Harris Hawks optimization algorithm based on nonlinear convergence factor and mutation quasi-reflected-based learning
-
摘要: 针对哈里斯鹰优化算法(Harris Hawks optimization, HHO)易早熟收敛、寻优精度低、收敛速度慢等问题，提出一种融合非线性收敛因子与变异准反射学习的哈里斯鹰优化算法（improved Harris Hawks optimization, IHHO）。首先，初始化阶段引入Circle混沌映射，提高初始化种群多样性和种群位置质量；其次，引入Sigmoid非线性收敛因子，平衡全局探索和局部开发能力；最后，针对HHO算法易陷入局部最优问题，提出变异准反射学习(quasi-reflection-based learning, QRBL)策略，提高种群活力，进一步提高算法局部收敛能力。仿真实验采用13个标准测试函数和1个经典工程问题对改进算法进行测试，结果表明改进算法收敛精度、收敛速度均有较大提高，适用于解决实际问题。Abstract: Due to the shortcomings of the Harris Hawks optimization (HHO) algorithm, such as premature convergence, low optimization precision, and slow convergence speed, an improved HHO (IHHO) algorithm integrating nonlinear convergence factor and mutation quasi-reflection-based learning (QRBL) is proposed. First, circle chaotic mapping is introduced in the initialization stage to improve the diversity of the initialization population and the location and quality of the population. Second, the sigmoid nonlinear convergence factor is introduced to balance the ability of global exploration and partial exploitation. Finally, because the HHO algorithm easily falls into the local optimum, mutation QRBL is proposed to improve the vigor of the population and further improve the local convergence ability of the algorithm. The simulation experiments are conducted by applying 13 standard test functions and one classical engineering problem to the evaluation of the proposed algorithm. The results show that the convergence accuracy and the convergence speed of the IHHO algorithm are greatly improved, and IHHO is suitable for solving practical problems.
-
随着科技的不断创新发展，不同领域产生诸多优化问题。近年来，众多学者通过分析生物种群或物理现象而提出的群智能优化算法不断涌现，如Kennedy等[1]受到鸟群觅食行为的规律性启发提出了粒子群优化算法（particle swarm optimization, PSO），PSO具有收敛速度快、参数少且算法简单易实现的优点。Mirjalili等[2]根据灰狼种群的等级制度和狩猎机制提出了灰狼优化算法（grey wolf optimization, GWO），GWO通过4种类型的灰狼模拟领导阶层，并实现了狩猎的3个主要步骤：寻找猎物、包围猎物和攻击猎物。Mirjalili等[3]通过模拟鲸鱼随机搜索捕食、气泡攻击与收缩包围行为提出的鲸鱼优化算法（whale optimization algorithm, WOA）。Mirjalili等[4]模拟了樽海鞘链的群体行为，通过领导者指导追随者，提出一种模拟链式行为向事物移动的樽海鞘群优化算法（salp swarm algorithm, SSA）。Mirjalili[5]为优化飞机机翼设计问题而提出的正余弦优化算法，主要基于数学中正余弦函数图像的概念，使最佳解向内或向外扩展，对应全局搜索和局部开发两个阶段，对最佳位置进行深度挖掘，最终达到全局最优的目的。Li等[6]基于黏菌的扩散和觅食行为提出黏菌优化算法（slime mould algorithm, SMA），SMA主要模拟了黏菌在觅食过程中的行为和形态变化，通过权值指标模拟黏菌静脉状管的形态变化和收缩模式之间的3种相关性。贾鹤鸣等[7]将遗传算法和乌燕鸥算法混合，应用到数据分类领域，并通过16组UCI数据和乳腺癌数据集验证算法在数据挖掘领域的应用。
2019年，Heidari等[8]提出了哈里斯鹰优化算法（Harris Hawks optimization, HHO），HHO是受自然界哈里斯鹰捕食行为启发的一种群智能优化算法，包含搜索、搜索与开发的转换、开发3个阶段。HHO是一种基于种群、无梯度的优化技术，具有较强的全局搜索能力，由于其简单易行、参数较少且寻优能力较强等特点，因此在图像分割[9]、神经网络训练[10]、电机控制[11]等领域广泛运用。但是HHO与其他群智能优化算法一样，在求解复杂优化问题时，存在收敛速度慢、寻优精度低、易陷入局部最优等缺陷。因此，很多学者针对HHO的不足进行改进研究。马一鸣等[12]利用Chan算法计算初始解，并替换单个个体位置，以减少不必要的全局搜索，提高了算法的收敛速度。Houssein等[13]引入交叉和变异合作基因操作符，并基于反向学习和随机反向学习策略提出HHOCM（Harris Hawks optimization via crossover and mutation）优化算法，有效提高解决方案的开发能力和种群的多样性。汤安迪等[14]引入Tent混沌映射、精英等级制度、非线性逃逸能量更新策略和高斯随机游走策略，以提升算法的收敛速度和收敛精度。Jia等[15]引入动态控制参数策略和突变机理，应用于HHO逃逸能量的计算和全局探索，通过调节不同参数，取得较好效果。上述改进策略对HHO算法的性能有一定提升，但对于HHO算法收敛速度慢、精度低、易陷入局部最优值的问题，依然具有较大的改进空间。
本文基于HHO算法存在的不足，首先，引入Circle混沌映射，提升初始化种群位置质量，其次引入Sigmoid非线性收敛因子，平衡全局探索和局部开发的转换，最后提出一种变异准反射学习策略，根据变异因子对求解进行变异和转换，并根据贪心策略保留最优解，有效增强了算法的寻优性能，并提升收敛速度和收敛精度。仿真实验部分采用13个标准测试函数以及1个经典工程问题对算法进行测试，结果表明改进算法寻优性能更佳，对跳出局部最优能力有一定增强。
1. 哈里斯鹰优化算法
1.1 探索阶段
HHO算法的灵感来自于哈里斯鹰探索、攻击猎物的不同攻击策略，主要由探索阶段、探索与开发的转换和开发阶段3部分组成。
在探索阶段，哈里斯鹰随机栖息在某些地方，它们栖息的地方基于其他成员或猎物的位置，具体计算方式为
$$ \begin{gathered} {\boldsymbol{X}}(t + 1) = \\ \left\{ \begin{gathered} {{\boldsymbol{X}}_{{{\rm{rand}}}}}(t) - {r_1}\left| {{{\boldsymbol{X}}_{{{\rm{rand}}}}}(t) - 2{r_2}{\boldsymbol{X}}(t)} \right|,\;{\kern 1pt} q \geqslant 0.5 \\ ({{\boldsymbol{X}}_{{{\rm{rabbit}}}}}(t) - {{\boldsymbol{X}}_{{\rm{m}}}}(t)) - {r_3}({{\boldsymbol{L}}_{{\rm{B}}}} + {r_4}({{\boldsymbol{U}}_{{\rm{B}}}} - {{\boldsymbol{L}}_{{\rm{B}}}})), \; q < 0.5 \\ \end{gathered} \right. \end{gathered}$$ (1) $$ {{\boldsymbol{X}}_{\rm{m}}}(t) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\boldsymbol{X}}_{\rm{i}}}(t)} $$ (2) 式中：
$\boldsymbol{X}(t+1)$ 是哈里斯鹰下一次迭代位置，${\boldsymbol{X}}_{\mathrm{r}\mathrm{a}\mathrm{b}\mathrm{b}\mathrm{i}\mathrm{t}}\left(t\right)$ 是猎物位置，$ {r}_{1} $ 、$ {r}_{2} $ 、$ {r}_{3} $ 、$ {r}_{4} $ 和$ q $ 是$ \left(\mathrm{0,1}\right) $ 间的随机数，UB和LB为变化范围的上下界，${\boldsymbol{X}}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}\left(t\right)$ 为当前种群中随机选择个体，${\boldsymbol{X}}_{\mathrm{m}}\left(t\right)$ 是当前鹰群的平均位置。1.2 探索到开发的转换
从全局搜索到局部开发的转换主要基于猎物的逃逸能量E，当
$ \left|E\right| \geqslant 1 $ 时算法进入探索阶段，当$ \left|E\right| < 1 $ 时算法进入开发阶段，E的计算公式为$$ {E_1}{\text{ = }}2\left(1 - \frac{t}{T}\right) $$ (3) $$ E{\text{ = }}{E_0}{E_1} $$ (4) 式中：E0为初始能量，为
$ -1 $ 到$ 1 $ 的随机数；t为当前迭代次数；T为最大迭代次数。1.3 开发阶段
在开发阶段，哈里斯鹰基于4种追捕策略进行狩猎。当
$ r \geqslant 0.5 $ 且$ \left|E\right| \geqslant 0.5 $ 时，表示猎物有足够的逃逸能量但是逃跑未成功，此时哈里斯鹰通过软包围的方式进行狩猎：$$ {\boldsymbol{X}}(t + 1) = \Delta {\boldsymbol{X}}(t) - E\left| {J{{\boldsymbol{X}}_{{{\rm{rabbit}}}}}(t) - {\boldsymbol{X}}(t)} \right| $$ (5) $$ \Delta {\boldsymbol{X}}(t){\text{ = }}{{\boldsymbol{X}}_{{{\rm{rabbit}}}}}(t) - {\boldsymbol{X}}(t) $$ (6) $$ J = 2(1 - {r_5}) $$ (7) 式中：
$ \Delta \boldsymbol{X}\left(t\right) $ 是猎物位置和当前位置的差值，$ {r}_{5} $ 是0~1的随机数，J表示猎物逃跑过程中的跳跃距离。当
$ r \geqslant 0.5 $ 且$ \left|E\right| < 0.5 $ 时，表示猎物没有足够的逃逸能量，也没有逃脱机会，此时哈里斯鹰通过硬包围的方式进行狩猎：$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{\rm{rabbit}}}(t) - E\left| {\Delta {\boldsymbol{X}}(t)} \right| $$ (8) 当
$ r < 0.5 $ 且$ \left|E\right| \geqslant 0.5 $ 时，表示猎物有足够的逃逸能量且成功逃脱，此时哈里斯鹰通过更智能的软包围方式进行狩猎，主要通过2个策略，首先执行：$$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{\rm{rabbit}}}(t) - E\left| {J{{\boldsymbol{X}}_{\rm{rabbit}}}(t) - {\boldsymbol{X}}(t)} \right| $$ (9) 当式（9）的策略无效时，执行如下策略：
$$ {\boldsymbol{Z}} = {\boldsymbol{Y}} + {\boldsymbol{S}} \times {{\boldsymbol{L}}_{{\rm{F}}}}(D) $$ (10) 式中：D是问题维度，S是一个
$ 1\times D $ 维的随机向量，LF为Levy飞行函数：$$ {{\boldsymbol{L}}_{{\rm{F}}}}(x) = 0.01 \times \frac{{{\boldsymbol{u}} \times \sigma }}{{{{\left| {\boldsymbol{v}} \right|}^{\frac{1}{\beta }}}}} $$ (11) $$ \sigma = {\left( {\frac{{\varGamma (1 + \beta ) \times \sin \dfrac{{{\text{π }}\beta }}{2}}}{{\varGamma \left(\dfrac{{1 + \beta }}{2}\right) \times \beta \times {2^{\frac{{\beta - 1}}{2}}}}}} \right)^{\frac{1}{\beta }}} $$ (12) 其中：u、v是
$ 1\times D $ 的随机正态分布向量，$ \beta $ 是取值为1.5的常数，因此该阶段的更新策略最终为$$ {\boldsymbol{X}}(t+1)=\left\{\begin{array}{l}{\boldsymbol{Y}}\text{，}{{F}}({\boldsymbol{Y}}) < {{F}}({\boldsymbol{X}}(t))\\ {\boldsymbol{Z}}\text{，}F({\boldsymbol{Z}}) < F({\boldsymbol{X}}(t))\end{array}\right. $$ (13) 当
$ r < 0.5 $ 且$ \left|E\right| < 0.5 $ 时，表示猎物有机会逃脱，但没有足够的逃逸能量，此时哈里斯鹰在突袭前形成硬包围以缩小它们和猎物的距离：$$ {\boldsymbol{X}}(t+1)=\left\{\begin{array}{l}{\boldsymbol{Y}}\text{，}\text{ }F({\boldsymbol{Y}}) < F({\boldsymbol{X}}(t))\\ {\boldsymbol{Z}}\text{，}\text{ }F({\boldsymbol{Z}}) < F({\boldsymbol{X}}(t))\end{array}\right. $$ (14) $$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{\rm{rabbit}}}(t) - E\left| {J{{\boldsymbol{X}}_{\rm{rabbit}}}(t) - {{\boldsymbol{X}}_{{\rm{m}}}}(t)} \right| $$ (15) $$ {\boldsymbol{Z}} = {\boldsymbol{Y}} + {\boldsymbol{S}} \times {{\boldsymbol{L}}_{{\rm{F}}}}(D) $$ (16) 2. 改进的哈里斯鹰优化算法
2.1 Circle混沌映射
混沌映射是一种由简单的确定性系统产生的随机性序列，具有一定的便利性和很高的随机性，可以产生(0,1)分布较为均匀的随机数。经过实验证明[16]，利用混沌序列进行种群初始化、选择、交叉和变异等操作会影响算法的整个过程，而且常常能取得比伪随机数更好的效果。产生混沌序列的映射有很多，Circle混沌映射是常用的映射之一，本文引入Circle混沌映射[16]初始化种群，以保证种群初始位置的质量：
$$ {{\boldsymbol{X}}_{i + 1}} = \text{mod} \left({{\boldsymbol{X}}_i} + b - \left(\frac{a}{{2{\text{π}}}}\sin 2{\text{π}}{{\boldsymbol{X}}_i}\right),1\right) $$ (17) 式中：a为0.5，b为0.2。
2.2 Sigmoid非线性收敛因子
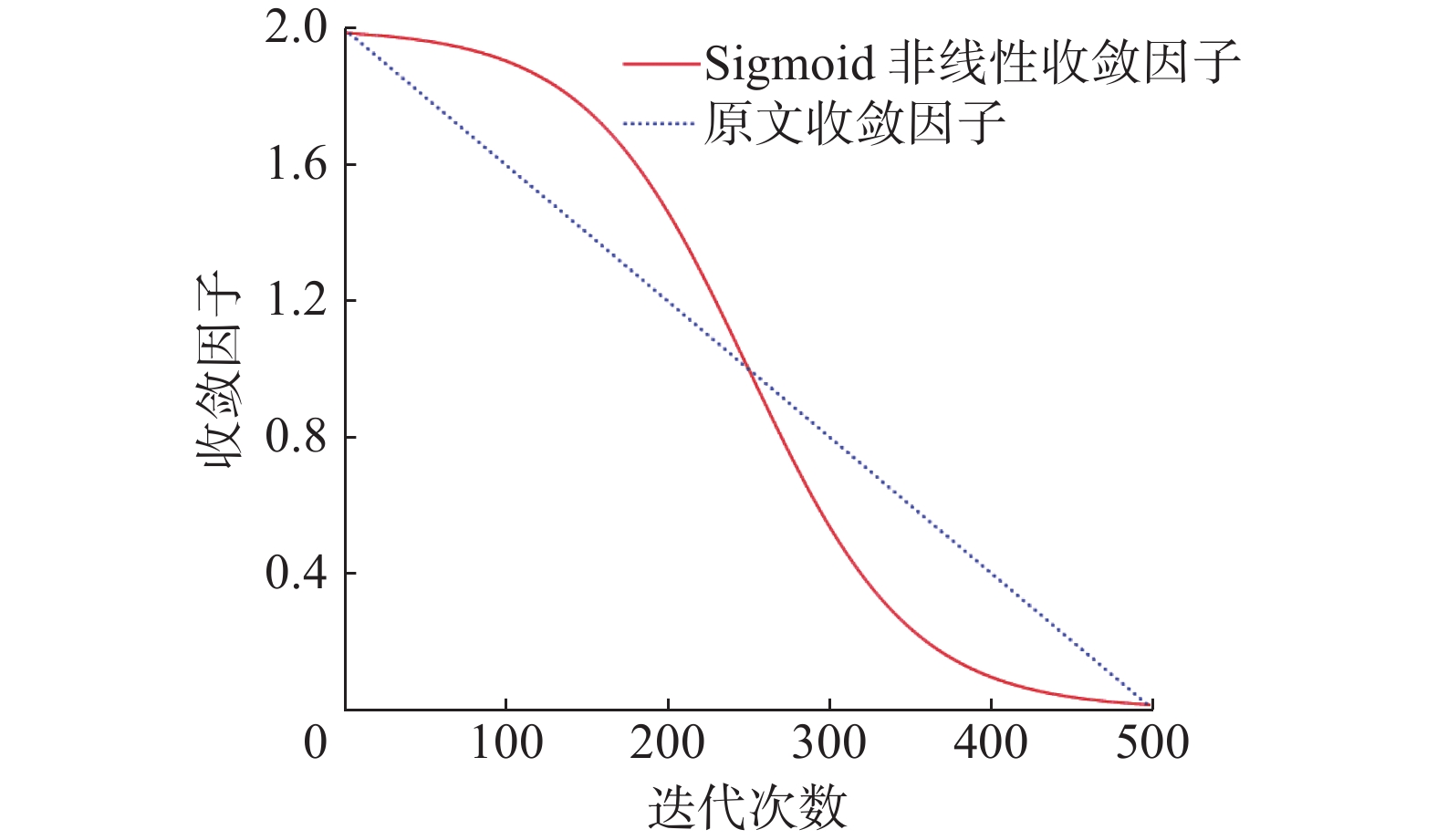
原算法的逃逸能量是探索到开发转换的关键性因素，主要通过式(3)、(4)计算，式(3)产生从2到0线性下降的值，虽然可以在一定程度上支持探索与开发的转换，但在迭代次数超过最大迭代次数一半的时候，就一定进入局部开发过程。然而实际的搜索过程是非常复杂的非线性过程，确定的转换边界容易降低算法寻优的性能。为平衡全局搜索和局部搜索，引入Sigmoid非线性收敛因子[17]。引入后，式(3)更新为
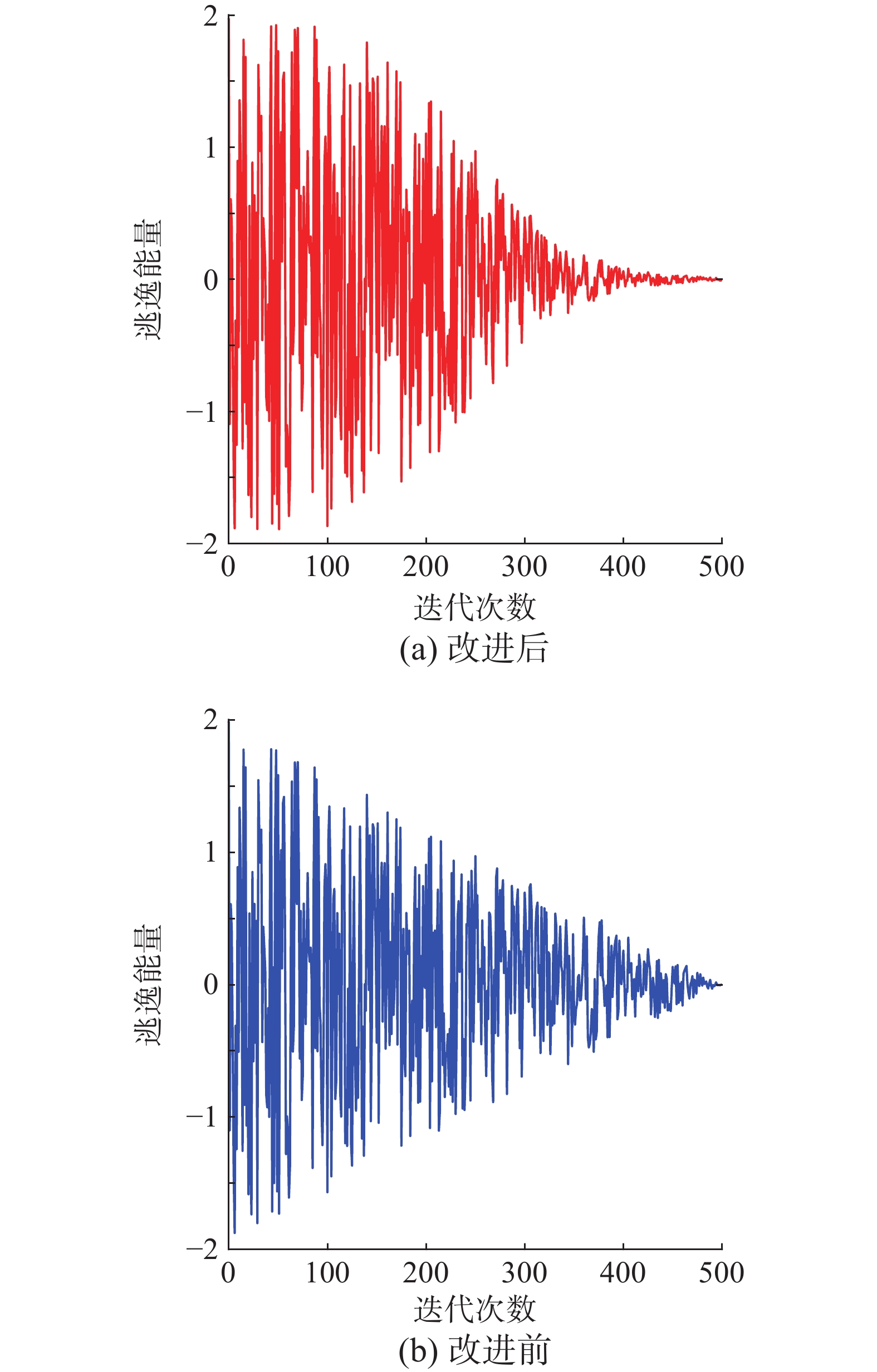
$$ {E_{{1\_{\rm{new}}}}}{\text{ = }}\frac{w}{{1 + \exp \left( {\dfrac{{t - {T \mathord{\left/ {\vphantom {T 2}} \right. } 2}}}{T} \times 10} \right)}} $$ (18) 式中：w为调节因子，本文选取w=2。Sigmoid非线性收敛因子和原文收敛因子对比如图1所示。
图 1 收敛因子曲线对比Fig. 1 Curve of convergence factor comparison
下载:
全尺寸图片
更新后逃逸能量对比如图2所示。前期种群保持个体较大自由度，增强全局寻优能力；后期自由度快速下降，增加局部开发能力。
图 2 逃逸能量曲线对比Fig. 2 Curve of escape energy comparison下载:
全尺寸图片
2.3 变异准反射学习策略
HHO算法中，哈里斯鹰通过4种追捕策略更新自身位置，重新计算适应度并择优进入下一次迭代，没有对更新位置进行干扰，容易导致算法陷入局部最优。据此，本文提出变异准反射学习策略，增加反射解和反向解对位置的干扰，增加种群多样性，提高算法跳出局部最优能力。
反向学习策略（opposition-based learning, OBL）[18-19] 主要思想是生成可行解的反向解，通过评估可行解和反向解，选择更好的候选解，具体公式为
$$ {{\boldsymbol{X}}_{\rm{o}}}(t) = {{\boldsymbol{L}}_{\rm{B}}} + {{\boldsymbol{U}}_{\rm{B}}} - {\boldsymbol{X}}(t) $$ (19) OBL的一种变体为准反向学习（quasi-opposition-based learning, QOBL）[20]，以往的研究证明，在寻找全局最优解时，使用准反向解比反向解更有效。准反向解的具体表达式为
$$ {{\boldsymbol{X}}_{{\rm{qo}}}}(t) = {\rm{rand}}\left(\frac{{{{\boldsymbol{L}}_{\rm{B}}} + {{\boldsymbol{U}}_{\rm{B}}}}}{2},{{\boldsymbol{X}}_{\rm{o}}}(t)\right) $$ (20) 基于OBL和QOBL，Ewees等[21]提出了一种新的准反射学习机制(QRBL)，准反射解是根据准反向解获得的，具体计算为
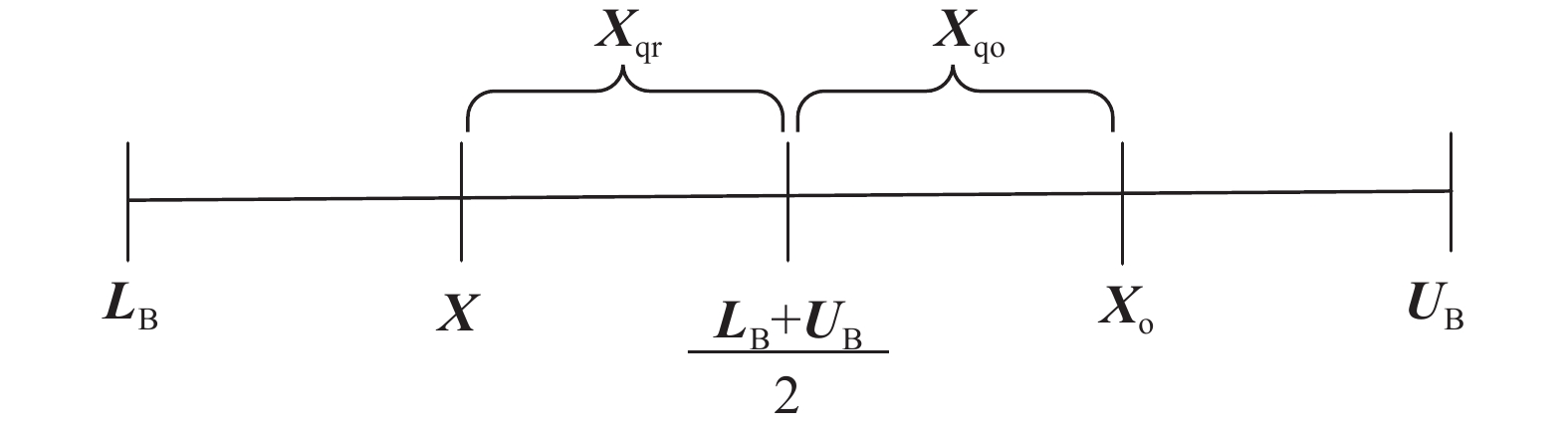
$$ {{\boldsymbol{X}}_{{\rm{qr}}}}(t) = {\rm{rand}}\left(\frac{{{{\boldsymbol{L}}_{\rm{B}}} + {{\boldsymbol{U}}_{\rm{B}}}}}{2},{\boldsymbol{X}}(t)\right) $$ (21) 三者的主要区别，如图3所示。
图 3 OBL、QOBL、QRBL区别Fig. 3 Differences between OBL, QOBL and QRBL下载:
全尺寸图片
Fan等[22]通过实验发现，对于HHO的优化，QRBL比QOBL和OBL更有优势，但在个别函数测试中，发现QOBL得出的解可以获得更好效果。为此提出变异QRBL算法，具体为
$$ {{\boldsymbol{X}}_{{\rm{new}}}}(t) = \left\{ \begin{gathered} {{\boldsymbol{X}}_{{\rm{qo}}}}(t),\quad b \leqslant {p_{\rm{r}}} \\ {{\boldsymbol{X}}_{{\rm{qr}}}}(t),\quad b > {p_{\rm{r}}} \\ \end{gathered} \right. $$ (22) 式中：b是（0,1）随机数；pr变异概率[23]是（0.01,0.1）之间的数，经测试pr=0.08算法性能最好。
经变异反射学习策略后，使用贪心策略将最好位置保留进入下一次迭代：
$$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {{\boldsymbol{X}}_{{\rm{new}}}}(t + 1),\;f({{\boldsymbol{X}}_{{\rm{new}}}}(t + 1)) < f({\boldsymbol{X}}(t + 1)) \\ {\boldsymbol{X}}(t + 1),\;f({{\boldsymbol{X}}_{{\rm{new}}}}(t + 1)) \geqslant f({\boldsymbol{X}}(t + 1)) \\ \end{gathered} \right. $$ (23) 2.4 IHHO算法实现过程
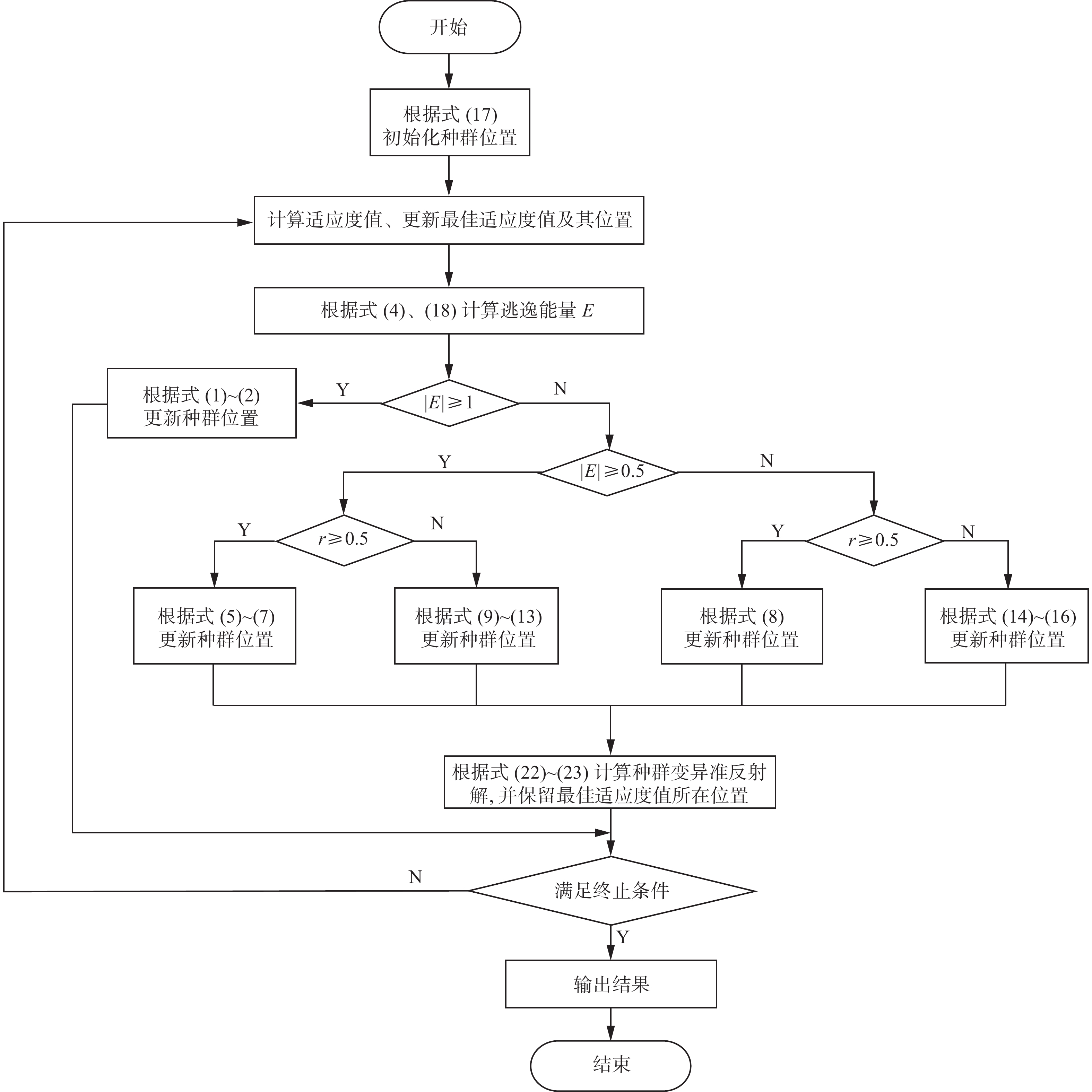
综上所述，IHHO算法在原始HHO算法的基础上进行改进，通过Circle混沌映射初始化种群，提升初始化位置质量，然后引入Sigmoid非线性收敛因子，平衡全局探索和局部开发，最后利用变异QRBL策略产生准反射或准反向位置，更新种群向最优个体位置进化，增强算法跳出局部最优的能力，使得算法获得更好的收敛速度和收敛精度，IHHO流程如图4所示。
图 4 IHHO算法流程Fig. 4 Flowchart of IHHO下载:
全尺寸图片
IHHO算法实现流程描述如下：
1） 使用Circle混沌映射初始化种群。
2） 计算个体适应度值，记录较优个体。
3） 如果
$ \left|E\right| \geqslant 1 $ ，个体根据式(1)、式(2)开始探索行为。4） 如果
$ \left|E\right| < 1 $ ，个体根据逃逸猎物能量值历史适应度值改善情况选择开发策略。
策略 1 软包围：当
$ r \geqslant 0.5 $ 且$ \left|E\right| \geqslant 0.5 $ ，子群个体采用式(5)~(7)更新位置；策略 2 硬包围：当
$ r \geqslant 0.5 $ 且$ \left|E\right| < 0.5 $ ，子群个体采用式(8)更新位置；策略 3 渐进式快速俯冲软包围：当
$ r < 0.5 $ 且$ \left|E\right| \geqslant 0.5 $ ，子群个体采用式(9)~(13)更新位置；策略 4 渐进式快速俯冲硬包围：当
$ r < 0.5 $ 且$ \left|E\right| < 0.5 $ ，子群个体采用式(14)~(16)更新位置；采用式(22)~(23)计算变异反射解，择优保留最好位置。
5） 判断是否满足终止条件，满足则跳出循环，否则返回步骤2。
6） 输出最佳位置及适应度值。
2.5 运算复杂度分析
IHHO算法主要由种群初始化、种群位置更新以及变异准反射解组成，假设种群规模N，维度D，最大迭代次数T，则IHHO初始阶段时间复杂度为O(N×D)，计算个体适应度为O(N)，迭代过程中利用变异QRBL生成解，复杂度为O(2×N×D×T)，更新最优解的时间复杂度为O(1)。综上所述，IHHO运算复杂度为O(2×N×D×T)。
表1为IHHO和HHO算法在13个标准测试函数[24]（F1—F13）上（每个函数迭代500次）运行时间的对比。从表1可以看到各算法用时与测试函数本身复杂度相关，时间差最大的为F13函数，算法运行时间相差0.3 s左右。虽然整体算法运行时间更长，但是IHHO算法在部分测试函数中收敛速度远大于原HHO算法，也就意味着IHHO在部分函数中不需要完整执行完500次迭代就已经达到最优效果，这也给IHHO在时间上进行了一个有效缩减。
表 1 IHHO和HHO运行时间对比Table 1 Riming time of IHHO and HHOs 算法 IHHO HHO F1 0.1789 0.0980 F2 0.1210 0.0799 F3 0.6220 0.3843 F4 0.0966 0.0852 F5 0.2055 0.1448 F6 0.1349 0.1000 F7 0.3227 0.2082 F8 0.2042 0.1379 F9 0.1496 0.1150 F10 0.1614 0.1199 F11 0.1923 0.1382 F12 0.7809 0.4953 F13 0.7845 0.4874 3. 实验仿真与分析
为验证IHHO算法的稳定性和有效性，使用13个标准测试函数对IHHO进行性能测试，其中，F1—F7为单峰测试函数，F8—F13为多峰测试函数，利用两种不同类型的测试函数，可充分验证算法的寻优性能。
3.1 对比算法与参数设置
为了更好的验证IHHO算法性能，选取6种性能良好的优化算法进行对比：HHO、SMA、WOA、SSA、GWO、SCA和其他HHO优化算法：CEHHO（chaotic elite Harris Hawk optimization）、HHOCM和DHHO/M（dynamic Harris Hawks optimization with a mutation mechanism）。算法选取平均值、标准差与Wilcoxon秩和检验作为评价指标。设定种群规模N=30，维度D=30，最大迭代次数T=500次，各算法独立运行30次，算法参数设置如表2所示。
3.2 求解精度分析
IHHO与经典算法标准函数测试结果对比如表3所示，与其他HHO优化算法标准函数测试结果对比如表4所示。Mean代表平均适应度值，Std为标准差，加粗的实验数据为最佳结果。
表 3 与经典算法标准函数测试结果对比Table 3 Test results of benchmark functions with classic algorithms函数 统计值 IHHO SMA HHO WOA SSA GWO SCA F1 Mean 0.00 9.28×10−308 9.70×10−97 1.36×10−72 3.23×10−7 1.55×10−27 1.15×101 Std 0.00 0.00 5.14×10−96 6.44×10−72 9.51×10−7 2.55×10−27 2.37×101 用时/s 0.1033 0.2145 0.0553 0.0403 0.0597 0.0960 0.0697 F2 Mean 0.00 5.82×10−146 1.93×10−50 2.54×10−50 2.05 1.16×10−16 1.58×10−2 Std 0.00 3.19×10−145 9.76×10−50 7.38×10−50 1.71 1.22×10−16 2.48×10−2 用时/s 0.1012 0.2258 0.0536 0.0414 0.0545 0.0990 0.0692 F3 Mean 0.00 1.59×10−315 9.01×10−68 4.10×104 1.42×103 1.03×10−5 9.57×103 Std 0.00 0.00 4.93×10−67 1.49×104 8.61×102 3.17×10−5 5.96×103 用时/s 0.4426 0.2887 0.2515 0.1188 0.1358 0.1583 0.1523 F4 Mean 0.00 6.95×10−165 1.34×10−48 5.10×101 1.17×101 7.13×10−7 3.83×101 Std 0.00 0.00 6.99×10−48 2.85×101 3.14 6.63×10−7 1.34×101 用时/s 0.1013 0.2388 0.0670 0.0404 0.0549 0.0997 0.0699 F5 Mean 2.24×10−3 3.73 1.80×10−2 2.80×101 1.76×102 2.72×101 8.17×104 Std 2.12×10−3 7.69 4.05×10−2 4.20×10−1 2.52×102 6.85×10−1 3.74×105 用时/s 0.2232 0.3149 0.13631 0.0690 0.0887 0.1361 0.1069 F6 Mean 1.05×10−5 4.90×10−3 1.63×10−4 3.70×10−1 1.31×10−7 8.74×10−1 1.68×101 Std 2.29×10−5 3.31×10−3 2.30×10−4 1.99×10−1 1.17×10−7 3.26×10−1 2.95×101 用时/s 0.1170 0.2711 0.0926 0.0414 0.0620 0.1307 0.0806 F7 Mean 1.07×10−4 2.07×10−4 1.15×10−4 3.81×10−3 1.60×10−1 2.10×10−3 1.00×10−1 Std 8.94×10−5 1.74×10−4 1.22×10−4 4.28×10−3 6.59×10−2 1.34×10−3 8.06×10−2 用时/s 0.3075 0.2675 0.1791 0.0895 0.1057 0.1496 0.1203 F8 Mean −1.26×104 −1.26×104 −1.26×104 −1.04×104 −7.48×103 −5.81×103 −3.79×103 Std 4.26×10−1 3.15×10−1 7.93×101 1.71×103 7.04×102 1.05×103 3.43×102 用时/s 0.1874 0.2838 0.1124 0.0538 0.0651 0.1106 0.0853 F9 Mean 0.00 0.00 0.00 0.00 5.09×101 3.12 4.55×101 Std 0.00 0.00 0.00 0.00 1.38×101 3.86 3.22×101 用时/s 0.1308 0.2461 0.0846 0.0428 0.0611 0.1003 0.0758 F10 Mean 8.88×10−16 8.88×10−16 8.88×10−16 4.68×10−15 2.31 1.02×10−13 1.48×101 Std 0.00 0.00 0.00 2.46×10−15 7.60×10−1 1.85×10−14 8.64 用时/s 0.1463 0.2390 0.0901 0.0457 0.0642 0.1060 0.0844 F11 Mean 0.00 0.00 0.00 1.94×10−2 1.57×10−2 2.81×10−3 1.06 Std 0.00 0.00 0.00 6.12×10−2 1.21×10−2 6.05×10−3 4.68×10−1 用时/s 0.1743 0.2583 0.1078 0.0554 0.0744 0.1079 0.1087 F12 Mean 6.63×10−7 5.56×10−3 7.65×10−6 2.02×10−2 6.00 4.62×10−2 5.35×104 Std 8.42×10−7 7.88×10−3 7.68×10−6 1.11×10−2 2.71 2.01×10−2 2.26×105 用时/s 0.7282 0.3451 0.4208 0.1752 0.1981 0.2313 0.2105 F13 Mean 1.02×10−5 3.84×10−3 8.08×10−5 5.59×10−1 1.23×101 6.65×10−1 3.96×105 Std 1.59×10−5 3.99×10−3 1.37×10−4 2.43×10−1 1.38×101 2.40×10−1 1.62×106 用时/s 0.6896 0.6896 0.4443 0.1786 0.2245 0.2339 0.2170 表 4 与其他HHO优化算法标准函数测试结果对比Table 4 Test results of benchmark functions with other HHO optimization algorithms函数 统计值 IHHO HHOCM CEHHO DHHO/M F1 Mean 0.00 0.00 0.00 8.16×10−92 Std 0.00 0.00 0.00 3.92×10−91 F2 Mean 0.00 2.06×10−198 0.00 5.26×10−48 Std 0.00 0.00 0.00 2.39×10−47 F3 Mean 0.00 0.00 0.00 4.62×10−60 Std 0.00 0.00 0.00 2.53×10−59 F4 Mean 0.00 4.90×10−192 0.00 1.89×10−45 Std 0.00 0.00 0.00 1.02×10−44 F5 Mean 2.24×10−3 1.80×10−2 4.26×10−3 1.15×10−2 Std 2.12×10−3 2.47×10−2 7.03×10−3 1.17×10−2 F6 Mean 1.05×10−5 4.82×10−4 1.65×10−5 6.56×10−5 Std 2.29×10−5 6.54×10−4 2.32×10−5 9.79×10−5 F7 Mean 1.07×10−4 1.52×10−4 1.33×10−4 1.58×10−4 Std 8.94×10−5 1.46×10−4 1.09×10−4 1.31×10−4 F8 Mean −1.26×104 −1.26×104 −1.26×104 −1.24×104 Std 4.26×10−1 7.51×10−1 6.03×101 9.65×102 F9 Mean 0.00 0.00 0.00 0.00 Std 0.00 0.00 0.00 0.00 F10 Mean 8.88×10−16 8.88×10−16 8.88×10−16 8.88×10−16 Std 0.00 0.00 0.00 0.00 F11 Mean 0.00 0.00 0.00 0.00 Std 0.00 0.00 0.00 0.00 F12 Mean 6.63×10−7 1.66×10−5 1.73×10−6 5.44×10−6 Std 8.42×10−7 2.41×10−5 2.37×10−6 6.46×10−6 F13 Mean 1.02×10−5 1.50×10−4 1.57×10−5 7.29×10−5 Std 1.59×10−5 1.42×10−4 3.16×10−5 9.17×10−5 从表3~4可以看出，在求解F1—F7单峰测试函数中，IHHO在F1—F4测试函数中达到理最优值，F5和F7中Mean和Std虽然没有达到理论最优值，但对比经典算法和其他HHO优化算法都取得最好结果。对于F6，IHHO虽然没有收敛到全局最优值，但求解精度仅次于SSA。可见，IHHO应用变异准反射学习对于提升局部收敛精度和稳定性有一定作用。在多峰测试函数中，对于F9—F13函数，IHHO在所有对比算法中表现最好；对于F8，IHHO平均适应度最优，方差仅次于SMA。可见IHHO算法在多峰测试函数中也取得较好效果，证明IHHO的全局搜索能力和跳出局部最优能力整体优于原始HHO和其他对比算法。结合测试函数的复杂性，证实了IHHO在平衡探索阶段和局部阶段的能力确实得到增强。通过表3还可以看到，IHHO对比HHO的收敛精度有非常大的提升，在多项测试函数中可以达到理论最优值，因此本文在性能上的提升有效弥补了运行时间的增加。
3.3 收敛曲线分析
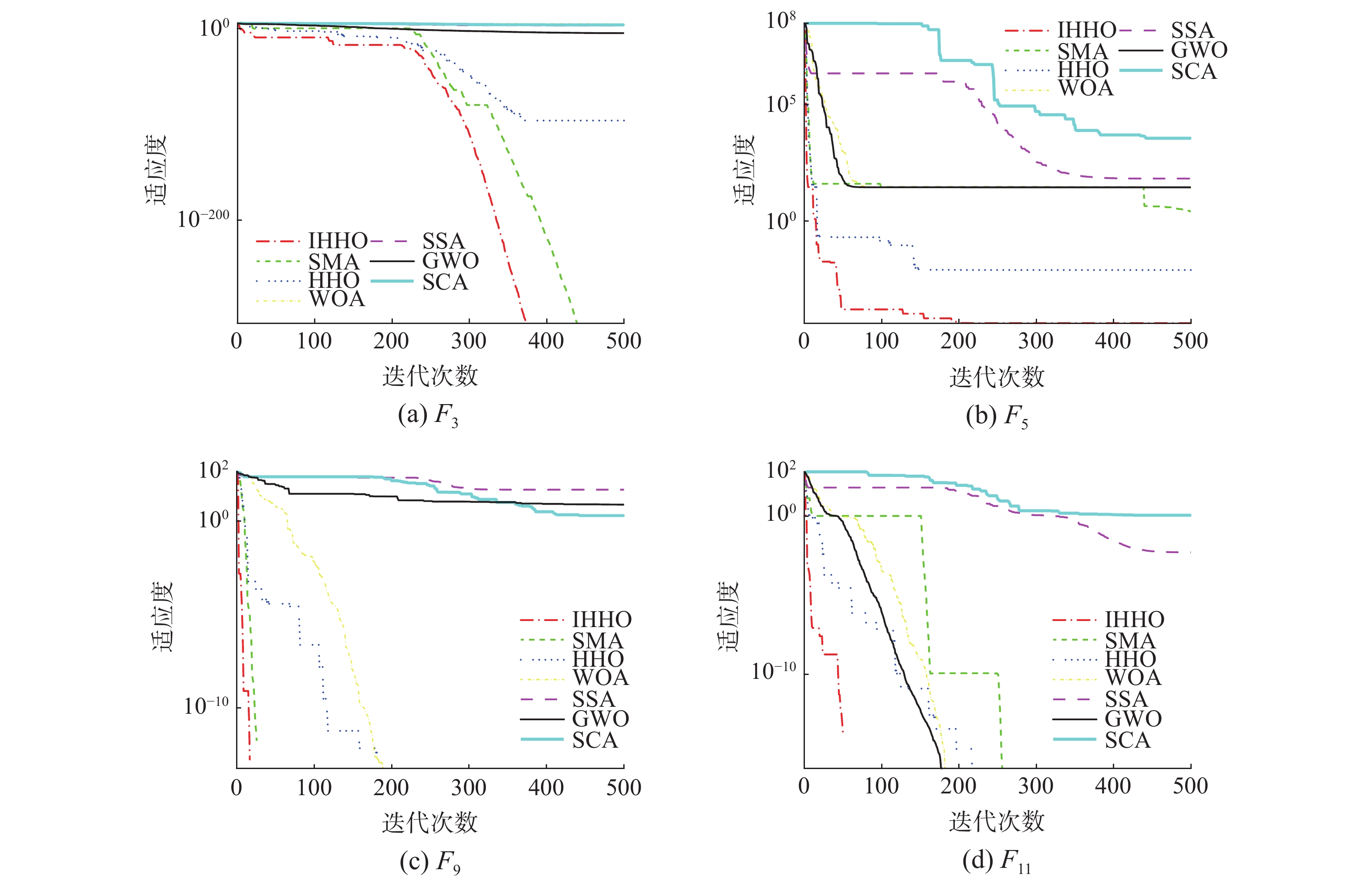
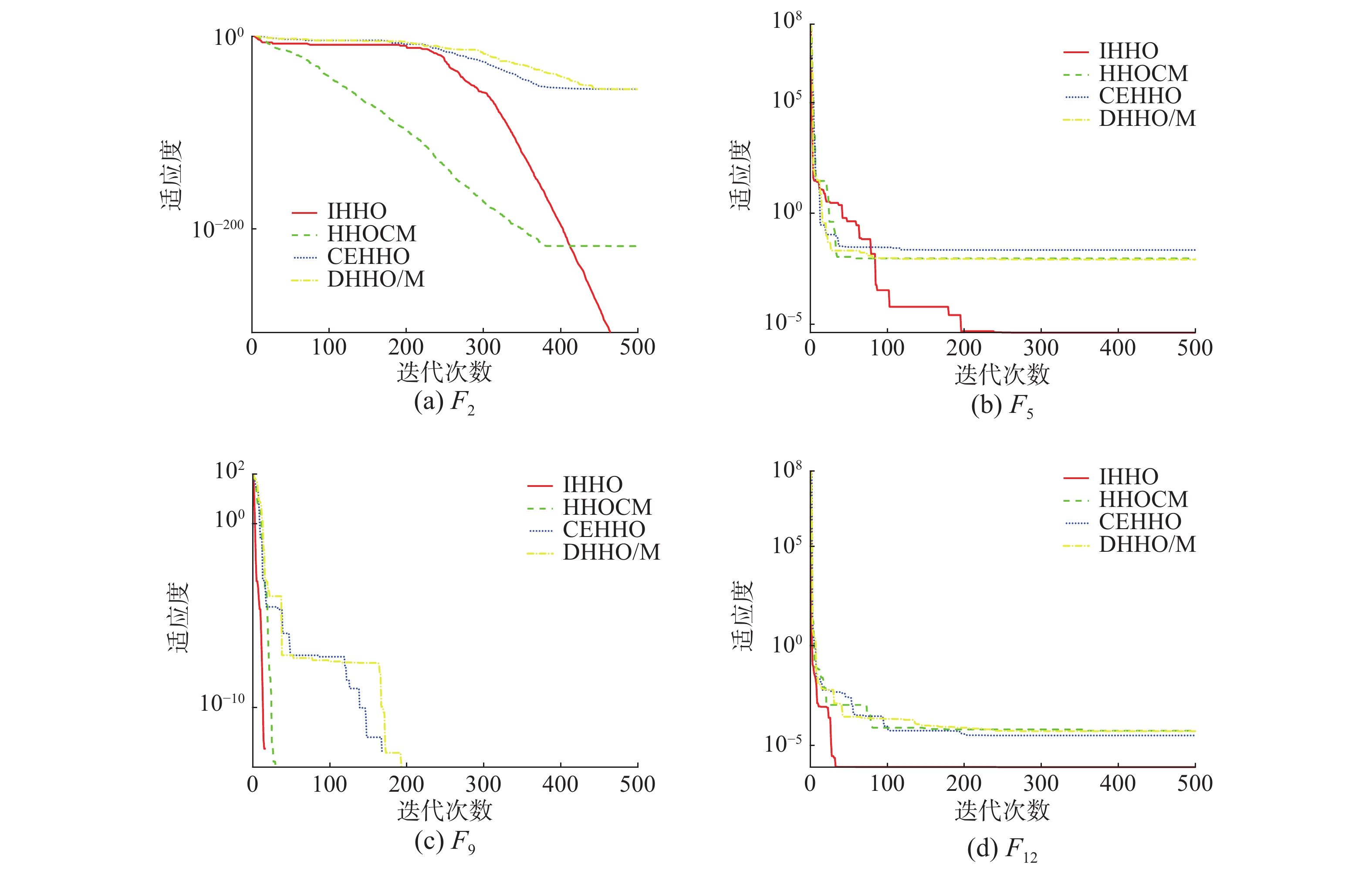
为了更直观地展示各算法的收敛速度及跳出局部最优能力，将IHHO与经典算法收敛曲线进行对比分析（图5），选取单峰函数F3、F5和多峰函数F9和F11。可以看到对于函数F3，IHHO在前期没有显示巨大优势，但是随着迭代增加，IHHO进入局部开发，收敛速度明显加快，迅速达到全局最优，证明变异准反射策略有效提高算法局部寻优的收敛速度。对于多峰测试函数F9和F11，IHHO在迭代初期（50次内）就迅速找到全局最优，证明算法稳定的全局探索能力。在与其他优秀的HHO改进算法的对比中（图6），选取单峰函数F2、F5和多峰函数F9和F12。对于函数F2，IHHO在前期没有很大优势，曲线与CEHHO和DHHO/M相当，略逊色于HHOCM，但是在250次迭代以后，IHHO迅速下降，最后收敛精度明显优于HHOCM，可见IHHO优秀的局部探索能力。F5函数同样在迭代前期就迅速下降，收敛精度远胜于其他对比算法。对于F9和F12，IHHO无论从收敛速度和收敛精度上都优于其他算法。可以看到IHHO对于多峰函数有效性。
图 5 与经典算法收敛曲线对比Fig. 5 Convergence curves with classic algorithms下载:
全尺寸图片
图 6 与其他HHO优化算法收敛曲线对比Fig. 6 Convergence curve with other HHO optimizer下载:
全尺寸图片
3.4 工程设计优化问题
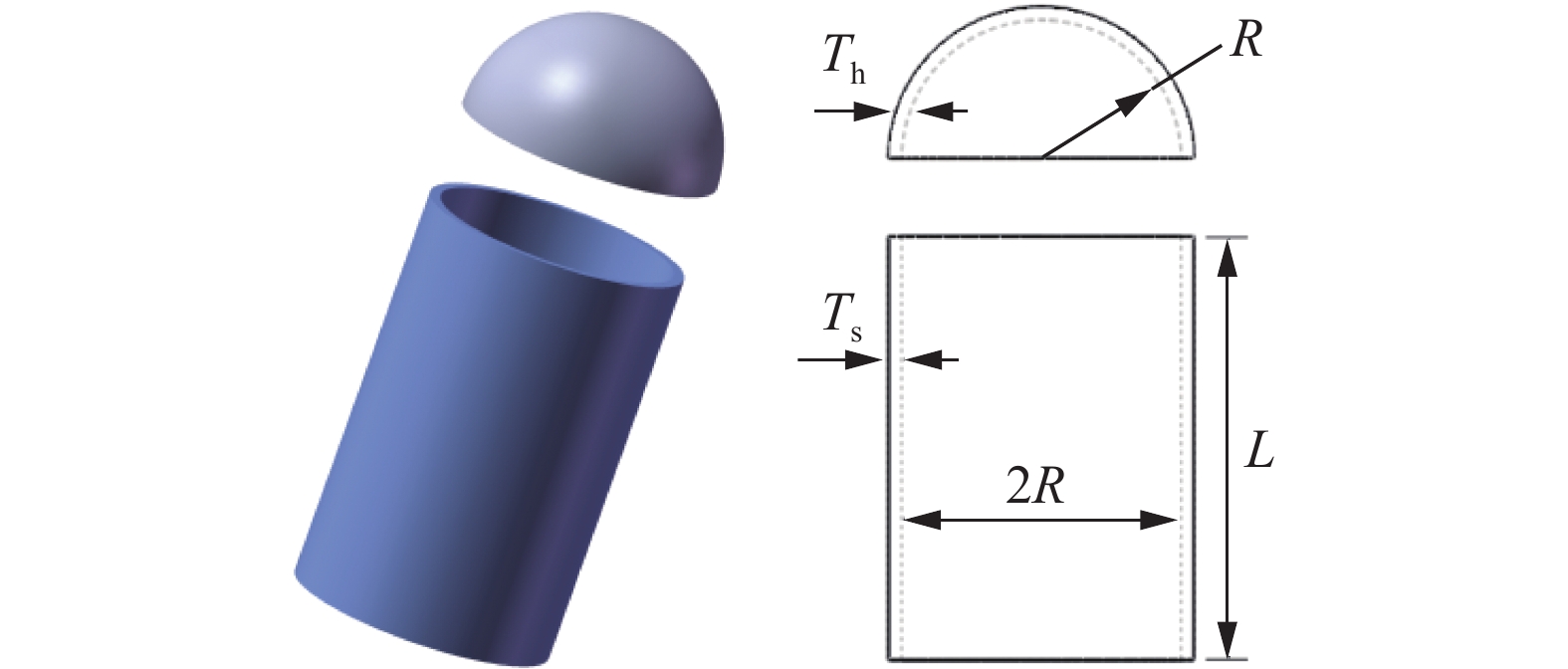
本节利用压力容器设计优化问题压力容器设计优化问题[25]（如图7）测试IHHO对于实际问题的优化性能，实验参数设置见表2。该问题是一个重要的研究领域，它旨在提高压力容器的性能、可靠性和成本效益。
图 7 压力容器设计问题Fig. 7 Pressure vessel design problem下载:
全尺寸图片
本章节内容旨在通过IHHO算法找到合适的优化容器壁厚度Ts、顶盖壁厚度Th、内径R和容器管深长度L，使容器在达到一定条件下付出成本最小，问题模型考虑：
$$ {\boldsymbol{X}} = [{x_1}\;\;\;{x_2}\;\;\;{x_3}\;\;\;{x_4}] = [{T_{\rm{s}}}\;\;\;{T_{\rm{h}}}{\text{ }}R\;\;\;L] $$ 使得下面条件最小：
$$ \begin{gathered} f({\boldsymbol{X}}) = 0.622\;4{x_1}{x_3}{x_4} + 1.778\;1{x_2}x_3^2 + \\ 3.166\;1x_1^2{x_4} + 19.84x_1^2{x_3} \end{gathered} $$ 满足：
$$ \begin{gathered} {\text{ }}{g_1}({\boldsymbol{x}}) = - {x_1} + 0.019\;3{x_3} \leqslant 0 \\ {\text{ }}{g_2}({\boldsymbol{x}}) = - {x_3} + 0.009\;54{x_3} \leqslant 0 \\ {g_3}({\boldsymbol{x}}) = - {\text{π}}x_3^2{x_4} - \frac{4}{3}{\text{π}}x_3^3 + 1\;296\;000 \leqslant 0 \\ {\text{ }}{g_4}({\boldsymbol{x}}) = {x_4} - 240 \leqslant 0 \end{gathered} $$ 变量范围为
$$ \begin{gathered} 0 \leqslant {x_1} \leqslant 99 \\ 0 \leqslant {x_2} \leqslant 99 \\ 10 \leqslant {x_3} \leqslant 200 \\ 10 \leqslant {x_4} \leqslant 200 \end{gathered} $$ 表5列出了IHHO及对比算法求解压力容器设计问题的实验结果。通过数据可以看出，IHHO收敛精度对比其他算法有不同程度的提升。可以看出，IHHO具备一定的工程优化能力，可应用于实际工程问题。
表 5 压力容器设计问题优化结果Table 5 The optimization results of pressure vessel problem算法 Ts(x1) Th(x2) R(x3) L(x4) 结果 IHHO 0.8251 0.4066 44.8326 145.5222 5928.67 HHO 0.8815 0.4267 47.2647 121.6444 6030.17 SMA 0.8656 0.4236 46.4191 129.5605 5989.18 WOA 0.7651 0.4534 41.1400 188.8871 5976.27 SSA 0.9038 0.4402 48.3157 112.2960 6078.02 GWO 0.8859 0.4345 47.4291 120.1625 6036.72 SCA 0.8320 0.3728 43.4836 161.8432 6031.48 HHOCM 0.8614 0.4219 46.2201 131.4779 5980.16 CEHHO 0.8972 0.4733 49.1172 105.5075 6234.97 DHHO/M 0.8189 0.4250 44.9023 144.7359 5969.54 4. 结束语
结合传统HHO算法的优势和不足，受变异反向学习启发，提出了一种新型改进的哈里斯鹰优化算法（IHHO）。IHHO融合Sigmoid非线性收敛因子，有效平衡了全局搜索和局部探索的转换能力，应用变异RQBL策略能够有效增强种群多样性，提高算法收敛速度和跳出局部最优的能力。通过13个标准函数和工程应用问题的测试结果表明，不论对于单峰函数、多峰函数还是实际优化问题，均具有较佳的收敛速度和精度。在后续研究中，尝试将变异准反射学习策略应用到其他优化算法，以验证该策略应用的广泛性。
-
图 1 收敛因子曲线对比
Fig. 1 Curve of convergence factor comparison
下载:
全尺寸图片
图 2 逃逸能量曲线对比
Fig. 2 Curve of escape energy comparison
下载:
全尺寸图片
图 3 OBL、QOBL、QRBL区别
Fig. 3 Differences between OBL, QOBL and QRBL
下载:
全尺寸图片
图 4 IHHO算法流程
Fig. 4 Flowchart of IHHO
下载:
全尺寸图片
图 5 与经典算法收敛曲线对比
Fig. 5 Convergence curves with classic algorithms
下载:
全尺寸图片
图 6 与其他HHO优化算法收敛曲线对比
Fig. 6 Convergence curve with other HHO optimizer
下载:
全尺寸图片
图 7 压力容器设计问题
Fig. 7 Pressure vessel design problem
下载:
全尺寸图片
表 1 IHHO和HHO运行时间对比
Table 1 Riming time of IHHO and HHO
s 算法 IHHO HHO F1 0.1789 0.0980 F2 0.1210 0.0799 F3 0.6220 0.3843 F4 0.0966 0.0852 F5 0.2055 0.1448 F6 0.1349 0.1000 F7 0.3227 0.2082 F8 0.2042 0.1379 F9 0.1496 0.1150 F10 0.1614 0.1199 F11 0.1923 0.1382 F12 0.7809 0.4953 F13 0.7845 0.4874 表 2 各算法参数设置
Table 2 Parameter setting of each algorithm
表 3 与经典算法标准函数测试结果对比
Table 3 Test results of benchmark functions with classic algorithms
函数 统计值 IHHO SMA HHO WOA SSA GWO SCA F1 Mean 0.00 9.28×10−308 9.70×10−97 1.36×10−72 3.23×10−7 1.55×10−27 1.15×101 Std 0.00 0.00 5.14×10−96 6.44×10−72 9.51×10−7 2.55×10−27 2.37×101 用时/s 0.1033 0.2145 0.0553 0.0403 0.0597 0.0960 0.0697 F2 Mean 0.00 5.82×10−146 1.93×10−50 2.54×10−50 2.05 1.16×10−16 1.58×10−2 Std 0.00 3.19×10−145 9.76×10−50 7.38×10−50 1.71 1.22×10−16 2.48×10−2 用时/s 0.1012 0.2258 0.0536 0.0414 0.0545 0.0990 0.0692 F3 Mean 0.00 1.59×10−315 9.01×10−68 4.10×104 1.42×103 1.03×10−5 9.57×103 Std 0.00 0.00 4.93×10−67 1.49×104 8.61×102 3.17×10−5 5.96×103 用时/s 0.4426 0.2887 0.2515 0.1188 0.1358 0.1583 0.1523 F4 Mean 0.00 6.95×10−165 1.34×10−48 5.10×101 1.17×101 7.13×10−7 3.83×101 Std 0.00 0.00 6.99×10−48 2.85×101 3.14 6.63×10−7 1.34×101 用时/s 0.1013 0.2388 0.0670 0.0404 0.0549 0.0997 0.0699 F5 Mean 2.24×10−3 3.73 1.80×10−2 2.80×101 1.76×102 2.72×101 8.17×104 Std 2.12×10−3 7.69 4.05×10−2 4.20×10−1 2.52×102 6.85×10−1 3.74×105 用时/s 0.2232 0.3149 0.13631 0.0690 0.0887 0.1361 0.1069 F6 Mean 1.05×10−5 4.90×10−3 1.63×10−4 3.70×10−1 1.31×10−7 8.74×10−1 1.68×101 Std 2.29×10−5 3.31×10−3 2.30×10−4 1.99×10−1 1.17×10−7 3.26×10−1 2.95×101 用时/s 0.1170 0.2711 0.0926 0.0414 0.0620 0.1307 0.0806 F7 Mean 1.07×10−4 2.07×10−4 1.15×10−4 3.81×10−3 1.60×10−1 2.10×10−3 1.00×10−1 Std 8.94×10−5 1.74×10−4 1.22×10−4 4.28×10−3 6.59×10−2 1.34×10−3 8.06×10−2 用时/s 0.3075 0.2675 0.1791 0.0895 0.1057 0.1496 0.1203 F8 Mean −1.26×104 −1.26×104 −1.26×104 −1.04×104 −7.48×103 −5.81×103 −3.79×103 Std 4.26×10−1 3.15×10−1 7.93×101 1.71×103 7.04×102 1.05×103 3.43×102 用时/s 0.1874 0.2838 0.1124 0.0538 0.0651 0.1106 0.0853 F9 Mean 0.00 0.00 0.00 0.00 5.09×101 3.12 4.55×101 Std 0.00 0.00 0.00 0.00 1.38×101 3.86 3.22×101 用时/s 0.1308 0.2461 0.0846 0.0428 0.0611 0.1003 0.0758 F10 Mean 8.88×10−16 8.88×10−16 8.88×10−16 4.68×10−15 2.31 1.02×10−13 1.48×101 Std 0.00 0.00 0.00 2.46×10−15 7.60×10−1 1.85×10−14 8.64 用时/s 0.1463 0.2390 0.0901 0.0457 0.0642 0.1060 0.0844 F11 Mean 0.00 0.00 0.00 1.94×10−2 1.57×10−2 2.81×10−3 1.06 Std 0.00 0.00 0.00 6.12×10−2 1.21×10−2 6.05×10−3 4.68×10−1 用时/s 0.1743 0.2583 0.1078 0.0554 0.0744 0.1079 0.1087 F12 Mean 6.63×10−7 5.56×10−3 7.65×10−6 2.02×10−2 6.00 4.62×10−2 5.35×104 Std 8.42×10−7 7.88×10−3 7.68×10−6 1.11×10−2 2.71 2.01×10−2 2.26×105 用时/s 0.7282 0.3451 0.4208 0.1752 0.1981 0.2313 0.2105 F13 Mean 1.02×10−5 3.84×10−3 8.08×10−5 5.59×10−1 1.23×101 6.65×10−1 3.96×105 Std 1.59×10−5 3.99×10−3 1.37×10−4 2.43×10−1 1.38×101 2.40×10−1 1.62×106 用时/s 0.6896 0.6896 0.4443 0.1786 0.2245 0.2339 0.2170 表 4 与其他HHO优化算法标准函数测试结果对比
Table 4 Test results of benchmark functions with other HHO optimization algorithms
函数 统计值 IHHO HHOCM CEHHO DHHO/M F1 Mean 0.00 0.00 0.00 8.16×10−92 Std 0.00 0.00 0.00 3.92×10−91 F2 Mean 0.00 2.06×10−198 0.00 5.26×10−48 Std 0.00 0.00 0.00 2.39×10−47 F3 Mean 0.00 0.00 0.00 4.62×10−60 Std 0.00 0.00 0.00 2.53×10−59 F4 Mean 0.00 4.90×10−192 0.00 1.89×10−45 Std 0.00 0.00 0.00 1.02×10−44 F5 Mean 2.24×10−3 1.80×10−2 4.26×10−3 1.15×10−2 Std 2.12×10−3 2.47×10−2 7.03×10−3 1.17×10−2 F6 Mean 1.05×10−5 4.82×10−4 1.65×10−5 6.56×10−5 Std 2.29×10−5 6.54×10−4 2.32×10−5 9.79×10−5 F7 Mean 1.07×10−4 1.52×10−4 1.33×10−4 1.58×10−4 Std 8.94×10−5 1.46×10−4 1.09×10−4 1.31×10−4 F8 Mean −1.26×104 −1.26×104 −1.26×104 −1.24×104 Std 4.26×10−1 7.51×10−1 6.03×101 9.65×102 F9 Mean 0.00 0.00 0.00 0.00 Std 0.00 0.00 0.00 0.00 F10 Mean 8.88×10−16 8.88×10−16 8.88×10−16 8.88×10−16 Std 0.00 0.00 0.00 0.00 F11 Mean 0.00 0.00 0.00 0.00 Std 0.00 0.00 0.00 0.00 F12 Mean 6.63×10−7 1.66×10−5 1.73×10−6 5.44×10−6 Std 8.42×10−7 2.41×10−5 2.37×10−6 6.46×10−6 F13 Mean 1.02×10−5 1.50×10−4 1.57×10−5 7.29×10−5 Std 1.59×10−5 1.42×10−4 3.16×10−5 9.17×10−5 表 5 压力容器设计问题优化结果
Table 5 The optimization results of pressure vessel problem
算法 Ts(x1) Th(x2) R(x3) L(x4) 结果 IHHO 0.8251 0.4066 44.8326 145.5222 5928.67 HHO 0.8815 0.4267 47.2647 121.6444 6030.17 SMA 0.8656 0.4236 46.4191 129.5605 5989.18 WOA 0.7651 0.4534 41.1400 188.8871 5976.27 SSA 0.9038 0.4402 48.3157 112.2960 6078.02 GWO 0.8859 0.4345 47.4291 120.1625 6036.72 SCA 0.8320 0.3728 43.4836 161.8432 6031.48 HHOCM 0.8614 0.4219 46.2201 131.4779 5980.16 CEHHO 0.8972 0.4733 49.1172 105.5075 6234.97 DHHO/M 0.8189 0.4250 44.9023 144.7359 5969.54 -
[1] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN'95 - International Conference on Neural Networks. Perth: IEEE, 2002: 1942–1948. [2] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007 [3] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95(C): 51–67. [4] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm[J]. Advances in engineering software, 2017, 114(C): 163–191. [5] MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge based systems, 2016, 96: 120–133. doi: 10.1016/j.knosys.2015.12.022 [6] LI Shimin, CHEN Huiling, WANG Mingjing, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future generation computer systems, 2020, 111: 300–323. doi: 10.1016/j.future.2020.03.055 [7] 贾鹤鸣, 李瑶, 孙康健. 基于遗传乌燕鸥算法的同步优化特征选择[J]. 自动化学报, 2022, 48(6): 1601–1615. JIA Heming, LI Yao, SUN Kangjian. Simultaneous feature selection optimization based on hybrid sooty tern optimization algorithm and genetic algorithm[J]. Acta automatica sinica, 2022, 48(6): 1601–1615. [8] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris Hawks optimization: algorithm and applications[J]. Future generation computer systems, 2019, 97: 849–872. doi: 10.1016/j.future.2019.02.028 [9] JIA Heming, PENG Xiaoxu, KANG Lifei, et al. Pulse coupled neural network based on Harris Hawks optimization algorithm for image segmentation[J]. Multimedia tools and applications, 2020, 79(37): 28369–28392. [10] FAN Chencheng, ZHOU Yongquan, TANG Zhonghua. Neighborhood centroid opposite-based learning Harris Hawks optimization for training neural networks[J]. Evolutionary intelligence, 2021, 14(4): 1847–1867. doi: 10.1007/s12065-020-00465-x [11] SARAVANAN G, IBRAHIM A, KUMAR D et al. Iot based speed control of BLDC motor with Harris hawks optimization controller[J]. International journal of grid and distributed computing, 2020, 13: 1902–1915. [12] 马一鸣, 石志东, 赵康, 等. 基于改进哈里斯鹰优化算法的TDOA定位[J]. 计算机工程, 2020, 46(12): 179–184. MA Yiming, SHI Zhidong, ZHAO Kang, et al. TDOA localization based on improved Harris hawk optimization algorithm[J]. Computer engineering, 2020, 46(12): 179–184. [13] HOUSSEIN E H, NEGGAZ N, HOSNEY M E, et al. Enhanced Harris Hawks optimization with genetic operators for selection chemical descriptors and compounds activities[J]. Neural computing and applications, 2021, 33(20): 13601–13618. doi: 10.1007/s00521-021-05991-y [14] 汤安迪, 韩统, 徐登武, 等. 混沌精英哈里斯鹰优化算法[J]. 计算机应用, 2021, 41(8): 2265–2272. doi: 10.11772/j.issn.1001-9081.2020101610 TANG Andi, HAN Tong, XU Dengwu, et al. Chaotic elite Harris Hawks optimization algorithm[J]. Journal of computer applications, 2021, 41(8): 2265–2272. doi: 10.11772/j.issn.1001-9081.2020101610 [15] JIA Heming, LANG Chunbo, OLIVA D, et al. Dynamic Harris Hawks optimization with mutation mechanism for satellite image segmentation[J]. Remote sensing, 2019, 11(12): 1421. doi: 10.3390/rs11121421 [16] MIRJALILI S, GANDOMI A H. Chaotic gravitational constants for the gravitational search algorithm[J]. Applied soft computing, 2017, 53(C): 407–419. [17] 王宁, 何庆. 融合黄金正弦与sigmoid连续化的海鸥优化算法[J]. 计算机应用研究, 2022, 39(1): 157–162,169. WANG Ning, HE Qing. Seagull optimization algorithm combining golden sine and sigmoid continuity[J]. Application research of computers, 2022, 39(1): 157–162,169. [18] WANG Shuang, LIU Qingxin, LIU Yuxiang, et al. A hybrid SSA and SMA with mutation opposition-based learning for constrained engineering problems[J]. Computational intelligence and neuroscience, 2021, 2021: 6379469. [19] TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Vienna: IEEE, 2006: 695–701. [20] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Quasi-oppositional differential evolution[C]//2007 IEEE Congress on Evolutionary Computation. Singapore: IEEE, 2007: 2229–2236. [21] EWEES A A, ABD ELAZIZ M, HOUSSEIN E H. Improved grasshopper optimization algorithm using opposition-based learning[J]. Expert systems with applications, 2018, 112: 156–172. doi: 10.1016/j.eswa.2018.06.023 [22] FAN Qian, CHEN Zhenjian, XIA Zhanghua. A novel quasi-reflected Harris Hawks optimization algorithm for global optimization problems[J]. Soft computing, 2020, 24(19): 14825–14843. doi: 10.1007/s00500-020-04834-7 [23] 李守玉, 何庆, 杜逆索. 分段权重和变异反向学习的蝴蝶优化算法[J]. 计算机工程与应用, 2021, 57(22): 92–101. doi: 10.3778/j.issn.1002-8331.2011-0409 LI Shouyu, HE Qing, DU Nisuo. Piecewise weight and mutation opposition-based learning butterfly optimization algorithm[J]. Computer engineering and applications, 2021, 57(22): 92–101. doi: 10.3778/j.issn.1002-8331.2011-0409 [24] 贾鹤鸣, 姜子超, 李瑶. 基于改进秃鹰搜索算法的同步优化特征选择[J]. 控制与决策, 2022, 37(2): 445–454. JIA Heming, JIANG Zichao, LI Yao. Simultaneous feature selection optimization based on improved bald eagle search algorithm[J]. Control and decision, 2022, 37(2): 445–454. [25] SONG Meijia, JIA Heming, ABUALIGAH L, et al. Modified Harris Hawks optimization algorithm with exploration factor and random walk strategy[J]. Computational intelligence and neuroscience, 2022, 2022: 4673665.
