Incremental dimensionality reduction algorithm based on data manifold boundaries and distribution state
-
摘要: 为了解决增量流形学习中的噪声干扰，以及对不同分布状态下的新数据进行流形降维问题，本文提出一种数据流形边界及其分布条件的增量式降维算法（incremental dimensionality reduction algorithm based on data manifold boundaries and distribution state, IDR-DMBDS）。该算法首先分析噪声概率分布同时对数据降噪，确定降噪数据的流形形态为主流形，并在主流形上表征出噪声的分布形式，以此获得近似的原数据流形边界，然后基于流形边界判别新数据的分布状态，最后将分布于原流形形态之上以及之外的新数据分别映射至低维空间。实验表明，该算法能够有效实现基于流形的增量式高维含噪数据的低维特征挖掘。Abstract: To eliminate the impact of noise on incremental manifold learning and conduct manifold dimensionality reduction on new data under different distribution states, an incremental dimensionality reduction algorithm is proposed based on data manifold boundaries and distribution state. In the algorithm, the probability distribution of noises is analyzed while simultaneously performing data noise reduction. The manifold shape of the data with noise reduction is determined as the main manifold, wherein the distribution form of noise is represented to obtain the approximate manifold boundary of the original data. Subsequently, the distribution state of the new data is determined based on the manifold boundary. Finally, the new data distributed inside and outside the original manifold shape are mapped to the low-dimensional space. Experiments reveal that the algorithm can effectively achieve the excavation of the low-dimensional features of incremental high-dimensional noisy data based on manifold learning.
-
近年来，流形学习在模式识别和机器学习中的应用越来越常见，如人脸识别[1]、文本检索[2]、故障检测[3]、以及隐私保护[4]等。流形学习是在流形假设的前提下，挖掘出高维数据的低维流形从而解决“维度灾难”问题[5]。经典流形学习算法有主成分分析(principal component analysis, PCA)[6]、等度量映射(isometric mapping, ISOMAP)[7]、局部线性嵌入(locally linear embedding, LLE)[8]、拉普拉斯特征映射(Laplacian eigenmaps, LE)[9]、局部切空间对齐(local tangent space alignment, LTSA)[10]等。在现代流形学习算法中，t-分布随机近邻嵌入(t-distributed stochastic neighbor embedding, t-SNE)[11]和一致的流形近似和投影(uniform manifold approximation and projection, UMAP)[12]将高维数据的拓扑结构进行低维映射以获得低维嵌入。此外，类似于变分自动编码器(variational suto-rncoder, VAE)[13]和生成对抗网络(generative sdversarial networks, GAN)[14]的深度生成模型，同样能有效地描述高维数据的低维特征，因此，深度生成模型也被证实具有良好的降维性能。然而，上述算法都是离线式的批量流形学习算法，无法适用于在线式的数据增量式学习问题。
为了改进批量流形学习算法的不足，增量式流形学习作为一种新兴的维数约简技术而出现，其思想是在实时地获得新数据后，通过构建与原数据的邻域关系，提取新数据的低维特征。目前，增量式流形学习算法可以归纳为两类。第一类是对新数据进行流形降维的同时，对原数据的低维表示进行同步更新，如Li等[15]将增量降维问题转化为矩阵的增量特征值计算问题，Bucak等[16]通过采用增量式非负矩阵分解理论，获得高维数据的低维坐标，其本质仍是批量式学习。第二类是处理新数据时，不更新原数据的低维表示，如Zhao等[17]基于字典学习提出了一种增量式降维算法，其实质是利用局部重构机制获得新数据的低维坐标。
虽然对增量式流形学习的研究已取得了一定进展，但是仍存在两个关键问题。一是当新数据分布于原数据所形成的流形形态之外时，即位于原流形形态的延伸结构上；二是数据受噪声干扰。以上两点均对增量式流形降维造成困难。针对上述问题，本文提出了一种新的增量式流形降维算法。该算法首先分析噪声概率分布，同时对数据进行降噪处理，确定降噪数据的流形形态为主流形，并在主流形上表征出噪声的分布形式，以此获得近似的原数据流形边界，然后基于流形边界判别新数据的分布状态。当新数据分布于原流形形态的延伸结构上时，根据新数据的局部空间位置构造映射函数，将新数据映射至低维空间；否则，通过构建与原数据的邻域关系，在低维空间对新数据进行加权重构，以此学习新数据的低维坐标。
本文贡献主要有以下两点：
1) 提出一种分布状态判别策略，根据新数据和流形边界的分布关系，判别新数据的分布状态；
2) 提出一种增量式降维算法，将不同分布状态的新数据分别映射至低维空间，揭示与原数据的低维本质特征，同时加入降噪流程，抑制噪声干扰。
1. IDR-DMBDS的流程及原理
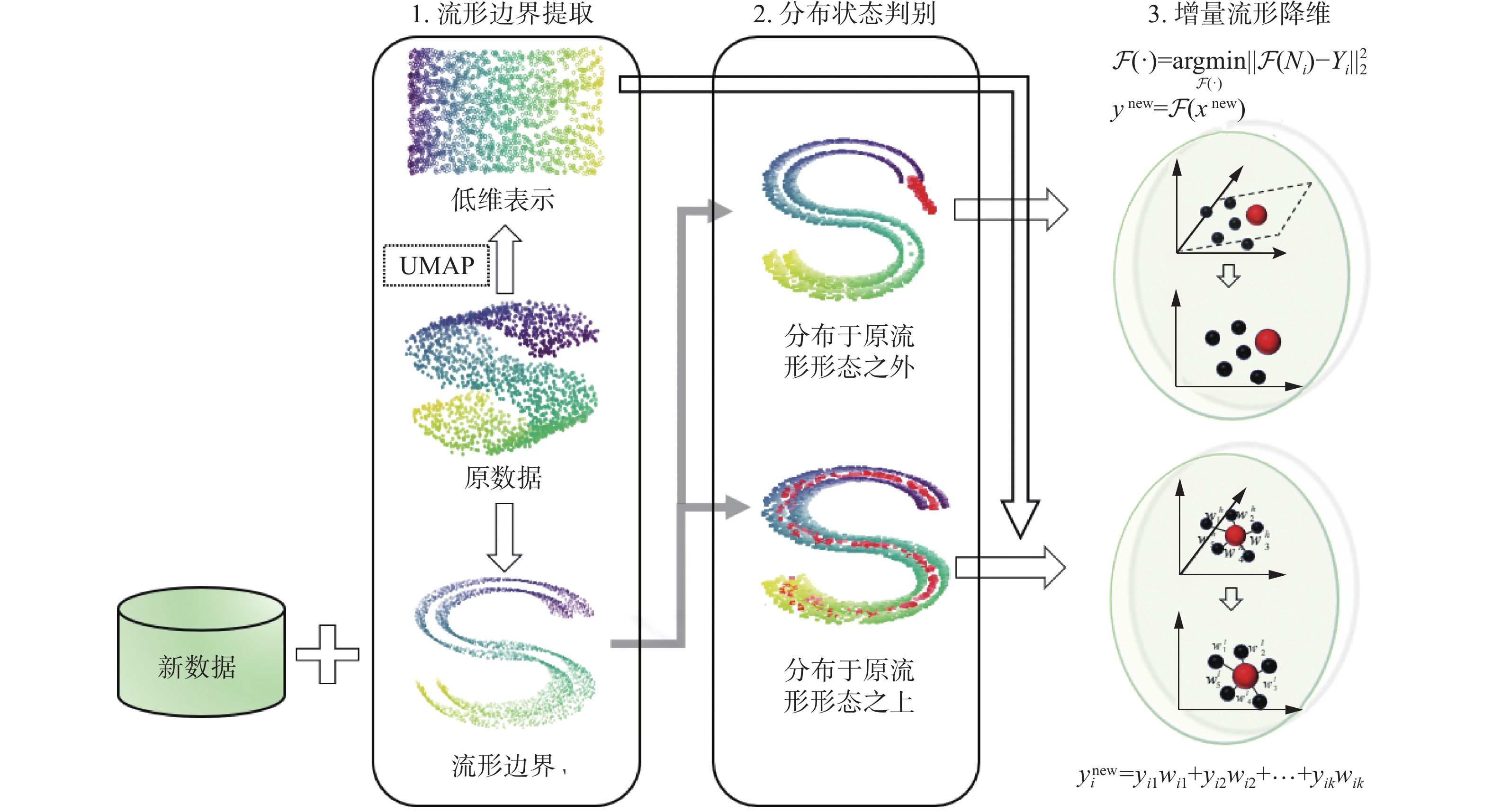
如图1所示，本文提出的算法分为3个阶段，包括：1）流形边界提取：所提取的流形边界以概率化表达方法描述数据；2）分布状态判别：判别新数据的分布状态；3）增量式流形降维：将不同分布状态下的新数据分别映射至低维空间。
图 1 IDR-DMBDS算法框架Fig. 1 Frame of the IDR-DMBDS
下载:
全尺寸图片
1.1 流形边界提取
假设在有限
$D$ 维流形上，含噪数据表示为${\boldsymbol{X}} = \{ {{\boldsymbol{x}}_i}|i = 1,2, \cdots , N\} ,{{\boldsymbol{x}}_i} \in {\bf{R}}^{\boldsymbol{D}}$ 。对原数据的流形边界提取主要分为2个步骤。1.1.1 降噪
为减少噪声干扰，采用相空间重构的投影算法，将高维欧式空间划分为局部流形空间和局部流形切空间，并将局部流形切空间之中的含噪数据投影至主流形，从而达到降噪的目的，流程为：
1）拟合主流形。
在流形学习理论中，若干具有线性结构的局部流形被拼接成分段线性流形，于是我们合理地将局部流形近似为超平面
${\boldsymbol{H}}$ ，然后通过拟合超平面来获得主流形。为拟合超平面，首先借用k-近邻算法获得含噪数据$ {{\boldsymbol{x}}_i} $ 的近邻点${{\boldsymbol{N}}_i} = \{ {\boldsymbol{x}}_i^j\left| {j = 1,2, \cdots, k} \right.\} , {\boldsymbol{x}}_i^j \in {\bf{R}}^{\boldsymbol{D}}$ 。然后，最小化重建距离保证近邻点至超平面${\boldsymbol{H}}$ 的距离之和最小，即$$ {\boldsymbol{H}} = \mathop {\arg} \;{\min \limits_{\boldsymbol{H}}} \sum\limits_{j = 1}^k {d{{({\boldsymbol{x}}_i^j,{\boldsymbol{H}})}^2}} $$ (1) 式中
$d({\boldsymbol{x}}_i^j,{\boldsymbol{H}})$ 表示${\boldsymbol{x}}_i^j$ 至${\boldsymbol{H}}$ 的欧氏距离。2）投影降噪过程。
拟合好超平面
${\boldsymbol{H}}$ 之后，计算${\boldsymbol{H}}$ 的法线方向并将其表示为$ {\boldsymbol{S}}$ 。然后，计算$ {{\boldsymbol{x}}_i} $ 沿法线方向$ {\boldsymbol{S}}$ 至超平面的欧氏距离，并表示为$d({{\boldsymbol{x}}_i},{\boldsymbol{H}})$ 。最后，将含噪数据$ {{\boldsymbol{x}}_i} $ 沿着法线方向$ {\boldsymbol{S}}$ 投影至超平面${\boldsymbol{H}}$ 从而达到降噪的目的。将该过程表示为$$ {{\boldsymbol{x}}_i} = {{\boldsymbol{x}}_i} - d({{\boldsymbol{x}}_i},{\boldsymbol{H}}) {\boldsymbol{S}} $$ (2) 1.1.2 提取流形边界
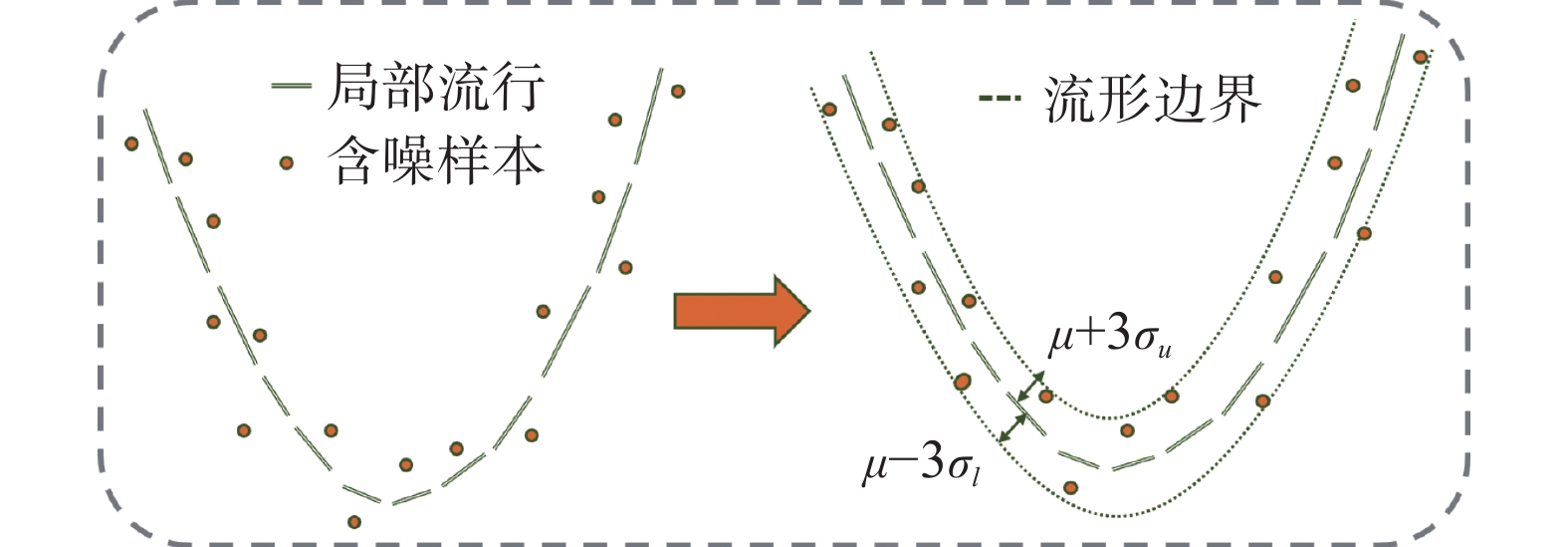
如图2所示，为了能更直观地描述噪声对不同流形空间位置的损伤程度，本文使用Parzen窗模型[18]对噪声进行概率分析，以此确定噪声在不同位置的均值
$\mu $ 和标准差$\sigma $ ，并在主流形上表征出噪声的分布形式，以此获得近似的原数据流形边界[19]。
图 2 流形边界提取过程Fig. 2 Process of extracting manifold boundary下载:
全尺寸图片
1.1.3 原数据的流形降维
增量式流形学习同样需要原数据的低维特征，本文使用UMAP算法对原数据进行降维，其核心是利用图布局算法，将构建在高维空间的加权
$k - $ 近邻图映射至低维空间，在低维空间挖掘出与其最相似的图。具体流程为：1）图构造(graph construction)。在高维空间构建加权
$k - $ 近邻图${\boldsymbol{G}} = ({\boldsymbol{V}},{\boldsymbol{E}},{\boldsymbol{w}})$ ，其中${\boldsymbol{V}}$ 表示图中对应于原数据$X$ 的节点集合，${\boldsymbol{E}}=\{({{\boldsymbol{x}}}_{i},{{\boldsymbol{x}}}_{ij})|1 \leqslant i \leqslant N,\text{ }1 \leqslant j \leqslant k\}$ 表示图中的边集合，并定义连接${{\boldsymbol{x}}_i}$ 与它近邻点${{\boldsymbol{N}}_i} = \{ {{\boldsymbol{x}}_{ij}}|j = 1,2, \cdots, k\}$ 边的权重$ {w_{ij}} $ 为$$ {w_{ij}} = \exp \left(\frac{{ - \max (0,d({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ij}}) - {\rho _i})}}{{{\sigma _i}}}\right) $$ (3) 式中：
$d({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ij}})$ 表示${{\boldsymbol{x}}_i}$ 和${{\boldsymbol{x}}_{ij}}$ 的欧氏距离，$ {\rho _i} $ 和${\sigma _i}$ 为两个超参数：$$ {\rho _i} = \min (d({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ij}})|1 \leqslant j \leqslant k,d({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ij}}) > 0) $$ (4) $$ \exp \left(\frac{{ - \max (0,d({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ij}}) - {\rho _i})}}{{{\sigma _i}}}\right) = {\log _2}(k) $$ (5) 2）图布局(graph layout)。定义目标函数：
$$ J = \sum\limits_{e \in E} {{{\boldsymbol{w}}_h}(e)} \log \left(\frac{{{{\boldsymbol{w}}_h}(e)}}{{{{\boldsymbol{w}}_l}(e)}}\right) + (1 - {{\boldsymbol{w}}_h}(e))\log \left(\frac{{1 - {{\boldsymbol{w}}_h}(e)}}{{1 - {{\boldsymbol{w}}_l}(e)}}\right) $$ (6) 其中
${{\boldsymbol{w}}_h}( \cdot )$ 和${{\boldsymbol{w}}_l}( \cdot )$ 分别表示在高维和低维空间之中的边的权重集合。为了能在降维后尽可能保留原$k - $ 近邻图蕴含的数据特征，利用梯度下降法最小化式（6），以此获得原数据的低维表示，记为${\boldsymbol{Y}} = \{ {{\boldsymbol{y}}_i}|i = 1,2, \cdots ,N\} ,{y_i} \in {{\bf{R}}}^{\boldsymbol{d}}$ 。1.2 分布状态判别
假设新数据表示为
${{\boldsymbol{X}}^{{\rm{new}}}} = \{ {\boldsymbol{x}}_i^{{\rm{new}}}|i = 1,2, \cdots, T\} ,{\boldsymbol{x}}_i^{{\rm{new}}} \in {\bf{R}}^{\boldsymbol{D}}$ 。通常，新数据和原数据具有独立同分布特性，新数据可能分布于原数据所形成的流形形态上，也可能分布于原流形形态的延伸结构上。因此，对新数据进行增量式流形降维前，需要先判别新数据的分布状态。为了有效判别新数据的分布状态，本文基于流形边界进行新数据的离群点检测。为避免因遍历所有新数据带来的计算量问题，利用k-means算法对新数据
${{\boldsymbol{X}}^{{\rm{new}}}}$ 进行聚类，得到$t$ 个聚类中心点${{\boldsymbol{X}}^c} = \{ {\boldsymbol{x}}_i^c|i = 1,2, \cdots, t\} ,{\boldsymbol{x}}_i^c \in {\bf{R}}^{\boldsymbol{D}}$ 作为新数据的代表点。离群点检测采用局部异常因子检测算法(local outlier hactor, LOF)[20]，通过量化聚类中心点与流形边界的密度差异进行离群点检测，并通过局部离群因子系数${\rm{Score}}( \cdot )$ 表征密度差异大小，${\rm{Score}}({\boldsymbol{x}}_i^c)$ 为1的聚类中心点将被识别为离群点。当聚类中心点被判别为离群点时，说明新数据分布于原流形形态的延伸结构上。
1.3 增量流形降维
对于分布于原流形形态之上的新数据，需保持降维前后表征数据距离的权值大小，而当新数据分布于原流形形态的延伸结构上时，则期望能够保持两者共同形成的全局低维流形结构不变。对新数据的增量流形降维的流程如下。
当新数据分布于原流形形态上时：首先，在原数据
${\boldsymbol{X}}$ 中寻找新数据${\boldsymbol{x}}_{i}^{{\rm{new}}}$ 的近邻点${{\boldsymbol{N}}_i} = \{ {{\boldsymbol{x}}_{ij}}|j = 1, 2, \cdots, k\}$ ，$ {{\boldsymbol{N}}_i} $ 的低维表示为$ {{\boldsymbol{Y}}_i} $ 。然后，根据式（3）计算${\boldsymbol{x}}_{i}^{{\rm{new}}}$ 与$ {{\boldsymbol{N}}_i} $ 的权重$ {{\boldsymbol{w}}_{ij}} $ 。最后，假设在高维欧式空间中，${\boldsymbol{x}}_{i}^{{\rm{new}}}$ 由$ {{\boldsymbol{N}}_i} $ 中的数据加权构成，并且${\boldsymbol{x}}_{i}^{{\rm{new}}}$ 的低维表示与$ {{\boldsymbol{Y}}_i} $ 同样保持这种权重关系。于是新数据的低维表示为$$ {\boldsymbol{y}}_{i}^{{\rm{new}}} = {{\boldsymbol{y}}_{i1}}{{\boldsymbol{w}}_{i1}} + {{\boldsymbol{y}}_{i2}}{{\boldsymbol{w}}_{i2}} \cdots + {{\boldsymbol{y}}_{ik}}{{\boldsymbol{w}}_{ik}} $$ (7) 当新数据分布于原流形形态的延伸结构上时：首先，在原数据
${\boldsymbol{X}}$ 中寻找新数据${\boldsymbol{x}}_{i}^{{\rm{new}}}$ 的近邻点$ {{\boldsymbol{N}}_i} = \{ {{\boldsymbol{x}}_{ij}}|j = 1,2, \cdots, k\} $ ，$ {{\boldsymbol{N}}_i} $ 的低维表示为$ {{\boldsymbol{Y}}_i} $ 。然后，设线性映射函数$\mathcal{F}\left( \cdot \right):{\bf{R}}^{\boldsymbol{D}} \to {\bf{R}}^{\boldsymbol{d}}$ ，该函数将$ {{\boldsymbol{N}}_i} $ 从高维空间线性映射至低维空间，且得到的低维表示$ \mathcal{F}\left( {{{\boldsymbol{N}}_i}} \right) $ 与$ {{\boldsymbol{Y}}_i} $ 差异最小，于是定义损失函数$$ \mathcal{F}\left( \cdot \right) = \mathop {\arg}{\min \limits_{\mathcal{F}\left( \cdot \right)}} \left\| {\mathcal{F}\left( {{{\boldsymbol{N}}_i}} \right) - {{\boldsymbol{Y}}_i}} \right\|_2^2 $$ (8) 将映射函数
$ \mathcal{F}\left( \cdot \right) $ 写为映射矩阵${\boldsymbol{B}}$ ，损失函数的矩阵形式为$$ {\boldsymbol{B}} = \mathop {\arg} {\min \limits_B} \left\| {{{\boldsymbol{N}}_i}{\boldsymbol{B}} - {{\boldsymbol{Y}}_i}} \right\|_2^2 $$ (9) 对式（9）进行最小化可得
$$ {\boldsymbol{B}} = {({({{\boldsymbol{N}}_i})^{\rm{T}}}{{\boldsymbol{N}}_i})^{ - 1}}{({{\boldsymbol{N}}_i})^{\rm{T}}}{{\boldsymbol{Y}}_i} $$ (10) 最后，将新数据映射至低维空间，其低维表示为
$$ {{\boldsymbol{y}}}_{i}^{{\rm{new}}}\text{ }={{\boldsymbol{x}}}_{i}^{{\rm{new}}}{\boldsymbol{B}} $$ (11) 本文所提算法的流程如下。
算法 IDR-DMBDS算法
输入 原数据
${\boldsymbol{X}}$ 、原数据的低维表示${\boldsymbol{Y}}$ 、新数据${{\boldsymbol{X}}^{{\rm{new}}}}$ 和数据边界。输出 新数据的低维特征
对
${{\boldsymbol{X}}^{{\rm{new}}}}$ 进行聚类，得到$ t $ 个聚类中心点$ {\boldsymbol{x}}_i^c $ For each
${\boldsymbol{x}}_i^c \in {{\boldsymbol{X}}^c}$ do$$ {\rm{Score}}({{\boldsymbol{x}}}_{i}^{c}) \text{ }\leftarrow \text{LOF}({{\boldsymbol{x}}}_{i}^{c}) $$ End for
If
${\rm{Score}}({\boldsymbol{x}}_i^c) \cap {\rm{Score}}({\boldsymbol{x}}_2^c) \cap {\rm{Score}}({\boldsymbol{x}}_t^c) = 1$ then$$ {\boldsymbol{y}}_{i}^{{\rm{new}}} \leftarrow {{\boldsymbol{y}}_{i1}}{{\boldsymbol{w}}_{i1}} + {{\boldsymbol{y}}_{i2}}{{\boldsymbol{w}}_{i2}} \cdots + {{\boldsymbol{y}}_{ik}}{{\boldsymbol{w}}_{ik}} $$ Else
$$ \mathcal{F}\left( \cdot \right){\text{ }} \leftarrow \mathop {{\text{ arg}}} {\min \limits_{\mathcal{F}\left( \cdot \right)}} \left\| {\mathcal{F}\left( {{{\boldsymbol{N}}_i}} \right) - {{\boldsymbol{Y}}_i}} \right\|_2^2 $$ $$ {\boldsymbol{y}}_{i}^{{\rm{new}}}{\text{ }} \leftarrow {\text{ }}\mathcal{F}\left( {{\boldsymbol{x}}_{i}^{{\rm{new}}}} \right) $$ End if
Return
$ {\boldsymbol{y}}_{i}^{{\rm{new}}} $ 1.4 计算复杂度分析
本算法将原数据
${\boldsymbol{X}} = \{ {{\boldsymbol{x}}_i}|i = 1,2, \cdots, N\} ,{{\boldsymbol{x}}_i} \in {\bf{R}}^{\boldsymbol{D}}$ 和新数据${{\boldsymbol{X}}^{{\rm{new}}}} = \{ {\boldsymbol{x}}_{i}^{{\rm{new}}}|i = 1,2, \cdots, T\} ,{\boldsymbol{x}}_{i}^{{\rm{new}}} \in {\bf{R}}^{\boldsymbol{D}}$ 降至$d$ 维包含5个步骤，其各自的计算复杂度以及总的计算复杂度分析如下。降噪：k-近邻搜索的平均计算成本为
$O(D\log (k)\cdot N\log (N))$ ，其中，$k$ 为近邻数。超平面拟合的计算成本为$O(N{D^3})$ 。含噪数据的投影过程的计算成本为$O(N)$ ；流形边界提取：流形边界提取的计算成本为$O(N)$ ；原数据的流形降维：原数据借用UMAP算法进行降维，其计算成本为$O({N^{1.14}})$ ；分布状态判别：利用k-means算法获取新数据$t$ 个聚类中心点的计算复杂度为$O(TDt)$ ，利用局部异常检测算法进行分布状态判别的计算复杂度为$O(2Nt)$ ；增量流形降维：获取新增数据的低维坐标的计算复杂度为$O(T{k^3})$ 。综上所述，本算法的总计算复杂度为
$O(D\log (k) \cdot N\log (N)) + O(N{D^3}) + 2O(N) + O({N^{1.14}})$ $ + O(TDt) + O(T{k^3})$ 。2. 实验结果与分析
2.1 实验设置
1）数据集说明。
为评估所提出算法的性能，我们选择两组具有可视化效果的合成数据集、一组文本数据集以及三组多类分图像数据集进行算法实现，数据集包括：
瑞士卷和“S”型数据集为服从流形结构的三维合成数据集；
MR数据集包含5000条电影评论，涉及正面/负面评论。
MNIST数据集是美国国家标准与技术研究院收集整理的大型手写数字数据库。其含有60000个训练样本和10000个测试样本，包含了0~9共10类手写数字图片，图像都做了尺寸归一化，为28像素×28像素大小的灰度图；
FASHION-MNIST数据集由Zalando旗下的研究部门提供。其含有60000个训练样本和10000个测试样本，涵盖了来自10种类别商品的正面图片，图像都为28像素×28像素大小的灰度图；
DSPRITES数据集是由6个不相关因素按程序产生的2D形状（心形、椭圆形和方形）图像数据集，这些因素包括颜色、形状、比例、方向、X坐标位置和Y坐标位置，图像大小都为64像素×64像素。
本文实验所用数据的信息描述如表1所示。
表 1 实验数据信息描述Table 1 Description of the experimental data数据集 维度 原数据
数量/个新数据
数量/个加入噪
声参数瑞士卷 3 2000 200 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ “S”型 3 2000 200 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ MR — 5000 — — MNIST $28 \times 28$ 5000 500 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ FASHION-MNIST $28 \times 28$ 5000 500 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ DSPRITES $64 \times 64$ 1500 600 $ \delta \sim \mathcal{N}(0,{0.3^2}) $ 2）对照算法说明。
本文实验选取4种降维算法作为对照算法。
ISOMAP：通过保持降维前后样本之间的“测地线”距离不变，挖掘出嵌入在高维空间的低维流形。加入增量新数据后，通过保持新增数据和原数据的测地距离来实现增量降维；
LLE：一种非线性降维算法，通过保持数据的局部线性结构来提取低维流形。加入增量新数据后，通过更新代价矩阵实现增量降维；
PCA：一种线性降维算法，依据样本在空间中的位置分布，保持样本点在多维空间中的最大方差并获得投影方向，实现维数约简。加入增量新数据后，重新计算均值向量并进行奇异值分解，更新特征值和特征向量实现增量降维；
UMAP：基于黎曼几何和代数拓扑的理论框架，将高维数据的拓扑结构进行低维映射以达到降维目的。本文通过局部加权重构算法实现对增量新数据的增量降维。
3）评估指标说明。
对于合成数据集，对实验结果进行可视化，以直观地展示算法流程以及降维性能。对于图像数据集，由于数据集为多类分数据集，使用高斯混合模型作为分类器对降维后的新数据进行分类，并将分类准确率作为评估指标，计算形式如下：
$$ {F_{{\rm{accuracy}}}} = \frac{{\displaystyle\sum\limits_{i = 1}^T {\delta ({{\hat y}_i},{y_i})} }}{T} $$ (12) 式中：
$ {\hat y_i} $ 和$ {y_i} $ 分别表示预测标签和真实标签，当$ {\hat y_i} $ =$ {y_i} $ 时，$ \delta ({\hat y_i},{y_i}) = 1 $ ，否则为0。4）涉及算法的参数设置。
k-近邻算法：近邻点个数设置为15；k-means算法：聚类数设置为20；LOF算法：近邻点个数设置为15，异常值比例设置为0.05；ISOMAP：该算法的近邻点个数设置为15；LLE：近邻点个数设置为15；UMAP：近邻点个数设置为15，低维空间中点之间的最小距离设置为0.2；高斯混合模型：在3个图像数据集的实验中，生成的聚类数分别设置为3、10、10。
2.2 合成数据集的实验结果分析
本节在2个合成数据集上评估所提算法的性能，图3对加入噪声的新数据和原数据进行可视化展示，图3(a)和图3(b)中的新数据分布于原流形形态之上，图3(c)和图3(d)中的新数据分布于原流形形态的延伸结构上。
图 3 数据集的可视化展示Fig. 3 Visual display of the datasets下载:
全尺寸图片
首先，对原数据进行投影降噪并获得流形边界，同时使用UMAP算法将降噪数据降至2维。然后，对新数据进行k-means聚类，得到新数据的聚类中心点，图4为聚类中心点与流形边界的分布关系，并基于流形边界判别新数据的分布状态。最后，根据判别结果，利用式（7）和式（11）对新数据进行降维，图5对降维后的新数据和原数据进行可视化展示。
图 4 聚类中心点与流形边界的分布关系Fig. 4 Distribution relationship between cluster centers and manifold boundary下载:
全尺寸图片
图 5 新数据和原数据的低维特征Fig. 5 Low-dimensional features of the new and original data下载:
全尺寸图片
由图4可知：当新数据分布于原流形形态上时，提取的流形边界能将聚类中心点包含进来，使用LOF算法对聚类中心点进行离群点检测，其都被判别为正常值。当新数据分布于原流形形态的延伸结构上时，聚类中心点分布于流形边界之外，因与周围的流形边界有较为明显的密度差异而被判别为离群点。
由图5可知：当新数据分布于原流形形态上时，对新数据进行降维后，其形态结构与原数据的保持一致，并且数据之间的权值关系也得以保留。当新数据分布于原流形形态的延伸结构上时，新数据降维之后的形态结构同样是对原数据的结构延伸，从而能够保持新数据和原数据的全局流形结构不变。
2.3 文本数据集的实验结果分析
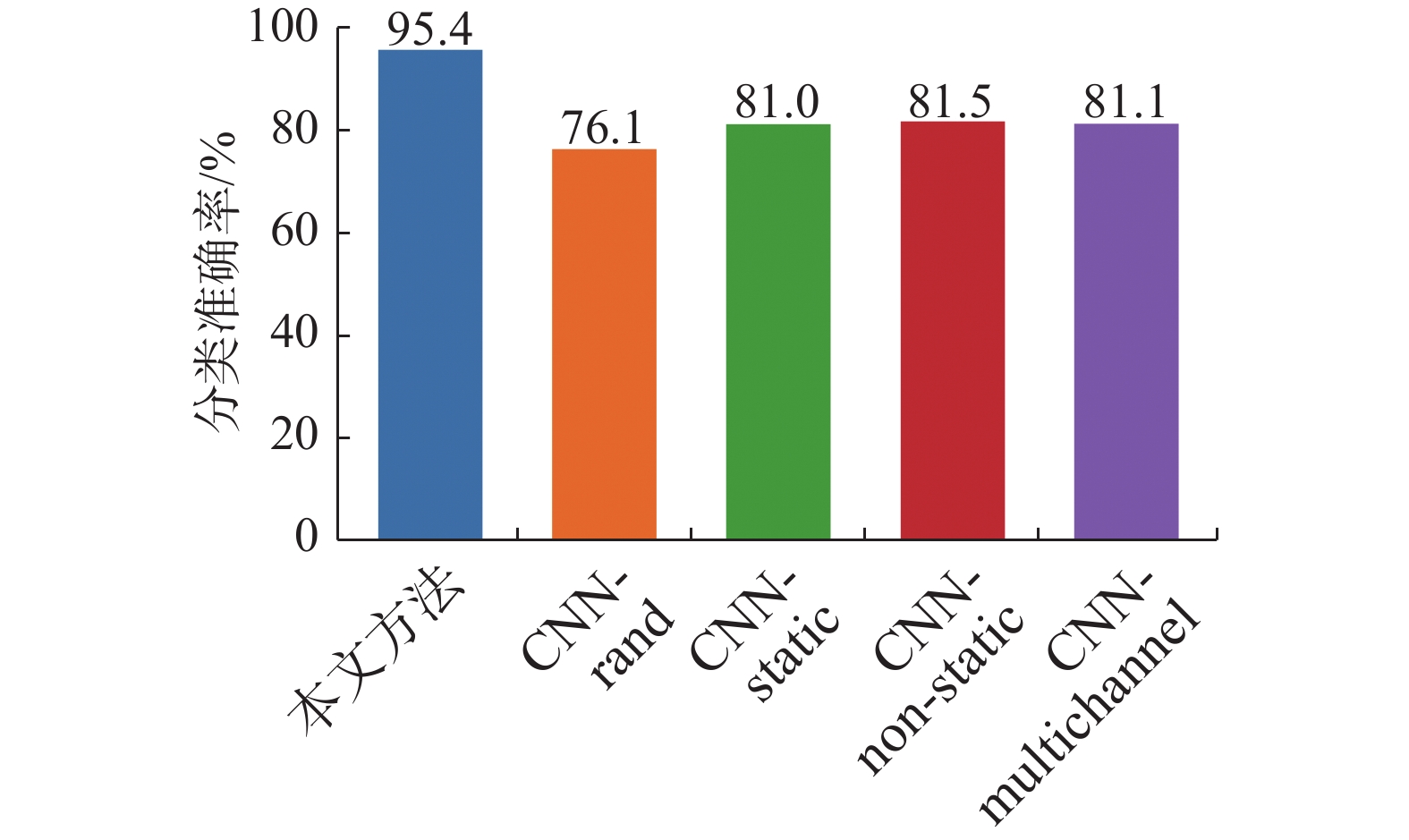
本节在MR数据集上评估所提算法的降维性能。本实验首先统计不同文本之间，两词在所有文本中相邻的次数，通过共现矩阵用于发现主题，解决词向量相近关系的表示[21]，然后使用本文算法将共现矩阵的行向量降至300维获得词向量，最后使用Text CNN模型[22]进行文本分类，并将分类准确率与文献[22]中的结果进行对比(文献[22]使用公开可用的word2vec词向量)，对比结果如图6所示。
图 6 MR数据集的分类准确率Fig. 6 Classification accuracy of the MR dataset下载:
全尺寸图片
由图6可知，本文算法在降维后能够保留更多的分类特征，在使用Text CNN模型进行分类后，具有更高的分类准确率。
2.4 图像数据集的实验结果分析
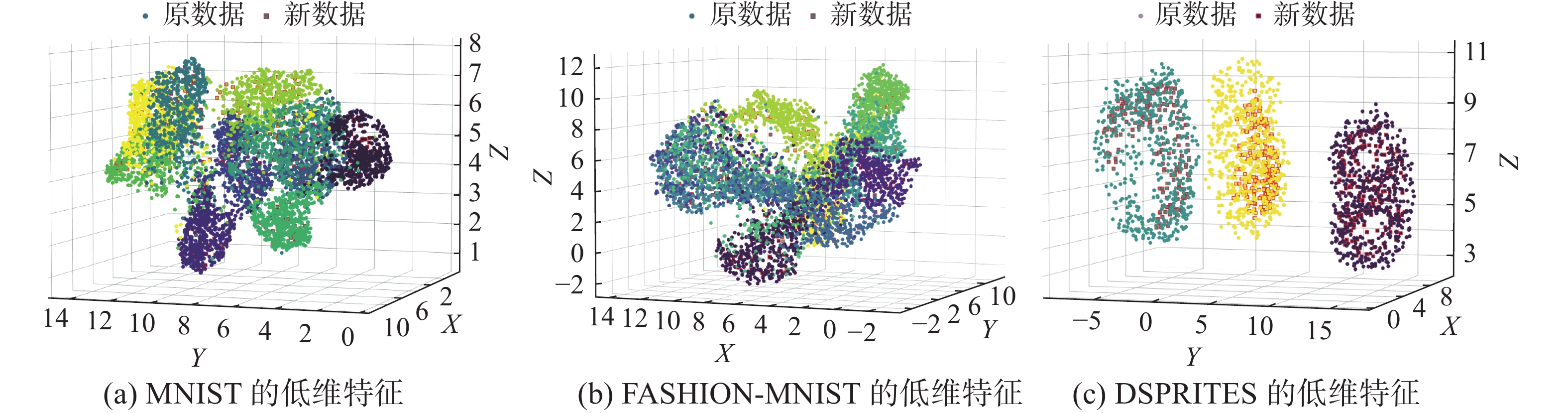
在3个图像数据集上来评估所提算法的性能，图7给出了3个数据集的部分图像示例。实验流程与合成数据集相同，用所提算法以及4种对照算法将数据降至3、5、10、80和200维，图8对算法获取的3维低维特征进行可视化。然后使用高斯混合模型对不同维度的低维表示进行分类，计算分类准确率。并将包括本文算法在内的5种不同算法的实验结果进行对比，图9给出对比结果。
图 7 数据集的图像示例Fig. 7 Examples of images in the datasets下载:
全尺寸图片
图 8 数据集的低维特征Fig. 8 Low-dimensional features of the datasets下载:
全尺寸图片
图 9 5种算法在数据集的分类准确率Fig. 9 Classification accuracy of five algorithms for the datasets下载:
全尺寸图片
由图8可知：与原数据相同类别的新数据，在降维后数据分布呈现类内聚敛的特性，而与原数据不同类别的新数据，在降维后呈现类间分离的特性，从而体现出较大的类别区分度。因此，在多类分含噪图像数据集上，本文提出的算法表现出较好的分类性能。
由图9可知：由于加入了投影降噪这一流程，相较于其他算法，本文算法在3个数据集上都取得了评估指标的最优值，尤其在MNIST数据集上，各个维度上的分类准确率均高于其他算法10%以上。另外，随着维度升高，LLE算法的分类准确率呈现逐渐降低的趋势，而本文的算法未出现这种问题。综上所述，在面对多类分含噪图像数据集时，本文算法具有更好的抗噪能力。
3. 结束语
本文针对含噪数据的增量式降维问题，提出一种新的流形降维算法。该算法引入投影降噪理论，将含噪数据投影至主流形，从而抑制噪声干扰；同时，基于流形边界判断新数据的分布状态，将不同分布状态下的新数据分别映射至低维空间，进而揭示与原数据的低维本质特征。实验表明，相较于其他流形降维算法，该算法能够适用于在线的增量式降维问题处理，同时表现出更好的分类性能和抗噪能力。另外，无论新数据分布于原流形形态之上或者是延伸结构之上，该算法都能揭示新数据和原数据共同蕴含的低维特征。进一步的研究将应用本文算法解决实际工程问题。
-
图 1 IDR-DMBDS算法框架
Fig. 1 Frame of the IDR-DMBDS
下载:
全尺寸图片
图 2 流形边界提取过程
Fig. 2 Process of extracting manifold boundary
下载:
全尺寸图片
图 3 数据集的可视化展示
Fig. 3 Visual display of the datasets
下载:
全尺寸图片
图 4 聚类中心点与流形边界的分布关系
Fig. 4 Distribution relationship between cluster centers and manifold boundary
下载:
全尺寸图片
图 5 新数据和原数据的低维特征
Fig. 5 Low-dimensional features of the new and original data
下载:
全尺寸图片
图 6 MR数据集的分类准确率
Fig. 6 Classification accuracy of the MR dataset
下载:
全尺寸图片
图 7 数据集的图像示例
Fig. 7 Examples of images in the datasets
下载:
全尺寸图片
图 8 数据集的低维特征
Fig. 8 Low-dimensional features of the datasets
下载:
全尺寸图片
图 9 5种算法在数据集的分类准确率
Fig. 9 Classification accuracy of five algorithms for the datasets
下载:
全尺寸图片
表 1 实验数据信息描述
Table 1 Description of the experimental data
数据集 维度 原数据
数量/个新数据
数量/个加入噪
声参数瑞士卷 3 2000 200 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ “S”型 3 2000 200 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ MR — 5000 — — MNIST $28 \times 28$ 5000 500 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ FASHION-MNIST $28 \times 28$ 5000 500 $ \delta \sim \mathcal{N}(0,{0.2^2}) $ DSPRITES $64 \times 64$ 1500 600 $ \delta \sim \mathcal{N}(0,{0.3^2}) $ -
[1] HUANG Likun, LU Jiwen, TAN Y P. Multi-manifold metric learning for face recognition based on image sets[J]. Journal of visual communication and image representation, 2014, 25(7): 1774–1783. doi: 10.1016/j.jvcir.2014.08.006 [2] 王莉军. 海量数据下的文本信息检索算法仿真分析[J]. 计算机仿真, 2016(4): 429–432. WANG Lijun. Simulation analysis of text Information retrieval algorithms under massive data[J]. Computer simulation, 2016(4): 429–432. [3] JIANG Quansheng, JIA Minping, HU Jianzhong, et al. Machinery fault diagnosis using supervised manifold learning[J]. Mechanical systems and signal processing, 2009, 23(7): 2301–2311. doi: 10.1016/j.ymssp.2009.02.006 [4] CHEN Zhenzhu, FU Anmin, DENG R H, et al. Secure and verifiable outsourced data dimension reduction on dynamic data[J]. Information sciences, 2021, 573: 182–193. doi: 10.1016/j.ins.2021.05.066 [5] IZENMAN A J. Introduction to manifold learning[J]. Wiley interdisciplinary reviews:computational statistics, 2012, 4(5): 439–446. doi: 10.1002/wics.1222 [6] BRO R, SMILDE A K. Principal component analysis[J]. Anal methods, 2014, 6(9): 2812–2831. doi: 10.1039/C3AY41907J [7] TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319–2323. doi: 10.1126/science.290.5500.2319 [8] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323–2326. doi: 10.1126/science.290.5500.2323 [9] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural computation, 2003, 15(6): 1373–1396. doi: 10.1162/089976603321780317 [10] ZHANG Zhenyue, ZHA Hongyuan. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J]. Journal of Shanghai University (english edition), 2004, 8(4): 406–424. doi: 10.1007/s11741-004-0051-1 [11] VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(11): 2579–2605. [12] MCINNES L, HEALY J, SAUL N, et al. UMAP: uniform manifold approximation and projection[J]. Journal of open source software, 2018, 3(29): 861. doi: 10.21105/joss.00861 [13] 张冀, 曹艺, 王亚茹, 等. VAE 和 Stack GAN的零样本图像分类方法[J]. 智能系统学报, 2021, 17(3): 593–601. ZHANG Ji, CAO Yi, WANG Yaru, et al. A zero sample image classification method combining VAE and Stack GAN[J]. CAAI transactions on intelligent systems, 2021, 17(3): 593–601. [14] 王坤峰, 苟超, 段艳杰, 等. 生成式对抗网络 GAN 的研究进展与展望[J]. 自动化学报, 2017, 43(3): 321–332. WANG Kunfeng, GOU Chao, DUAN Yanjie, et al. Research progress and prospects of generative adversarial networks[J]. IEEE/CAA journal of automatica sinica (JAS), 2017, 43(3): 321–332. [15] LI Housen, JIANG Hao, BARRIO R, et al. Incremental manifold learning by spectral embedding methods[J]. Pattern recognition letters, 2011, 32(10): 1447–1455. doi: 10.1016/j.patrec.2011.04.004 [16] BUCAK S S, GUNSEL B. Incremental subspace learning via non-negative matrix factorization[J]. Pattern recognition, 2009, 42(5): 788–797. doi: 10.1016/j.patcog.2008.09.002 [17] ZHAO Zhong, FENG Guocan, ZHU Jiehua, et al. Manifold learning: Dimensionality reduction and high dimensional data reconstruction via dictionary learning[J]. Neurocomputing, 2016, 216: 268–285. doi: 10.1016/j.neucom.2016.07.045 [18] KWAK N, CHOI C H. Input feature selection by mutual information based on Parzen window[J]. IEEE transactions on pattern analysis and machine intelligence, 2002, 24(12): 1667–1671. doi: 10.1109/TPAMI.2002.1114861 [19] YANG Tao, FU Dongmei, MENG Jintao, et al. A manifold-based dimension reduction algorithm framework for noisy data using graph sampling and spectral graph[J]. Complexity, 2020, 2020: 1–18. [20] MA Hehe, HU Yi, SHI Hongbo. Fault detection and identification based on the neighborhood standardized local outlier factor method[J]. Industrial & engineering chemistry research, 2013, 52(6): 2389–2402. [21] ELEYAN A, DEMIREL H. Co-occurrence matrix and its statistical features as a new approach for face recognition[J]. Turkish journal of electrical engineering and computer sciences, 2011, 19(1): 97–107. [22] YOON K. Convolutional Neural Networks for Sentence[C]// Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. Doha: Association for Computational Linguistics, 2014: 1746–1751.
