A multimodal multi-objective optimization algorithm with clustering and niching searching
-
摘要: 针对多模态多目标优化中种群多样性难以维持和所得等价Pareto最优解数量不足问题，提出一种融合聚类和小生境搜索的多模态多目标优化算法(multimodal multi-objective optimization algorithm with clustering and niching searching, CSSMPIO)。首先利用基于聚类的特殊拥挤距离非支配排序方法(clustering-based special crowding distance, CSCD)初始化种群；引入自适应物种形成策略生成稳定的小生境，在不同的小生境子空间并行搜索和保持等价Pareto最优解；采用特殊拥挤距离非支配排序策略实现个体选优、精英学习策略避免过早收敛。通过在14个多模态多目标函数上进行测试，并与7种新提出的多模态多目标优化算法进行对比实验以及Wilcoxon秩和检验发现，CSSMPIO的总体性能优于对比算法。最后将算法用于基于地图的测试问题，进一步证明了算法的有效性。Abstract: In order to address the problems associated with maintaining population diversity and the insufficient number of equivalent Pareto-optimal solutions for multimodal multi-objective optimization, this study proposes a multimodal multi-objective optimization algorithm combining clustering and niche search (CSSMPIO). In the proposed algorithm, a clustering-based special crowding distance method is designed to initialize the population. Additionally, self-organized speciation is introduced to form stable niches, facilitating parallel searching and maintaining equivalent Pareto-optimal solutions. Subsequently, a non-dominated special crowding distance is introduced to realize individual selection and an elite learning strategy, circumventing premature convergence. The algorithm has been simulated using seven other state-of-the-art algorithms on 14 multimodal multi-objective optimization problems and was tested and analyzed using the Wilcoxon rank sum test. The results reveal that the general performance of CSSMPIO is superior to that of the compared algorithms. Finally, the CSSMPIO algorithm is applied to the map-based test problem, which confirms the effectiveness of the algorithm.
-
多模态多目标优化问题（multimodal multi-objective optimization problem, MMOP）[1]是一类特殊的多目标优化问题（mmulti-objective optimization problem, MOP）[2]，它着重于获取具有相同目标值的帕累托最优解集（Pareto-optimal sets, PSs）。如何获取并保持决策空间更多的PSs，提高决策空间的多样性以及算法的搜索能力一直是多模态多目标优化问题存在的难点。
目前，多模态多目标问题主要从两个方面来优化：一是提高算法的搜索能力。最早有学者提出通过改进粒子群算法来提高搜索能力，如CLPSO（comprehensive learning particle swarm optimization）[3]和AMPSO（modified particle swarm optimization）[4]通过优化粒子的学习方式以提高算法的搜索能力；STMOPSO（star-structured multi-objective particle swarm optimization）[5]基于星型拓扑结构提出一种非支配解集分布均匀程度的评价方法，提高了算法的收敛速度。小生境策略可以提高算法的搜索能力，如Qu等[6]提出的LIPS（distance-based locally informed particle swarm）利用邻域信息在小生境空间内粒子根据局部最优粒子进行搜索，提高了算法的精细搜索能力；SS-MOPSO（self-organized speciation based multi-objective particle swarm optimizer）[7]基于物种形成策略形成多个稳定的物种，物种与物种之间互不重叠，分别搜索并保持Pareto最优解；Liang等[8]在NSGAII的基础上提出DN-NSGAII（decision space based niching NSGAII），在决策空间小生境内分别搜索不同的Pareto最优解，有效防止了过早收敛，但该算法仅考虑决策空间的拥挤程度；DN-MMOES（two-stage double niched evolution strategy）[9]采用两阶段策略，分别在决策和目标空间中都采用小生境。此外，还设计了决策密度自适应策略来改善不平衡的决策空间密度，该算法提高了搜索能力，但该算法的某些局部最优解可能被全局最优解支配；MO-Ring-PSO-SCD（multi-objective particle swarm optimization algorithm with ring topology）[10]和MO-Ring-CSO-SCD（multi-objective competitive swarm optimization algorithm with ring topology）[11]采用环形拓扑结构形成稳定的小生境，且不需要定义小生境参数，算法能够搜索到更多的Pareto最优解，能在决策空间和目标空间中获得良好的分布；SMPSO-MM（multi-objective particle swarm optimizer with a self-organizing mechanism）[12]和MMOPIO（multimodal multi-objective pigeon-inspired optimization）[13]都引入自组织映射机制（self-organizing map, SOM），将决策空间转化到目标空间，使粒子在映射空间进行邻域搜索，有效提高了算法的搜索能力，但算法引入的SOM机制，映射机理较复杂；MOMMOP（transformation technique based on multi-objective optimization）[14]将MMOP转化为具有两个冲突目标的MOP，因此MMOP的所有最优解都转化成优化问题的Pareto最优解；Luo等[15]提出的MMOEA-CAS（evolutionary algorithm with clustering-based assisted selection strategy）在决策空间采用添加算子增加多样性，在目标空间采用删除算子删除最差解，提高了算法的搜索能力；近来，有学者为了保留更多的全局和局部Pareto最优解，提出MMOMA-DM&CS（multimodal multi-objective memetic algorithm based on a local detection mechanism and a clustering-based selection strategy）[16]算法在局部检测机制中采用了基于密度的聚类方法，帮助收集局部聚类中的解；MMOHEA（efficient two-archive model based multimodal evolutionary algorithm）[17]结合竞争粒子群和差分进化算法的策略并行生成子代解，扩展了具有不同进化需求的决策空间和目标空间，有效改善了算法搜索能力。
上述提高算法搜索能力的策略可以搜索到更多的Pareto最优解，此外通过提高决策空间的多样性也能解决多模态多目标优化问题。如TriMOEA-TA&R（multi-modal multi-objective evolutionary algorithm using two-archive and recombination strategies）[18]引入新的环境选择机制即特殊拥挤距离非支配排序法（special crowding distance, SCD）计算决策空间和目标空间的拥挤距离，建立收敛性和多样性两个档案分别处理空间的变量关系，最后还对档案中的解进行重组，实验证明该算法同时保证了决策空间和目标空间的多样性，DN_NSGAII[8]、MO_Ring_PSO_SCD[10]和MO_Ring_CSO_SCD[11]算法也同样引入了SCD方法；Yang等[19]提出EMO-DD（evolutionary multi-objective optimization algorithm with a decomposition strategy in the decision space）将整个种群分解为若干子种群对收敛程度和分布密度协同优化，从而筛选出决策空间收敛性和多样性好的解；ZLS-SMPSO-MM（multimodal multi-objective particle swarm optimization combing zoning search and local search）[20]在SOM机制前对决策空间进行处理，将决策空间分为多个子种群并用协方差矩阵自适应算法，缩短了算法的计算时间；MMODE（multimodal multi-objective Differential Evolution optimization algorithm）[21]制定决策变量预选档案，对边界解引入一个边界突变机制，提高了决策空间的多样性；此外，基于聚类的方法也可以改善多样性，如MMO-CLRPSO（cluster based PSO with leader updating mechanism and ring-topology）[22]引用一种决策变量聚类方法在决策空间形成多个子种群，子种群同时考虑到全局最优粒子和局部最优粒子进行信息交流，在探索与开发阶段实现了较好的平衡；Lin等[23]提出MMOEA/DC（novel MMOEA with dual clustering in decision and objective spaces）首先在决策空间和目标空间分别采用NCM（neighborhood-based clustering method）聚类和HCM（hierarchical clustering method）聚类方法，再选择收敛性好的解进行二次聚类，该算法同时在两空间实现了较好的性能；MMODE-CSCD（differential evolution algorithm based on the clustering technique and an elite selection mechanism）[24]将差分进化算法与聚类策略结合，采用基于聚类的特殊拥挤距离计算决策空间与目标空间的综合拥挤程度，从而提高种群分布的均匀性；MOEA-GA（multimodal multi-objective evolutionary algorithm using a density-based one-by-one update strategy）[25]采用谐波平均距离估计决策空间中解的平均密度，只允许粒子与决策空间邻域内的个体进行信息交互，并基于密度逐步更新粒子，实验证明算法提高了决策空间的多样性。
以上算法大多基于粒子群的搜索方式更新粒子的位置，而鸽群优化算法（pigeon-inspired optimization algorithm PIO）[26] 的局部搜索能力强，对求解多模态多目标优化问题有较好的性能。PIO自提出以来, 有许多文献对其进行改进研究，例如，利用反向学习策略[27]、混沌映射策略[28]初始化种群，引入高斯因子[29]、非线性变异策略[30]等。PIO虽然得到了许多改进，但对于多模态多目标优化问题的研究仍不多见。基于此，为解决多模态多目标优化问题，提高种群多样性以及寻找更多的Pareto最优解，本文引入聚类、自适应物种形成策略结合改进的鸽群算法，提出一种融合聚类和小生境搜索的多模态多目标优化算法（multimodal multi-objective pigeon-inspired optimization algorithm with clustering and searching strategy, CSSMPIO）。
1. 相关理论
1.1 多模态多目标优化
最小化多目标优化问题[2]定义如下：
$$ \begin{gathered} {\rm{min}}F({\boldsymbol{x}}) = \{ {f_1}({{x}}),{f_2}(x),\cdots,{f_m}(x)\} \\ {g_i}({\boldsymbol{x}}) \leqslant 0,i = 1,2,\cdots,k \\ {h_j}({\boldsymbol{x}}) = 0,j = 1,2,\cdots,p \\ \end{gathered} $$ (1) 式中：
$ m $ 表示待优化的目标个数，${\boldsymbol{x}} = \left[ {x_1}\;{x_2}\; \cdots\;{x_n}\right]$ 是$ n $ 维决策变量，${g_i}({\boldsymbol{x}}) \leqslant 0,$ $i = 1,2,\cdots,k$ 为$ k $ 个不等式约束，${h_j}({\boldsymbol{x}}) = 0,$ $j = 1,2,\cdots,p$ 为$ p $ 个等式约束。在多目标优化问题中，根据Pareto解的支配关系可以比较不同解的优劣，若有两个可行解
${{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2} \in {\boldsymbol{X}}$ ，对$\forall i = 1,2,\cdots,m$ ，都有${f_i}({{\boldsymbol{x}}_1}) \leqslant {f_i}({{\boldsymbol{x}}_2})$ ，则称$ {x_1} $ 支配$ {x_2} $ 。如果一个解不受任何其他解的支配，那么它就被称为非支配解，决策空间中非支配解组成的集合称为非支配解集，即PSs，Pareto最优前端（Pareto-optimal front, PF）是目标空间中与Pareto最优解对应的所有向量的集合。多模态多目标优化[31]是一种特殊的多目标优化，如果一个多目标优化问题[2]满足以下条件之一就属于多模态多目标优化问题：
1) 存在至少一个局部最优解；
2) 存在两个以上全局最优解。
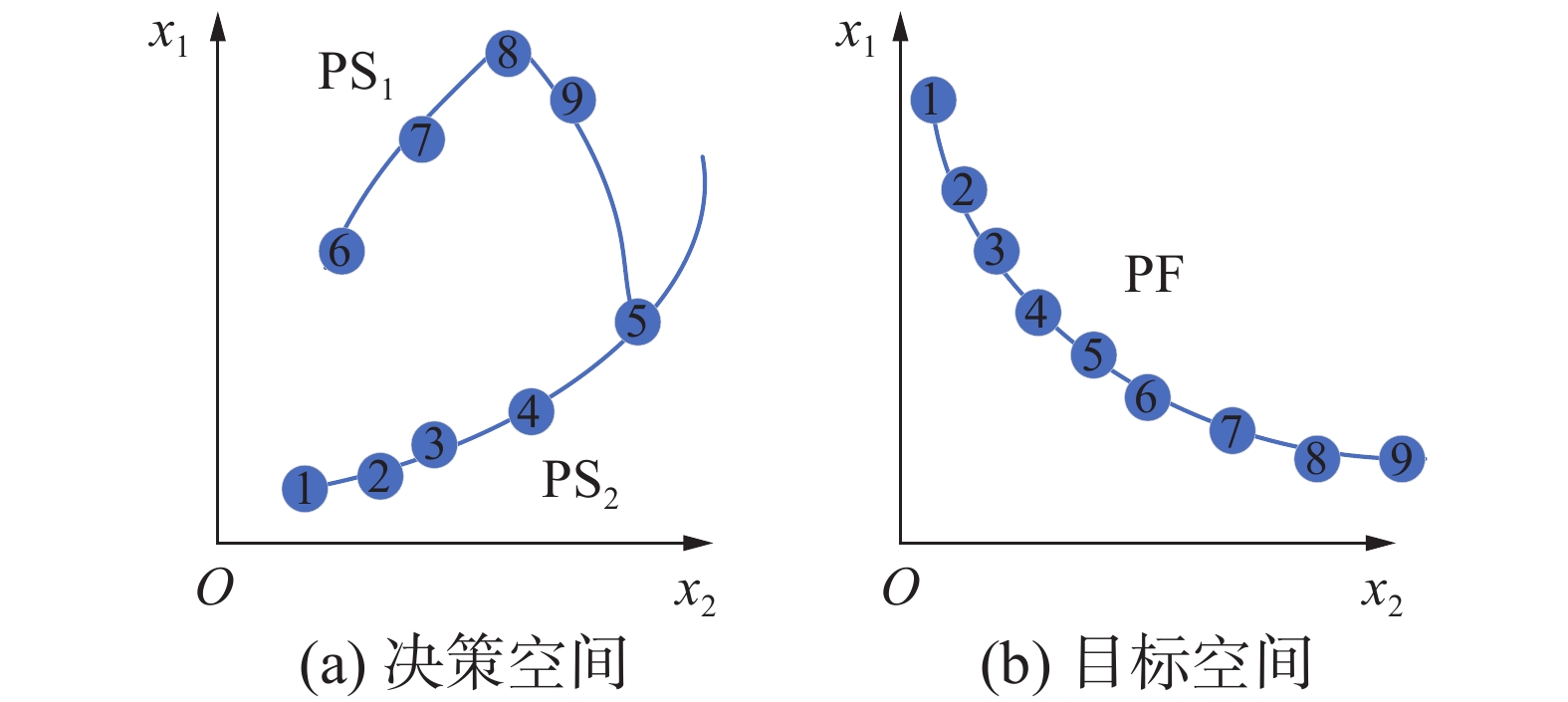
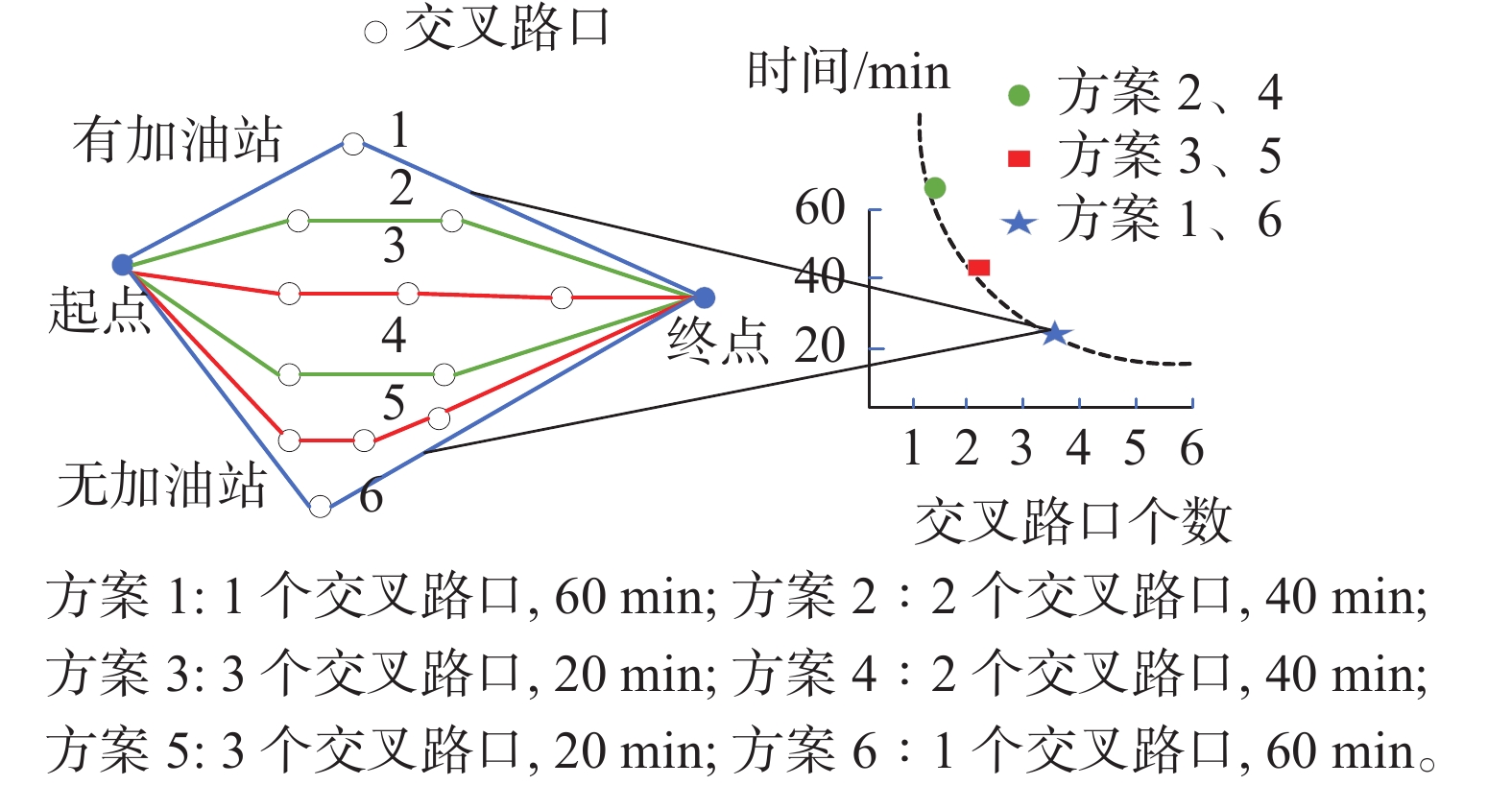
同一问题最优目标值，可能对应着多个不同的解决方案，即PF中的某一点可能对应着决策空间中至少一个局部最优解或两个以上的全局最优解。路径规划问题[22]就是典型的多模态多目标优化，如图1所示，出行者想要在最短的时间从起点到终点，方案1和方案6、方案2和方案4、方案3和方案5分别对应目标空间的同一点，各自的区别在于有无加油站以及交叉路口的个数，出行者可以根据不同的需求选择适合自己的出行路线，由此可见，仅得到一个Pareto最优解是不能满足出行者的需求的。多模态多目标问题的重点就是在保证目标空间PF优越性的同时，找到决策空间更多的PSs。
图 1 路径优化问题Fig. 1 Path planning problem
下载:
全尺寸图片
1.2 鸽群优化算法
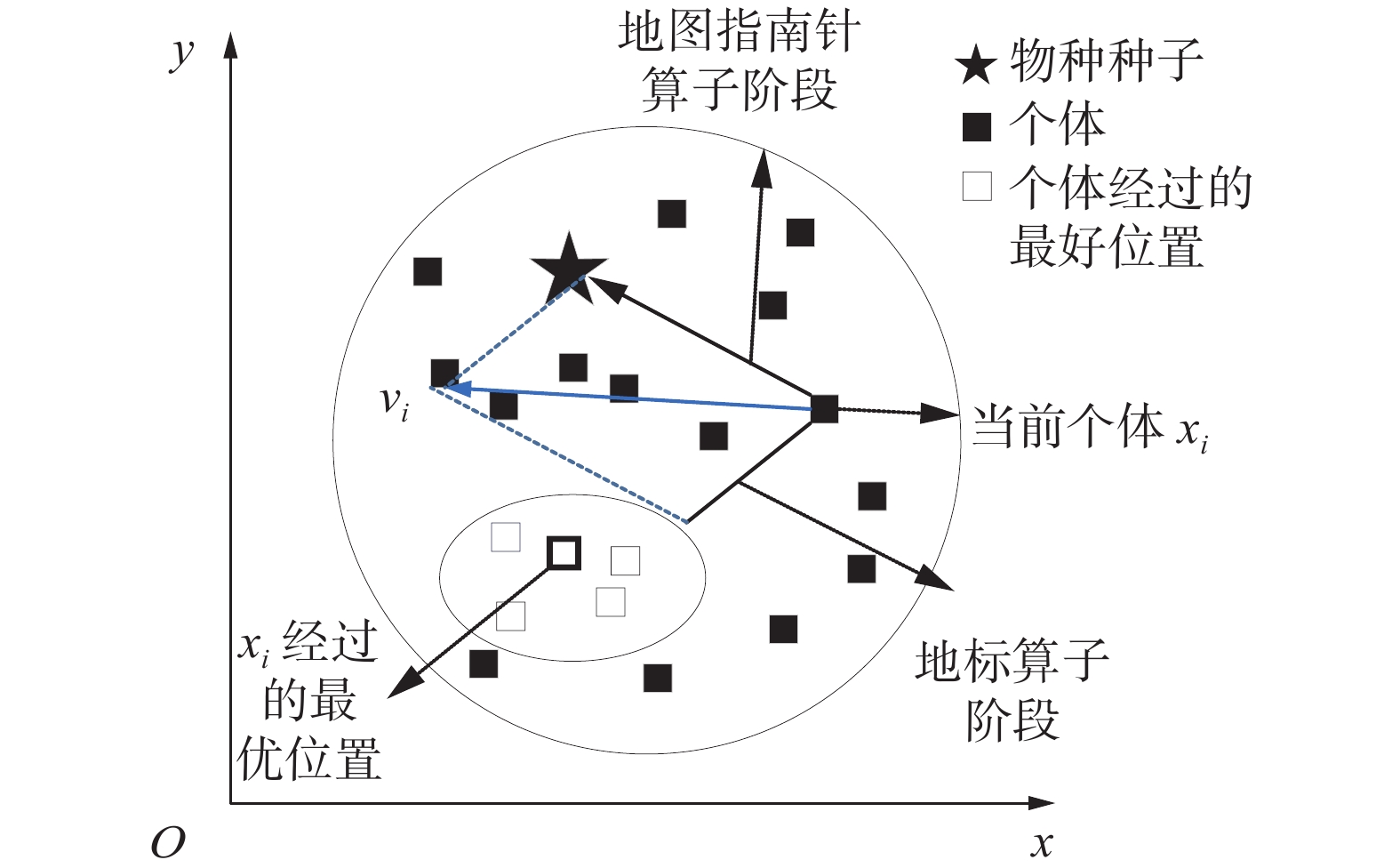
鸽群算法[26]由地图指南针算子和地标算子两阶段组成，这两个算子处于独立运行阶段，即先在地图指南针算子阶段对鸽子的位置和速度进行初始化并迭代更新，然后在地标算子阶段，每次迭代都会使鸽子数量减少一半，舍弃远离目标的鸽子，对于剩余中心位置的鸽子作为飞行参考方向。
地图指南针算子阶段（Map/compass operator）:
$$ \begin{gathered} {v_i}(t + 1) = {v_i}(t) \cdot {{\rm{e}}^{( - {R_s}\cdot t)}} + {r_{{\rm{and}}}} \cdot ({x_{{\rm{gbest}}}}(t) - {x_i}(t)), \\ i = 1,2,\cdots,N \\ \end{gathered} $$ (2) $$ {x_i}(t + 1) = {x_i}(t) + {v_i}(t + 1) $$ (3) 式中：
$ {R_s} $ 为地图指南针算子，通常取（0,1）；$ t $ 为当前迭代次数；$ {x_{{\rm{gbest}}}} $ 为全局最佳位置；$ N $ 为假设的鸽子数量；$ {r_{{\rm{and}}}}() $ 为介于（0,1）之间均匀分布的随机数。地标算子阶段（LandMark operator）：
$$ N(t + 1) = \frac{{N(t)}}{2} $$ (4) $$ {x_{{\rm{center}}}}(t + 1) = \frac{{\sum {{x_i}(t + 1)} \cdot {\rm{fitness}}({x_i}(t + 1))}}{{N \cdot \sum {{\rm{fitness}}({x_i}(t + 1))} }} $$ (5) $$ {x_i}(t + 1) = {x_i}(t) + {r_{{\rm{and}}}} \cdot ({x_{{\rm{center}}}}(t + 1) - {x_i}(t)) $$ (6) 其中
${\rm{fitness}}(x)$ 为每只鸽子的适应度值。2. 融合聚类和小生境搜索的优化 算法
本文提出融合聚类和小生境搜索的多模态多目标优化算法，称作CSSMPIO算法。主要由基于聚类的特殊拥挤距离排序和自适应物种形成多个子种群两部分组成。
2.1 聚类排序初始化种群
聚类算法将同一非支配层的解划分为多个类，同一类中的个体将来自同一局部区域。将聚类算法与特殊拥挤距离非支配排序（special crowding distance, SCD）方法[10]结合，形成基于聚类的特殊拥挤距离排序（cluster special crowding distance, CSCD）[24]方法，可以有效地解决SCD不能正确识别邻域解的问题。在CSCD中，个体的邻域解只能从同一类中识别出来。如图2（a），把解分成3类，第1类（1, 2, 3, 4, 5）第2类（6, 7, 8），第3类（9）。
图 2 多模态多目标优化问题Fig. 2 Multimodal multi-objective optimization problem下载:
全尺寸图片
以解4为例，则基于聚类的特殊拥挤距离值
${C_{{\rm{SCD}}}}_{(4)}$ 的计算公式如下：$$ {C_D}_{(4,x)} = \frac{{|{x_{3,1}} - {x_{5,1}}|}}{{|{x_{1,1}} - {x_{5,1}}|}} + \frac{{|{x_{3,2}} - {x_{5,2}}|}}{{|{x_{1,2}} - {x_{5,2}}|}} $$ (7) $$ {C_D}_{(4,y)} = \frac{{|{x_{3,1}} - {x_{5,1}}|}}{{|{x_{1,1}} - {x_{9,1}}|}} + \frac{{|{x_{3,2}} - {x_{5,2}}|}}{{|{x_{1,2}} - {x_{9,2}}|}} $$ (8) $$ \left\{\begin{split} &{C}_{{\rm{SCD}}}{}_{(4)}=\mathrm{max}({C}_{D(}{}_{4,x)},{C}_{D(}{}_{4,y)}),\\ &\qquad\quad {C}_{D(}{}_{4,x)} > {C}_{D(}{}_{{\rm{avg}},x)}或{C}_{D(}{}_{4,y)} > {C}_{D(}{}_{{\rm{avg}},f)}\\ &{C}_{{\rm{SCD}}(}{}_{4)}=\mathrm{min}({C}_{D(}{}_{4,x)},{C}_{D(}{}_{4,y)}),\\ &\qquad\quad {C}_{D(}{}_{4,x)}\leqslant {C}_{D(}{}_{{\rm{avg}},x)}或{C}_{D(}{}_{4,y)}\leqslant {C}_{D(}{}_{{\rm{avg}},f)}\end{split}\right. $$ (9) 式中：
$ {C_{D(}}_{4,x)} $ 为解4在决策空间的拥挤距离，$ {C_{D(}}_{4,y)} $ 为解4在目标空间的拥挤距离，$ {C_{D(}}_{{\rm{avg}},x)} $ 和$ {C_{D(}}_{{\rm{avg}},y)} $ 分别为决策空间和目标空间的平均拥挤距离。基于聚类的特殊拥挤距离初始化种群步骤如下：
输入 种群P
1) 种群P进行非支配排序，得到多个非支配层次，定义为F1, F2,···,
${{\boldsymbol{F}}_{{n}_{\rm{um}}}}$ （num为层数），$j = 1, 2,\cdots, {n_{{\rm{um}}}}$ 表示个体在Fj中的非支配排序；2) 计算
$ {k_j} $ 值：$ {k_j} = {{|{F_j}|} \mathord{\left/ {\vphantom {{|{F_j}|} n}} \right. } n} $ ，$ |{F_j}| $ 表示Fj中的个体数，$ n $ 为正整数；3) 根据k-means算法将Fj分成多个聚类；
4) 利用同一类内的邻域关系计算每个个体的
$ {C_{{\rm{SCD}}}} $ 值。输出 根据种群的非支配排序和
${C_{{\rm{SCD}}}}$ 值对种群P进行排序，输出一个新的种群P$ * $ 。2.2 小生境搜索过程
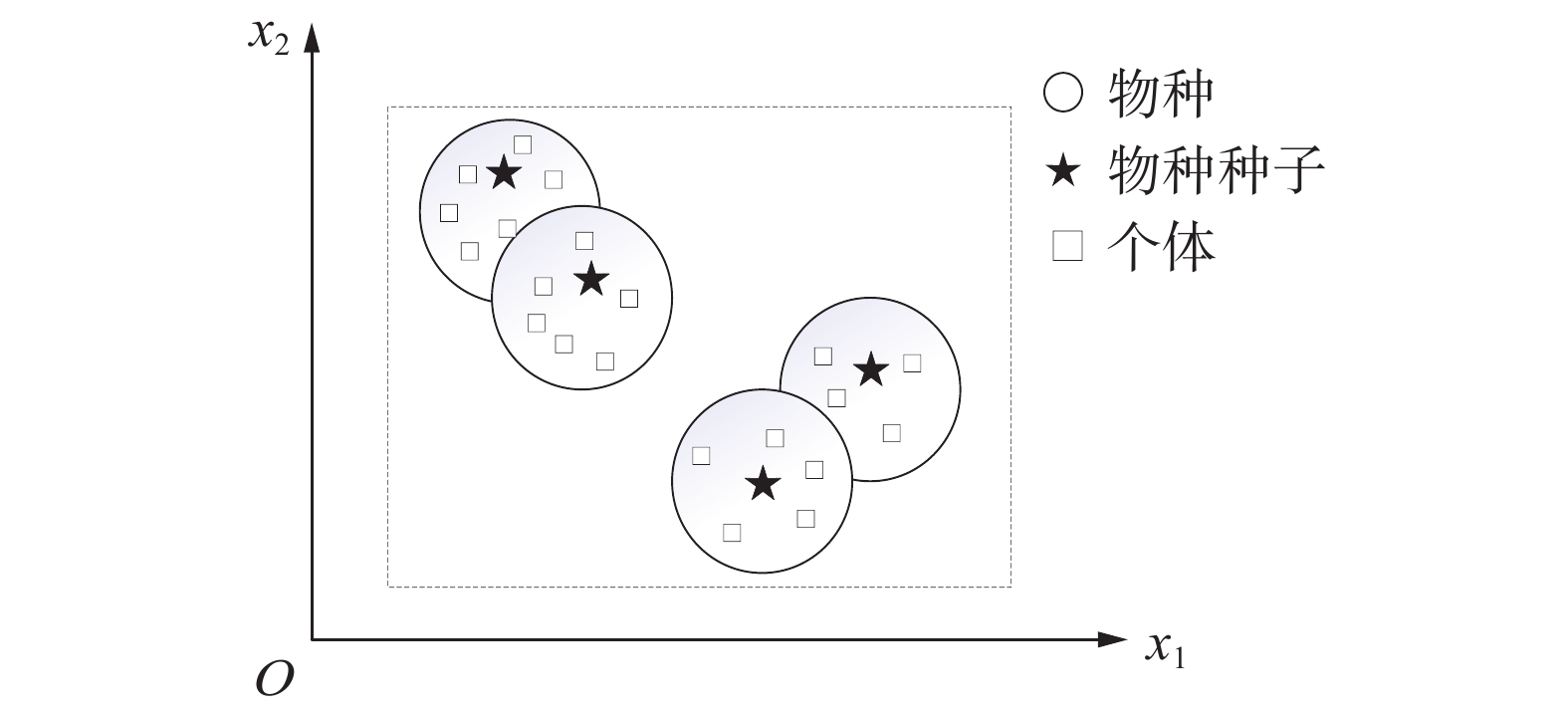
种群经过基于聚类的特殊拥挤距离排序初始化后，被分成了多个类，然后采用自适应物种形成策略生成稳定的小生境，物种形成是根据个体之间相似性将个体划分为多个子种群。如把S1, S2,···, Sk种群划分为多个子种群，个体
${{\boldsymbol{x}}^*} \in {{\boldsymbol{S}}_i}$ ，若对于个体${\boldsymbol{y}} \in {{\boldsymbol{S}}_i}$ ，都有个体$ {x^*} $ 的非支配等级高于个体$ y $ ，且个体$ {x^*} $ 到个体$ y $ 的欧氏距离$ {d_{{\rm{is}}}} $ 小于物种半径$ R $ ，则个体$ y $ 向$ {x^*} $ 学习：$$ {d_{{\rm{is}}}}({{\boldsymbol{x}}^*},{\boldsymbol{y}}) = \sqrt {{{(({{\boldsymbol{x}}^*}) - {\boldsymbol{y}})}^2}} \leqslant R $$ (10) 该定义并不意味着如果一个物种Si以非支配个体
$ {x^*} $ 为中心，则$ {x^*} $ 的物种半径范围内的所有个体都属于该物种。如图3所示，一个占优势的个体可能会支配多个物种内的个体。
图 3 物种在二维区域的分布Fig. 3 Distribution of species in a two-dimensional region下载:
全尺寸图片
自适应物种形成中，物种种子经过特殊拥挤距离排序选择后，直接根据物种半径确定其物种内所包含的个体。若个体同时在两个物种种子的物种半径内，则由非支配等级更高的物种种子支配该个体。其主要步骤如下：
1) 种群进行基于聚类的非支配特殊拥挤距离升序排序，输出新种群，存储到spop中；
2) 将NPspop作为spop中集合的数目，spop中的第一个个体记为物种种子
${x_{{\rm{species}}{\text{ }}{\rm{seed}}}}_{(j)}$ ；3) 获得物种种子
$ {x_{{\rm{species}}{\text{ }}{\rm{seed}}}}_{(j)} $ 后，迭代更新形成互不重叠的物种；4) 当NPspop≠0时，执行以下操作：
计算
${x_{{\rm{species}}{\text{ }}{\rm{seed}}}}_{(j)}$ 与${s_{{\rm{pop}}}}_{(j)}$ 的欧氏距离；若${d_{{\rm{is}}}} \leqslant R$ ，则个体$ i $ 位于该物种；同时清除spop中已经分配给第$ j $ 个物种种子的个体，spop得到更新。输出 更新后的多个子种群。
2.3 改进的位置更新策略
为平衡个体的探索与开发过程，受多目标鸽群启发算法（multi-objective pigeon-inspired optimization algorithm, MPIO）[32]的影响，结合粒子群优化算法，将地图指南针算子和地标算子结合起来，个体在每个子种群的位置更新如图4。
图 4 单个物种中个体位置更新方式Fig. 4 Individual position updating in a single species下载:
全尺寸图片
个体的速度更新公式如下：
$$ \begin{gathered} {v_i}(t + 1) = {v_i}(t) \cdot {i_{{\rm{wt}}}} + \left(1 - \log \left(\dfrac{t}{T}\right)\right) \cdot {r_{{\rm{and}}}} \cdot ({x_{{\rm{speciesseed}},i}}(t) - \\{x_i}(t)) + \log \left(\frac{t}{T}\right) \cdot {r_{{\rm{and}}}} \cdot ({x_{{\rm{center}}}}(t) - {x_i}(t)) \end{gathered} $$ (11) $$ {i_{{\rm{wt}}}} = {w_{{\rm{max}}}} + ({w_{{\rm{min}}}} - {w_{{\rm{max}}}}) \cdot \frac{{T - t}}{T} + {w_{{\rm{min}}}} $$ (12) 式中：wmax与wmin分别表示惯性权重的最大最小值；xspeciesseed为物种种子；rand为0~1之间的随机数；xcenter表示鸽群中心坐标位置；T为最大迭代次数；iwt为非线性惯性权重。
为了保留更多的解，对最优解执行精英学习策略，避免早熟收敛，公式如下：
$$ {x_i}(t + 1) = {x_{{\rm{species}}{\text{ }}{\rm{seed}},i}}(t) + \left({u_{{\rm{b}}(i)}} - {l_{{\rm{b}}(i)}}\right)\cdot{\rm{Guass}}(0,{p_r}^2) $$ (13) $$ {p_{\rm{r}}} = {p_{\rm{r}}}0 - \frac{{({p_{\rm{r}}}0(1) - {p_{\rm{r}}}0(2)) \cdot 2}}{T} $$ (14) 式中：
$ {u_{\rm{b}}} $ 、$ {l_{\rm{b}}} $ 分别为变量的上下界；$ {\rm{Guass}}(0,{p_{\rm{r}}}^2) $ 为均值为0，标准差为$ {p_{\rm{r}}} $ 的高斯分布，$ {p_{\rm{r}}}0 $ 值从0.2线性下降到0.05。进化初期，较大的变异范围有利于算法的全局搜索，随着迭代的进行，算法需要在局部范围找到更精确的解，因此小的变异范围更适合。2.4 CSSMPIO算法流程
输入 种群规模Popsize；最大评估次数MaxGen；鸽群参数：wmax、wmin；变异算子pr0；外部存档集Pachive；
1) 初始化个体的速度和位置，记为POA，并评估POA；
2) 种群P=POA；
3) 当迭代t≤MaxGen时，执行以下操作：
种群P执行2.2节操作，输出新种群P
$* $ ；对新种群P$* $ 执行步骤2.3节操作；4) 更新个体的位置和速度，步骤如下：
选出pbest和
$ {x_{{\rm{species}}{\text{ }}{\rm{seed}}}}_{(j)} $ ；pbest为种群P中的最优个体，$ {x_{{\rm{species}}{\text{ }}{\rm{seed}}}}_{(j)} $ 物种中的最优个体；对pbest进行非支配排序，依据式(5)将其转换成$ {x_{{\rm{center}}}} $ ；依据式(11)、(3)更新个体的速度和位置，式(13)对子代执行精英学习策略，更新P$* $ ；对更新后的P$ * $ 进行评估；将P$* $ 放入POA中，对POA中的个体进行排序；5）当前迭代次数满足t>MaxGen时，结束循环，否则返回3）。
输出 PS，PF。
在CSSMPIO中，聚类排序首先对粒子进行初始化，然后采用自适应物种形成策略在决策空间生成稳定的小生境子种群，鸽群算法的局部搜索能力强，因此可以增强子种群的局部搜索能力，在决策空间中搜索到大量的PSs，最后再引入精英学习策略，对子种群中的最优解进行变异，避免早熟收敛。
2.5 CSSMPIO时间复杂度分析
CSSMPIO算法的主要时间成本来源于基于聚类的特殊拥挤距离排序初始化种群和自适应物种形成策略两部分组成。设种群规模为N，目标维数为M。基于聚类的特殊拥挤距离排序初始化种群时间复杂度为O(N)。自适应物种形成策略中假设有N个个体被排序并存储在spop中，其大小为NPspop，for循环NPspop次，以查看该个体是否在当前种子的半径
$ R $ 内。最好的情况是，所有的个体都在第一个种子的物种半径中，因此for循环只执行了N次。在最坏的情况下，当所有N个个体都是N个独立物种的种子时，for循环执行$ {{N(N + 1)} \mathord{\left/ {\vphantom {{N(N + 1)} 2}} \right. } 2} $ 次。表明该过程的复杂度最高为O(N2)。并且自适应物种形成过程中，已分配给某些物种的个体被从种群中移除，种群中剩余的个体不再计算与之前物种种子的欧氏距离。因此，其复杂度仅依赖于N，计算次数在物种形成过程中迅速减少。因此，CSSMPIO最坏的时间复杂度为O(MN3)。3. 实验结果与分析
3.1 评价指标
多模态多目标优化问题既要求目标空间的分布性能良好，又要保证找到决策空间更多的等价PSs，因此本文采用了以下评价指标对所提算法进行评价。
1) PSP （Pareto set proximity）[31]：
$$ {{P}}_{{{\rm{PS}}}} = \frac{{{{R}_{\rm{c}}}}}{{x_{{{\rm{IGD}}}}}} $$ (15) 式中：Rc（cover rate, CR）表示算法求得的PSs对真实PSs的覆盖率；xIGD为求得的PSs与真实PSs之间的欧氏距离IGDx，因此PSP反映的是真实PSs与获得的PSs之间的相似性，PSP越大算法性能越好。
2) IGDx[31]：
$$ x_{\rm{IGD}}(O,{P^ * }) = \frac{{\displaystyle\sum_{v \in {P^ * }}{d_{(v,O}}_)} }{{|{P^ * }|}} $$ (16) 式中：
$ |{P^*}| $ 表示参考点的数目，$ O $ 表示一组已得到的解，$ {d_{(v,O)}} $ 表示$ v $ 和$ O $ 中所有点之间最小的欧氏距离。如果参考解集能很好地表示真实PSs，那么IGDx就能较好地衡量决策空间的收敛性和多样性。IGDx的值越小，说明算法求得的PSs和实际PSs越接近。3.2 实验设置
为进一步验证所提算法的性能，将CSSMPIO算法与自适应物种形成粒子群优化算法SS_MOPSO[7]、基于决策空间小生境算法DN_NSGAII[8]、基于环形拓扑结构的多模态多目标粒子群优化算法MO-Ring-PSO-SCD（MRPS）[10]、自组织多模态多目标粒子群优化算法SMOPSO-MM[12]、自组织多模态多目标鸽群优化算法 MMOPIO[13]、基于双存档模型的高效混合进化多模态多目标优化算法MMOHEA[17]算法和多目标优化算法MOEAD[33]进行对比实验研究。所有算法的最大评估次数为80000次，种群规模为800，算法在每个测试函数上运行20次，算法参数设置如表1。
表 1 算法的参数设置Table 1 Parameters setting of algorithms算法 参数 CSSMPIO $R = {1 \mathord{\left/ { {1 {20 {{V} }_{{R} };k = 10;{c_1} = {c_2} = 2.05} } } \right. } }$ MMOHEA[17] ${{c} }_{{r} } = 0.9;F = 0.5$ MRPS[10] ${c_1} = {c_2} = 2.05;w = 0.729\;8$ MMOPIO[13] $\lambda = 7;{{R} }_{{s} } = 0.3$ SMOPSO-MM[12] ${c_1} = {c_2} = 2.05;w = 0.729\;8$
拓扑结构= $1 \times 100;\eta_0=0.7$；
$\sigma_0=\dfrac{ {\rm{sqrt} }\left({1}^{2}+{100}^{2}\right)}{2}$SS_MOPSO[7] $R = {1 \mathord{\left/ { {1 {20 {{V} }_{{R} } } } } \right. } };w = 0.729\;8;{c_1} = {c_2} = 2.05$ DN_NSGAII[8] ${{C} }_{{F} } = 0.5;{\eta _c} = {\eta _m} = 20;{p_c} = 1;{p_m} = {1 \mathord{\left/ {\vphantom {1 n} } \right. } n}$ MOEAD[33] $ {p_m} = 0.5;{\eta _m} = 20 $ 选取14个多模态多目标问题[31]进行测试。其中，8个MMF函数[10]、3个SYM-PART函数[34]、3个OMNI函数[35]。所有优化问题的目标个数均为2，MMF函数与SYM-PART函数的空间维度为2，OMNI函数的空间维度分别为3、4、5。一般来说，在每个维度上PSs重叠的测试函数比没有重叠的测试函数更复杂，此外，当一个函数的PSs数目较多时，它也会变得更加复杂。MMF1和MMF2是相对简单的测试函数，MMF3比MMF1和MMF2复杂。MMF4和MMF8与表中其他测试函数相比，PF是凹的，它们有4个PSs，每个维度都不重叠。MMF6有4个PSs，它们在每个维度上重叠，MMF7的PSs呈不规则曲线。SYM-PART2测试函数是由SYM-PART1旋转生成的，因此比SYM-PART1更复杂。在SYM-PART函数中，PSs的数量都是9个。Omni-test中PSs的数量最多，分别为27、72、360，而且每个维数都有重叠。因此，Omni-test是14个测试函数中最复杂的。测试系数特征如表2。
表 2 测试函数特征Table 2 The characteristics of test problems函数名称 PSs的数量 每个维度的重叠 MMF1 2 × MMF2 2 × MMF3 2 √ MMF4 4 × MMF5 4 × MMF6 4 √ MMF7 2 × MMF8 4 × SYM-PART 9 √ Omni-test1 27 √ Omni-test2 72 √ Omni-test3 360 √ 3.2.1 种群规模popsize分析
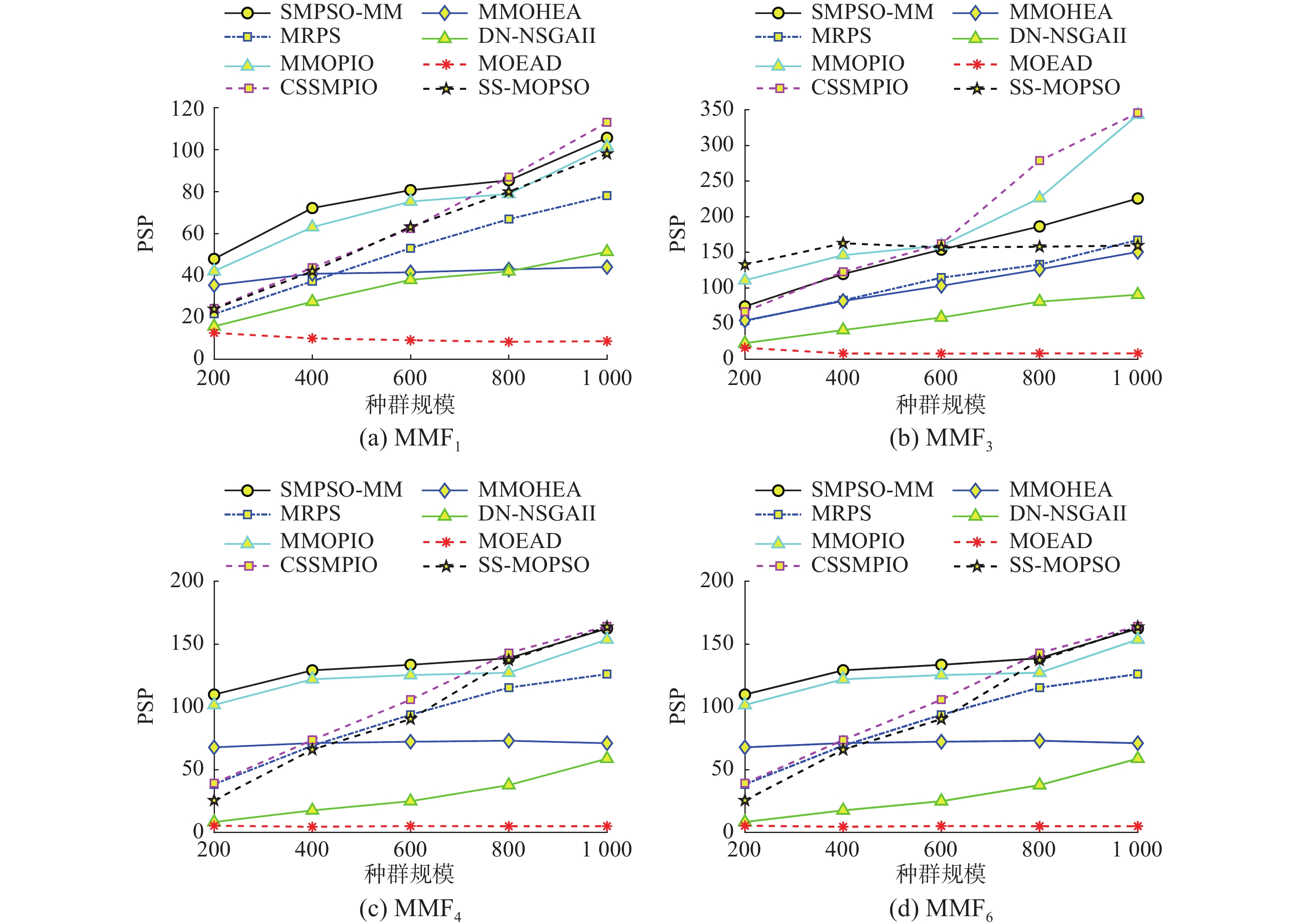
在本节中，分析种群规模popsize对算法性能PSP的影响，由于MMF1、MMF3、MMF4和MMF6这4个测试函数的PSs的数量以及维度重叠是不同的，因此对比算法性能在该4个测试函数上随种群规模的变化情况，并将种群规模设置为200、400、600、800、1000，其他参数设置如表1。
实验结果如图5所示，可以看出，MOEAD作为多目标优化算法，种群规模的改变对算法性能没有多大的影响。虽然DN_NSGAII的PSP值较低，但算法性能随种群规模的增大而增大。MMOHEA仅在MMF3上算法性能随种群规模有所改变，这是因为MMF3的测试函数复杂，且PSs的曲线更加平滑。MMF3测试函数中，除SS-MOPSO算法，算法性能都随种群规模的增大而增大，在种群规模小于600时，SS_MOPSO性能最好，但当种群规模高于600时，算法性能几乎不变。除以上算法，其他算法性能都随种群规模的增大而变化，由于MMOPIO和SMPSO_MM采用SOM机制来获得更好的解集，所以在种群规模小于800时，MMOPIO和SMPSO_MM性能优于CSSMPIO，MRPS算法性能变化明显，且一直低于CSSMPIO。
图 5 不同种群规模的PSP值Fig. 5 PSP values with different population sizes下载:
全尺寸图片
综合来看CSSMPIO的性能随种群规模的变化更优于对比算法，并且所有算法性能在不同的测试函数上大都受种群规模的影响，在计算资源有限的情况下，所提算法的种群规模仍设置为800。
3.2.2 物种半径R分析
自适应物种形成策略生成小生境子空间，其中物种半径确定子种群的大小，物种半径的大小对算法的性能有一定的影响，一般情况下，物种半径设置为决策变量范围的1/20~1/10，因此本小节验证在不同测试函数上算法性能随物种半径变化情况。本实验选定MMF2、MMF5、SYM-PART1和Omni-test1测试函数分析不同物种半径对CSSMPIO性能的影响，10次实验的平均PSP值如图6，其他参数设置同表1。图中显示，测试函数的PSP值都随物种半径的增大而减小，这是因为随着物种半径的增大，决策空间中形成的物种数量减少。此外，与SYM-PART1和Omni-test1相比，随着半径的增加，MMF2、SYM-PART1和Omni-test1的PSP值显示出较小的变化。产生这种现象的原因是测试函数决策变量变化范围小，因此半径的变化很小，这对算法的性能影响很小。因此将物种半径设置为决策变量范围的1/20时，CSSMPIO可以找到决策空间更多Pareto解集，提高决策空间的种群多样性。
图 6 不同物种半径的PSP值Fig. 6 PSP values with different radius下载:
全尺寸图片
3.2.3 聚类数目k分析
在所提算法中，初始化种群中聚类数目
$ k $ 值的确定也会影响算法的性能。如2.1小节所示，$ k = {{|{F_j}|} \mathord{\left/ {\vphantom {{|{F_j}|} n}} \right. } n} $ ，$ |{F_j}| $ 表示Fj中的个体数，$ n $ 为正整数，可以看出，参数$ n $ 间接决定了$ k $ 的值，当$ n $ 较大时，$ k $ 越小。本小节验证不同$ n $ 值[24]对算法性能的影响，参数设置如表1，实验结果如表3。从表3可以看出，大多数测试函数在$ n $ =10时，算法性能最好，尤其是表现在复杂函数中。即使$ n $ =10时MMF2和MMF8函数的PSP值不是最高的，但与表现最好的也相差不大。由于一个解和它的邻域解应来自同一局部区域，所以参数$ n $ 越小越好，但如果同一类中解的个数过少，则会影响边界解的CSCD值。综合考虑，取参数$ n $ =10。表 3 CSSMPIO使用不同参数$n $ 获得的PSP值Table 3 PSP values obtained by CSSMPIO with different$n $ values测试问题 $ n = 5 $ $ n = 10 $ $ n = 15 $ $ n = 20 $ MMF1 79.97±2.39 83.19±2.24 82.68±2.87 77.75±3.29 MMF2 274.14±63.78 275.76±37.53 282.44±51.37 268.65±57.27 MMF3 298.12±84.37 305.08±29.13 272.72±36.95 273.78±43.89 MMF4 128.64±6.05 132.78±7.88 116.78±10.28 110.12±11.95 MMF5 39.22±1.35 43.11±1.35 40.99±0.83 34.49±1.11 MMF6 38.77±1.85 41.60±1.77 40.16±1.73 39.80±1.09 MMF7 110.29±7.81 113.60±5.99 102.62±8.65 110.38±6.87 MMF8 60.59±2.45 57.55±3.21 53.24±5.22 57.62±2.32 SYM-PART1 42.71±3.73 52.01±3.58 42.85±1.97 42.29±3.53 Omni-test1 10.39±1.24 11.73±1.25 5.64±2.73 8.10±2.60 3.3 实验结果与对比
3.3.1 PSP指标对比实验和分析
CSSMPIO与其他比较算法所得的PSP值的平均值与标准方差的统计结果如表4所示，其中最佳结果被突出显示。同时，采用Wilcoxon秩和检验[36]表明CSSMPIO的结果与其他比较算法在0.05显著水平上的差异性，“+”“−”和“=”分别表示比较算法与CSSMPIO相比体现出明显优越、明显差、没有显著差异的性能。从表4可以看出，CSSMPIO取得的PSP最优值数量为8个，SMPSO_MM取得的最优值数量为3个，SS_MOPSO求得的最优值数量为3个。CSSMPIO在14个测试函数上的PSP结果显著优于MOEAD和DN_NSGAII。MOEAD是典型的多目标算法，对于求解多模态多目标测试函数的效果最差。DN_NSGAII在所有函数上的性能表现都较差，这是因为DN_NSGAII只考虑了决策空间的拥挤距离，而忽略了目标空间。MMOHEA算法在Omni-test测试函数上的性能较好，虽然在其他测试函数上PSP性能较差，但是算法运行所需的时间较短，并且算法性能比较稳定。而MRPS性能略低的原因在于仅考虑了环形拓扑邻域结构，没有进行非支配特殊拥挤距离排序，在决策空间的解分布不够均匀。SMPSO_MM和MMOPIO采用SOM机制来建立粒子的邻域，使其更适合求解较复杂的问题。在SS_MOPSO中，不同物种重叠粒子的分配仅取决于物种种子的非支配等级，粒子会向非支配等级更高的物种种子学习，这会影响种群的多样性，得到的PSs是不完整、不均匀的。
表 4 所有算法得到的PSP平均值与标准方差Table 4 Mean and standard variance of PSP obtained by all algorithms测试
问题mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SS_MOPSO MMOHEA CSSMPIO MMF1 41.88±2.80
(−)8.02±4.89
(−)67.05±3.12
(−)85.34±2.34
(=)73.83±2.78
(−)83.11±3.27
(−)42.78±1.43
(−)86.86±4.15 MMF2 61.55±33.31
(−)4.62±3.24
(−)107.53±11.92
(−)152.69±15.35
(−)167.78±45.24
(−)163.28±18.06
(−)116.75±16.14
(−)277.15±34.30 MMF3 75.11±28.88
(−)7.00±3.79
(−)128.63±17.06
(−)186.24±15.19
(−)226.06±32.79
(−)189.94±12.67
(−)125.96±16.67
(−)305.44±24.93 MMF4 38.45±8.59
(−)1.93±0.97
(−)114.51±3.29
(−)132.78±3.82
(−)120.15±3.91
(−)139.40±3.49
(+)73.03±3.99
(−)135.90±5.95 MMF5 14.57±1.47
(−)3.35±1.35
(−)33.11±1.35
(−)40.12± 1.33
(−)30.24±1.46
(−)40.11±1.19
(−)22.21±0.41
(−)43.62±1.50 MMF6 18.89±1.37
(−)4.97±2.37
(−)36.44±1.59
(−)42.42±1.08
(=)36.23±1.99
(−)42.19±1.29
(=)24.16±0.59
(−)41.74±1.39 MMF7 95.55±17.79
(−)7.49±4.78
(−)108.77±3.89
(−)141.13±5.14
(+)136.49±4.78
(+)123.73±6.27
(+)78.05±2.87
(−)119.82±6.11 MMF8 18.01±5.89
(−)0.25±0.12
(−)47.64±2.22
(−)62.53±2.34
(+)54.78±7.12
(−)59.34±22.39
(=)33.78±3.40
(−)58.38±2.76 SYM-PART1 0.44±0.59
(−)0.01±0.01
(−)21.95±1.67
(−)30.37±2.77
(−)59.97±0.24
(+)34.50±1.30
(−)31.22±1.48
(−)52.01±3.58 SYM-PART2 3.07±4.00
(−)0.01±0.01
(−)18.73±0.94
(−)16.88 ±1.33
(−)43.18±3.16
(−)30.77±1.19
(−)31.82±0.70
(−)47.08±3.79 SYM-PART3 5.57±9.97
(−)0.01±0.01
(−)9.37±2.19
(−)15.78±2.80
(−)41.15±1.78
(−)28.17±2.45
(−)11.34±2.34
(−)56.94±2.78 Omni-test1 1.16±0.23
(−)0.03±0.01
(−)8.04±1.06
(−)7.69±1.48
(−)1.15±0.08
(−)11.75±1.10
(−)12.09±0.54
(=)12.15±2.23 Omni-test2 0.44±0.08
(−)0.03±0.01
(−)0.98±0.07
(=)0.95±0.07
(=)0.95±0.04
(−)1.46±0.05
(+)1.01±0.00
(=)0.99±0.07 Omni-test3 0.28±0.09
(−)0.02±0.01
(−)0.51±0.02
(+)0.49±0.02
(+)0.50±0.01
(+)0.58±0.02
(+)0.47±0.01
(=)0.46±0.02 +/=/− 0/0/14 0/0/14 1/1/12 3/3/8 3/0/11 4/2/8 0/3/11 — 此外，CSSMPIO对MMF2、MMF3、MMF4、SYM-PART与Omni-test1测试函数的性能显著优越，尤其是对SYM-PART和MMF8测试函数，CR值达到1.0，这意味着求得的PSs全部覆盖了真实PSs。CSSMPIO与SMPSO_MM在MMF1、MMF5和MMF6上的结果相近，这是因为算法在决策空间表现相似，而CSSMPIO在MMF7表现较差的原因是MMF7的PSs的分布呈不规则曲线。由于鸽群算法的局部搜索能力强，CSSMPIO与MMOPIO都适于求解SYM-PART测试函数，并且对于多个PSs的Omni-test测试函数CSSMPIO也表现较好。
表5反映了CSSMPIO与对比算法的HV值，HV反映了目标空间的收敛性和多样性[31]。从表5可以看出，CSSMPIO在MMF5、SYM-PART2和SYM-PART3测试函数上的HV最高；DN_NSGAII和MOEAD的HV大都表现较好，原因是这两个算法都是多目标算法，考虑了目标空间而未考虑决策空间。虽然CSSMPIO与其他算法相比没有表现出最佳HV，但从统计结果来看，结果相差不大。综合来讲CSSMPIO不仅在决策空间有较好的收敛性和多样性，而且也考虑到在目标空间的分布。
表 5 所有算法得到的HV平均值与标准方差Table 5 The mean and standard variance of HV obtained by all algorithms测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SS_MOPSO MMOHEA CSSMPIO MMF1 3.66±1.30×10−3 3.67±4.79×10−4 3.66±4.63×10−4 3.67±3.99×10−4 3.66±2.84×10−4 3.66±4.55×10−4 3.66±5.40×10−4 3.66±1.31×10−4 MMF2 3.66±6.20×10−3 3.67±5.34×10−4 3.65±8.10×10−3 3.66±4.16×10−3 3.65±2.07×10−3 3.66±4.20×10−3 3.65±4.80×10−3 3.66±4.02×10−4 MMF3 3.66±4.90×10−3 3.67±7.72×10−4 3.65±5.10×10−3 3.66±3.34×10−3 3.66±1.41×10−3 3.66±3.28×10−3 3.66±2.25×10−3 3.66±1.96×10−3 MMF4 3.33±3.60×10−4 3.33±1.63×10−4 3.33±1.20×10−3 3.33±8.88×10−4 3.33±3.88×10−4 3.33±8.45×10−4 3.33±1.34×10−4 3.33±3.14×10−4 MMF5 3.67±2.70×10−3 3.67±6.81×10−4 3.66±3.52×10−4 3.66±4.89×10−4 3.66±6.98×10−5 3.67±3.03×10−4 3.66±3.72×10−4 3.67±3.10×10−4 MMF6 3.66±1.10×10−3 3.67±5.53×10−4 3.66±3.31×10−4 3.66±3.74×10−4 3.66±3.19×10−4 3.66±3.19×10−4 3.66±3.24×10−4 3.66±3.24×10−4 MMF7 3.66±7.10×10−4 3.67±2.39×10−4 3.67±2.38×10−4 3.66±3.00×10−4 3.66±6.24×10−4 3.66±2.88×10−4 3.66±3.61×10−4 3.66±4.16×10−4 MMF8 3.21±1.30×10−3 3.21±1.44×10−4 3.21±1.50×10−4 3.21±1.58×10−4 3.21±4.14×10−5 3.21±7.30×10−4 3.21±3.99×10−4 3.21±7.30×10−4 SYM-PART1 1.32±3.09×10−4 1.32±8.35×10−5 1.30±1.90×10−4 1.27±4.86×10−3 1.32±8.20×10−5 1.32±8.30×10−4 1.31±7.72×10−4 1.32±2.29×10−4 SYM-PART2 1.32±4.92×10−4 1.32±6.85×10−4 1.29±2.20×10−3 1.27±4.39×10−3 1.32±5.16×10−4 1.31±1.12×10−3 1.31±1.02×10−3 1.32±4.26×10−4 SYM-PART3 1.32±5.00×10−4 1.32±1.40×10−3 1.29±2.50×10−3 1.25±6.48×10−3 1.31±2.04×10−3 1.31±2.04×10−3 1.30±1.88×10−3 1.26±6.60×10−3 Omni-test1 62.06±3.98×10−4 62.06±4.80×10−3 61.97±1.24×10−2 61.95±1.56×10−2 61.99±5.33×10−3 62.02±5.33×10−3 61.01±1.81×10−2 62.06±2.16×10−4 Omni-test2 77.54±2.10×10−3 77.53±9.80×10−3 77.03±8.52×10−2 76.84±1.09×10−1 77.49±1.35×10−2 77.35±2.53×10−2 77.01±1.34×10−1 77.39±4.98×10−2 Omni-test3 94.59±8.80×10−3 94.55±2.42×10−2 92.88±2.72×10−1 92.29±3.06×10−1 94.31±6.65×10−1 93.86±1.08×10−1 92.61±2.41×10−1 93.78±2.11×10−1 3.3.2 IGDx指标对比实验和分析
CSSMPIO与其他比较算法所得的IGDx值的平均值和标准方差见表6。同时， Wilcoxon得到的统计分析结果也在表6中显示。从表中可以看出，相比于MOEAD和DN_NSGAII，CSSMPIO在14个测试函数上都表现出了较好的性能。CSSMPIO在MMF1、MMF5和MMF6测试函数上的IGDx值与SMPSO_MM算法相比没有显著差异。CSSMPIO在规则曲线测试函数MMF2和MMF3上的IGDx值较小，说明在这两个测试函数上获得的PSs与真实PSs值的欧氏距离较小，算法求得的解集和参考解集越接近。在MMF4上，SMPSO_MM取得了较好的效果，由于MMF7和MMF8的解分布为不规则的曲线，而SOM映射网络适于求解此类问题，所以SMPSO_MM和MMOPIO求得的解集和参考解集更接近。在更复杂、空间维度更高的测试函数SYM-PART与Omni-test上的性能指标表示，CSSMPIO却取得了更好的结果，这意味着更接近真正的PSs。并且MMF1、MMF4、MMF5、MMF7和MMF8是除MMF6之外在每个维度上没有重叠的简单测试函数，从结果中可以看出，CSSMPIO对求解复杂的测试函数效果更优越一些。
表 6 所有算法得到的IGDx平均值与标准方差Table 6 Mean and standard variance of IGDx obtained by all algorithms测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SSMOPSO MMOHEA CSSMPIO MMF1 0.0237±
0.0033(−)0.1503±
0.0685(−)0.0149±
0.0007(−)0.0117±
0.0003(=)0.0129±
0.0003(−)0.0119±
0.0005(−)0.0233±
1.4303(−)0.0115±
0.0005MMF2 0.0223±
0.0150(−)0.2645±
0.1163(−)0.0092±
0.0010(−)0.0065±
0.0007(−)0.0056±
0.0006(−)0.0061±
0.0006(−)0.0085±
0.0012(−)0.0043±
0.0006MMF3 0.0166±
0.0071(−)0.1378±
0.0467(−)0.0072±
0.0010(−)0.0053±
0.0005(−)0.0056±
0.0001(−)0.0059±
0.0010(−)0.0079±
0.0011(−)0.0049±
0.0007MMF4 0.0268±
0.0063(−)0.4262±
0.1235(−)0.0087±
0.0003(−)0.0053±
0.0005(+)0.0083±
0.0003(−)0.0076±
0.0003(−)0.0136±
0.0007(−)0.0071±
0.0003MMF5 0.0689±
0.0071(−)0.2985±
0.1263(−)0.0302±
0.0013(−)0.0246±
0.0009(=)0.0331±
0.0016(−)0.0248±
0.0007(=)0.0448±
0.0007(−)0.0250±
0.0008MMF6 0.0109±
0.0024(−)0.2045±
0.0708(−)0.0275±
0.0012(−)0.0238±
0.0006(=)0.0286±
0.0016(−)0.0235±
0.0008(+)0.0412±
0.0010(−)0.0239±
0.0008MMF7 0.0643±
0.0352(−)0.1522±
0.0662(−)0.0092±
0.0003(−)0.0071±
0.0003(+)0.0072±
0.0003(+)0.0081±
0.0004(=)0.0128±
0.0004(−)0.0081±
0.0004续表 6 测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SSMOPSO MMOHEA CSSMPIO MMF8 3.0256±
1.0730(−)2.7114±
0.5862(−)0.0210±
0.0010(−)0.0160±
0.0006(+)0.0174±
0.0009(=)0.0167±
0.0006(+)0.0298±
0.0034(−)0.0174±
0.0008SYM-PART1 1.0513±
0.8300(−)12.6877±
2.7300(−)0.0458±
0.0035(−)0.0323±
0.0003(−)0.0167±
0.2402(+)0.0290±
0.0061(−)0.0321±
0.0015(−)0.0193±
0.0013SYM-PART2 0.9538±
0.0756(−)12.7889±
2.4800(−)0.0533±
0.0028(−)0.0597±
0.0005(−)0.0231±
0.0015(−)0.0326±
0.0105(−)0.0314±
0.0006(−)0.0213±
0.0017SYM-PART3 0.9556±
0.7563(−)10.3697±
2.4900(−)0.1094±
0.0241(−)0.0651±
0.0133(−)0.0241±
0.0089(−)0.0357±
0.0042(−)0.0842±
0.0167(−)0.0123±
0.0007Omni-test1 0.8899±
0.1652(−)3.4183±
0.4137(−)1.2623±
0.0212(−)0.1345±
0.0316(−)0.8706±
0.0618(−)0.0810±
0.0274(−)0.0824±
0.0038(−)0.0786±
0.0181Omni-test2 2.1976±
0.2923(−)3.9763±
0.4832(−)1.0132±
0.0651(−)1.0473±
0.0762(−)0.9987±
0.0339(=)0.7887±
0.0689(+)0.9899±
0.1004(+)0.9983±
0.1038Omni-test3 3.1630±
0.5124(−)4.6964±
0.4551(−)1.9423±
0.0862(+)2.0288±
0.0815(+)1.9684±
0.0503(+)1.7224±
0.0649(+)2.1185±
0.0118(+)2.1244±
0.0909+/=/− 0/0/14 0/0/14 1/0/13 4/3/7 3/2/9 4/2/8 2/0/12 — 3.3.3 决策空间PSs分布分析
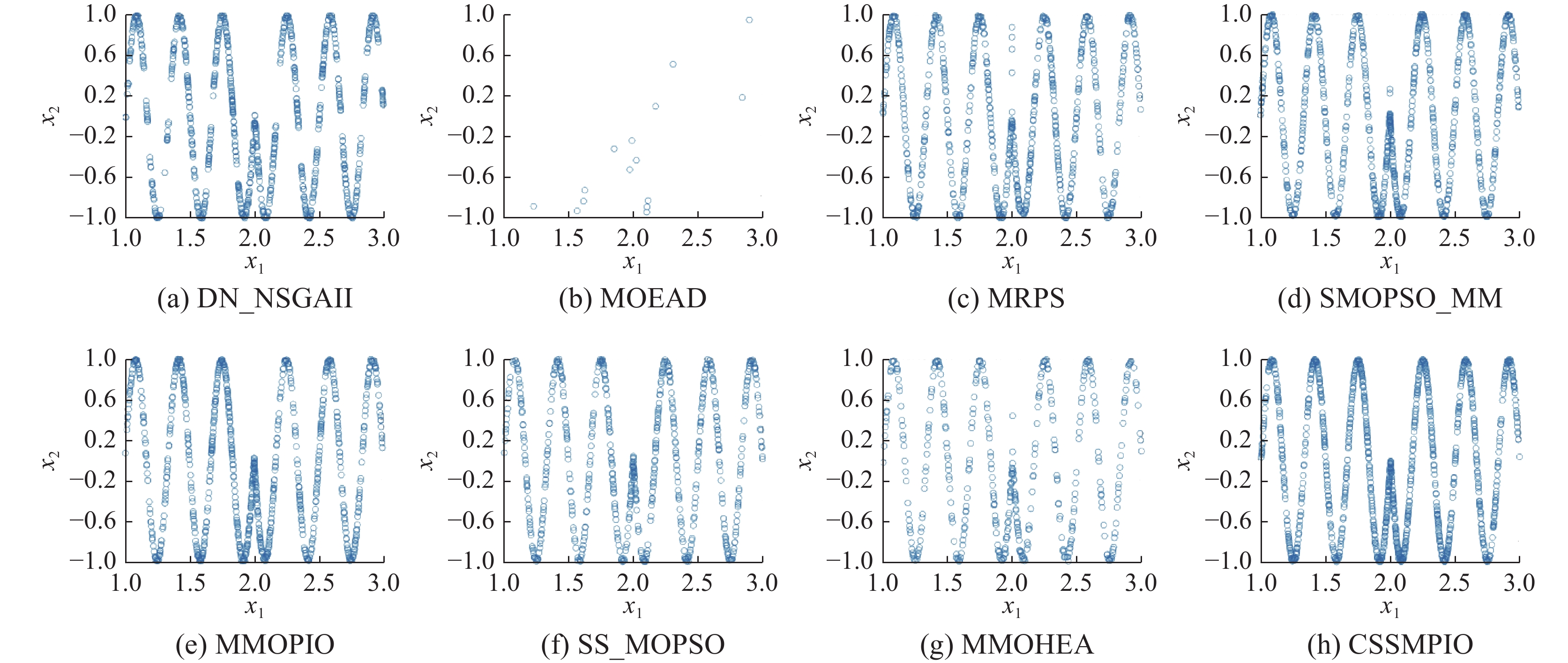
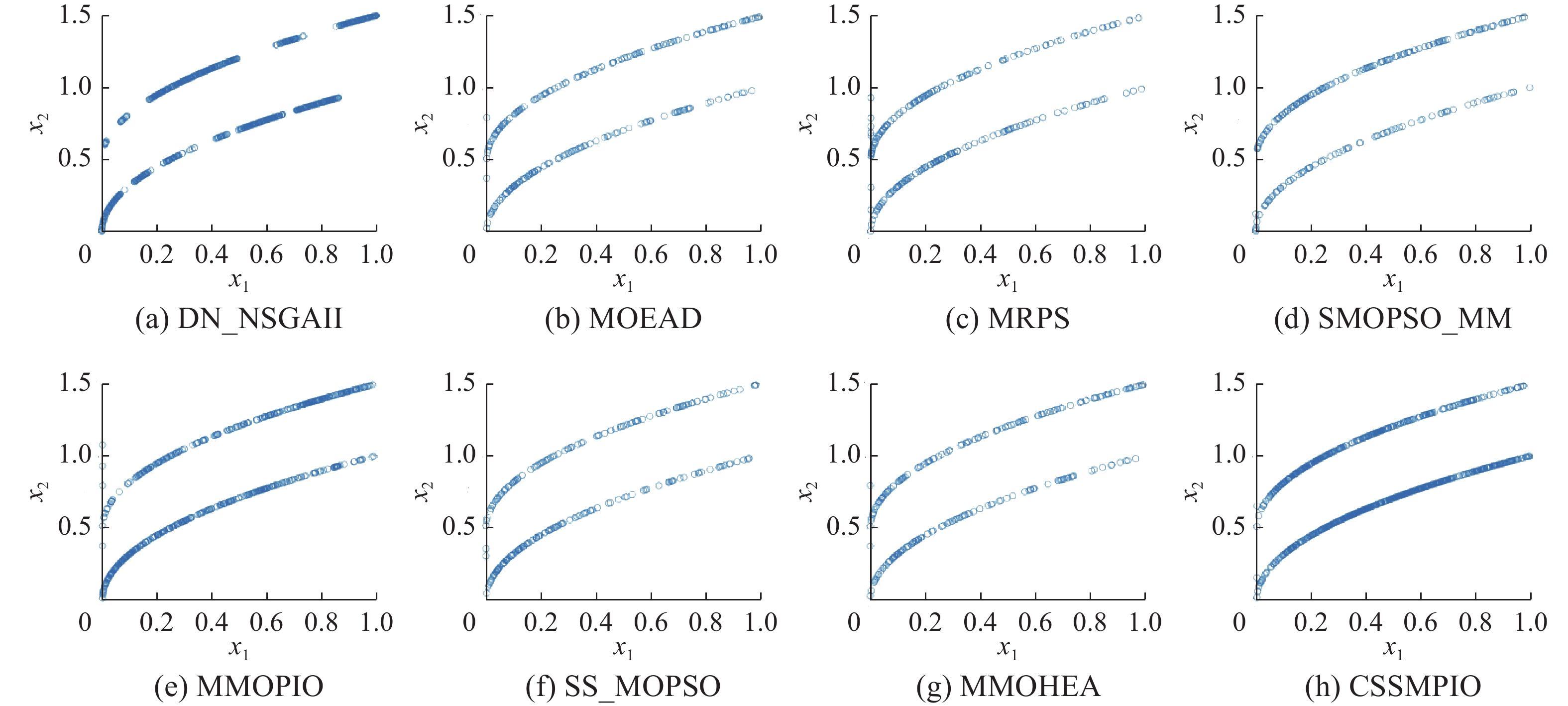
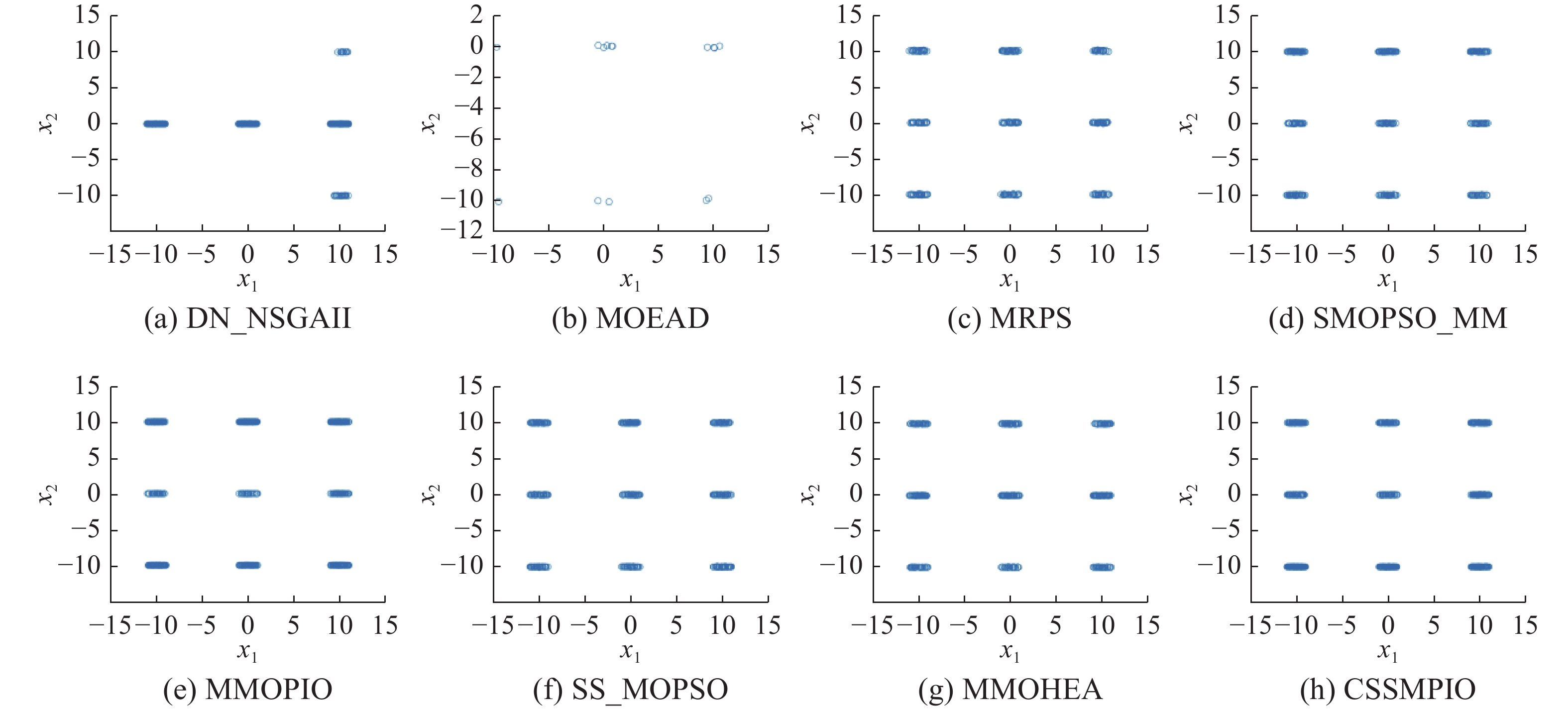
图7~9比较了算法在MMF1、MMF3和SYM-PART1测试函数上得到的PSs，图中的水平坐标和垂直坐标分别表示对应决策变量的边界范围。从图中可以看出，MOEAD求得的PSs最差。在MMF1测试函数上，不仅3.3.1和3.3.2小节部分CSSMPIO求得PSP值和IGDx值更优越，而且从图7可以看出CSSMPIO求得的PSs分布也更均匀。对于性能表现较好的MMF3和SYM-PART1测试函数来说，图8、图9更直观地体现了CSSMPIO找到更多的Pareto最优解，且解的分布也更均匀。
图 7 不同算法在MMF1上得到的PSsFig. 7 PSs obtained on MMF1 with different algorithms下载:
全尺寸图片
图 8 不同算法在MMF3上得到的PSsFig. 8 PSs obtained on MMF3 with different algorithms下载:
全尺寸图片
图 9 不同算法在SYM-PART1上得到的PSsFig. 9 PSs obtained on SYM-PART1 with different algorithms下载:
全尺寸图片
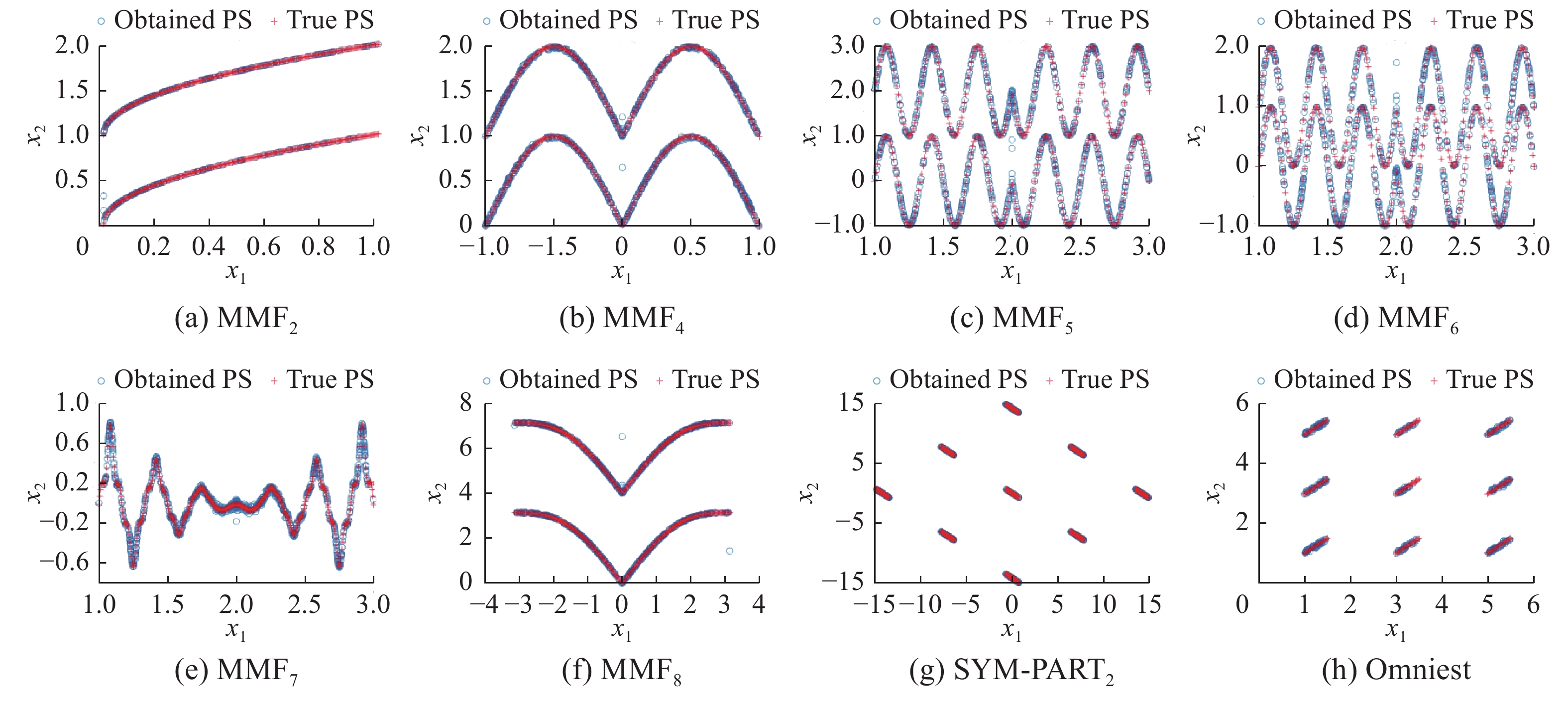
为了更准确地说明这一点，图10表示CSSMPIO在其他测试函数上得到的决策空间Pareto解集的分布和真实Pareto解集分布的图像，“○”代表的是获得的PS，“+”代表的是真实PS。从图中可以看出，CSSMPIO求得的PSs大多可以覆盖于真实的PSs，且PSs的分布是均匀的。尤其在复杂函数SYM-PART2上取得了更优的效果。综合各算法的PSP值和IGDx值以及Pareto解集的分布结果，所提CSSMPIO获得的PSs能够较好地覆盖真实PSs，相比于其他算法具有更好的收敛性和多样性，在决策空间和目标空间上实现更好的平衡。
图 10 CSSMPIO在测试函数上得到的决策空间PSs分布Fig. 10 The PSs distribution of decision space obtained by the CSSMPIO algorithm in test functions下载:
全尺寸图片
3.4 算法运行时间对比分析
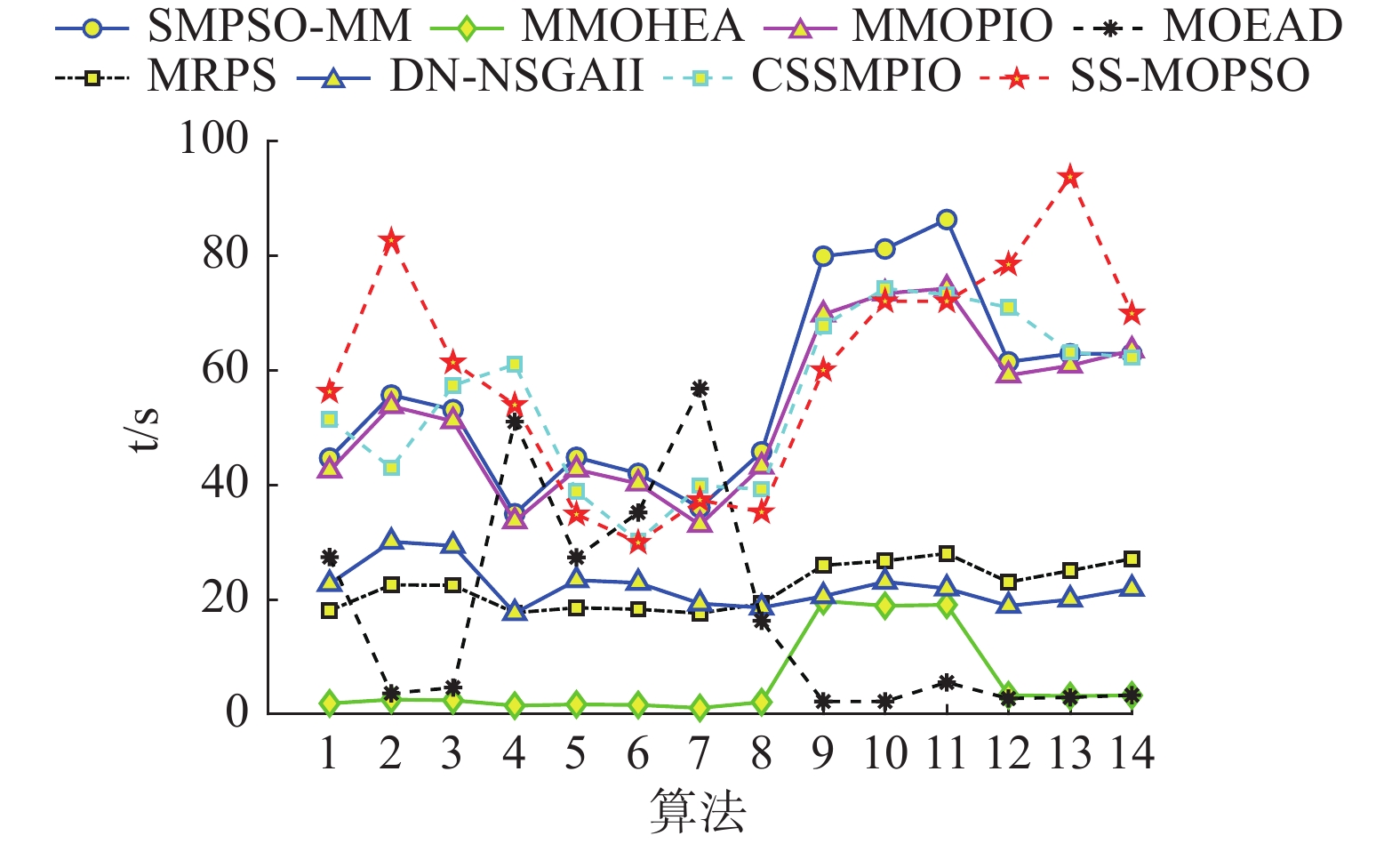
图11可视化了不同算法在测试问题上计算一次的平均运行时间，运行时间刻度设置为log10。从图11可以看出，MMOHEA的时间成本最低，这是因为算法采用了有效支配排序策略，但是该算法的计算结果较差。MOEAD的运行时间是不稳定的；CSSMPIO采用了小生境搜索策略，算法运行时间相较MRPS、DN_NSGAII较长；相较于SMPSO_MM、MMOPIO来说，CSSMPIO算法的运行时间相差不多，但是算法的求解结果更好，综合来看，CSSMPIO算法的效率较高。
图 11 比较算法在14个测试函数上的运行时间Fig. 11 Runtime of different comparison algorithms on 14 test functions下载:
全尺寸图片
4. 基于地图测试问题的应用
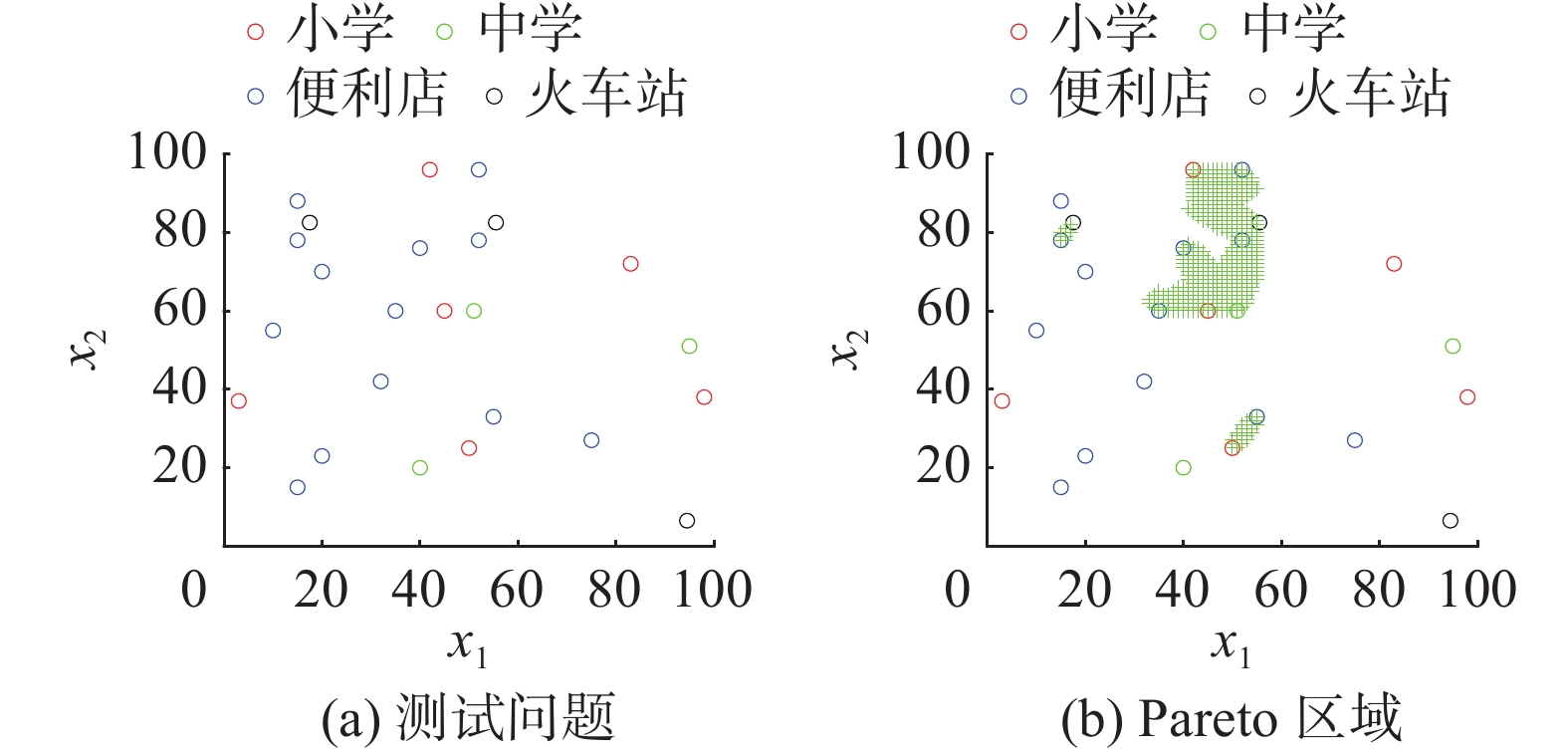
为验证CSSMPIO的性能，采用基于地图的测试问题[37]，测试问题是从实际地图生成的，如图12（a）所示，涉及6所小学（红色圆圈）、3所中学（绿色圆圈）、13家便利店（蓝色圆圈）和3个火车站（黑色圆圈），利用决策空间（即地图中的点）中解
$ x $ 的欧氏距离定义了4个最小化目标：$ {f_1}(x) $ ：距离最近的小学（红色圆圈）；$ {f_2}(x) $ ：距离最近的中学（绿色圆圈）；$ {f_3}(x) $ ：距离最近的便利店（蓝色圆圈）；$ {f_4}(x) $ ：距离最近的火车站（黑色圆圈）。
图 12 基于地图的测试问题及Pareto区域Fig. 12 The map-based test problems and the Pareto regions下载:
全尺寸图片
图12（b）中的绿色部分表示该问题的帕累托最优区域，并通过检查101×101个点
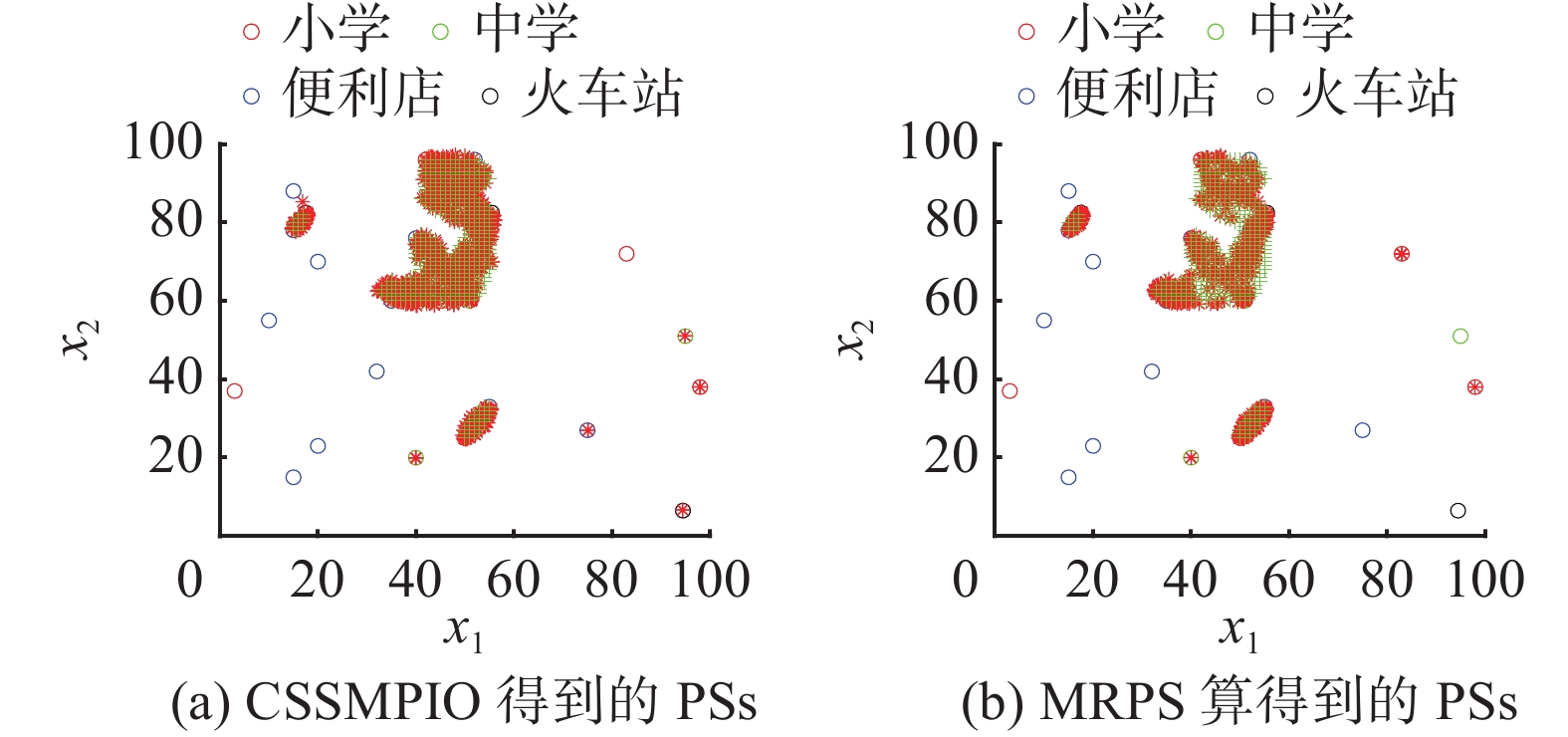
$({x_1} = 0,\; 1, \;\cdots, 100$ ；${x_2} = 0,\;1,\;\cdots,\;100)$ 中每个点的Pareto最优性来描述。为了证明CSSMPIO的有效性，将CSSMPIO与MRPS在基于地图的问题上进行了比较，参数设置如表1。结果如图13所示，CSSMPIO可以覆盖所有Pareto区域，而MRPS获得的Pareto区域是不完整的。这表明CSSMPIO的性能优于MRPS，证明了CSSMPIO的有效性。
图 13 两种算法得到的解Fig. 13 Obtained solutions by two algorithms下载:
全尺寸图片
5. 结束语
针对多模态多目标优化中种群多样性难以维持以及等价Pareto最优解数量不足问题，本文提出一种融合聚类和小生境搜索的多模态多目标优化算法（CSSMPIO）。CSSMPIO采用基于聚类的特殊拥挤距离排序（CSCD）克服了非支配特殊拥挤排序（SCD）不能正确识别邻域的缺点，并且考虑到了决策空间和目标空间的拥挤距离，个体在自适应形物种形成策略中形成的小生境子种群中利用改进的鸽群优化算法并行搜索等价Pareto最优解，最后执行精英学习策略，从而在决策空间和目标空间中获得一个均匀分布的群体。
综合分析CSSMPIO算法与其他7种多模态多目标算法在14个测试函数上的结果发现，CSSMPIO算法能够找到更多的PSs，提高了决策空间的多样性以及算法搜索能力。另外求得的解集接近于真实解集，具有较好的收敛性和多样性，在决策空间和目标空间上实现更好的平衡。
但是本文所提算法是连续优化算法，不适于求解离散优化问题，在未来的工作中，设计出离散优化多模态算法将是研究的方向。
-
图 1 路径优化问题
Fig. 1 Path planning problem
下载:
全尺寸图片
图 2 多模态多目标优化问题
Fig. 2 Multimodal multi-objective optimization problem
下载:
全尺寸图片
图 3 物种在二维区域的分布
Fig. 3 Distribution of species in a two-dimensional region
下载:
全尺寸图片
图 4 单个物种中个体位置更新方式
Fig. 4 Individual position updating in a single species
下载:
全尺寸图片
图 5 不同种群规模的PSP值
Fig. 5 PSP values with different population sizes
下载:
全尺寸图片
图 6 不同物种半径的PSP值
Fig. 6 PSP values with different radius
下载:
全尺寸图片
图 7 不同算法在MMF1上得到的PSs
Fig. 7 PSs obtained on MMF1 with different algorithms
下载:
全尺寸图片
图 8 不同算法在MMF3上得到的PSs
Fig. 8 PSs obtained on MMF3 with different algorithms
下载:
全尺寸图片
图 9 不同算法在SYM-PART1上得到的PSs
Fig. 9 PSs obtained on SYM-PART1 with different algorithms
下载:
全尺寸图片
图 10 CSSMPIO在测试函数上得到的决策空间PSs分布
Fig. 10 The PSs distribution of decision space obtained by the CSSMPIO algorithm in test functions
下载:
全尺寸图片
图 11 比较算法在14个测试函数上的运行时间
Fig. 11 Runtime of different comparison algorithms on 14 test functions
下载:
全尺寸图片
图 12 基于地图的测试问题及Pareto区域
Fig. 12 The map-based test problems and the Pareto regions
下载:
全尺寸图片
图 13 两种算法得到的解
Fig. 13 Obtained solutions by two algorithms
下载:
全尺寸图片
表 1 算法的参数设置
Table 1 Parameters setting of algorithms
算法 参数 CSSMPIO $R = {1 \mathord{\left/ { {1 {20 {{V} }_{{R} };k = 10;{c_1} = {c_2} = 2.05} } } \right. } }$ MMOHEA[17] ${{c} }_{{r} } = 0.9;F = 0.5$ MRPS[10] ${c_1} = {c_2} = 2.05;w = 0.729\;8$ MMOPIO[13] $\lambda = 7;{{R} }_{{s} } = 0.3$ SMOPSO-MM[12] ${c_1} = {c_2} = 2.05;w = 0.729\;8$
拓扑结构= $1 \times 100;\eta_0=0.7$；
$\sigma_0=\dfrac{ {\rm{sqrt} }\left({1}^{2}+{100}^{2}\right)}{2}$SS_MOPSO[7] $R = {1 \mathord{\left/ { {1 {20 {{V} }_{{R} } } } } \right. } };w = 0.729\;8;{c_1} = {c_2} = 2.05$ DN_NSGAII[8] ${{C} }_{{F} } = 0.5;{\eta _c} = {\eta _m} = 20;{p_c} = 1;{p_m} = {1 \mathord{\left/ {\vphantom {1 n} } \right. } n}$ MOEAD[33] $ {p_m} = 0.5;{\eta _m} = 20 $ 表 2 测试函数特征
Table 2 The characteristics of test problems
函数名称 PSs的数量 每个维度的重叠 MMF1 2 × MMF2 2 × MMF3 2 √ MMF4 4 × MMF5 4 × MMF6 4 √ MMF7 2 × MMF8 4 × SYM-PART 9 √ Omni-test1 27 √ Omni-test2 72 √ Omni-test3 360 √ 表 3 CSSMPIO使用不同参数
$n $ 获得的PSP值Table 3 PSP values obtained by CSSMPIO with different
$n $ values测试问题 $ n = 5 $ $ n = 10 $ $ n = 15 $ $ n = 20 $ MMF1 79.97±2.39 83.19±2.24 82.68±2.87 77.75±3.29 MMF2 274.14±63.78 275.76±37.53 282.44±51.37 268.65±57.27 MMF3 298.12±84.37 305.08±29.13 272.72±36.95 273.78±43.89 MMF4 128.64±6.05 132.78±7.88 116.78±10.28 110.12±11.95 MMF5 39.22±1.35 43.11±1.35 40.99±0.83 34.49±1.11 MMF6 38.77±1.85 41.60±1.77 40.16±1.73 39.80±1.09 MMF7 110.29±7.81 113.60±5.99 102.62±8.65 110.38±6.87 MMF8 60.59±2.45 57.55±3.21 53.24±5.22 57.62±2.32 SYM-PART1 42.71±3.73 52.01±3.58 42.85±1.97 42.29±3.53 Omni-test1 10.39±1.24 11.73±1.25 5.64±2.73 8.10±2.60 表 4 所有算法得到的PSP平均值与标准方差
Table 4 Mean and standard variance of PSP obtained by all algorithms
测试
问题mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SS_MOPSO MMOHEA CSSMPIO MMF1 41.88±2.80
(−)8.02±4.89
(−)67.05±3.12
(−)85.34±2.34
(=)73.83±2.78
(−)83.11±3.27
(−)42.78±1.43
(−)86.86±4.15 MMF2 61.55±33.31
(−)4.62±3.24
(−)107.53±11.92
(−)152.69±15.35
(−)167.78±45.24
(−)163.28±18.06
(−)116.75±16.14
(−)277.15±34.30 MMF3 75.11±28.88
(−)7.00±3.79
(−)128.63±17.06
(−)186.24±15.19
(−)226.06±32.79
(−)189.94±12.67
(−)125.96±16.67
(−)305.44±24.93 MMF4 38.45±8.59
(−)1.93±0.97
(−)114.51±3.29
(−)132.78±3.82
(−)120.15±3.91
(−)139.40±3.49
(+)73.03±3.99
(−)135.90±5.95 MMF5 14.57±1.47
(−)3.35±1.35
(−)33.11±1.35
(−)40.12± 1.33
(−)30.24±1.46
(−)40.11±1.19
(−)22.21±0.41
(−)43.62±1.50 MMF6 18.89±1.37
(−)4.97±2.37
(−)36.44±1.59
(−)42.42±1.08
(=)36.23±1.99
(−)42.19±1.29
(=)24.16±0.59
(−)41.74±1.39 MMF7 95.55±17.79
(−)7.49±4.78
(−)108.77±3.89
(−)141.13±5.14
(+)136.49±4.78
(+)123.73±6.27
(+)78.05±2.87
(−)119.82±6.11 MMF8 18.01±5.89
(−)0.25±0.12
(−)47.64±2.22
(−)62.53±2.34
(+)54.78±7.12
(−)59.34±22.39
(=)33.78±3.40
(−)58.38±2.76 SYM-PART1 0.44±0.59
(−)0.01±0.01
(−)21.95±1.67
(−)30.37±2.77
(−)59.97±0.24
(+)34.50±1.30
(−)31.22±1.48
(−)52.01±3.58 SYM-PART2 3.07±4.00
(−)0.01±0.01
(−)18.73±0.94
(−)16.88 ±1.33
(−)43.18±3.16
(−)30.77±1.19
(−)31.82±0.70
(−)47.08±3.79 SYM-PART3 5.57±9.97
(−)0.01±0.01
(−)9.37±2.19
(−)15.78±2.80
(−)41.15±1.78
(−)28.17±2.45
(−)11.34±2.34
(−)56.94±2.78 Omni-test1 1.16±0.23
(−)0.03±0.01
(−)8.04±1.06
(−)7.69±1.48
(−)1.15±0.08
(−)11.75±1.10
(−)12.09±0.54
(=)12.15±2.23 Omni-test2 0.44±0.08
(−)0.03±0.01
(−)0.98±0.07
(=)0.95±0.07
(=)0.95±0.04
(−)1.46±0.05
(+)1.01±0.00
(=)0.99±0.07 Omni-test3 0.28±0.09
(−)0.02±0.01
(−)0.51±0.02
(+)0.49±0.02
(+)0.50±0.01
(+)0.58±0.02
(+)0.47±0.01
(=)0.46±0.02 +/=/− 0/0/14 0/0/14 1/1/12 3/3/8 3/0/11 4/2/8 0/3/11 — 表 5 所有算法得到的HV平均值与标准方差
Table 5 The mean and standard variance of HV obtained by all algorithms
测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SS_MOPSO MMOHEA CSSMPIO MMF1 3.66±1.30×10−3 3.67±4.79×10−4 3.66±4.63×10−4 3.67±3.99×10−4 3.66±2.84×10−4 3.66±4.55×10−4 3.66±5.40×10−4 3.66±1.31×10−4 MMF2 3.66±6.20×10−3 3.67±5.34×10−4 3.65±8.10×10−3 3.66±4.16×10−3 3.65±2.07×10−3 3.66±4.20×10−3 3.65±4.80×10−3 3.66±4.02×10−4 MMF3 3.66±4.90×10−3 3.67±7.72×10−4 3.65±5.10×10−3 3.66±3.34×10−3 3.66±1.41×10−3 3.66±3.28×10−3 3.66±2.25×10−3 3.66±1.96×10−3 MMF4 3.33±3.60×10−4 3.33±1.63×10−4 3.33±1.20×10−3 3.33±8.88×10−4 3.33±3.88×10−4 3.33±8.45×10−4 3.33±1.34×10−4 3.33±3.14×10−4 MMF5 3.67±2.70×10−3 3.67±6.81×10−4 3.66±3.52×10−4 3.66±4.89×10−4 3.66±6.98×10−5 3.67±3.03×10−4 3.66±3.72×10−4 3.67±3.10×10−4 MMF6 3.66±1.10×10−3 3.67±5.53×10−4 3.66±3.31×10−4 3.66±3.74×10−4 3.66±3.19×10−4 3.66±3.19×10−4 3.66±3.24×10−4 3.66±3.24×10−4 MMF7 3.66±7.10×10−4 3.67±2.39×10−4 3.67±2.38×10−4 3.66±3.00×10−4 3.66±6.24×10−4 3.66±2.88×10−4 3.66±3.61×10−4 3.66±4.16×10−4 MMF8 3.21±1.30×10−3 3.21±1.44×10−4 3.21±1.50×10−4 3.21±1.58×10−4 3.21±4.14×10−5 3.21±7.30×10−4 3.21±3.99×10−4 3.21±7.30×10−4 SYM-PART1 1.32±3.09×10−4 1.32±8.35×10−5 1.30±1.90×10−4 1.27±4.86×10−3 1.32±8.20×10−5 1.32±8.30×10−4 1.31±7.72×10−4 1.32±2.29×10−4 SYM-PART2 1.32±4.92×10−4 1.32±6.85×10−4 1.29±2.20×10−3 1.27±4.39×10−3 1.32±5.16×10−4 1.31±1.12×10−3 1.31±1.02×10−3 1.32±4.26×10−4 SYM-PART3 1.32±5.00×10−4 1.32±1.40×10−3 1.29±2.50×10−3 1.25±6.48×10−3 1.31±2.04×10−3 1.31±2.04×10−3 1.30±1.88×10−3 1.26±6.60×10−3 Omni-test1 62.06±3.98×10−4 62.06±4.80×10−3 61.97±1.24×10−2 61.95±1.56×10−2 61.99±5.33×10−3 62.02±5.33×10−3 61.01±1.81×10−2 62.06±2.16×10−4 Omni-test2 77.54±2.10×10−3 77.53±9.80×10−3 77.03±8.52×10−2 76.84±1.09×10−1 77.49±1.35×10−2 77.35±2.53×10−2 77.01±1.34×10−1 77.39±4.98×10−2 Omni-test3 94.59±8.80×10−3 94.55±2.42×10−2 92.88±2.72×10−1 92.29±3.06×10−1 94.31±6.65×10−1 93.86±1.08×10−1 92.61±2.41×10−1 93.78±2.11×10−1 表 6 所有算法得到的IGDx平均值与标准方差
Table 6 Mean and standard variance of IGDx obtained by all algorithms
测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SSMOPSO MMOHEA CSSMPIO MMF1 0.0237±
0.0033(−)0.1503±
0.0685(−)0.0149±
0.0007(−)0.0117±
0.0003(=)0.0129±
0.0003(−)0.0119±
0.0005(−)0.0233±
1.4303(−)0.0115±
0.0005MMF2 0.0223±
0.0150(−)0.2645±
0.1163(−)0.0092±
0.0010(−)0.0065±
0.0007(−)0.0056±
0.0006(−)0.0061±
0.0006(−)0.0085±
0.0012(−)0.0043±
0.0006MMF3 0.0166±
0.0071(−)0.1378±
0.0467(−)0.0072±
0.0010(−)0.0053±
0.0005(−)0.0056±
0.0001(−)0.0059±
0.0010(−)0.0079±
0.0011(−)0.0049±
0.0007MMF4 0.0268±
0.0063(−)0.4262±
0.1235(−)0.0087±
0.0003(−)0.0053±
0.0005(+)0.0083±
0.0003(−)0.0076±
0.0003(−)0.0136±
0.0007(−)0.0071±
0.0003MMF5 0.0689±
0.0071(−)0.2985±
0.1263(−)0.0302±
0.0013(−)0.0246±
0.0009(=)0.0331±
0.0016(−)0.0248±
0.0007(=)0.0448±
0.0007(−)0.0250±
0.0008MMF6 0.0109±
0.0024(−)0.2045±
0.0708(−)0.0275±
0.0012(−)0.0238±
0.0006(=)0.0286±
0.0016(−)0.0235±
0.0008(+)0.0412±
0.0010(−)0.0239±
0.0008MMF7 0.0643±
0.0352(−)0.1522±
0.0662(−)0.0092±
0.0003(−)0.0071±
0.0003(+)0.0072±
0.0003(+)0.0081±
0.0004(=)0.0128±
0.0004(−)0.0081±
0.0004续表 6 测试问题 mean±std DN_NSGAII MOEAD MRPS SMPSO_MM MMOPIO SSMOPSO MMOHEA CSSMPIO MMF8 3.0256±
1.0730(−)2.7114±
0.5862(−)0.0210±
0.0010(−)0.0160±
0.0006(+)0.0174±
0.0009(=)0.0167±
0.0006(+)0.0298±
0.0034(−)0.0174±
0.0008SYM-PART1 1.0513±
0.8300(−)12.6877±
2.7300(−)0.0458±
0.0035(−)0.0323±
0.0003(−)0.0167±
0.2402(+)0.0290±
0.0061(−)0.0321±
0.0015(−)0.0193±
0.0013SYM-PART2 0.9538±
0.0756(−)12.7889±
2.4800(−)0.0533±
0.0028(−)0.0597±
0.0005(−)0.0231±
0.0015(−)0.0326±
0.0105(−)0.0314±
0.0006(−)0.0213±
0.0017SYM-PART3 0.9556±
0.7563(−)10.3697±
2.4900(−)0.1094±
0.0241(−)0.0651±
0.0133(−)0.0241±
0.0089(−)0.0357±
0.0042(−)0.0842±
0.0167(−)0.0123±
0.0007Omni-test1 0.8899±
0.1652(−)3.4183±
0.4137(−)1.2623±
0.0212(−)0.1345±
0.0316(−)0.8706±
0.0618(−)0.0810±
0.0274(−)0.0824±
0.0038(−)0.0786±
0.0181Omni-test2 2.1976±
0.2923(−)3.9763±
0.4832(−)1.0132±
0.0651(−)1.0473±
0.0762(−)0.9987±
0.0339(=)0.7887±
0.0689(+)0.9899±
0.1004(+)0.9983±
0.1038Omni-test3 3.1630±
0.5124(−)4.6964±
0.4551(−)1.9423±
0.0862(+)2.0288±
0.0815(+)1.9684±
0.0503(+)1.7224±
0.0649(+)2.1185±
0.0118(+)2.1244±
0.0909+/=/− 0/0/14 0/0/14 1/0/13 4/3/7 3/2/9 4/2/8 2/0/12 — -
[1] QU B, SUGANTHAN P N. Novel multimodal problems and differential evolution with ensemble of restricted tournament selection[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Barcelona: IEEE, 2010: 1−7. [2] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017 [3] LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE transactions on evolutionary computation, 2006, 10(3): 281–295. doi: 10.1109/TEVC.2005.857610 [4] ZHANG Xuwei, LIU Hao, TU Liangping. A modified particle swarm optimization for multimodal multi-objective optimization[J]. Engineering applications of artificial intelligence, 2020, 95: 103905. doi: 10.1016/j.engappai.2020.103905 [5] 高海军, 潘大志. 星型结构的多目标粒子群算法求解多模态多目标问题[J]. 计算机工程与科学, 2020, 42(8): 1472–1481. GAO Haijun, PAN Dazhi. A multi-objective particle swarm optimization algorithm with star structure to solve the multi-modal multi-objective problem[J]. Computer engineering and science, 2020, 42(8): 1472–1481. [6] QU B Y, SUGANTHAN P N, DAS S. A distance-based locally informed particle swarm model for multimodal optimization[J]. IEEE transactions on evolutionary computation, 2013, 17(3): 387–402. doi: 10.1109/TEVC.2012.2203138 [7] QU Boyang, LI Chao, LIANG Jing, et al. A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems[J]. Applied soft computing, 2020, 86: 105886. doi: 10.1016/j.asoc.2019.105886 [8] LIANG Jing, YUE Caitong, QU Boyang. Multimodal multi-objective optimization: a preliminary study[C]//2016 IEEE Congress on Evolutionary Computation. Vancouver: IEEE, 2016: 2454−2461. [9] ZHANG Kai, SHEN Chaonan, YEN G G, et al. Two-stage double niched evolution strategy for multimodal multiobjective optimization[J]. IEEE transactions on evolutionary computation, 2021, 25(4): 754–768. doi: 10.1109/TEVC.2021.3064508 [10] YUE Caitong, QU Boyang, LIANG Jing. A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems[J]. IEEE transactions on evolutionary computation, 2018, 22(5): 805–817. doi: 10.1109/TEVC.2017.2754271 [11] WANG Ying, YANG Zhile, GUO Yuanjun, et al. A novel multi-objective competitive swarm optimization algorithm for multi-modal multi objective problems[C]//2019 IEEE Congress on Evolutionary Computation. Wellington: IEEE, 2019: 271−278. [12] LIANG Jing, GUO Qianqian, YUE Caitong, et al. A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems[C]//International Conference on Swarm Intelligence. Cham: Springer, 2018: 550−560. [13] HU Yi, WANG Jie, LIANG Jing, et al. A self-organizing multimodal multi-objective pigeon-inspired optimization algorithm[J]. Science China information sciences, 2019, 62(7): 70206. doi: 10.1007/s11432-018-9754-6 [14] WANG Yong, LI Hanxiong, YEN G G, et al. MOMMOP: multiobjective optimization for locating multiple optimal solutions of multimodal optimization problems[J]. IEEE transactions on cybernetics, 2015, 45(4): 830–843. doi: 10.1109/TCYB.2014.2337117 [15] LUO Naili, LIN Wu, HUANG Peizhi, et al. An evolutionary algorithm with clustering-based assisted selection strategy for multimodal multiobjective optimization[J]. Complexity, 2021, 2021: 1–13. [16] LUO Naili, YE Yulong, LIN Wu, et al. A novel multimodal multiobjective memetic algorithm with a local detection mechanism and a clustering-based selection strategy[J]. Memetic computing, 2023, 15(1): 31–43. doi: 10.1007/s12293-022-00353-0 [17] HU Yi, WANG Jie, LIANG Jing, et al. A two-archive model based evolutionary algorithm for multimodal multi-objective optimization problems[J]. Applied soft computing, 2022, 119: 108606. doi: 10.1016/j.asoc.2022.108606 [18] LIU Yiping, YEN G G, GONG Dunwei. A multimodal multiobjective evolutionary algorithm using two-archive and recombination strategies[J]. IEEE transactions on evolutionary computation, 2019, 23(4): 660–674. doi: 10.1109/TEVC.2018.2879406 [19] YANG Qite, WANG Zhenkun, LUO Jianping, et al. Balancing performance between the decision space and the objective space in multimodal multiobjective optimization[J]. Memetic computing, 2021, 13(1): 31–47. doi: 10.1007/s12293-021-00325-w [20] 胡洁, 范勤勤, 王直欢. 融合分区和局部搜索的多模态多目标优化[J]. 智能系统学报, 2021, 16(4): 774–784. HU Jie, FAN Qinqin, WANG Zhihuan. Multimodal multi-objective optimization combining zoning and local search[J]. CAAI transactions on intelligent systems, 2021, 16(4): 774–784. [21] LIANG Jing, XU Weiwei, YUE Caitong, et al. Multimodal multiobjective optimization with differential evolution[J]. Swarm and evolutionary computation, 2019, 44: 1028–1059. doi: 10.1016/j.swevo.2018.10.016 [22] ZHANG Weizheng, LI Guoqing, ZHANG Weiwei, et al. A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization[J]. Swarm and evolutionary computation, 2019, 50: 100569. doi: 10.1016/j.swevo.2019.100569 [23] LIN Qiuzhen, LIN Wu, ZHU Zexuan, et al. Multimodal multiobjective evolutionary optimization with dual clustering in decision and objective spaces[J]. IEEE transactions on evolutionary computation, 2021, 25(1): 130–144. doi: 10.1109/TEVC.2020.3008822 [24] LIANG Jing, QIAO Kangjia, YUE Caitong, et al. A clustering-based differential evolution algorithm for solving multimodal multi-objective optimization problems[J]. Swarm and evolutionary computation, 2021, 60: 100788. doi: 10.1016/j.swevo.2020.100788 [25] SHI Ruizhi, LIN Wu, LIN Qiuzhen, et al. Multimodal multi-objective optimization using A density-based one-by-one update strategy[C]//2019 IEEE Congress on Evolutionary Computation. Wellington: IEEE, 2019: 295−301. [26] DUAN Haibin, QIAO Peixin. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1): 24–37. doi: 10.1108/IJICC-02-2014-0005 [27] 陶国娇, 李智. 带认知因子的交叉鸽群算法[J]. 四川大学学报(自然科学版), 2018, 55(2): 295–300. TAO Guojiao, LI Zhi. A crossed pigeon-inspired optimization algorithm with congnitive factor[J]. Journal of Sichuan university (natural science edition), 2018, 55(2): 295–300. [28] 尹德鑫, 张达敏, 蔡朋宸, 等. 基于鸽群算法的Fuch混沌蝗虫算法[J]. 计算机应用研究, 2021, 38(7): 2013–2017. YIN Dexin, ZHANG Damin, CAI Pengchen, et al. Fuch chaotic grasshopper algorithm based on pigeon swarm algorithm[J]. Application research of computers, 2021, 38(7): 2013–2017. [29] LIU Hanmin, YAN Xuesong, WU Qinghua. An improved pigeon-inspired optimisation algorithm and its application in parameter inversion[J]. Symmetry, 2019, 11(10): 1291. doi: 10.3390/sym11101291 [30] 马龙, 卢才武, 顾清华, 等. 引入改进鸽群搜索算子的粒子群优化算法[J]. 模式识别与人工智能, 2018, 31(10): 909–920. MA Long, LU Caiwu, GU Qinghua, et al. Particle swarm optimization with search operator of improved pigeon-inspired algorithm[J]. Pattern recognition and artificial intelligence, 2018, 31(10): 909–920. [31] 岳彩通, 梁静, 瞿博阳, 等. 多模态多目标优化综述[J]. 控制与决策, 2021, 36(11): 2577–2588. YUE Caitong, LIANG Jing, QU Boyang, et al. A survey on multimodal multiobjective optimization[J]. Control and decision, 2021, 36(11): 2577–2588. [32] QIU Huaxin, DUAN Haibin. Multi-objective pigeon-inspired optimization for brushless direct current motor parameter design[J]. Science China technological sciences, 2015, 58(11): 1915–1923. doi: 10.1007/s11431-015-5860-x [33] ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712–731. doi: 10.1109/TEVC.2007.892759 [34] RUDOLPH G, NAUJOKS B, PREUSS M. Capabilities of EMOA to detect and preserve equivalent Pareto subsets[C]//Proceedings of the 4th international conference on Evolutionary multi-criterion optimization. New York: ACM, 2007: 36–50. [35] DEB K, TIWARI S. Omni-optimizer: a procedure for single and multi-objective optimization[C]//Proceedings of the Third international conference on Evolutionary Multi-Criterion Optimization. New York: ACM, 2005: 47–61. [36] DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and evolutionary computation, 2011, 1(1): 3–18. doi: 10.1016/j.swevo.2011.02.002 [37] ISHIBUCHI H, AKEDO N, NOJIMA Y. A many-objective test problem for visually examining diversity maintenance behavior in a decision space[C]//Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2011: 649–656.
