Real time fault diagnosis method of rolling bearing based on CWT and LightweightNet
-
摘要: 针对普通的深度学习算法用于轴承故诊断分类时计算量大、消耗成本高的问题，提出一种结合连续小波变换和轻量级神经网络的滚动轴承实时故障诊断方法。首先，使用Morlet母小波函数对轴承振动加速度数据进行连续小波变换，提取出时频域特征并将一维信号转换成二维图片；然后，结合分组卷积、通道混洗、倒残差结构等轻量级神经网络设计元素设计一个轻量级卷积神经网络LightweightNet用于时频图片的故障分类，LightweightNet网络在保证具有足够特征提取能力的同时还具有轻量级特点。使用凯斯西储大学轴承故障数据集进行实验表明，本方法相比于其他使用经典轻量级神经网络的方法具有更少的参数、最高的准确率和更快的诊断速度，基本可以实现滚动轴承的实时故障诊断，且在内存消耗与模型存储占用空间方面远小于其他同类方法。Abstract: In order to solve the problem of large computation and high cost when common deep learning algorithm is applied to bearing fault diagnosis and classification, a real-time rolling bearing fault diagnosis method combining continuous wavelet transform and lightweight neural network is proposed in this paper. Firstly, the Morlet mother wavelet function is used to carry out continuous wavelet transform on the bearing vibration acceleration data, extracting the time-frequency domain features and converting the one-dimensional signals into two-dimensional images. Then, LightweightNet, a lightweight convolutional neural network, is designed for time-frequency image fault classification by combining lightweight neural network design elements such as group convolution, channel shuffle and inverted residual structure. LightweightNet not only ensures sufficient feature extraction ability, but also has lightweight characteristics. The bearing failure experiment data sets from Case Western Reserve University show that, compared with other methods using classic lightweight neural network, this method has less parameters, the highest degree of accuracy and faster diagnosis speed, the real-time fault diagnosis of rolling bearing can be achieved basically, far less than other similar methods in memory consumption and model storage space.
-
作为现代工业的重要组成部分，滚动轴承广泛应用在军工、制造和交通运输等各个领域[1]。由于在各种机械中使用广泛且最易磨损，一旦发生故障则会对整个机械的稳定运行带来巨大的威胁，因此对其进行快速、有效的故障诊断可以极大地保证整个机械系统的稳定运行，避免突发故障引起的各种事故和损失。而对于滚动轴承的故障诊断，现代化的解决方案是利用传感器技术和人工智能算法对其进行基于状态的维护，这其中智能故障诊断在其中扮演着关键的角色。
智能故障诊断一般分为3个步骤：信号处理、特征提取、模式分类。信号处理是指运用各种信号分析方法对轴承运行时采集到的状态信号加以分析与处理，从而获得对轴承正常运行与故障状态的综合性评估，一般有小波变换法(wavelet transform, WT)、经验模式分解法(empirical mode decomposition, EMD)、形态信息处理过程法(morphological signal processing，MSP)和谱分析法(spectrum analysis, SA)等，其中小波变换法可以获得故障信息的特征信号，经常结合其他方法使用。例如，文献[2-3]分别使用小波变换结合极限学习机和深度Q学习对滚动轴承进行故障诊断。
对于特征提取和模式分类，随着人工智能的发展，各种深度学习算法显示出巨大的优势。针对工业过程中的传感器数据，例如振动数据、电流数据，深度学习算法利用深层神经网络模型的超强特征提取能力，从中提取故障特征，之后再使用分类模型对样本数据进行故障分类，从而诊断出轴承的健康状态，是现代装备故障诊断的主流和前沿处理方式。常用的有卷积神经网络（convolutional neural network, CNN）算法[4-11]、自编码器（auto encoder, AE）方法[12-13]、生成对抗网络[14]（generative adversarial networks，GAN），循环神经网络类[15-17]等。其中比较经典的有：文献[9]使用多通道卷积神经网络从多个维度提取更一般的故障特征；文献[14]提出基于深度卷积和对抗网络的故障转移诊断模型，可用于不同类别自适应地对齐特征，用于多工况的故障诊断；Zou等[7]使用一维卷积神经网络直接针对时域信号进行故障诊断。Xu等[18]提出了结合CNN与gcForest，利用连续的小波变换技术(continuous wavelet transform，CWT)将轴承振动信号转换为二维图片，然后利用CNN提取图像故障特征，并将其输入gcForest分类器进行分类。
而现有的深度学习方法也有缺陷，例如文献[4-5, 7]使用一维卷积进行故障特征提取，这些方法直接处理一维振动时序信号，没有考虑到信号中的频域信息。文献[6, 8]分别使用图像映射、短时傅里叶变换将一维振动数据变换为时频图，然后再通过CNN进行故障诊断，取得95%以上的准确率，但这些方法没有考虑到计算开销和诊断时间。在实际工业应用中，特别是终端硬件中对内存、存储、计算量的要求是苛刻的，参数多、开销大的深度学习模型难以直接部署到工业生产线上。基于以上分析，本文使用CWT对轴承振动信号进行时频域处理并将一维信号转化为二维时频图片，使用深度可分离卷积、分组卷积等轻量化神经网络元素设计一种轻量级卷积神经网络用于对时频域图片进行故障分类。结合CWT对信号的时频域分析能力和轻量级神经网络的分类能力，该方法可进行快速准确的轴承故障分类。
1. 相关预备知识
1.1 小波变换原理
连续小波变换（CWT）可以将振动信号的时频特征显示在图像上。对于一个母小波函数
$\psi({t}) \in L^{2}(R)$ ，则$\psi({t})$ 的傅里叶变换满足：$$ {{{\displaystyle \int }}^{\text{}}}_{-\infty }^{+\infty }\frac{|\widehat{\psi }(\omega ){|}^{2}}{\omega }\text{d}\omega < \infty $$ 式中：
$ \omega $ 表示频率，$ \hat{\psi}(\omega) $ 表示$\psi({t})$ 的傅里叶变换。对$\psi({t})$ 进行拉伸和平移即可获得一个小波函数族：$$ \psi_{a, b}(t)=\frac{1}{\sqrt{a}} \psi\left(\frac{t-b}{a}\right)\quad a, b \in R, a>0 $$ $$ t=a t_{0}+b $$ 式中：
$ a $ 是尺度因子；$ b $ 是位移因子；$ \psi_{a, b}(t) $ 是分析小波。尺度因子限制了小波函数的尺度，对应频域，位移因子限制了小波函数的位移，对应时域。结合以上说明，任意有限能量信号$ x(t) \in L^{2}(R) $ 的CWT变换定义为$$ \begin{array}{l}{\text{CWT}}_{x}(a,b)=\left[x(t),{\psi }_{a,b}(t)\right] =\dfrac{1}{\sqrt{a}}{{\displaystyle \int }}_{-\infty }^{+\infty }x(t){\psi }^{\ast }\left(\dfrac{t-b}{a}\right){\rm{d}}t\end{array} $$ 式中：
$\psi^{*}\left(\dfrac{t-b}{a}\right)$ 表示$\psi\left(\dfrac{t-b}{a}\right)$ 的共轭；${\rm{C W T}}_{x}(a, b)$ 表示信号$ x(t) $ 和小波$ \psi_{a, b}(t) $ 的内积。1.2 深度可分离卷积
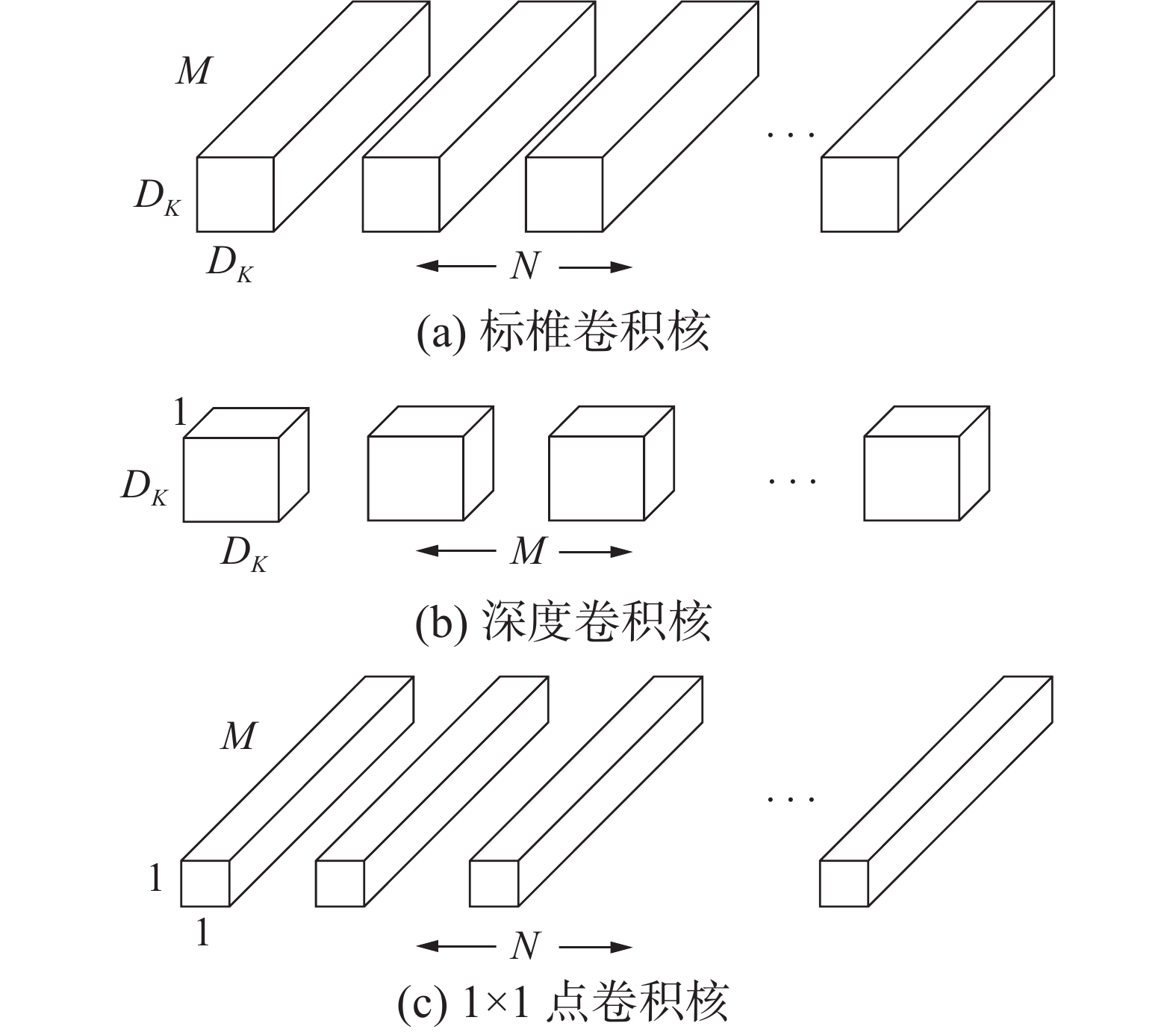
一个标准的卷积具有滤波和特征组合两种功能，深度可分离卷积[19]将标准卷积分解成深度卷积（depthwise convolution，DWConv）和被称为逐点卷积的
$ 1 \times 1 $ 卷积，从而大大减少计算量和模型尺寸。如图1(a)显示了一个标准卷积核，图1(b)为深度卷积核，图1(c)为$ 1 \times 1 $ 点卷积核。标准卷积K使尺寸为$ D_{F} \times D_{F} \times M $ 的特征图F转化为尺寸为$ D_{F} \times D_{F} \times N $ 的特征图G，计算量为${D_K} \cdot {D_K} \cdot M \cdot N \cdot {D_F} \cdot {D_F}$ ，其中：输入特征图方块的宽度和高度均为$ D_{F} $ ，$ M $ 表示输入通道数，$ N $ 表示输出通道数，$ D_{K} $ 是卷积核的大小。深度可分卷积将标准卷积的滤波和合并过程分步骤进行。首先使用深度卷积为每个输入通道应用单个过滤器，若用K表示大小为$ {D_K} \times {D_K} \times M $ 的深度卷积核，K的第$ m $ 卷积核与输入特征图F的第$ m $ 通道做运算的计算量为${D_K} \cdot {D_K} \cdot M \cdot {D_F} \cdot {D_F}$ 然后用卷积核大小为$ 1 \times 1 $ ，个数与标准卷积核个数一致的点卷积合并所有通道的输出，计算量为$ M \cdot N \cdot {D_F} \cdot {D_F} $ 。
图 1 标准卷积核与深度可分离卷积核Fig. 1 Standard convolution kernel and deep separable convolution kernel
下载:
全尺寸图片
由以上分析可知，采用深度可分卷积代替标准卷积计算完成同样效果的卷积运算，两者的计算量之比为
$$ \begin{gathered} \frac{{{D_K} \cdot {D_K} \cdot M \cdot {D_F} \cdot {D_F} + M \cdot N \cdot {D_F} \cdot {D_F}}}{{{D_K} \cdot {D_K} \cdot M \cdot N \cdot {D_F} \cdot {D_F}}} = \frac{1}{N} + \frac{1}{{D_K^2}} \end{gathered} $$ 1.3 分组卷积
组卷积[20]（group convolution，GConv）是一种用于减少模型参数和计算量的操作方式，如图2。具体做法为将卷积核和特征图通道进行分组，每个组的特征图与卷积核进行运算，最后合并输出结果。对于大小为
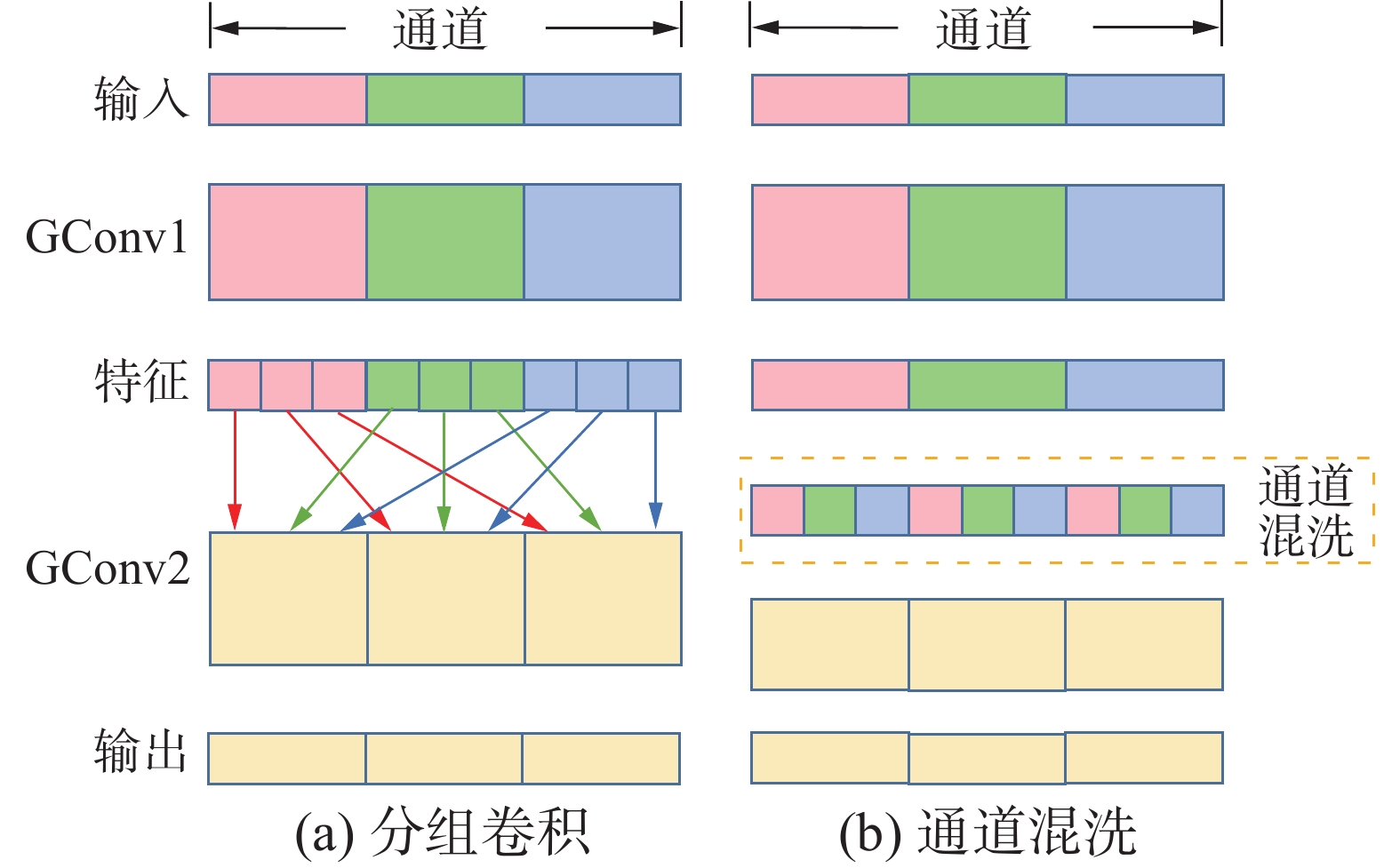
$ H \times W \times M $ 的输入特征图，使用$ M $ 个$ K \times K $ 卷积核进行组别为$ G $ 的组卷积，得到$ H \times W \times N $ 的输出特征图，对应的参数量和计算量仅为$ K^{2} M N / G $ 和$ H W N K^{2} M / G $ 。而使用标准卷积运算则为$ K^{2} M N $ 和$ H W N K^{2} M $ ，即组卷积运算的参数量和计算量均为标准卷积的$ 1 / G $ 。组卷积可以看作一种稀疏的卷积连接，可以明显地降低计算量，但多个组卷积连在一起会导致通道之间的信息不能流通，可能会造成全局信息的丢失。
图 2 分组卷积Fig. 2 Group convolution下载:
全尺寸图片
1.4 通道混洗
通道混洗（channel shuffle）可在一定程度上解决分组卷积全局信息丢失的问题，图3左图中间部分为一般的分组卷积。图3右图的中间部分为混洗后的通道示意图，将分组卷积中的所有分组通道划分为更小的子组，然后将不同的子组提供给下一层的所有的分组。具体实现为：分组卷积层将
$ g \times n $ 个信道先分成$ g $ 组，然后转置、打平再输出到下一层即可，这是一个优雅而高效的操作，却可以有效地解决上述信息分隔的问题，使构建多个组卷积的轻量化网络成为可能。
图 3 通道混洗Fig. 3 Channel shuffle下载:
全尺寸图片
2. 算法描述
算法分成两部分，第1部分为使用CWT对信号进行时频域特征提取并转成二维图片，第2部分构建轻量级卷积神经网络进行快速故障分类，下面分别进行说明。
2.1 轴承振动信号处理
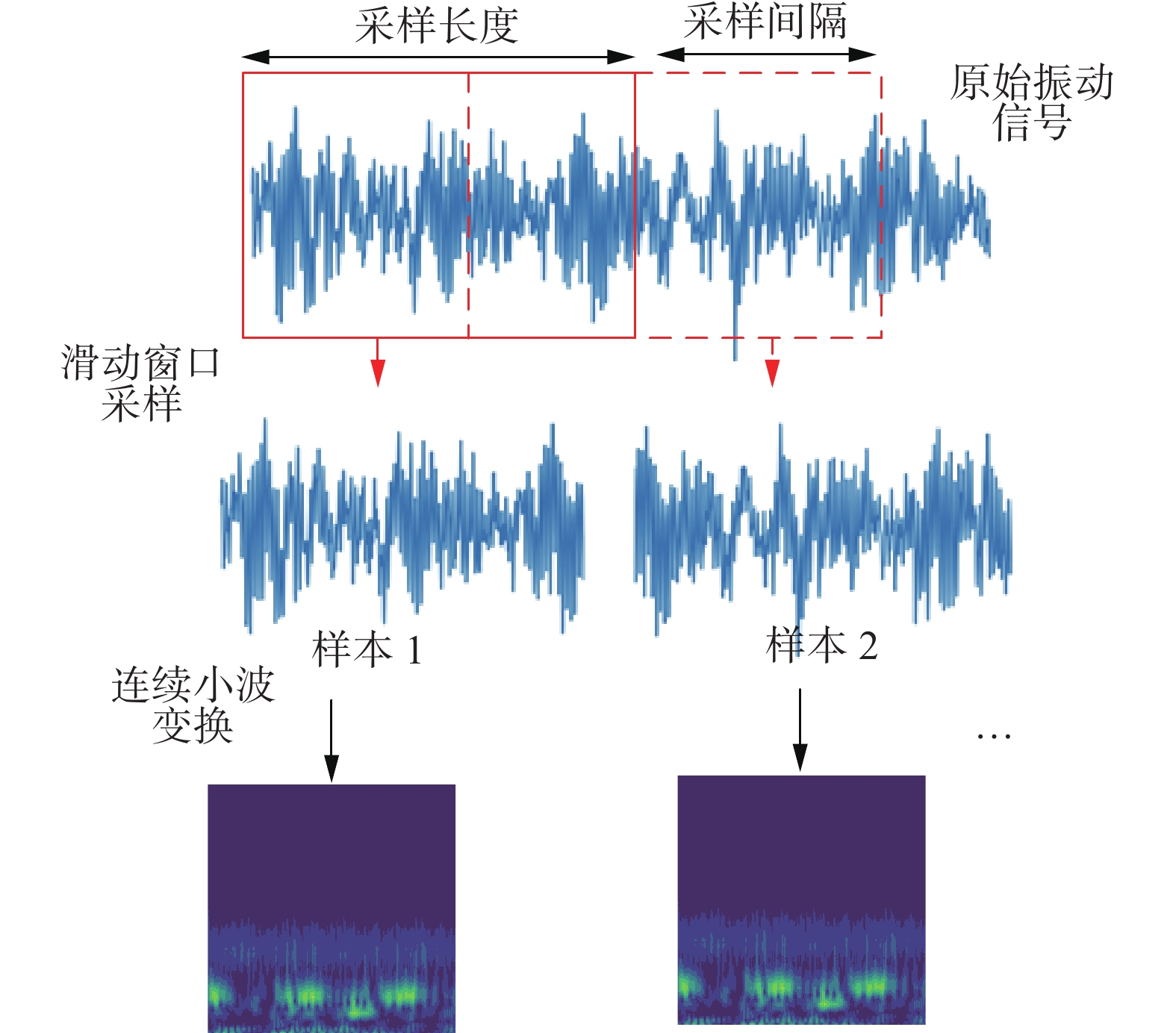
如图4所示，首先对原始振动信号进行滑动窗口采样处理。即振动信号文件中从头开始以sample_interval为滑动步长，sample_length为窗口长度，逐个截取振动信号作为一个独立的样本，而每一个样本的标签即为原始振动信号文件的标签。然后对上一步得到的单独样本进行CWT处理。即使用小波函数
$\psi (t)$ 对信号样本$x(t)$ 执行连续小波变换的过程。选择合适的母小波是连续小波变换的关键。常用的母小波函数包括Haar、Meyer、Coiflet和Morlet。由于Morlet函数与轴承缺陷产生的冲击特性相匹配，因此本研究采用Morlet函数进行连续波变换。Morlet函数在时域的定义是：
图 4 滑动窗口采样示意Fig. 4 sliding window sampling下载:
全尺寸图片
$$ \psi (t) = C{{\rm{e}}^{ - \tfrac{{{t^2}}}{2}}}\cos 5x $$ 其中
$ C $ 是标准化常数。Morlet连续小波变化即将1.1节的小波函数使用Morlet函数的代替，可以将一个一维振动信号转化为关于时域和频域的二维数据，之后用Matplotlib画出能量热力图作为一个时频域图片样本。图4为对一维振动样本采样后再进行连续小波变换的处理结果。2.2 Lightweight模型设计
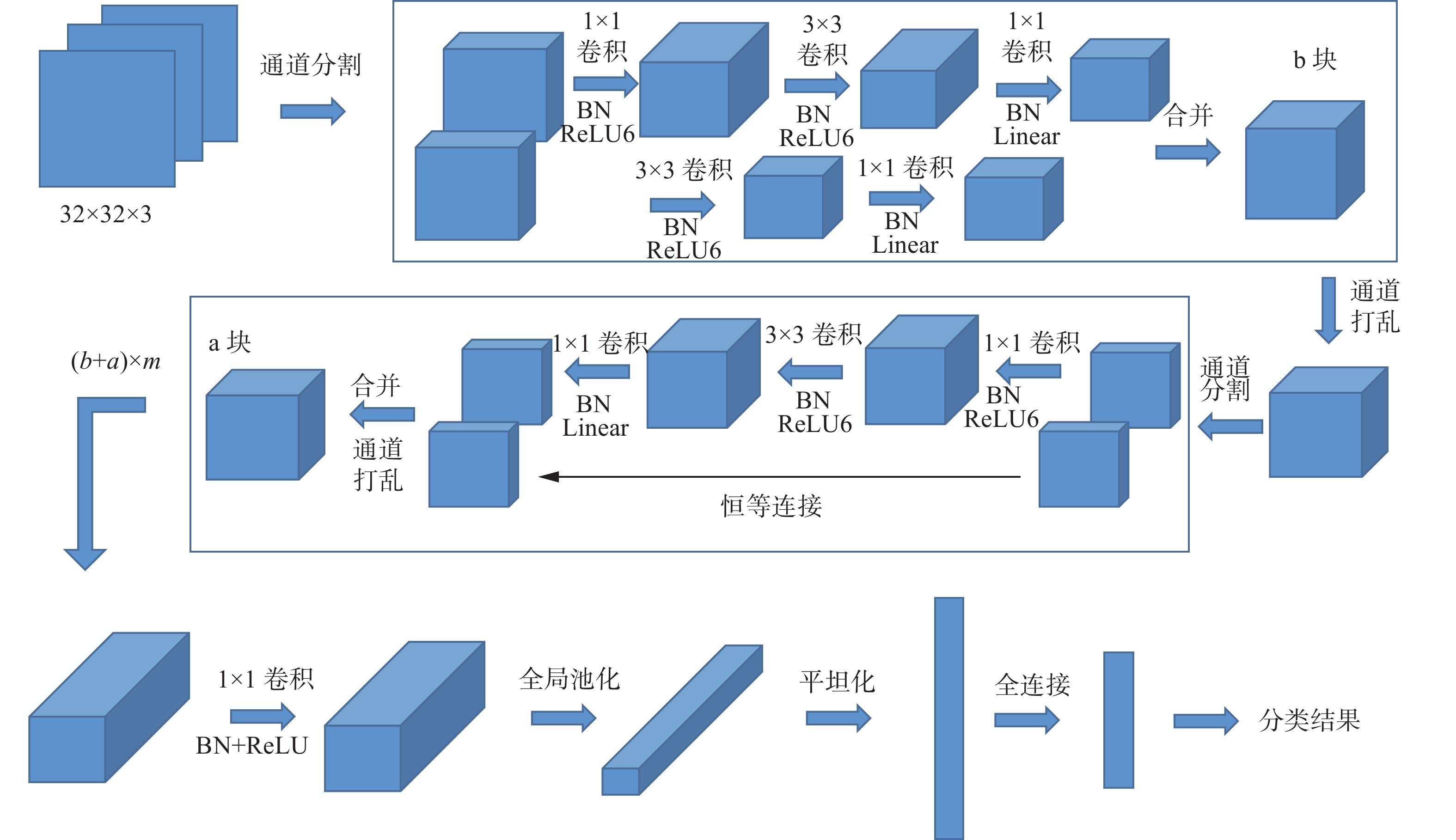
许多经典的轻量化神经网络通过大幅度的尺寸缩减来减少总参数量[21]，现有的研究已经表明，这样操作会导致准确率的损失。与大大降低参数的方法不同，本文方法应用了分组卷积和通道混洗可以在不损失模型特征提取能力的同时显著的降低计算量的特性[20]。所提出的LightweightNet由2个模块组成：轻量级特征提取器和分类器。轻量级特征提取器主要由LightweightNet块组成。
2.2.1 Lightweight块
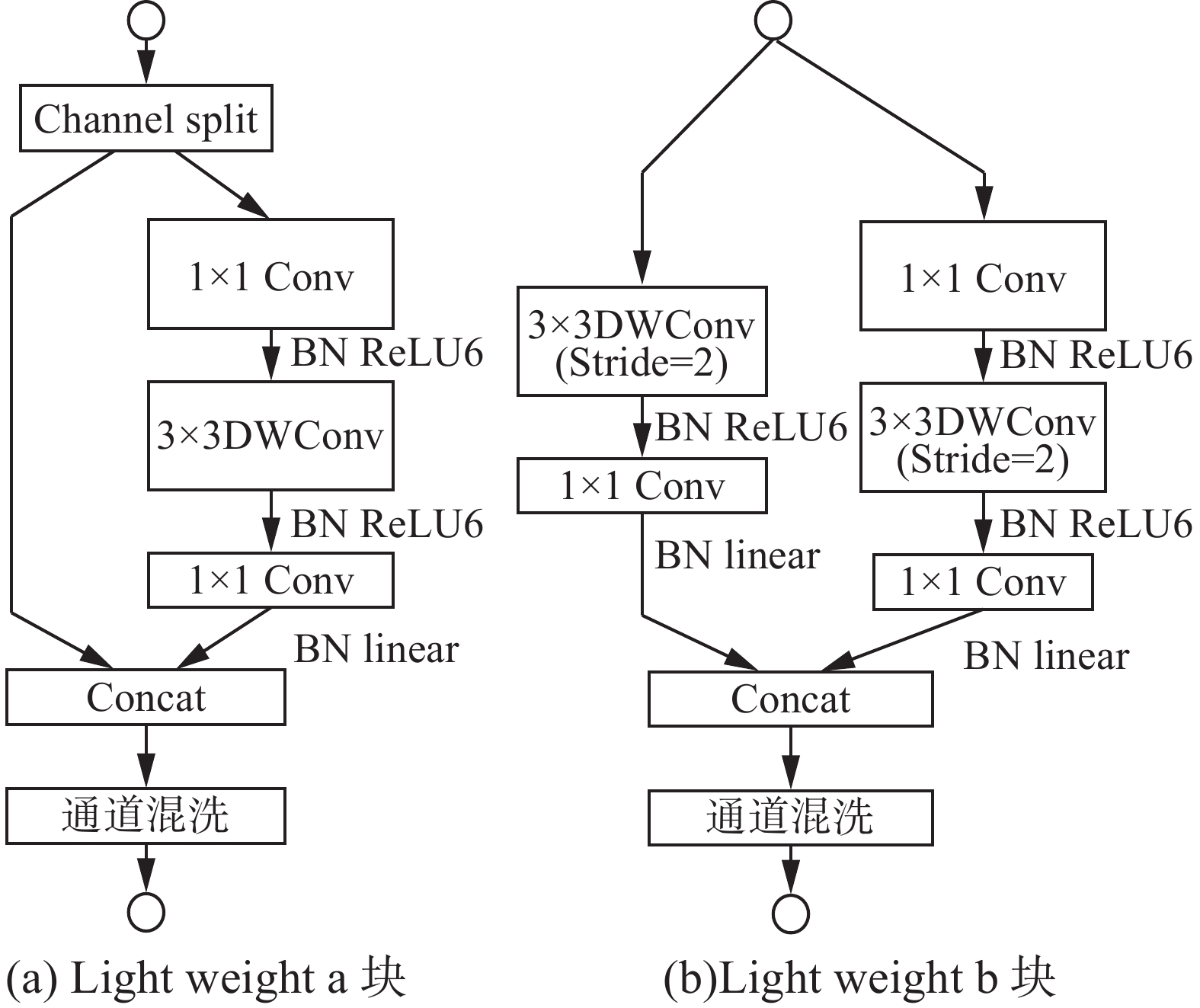
如图5为LightweightNet块结构，其中包含第一节描述的分组卷积、逐点卷积和通道混洗等操作。Lightweight块分a、b块，其中a块中
$ 3 \times 3 $ 的DWCov步长为1，不会改变特征向量的大小，主要用来提取故障特征；b块中$ 3 \times 3 $ 的DWCov步长为2，会将特征向量的长度和宽度变为原来的1/2，除了可以提取特征，还可以用来降维。
图 5 LightweightNet块结构Fig. 5 Lightweightnet block structure下载:
全尺寸图片
LightweightNet块本质上是残差块，但加入了通道分组、倒残差结构等经量化网络设计元素。对于a块，首先进行通道分割，即一半的通道特征经过右边主路径的处理，另一部分的通道直接进行恒等映射。对于右边的主路径中，整体的形状是一个倒残差，首先进行
$ 1 \times 1 $ 的点卷积，提升特征向量的通道，然后使用$ 3 \times 3 $ 的DWCov进行故障特征提取，最后使用$ 1 \times 1 $ 的点卷积将特征向量的通道数恢复至原先的大小。然后将主路径处理后到的特征向量与分支路径的特征向量进行拼接，最后添加通道混洗操作将合并后的特征向量进行通道打乱。由MobileNetV2论文[22]可知，ReLU函数会对低维特征造成大量损失，而对高维特征信息造成损失较小，因此在a块主路径的前两个卷积计算后，采用了BN层和ReLU6激活函数，在最后的卷积层后添加了BN层和线性激活。对于b块，与a不同的是首先并没有最开始的通道分割操作，即主路径与分支路径均处理同样的输入特征向量，右侧主路径与a块一致为同样的3个卷积层，但中间的
$ 3 \times 3 $ 的DWCov步长设为2，使输出向量的长宽均变为原来的1/2。左侧分支路径的处理为两层卷积层，分别是步长为2的$ 3 \times 3 $ 的DWCov和$ 1 \times 1 $ 的点卷积。这里2个分支中最后的$ 1 \times 1 $ 点卷积个数均在之后整个模型建立时设置，用来增加通道数。最后两个分支的输出经过向量拼接和通道混洗后输出，由此可知，经过b块处理后的特征向量，长宽会变为原来的1/2，通道数相应增加。2.2.2 LightweightNet整体结构
如图6，本文提出的 LightweightNet模型由轻量级特征提取器和分类器组成。轻量级特征提取器包含LightweightNet a块、b块，既考虑到模型的轻量化，又保证模型具有足够的特征提取能力。具体是一个b块后跟若干个a块组成一个小的特征处理单元，然后重复类似的特征处理单元使模型具有足够的特征提取能力。经过轻量级特征提取器处理后的向量输出，进行一次卷积降维然后再进行全局池化操作，最后输入到分类器中进行故障分类。此处的分类器由一层全连接神经网络组成，主要作用是进行故障分类，最后一层全连接节点的个数由分类的类别数决定，例如对于本文实验要进行的CWRU数据集故障诊断任务是10个故障类别，故对应的全连接节点个数为10。对于其他不同的分类数，动态调整最后一层神经节点的个数即可，具有非常大的灵活性。
图 6 LightweighNet结构Fig. 6 LightweightNet structure下载:
全尺寸图片
2.2.3 时间复杂度分析
LightweightNet块的具有轻量级的计算开销。与经典卷积神经网络ResNet[23] (瓶颈设计)和ResNeXt[24]相比，在相同的设置下，本文的LightweightNet块结构的复杂性更小。对于给定的输入维度为
$ c \times h \times w $ 的特征图，$ 3 \times 3 $ DWCov处的通道数为$ m $ ，ResNet需要的计算量为$ hw\left( {2cm + 9{m^2}} \right) $ FLOPs，ResNeXt需要的计算量为$ hw\left( {2cm + 9{m^2}/g} \right) $ FLOPs，而本文的LightweightNet a块计算开销仅为$ hw(cm + 9m) $ FLOPs。2.3 基于CWT-LightweightNet的轴承故障诊断流程
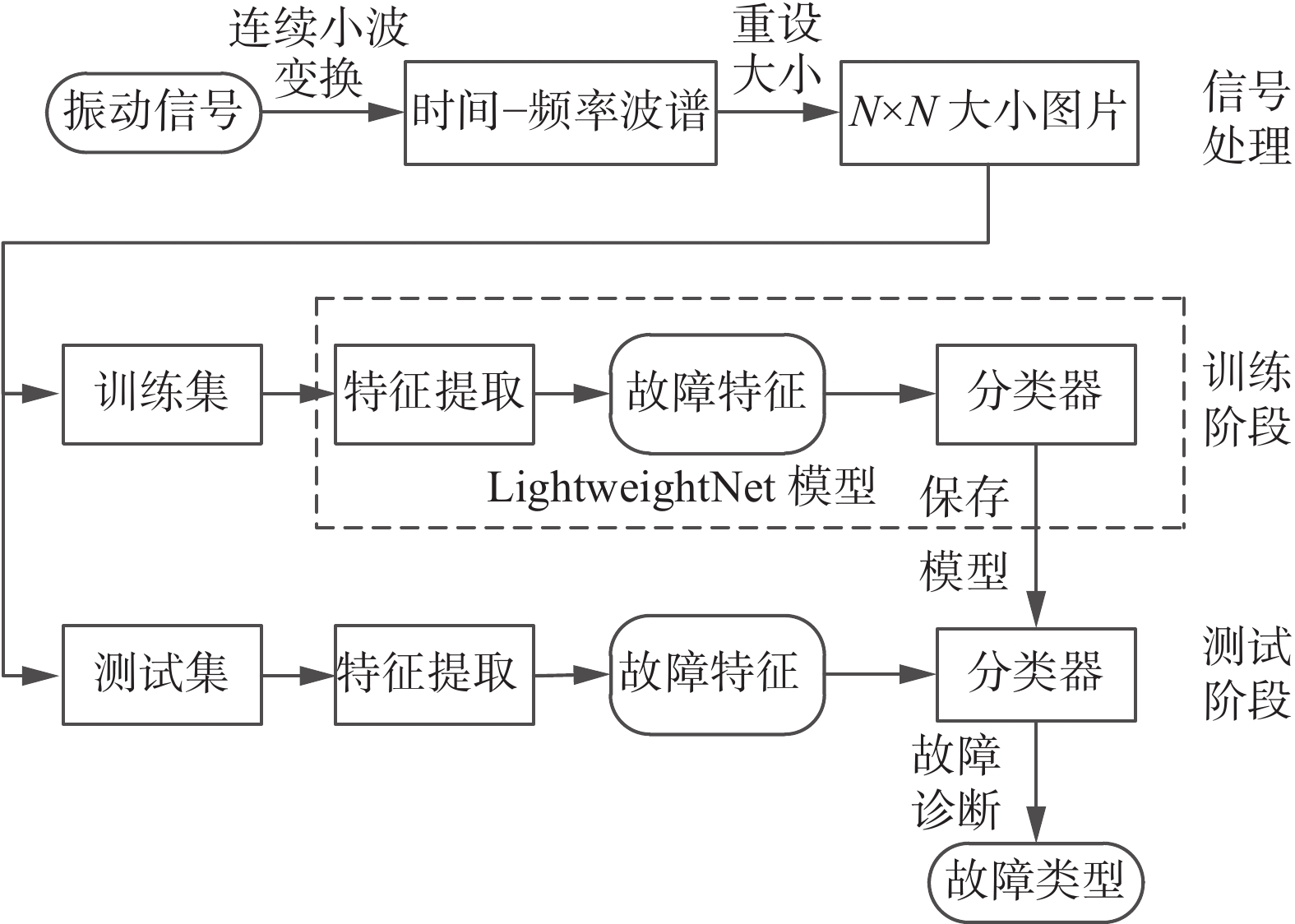
如图7所示，结合 CWT和LightweightNet的轴承实时故障诊断方法整体流程如下：
图 7 故障诊断流程Fig. 7 Fault diagnosis process下载:
全尺寸图片
1）滑动窗口样本生成：对于原始振动信号数据文件，每sample_length连续的数据点作为一个样本，将滑动步长设定为sample_interval不间断地从原始数据文件中进行滑动窗口采样，样本故障标签为数据文件标签。
2）连续小波变换生成图片：对于步骤1）的每一个样本，将一维振动数据样本经过连续小波变换后转成二维样本，再使用Matplotlib做图库画出彩色的三通道时频图，并调整图片的大小以适合后续的模型输入。按照合适的比例把每个图片样本打乱并分割为练习集和测试集,分别进行后面的训练和测试。
3）模型训练：将步骤2）中选择的训练集样本输入本文设计的LightweightNet模型进行前向传播计算和反向传播权重更新，选择各种不同的超参数进行多次实验后，确定效果最好的超参数并将对应的神经网络模型保存。
4）模型测试：将步骤2）中选择的测试集样本输入到本文设计的LightweightNet模型中进行前向传播，得到最后一层的全连接层的输出即为模型的诊断结果。
3. 实验与结果分析
为了验证本文方法（CWT-LightweightNet）的优越性，选择凯斯西储大学故障轴承数据集[25]（Case Western Reserve University, CWRU）为验证数据集，选择文献[19]方法，CWT-CNN，CWT-MobileNet，CWT-ShuffleNet方法作为对比方法进行试验验证。文献[19]使用CWT和CNN进行特征提取，最后使用gcForest进行故障分类，其他几种对比方法为使用普通CNN或经典轻量级卷积神经网络代替LightweightNet。
3.1 数据集选择与处理
CWRU数据集由美国凯斯西储大学轴承数据中心提供，其中每个信号数据均使用mat格式文件存储，由不同状态的轴承在具体运行条件下放在试验台上运行并采集而来，每种条件用故障位置、故障深度、电机负载和采样频率4个实验变量表述。对于轴承故障位置，分为内环故障（inner fault, IF）、球故障（ball fault, BF）和外环故障（outer fault, OF）3种，无故障的情况记为正常（normal, NO）；对于故障深度，电火花单点加工故障分为7、14、21、28和40 mil（1 mil =0.00254 cm），对于电机负载，电机在4种不同的负载（0、735.499、1470.998、2206.497 W）以恒定的速度运行；针对采样频率，驱动端轴承有12 kHz和48 kHz。
由于实际生产中旋转轴承大多数时间负载不为0，本实验考虑所有非零负载下的轴承故障诊断。诊断目标为从振动信号中诊断出具体的10种健康状态，包括3种故障位置与3种故障深度组合的9种故障状态（7 mil内环故障、7 mil外环故障、7 mil球故障、14 mil内环故障、14 mil外环故障、14 mil球故障、21 mil内环故障、21 mil外环故障、21 mil球故障）和一种正常状态。考虑到CWRU数据集在个别条件下的数据缺失，选择负载为735.499、1470.998、2206.497 W，采样频率12 kHz的驱动端轴承故障数据和正常数据。具体样本文件如表1和表2表示。
表 1 本文使用的正常数据文件Table 1 Normal data files used in this paper电机负载
(HP)马达速度/
$\left( {{\text{r}} \cdot {\text{mi}}{{\text{n}}^{ - 1}}} \right)$正常基准
数据文件1 1772 Normal_1(98.mat) 2 1750 Normal_2(99.mat) 3 1730 Normal_3(100.mat) 表 2 本文使用的故障数据文件Table 2 Fault data file used in this paper故障深度/
mil电机负载/
W马达速度/
$\left( {{\text{r}} \cdot {\text{mi}}{{\text{n}}^{ - 1}}} \right)$内环故障(IF)
数据文件球故障(BF)
数据文件外环故障(OF)
@6:00数据文件7 735.499 1772 106.mat 119.mat 131.mat 1470.998 1750 107.mat 120.mat 132.mat 2206.497 1730 108.mat 121.mat 133.mat 14 735.499 1772 170.mat 186.mat 198.mat 1470.998 1750 171.mat 187.mat 199.mat 2206.497 1730 172.mat 188.mat 200.mat 21 735.499 1772 210.mat 223.mat 235.mat 1470.998 1750 211.mat 224.mat 236.mat 2206.497 1730 212.mat 225.mat 237.mat 由于数据集每个文件含有240 000个数据点，对于诊断任务过大。使用2.1节描述的滑动窗口采样方法，窗口大小sample_length设置为1024，滑动步长sample_internal设置为384，每个数据文件生成的样本取前300个，则根据表1和表2选择的数据集，一共可以生成9 000个样本，这些样本对应的标签为原数据文件的故障标签。
对于上述经过滑动窗口生成的9 000个单独的数据样本，选择Morlet母小波函数进行连续小波变换，并使用Python的Matplotlib作图库画出三通道彩色能量图。如图8为不同健康状态的数据样本经过CWT后生成的彩色图片，从中可以看出，健康状态的轴承随着时间的推移能量呈现均匀的趋势，而故障状态的能量分布规律与正常状态的具有明显的不同。这说明，CWT可以提取故障的一般特征规律显示到时频图片中。
图 8 连续小波变换处理结果Fig. 8 Continuous wavelet transform processing results下载:
全尺寸图片
3.2 实验设置
为了减小神经网络的计算量，将上一步生成的9 000张彩色图片大小设定成为32像素×32像素。并打乱顺序，再根据训练集：验证集：测试集为8∶1∶1的比例分割。构建2.2.2节描述的 LightweightNet神经网络模型，其中LightweightNet b块使用3个，LightweightNet a块使用一个，且位置跟在第1个b块后面，3个b块的输出通道数依次设置为16、32、48，分类器中卷积层输出通道数设为96，模型的最后一层节点个数设置为10。表3为模型各层输出维度和参数量。
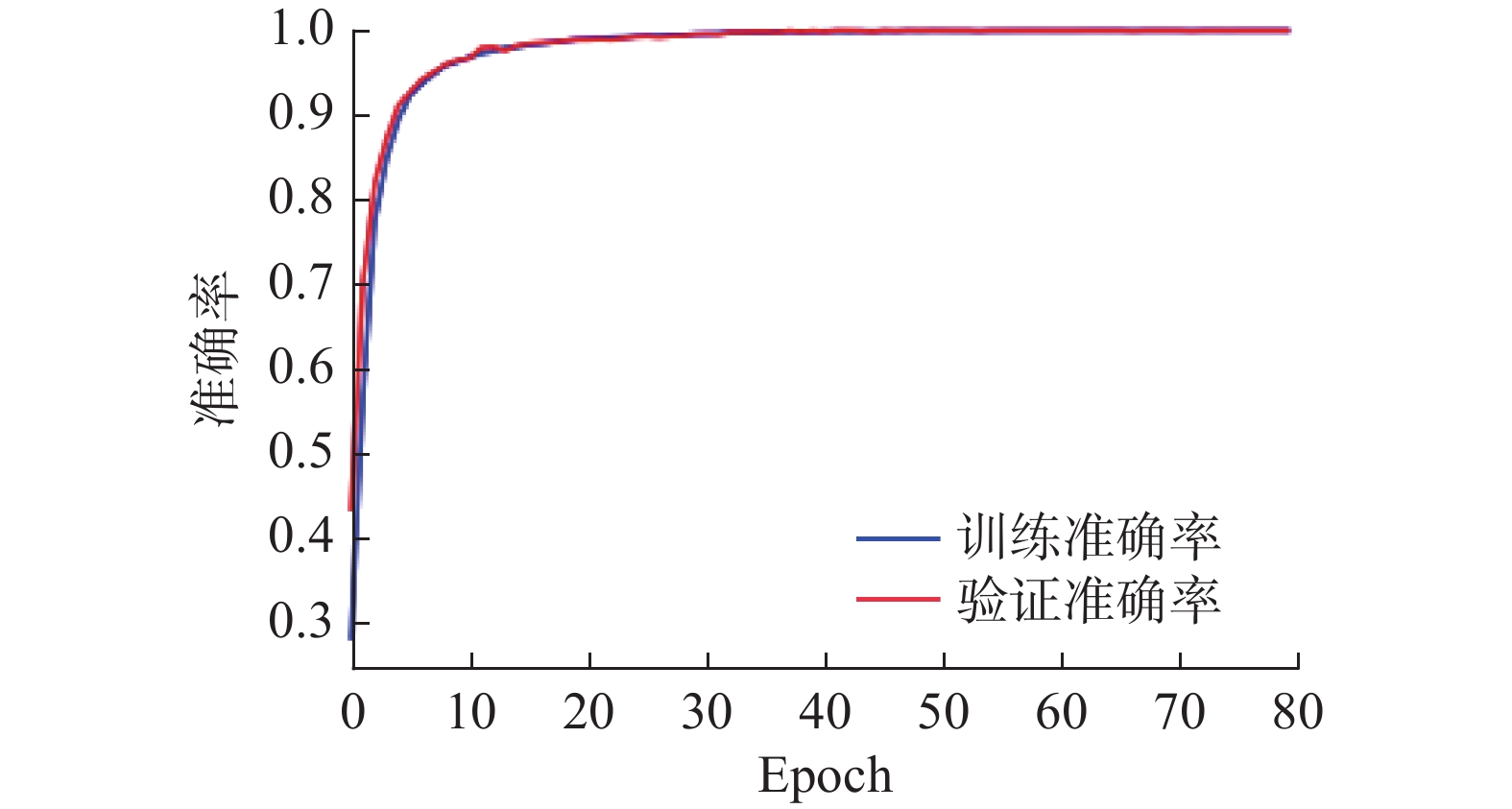
表 3 神经网络各层输出维度和参数数量Table 3 Output dimension and parameter quantity of each layer of neural network层（类型） 输出维度 参数量 input (InputLayer) (_, 32, 32, 3) 0 LightweightBblock0 (_, 16, 16, 16) 959 LightweightAblock0 (_, 16, 16, 16) 1 056 LightweightBblock1 (_, 8, 8, 32) 3 600 LightweightBblock2 (_, 4, 4, 48) 8 192 conv5 (ConvBNReLU) (_, 4, 4, 96) 4 992 globalpool (GAP) (_, 96) 0 fc (Dense) (_, 10) 970 softmax_6 (Softmax) (_, 10) 0 训练模型使用Adam优化器，基本参数设置分别为lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon= 1×10−8；训练轮次epochs=80，批处理训练参数batch_size=128，将训练集输入到模型中进行参数训练。本文所有实验均在具有GPU的Windows 10，64位操作系统计算机上进行，CPU型号为i5-10600，运行内存为16 GB。编程语言使用的是Python 3.7，神经网络模型构建使用TensorFlow 2.3和Keras 2.4；矩阵处理使用numpy和pandas库；小波变换使用的是pywt库；如图9和10为模型训练过程的损失曲线和准确率曲线变化示意图。经过多次训练模型在验证集上的准确率可达到100%，在训练后将模型保存可用于之后的测试过程。
图 9 模型训练损失曲线Fig. 9 Model training loss curve下载:
全尺寸图片
图 10 模型训练准确率曲线Fig. 10 Model training accuracy curve下载:
全尺寸图片
3.3 对比分析
实现本节开头说明的五种对比模型并使用上述训练集进行训练，在模型达到最优时确定参数保存模型，之后使用测试集进行多次测试，将本文模型和5种对比模型测试集准确率结果记录到表4，其中平均准确率
$ {{{A}}_{{\text{ave}}}} $ 为多次实验准确的平均值：表 4 6种模型的测试集故障诊断准确率结果Table 4 Fault diagnosis accuracy results of test sets of six models模型 第1次/% 第2次/% 第3次/% 第4次/% 第5次/% 平均准确率/% 方差 CWT-LightweightNet 99.72 99.72 99.77 99.72 99.77 99.74 0.0006 CWT-CNN-GCF 98.00 98.89 98.67 99.11 99.33 98.80 0.2084 CWT-CNN 97.77 98.44 98.22 98.66 97.55 98.13 0.1702 CWT-AlexNet 99.30 99.44 99.66 99.77 99.56 99.55 0.0270 CWT-MobileNet 98.20 99.30 99.30 98.67 97.78 98.65 0.3610 CWT-ShuffletNet 95.33 90.22 94.00 95.77 91.55 93.37 4.6467 $$ {{{A}}_{{\text{ave}}}} = \frac{1}{5}\sum\limits_{i = 1}^5 {{{{A}}_i}} $$ 表5记录模型的平均诊断时间、模型参数量和模型占用内存和存储空间大小信息。参数量
$ {N_{{\text{par}}}} $ 为表 5 6种模型的测试集故障诊断其他指标Table 5 Other indicators of fault diagnosis of six models on the test set模型 诊断时间/ms 参数量 所占内存/MB 模型存储/MB CWT-LightweightNet 82 19769 0.5808 0.20 CWT-CNN-GCF 1134 1261450 5.3677 5.07 CWT-CNN 320 1261450 5.3677 5.07 CWT-AlexNet 531 46787978 181.2720 187 CWT-MobileNet 472 2270794 13.2001 9.34 CWT-ShuffletNet 358 359994 9.7692 1.91 $$ {N_{{\text{par}}}} = {N_{{\text{tra}}}} + {N_{{\text{untra}}}} $$ 式中：
$ {N_{{\text{tra}}}} $ 表示神经网络可训练参数量；$ {N_{{\text{untra}}}} $ 表示不可训练参数量。从表4中可以看出，本文提出的方法在多次测试集的诊断任务上具有最高的平均准确率99.74%，且多次实验结果最为稳定。这说明设计的LightweightNet b块和a块具有非常好的故障特征提取能力。其次效果比较好的是CWT-AlexNet，平均值为99.55%，因为AlexNet是一个大型的卷积神经网络，具有上千万的参数量和深层的卷积来对数据集进行拟合。对比模型效果最差的是CWT-CNN方法，这是因为一般的CNN层数少且没有使用优化手段，而文献[19]对CWT-CNN方法进行改进，使用gcForest进行故障分类并提升一定的效果，但整体效果还是差于本文算法，且运行时间比较长。对于使用经典轻量级卷积神经网路的CWT-MobileNet方法，在保证参数量小于CWT-AlexNet方法的同时，准确率没有过多的下降，说明使用的轻量级设计元素可以在保证降低参数量的同时不会损失过多的特征提取能力，但由于MobileNet没有经过针对故障特征提取任务的专门设计，所以在轴承故障诊断任务中效果不如本文的LightweightNet网络。
此外，本文方法在CWRU数据集上可以实现平均99.74%的准确率，均高于其他5种对比模型；并且具有最小的方差，为0.0006，即本方法的稳定性也是最好的；在诊断用时方面，本方法多次实验的平均诊断时间为82 ms，是CWT-CNN方法的3/10，不到文献[19]方法的1/10，基本实现实时的故障诊断。如表5所示，模型存储方面，LightweightNet模型参数量不到2×104，模型参数存储只需要0.2 MB的空间，远远小于CWT-AlexNet的187 MB和CWT-MobileNet的9.34 MB，不到CWT-ShuffletNet模型的1/9，不到CWT-CNN的1/25；占用内存方面， LightweightNet模型占用内存极小，诊断时参数特征图总占用总内存仅为0.58 MB，不到CNN的1/9，不到ShuffleNet的1/16，是MobileNet的1/22，大约是AlexNet的1/312，在各种对比模型中占据绝对的优势。
4. 结束语
本文针对滚动轴承的快速故障诊断问题，考虑到一般的卷积神经网络参数量大、占用硬件资源多，提出一种结合CWT和LightweightNet的方法，使用CWT提取时频域特征，构建轻量级神经网络模型LightweightNet用于故障分类。使用CWRU数据集进行方法验证表明，本方法的诊断准确率高达99.74%，诊断用时仅用82 ms，基本可以实现实时的故障诊断，且模型参数、内存使用和模型存储空间都远小于普通或经典轻量级卷积神经网络模型。
-
图 1 标准卷积核与深度可分离卷积核
Fig. 1 Standard convolution kernel and deep separable convolution kernel
下载:
全尺寸图片
图 2 分组卷积
Fig. 2 Group convolution
下载:
全尺寸图片
图 3 通道混洗
Fig. 3 Channel shuffle
下载:
全尺寸图片
图 4 滑动窗口采样示意
Fig. 4 sliding window sampling
下载:
全尺寸图片
图 5 LightweightNet块结构
Fig. 5 Lightweightnet block structure
下载:
全尺寸图片
图 6 LightweighNet结构
Fig. 6 LightweightNet structure
下载:
全尺寸图片
图 7 故障诊断流程
Fig. 7 Fault diagnosis process
下载:
全尺寸图片
图 8 连续小波变换处理结果
Fig. 8 Continuous wavelet transform processing results
下载:
全尺寸图片
图 9 模型训练损失曲线
Fig. 9 Model training loss curve
下载:
全尺寸图片
图 10 模型训练准确率曲线
Fig. 10 Model training accuracy curve
下载:
全尺寸图片
表 1 本文使用的正常数据文件
Table 1 Normal data files used in this paper
电机负载
(HP)马达速度/
$\left( {{\text{r}} \cdot {\text{mi}}{{\text{n}}^{ - 1}}} \right)$正常基准
数据文件1 1772 Normal_1(98.mat) 2 1750 Normal_2(99.mat) 3 1730 Normal_3(100.mat) 表 2 本文使用的故障数据文件
Table 2 Fault data file used in this paper
故障深度/
mil电机负载/
W马达速度/
$\left( {{\text{r}} \cdot {\text{mi}}{{\text{n}}^{ - 1}}} \right)$内环故障(IF)
数据文件球故障(BF)
数据文件外环故障(OF)
@6:00数据文件7 735.499 1772 106.mat 119.mat 131.mat 1470.998 1750 107.mat 120.mat 132.mat 2206.497 1730 108.mat 121.mat 133.mat 14 735.499 1772 170.mat 186.mat 198.mat 1470.998 1750 171.mat 187.mat 199.mat 2206.497 1730 172.mat 188.mat 200.mat 21 735.499 1772 210.mat 223.mat 235.mat 1470.998 1750 211.mat 224.mat 236.mat 2206.497 1730 212.mat 225.mat 237.mat 表 3 神经网络各层输出维度和参数数量
Table 3 Output dimension and parameter quantity of each layer of neural network
层（类型） 输出维度 参数量 input (InputLayer) (_, 32, 32, 3) 0 LightweightBblock0 (_, 16, 16, 16) 959 LightweightAblock0 (_, 16, 16, 16) 1 056 LightweightBblock1 (_, 8, 8, 32) 3 600 LightweightBblock2 (_, 4, 4, 48) 8 192 conv5 (ConvBNReLU) (_, 4, 4, 96) 4 992 globalpool (GAP) (_, 96) 0 fc (Dense) (_, 10) 970 softmax_6 (Softmax) (_, 10) 0 表 4 6种模型的测试集故障诊断准确率结果
Table 4 Fault diagnosis accuracy results of test sets of six models
模型 第1次/% 第2次/% 第3次/% 第4次/% 第5次/% 平均准确率/% 方差 CWT-LightweightNet 99.72 99.72 99.77 99.72 99.77 99.74 0.0006 CWT-CNN-GCF 98.00 98.89 98.67 99.11 99.33 98.80 0.2084 CWT-CNN 97.77 98.44 98.22 98.66 97.55 98.13 0.1702 CWT-AlexNet 99.30 99.44 99.66 99.77 99.56 99.55 0.0270 CWT-MobileNet 98.20 99.30 99.30 98.67 97.78 98.65 0.3610 CWT-ShuffletNet 95.33 90.22 94.00 95.77 91.55 93.37 4.6467 表 5 6种模型的测试集故障诊断其他指标
Table 5 Other indicators of fault diagnosis of six models on the test set
模型 诊断时间/ms 参数量 所占内存/MB 模型存储/MB CWT-LightweightNet 82 19769 0.5808 0.20 CWT-CNN-GCF 1134 1261450 5.3677 5.07 CWT-CNN 320 1261450 5.3677 5.07 CWT-AlexNet 531 46787978 181.2720 187 CWT-MobileNet 472 2270794 13.2001 9.34 CWT-ShuffletNet 358 359994 9.7692 1.91 -
[1] LI Chuan, DE OLIVEIRA J V, CERRADA M, et al. A systematic review of fuzzy formalisms for bearing fault diagnosis[J]. IEEE transactions on fuzzy systems, 2019, 27(7): 1362–1382. doi: 10.1109/TFUZZ.2018.2878200 [2] 姚峰林, 谢长开, 吕世宁, 等. 基于小波包变换和ELM的滚动轴承故障诊断研究[J]. 安全与环境学报, 2021, 21(6): 2466–2472. doi: 10.13637/j.issn.1009-6094.2020.0999 YAO Fenglin, XIE Changkai, LYU Shining, et al. Research on fault diagnosis of rolling bearings based on wavelet packet transform and ELM[J]. Journal of safety and environment, 2021, 21(6): 2466–2472. doi: 10.13637/j.issn.1009-6094.2020.0999 [3] 陈仁祥, 周君, 胡小林, 等. 基于深度Q学习和连续小波变换的旋转机械故障诊断方法[J]. 振动工程学报, 2021, 34(5): 1092–1100. CHEN Renxiang, ZHOU Jun, HU Xiaolin, et al. Fault diagnosis method of rotating machinery based on deep Q-learning and continuous wavelet transform[J]. Journal of vibration engineering, 2021, 34(5): 1092–1100. [4] WANG Xin, MAO Dongxing, LI Xiaodong. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network[J]. Measurement, 2021, 173: 108518. doi: 10.1016/j.measurement.2020.108518 [5] 潘琳鑫, 巩永旺, 晏生莲. 基于改进一维卷积神经网络的轴承故障诊断方法[J/OL]. 软件导刊: 1−5.[2023−04−05].http://kns.cnki.net/kcms/detail/42.1671.TP.20221207.1119.014.html. Pan Linxin, Gong Yongwang, Yan Shenglian. A bearing fault diagnosis method based on improved one-dimensional convolutional neural network [J/OL]. Software Guide: 1−5.[2023−04−05].http://kns.cnki.net/kcms/detail/42.1671.TP.20221207.1119.014.html. [6] YANG Zhibo, ZHANG Junpeng, ZHAO Zhibin, et al. Interpreting network knowledge with attention mechanism for bearing fault diagnosis[J]. Applied soft computing, 2020, 97: 106829. doi: 10.1016/j.asoc.2020.106829 [7] ZOU Fengqian, ZHANG Haifeng, SANG Shengtian, et al. An anti-noise one-dimension convolutional neural network learning model applying on bearing fault diagnosis[J]. Measurement, 2021, 186: 110236. doi: 10.1016/j.measurement.2021.110236 [8] ZHAO Jing, YANG Shaopu, LI Qiang, et al. A new bearing fault diagnosis method based on signal-to-image mapping and convolutional neural network[J]. Measurement, 2021, 176: 109088. doi: 10.1016/j.measurement.2021.109088 [9] BAI Ruxue, XU Quansheng, MENG Zong, et al. Rolling bearing fault diagnosis based on multi-channel convolution neural network and multi-scale clipping fusion data augmentation[J]. Measurement, 2021, 184: 109885. doi: 10.1016/j.measurement.2021.109885 [10] 高淑芝, 裴志明, 张义民. 动态自适应学习率优化的卷积神经网络轴承故障诊断方法[J/OL]. 机械设计与制造: 1−5.[2023−04−05].DOI: 10.19356/j.cnki.1001-3997.20230210.031. GAO Shuzhi, PEI Zhiming, ZHANG Yimin. Dynamic adaptive learning rate optimized convolutional neural network bearing fault diagnosis method [J/OL]. Mechanical design and manufacturing: 1−5.[2023−04−05].DOI: 10.19356/j.cnki.1001-3997.20230210.031. [11] 李欢, 吕勇, 袁锐, 等. 基于深度卷积神经网络的滚动轴承迁移故障诊断[J]. 组合机床与自动化加工技术, 2023(2): 90–94. LI Huan, LYU Yong, YUAN Rui, et al. Fault diagnosis of rolling bearing migration based on deep convolution neural network[J]. Modular machine tool and automatic processing technology, 2023(2): 90–94. [12] MENG Zong, ZHAN Xuyang, LI Jing, et al. An enhancement denoising autoencoder for rolling bearing fault diagnosis[J]. Measurement, 2018, 130: 448–454. doi: 10.1016/j.measurement.2018.08.010 [13] CLAESSENS B J, VRANCX P, RUELENS F. Convolutional neural networks for automatic state-time feature extraction in reinforcement learning applied to residential load control[J]. IEEE transactions on smart grid, 2018, 9(4): 3259–3269. doi: 10.1109/TSG.2016.2629450 [14] ZOU Yisheng, LIU Yongzhi, DENG Jialin, et al. A novel transfer learning method for bearing fault diagnosis under different working conditions[J]. Measurement, 2021, 171: 108767. doi: 10.1016/j.measurement.2020.108767 [15] HAO Shijie, GE Fengxiang, LI Yanmiao, et al. Multisensor bearing fault diagnosis based on one-dimensional convolutional long short-term memory networks[J]. Measurement, 2020, 159: 107802. doi: 10.1016/j.measurement.2020.107802 [16] XU Zifei, MEI Xuan, WANG Xinyu, et al. Fault diagnosis of wind turbine bearing using a multi-scale convolutional neural network with bidirectional long short term memory and weighted majority voting for multi-sensors[J]. Renewable energy, 2022, 182: 615–626. doi: 10.1016/j.renene.2021.10.024 [17] WU Zhenghong, JIANG Hongkai, LIU Shaowei, et al. A deep reinforcement transfer convolutional neural network for rolling bearing fault diagnosis[J]. ISA transactions, 2022, 129: 505–524. doi: 10.1016/j.isatra.2022.02.032 [18] XU Yang, LI Zhixiong, WANG Shuqing, et al. A hybrid deep-learning model for fault diagnosis of rolling bearings[J]. Measurement, 2021, 169: 108502. doi: 10.1016/j.measurement.2020.108502 [19] PENG Xu, ALEXANDER H K. RALF B, et al. Measurement of the topological Chern number by continuous probing of a qubit subject to a slowly varying Hamiltonian[EB/OL]. (2017−04−03)[2022−04−12].https://arxiv.org/abs/1704.0486. [20] ZHANG Xiangyu, ZHOU Xinyu, LIN Mengxiao, et al. ShuffleNet: an extremely efficient convolutional neural network for mobile devices[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6848−6856. [21] YAO Dechen, LIU Hengchang, YANG Jianwei, et al. A lightweight neural network with strong robustness for bearing fault diagnosis[J]. Measurement, 2020, 159: 107756. doi: 10.1016/j.measurement.2020.107756 [22] SANDLER M, HOWARD A, ZHU Menglong, et al. MobileNetV2: inverted residuals and linear bottlenecks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 4510−4520. [23] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [24] XIE Saining, GIRSHICK R, DOLLÁR P, et al. Aggregated residual transformations for deep neural networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 5987−5995. [25] SMITH W A, RANDAL R B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study[J]. Mechanical Systems and Signal Processing, 2015(64−65): 100–131.
