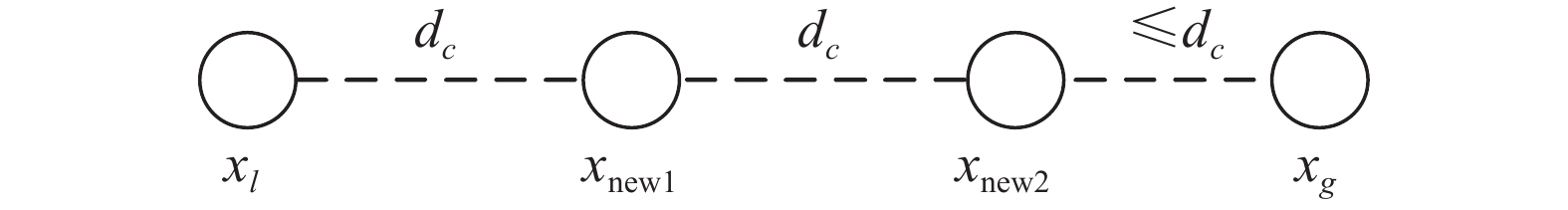DC-SMOTE oversampling method for an imbalanced dataset
-
摘要: 针对不平衡数据集在分类任务中表现不佳的问题，提出基于局部密度与集中度的过采样算法。针对数据集中所有的少数类样本点，分别利用高斯核函数与局部引力来计算局部密度与集中度；对于局部密度较小的部分有针对性地合成第一类新样本，解决类内不平衡问题。根据集中度的不同，区分出少数类样本的边界，有针对性地合成第二类新样本，达到强化边界的作用；同时，通过自适应生成新样本，有效解决大部分过采样算法没有明确过采样量或者盲目追求样本平衡度相等的问题。最后，在公开的12个不平衡数据集上进行了实验，实验结果表明，本算法在低不平衡数据集与高不平衡数据集上的应用均拥有良好的表现。Abstract: Inspired by the poor performance of imbalanced datasets in classification tasks, an oversampling algorithm based on local density and centrality is proposed. First, for all the minority sample points in the dataset, the Gaussian kernel function and local gravity are used to calculate the local density and centrality, respectively. Furthermore, the first type of new samples is synthesized for the portion with small local density to solve the imbalance problem within this kind. According to the difference of centrality, the boundaries of minority samples are distinguished, and the second kind of samples are specifically synthesized to strengthen the boundaries. Meanwhile, new samples are generated adaptively, which solves the problem that most oversampling algorithms fail to clearly define the oversampling quantity or blindly pursue the balance of the number of samples of two categories. Finally, experiments are conducted on 12 public imbalanced datasets and results reveal that the algorithm has good performance in low- and high-imbalanced datasets.
-
Keywords:
- imbalanced dataset /
- oversampling /
- Gaussian kernel /
- local gravity /
- high-imbalanced data /
- SMOTE /
- imbalance ratio /
- classification
-
现如今人类处在一个信息大爆炸的时代，伴随着科技的进步与发展，各行各业都已经积累了大量的数据，在这当中，类不平衡的数据引起了研究人员的广泛关注。类不平衡是指在数据集中，不同类别的数据在整体数据中占比悬殊的一种情况，这种关于数据的类不平衡情况广泛出现在网络入侵检测[1]、金融诈骗检测[2]、疾病诊断[3-4]、垃圾邮件的识别与过滤[5]等问题中。对于类不平衡问题来说，重要的是如何准确地判断出少数类。截至目前为止，研究人员已经在类不平衡问题的解决上有了一定的研究，主要采用两种方法，分别为数据层面的方法与算法层面的方法。
对于应用于数据层面的方法，主要有过采样和欠采样两种，原理是通过改变数据集中少数类与多数类样本的不平衡比例达到两类数据在数量上的平衡。其中对于过采样方法来说，合成少数类过采样技术(synthetic minority oversmpling technique, SMOTE)最为经典，其原理是通过人工合成新的少数类样本来达到平衡数据集的效果[6]。由于SMOTE算法的精妙设计，学者们又针对SMOTE算法的不足提出了一系列改进算法。例如：针对少数类边界的过采样算法Borderline-SMOTE[7]，该算法通过对少数类的边界针对性过采样来强化少数类边界；基于聚类的过采样算法KMeans-SMOTE[8]选择先将少数类划分为几个不同的子集，然后分别在子集中进行过采样；同样基于聚类的过采样还有谢子鹏等[9]的OEMC方法和王亮等[10]的DB-MCSMOTE方法；针对处理类内不平衡的过采样算法Knnor[11]，主要是通过识别出少数类聚集稠密区域，在该区域生成过采样点。对于欠采样方法来说，其主要原理是从多数类样本中选择一些数据进行删除来平衡数据集。最简单的欠采样方法就是随机欠采样(random undersampling, RUS)，该方法随机地在多数类样本中采样，直接删除选中的多数类样本，直到达到类间平衡。与过采样方法类似，同样对于欠采样来说也存在基于聚类的欠采样方法，如CBIS (cluster-based instance selection)[12]方法以及AUSDPC (adaptive undersampling based on density peak clustering)[13]方法，其主要原理是先对多数类聚类为多个簇，然后利用欠采样的方法移除簇内的一些样本来平衡不同类的样本。除此之外还有一些高级的采样算法，如Das等[14]考虑了少数类样本的原始分布提出的RACOG，以及Yu等[15]利用蚁群算法的ACOSampling，充分考虑多数类样本的重要程度以保证欠采样时保留重要程度较大的样本。
对于应用于算法层面的方法，第一种为敏感代价学习，原理是通过改变训练器的训练指标，将误分代价最小化作为分类器的训练目标，即在训练时过程中，为少数类误分为多数类施加较大的惩罚，而对多数类误分为少数类施加较小的惩罚[16]。另一种为集成学习法，原理是将采样技术与集成学习的理论相结合，使得分类器具有更强的泛化能力[17-18]。
截至目前为止，虽然并没有一个可以完美解决不平衡问题的方法出现，但在这其中，采样方法已经表现出了巨大的潜力。采样方法由于其针对的是数据集而不是分类器，这一优势使得采样方法可以从分类器中独立出来，不必受到分类器的限制，因而使得采样方法拥有更强的适用性。
对于类不平衡问题来说，除了类间不平衡之外，类内不平衡也是值得关注的一个难点。已经有研究表明[19]，类内不平衡往往是影响最终分类效果的关键因素。少数类样本由于分布位置不平衡以及分布密度不均匀，形成了一些位置不相邻，密度不相等的小样本子集。根据类内不平衡样本的特征，少数类与多数类样本不仅在数量上存在着较大差距，而且如果少数类样本子集中的数量过于稀少或者分布位置偏离样本空间太远的话，那么分类器在分类的过程中有可能会将这样偏离少数类样本空间的子集当作噪声样本处理，但是如果将这些子集删除，那么则会降低少数类的分类效果。所以，如何解决类内不平衡也是一个值得关注的课题。
针对以上不平衡分类中存在类间不平衡与类内不平衡的问题，本文提出了基于局部密度与集中度的过采样方法DC-SMOTE (SMOTE based on local density and centrality)。
1. 局部密度与集中度
1.1 局部密度
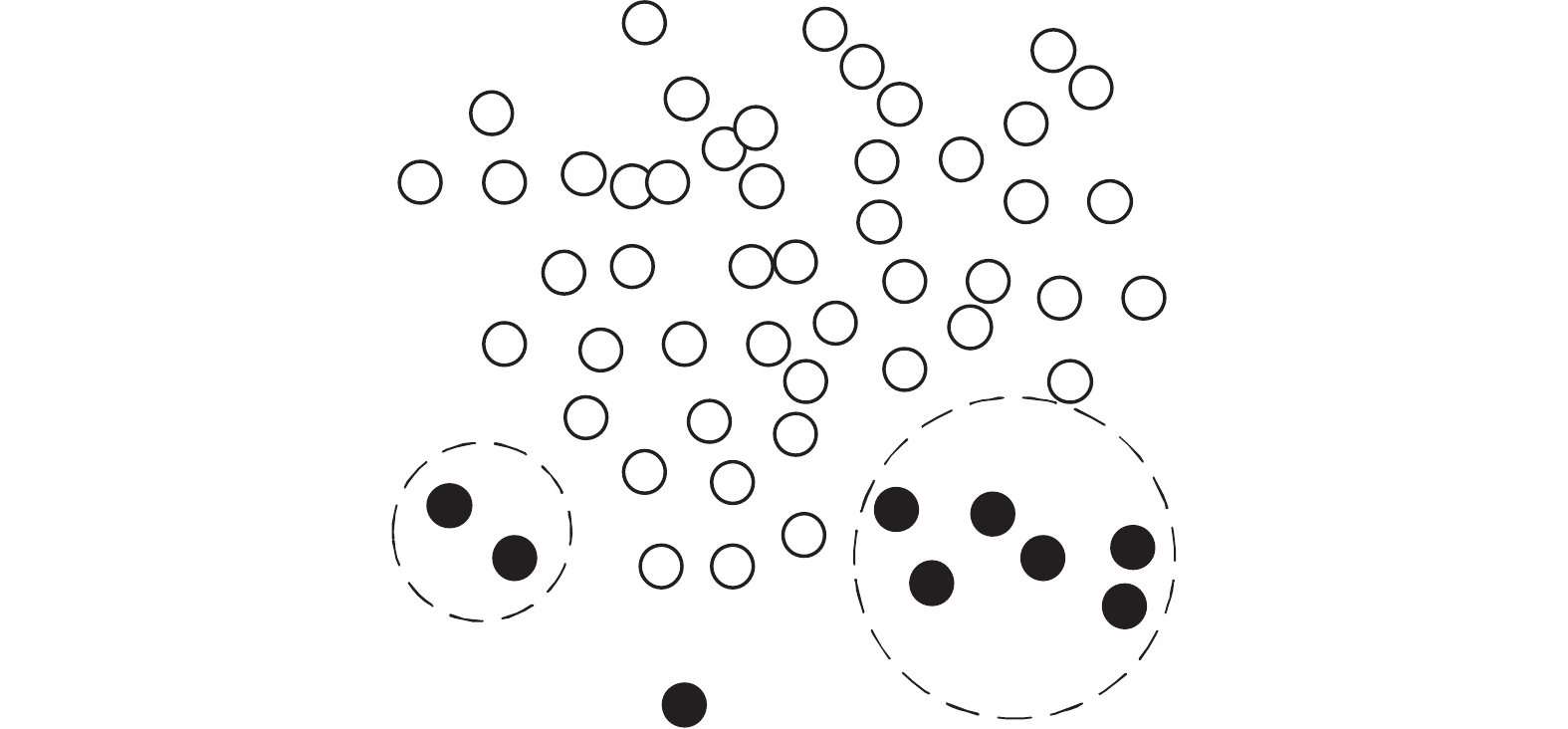
由Rodriguez等[20]在2014年提出了密度峰值聚类(density peak clustering, DPC)算法，它是一种基于密度的聚类算法，可以识别任意形状的簇。该算法假定了两个前置条件：1）簇中心的局部密度高于周围点的局部密度，2）簇中心之间有较大的距离。DPC通过计算每个样本的局部密度和它到更高密度点的最小距离画出决策图进行决策，如图1为类内不平衡示意。
图 1 类内不平衡Fig. 1 Within class imbalance
下载:
全尺寸图片
由图1可以看到在少数类内部存在着密度不均的问题。为了得到少数类中的类内密度信息，使用局部密度的概念来衡量数据点在少数类空间中的分布[21]。假设数据集为
$X = \left( {{x_1},{x_2}, \cdot \cdot \cdot ,{x_n}} \right)$ ，其中n为数据集的样本个数，对于其中的每一个样本xi，利用高斯核函数来计算它的局部密度ρi：$$ {\rho _{ {i}}}{ t{ = }}\sum\limits_j^{} {\exp \left[ { - {{\left( {\frac{{{d_{ij}}}}{{{d_c}}}} \right)}^2}} \right]} $$ (1) 式中：dij是样本点xi与样本点xj之间的距离，dc是截断距离，其数值通常为所有样本点两两之间距离升序排列的1%~2%。通过获得所有少数类数据点的局部密度，可以有效衡量少数类样本的密度分布。
1.2 局部合力与集中度
受到牛顿万有引力的启发，数据点之间的局部引力可以反映出数据点和其周围邻近数据点之间的关系。类比于万有引力定律可得两质点之间的引力F12定义为
$$ {{\boldsymbol{F}}_{12}} = G\frac{{{m_1}{m_2}}}{{D_{{\text{12}}}^{\text{2}}}}{\widehat {\boldsymbol{D}}_{12}} $$ (2) 其中：F12表示质点1与质点2之间的引力，G为引力系数，m1和m2分别为两质点的质量，D12表示质点1与质点2之间的距离，
${\widehat {\boldsymbol{D}}_{12}}$ 表示两点之间的单位向量。因为计算的是局部范围内的引力[22-23]，可以考虑数据点与其邻域内的点的距离相接近，也即数据点与于其近邻点之间的距离没有明显差异，所以式(2)简化为$$ {{\boldsymbol{F}}_{12}} = G{m_1}{m_2}{\widehat {\boldsymbol{D}}_{12}} $$ (3) 进一步将式(3)引入数据集
$X = \left( {x_1}, {x_2}, \cdots , {x_n} \right)$ 中，质点1与质点2样本点xi与样本点xj来代替。选取距离数据点xi的k个最近邻点对它产生局部合力LRF表示为$$ {{\boldsymbol{F}}_i} = \sum\limits_{j = 1}^k {{{\boldsymbol{F}}_{ij}} = G{m_i}\sum\limits_{j = 1}^k {{m_j}{{\widehat {\boldsymbol{D}}}_{ij}}} } $$ (4) 从式(4)可得出，拥有较大质量的数据点对其邻域内的近邻点的影响越大；拥有较小质量的数据点受其领域内的近邻点影响越大。由此LRF简化为
$$ {{\boldsymbol{F}}_i} = \frac{1}{{{m_i}}}\sum\limits_{j = 1}^k {{{\widehat {\boldsymbol{D}}}_{ij}}} $$ (5) 样本点xi的质量定义为
$$ {m_i} = \frac{1}{{\displaystyle\sum\limits_{j = 1}^k {{D_{ij}}} }} $$ (6) 为了区分少数类的边界点和非边界点，利用局部合力LRF所包含的信息计算数据点xi的集中度Ci，定义如下：
$$ {C_i} = \frac{1}{k}\sum\limits_{j = 1}^k {\cos \left( {{{\boldsymbol{F}}_{j,}} - {{\boldsymbol{D}}_{ij}}} \right)} $$ (7) 式中：k表示近邻点的数量，
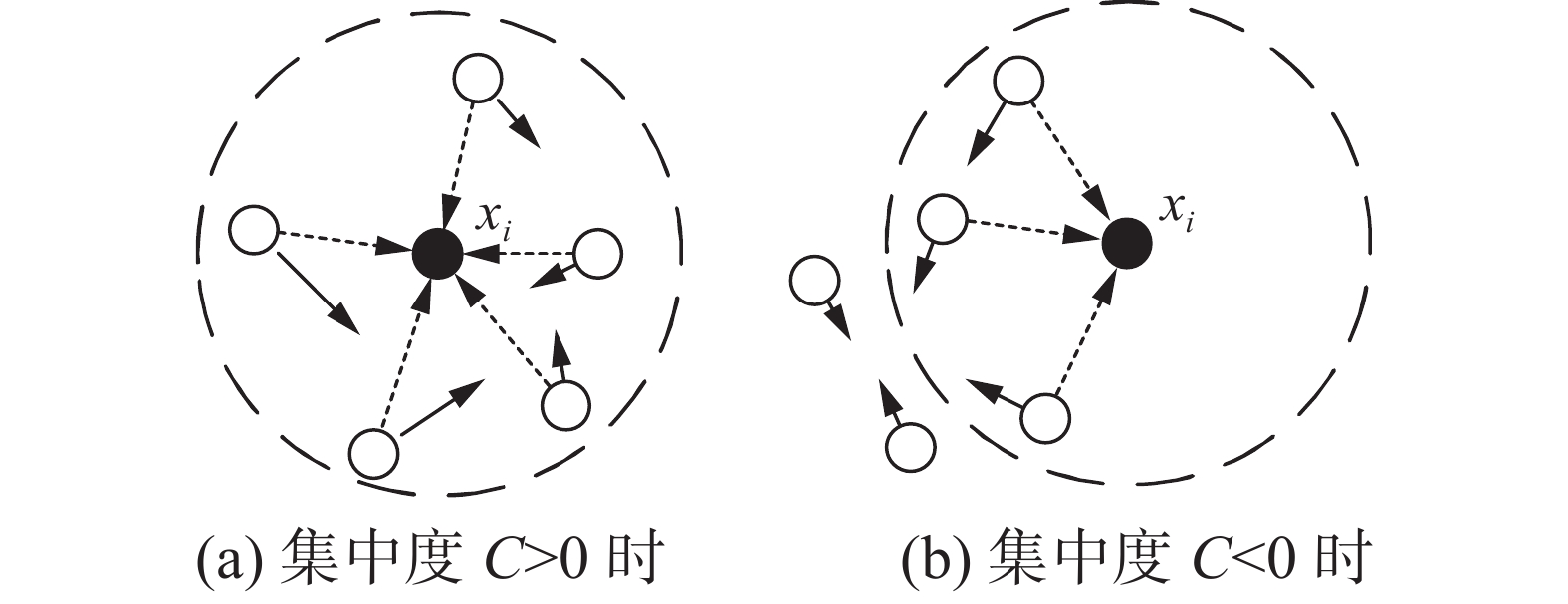
$ - {{\boldsymbol{D}}_{ij}}$ 表示从xj向xi的距离向量。由集中度Ci的定义可得，当xi集中度Ci>0时，其近邻点对于xi的集中度较大，则认为xi为内部点的可能性较大；相反，若Ci<0时，则说明其近邻点对于xi的集中度较小，则xi为边界点的可能性较大。在得出位于少数类边界的样本之后，可以设置重采样策略在边界生成样本以达到强化边界的效果。数据点位置与集中度C的关系如图2所示，其中带箭头的实线表示每个数据点的局部合力，带箭头的虚线表示两数据点之间的距离向量。图2(a)表示了一种集中度C>0的情况，其中黑色圆点xi为内部点的可能性较大；图2(b)表示了一种集中度C<0的情况，其中黑色圆点xi为边界点的可能性较大。
图 2 数据点位置与集中度C的关系Fig. 2 Relationship between data point location and C下载:
全尺寸图片
2. 基于截断距离及集中度的过采样
为了打破少数类的类内不平衡，在确定出所有少数类样本点的局部密度之后，需要提高局部密度较小点的密度来实现少数类内样本的相对平衡。在使用过采样算法时，将新生成的少数类样本设置在样本空间中的哪些位置是一个关键问题。
分别设置两个不同的部分来实现DC-SMOTE算法的过采样，实现打破类内不平衡与强化边界的作用，同时由于算法的设置可根据不同的数据集自适应确定过采样量，避免过分追求少数类样本与多数类样本在数量上的平衡而消耗过多算力，也避免了生成过多的少数类造成分类过程中的过拟合。
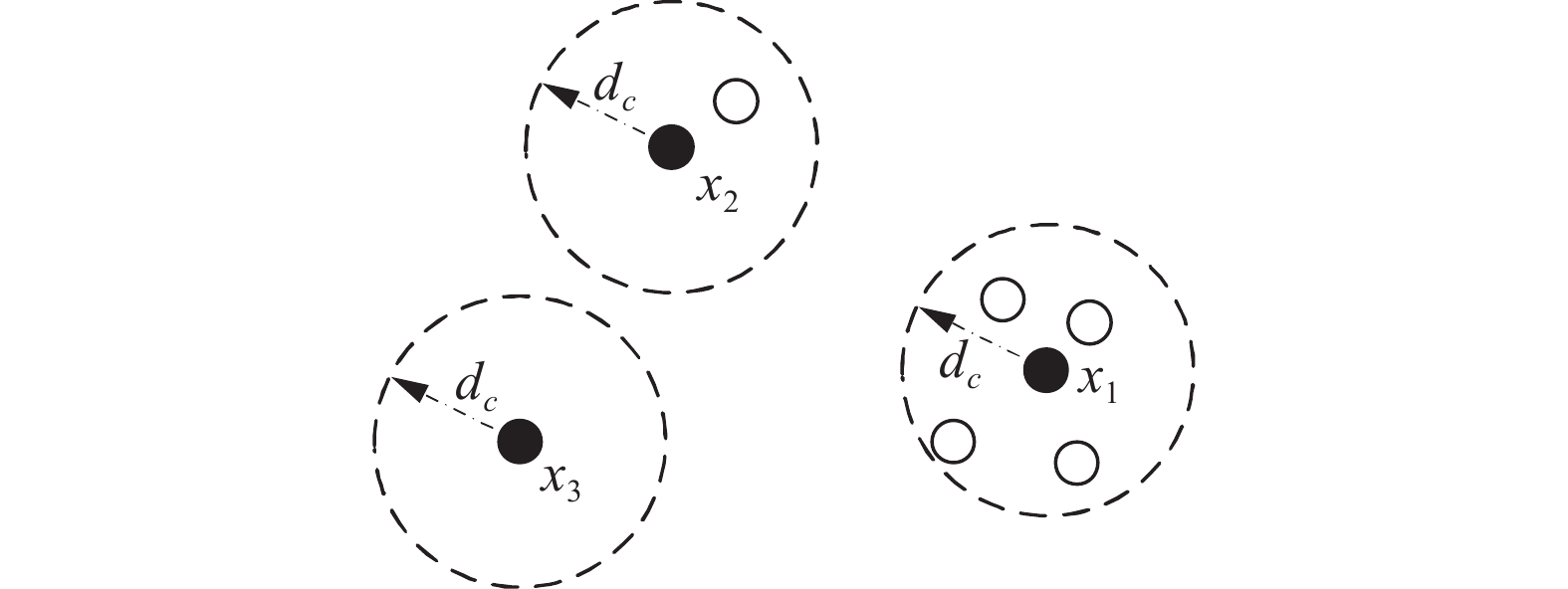
由式(1)可知，当样本点xi与样本点xj两者之间的距离小于dc时，样本点xj对于样本点xi的局部密度ρi产生的贡献较大。如图3所示，以x1、x2、x3这3个点为例，由于在这3个点周围的数据点聚集程度不同，导致在截断距离dc范围内出现的数据点数量的不同，从而使得局部密度各异。
图 3 局部密度ρ各异的数据点Fig. 3 Data points with different ρ下载:
全尺寸图片
为了生成的第一型过采样点对局部密度小的数据点产生较大的贡献，选择集合了所有原始少数类样本信息的dc作为新生成的少数类与原始少数类之间的距离，避免了SMOTE等算法随机生成的少数类没有意义的情况。如图4所示，xl与xg分别表示少数类样本中的一个小密度点和它的一个大密度点近邻，在它们之间生成了以dc为距离的2个少数类点xnew1与xnew2。
图 4 生成第一型过采样点示意Fig. 4 Schematic of creating type-1 points下载:
全尺寸图片
生成第一型过采样点的具体步骤见算法1。
算法 1 合成第一型过采样点
输入 训练集X，近邻数量k。
输出 采样后的第一型过采样点集X1，合成的第一型过采样点的数量n。
1) 将训练集按标签划分为少数类集Xmin与多数类集Xmaj；
2) 利用式(1)计算得出所有少数类样本点的局部密度P；
3) 分离出所有少数类样本局部密度P中密度ρ<0.36的样本点设置为小密度点集Xl，剩余的为大密度点集Xg，根据式(1)，为了确保样本点周围至少存在一个满足二者距离小于截断距离dc的近邻点，取极限情况dij=dc，由此取得ρ的临界值为0.36；
4) 对所有的小密度点xl，在大密度点xg中选择k个近邻；
5) 在每个小密度点xl，与它的k个近邻间生成第一型过采样点；
6) 返回生成的第一型过采样点集X1，计算平均两样本点之间生成的第一型少数类点的数量值n。
由式(7)可知，原始少数类样本点可依据集中度C的大小来判断出其中的样本点是否位于少数类的边界。由于位于少数类样本边界，尤其是与多数类样本相接近的少数类分类判断尤其困难，所以需要对边界进行强化以达到更高的分类精度，第二型少数类的生成采取如下公式：
$$ {x_{{\rm{new}}}} = {x_i} + \left( {{x_j} - {x_i}} \right) \times {\rm{Rand}} $$ (8) 式中：xi为C<0的样本点，xj为C>0的样本点中距离xi的近邻点，Rand取区间(0, 1)中的随机值。
合成第二型过采样点的具体步骤见算法2。
算法 2 合成第二型过采样点
输入 训练集X，近邻数量k，两点间平均生成少数类数量
$n$ 。输出 采样后的第二型过采样点集X2。
1) 将训练集按标签划分为少数类集Xmin与多数类集Xmaj；
2) 计算少数类集合中所有少数类样本点的集中度C；
3) 选择出集中度
$C < 0$ 的少数类集，与它的k个集中度$C > 0$ 的近邻；4) 按照式(8)与生成第二型过采样点，任意两点之间生成n个过采样点；
5) 返回生成的第二型过采样点集X2。
将算法1与算法2串行执行的同时，将算法1得到的参数n传递至算法2，随后调整不平衡度，也就产生了DC-SMOTE算法。
DC-SMOTE算法
输入 训练集X，近邻数量
$k$ 。输出 处理后的数据集。
1) 执行算法1；
2) 执行算法2；
3) 判断新数据集的不平衡度IBR是否小于1，如果是，则随机删除部分新合成的少数类至不平衡度IBR为1后输出数据集；如果不是，则直接输出数据集。
对于DC-SMOTE算法的复杂度来说，主要由算法1与算法2共同决定。根据分析得到，算法1的时间复杂度主要受到其步骤2与步骤4的影响，二者的时间复杂度为O(M2)与O(L×G+L×k×log k)，算法2的时间复杂度主要受到其步骤2与步骤3的影响，分别为O(M×k2)与O(M×k×logk)的影响，其中M是少数类样本的数量，L是小密度点的数量，G是大密度点的数量，k为近邻数量。由于少数类样本数量M为小密度点数量L与大密度点数量G的加和，所以可见DC-SMOTE算法的复杂度主要集中于局部密度与集中度的求解。
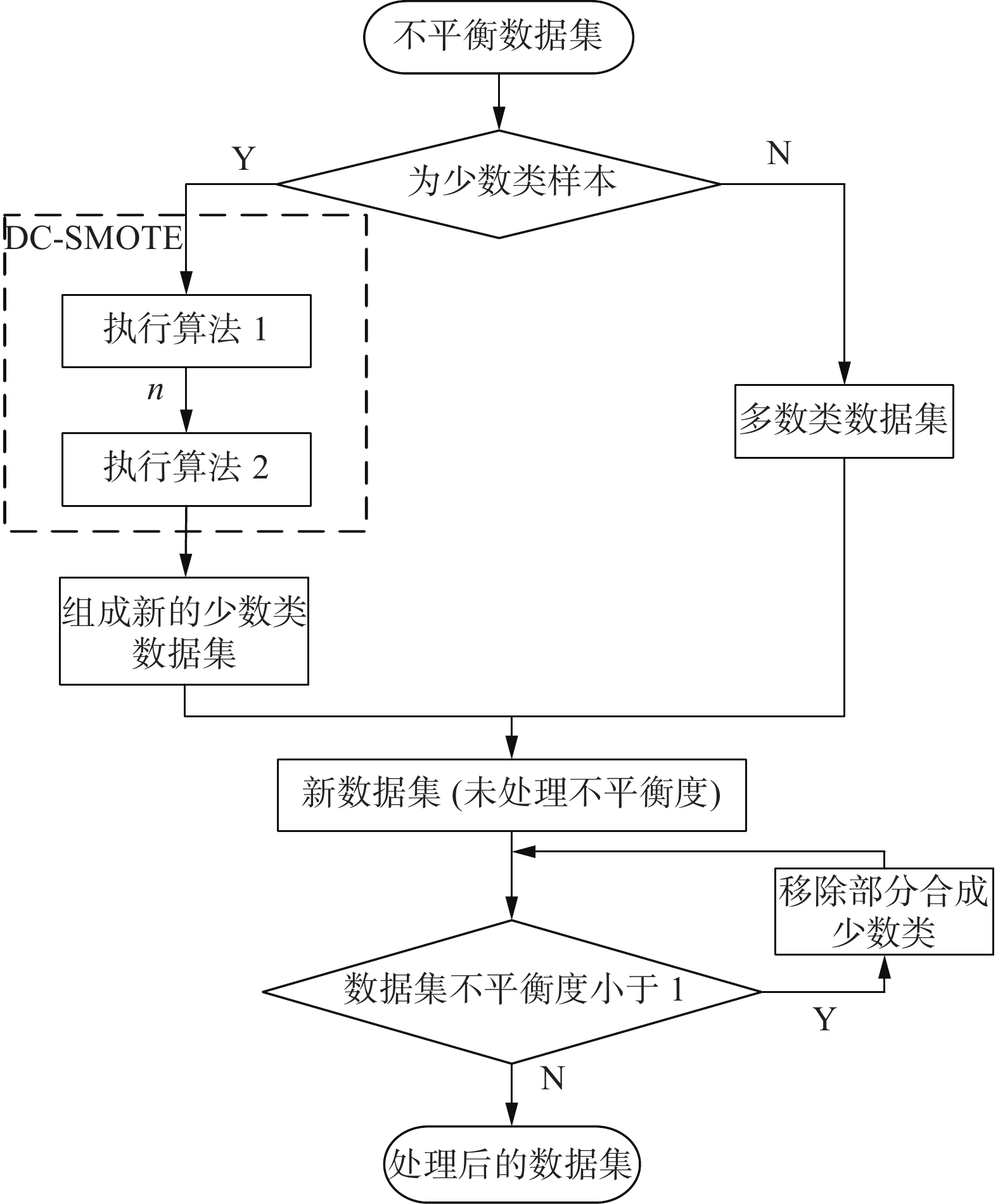
DC-SMOTE算法整体流程如图5所示。
图 5 DC-SMOTE算法流程Fig. 5 Flow of DC-SMOTE algorithm下载:
全尺寸图片
3. 实验与结果分析
3.1 实验数据
本文在公开数据库KEEL数据库以及UCI数据集里共选用了12个二分类数据集作为实验数据集。数据集的详细信息如表1所示。
表 1 数据集信息Table 1 Dataset information数据集 特征数 样本数 不平衡度 Ecoli 1 7 336 3.36 Ecoli 2 7 336 5.46 Segment 0 19 2 308 6.02 Ecoli 046vs5 6 203 9.15 Yeast 1vs7 7 459 13.81 yeast 2vs8 8 482 23.10 Letter-A 16 20 000 24.35 Yeast 4 8 1 484 28.41 Yeast 6 8 1 484 39.15 Winequality 3vs7 11 900 44.00 Poker 8-9vs6 10 1 485 58.40 Poker 8vs6 10 1 477 85.88 3.2 对比方法与评价指标
为了充分评估本文方法的稳定性与有效性，实验采用了几种过采样方法来进行对比，分别为SMOTE、ADASYN[24]、Borderline-SMOTE、CCR[25]、Kmeans-SMOTE以及Knnor。由于DC-SMOTE方法属于数据层面的分类方法，并不受具体的分类器限制，所以本文选择被广泛用于解决不平衡问题的决策树模型作为分类器。
传统的分类器评价指标是利用少数类与多数类整体分类的准确率，但是对于不平衡分类问题来看，整体的准确率在数值上通常接近100%，然而这样看似完美的结果并没有实际意义。对于不平衡问题，通常选择混淆矩阵来对实验结果进行分析，它也被称为误差矩阵，是一种计算分类精度的工具[26]，具体结构如表2所示。
表 2 混淆矩阵Table 2 Confusion matrix样本类别 预测为多数类 预测为少数类 实际为多数类 NTN NFP 实际为少数类 NFN NTP 本文选择两种建立在混淆矩阵上的评价指标作为本文的评价指标衡量算法的优劣：ROC曲线下的面积(area under ROC curve, AUC) AUC以及几何平均值 (geometric mean, G-mean)Gmean。
召回率/真阳率(RRecall/RTP)，分类正确的正样本占所有正样本的比例：
$$ {R_{{\text{Recall}}}} = {R_{{\text{TP}}}} = \frac{{{N_{{\text{TP}}}}}}{{{N_{{\text{TP}}}} + {N_{{\text{FN}}}}}} $$ (9) 假阳率(RFP)，分类错误的正样本占所有样本的比例：
$$ {R_{{\text{FP}}}} = \frac{{{N_{{\text{FP}}}}}}{{{N_{{\text{FP}}}} + {N_{TN}}}} $$ (10) 特异度/真负率(RTN)，分类正确的负样本占所有负样本的比例：
$$ {R_{{\text{TN}}}} = \frac{{{N_{{\text{TN}}}}}}{{{N_{{\text{TN}}}} + {N_{{\text{FP}}}}}} $$ (11) 几何平均值Gmean，正精度与负精度的几何平均：
$$ {G_{{\text{mean}}}} = \sqrt {{R_{{\text{Recall}}}} \times {R_{{\text{TN}}}}} $$ (12) 几何平均值通常作为评价正类和负类样本准确性的综合评价指标来使用。
利用ROC曲线，同时将其真阳率(RTP)与假阳率(RFP)作为参考，计算AUC：
$$ {A_{{\text{UC}}}} = \frac{{1 + {R_{{\text{TP}}}} - {R_{{\text{FP}}}}}}{2} $$ (13) 其中真阳率越高，假阳率越低，说明分类器分类性能更好。
不平衡度RIB的计算方法为
$$ {R_{{\text{IB}}}} = \frac{{\left| {{X_{{\text{maj}}}}} \right|}}{{\left| {{X_{\min }}} \right|}} $$ (14) 其中
$ \left|X_{\text {maj }}\right| $ 与$ \left|X_{\min }\right| $ 分别表示数据集中多数类样本点与少数类样本点的数量。3.3 实验结果
为了尽可能避免随机性对实验造成的影响，实验采用五折交叉验证的办法重复进行多次实验取平均结果作为最终结果。
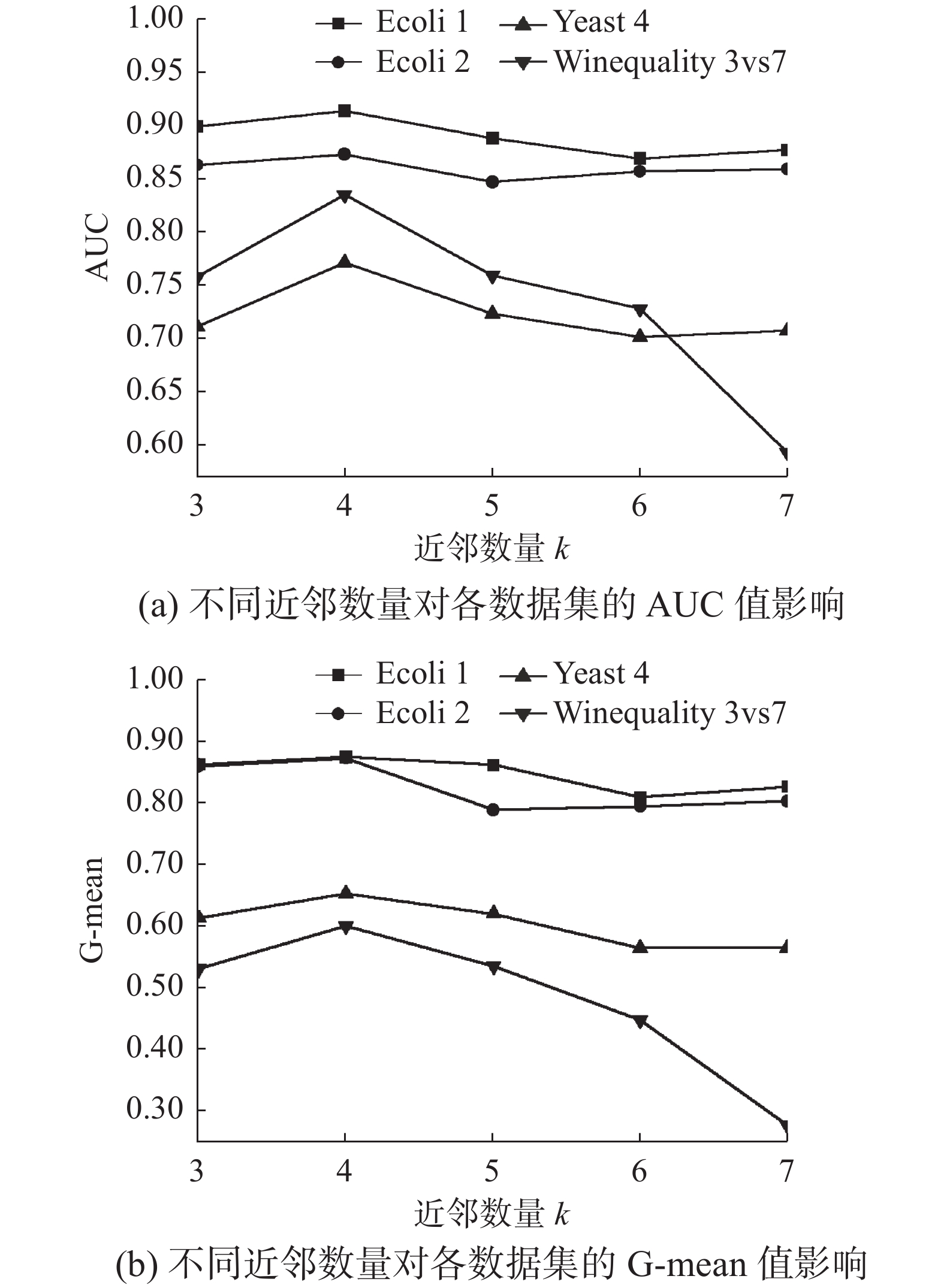
在实验中，近邻数量k的选取也是一个关键问题。为了选择较为合适的最佳近邻数量，选取了两个低不平衡度数据集Ecoli1、Ecoli2与两个高不平衡度数据集Yeast 4、Winequality 3vs7。使用这2个数据集为代表数据集，利用本文提出的DC-SMOTE算法进行不同近邻数量下的分类性能测试。采用不同近邻数量下的各个数据集分类性能如图6所示。从图中可以看出，当选取近邻数量为4时，测试数据集所表现出的性能较优，所以选取近邻数量为4作为适合DC-SMOTE算法的最佳近邻数量。
图 6 近邻数量测试Fig. 6 The test of the number of nearest neighbors下载:
全尺寸图片
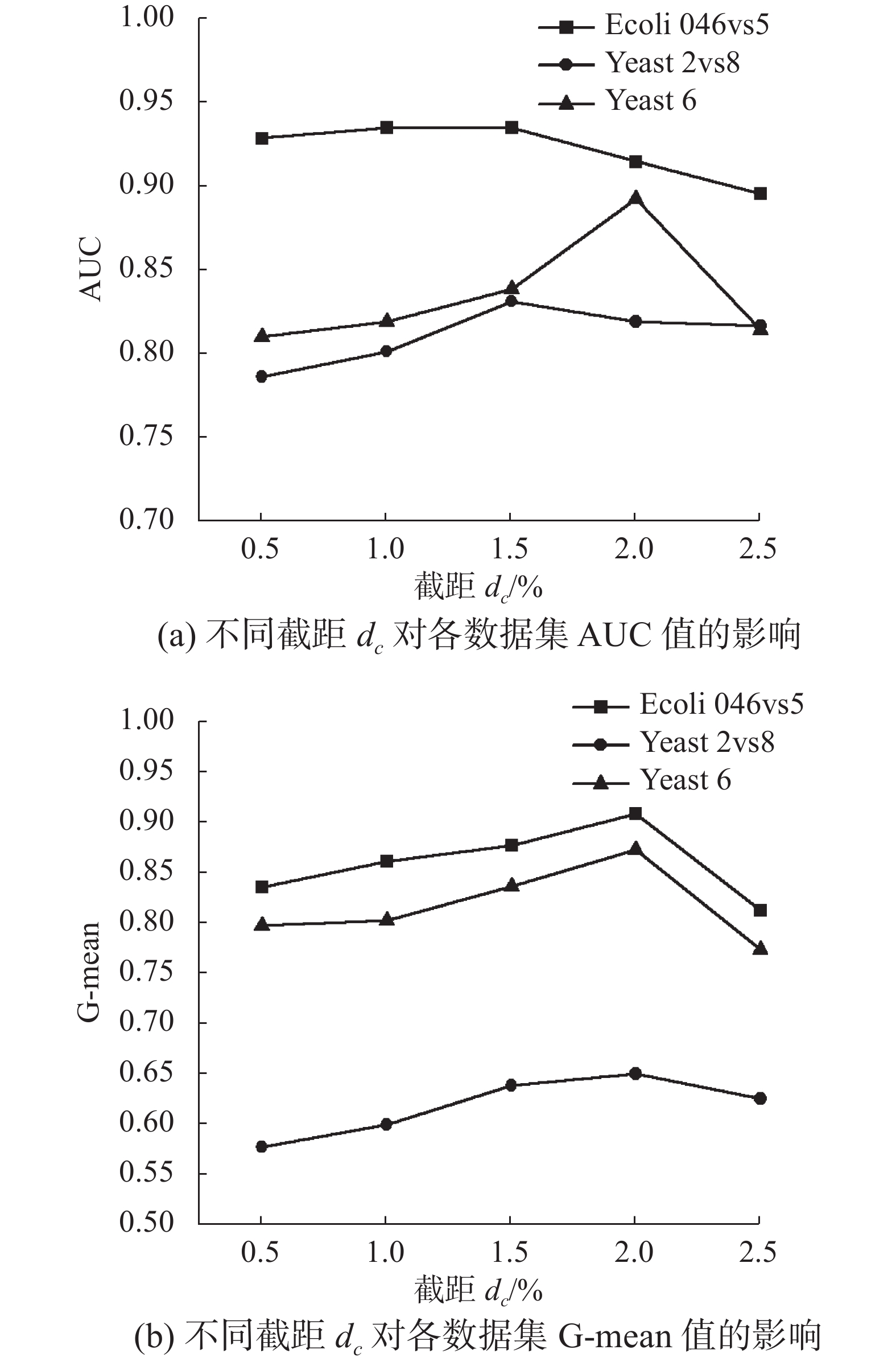
截断距离dc作为影响算法性能的另一个因素，选择数据集Ecoli 046vs5、Yeast 2vs8和Yeast 6，以及分别取位于数据集中两两样本点距离升序排列的0.5%、1%、1.5%、2%、2.5%位置上的距离作为截断距离dc进行实验，结果如图7所示。由图7可知，选择不同的截断距离会对试验结果造成影响，但当其处于样本点间距离升序排列的1%~2%时效果最佳，其原因是当dc过小时，算法会产生较多的过采样点，使得原本数据集的小密度样本区域平衡过度导致算法效果不佳；而当dc从0.5%位置增大到2.5%位置上时，除Ecoli 046vs5以外，Yeast 2vs8与Yeast 6所产生的数据量分别减少了46.2%与64.6%，产生的少数类样本不足的原因同样会影响算法性能。为了可以使生成的过采样点数量可以较好地平衡原始数据集，同时为了将截断距离dc限制在该区间内而不是限定于某一具体的值，选择采用二分查找法迭代获取dc值，使其处于样本点间距离升序排列的1%~2%。
图 7 截断距离dc测试Fig. 7 The test of cut-off distance dc下载:
全尺寸图片
从表3中可以看出，对于不同的数据集，DC-SMOTE算法会自适应地过采样来打破类间不平衡，不需要因为没有明确过采样量而盲目生成少数类样本，也不需要过分追求少数类和多数类样本在不平衡度上达到1来生成过量的无意义样本。这也就说明了DC-SMOTE算法只需要生成较少量的样本就可以实现分类器效果的提升，避免了盲目采样导致模型分类性能不佳的问题。对于原始不平衡度极低的数据集，如数据集Ecoli 1、Ecoli 2、Segment 0与Ecoli 046vs5来说，其原始数据集本身的不平衡度已经非常接近1，为了进一步改善不平衡度，在经过本算法处理过后，将不平衡度调整为1。在高不平衡度数据集中，本算法根据不同数据集自身的数据特征生成了相应不平衡度的新数据集，过采样后的数据集不平衡度各异。结合低不平衡度与高不平衡度数据集处理前后的不平衡度数值来看，DC-SMOTE算法实现了对于不同数据集自适应地产生适合自身数据集特征的过采样少数类样本，使生成的样本更有意义。
表 3 不平衡度数据集处理前后IBR对比Table 3 IBR comparison before and after imbalance data set processing数据集 原始IBR 处理后IBR Ecoli 1 3.36 1.00 Ecoli 2 5.46 1.00 Segment 0 6.02 1.00 Ecoli 046vs5 9.15 1.00 yeast 1 vs 7 13.87 1.40 Yeast 2vs8 23.10 1.69 Letter-A 24.35 2.35 yeast 4 28.41 5.01 Yeast 6 39.15 4.13 Winequality 3vs7 44.00 1.52 Poker 8-9vs6 58.40 9.97 Poker 8vs6 85.88 11.01 从表4与表5可以看出，本文所提出的方法在所有的数据集上都获得了最优的G-mean值和AUC值，同时可获得较稳定的结果。尤其在处理高不平衡数据集，如Yeast 4、Winequality 3vs7、Poker 8-9vs6时，本文算法的G-mean值相较与对比的所有过采样算法均有较大提升，优势明显，说明本算法在高不平衡度数据集的处理过程中尤其可以获得较大的召回率/真阳率与特异度/真负率，保证了算法的综合性能。
表 4 各算法在数据集上G-mean值对比Table 4 Comparison of G-mean values of each algorithm on the data set数据集 SMOTE ADASYN B-SMO CCR K-SMO KNNOR D-SMO Ecoli 1 0.800 0.816 0.812 0.824 0.783 0.845 0.877 Ecoli 2 0.805 0.764 0.780 0.778 0.834 0.842 0.875 Segment 0 0.856 0.844 0.875 0.744 0.799 0.846 0.899 Ecoli 046vs5 0.783 0.808 0.828 0.850 0.796 0.855 0.869 yeast 1 vs 7 0.430 0.358 0.443 0.510 0.492 0.501 0.546 Yeast 2vs8 0.535 0.436 0.499 0.676 0.603 0.741 0.814 Letter-A 0.732 0.732 0.456 0.525 0.632 0.766 0.811 yeast 4 0.490 0.449 0.476 0.560 0.494 0.518 0.654 Yeast 6 0.512 0.504 0.589 0.640 0.588 0.625 0.665 Winequality 3vs7 0.215 0.235 0.230 0.409 0.295 0.380 0.602 Poker 8-9vs6 0.500 0.372 0.356 0.605 0.214 0.614 0.801 Poker 8vs6 0.703 0.661 0.385 0.762 0.400 0.382 0.799 表 5 各算法在数据集上AUC值对比Table 5 Comparison of AUC values of each algorithm on the data set数据集 SMOTE ADASYN B-SMO CCR K-SMO KNNOR D-SMO Ecoli 1 0.813 0.860 0.810 0.836 0.807 0.844 0.914 Ecoli 2 0.852 0.824 0.830 0.869 0.867 0.862 0.873 Segment 0 0.724 0.734 0.814 0.822 0.733 0.823 0.853 Ecoli 046vs5 0.826 0.900 0.811 0.858 0.828 0.836 0.908 yeast 1 vs 7 0.632 0.575 0.627 0.663 0.646 0.635 0.709 Yeast 2vs8 0.746 0.699 0.659 0.737 0.715 0.786 0.864 Letter-A 0.734 0.747 0.788 0.715 0.805 0.822 0.854 yeast 4 0.701 0.652 0.648 0.650 0.611 0.633 0.771 Yeast 6 0.779 0.779 0.732 0.707 0.745 0.760 0.828 Winequality 3vs7 0.555 0.579 0.564 0.644 0.612 0.615 0.835 Poker 8-9vs6 0.694 0.651 0.630 0.710 0.535 0.694 0.738 Poker 8vs6 0.723 0.722 0.662 0.773 0.695 0.654 0.798 DC-SMOTE算法可以获得较大优势的原因在于：在有效描述少数类样本的密度之后，有针对性地以小密度样本为核心，以截断距离为参考距离生成过采样点，使生成的第一类少数类样本由于采用了全体少数类的信息而更加有意义且具有代表性；同时通过集中度来区分样本的位置，在少数类边界位置设置过采样点以强化边界，从而保护边界少数类的正确区分；从数据集本身性质出发，自适应产生相应数量的过采样少数类，避免了盲目生成大量无意义的少数类样本。综上所述，不论原始数据集不平衡度的高低，相比较于其他过采样算法，本文方法的G-mean值、AUC值较高，表明整体分类性能较好。
4. 结束语
在现如今的分类问题中，分类数据在数量上的不平衡给许多领域都带来了不小的挑战。传统方法应对不平衡分类通常由以下问题：一方面不对新生成的少数类在质量上加以控制，常常会产生具有干扰性的样本；另一方面不对新生成的少数类在数量上进行限制，使生成的大部分样本由于盲目性和无意义性而导致模型分类性能下降。本文提出的DC-SMOTE算法在充分考虑原始少数类样本性质的前提下，生成了具有代表性的过采样点，防止噪声的引入；在采样时利用不同数据集特有的分布信息，自适应生成相应数量的少数样本。因为所有新生成的少数类样本都是来自于原始的少数类样本，所以不会有异常值的产生。通过实验可以看出在不平衡度各异的数据集上应用本算法来提升分类效果是可行且有效的。但本文也存在着不足，一方面本文仅仅关注二分类的数据不平衡问题，在实际的生活与应用中，往往更多出现的情况是多分类的数据不平衡，另一方面，由于原始的数据集中或多或少可能存在着噪声，多余出来的噪声通常是导致分类器分类效果差的重要原因。综上所述，在今后的研究中可以将本文的算法推广至多分类的同时还可以就原始数据的噪声问题进行进一步讨论。
-
图 1 类内不平衡
Fig. 1 Within class imbalance
下载:
全尺寸图片
图 2 数据点位置与集中度C的关系
Fig. 2 Relationship between data point location and C
下载:
全尺寸图片
图 3 局部密度ρ各异的数据点
Fig. 3 Data points with different ρ
下载:
全尺寸图片
图 4 生成第一型过采样点示意
Fig. 4 Schematic of creating type-1 points
下载:
全尺寸图片
图 5 DC-SMOTE算法流程
Fig. 5 Flow of DC-SMOTE algorithm
下载:
全尺寸图片
图 6 近邻数量测试
Fig. 6 The test of the number of nearest neighbors
下载:
全尺寸图片
图 7 截断距离dc测试
Fig. 7 The test of cut-off distance dc
下载:
全尺寸图片
表 1 数据集信息
Table 1 Dataset information
数据集 特征数 样本数 不平衡度 Ecoli 1 7 336 3.36 Ecoli 2 7 336 5.46 Segment 0 19 2 308 6.02 Ecoli 046vs5 6 203 9.15 Yeast 1vs7 7 459 13.81 yeast 2vs8 8 482 23.10 Letter-A 16 20 000 24.35 Yeast 4 8 1 484 28.41 Yeast 6 8 1 484 39.15 Winequality 3vs7 11 900 44.00 Poker 8-9vs6 10 1 485 58.40 Poker 8vs6 10 1 477 85.88 表 2 混淆矩阵
Table 2 Confusion matrix
样本类别 预测为多数类 预测为少数类 实际为多数类 NTN NFP 实际为少数类 NFN NTP 表 3 不平衡度数据集处理前后IBR对比
Table 3 IBR comparison before and after imbalance data set processing
数据集 原始IBR 处理后IBR Ecoli 1 3.36 1.00 Ecoli 2 5.46 1.00 Segment 0 6.02 1.00 Ecoli 046vs5 9.15 1.00 yeast 1 vs 7 13.87 1.40 Yeast 2vs8 23.10 1.69 Letter-A 24.35 2.35 yeast 4 28.41 5.01 Yeast 6 39.15 4.13 Winequality 3vs7 44.00 1.52 Poker 8-9vs6 58.40 9.97 Poker 8vs6 85.88 11.01 表 4 各算法在数据集上G-mean值对比
Table 4 Comparison of G-mean values of each algorithm on the data set
数据集 SMOTE ADASYN B-SMO CCR K-SMO KNNOR D-SMO Ecoli 1 0.800 0.816 0.812 0.824 0.783 0.845 0.877 Ecoli 2 0.805 0.764 0.780 0.778 0.834 0.842 0.875 Segment 0 0.856 0.844 0.875 0.744 0.799 0.846 0.899 Ecoli 046vs5 0.783 0.808 0.828 0.850 0.796 0.855 0.869 yeast 1 vs 7 0.430 0.358 0.443 0.510 0.492 0.501 0.546 Yeast 2vs8 0.535 0.436 0.499 0.676 0.603 0.741 0.814 Letter-A 0.732 0.732 0.456 0.525 0.632 0.766 0.811 yeast 4 0.490 0.449 0.476 0.560 0.494 0.518 0.654 Yeast 6 0.512 0.504 0.589 0.640 0.588 0.625 0.665 Winequality 3vs7 0.215 0.235 0.230 0.409 0.295 0.380 0.602 Poker 8-9vs6 0.500 0.372 0.356 0.605 0.214 0.614 0.801 Poker 8vs6 0.703 0.661 0.385 0.762 0.400 0.382 0.799 表 5 各算法在数据集上AUC值对比
Table 5 Comparison of AUC values of each algorithm on the data set
数据集 SMOTE ADASYN B-SMO CCR K-SMO KNNOR D-SMO Ecoli 1 0.813 0.860 0.810 0.836 0.807 0.844 0.914 Ecoli 2 0.852 0.824 0.830 0.869 0.867 0.862 0.873 Segment 0 0.724 0.734 0.814 0.822 0.733 0.823 0.853 Ecoli 046vs5 0.826 0.900 0.811 0.858 0.828 0.836 0.908 yeast 1 vs 7 0.632 0.575 0.627 0.663 0.646 0.635 0.709 Yeast 2vs8 0.746 0.699 0.659 0.737 0.715 0.786 0.864 Letter-A 0.734 0.747 0.788 0.715 0.805 0.822 0.854 yeast 4 0.701 0.652 0.648 0.650 0.611 0.633 0.771 Yeast 6 0.779 0.779 0.732 0.707 0.745 0.760 0.828 Winequality 3vs7 0.555 0.579 0.564 0.644 0.612 0.615 0.835 Poker 8-9vs6 0.694 0.651 0.630 0.710 0.535 0.694 0.738 Poker 8vs6 0.723 0.722 0.662 0.773 0.695 0.654 0.798 -
[1] LIU Lan, WANG Pengcheng, LIN Jun, et al. Intrusion detection of imbalanced network traffic based on machine learning and deep learning[J]. IEEE access, 2020, 9: 7550–7563. [2] AWOYEMI J O, ADETUNMBI A O, OLUWADARE S A. Credit card fraud detection using machine learning techniques: a comparative analysis[C]//2017 International Conference on Computing Networking and Informatics (ICCNI). Lagos, Nigeria. IEEE, 2017: 1–9. [3] ZHANG Jue, CHEN Li. Clustering-based undersampling with random over sampling examples and support vector machine for imbalanced classification of breast cancer diagnosis[J]. Computer assisted surgery, 2019, 24(sup2): 62–72. doi: 10.1080/24699322.2019.1649074 [4] FOTOUHI S, ASADI S, KATTAN M W. A comprehensive data level analysis for cancer diagnosis on imbalanced data[J]. Journal of biomedical informatics, 2019, 90: 103089. doi: 10.1016/j.jbi.2018.12.003 [5] MA Zhiqiang, YAN Rui, YUAN Donghong, et al. An imbalanced Spam mail filtering method[J]. International journal of multimedia and ubiquitous engineering, 2015, 10(3): 119–126. doi: 10.14257/ijmue.2015.10.3.12 [6] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16: 321–357. doi: 10.1613/jair.953 [7] HAN Hui, WANG Wenyuan, MAO Binghuan. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[M]//Lecture Notes in Computer Science. Berlin: Springer Berlin Heidelberg, 2005: 878−887. [8] DOUZAS G, BACAO F, LAST F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE[J]. Information sciences: an international journal, 2018, 465(C): 1–20. [9] 谢子鹏, 包崇明, 周丽华, 等. 类不平衡数据的EM聚类过采样算法[J]. 计算机科学与探索, 2023, 17(1): 228–237. XIE Zipeng, BAO Chongming, ZHOU Lihua, et al. EM clustering oversampling algorithm for class imbalanced data[J]. Journal of frontiers of computer science and technology, 2023, 17(1): 228–237. [10] 王亮, 冶继民. 整合DBSCAN和改进SMOTE的过采样算法[J]. 计算机工程与应用, 2020, 56(18): 111–118. doi: 10.3778/j.issn.1002-8331.1906-0441 WANG Liang, YE Jimin. Hybrid algorithm of DBSCAN and improved SMOTE for oversampling[J]. Computer engineering and applications, 2020, 56(18): 111–118. doi: 10.3778/j.issn.1002-8331.1906-0441 [11] ISLAM A, BELHAOUARI S B, REHMAN A U, et al. KNNOR: an oversampling technique for imbalanced datasets[J]. Applied soft computing, 2022, 115: 108288. doi: 10.1016/j.asoc.2021.108288 [12] TSAI C F, LIN Weichao, HU Yahan, et al. Under-sampling class imbalanced datasets by combining clustering analysis and instance selection[J]. Information sciences, 2019, 477: 47–54. doi: 10.1016/j.ins.2018.10.029 [13] 崔彩霞, 曹付元, 梁吉业. 基于密度峰值聚类的自适应欠采样方法[J]. 模式识别与人工智能, 2020, 33(9): 811–819. CUI Caixia, CAO Fuyuan, LIANG Jiye. Adaptive undersampling based on density peak clustering[J]. Pattern recognition and artificial intelligence, 2020, 33(9): 811–819. [14] DAS B, KRISHNAN N C, COOK D J. RACOG and wRACOG: two probabilistic oversampling techniques[J]. IEEE transactions on knowledge and data engineering, 2015, 27(1): 222–234. doi: 10.1109/TKDE.2014.2324567 [15] YU Hualong, NI Jun, ZHAO Jing. ACOSampling: an ant colony optimization-based undersampling method for classifying imbalanced DNA microarray data[J]. Neurocomputing, 2013, 101: 309–318. doi: 10.1016/j.neucom.2012.08.018 [16] TAO Xinmin, LI Qing, GUO Wenjie, et al. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification[J]. Information sciences:an international journal, 2019, 487(C): 31–56. [17] HE Hongliang, ZHANG Wenyu, ZHANG Shuai. A novel ensemble method for credit scoring: Adaption of different imbalance ratios[J]. Expert systems with applications, 2018, 98(8): 105–117. [18] 平瑞, 周水生, 李冬. 高度不平衡数据的代价敏感随机森林分类算法[J]. 模式识别与人工智能, 2020, 33(3): 249–257. PING Rui, ZHOU Shuisheng, LI Dong. Cost sensitive random forest classification algorithm for highly unbalanced data[J]. Pattern recognition and artificial intelligence, 2020, 33(3): 249–257. [19] JO T, JAPKOWICZ N. Class imbalances versus small disjuncts[J]. ACM SIGKDD explorations newsletter, 2004, 6(1): 40–49. doi: 10.1145/1007730.1007737 [20] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. doi: 10.1126/science.1242072 [21] DU Mingjing, DING Shifei, JIA Hongjie. Study on density peaks clustering based on k-nearest neighbors and principal component analysis[J]. Knowledge-based systems, 2016, 99(9): 135–145. [22] WANG Zhiqiang, YU Zhiwen, CHEN C L P, et al. Clustering by local gravitation[J]. IEEE transactions on cybernetics, 2018, 48(5): 1383–1396. doi: 10.1109/TCYB.2017.2695218 [23] JIANG Jianhua, HAO Dehao, CHEN Yujun, et al. GDPC: gravitation-based Density Peaks Clustering algorithm[J]. Physica A statistical mechanics and its applications, 2018, 502: 345–355. doi: 10.1016/j.physa.2018.02.084 [24] HE Haibo, BAI Yang, GARCIA E A, et al. ADASYN: adaptive synthetic sampling approach for imbalanced learning[C]//2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence). Hong Kong: IEEE, 2008: 1322−1328. [25] KOZIARSKI M, WOŻNIAK M. CCR: a combined cleaning and resampling algorithm for imbalanced data classification[J]. International journal of applied mathematics and computer science, 2017, 27(4): 727–736. doi: 10.1515/amcs-2017-0050 [26] PIRYONESI S M, EL-DIRABY T E. Data analytics in asset management: cost-effective prediction of the pavement condition index[J]. Journal of infrastructure systems, 2020, 26(1): 4019036. doi: 10.1061/(ASCE)IS.1943-555X.0000512
