Hierarchical sliding mode control of a double pendulum crane with an extended state observer
-
摘要: 吊车系统在大尺寸货物运送过程中会呈现出双摆效应，同时更易受到外部干扰影响，导致控制难度更大。 针对双摆吊车系统控制难题，提出一种基于扩张状态观测器的分层滑模控制方法，在保证负载快速平稳运送的同时有效抑制吊钩和负载的摆动。基于吊车系统的动力学模型设计扩张状态观测器对系统的状态变量和干扰集合项进行估计，利用系统的状态误差和观测器的估计信号设计分层滑模控制器。此外，控制方法通过在滑模面中引入干扰补偿项，进一步提高系统的抗干扰能力。通过数值仿真，与已有方法进行对比，充分验证该研究方法在工作效率和鲁棒性方面均具有良好的控制性能。Abstract: During the oversized cargo transportation process, the crane system may act like a double pendulum system, which would also be easily affected by external disturbances and result in greater control difficulty. To deal with this control problem of the double pendulum crane system, a hierarchical sliding mode control method based on an extended state observer is proposed in this work to attain fast and smooth payload transportation while effectively suppressing the swing of the payload and the hook. Particularly, the state variables and disturbance terms are estimated by the designed extended state observer, and afterward, a hierarchical sliding mode controller is proposed by using the state error signals and the estimated signals of the observer. Moreover, the disturbance compensation term is contained in the designed sliding surface to further enhance the anti-disturbance ability of the system. In comparison to current methods by simulation tests, the proposed method can bring suitable control performance regarding working efficiency and robustness.
-
欠驱动系统[1-2]是指待控自由度多于独立控制输入的一类系统，如无人机系统[3-5]、欠驱动机械臂系统[6-7]和欠驱动外骨骼系统[8-9]等。吊车作为工业制造中应用最普遍的运输工具之一，能够承担不同类型的运送任务，例如港口集装箱、钢厂铁水包和工地建筑材料等大型货物的搬运。同时，随着生产技术水平的提高，越来越多不同类型的吊车被应用于各个行业，根据其机械结构的不同，可以细分为桥式吊车[10-11]、塔式吊车[12-13]和桅杆式吊车[14-15]等，吊车也正朝着智能化、大型化和快速化等方向发展。现阶段工业生产所使用的吊车控制算法主要为轨迹规划、输入整形等开环控制方法。然而，此类控制算法在实际的应用中存在鲁棒性和可靠性不足的问题。同时，传统的闭环比例微分(proportional-derivative，PD)控制算法也被应用于吊车的控制中，但无法有效抑制负载摆动。对吊车系统而言，由于自身的欠驱动特性、非线性和强耦合特性导致系统控制器设计的难度大大提高。同时，可能存在的外部干扰会导致负载发生大幅度摆动，这不仅会影响负载的准确定位和吊车系统的工作效率，还可能造成意外碰撞等安全事故。因此，为吊车系统设计安全可靠的自动控制方法具有实际意义。
对于桥式吊车系统，其主要的控制目标包括：1) 快速精准的台车定位；2) 负载摆动的抑制和消除。在过去的几十年里，国内外的研究学者为解决吊车的控制问题提出了很多有效的控制方法，根据是否需要状态反馈可分为开环控制和闭环控制两类。开环控制方法指无需信号反馈的控制方法，一般包括轨迹规划[16]、输入整形[17]等。Yang等[16]针对吊车系统复杂的非线性动力学模型和保证系统瞬态性能的控制问题，提出一种新的非线性时间次优轨迹规划方法。Ramli等[17]通过分析吊车系统的动力学模型，利用粒子群优化训练的神经网络设计了一个新的输入整形器，有效解决了系统参数变化对控制性能的影响。然而，开环控制方法依赖精准的吊车模型，并且当存在外部干扰时，系统的控制性能可能会下降。为提高系统的鲁棒性，研究人员利用信号反馈，提出一系列的闭环控制方法，包括自适应控制方法[18-19]、基于能量的控制方法[20-21]和滑模控制方法[22-23]等。Zhang等[18]和Frikha等[19]为解决吊车系统中参数不确定性的问题，分别针对2种不同的吊车模型，结合自适应控制方法和滑模控制方法设计出控制器，在实现对系统未知参数进行有效估计的同时完成系统的控制目标。Zhang等[20]和Wu等[21]针对三维桥式吊车系统，基于无源性理论构造了系统的储能函数，利用耦合−耗散不等式设计了可以有效抑制负载摆动的控制器。Wu等[22]利用系统的状态反馈和干扰观测器的估计值设计一种新的连续全局滑模控制器，试验结果表明该控制器对外部干扰具有良好的鲁棒性。Chwa[23]基于滑模控制方法提出一种有限时间跟踪防摆控制策略，可以有效抑制瞬态时间的负载摆角。近年来，一些智能控制方法同样用于吊车的控制设计中，如模糊控制[24]、神经网络控制[25]等。
上述方法需要假设吊钩和负载为一个质点，并将吊车系统的负载摆动视为单摆系统。然而，在一些情况下, 负载尺寸太大不能视为质点或者吊钩的质量不能忽视，吊车系统将出现吊钩围绕台车摆动和负载围绕吊钩摆动的现象，即双摆效应。相比单摆吊车系统，由于增加了一个欠驱动的状态变量，很大程度上提升了对系统动态性能分析和控制器设计的难度。目前，学者们针对双摆吊车系统的控制问题也提出一些控制策略，Ouyang等[26]通过分析双摆吊车系统台车与吊钩和负载之间的耦合关系，提出一种包含定位和防摆功能的在线轨迹规划方法。Chen等[27]提出了一种考虑各种约束条件的最优时间轨迹规划方法，可以实现台车定位的同时有效抑制吊钩和负载的摆动。Tian等[28]针对吊车系统执行器的初始输出值受到物理约束的问题, 提出一种具有初始饱和度的部分增强耦合非线性控制器，仿真结果表明该控制器具有良好的控制性能。
为提高双摆吊车系统的抗干扰能力，本研究提出一种基于扩张状态观测器的分层滑模控制方法。首先通过分析双摆吊车动力学方程，将其转化为方便控制器设计的二阶系统形式。然后，为解决实际工程应用中系统状态变量的速度信号和加速度信号以及外部干扰信号很难直接得到的问题，针对双摆吊车系统设计了一种有效观测相关信号的扩张状态观测器，降低控制系统的成本的同时提高了控制方法的可行性。在此基础上，为了实现准确的台车定位并抑制吊钩和负载的摆动，根据扩张状态观测器的估计值，利用滑模控制方法分别设计可驱动部分和欠驱动部分滑模面，并通过合适的方式构造系统总的滑模面。同时为了提高系统的抗干扰能力，在滑模面的设计中加入干扰补偿项。最后，通过Lyapunov方法对控制器的稳定性进行理论分析，并通过一系列的仿真验证本研究设计的控制器具有良好的控制性能。本研究的主要贡献如下：1) 针对双摆吊车系统，提出了一种基于扩张状态观测器的分层滑模控制方法，并结合扩张状态观测器设计干扰补偿策略。2) 所设计的控制器基于非线性系统模型，不需要对系统的状态变量进行线性化处理。3) 通过理论证明和仿真验证，均表明所提控制方法可实现台车准确定位的同时有效抑制吊钩和负载的摆动，且具有较强的鲁棒性。
1. 问题描述
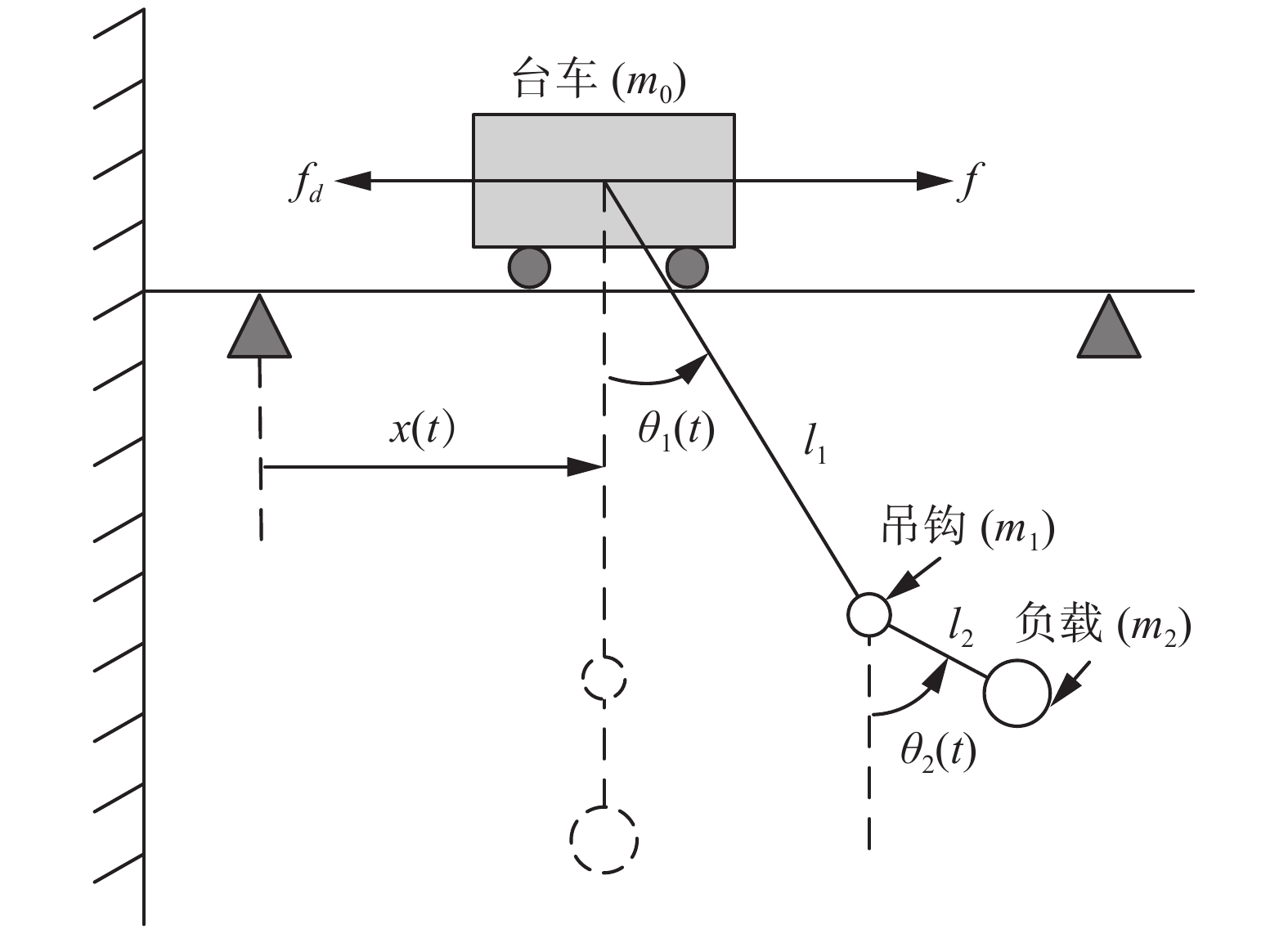
在本研究中，考虑图1中的固定绳长双摆吊车系统，利用拉格朗日方程，其动力学模型可建立如下[29]
图 1 双摆吊车模型示意Fig. 1 Schematic diagram of double pendulum cranes
下载:
全尺寸图片
$$ \begin{split} &({m_0} + {m_1} + {m_2})\ddot x + {m_2}{l_2}\left({{\ddot \theta }_2}\cos {\theta _2} - \dot \theta _2^2\sin {\theta _2}\right) + \\ &\quad ({m_1} + {m_2}){l_1}\left({{\ddot \theta }_1}\cos {\theta _1} - \dot \theta _1^2\sin {\theta _1}\right) = f - {f_d} \end{split} $$ (1) $$ \begin{split} &\;\;({m_1} + {m_2}){l_1}\cos {\theta _1}\ddot x + ({m_1} + {m_2})l_1^2{{\ddot \theta }_1} + \\ &{m_2}{l_1}{l_2}\left[{{\ddot \theta }_2}\cos \left({\theta _1} - {\theta _2}\right) + \dot \theta _2^2\sin ({\theta _1} - {\theta _2})\right] + \\ &\quad \left({m_1} + {m_2}\right)g{l_1}\sin {\theta _1} + {d_1}{{\dot \theta }_1} = 0 \end{split} $$ (2) $$ \begin{split} &{m_2}{l_2}\left[\cos {\theta _2}\ddot x + {l_1}\cos ({\theta _1} - {\theta _2}){{\ddot \theta }_1} + {l_2}{{\ddot \theta }_2} -\right. \\ &\left.{l_1}\dot \theta _1^2\sin ({\theta _1} - {\theta _2}) + g\sin {\theta _2}\right] + {d_2}{{\dot \theta }_2} = 0 \\ \end{split} $$ (3) 式中：
${m_0}$ 、${m_1}$ 、${m_2}$ 分别表示台车质量、吊钩质量以及负载质量；${l_1}$ 和${l_2}$ 分别表示吊绳长度和吊钩质心到负载质心之间的长度；$x(t)$ 表示台车位移；${\theta _1}(t)$ 和${\theta _2}(t)$ 分别表示吊钩摆角和负载绕吊钩的摆角；$g$ 表示重力加速度常数；$f(t)$ 表示作用在台车上的驱动力；${f_d}$ 表示由外部干扰和摩擦等不确定因素构成的集干扰项；${d_1}$ 和${d_2}$ 表示摩擦系数。为方便后续描述；使用了如下的简化形式$$ \begin{gathered} {m_0} + {m_1} + {m_2} = {m_{0 - 2}}{\text{, }} {m_1} + {m_2} = {m_{1 - 2}}{\text{, }}\sin {\theta _1} = {S_1}, \\ {S_2} = \sin {\theta _2},{\text{ }}\cos {\theta _1} = {C_1},{\text{ }}\cos {\theta _2} = {C_2}, \\ \cos ({\theta _1} - {\theta _2}) = {C_{1 - 2}},{\text{ }}\sin ({\theta _1} - {\theta _2}) = {S_{1 - 2}} \end{gathered} $$ 为方便控制器和扩张状态观测器设计，将式(1)~(3)改写为如下的二阶系统形式
$$ \left\{ \begin{gathered} {{\dot {\boldsymbol{q}}}_1}(t) = {{\boldsymbol{q}}_2}(t), \\ {{\dot {\boldsymbol{q}}}_2}(t) = {\boldsymbol{a}}f + {{\boldsymbol{q}}_3}(t), \\ {{\boldsymbol{q}}_3}(t) = {\boldsymbol{b}} - {\boldsymbol{\varpi}} , \\ \end{gathered} \right. $$ (4) 式中：
${{\boldsymbol{q}}_1} = {[\begin{array}{*{20}{c}} x&{{\theta _1}}&{{\theta _2}} \end{array}]^{\rm{T}}}$ 和${{\boldsymbol{q}}_2} = {[\begin{array}{*{20}{c}} {\dot x}&{{{\dot \theta }_1}}&{{{\dot \theta }_2}} \end{array}]^{\rm{T}}}$ 分别表示系统的状态向量和速度向量；${{\boldsymbol{q}}_3} = {[\begin{array}{*{20}{c}} {{\omega _1}}&{{\omega _2}}&{{\omega _3}} \end{array}]^{\rm{T}}}$ 表示包含系统非线性函数项和干扰项的集总扰动项向量；${\boldsymbol{\varpi}} = {[\begin{array}{*{20}{c}} {{\varpi _1}}&{{\varpi _2}}&{{\varpi _3}} \end{array}]^{\rm{T}}} = {[\begin{array}{*{20}{c}} {{a_1}{f_d}}&{{a_2}{f_d}}&{{a_3}{f_d}} \end{array}]^{\rm{T}}}$ 表示影响系统不确定干扰项向量；${\boldsymbol{a}} = {[\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}} \end{array}]^{\rm{T}}}$ 和${\boldsymbol{b}} = {[\begin{array}{*{20}{c}} {{b_1}}&{{b_2}}&{{b_3}} \end{array}]^{\rm{T}}}$ 分别表示吊车动力学模型的非线性函数项。具体如下$$ {a_i} = \frac{{{H_i}}}{\varDelta },{\text{ }}{b_i} = \frac{{{T_i}}}{\varDelta },\; i = 1,2,3 $$ 其中，
$$ \begin{gathered} \varDelta = {m_{1 - 2}}{m_2}l_1^2l_2^2\left({m_{0 - 2}} - {m_{1 - 2}}C_1^2\right) - m_2^2l_1^2l_2^2\left({m_{1 - 2}}C_2^2 +\right. \\ \left. {m_{0 - 2}}C_{1 - 2}^2 - 2{m_{1 - 2}}{C_1}{C_2}{C_{1 - 2}}\right) \end{gathered} $$ $$ \begin{gathered} {T_1}= \left({m_{1 - 2}}{m_2}l_1^2l_2^2 - m_2^2l_1^2l_2^2C_{1 - 2}^2\right)\left({m_{1 - 2}}{l_1}\dot \theta _1^2{S_1} + {m_2}{l_2}\dot \theta _2^2 \times\right. \\ \left.{S_2}\right) + \left({m_{1 - 2}}{m_2}{l_1}l_2^2{C_1} - m_2^2{l_1}l_2^2{C_2}{C_{1 - 2}}\right)\left({m_2}{l_1}{l_2}\dot \theta _2^2{S_{1 - 2}}+ \right.\\ \left.{m_{1 - 2}}g{l_1}{S_1} + {d_1}{{\dot \theta }_1}\right) + \left({m_{1 - 2}}{m_2}l_1^2{l_2}{C_2} - {m_2}l_1^2{l_2}{C_1}{C_{1 - 2}}\right) \times\\ \left({m_2}g{l_2}{S_2} - {m_2}{l_1}{l_2}\dot \theta _1^2{S_{1 - 2}} + {d_2}{{\dot \theta }_2}\right) \end{gathered} $$ $$ {H_1} = {m_2}l_1^2l_2^2({m_1} + {m_2}S_{1 - 2}^2) $$ $$ \begin{gathered} {T_2} = \left(m_2^2{l_1}l_2^2{C_2}{C_{1 - 2}} - {m_{1 - 2}}{m_2}{l_1}l_2^2{C_1}\right)\left({m_{1 - 2}}{l_1}\dot \theta _1^2{S_1} + {m_2}{l_2} \times \right. \\ \left. \dot \theta _2^2{S_2}\right) + \left(m_2^2l_2^2C_2^2 - {m_{0 - 2}}{m_2}l_2^2\right)\left({m_2}{l_1}{l_2}\dot \theta _2^2{S_{1 - 2}} + {m_{1 - 2}} \times \right. \\ \left. g{l_1}{S_1} + {d_1}{{\dot \theta }_1}\right) + \left({m_{0 - 2}}{m_2}{l_1}{l_2}{C_{1 - 2}} - {m_{1 - 2}}{m_2}{l_1}{l_2}{C_1}{C_2}\right) \times \\ \left({m_2}g{l_2}{S_2} - {m_2}{l_1}{l_2}\dot \theta _1^2{S_{1 - 2}} + {d_2}{{\dot \theta }_2}\right) \end{gathered} $$ $${H_2} = {m_2}l_1^2l_2^2({m_2}{S_2}{S_{1 - 2}} + {m_1}{C_1}) $$ $$ \begin{gathered} {T_3} = \left[{m_{1 - 2}}{m_2}l_1^2{l_2}\left({C_1}{C_{1 - 2}} - {C_2}\right)\right]\left({m_{1 - 2}}{l_1}\dot \theta _1^2{S_1} + {m_2}{l_2}\dot \theta _2^2 \times \right. \\ \left.{S_2}\right) + \left({m_{0 - 2}}{m_2}{l_1}{l_2}{C_{1 - 2}} - {m_{1 - 2}}{m_2}{l_1}{l_2}{C_1}{C_2}\right)\left({m_2}{l_1}{l_2}\dot \theta _2^2 \times \right.\\ \left. {S_{1 - 2}} + {m_{1 - 2}}g{l_1}{S_1} + {d_1}{{\dot \theta }_1}\right) + \left(m_{1 - 2}^2l_1^2C_1^2 - {m_{0 - 2}}{m_{1 - 2}}l_1^2\right) \times \\ \left({m_2}g{l_2}{S_2} - {m_2}{l_1}{l_2}\dot \theta _1^2{S_{1 - 2}} + {d_2}{{\dot \theta }_2}\right) \end{gathered} $$ $$ {H_3} = {m_{1 - 2}}{m_2}l_1^2{l_2}{S_{1 - 2}} $$ 对于双摆吊车系统，由于系统本身的欠驱动特性，无法直接控制吊钩和负载的运动，只有利用台车与吊钩和负载之间的耦合关系来间接抑制吊钩和负载的摆动，因此需要充分分析系统的动力学特性设计合适的控制方法，驱动台车到达目标位置
${x_d}$ 的同时有效抑制吊钩和负载的摆动。系统的控制目标描述如下$$ \begin{gathered} \mathop {\lim }\limits_{t \to \infty } x(t) = {x_d},{\text{ }}\mathop {\lim }\limits_{t \to \infty } {\theta _1}(t) = 0,{\text{ }}\mathop {\lim }\limits_{t \to \infty } {\theta _2}(t) = 0, \\ \mathop {\lim }\limits_{t \to \infty } \dot x(t) = 0,{\text{ }}\mathop {\lim }\limits_{t \to \infty } {{\dot \theta }_1}(t) = 0,{\text{ }}\mathop {\lim }\limits_{t \to \infty } {{\dot \theta }_2}(t) = 0 \\ \end{gathered} $$ (5) 接下来，将设计合适的控制器，实现双摆吊车的控制目标(式5)。
2. 主要结果
本节将提出一种基于扩张状态观测器的分层滑模控制方法。首先基于转换后的系统动力学方程(4)和状态变量误差信号设计一种扩张状态观测器，对系统状态变量和外部干扰进行估计。然后，基于扩张状态观测器的估计信号设计保证台车准确定位和有效抑制吊钩和负载摆动的分层滑模控制器。最后, 通过Lyapunov方法对控制器性能进行理论分析。
2.1 扩张状态观测器设计
将设计扩张状态观测器对系统的状态变量和外部干扰信号进行估计。首先，根据系统的控制目标(5)定义如下的误差向量
${\boldsymbol{e}}$ $$ {\boldsymbol{e}} = {\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{e_2}}&{{e_3}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {x - {x_d}}&{{\theta _1}}&{{\theta _2}} \end{array}} \right]^{\rm{T}}} $$ (6) 然后，由式(4)所描述的二阶系统和系统的状态误差向量(6)，为台车位移
$x$ 、吊钩摆角${\theta _1}$ 和负载摆角${\theta _2}$ 设计扩张状态观测器$$ \left\{ \begin{gathered} {{\dot {\boldsymbol{z}}}_{1j}} = {{\boldsymbol{z}}_{2j}} + \frac{3}{\zeta }{\boldsymbol{e}} \\ {{\dot {\boldsymbol{z}}}_{2j}} = {{\boldsymbol{z}}_{3j}} + f + \frac{3}{{{\zeta ^2}}}{\boldsymbol{e}} \\ {{\dot {\boldsymbol{z}}}_{3j}} = \frac{1}{{{\zeta ^3}}}{\boldsymbol{e}} \\ \end{gathered} \right. $$ (7) 式中：
${{\boldsymbol{z}}_{1j}}、{{\boldsymbol{z}}_{2j}}、{{\boldsymbol{z}}_{3j}}(j = x,{\text{ }}{\theta _1},{\text{ }}{\theta _2})$ 分别表示状态变量的估计向量；$\zeta $ 为观测器控制增益；${{\textit{z}}_{1x}}、{\text{ }}{{\textit{z}}_{1{\theta _1}}}、{\text{ }}{{\textit{z}}_{1{\theta _2}}}$ 分别表示对状态变量$x、{\text{ }}{\theta _1}、{\text{ }}{\theta _2}$ 的估计；${{\textit{z}}_{2x}}、{\text{ }}{{\textit{z}}_{2{\theta _1}}}、{\text{ }} {{\textit{z}}_{2{\theta _2}}}$ 分别表示对$\dot x、{\text{ }}{\dot \theta _1}、{\text{ }}{\dot \theta _2}$ 的估计；${{\textit{z}}_{3x}}、{\text{ }}{{\textit{z}}_{3{\theta _1}}}、{\text{ }}{{\textit{z}}_{3{\theta _2}}}$ 分别表示集总扰动项${\omega _1}、{\text{ }}{\omega _2}、{\text{ }}{\omega _3}$ 的估计。定理 1[30] 扩张状态观测器(7)具有严格意义的收敛性，可以对二阶系统(4)中状态变量和不确定干扰项进行有效估计，即
$$ \mathop {\lim }\limits_{t \to \infty } \left\| {{{\boldsymbol{q}}_i}(t) - {{\boldsymbol{z}}_{ij}}(t)} \right\| = 0 $$ 2.2 滑模控制器设计
本小节为双摆吊车系统设计一个分层滑模控制器，进而实现台车的精准定位的同时有效抑制负载和吊钩摆动的控制目标。
利用系统的状态误差(6)和扩张状态观测器(7)，设计吊车系统的第一层滑模面为
$$ {s_i} = {{\textit{z}}_{2j}} + {c_i}{e_i} - \int_0^t {{{\textit{z}}_{3j}}{\rm{d}}\tau } $$ (8) 式中：
${s_i}{\text{ }}(i = 1,2,3)$ 分别表示针对系统状态变量设计的子滑模面；$ {c_1}、{c_2}、{c_3} \in {\bf{R}^ + } $ 为第一层滑模面的控制增益。对式(8)两边关于时间求导数，并代入式(4)整理得
$$ {\dot s_i} = {c_i}{{\textit{z}}_{2j}} + {a_i}f + {\omega _i} - {{\textit{z}}_{3j}} $$ (9) 式中，
${{\textit{z}}_{3j}}{\text{ }}(j = x,{\theta _1},{\theta _2})$ 分别是${\omega _i}{\text{ }}(i = 1,2,3)$ 的估计值，由定理1扩张状态观测器的收敛性可得${{\textit{z}}_{3j}} = {\omega _i}$ 。因此，根据式(9)可求得第一层滑模面的等效控制量${f_{{\rm{ueq}}1}}、{\text{ }}{f_{{\rm{ueq}}2}}、{\text{ }}{f_{{\rm{ueq}}3}}$ ：$$ {f_{{\rm{ueq}}1}} = - {c_1}a_1^{ - 1}{{\textit{z}}_{2x}} $$ (10) $$ {f_{{\rm{ueq2}}}} = - {c_2}a_2^{ - 1}{{\textit{z}}_{2{\theta _1}}} $$ (11) $$ {f_{\rm{{ueq3}}}} = - {c_3}a_3^{ - 1}{{\textit{z}}_{2{\theta _2}}} $$ (12) 为保证系统的稳定性，系统总的控制量必须包含第一层滑模面的等效控制量，则设计控制器为
$$ f = {f_{{\rm{ueq1}}}} + {f_{{\rm{ueq2}}}} + {f_{{\rm{ueq3}}}} + {f_{{\rm{usw}}}} $$ (13) 其中，
${f_{{\rm{usw}}}}$ 为切换控制量。然后，根据式(8)构造系统的第二层滑模面$$ S = \alpha {s_1} + \beta {s_2} + \gamma {s_3} $$ (14) 其中，
$\alpha 、\beta、\gamma $ 是第二层滑模面控制增益。对式(14)两边关于时间求导数，并将式(9)代入整理得
$$ \begin{gathered} \dot S = \alpha ({c_1}{{\textit{z}}_{2x}} + {a_1}f) + \beta ({c_2}{{\textit{z}}_{2{\theta _1}}} + {a_2}f) + \gamma ({c_3}{{\textit{z}}_{2{\theta _2}}} + {a_3}f) \end{gathered} $$ (15) 然后，在所设计滑模面的基础上，整理可得系统的切换控制量
${f_{{\rm{usw}}}}$ 为$$ {f_{{\rm{usw}}}} = - \psi _1^{ - 1}[{\psi _2} + \kappa S + \eta {\text{sgn}}(S)] $$ (16) 式中：
$\kappa $ ，$\eta \in {\rm{R}^ + }$ 为系统控制增益；${\psi _1}$ 和${\psi _2}$ 的具体形式为$$ {\psi _1} = \alpha {a_1} + \beta {a_2} + \gamma {a_3} $$ $$ \begin{gathered} {\psi _2} = (\beta {a_2} + \gamma {a_3}){f_{{\rm{ueq1}}}} + (\alpha {a_1} + \gamma {a_3}){f_{{\rm{ueq2}}}}+ (\alpha {a_1} + \beta {a_2}){f_{{\rm{ueq3}}}} \end{gathered} $$ ${\text{sgn}}( * )$ 代表标准符号函数$$ {\text{sgn}}( * ) = \left\{ \begin{array}{*{20}{l}} {{\text{1, }} * {{ > 0}}} \\ {{\text{0, }} * {{ = 0}}} \\ - {\text{1, }} * {{ < 0}} \end{array} \right. $$ (17) 将式(10)~(12)和(16)代入式(13)整理可得系统总的控制量为
$$ \begin{aligned} f = - \psi _1^{ - 1}[\alpha {c_1}{{\textit{z}}_{2x}} + \beta {c_2}{{\textit{z}}_{2{\theta _1}}} + \gamma {c_3}{{\textit{z}}_{2{\theta _2}}} + \kappa S + \eta {\text{sgn}}(S)] \end{aligned} $$ (18) 其中，系统的控制参数满足如下条件
$$ \kappa {\text{, }}\eta {\text{, }}{c_2},{\text{ }}{c_3},{\text{ }}\alpha {c_1},\gamma ,\beta > 0 $$ 注1 本研究所提方法所需信号可直接通过编码器等方式获得，而不需要进一步利用差分方程获得速度和加速度等信号，避免了可能出现的噪声信号对系统的影响，提高了所提方法可行性和鲁棒性。
2.3 稳定性分析
定理 2 对于双摆吊车系统(1)−(3)，采用所设计的分层滑模控制器(18)，在保证系统稳定性的同时可以实现台车快速精准定位并有效抑制吊钩和负载的摆动，即
$$ x \to {x_d}\text{，}{\theta _1} \to 0\text{，}{\theta _2} \to 0 $$ 证明 首先，选取如下的Lyapunov候选函数
$$ V(t) = \frac{1}{2}{S^2} $$ (19) 对式(19)两边关于时间求导数，将式(15)和(18)代入并利用式(17)的关系整理可得
$$ \begin{split}& \begin{gathered} \dot V(t) = S\dot S = - \kappa {S^2} - \eta S{\text{sgn}}(S) \leqslant - \kappa {S^2} - \\ \eta \left| S \right| \leqslant - \eta \left| S \right| \leqslant 0 \end{gathered}\\[-6pt]& \end{split} $$ (20) 进一步由式(20)可得
$$ \begin{gathered} \dot V(t) \leqslant - \eta \sqrt {2V(t)} \Rightarrow \sqrt {V(t)} - \sqrt {V(0)} \leqslant - \frac{{\sqrt 2 \eta }}{2}t \end{gathered} $$ (21) 然后，假设存在时间
${t_f}$ 系统的状态变量收敛到滑模面$S = 0$ ，即$V({t_f}) = 0$ 。由式(21)可得$$ {t_f} \leqslant \frac{{\sqrt 2 }}{\eta }\sqrt {V(0)} $$ (22) 由式(22)可知滑模面
$S$ 的收敛时间${t_f}$ 是有界的。此外，由式(20)中$\dot V(t) \leqslant 0$ ，可得对于$\forall t \geqslant {t_f}$ 存在如下关系$$ 0 \leqslant V(t) \leqslant V({t_f}) = 0 \Rightarrow V(t) = 0 \Rightarrow S = 0 $$ (23) 因此，系统在时间
${t_f}$ 后滑模面$ S $ 的不变集中存在如下关系$$ \dot S = 0,{\text{ }}\forall t \geqslant {t_f} $$ (24) 由式(24)并结合式(11)~(13)和(23)整理可得
$$ \begin{gathered} \ddot x =- ({c_1} + 1)\dot x - {c_1}{e_1} + {\alpha ^{ - 1}}\left[ - \left(\beta + \beta {c_2}\right){{\dot \theta }_1} - \right.\\ \left. \beta {c_2}{\theta _1} - \left(\gamma + \gamma {c_3}\right){{\dot \theta }_2} - \gamma {c_3}{\theta _2}\right] \\ \end{gathered} $$ (25) 将式(25)代入式(2)和(3)并整理可得
$$ \begin{gathered} {{\ddot \theta }_1} = {\left({m_1}{l_1} + {m_2}{l_1}S_{1 - 2}^2\right)^{ - 1}}\{ [{m_2}({C_2}{C_{1 - 2}} - {C_1}) -\\ ({m_1} + {m_1}){C_1}][ - {c_1}{e_1} - ({c_1} + 1)\dot x - {\alpha ^{ - 1}}\beta {c_2}{\theta _1}- \\ {\alpha ^{ - 1}}(\beta + \beta {c_2}){{\dot \theta }_1} - {\alpha ^{ - 1}}(\gamma + \gamma {c_3}){{\dot \theta }_2}- \\ {\alpha ^{ - 1}}\gamma {c_3}{\theta _2}] - {m_2}{l_1}{S_{1 - 2}}{C_{1 - 2}}\dot \theta _1^2 - {m_2}{l_2}{S_{1 - 2}}\dot \theta _2^2+ \\ g{S_1}({m_2}{C_{1 - 2}} - {m_1} - {m_2}) - {d_1}l_1^{ - 1}{{\dot \theta }_1}- \\ {d_2}l_2^{ - 1}{C_{1 - 2}}{{\dot \theta }_1}\} \\ \end{gathered} $$ (26) $$ \begin{gathered} {{\ddot \theta }_2} = {\left({m_1}{l_2} + {m_2}{l_2}S_{1 - 2}^2\right)^{ - 1}}\{ - ({m_1} + {m_2}){S_1}{S_{1 - 2}} \; \cdot \\ [ - {c_1}{e_1} - ({c_1} + 1)\dot x - {\alpha ^{ - 1}}(\beta + \beta {c_2}){{\dot \theta }_1} - \\ {\alpha ^{ - 1}}\beta {c_2}{\theta _1} - {\alpha ^{ - 1}}(\gamma + \gamma {c_3}){{\dot \theta }_2} - {\alpha ^{ - 1}}\gamma {c_3} \cdot \\ {\theta _2}] - {d_1}l_1^{ - 1}{C_{1 - 2}}{{\dot \theta }_1} + ({m_1} + {m_2}){l_1}{S_{1 - 2}}\dot \theta _1^2 +\\ {m_2}{l_2}{S_{1 - 2}}{C_{1 - 2}}\dot \theta _2^2 + ({m_1} + {m_2})g{C_{1 - 2}}{S_1}- \\ ({m_1} + {m_2})g{S_2} + ({m_1} + {m_2}){({m_2}{l_2})^{ - 1}}{d_2}{{\dot \theta }_2}\} \\ \end{gathered} $$ (27) 重新定义系统的状态变量矩阵
${\boldsymbol{p}} \in {\bf{R}^6}$ 如下$$ \begin{gathered} {\boldsymbol{p}}= {[\begin{array}{*{20}{c}} {{p_1}}&{{p_2}}&{{p_3}}&{{p_4}}&{{p_5}}&{{p_6}} \end{array}]^{\rm{T}}} =\\ {[\begin{array}{*{20}{c}} {{e_1}}&{\dot x}&{{\theta _1}}&{{{\dot \theta }_1}}&{{\theta _2}}&{{{\dot \theta }_2}} \end{array}]^{\rm{T}}} \\ \end{gathered} $$ (28) 进一步利用式(25)~(27)存在如下的关系
$$ {\dot p_1} = {p_2} $$ (29) $$ \begin{gathered} {{\dot p}_2} = - ({c_1} + 1){p_2} - {c_1}{p_1} + {\alpha ^{ - 1}}[ - (\beta + \beta {c_2}){p_4}- \\ \beta {c_2}{p_3} - (\gamma + \gamma {c_3}){p_6} - \gamma {c_3}{p_5}] = v({\boldsymbol{p}}) \\ \end{gathered} $$ (30) $$ {\dot p_3} = {p_4} $$ (31) $$ \begin{gathered} {{\dot p}_4} = {\left({m_1}{l_1} + {m_2}{l_1}S_{1 - 2}^2\right)^{ - 1}}\{ [{m_2}({C_2}{C_{1 - 2}} - {C_1})- \\ ({m_1} + {m_1}){C_1}]\left[ - {c_1}{p_1} - ({c_1} + 1){p_2} - {\alpha ^{ - 1}}\beta {c_2}{p_3}- \right.\\ {\alpha ^{ - 1}}(\beta + \beta {c_2}){p_4} - {\alpha ^{ - 1}}(\gamma + \gamma {c_3}){p_6} -\\ \left.{\alpha ^{ - 1}}\gamma {c_3}{p_5}\right] - {m_2}{l_2}{S_{1 - 2}}p_6^2 - {m_2}{l_1}{S_{1 - 2}}{C_{1 - 2}}p_4^2 +\\ g{S_1}({m_2}{C_{1 - 2}} - {m_1} - {m_2}) - {d_1}l_1^{ - 1}{p_4} -\\ {d_2}l_2^{ - 1}{C_{1 - 2}}{p_6}\} , = m({\boldsymbol{p}}) \\ \end{gathered} $$ (32) $$ {\dot p_5} = {p_6} $$ (33) $$ \begin{gathered} {{\dot p}_6} = {\left({m_1}{l_2} + {m_2}{l_2}S_{1 - 2}^2\right)^{ - 1}}\{ - ({m_1} + {m_2}){S_1}{S_{1 - 2}} \;{\boldsymbol{\cdot}} \\ [ - {c_1}{p_1} - ({c_1} + 1){p_2} - {\alpha ^{ - 1}}(\beta + \beta {c_2}){p_4}- \\ {\alpha ^{ - 1}}\beta {c_2}{p_3} - {\alpha ^{ - 1}}(\gamma + \gamma {c_3}){p_6} - {\alpha ^{ - 1}}\gamma {c_3}{p_5}]- \\ {d_1}l_1^{ - 1}{C_{1 - 2}}{p_4} + ({m_1} + {m_2}){l_1}{S_{1 - 2}}p_4^2 + {m_2}{l_2}{S_{1 - 2}} \;{\boldsymbol{\cdot}} \\ {C_{1 - 2}}p_6^2 + + ({m_1} + {m_2})g{C_{1 - 2}}{S_1} - ({m_1} + {m_2})g{S_2}+ \\ ({m_1} + {m_2}){({m_2}{l_2})^{ - 1}}{d_2}{p_6}\} = n({\boldsymbol{p}}) \\ \end{gathered} $$ (34) 因此，根据式(29)~(34)可得一个关于
${\boldsymbol{p}}$ 的状态空间表达式，将其在平衡点${{\boldsymbol{p}}_0} = 0$ 处线性化处理，整理可得如下的线性系统$$ \dot {\boldsymbol{p}} = {\boldsymbol{A}}{\boldsymbol{p}} $$ (35) 其中
$$ \begin{gathered} {\boldsymbol{A}} = {\left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0 \\ {\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_1}}}}&{\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_2}}}}&{\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_3}}}}&{\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_4}}}}&{\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_5}}}}&{\dfrac{{v({\boldsymbol{p}})}}{{\partial {p_6}}}} \\ 0&0&0&1&0&0 \\ {\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_1}}}}&{\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_2}}}}&{\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_3}}}}&{\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_4}}}}&{\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_5}}}}&{\dfrac{{m({\boldsymbol{p}})}}{{\partial {p_6}}}} \\ 0&0&0&0&0&1 \\ {\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_1}}}}&{\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_2}}}}&{\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_3}}}}&{\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_4}}}}&{\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_5}}}}&{\dfrac{{n({\boldsymbol{p}})}}{{\partial {p_6}}}} \end{array}} \right]_{{{\boldsymbol{p}}_0} = 0}}= \\ \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0 \\ { - {c_1}}&{ - ({c_1} + 1)}&{{A_{23}}}&{{A_{24}}}&{{A_{25}}}&{{A_{26}}} \\ 0&0&0&1&0&0 \\ {{A_{41}}}&{{A_{42}}}&{{A_{43}}}&{{A_{44}}}&{{A_{45}}}&{{A_{46}}} \\ 0&0&0&0&0&1 \\ 0&0&{{A_{63}}}&{{A_{64}}}&{{A_{65}}}&{{A_{66}}} \end{array}} \right] \\ \end{gathered}$$ (36) 其中，
$$ \begin{gathered} {A_{23}} = - {\alpha ^{ - 1}}\beta {c_2},\;{A_{24}} = - {\alpha ^{ - 1}}(\beta + \beta {c_2}),\; \\ {A_{25}} = - {\alpha ^{ - 1}}\gamma {c_3},\;{A_{26}} = - {\alpha ^{ - 1}}(\gamma + \gamma {c_3}),\; \\ {A_{41}} = {c_1}{l_1}^{ - 1},\;{A_{42}} = ({c_1} + 1){l_1}^{ - 1},\;{\text{ }}{A_{43}} = {(\alpha {l_1})^{ - 1}}\beta {c_2},\; \\ {A_{44}} = {(\alpha {m_1}l_1^2)^{ - 1}}[{l_1}(\beta + \beta {c_2}) + \alpha {d_1}],\;{\text{ }} \\ {A_{45}} = {(\alpha {l_1})^{ - 1}}\gamma {c_3},\;{A_{63}} = {({m_1}{l_2})^{ - 1}}({m_1} + {m_2})g \\ {A_{46}} = {(\alpha {m_1}{l_1}{l_2})^{ - 1}}[{m_1}{l_2}(\gamma + \gamma {c_3}) + \alpha {d_2}],\;{\text{ }} \\ {A_{64}} = {({m_1}{l_1}{l_2})^{ - 1}}{d_1},\;{A_{65}} = {({m_1}{l_2})^{ - 1}}({m_1} + {m_2})g,\; \\ {A_{66}} = {({m_1}{m_2}l_2^2)^{ - 1}}({m_1} + {m_2}){d_2} \end{gathered} $$ 利用Routh-Hurwitz判据计算可得矩阵
${\boldsymbol{A}}$ 的特征值为$$ \begin{gathered} \lambda = - \frac{1}{2}\left[ {({c_1} + 1) \pm \sqrt {{{({c_1} + 1)}^2} - 4{c_1}} } \right], \\ - \frac{1}{2}\left[ {{A_{44}} \pm \sqrt {A_{44}^2 - 4{A_{43}}} } \right], \\ - \frac{1}{2}\left[ {{A_{66}} \pm \sqrt {A_{66}^2 - 4{A_{65}}} } \right] < 0. \\ \end{gathered} $$ (37) 由式(18)中控制参数关系可判定矩阵
${\boldsymbol{A}}$ 为Hurwitz矩阵。因此，可得线性系统(35)具有严格意义上的稳定，进一步可得吊车系统(1)~(3)在平衡点处渐近稳定，同时系统各个状态变量在平衡点处收敛。注2 基于李雅普诺夫理论所设计的复杂非线性系统控制方法通常没有标准的调优准则。通过分析控制器设计和稳定性证明的过程以及大量的仿真可以得到系统控制参数的调优准则和选取范围。首先，为保证系统的稳定性，所有控制增益的选择都要在文中给定的范围内。然后，通过滑模控制的控制规律和大量仿真可以总结出系统控制增益选择的规律，通过增大
$ {c_1}、{c_2}、{c_3} $ 可以减少台车的定位误差和增大吊钩和负载摆角的收敛速度，但$ {c_1}、{c_2}、{c_3} $ 的取值过大可能会造成系统的超调和振荡，$ \alpha 、\beta、\gamma $ 越大系统子滑模面之间的耦合程度越强，对状态变量的影响越明显，$\kappa、\eta $ 为指数趋近律的控制增益，通过减少$\eta $ 可以有效抑制滑模面的振荡，增大$\kappa $ 可以提高滑模面的收敛速度，为提高系统的收敛速度和减少振荡应在增大$\kappa $ 的同时减小$\eta $ ，在一定范围内，扩张状态观测器控制增益$\xi $ 的值越小，观测器的收敛速度越快，但同时要保证观测器的有效估计。3. 仿真结果
为测试所设计的分层滑模控制器(18)对双摆吊车系统的控制性能，通过一系列的仿真结果验证控制器的有效性。在仿真中，双摆吊车系统的参数设置如下
$$ \begin{gathered} {m_0} = 5\;{\rm{kg}},{\text{ }}{m_1} = 2\;{\rm{kg}},{\text{ }}{m_2} = 2.5\;{\rm{kg}}, \\ {l_1} = 1\;{\rm{m}},{\text{ }}{l_2} = 0.4\;{\rm{m}},{\text{ }}g = 9.8\;{\rm{m}}/{{\rm{s}}^2} \\ \end{gathered} $$ 经过仔细的调试，本研究所提方法的控制增益选取如下
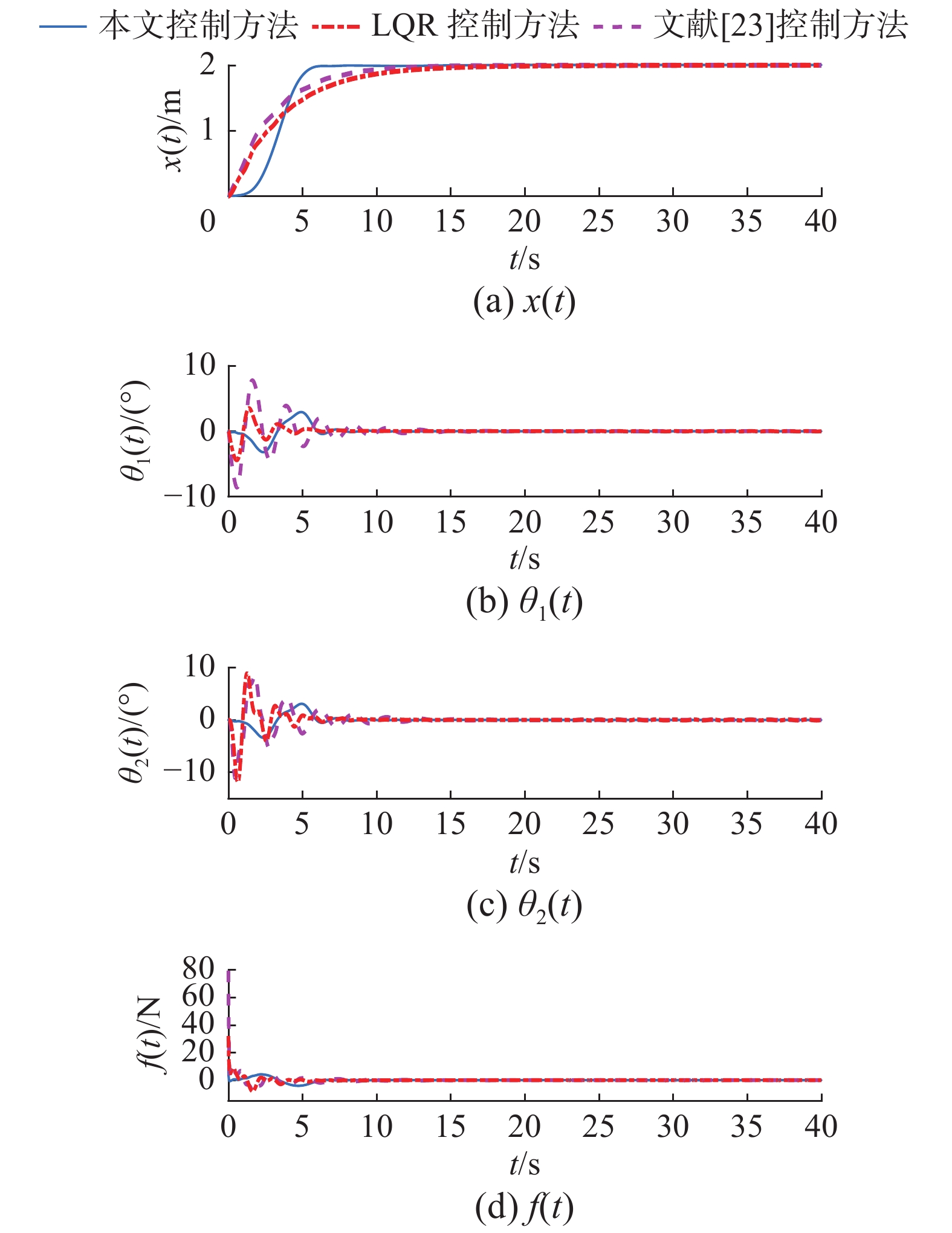
$$ \begin{gathered} {c_1} = 2.5,{\text{ }}{c_2} = 0.2,{\text{ }}{c_3} = 5,{\text{ }}\alpha = 1.5,{\text{ }}\beta = 1, \\ {d_1} = 0.05,{\text{ }}{d_2} = 0.05,{\text{ }}\gamma = 0.1,{\text{ }}\eta = 12, \\ \kappa {\text{ = 50, }}\zeta = 0.15 \\ \end{gathered} $$ 为验证本研究所提控制方法具有良好的控制性能，拟设计3组仿真测试。首先，在第1组仿真中，为在运输效率和吊钩与负载摆角抑制方面的良好性能，作为对比，选取文献[23]的控制方法和广泛用于解决机械系统控制问题的线性二次型调节器(linear quadratic regulator，LQR)控制方法进行仿真测试。然后, 在第2组仿真中，为进一步验证在实际工程中的实用性，分别改变负载的质量和台车目标位置的仿真测试，并与第1组仿真结果进行对比。最后，为验证其鲁棒性，在第3组仿真中，设计对吊钩和负载施加初始摆角干扰和外部摆角干扰的仿真测试，验证存在干扰的条件下控制器的性能。
第1组 对比仿真测试。将通过与文献[23]中控制方法和LQR控制方法进行仿真对比。对于LQR控制方法，其控制器的表达式如下
$$ f = - {k_1}{e_1} - {k_2}\dot x - {k_3}{\theta _1} - {k_4}{\dot \theta _1} - {k_5}{\theta _2} - {k_6}{\dot \theta _2} $$ 其中，
${k_1}、{k_2}、{k_3}、{k_4}、{k_5}、{k_6}$ 为控制增益。代价函数选取为
$$ J = \int_0^\infty {\left({{\boldsymbol{p}}^{\rm{T}}}{\boldsymbol{Qp}} + R{F^2}\right)} {\rm{d}}t $$ 式中：矩阵
${\boldsymbol{Q}} \in {{\bf{R}}^{6 \times 6}},{\text{ }}R \in \rm{R}$ 的选择如下$$ {\boldsymbol{Q}} = {\rm{diag}}( 45,{\text{ }}7,{\text{ }}102,{\text{ }}1,{\text{ }}78,{\text{ }}0) ,{\text{ }}R = 0.01。 $$ 利用MATLAB计算得到控制器的增益为
$$ \begin{array}{*{20}{l}} {{k_1} = 39.772,{\text{ }}{k_2} = 120.364,{\text{ }}{k_3} = - 200.19,} \\ {{k_4} = - 15.55,{\text{ }}{k_5} = 145.168,{\text{ }}{k_6} = - 0.041。} \end{array} $$ 对于文献[23]控制方法，其控制器表达式如下
$$ \begin{gathered} f = \left({m_0} + \frac{{{m_1}({m_1} + {m_2})S_1^2}}{{{m_1} + {m_2}S_{1 - 2}^2}}\right)\bigg[ - \varphi {k_p}\dot e\tanh ({k_p}e) - \tau \sigma - \\ \varphi {{{\rm{sech}}} ^2}(k{k_p}e)\bigg] -\frac{1}{{{m_1} + {m_2}S_{1 - 2}^2}}\bigg[{m_1}({m_1} + {m_2}){S_1} \cdot\\ \left(\dot \theta _1^2 + {C_1}g\right) + {m_1}{m_2}{l_2}\left({S_2} + {C_1}{S_{1 - 2}}\right)\dot \theta _2^2\bigg] \\ \end{gathered} $$ 式中：
$\varphi 、{k_s}、\tau $ 为控制增益；$\sigma $ 为系统设计的滑模面，具体算法如下$$ \sigma = \dot e + k\tanh ({k_p}e),\; e = x - {x_d} $$ 控制增益选择为
$$ \varphi = 22.5,\; {k_s} = 16,\; \tau = 3 。$$ 仿真结果如图2所示。由图2可知，本研究所提控制方法在
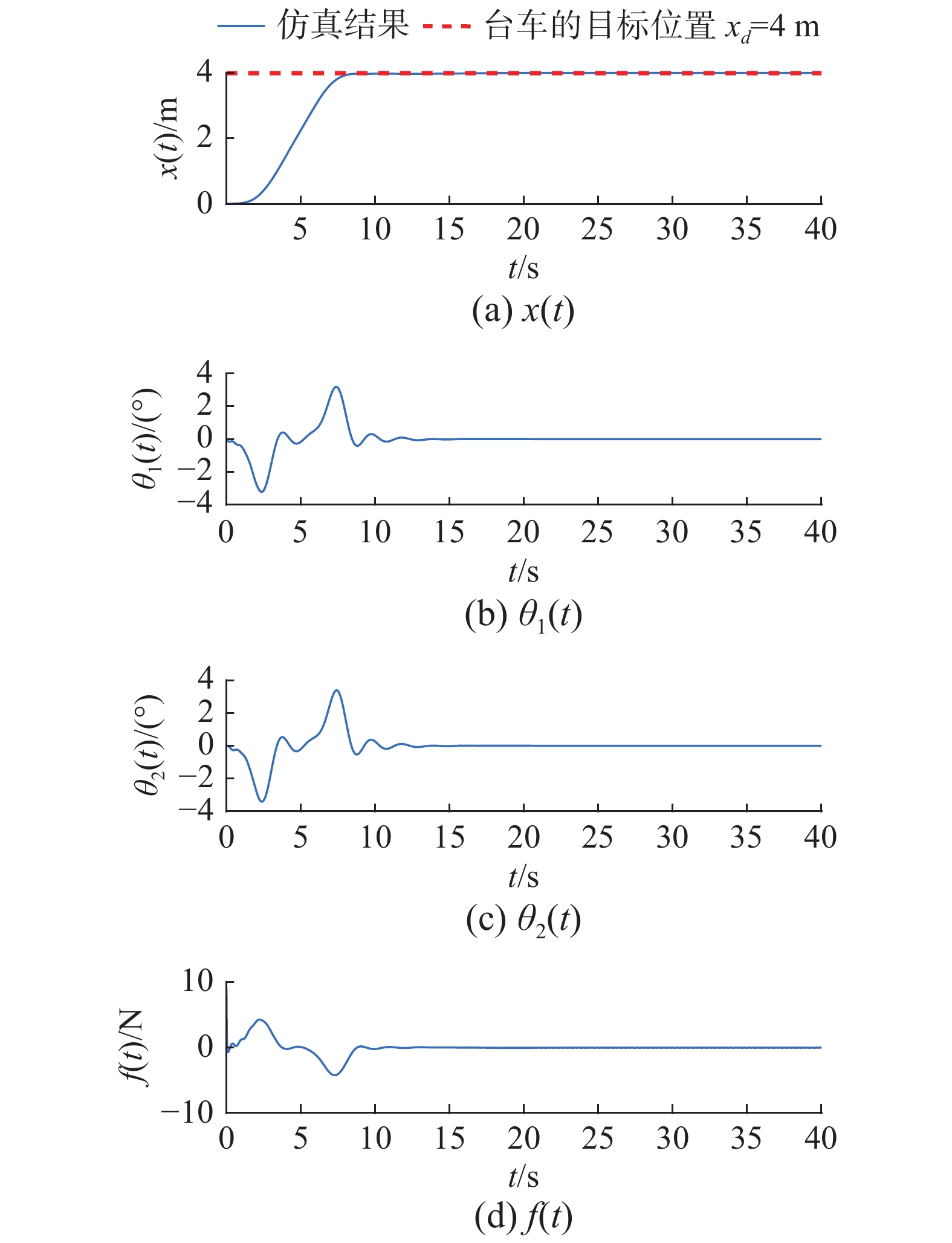
$5.8{\text{ }}{\rm{s}}$ 将台车准确驱动到目标位置，并且吊钩和负载摆角始终保持在3.5°之内且没有残余摆动。相比之下，LQR控制方法和文献[23]的控制方法，虽然也可以驱动台车到达目标位置，但运送时间增加${\text{4}}{\text{.9 }}{\rm{s}}$ 和${\text{5}}{\text{.5 }}{\rm{s}}$ ，同时吊钩的最大摆角达到8.5°和4.5°，负载的最大摆角达到11°和12°，明显大于本研究所提方法的摆角，并且负载存在明显的残余摆动。因此，本研究所提控制方法，在运送效率和抑制吊钩和负载摆动方面具有更好的控制性能。
图 2 第1组仿真结果Fig. 2 Simulation results in Group 1下载:
全尺寸图片
第2组 修改系统参数。在实际的工业生产中，吊车系统需要承担不同情况的运送任务，包括不同距离的台车目标位置和运送不同质量的负载等。为验证所提控制方法在工业生产中的实用性，在控制参数选取与第1组仿真保持一致的前提下，分别进行驱动台车到达目标位置
${x_d} = 4{\text{ }}{\rm{m}}$ 和运送不同质量的负载$m'_2 $ =5 kg的仿真测试。仿真结果分别如图3和图4所示。对比图3和图2的仿真结果可以发现，在台车目标距离增加一倍的情况下，台车到达目标位置的时间增加
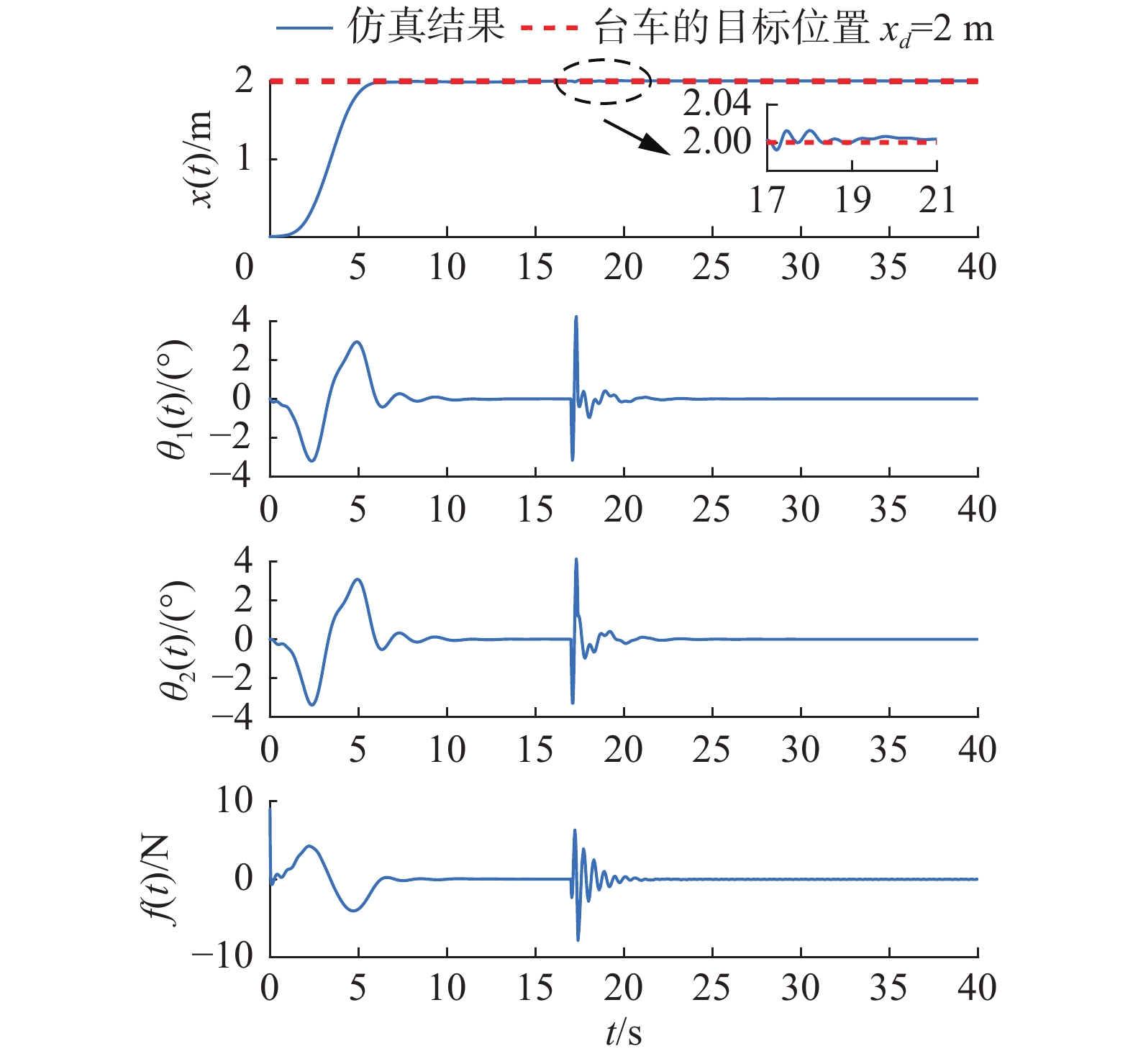
${\text{2}}{\text{.1 }}{\rm{s}}$ 左右，吊钩和负载的最大摆角仅增加0.3°左右，且吊钩与负载摆角均迅速收敛到零。由图4可以发现, 在增加负载质量的仿真测试中，与第1组仿真相比台车的运送时间、吊钩和负载的最大摆角以及摆动消除的时间几乎相同，仅作用于台车的初始驱动力出现细微改变。因此，本研究所提控制方法在运输远距离负载任务时在保证高运输效率的同时有效抑制吊钩和负载的摆动，同时在承担不同质量负载的运送任务时，具有良好的控制性能。
图 3 第2组仿真结果：改变台车目标位置Fig. 3 Simulation results in Group 2: changing the target position of the trolley下载:
全尺寸图片
图 4 第2组仿真结果：改变负载质量${m_2} = 5 \;{\rm{kg}}$ Fig. 4 Simulation results in Group 2: changing the mass of the payload${m_2} = 5\; {\rm{kg}}$ 下载:
全尺寸图片
第3组 鲁棒性仿真测试。当吊车系统在室外环境工作时，很可能会遭受外部干扰(如风)的影响导致吊钩和负载发生摆动，进而产生安全风险。因此，为验证所提控制方法的鲁棒性，在控制目标和控制参数与第1组仿真保持一致的前提下，引入2种不同方式的干扰对吊车系统进行鲁棒性测试。具体而言，首先为测试控制器针对初始摆角干扰的鲁棒性，同时对吊钩摆角和负载摆角施加2°的初始摆角干扰。接着，为测试控制器在稳定状态下的鲁棒性，在无初始摆角干扰的前提下，在仿真进行到
$17{\text{ }}{\rm{s}}$ 处同时对吊钩和负载施加4°左右的外部摆动干扰。仿真结果如图5和图6所示。通过对比图5和图2的仿真结果可以发现，在对吊钩和负载施加初始摆角干扰的情况下，台车到达目标位置的时间和吊钩和负载的最大摆角与第1组仿真结果相同，仅作用在台车上的驱动力发生可接受的变化。由图6中可以看出，在吊车系统处于稳定状态下吊钩和负载遭受外部摆角干扰时，本研究所提控制方法能够通过改变台车的位移(图6第1个子图中的局部放大图)有效抑制干扰对吊车系统的影响，并且在干扰结束后
$2{\text{ }}{\rm{s}}$ 内消除吊钩和负载的摆动，且最终不存在台车定位误差。综上所述, 本研究所提控制方法具有良好的鲁棒性。
图 5 第3组仿真结果：初始摆角扰动Fig. 5 Simulation results in Group 3: initial swing angle disturbances下载:
全尺寸图片
图 6 第3组仿真结果：外部摆角扰动Fig. 6 Simulation results in Group 3: external swing angle disturbances下载:
全尺寸图片
4. 结束语
本研究针对具有双摆效应的欠驱动吊车系统，提出一种基于扩张状态观测器的分层滑模控制方法。首先，将双摆吊车动力学模型转化为方便观测器和控制器设计的形式。然后，基于转换后的二阶系统结构和状态变量误差设计一种扩张状态观测器对系统干扰信号进行有效估计。最后，设计出可以实现台车精准定位和抑制负载与吊钩摆动的分层滑模控制器。通过与已有的控制方法进行对比，仿真结果表明本研究所提控制方法在运输效率和鲁棒性方面具有良好的控制性能。在接下来的研究工作中，将考虑双摆吊车系统具有未知参数的抗干扰控制问题，搭建有效的吊车系统试验原理样机并进行试验测试，更好地验证所提方法的有效性。
-
图 1 双摆吊车模型示意
Fig. 1 Schematic diagram of double pendulum cranes
下载:
全尺寸图片
图 2 第1组仿真结果
Fig. 2 Simulation results in Group 1
下载:
全尺寸图片
图 3 第2组仿真结果：改变台车目标位置
Fig. 3 Simulation results in Group 2: changing the target position of the trolley
下载:
全尺寸图片
图 4 第2组仿真结果：改变负载质量
${m_2} = 5 \;{\rm{kg}}$ Fig. 4 Simulation results in Group 2: changing the mass of the payload
${m_2} = 5\; {\rm{kg}}$ 下载:
全尺寸图片
图 5 第3组仿真结果：初始摆角扰动
Fig. 5 Simulation results in Group 3: initial swing angle disturbances
下载:
全尺寸图片
图 6 第3组仿真结果：外部摆角扰动
Fig. 6 Simulation results in Group 3: external swing angle disturbances
下载:
全尺寸图片
-
[1] YE Huawen. Stabilization of uncertain feedforward nonlinear systems with application to underactuated systems[J]. IEEE transactions on automatic control, 2019, 64(8): 3484–3491. doi: 10.1109/TAC.2018.2882479 [2] THAKAR P S, TRIVEDI P K, BANDYOPADHYAY B, et al. A new nonlinear control for asymptotic stabilization of a class of underactuated systems: an implementation to slosh-container problem[J]. IEEE/ASME transactions on mechatronics, 2017, 22(2): 1082–1092. doi: 10.1109/TMECH.2016.2636251 [3] 何杭轩, 段海滨, 张秀林, 等. 基于扩张鸽群优化的舰载无人机横侧向着舰自主控制[J]. 智能系统学报, 2022, 17(1): 151–157. HE Hangxuan, DUAN Haibin, ZHANG Xiulin, et al. Lateral automatic carrier landing control based on expanded pigeon inspired optimization[J]. CAAI transactions on intelligent systems, 2022, 17(1): 151–157. [4] STEWART W, WEISLER W, ANDERSON M, et al. Dynamic modeling of passively draining structures for aerial-aquatic unmanned vehicles[J]. IEEE journal of oceanic engineering, 2020, 45(3): 840–850. doi: 10.1109/JOE.2019.2898069 [5] DING Caiwu, LU Lu. A tilting-rotor unmanned aerial vehicle for enhanced aerial locomotion and manipulation capabilities: design, control, and applications[J]. IEEE/ASME transactions on mechatronics, 2021, 26(4): 2237–2248. doi: 10.1109/TMECH.2020.3036346 [6] 王琥, 胡立坤, 谭颖. PSO优化的六自由度机械臂全局快速终端滑模控制[J]. 智能系统学报, 2017, 12(2): 266–271. doi: 10.11992/tis.201605024 WANG Hu, HU Likun, TAN Ying. A PSO-based global fast terminal sliding mode controller for 6-DOF manipulators[J]. CAAI transactions on intelligent systems, 2017, 12(2): 266–271. doi: 10.11992/tis.201605024 [7] BARBAZZA L, ZANOTTO D, ROSATI G, et al. Design and optimal control of an underactuated cable-driven micro-macro robot[J]. IEEE robotics and automation letters, 2017, 2(2): 896–903. doi: 10.1109/LRA.2017.2651941 [8] 衣淳植, 郭浩, 丁振, 等. 下肢外骨骼研究进展及关节运动学解算综述[J]. 智能系统学报, 2018, 13(6): 878–888. doi: 10.11992/tis.201804063 YI Chunzhi, GUO Hao, DING Zhen, et al. Research progress of lower-limb exoskeleton and joint kinematics calculation[J]. CAAI transactions on intelligent systems, 2018, 13(6): 878–888. doi: 10.11992/tis.201804063 [9] SUN Wei, LIN J W, SU Shunfeng, et al. Reduced adaptive fuzzy decoupling control for lower limb exoskeleton[J]. IEEE transactions on cybernetics, 2021, 51(3): 1099–1109. doi: 10.1109/TCYB.2020.2972582 [10] KIM J, LEE D, KISS B, et al. An adaptive unscented Kalman filter with selective scaling (AUKF-SS) for overhead cranes[J]. IEEE transactions on industrial electronics, 2021, 68(7): 6131–6140. doi: 10.1109/TIE.2020.2996150 [11] CHEN He, SUN Ning. Nonlinear control of underactuated systems subject to both actuated and unactuated state constraints with experimental verification[J]. IEEE transactions on industrial electronics, 2020, 67(9): 7702–7714. doi: 10.1109/TIE.2019.2946541 [12] RAUSCHER F, SAWODNY O. Modeling and control of tower cranes with elastic structure[J]. IEEE transactions on control systems technology, 2021, 29(1): 64–79. doi: 10.1109/TCST.2019.2961639 [13] WU T S, KARKOUB M, WANG Huiwei, et al. Robust tracking control of MIMO underactuated nonlinear systems with dead-zone band and delayed uncertainty using an adaptive fuzzy control[J]. IEEE transactions on fuzzy systems, 2017, 25(4): 905–918. doi: 10.1109/TFUZZ.2016.2586970 [14] FU Yu, SUN Ning, YANG Tong, et al. Adaptive coupling anti-swing tracking control of underactuated dual boom crane systems[J]. IEEE transactions on systems, man, and cybernetics:systems, 2022, 52(7): 4697–4709. doi: 10.1109/TSMC.2021.3102244 [15] CAI Panpan, CHANDRASEKARAN I, ZHENG Jianmin, et al. Automatic path planning for dual-crane lifting in complex environments using a prioritized multiobjective PGA[J]. IEEE transactions on industrial informatics, 2018, 14(3): 829–845. doi: 10.1109/TII.2017.2715835 [16] YANG Tong, SUN Ning, CHEN He, et al. Motion trajectory-based transportation control for 3-D boom cranes: analysis, design, and experiments[J]. IEEE transactions on industrial electronics, 2019, 66(5): 3636–3646. doi: 10.1109/TIE.2018.2853604 [17] RAMLI L, MOHAMED Z, JAAFAR H I. A neural network-based input shaping for swing suppression of an overhead crane under payload hoisting and mass variations[J]. Mechanical systems and signal processing, 2018, 107: 484–501. doi: 10.1016/j.ymssp.2018.01.029 [18] ZHANG Menghua, MA Xin, SONG Rui, et al. Adaptive proportional-derivative sliding mode control law with improved transient performance for underactuated overhead crane systems[J]. IEEE/CAA journal of automatica sinica, 2018, 5(3): 683–690. doi: 10.1109/JAS.2018.7511072 [19] FRIKHA S, DJEMEL M, DERBEL N. A new adaptive neuro-sliding mode control for gantry crane[J]. International journal of control, automation and systems, 2018, 16(2): 559–565. doi: 10.1007/s12555-017-0070-x [20] ZHANG Shengzeng, HE Xiongxiong, CHEN Qiang. Energy coupled-dissipation control for 3-dimensional overhead cranes[J]. Nonlinear dynamics, 2020, 99(3): 2097–2107. doi: 10.1007/s11071-019-05451-2 [21] WU Xianqing, HE Xiongxiong. Nonlinear energy-based regulation control of three-dimensional overhead cranes[J]. IEEE transactions on automation science and engineering, 2017, 14(2): 1297–1308. doi: 10.1109/TASE.2016.2542105 [22] WU Xianqing, XU Kexin, LEI Meizhen, et al. Disturbance-compensation-based continuous sliding mode control for overhead cranes with disturbances[J]. IEEE transactions on automation science and engineering, 2020, 17(4): 2182–2189. doi: 10.1109/TASE.2020.3015870 [23] CHWA D. Sliding-mode-control-based robust finite-time antisway tracking control of 3-D overhead cranes[J]. IEEE transactions on industrial electronics, 2017, 64(8): 6775–6784. doi: 10.1109/TIE.2017.2701760 [24] AGUIAR C, LEITE D, PEREIRA D, et al. Nonlinear modeling and robust LMI fuzzy control of overhead crane systems[J]. Journal of the Franklin Institute, 2021, 358(2): 1376–1402. doi: 10.1016/j.jfranklin.2020.12.003 [25] YAVUZ H, BELLER S. An intelligent serial connected hybrid control method for gantry cranes[J]. Mechanical systems and signal processing, 2021, 146: 107011. doi: 10.1016/j.ymssp.2020.107011 [26] OUYANG Huimin, TIAN Zheng, YU Lili, et al. Motion planning approach for payload swing reduction in tower cranes with double-pendulum effect[J]. Journal of the Franklin Institute, 2020, 357(13): 8299–8320. doi: 10.1016/j.jfranklin.2020.02.001 [27] CHEN He, FANG Yongchun, SUN Ning. A swing constrained time-optimal trajectory planning strategy for double pendulum crane systems[J]. Nonlinear dynamics, 2017, 89(2): 1513–1524. doi: 10.1007/s11071-017-3531-0 [28] TIAN Zheng, YU Lili, OUYANG Huimin, et al. Transportation and swing reduction for double-pendulum tower cranes using partial enhanced-coupling nonlinear controller with initial saturation[J]. ISA transactions, 2021, 112: 122–136. doi: 10.1016/j.isatra.2020.11.028 [29] SUN Ning, YANG Tong, FANG Yongchun, et al. Transportation control of double-pendulum cranes with a nonlinear quasi-PID scheme: design and experiments[J]. IEEE transactions on systems, man, and cybernetics:systems, 2019, 49(7): 1408–1418. doi: 10.1109/TSMC.2018.2871627 [30] GUO Baozhu, ZHAO Zhiliang. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & control letters, 2011, 60(6): 420–430.
