Concept-driven discriminative feature learning for few-shot learning
-
摘要: 小样本学习旨在让模型能够在仅有少量标记数据的新类中进行分类。基于度量学习的方法是小样本学习的一种有效方法，该类方法利用有标签的支持集样本构建类表示，再基于查询样本和类表示的相似性进行分类。因此，如何构建判别性更强的类表示是这类方法的关键所在。多数工作在构建类表示时，忽略了类概念相关信息的挖掘，这样容易引入样本中类别无关信息，从而降低类表示的判别性。为此本文提出一种概念驱动的小样本判别特征学习方法。该方法首先利用类别的语义信息来指导模型挖掘样本中类概念相关信息，进而构建更具判别性的类表示。其次，设计了随机掩码混合机制增加样本的多样性和识别难度，进一步提升类表示的质量。最后对处于决策边界附近的查询样本赋予更大的权重，引导模型关注难样本，从而更好地进行类表示学习。大量实验的结果表明本文提出的方法能够有效提升小样本分类任务的准确率，并且在多个数据集上优于当前先进的算法。Abstract: Few-shot learning (FSL) aims to recognize unlabeled samples from novel classes with few labeled samples. Metric-based methods, which obtain favorable results in FSL, construct class representations with labeled samples and classify the query samples based on the similarity between class representations and query samples. Therefore, constructing discriminative class representations is the key to these approaches. Most of the existing work ignores the mining of concept-relevant discriminative sample information when constructing class representations, which may bring noise information in samples to the class representations. To alleviate these problems, a concept-driven discriminative feature learning method tailored for FSL is proposed in this work. First, this method incorporates semantic category information to guide the mining of the class-sensitive information of labeled samples and thereby establishes a more discriminative class representation. Then, a random mask mixing mechanism is designed to increase data diversity and the identification difficulty of query samples to further improve class representation quality. Finally, it assigns higher weights to the samples near the decision boundary to guide the model to focus on difficult samples, which helps to learn better class representations. Extensive experiments show that the framework proposed in this work can effectively improve recognition accuracy, and it outperforms state-of-the-art methods on many benchmarks.
-
随着信息技术的发展，社会数字化进程在加速，社会各部门每天产生的数据量及其增长量都远超以往．在此背景下，依托于大规模数据的深度学习技术在推荐系统、自然语言处理、机器视觉[1]、控制自动化等应用场景取得了显著成就。 但是这些机器的智能还并不能和人类智能相媲美，相比之下，人类对于新概念新知识的认知理解并不需要如此大的数据量。此外，在某些领域如医疗、军事等，手动收集和标记大量数据耗费大量的人力物力，人们无法搜集到足够的数据。如何在小数据量的情况下进行快速学习对于计算机来说依旧是一个挑战。因此小样本学习[2-11]成为学术界和工业界近年来关注的重点问题。
小样本学习的关键问题在于训练样本不足，模型容易过拟合，泛化性能差。元学习[9-10]是在数据匮乏情况下缓解模型过拟合的一种有效途径。具体来说就是，模型通过设置一系列小样本学习的任务[11] (episode)，在训练中模拟低数据量的任务，在多轮的迭代中学习解决这类任务的元知识并将这种知识迁移到新类中，例如嵌入空间[2-8,11-13](embed-ding space)等。基于度量学习的小样本学习方法简单有效，受到研究者的广泛认可。嵌入空间则是在元学习框架下基于度量学习的方法进行小样本学习所要学习的元知识，在该空间中同类的样本相互靠近，不同类的样本相互远离。在测试时，利用有标签的支持集样本构建类表示，通过最近邻的原则为查询集的每个样本分配一个支持集类别所对应的标签。因此这类方法的一个关键问题在于如何学习一个好的类表示。例如，原型网络[2]认为每个类的类表示可以由一个进行原型表示，以同类样本在嵌入空间的质心为类原型。然而模型将每个样本表示成向量，忽略了样本的空间信息和局部信息，导致在构建类原型过程缺乏对类概念相关判别信息的挖掘，在复杂语义的场景中泛化性能较差。对于小样本学习来说，丰富的局部信息可以更好地帮助构建该类表示。因此后续有一些方法将样本表示成张量，利用样本的局部信息来构建最终的类表示[7]。虽然这类方法考虑了更丰富的信息，但由于图片的局部信息中不仅包含目标物体，通常也包含着很多与类别无关的背景信息，可以看到直接利用全部局部信息构造的类表示容易引入图片中的噪音信息，从而降低类表示的判别性。因此在构建类表示的学习过程中需要有效挖掘类概念相关区域，去除无关信息对类表示的影响。在类表示学习的过程中，模型仅仅利用少量的有标签样本和查询集样本进行训练对于提升类概念敏感特征挖掘能力的泛化性有限，增加数据多样性可以增加模型的识别难度，从而提示类表示的判别性。此外，小样本学习由于样本数目少，模型在学习构建类表示的过程中距离决策边界更近的样本对类表示的构建学习更重要，所有的样本不是同样重要。因此模型需要更有效地利用信息价值更高的样本进行判别特征进行挖掘，同时这也有利于减小类内方差。
从上述问题出发，本文提出一种概念驱动的小样本判别特征表示学习方法，该方法旨在充分挖掘样本中和类概念相关的信息，从而构建更具判别性的类表示，以提升相似性度量的准确性。具体来说，对于有标签的支持集样本，利用语义标签引导模型对类概念敏感信息进行挖掘从而构建判别性更强的类表示。对于无标签的查询样本，通过随机掩码混合机制增加查询样本的多样性和识别难度，进一步提升类表示的判别性能以及模型的泛化能力。最后，在不引入参数的情况下，在局部任务损失的计算中引入了代价敏感策略，对查询集的每个样本依据任务的难易程度自适应的设置不同的权重，合理利用信息价值更高的难样本难任务进行类概念敏感信息的判别特征挖掘。同时本文采用了稠密预测[14](dense classification)的训练策略，有效地利用到局部特征的信息，能够从有限的训练数据中获取更多的知识。
具体而言，本文的贡献点如下：
1）提出概念驱动的小样本学习判别特征学习方法，利用类概念信息引导模型在少量数据的情况下对类概念敏感的判别特征的挖掘，从而构建判别性的更强类表示，提升小样本图像分类任务的准确度。 在类表示构建的学习过程中，利用随机掩码混合机制及代价敏感策略使模型更高效地进行判别特征的挖掘从而提升模型的泛化性。
2）通过大量实验表明本文模型在标准小样本分类任务上的有效性。同时在跨领域小样本分类任务的实验结果也表明模型具有良好的泛化性。
1. 相关工作
本节首先对小样本学习的N-way K-shot任务进行介绍及其他相关专业术语进行描述，再介绍与本文模型密切相关的基于度量学习的小样本学习方法以及数据增强在小样本学习中的应用。
1.1
$ N $ -way$ K $ -shot任务与传统的机器学习数据划分方式不同，在小样本学习中通常将数据集划分为两个类别不相交的集合，分别为训练时所用的基类数据集
$ {\mathcal{D}}_{\text{base}} $ 和测试时所用的新类数据集$ {\mathcal{D}}_{\text{novel}} $ ，分别有类别$ {C}_{\text{base}} $ 和$ {C}_{\text{novel}} $ ，且有$ {C}_{\text{base}}\cap {C}_{\text{novel}}=\varnothing $ 。在基类数据集中${\mathcal{D}}_{{\rm{base}}}=\left(x,y\right)\subset {X}_{b}\times {Y}_{b}$ ，在新类数据集中${D}_{{\rm{novel}}}=\left(x,y\right)\subset {X}_{n}\times {Y}_{n}$ ，$ \left(x,y\right) $ 分别为样本及对应的标签。特别地，小样本学习采用元学习训练机制，通过构建一系列任务进行学习，每个任务由支持集和查询集组成的二元组$ （S,Q） $ 构成，其中支持集$ S $ 包含个$ N $ 不同的类别，每个类别有$ K $ 个样本，每个任务旨在利用支持集的样本，对查询集的样本$ {x}_{q}\in Q $ 进行分类，即划分到相应任务所属的支持集的类别。在多数研究工作中$ N $ 通常取值为5，$ K $ 的取值为1或5。1.2 基于度量学习的小样本学习
基于度量学习的小样本学习方法希望学习一个好的嵌入空间，在该空间中同类的样本距离更近，不同类的样本距离更远。在测试时，通过比较查询样本与类表示之间的相似性对其进行分类。因此，这类方法的两个关键问题是类表示构建[2,13,15-16] 和相似性度量[2,3,17]。
在类表示构建方面，原型网络将图像映射到特征空间中，以同类样本的质心作为类表示，利用最近邻原则预测查询集的样本的标签。然而在某些复杂场景的数据集中，基于少量样本质心构建的类表示是有偏的。为此后续有相关工作提出一些关于类表示的修正方法。文献[18]认为支持集的样本对类表示的构建贡献不一样，因此需要对同类的不同样本设置不同的权重，以加权平均的形式得到类表示。文献[13]则考虑到仅利用少量有标签的图像信息无法很好地构建类表示，因此引入类相关的其他模态信息如类别语义标签来辅助构建类表示。
上述提及的原型网络及其改进工作通常基于特征图全局池化得到的样本的表示，忽略了局部特征给模型判别性以及迁移性带来的增益。因此Li等[7]的DN4则引入了图像的局部信息来构建类表示，DeepEMD[5]在保持局部特征的情况下，引入推土距离(EMD)距离进行度量，与此同时在训练和测试阶段中都带来了更高的计算复杂度。
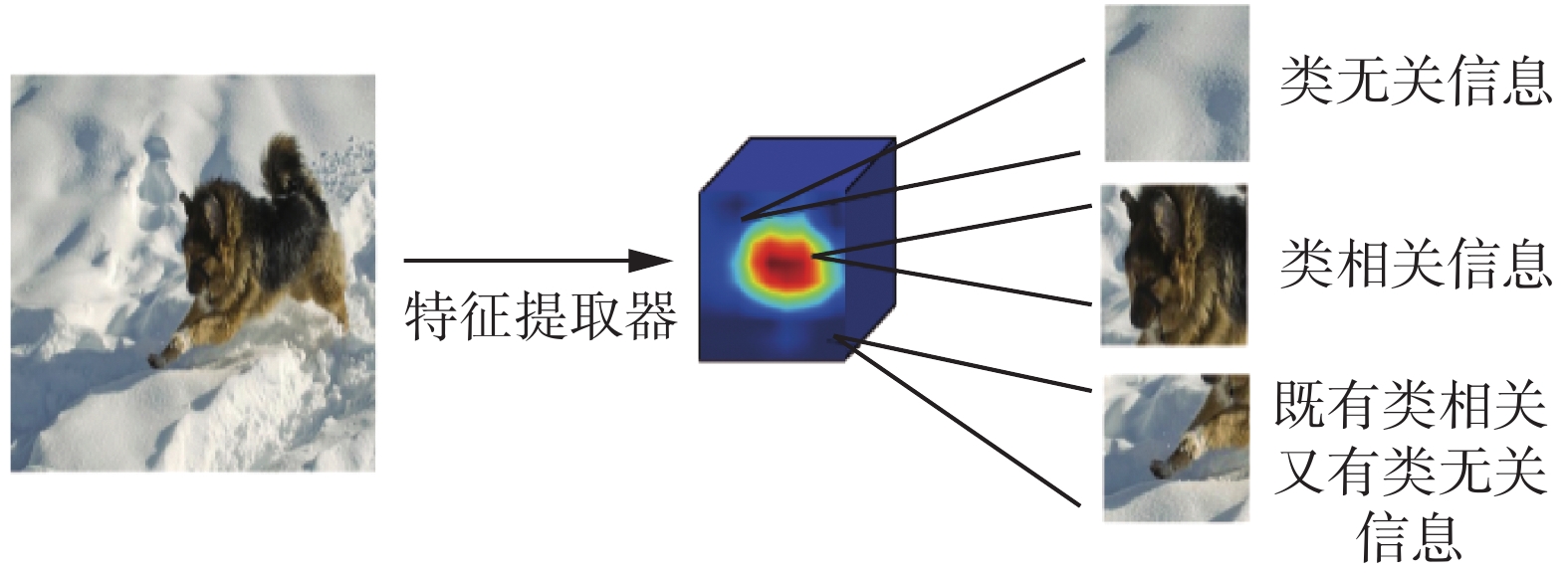
在使用局部信息进行类表示构建时，由于背景等与类别无关信息的存在可能会给类表示带来噪声信息，如图1所示。因此需要一个判别特征挖掘的过程。Ye等[6]和Oreshkin等[8]的工作则引入任务自适应模块利用查询集样本特征对类表示进行任务相关自适应调整。CAM[12]模型则是在利用查询集样本对类表示进行调整的同时也利用类表示对查询集样本间进行调整从而实现特征对齐。文献[19]则利用神经常微分方程(NDE)实现这一过程。 然而，这些方法在利用查询集样本对类表示进行调整时，由于查询样本标签未知，其他类别的样本可能会作为噪音引入到类表示中，从而影响模型性能。为此本文在基于局部信息构建判别性的类表示时利用的是类概念信息而不是无标签的查询集样本。
图 1 类相关局部区域与类无关局部区域示意图Fig. 1 Illustrations of class relevant local regions and class irrelevant local regions
下载:
全尺寸图片
针对相似性度量，大部分方法都是采用传统的距离计算方式，简单有效，在数据有限的情况下，可以很好地缓解模型过拟合问题。也有一些工作针对相似性度量进行改进，例如关系网络[3]则认为简单的度量方式无法很好地度量高维数据间复杂的关系，因此引入神经网络自适应学习相似性度量模块。文献[20]则利用图神经网络建模类表示与查询样本间的相似性。本文主要针对类表示学习进行研究，故采用余弦距离进行作为相似性的度量方式。
1.3 小样本学习中的数据增强
在深度学习中，数据增强是提升数据多样性和缓解模型过拟合的有效途径。传统的数据增强方式，如图像裁剪、图像翻转、颜色变换以及Mixup[21]及其改进工作(Cutmix[22]、Manifold mixup[23])等可以有效提升模型的泛化性能。
利用数据增强技术来提高小样本数据的多样性和小样本学习模型的泛化性也是小样本学习中的常用手段。Wang等[24]的工作中均提出生成对抗网络与小样本学习相结合的方法利用有标签的少量样本生成新的样本来扩充数据集。在Goldblum [25]的工作中则把MixUp以及CutMix引入到小样本学习中的多个环节中。Seo等[26]提出的 Self-Mix策略，旨在防止小样本学习模型只记住训练集中出现过的样本结构。上述工作的数据增强方式是基于原始图像样本，文献[27]表明特征空间中的数据增强可以作为模型正则化的一种有效方式，其中的S2M2模型则将流形混合(Manifold mixup)首次应用到小样本学习研究中，利用两个样本在神经网络中间层的输出的凸组合来提升模型的泛化性和鲁棒性。此外，在元学习中，数据是以任务为单位进行组织的，且在测试阶段需要预测不可见的类。因此Liu等[28]通过任务级别的数据扩充，增加任务的多样性提升模型在不可见的类上的预测性能。
2. 本文方法
本节首先介绍本文所提出的概念驱动的小样本判别特征学习方法，然后再分别介绍训练流程及标签预测流程。
2.1 模型描述
概念驱动的小样本判别特征学习方法旨在通过对类概念的判别信息的挖掘，提升类表示的质量，以更好地进行相似性度量，进而提升小样本学习的分类性能，模型结构图如图2所示。
图 2 模型结构Fig. 2 Model architecture下载:
全尺寸图片
首先利用类概念融合模块融合类概念信息到特征图中，引导模型关注特征图中与类别相关的区域，用于构建类别语义相关的类表示，有利于后续的更精确的相似性度量。同时在训练过程中，为更高效地挖掘样本的判别特征以及提升模型的泛化性能，对查询集样本设计了一种数据增强方式并对每个样本设置了不同的权重，赋予难样本更大的权重，简单样本较小的权重，详细介绍如下：
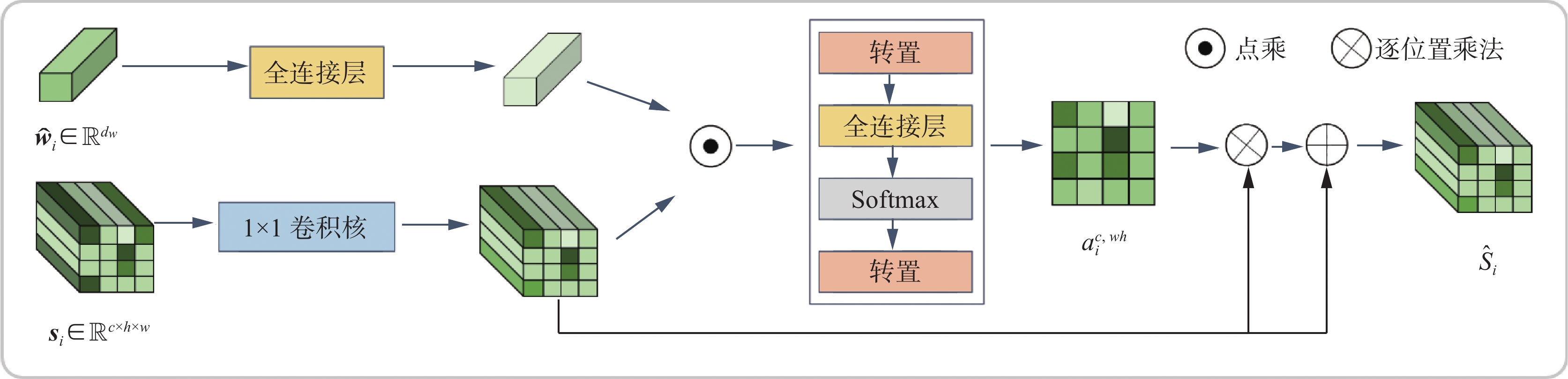
类概念融合模块 当支持集样本中所包含复杂的背景信息或者多个对象时，利用样本的全部信息构建类表示会得到判别性不强的类表示，从而给查询样本的分类带来干扰。为此，本文设计了类概念融合模块使模型关注类别相关的区域，实现图像语义解耦，以构建判别性更强的类表示。该模块主要基于双线性池化模型[29]改进实现，其结构如图3所示。
图 3 类概念融合模块结构Fig. 3 Concept fusion module architecture下载:
全尺寸图片
具体步骤如下：
首先对于任务
$ T $ 中支持集样本${\boldsymbol{X}}_{i}^{{S}}\in {\mathbb{R}}^{3\times h\times w}(i\in \mathrm{1,2},\cdots, N\times K)$ 和查询集中的样本${\boldsymbol{X}}_{{i}}^{{Q}}\in {\mathbb{R}}^{3\times h\times w}(i\in 1, 2,\cdots, N\times {n}_{q})$ 利用特征提取器$ {f}_{\theta } $ 提取特征得张量${\boldsymbol{s}}_{{i}}= {f}_{\theta }\left({\boldsymbol{X}}_{i}^{{S}}\right)\in {\mathbb{R}}^{c\times h\times w}$ 和${\boldsymbol{q}}_{{i}}={f}_{\theta }\left({\boldsymbol{X}}_{i}^{Q}\right)\in {\mathbb{R}}^{c\times h\times w}$ ，其中$ c,w,h $ 分别为特征图的通道数、宽和高。相比于向量表示，该表示包含了图片更丰富的局部信息,更利于小样本学习。虽然张量表示包含了更丰富的局部信息，但这些信息中有可能是背景信息，如果利用背景信息构建类表示，会降低类表示的判别性和泛化性。因此本文利用类别语义标签作为类概念信息引导模型关注图像中的类相关区域。类别的语义标签可以看作类概念在人类语言层面的高度凝练，高度概括同类样本所包含的语义信息。对于每个类别
$ {C}_{i} $ ，本文首先利用GloVe[30]的预训练模型提取特征得到$ {d}_{w} $ 维类标签语义向量，并以此作为类概念编码：$$ \begin{array}{c}{\widehat{\boldsymbol{w}}}_{{i}}={f}_{g}\left({\boldsymbol{w}}_{i}\right)\end{array} $$ 式中：
$ {\boldsymbol{w}}_{i} $ 是类别$ {C}_{i} $ 的语义标签。接下来利用双线性池化来挖掘样本表示中与类相关的信息。双线性池化通过特征融合可以充分挖掘类概念编码和样本表示的直接相关性：
$$ \begin{array}{c}{\tilde {\boldsymbol{s}}}_{i}^{c,wh}={\boldsymbol{P}}^{\rm{T}}\left({\rm{tanh}}\left(\psi \left({\boldsymbol{s}}_{i}\right)\odot \left({\boldsymbol{V}}^{\rm{T}}{\widehat{\boldsymbol{w}}}_{i}\right)\right)\right)+{\boldsymbol{b}}\end{array} $$ 式中：
$ \mathrm{\psi } $ 为$ 1\mathrm{ }\times 1 $ 的卷积，$\boldsymbol{V}\in {\mathbb{R}}^{{{d}}_{{w}}\times {{d}}_{1}}$ 、$\boldsymbol{P}\in {\mathbb{R}}^{{{d}}_{1}\times {{d}}_{2}}$ 与$\boldsymbol{b}\in {\mathbb{R}}^{{{d}}_{2}}$ 均为可学习参数，$ \odot $ 为逐位置乘法操作。接着将${\tilde {\boldsymbol{s}}}_{i}^{{c},{w}{h}}$ 进行转置操作，再按空间位置划分为${ \tilde {\boldsymbol{s}}}_{i}=\left[ { \tilde {\boldsymbol{s}}}_{i}^{1} { \tilde {\boldsymbol{s}}}_{i}^{2}\cdots { \tilde {\boldsymbol{s}}}_{i}^{hw}\right]$ ，在得到类概念编码和样本表示直接的相关性${\tilde {{\boldsymbol{s}}}}_{i}$ 之后计算特征图上每一个位置$ (w,h) $ 的重要性，如式(1)所示，再进行归一化处理，归一化后的权重体现了特征图上的每一个位置相对于类概念的重要程度。$$ \begin{array}{c} { \tilde a}_{i}^{c,wh}={f}_{a}\left( { \tilde {\boldsymbol{s}}}_{i}\right)\end{array} $$ (1) $$ \begin{array}{c}{a}_{i}^{c,wh}=\dfrac{\mathrm{exp}\left({{ \tilde a}}_{i}^{c,wh}\right)}{\displaystyle\sum _{w,h} \mathrm{exp}\left({{ \tilde a}}_{i}^{c,wh}\right)}\end{array} $$ 式中：
$ {f}_{a} $ 为重要性权重生成函数，由单层全连接网络实现。最后将生成的注意力权重作用在特征上，这里使用了类似残差连接的机制：$$ \begin{array}{c}{\hat {\boldsymbol{s}}}_{{i}}={\boldsymbol{s}}_{{i}}+{a}_{i}^{c,wh}\odot {\boldsymbol{s}}_{{i}}\end{array} $$ 最终得到的支持集特征为
${\hat {\boldsymbol{s}}}_{{i}}$ ，该特征显式地利用了类概念信息挖掘样本中类相关的判别特征，以此特征进行类表示的构建可以减少类无关信息的干扰，有利于后续的相似性度量。基于随机掩码混合的数据增强 样本量少是小样本学习的本质问题，为了增加数据的多样性，本文设计了基于随机掩码混合的数据增强策略对查询集进行数据增强。本文只对查询集进行数据增强，是为了防止对支持集进行数据增强可能会对类表示学习引入更多噪音，从而得到不准确的类表示。具体做法如下：给定一张输入图片
$ X $ ，其尺寸为$ 3\times H \times W $ ，将图片$ X $ 划分为大小为$ S\times S $ 的图像块，总共有$(H\times W)/\left(S\times S\right)$ 个图像块，生成$ S\times S $ 的随机掩码$ \widehat{\boldsymbol{M}} $ ，接下来放大为$ H \times W $ 的随机掩码$ \boldsymbol{M} $ ，将$ \boldsymbol{M} $ 与$ 1-\boldsymbol{M} $ 分别作用在两个样本上，得到增强后的样本$ {\widehat{\boldsymbol{X}}}_{\boldsymbol{i}}^{\boldsymbol{q}} $ ：$$ \begin{array}{c}{\widehat{\boldsymbol{X}}}_{\boldsymbol{i}}^{\boldsymbol{q}}=\left(1-\boldsymbol{M}\right)\odot {\boldsymbol{X}}_{\boldsymbol{i}}^{\boldsymbol{q}}+{\boldsymbol{M}}\odot {\boldsymbol{X}}_{\boldsymbol{j}}^{\boldsymbol{q}}\end{array} $$ (2) 式中：
$ {{\boldsymbol{X}}}_{i}^{q} $ 和$ {{\boldsymbol{X}}}_{j}^{q} $ 为同一任务的两个样本；$ \boldsymbol{M} \in {\left\{\mathrm{0,1}\right\}}^{H\times W} $ 为$ H \times W $ 随机的二进制掩码；$ \odot $ 为逐位置乘法。对于二进制掩码$ \boldsymbol{M} $ ，如果$ {\boldsymbol{M}}_{i,j}=1 $ ，则对图像$ (i,j) $ 坐标处的像素保留，否则移除该像素点。由于本文采用了稠密分类的训练策略，因此需要对${\widehat{{\boldsymbol{X}}}}_{i}^{q}$ 的每一个位置设置相应的标签：$$ \begin{array}{c}{\widehat{\boldsymbol{Y}}}_{\boldsymbol{i}}^{\boldsymbol{q}}=\left(1-\boldsymbol{M}\right)\odot {\boldsymbol{Y}}_{\boldsymbol{i}}^{\boldsymbol{q}}+M\odot {\boldsymbol{Y}}_{\boldsymbol{j}}^{\boldsymbol{q}}\end{array} $$ 随机掩码混合的引入一方面可以增加数据多样性；另一方面可以增加识别难度，在最具鉴别性的内容被隐藏时，迫使网络寻找其他相关内容，从而提升模型在不同任务上的泛化性。该策略的思路与Cutmix以及文献[31]中的PatchMix类似，都是通过混合两个样本进行数据增强。然而在上述两个工作中采用的是连续区域混合，过多删除一个或几个区域可能会导致对象的完整删除。但是本文使用的是基于网格的混合方式，可以在一定程度上保持局部区域的完整性。
代价敏感自适应损失 由于小样本学习采用基于元学习的训练机制，从数据集中抽取任务进行模型训练，这种机制抽取出来的任务，其难易程度各不相同，对度量空间的学习的影响也各不相同。在所抽取出来的任务中，
$ N $ 个类在特征空间中相近时，将查询集样本分类到各个类的概率值相近，其困难程度较大。根据边界分布理论，越处于决策边界的样本，信息价值越高，即挖掘难样本、难任务对类判别特征的提取和类表示的构建的学习过程至关重要。为此本文引入代价敏感策略，在任务层面上不同的样本赋予不同的权重，赋予难样本更大的权重，适当降低简单样本的权重系数。具体做法是在交叉熵损失函数的基础上引入代价敏感惩罚系数，最终的损失函数形式为$${\cal L}\left(y,p\right)={\rm{Sigmoid}}\left({p}^{\ell}-{p}^{i}\right){L}_{ce}\left(y,p\right)$$ $$ \begin{array}{c}{p}^{i}=p\left[\kern-0.15em\left[ {y}_{i}=1 \right]\kern-0.15em\right]\end{array} $$ 式中：
$\left[\kern-0.15em\left[ \cdot \right]\kern-0.15em\right]$ 为艾弗森括号，即从预测分布中取出样本标签对应的预测结果$ {p}^{i} $ ，${p}^{\ell}{=1-p}^{i}$ 则为分错的概率。从上面的式子可以看到，当某个样本$ {p}_{i} $ 和$ {p}_{l} $ 有较大间隔时即${p}^{\ell}-{p}^{i}$ ，其惩罚系数较小，当$ {p}_{i} $ 和$ {p}_{l} $ 相近时，其惩罚系数较大。同时当整个任务比较困难时，任务总体的惩罚系数较大，相当于给任务赋予了更大的权重，反之则赋予了更小的权重。2.2 模型训练
模型的损失函数如图2所示分为两个部分，其中一部分为全局损失，通过对样本的全局分类，可以建模类间的关系，另一部分为各个任务内的分类损失。令
$\widehat{\mathcal{T}}=\{\widehat{\boldsymbol{S}},\widehat{\boldsymbol{Q}} \}$ ，$ \widehat{{\boldsymbol{S}}} $ 为融合类概念特征的支持集样本，$ \widehat{\boldsymbol{Q}} $ 则为经过随机掩码混合后的查询集样本特征。与之前利用全局池化在输入到分类层进行分类的方式不同，本文使用的是稠密分类[14]的训练策略。在特征图后使用$ 1\times 1 $ 卷积作分类器，即对于特征张量${{\boldsymbol{x}}}_{i}\in \widehat{\mathcal{T}}$ ，对特征图每一个位置$ \left(p,q\right) $ 的局部特征做出预测，即$$ \begin{array}{c}P\left({y}_{i}=y\mid {\boldsymbol{x}}_{i}^{\left(p,q\right)}\right)={\rm{softmax}}\left({\varPhi }\left({\boldsymbol{x}}_{i}^{\left(p,q\right)}\right)\right)\end{array} $$ 式中：
${\varPhi }$ 为$ 1\mathrm{ }\times \mathrm{ }1 $ 卷积层。 以整个任务的负对数似然的平均值为全局分类损失${\mathcal{L}}_{\rm{CLS}}$ :$$ \begin{array}{c}{\mathcal{L}}_{\rm{CLS}}=\underset{\left({x}_{i},{y}_{i}\right)\in \widehat{\mathcal{T}}}{\mathbb{E}}\dfrac{1}{w\times h}\displaystyle\sum _{\genfrac{}{}{0pt}{}{p=1}{q=1}}^{w,h} -{y}_{i}{\mathrm{log}}_{2}P\left({y}_{i}=y\mid {\boldsymbol{x}}_{i}^{\left(p,q\right)}\right)\end{array} $$ 对于任务内的分类，采用度量学习的思想基于最近邻的策略进行分类，将每一个查询集样本分配与它距离最近的类表示的标签。与原型网络[2]类似，本文利用同类样本特征的质心构建类表示，
$$ \begin{array}{c}{\boldsymbol{c}}_{{k}}=\dfrac{1}{\left|{\widehat{\boldsymbol{S}}}_{{k}}\right|}\displaystyle \sum _{{y}_{i}=k} {\rm{GAP}}\left({\widehat{\boldsymbol{s}}}_{{i}}\right)\end{array} $$ 式中：
${\boldsymbol{c}}_{{k}}\in {\bf{R}}^{{h}}$ ，GAP为全局平均池化。计算查询集中每个样本
$ {\boldsymbol{q}}_{i} $ 到所有类原型${\boldsymbol{c}}_{{j}}$ 的距离。则样本属于支持集中第$ i $ 个类的概率为$$ \begin{array}{c}P\left({y}_{i}=k\mid {\boldsymbol{q}}_{i}\right)=\dfrac{{\rm exp}\left[-\mathcal{M}\left({\boldsymbol{c}}_{k},{\boldsymbol{q}}_{i}\right)/\tau \right]}{\displaystyle\sum _{j=1}^{N} {\rm exp}\left[-\mathcal{M}\left({\boldsymbol{c}}_{j},{\boldsymbol{q}}_{i}\right)/\tau \right]}\end{array} $$ 式中：
$ \tau $ 为温度系数，$ \mathcal{M} $ 为距离度量方式，本文采用的是余弦距离，可以限制和减少神经元的方差，从而得到具有更好泛化能力的模。同时这里也采用保留局部特征的稠密分类的训练策略。因此，小样本学习分类任务的损失函数$ {\mathcal{L}}_{\text{FSL}} $ 定义为$$ \begin{array}{c}{\mathcal{L}}_{\rm{FSL}}=\underset{\left({x}_{i},{y}_{i}\right)\in \widehat{Q}}{\mathbb{E}}\dfrac{1}{w\times h}\displaystyle\sum _{\genfrac{}{}{0pt}{}{p=1}{q=1}}^{w,h} -{\rm{log}}_{2}P\left(y={y}_{i}^{\left(p,q\right)}\mid {\boldsymbol{q}}_{i}^{\left(p,q\right)}\right)\end{array} $$ 结合式(2)中的代价敏感自适应损失函数，
$ {\mathcal{L}}_{\text{FSL}\text{}} $ 最终的形式如下：$$ \begin{array}{c}{\mathcal{L}}_{\rm{FSL}}=\underset{\left({x}_{i},{y}_{i}\right)\in \widehat{Q}}{\mathbb{E}}\dfrac{1}{w\times h}\displaystyle\sum _{\genfrac{}{}{0pt}{}{p=1}{q=1}}^{w,h} \dfrac{-{\rm{log}}_2{p}^{i}}{1+\mathrm{exp}\left(-\beta \left({p}^{\ell}-{p}^{i}\right)\right)}\end{array} $$ 式中：
$ {p}^{i}=P\left(y={y}_{i}^{\left(p,q\right)}\mid {\boldsymbol{q}}_{i}^{\left(p,q\right)}\right) $ ，${p}^{\ell}=1-{p}^{i}$ 。最终的整体损失函数$ {\mathcal{L}}_{\text{total}} $ 定义为$$ \begin{array}{c}{\mathcal{L}}_{\text{total}}=\alpha {\mathcal{L}}_{\rm{CLS}\text{}}+\gamma {\mathcal{L}}_{\rm{FSL}}\end{array} $$ 式中
$ \alpha $ 和$ \gamma $ 为损失函数的权重系数。2.3 结果预测
在测试阶段，从测试集中抽样出来的任务，包含有标签的支持集样本和无标签的查询集样本，利用特征提取器分别得到特征图
${\boldsymbol{s}}_{{i}}^{{n}}\in {\mathbb{R}}^{c\times h\times w}$ 和${\boldsymbol{q}}_{{j}}^{{n}}\in {\mathbb{R}}^{c\times h\times w}$ 。对支持集样本，还需要利用类概念融合模块融合类概念信息，得到支持集样本的特征图${\hat{\boldsymbol{s}}}_{i}^{n}\in {\mathbb{R}}^{c\times h\times w}$ ，并以同类样本的质心构建类表示，最后通过最近邻分类器预测每个查询集样本的标签：$$ \begin{array}{c}{\hat{y}}_{j}^{q}={\rm{arg}}\underset{i}{\;{\rm{min}}} M\left(\mathrm{GAP}\left({\hat{\boldsymbol{s}}}_{{i}}^{{n}}\right),\mathrm{GAP}\left({\boldsymbol{q}}_{{j}}^{{n}}\right)\right)\end{array} $$ 式中：
$ \mathrm{G}\mathrm{A}\mathrm{P} $ 为全局池化，$ \mathcal{M} $ 为距离度量方式，本文采用的是余弦距离。3. 实验与结果
在本节，将介绍实验所用到的数据集以及实验的设置与细节，然后评估本文方法在多种场景下有效性，包括标准小样本学习设置和跨领域小样本。学习设置和最后通过详细的消融实验证明本文所提出的模型的各个组件的有效性。
3.1 数据集介绍
本文在小样本学习的基准数据集上进行了实验，包括miniImageNet[11]，tieredImageNet[32]，CIFAR-FS[8]，FC100 [8] 等，各数据集规模与划分方式细节如表1所示。
表 1 4个基准数据集汇总Table 1 Summarization of four benchmarks数据集 样本数 类别数 数据集划分 miniImageNet 60000 100 64/16/20 tieredImageNet 779165 608 351/97/160 CIFAR-FS 60000 100 60/16/20 FC100 60000 100 60/20/20 数据集miniImageNet与tieredImageNet均为数据集ILSVRC-12[33]的子集。tieredImageNet比miniImageNet更大，且类别具有层级结构，包含34个超类，每个超类又包含10~30个子类，每个类的图片数量不等。CIFAR-FS和FC100均是CIFAR100[34]的子集，图片大小为
$ 32\times 32 $ 像素。相比于CIFAR-FS的数据集划分方式，FC100是按照超类划分的，训练集和测试集之间的类别属于完全不同的超类，领域跨度更大，因此更具挑战性。3.2 实验设置与训练细节
实验设置 本文在 5-way 1-shot 和 5-way 5-shot 设置上测试本文所提出的模型。对于 N-way K-shot 设置，每个任务由N类构成，每个类都包含 K个支持集样本和6个查询样本。测试时，在所有1-shot和5-shot的实验中，在测试集中随机抽取2000个任务，每个类有15个查询样本，并记录相应的95%置信区间的平均准确度。
网络架构 与之前的相关工作[12,14, 31]类似，本文使用ResNet12[1]作为主干特征提取网络，该网络包含 4 个残差块。每个残差块包含 3 个卷积层以及1个池化层，卷积核尺寸3×3， 最大池化层窗口为2×2。同时与文献[35]类似，本文也使用 Dropblock 作为正则化模块，每个残差块的卷积核的数量设置为 (64, 128, 256,512)。
训练细节 各数据集的输入图像尺寸大小均调整为 84 × 84像素。在训练过程中，我们采用与文献[12,19]等工作相同的数据增强方式包括水平翻转、随机裁剪和随机擦除等简单图像变换。使用带动量的SGD优化器，优化模型，权重衰减系数设置为5×10−4。每个小批次包含5个任务。该模型在所有数据集上均训练80个轮次，初始学习率为 0.1。对于miniImageNet，分别在 60 和 70轮次时学将习率降低到 0.006 和 0.0012。对于tieredImageNet，学习率的衰减因子为0.1，每20轮衰减一次。温度超参数
$ \tau $ 设置为5，在参考相关文献[12]的基础上通过多次实验比较，超参数$ \mathrm{\alpha } $ 和$ \gamma $ 设置为1和0.5取得最好性能。本文的所有的模型实现与实验均使用Pytorch，并且使用NVIDIA 2080Ti GPU。3.3 实验结果比较
标准小样本学习实验结果 为了验证本文提出方法在N-way K-shot小样本学习任务上的有效性与优异性，在多个数据集上与小样本学习领域的一些经典方法和先进方法进行了对比，如原型网络，匹配网络，MAML，CAN， DeepEMD等。在miniImageNet和tieredImageNet数据集上的实验结果如表2所示。本文的模型在这两个数据集上1-shot场景下的平均准确度为68.91%和71.75%均优于同类型的算法。模型在5-shot的实验设置下也与先进算法的性能相近。可以看出在数据较少的场景下，本文方法可以提取到更具判别性的特征，从而提升模型的性能。这也表明了显式地利用类概念信息引导模型关注类相关的区域，可以有效提升类表示的构建质量，在后续的相似性度量中得到更准确的相似性度量，更好地体现支持集样本和查询集样本的关系。
表 2 miniImageNet和 tieredImageNet数据集上的实验结果对比Table 2 Comparison of experimental result on miniImageNet and tieredImageNet datasets% 模型 主干特征提取网络 miniImageNet tieredImageNet 5-way 1-shot 5-way 5-shot 5-way 1-shot 5-way 5-shot MatchingNet[4] ResNet10 54.49±0.81 68.82±0.65 — — ProtoNet[4] ResNet10 51.98±0.84 72.64±0.64 — — RelationNet[4] ResNet10 52.19±0.83 70.20±0.66 — — MAML[4] ResNet10 51.98±0.84 66.62±0.83 — — MetaOptNet[35] ResNet10 64.09±0.62 80.00±0.45 65.99±0.72 81.56±0.53 DC [14] ResNet12 61.26±0.20 79.01±0.13 — — LEO[36] WRN-28 61.76±0.08 77.59±0.12 66.33±0.05 81.44±0.09 TADAM[8] ResNet12 58.50±0.30 76.70±0.30 — — AM3 [13] ResNet12 65.30±0.49 78.10±0.36 69.08±0.47 82.58±0.31 FEAT[6] ResNet12 66.78±0.20 82.08±0.14 70.80±0.23 84.79±0.16 CAN[12] ResNet12 63.85±0.48 79.44±0.34 69.89±0.51 84.23±0.37 DeepEMD[5] ResNet12 65.91±0.82 82.41±0.56 71.16±0.87 86.03±0.58 infoPatch[31] ResNet12 67.67±0.45 82.44±0.31 71.51±0.52 85.44±0.35 DAM[19] ResNet12 67.76±0.46 82.71±0.31 71.89±0.52 85.96±0.35 本文算法 ResNet12 68.91±0.45 83.02±0.30 71.75±0.51 84.37±0.36 本文模型在FC100数据集及CIFAR-FS数据集上的结果如表3~4所示。模型在FC100数据集在1-shot和5-shot的实验结果为79.93%和88.74%均超过已有的方法，同时在CIFAR-FS数据集上也取得和先进方法相似的性能，分别为45.34%和59.38%。
表 3 CIFAR-FS上的实验结果对比Table 3 Comparison of experimental results on CIFAR-FS% 模型 主干特征
提取网络CIFAR-FS 5-way 1-shot 5-way 5-shot MAML[10] ConvNet 58.90±1.90 71.50±1.00 ProtoNet[2] ConvNet 55.50±0.70 72.00±0.60 RelationNet[3] ConvNet 55.00±1.00 69.30±0.80 LR+ICI[37] ResNet12 73.97±n/a 84.13±0.n/a Rethink[38] ResNet12 73.90±0.80 86.90±0.50 BML[39] ResNet12 73.45±0.47 88.04±0.33 本文算法 ResNet12 79.93±0.45 88.74±0.31 表 4 FC100数据集上的实验结果对比Table 4 Comparison of experimental results on FC100% 跨领域小样本学习实验结果 跨领域是一个更有挑战性的实验场景。本文根据文献[4]中的实验设置，以miniImageNet数据集为训练集，以CUB-200-2011[40]数据集为测试集，测试模型的跨领域泛化能力。表5显示了本文算法与现有方法相比的实验结果。本文方法在5-way 1-shot和5-way 5-shot设置下，达到51.63%和71.37%。当训练集和测试集来自不同领域时，相比于其他方法仍然具有较高分类精度，可以看出，该方法具有较强的领域泛化的能力，可以有效缓解领域漂移的问题。
表 5 CUB-200-2011跨领域实验结果对比Table 5 Cross Domain Comparison of experimental results on CUB-200-2011% 模型 miniImageNetCUB 5-way 1-shot 5-way 5-shot ProtoNet[2] — 53.07±0.74 MatchingNet[11] 51.65±0.84 69.14±0.72 CloserLook[4] — 51.34±0.72 ClosserLook++[4] — 62.04±0.76 Cosine classifier[4] 44.17±0.78 69.01±0.74 Neg-Softmax[41] — 69.30±0.73 KNN[7] 50.84±0.81 71.25±0.69 BML[39] — 72.42±0.54 本文算法 51.63±0.48 71.37±0.39 3.4 消融实验
为了证明我们提出的模型各个组件的有效性，本文进行了消融实验，如表6所示。
表 6 在miniImageNet数据集上的消融实验Table 6 Ablation study on on miniImageNet dataset% CFM Ltask MaskMix miniImageNet 5-way 1-shot 5-way 5-shot 65.66±0.46 79.85±0.33 √ 67.27±0.45 81.06±0.32 √ √ 68.21±0.45 81.74±0.32 √ √ √ 68.91±0.45 83.02±0.30 基线模型 本文的基线模型基于原型网络，采用最近邻分类器，以余弦相似度为度量方式。与之前的大多数方法相比，该方法已有一定的提升，这主要是由于在训练时采用了稠密分类的训练策略，保留了局部特征的信息，避免了全局池化带来的信息丢失，基线模型在 miniImageNet数据集1-shot和5-shot设置下的平均准确率分别为65.66%和79.85%。
类概念混合模块 该模块在基线模型的基础上引入类概念信息引导模型关注类概念相关区域，从而构建判别性更强的类表示，带来了较大的性能增益，在1-shot上效果更加显著，分类精度提升了1.61%，同时在5-shot上也有1.21%性能增益。这也说明了更准确的类表示在相似性度量阶段可以更好地判断样本间的关系。
代价敏感自适应损失 模型在类表示构建的学习过程中，代价敏感自适应损失使得模型更加注重于难任务难样本的挖掘，可以增大易混淆的不同类样本的间隔，可以学习到一个更好的度量空间，是的难样本的可区分性更高，在1-shot和5-shot的提升分别为0.93%和0.68%。
基于随机掩码混合的数据增强 基于随机掩码混合的数据增强策略通过提升数据多样性来提升模型的泛化性。在实验结果上也很好地体现了这一作用，在5-shot设置下分类精度提升更为显著，提升了1.28%。
基于随机掩码混合的数据增强网格尺寸 在训练过程中基于随机掩码混合的数据增强网格尺寸对模型的性能有重要影响，如表7所示。在3×3时达到了最好的性能，使用更小的网格尺寸进行随机掩码混合，即将图片划分为更多的局部图像块，如5×5，此时进行数据增强，则可能会引入噪声，使得图片丢失了原有的语义信息，从而影响模型性能。
表 7 miniImageNet数据集上不同网格尺寸的实验结果Table 7 Result of different grid size on miniImageNet% 随机掩码混合网格尺寸 5-way 5-shot 2×2 82.57±0.32 3×3 83.02±0.31 4×4 82.74±0.31 5×5 80.53±0.31 3.5 特征图可视化
类概念融合模块可以有效地引导模型对类敏感特征的挖掘，进而得到更具判别性的类原型表征。为了更直观体现这一效果，本文在miniImageNet随机抽取了一个任务进行展示。该任务的支持集样本类概念融合模块响应激活图如图4所示，第一行为原始图片，第二行为类概念融合模块响应图。从图中可以看出，该模块可以有效地引导模型关注模型的图像类别相关的区域，降低了无关信息的干扰，从而可以得到更具代表性的类表示。
图 4 类概念融合模块响应图可视化Fig. 4 Concept fusion module activation map visualization下载:
全尺寸图片
4. 结束语
本文提出了一种概念驱动的小样本判别特征学习方法。通过在保留局部特征的基础上，对支持集样本设计了类概念融合模型，融合类概念信息，提升了模型类判别特征的挖掘能力。对查询集样本设计了随机掩码混合数据增强，在保留空间信息的基础上提升了数据多样性，从而提升了模型的泛化性能。在小样本量少的场景下引入基于任务的代价敏感损失函数，有效挖掘任务内样本间的关系。最后在多个小样本学习领域的基准数据集上验证了本文提出的模型的有效性。
-
图 1 类相关局部区域与类无关局部区域示意图
Fig. 1 Illustrations of class relevant local regions and class irrelevant local regions
下载:
全尺寸图片
图 2 模型结构
Fig. 2 Model architecture
下载:
全尺寸图片
图 3 类概念融合模块结构
Fig. 3 Concept fusion module architecture
下载:
全尺寸图片
图 4 类概念融合模块响应图可视化
Fig. 4 Concept fusion module activation map visualization
下载:
全尺寸图片
表 1 4个基准数据集汇总
Table 1 Summarization of four benchmarks
数据集 样本数 类别数 数据集划分 miniImageNet 60000 100 64/16/20 tieredImageNet 779165 608 351/97/160 CIFAR-FS 60000 100 60/16/20 FC100 60000 100 60/20/20 表 2 miniImageNet和 tieredImageNet数据集上的实验结果对比
Table 2 Comparison of experimental result on miniImageNet and tieredImageNet datasets
% 模型 主干特征提取网络 miniImageNet tieredImageNet 5-way 1-shot 5-way 5-shot 5-way 1-shot 5-way 5-shot MatchingNet[4] ResNet10 54.49±0.81 68.82±0.65 — — ProtoNet[4] ResNet10 51.98±0.84 72.64±0.64 — — RelationNet[4] ResNet10 52.19±0.83 70.20±0.66 — — MAML[4] ResNet10 51.98±0.84 66.62±0.83 — — MetaOptNet[35] ResNet10 64.09±0.62 80.00±0.45 65.99±0.72 81.56±0.53 DC [14] ResNet12 61.26±0.20 79.01±0.13 — — LEO[36] WRN-28 61.76±0.08 77.59±0.12 66.33±0.05 81.44±0.09 TADAM[8] ResNet12 58.50±0.30 76.70±0.30 — — AM3 [13] ResNet12 65.30±0.49 78.10±0.36 69.08±0.47 82.58±0.31 FEAT[6] ResNet12 66.78±0.20 82.08±0.14 70.80±0.23 84.79±0.16 CAN[12] ResNet12 63.85±0.48 79.44±0.34 69.89±0.51 84.23±0.37 DeepEMD[5] ResNet12 65.91±0.82 82.41±0.56 71.16±0.87 86.03±0.58 infoPatch[31] ResNet12 67.67±0.45 82.44±0.31 71.51±0.52 85.44±0.35 DAM[19] ResNet12 67.76±0.46 82.71±0.31 71.89±0.52 85.96±0.35 本文算法 ResNet12 68.91±0.45 83.02±0.30 71.75±0.51 84.37±0.36 表 3 CIFAR-FS上的实验结果对比
Table 3 Comparison of experimental results on CIFAR-FS
% 模型 主干特征
提取网络CIFAR-FS 5-way 1-shot 5-way 5-shot MAML[10] ConvNet 58.90±1.90 71.50±1.00 ProtoNet[2] ConvNet 55.50±0.70 72.00±0.60 RelationNet[3] ConvNet 55.00±1.00 69.30±0.80 LR+ICI[37] ResNet12 73.97±n/a 84.13±0.n/a Rethink[38] ResNet12 73.90±0.80 86.90±0.50 BML[39] ResNet12 73.45±0.47 88.04±0.33 本文算法 ResNet12 79.93±0.45 88.74±0.31 表 4 FC100数据集上的实验结果对比
Table 4 Comparison of experimental results on FC100
% 表 5 CUB-200-2011跨领域实验结果对比
Table 5 Cross Domain Comparison of experimental results on CUB-200-2011
% 模型 miniImageNetCUB 5-way 1-shot 5-way 5-shot ProtoNet[2] — 53.07±0.74 MatchingNet[11] 51.65±0.84 69.14±0.72 CloserLook[4] — 51.34±0.72 ClosserLook++[4] — 62.04±0.76 Cosine classifier[4] 44.17±0.78 69.01±0.74 Neg-Softmax[41] — 69.30±0.73 KNN[7] 50.84±0.81 71.25±0.69 BML[39] — 72.42±0.54 本文算法 51.63±0.48 71.37±0.39 表 6 在miniImageNet数据集上的消融实验
Table 6 Ablation study on on miniImageNet dataset
% CFM Ltask MaskMix miniImageNet 5-way 1-shot 5-way 5-shot 65.66±0.46 79.85±0.33 √ 67.27±0.45 81.06±0.32 √ √ 68.21±0.45 81.74±0.32 √ √ √ 68.91±0.45 83.02±0.30 表 7 miniImageNet数据集上不同网格尺寸的实验结果
Table 7 Result of different grid size on miniImageNet
% 随机掩码混合网格尺寸 5-way 5-shot 2×2 82.57±0.32 3×3 83.02±0.31 4×4 82.74±0.31 5×5 80.53±0.31 -
[1] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [2] SNELL J, SWERSKY K, ZEMEL R S. Prototypical networks for few-shot learning[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 4077− 4087. [3] SUNG F, YANG Yongxin, ZHANG Li, et al. Learning to compare: relation network for few-shot learning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 1199−1208. [4] CHEN Weiyu, LIU Yencheng, KIRA Z, et al. A closer look at few-shot classification[C]//Proceedings of the International Conference on Learning Representations. LaJolla, CA: ICLR, 2018. [5] ZHANG Chi, CAI Yujun, LIN Guosheng, et al. DeepEMD: few-shot image classification with differentiable earth mover's distance and structured classifiers[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 12200−12210. [6] YE Hanjia, HU Hexiang, ZHAN Dechuan, et al. Few-shot learning via embedding adaptation with set-to-set functions[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 8805−8814. [7] LI Wenbin, WANG Lei, XU Jinglin, et al. Revisiting local descriptor based image-to-class measure for few-shot learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 7253−7260. [8] ORESHKIN B N, RODRIGUEZ P, LACOSTE A. TADAM: Task dependent adaptive metric for improved few-shot learning[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2018: 719−729 [9] SACHIN Ravi, HUGO Larochelle. Optimization as a model for few-shot learning [C]//Proceedings of the International Conference on Learning Representations. LaJolla: ICLR, 2017. [10] FINN C, ABBEEL P, LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//International Conference on Machine Learning. New York: ACM, 2017: 1126−1135. [11] VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching networks for one shot learning[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2016: 3637−3645. [12] HOU R, CHANG H, MA B, et al. Cross attention network for few-shot classification[C]//Advances in Neural Informa-tion Processing Systems. Cambridge: MIT Press, 2019: 4003−4014. [13] XING C, ROSTAMZADEH N, ORESHKIN B N, et al. Adaptive cross-modal few-shot learning[C]//Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019: 4847−4857. [14] LIFCHITZ Y, AVRITHIS Y, PICARD S, et al. Dense classification and implanting for few-shot learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 9250−9259. [15] 王德文, 魏波涛. 基于孪生变分自编码器的小样本图像分类方法[J]. 智能系统学报, 2021, 16(2): 254–262. WANG Dewen, WEI Botao. A small-sample image classification method based on a Siamese variational auto-encoder[J]. CAAI Transactions on Intelligent Systems, 2021, 16(2): 254–262. [16] 张玲玲, 陈一苇, 吴文俊, 等. 基于对比约束的可解释小样本学习[J]. 计算机研究与展, 2021, 58(12): 2573–2584. ZHANG Lingling, CHEN Yiwei, WU Wenjun, et al. Interpretable few-shot learning with contrastive constraint[J]. Journal of computer research and development, 2021, 58(12): 2573–2584. [17] 韦世红, 刘红梅, 唐宏, 等. 多级度量网络的小样本学习[J/OL]. 计算机工程与应用, 2021: 1−10. (2021−10−12) [2023−01−05]. https://kns.cnki.net/kcms/detail/11.2127.TP.20211012.1508.008.html. WEI Shihong, LIU Hongmei, TANG Hong, et al. Multilevel metric networks for few-ShotLearning[J/OL]. Computer engineering and applications, 2021: 1−10. (2021−10−12) [2023−01−05]. https://kns.cnki.net/kcms/detail/11.2127.TP.20211012.1508.008.html. [18] ZHENG Yan, WANG Ronggui, YANG Juan, et al. Principal characteristic networks for few-shot learning[J]. Journal of visual communication and image representation, 2019, 59: 563–573. doi: 10.1016/j.jvcir.2019.02.006 [19] XU Chengming, FU Yanwei, LIU Chen, et al. Learning dynamic alignment via meta-filter for few-shot learning[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Nashville. IEEE, 2021: 5178−5187. [20] GARCIA V, BRUNA J. Few-shot learning with graph neural networks[C]//Proceedings of the International Conference on Learning Representations. LaJolla: ICLR, 2018. [21] ZHANG H, CISSE M, DAUPHIN Y N, et al. Mixup: Beyond empirical risk minimization[C]//Proceedings of the Interna-tional Conference on Learning Representations. LaJolla: ICLR, 2018. [22] YUN S, HAN D, CHUN S, et al. CutMix: regularization strategy to train strong classifiers with localizable features[C]//2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 6022−6031. [23] VERMA V, LAMB A, BECKHAM C, et al. Manifold mixup: Better representations by interpolating hidden states[C]// International Conference on Machine Learning. New York: ACM, 2019: 6438−6447. [24] WANG Yuxiong, GIRSHICK R, HEBERT M, et al. Low-shot learning from imaginary data[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 7278−7286. [25] NI R, GOLDBLUM M, SHARAF A, et al. Data augmentation for meta-learning[C]//International Conference on Machine Learning. New York: ACM, 2021: 8152−8161. [26] SEO J W, JUNG H G, LEE S W. Self-augmentation: Generalizing deep networks to unseen classes for few-shot learning[J]. Neural networks, 2021, 138: 140–149. doi: 10.1016/j.neunet.2021.02.007 [27] MANGLA P, SINGH M, SINHA A, et al. Charting the right manifold: manifold mixup for few-shot learning[C]//2020 IEEE Winter Conference on Applications of Computer Vision. Snowmass: IEEE, 2020: 2207−2216. [28] LIU Jialin, CHAO Fei, LIN C M. Task augmentation by rotating for meta-learning[EB/OL]. (2020−02−08)[2022−03−01].https://arxiv.org/abs/2003.00804. [29] KIM J H, ON K W, LIM W, et al. Hadamard product for low-rank bilinear pooling[C] //Proceedings of the International Conference on Learning Representations. LaJolla: ICLR, 2017 : 04325. [30] PENNINGTON J, SOCHER R, MANNING C. Glove: global vectors for word representation[C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. Doha: Association for Computational Linguistics, 2014: 1532−1543. [31] LIU Chen, FU Yanwei, XU Chengming, et al. Learning a few-shot embedding model with contrastive learning[J]. Proceedings of the AAAI conference on artificial intelligence, 2021, 35(10): 8635–8643. doi: 10.1609/aaai.v35i10.17047 [32] REN Mengye, TRIANTAFILLOU E, RAVI S, et al. Meta-learning for semi-supervised few-shot classification[EB/OL]. (2018−03−02)[2022−03−01].https://arxiv.org/abs/1803.00676. [33] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//NIPS’12: Proceedings of the 25th International Conference on Neural Information Processing Systems - Volume 1. New York: ACM, 2012: 1097−1105. [34] KRIZHEVSKY A. Learning multiple layers of features from tiny images[M]. Cambridge: MIT Press, 2009. [35] LEE K, MAJI S, RAVICHANDRAN A, et al. Meta-learning with differentiable convex optimization[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 10649−10657. [36] RUSU A A, RAO D, SYGNOWSKI J, et al. Meta-Learning with Latent Embedding Optimization[C]//International Conference on Learning Representations. LaJolla: ICLR, 2018. [37] WANG Yikai, XU Chengming, LIU Chen, et al. Instance credibility inference for few-shot learning[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 12833−12842. [38] TIAN Yonglong, WANG Yue, KRISHNAN D, et al. Rethinking few-shot image classification: a good embedding is all you need? [M]//Computer Vision ECCV 2020. Cham: Springer International Publishing, 2020: 266−282. [39] ZHOU Ziqi, QIU Xi, XIE Jiangtao, et al. Binocular mutual learning for improving few-shot classification[C]//2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 8382−8391. [40] WAH C, BRANSON S, WELINDER P, et al. The caltech-ucsd birds-200-2011 dataset[EB/OL]. (2011−10−26)[2022−03−01]. https://authors.library.caltech.edu/27452. [41] LIU Bin, CAO Yue, LIN Yutong, et al. Negative margin matters: understanding margin in few-shot classification[M]//Computer Vision – ECCV 2020. Cham: Springer International Publishing, 2020: 438−455.
