Deep mutual information maximization method for incomplete multi-view clustering
-
摘要: 多视图聚类是无监督学习领域研究热点之一，近年来涌现出许多优秀的多视图聚类工作，但其中大多数方法均假设各视图是完整的，然而真实场景下数据收集过程极容易发生缺失，造成部分视图不完整。同时，很多方法采取传统机器学习方法（即浅层模型）对数据进行特征学习，这导致模型难以挖掘高维数据内的复杂信息。针对以上问题，本文提出一种面向不完整多视图聚类的深度互信息最大化方法。首先利用深度自编码器挖掘各视图深层次的隐含特征，并通过最大化潜在表示间的互信息来学习各视图间的一致性知识。然后，对于不完整视图中的缺失数据，利用多视图的公共潜在表示进行补全。此外，本文采用一种自步学习策略对网络进行微调，从易到难地学习数据集中的样本，得到更加宜于聚类的特征表示。最后，在多个真实数据集上进行实验，验证了本文方法的有效性。Abstract: Multi-view clustering is a research hotspot in the field of unsupervised learning. Of the many excellent multi-view clustering studies that have recently arisen, most assume that each view is complete. However, in a real scene, the data are extremely easily missed in the collection process, resulting in partially incomplete views. Simultaneously, many methods use traditional machine learning, i.e., the shallow-layer model, to learn data features, which makes it difficult for the model to mine the complex information of high-dimensional data. To solve these problems, in this paper, a novel deep mutual information maximization method is proposed for incomplete multi-view clustering. First, a deep autoencoder is used to learn the rich complex information of each view, and the knowledge of consistency among views is learned by the mutual information between potential representations. Then, the missing data are fixed up by the common latent representation of multi-view data. Additionally, this paper uses a self-paced strategy to fine-tune the model as it learns the samples from easy to difficult, obtaining a more clustering-friendly representation. Experiments performed on several real datasets show the effectiveness of our proposed method.
-
随着科技的发展，对于同一个物体可以有多种的数据采集方式，这种来自不同域或不同特征提取器的数据称为多视图数据。多视图数据往往是从不同角度/视角来描述同一个物体，可以获得比单一视图更加完整的信息。例如：一个图像，可以用色彩信息进行描述，也可以用其纹理信息进行表示；对于同一新闻事件，不同报社的新闻报道也可以给出不同的内容描述。多视图聚类（multi-view clustering，MvC）是多视图数据的重要应用研究方向之一，它的关键在于挖掘多视图数据间的一致性信息和互补性信息，从而将相似的样本划分到同一簇，而不相似的样本划分到不同簇。
近年来有许多优秀的多视图聚类方法[1-14]被提出，其中大部分工作都假设各视图数据是完整的，然而在现实多视图数据收集的过程中，容易出现数据缺失的情况，这种具有缺失数据的聚类任务被称为不完整多视图聚类。如何有效地在不完整多视图数据上挖掘视图间的一致性和互补性是一项具有挑战性的任务。Shao等[3]首先利用全局特征均值来对缺失数据进行填充，然后采用加权非负矩阵（nonnegative matrix factorization, NMF）分解的方式去建模，并引入
${L_{2,1}}$ 范数消除数据噪声和异常值对结果的影响。但是当缺失率较大时，基于均值的填充方法会导致较大的误差。Yin等[4]通过将多视图数据分成完整的和不完整的部分，通过对齐完整部分的数据来最大化各视图间的一致性从而解决缺失数据的问题。然而这种处理缺失的方式目标函数过于复杂，尤其随着视图数目的增多，需考虑的情况也会随之剧增。Wang等[5]将视图数据的缺失转为相似度矩阵的缺失，又通过各视图之间一致性假设对相似度矩阵进行补全提出了PIC（perturbation-oriented incomplete multi-view clustering）算法。但PIC假设至少有一个视图是完整的，这对任意缺失的不完整多视图数据是一个考验。Hu等[6]扩展了 PVC（partial multi-view clustering）[7]提出了DAIMC（doubly aligned incomplete multi-view clustering），利用加权非负矩阵分解对缺失数据设置零权重以消除其对模型学习的影响。然后利用Semi-NMF和${L_{2,1}}$ 范数正则化去建模，同时考虑样本对齐信息和基矩阵对齐信息。尽管以上的方法都在不完整多视图任务上具有良好的表现，然而它们仍面临以下问题：大多现存方法是利用浅层模型来获得多视图间的共同特征表示，而这难以从复杂的高维多视图数据中捕获更深层次的内在信息。对此现有部分多视图聚类方法[8-17]利用深度网络挖掘数据内在信息。Shaham等[15]将传统的谱聚类利用神经网络的方式来实现提出了SpectralNet，通过深度网络直接输出对应的特征矩阵。Huang等[8]将SpectralNet扩展到多视图聚类任务提出了MvSCN（multi-view spectral clustering network）。MvSCN对每个视图构造一个深度网络，并对视图间的特征表示设计了一个回归损失，同时学习视图内和视图内的一致性信息。Ji等[16]基于子空间聚类的思想提出DSC-Nets（deep subspace clustering networks），其利用自编码器在中间引入一个自表示层，学习得到低维特征表示的相似度矩阵。Sun等[9]提出S2DMVSC(self-supervised deep multi-view subspace clustering）直接将各视图共享同一个自表示层学习一致的相似度矩阵，并加入谱聚类指导网络的学习，进一步提升最终聚类性能。不同于其他多视图子空间聚类模型对每个视图单独产生子空间表示，Zhang等[10]通过学习一个潜在的公共子空间表示，来探索多视图样本间互补性和一致性信息，并有效地处理各视图内的噪声。此外，Zhang等[11]基于多视图数据都是由一个潜在特征表示映射而来构造了AE2-Net（autoencoder in autoencoder networks），包含内部和外部两个自编码器。同时，Zhang等[12]还基于学习多视图数据的完备特征表示提出了针对缺失多视图数据集的CPM-GAN（cross partial multi-view generative adversarial network）算法，该算法通过引入一种对抗学习策略来有效地处理数据缺失的问题。然而现有基于深度学习的MvC方法往往将特征学习和聚类任务分为两个阶段，这难以保证模型学习到的特征是有利于聚类任务的。除了前述问题外，现有的MvC方法几乎没有模型考虑聚类簇边缘样本在聚类任务中所带来的干扰，因为这些方法都等同地向所有样本进行学习。因此本文提出一种面向不完整多视图聚类的深度互信息最大化方法，该方法主要思想是利用深度网络强大的特征学习能力挖掘高维复杂多视图数据内更丰富的信息，并通过最大化潜在表示的互信息来学习各视图间的一致性。然后，对于缺失视图，一般假设各视图都是由同一低维潜在表示映射而来，利用多视图的公共表示通过特征映射补全缺失数据。此外，本文采用一种根据自步学习策略思想改进的K-Means(self-paced K-Means)，对网络进行微调，从易到难地学习数据集中的样本，得到更加聚类友好的特征表示。最后，在多个数据集上得到的实验结果表明该算法的优越性。
1. 预备知识
为了后期能更加准确地描述本文所提出的方法，本章将简要回顾互信息和K-Means聚类算法的相关概念与定义。
1.1 互信息
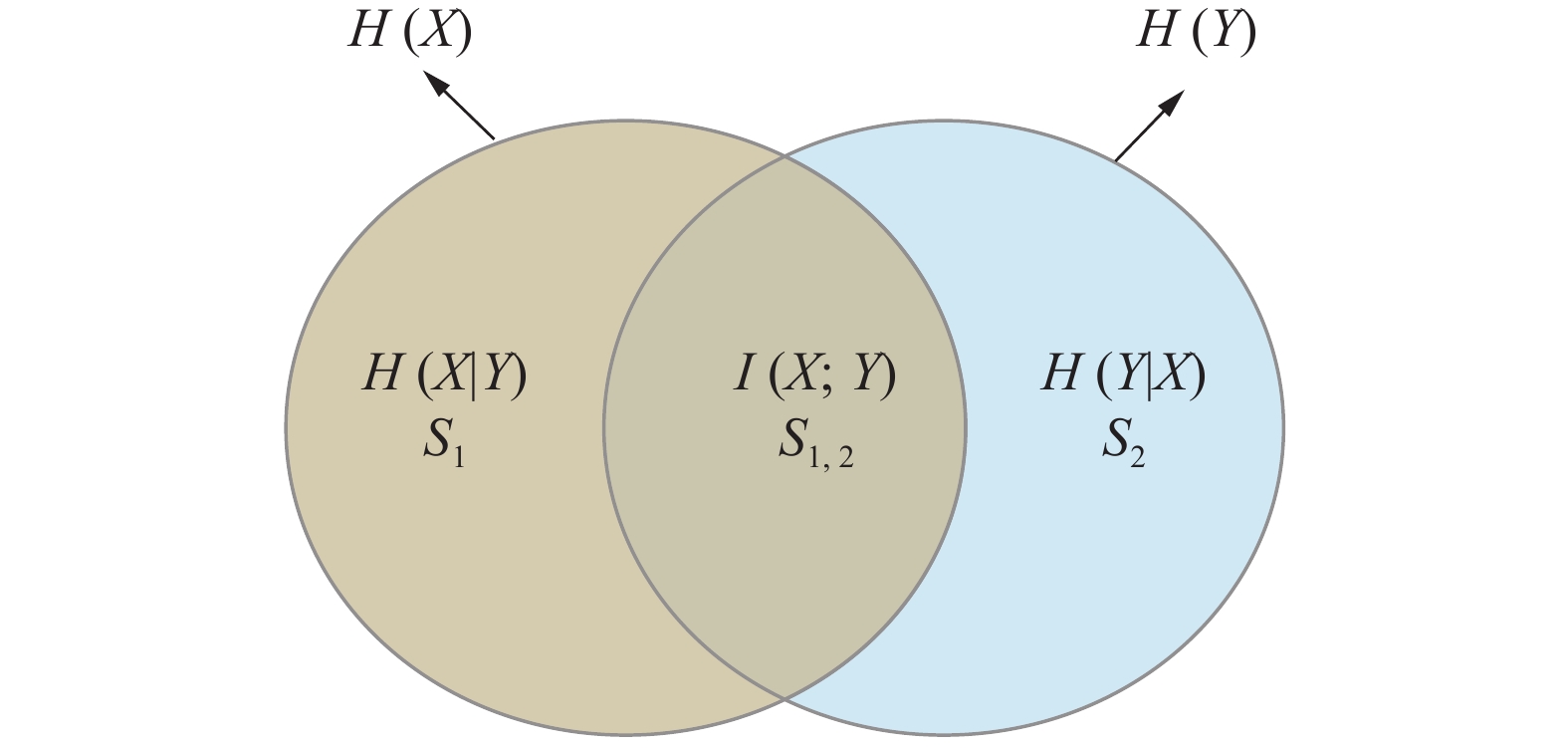
互信息是源于信息论的一个概念，是度量两个随机变量相互依赖程度的一个量。用图1形象地说明互信息，其中用两个圆形分别表示随机变量X和Y各自所包含的所有信息，也即各自的熵，
${S_{1,2}}$ 就代表了X和Y的互信息，即变量X和Y相互依赖的部分，${S_1}$ 和${S_2}$ 则是X和Y独自包含的信息，在信息论中表示为条件熵H(X|Y)和H(Y|X)。这与多视图聚类非常相似，视图间一致的信息即是视图间相互依赖的互信息，而视图间互补的信息即是各视图的条件熵。受此想法启发，本文采用最大化视图间的互信息来学习各视图间的一致性。值得一提的是，Zhong等[17]证明，目前在无监督学习领域被广泛应用的对比学习也是旨在优化互信息的下界。
图 1 互信息阐述Fig. 1 Illustration of mutual information
下载:
全尺寸图片
1.2 K-Means聚类方法
K-Means[18]是传统的聚类方法之一，也是被广泛使用的一种聚类方法。对于输入的数据矩阵
${{\boldsymbol{X}}} \in {{\bf{R}}^{m \times n}}$ ，K-Means的核心思想是寻找k个聚类中心使得所有n个样本到其对应中心的欧氏距离的平均值最小。引入${\boldsymbol{U}} \in {{\bf{R}}^{m \times k}}$ 表示聚类中心矩阵，${{\boldsymbol{S}}} \in {\{ 0,1\} ^{k \times n}}$ 表示聚类指示矩阵，即样本被划分到的类，即当样本i被划分到第j类时$ {s_{j,i}} = 1,{s_{ \ne j,i}} = 0 $ ，则K-Means可以用数学符号表示为$$ \underset{U,S}{\rm{min}}\Vert {\boldsymbol{X}}-{\boldsymbol{US}}{\Vert }_{F}^{2},\;{\rm{s.t.}}{\boldsymbol{S}}\in {\{0,1\}}^{k\times n},{{\boldsymbol{S}}}^{\text{T}}{\boldsymbol{1}}=1 $$ 式中：
$ \Vert \cdot {\Vert }_{F}^{2} $ 表示 Frobenius范数，1表示全一向量。1.3 自步学习
自步学习[19] (self-paced learning, SPL)是自课程式学习[20] (curriculum learning, CL)发展出来的一种模型训练方式。受人类认知学习模式启发，CL利用先验知识确定样本对于学习任务的复杂程度，决定其训练的优先级，让模型从易到难地从数据集样本中学习。然而这忽略了样本在训练中习得的知识，SPL则是在迭代过程中决定下一步样本学习的优先级，同时还能有助于弱化样本中的噪声。具体地，SPL旨在优化以下目标：
$$ \mathop {\min }\limits_{\omega ,v} E(\omega ,v;\lambda ) = \sum\limits_{i = 1}^n {({v_i}\mathcal{L}({y_i},g({x_i},\omega ))) + f({v_i},\lambda )} $$ 式中：
${v_i}$ 表示${x_i}$ 的权重，即样本训练优先级；$ f({v_i},\lambda ) $ 是正则项；$ \mathcal{L}({y_i},g({x_i},\omega )) $ 是模型的目标函数，其值越小${v_i}$ 的值就越大，也就是说，如果${x_i}$ 经过训练后的结果越接近与期待的值则在下一步训练中样本在训练中的参与度就越高。在每次迭代中，$v$ 和模型参数的更新采用交替优化的策略。2. 基于互信息的深度不完整多视图聚类方法
2.1 符号与问题定义
为了便于后续描述提出的方法，本文将以两视图的不完整多视图为例，将不完整多视图数据集表示为
${\boldsymbol{X}} = [{{\boldsymbol{X}}^{[1]}},{{\boldsymbol{X}}^{[2]}}]$ ，其中${{\boldsymbol{X}}^{[1]}}$ 和${{\boldsymbol{X}}^{[2]}}$ 分别为视图1和视图2的数据矩阵。为了能更好地从不完整数据集中学习，进一步将${{\boldsymbol{X}}^{[1]}},{{\boldsymbol{X}}^{[2]}}$ 表示为$\{ {\boldsymbol{X}}_c^{[1]},{\bar {\boldsymbol{X}}^{[1]}}\}$ 和$\{ {\boldsymbol{X}}_c^{[2]},{\bar {\boldsymbol{X}}^{[2]}}\}$ ，其中${{\boldsymbol{X}}_c}^{[v]}$ 表示无视图缺失部分数据矩阵，${\bar {\boldsymbol{X}}^{[v]}}$ 表示该视图独有部分的数据矩阵。本文所提出的方法即先在完整部分数据集上进行训练，再利用训练好的模型对缺失数据进行补全然后计算得出最后的聚类结果。2.2 方法论
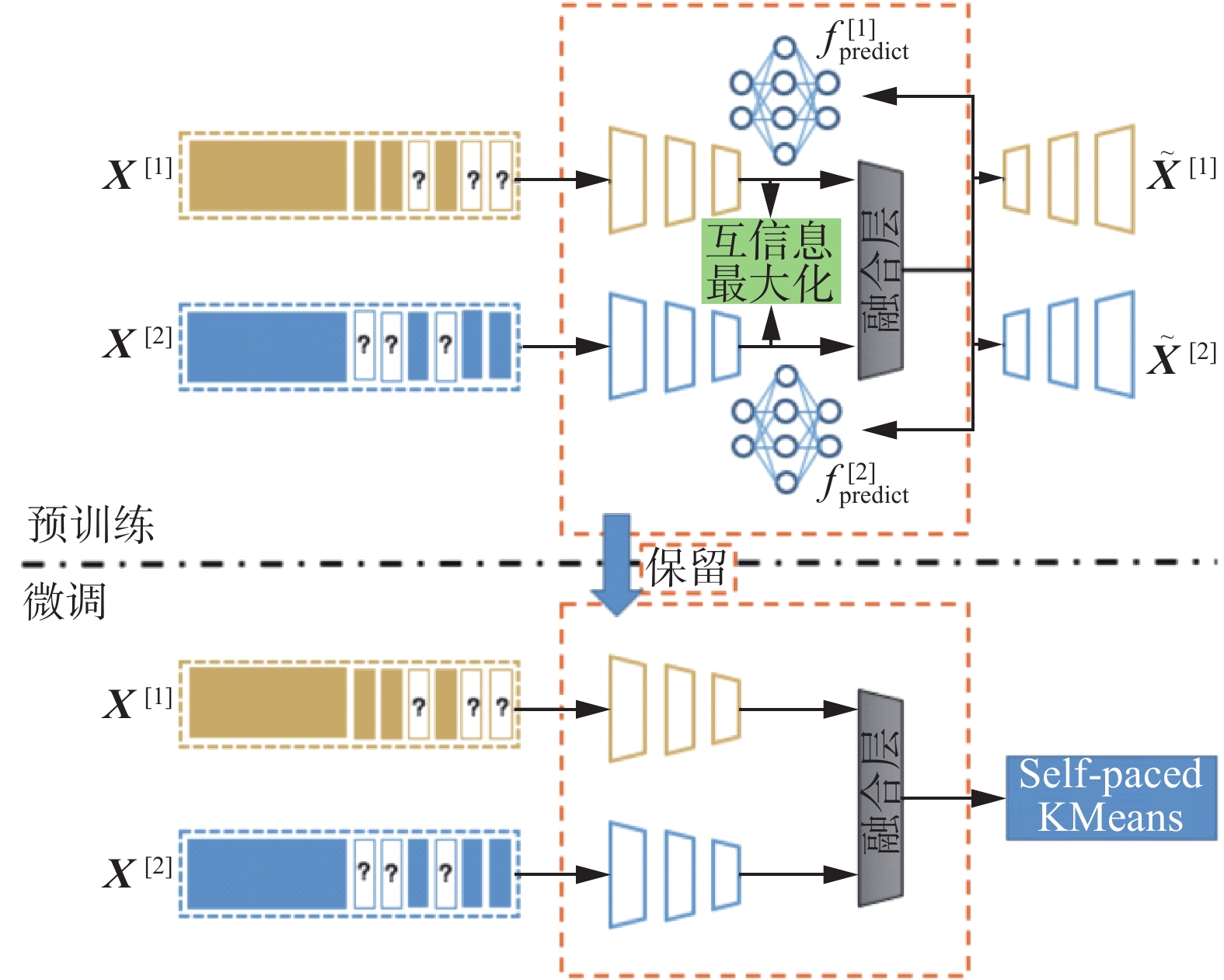
本文提出了一种面向不完整多视图聚类的深度互信息最大化方法，模型的整体框架如图2所示，大致可以分为两个阶段：1）预训练阶段，通过最大化互信息学习视图间的一致性；2）微调阶段，在预训练好的模型上利用Self-paced K-Means方法微调，学习到聚类友好的特征表示。接下来将详细对模型各部分进行介绍。
图 2 基于互信息最大化的不完整多视图聚类方法模型Fig. 2 Framework of incomplete multi-view clustering model based on mutual information maximization下载:
全尺寸图片
2.2.1 基于互信息最大化的一致性学习
在预训练阶段，本文的模型采用传统的自编码器作为基础结构，分别对各视图学习其内在的信息。其中引入加权融合层来学习多视图的公共特征表示，并引入互信息来增强视图间的一致性信息。
1)各视图的编码与解码： 自编码器一般包括两个部分，编码器和解码器。编码器从高维数据中捕获潜在特征，同时解码器网络旨在从编码的特征中恢复数据。由于多视图数据一般来自不同域，故对各视图设计一个自编码器，学习各自独有的信息，其目标函数为
$$ {\cal L}_{{\rm{rec}}}={\displaystyle\sum _{v=1}^{2}\Vert {\boldsymbol{X}}^{[v]}-{f}_{{\rm{de}}}^{[v]}({f}_{{\rm{en}}}^{[v]}({\boldsymbol{X}}^{[v]})){\Vert }_{2}^{2}} $$ 式中：
$f_{{\rm{en}}}^{[v]}( \cdot ),f_{{\rm{de}}}^{[v]}( \cdot )$ 分别表示视图v对应的编码器和解码器。2)视图融合层：大量多视图工作[21-24]都假设所有视图共享同一样本的共同语义，如公共表示或聚类标签。受此启发，本文引入了一个简单的加权融合层获得所有视图共享的公共表示：
$$ {{\boldsymbol{H}}} = \sum\limits_{v = 1}^2 {{w_v}{{{\boldsymbol{H}}}^{[v]}}} ,\;{\rm{s.t.}}\quad {w_1} + {w_2} = 1 $$ 式中：
${{{\boldsymbol{H}}}^{[v]}}$ 表示${{{\boldsymbol{X}}}^{[v]}}$ 经过$f_{{\rm{en}}}^{[v]}( \cdot )$ 后获得的潜在表示，即${{{\boldsymbol{H}}}^{[v]}} = f_{{\rm{en}}}^{[v]}({{{\boldsymbol{X}}}^{[v]}})$ 。${w_v}$ 表示视图v的权重，在本文中，将${w_v}$ 设置为均值权重。仅通过加权融合获得的公共表示H还无法保证其包含了各视图间共享的共同语义。为此，将其作为各视图解码器
$f_{{\rm{de}}}^{[v]}( \cdot )$ 的输入，期待由公共表示H还原到对应的视图，即${{{\boldsymbol{X}}}^{[v]}}$ 的重构${{\tilde {\boldsymbol{X}}}^{[v]}} = f_{{\rm{de}}}^{[v]}({{\boldsymbol{H}}})$ 。3)视图间的一致性学习：在经过自编码器学习到的潜在空间，采用互信息的方式学习视图间的一致性。已知对于随机变量M和N其互信息I(M;N)的计算方式为
$$ {{I(M;N)}} = \sum\limits_{m \in {M}} {\sum\limits_{n \in {N}} {p(m,n){{\log }_2}\frac{{p(m,n)}}{{p(m)p(n)}}} } $$ 式中：
$p(m,n)$ 为M和N的联合概率密度函数；$p(m)、 p(n)$ 分别为M和N的边缘概率密度函数。为了能够具体计算视图间的互信息，需要定义${{{\boldsymbol{H}}}^{[1]}}$ 和${{{\boldsymbol{H}}}^{[2]}}$ 的联合概率密度函数以及边缘概率密度函数，这里采用Lin等[25]中所提出的方式，即$$ {{\boldsymbol{P}}} = {{{\boldsymbol{H}}}^{[1]}} \times {({{{\boldsymbol{H}}}^{[2]}})^{\rm{T}}} $$ 式中：P即为联合概率分布，
${{\boldsymbol{P}}} \in {\mathbb{R}^{D \times D}}$ ，D为潜在空间的维度。对于各视图的编码器输出${{{\boldsymbol{H}}}^{[1]}}$ 和${{{\boldsymbol{H}}}^{[2]}}$ 的边缘概率分布${{{\boldsymbol{P}}}_d}$ 和${{\boldsymbol{P}}}_d^ \star$ ，则通过在P的基础上计算得到，即分别对P在第d行和第d列的维度上进行求和。至此，可以给出基于互信息最大化的多视图一致性学习目标函数：$$ {\mathcal{L}_{{\rm{MI}}}} = - {{I(}}{{{\boldsymbol{H}}}^{[1]}};{{{\boldsymbol{H}}}^{[2]}}{\text{)}} = - \sum\limits_{{d_1} = 1}^D {\sum\limits_{{d_2} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}{d_2}}}\ln \frac{{{{{\boldsymbol{P}}}_{{d_1}{d_2}}}}}{{{{{\boldsymbol{P}}}_{{d_1}}} \cdot {{\boldsymbol{P}}}_{{d_2}}^ \star }}} } $$ 式中：
${{{\boldsymbol{P}}}_{{d_1}{d_2}}}$ 表示P中第${d_1}$ 行${d_2}$ 列的元素。同时为了避免模型陷入平凡解问题，在目标函数中加入${{{\boldsymbol{H}}}^{[1]}}$ 和${{{\boldsymbol{H}}}^{[2]}}$ 的熵${{H(}}{{{\boldsymbol{H}}}^{[1]}}{\text{)}}$ 和${{H(}}{{{\boldsymbol{H}}}^{[2]}}{\text{)}}$ ，即$$ \begin{gathered} {\mathcal{L}_{{\rm{MI}}}} = - {{I(}}{{{\boldsymbol{H}}}^{[1]}},{{{\boldsymbol{H}}}^{[2]}}{\rm{)}} - \alpha ({{H(}}{{{\boldsymbol{H}}}^{[1]}}{{) + H(}}{{{\boldsymbol{H}}}^{[2]}}{\rm{)}})= - \\ \left( \sum\limits_{{d_1} = 1}^D {\sum\limits_{{d_2} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}{d_2}}}\ln \frac{{{{{\boldsymbol{P}}}_{{d_1}{d_2}}}}}{{{{{\boldsymbol{P}}}_{{d_1}}} \cdot {{\boldsymbol{P}}}_{{d_2}}^ \star }}} }\right. +\\ \left. \alpha \left(\sum\limits_{{d_1} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}}}\ln {{{\boldsymbol{P}}}_{{d_1}}} + \sum\limits_{{d_2} = 1}^D {{{\boldsymbol{P}}}_{{d_2}}^ \star \ln {{\boldsymbol{P}}}_{{d_2}}^ \star } } \right) \right) = - \\ \sum\limits_{{d_1} = 1}^D {\sum\limits_{{d_2} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}{d_2}}}\left( {\ln \frac{{{{{\boldsymbol{P}}}_{{d_1}{d_2}}}}}{{{{{\boldsymbol{P}}}_{{d_1}}} \cdot {{\boldsymbol{P}}}_{{d_2}}^ \star }} + \alpha \left(\ln \frac{1}{{{{{\boldsymbol{P}}}_{{d_1}}}}} + \ln \frac{1}{{{{{\boldsymbol{P}}}_{{d_2}}}}}\right)} \right)} } = - \\ \sum\limits_{{d_1} = 1}^D {\sum\limits_{{d_2} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}{d_2}}}\ln \frac{{{{{\boldsymbol{P}}}_{{d_1}{d_2}}}}}{{{{\boldsymbol{P}}}_{{d_1}}^{\alpha + 1} \cdot {{({{\boldsymbol{P}}}_{{d_2}}^ \star )}^{\alpha + 1}}}}} } \\ \end{gathered} $$ 式中
$\alpha $ 为平衡互信息和熵之间的参数。综上，预训练阶段的目标函数即为
$$ {\mathcal{L}_{{\rm{preTrain}}}} = {\mathcal{L}_{{\rm{MI}}}} + {\lambda _1}{\mathcal{L}_{{\rm{rec}}}} $$ (1) 式中
${\lambda _1}$ 为平衡参数。2.2.2 基于一致性表示的缺失数据补全
上一节中，假设多视图都共享同一样本的共同语义，并通过视图融合层得到公共一致性表示H，同时将其作为解码器的数据还原视图数据。在此，可以合理认为同样可以由公共表示H补全缺失的数据。即若视图v的样本i缺失，可以由公共表示
${{{\boldsymbol{h}}}_i}$ 通过一个缺失补全网络$f_{{\rm{predict}}}^{[v]}( \cdot )$ 学习得到：$$ {\tilde {\boldsymbol{h}}}_i^{[v]} = f_{{\rm{predict}}}^{[v]}({{{\boldsymbol{h}}}_i}) $$ 式中，
$\tilde h_i^{[v]}$ 表示样本的潜在表示。而对于这一缺失补全网络，目标函数为$$ {\mathcal{L}}_{{\rm{predict}}}={\displaystyle \sum _{v=1}^{2}\Vert {\boldsymbol{H}}^{[v]}-{f}_{{\rm{predict}}}^{[v]}({\boldsymbol{H}}^{[v]}){\Vert }_{2}^{2}} $$ (2) 对于
$f_{{\rm{predict}}}^{[v]}( \cdot )$ 的训练，先在$\{ {{\boldsymbol{X}}}_c^{[1]},{{\boldsymbol{X}}}_c^{[2]}\}$ 上进行训练，然后用于缺失数据补全。值得一提的是，由于补全得到的数据表示是从公共表示H学习而来，最大程度地包含了视图间的一致性信息，在一定程度上增加了视图间的互信息，与上一节的学习目标相辅相成。
2.2.3 基于Self-Paced K-Means的微调
现有的多视图聚类算法，大多先对原始数据进行挖掘得到潜在表示，然后在潜在表示上应用传统聚类。但是这样的两阶段方式，难以保证获得的潜在表示是有利于聚类任务的。因此，本文在预训练阶段后利用Self-Paced K-Means对算法模型进行微调，它能够有效避免聚类边缘样本干扰，同时学习得到更加聚类友好的表示。它的目标函数表示为
$$ \begin{array}{c}{\mathcal{L}}_{{\rm{spKMeans}}}=\dfrac{1}{nk}{\displaystyle \sum _{i=1}^{n}({r}_{i}\Vert {\boldsymbol{h}}_{i}-{{\boldsymbol{US}}}_{:,i}{\Vert }_{2}^{2}-{r}_{i}\tau )}\\ {\rm{s.t.}}\quad {r}_{i}\in \{0,1\},{\boldsymbol{S}}\in \{0,1\},{\boldsymbol{S}}^{{\rm{T}}}{{\boldsymbol{1}}}=1\end{array} $$ (3) 式中：U和S分别表示聚类的中心和类指示矩阵，在训练中设置为每20次迭代由K-Means算法更新一次；
${r_i}$ 则是一个指示量，当$\Vert {{{\boldsymbol{h}}}}_{i}-{{\boldsymbol{U}}}{{{\boldsymbol{S}}}}_{:,i}{\Vert }_{2}^{2}$ 小于阈值时为1，大于阈值时为0；而$\tau $ 表示一个阈值，当${{{\boldsymbol{h}}}_i}$ 与其对应中心点的距离大于$\tau $ 时则认为此样本为聚类边缘样本，较难以被正确划分：$$ \tau = \mu ({{{\boldsymbol{l}}}^t}) + \frac{t}{T}\sigma ({{{\boldsymbol{l}}}^t}) $$ 式中：
${{{\boldsymbol{l}}}^t}$ 表示第t次迭代的样本损失向量，具体地向量中第i个值${{{\boldsymbol{l}}}}_{i}^{t}=\Vert {{{\boldsymbol{h}}}}_{i}^{t}-{{{\boldsymbol{U}}}}^{t}{{{\boldsymbol{S}}}}_{:,i}^{t}{\Vert }_{2}^{2}$ ；$\mu ( \cdot ),\sigma ( \cdot )$ 分别代表了求均值和方差，t和T分别代表了当前迭代次数和总的迭代次数。由此可以看出，Self-Paced K-Means采用了一种自步学习策略，由易到难地从样本中学习，这更加近似于人类的学习方式，并且大量研究[26-30]证明了这种方式的有效性。具体的算法过程如下：
输入 不完整多视图数据集
${\boldsymbol{X}} = [{{\boldsymbol{X}}^{[1]}},{{\boldsymbol{X}}^{[2]}}]$ ，聚类数k，参数${\lambda _1}$ ，$\alpha $ ，预训练迭代次数${T_1}$ ，微调迭代次数${T_2}$ ，缺失补全网络开始迭代次数${T_3}$ ；输出 不完整多视图聚类结果。
阶段一：预训练网络
1）当迭代次数
$t \leqslant {T_3}$ 时，通过式(1)更新网络$f_{{\rm{en}}}^{[1]}( \cdot )$ 、$f_{{\rm{en}}}^{[2]}( \cdot )$ 、${f}_{{\rm{de}}}^{[1]}(\cdot )$ 、$f_{{\rm{de}}}^{[2]}( \cdot )$ 。2）当迭代次数
${T_3} < t < {T_1}$ 时，通过式(1)和式(2)更新网络$f_{{\rm{en}}}^{[1]}( \cdot )$ 、$f_{{\rm{en}}}^{[2]}( \cdot )$ 、$f_{{\rm{de}}}^{[1]}( \cdot )$ 、$f_{{\rm{de}}}^{[2]}( \cdot )$ 、$f_{{\rm{predict}}}^{[1]}( \cdot )$ 及$f_{{\rm{predict}}}^{[2]}( \cdot )$ 。3）重复执行1）、2）直到指定迭代次数。
阶段二：微调网络
1）当迭代次数
$t < {T_2}$ 时，通过式(3)更新网络$f_{{\rm{en}}}^{[1]}( \cdot )$ 、$f_{{\rm{en}}}^{[2]}( \cdot )$ 。阶段三：获得聚类结果
1）通过网络
$f_{{\rm{en}}}^{[1]}( \cdot )$ 、$f_{{\rm{en}}}^{[2]}( \cdot )$ 、$f_{{\rm{predict}}}^{[1]}( \cdot )$ 及$f_{{\rm{predict}}}^{[2]}( \cdot )$ 获得公共表示H。2）通过在H上应用K-Means算法获得聚类结果。
2.3 损失函数
前文通过两视图的情况对本文所提出模型进行了详细的描述，模型整体分为两个阶段，即预训练阶段和微调网络阶段。在预训练阶段利用传统的自编码器分别对各视图学习其内在的信息，并引入互信息来增强视图间的一致性信息。相应地其目标函数为
$$ {\mathcal{L}_{{\text{pre - train}}}} = {\mathcal{L}_{{\rm{rec}}}} + {\mathcal{L}_{{\rm{MI}}}} + {\mathcal{L}_{{\rm{predict}}}} $$ 式中：
${\mathcal{L}_{{\rm{predict}}}}$ 为学习缺失样本的目标函数，预训练和微调阶段均包含此项。在微调阶段为了学习得到更加聚类友好的表示，加入Self-Paced K-Means对算法模型进行微调：$$ {\mathcal{L}_{{\text{fine - tine}}}} = {\mathcal{L}_{{\rm{spKMaens}}}} + {\mathcal{L}_{{\rm{predict}}}} $$ 于此同时本文的模型还可以扩展到两视图以上的情况，这里给出模型各个模块在多视图数据集上对应的目标函数。
各视图编码和解码模块，同样多视图各自维护一个自编码器网络，其重构损失为
$$ {\cal L}_{{\rm{rec}}}={\displaystyle \sum _{v=1}^{V}\Vert {\boldsymbol{X}}^{[v]}-{f}_{{\rm{de}}}^{[v]}({f}_{{\rm{en}}}^{[v]}({\boldsymbol{X}}^{[v]})){\Vert }_{2}^{2}} $$ 式中：
$V$ 表示视图总数，$f_{{\rm{en}}}^{[v]}( \cdot )$ 和$f_{{\rm{de}}}^{[v]}( \cdot )$ 分别表示各视图的编码器和解码器。类似地，视图融合层采用对多个视图加权求和得到，其计算公式可表示为
$$ {{\boldsymbol{H}}} = \sum\limits_{v = 1}^V {{w_v}{{{\boldsymbol{H}}}^{[v]}}} ,{\rm{s.t.}}\sum\limits_{v = 1}^V {{w_v}} = 1 $$ 而对于视图间一致性的学习，由于互信息只能计算两个随机变量之间的相互依赖程度，故对于两视图以上的情况采用对两两视图间的互信息求和来学得多视图间的一致性信息，即
$$ \begin{gathered} {\mathcal{L}_{{\rm{MI}}}} = - \sum\limits_i^V {\sum\limits_{j( \ne i)}^V {{{I(}}{{{\boldsymbol{H}}}^{[i]}};{{{\boldsymbol{H}}}^{[j]}}{\text{)}}} } = \\ - \sum\limits_i^V {\sum\limits_{j( \ne i)}^V {\sum\limits_{{d_1} = 1}^D {\sum\limits_{{d_2} = 1}^D {{{{\boldsymbol{P}}}_{{d_1}{d_2}}}\ln \frac{{{{{\boldsymbol{P}}}_{{d_1}{d_2}}}}}{{{{P}_{{d_1}}} \cdot {{\boldsymbol{P}}}_{{d_2}}^ \star }}} } } } \\ \end{gathered} $$ 在前面两视图的场景中，模型利用视图融合层得到的公共一致性表示H作为解码器的输入对缺失数据进行补全。在多视图场景同样采用这样的策略，对缺失视图的样本，利用与其对应的其他视图样本的平均加权值来学习得到：
$$ {\cal L}_{{\rm{predict}}}={\displaystyle \sum _{v=1}^{V}\Vert {\boldsymbol{H}}^{[v]}-{f}_{{\rm{predict}}}^{[v]}({\boldsymbol{H}}^{[{\rm{other}}]}){\Vert }_{2}^{2}} $$ 式中：
${{{\boldsymbol{H}}}^{[{\rm{other}}]}}$ 表示可获得的视图样本的平均加权值，即${{{\boldsymbol{H}}}^{[{\rm{other}}]}} = \dfrac{1}{{{V_{{\rm{other}}}}}}\displaystyle\sum\limits_{v = 1}^{{V_{{\rm{other}}}}} {{H^{[v]}}}$ ，将其作为视图$v$ 的预测网络$f_{{\rm{predict}}}^{[v]}( \cdot )$ 的输入来学习重构其对应的缺失样本的表示。至此，已给出本文模型每个模块对应的多视图场景下的目标函数，根据2.2.3节中所述的具体算法流程即可将本模型应用于两视图以上的多视图学习任务。
3. 实验与结果分析
为了验证本文所提出算法的有效性，分别在4个多视图数据集上，与11个现有算法进行了对比实验，并采用准确率(accuracy, ACC)、标准化互信息(normalized mutual information, NMI)和调整后的兰德指数(adjusted rand index, ARI)3个聚类常用指标作为评价算法的效果。本章将依次对数据集、对比方法、实验设置、对比结果分析进行介绍。
3.1 数据集
具体的4个数据集分别是：Caltech101-20、Scene-15、LandUse-21和NoisyMNIST，其中前3个为真实数据集，最后一个是根据DCCAE (deep canonically correlated autoencoders)[31]中的方法生成的多视图数据集。实验中，对前3个数据集，选取其中两个视图用于实验，详细的数据集信息参见表1。
表 1 数据集详细信息Table 1 Information of datasets数据集 样本数 实验视图 视图维度 类数 Caltech101-20 2386 HOG,GIST 1984/512 20 Scene-15 4485 PHOG,GIST 20/59 15 LandUse-21 2100 PHOG,GIST 59/40 21 NoisyMNIST 20000 — 784/784 10 对于缺失数据集，实验中采用按照设定的缺失率对完整的数据集随机抽取缺失值。这里的缺失率指各视图的缺失数据占完整样本数的比率，由于本文主要对两视图进行研究，故实验中缺失率最高取到0.4。
3.2 对比方法
此次选取11个多视图聚类算法作为对比方法，其中有针对完整多视图的，同时也有针对不完整多视图的。它们分别是：DCCA (deep canonically correlated analysis)[32]、DCCAE[31]、BMVC(binary multi-view clustering)[33]、AE2-Net[11]、PVC[7]、EERIMVC (efficient and effective regularized incomplete multi-view clustering)[34]、DAIMC[6]、IMG(incomplete multi-modal visual data grouping)[35]、UEAF (unified embedding alignment framework)[36]、CPM-GAN[12]、PIC[5]和COMPLETER (incomplete multi-view clustering via contrastive prediction)[25]。其中前4个不是针对不完整多视图数据的方法，对此，先采用均值对缺失数据补全，然后再在模型上验证。为了获得更具说服力的结果，对所有的对比的算法，均采用其论文中推荐的模型结构以及参数设置。
3.3 实验设置
本文的方法基于Pytorch 1.6.0，Python 3.7实现，并在网络中间层应用ReLU函数进行非线性映射，同时添加了归一化操作用于提高模型的训练速度以及缓解训练中的梯度消失问题，而对于编码器的输出层采用SoftMax函数进行非线性映射。所有模型在Ubuntu 18.04系统采用单块NVIDIA Tesla K80 GPU的服务器上运行。同时，对预训练模型采用400次迭代，并且对式(1)中的参数
${\lambda _1}$ 分别为Caltech101-20、Scene-15、LandUse-21和NoisyMNIST设置为0.01, 0.1, 0.01, 0.2。在第100次迭代后在目标函数中加入式(3)，学习缺失补全网络。微调阶段，仅保留模型编码器模块训练100次。整个实验重复5次，最后取平均值作为实验结果。3.4 实验结果分析
实验首先在缺失率为0（即完整数据集）和0.25上对所有的方法进行了对比实验，详细的实验结果见表2、3，表3的缺失率为0.25，其中黑色粗体表示每种实验设置下的最佳结果。通过对比表中不同模型的聚类指标，可以发现：
表 2 完整多视图聚类效果对比Table 2 Comparison of model effects on complete multi-view datasets% 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI AE2-Net 49.10 65.38 35.66 56.98 46.83 36.98 24.79 30.36 10.35 36.10 40.39 22.08 IMG 44.51 61.35 35.74 — — — 16.40 27.11 5.10 24.20 25.64 9.57 表 3 不完整多视图聚类效果对比Table 3 Comparison of model effects on incomplete multi-view datasets% 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI AE2-Net 33.61 49.20 24.99 38.67 33.79 19.99 19.22 23.03 5.75 27.88 31.35 13.93 IMG 42.29 58.26 33.69 — — — 15.52 22.54 3.73 23.96 25.70 9.21 UEAF 47.35 56.71 37.08 34.56 33.13 24.04 16.38 18.42 3.80 28.20 27.01 8.70 DAIMC 44.63 59.53 32.70 34.44 27.15 16.42 19.30 19.45 5.80 23.60 21.88 9.44 EERIMVC 40.66 51.38 27.91 54.97 44.91 35.94 22.14 25.18 9.10 33.10 32.11 15.91 DCCAE 40.01 52.88 30.00 61.79 59.49 33.49 14.94 20.95 3.67 31.75 34.42 15.80 PVC 41.42 56.53 31.00 35.97 27.74 16.99 21.33 23.14 8.10 25.61 25.31 11.25 BMVC 32.13 40.58 12.20 24.36 15.11 6.50 18.76 18.73 3.70 30.91 30.23 10.93 DCCA 38.59 52.51 29.81 61.82 60.55 37.71 14.08 20.02 3.38 31.83 33.19 14.93 CPM-GAN 41.42 55.89 33.74 — — — 19.02 21.58 6.11 27.30 27.18 11.93 PIC 57.53 64.32 45.22 — — — 23.60 26.52 9.45 38.70 37.98 21.16 COMPLETER 68.44 67.39 75.44 80.01 75.23 70.66 22.16 27.00 10.39 39.50 42.35 23.51 Ours 71.25 69.72 77.41 84.54 77.68 74.72 21.38 28.89 11.30 40.30 42.10 23.33 1）本文的方法在数据集Caltech101-20上效果提升最为显著，无论在完整和缺失的情况均有2%以上提升。同时相较于其他模型，本文提出的模型从完整数据到缺失数据的效果降低较少，这证明本文的模型对于数据缺失更加稳定。
2）本文的方法在Scene-15数据集和LandUse-21数据集提升较少，这是因为这两个数据集的各类样本较少，维度较低，深度方法对其的效果不明显。同时从其他多视图聚类算法在这两个数据集上的表现，可以发现这两个数据集本身较难以被聚类，所以本文的Self-paced K-Means策略对其的优化能力有限。
续表 2 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI UEAF 47.40 57.90 38.98 67.33 65.37 55.81 23.00 27.05 8.79 34.37 36.69 18.52 DAIMC 45.48 61.79 32.40 39.18 35.69 23.65 24.35 29.35 10.26 32.09 33.55 17.42 EERIMVC 43.28 55.04 30.42 65.47 57.69 49.54 24.92 29.57 12.24 39.60 38.99 22.06 DCCAE 44.05 59.12 34.56 81.60 84.69 70.87 15.62 24.41 4.42 36.44 39.78 21.47 PVC 44.91 62.13 35.77 41.94 33.90 22.93 25.22 30.45 11.72 30.83 31.05 14.98 BMVC 42.55 63.63 32.33 81.27 76.12 71.55 25.34 28.56 11.39 40.50 41.20 24.11 DCCA 41.89 59.14 33.39 85.53 89.44 81.87 15.51 23.15 4.43 36.18 38.92 20.87 CPM-GAN 43.18 62.00 34.57 — — — 22.34 29.18 9.49 30.87 31.54 15.27 PIC 62.27 67.93 51.56 — — — 24.86 29.74 10.48 38.72 40.46 22.12 COMPLETER 70.18 68.06 77.88 89.08 88.86 85.47 25.63 31.73 13.05 41.07 44.68 24.78 Ours 72.50 71.23 80.97 88.73 88.87 85.32 24.90 33.07 13.95 41.59 45.49 26.40 3.5 不同缺失率下的性能对比
为了进一步在更细粒度地缺失率上观察模型的效果，选取表中表现较好的3个方法：PIC[5]、COMPLETER[24]和本文提出的方法，在缺失率为0.1、0.2、0.3、0.4时进行实验，图3展示了其实验结果。 结果表明: 1) 随着缺失率的增加, 3种方法的性能均有一定程度的下降；2）相较于PIC[5]和COMPLETER[24]，本文所提出的方法更加稳定。
图 3 多种缺失率下效果对比Fig. 3 Comparison of model effects on more missing rate下载:
全尺寸图片
3.6 消融实验
为了探究本文所提出模型各部分对不完整多视图聚类任务的贡献，设计了消融实验。实验分别在无互信息最大化模块、无视图融合模块、无Self-paced K-Means模块这3种情况下进行实验，并与完整的模型进行对比，结果见表4。从表4中可以看出完整模型的效果是最好的，其余均有一定程度的效果衰退。
表 4 消融实验结果Table 4 Result of ablation experiments% 消融实验模型 ACC NMI ARI 无互信息最大化 42.44 48.02 34.36 无视图融合模块 68.55 68.53 72.13 无Self-paced K-Means 68.03 69.39 72.29 完整模型 71.25 69.72 77.41 对比无互信息最大化的消融模型和完整模型，其ACC、NMI和ARI分别降低了28.81%、21.7%和43.05%，由此证明了通过最大化互信息的方式学习视图间的公共语言是切实有效的。
对比无视图融合模块的消融模型和完整模型，其ACC、NMI和ARI分别有一定程度的减弱，由此证明了在训练过程中加入视图融合层自动学习融合表示，同时更好地辅助学习视图间的一致性。
对比无Self-paced K-Means微调的消融模型和完整模型，其ACC和ARI分别降低了3.22%和5.12%，这得益于Self-Paced K-Means是一种从易到难的样本学习模式，区别地对待对聚类中间样本和边缘样本，同时使模型学习得到更加聚类友好的表示。
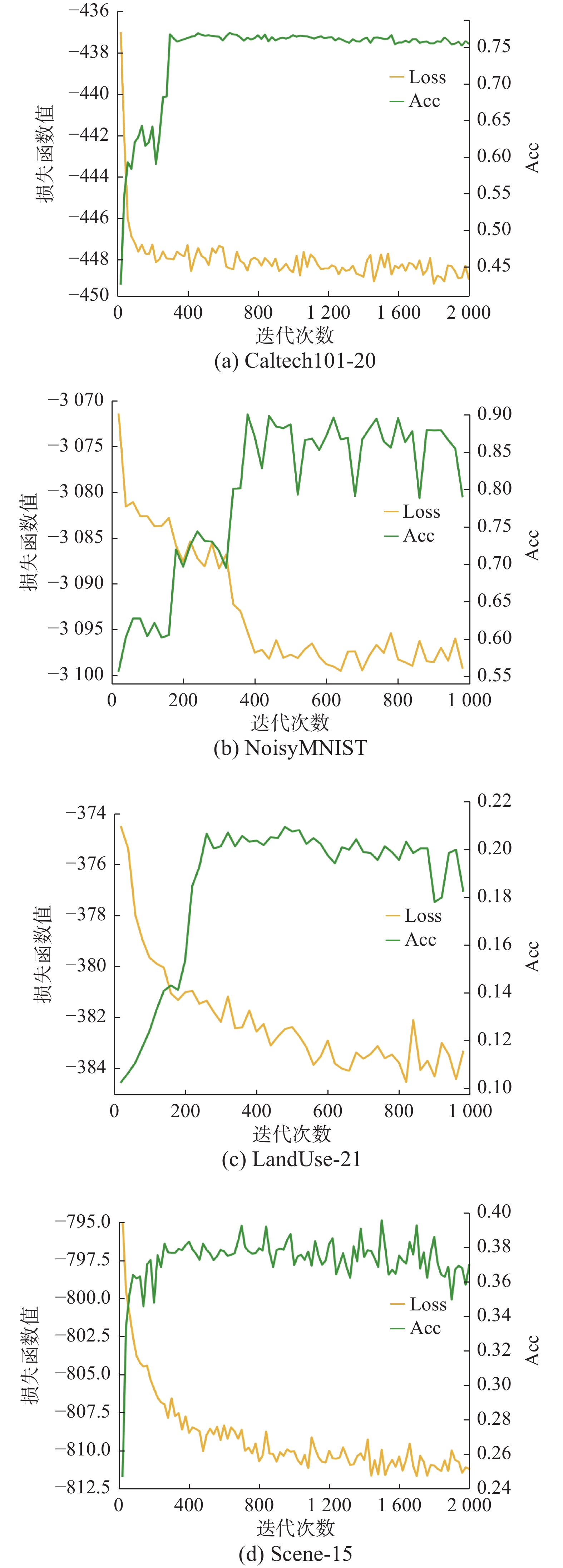
3.7 收敛性分析
在本节中，为了验证本文提出模型的收敛性，图4给出了在4个数据集的损失函数值的收敛曲线及ACC指标的表现。损失函数值与迭代次数成反比，并且都能在第 300次迭代内急剧下降达到最小值并趋于稳定；同时ACC持续增加。这表明模型具有良好的收敛性。其中NoisyMNIST的ACC曲线在后期波动较大，这可能由于较之其他数据集NoisyMNIST的数据量较大，同时NoisyMNIST的一个视图是加高斯噪声生成，为聚类带来了挑战，但是从图中也可以看出瓶颈效果还是不错的。
图 4 模型在4个数据集上的收敛曲线Fig. 4 Convergence curves of model on 4 datasets下载:
全尺寸图片
3.8 可视化分析
为了更直观地展现本文提出模型的聚类效果，分别在迭代20次、200次和500次利用t-SNE[37]方法对缺失率为0.25的NoisyMNIST的结果进行可视化，见图5。从迭代20次的可视化图中可以明显看出NoisyMNIST的各类分布是较为混乱的，存在同类样本分隔较远以及不同类样本距离较近的情况，同时类与类之间间隔不明显。在迭代200次的可视化图中各类就明显地聚集在一起。最后，迭代500次的可视化图各类更紧密地聚集在了一起，同时类与类之间间隔更加明显。
图 5 对Noisy MNIST的聚类可视化Fig. 5 Multi-view clustering visualization on Noisy MNIST下载:
全尺寸图片
4. 结束语
本文提出一种新颖的针对不完整多视图的深度聚类方法，在利用深度自编码器学习各视图复杂的内在信息的同时引入了互信息和视图融合层来最大化视图间的一致性，同时提出了一种有效且合理的缺失数据补全策略。最后，利用一种Self-paced K-Means的目标函数对模型进行微调，使获得的潜在公共表示更加聚类友好。在多个数据集上的实验结果证明了本文方法的有效性。
本文提出的模型虽然在一些基准数据集上取得了一定的提升，但还是存在部分局限性，例如，没有将其应用到更实际的数据集上，同时对于两视图以上的情况，本文方法的复杂度将随视图数急剧增加。下一步我们将考虑从这两个方向来优化模型，同时进一步提高不完整多视图聚类性能。
-
图 1 互信息阐述
Fig. 1 Illustration of mutual information
下载:
全尺寸图片
图 2 基于互信息最大化的不完整多视图聚类方法模型
Fig. 2 Framework of incomplete multi-view clustering model based on mutual information maximization
下载:
全尺寸图片
图 3 多种缺失率下效果对比
Fig. 3 Comparison of model effects on more missing rate
下载:
全尺寸图片
图 4 模型在4个数据集上的收敛曲线
Fig. 4 Convergence curves of model on 4 datasets
下载:
全尺寸图片
图 5 对Noisy MNIST的聚类可视化
Fig. 5 Multi-view clustering visualization on Noisy MNIST
下载:
全尺寸图片
表 1 数据集详细信息
Table 1 Information of datasets
数据集 样本数 实验视图 视图维度 类数 Caltech101-20 2386 HOG,GIST 1984/512 20 Scene-15 4485 PHOG,GIST 20/59 15 LandUse-21 2100 PHOG,GIST 59/40 21 NoisyMNIST 20000 — 784/784 10 表 2 完整多视图聚类效果对比
Table 2 Comparison of model effects on complete multi-view datasets
% 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI AE2-Net 49.10 65.38 35.66 56.98 46.83 36.98 24.79 30.36 10.35 36.10 40.39 22.08 IMG 44.51 61.35 35.74 — — — 16.40 27.11 5.10 24.20 25.64 9.57 表 3 不完整多视图聚类效果对比
Table 3 Comparison of model effects on incomplete multi-view datasets
% 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI AE2-Net 33.61 49.20 24.99 38.67 33.79 19.99 19.22 23.03 5.75 27.88 31.35 13.93 IMG 42.29 58.26 33.69 — — — 15.52 22.54 3.73 23.96 25.70 9.21 UEAF 47.35 56.71 37.08 34.56 33.13 24.04 16.38 18.42 3.80 28.20 27.01 8.70 DAIMC 44.63 59.53 32.70 34.44 27.15 16.42 19.30 19.45 5.80 23.60 21.88 9.44 EERIMVC 40.66 51.38 27.91 54.97 44.91 35.94 22.14 25.18 9.10 33.10 32.11 15.91 DCCAE 40.01 52.88 30.00 61.79 59.49 33.49 14.94 20.95 3.67 31.75 34.42 15.80 PVC 41.42 56.53 31.00 35.97 27.74 16.99 21.33 23.14 8.10 25.61 25.31 11.25 BMVC 32.13 40.58 12.20 24.36 15.11 6.50 18.76 18.73 3.70 30.91 30.23 10.93 DCCA 38.59 52.51 29.81 61.82 60.55 37.71 14.08 20.02 3.38 31.83 33.19 14.93 CPM-GAN 41.42 55.89 33.74 — — — 19.02 21.58 6.11 27.30 27.18 11.93 PIC 57.53 64.32 45.22 — — — 23.60 26.52 9.45 38.70 37.98 21.16 COMPLETER 68.44 67.39 75.44 80.01 75.23 70.66 22.16 27.00 10.39 39.50 42.35 23.51 Ours 71.25 69.72 77.41 84.54 77.68 74.72 21.38 28.89 11.30 40.30 42.10 23.33 续表 2 对比方法 Caltech101-20 NoisyMNIST LandUse-21 Scene-15 ACC NMI ARI ACC NMI ARI ACC NMI ARI ACC NMI ARI UEAF 47.40 57.90 38.98 67.33 65.37 55.81 23.00 27.05 8.79 34.37 36.69 18.52 DAIMC 45.48 61.79 32.40 39.18 35.69 23.65 24.35 29.35 10.26 32.09 33.55 17.42 EERIMVC 43.28 55.04 30.42 65.47 57.69 49.54 24.92 29.57 12.24 39.60 38.99 22.06 DCCAE 44.05 59.12 34.56 81.60 84.69 70.87 15.62 24.41 4.42 36.44 39.78 21.47 PVC 44.91 62.13 35.77 41.94 33.90 22.93 25.22 30.45 11.72 30.83 31.05 14.98 BMVC 42.55 63.63 32.33 81.27 76.12 71.55 25.34 28.56 11.39 40.50 41.20 24.11 DCCA 41.89 59.14 33.39 85.53 89.44 81.87 15.51 23.15 4.43 36.18 38.92 20.87 CPM-GAN 43.18 62.00 34.57 — — — 22.34 29.18 9.49 30.87 31.54 15.27 PIC 62.27 67.93 51.56 — — — 24.86 29.74 10.48 38.72 40.46 22.12 COMPLETER 70.18 68.06 77.88 89.08 88.86 85.47 25.63 31.73 13.05 41.07 44.68 24.78 Ours 72.50 71.23 80.97 88.73 88.87 85.32 24.90 33.07 13.95 41.59 45.49 26.40 表 4 消融实验结果
Table 4 Result of ablation experiments
% 消融实验模型 ACC NMI ARI 无互信息最大化 42.44 48.02 34.36 无视图融合模块 68.55 68.53 72.13 无Self-paced K-Means 68.03 69.39 72.29 完整模型 71.25 69.72 77.41 -
[1] 赵博宇, 张长青, 陈蕾, 等. 生成式不完整多视图数据聚类[J]. 自动化学报, 2021, 47(8): 1867–1875. doi: 10.16383/j.aas.c200121 ZHAO Boyu, ZHANG Changqing, CHEN Lei, et al. Generative model for partial multi-view clustering[J]. Acta automatica sinica, 2021, 47(8): 1867–1875. doi: 10.16383/j.aas.c200121 [2] 张熠玲, 杨燕, 周威, 等. CMvSC: 知识迁移下的深度一致性多视图谱聚类网络[J]. 软件学报, 2022, 33(4): 1373–1389. ZHANG Yiling, YANG Yan, ZHOU Wei, et al. CMvSC: knowledge transferring based deep consensus network for multi-view spectral clustering[J]. Journal of software, 2022, 33(4): 1373–1389. [3] SHAO Weixiang, HE Lifang, YU P S. Multiple incomplete views clustering via weighted nonnegative matrix factorization with L2, 1 regularization[M]//Machine Learning and Knowledge Discovery in Databases. Cham: Springer International Publishing, 2015: 318−334. [4] YIN Qiyue, WU Shu, WANG Liang. Incomplete multi-view clustering via subspace learning[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. Melbourne: ACM, 2015: 383−392. [5] WANG HAO, ZONG LINLIN, LIU BING, et al. Spectral perturbation meets incomplete multi-view data[EB/OL]. (2019−03−31)[2022−03−23].https://arxiv.org/abs/1906.00098. [6] HU MENGLEI, CHEN SONGCAN. Doubly aligned incomplete multi-view clustering[EB/OL]. (2019−03−07)[2022−03−23].https://arxiv.org/abs/1903.02785. [7] LI Shaoyuan, JIANG Yuan, ZHOU Zhihua. Partial multi-view clustering[C]//Proceedings of the AAAI conference on artificial intelligence. Québec: AAAI Press, 2014, 28(1): 1968−1974. [8] HUANG Zhenyu, ZHOU Tianyi, PENG Xi, et al. Multi-view spectral clustering network[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. Macao: International Joint Conferences on Artificial Intelligence Organization, 2019: 2563−2569. [9] SUN Xiukun, CHENG Miaomiao, CHEN Min, et al. Self-supervised deep multi-view subspace clustering [C]//Proceedings of the 8th Asian Conference on Machine Learning. Nagoya: PMLR, 2019: 1001−1016. [10] ZHANG Changqing, FU Huazhu, HU Qinghua, et al. Generalized latent multi-view subspace clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2020, 42(1): 86–99. doi: 10.1109/TPAMI.2018.2877660 [11] ZHANG Changqing, LIU Yeqing, FU Huazhu. AE2-nets: autoencoder in autoencoder networks[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 2572−2580. [12] ZHANG Changqing, CUI Yajie, HAN Zongbo, et al. Deep partial multi-view learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(5): 2402–2415. [13] PAN Erlin, ZHAO Kang. Multi-view Contrastive Graph Clustering[J]. Advances in neural information processing systems, 2021, 34: 2148–2159. [14] WAN Zhibin, ZHANG Changqing, ZHU Pengfei, et al. Multi-view information-bottleneck representation learning[C]//Proceedings of the AAAI conference on artificial intelligence. Van couver: AAAI Press, 2021, 35(11): 10085−10092. [15] SHAHAM U, STANTON K, LI H, et al. Spectralnet: Spectral clustering using deep neural networks[EB/OL]. (2018−01−04) [2022−03−23].https://arxiv.org/abs/18012021. [16] PAN Ji, ZHANG Tong, LI Hongdong, et al. Deep subspace clustering networks[J]. Advances in neural information processing systems, 2017: 30. [17] ZHONG HUASONG, CHEN CHONG, JIN ZHONGMING, et al. Deep robust clustering by contrastive learning[EB/OL]. (2020−08−07)[2022−03−23].https://arxiv.org/abs/2008.03030. [18] MACQUEEN J. Classification and analysis of multivariate observations[C]//Fifth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: The Regents of the University of California, 1967: 281−297. [19] KUMAR M P, PACKER B, KOLLER D. Self-paced learning for latent variable models[C]// Advances in neural information processing systems. NIPS, 2010. [20] BENGIO Y, LOURADOUR J, COLLOBERT R, et al. Curriculum learning[C]//ICML’09: Proceedings of the 26th Annual International Conference on Machine Learning. New York: ACM, 2009: 41−48. [21] HU Menglei, CHEN Songcan. One-pass incomplete multi-view clustering[C]//Proceedings of the AAAI conference on artificial intelligence. Honolulu, AAAI Press: 2019, 33: 3838−3845. [22] ZHAO Liang, CHEN Zhikui, YANG Yi, et al. Incomplete multi-view clustering via deep semantic mapping[J]. Neurocomputing, 2018, 275: 1053–1062. doi: 10.1016/j.neucom.2017.07.016 [23] 刘相男, 丁世飞, 王丽娟. 基于深度图正则化矩阵分解的多视图聚类算法[J]. 智能系统学报, 2022, 17(1): 158–169. doi: 10.11992/tis.202104046 LIU Xiangnan, DING Shifei, WANG Lijuan. A multi-view clustering algorithm based on deep matrix factorization with graph regularization[J]. CAAI transactions on intelligent systems, 2022, 17(1): 158–169. doi: 10.11992/tis.202104046 [24] 郭圣, 仲兆满, 李存华. 基于深度自编码的多视图子空间聚类网络[J]. 计算机工程与应用, 2020, 56(17): 60–68. GUO Sheng, ZHONG Zhaoman, LI Cunhua. Multi-view subspace clustering network based on deep autoencoder[J]. Computer engineering and applications, 2020, 56(17): 60–68. [25] LIN Yijie, GOU Yuanbiao, LIU Zitao, et al. COMPLETER: incomplete multi-view clustering via contrastive prediction[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 11169−11178. [26] GE Yixiao, ZHU Feng, CHEN Dapeng, et al. Self-paced contrastive learning with hybrid memory for domain adaptive object re-id[J]. Advances in neural information processing systems, 2020, 33: 11309−11321. [27] JIANG Lu, MENG Deyu, ZHAO Qian, et al. Self-paced curriculum learning[C]//Proceedings of the AAAI conference on artificial intelligence. Buenos Aires: AAAI Press, 2015, 29(1). [28] CHU Guanyi, WANG Xiao, SHI Chuan, et al. CuCo: graph representation with curriculum contrastive learning[C]//Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2021: 2300−2306. [29] PENG Jizong, WANG Ping, DESROSIERS C, et al. Self-paced contrastive learning for semi-supervised medical image segmentation with meta-labels[J]. Advances in neural information processing systems, 2021, 34: 16686–16699. [30] 许子微, 陈秀宏. 自步稀疏最优均值主成分分析[J]. 智能系统学报, 2021, 16(3): 416–424. doi: 10.11992/tis.201911028 XU Ziwei, CHEN Xiuhong. Sparse optimal mean principal component analysis based on self-paced learning[J]. CAAI transactions on intelligent systems, 2021, 16(3): 416–424. doi: 10.11992/tis.201911028 [31] WANG Weiran, RAMAN Arora, LIVESCU, K, et al. On deep multi-view representation learning[C]//Proceedings of the 32nd International Conference on Machine Learning. Lille: PMLR, 2015: 1083−1092. [32] ANDREW G, ARORA R, BILMES J, et al. Deep canonical correlation analysis[C]//ICML’13: Proceedings of the 30th International Conference on International Conference on Machine Learning-Volume 28. New York: ACM, 2013: 1247–1255. [33] ZHANG Zheng, LIU Li, SHEN Fumin, et al. Binary multi-view clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(7): 1774–1782. doi: 10.1109/TPAMI.2018.2847335 [34] LIU Xinwang, LI Miaomiao, TANG Chang, et al. Efficient and effective regularized incomplete multi-view clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 43(8): 2634–2646. [35] ZHANG Handong, LIU Hongfu, FU Yun. Incomplete multi-modal visual data grouping[C]// International Joint Conference on Artificial Intelligence. New York: AAAI, 2016: 2392−2398. [36] WEN Jie, ZHANG Zheng, XU Yong, et al. Unified embedding alignment with missing views inferring for incomplete multi-view clustering[C]//Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019: 5393−5400. [37] VAN der Maaten L, HINTON G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(11): 2579−2605.
