Detection model of target motion direction simulating the optic lobe neural network of compound eyes
-
摘要: 如何对杂乱背景中物体（目标）的运动方向做出准确可靠的检测与感知，是计算机视觉研究领域中一个重要问题。自然界中，飞虫（如苍蝇、蜻蜓等）高适应性和高可靠性的感知目标运动是一种自然特性，本文基于飞虫−果蝇视叶神经纤维网最新的生理学研究成果，提出一种基于果蝇视觉感知目标运动方向的多层级检测模型系统。通过对不同场景下拍摄的视频序列样本进行实验和测试，并与2-Q运动检测器模型、基于ON和OFF信号通道处理运动信息的检测模型等进行了对比，验证了其在杂乱背景下对于目标水平和垂直方向运动检测的有效性和鲁棒性。Abstract: How to detect and perceive the motion direction of objects (targets) in a chaotic background accurately and reliably is an important research area in the field of computer vision. In nature, flying insects (such as flies and dragonflies) can sense the movements of their target with high adaptability and reliability . Based on the latest research results of the physiology of the optic lobe neuropile layer of the flying insect drosophila, a multilevel model system for detecting target motion direction based on visual perception of drosophila is proposed. By shooting the video sequence of samples under different scenarios for experiment and test and comparing with the 2-Q motion detector model based on ON and OFF signal channel processing motion information, the effectiveness and robustness of the proposed system for horizontal and vertical motion detection of video targets under a chaotic background are confirmed.
-
自然界中飞虫（如苍蝇、蜻蜓、蜜蜂、蝗虫等）复眼视觉系统对于目标（物体）/图形（figure）分辨与运动感知的高适应性和高可靠性是一种自然特性。与灵长类动物的视觉系统相比，飞虫复眼分辨力和计算资源尽管有限，对杂乱场景中目标的分辨和追踪或逃逸过程本质上却是良态和适定的[1-3]。在以复眼视觉神经计算为基础的运动感知方面，几十年来一直是科学研究的焦点。当今，复眼视觉系统已成为研究设计人工运动感知视觉系统的重要模型范式[4-8]。
为阐明飞虫复眼视觉运动感知的神经计算过程，早在1956年，Hassenstein和Reichardt开创性地提出运动相关器（Hassenstein-Reichardt correlator模型），也称初级运动检测器（elementary motion detector，EMD）模型[8]。在之后的几十年里，许多学者陆续又提出了一些EMD的变体模型[9-10]。近十多年来，在揭示飞虫复眼运动视觉系统中有关ON和OFF信号通道（亮色通道和暗色通道），髓质层的跨层神经元T4，小叶层的小叶柱LCs神经元和跨层神经元T5，小叶板层LPTCs（lobula plate tangential cells）中一类STMD（small target motion detector），方向选择（direction selective）和FD（figure detection）神经元，以及对于目标大小（尺寸）及边缘和纹理、运动强度和方向等选择性反应机理等方面，又进一步地取得了新进展[3-4,11-15]。这为精细化阐明目标运动感知的视觉神经计算过程提供了生物学基础。2011年Eichner等[16]根据昆虫视叶神经系统ON和OFF通道机制的电生理学发现，提出四象限检测（4-Quadrant detector）模型。2012年Hennig等[17]提出一种基于自然光流处理的图形检测FD电路模型，仿真模拟了果蝇FD神经元利用相对运动对目标分辨及相互间距离推断做出的显著反应。2013年Wiederman等[18]提出ESTMD（elementary small target motion detector）与经典的EMD级联的混合模型，通过ESTMD-EMD级联的方案封装STMD神经元的生物特性，将运动视觉路径中的ON和OFF通道关联起来检测自然场景中小物体运动，可以同时对大小和方向表现出明显的选择性。2017年Yue等[19]提出一种基于果蝇视叶中DSNs（direction selective neurons）的视觉神经网络模型，能够在杂乱背景中感知四个基本方向上的目标运动，并具有优良的速度响应性能。2020年Fu等[20]提出了一种基于ON和OFF信号通道处理运动信息的检测模型，实现了杂乱运动背景下目标运动方向的检测。2022年李柯等[21]基于视叶结构中一类特定小目标检测器神经元LC11对运动做出精细的选择性响应等昆虫生理学研究的新发现，提出了一种杂乱移动背景下暗色小目标运动检测方法。
上述的仿复眼感知运动目标建模是随着近年来视叶结构神经元细节和连接功能、视觉信号传导与响应等研究新成果为基础而不断优化发展的，如Fu等[20]提出的模型是基于昆虫生理学新的研究成果而建立的。但使用相对简单的结构和少量神经元的简约复眼视觉神经计算范式，建立更有效的复眼形态感知模型来处理杂乱的运动背景和鲁棒性的检测目标运动方向，仍然是一个具有挑战性的问题。本文基于最新的昆虫生理学研究成果，提出一种目标运动方向检测的多层级模型系统（multi-level model system for target motion direction detection，MLMS）。新模型的优点如下：
1）在保证目标运动方向有效性检测的前提下，仅对复眼视网膜层帧差处理后的低频子图进行处理，降低了模型算法的计算复杂度及计算耗时。
2）通过模拟和解析薄板层，首先对低频子图序列做初级视觉滤波（primary visual filtering，PVF），然后，对被分解成两条平行的ON和OFF通道的运动视觉信号分别做二次视觉滤波（secondary visual filtering，SVF），降低噪声的同时提高了运动边缘的对比度，增强了杂乱的运动背景下目标运动方向检测的抗干扰性能。
3）基于方向选择(direction selection, DS)和方向对抗(direction opposition, DO)响应机制，通过T4和T5小视场(small-field)的方向敏感信号与LPTCs宽视场的水平敏感(horizontal-sensitive，HS)和垂直敏感(vertical-sensitive，VS)的整合计算，提升了杂乱的运动背景下目标运动方向检测的敏感性和鲁棒性性能。
1. 运动方向检测模型框架
1.1 果蝇视叶的目标运动感知神经回路
果蝇复眼视网膜细胞发送光感信号通向脑内两侧的薄板（lamina），与下游髓质（medulla）、小叶（lobula）及小叶板（lobula plate）神经节层连续依次相连，而后汇聚到达中央脑（central brain）的各个脑结构，形成视觉信息加工处理的神经回路[2,4]。位于视叶结构最外层的薄板对各个小眼R1～R6光感信号进行整合，以及将运动视觉信息分解成两条平行的ON和OFF通道，然后向下游层髓质传递。髓质层的跨髓神经元Tm、固有神经元Mi等，分别接收ON和OFF两条通道的信号，并分别向下游层小叶和小叶板投射，小叶和小叶板层并局部信号整合产生宽视场的精确响应信号[2,14-15]。进一步的，LPTCs轴突大多数投射到原脑区或与颈及足、翅运动有关的神经元。
1.2 方向检测的多层级模型系统框架
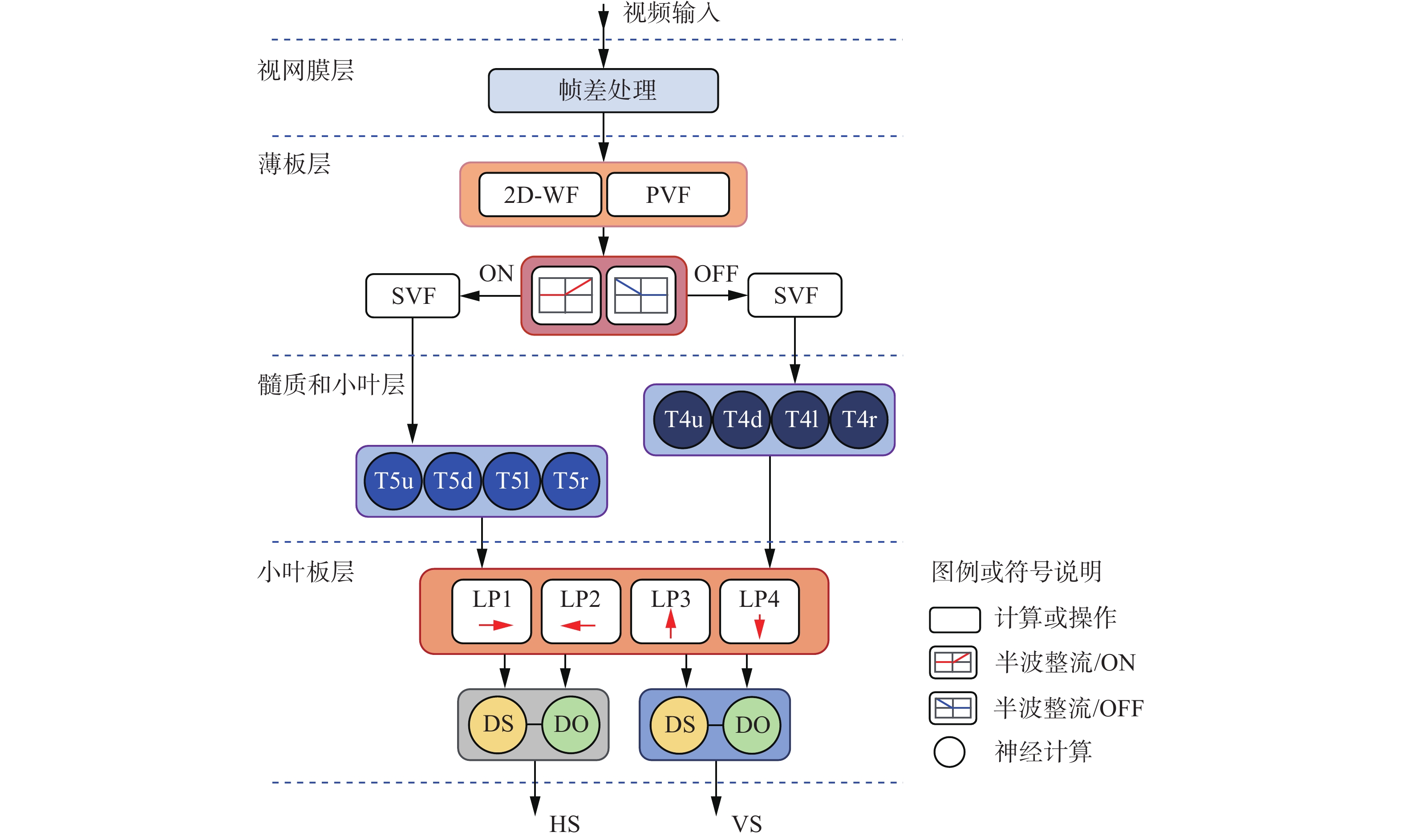
构建的目标运动方向检测的多层级模型系统（MLMS）的框架，如图1所示。
图 1 多层级模型系统MLMS框架Fig. 1 Multi-level model system MLMS framework
下载:
全尺寸图片
系统各层级具体的模拟与计算如下。
1）视网膜层的模拟与计算：基于视网膜感光细胞光电转换响应，对视频输入进行帧差处理，获取目标运动信息。
2）薄板层的模拟与计算[10,22]：a) 采用二维小波变换（two-dimensional wavelet transform，2D-WF），将帧差处理后的图像序列，分解为高频子图和低频子图，考虑到算法的轻量化，仅对被分解的低频子图进行处理。b) 模拟薄板层相近神经元彼此之间侧抑制效应，以及选择性地调节信号强度和频率分布，完成初级视觉滤波（PVF）。c) 通过半波整流形式分解成两条平行的ON、OFF信号通道。d) 基于快速去极化和慢速重极化的生物适应性视觉处理机制，分别对ON、OFF信号做二次视觉滤波（SVF）。
3）髓质和小叶层的模拟与计算[20,22]：模拟位于髓质的跨层神经元T4和位于小叶的跨层神经元T5，分别对ON、OFF通道信号计算出方向选择性响应，并向下游的小叶板投射。
4）小叶板层的模拟与计算[4,20,22]：模拟小叶板从上游T4、T5获取小视场下不同运动方向信号作为输入，整合了方向选择（DS）和方向对抗（DO）响应信号，从而产生宽视场下的水平敏感（HS）和垂直敏感（VS）运动方向分量。
2. 视叶计算的各层级
2.1 视网膜计算层
视网膜感光细胞接收输入光信号，比较各像素点相邻时间内的亮度变化，其神经元产生膜电位，完成帧间差分处理，帧间差分的像素点P计算式：
$$ P(x,y,t) = L(x,y,t) - L(x,y,t - 1) + \sum\limits_{i = 1}^{_{{n_p}}} {{a_i}} \cdot P(x,y,t - i) $$ (1) $$ {a_i} = {(1 + {{\text{e}}^i})^{ - 1}} $$ (2) 式中：(x,y)代表像素点坐标，L(x,y,t)表示t时刻像素值，
${n_p}$ 为持续影响的帧数[0, 2]，${a_i}$ 为衰减系数。2.2 薄板计算层
2.2.1 低频子图和高频子图的二维小波变换分解
果蝇运动视觉系统中薄板层具有区分高频信号中视觉杂乱的背景及噪点，及低频信号中能反映目标轮廓和有效保留运动边缘信息的功能特性[2,4,12]。借助二维小波变换，将帧间差分图像分解为低频子图和高频子图，且仅对被分解的低频子图进行处理，以减少计算负担。
2.2.2 初级视觉滤波
基于中心−周围对抗（centre-surrounding antagonism）的互抑制计算机理[10]，模拟薄板层单极细胞LMCs功能，通过高斯差分形式模拟初级视觉滤波，去除冗余的背景运动，提高目标运动细节的视锐度。相关研究表明，两个高斯函数的核半径比为5∶1时，近似为视网膜层上的视像。高斯差分的二维表达式为
$$ {P_e}(x,y,t) = \sum\limits_{u = - 2}^2 {\sum\limits_{v = - 2}^2 {{P_L}(x - u,y - v,t) \cdot \frac{1}{{2{\text{π}}\sigma _{ e}^2}}\exp \left( - \frac{{{u^2} + {v^2}}}{{2\sigma _{ e}^2}}\right)} } $$ (3) $$ {P_i}(x,y,t) = \sum\limits_{u = - 5}^5 {\sum\limits_{v = - 5}^5 {{P_L}(x - u,y - v,t) \cdot \frac{1}{{2{\text{π}}\sigma _{ i}^2}}\exp \left( - \frac{{{u^2} + {v^2}}}{{2\sigma _{ i}^2}}\right)} } $$ (4) 式中：
${P_L}$ 为经过二维小波变换获得的低频子图，${P_e}$ 代表中心正高斯的兴奋信号，${P_i}$ 代表周围负高斯的抑制信号。${\sigma _i}$ 和${\sigma _e}$ 表示抑制和兴奋信号的标准差，分别取${\sigma _i}$ =10、${\sigma _e}$ =2。基于中心−周围对抗的互抑制可由下式解析：$$ \begin{gathered} {L_A}(x,y,t) = \\ \left\{ \begin{array}{l} {|{P_e}(x,y,t) - {P_i}(x,y,t)|{,\;^{}}{P_e}(x,y,t) \geqslant 0,\;{P_i}(x,y,t) \geqslant 0}\\ { - |{P_e}(x,y,t) - {P_i}(x,y,t)|{,\;^{}}{P_e}(x,y,t) < 0,\;{P_i}(x,y,t) < 0} \end{array} \right. \end{gathered} $$ (5) 为提高运动边缘的对比度，最大限度地从杂乱视觉背景中提取出有用的运动信息，这里采用平滑滤波和设置阈值的方式进行预处理：
$$ Z(x,y,t) = \sum\limits_{ - 1}^1 {\sum\limits_{ - 1}^1 {{L_A}(x,y,t) \cdot \omega (x,y)} } $$ (6) $$ \omega = \frac{1}{{{\text{16}}}}\left[ \begin{gathered} {1_{}}\mathop {}\nolimits_{}\;\; {{\text{2}}_{}}\;\; \mathop {}\nolimits_{} 1 \\ {{\text{2}}_{}}\mathop {}\nolimits_{} \;\;{{\text{4}}_{}}\;\; \mathop {}\nolimits_{} {\text{2}} \\ {1_{}}\mathop {}\nolimits_{} \;\;{{\text{2}}_{}}\;\; \mathop {}\nolimits_{} 1 \\ \end{gathered} \right] $$ (7) 在设置卷积核
$\omega $ 时（见式(7)），赋予中心点最高权重系数，然后随着距离中心点距离的增加而减小系数值，使得在对图像进行平滑处理降噪的过程中，尽可能地降低图像模糊。接着，设置一个阈值T来过滤掉较弱的兴奋点：$$ \hat Z (x,y,t) = \left\{ \begin{gathered} Z(x,y,t) \cdot A{,\;^{}}|Z(x,y,t)| \geqslant T \\ 0{,\;^{}}|Z(x,y,t)| < T \\ \end{gathered} \right. $$ (8) 式中：
$\hat Z (x,y,t)$ 为初级视觉滤波的预处理后，在图像某像素点的灰度值；A为增强系数；T 为过滤的阈值。2.2.3 半波整流
采用半波整流方式，将运动视觉信号分解成两条平行的ON和OFF通道进行处理：
$$ \begin{gathered} {L_1}(x,y,t) = \hat Z (x,y,t),\;\;\hat Z (x,y,t) > 0 \\ {L_2}(x,y,t) = - \hat Z (x,y,t),\;\;\hat Z (x,y,t) < 0 \\ \end{gathered} $$ (9) 式中：L1代表ON通道的信号，L2代表OFF通道的信号。
2.2.4 二次视觉滤波
模拟果蝇视觉系统中快速去极化–慢速重极化的神经计算过程，实现二次视觉滤波。首先，对来自ON和OFF的输入信号在时间t时刻求导数，因数字信号不可导，因此，比较每两个连续帧之间的神经元响应：
$$ \begin{gathered} \Delta {L_1}(x,y) = {L_1}(x,y,t) - {L_1}(x,y,t - 1) \\ \Delta {L_2}(x,y) = {L_2}(x,y,t) - {L_2}(x,y,t - 1) \\ \end{gathered} $$ (10) 随后，对来自ON和OFF的输入信号L1和L2，由下式分别完成非负信号的快速去极化和负信号的慢速重极化的处理。
$$ {{\hat L_1}} (x,y,t) = \left\{ \begin{gathered} {L_1}(x,y,t) + \exp (\Delta \tau /{\xi _2}){,\;^{}}\Delta {L_1}(x,y) \geqslant 0 \\ {L_1}(x,y,t) - \exp ( - \Delta \tau /{\xi _1}){,\;^{}}\Delta {L_1}(x,y) < 0 \\ \end{gathered} \right. $$ (11) $$ {{\hat L_{\text{2}}}} (x,y,t) = \left\{ \begin{gathered} {L_{\text{2}}}(x,y,t) + \exp (\Delta s/{\xi _2}){,\;^{}}\Delta {L_{\text{2}}}(x,y) \geqslant 0 \\ {L_{\text{2}}}(x,y,t) - \exp ( -\Delta s/{\xi _1}){,\;^{}}\Delta {L_{\text{2}}}(x,y) < 0 \\ \end{gathered} \right. $$ (12) 式中：
$\Delta \tau$ 为帧间的时间差，即视频输入帧率的倒数，单位为ms。${\xi _1}、{\xi _2}$ 是响应衰减（增强）系统。最后，用原始信号减去延迟信号得：
$$ \begin{gathered} {M_1}(x,y,t) = {L_1}(x,y,t) - {{\hat L_1}} (x,y,t) \\ {M_2}(x,y,t) = {L_2}(x,y,t) - {{\hat L_2}} (x,y,t) \\ \end{gathered} $$ (13) 式中：M1表示在ON信号通道，经二次视觉滤波后的运动信息；M2表示在OFF信号通道，经二次视觉滤波后的运动信息。
2.3 髓质和小叶计算层
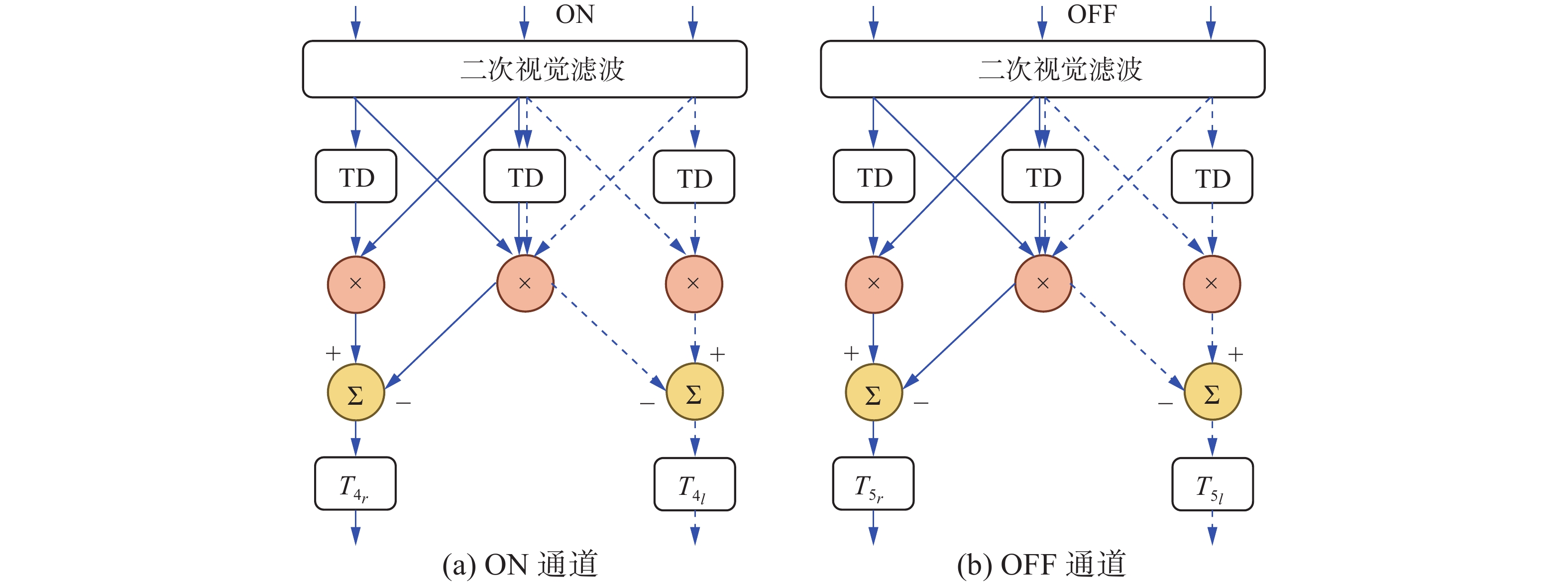
基于近年来昆虫生理学最新的研究成果，研究建立有关运动方向选择（motion direction selection，MDS）模型[3,4,11,13]。图2给出了在髓质和小叶层中MDS模型的结构。图中以左、右水平方向为例（垂直方向同理），输入信号代表每个像素点(x,y)的灰度值，ON和OFF通道的3个输入信号分别代表2个像素点的灰度值，TD为时间延迟单元，带箭头的实线代表向右平移运动分量的路径，箭头虚线代表向左平移运动分量的路径。T4r和T4l神经元代表ON通道中目标向右和向左移动的分量，T5r和T5l代表OFF通道中目标向右和向左移动的运动分量。
图 2 髓质和小叶层中运动方向选择性建模Fig. 2 Selective modeling of the motion direction in the medulla and lobule下载:
全尺寸图片
综合考虑ON或OFF通道内8邻域相关细胞的影响，计算髓质层T4在up（T4u）、down（T4d）、left（T4l）、right（T4r）4个基本方向的响应：
$$ \begin{gathered} {T_{4u}}(x,y,t) = \sum\limits_{i = {{ - }}1}^{\text{1}} { {{\hat M_1}} } (x + {s_d},y + i \cdot {s_d},t) \cdot {M_1}(x,y,t) - \\ {{\hat M_1}} (x,y,t) \cdot {M_1}(x + {s_d},y + i \cdot {s_d},t) \end{gathered} $$ (14) $$ \begin{gathered} {T_{4d}}(x,y,t) = \sum\limits_{i = { { - 1}}}^{\text{1}} { {{\hat M_1}} } (x - {s_d},y + i \cdot {s_d},t) \cdot {M_1}(x,y,t) -\\ {{\hat M_1}} (x,y,t) \cdot {M_1}(x - {s_d},y + i \cdot {s_d},t) \end{gathered} $$ (15) $$ \begin{gathered} {T_{4l}}(x,y,t) = \sum\limits_{i = { { - }}1}^{\text{1}} { {{\hat M_1}} } (x + i \cdot {s_d},y + {s_d},t) \cdot {M_1}(x,y,t) -\\ {{\hat M_1}} (x,y,t) \cdot {M_1}(x + i \cdot {s_d},y + {s_d},t) \end{gathered} $$ (16) $$ \begin{gathered} {T_{4r}}(x,y,t) = \sum\limits_{i = { { - }}1}^{\text{1}} { {{\hat M_1}} } (x + i \cdot {s_d},y - {s_d},t) \cdot {M_1}(x,y,t) - \\ {{\hat M_1}} (x,y,t) \cdot {M_1}(x + i \cdot {s_d},y - {s_d},t) \end{gathered} $$ (17) 式中：
${s_d}$ 代表采样距离，与中心−周围对抗互抑制机制中的参数${\sigma _i}$ 有关，$ {{\hat M_1}} $ 表示延迟信号，计算如下：$$ {{\hat M_1}} (x,y,t) = {M_1}(x,y,t) + \exp ( \Delta \tau /{\xi _2}) $$ (18) 同样的，小叶层中的T5计算公式与T4类同，此处不再赘述。
2.4 小叶板计算层
模拟小叶板4个子层（LP1～LP4）对来自上游T4和T5方向选择性响应的投射进行整合计算，计算输出为[4,19-21]
$$ \begin{gathered} {L_{{P_u}}}(t) = \sum\limits_{x = 1}^C {\sum\limits_{y = 1}^R {{T_{{4_u}}}(x,y,t) + {T_{{5_u}}}(x,y,t)} } \\ {L_{{P_d}}}(t) = \sum\limits_{x = 1}^C {\sum\limits_{y = 1}^R {{T_{{4_d}}}(x,y,t) + {T_{{5_d}}}(x,y,t)} } \\ \end{gathered} $$ (19) $$ \begin{gathered} {L_{{P_l}}}(t) = \sum\limits_{x = 1}^C {\sum\limits_{y = 1}^R {{T_{{4_l}}}(x,y,t) + {T_{{5_l}}}(x,y,t)} } \\ {L_{{P_r}}}(t) = \sum\limits_{x = 1}^C {\sum\limits_{y = 1}^R {{T_{{4_r}}}(x,y,t) + {T_{{5_r}}}(x,y,t)} } \\ \end{gathered} $$ (20) 式中：C和R分别表示二维视野（即，输入的二维像）的列和行，相反方向的运动产生方向对抗响应，垂直敏感分量VS和水平敏感HS分量为[20,22-23]
$$ \begin{gathered} {H_S}(t) = {L_{{P_r}}}(t) - {L_{{P_l}}}(t) \\ {V_S}(t) = {L_{{P_d}}}(t) - {L_{{P_u}}}(t) \\ \end{gathered} $$ (21) 使用Sigmoid函数作为激活函数，定义为[20]
$$ f(x) = 2 \cdot {{\rm{sgn}}} (x) \cdot ({(1 + {{\text{e}}^{ - |x| \cdot {{(C \cdot R \cdot k)}^{ - 1}}}})^{ - 1}} - 0.5) $$ (22) 式中k是比例系数。将HS和VS作为函数f(x)的输入变量x，则f(x)的输出对应水平方向和垂直方向的输出响应值。水平方向的响应值为正时，代表目标向右运动；反之，代表目标向左运动。垂直方向的响应值为正时，代表目标向下运动；反之，代表目标向上运动。对输入变量进行归一化处理后，运动方向检测模型的响应值为[−1,1]。考虑到方向检测模型的响应较为敏感，且有噪声干扰的影响，本文对模型的响应设置有效值（u=0.4）。当响应值的绝对值大于u时，表示目标做平移运动；否则，表示目标无平移运动。
3. 仿真实验与分析
3.1 仿真实验环境及参数设置
仿真实验是在CPU/2.30GHz、内存4GB、Microsoft Windows 10操作系统运行环境下进行的。为验证多层级模型系统（MLMS）的性能，设置了多组不同场景的视频序列作为检测模型的输入，进行仿真实验和测试。MLMS新模型的主要参数设置列表1。
表 1 MLMS新模型的主要参数设置Table 1 Main parameters setting of the new MLMS model参数 含义 取值 ${n_p}$ 持续影响的帧数 [0,2] ${\tau _i}$ 连续帧之间时间间隔/ms 1000 ${s_d}$ 采样距离 4.00 ${\sigma _e},{\text{ }}{\sigma _i}$ vDoG机制中的标准方差 2,40 ${\tau _s}$ 动态延迟/ms [10,200] k Sigmoid函数中的比例系数 0.01 A 增强系数 10.00 T 阈值 15.00 3.2 实验测试与分析
实验 1 PPT生成动画视频的运动方向检测
借助Microsoft Office PowerPoint（PPT）生成4段动画视频（技术参数列于表2），对MLMS新模型做性能测试，合成的动画视频序列是在白颜色背景下黑颜色方块沿4个基本方向（上、下、左、右）移动的动画视频。黑色方块设置为运动目标，白色为背景，合成的动画中目标与背景的对比度极高，排除了杂乱背景下干扰的因素。
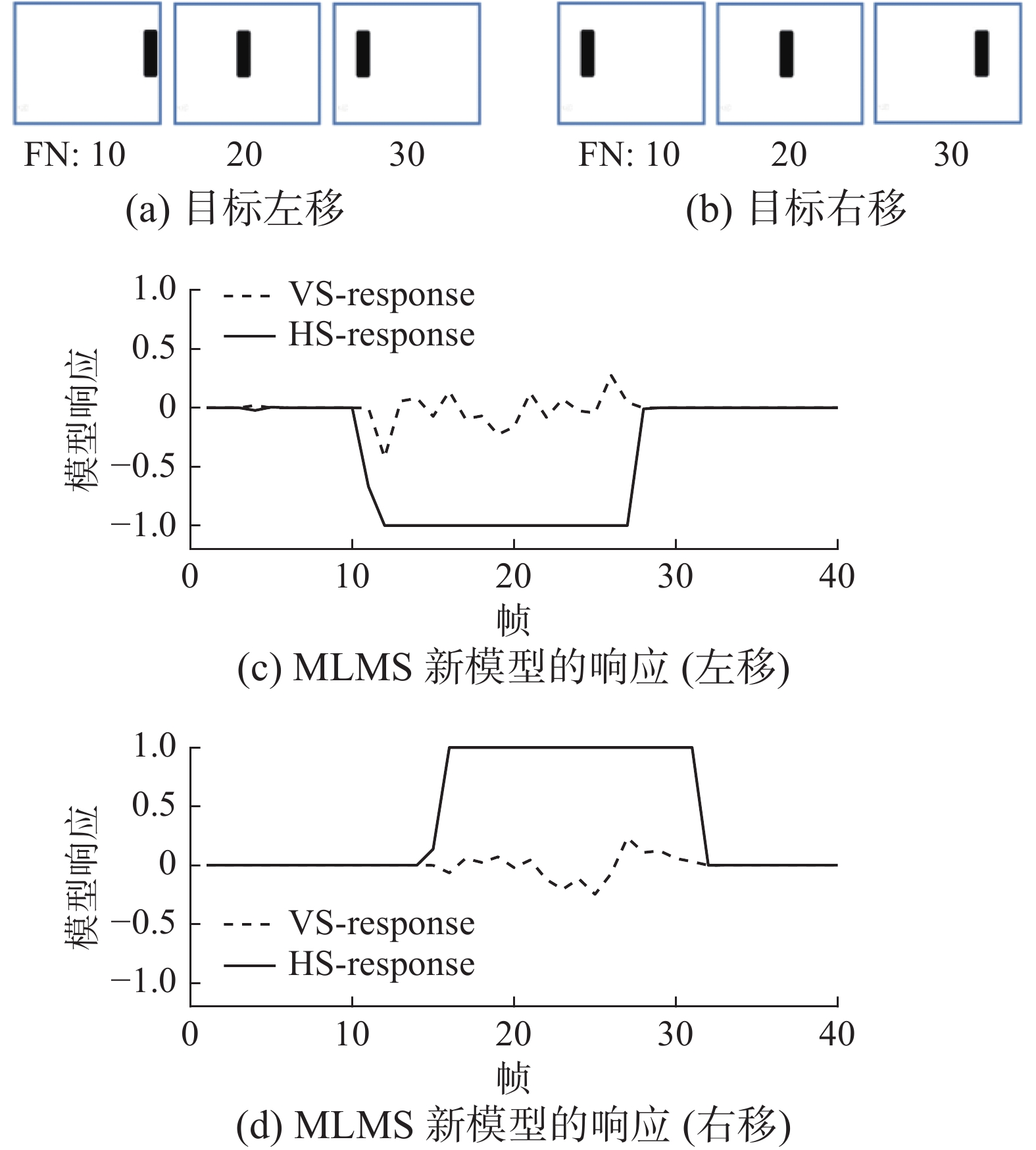
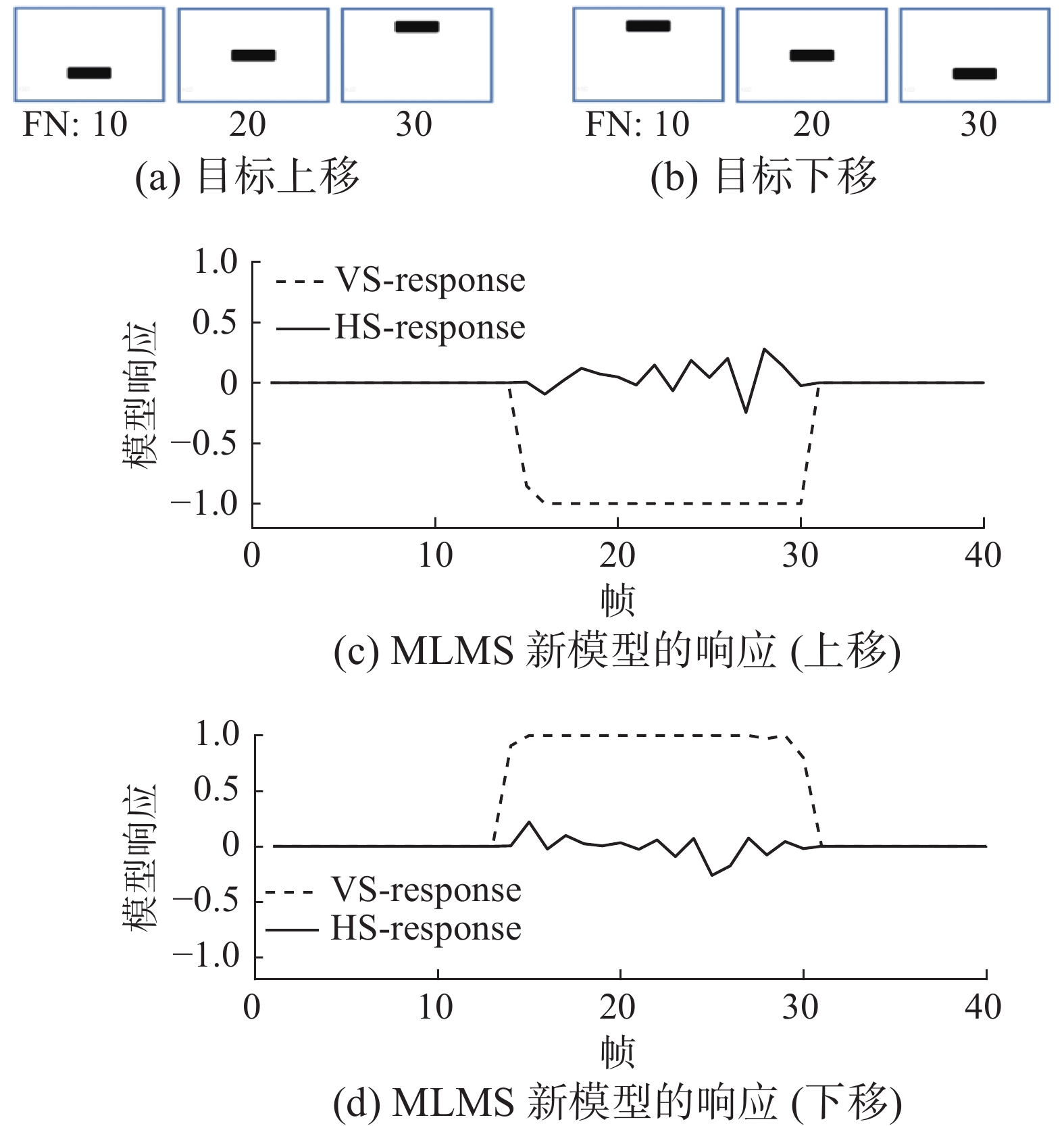
表 2 合成的4段动画视频技术参数Table 2 Technical parameters of four animated videos synthesized技术参数 动画视频/目标运动 左移 右移 上移 下移 帧速率/(f/s) 20 15 图像尺寸/(像素×像素) 1280×720 1280×720 长度/帧 40 40 图3(a)、图3(b)分别是从各自的动画视频中截取的3帧代表图像，示意了目标左移和目标右移。图4(a)、图4(b)示意了目标上移和目标下移。图4(c)、图4(d)分别是MLMS新模型与之对应目标运动方向的选择性响应曲线图，横坐标代表动画视频帧数，纵坐标代表MLMS的响应输出值，即MLMS的方向选择性响应值表示目标随帧变化的运动方向。实线代表水平敏感HS的方向响应，值为负，表示目标向左移动，值为正，表示目标向右移动。虚线代表垂直敏感VS的方向响应，值为负，表示目标向上移动，值为正，表示目标向下移动。
图 3 动画视频中目标（物体）左右运动方向检测的实验测试Fig. 3 Experimental test of target (object) left-right motion direction detection in animated video下载:
全尺寸图片
图 4 动画视频中目标（物体）上下运动方向检测的实验测试Fig. 4 Experimental test of target (object) up-down motion direction detection in animated video下载:
全尺寸图片
由动画视频的运动方向检测实验结果可看出，在简单背景（白底、黑色目标）下MLMS新模型能够准确地检测出目标运动方向，但在第10～35帧之间，非运动方向上也有微弱的响应，曲线在零值附近有小的上下波动，分析原因，是在合成的动画视频中，难以保证黑色方块（目标）的移动是绝对水平或绝对垂直所导致的，这也说明了MLMS新模型也具有显著的垂直方向敏感性。
实验 2 室内人行走动的运动方向检测
使用摄像机拍摄室内人行走动作为实验和测试视频，视频帧速率：27f/s，图像尺寸：960像素×544像素。如图5所示，图5(a)、(b)分别给出了MLMS对室内人行向右和向左运动的方向选择性响应曲线图。图5(a)中MLMS对水平敏感方向响应的实线从第10帧时开始变化且数值大于零，表示目标向右运动，这与人向右行方向相符。虚线反映垂直敏感方向响应的波动幅度较大，这是由于人右行时摆手晃动和身体高低起伏原因。人向左行走较平稳，在垂直敏感方向上几乎无响应。
图 5 室内人行走动视频、水平和垂直运动方向检测实验测试Fig. 5 Indoor pedestrian walking video and experimental test of horizontal and vertical movement direction detection下载:
全尺寸图片
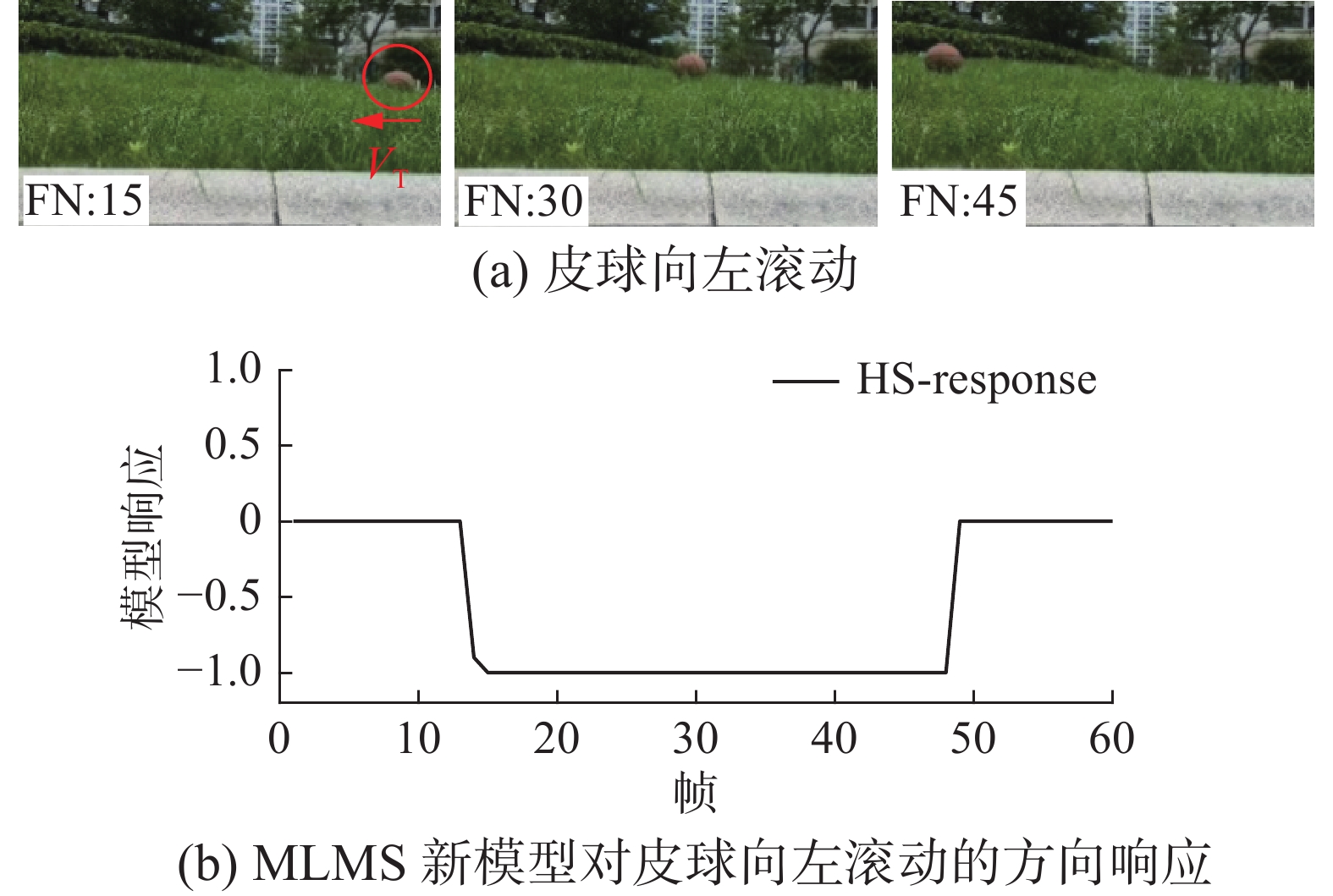
实验 3 皮球滚动方向检测
使用摄像机拍摄在路边草地上滚动的皮球。拍摄的视频帧速率为23 f/s，图像尺寸为960像素×544 像素，视频序列长度为60帧。皮球向左滚动的视频序列中分别截取第15、30和45帧代表图像示于图6(a)，箭头VT表示皮球运动方向。图6(b) 给出了MLMS新模型对皮球在水平方向向左滚动的检测结果。在第15～45帧区间，MLMS的响应输出值保持为负数，与皮球滚动方向相符，且草丛中滚动的皮球受到部分遮挡时，响应值仍然稳定。
图 6 皮球向左滚动的视频和方向检测的实验测试Fig. 6 Video of ball rolling to the left and experimental test of direction detection下载:
全尺寸图片
实验 4 杂乱背景下人行走动的运动方向检测
视频拍摄场景如图7所示，是人在树丛中向右行行走或向左走的视频，分别截取了其中4帧代表图像，箭头VT表示人行走方向。拍摄场景的树丛及地物背景较为杂乱，地面起伏不平、人行走起伏晃动、目标被树木遮挡等干扰因素。对MLMS新模型与其他3种果蝇视觉运动检测器模型，即双向EMD模型[24]、2-Q运动检测器模型[25]、文献[20]的模型进行了实验测试，不同模型计算所耗用的时间如表3所示。
图 7 杂乱视觉背景下人行走动的视频Fig. 7 Video of pedestrians walking in a chaotic visual background下载:
全尺寸图片
从表3看出，双向EMD模型和2-Q模型计算耗时较少，文献[20]的模型和MLMS新模型相比，因MLMS仅对低频子图进行处理，故计算耗时相对较少。
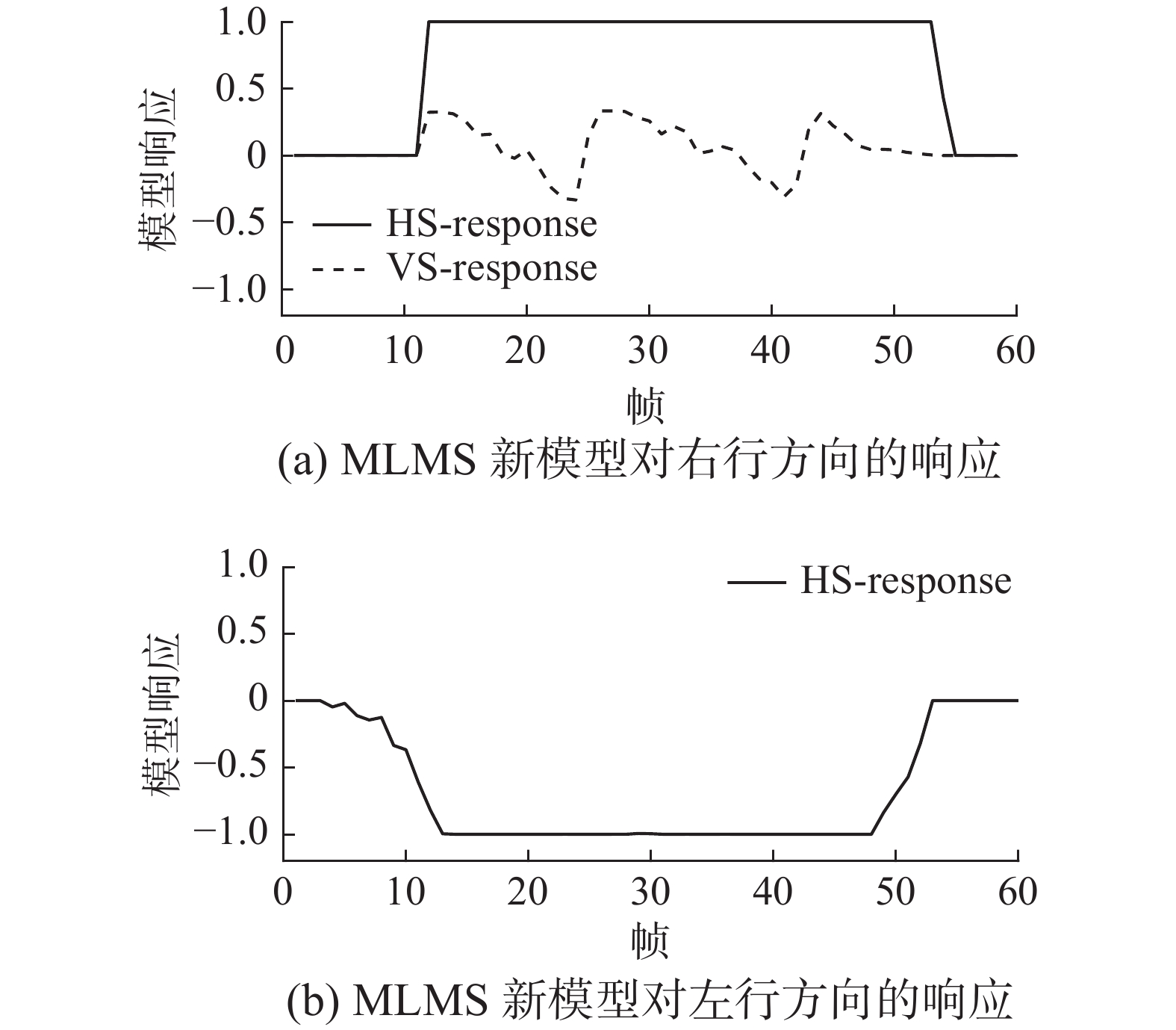
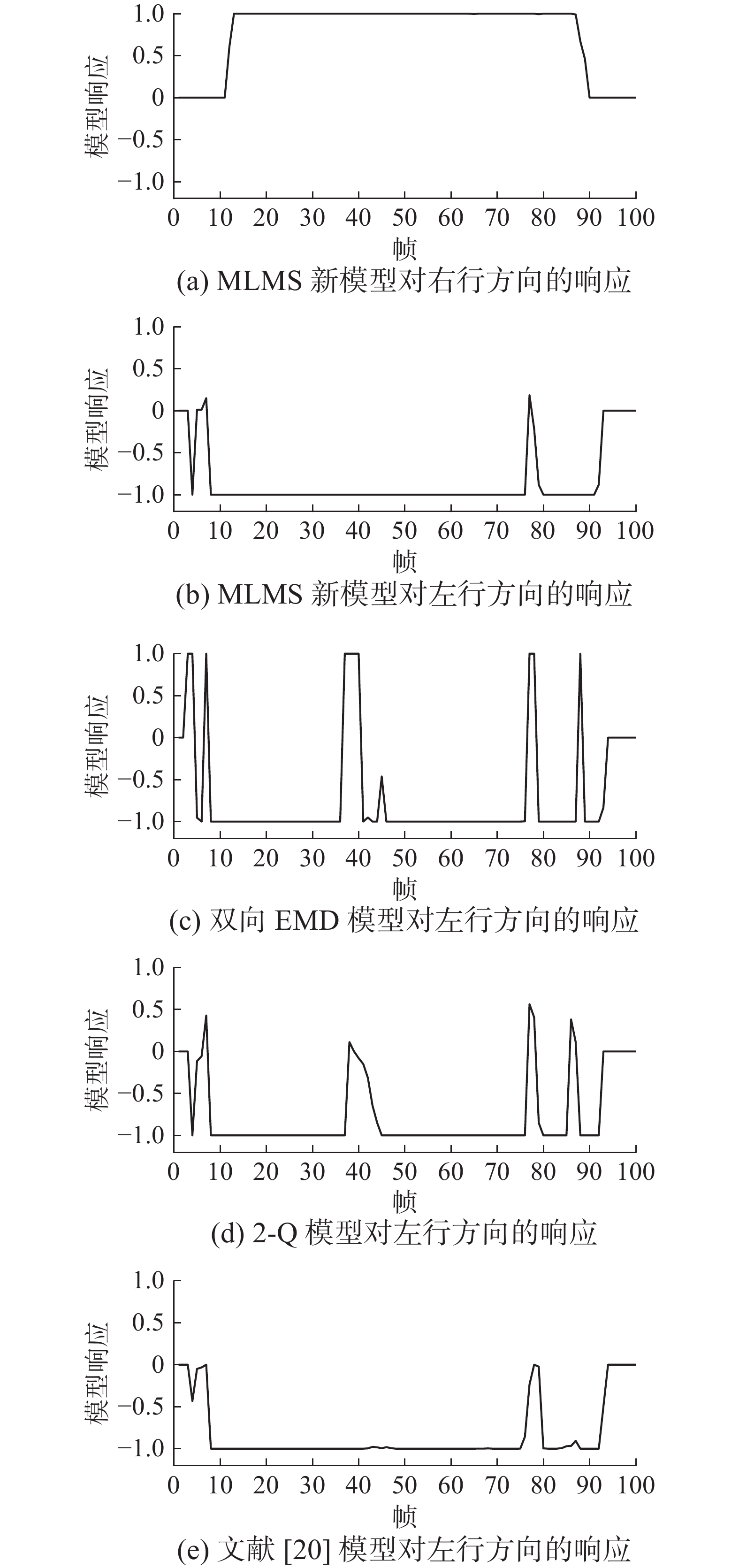
MLMS与其他3种模型的方向检测结果如图8所示。图8(a)和图8(b)曲线图分别是MLMS对人向右或向左行走方向的选择性响应输出，曲线为正值时，表示人向右走，为负值时，表示人向左走。
图 8 杂乱背景下人行走动方向检测的实验测试Fig. 8 Experimental test of pedestrian walking direction detection under chaotic background下载:
全尺寸图片
在杂乱视觉背景下，及人行走时身体晃动、人体局部被遮挡等影响，人向左行时，双向EMD模型和2-Q运动检测器模型输出的水平方向HS选择性响应值出现3次正值，即响应值大于0的情况，参见图8(c)和图8(d)，这与拍摄视频中人向左运动方向不符，其中双向EMD模型出现3次响应值达到1，2-Q模型出现3次响应值接近或小于0.6，这两种果蝇视觉运动检测器模型均存在检测出人向右运动的错误，说明其抗干扰能力较差，或者说，在杂乱背景和受干扰条件下，对于检测目标运动方向的鲁棒性差。
图8(e)是文献[20]的模型对左行方向的响应。第5～9帧区间，人正在走上小土坡，有向上的起伏晃动，第76～85帧区间，人体被树干遮挡，模型响应值出现了波动。这是在杂乱视觉背景下抗扰动方向检测出现偏差的主要原因。但文献[20]的模型响应值未超过0，而MLMS新模型出现了2次超过0.1，且小于0.3的响应值，说明文献[20]的模型略好于MLMS新模型。
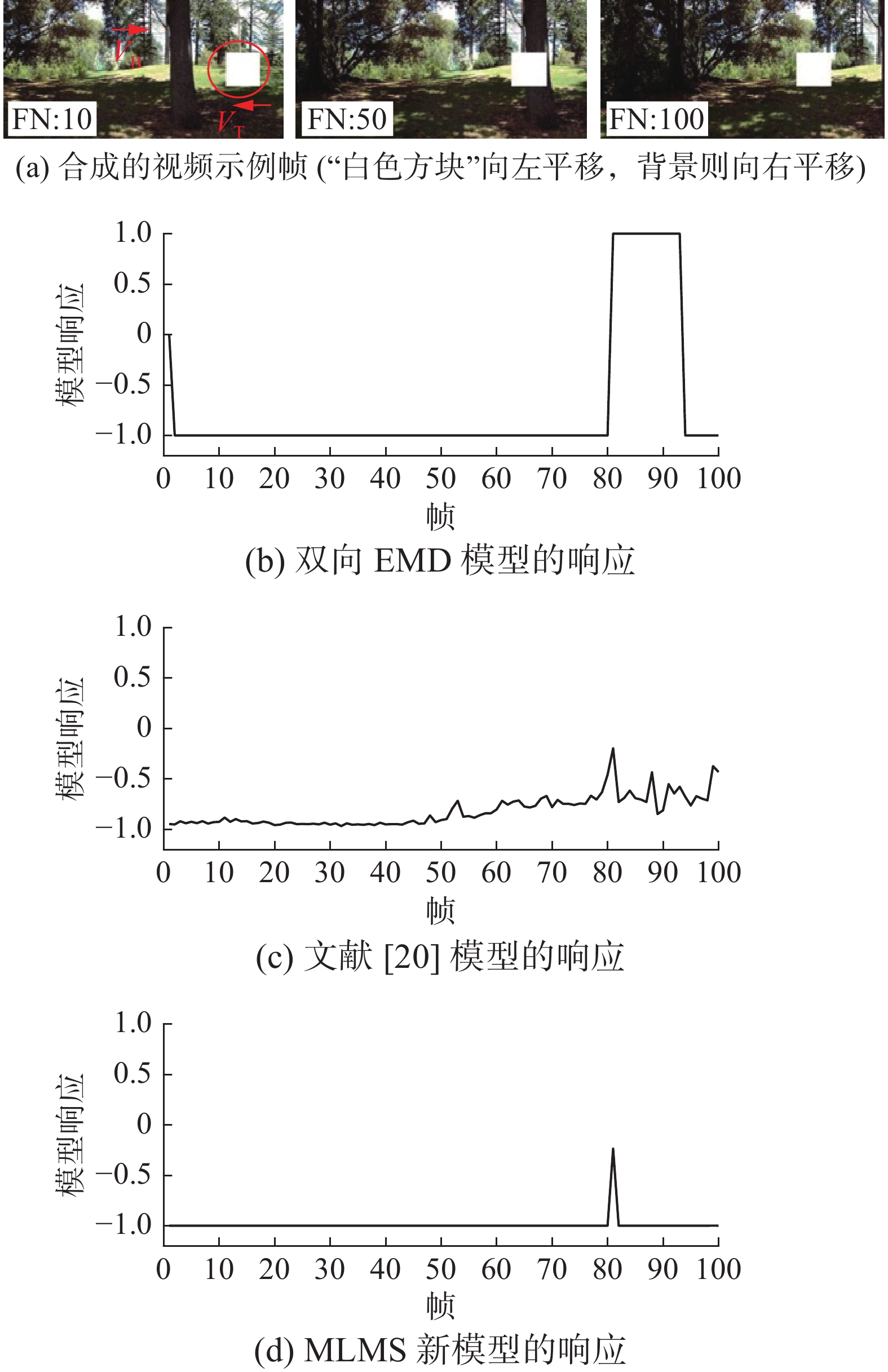
实验 5 杂乱的移动背景下目标运动方向检测
借助Vision Egg，（一款用于视觉研究与实验的程序库，它带有演示应用程序，可通过普通的计算机图形卡，及使用Egg的函数等生成实验视频）合成了动态场景下目标运动的视频，帧速率为50 f/s，图像尺寸为500像素×250像素，视频序列长度/大小为100帧。视频中设置白色方块，代表运动目标，向左平移，而背景则向右平移。目标尺寸大小为80像素×80像素，目标的运动速度为 −27(°)/s，背景的运动速度为40(°)/s（速度值为负值代表向左运动，为正值代表向右运动）。分别截取视频中3帧代表图像（分别是第10、50、100帧图像）示于图9(a)，箭头VT和VB分别表示目标和背景的运动方向。不同模型的响应输出结果分别示于图9(b)、图9(c)和图9(d)。从图9中响应曲线可看出，约在81帧附近，响应曲线会出现波动。
图 9 杂乱的移动背景下方向检测的实验测试Fig. 9 Experimental test of direction detection in a chaotic moving background下载:
全尺寸图片
4. 结束语
本文通过模拟和解析视叶结构中薄板的初级视觉滤波，ON和OFF通道的平行分解，快速去极化和慢速重极化的二次视觉滤波，髓质层T4和小叶层T5对于小视场的方向敏感信号与小叶板层LPTCs宽视场的水平敏感HS和垂直敏感VS的整合等一系列计算，所提出的MLMS新模型，经不同场景拍摄的视频序列的实验测试，验证了其在杂乱背景下目标运动方向检测具有的优良性能。
-
图 1 多层级模型系统MLMS框架
Fig. 1 Multi-level model system MLMS framework
下载:
全尺寸图片
图 2 髓质和小叶层中运动方向选择性建模
Fig. 2 Selective modeling of the motion direction in the medulla and lobule
下载:
全尺寸图片
图 3 动画视频中目标（物体）左右运动方向检测的实验测试
Fig. 3 Experimental test of target (object) left-right motion direction detection in animated video
下载:
全尺寸图片
图 4 动画视频中目标（物体）上下运动方向检测的实验测试
Fig. 4 Experimental test of target (object) up-down motion direction detection in animated video
下载:
全尺寸图片
图 5 室内人行走动视频、水平和垂直运动方向检测实验测试
Fig. 5 Indoor pedestrian walking video and experimental test of horizontal and vertical movement direction detection
下载:
全尺寸图片
图 6 皮球向左滚动的视频和方向检测的实验测试
Fig. 6 Video of ball rolling to the left and experimental test of direction detection
下载:
全尺寸图片
图 7 杂乱视觉背景下人行走动的视频
Fig. 7 Video of pedestrians walking in a chaotic visual background
下载:
全尺寸图片
图 8 杂乱背景下人行走动方向检测的实验测试
Fig. 8 Experimental test of pedestrian walking direction detection under chaotic background
下载:
全尺寸图片
图 9 杂乱的移动背景下方向检测的实验测试
Fig. 9 Experimental test of direction detection in a chaotic moving background
下载:
全尺寸图片
表 1 MLMS新模型的主要参数设置
Table 1 Main parameters setting of the new MLMS model
参数 含义 取值 ${n_p}$ 持续影响的帧数 [0,2] ${\tau _i}$ 连续帧之间时间间隔/ms 1000 ${s_d}$ 采样距离 4.00 ${\sigma _e},{\text{ }}{\sigma _i}$ vDoG机制中的标准方差 2,40 ${\tau _s}$ 动态延迟/ms [10,200] k Sigmoid函数中的比例系数 0.01 A 增强系数 10.00 T 阈值 15.00 表 2 合成的4段动画视频技术参数
Table 2 Technical parameters of four animated videos synthesized
技术参数 动画视频/目标运动 左移 右移 上移 下移 帧速率/(f/s) 20 15 图像尺寸/(像素×像素) 1280×720 1280×720 长度/帧 40 40 -
[1] 郭爱克. 探索自然智慧本质, 照亮类脑智能之路: 果蝇学习记忆与抉择的神经环路机制研究[J]. 中国科学:生命科学, 2019, 49(10): 1354–1374. GUO Aike. A cross-species review of cognitive neural circuits to illuminate the way to brain-inspired intelligence[J]. Scientia sinica (vitae), 2019, 49(10): 1354–1374. [2] PAULK A, MILLARD S S, VAN SWINDEREN B. Vision in Drosophila: seeing the world through a model’s eyes[J]. Annual review of entomology, 2013, 58: 313–332. doi: 10.1146/annurev-ento-120811-153715 [3] WINDING M, PEDIGO B D, BARNES C L, et al. The connectome of an insect brain[J]. Science, 2023, 379(6636): eadd9330. doi: 10.1126/science.add9330 [4] BORST A, HAAG J, MAUSS A S. How fly neurons compute the direction of visual motion[J]. Journal of comparative physiology A, neuroethology, sensory, neural, and behavioral physiology, 2020, 206(2): 109–124. doi: 10.1007/s00359-019-01375-9 [5] 章盛, 沈洁, 郑胜男, 等. 类果蝇复眼视觉神经计算建模及仿生应用研究综述[J]. 红外技术, 2023, 45(3): 229–240. ZHANG Sheng, SHEN Jie, ZHENG Shengnan, et al. Research review of drosophila-like compound eye visual neural computational modeling and bionic applications[J]. Infrared technology, 2023, 45(3): 229–240. [6] 徐梦溪, 施建强. 仿生复眼型多源监测数据融合与专题信息提取[J]. 水利信息化, 2021(1): 71–75. XU Mengxi, SHI Jianqiang. Bionic compound eye based multi-source monitoring data fusion and thematic information extraction[J]. Water resources informatization, 2021(1): 71–75. [7] 胡雪蕾, 高明, 陈阳. 大视场曲面仿生复眼光学系统设计[J]. 红外与激光工程, 2020, 49(1): 0114002. HU Xuelei, GAO Ming, CHEN Yang. Design of curved bionic compound eye optical system with large field of view[J]. Infrared and laser engineering, 2020, 49(1): 0114002. [8] 王申奥, 王汉熙. “人造复眼” 英文学术文献展现的学术研究整体态势[J]. 武汉理工大学学报, 2020, 42(2): 90–102. WANG Shen’ao, WANG Hanxi. Academic research situation and development direction of the “artificial compound eyes” in English academic literature[J]. Journal of Wuhan University of Technology, 2020, 42(2): 90–102. [9] FU Qinbing, WANG Hongxin, HU Cheng, et al. Towards computational models and applications of insect visual systems for motion perception: a review[J]. Artificial life, 2019, 25(3): 263–311. doi: 10.1162/artl_a_00297 [10] 黄凤辰, 李敏, 石爱业, 等. 受昆虫视觉启发的多光谱遥感影像小目标检测[J]. 通信学报, 2011, 32(9): 88–95. HUANG Fengchen, LI Min, SHI Aiye, et al. Insect visual system inspired small target detection for multi-spectral remotely sensed images[J]. Journal on communications, 2011, 32(9): 88–95. [11] JOESCH M, SCHNELL B, RAGHU S V, et al. ON and OFF pathways in Drosophila motion vision[J]. Nature, 2010, 468(7321): 300–304. doi: 10.1038/nature09545 [12] KELEŞ M F, FRYE M A. Object-detecting neurons in drosophila[J]. Current biology:CB, 2017, 27(5): 680–687. doi: 10.1016/j.cub.2017.01.012 [13] HAAG J, ARENZ A, SERBE E, et al. Complementary mechanisms create direction selectivity in the fly[J]. eLife, 2016, 5: e17421. doi: 10.7554/eLife.17421 [14] STROTHER J A, WU S T, WONG A M, et al. The emergence of directional selectivity in the visual motion pathway of drosophila[J]. Neuron, 2017, 94(1): 168–182. doi: 10.1016/j.neuron.2017.03.010 [15] FISHER Y E, LEONG J C S, SPORAR K, et al. A class of visual neurons with wide-field properties is required for local motion detection[J]. Current biology: CB, 2015, 25(24): 3178–3189. doi: 10.1016/j.cub.2015.11.018 [16] EICHNER H, JOESCH M, SCHNELL B, et al. Internal structure of the fly elementary motion detector[J]. Neuron, 2011, 70(6): 1155–1164. doi: 10.1016/j.neuron.2011.03.028 [17] HENNIG P, EGELHAAF M. Neuronal encoding of object and distance information: a model simulation study on naturalistic optic flow processing[J]. Frontiers in neural circuits, 2012, 6: 14. [18] WIEDERMAN S D, O’CARROLL D C. Biologically inspired feature detection using cascaded correlations of off and on channels[J]. Journal of artificial intelligence and soft computing research, 2013, 3(1): 5–14. doi: 10.2478/jaiscr-2014-0001 [19] YUE Shigang, FU Qinbing. Modeling direction selective visual neural network with ON and OFF pathways for extracting motion cues from cluttered background[C]//2017 International Joint Conference on Neural Networks. Anchorage: IEEE, 2017: 831−838. [20] FU Qinbing, YUE Shigang. Modelling Drosophila motion vision pathways for decoding the direction of translating objects against cluttered moving backgrounds[J]. Biological cybernetics, 2020, 114(4/5): 443–460. [21] 李柯, 沈克永, 刘宝, 等. 模拟飞虫复眼视觉的小目标运动检测与跟踪系统研究[J]. 图像与信号处理, 2022, 11(3): 92–100. doi: 10.12677/JISP.2022.113011 LI Ke, SHEN Keyong, LIU Bao, et al. Research on moving small target detection and tracking system of simulated flying insect compound eye vision[J]. Journal of image and signal processing, 2022, 11(3): 92–100. doi: 10.12677/JISP.2022.113011 [22] 施建强, 徐扬, 徐梦溪, 等. 一种用于感知目标运动方向的人工苍蝇视觉神经网络模型[C]// 2021年中国仪器仪表学会学术年会. 上海: 中国仪器仪表学会, 2021: 1−4. SHI Jianqiang, XU Yang, XU Mmengxi, et al. An artificial neural network model simulating fly vision for sensing target motion direction[C]//2021 Annual Conference of China Instrument and Control Society. Shanghai: China Instrument and Control Society, 2021: 1−4. [23] SHEN Keyong, YANG Yang, LIANG Yuying, et al. Modeling Drosophila vision neural pathways to detect weak moving targets from cluttered backgrounds[J]. Computers and electrical engineering, 2022, 99: 107678. doi: 10.1016/j.compeleceng.2021.107678 [24] BORST A, EGELHAAF M. Principles of visual motion detection[J]. Trends in neurosciences, 1989, 12(8): 297–306. doi: 10.1016/0166-2236(89)90010-6 [25] FRANCESCHINI N, RIEHLE A, LE NESTOUR A. Directionally selective motion detection by insect neurons[C]//Facets of Vision. Heidelberg: Springer, 1989: 360−390.
