Influence of spacecraft flexibility on imaging area in space remote sensing
-
摘要: 针对遥感敏捷卫星机动模式对地成像观测，分析挠性附件振动对卫星成像区域和质量的影响。首先利用有限元法和拉格朗日法建立带挠性附卫星的动力学模型；然后通过星地几何法计算成像条带；最后分别选取太阳同步轨道和地球同步轨道，以两个对称的太阳能帆板作为挠性附件，给出数值仿真结果。仿真结果表明，卫星机动完成后，成像区域横滚方向与俯仰方向均偏差较大，导致成像区域错位；太阳帆板振动对成像区域的影响随着其振动减弱而减弱，并逐渐趋于稳定。卫星轨道高度越高，扰动对于卫星成像区域的影响越大，需要更长时间稳定自身姿态。Abstract: Aiming at the earth imaging observation of remote sensing agile satellite maneuvering mode, the influence of flexible accessory vibration on satellite imaging area and quality is analyzed in this paper. Firstly, the dynamics model of satellite with flexible appendage is established by using finite element method and Lagrange method; Then, the imaging strip is calculated by satellite earth geometry method; Finally, the numerical simulation results are derived by selecting the sun-synchronous orbit and geostationary orbit as examples, and using two symmetrical solar panels as flexible accessories. The simulation results show that after the satellite maneuver is completed, the deviation between the roll direction and the pitch direction of the imaging area is large, resulting in dislocation of the imaging area; The influence of solar panel vibration on the imaging area decreases with the weakening of its vibration, and tends to stability gradually. The higher the altitude of satellite orbit, the greater the impact of disturbance on the satellite imaging area, which takes longer time to stabilize the attitude.
-
天基遥感因其具有观测覆盖范围广、波段多、全天时和全天候获取全球观测数据的独特优势，在自然灾害监测、评估与预警等领域得到广泛地研究与应用[1-4]。近年来，随着光学遥感相机分辨率的不断提升，成像条带变窄，遥感卫星应用模式由被动推扫模式向主动机动成像模式方向发展[5]。该机动成像模式利用敏捷卫星的高姿态机动特性，快速指向多个重点成像区域，对其实施更高效和更精细化的成像观测[6-8]。为了实现快速机动成像，往往需要敏捷卫星以大角度和高角速度进行姿态机动，这将激发挠性附件的强烈动态响应[9]，并对成像区域和质量产生影响，尤其对于高轨敏捷卫星，影响更为显著。因此，研究大角度和高角速度机动下挠性附件对卫星成像区域和质量的影响具有重要价值。
目前国内外学者针对挠性航天器研究主要集中在姿态控制挠性附件的力学参数辨识方面，文献[10-11]分别对姿态控制与挠性附件的力学参数辨识进行了详细的文献综述，仅有少量文献研究航天器姿态对成像区域和质量的影响。贾桂敏[12]提出了三轴姿态变化时三线阵CCD相机成像像移数学模型，研究了姿态变化对成像像移的影响。周伟敏[13]建立了完备像移模型并提出了一种路径规划以减弱挠性附件振动对像移的影响。尉文龙[14]研究了卫星势能和地球引力的共同作用所产生的摆动现象对CCD相机的成像效果影响。吴亮等[15]分析了在不同视角下偏航、俯仰、横滚3个方向的姿态误差对SAR成像质量产生的影响。张普中[16]研究了带挠性附件卫星平台振动对成像性能的影响。
上述的研究并未涉及和分析敏捷卫星机动模式下挠性附件对成像区域和质量的影响，而该模式为实际工程发展的主要应用模式。
针对以上问题以及工程发展的需求，本文以敏捷卫星为研究对象，分别建立挠性附件的有限元模型和带挠性附件卫星刚柔耦合动力学模型，分析机动后挠性附件对成像区域和质量产生影响。
1. 挠性附件有限元模型
本节采用有限元法中的模态叠加法建立挠性附件的动力学方程。考虑到航天器的挠性附件多为薄板结构，例如大型太阳能帆板。因此，本文假设挠性附件为薄板结构，采用4节点四边形单元对其进行离散。每个节点为3个自由度，分别为扰度
$\varOmega $ ，绕x轴转角$ {\theta _x} $ 和绕y轴转角${\theta _y}$ ，单元节点位移可表示为$$ {{\boldsymbol{u}}^{\text{e}}} = {\left[ {{w_1}\,\,{\theta _{x1}}\,\,{\theta _{y1}} \cdots {w_4}\,\,{\theta _{x4}}\,\,{\theta _{y4}}} \right]^{\text{T}}}\, $$ 式中
${{\boldsymbol{u}}^{\text{e}}}$ 为单元节点位移向量。利用形函数插值，单元内一点位移可表示为
$$ w = {\boldsymbol{N}}{{\boldsymbol{u}}^{\text{e}}} $$ 式中：
${\boldsymbol{N}} = \left[ {{{\boldsymbol{N}}_i}}\;\;{{{\boldsymbol{N}}_j}}\;\;{{{\boldsymbol{N}}_l}}\;\;{{{\boldsymbol{N}}_m}} \right]$ 为形函数矩阵，${{\boldsymbol{N}}_i}$ 、${{\boldsymbol{N}}_j}$ 、${{\boldsymbol{N}}_l}$ 和${{\boldsymbol{N}}_m}$ 的具体表示式为$$ \begin{gathered} {{\boldsymbol{N}}_i} =\\ \frac{{{X_1}{Y_1}}}{{16}}[ {{X_1}{Y_1} - {X_2}{Y_2} + 2{X_1}{X_2} + 2{Y_1}{Y_2}}\;\;{2b{Y_1}{Y_2}} - 2a{X_1}{X_2}] \\ {{\boldsymbol{N}}_j} =\\ \frac{{{X_2}Y}}{{16}}[ {{X_2}{Y_1} - {X_1}{Y_2} + 2{X_1}{X_2} + 2{Y_1}{Y_2}}\;\;{2b{Y_1}{Y_2}} 2a{X_1}{X_2}] \\ {{\boldsymbol{N}}_l} =\\ \frac{{{X_2}{Y_2}}}{{16}}[ {{X_2}{Y_2} - {X_1}{Y_1} + 2{X_1}{X_2} + 2{Y_1}{Y_2}}\;\;{ - 2b{Y_1}{Y_2}} 2a{X_1}{X_2}] \\ {{\boldsymbol{N}}_m} = \\ \frac{1}{{16}}{X_1}{Y_2}[ {{X_1}{Y_2} - {X_2}{Y_1} + 2{X_1}{X_2} + 2{Y_1}{Y_2}}\;\;{ - 2b{Y_1}{Y_2}} - 2a{X_1}{X_2}] \end{gathered} $$ 其中
${X_1}$ 、${X_2}$ 、${Y_1}$ 和${Y_2}$ 为中间标量，其具体表达式为$$ \begin{gathered} {X_1} = 1 - \frac{\tau }{a} \\ {X_2} = 1 + \frac{\tau }{a} \\ {Y_1} = 1 - \frac{\upsilon }{b} \\ {Y_2} = 1 + \frac{\upsilon }{b} \end{gathered} $$ 其中
$\tau $ 和$\upsilon $ 分别表示单元坐标系。利用一般有限元法可得挠性附件单元的动力学平衡方程为
$$ {{\boldsymbol{M}}^{\text{e}}}{{\boldsymbol{\ddot u}}^{\text{e}}}(t) + {{\boldsymbol{K}}^{\text{e}}}{{\boldsymbol{u}}^{\text{e}}}(t) = {{\boldsymbol{f}}^{\text{e}}}(t) $$ 式中：
$ {{\boldsymbol{u}}^{\text{e}}}(t) $ 为单元节点位移向量；$ {{\boldsymbol{f}}^{\text{e}}}(t) $ 为单元节点外载荷向量；$ {{\boldsymbol{M}}^{\text{e}}} $ 和$ {{\boldsymbol{K}}^{\text{e}}} $ 分别为挠性附件单元质量阵和刚度阵，其具体表达式为$$ \begin{gathered} {{\boldsymbol{M}}^{\text{e}}} = {\int_{{{{V}}_{\text{e}}}} {\rho {\boldsymbol{N}}} ^{\text{T}}}{\boldsymbol{N}}{\text{d}}V \\ {{\boldsymbol{K}}^{\text{e}}} = {\int_{{{{V}}_{\rm{e}}}} {\boldsymbol{B}} ^{\text{T}}}{\boldsymbol{DB}}{\text{d}}V \\ \end{gathered} $$ 式中：
$\rho $ 为密度；${\boldsymbol{D}}$ 为弹性矩阵；${\boldsymbol{B}}$ 为形函数矩阵的导数阵。通过组装所有单元矩阵并消除固定自由度，可得到挠性附件的动力学平衡方程为[17]
$$ {\boldsymbol{M\ddot u}}(t) + {\boldsymbol{Ku}}(t) = {\boldsymbol{f}}(t) $$ (1) 式中：M和K分别结构的质量阵和刚度阵；u
$ (t) $ 和f$ (t) $ 分别为节点位移向量和载荷向量。对式（1）求解其广义特征值问题，得到特征值
${\varOmega _i}$ 和特征向量$ {{\boldsymbol{\varPhi}} _i} $ ，引入系统阻尼矩阵，并将其转化为模态坐标描述下的振动平衡方程为[13]$$ {\boldsymbol{\ddot \eta }}(t) + {{\boldsymbol{C}}_{\eta}}{\boldsymbol{\dot \eta }}(t) + {\boldsymbol{\varOmega \eta }}(t) = {\boldsymbol{Q}} $$ (2) 式中：
${\boldsymbol{\eta }}(t) = {\left[ {{\eta _1}(t)}\;\;{{\eta _2}(t)}\;\; \cdots \;\;{{\eta _n}(t)} \right]^{\text{T}}}$ 为模态坐标向量；${\boldsymbol{\varPhi }} = \left[ {{\varPhi _1}}\;\;{{\varPhi _2}}\;\;\cdots \;\;{{\varPhi _n}} \right]$ 为模态矩阵；${\boldsymbol{\varOmega }} = {\text{diag}}[ {\varOmega _1^2}\;\;{\varOmega _2^2}\;\; \cdots {\varOmega _n^2} ]$ ；$ {\boldsymbol{Q}} = {{\boldsymbol{\varPhi }}^{\text{T}}}{\boldsymbol{f}}(t) $ 为广义力向量；${{\boldsymbol{C}}_\eta } = {\text{diag}}[ {2{\varOmega _1}{\xi _1}}\;\; {2{\varOmega _2}{\xi _2}}\cdots {2{\varOmega _n}{\xi _n}} ]$ ，${\xi _i}$ 为结构阻尼比；n为模态阶数。式(2)为互相不耦合的二阶微分方程组，对其进行求解，并利用模态叠加法，可得到每个节点的位移响应为
$$ {\boldsymbol{u}}(t) = \sum\limits_{i = 1}^n {{\eta _i}} (t){{\boldsymbol{\varPhi}} _i} $$ 2. 带挠性附件卫星刚柔耦合动力学模型
本节综合考虑带挠性附件卫星平动和转动建立其刚柔耦合动力学模型。首先定义建模过程中的坐标系，采用四元数法描述卫星姿态[18]；然后推导出系统的动能和势能；最后利用拉格朗日法建立其动力学模型[19]。
2.1 坐标系定义
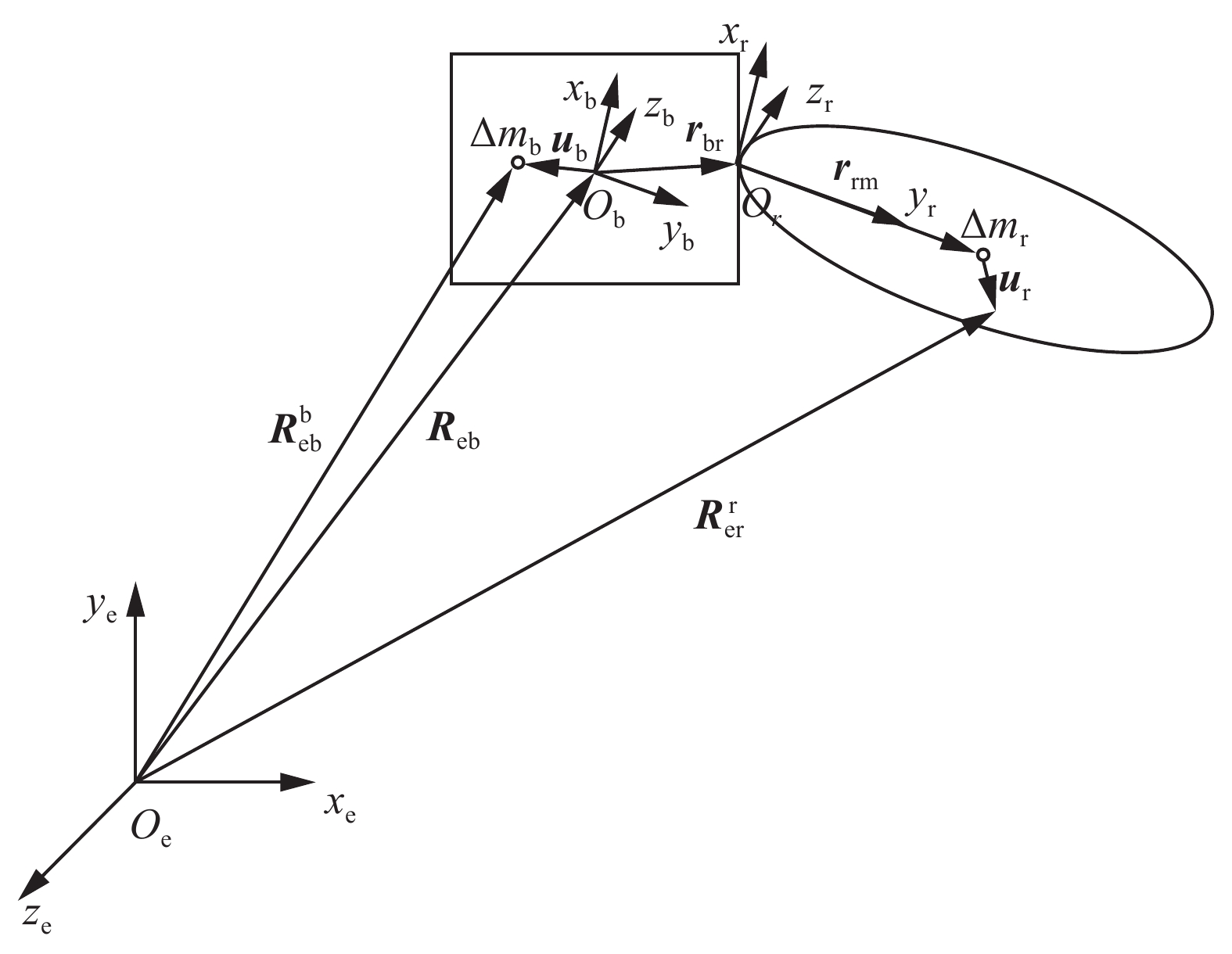
带挠性附件的卫星可简化为中心刚体加挠性附件结构，如图1所示。为了方便描述和分析，定义
${o_{\text{e}}}{x_{\text{e}}}{y_{\text{e}}}{z_{\text{e}}}$ 为地心惯性坐标系。${o_{\text{f}}}{x_{\text{f}}}{y_{\text{f}}}{z_{\text{f}}}$ 为附件坐标系，坐标原点${o_{\text{f}}}$ 位于挠性附件与中心刚体的连接点，${x_{\text{f}}}$ 轴和${y_{\text{f}}}$ 轴平行挠性附件平面，${y_{\text{f}}}$ 沿着挠性附件轴向方向，${z_{\text{f}}}$ 按右手定则定义。${o_{\text{b}}}{x_{\text{b}}}{y_{\text{b}}}{z_{\text{b}}}$ 为卫星体坐标系，坐标原点${o_{\text{b}}}$ 位于卫星的质心，${x_{\text{b}}}$ 轴、${y_{\text{b}}}$ 轴和${z_{\text{e}}}$ 轴分别与附件坐标系轴方向一致。
图 1 带挠性附件卫星简化模型Fig. 1 Simplified model of satellite with flexible appendix
下载:
全尺寸图片
2.2 带挠性附件卫星的动力学建模
本节分别推导出刚体运动和挠性附件运动的动能和势能，利用拉格朗日法建立带挠性附件卫星的刚柔耦合动力学模型。
如图1所示，设
$\Delta {m_{\text{b}}}$ 为卫星本体上任意质量单元，${{\boldsymbol{u}}_{\text{b}}}$ 为卫星本体坐标系描述下坐标原点到质量单元向量，${\boldsymbol{R}}_{{\text{em}}}^{\text{b}}$ 为卫星本体质量单元在惯性坐标系下的位移向量。${{\boldsymbol{R}}_{{\text{eb}}}}$ 为惯性坐标系描述下惯性坐标系原点指向卫星本体坐标系原点向量。$\Delta {m_{\text{r}}}$ 为挠性附件上任意质量单元，${{\boldsymbol{u}}_{\text{r}}}$ 为挠性附件质量单元的位移向量，${{\boldsymbol{r}}_{{\text{rm}}}}$ 为挠性坐标系原点指向质量单元向量，${{\boldsymbol{r}}_{{\text{br}}}}$ 为卫星本体坐标系原点指向挠性附件坐标系原点向量，${\boldsymbol{R}}_{{\text{em}}}^{\text{r}}$ 为挠性附件上质量单元在惯性坐标系下的位移向量。${{\boldsymbol{u}}_{\text{r}}}$ 、${{\boldsymbol{r}}_{{\text{rm}}}}$ 和${{\boldsymbol{r}}_{{\text{br}}}}$ 均在挠性附件坐标系下描述。根据图1中的描述，在惯性坐标系下卫星本体和挠性附件质量单元位移向量可表示为[20]
$$ {\boldsymbol{R}}_{{\text{em}}}^{\text{b}} = {{\boldsymbol{R}}_{{\text{eb}}}} + {\boldsymbol{A}}({\boldsymbol{q}}){{\boldsymbol{u}}_{\text{b}}} $$ $$ {\boldsymbol{R}}_{{\text{em}}}^{\text{r}} = {{\boldsymbol{R}}_{{\text{eb}}}} + {\boldsymbol{A}}({\boldsymbol{q}})({{\boldsymbol{r}}_{{\text{br}}}} + {{\boldsymbol{r}}_{{\text{rm}}}} + {{\boldsymbol{u}}_{\text{r}}}) $$ (3) 式中
$ {\boldsymbol{A}}({\boldsymbol{q}}) $ 为卫星本体坐标系和挠性附件坐标系到惯性坐标系的旋转矩阵，具体表达式为[21]$$\begin{gathered} {\boldsymbol{A}}({\boldsymbol{q}}) = \\ \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2}&{2({q_1}{q_2} - {q_0}{q_3})}&{2({q_1}{q_3} + {q_0}{q_2})} \\ {2({q_1}{q_2} + {q_0}{q_3})}&{q_0^2 - q_1^2 + q_2^2 - q_3^2}&{2({q_2}{q_3} - {q_0}{q_1})} \\ {2({q_1}{q_3} - {q_0}{q_2})}&{2({q_2}{q_3} + {q_0}{q_1})}&{q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right] \end{gathered}$$ 其中
${\boldsymbol{q}} = {[ {{q_0}}\;\;{{q_1}}\;\;{{q_2}}\;\;{{q_3}} ]^{\text{T}}}$ 为单位四元数。令
${{\boldsymbol{r}}_{\text{d}}} = {{\boldsymbol{r}}_{{\text{br}}}} + {{\boldsymbol{r}}_{{\text{rm}}}} + {{\boldsymbol{u}}_{\text{r}}}$ ，式(3)可重写为$$ {\boldsymbol{R}}_{{\text{em}}}^{\text{r}} = {{\boldsymbol{R}}_{{\text{eb}}}} + {\boldsymbol{A}}({\boldsymbol{q}}){{\boldsymbol{r}}_{\text{d}}} $$ 卫星本体和挠性附件质量单元速度向量可分别表示为
$$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{b}} = {{\boldsymbol{\dot R}}_{{\text{eb}}}} + {\boldsymbol{A}}({\boldsymbol{q}}){\boldsymbol{\tilde \varOmega }}{{\boldsymbol{u}}_{\text{b}}} $$ (4) $$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{r}} = {{\boldsymbol{\dot R}}_{{\text{eb}}}} + {\boldsymbol{A}}({\boldsymbol{q}}){\boldsymbol{\tilde \varOmega }}{{\boldsymbol{r}}_{\text{d}}} + {\boldsymbol{A}}({\boldsymbol{q}}){{\boldsymbol{\dot r}}_{\text{d}}} $$ (5) 式中：
$ {\boldsymbol{\tilde \varOmega }} $ 为角速度反对称矩阵，其表达式为$$ {\boldsymbol{\tilde \varOmega }} = \left[ {\begin{array}{*{20}{c}} 0&{ - {\varOmega _3}}&{{\varOmega _2}} \\ {{\varOmega _3}}&0&{ - {\varOmega _1}} \\ { - {\varOmega _2}}&{{\varOmega _1}}&0 \end{array}} \right] $$ 根据反对称阵乘法性质，并令
${\boldsymbol{\varOmega }} = 2{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}}$ ，式(4)和式(5)可分别表示为[22]$$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{b}} = {{\boldsymbol{\dot R}}_{{\text{eb}}}} - 2{\boldsymbol{A}}({\boldsymbol{q}}){{\boldsymbol{\tilde u}}_{\text{b}}}{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}} $$ (6) $$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{r}} = {{\boldsymbol{\dot R}}_{{\text{eb}}}} - 2{\boldsymbol{A}}({\boldsymbol{q}}){{\boldsymbol{\tilde r}}_{\text{d}}}{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}} + {\boldsymbol{A}}({\boldsymbol{q}}){\boldsymbol{eN}}{{\boldsymbol{P}}_i}{\boldsymbol{S\varPhi \dot \eta }} $$ (7) 式中：
$ {{\boldsymbol{\tilde u}}_{\text{b}}} $ 和$ {{\boldsymbol{\tilde r}}_{\text{d}}} $ 分别为向量${{\boldsymbol{u}}_{\text{b}}}$ 和${{\boldsymbol{r}}_{\text{d}}}$ 反对称矩阵；${\boldsymbol{\varOmega }} = {\left[ {{\varOmega _1}}\;\;{{\varOmega _2}}\;\;{{\varOmega _3}} \right]^{\text{T}}}$ 为角速度向量；${\boldsymbol{S}}$ 为扩维矩阵；${{\boldsymbol{P}}_i}$ 为第i个单元的单元联系矩阵；${\boldsymbol{e}}$ 为列阵，若仅考虑挠度位移${\boldsymbol{e}} = {\left[ 0\;\;0\;\;1 \right]^{\text{T}}}$ ；${\boldsymbol{L}}({\boldsymbol{q}})$ 的具体表达式为$$ {\boldsymbol{L}}({\boldsymbol{q}}) = \left[ {\begin{array}{*{20}{c}} { - {q_1}}&{{q_0}}&{{q_3}}&{ - {q_2}} \\ { - {q_2}}&{ - {q_3}}&{{q_0}}&{{q_1}} \\ { - {q_3}}&{{q_2}}&{ - {q_1}}&{{q_0}} \end{array}} \right] $$ 将式(6)和式(7)写成矩阵形式为
$$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{b}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{3 \times 3}}}&{ - 2{\boldsymbol{A}}({\boldsymbol{q}}){{{\boldsymbol{\tilde u}}}_{\text{b}}}{\boldsymbol{L}}({\boldsymbol{q}})}&{\boldsymbol{0}} \end{array}} \right]{\boldsymbol{\dot a}} $$ (8) $$ {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{r}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{3 \times 3}}}&{ - 2{\boldsymbol{A}}({\boldsymbol{q}}){{{\boldsymbol{\tilde u}}}_{\text{b}}}{\boldsymbol{L}}({\boldsymbol{q}})}&{{\boldsymbol{A}}({\boldsymbol{q}}){\boldsymbol{eN}}{{\boldsymbol{P}}_i}{\boldsymbol{S\varPhi }}} \end{array}} \right]{\boldsymbol{\dot a}} $$ 式中：
$ {{\boldsymbol{I}}_{3 \times 3}} $ 代表维度为3的单位阵；${\boldsymbol{\dot a}} = \left[ {{{{\boldsymbol{\dot R}}}_{{\text{eb}}}}}\;\;{{\boldsymbol{\dot q}}}\;\;{{\boldsymbol{\dot \eta }}} \right]$ ，由于卫星本体为刚体，对于式(8)$ {\boldsymbol{\dot \eta }} $ 为0向量。假设卫星本体关于其本体坐标系原点对称，卫星本体和挠性附件的动能分别可表示为
$$ \begin{gathered} {T_{\rm{b}}} = \int_{\rm{b}} {({\boldsymbol{\dot R}}_{{\text{em}}}^{\rm{b}}} {)^{\text{T}}}{\boldsymbol{\dot R}}_{{\text{em}}}^{\rm{b}}{\text{d}}{m_{\text{b}}} =\\ \frac{1}{2}{\boldsymbol{\dot R}}_{{\text{em}}}^{\text{T}}{{\boldsymbol{M}}_{\text{b}}}{\boldsymbol{\dot R}}_{{\text{em}}}^{} + 2{{{\boldsymbol{\dot q}}}^{\text{T}}}{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}}){{\boldsymbol{J}}_{\text{b}}}{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}} \end{gathered} $$ $$ \begin{gathered} {T_r} = \sum {T_{\text{r}}^{\text{e}}} = \int_b {({\boldsymbol{\dot R}}_{{\text{em}}}^{\text{r}}} {)^{\text{T}}}{\boldsymbol{\dot R}}_{{\text{em}}}^{\text{r}}{\text{d}}{m_{\text{r}}} =\\ \frac{1}{2}{\boldsymbol{\dot R}}_{{\text{em}}}^{\text{T}}{{\boldsymbol{M}}_{\text{r}}}{\boldsymbol{\dot R}}_{{\text{em}}}^{} + 2{{{\boldsymbol{\dot q}}}^{\text{T}}}{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}}){{\boldsymbol{J}}_{\text{r}}}{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}} + \frac{1}{2}{{{\boldsymbol{\dot \eta }}}^{\text{T}}}{{\boldsymbol{M}}_{\eta}}{\boldsymbol{\dot \eta }} - \\ 2{\boldsymbol{\dot R}}_{{\text{em}}}^{\text{T}}{\boldsymbol{A}}{{\boldsymbol{H}}_1}{\boldsymbol{L}}({\boldsymbol{q}}){\boldsymbol{\dot q}} + {\boldsymbol{\dot R}}_{{\text{em}}}^{\text{T}}{\boldsymbol{A}}{{\boldsymbol{H}}_2}{\boldsymbol{\dot \eta }} + 2{{{\boldsymbol{\dot q}}}^{\text{T}}}{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}}){{\boldsymbol{H}}_3}{\boldsymbol{\dot \eta }} \end{gathered} $$ 式中：
${{\boldsymbol{M}}_{\text{b}}} = {\text{diag}}\left[ {{m_{\text{b}}}}\;\;{{m_{\text{b}}}}\;\;{{m_{\text{b}}}} \right]$ 为卫星本体的质量对角阵；${{\boldsymbol{M}}_{\text{r}}} = {\text{diag}}\left[ {{m_{\text{r}}}}\;\;{{m_{\text{r}}}}\;\;{{m_{\text{r}}}} \right]$ 为挠性附件的质量对角阵；${m_{\rm{b}}}$ 和${m_{\rm{r}}}$ 分别为卫星本体和挠性附件质量；${{\boldsymbol{J}}_{\rm{b}}}$ 和${{\boldsymbol{J}}_{\rm{r}}}$ 分别为卫星本体和挠性附件的转动惯量矩阵；${{\boldsymbol{H}}_1} = \sum {\int_{\text{e}} {{{{\boldsymbol{\tilde r}}}_{\text{d}}}} } {\text{d}}m$ ；${{\boldsymbol{H}}_2} = {\boldsymbol{e}}\sum {(\int_{\text{e}} {\boldsymbol{N}} } {\text{d}}m{{\boldsymbol{P}}_i}){\boldsymbol{S\varPhi }}$ ；${{\boldsymbol{H}}_3} = \sum {(\int_{\text{e}} {{{{\boldsymbol{\tilde r}}}_{\text{d}}}^{\text{T}}{\boldsymbol{eN}}} } {\text{d}}m{{\boldsymbol{P}}_i}) {\boldsymbol{S\varPhi }}$ ；${{\boldsymbol{M}}_{\eta}} = {{\boldsymbol{I}}_{n \times n}}$ 。卫星整体系统的动能可表示为卫星本体和挠性附件的动能之和:
$$ T = {T_{\text{b}}} + {T_{\text{r}}} $$ (9) 系统势能为挠性附件的弹性势能，其表达式为
$$ U = \frac{1}{2}{{\boldsymbol{\eta }}^{\text{T}}}{\boldsymbol{\varOmega \eta }} $$ (10) 将系统动能式(9)和系统势能式(10)代入第一类拉格朗日方程可得到带挠性附件卫星的动力学方程为[23]
$$ \begin{gathered} {{\boldsymbol{M}}_{\text{t}}}{\boldsymbol{\ddot a}} + {\boldsymbol{V\dot a}} + \frac{{\partial U}}{{\partial {\boldsymbol{a}}}} + {\left(\frac{{\partial \psi }}{{\partial {\boldsymbol{a}}}}\right)^{\text{T}}}\lambda = {\boldsymbol{Q}} \\ \psi = 0 \end{gathered} $$ (11) 式中：
${\boldsymbol{V}} = \dfrac{{\partial ({{\boldsymbol{M}}_{\text{t}}}{\boldsymbol{\dot a}})}}{{\partial {\boldsymbol{a}}}} - \dfrac{1}{2}{\left(\dfrac{{\partial ({{\boldsymbol{M}}_{\text{t}}}{\boldsymbol{\dot a}})}}{{\partial {\boldsymbol{a}}}}\right)^{\text{T}}} + {{\boldsymbol{C}}_\eta }$ ；$ \psi = {{\boldsymbol{q}}^{\text{T}}}{\boldsymbol{q}} - 1 $ ；$\lambda $ 为拉格朗日乘子；Mt的表达式为$$ {{\boldsymbol{M}}_{\text{t}}} = \left[ {\begin{array}{*{20}{c}} {({m_{\text{b}}} + {m_{\text{r}}}){{\boldsymbol{I}}_{3 \times 3}}} & { - 2{\boldsymbol{A}}{{\boldsymbol{H}}_1}{\boldsymbol{L}}({\boldsymbol{q}})} & {{\boldsymbol{A}}{{\boldsymbol{H}}_2}} \\ { - 2{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}}){\boldsymbol{H}}_1^{\text{T}}{{\boldsymbol{A}}^{\text{T}}}} & {4{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}})({{\boldsymbol{J}}_{\text{b}}} + {{\boldsymbol{J}}_{\text{r}}}){\boldsymbol{L}}({\boldsymbol{q}})} & {2{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}}){{\boldsymbol{H}}_3}} \\ {{\boldsymbol{H}}_2^{\text{T}}{{\boldsymbol{A}}^{\text{T}}}} & {2{\boldsymbol{H}}_3^{\text{T}}{{\boldsymbol{L}}^{\text{T}}}({\boldsymbol{q}})} & {{{\boldsymbol{I}}_{n \times n}}} \end{array}} \right] 。 $$ 对于式(11)的微分方程可采用广义
$\alpha $ 法进行求解[24-25]。3. 成像区域计算
假设卫星搭载光学遥感相机的视场为矩形，卫星轨道高度为
$h$ ，星下点经纬度分别为llon和llat，卫星瞬时的横滚角和瞬时俯仰角分别为$\alpha $ 和$\beta $ ，相机水平半张角和垂直半张角分别为$\varphi $ 和$\gamma $ ，成像区域计算方法如下：1) 以llon为基准经度，将卫星星下点经纬度坐标(llon, llat)转换为高斯坐标(xsat, ysat)。
2) 设中心点高斯坐标为(ximg, yimg)，通过式(27)计算卫星成像中心点在地面位置。
$$ \begin{gathered} {x_{{\text{img}}}} = {x_{{\text{sat}}}} - h\tan \alpha \\ {y_{{\text{img}}}} = {y_{{\text{sat}}}} + h\tan \beta \\ \end{gathered} $$ 3) 计算矩形成像区域中心点与视场边界的距离和视场顶点坐标，其计算公式为
$$ \left\{ {\begin{aligned} &{{d_{\rm{l}}} = h \cdot \tan \left( {\alpha + \gamma } \right) - h \cdot \tan \alpha } \\ & {{d_{\rm{r}}} = h \cdot \tan \alpha - h \cdot \tan \left( {\alpha - \gamma } \right), \quad \alpha \geqslant \gamma } \\ &{{d_{\rm{r}}} = h \cdot \tan \alpha + h \cdot \tan \left( {\gamma - \alpha } \right), \quad\alpha < \gamma } \end{aligned}} \right. $$ $$ \left\{ {\begin{aligned} &{{d_{\rm{u}}} = h \cdot \tan \left( {\beta + \varphi } \right) - h \cdot \tan \beta } \\ & {{d_{\rm{d}}} = h \cdot \tan \beta - h \cdot \tan \left( {\beta - \varphi } \right),\quad \beta \geqslant \varphi } \\ &{{d_{\rm{d}}} = h \cdot \tan \beta + h \cdot \tan \left( {\varphi - \beta } \right),\quad \beta < \varphi } \end{aligned}} \right.$$ 式中：dl、dr、du和dd分别表示为成像区域中心点距离左侧、右侧、前方和后方视场边缘的距离。
根据中心点高斯坐标以及中心点与视场边界的距离，视场顶点坐标为
$$ \begin{gathered} {p_{{\text{rf}}}} = \left( {{x_{{\text{img}}}} - {d_{\text{r}}},{y_{{\text{img}}}} + {d_{\text{u}}}} \right) \\ {p_{{\text{lf}}}} = \left( {{x_{{\text{img}}}} + {d_{\text{l}}},{y_{{\text{img}}}} + {d_{\text{u}}}} \right) \\ {p_{{\text{rr}}}} = \left( {{x_{{\text{img}}}} - {d_{\text{r}}},{y_{{\text{img}}}} - {d_{\text{d}}}} \right) \\ {p_{{\text{lr}}}} = \left( {{x_{{\text{img}}}} + {d_{\text{l}}},{y_{{\text{img}}}} - {d_{\text{d}}}} \right) \\ \end{gathered} $$ 其中，
$ {p_{{\text{rf}}}} $ 、$ {p_{{\text{lf}}}} $ 、$ {p_{{\text{rr}}}} $ 和$ {p_{{\text{lr}}}} $ 分别表示为视场右前顶点、左前顶点、右后顶点和左后顶点高斯坐标。4) 将视场顶点高斯坐标重新转换为经纬度。
4. 数值仿真
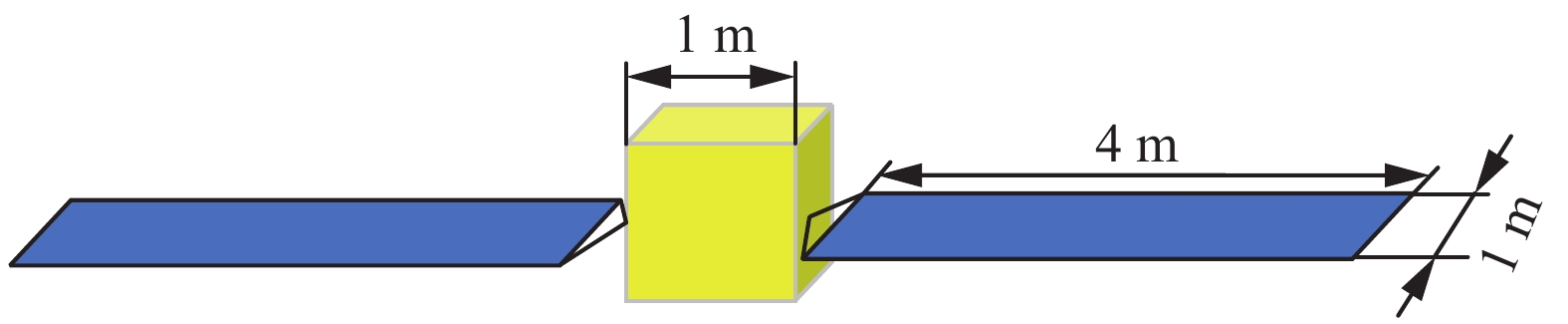
仿真算例以某型号敏捷卫星简化模型为对象，开展挠性附件对成像区域和质量的影响研究。如图2所示，卫星主要的挠性附件为两个对称的太阳能帆板，帆板长为4 m，宽为1 m，厚度为0.02 m。卫星本体简化为边长为1 m的正方体，质量为500 kg。帆板通过桁架与卫星本体固定连接，帆板边缘到卫星本体中心距离为0.75 m，太阳能帆板的主要的力学参数如表1所示。
图 2 卫星简化模型Fig. 2 Simplified model of satellite下载:
全尺寸图片
表 1 太阳能帆板力学参数Table 1 Parameters of solar panel参数 数值 弹性模量/Pa $1 \times {10^8}$ 泊松比 0.3 密度/(kg·m−3) 150 阻尼系数 0.05 数值仿真中分别选取的太阳同步轨道和地球同步轨道研究帆板残余振动对成像区域的影响。表2和表3分别给出了太阳同步轨道和地球同步轨道参数。对于太阳同步轨道，相机的水平半张角和垂直半张角分别为1°和2°。对于地球同步轨道，相机的水平半张角和垂直半张角分别为0.1°和0.2°。为了模拟敏捷卫星机动成像模式，设计仿真工况如下：
表 2 太阳同步轨道参数Table 2 Sun-synchronous orbital parameters参数 数值 历元时间(UTC) 2022/01/26 15:03:16 半长轴/km 7178.14 偏心率 0 轨道倾角/ (°) 98.608 升交点赤经/ (°) 305.432 近地点幅角/ (°) 0 平近点角/ (°) 0 表 3 地球同步轨道参数Table 3 Geostationary orbital parameters参数 数值 历元时间(UTC) 2022/03/01 15:03:12 半长轴/km 42166.3 偏心率 0 轨道倾角/ (°) 0 升交点赤经/ (°) 351.758 近地点幅角/ (°) 0 平近点角/ (°) 0 1) 卫星本体
${x_{\text{b}}}$ 和${y_{\text{b}}}$ 方向各施加10 N/m的力矩，持续时间1 s，卫星开始机动；2) 卫星姿态机动过程，持续时间1 s，无力矩；
3) 卫星本体
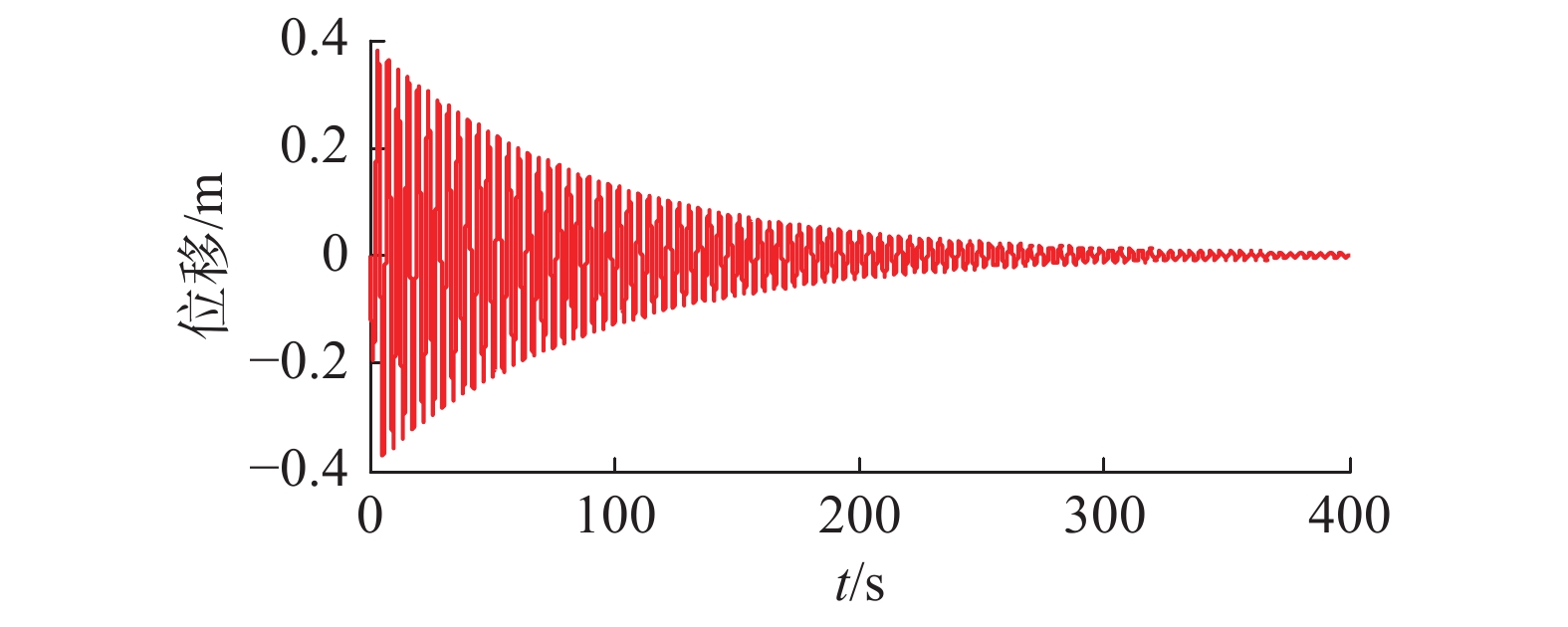
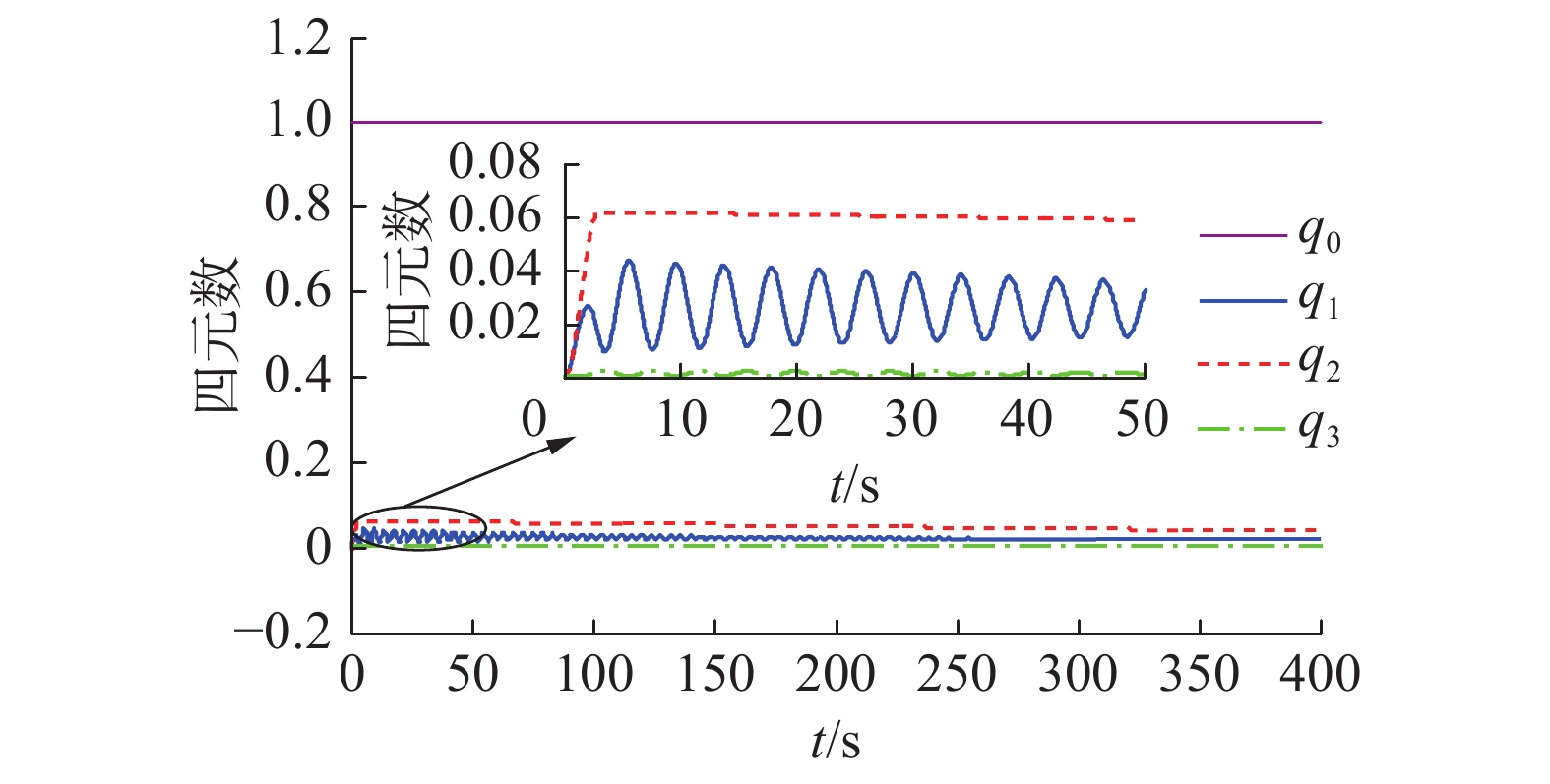
${x_{\text{b}}}$ 和${y_{\text{b}}}$ 方向各施加−10 N/m的力矩，持续时间1 s，机动结束。图3给出了太阳帆板尖端挠度振动曲线。从图中可以看出，太阳帆板尖端最大挠度超过了0.3 m，发生在机动开始阶段。卫星机动结束后，由于帆板结构阻尼帆板尖端挠度而逐渐衰减。图4给出了四元数变化曲线。从图中可以看出，卫星机动结束后太阳帆板的残余振动导致卫星姿态不稳定。
图 3 太阳帆板尖端挠度振动Fig. 3 Deflection vibration of solar panel tip下载:
全尺寸图片
图 4 四元数变化曲线Fig. 4 Quaternion curves下载:
全尺寸图片
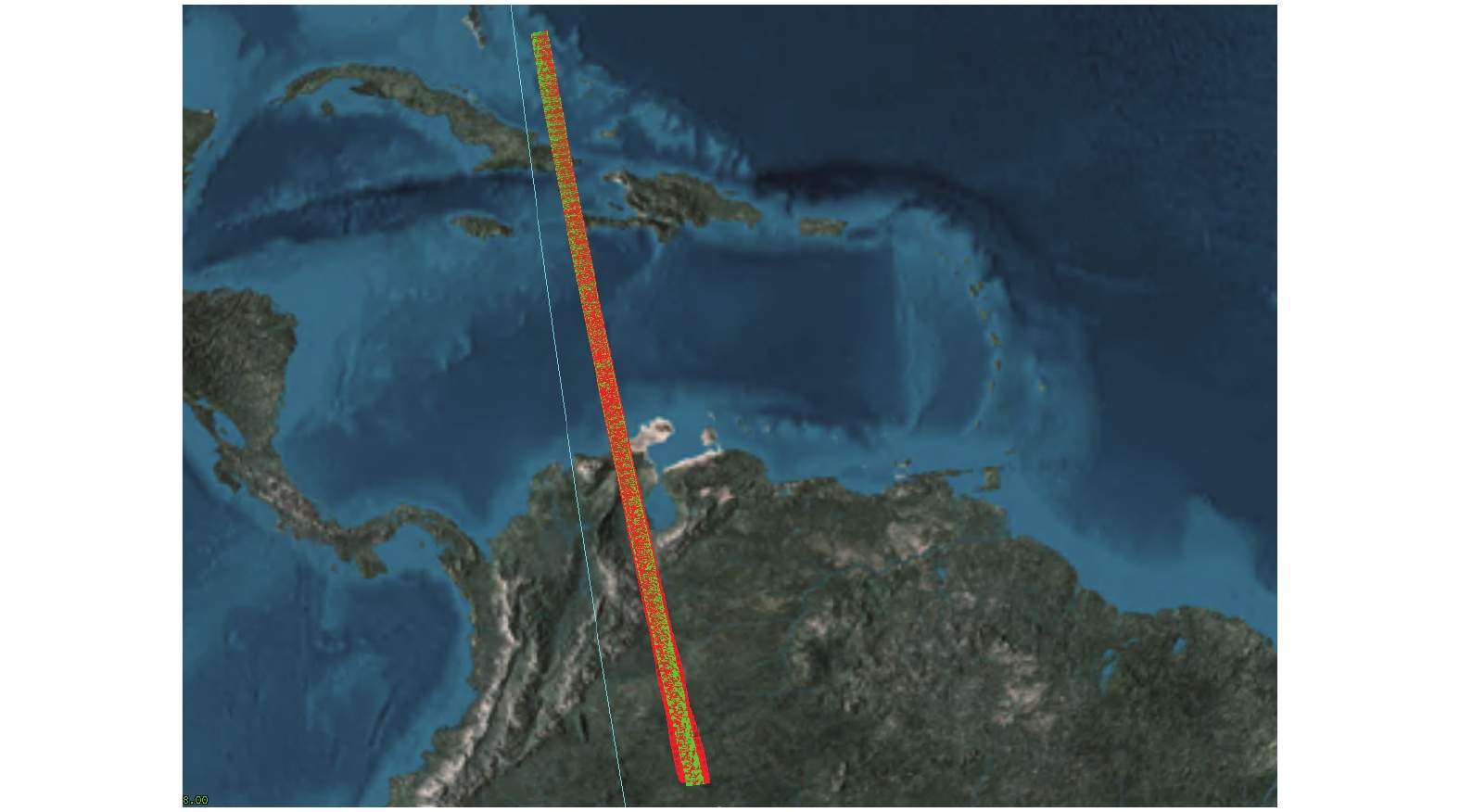
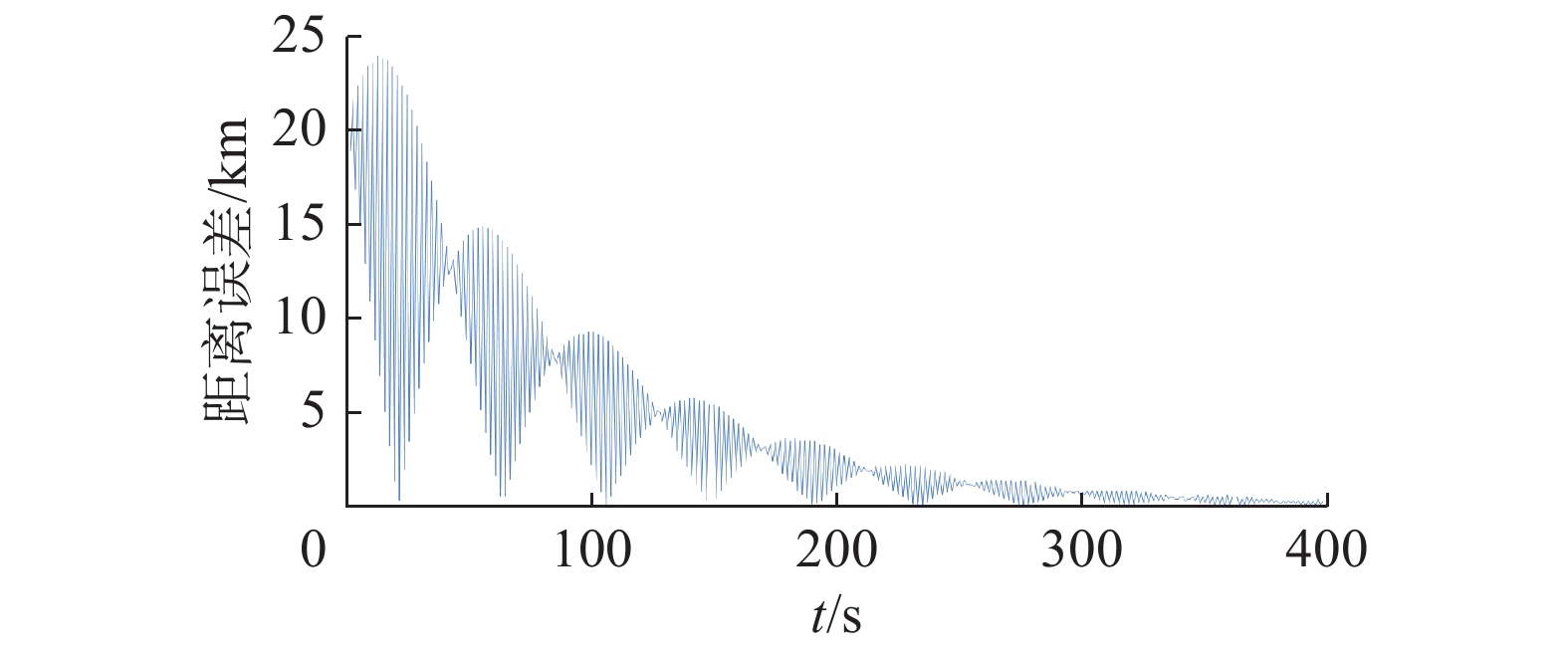
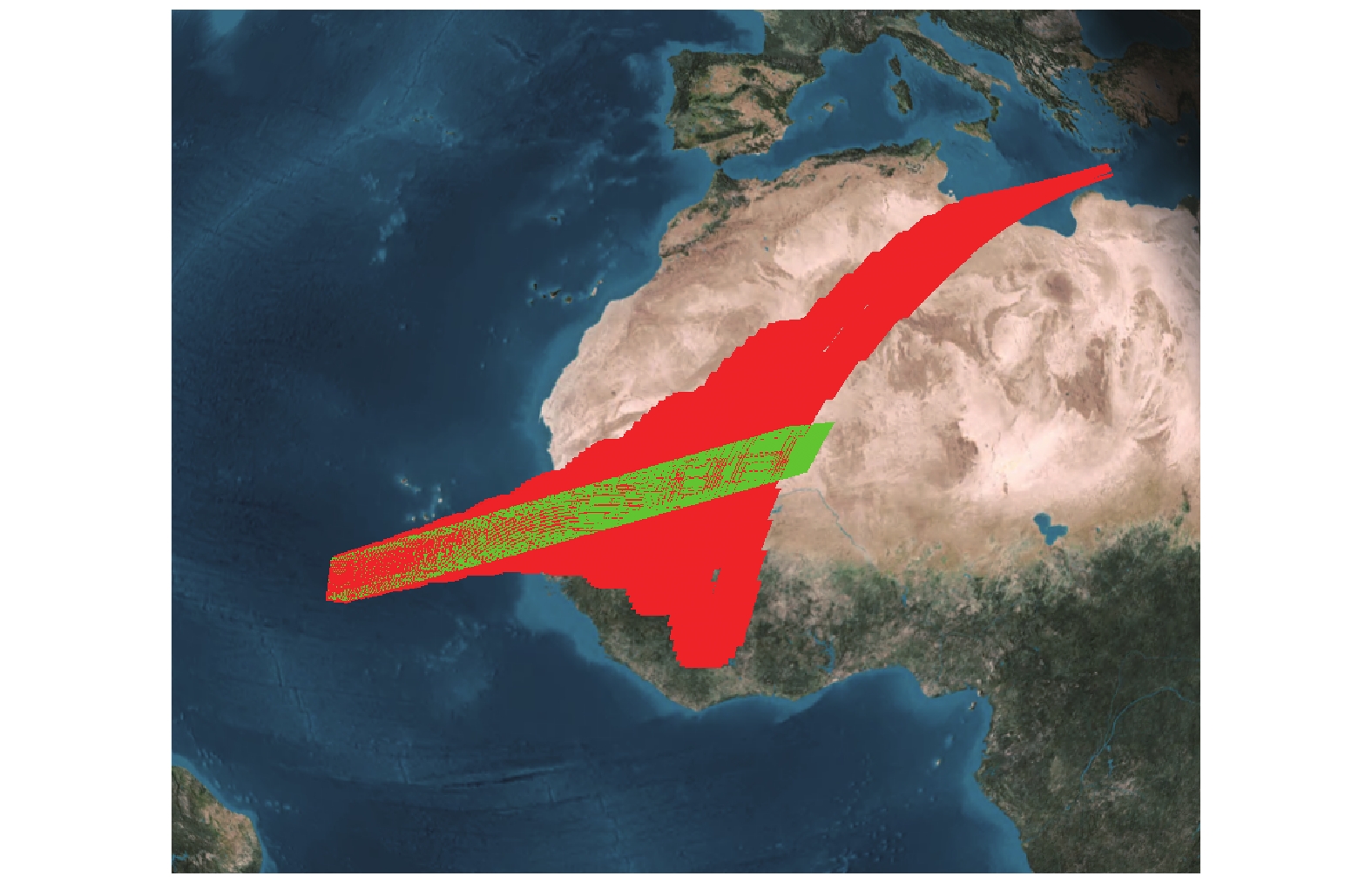
图5给出了太阳同步轨道成像条带，绿色部分为无扰动时卫星的成像条带，红色部分为添加扰动时卫星的成像条带。从图中可以看出卫星姿态机动引起太阳帆板的振动对成像区域有影响。机动结束后，立刻对地面进行观测，成像区域横滚方向与俯仰方向均偏差较大，红色成像区域在横向与纵向上产生大面积错位，并呈现出反复震荡。随着成像时间增加，帆板振动趋于稳定，红色成像区域逐渐向绿色区域靠拢直至重合。图6给出了太阳同步轨道卫星成像中心点偏移距离随时间变化的曲线，其中最大偏差为24.4 km，经过289 s的姿态稳定后，距离偏差小于1 km。
图 5 太阳同步轨道卫星成像条带偏移情况Fig. 5 Strip displacement of Sun-synchronous orbit下载:
全尺寸图片
图 6 太阳同步轨道卫星成像中心点偏移距离曲线Fig. 6 Distance error of imaging center point of Sun-synchronous orbital satellite下载:
全尺寸图片
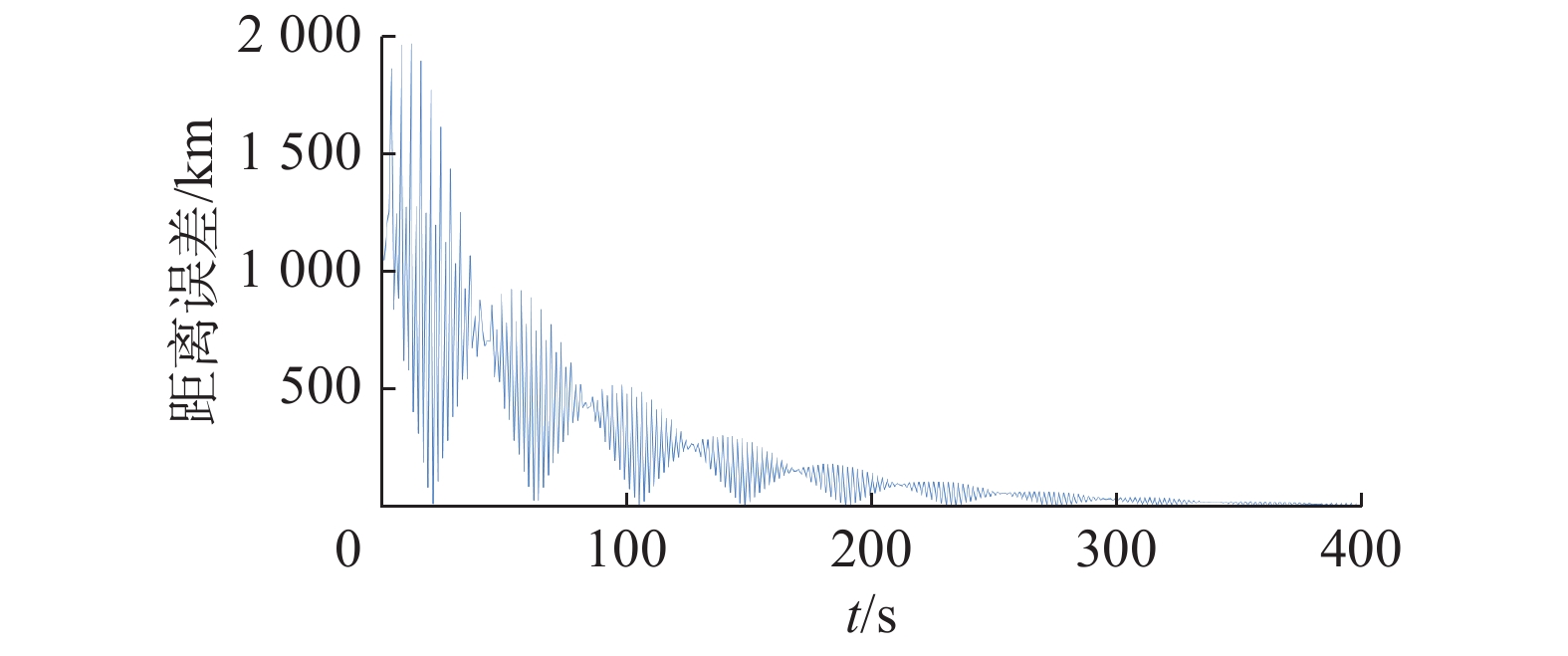
图7给出了地球同步轨道成像条带，绿色部分为无扰动时卫星的成像条带，红色部分为添加扰动时卫星的成像条带。从图中可以看出，卫星姿态机动引起太阳帆板的振动对成像区域有较大的影响，尤其是初始阶段，影响显著。对比图5与图6可以看出，卫星轨道高度越高，扰动对于卫星成像区域的影响越大。图8给出了地球同步轨道下卫星成像中心点偏移距离随时间变化的曲线，其中最大偏差高达1967.5033 km，经过400 s的姿态稳定后，偏差仍大于15 km。显然，卫星轨道高度越高，扰动对于其成像区域的影响越大，需要更长时间稳定自身姿态。
图 7 地球同步轨道卫星成像条带偏移情况Fig. 7 Strip displacement of Geostationary orbital下载:
全尺寸图片
图 8 地球同步轨道卫星成像中心点偏移距离曲线Fig. 8 Distance error of imaging center point of Geostationary orbital satellite下载:
全尺寸图片
经过仿真验证，在这两种工况下，卫星经过约300 s的稳定后，姿态趋于稳定，此时扰动对于低轨卫星的观测区域基本无影响，但高轨卫星需要更长时间使得期望观测区域与实际观测区域的位置误差小于距离阈值。
5. 结束语
本文建立了带挠性附件卫星刚柔耦合动力学模型，分析了遥感敏捷卫星机动模式挠性附件振动对成像区域的影响。选取太阳同步轨道和地球同步轨道，以两个对称的太阳能帆板作为挠性附件给出数值仿真结果。仿真结果表明，卫星姿态机动结束成像区域横滚方向与俯仰方向均偏差较大，导致成像区域产生错位；在这两种工况下，卫星经过约300 s的稳定后，姿态趋于稳定，此时扰动对于低轨卫星的观测区域基本无影响，但高轨卫星需要更长时间使得期望观测区域与实际观测区域的位置误差小于距离阈值。
-
图 1 带挠性附件卫星简化模型
Fig. 1 Simplified model of satellite with flexible appendix
下载:
全尺寸图片
图 2 卫星简化模型
Fig. 2 Simplified model of satellite
下载:
全尺寸图片
图 3 太阳帆板尖端挠度振动
Fig. 3 Deflection vibration of solar panel tip
下载:
全尺寸图片
图 4 四元数变化曲线
Fig. 4 Quaternion curves
下载:
全尺寸图片
图 5 太阳同步轨道卫星成像条带偏移情况
Fig. 5 Strip displacement of Sun-synchronous orbit
下载:
全尺寸图片
图 6 太阳同步轨道卫星成像中心点偏移距离曲线
Fig. 6 Distance error of imaging center point of Sun-synchronous orbital satellite
下载:
全尺寸图片
图 7 地球同步轨道卫星成像条带偏移情况
Fig. 7 Strip displacement of Geostationary orbital
下载:
全尺寸图片
图 8 地球同步轨道卫星成像中心点偏移距离曲线
Fig. 8 Distance error of imaging center point of Geostationary orbital satellite
下载:
全尺寸图片
表 1 太阳能帆板力学参数
Table 1 Parameters of solar panel
参数 数值 弹性模量/Pa $1 \times {10^8}$ 泊松比 0.3 密度/(kg·m−3) 150 阻尼系数 0.05 表 2 太阳同步轨道参数
Table 2 Sun-synchronous orbital parameters
参数 数值 历元时间(UTC) 2022/01/26 15:03:16 半长轴/km 7178.14 偏心率 0 轨道倾角/ (°) 98.608 升交点赤经/ (°) 305.432 近地点幅角/ (°) 0 平近点角/ (°) 0 表 3 地球同步轨道参数
Table 3 Geostationary orbital parameters
参数 数值 历元时间(UTC) 2022/03/01 15:03:12 半长轴/km 42166.3 偏心率 0 轨道倾角/ (°) 0 升交点赤经/ (°) 351.758 近地点幅角/ (°) 0 平近点角/ (°) 0 -
[1] 雷涛, 王洁, 薛丁华, 等. 差异特征融合的无监督SAR图像变化检测[J]. 智能系统学报, 2021, 16(3): 595–604. doi: 10.11992/tis.202103011 LEI Tao, WANG Jie, XUE Dinghua, et al. Unsupervised SAR image change detection based on difference feature fusion[J]. CAAI transactions on intelligent systems, 2021, 16(3): 595–604. doi: 10.11992/tis.202103011 [2] 杨舒, 陈浩, 李军, 等. 一种面向任务的对地观测卫星Agent团队构建方法[J]. 智能系统学报, 2017, 12(5): 653–660. doi: 10.11992/tis.201706017 YANG Shu, CHEN Hao, LI Jun, et al. Agent team formation approach for task-oriented earth observation satellite[J]. CAAI transactions on intelligent systems, 2017, 12(5): 653–660. doi: 10.11992/tis.201706017 [3] REDDY C S, KURIAN A, SRIVASTAVA G, et al. Remote sensing enabled essential biodiversity variables for biodiversity assessment and monitoring: technological advancement and potentials[J]. Biodiversity and conservation, 2021, 30(1): 1–14. doi: 10.1007/s10531-020-02073-8 [4] SABETGHADAM S, KHOSHSIMA M, PIERLEONI A. Aerosol climatology and determination of different types over the semi-arid urban area of Tehran, Iran: application of multi-platform remote sensing satellite data[J]. Atmospheric pollution research, 2020, 11(9): 1625–1636. doi: 10.1016/j.apr.2020.06.029 [5] 王跃, 范立佳, 李雨廷. 高分多模卫星敏捷遥感技术研究及应用[J]. 航天器工程, 2021, 30(3): 27–35. doi: 10.3969/j.issn.1673-8748.2021.03.004 WANG Yue, FAN Lijia, LI Yuting. Research and application of agile remote sensing technologies in GFDM-1 satellite[J]. Spacecraft engineering, 2021, 30(3): 27–35. doi: 10.3969/j.issn.1673-8748.2021.03.004 [6] 宝音贺西, 印明威. 敏捷卫星时间最优姿态机动研究综述[J]. 动力学与控制学报, 2020, 18(4): 1–11. BAOYIN Hexi, YIN Mingwei. Review on time-optimal reorientation of agile satellites[J]. Journal of dynamics and control, 2020, 18(4): 1–11. [7] 赵键, 杨芳. 中国高分辨率敏捷小卫星的技术创新及应用实践[J]. 航天器工程, 2021, 30(6): 23–30. doi: 10.3969/j.issn.1673-8748.2021.06.003 ZHAO Jian, YANG Fang. Technical innovation and application of Chinese agile small satellites[J]. Spacecraft engineering, 2021, 30(6): 23–30. doi: 10.3969/j.issn.1673-8748.2021.06.003 [8] 梁健, 张润宁, 王大伟, 等. 敏捷SAR卫星视频成像模式的姿态机动策略[J]. 中国科学院大学学报, 2019, 36(1): 125–130. doi: 10.7523/j.issn.2095-6134.2019.01.017 LIANG Jian, ZHANG Running, WANG Dawei, et al. Attitude maneuver strategy of video mode based on agile SAR satellite[J]. Journal of university of Chinese academy of sciences, 2019, 36(1): 125–130. doi: 10.7523/j.issn.2095-6134.2019.01.017 [9] 武晓雯. 敏捷卫星姿态机动规划方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016. WU Xiaowen. Research on attitude maneuvering planning method of agile satellite[D]. Harbin: Harbin Engineering University, 2016. [10] 曹登庆, 白坤朝, 丁虎, 等. 大型柔性航天器动力学与振动控制研究进展[J]. 力学学报, 2019, 51(1): 1–13. doi: 10.6052/0459-1879-18-054 CAO Dengqing, BAI Kunchao, DING Hu, et al. Advances in dynamics and vibration control of large-scale flexible spacecraft[J]. Chinese journal of theoretical and applied mechanics, 2019, 51(1): 1–13. doi: 10.6052/0459-1879-18-054 [11] 黄龙飞, 尚志, 柳宁. 变结构航天器动力学特性在轨辨识方法综述[J]. 航天器工程, 2015, 24(3): 100–106. doi: 10.3969/j.issn.1673-8748.2015.03.016 HUANG Longfei, SHANG Zhi, LIU Ning. Discussion on method of on-orbit identification of dynamic characteristics for variable structure spacecraft[J]. Spacecraft engineering, 2015, 24(3): 100–106. doi: 10.3969/j.issn.1673-8748.2015.03.016 [12] 贾桂敏. 姿态变化对遥感推扫式三线阵立体测量精度的影响研究[D]. 天津: 天津大学, 2013. JIA Guimin. Research of attitude variation effects on three-line-array cameras in remote sensing push-broom stereo photogrammetry[D]. Tianjin: Tianjin University, 2013. [13] 周伟敏. 挠性结构卫星姿态机动与成像控制技术研究[D]. 长沙: 国防科技大学, 2019. ZHOU Weimin. Research on attitude maneuver and image compensation control for flexible satellite[D]. Changsha: National University of Defense Technology, 2019. [14] 尉文龙. 卫星摆动造成的图像退化及其修复研究[D]. 兰州: 兰州大学, 2017. YU Wenlong. Image degradation caused by satellite swing and its correction[D]. Lanzhou: Lanzhou University, 2017. [15] 吴亮, 雷斌, 韩冰, 等. 卫星姿态误差对多通道SAR成像质量的影响[J]. 测绘通报, 2015(1): 124–130. WU Liang, LEI Bin, HAN Bing, et al. The impact of satellite attitude error on multi-channel SAR image quality[J]. Bulletin of surveying and mapping, 2015(1): 124–130. [16] 张普中. 考虑飞轮动态特性的卫星平台控制策略与成像性能分析[D]. 北京: 北京理工大学, 2016. ZHANG Puzhong. Control strategy of the satellite platform considering the dynamic characteristics of flywheel and imaging performance analysis[D]. Beijing: Beijing Institute of Technology, 2016. [17] 王钦, 何星星, 文援兰. 带挠性附件的航天器结构−姿态耦合动力学[J]. 上海航天, 2011, 28(2): 12–16,49. doi: 10.19328/j.cnki.1006-1630.2011.02.003 WANG Qin, HE Xingxing, WEN Yuanlan. Spacecraft structures-attitude coupling dynamics with flexible appendages[J]. Aerospace Shanghai, 2011, 28(2): 12–16,49. doi: 10.19328/j.cnki.1006-1630.2011.02.003 [18] CHELNOKOV Y N. Quaternion equations of disturbed motion of an artificial earth satellite[J]. Cosmic research, 2019, 57(2): 101–114. doi: 10.1134/S0010952519020023 [19] HUSSEIN M, QIAN Longjun. Dynamic modeling and attitude control system of underactuated fuel slosh with flexible appendages[J]. IOP conference series:materials science and engineering, 2019, 631(3): 032055. doi: 10.1088/1757-899X/631/3/032055 [20] XU Xiaoming, ZHONG Wanxie. On the numerical influences of inertia representation for rigid body dynamics in terms of unit quaternion[J]. Journal of applied mechanics, 2016, 83(6): 061006. doi: 10.1115/1.4033031 [21] ISLAM M, OKASHA M, SULAEMAN E. A model predictive control (MPC) approach on unit quaternion orientation based quadrotor for trajectory tracking[J]. International journal of control, automation and systems, 2019, 17(11): 2819–2832. doi: 10.1007/s12555-018-0860-9 [22] 孙禄君. 双柔性帆板卫星分力合成主动振动抑制研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. SUN Lujun. Active vibration suppression based on component synthesis method for the satellite with double flexible sail[D]. Harbin: Harbin Institute of Technology, 2013. [23] YANG Jinzhao, PENG Haijun, ZHOU Wenya, et al. A modular approach for dynamic modeling of multisegment continuum robots[J]. Mechanism and machine theory, 2021, 165: 104429. doi: 10.1016/j.mechmachtheory.2021.104429 [24] AZIMI M, SHAHRAVI M, JOUBANEH E F. Dynamic analysis of maneuvering flexible spacecraft appendage using higher order sandwich panel theory[J]. Latin American journal of solids and structures, 2016, 13(2): 296–313. doi: 10.1590/1679-78252326 [25] ARNOLD M, BRÜLS O. Convergence of the generalized-α scheme for constrained mechanical systems[J]. Multibody system dynamics, 2007, 18(2): 185–202. doi: 10.1007/s11044-007-9084-0
