Script event prediction based on a quaternion-gated graph neural network
-
摘要: 脚本事件预测需要考虑两类信息来源：事件间的关联与事件内的交互。针对于事件间的关联，采用门控图神经网络对其进行建模。而对于事件内的交互，采用四元数对事件进行表征，接着通过四元数的哈密顿乘积来捕捉事件4个组成部分之间的交互。提出结合四元数和门控图神经网络来学习事件表示，它既考虑了外部事件图的交互作用，又考虑了事件内部的依赖关系。得到事件表示后，利用注意机制学习上下文事件表示和每个候选上下文表示的相对权值。然后通过权重计算上下文事件表示的和，再计算其与候选事件表示的欧氏距离。最后选择距离最小的候选事件作为正确的候选事件。在纽约时报语库上进行了实验，结果表明，通过多项选择叙事完形填空评价，本文的模型优于现有的基线模型Abstract: Two types of information sources are essential for script event prediction: the correlation between events and the inner interactions within one event. For the first information source, we use a gated graph neural network to model the correlation between events. For the inner interactions within one event, we use quaternion to model the event, and then we use the Hamilton product of quaternion to capture the inner interactions of four components. We propose to learn event representation by combining quaternion and a gated graph neural network. This approach considers the interaction of external event diagrams and the dependence within an event. After obtaining the event representation, we use an attention mechanism to learn the context event representation and the relative weight of each candidate context representation. Next, we calculate the sum of the context event embeddings through the weights, and then we calculate the Euclidean distance between the context event embedding sum and the candidate event embedding. Finally, we choose the candidate event with the smallest distance as the right candidate event. The results of experiments conducted on the New York Times corpus show that our proposed model is superior to the existing state-of-the-art baseline models through evaluation using a multiple-choice narrative cloze test.
-
脚本事件包含许多有关人类语言的信息和文化[1]，有时也称为框架[2]和纲要[3]。了解脚本事件，对于迈向真正的人工智能至关重要，其具有许多应用，例如阅读理解、意图识别和对话管理[1]。具体来说，脚本事件预测是基于上下文背景事件，然后从若干个后续待选事件中选择一个最有可能发生的后续事件[4]。
脚本事件预测的第一步是获取事件表示。获得高质量的事件表示需要考虑事件内部的交互与事件之间的关联。 在许多已有的事件预测模型中，一个事件的嵌入表示为4个分量(谓语动词、主语、宾语以及与谓语动词有介词关系的实体)的嵌入[1]的拼接，或者是4个分量嵌入的非线性变换[4]。 然而，由于1个事件是1个复杂的多参数结构，1个事件内部的4个组成成分也会互相影响，互相作用，这样的直接耦合或非线性转换不能捕捉到事件4个部分之间的交互关系，从而使模型丢失这方面的信息。
为了捕获多维特征的内部依赖关系，许多信号处理和机器学习算法更加关注四元数和超复杂域[5-7]。一些四元数神经网络在不同的应用中显示了良好的效果。具体来说，四元数网络[8]、四元数递归神经网络[9]和深度四元数卷积网络[10]在图像、语音和自然语言处理方面表现良好。
针对于事件之间的关联，由于其可以建模成图结构形式，本文采用图神经网络对其进行建模。近年来，图形神经网络受到越来越多的关注。由于其能够学习不同节点之间的在给定图中的交互信息，图神经网络在处理图形结构数据上得到了广泛的应用，例如在社交网络上[11]、机器人设计上[12]、知识图谱上[13]。受CNN、RNN和自动编码器在深度学习中的启发，将卷积、门控等机制应用于图神经网络就引出了图卷积网络(graph convolutional network, GCN)[11]，门控图神经网络(gated graph neural network, GGNN)[14]等经典算法。
本文的主要贡献包括3个方面：
1）提出基于四元数的事件表示模型，该模型将四元数的4个不同组成部分与事件描述中4个组成部分一一对应，然后可以利用四元数代数运算中的哈密顿乘积权重共享的机制，捕捉到事件四个不同部分的内在依赖关系。
2）将四元数事件表示模型与门控图神经网络相结合，借助于图神经网络可以捕捉不同事件之间的交互关系。
3）所提出的四元数门控图神经网络的事件预测模型在《纽约时报》语料库上的实验结果表明，该方法可以取得比之前方法更优越的性能。
1. 相关工作
1.1 脚本事件预测
在人工智能领域中使用脚本的历史可以追溯到1970年[10]。在这个概念中，脚本由没有概率语义的复杂事件组成。近年来，越来越多的研究调查了带有脚本事件的基于学习的基于概率的共现模型。文献[15]提出了从原始新闻通讯录文本中无监督地引入叙事事件链的方法，使用叙事完形填空作为评估指标，并开创了统计脚本学习的最新工作。文献[9]使用bigram模型来显式地建模事件对的时间顺序。但是，他们都以（动词，从属）形式利用了非常有限的事件表示形式。为了克服这种事件表示的缺点，文献[16]提出了一种使用带有多个参数的事件的方法。
近些年来，随着神经网络在自然语言处理得到越来越广泛的应用。很多学者也试图将神经网络的方法与脚本事件预测模型相结合。文献[5]指出，基于LSTM的事件序列模型优于以前的基于共现的方法。文献[6]描述了一种前馈神经网络，该神经网络将动词和自变量组成低维向量，并根据叙述性完形填空任务的多项选择进行评估。文献[5]通过使用LSTM隐藏状态计算成对事件相关性得分，将事件顺序信息和成对事件关系集成在一起。文献[17]将自监督学习引入到脚本事件预测模型中，并且提出多任务框架来对模型进行联合训练。文献[18]将因果推断引入到事件预测模型中并且取得了显著的性能。
1.2 图神经网络
不同于语音、文本等序列数据，以及图像等网格数据，图结构数据是一种非欧氏空间的数据。 图结构数据在生活中有着广泛的应用, 很多数据可以以图的形式进行建模，例如，社交网络、蛋白质分子结构、知识图谱等。之前的模型在建模这种图结构数据时一般通过随机游走的方式抽取出链状形式的数据，再通过skim-gram等方式对图数据进行表示学习。近些年来，随着神经网络的广泛应用，一些研究者将深度学习与图结构数据相结合提出了图神经网络模型。
图卷积网络是其中的图神经网络的经典代表[14,19]，图卷积网络考虑图集点的一阶邻居，其将卷积网络的思想进行泛化，以一个具体的节点表示学习为例，将节点的邻居表示进行融合得到该节点的表示。门控图神经网络[14]将循环神经网络[20-21]的门控机制引入到图神经网络的消息传递过程，可以用来处理时序的图结构数据。
2. 四元数
在本节中，本文主要介绍四元数的具体表现形式以及一些常规的数学运算，例如四元数的共轭、标准化、哈密顿乘积等。
2.1 基本定义
四元数是超复数系统[9]的代表，它将传统的复数系统扩展到四维空间。四元数
$ Q $ 由1个实分量和3个虚分量组成，定义为$$ Q = a + b{\rm{i}} + c{\rm{j}} + d{\rm{k}} $$ 式中：
$a、b、c、d$ 是实数；${\rm{i}}、{\rm{j}}、{\rm{k}}$ 是复数单位。${\rm{ i}} 、{\rm{j}}、 {\rm{k}}$ 满足哈密顿规则并且有等式：${\rm{{i^2} }}= {\rm{{j^2}}} = {\rm{{k^2}}} = {\rm{ijk}} = - 1$ 。2.2 共轭
若
$ {Q^*} $ 是$ Q $ 的共轭，其定义为$$ {Q^*} = a - b{\rm{i}} - c{\rm{j}} - d{\rm{k}} $$ 2.3 标准化
将四元数
$ Q $ 进行标准化后可以得到单位四元数$ {Q'} $ 其定义为$$ {Q'} = \frac{Q}{{\sqrt {{a^2} + {b^2} + {c^2} + {d^2}} }} $$ 2.4 哈密顿乘积
哈密顿乘积为四元数
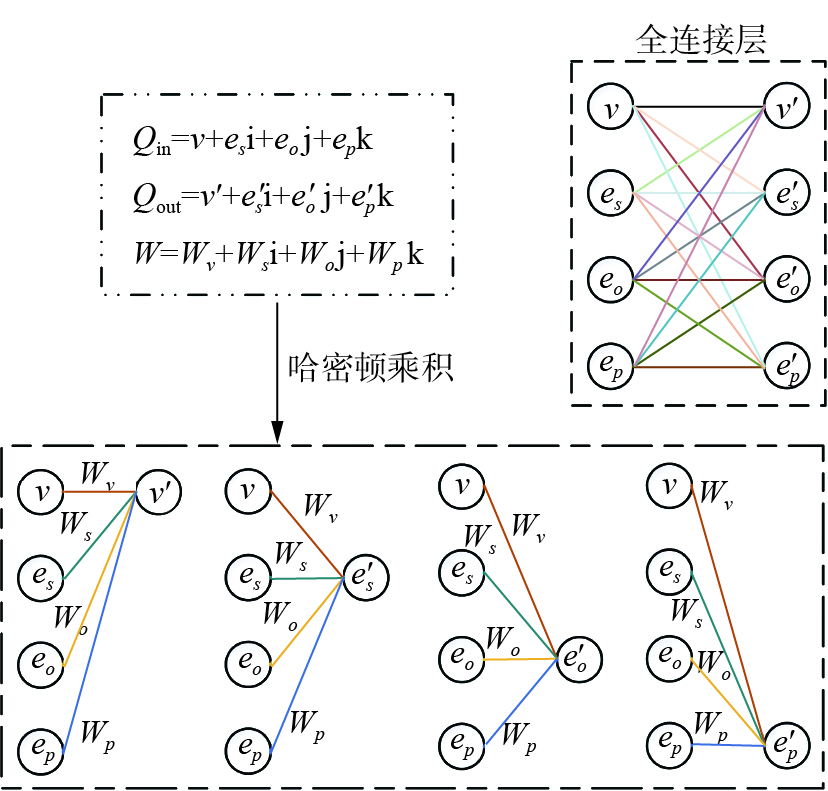
${Q_1} = {a_1} + {b_1}{\rm{i}} + {c_1}{\rm{j}} + {d_1}{\rm{k}}$ 与${Q_2} = {a_2} + {b_2}{\rm{i}} + {c_2}{\rm{j}} + {d_2}{\rm{k}}$ 之间的乘积。哈密顿乘积不满足交换律，具体的运算步骤如下：$$ \begin{gathered} {Q_1} \otimes {Q_2} = ({a_1}{a_2} - {b_1}{b_2} - {c_1}{c_2} - {d_1}{d_2})+\\ ({a_1}{b_2} + {b_1}{a_2} + {c_1}{d_2} - {d_1}{c_2}){\rm{i}} +\\ ({a_1}{a_2} - {b_1}{b_2} - {c_1}{c_2} - {d_1}{d_2}){\rm{j}} +\\ ({a_1}{d_2} + {b_1}{c_2} - {c_1}{b_2} + {d_1}{a_2}){\rm{k}} \\ \end{gathered} $$ 相比于一般的矩阵运算，四元数的哈密顿乘积运算可以通过共享参数的形式捕捉模块之间的互相依赖关系。图1通过图示的方式展示了哈密顿乘积运算与全连接层的矩阵运算之间的区别。在实数空间中，权重矩阵的所有元素都是不同的，对于图中所示的连接可以有4×4 = 16个自由度。在四元数空间中只有4个自由度，因为
$ {w_v}, {w_s},{w_o},{w_p} $ 是共享的权重系数。这种共享机制可以减少75%的参数量，并且捕捉到$v、{e_s}、{e_o}、{e_p}$ 组成部分的内在交互。
图 1 哈密顿乘积层与一般全连接乘积层的比较Fig. 1 Comparsion of Hamilton product layer and fully connected layer
下载:
全尺寸图片
2.5 激活函数
四元数划分激活函数
$ \partial (Q)$ 定义为$$ \partial (Q) = f(r) + f(x){\rm{i}} + f(y){\rm{j}} + f(z){\rm{k}} $$ 式中：
$ f $ 对应着一般的激活函数，例如relu激活函数或sigmoid激活函数。3. 四元数门控图神经网络
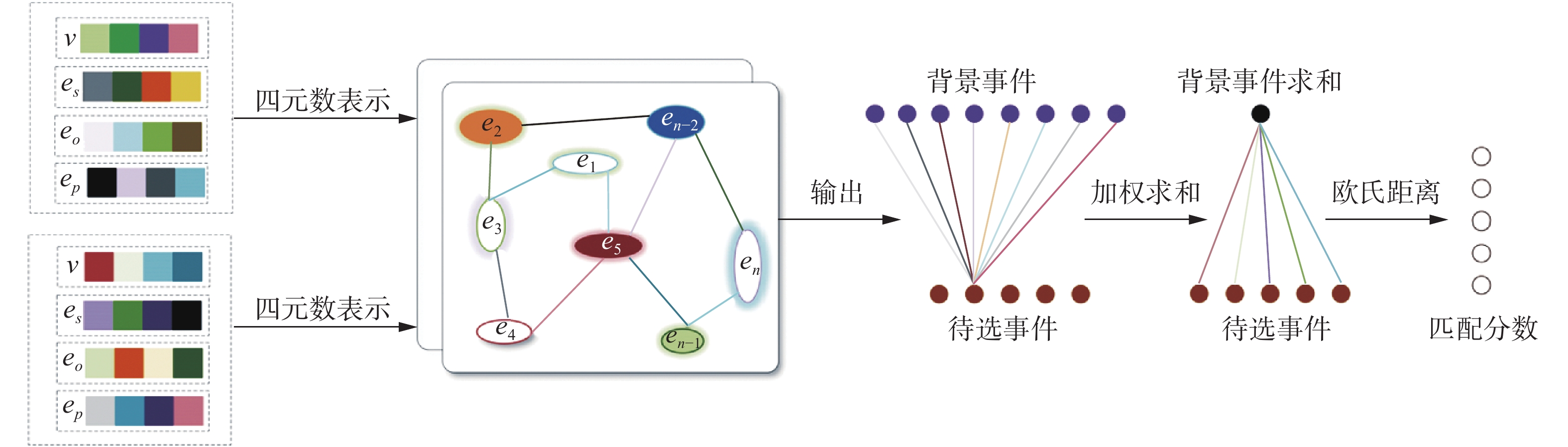
在本节中，首先对四元数门控图神经网络(QGGNN, quaternion gated graph neural network)进行具体介绍，整个算法流程如图2所示。首先，
$ v、{e_s}、{e_o}、{e_p} $ 被转化成四元数表示，然后输入到两层的四元数门控图神经网络中。网络的输出是8个背景事件向量和5个待选事件向量。然后这8个背景事件向量与5个待选事件向量中的每一个进行注意力机制计算，即可得到这8个背景向量与5个待选事件向量的相对重要程度的权值，从而得到背景事件的整体表示。再用背景事件的整体表示与每一个待选事件求分数，选出分数最大的待选事件即为将要预测的事件。
图 2 QGGNN的示意图Fig. 2 Illustration of QGGNN下载:
全尺寸图片
3.1 获取事件表示
模型的第一步就是通过四元数门控图神经网络将输入的脚本事理图谱转化为高质量的事件表示向量。
为了获取高质量的事件表示，需要根据其数据结构形式的特点对模型进行相应的设计。 总体来说，背景事件中有两类事件交互信息：一类是事件与事件之间的交互信息，本文称之为事件间的交互；第二类是1个事件内部4个组成成分之间的交互，本文称之为事件内的交互。因为事件间的交互可以建模成图结构形式，所以很适合采用图神经网络对其进行建模。 针对于事件内的交互，本文将一个事件表示成四元数的形式，然后通过四元数中哈密顿乘积中的共享参数机制捕捉事件内部不同组成部分的关系。
基于此，本文结合四元数和门控图神经网络[14]来学习事件表示。 门控图神经网络的输入是初始的事件表示
${{\boldsymbol{h}}^{(0)}}$ 和邻接矩阵${\boldsymbol{A}}$ 。${{\boldsymbol{h}}^{(0)}}$ 包含8个背景事件向量和5个后续待选事件向量。${\boldsymbol{A}} \in {{\rm{R}}^{13\times 13}}$ 表示图中不同节点之间的交互。 门控图神经网络的信息处理过程为$$ {a^{(t)}} = {{\boldsymbol{A}}^{\rm{T}}}{{\boldsymbol{h}}^{(t - 1)}} + b $$ (1) $$ {z^{(t)}} = \sigma (Q_1^z \otimes {a^{(t)}} + Q_2^z \otimes {{\boldsymbol{h}}^{(t - 1)}}) $$ (2) $$ {r^{(t)}} = \sigma (Q_1^r \otimes {a^{(t)}} + Q_2^r \otimes {{\boldsymbol{h}}^{(t - 1)}}) $$ (3) $$ {c^{(t)}} = \tanh (Q_1^z \otimes {a^{(t)}} + Q_2^z \otimes ({r^{(t)}} \odot {{\boldsymbol{h}}^{(t - 1)}})) $$ (4) $$ {{\boldsymbol{h}}^{(t)}} = (1 - {z^{(t)}}) \odot {{\boldsymbol{h}}^{(t - 1)}} + {z^{(t)}} \odot {c^{(t)}} $$ (5) 式中：
$ \otimes $ 代表哈密顿乘积；$ \odot $ 表示元素级别的乘法；$ \sigma $ 和$ \tanh $ 是四元数划分激活函数。门控图神经网络的门结构类似于门控循环单元(GRU)的门控结构。 四元数门控图神经网络的参数是$ Q_1^z、Q_2^z、 Q_1^r、Q_2^r、{Q_1}、{Q_2} $ , 这些参数的结构都是四元数。式(1)表示图中不同节点之间的信息交互。式(2)~(5)类似于GRU的信息迭代，通过上一个时间步其他节点的表示更新当前的节点表示。
$ {z^{(t)}} $ 和$ {r^{(t)}} $ 是更新门和重置门。上述公式循环的更新的步数是一个固定的数值K。四元数门控图神经网络的输出$ {{\boldsymbol{h}}^{(t)}} $ 是背景事件和待选事件新的表示，这些新的表示利用了事件内部的依赖信息与事件之间的交互信息。3.2 待选事件相似度匹配
背景事件经过四元数门控图神经网络后，可以得到高质量的事件表示。对于每一个子图, 四元数门控图神经网络的输出是8个背景事件向量
${{\boldsymbol{h}}_1},{{\boldsymbol{h}}_2},\cdots,{{\boldsymbol{h}}_8}$ 和5个待选事件向量${{\boldsymbol{h}}_{c1}},{{\boldsymbol{h}}_{c2}},\cdots,{{\boldsymbol{h}}_{c5}}$ 。为了计算每个背景事件的相对重要性，本文利用注意力神经网络来获取上下文事件与后续事件候选者的权重：
$$ {u_{ij}} = \tanh ({W_h}{h_i} + {W_c}{h_{cj}} + {b_u}) $$ $$ {\partial _{ij}} = \dfrac{{\exp ({u_{ij}})}}{{ \displaystyle\sum_k {\exp ({u_{kj}})} }} $$ 得到背景事件的权重系数
$ {\partial _{ij}} $ , 每一个待选事件${h_{cj}}$ 图中的背景事件的距离可以用如下公式计算：$$ {s_j} = g\left(\sum_i {{\partial _{ij}}{h_i}} ,{h_{cj}}\right) $$ 式中g() 表示两个事件的欧氏距离：
$$ g(a,b) = ||a - b|| $$ 模型根据匹配距离选择出与背景事件最接近的待选事件作为预测结果。
3.3 模型训练
给定一系列事件，每个事件都有其最合理的后续事件，模型的目标函数是margin loss，具体表示为
$$ L(\theta ) = \sum_{I = 1}^N {\sum_{j = 1}^k {(\max (0,{\text{margin}} - {s_{Iy}} + {s_{Ij}}))} } + \frac{\lambda }{2}||\theta |{|^2} $$ 式中：
$ {s_{Ij}} $ 是第$ I $ 个背景事件与第$ j $ 个后续待选事件的相关分数；$ y $ 是正确待选事件的索引；$ \lambda $ 是L2正则化的参数。模型的参数用 RMSprop 算法进行优化。4. 实验
4.1 数据集及实验设置
在脚本事件预测任务中，事件链摘自Gigaword语料库的《纽约时报》，本文使用C＆C工具进行POS标记和依赖性解析[22]，然后将OpenNlp用于相结构解析和指代消解。在训练集中，有140331个事件图，开发和测试集分别有10000个事件图。对于每个事件图，有8个上下文事件和5个候选事件。
本文在开发集上使用网格搜索来选择最佳的超参数。正则化权重为1×10−7，初始学习率为0.0015。本文的批处理大小为1000。
4.2 实验结果
结果如表1。首先简要介绍几个基线模型，然后分析结果。
1) PMI基于逐点相互信息（PMI），并通过上下文事件和候选事件之间的PMI分数之和对每个候选事件进行评分。
2) Bigram使用最大似然估计基于跳过的Bigram概率来计算事件对关系。
3) Word2vec从大型文本语料库学习单词嵌入。成对事件相关性分数是使用动词和自变量嵌入来计算的。
4) Event-Comp使用孪生网络来计算事件表示的成对事件得分。
5) PairLSTM提出了一种动态内存网络，以将链顺序信息集成到事件关系度量中，并通过使用LSTM隐藏状态表示链中的事件来计算事件对关系。
6) SGNN提出构造事件图以解决基于门控图神经网络嵌入的脚本事件预测问题。
从SGNN和其他基线模型的实验结果可以看出，SGNN可以取得更好的实验性能，这是因为事件图可以捕获更多的事件交互。 而本文所提出的QGGNN既利用了事件图的交互作用，又通过四元数利用了动词与事件中其他成分之间的潜在关系。与现有的最新SGNN相比，QGGNN在SGNN上的占比从52.45％提高到53.31％，这表明四元数可以有效地表示事件，捕捉到事件不同部分之间的交互关系。 并且由于哈密顿乘积中的权重共享机制，模型所需要的参数量也小于SGNN。除SGNN和PairLSTM外，使用t检验的QGGNN效果显著（P<0.01）。
5. 结束语
本文的主要贡献是将四元数这种数据类型的特点与脚本事件的组成特点相结合，以学习到高质量的脚本事件表示。 具体来说，四元数包含1个实部和3个虚部，而1个事件也恰恰是由1个谓语动词和其他3个事件基元组成。基于此，四元数在进行运算的时候由于是采用哈密顿乘积法则，而这种运算法的参数共享机制就可以捕捉到事件内部不同组成部分之间的关联。实验表明，基于事件中不同组件的共存性，该方法明显优于当前最新的SGNN。
-
图 1 哈密顿乘积层与一般全连接乘积层的比较
Fig. 1 Comparsion of Hamilton product layer and fully connected layer
下载:
全尺寸图片
图 2 QGGNN的示意图
Fig. 2 Illustration of QGGNN
下载:
全尺寸图片
-
[1] LI ZHONGYANG, DING XIAO, LIU TING. Constructing narrative event evolutionary graph for script event prediction[EB/OL]. (2018−05−14)[2022−03−23].https://arxiv.org/abs/1805.05081. [2] GEERAERTS, DIKR. Cognitive Linguistics: Basic Readings[M]. Berlin: De Gruyter Mouton, 2008. : 373–400. [3] RUMELHART D E. Notes on a schema for stories[M]//Representation and Understanding. Amsterdam: Elsevier, 1975: 211−236. [4] WANG Zhongqing, ZHANG Yue, CHANG C Y. Integrating order information and event relation for script event prediction[C]//Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Copenhagen: Association for Computational Linguistics, 2017: 57–67. [5] MIZOGUCHI T, YAMADA I. Hyper complex tensor completion with cayley-dickson singular value decomposition[C]//2018 IEEE International Conference on Acoustics, Speech and Signal Processing. Calgary: IEEE, 2018: 3979−3983. [6] XIANG Min, KANNA S, MANDIC D P. Performance analysis of quaternion-valued adaptive filters in nonstationary environments[J]. IEEE transactions on signal processing, 2018, 66(6): 1566–1579. doi: 10.1109/TSP.2017.2787102 [7] ORTOLANI F, COMMINIELLO D, SCARPINITI M, et al. Frequency domain quaternion adaptive filters: Algorithms and convergence performance[J]. Signal processing, 2017, 136: 69–80. doi: 10.1016/j.sigpro.2016.11.002 [8] PARCOLLET T, MORCHID M, BOUSQUET P M, et al. Quaternion neural networks for spoken language understanding[C]//2016 IEEE Spoken Language Technology Workshop. San Diego: IEEE, 2016: 362−368. [9] TITOUAN Parcollet, MIRCO Ravanelli, MOHAMED Morchid, et al. Quaternion recurrent neural networks[EB/OL] (2018−06−12) [2022−03−23].https://arxiv.org/abs/1806.04418. [10] GAUDET C J, MAIDA A S. Deep quaternion networks[C]//2018 International Joint Conference on Neural Networks. Rio de Janeiro: IEEE, 2018: 1−8. [11] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: online learning of social representations[C]// Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. New York: Association for Computing Machinery, 2014: 701–710. [12] KIPF T, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2016−09−09) [2022−03−23].https://arxiv.org/abs/1609.02907. [13] WANG Tingwu, ZHOU Yuhao, FIDLER S, et al. Neural graph evolution: towards efficient automatic robot design[EB/OL]. (2016−06−12) [2022−03−23].https://arxiv.org/abs/1906.05370. [14] LI YUJIA, TARLOW D, BROCKSCHMIDT M, et al. Gated graph sequence neural networks[EB/OL]. (2015−11−17) [2022−03−23].https://arxiv.org/abs/1511.05493. [15] NATHANAEL Chambers, DAN Jurafsky. Unsupervised learning of narrative event chains[C]//Proceedings of ACL-08: HLT. Columbus: Association for Computational Linguistics, 2008: 789–797. [16] XU Dongpo, ZHANG Lina, ZHANG Huisheng. Learning algorithms in quaternion neural networks using ghr calculus[J]. Neural network world, 2017, 27(3): 271–282. doi: 10.14311/NNW.2017.27.014 [17] CHO K, VAN MERRIENBOER B, BAHDANAU D, et al. On the properties of neural machine translation: encoder-decoder approaches[EB/OL]. (2014−09−03) [2022−03−23].https://arxiv.org/abs/1409.1259. [18] ZHOU Bo, CHEN Yubo, LIU Kang, et al. Multi-task self-supervised learning for script event prediction[C]//CIKM’21: Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM, 2021: 3662−3666. [19] SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks[M]//The Semantic Web. Cham: Springer International Publishing, 2018: 593−607. [20] CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[EB/OL]. (2014−06−03) [2022−03−23].https://arxiv.org/abs/1406.1078. [21] BAHDANAU D, CHO K, BENGIO Y. Neural machine translation by jointly learning to align and translate[EB/OL]. (2014−09−01) [2022−03−23].https://arxiv.org/abs/1409.0473. [22] CURRAN J R, CLARK S, BOS J. Linguistically motivated large-scale NLP with C&C and boxer[C]//ACL’07: Proceedings of the 45th Annual Meeting of the ACL on Interactive Poster and Demonstration Sessions. New York: ACM, 2007: 33−36. [23] JANS B, BETHARD S, VULIĆ I, et al. Skip n-grams and ranking functions for predicting script events[C]//EACL’12: Proceedings of the 13th Conference of the European Chapter of the Association for Computational Linguistics. New York: ACM, 2012: 336−344. [24] MIKOLOV T, SUTSKEVER I, CHEN KAI, et al. Distributed representations of words and phrases and their compositionality[EB/OL]. (2013−10−16)[2022−03−23].https://arxiv.org/abs/1310.4546. [25] GRANROTH-WILDING M, CLARK S. What happens next? event prediction using a compositional neural network model[C]// Proceedings of the 30th AAAI Conference on Artificial Intelligence and the 28th Innovative Applications of Artificial Intelligence Conference. Phoenix: AAAI Press, 2016, 30(1).
