Collaborative filtering recommendation approach fused with graph convolutional attention mechanism
-
摘要: 图卷积神经网络(graph convolutional neural network ,GCN)因其强大的建模能力引起了广泛关注,在商品推荐中，现有的图卷积协同过滤技术忽略了邻居节点在传播聚合过程中的重要性，使得用户和商品的嵌入向量表达不够合理。为了解决这一问题，本文提出一种融合图卷积注意力机制的协同过滤推荐模型。首先通过图嵌入技术将用户−项目的交互信息映射到低维稠密的向量空间；其次通过堆叠多层的图卷积网络学习用户与项目间的高阶交互信息；同时融合注意力机制为邻居节点自适应地分配权重，不仅可以捕获更具代表性的邻居影响，还使得在聚合邻居节点的特征信息时，仅依赖于节点之间的特征表达，使其独立于图结构，提高了模型的泛化能力；最后设计了分层聚合函数，将图卷积层学习到的多个嵌入向量加权聚合，使用内积函数得到用户−项目之间的关联分数。在3个真实数据上进行的泛化实验，实验结果验证了该方法的有效性。Abstract: The graph convolutional neural network (GCN) has attracted extensive attention due to its powerful modeling capabilities. In item recommendation, existing graph convolution collaborative filtering techniques ignore the importance of neighbor nodes in the propagation aggregation process, making the embedding vector representation of user and item unreasonable. Therefore, this paper proposes a collaborative filtering recommendation model fused with graph convolutional attention to address this problem. First, user-item interaction information was mapped to a low-dimensional, dense vector space using graph embedding techniques. Further, the high-order interaction information between the user and the item was learned using stacking multiple layers of GCN. The model also fused attention mechanisms to adaptively assign weights to neighbor nodes, thereby capturing the influence of highly representative neighbors. Simultaneously, the model could rely only on feature expressions between nodes when aggregating feature information from neighboring nodes, increasing the independence of the graph structure and improving the generalization capability of the model. Finally, a hierarchical aggregation function that aggregated multiple embedding vectors, which was learned from the graph convolution layer by weighting, was designed, and the inner product function was used to obtain the association score between the user and the item. Results of the extensive experiments conducted on three real datasets have demonstrated the effectiveness of the proposed approach.
-
大数据时代下，为了缓解信息过载问题，推荐系统被广泛应用于个性化信息过滤。协同过滤(collaborative filtering, CF)是应用最广泛的推荐算法，核心思想是从兴趣相似的用户中预测用户偏好。早期的协同过滤推荐模型[1-2]直接使用用户和项目ID作为嵌入向量，嵌入函数缺乏对用户与项目间交互信息的明确编码，导致所学习的嵌入表达具有局限性，不足以产生令人满意的CF嵌入。随后，SequentialMF模型[3]将更多的邻居信息整合到嵌入过程，提高了嵌入质量，但模型受线性乘积的影响，无法有效地捕捉交互数据中的非线性结构。广义矩阵分解模型[4]在浅层结构引入的神经网络赋予模型具有学习非线性交互的能力，使得它可以捕获用户与项目间的二阶交互关系，但却无法捕获包含更多信息的高阶交互，导致模型性能受限。
图卷积神经网络是一种针对图结构数据的深度学习模型[5]，具有更抽象的学习能力，其强大的表征能力，可以捕获包含许多丰富信息且更为抽象的高阶关系。通过多次迭代图卷积层还可以学习嵌入表征的全局结构，挖掘海量数据中深层次的属性特征，建模用户与项目之间的高阶交互的非线性关系。PinSage[6]、NGCF[7]和LightGCN[8]等均为典型的图卷积协同过滤技术。但是，它们聚合邻居节点的方式依赖于图结构，局限了模型的泛化能力，并且为所有邻居统一分配固定的权重，不能区分邻居信息的重要性。另外，数据稀疏性对模型的推荐效果也会产生一定的消极影响。
为了解决上述提到的问题，本文提出一种融合图卷积注意力机制的协同过滤推荐模型，利用图嵌入技术将初始的用户和项目信息嵌入到低维稠密的向量空间，缓解了数据稀疏性对模型性能的消极影响，通过构建用户−项目交互图使得嵌入函数可以显式地学习用户与项目间的交互信息，以产生令人满意的CF嵌入；其次利用用户−项目交互图的拓扑结构来建模用户与项目间的高阶交互信息，通过堆叠多层图卷积网络以递归的方式学习此类高阶关系，以此揭示用户与项目之间的耦合关系；此外融合注意力机制聚合邻居节点信息，根据邻居节点的贡献值为其动态分配权重，捕获更具代表性的邻居影响，提高推荐结果的可解释性，而且这种聚合方式仅依赖于节点之间的特征表达，独立于图结构，可以提高模型的泛化能力；并设计了分层聚合函数，将图卷积层学习到的多个嵌入向量加权聚合，学习每一层嵌入向量对最终嵌入向量的影响；最后使用内积函数得到用户−项目之间的关联分数。
1. 相关工作
基于协同过滤的推荐算法。矩阵分解[9]是经典的协同过滤方法，它将用户/项目表示在潜在向量的低维空间，通过用户/项目的潜在向量的内积来预测用户对项目的评分。随着深度学习的发展，基于深度学习的推荐模型可以更好地增强模型的表达能力。它将用户/项目信息经神经网络的表征学习，得到更具代表的用户/项目表达。文献[10]和文献[11]是经典的基于深度学习的协同过滤推荐模型。
基于图嵌入的推荐算法。图嵌入的基本思想是使用降维技术将节点的高维信息映射到低维稠密的向量空间，以此完成聚类[12]和分类[13]等任务。最初的嵌入方式使用随机游走[14]来映射向量的低维嵌入，但是随机游走每一步生成所有项目的排名分数，导致了效率低下问题。随后研究者开始利用网络嵌入模型[15-16]来缓解这一限制。文献[15]提出了异构偏好嵌入模型，将用户偏好和查询意图编码到低维向量空间中，通过相似度计算来生成推荐列表。Hop-Rec[16]将矩阵分解和基于图的学习模型融合在一起，通过将观察到的用户−项目的直接交互因子化来获取用户偏好，从用户−项目交互图中随机游走来提取间接偏好。
基于图卷积神经网络的推荐算法。图卷积网络已经在多种领域取得了成功，最近的研究趋势是将卷积推广到不满足平移不变性的图结构数据中，使用卷积算子学习图结构数据。GraphSage[17]是一个通用的图卷积推荐框架，利用一个广义聚合函数从节点的局部邻域采样并聚集特征来生成嵌入向量，使得图卷积网络在推荐领域取得了进一步成功。文献[18]通过将用户−项目的交互数据转换为3个异构图来学习异构图之间的共享特征表示，利用图卷积技术来聚集邻居的特征，保持了图数据的局部性质。
基于注意力机制的推荐算法。图注意力网络(graph attention network, GAT)[19]不仅可以过滤输入数据中的噪声数据，还可以加强某些代表性数据的权重，因此在推荐系统中应用注意力机制逐渐成为推荐新技术。文献[20]提出一种基于自注意力机制的属性异构信息网络嵌入的商品推荐模型，模型通过属性异构信息网络嵌入学习用户与项目的低维嵌入表示，利用自注意力机制考虑不同的属性信息对推荐结果有不同程度的影响，克服了传统属性异构信息网络嵌入推荐模型的局限性。文献[21]是一种基于双层注意力机制的推荐模型，通过引入局部注意力和相互注意力学习用户与评论之间所存在的潜在相关性，提高了推荐结果的可解释性。
2. 问题定义与解决方案
2.1 问题定义
定义1 用户集与项目集：用U={u1, u2, …, uM}表示用户集，I={i1, i2, …, iN}表示项目集，其中，M为用户数量，N为项目数量。
定义2 用户−项目交互图：令Gui={U∪I, Eui}表示用户−项目交互图，其中U和I为顶点集合，|U|和|I|分别表示用户与项目的数量，Eui为用户与项目之间边的集合。
2.2 解决方案
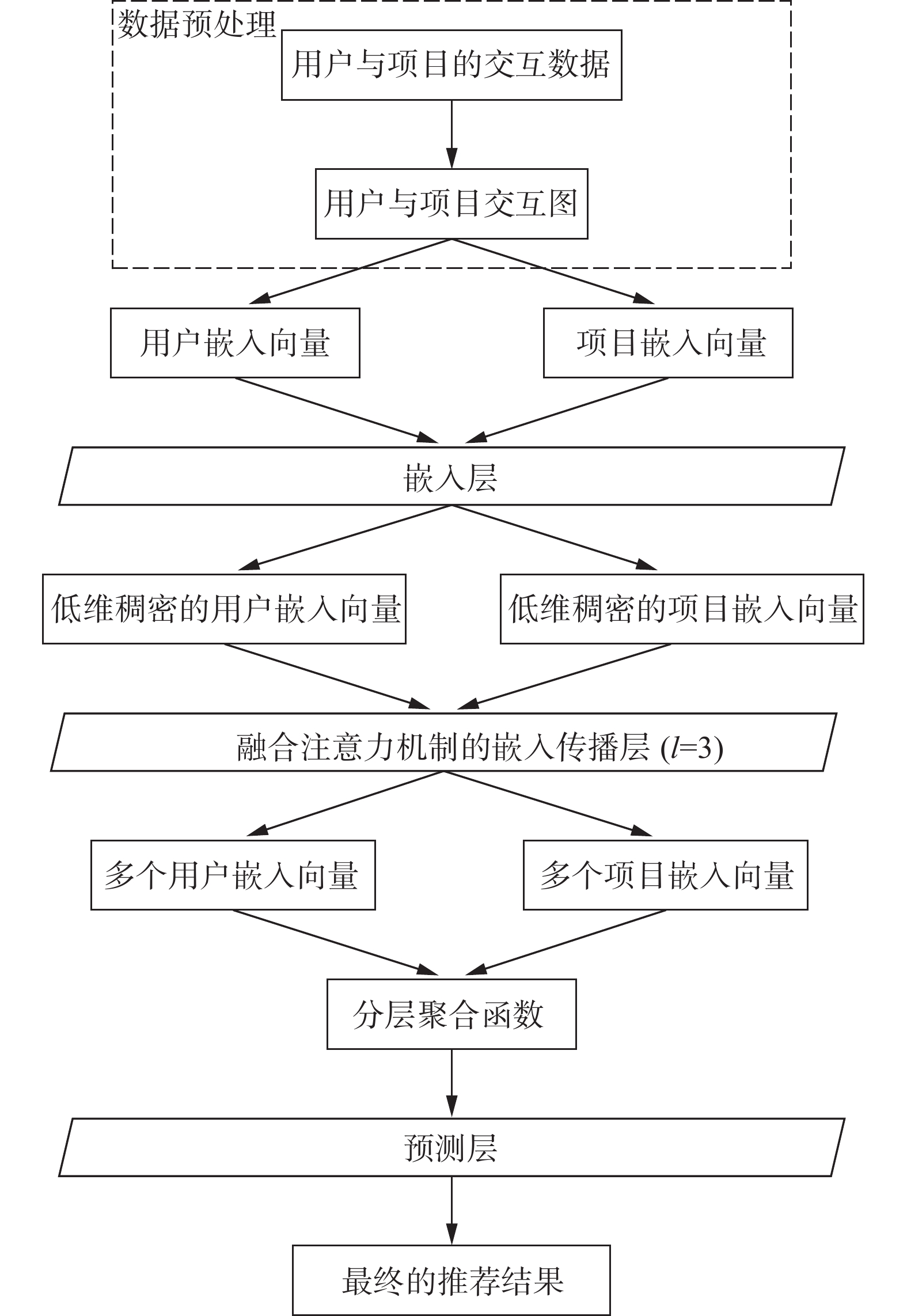
本文的总体解决方案的流程图如图1。
图 1 模型流程Fig. 1 Model flow
下载:
全尺寸图片
模型流程共分3步。
1）构建模型的嵌入层。首先将用户与项目的原始交互数据，以one-hot编码的方式将其转换为数据；其次根据用户与项目间的交互记录构造用户−项目交互图；最后利用图嵌入技术将用户与项目信息嵌入到低维稠密的向量空间。
2）构建融合注意力机制的嵌入传播层。将嵌入层得到的低维稠密向量送入嵌入传播层，通过堆叠多层图卷积网络在嵌入空间构建信息交互流，强化用户与项目间的传播嵌入；融合注意力机制根据邻居节点的贡献值为其动态的分配权重。
3）构建预测层。经嵌入传播层学习将得到多个用户和项目的嵌入向量，将其送入分层聚合函数得到最终的嵌入向量表达；最后采用内积交互函数，得到最终的推荐结果。
本文设计的融合图卷积注意力机制的协同过滤模型，框架如图2，主要由3个模块组成：1）嵌入层、初始化用户和项目的嵌入向量；2）融合注意力机制的嵌入传播层，通过图卷积技术细化用户与项目间的高阶交互信息，融合注意力机制学习邻居节点在传播聚合过程中的重要性；3）预测层，采用内积交互函数，得到用户与项目之间的关联分数。
图 2 融合图卷积注意力机制的协同过滤推荐模型框架Fig. 2 Framework of collaborative filtering recommendation model fused with graph convolutional attention下载:
全尺寸图片
2.2.1 嵌入层
模型在嵌入层通过在用户−项目交互图上传播嵌入来强化嵌入向量的潜在特征。根据嵌入模型[22-23]，一个用户u（或项目i）的嵌入向量可表示为cu∈Rd(ci∈Rd)，其中d表示嵌入维度，那么由用户和项目嵌入向量组成的参数矩阵作为初始嵌入向量查找表，如下式：
$$ {\boldsymbol{E}}_m = [{\boldsymbol{e}}_{u_1}\;{\boldsymbol{e}}_{u_2}\; \cdots \;{\boldsymbol{e}}_{u_M}\;{\boldsymbol{e}}_{i_1}\;{\boldsymbol{e}}_{i_2}\; \cdots \;{\boldsymbol{e}}_{i_N}] $$ (1) 式中：M表示用户数量，N为项目数量。嵌入查找表作为用户嵌入和项目嵌入的初始状态，以端到端的方式进行传递和优化。
2.2.2 融合注意力机制的嵌入传播层
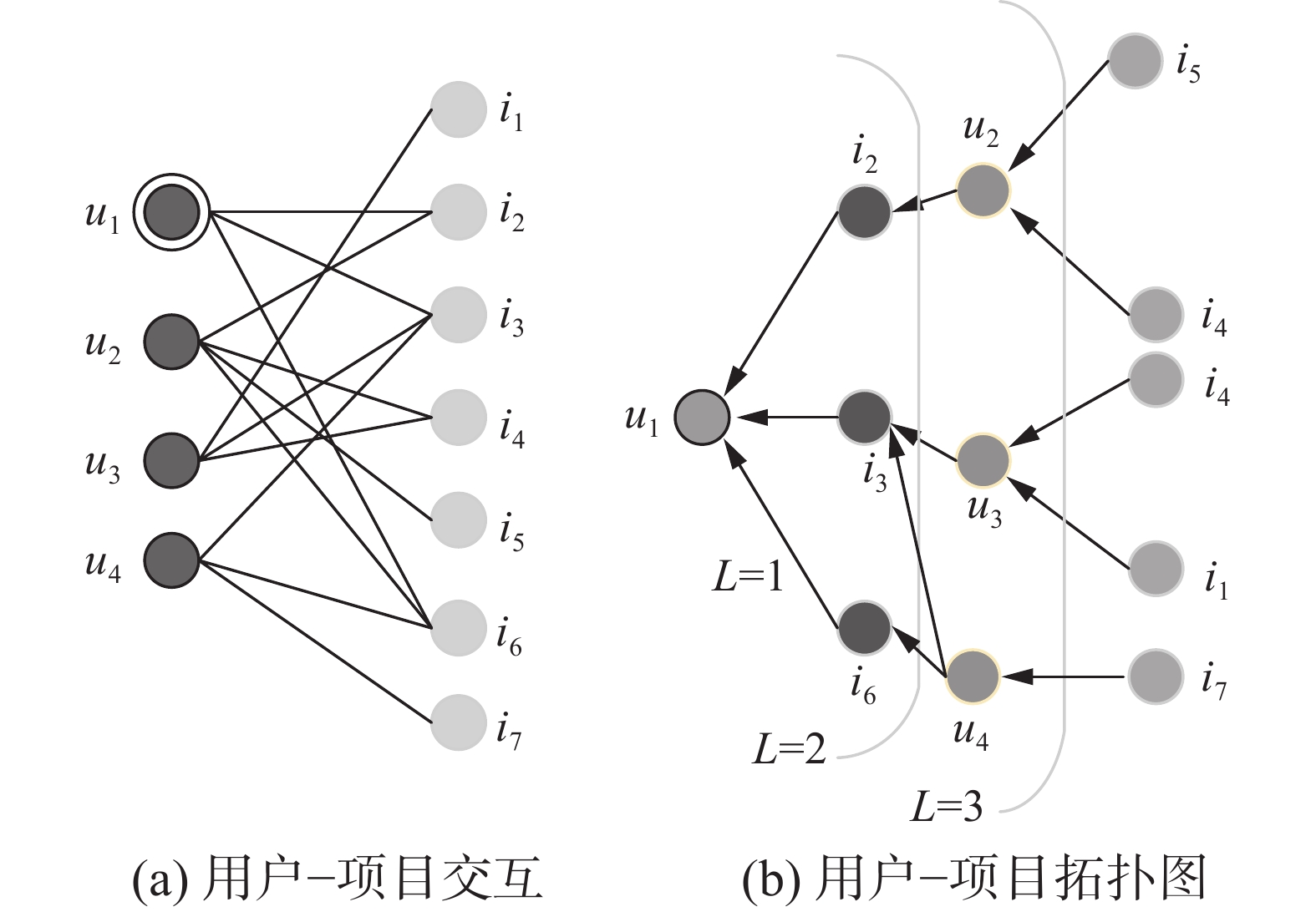
本文设计了融合注意力机制的嵌入传播层，通过学习用户−项目交互图的拓扑结构来构建用户与项目间的高阶交互信息，图3给出了用户−项目交互图。
图 3 用户−项目交互图Fig. 3 User-Item interaction diagram下载:
全尺寸图片
图3 (a)为用户−项目交互图，图3 (b)为目标用户u1的高阶交互关系图（即交互图的拓扑结构）。u1的高阶交互是指从路径长度L>1的任何节点到达目标节点u1的路径，此类高阶交互承载着u1更为丰富的交互信号。例如，路径u1←i3←u3和u1←i3/i6←u4表示u1与u3和u4之间具有行为相似性，但u1与u4之间有两次交互，由此可以推断u1与u4具有更高的亲密度，u4更能影响u1的决策，也就是说u4应该被分配更高的权重。然而，以往的模型[7-8]为邻居节点分配统一的静态权重，无法区分用户亲密度对用户决策的影响。例如，i4(u1←i2←u2←i4和u1←i3←u3←i4)与i7(u1←i3←u4←i7和u1←i6←u4←i7)均有两条路径可以到达u1，传统模型无法区分i4与i7哪一个项目更能引起u1的兴趣。本文模型融合注意力机制，可以根据用户与邻居节点的亲密度，自适应地为其分配权重。因此，邻居节点u4相较于u2拥有更高的权重，由此预测i7更能引起u1的兴趣。
此外，随着路径的增加每一层嵌入传播层在反映用户偏好时有不同的贡献，例如，路径L=1为用户直接交互的项目，此类信息更能反映用户偏好，因此在聚合多个嵌入向量对最终嵌入向量的影响时，应该被赋予更高的比重。本文设计的分层聚合函数可以捕获不同层的嵌入表达，以实现路径越短对最终向量的影响越大。例如，由图3 (b)可知i4的两条路径在L=3层分化，而i7的两条路径在L=2层分化，则可以预测i7更能引起u1的兴趣。
模型通过堆叠多层图卷积层来构建嵌入传播层，为了更好地构建高阶传播，首先建模单阶传播。在现实世界中，用户交互的项目直接反映了用户偏好。由图3可知对于用户−项目交互图中存在连接的用户−项目对(u，i)，可将从项目i到用户u 的消息传递定义为
$$ {\boldsymbol{m}}_{u \leftarrow i} = f({\boldsymbol{e}}_{{i}},{\boldsymbol{e}}_{{u}},p_{ui}) $$ (2) 式中：u ← i表示从项目到用户的方向传递，m表示传递消息的嵌入向量，
$ f( \bullet ) $ 是一个消息编码函数，pui为相关系数控制(u，i)边上每次传播时的衰减因子。根据经典的图卷积推荐技术原理[7-8]，相关性系数p可定义为拉普拉斯范数：
$$ p_{ui} = \frac{1}{{\sqrt {|N_u||N_i|} }} $$ (3) 其中Nu和Ni分别表示用户u交互的项目集以及与项目i交互的用户集。
本文的嵌入传播层为了更好的建模用户与项目间的交互信息，利用哈达玛积(
$ {\boldsymbol{e}}_{{i}} \odot {\boldsymbol{e}}_{{u}} $ )将用户与项目的交互编码到消息传递机制中，考虑了$ {\boldsymbol{e}}_{{i}} $ 与$ {\boldsymbol{e}}_{{u}} $ 之间的交互信息，使得模型在传递消息时依赖于$ {\boldsymbol{e}}_{{i}} $ 和$ {\boldsymbol{e}}_{{u}} $ 之间的亲密度值，也就是说相似的用户/项目之间可以传递更多的消息。此外，融合注意力机制自适应地为邻居节点分配权重，以此捕获邻居节点的重要性。由此消息编码函数$ f( \bullet ) $ 可定义为$$ {\boldsymbol{m}}_{u \leftarrow i} = p_{ui}\left(\sigma \left(\sum\limits_{i \in {N_u}} {\alpha _{ui}{{{\boldsymbol{W}}}}_1{\boldsymbol{e}}_i} + {\boldsymbol{W}}_2\left({{{\boldsymbol{e}}_i}} \odot {{{\boldsymbol{e}}_u}}\right)\right)\right. $$ (4) 式中：W1、W2∈
$ {{\bf{R}}^{d' \times d}} $ 为可训练的权重矩阵，用于提取重要的嵌入信息；矩阵维度为$ d' \times d $ ；$ d' $ 为转换大小；$\alpha _{ui }$ 为注意力权重；$ \odot $ 表示逐元素相乘。依据GAT[19]原理，在构建单阶传播时，邻居节点i对目标节点u的影响，可以由注意力相关分数表示：
$$ {\boldsymbol{e}}_{ui} = {\text{LeakyReLu}}({\boldsymbol{e}}_u||{\boldsymbol{e}}_i) $$ (5) 式中：||表示向量的拼接，LeakyReLu[24]为激活函数。为了得到对应的注意力权重，模型使用softmax函数计算目标用户u的所有邻居信息，对各个邻居节点的贡献值进行归一化，获得每个邻居节点i的权重，计算方式为
$$ \alpha _{ui} = {\text{softmax}}({\boldsymbol{e}}_{ui}) = \frac{{\exp ({\boldsymbol{e}}_{ui})}}{{\displaystyle\sum\limits_{k \in {N_u}} {\exp ({\boldsymbol{e}}_{uk})} }} $$ (6) 模型通过聚合目标用户u的邻居节点特征来更新用户u的嵌入表达eu，采用LeakyRelu激活函数显式地利用mu ← i连接信息来关联用户和项目嵌（LeakyRelu函数允许对消息传递过程中的正负信号进行编码），则聚合函数可以抽象为
$$ {\boldsymbol{e}}_u^{(1)} = {\text{LeakyReLu}}({\boldsymbol{m}}_{u \leftarrow i}) $$ (7) 其中eu表示用户u在单层传播之后得到的用户嵌入向量。
本文模型通过叠加多个单阶传播层来挖掘高阶的交互信息，以此构建模型的高阶传播。由图3(b)可知，堆叠两层可捕获用户间的行为相似性（如u1−i3/i6−u4），堆叠3层可挖掘潜在的推荐优先级（如i7的两条路径u1←i3←u4←i7和u1←i6←u4←i7）。模型利用堆叠的l层融合注意力机制的嵌入传播层，获得用户（或项目）l-阶邻居节点的特征信息，在第l层以递归的方式传播此类特征信息，计算方式为
$$ {{e}}_u^{(l)} = {\text{LeakyReLu}}\left(\sum\limits_{i \in N_u} {{\text{m}}_{u \leftarrow i}^{(l)}} \right) $$ (8) 其中，根据单阶嵌入传播层的构建，高阶邻居节点影响
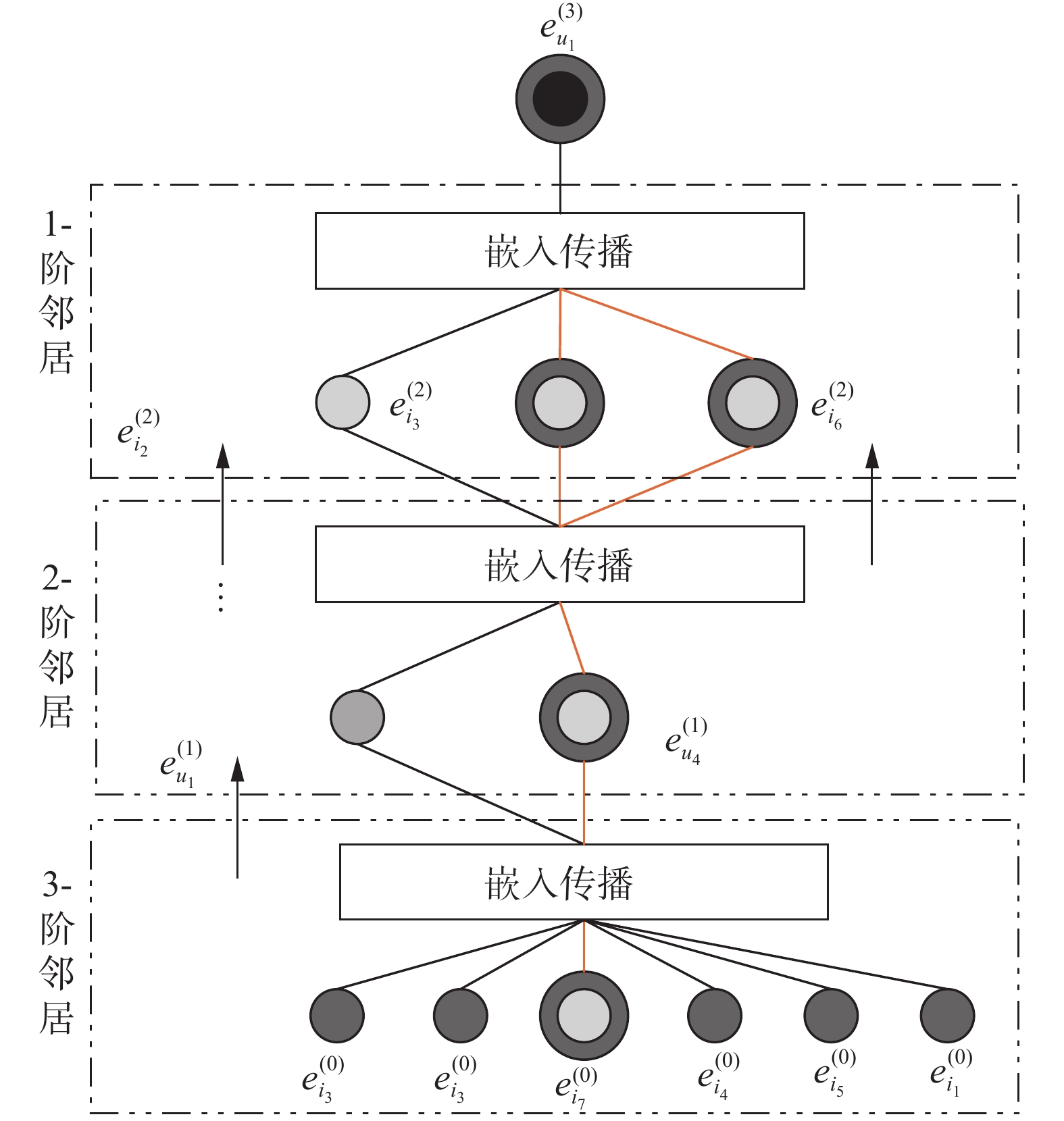
$\displaystyle\sum\limits_{i \in N_u} {m_{u \leftarrow i}^{(l)}}$ 的具体表达形式可定义为$$ \sum\limits_{i \in N_u} {{{m}}_{{{u}} \leftarrow {{i}}}^{({{l}})}} = p_{ui}\left({\left(\sigma \left(\sum\limits_{i \in N_u} {\alpha _{ui}{{{\boldsymbol{W}}}}_1{{{\boldsymbol{e}}_i}}} \right)\right)^{(l - 1)}} + {{{\boldsymbol{W}}}}_2\left({{{\boldsymbol{e}}}}_i^{(l - 1)} \odot {{{\boldsymbol{e}}}}_u^{(l - 1)}\right)\right) $$ (9) 图4给出了图3(b)中三阶路径u1 ←i3/i6 ←u4 ←i7在嵌入传播时被捕获的过程。分析图3(b)可知，u1与u4具有更高的亲密度，也就是说在采用注意力机制聚合邻居节点的贡献值时，u4被分配了更高的权重，由此预测i7更能引起u1的兴趣。因此，在所有到达u1的三阶路径中，路径u1 ←i3/i6 ←u4 ←i7被捕获。同样，当堆叠l层嵌入传播层时，用户与项目之间的高阶交互信息仍可以在嵌入传播的过程中被捕获。
图 4 三阶嵌入传播Fig. 4 Illustration of third-order embedding propagation下载:
全尺寸图片
2.2.3 模型预测层
在经过l层传播后，得到了用户u的多个嵌入表达，即
$\left\{ {\boldsymbol{e}}_u^{(1)}, {\boldsymbol{e}}_u^{(2)},\cdots ,{\boldsymbol{e}}_u^{(l)}\right\} $ 。由图3分析可知不同嵌入层获得的嵌入向量对用户偏好有不同的影响，因此本文设计了分层聚合函数进一步结合在每一层捕获的嵌入向量，构成用户最终的向量表达。对经过l层传播后得到的多个项目嵌入表达，同理得到最终的项目嵌入向量表达，分别如下所示：$$ {\boldsymbol{e}} _u= \sum\limits_{i = 0}^L {\beta_ l \times {\boldsymbol{e}}_{{u}}^{({{l}})}} $$ (10) $$ {\boldsymbol{e}}_{i} = \sum\limits_{i = 0}^L {\beta _l \times {\boldsymbol{e}}_{{i}}^{({{l}})}} $$ (11) 式中：βl≥0表示第l层嵌入对最终嵌入表达的重要性，在本文中设置βl =1/(1+L)。
最后，在模型预测层，采用内积交互函数得到用户对目标项目的偏好，计算方式如下：
$$ \hat y_{ui} = {\boldsymbol{e}}_{{u}}^{\rm{T}} \times {\boldsymbol{e}}_i $$ (12) 2.2.4 模型优化
本文模型使用贝叶斯损失函数[25]对模型进行优化，原因是贝叶斯损失函数考虑了观察到的交互和未观察到的交互之间的相对顺序。具体地说，它假设观察到的交互对用户偏好的影响更大，优化目标如下：
$$L = \sum\limits_{u,i,j \in O} { - \ln \sigma ( {\hat y_{ui}} -\hat y_{uj})} + \lambda ||{{\varTheta }}|{|^2}$$ (13) 其中，
$O = \{ (u,i,j)|(u,i) \in {{\text{R}}^ + },(u,j) \in {{\mathbf{R}}^ - }\}$ 被定义为用户与项目交互数据集合，每一个数据都是一个三元组。${{\mathbf{R}}^ + }$ 表示观察到的用户−项目交互，${{\mathbf{R}}^ - }$ 表示未观察到的用户−项目交互，$ \sigma () $ 是sigmoid函数。$\lambda ||{{\varTheta }}|{|^2}$ 为L2正则化项，$ \lambda $ 为正则化系数，它控制L2正则化强度防止过拟合，${{\varTheta }}\left\{ {E,\left\{ {{\boldsymbol{W}}_1^{\left( {{l}} \right)},{\boldsymbol{W}}_2^{\left( {{l}} \right)}} \right\}_{{{l}} = 1}^L} \right\}$ 表示所有可训练的模型参数。Dropout策略可以在模型训练时有效防止模型的过拟合，本文采用消息丢弃的Dropout策略。在消息丢弃方法中，按照概率p 随机舍弃式(9)计算出的消息，使其不聚合到用户/项目的嵌入向量中。
3. 实验及仿真结果
3.1 数据集
实验数据集采用Gowalla、Yelp2018以及Amazon-Book 3个公开的数据集，对于每一个数据集，随机选择每个用户的80%的交互历史构成训练集，剩下的20%作为测试集，随机选取训练集中的10%作为验证集，用于参数的调试。表1给出了3个数据集的统计信息。
表 1 实验数据信息Table 1 Statistics of the datasets数据集 用户 项目 交互记录 稀疏度 Gowalla 29858 40981 1027370 0.00084 Yelp2018 31831 40841 1666869 0.00128 Amazon-Book 52643 91599 2984108 0.00062 3.2 对比算法
本文提出的图卷积注意力机制协同过滤（GACF）模型分别与5种推荐模型比较：
1）MF[9]模型：该模型利用奇异值方法对矩阵进行分解，通过贝叶斯个性化排名损失函数对模型进行优化，并将用户−项目交互作为交互函数的目标值。
2）NeuMF[11]模型：该模型是一个经典的基于深度学习的协同过滤推荐算法，它结合了传统矩阵分解和多层感知机，通过元素层面上的用户和项目嵌入和串联多个隐藏层来捕获用户−项目之间的非线性特征交互，能够捕获用户和项目间的关联关系。
3）Hop-Rec[10]模型：该模型基于图神经网络，通过在图上的随机游走并结合图顶点的度，以一定概率采样用户和项目的高阶关系，可以显式地捕获用户和项目之间的高阶偏好，丰富了训练数据，提高了推荐结果的可解释性。
4）GC-MC[26]模型：该模型基于消息传递的图自动编码，通过编码器生成用户和项目表示，并利用用户和项目的一阶交互信息来捕捉它们之间的隐性特征，提高了推荐模型的泛化能力。
5）LightGCN[8]：该模型基于文献[7]所提出 的模型，文献[7]模型中特征变换和非线性激活两个复杂的设计，降低了模型的训练难度。
6）NGCF[7]模型：该模型是基于图卷积神经网络的最新推荐模型，它利用了用户与项目交互图的拓扑结构将交互信息嵌入到学习过程中，并构建了3层图卷积神经网络对交互信息进行嵌入传播学习，通过将传播层学习的嵌入向量进行聚合，得到用户与项目之间的关联分数。
3.3 实验设置
本文模型和算法使用Python语言基于TensorFlow框架实现，机器配置为CPU i7-8700K 3.7 GHz，操作系统为Windows 10。在实验中，基于以往模型[7]的经验，正则化系数设置为1×10−4，每次处理的数据量大小为1024，嵌入大小为64，使用64×64的图卷积层，迭代次数为100 次时模型收敛。采用Adam[27]作为优化器，参数初始化采用Xavier方式。经验证集测试后，学习率lr设置为0.001，Dropout率p设置为0.1。
3.4 评估指标
对于测试集中的每个用户，将用户未交互的所有项目视为负样本，将用户已经交互的项目作为正样本。本文中每种模型均输出用户对所有项目的偏好分数，为了评估模型在top-k推荐效果方面的优越性，实验采用召回率(RRecall@K)和归一化折现积累收益(NNDCG@K)作为推荐效果方面的评价指标。实验中，k分别取值为20、40、60、80、100，模型总体推荐效果取其平均值。
召回率计算的是所有“被正确推荐的项目”占所有“应该被推荐的正确的项目”的比例，计算公式为
$$ R_{{\rm{Recall}}@K} = \frac{{\displaystyle\sum\limits_u {|R(u) \cap T(u)|} }}{{\displaystyle\sum\limits_u {T(u)} }} $$ (14) 式中：R(u)是为用户推荐的项目集合，T(u)为测试集上用户感兴趣的项目的集合。
NNDCG@K是一种基于排名的测试指标，排名靠前的项目得分更高。
$$ N_{\rm{NDCG}@K} = \frac{1}{n}\sum\limits_{i = 1}^K {\frac{{{2^{{R_{{\text{reli}}}}}} - 1}}{{\log_2(i + 1)}}} $$ (15) 式中：
$ {R_{{\text{reli}}}} $ 表示用户对第i个项目的评分，$\log_2(i + 1)$ 是一个位置递减权重。3.5 模型推荐效果比较
3.5.1 总体比较
将本文模型与对比模型分别在3个不同的数据集进行实验，实验结果如表2所示。从模型推荐效果的总体比较来看，本文提出的模型在3种数据集上的2种评价指标的表现均大幅度优于其他对比方法，说明了模型设计的合理性，同时也证明了模型的高效性和良好的泛化能力。
表 2 总体比较Table 2 Overall performance comparison模型 Gowalla Yelp2018 Amazon-Book RRecall@K NNDCG@K RRecall@K NNDCG@K RRecall@K NNDCG@K MF 0.1291 0.1878 0.0317 0.0617 0.0250 0.0518 NeuMF 0.1326 0.1985 0.0331 0.0840 0.0253 0.0535 GC-MC 0.1395 0.1960 0.0365 0.0812 0.0288 0.0551 Hop-Rec 0.1399 0.2128 0.0388 0.0857 0.0309 0.0606 LightGCN 0.1830 0.1554 0.0649 0.0530 0.0411 0.0315 NGCF 0.1547 0.2237 0.0438 0.0926 0.0344 0.0630 GACF 0.2285 0.2597 0.1038 0.1455 0.0634 0.0936 GACF较NGCF的提升率/% 47.51 16.09 136.99 57.13 84.30 48.57 3.5.2 嵌入传播层数的影响
实验通过改变模型的深度，探究最佳的嵌入传播层数，在实验中，分别设置了{1,2,3,4}等不同的层数。观察表3可知，GACF模型相较于NGCF模型均取得了更好的推荐效果。此外，随着图卷积层的层数的增加，模型的推荐效果也有显著的提升。但是当层数增加到4层时，在Gowalla数据集和Amazon-Book数据集上，模型出现了过拟合现象。原因是当嵌入传播层加深时，导致节点间的特征表达过度平滑化，使之缺少节点表征，进而缺少区分性，降低了模型的推荐效果，其次当堆叠过深的嵌入传播层，导致过多的噪声数据参与模型训练，使模型出现过拟合现象，也从侧面验证了堆叠三层的嵌入传播层足以捕获有效的CF 信号。
表 3 层数对模型推荐效果的影响Table 3 Effect of number of layers on the model recommendation层数 方法 Gowalla Yelp2018 Amazon-Book RRecall@K NNDCG@K RRecall@K NNDCG@K RRecall@K NNDCG@K 1 层 NGCF 0.1511 0.2218 0.0417 0.0889 0.0315 0.0618 GACF 0.2197 0.2557 0.0975 0.1383 0.0579 0.0916 提升率/% +45.4 +15.28 +133.81 +55.57 +83.81 +48.22 2层 NGCF 0.1535 0.2238 0.0429 0.0926 0.0319 0.0622 GACF 0.2246 0.2587 0.1005 0.1448 0.0588 0.0924 提升率/% +46.32 +15.59 +134.27 +56.37 +84.33 +48.55 3层 NGCF 0.1547 0.2237 0.0438 0.0926 0.0344 0.0630 GACF 0.2285 0.2597 0.1038 0.1455 0.0634 0.0936 提升率/% +47.51 +16.09 +136.99 +57.13 +84.3 +48.57 4层 NGCF 0.1560 0.2240 0.0427 0.0907 0.0342 0.0636 GACF 0.2294 0.2600 0.1010 0.1424 0.0630 0.0945 提升率/% +47.05 +16.07 +136.53 +57.00 +84.21 +48.58 3.5.3 模型top-k推荐有效性评估
为了探究融合注意力机制的有效性以及分层聚合函数的合理性，实验对模型的top-k推荐进行了RRecall@K和NNDCG@K两方面的评估。图5的实验结果表明，本文模型在3个数据集上所表现出的推荐效果均远高于其他模型，表明本文方法所推荐的前top-k列表更具个性化。原因是模型在嵌入传播层融合注意力机制，衡量了邻居节点的重要性，自适应地为其动态分配权重，帮助目标用户选择更具代表性的项目。其次，模型通过分层聚合函数，将图卷积层学习到的多个嵌入向量加权聚合，学习其对最终嵌入表达的重要性，实现了路径越短对最终向量的影响越大。
图 5 两个不同数据集上top-k推荐效果Fig. 5 top-k recommendation performance on two different data sets下载:
全尺寸图片
3.6 超参数学习
3.6.1 学习率的影响
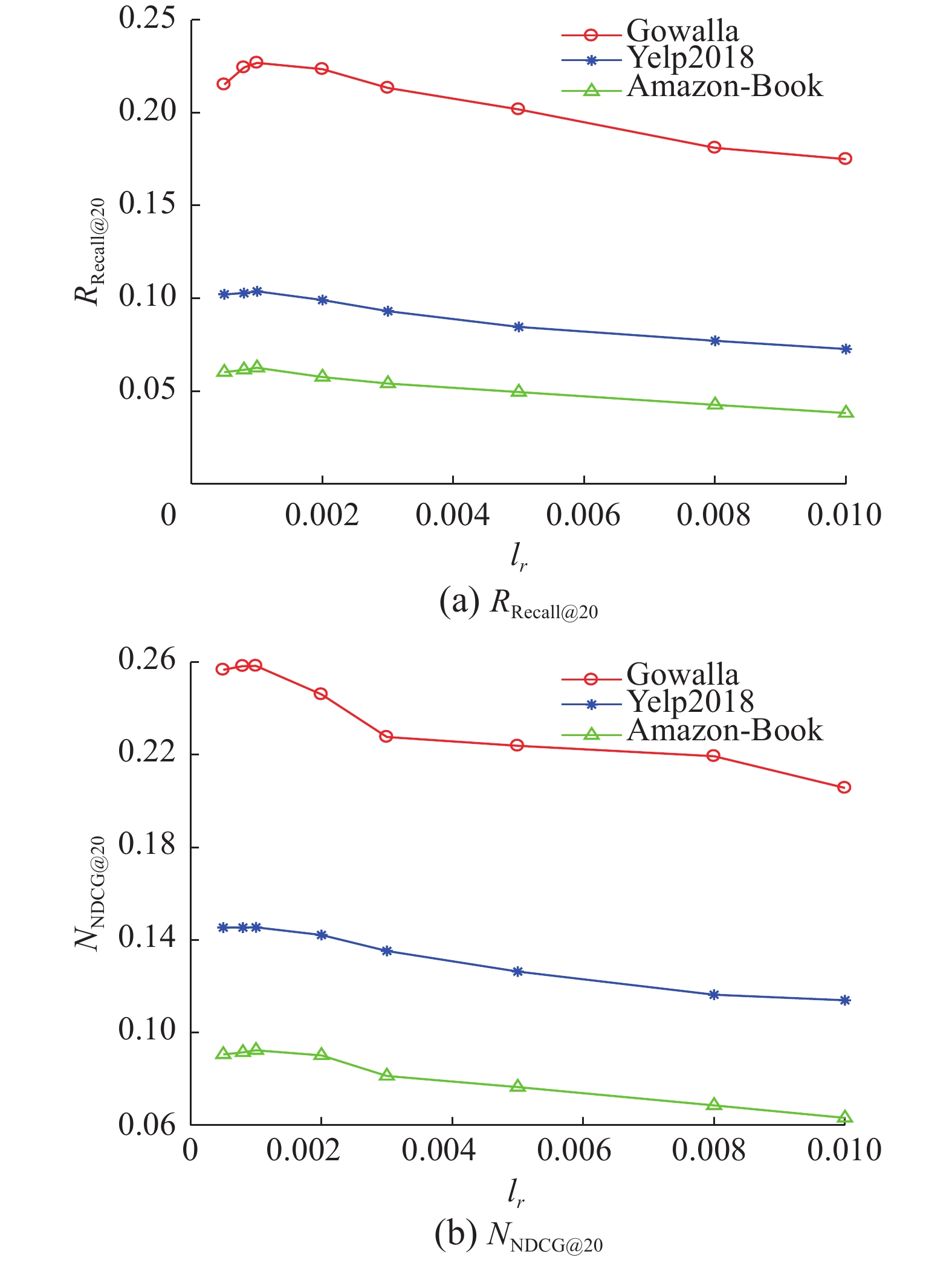
模型的学习率直接影响着神经网络模型的收敛状态，进而影响着模型学习的性能表现，因此选择一个合适的学习率对于一个神经网络模型的影响至关重要。本文在实验中，将其设置为一个超参数，通过动态学习率策略调整训练出一个最优的学习率大小。
从图6的实验结果观察可知当学习率lr=0.001时，模型的总体效果达到最佳，当学习率lr=0.01时，模型的总体效果最差。在Gowalla数据集上，当lr=0.01时RRecall@20和NNDCG@20的结果分别为0.1750和0.2057；当lr=0.001时RRecall@20和NNDCG@20的结果分别为0.2269和0.2584，评价指标分别提高了29.66%和25.62%。在Yelp2018数据集上，当lr=0.01时RRecall@20和NNDCG@20的结果分别为0.0727和0.1140；当lr=0.001时RRecall@20和NNDCG@20的结果分别为0.1028和0.1455，评价指标分别提高了41.40%和27.63%。在Amazon-Book数据集上，当lr=0.01时RRecall@20和NNDCG@20的结果分别为0.0382和0.0623；当lr=0.001时RRecall@20和NNDCG@20的结果分别为0.0611和0.0924，评价指标分别提高了59.95%和48.31%。由此可见，合适的学习率对于模型效果的表现有直接影响。
图 6 学习率测试结果Fig. 6 Learning rate test results下载:
全尺寸图片
3.6.2 Dropout率学习
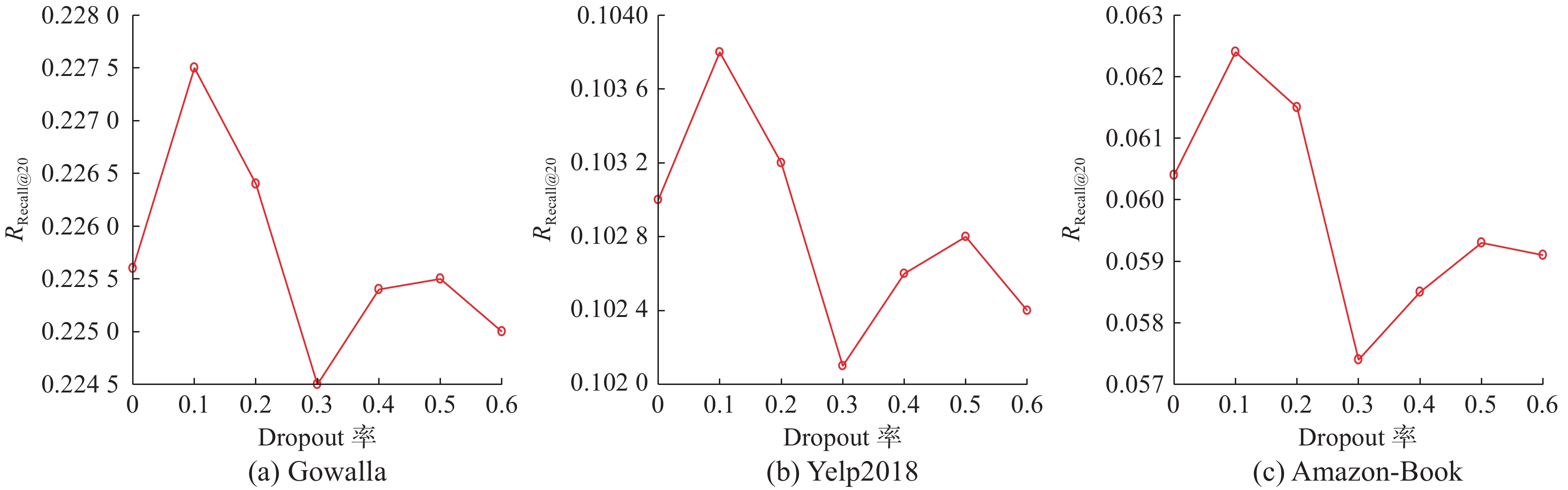
Dropout策略可以在模型训练时有效防止模型的过拟合，本文采用消息丢弃Dropout策略。图7给出节点丢弃率p作用于3个数据集上所产生的不同影响。在Gowalla、Yelp2018和Amazon-Book数据集上，当p=0.1时获得了最佳的召回率，当p=0.3时获得了最差的召回率。
图 7 节点丢弃率的影响Fig. 7 Effect of message dropout ratios下载:
全尺寸图片
4. 结束语
本文提出了一种图卷积注意力机制协同过滤推荐模型，模型首先在嵌入层考虑用户与项目的交互信息，其中在嵌入传播层融合注意力机制，综合考虑了邻居节点对目标节点影响的重要性，通过分层聚合函数将嵌入层学习到的多个嵌入向量加权聚合，学习其对最终嵌入表达的重要性。最后，利用内积运算对用户与项目之间的关联分数进行预测。实验结果表明，与现有的主流协同过滤推荐模型相比，本文模型取得了更好的推荐效果。在未来的工作中，将考虑影响推荐性能的更多属性，如用户的社会关系、用户兴趣的动态变化等，尝试通过图卷积神经网络协同过滤技术缓解推荐系统中的冷启动问题，进一步提升推荐的准确性。
-
图 1 模型流程
Fig. 1 Model flow
下载:
全尺寸图片
图 2 融合图卷积注意力机制的协同过滤推荐模型框架
Fig. 2 Framework of collaborative filtering recommendation model fused with graph convolutional attention
下载:
全尺寸图片
图 3 用户−项目交互图
Fig. 3 User-Item interaction diagram
下载:
全尺寸图片
图 4 三阶嵌入传播
Fig. 4 Illustration of third-order embedding propagation
下载:
全尺寸图片
图 5 两个不同数据集上top-k推荐效果
Fig. 5 top-k recommendation performance on two different data sets
下载:
全尺寸图片
图 6 学习率测试结果
Fig. 6 Learning rate test results
下载:
全尺寸图片
图 7 节点丢弃率的影响
Fig. 7 Effect of message dropout ratios
下载:
全尺寸图片
表 1 实验数据信息
Table 1 Statistics of the datasets
数据集 用户 项目 交互记录 稀疏度 Gowalla 29858 40981 1027370 0.00084 Yelp2018 31831 40841 1666869 0.00128 Amazon-Book 52643 91599 2984108 0.00062 表 2 总体比较
Table 2 Overall performance comparison
模型 Gowalla Yelp2018 Amazon-Book RRecall@K NNDCG@K RRecall@K NNDCG@K RRecall@K NNDCG@K MF 0.1291 0.1878 0.0317 0.0617 0.0250 0.0518 NeuMF 0.1326 0.1985 0.0331 0.0840 0.0253 0.0535 GC-MC 0.1395 0.1960 0.0365 0.0812 0.0288 0.0551 Hop-Rec 0.1399 0.2128 0.0388 0.0857 0.0309 0.0606 LightGCN 0.1830 0.1554 0.0649 0.0530 0.0411 0.0315 NGCF 0.1547 0.2237 0.0438 0.0926 0.0344 0.0630 GACF 0.2285 0.2597 0.1038 0.1455 0.0634 0.0936 GACF较NGCF的提升率/% 47.51 16.09 136.99 57.13 84.30 48.57 表 3 层数对模型推荐效果的影响
Table 3 Effect of number of layers on the model recommendation
层数 方法 Gowalla Yelp2018 Amazon-Book RRecall@K NNDCG@K RRecall@K NNDCG@K RRecall@K NNDCG@K 1 层 NGCF 0.1511 0.2218 0.0417 0.0889 0.0315 0.0618 GACF 0.2197 0.2557 0.0975 0.1383 0.0579 0.0916 提升率/% +45.4 +15.28 +133.81 +55.57 +83.81 +48.22 2层 NGCF 0.1535 0.2238 0.0429 0.0926 0.0319 0.0622 GACF 0.2246 0.2587 0.1005 0.1448 0.0588 0.0924 提升率/% +46.32 +15.59 +134.27 +56.37 +84.33 +48.55 3层 NGCF 0.1547 0.2237 0.0438 0.0926 0.0344 0.0630 GACF 0.2285 0.2597 0.1038 0.1455 0.0634 0.0936 提升率/% +47.51 +16.09 +136.99 +57.13 +84.3 +48.57 4层 NGCF 0.1560 0.2240 0.0427 0.0907 0.0342 0.0636 GACF 0.2294 0.2600 0.1010 0.1424 0.0630 0.0945 提升率/% +47.05 +16.07 +136.53 +57.00 +84.21 +48.58 -
[1] SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. New York: ACM, 2001: 285−295. [2] AMBULGEKAR H P, PATHAK M K, KOKARE M B. A survey on collaborative filtering: tasks, approaches and applications[C]//Proceedings of International Ethical Hacking Conference 2018. Singapore: Springer, 2019: 289−300. [3] SUN Guangfu, WU Le, LIU Qi, et al. Recommendations based on collaborative filtering by exploiting sequential behaviors[J]. Journal of software, 2014, 24(11): 2721–2733. doi: 10.3724/SP.J.1001.2013.04478 [4] HE Xiangnan, LIAO Lizi, ZHANG Hanwang, et al. Neural collaborative filtering[C]//Proceedings of the 26th International Conference on World Wide Web. New York: ACM, 2017: 173−182. [5] SHUMAN D I, NARANG S K, FROSSARD P, et al. The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains[C]//IEEE Signal Processing Magazine. New York: IEEE, 2013: 83−98. [6] YING R, HE Ruining, CHEN Kaifeng, et al. Graph convolutional neural networks for web-scale recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2018: 974−983. [7] WANG Xiang, HE Xiangnan, WANG Meng, et al. Neural graph collaborative filtering[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2019: 165−174. [8] HE Xiangnan, DENG Kuan, WANG Xiang, et al. LightGCN: simplifying and powering graph convolution network for recommendation[C]//Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2020: 639−648. [9] KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems[J]. Computer journal, 2009, 42(8): 30–37. [10] KOREN Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2008: 426−434. [11] HE Xiangnan, DU Xiaoyu, WANG Xiang, et al. Outer product-based neural collaborative filtering[C]//Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2018: 2227−2233. [12] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 701−710. [13] GROVER A, LESKOVEC J. Node2vec: scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 855−864. [14] GORI M, PUCCI A. ItemRank: a random-walk based scoring algorithm for recommender engines[C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence. New York: ACM, 2007: 2766−2771. [15] CHEN C M, TSAI M F, LIN Y C, et al. Query-based music recommendations via preference embedding[C]//Proceedings of the 10th ACM Conference on Recommender Systems. New York: ACM, 2016: 79−82. [16] YANG J H, CHEN C M, WANG Chuanju, et al. HOP-rec: high-order proximity for implicit recommendation[C]//Proceedings of the 12th ACM Conference on Recommender Systems. New York: ACM, 2018: 140−144. [17] HAMILTON W L, YING R, LESKOVEC J. Inductive representation learning on large graphs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 1025−1035. [18] XU Yanan, ZHU Yanmin, SHEN Yanyan, et al. Learning shared vertex representation in heterogeneous graphs with convolutional networks for recommendation[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2019: 4620−4626. [19] PETAR V, GUILLEM C, ARANTXA C, et al. Graph attention networks[C]//Proceedings of International Conference on Learning Representations. Vancouver: ICLR, 2018, 23−35. [20] 王宏琳, 杨丹, 聂铁铮, 等. 自注意力机制的属性异构信息网络嵌入的商品推荐[J]. 计算机研究与发展, 2022, 59(7): 1509–1521. WANG Honglin, YANG Dan, NIE Tiezheng, et al. Attributed heterogeneous information network embedding with self-attention mechanism for product recommendation[J]. Journal of computer research and development, 2022, 59(7): 1509–1521. [21] LIU Donghua, LI Jing, DU Bo, et al. DAML: dual attention mutual learning between ratings and reviews for item recommendation[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2019: 344−352. [22] 高海燕, 毛林, 窦凯奇, 等. 基于图嵌入模型的协同过滤推荐算法[J]. 数据采集与处理, 2020, 35(3): 483–493. doi: 10.16337/j.1004-9037.2020.03.011 GAO Haiyan, MAO Lin, DOU Kaiqi, et al. Graph embedding model based collaborative filtering algorithm[J]. Journal of data acquisition and processing, 2020, 35(3): 483–493. doi: 10.16337/j.1004-9037.2020.03.011 [23] 邢长征, 赵宏宝, 张全贵, 等. 融合评论文本层级注意力和外积的推荐方法[J]. 计算机科学与探索, 2020, 14(6): 947–957. doi: 10.3778/j.issn.1673-9418.1906067 XING Changzheng, ZHAO Hongbao, ZHANG Quangui, et al. Review text hierarchical attention and outer product for recommendation method[J]. Journal of frontiers of computer science and technology, 2020, 14(6): 947–957. doi: 10.3778/j.issn.1673-9418.1906067 [24] MAAS A L. Rectifier nonlinearities improve neural network acoustic models[C]//Proceedings of International Conference on Machine Learning. New York: ACM, 2013, 28−34. [25] RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback[C]//Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence. New York: ACM, 2009: 452−461. [26] VAN DEN BERG R, KIPF T, WELLING M. Graph convolutional matrix completion[C]// Proceedings of Computing Research Repository. New York: ACM, 2017, 1706−02263. [27] KINGMA D, BA J. Adam: a method for stochastic optimization[C]//Proceedings of the International Conference on Learning Representations. San Diego: ICLR, 2015, 1412−1427.
