Mixed data clustering initialization method using outlier detection technology
-
摘要: 近年来,混合型数据的聚类问题受到广泛关注。作为处理混合型数据的一种有效方法,K-prototype聚类算法在初始化聚类中心时通常采用随机选取的策略,然而这种策略在很多实际应用中难以保证聚类结果的质量。针对上述问题,采用基于离群点检测的策略来为K-prototype算法选择初始中心,并提出一种新的混合型数据聚类初始化算法(initialization of K-prototype clustering based on outlier detection and density, IKP-ODD)。给定一个候选对象,IKP-ODD通过计算其距离离群因子、加权密度以及与已有初始中心之间的加权距离来判断候选对象是否是一个初始中心。IKP-ODD通过采用距离离群因子和加权密度,防止选择离群点作为初始中心。在计算对象的加权密度以及对象之间的加权距离时,采用邻域粗糙集中的粒度邻域熵来计算每一个属性的重要性,并根据属性重要性的大小为不同属性赋予不同的权重,有效地反映不同属性之间的差异性。在多个UCI数据集上的实验表明,相对于现有的初始化方法,IKP-ODD能够更好地解决K-prototype聚类的初始化问题。Abstract: In recent years, the clustering problem of mixed-type data has received wide attention. As an effective method to process mixed-type data, K-prototype clustering algorithm usually uses the strategy of random selection to initialize cluster centers. However, it is difficult to guarantee the quality of clustering results in many practical applications. To solve above problem, in this paper we select initial centers for K-prototype algorithm based on outlier detection, and present a new initialization algorithm (Initialization of K-prototype Clustering Based on Outlier Detection and Density, denoted as IKP-ODD) for mixed-type data clustering. Given a candidate object, IKP-ODD determines whether the candidate object is an initial center by calculating its distance outlier factor, weighted density and weighted distances from existing initial centers. IKP-ODD prevents outliers from being selected as initial centers by using distance outlier factor and weighted density. When calculating the weighted densities of objects and the weighted distances between objects, we use the granular neighborhood entropy in neighborhood rough sets to calculate the significance of each attribute, and assign different weights to different attributes according to the significances of attributes, which can effectively reflect the difference between different attributes. Experiments on several UCI datasets show that IKP-ODD performs better than the existing initialization methods when solving the initialization problem of K-prototype clustering.
-
聚类是数据挖掘中的一项重要任务,其目的在于将一些样本划分为若干个簇。通过计算簇内相似性和簇间相似性对样本进行划分,使得同一个簇中样本之间的相似性尽可能大,而不同簇中样本之间的相似性尽可能小[1]。目前,聚类技术已被应用到模式识别[2]、特征选择[3-4]、图像分析[5-7]、生物医学[8-9]等众多领域。
在现实应用中,存在着很多同时包含数值型属性和类别型属性的混合型数据。传统的K-means算法和K-modes算法分别仅限于处理包含数值型属性的数据和包含类别型属性的数据,并不适合于处理这种混合型数据。为了解决混合型数据的聚类问题,Huang[10]提出了一种用于处理混合型数据的K-prototype聚类算法。K-prototype算法简单、高效,已成为处理混合型数据聚类的代表性算法。不过,K-prototype算法也存在一些局限,例如,初始化问题缺乏有效解决办法,随机选择初始聚类中心难以保证算法的稳定性和准确率。为了更好地发挥K-prototype算法的作用,有必要对其初始化问题进行系统的研究。
目前,针对K-prototype聚类初始化问题的研究还比较少,只有少数几位学者开展了相关研究。例如,Jia等[11]提出了一种基于混合相异系数的加权聚类算法WKPCA,该方法利用平均距离、局部邻域密度和相对距离自动选择初始中心。Guo等[12]提出了一种基于邻域密度和距离的混合型数据聚类算法,该方法通过计算每个样本的邻域密度和样本之间的距离自适应确定初始中心。赵立江等[13]提出了一种对初始点分组取样的方法,然而,该方法可能导致多个初始中心来自同一个簇。Zhou等[14]提出了一种通过计算等分间隔点和取值出现频率确定初始中心的方法,然而,该方法没有考虑不同属性之间的差异性。
从以上分析可以看出,现有的K-prototype聚类初始化方法还存在多个初始中心来自同一个簇,将离群点选为初始中心等问题。针对这些问题,本文将从离群点检测的角度出发,提出一种新的混合型数据聚类初始化算法IKP-ODD。离群点检测是数据挖掘的主要研究方向之一,其目的是从大量复杂的数据中发现一小部分离群的、与常规数据模式显著不同的模式。离群点检测最早出现在统计学领域,并由此出现了众多的基于统计的离群点检测方法。基于统计的方法其主要缺点是很多数据集本身并不符合某种特定的概率分布模型。针对基于统计的方法的不足,Knorr等[15]从数据挖掘的角度来研究离群点,并提出了基于距离的离群点检测方法。基于距离的离群点检测方法直观、易于理解且实现简单,并且不受数据空间结构的影响。
IKP-ODD算法的基本思路如下:离群点不应该被选为初始中心,初始中心应该具有代表性,并且任意两个初始中心不能来自于同一个簇。基于这一思路,IKP-ODD算法首先采用基于距离的方法来计算每个候选对象x在数值型属性上以及类别型属性上的离群因子;然后,计算x在数值型属性上以及类别型属性上的加权密度,并且计算x与已有初始中心在数值型属性上以及类别型属性上的加权距离;最后,通过综合考虑上述6个因素来确定x成为初始中心的可能性。通过计算每个对象x的离群因子,就可以避免将离群点选为初始中心,而计算对象x的加权密度,则可以保证所选择的初始中心具有代表性,另外,计算对象x与已有初始中心的加权距离,则可以让任意2个初始中心之间的距离足够大,从而避免两个初始中心来自于同一个簇的问题。需要指出的是,IKP-ODD算法在计算对象的加权密度以及对象之间的加权距离时,不同属性将根据其重要性的大小被赋予不同的权重。为了准确地计算出混合型数据集中每一个属性的重要性,本文在邻域粗糙集模型中定义一种新的信息熵——粒度邻域熵,并提出一种基于粒度邻域熵的属性重要性度量。粒度邻域熵是对现有的邻域熵的一种扩展,它将邻域知识粒度的概念引入到邻域熵中,可以更好地刻画邻域粗糙集中的不确定性。
本文的主要贡献如下:1)提出了一种针对混合型数据聚类的初始化算法IKP-ODD。在选择初始中心时,IKP-ODD采用基于距离的离群点检测方法来计算每个候选对象x的离群程度,可以避免离群点被选作初始中心。2) IKP-ODD在选择初始中心时还考虑到对象x的加权密度以及x与已有初始中心的加权距离。在计算加权密度和加权距离时,不同属性的权重通过粒度邻域熵来进行计算。由于属性权重能够有效反应不同属性在选择初始中心时所发挥的不同作用,从而提高了所选择的初始中心的质量。
1. 基本概念
本节引入与邻域粗糙集相关的一些主要概念。在邻域粗糙集中,一般使用邻域信息系统[16-18]来存储数据。当一个邻域信息系统中同时包含数值型属性和类别型属性,则称之为一个混合邻域信息系统。本文主要研究混合型数据聚类的初始化问题,因此,所考虑的都是混合邻域信息系统。
给定一个混合邻域信息系统
$I=(U, A) $ ,令$\delta $ 为邻域半径,假设属性集A又分成类别型属性集$A^C $ 和数值型属性集$A^N $ ,其中,$A=A^C \cup A^N $ ,$A^C \cap A^N = \varnothing$ 。对任意属性子集$B \subseteq A $ ,假设B又分成类别型属性子集$B^C $ 和数值型属性子集$B^N $ ,其中,$B^C= A^C \cap B$ ,$B^N=A^N \cap B $ 。论域U上的二元关系$N_B^{\delta }=\{(x, y) \in U \times U: {d_{{B^N}}}(x,y) \leqslant \delta \wedge {d_{{B^C}}}(x,y) = 0 \}$ 被称为混合邻域关系[16,18]。对于任意对象$x \in U $ ,x在混合邻域关系$N_B^{\delta } $ 下的混合邻域类被定义为:$\delta _B(x)=\{y \in U: (x, y) \in N_B^{\delta }\}$ [16-18]。利用混合邻域关系,可以进一步定义邻域熵$E_{\delta} (B) $ ,具体定义见文献[19]。定义1邻域知识粒度 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径。对任意属性子集
$B \subseteq A$ ,假设B在论域U上所确定的混合邻域关系为$N_B^{\delta } $ ,属性子集B所对应的邻域知识粒度$G_{\delta }(B) $ 定义为$$ G_{\delta }(B) = \frac{1}{{|U|}}\sum\limits_{x \in U} {\frac{{|{\delta _B}(x){|^2}}}{{|U{|^2}}}} $$ 对任意
$x \in U $ ,由于$\delta_B(x) \subseteq U $ 且${\delta _B}(x) \ne \varnothing$ ,因此有$\dfrac{1}{{|U{|^{\text{2}}}}} \leqslant \dfrac{{|{\delta _B}(x){|^2}}}{{|U{|^{\text{2}}}}} \leqslant 1$ 。从上述结果可以进一步得出:$\dfrac{1}{{|U{|^2}}} \leqslant {G_\delta }(B) \leqslant 1$ 。当对每一个$x \in U $ 都有$\delta _B(x) = U $ 时,$G_{\delta }(B)$ 得到其最大值1。当对每一个$x \in U $ 都有$\delta _B(x) = \{x\} $ 时,$G_{\delta }(B)$ 得到其最小值$\dfrac{1}{{|U{|^2}}}$ 。2. 基于粒度邻域熵的属性重要性
定义2粒度邻域熵 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径。对任意属性子集B
$ \subseteq $ A,假设B在论域U上所确定的混合邻域关系为$N_B^{\delta } $ ,本文将属性子集B所对应的粒度邻域熵定义为$$ E_{\delta }^G(B) = (1 - {G_\delta }(B)) \times {E_\delta }(B) $$ 由定义2可知,当对每一个
$x \in U $ 都有$\delta _B(x)= U$ 时,$E_{\delta }^G(B)$ 得到其最小值0。当对每一个$x \in U $ 都有$\delta _B(x)=U $ 时,$E_{\delta }^G(B)$ 得到其最大值$\left(1 - \dfrac{1}{{|U{|^2}}}\right) \times \log_2 |U|$ 。定义3基于粒度邻域熵的属性重要性 给定一个混合邻域信息系统
$I=(U, A)$ ,令δ为邻域半径。对任意属性$a \in A$ ,属性a在$I_S $ 中的重要性定义为$$ {S_\delta }(a) = \frac{{{E_{\delta}^G }(A) - {E_{\delta}^G }(A - \{ a\} )}}{{{E_{\delta}^G }(A) + {E_{\delta}^G }(A - \{ a\} )}} $$ 根据定义2,可以证明粒度邻域熵是单调的,因此,对任意
$B_1 $ ,$B_2 \subseteq A$ 如果$B_1 \subseteq B_2$ ,则${E_{\delta}^G }(B_1) \leqslant {E_{\delta}^G }(B_2)$ 。由于$A-\{a\} \subset A$ ,因此,可以进一步得出:对任意$a \in A$ ,$0 \leqslant S_{\delta }(a)\leqslant 1$ 。本文提出的IKP-ODD算法需要计算对象的加权密度以及对象之间的加权距离。为了反映不同属性之间的差异,本文在计算加权密度和加权距离时要为不同的属性赋予不同的权重。给定一个混合信息系统
$I=(U, A)$ ,本文采用基于粒度邻域熵的属性重要性来计算属性集A中每个属性的权重。定义4属性权重 给定一个混合邻域信息系统
$I=(U, A)$ ,令δ为邻域半径。对任意$a \in A$ ,令$S_{\delta }(a)$ 表示属性a在I中的重要性,属性a的权重定义为$$ w(a) = \left\{ \begin{aligned} & \frac{2}{3},\quad {S_\delta }(a) = 0 \\ & 1 + \sqrt {{S_\delta }(a)} ,\quad {S_\delta }(a) \ne 0 \end{aligned} \right. $$ 由于对任意
$a \in A $ ,有$0 \leqslant S_{\delta }(a) \leqslant 1$ ,因此可以得出:$2/3 \leqslant w (a) \leqslant 2$ 。3. 混合型数据聚类初始化的6个因素
在为混合型数据聚类选择初始中心的过程中,IKP_ODD算法主要考虑了以下6个因素:每一个候选对象x在数值型属性上以及类别型属性上的距离离群因子;x在数值型属性上以及类别型属性上的加权密度;x与现有初始中心在数值型属性上以及类别型属性上的加权距离。本节首先给出加权距离和加权密度的定义,然后给出距离离群因子的定义,最后基于以上6个因素来计算候选对象x成为初始中心的可能性。
3.1 加权距离和加权密度
定义5数值型属性上的加权距离 给定一个混合邻域信息系统
$I=(U, A)$ ,令δ为邻域半径,并且令$A^N \subseteq A $ 表示数值型属性集。对任意2个对象$x, y \in U $ ,x与y在数值型属性上的加权距离定义为$$ {d_N^w}(x,y) = \sqrt {\sum\limits_{a \in {A^N}} {w(a) \times {{({x_a} - {y_a})}^2}} } $$ 式中:对任意
$a \in A^N $ ,$w(a)$ 表示数值型属性a的权重;$x_a $ 和$y_a $ 分别表示对象x与y在属性a上的取值。定义6数值型属性上的加权平均距离 给定一个混合邻域信息系统
$I=(U, A)$ ,令δ为邻域半径,并且令$A^N \subseteq A $ 表示数值型属性集。数据集U中任意2个对象在数值型属性上的加权平均距离定义为$$ \overline {d_N^w} = \dfrac{{\displaystyle\sum\limits_{({u_1},{u_2}) \in U \times U} {{d_N^w}({u_1},{u_2})} }}{{|U{|^2}}} $$ (1) 定义7数值型属性上的加权密度 给定一个混合邻域信息系统
$I=(U, A)$ ,令δ为邻域半径,并且令$A^N \subseteq A $ 表示数值型属性集。对任意对象$x \in U $ ,x在数值型属性上的加权密度定义为$$ \rho _N^w(x) = \dfrac{\overline {d_N^w} }{{\displaystyle\sum_{y \in U} {d^w(x,y)} /|U| + \overline {d_N^w} }} $$ 式中
$\overline {d_N^w} $ 为数据集U中所有对象的加权平均距离。从定义7可以很容易得出:$0 < \rho _N^w(x)\leqslant 1$ 。定义8类别型属性上的加权距离 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径,并且令AC
$ \subseteq $ A表示类别型属性集。对任意2个对象x, y$\in $ U,x与y在类别型属性上的加权距离定义为$$ {d_C^w}(x,y) = \sum\limits_{a \in {A^C}} {w(a) \times m({x_a},{y_a})} $$ 式中:对任意a∈AC,w(a)表示类别型属性a的权重;xa和ya分别表示对象x与y在属性a上的取值;m(xa, ya)表示对象x与y在类别型属性a上的简单匹配距离,具体定义为
$$ m({x_a},{y_a}) = \left\{ \begin{split} & 0,\quad {x_a} = {y_a} \\ & 1,\quad {x_a} \ne {y_a} \\ \end{split} \right. $$ 定义9类别型属性上的加权密度 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径,并且令AC
$ \subseteq $ A表示类别型属性集。对任意对象x$\in $ U,x在类别型属性上的加权密度定义为$$ \rho _C^w(x) = \sum\nolimits_{a \in {A^C}} {w(a)} \times \frac{{\left| {y \in U:{x_a} = {y_a}} \right|/\left| U \right|}}{{\left| {{A^C}} \right|}}$$ 式中:对任意a
$\in $ AC,w(a)表示类别型属性a的权重;xa和ya分别表示对象x与y在属性a上的取值。3.2 距离离群因子与对象成为初始中心的可能性
定义10数值型属性上的距离离群因子 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径,并且令AN
$ \subseteq $ A表示数值型属性集。对任意对象x$\in $ U,x在数值型属性上的距离离群因子定义为$$ {O_N}(x) = \frac{{|\{ y \in U:{d_N^w}(x,y) > \overline {d_N^w} \} |}}{{|U|}} $$ 式中:对任意对象
$y \in U$ ,${d_N^w}(x,y) $ 表示对象x与y在数值型属性上的加权距离;$\overline {d_N^w}$ 如式(1)所示,表示U中任意2个对象在数值型属性上的加权平均距离。定义11类别型属性上的距离离群因子 给定一个混合邻域信息系统I=(U, A),令δ为邻域半径,并且令AC
$ \subseteq $ A表示类别型属性集。对任意对象$x \in U$ ,x在类别型属性上的距离离群因子定义为$$ {O_C}(X) = \frac{{|\{ y \in U:{d_C^w}(x,y) > d_{{\rm{is}}}\} |}}{{|U|}} $$ 式中:对任意对象
$y \in U$ ,${d_C^w}(x,y) $ 表示对象x与y在类别型属性上的加权距离;dis为一个给定的阈值,其取值范围为[0,$\sum\nolimits_{a \in {A^C}} {w(a)}$ ]。定义12 给定一个混合邻域信息系统I=(U, A),令T={s1, s2,···, sq}为已有的初始中心集,对任意候选对象
$y \in U$ − T,y被选为初始中心的可能性P_I(y)定义为$$ \begin{gathered} P\_I(y) = \dfrac{{\displaystyle\sum_{j = 1}^q {(d_N^w(y,{s_j}) + d_C^w(y,{s_j}))} }}{q} - \\ {\tau _1}\sqrt {{O_N}(y) + {O_C}(y)} + {\tau _2}(\rho _N^w(y) + \rho _C^w(y)) + \\ \dfrac{{\displaystyle\sum_{j = 1}^q {(d_N^w(y,{s_j}) + d_C^w(y,{s_j}))} }}{{q \times (1 + {\tau _1}\sqrt {{O_N}(y) + {O_C}(y)} - {\tau _2}(\rho _N^w(y) + \rho _C^w(y)))}} \end{gathered} $$ 式中:对任意1
$\leqslant $ j$\leqslant $ q,$d_N^w(y,{s_j}) $ 表示对象y与初始中心sj在数值型属性上的加权距离;$d_C^w(y, s_j) $ 表示对象y与初始中心sj在类别型属性上的加权距离;τ1和τ2是2个给定的参数,分别用于调节ON(y)+OC(y)和$\rho _N^w (y) + \rho _C^w $ (y)在计算P_I(y)时的影响力。从定义12可知,候选对象y的距离离群因子越小,则其成为初始中心的可能性越大,而y的加权密度越大,则其成为初始中心的可能性也越大。此外,y与已有的初始中心的距离越大,则其成为初始中心的可能性也越大。
4. 聚类中心初始化算法IKP-ODD
给定1个数据集T和候选对象x,IKP-ODD算法通过以下5个步骤来计算P_I(x) (x成为初始中心的可能性):1)根据粒度邻域熵计算每个属性a的重要性,并得到a的权重;2)采用基于距离的离群点检测方法计算x在数值型属性上的距离离群因子ON (x)以及x在类别型属性上的距离离群因子OC (x);3)计算x在数值型属性上的加权密度
$\rho _N^w $ (x)以及x在类别型属性上的加权密度$\rho _C^w $ (x);4)假设T={s1, s2,···, sq}表示当前已有的初始中心集,计算x与初始中心sj在数值型属性上的加权距离$d_N^w\left( {x,{s_j}} \right) $ ;以及x与sj在类别型属性上的加权距离$ d_C^w(x, s_j)$ ,其中,sj$\in $ S,1$\leqslant $ j$\leqslant $ q;5)利用ON (x),$\rho _N^w $ (x)和{$d_N^w(x, s_j)$ : 1$\leqslant $ j$\leqslant $ q}以及OC (x),$\rho _C^w $ (x)和{$d_C^w(x, s_j)$ : 1$\leqslant $ j$\leqslant $ q}来计算x在所有属性上被选为初始中心的可能性P_I (x)。根据算法,下面首先给出一个用于计算属性权重的算法(算法1),在算法1的基础上,进一步给出IKP-ODD算法(算法2)。
算法1 属性权重计算
输入 混合邻域信息系统I=(U, A),其中论域U={x1,x2, ···, xn},属性集A={a1,a2, ···, am};邻域半径δ。
输出 所有属性的权重,即集合{w(a): a
$\in $ A}。1) 对每一个对象x
$\in $ U,利用ball-tree[20]的方法计算x在混合邻域关系$N_A^\delta $ 下的混合邻域类δA(x)。2) 计算属性集A对应的的粒度邻域熵
$E_\delta ^G $ (A)。3) 对每一个属性a
$\in $ A,反复执行下列语句:① 对每一个对象x
$\in$ U,利用ball-tree[20]的方法计算x在混合邻域关系$N_{A - \left\{ a \right\} }^\delta$ 下的混合邻域类δA−{a}(x);②计算属性子集A−{a}所对应的粒度邻域熵
$E_\delta ^G $ (A−{a})。4) 对每一个属性a
$\in $ A,计算属性a在I中的重要性Sδ (a)。5) 对每一个属性a
$\in $ A,计算属性a的权重w(a)。6) 算法结束,返回集合{w(a): a
$ \in $ A}。算法1的1)采用了ball-tree[20]的方法来计算对象x在混合邻域关系
$N_A^\delta $ 下的混合邻域类δA(x)。1)的时间复杂度为O(m×log2n×n),其中n=|U|,m=|A|。3)中同样采用了ball-tree[20]的方法来计算对象x在混合邻域关系$N_{A - \left\{ {\left. a \right\}} \right.}^\delta $ 下的混合邻域类δA−{a}(x)。3)的时间复杂度为O(m2×log2n×n)。此外, 4)和5)的时间复杂度均为O(m)。综上可知,算法1的时间复杂度为O(m2×log2n×n),空间复杂度为O(m+n)。算法2 IPK-ODD
输入 混合邻域信息系统I=(U, A),其中,论域
$U = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\} $ ,属性集$A = \left\{ {{a_1},{a_2}, \cdots ,{a_m}} \right\} $ 又分成类别型属性集${A^C} = \left\{ {a_1^C,a_2^C, \cdots ,a_p^C} \right\}$ 和数值型属性集${A^N} = \left\{ {a_1^N,a_2^N, \cdots ,a_q^N} \right\} $ ,邻域半径δ,阈值dis,参数τ1和τ2。输出 集合T,即K个初始中心的集合。
初始化 令T=
$\varnothing$ 。1) 利用算法1得到属性集A中每个属性a的权重w(a)。
2) 利用ball-tree[20]的方法计算U中任意2个对象在数值型属性上的加权平均距离
$\overline {d_N^w} $ 。// 2)和3)用于处理数值型属性
3) 对每一个对象x∈U,反复执行下列语句:
① 利用ball-tree[20]的方法计算对象x与U−{x}中每一个对象在数值型属性上的加权距离;
② 计算x在数值型属性上的加权密度
$\rho _N^w\left( x \right) $ ;③ 在集合U−{x}中统计与对象x在数值型属性上的加权距离大于
$\overline {d_N^w} $ 的对象个数;④ 计算对象x在数值型属性上的距离离群因子ON(x)。
4) 对每一个对象x
$\in $ U,反复执行下列语句:// 4)~6)用于处理类别型属性
① 利用ball-tree[20]的方法计算对象x与U−{x}中每个对象在类别型属性上的加权距离;
② 在集合U−{x}中统计与对象x在类别型属性上的加权距离大于dis的对象个数;
③ 计算对象x在类别型属性上的距离离群因子OC(x)。
5) 对每一个类别型属性a
$\in $ AC,反复执行下列语句:① 利用计数排序[21]的方法计算不可区分关系ND({a})对论域U的划分U/ND({a});
② 对每一个对象x
$\in $ U,利用U/IND({a})来统计U中与x在属性a上取值相等的对象个数。6) 对每一个对象x
$\in $ U,计算x在类别型属性上的加权密度$\rho _C^w $ (x)。7) 对每一个对象x
$\in $ U,令O(x)=ON(x)+ OC(x)表示x的总体离群因子。从U中选择总体离群因子最小的对象y,并且令T=T$ \cup $ {y},即将对象y选为第一个初始中心。// 如果有多个对象同时具有最小的总体离群因子,则从这些对象中随机选择一个。
8) 如果|T| < K,则转到9),否则转到12)。
9) 对每一个对象x
$\in $ U−T,反复执行下列语句://令T={s1, s2, ···, sq}表示当前已选择的初始中心集① 对每一个si
$\in $ T,计算对象x与初始中心si在数值型属性上的加权距离,其中,1$\leqslant $ i$\leqslant $ q;② 对每一个si
$\in $ T,计算对象x与初始中心si在类别型属性上的加权距离,其中,1$\leqslant $ i$\leqslant $ q;③ 计算对象x被选为初始中心的可能性P_I(x)。
10) 从U−S中选择最有可能成为初始中心的对象z,即P_I(z) = max({P_I(y): y
$\in $ U−T}),并且令T=T$\cup $ {z}。11) 如果|T|<K,则转到9),否则转到12)。
12) 算法结束,返回集合T。
在算法2的2)和3)中,采用了ball-tree[20]的方法来分别计算U中任意2个对象在数值型属性上的加权平均距离
$\overline {d_N^w} $ ,以及对象x与U−{x} 中每个对象在数值型属性上的加权距离。在最坏的情况下,2)和3)的时间复杂度为O(q×log2n×n),其中q=|AN |。在4)中,同样采用了ball-tree[20]的方法来计算对象x与U−{x}中每个对象在类别型属性上的加权距离。4)的时间复杂度为O(p×log2n×n),其中p=|AC |。此外, 5)和6)的时间复杂度为O(p×n), 7)~12)的时间复杂度为O(K2×m×n)。综上所述,在最坏的情况下,算法2的时间复杂度为O(m×n×(mlog2n+K2)),空间复杂度为O((m+K)×n)。5. 实验结果和分析
为了验证IKP-ODD的性能,在以下10个UCI数据集上进行了实验[22]: Credit Approval(Credit),Statlog (Heart) (SH),Hepatitis,Statlog (German Credit,SG),Heart failure clinical records (HFCR),Statlog (Australian Credit Approval,SA),Teaching Assistant Evaluation (TAE),Acute Inflammations (Acute),Immunotherapy (Immu),Cylinder Bands (Bands)。上述10个数据集的详细信息如表1所示。
表 1 10个UCI数据集的详细信息Table 1 Description of the 10 data sets数据集 类别个数 对象个数 属性个数 Credit 2 690 15 SH 2 270 13 Hepatitis 2 155 19 SG 2 150 20 HFCR 2 299 13 SA 2 690 14 TAE 2 151 5 Acute 2 120 6 Immu 2 90 8 Bands 2 512 39 除了在上述10个UCI数据集上进行实验,本文还通过scikit-learn生成了2个人工数据集genereted dataset 1(GD1)和generated dataset 2(GD2),用于展示不同的初始中心对聚类结果的影响。GD1和GD2分别包含800个样本,这些样本分别属于4个不同的簇。
5.1 实验设计
本文基于Python语言实现了IKP-ODD,并将该算法的实验结果与现有的6种具有代表性的聚类初始化方法进行了比较,这6种方法分别是:随机方法(Random),Cao[24]的方法,Huang[10]的方法,Sajidha[23]的方法,Peng[25]的方法,Dinh[26]的方法。其中,Cao的方法是一种基于密度的初始化方法,Huang的方法将取值频率最高的K个点作为初始中心,Sajidha的方法是一种基于密度和距离的初始化方法,Peng的方法是一种基于加权密度和加权距离的初始化方法,Dinh的方法是一种基于最大频繁项集挖掘的初始化方法。
不同算法的参数设置情况如下:首先,关于IKP-ODD的参数设置,通过多次实验来逐步调节dis、τ1、τ2的值,并选择能够获得最优实验结果的参数值。最终,将dis的值设置为0.55,并且将τ1和τ2的值分别设置为1.0和0.1;其次,对于6个对比算法,它们也包括一些需要提前设置的参数。这6个对比算法的每个参数均根据相关文献中所提供的参数值来进行设置[10,23-26]。
实验分为3个阶段:1)数据预处理;2)选择初始中心;3)聚类。在第1阶段,为了避免噪声数据对离群点检测的影响,在数据预处理中利用多元线性回归方法对每一个数据集中的噪声数据进行剔除。在第2阶段,分别采用不同的方法来初始化聚类中心。在第3阶段,根据前面所得到的初始中心来执行K-prototype算法。最后,比较不同初始化方法的聚类结果。
为了评价不同聚类初始化方法所产生的聚类结果的好坏,本文采用了文献[27]中所提出的3种性能度量指标:正确率A、精度P和召回率R。给定一个混合邻域信息系统I=(U, A),假设U中实际包含K个类:{C1,C2, ···, CK},而由给定的聚类算法M所生成的K个簇分别为:{C1', C2', ···, CK'},A、P和R分别被定义为
$$\begin{gathered} {A} = \dfrac{{\displaystyle\sum_{j = 1}^K {{p_j}} }}{{|U|}}\\ {P} = \dfrac{{\displaystyle\sum_{j = 1}^K {\frac{{{p_j}}}{{{p_j} + {q_j}}}} }}{K}\\ {R} = \dfrac{{\displaystyle\sum_{j = 1}^K {\frac{{{p_j}}}{{{p_j} + {r_j}}}} }}{K} \end{gathered}$$ 式中:对任意 1
$\leqslant $ j$\leqslant $ K,pj = |Cj$ \cap $ Cj' | (pj表示U中被算法M正确分配到簇Cj的对象个数);qj = |Cj'| − pj (qj表示U中被M错误分配到簇Cj的对象个数);rj = |Cj| − pj (rj表示U中本来应该被M分配到簇Cj中,但被其错误分配到其他簇的对象个数)。5.2 实验结果
表2~4给出了不同初始化方法在不同数据集上所产生的K-prototype聚类结果,其中,表2给出了不同初始化方法所产生的正确率值,表3给出了不同初始化方法所产生的精度值,而表4则给出了不同初始化方法所产生的召回率值。
表 2 不同初始化方法所产生的正确率值Table 2 Accuracy values produced by different methods数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5279 0.8087 0.8072 0.5648 0.7982 0.7541 0.8102 SH 0.5200 0.7963 0.7963 0.5519 0.7926 0.7876 0.8037 Hepatitis 0.6948 0.7000 0.7028 0.6875 0.7000 0.6500 0.7250 SG 0.5918 0.5690 0.5337 0.5750 0.5280 0.5260 0.6420 HFCR 0.5300 0.5452 0.6010 0.6355 0.6263 0.6388 0.7191 SA 0.5253 0.8029 0.7999 0.5565 0.8000 0.7740 0.7884 TAE 0.6657 0.6755 0.6596 0.6755 0.6755 0.6661 0.6954 Acute 0.5917 0.5917 0.5917 0.5917 0.7125 0.5917 0.8250 Immu 0.5491 0.5456 0.5493 0.5761 0.5739 0.5556 0.5889 Bands 0.5202 0.6209 0.6209 0.6101 0.6083 0.6032 0.6173 GD1 0.8163 0.8551 0.8636 0.8631 0.8645 0.8626 0.8788 GD2 0.8139 0.8262 0.8260 0.8373 0.83775 0.8371 0.8513 表 3 不同初始化方法所产生的精度值Table 3 Precision values produced by different methods数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5029 0.8067 0.8052 0.6223 0.7975 0.7626 0.8082 SH 0.5198 0.7938 0.7938 0.5593 0.7910 0.7860 0.8012 Hepatitis 0.6946 0.7023 0.7019 0.6767 0.6918 0.6523 0.7230 SG 0.4976 0.5095 0.5091 0.5152 0.4866 0.4504 0.5545 HFCR 0.5134 0.4897 0.5522 0.6646 0.6168 0.6665 0.6847 SA 0.5012 0.8004 0.7976 0.7779 0.7983 0.7763 0.7871 TAE 0.7821 0.7876 0.7790 0.7876 0.7876 0.7785 0.7970 Acute 0.5931 0.5931 0.5931 0.5931 0.7250 0.5931 0.8846 Immu 0.4403 0.4371 0.4587 0.5286 0.5219 0.5958 0.6086 Bands 0.5097 0.6090 0.6090 0.5919 0.6003 0.5956 0.6062 GD1 0.8416 0.8512 0.8630 0.8629 0.8646 0.8623 0.8786 GD2 0.8121 0.8252 0.8261 0.8376 0.8381 0.8377 0.8518 表 4 不同初始化方法所产生的召回率值Table 4 Recall values produced by different methods数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5021 0.8079 0.8065 0.5911 0.8004 0.7592 0.8096 SH 0.5200 0.7933 0.7933 0.5592 0.7875 0.7855 0.8017 Hepatitis 0.7005 0.7086 0.7078 0.6709 0.6770 0.6570 0.7299 SG 0.4978 0.5102 0.5108 0.5164 0.4848 0.4481 0.5481 HFCR 0.5151 0.4893 0.5552 0.6849 0.6301 0.6873 0.6970 续表 4 数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD SA 0.5010 0.8014 0.7992 0.5016 0.8014 0.7763 0.7903 TAE 0.6668 0.6733 0.6627 0.6733 0.6733 0.6671 0.6965 Acute 0.5957 0.5957 0.5957 0.5957 0.7107 0.5957 0.7900 Immu 0.4240 0.4186 0.4488 0.5461 0.5369 0.6412 0.6623 Bands 0.5101 0.6176 0.6176 0.5980 0.6083 0.6032 0.6148 GD1 0.8162 0.8551 0.8636 0.8631 0.8645 0.8626 0.8787 GD2 0.8139 0.8262 0.8260 0.8373 0.83775 0.8371 0.8513 在表2中,每个数据集上的最高值都用加粗表示。从表2中可以看出,当使用正确率来评估聚类初始化方法的性能时,IKP-ODD的性能要优于其他6种已有的初始化方法。除了在SA和Bands这2个数据集上,IKP-ODD在其余10个数据集上都获得了最高的正确率值(约占所有数据集的83%)。具体来说,IKP-ODD的性能在所有12个数据集上都要优于随机方法。随机方法不能保证聚类结果的唯一性,但IKP-ODD可以产生唯一的聚类结果,解决了聚类结果的不稳定问题。除了随机方法之外,IKP-ODD的性能也要优于Cao、Huang、Sajidha、Peng和Dinh这5种方法,例如,IKP-ODD的性能在10个数据集上要优于Cao和Huang的方法,在11个数据集上要优于Peng的方法,并且在所有数据集上都要优于Sajidha和Dinh的方法。上述结果表明,从正确率的角度来看,IKP-ODD是解决K-prototype聚类初始化问题的一种有效策略。
从表3中可以看出,当使用精度来评估聚类初始化方法的性能时,IKP-ODD的性能要优于其他6种已有的初始化方法。除了在SA和Bands这2个数据集上,IKP-ODD在其余10个数据集上都获得了最高的精度值。具体来说,IKP-ODD的性能在所有12个数据集上都要优于随机方法、Sajidha和Dinh的方法。此外,IKP-ODD的性能在10个数据集上要优于Cao和Huang的方法,并且在11个数据集上要优于Peng的方法。上述结果表明,从精度的角度来看,IKP-ODD在解决K-prototype聚类的初始化问题上是有效的。
从表4中可以看出,当使用召回率来评估聚类初始化方法的性能时,IKP-ODD的性能要优于其他6种已有的初始化方法。除了在SA和Bands这2个数据集上,IKP-ODD在其余10个数据集上都获得了最高的召回率值。具体来说,IKP-ODD的性能在所有12个数据集上都要优于随机方法、Sajidha和Dinh的方法。此外,IKP-ODD的性能在10个数据集上要优于Cao和Huang的方法,并且在11个数据集上要优于Peng的方法。上述结果表明,从召回率的角度来看,IKP-ODD在解决K-prototype聚类的初始化问题上是有效的。
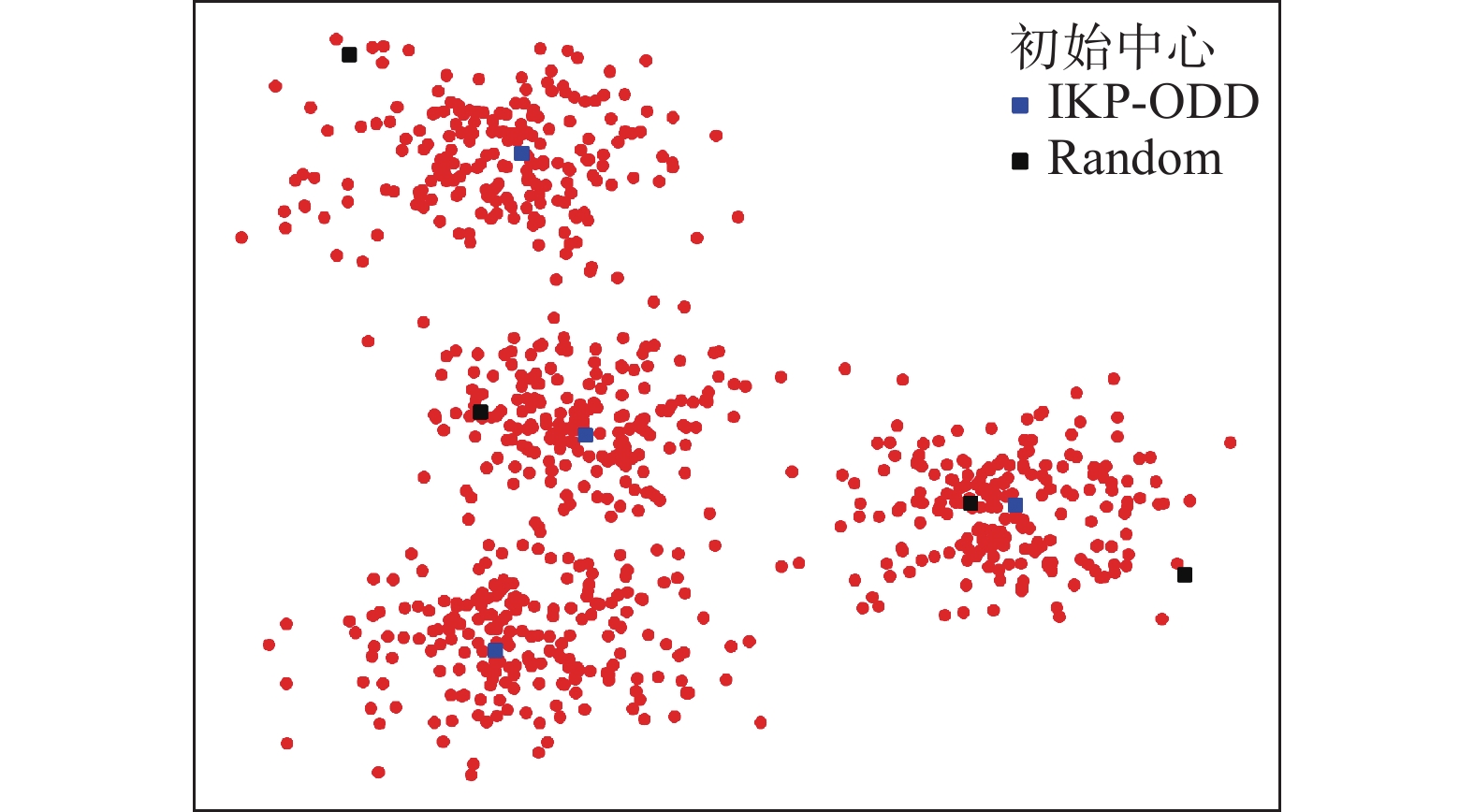
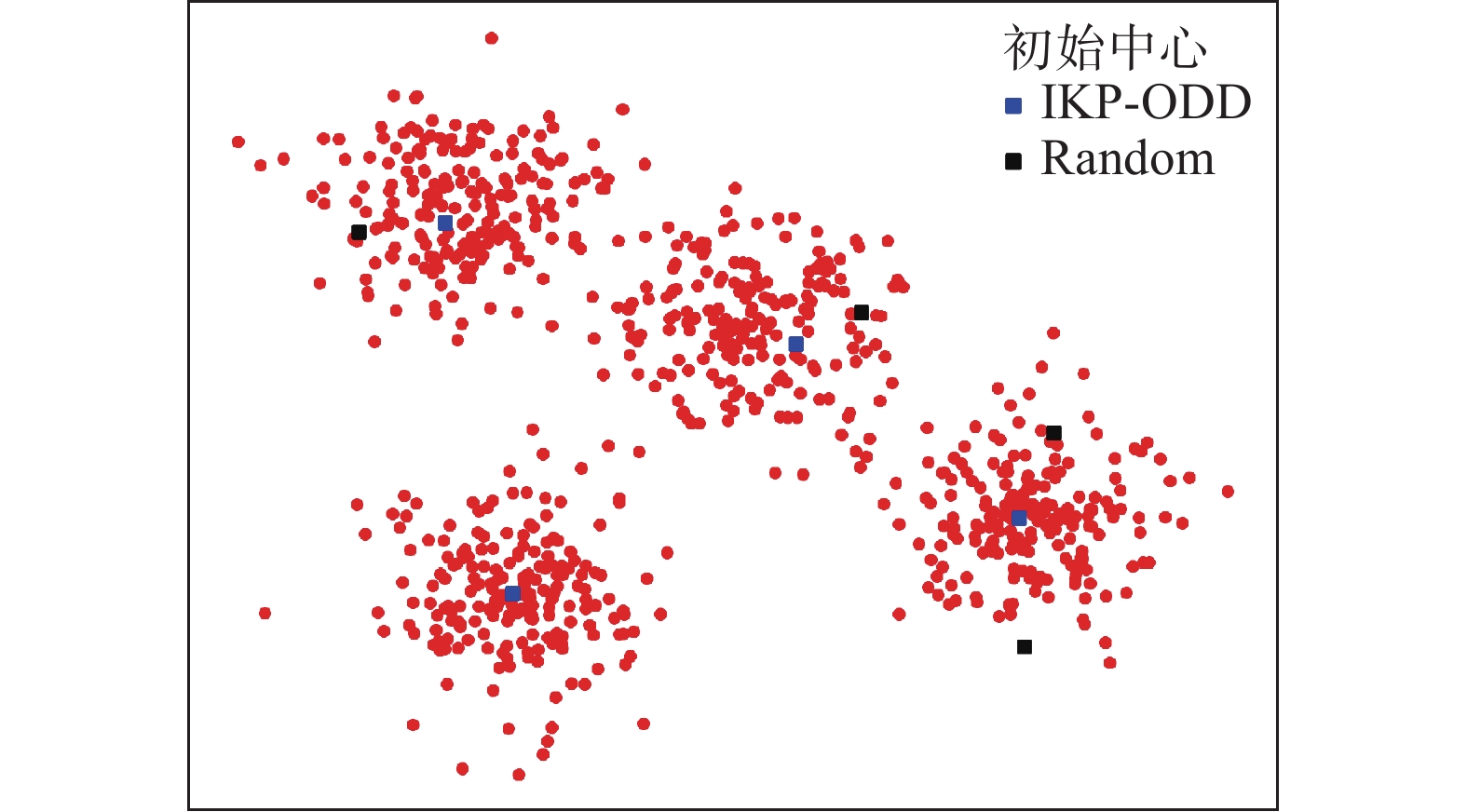
为了更直观地反映聚类中心初始化对聚类结果的影响,下面以IKP-ODD和Random这2个方法为例,利用图1和图2分别给出了在人工数据集GD1和GD2上使用IKP-ODD和Random这2种方法选出的初始中心在数据集中对应的位置。
在图1~2中,人工数据集中的样本由红色圆点表示,IKP-ODD和Random所选取的初始中心分别由蓝色正方形和黑色正方形表示。从图1~2可以看出,随机方法选择了远离簇中心的点作为初始中心,并且从同一个簇中选取了2个初始中心。IKP-ODD在每个簇中只选取了1个初始中心,且初始中心的位置均接近于簇中心。由图1~2可知,当使用随机方法选择初始中心时,无法避免离群点被选为初始中心;同时,选取的多个初始中心可能来自于同一个簇。而当使用IKP-ODD时,不仅避免了离群点被选为初始中心,并且避免了多个初始中心来自一个簇,这使得所选择的初始中心在每个簇中更具代表性,从而提升了聚类效果。
为了检验本文方法与现有方法之间的性能差异是否具有统计学意义,对表2~4中列出的结果进行了配对t–检验[28],即对已有的初始化方法和IKP-ODD产生的聚类结果进行配对t–检验,其中显著性水平为0.05。配对t–检验的结果如表5所示。
表 5 配对t–检验结果Table 5 Paired t-test results对比方法 正确率下
的p值精度下
的p值召回率下
的p值IKP-OOD vs. Random 0.0013 0.0011 0.0006 IKP-OOD vs. Cao 0.0414 0.0425 0.0346 IKP-OOD vs. Huang 0.0342 0.0465 0.0297 IKP-OOD vs. Sajidha 0.0065 0.0180 0.0059 IKP-OOD vs. Peng 0.0168 0.0182 0.0066 IKP-OOD vs. Dinh 0.0095 0.0462 0.0143 从表5可以看出,在正确率、精度和召回率这3个评价指标下,IKP-ODD与每一个对比方法的p值总是小于0.05,因此,上述结果表明本文方法与现有方法的差异性具有统计学意义。
6. 结束语
目前关于K-prototype聚类的初始化问题还缺少有效解决办法。对此,本文提出了一种新的混合型数据聚类初始化算法。该算法假设离群点不应被选为初始中心。因此,在选择初始中心时,本文首先计算每个候选对象x的离群程度。此外,为了避免不同的初始中心来自于同一个簇并保证所选择的初始中心具有代表性,对象x与已有初始中心的加权距离以及x的加权密度也被考虑进去。在多个数据集上的实验表明本文算法是有效的。
虽然基于距离的方法是一种非常有效的离群点挖掘方法,但是其缺点是需要选择一个合适的距离阈值dis。在实际应用中,dis的选取需要经过多次尝试才能最终确定。因此,在下一步研究中,计划采用其他一些具有代表性的离群点检测方法来为K-prototype聚类选择初始中心。此外,在属性重要性的度量方面,也可以考虑采用其他一些方式,例如,基于模糊粗糙集来度量属性重要性并计算属性权重。
-
表 1 10个UCI数据集的详细信息
Table 1 Description of the 10 data sets
数据集 类别个数 对象个数 属性个数 Credit 2 690 15 SH 2 270 13 Hepatitis 2 155 19 SG 2 150 20 HFCR 2 299 13 SA 2 690 14 TAE 2 151 5 Acute 2 120 6 Immu 2 90 8 Bands 2 512 39 表 2 不同初始化方法所产生的正确率值
Table 2 Accuracy values produced by different methods
数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5279 0.8087 0.8072 0.5648 0.7982 0.7541 0.8102 SH 0.5200 0.7963 0.7963 0.5519 0.7926 0.7876 0.8037 Hepatitis 0.6948 0.7000 0.7028 0.6875 0.7000 0.6500 0.7250 SG 0.5918 0.5690 0.5337 0.5750 0.5280 0.5260 0.6420 HFCR 0.5300 0.5452 0.6010 0.6355 0.6263 0.6388 0.7191 SA 0.5253 0.8029 0.7999 0.5565 0.8000 0.7740 0.7884 TAE 0.6657 0.6755 0.6596 0.6755 0.6755 0.6661 0.6954 Acute 0.5917 0.5917 0.5917 0.5917 0.7125 0.5917 0.8250 Immu 0.5491 0.5456 0.5493 0.5761 0.5739 0.5556 0.5889 Bands 0.5202 0.6209 0.6209 0.6101 0.6083 0.6032 0.6173 GD1 0.8163 0.8551 0.8636 0.8631 0.8645 0.8626 0.8788 GD2 0.8139 0.8262 0.8260 0.8373 0.83775 0.8371 0.8513 表 3 不同初始化方法所产生的精度值
Table 3 Precision values produced by different methods
数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5029 0.8067 0.8052 0.6223 0.7975 0.7626 0.8082 SH 0.5198 0.7938 0.7938 0.5593 0.7910 0.7860 0.8012 Hepatitis 0.6946 0.7023 0.7019 0.6767 0.6918 0.6523 0.7230 SG 0.4976 0.5095 0.5091 0.5152 0.4866 0.4504 0.5545 HFCR 0.5134 0.4897 0.5522 0.6646 0.6168 0.6665 0.6847 SA 0.5012 0.8004 0.7976 0.7779 0.7983 0.7763 0.7871 TAE 0.7821 0.7876 0.7790 0.7876 0.7876 0.7785 0.7970 Acute 0.5931 0.5931 0.5931 0.5931 0.7250 0.5931 0.8846 Immu 0.4403 0.4371 0.4587 0.5286 0.5219 0.5958 0.6086 Bands 0.5097 0.6090 0.6090 0.5919 0.6003 0.5956 0.6062 GD1 0.8416 0.8512 0.8630 0.8629 0.8646 0.8623 0.8786 GD2 0.8121 0.8252 0.8261 0.8376 0.8381 0.8377 0.8518 表 4 不同初始化方法所产生的召回率值
Table 4 Recall values produced by different methods
数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD Credit 0.5021 0.8079 0.8065 0.5911 0.8004 0.7592 0.8096 SH 0.5200 0.7933 0.7933 0.5592 0.7875 0.7855 0.8017 Hepatitis 0.7005 0.7086 0.7078 0.6709 0.6770 0.6570 0.7299 SG 0.4978 0.5102 0.5108 0.5164 0.4848 0.4481 0.5481 HFCR 0.5151 0.4893 0.5552 0.6849 0.6301 0.6873 0.6970 续表 4 数据集 Random Cao Huang Sajidha Peng Dinh IKP-ODD SA 0.5010 0.8014 0.7992 0.5016 0.8014 0.7763 0.7903 TAE 0.6668 0.6733 0.6627 0.6733 0.6733 0.6671 0.6965 Acute 0.5957 0.5957 0.5957 0.5957 0.7107 0.5957 0.7900 Immu 0.4240 0.4186 0.4488 0.5461 0.5369 0.6412 0.6623 Bands 0.5101 0.6176 0.6176 0.5980 0.6083 0.6032 0.6148 GD1 0.8162 0.8551 0.8636 0.8631 0.8645 0.8626 0.8787 GD2 0.8139 0.8262 0.8260 0.8373 0.83775 0.8371 0.8513 表 5 配对t–检验结果
Table 5 Paired t-test results
对比方法 正确率下
的p值精度下
的p值召回率下
的p值IKP-OOD vs. Random 0.0013 0.0011 0.0006 IKP-OOD vs. Cao 0.0414 0.0425 0.0346 IKP-OOD vs. Huang 0.0342 0.0465 0.0297 IKP-OOD vs. Sajidha 0.0065 0.0180 0.0059 IKP-OOD vs. Peng 0.0168 0.0182 0.0066 IKP-OOD vs. Dinh 0.0095 0.0462 0.0143 -
[1] SEAL A, KARLEKAR A, KREJCAR O, et al. Fuzzy c-means clustering using Jeffreys-divergence based similarity measure[J]. Applied soft computing, 2020, 88: 106016. doi: 10.1016/j.asoc.2019.106016 [2] 常思源, 白晓征, 刘君. 一种基于聚类分析的二维激波模式识别算法[J]. 航空学报, 2020, 41(8): 162–175. CHANG Siyuan, BAI Xiaozheng, LIU Jun. A two-dimensional shock wave pattern recognition algorithm based on cluster analysis[J]. Acta aeronautica et astronautica sinica, 2020, 41(8): 162–175. [3] MOSLEHI F, HAERI A. A novel feature selection approach based on clustering algorithm[J]. Journal of statistical computation and simulation, 2021, 91(3): 581–604. doi: 10.1080/00949655.2020.1822358 [4] 谢娟英, 丁丽娟, 王明钊. 基于谱聚类的无监督特征选择算法[J]. 软件学报, 2020, 31(4): 1009–1024. doi: 10.3390/math9050570 XIE Juanying, DING Lijuan, WANG Mingzhao. Spectral clustering based unsupervised feature selection algorithms[J]. Journal of software, 2020, 31(4): 1009–1024. doi: 10.3390/math9050570 [5] 路皓翔, 刘振丙, 张静, 等. 结合多尺度循环卷积和多聚类空间的红外图像增强[J]. 电子学报, 2022, 50(2): 415–425. LU Haoxiang, LIU Zhenbing, ZHANG Jing, et al. Infrared image enhancement based on multi-scale cyclic convolution and multi-clustering space[J]. Acta electronica sinica, 2022, 50(2): 415–425. [6] ZHANG Xiaofeng, SUN Yujuan, LIU Hui, et al. Improved clustering algorithms for image segmentation based on non-local information and back projection[J]. Information sciences, 2021, 550: 129–144. doi: 10.1016/j.ins.2020.10.039 [7] HUA Lei, GU Yi, GU Xiaoqing, et al. A novel brain MRI image segmentation method using an improved multi-view fuzzy c-means clustering algorithm[J]. Frontiers in neuroscience, 2021, 15: 662674. doi: 10.3389/fnins.2021.662674 [8] ZOU Quan, LIN Gang, JIANG Xingpeng, et al. Sequence clustering in bioinformatics: an empirical study[J]. Briefings in bioinformatics, 2020, 21(1): 1–10. [9] TENG Haotian, YUAN Ye, BAR-JOSEPH Z. Clustering spatial transcriptomics data[J]. Bioinformatics, 2022, 38(4): 997–1004. doi: 10.1093/bioinformatics/btab704 [10] HUANG Zhexue. Extensions to the k-means algorithm for clustering large data sets with categorical values[J]. Data mining and knowledge discovery, 1998, 2(3): 283–304. doi: 10.1023/A:1009769707641 [11] JIA Ziqi, SONG Ling. Weighted k-prototypes clustering algorithm based on the hybrid dissimilarity coefficient[J]. Mathematical problems in engineering, 2020, 2020: 1–13. [12] GUO Dongwei, CHEN Yingjie, CHEN Jingwen. A K-prototypes algorithm based on adaptive determination of the initial centroids[C]//Proceedings of the 2018 10th International Conference on Machine Learning and Computing. New York: ACM, 2018: 116−121. [13] 赵立江, 黄永青, 刘玉龙. 改进的混合属性数据聚类算法[J]. 计算机工程与设计, 2007, 28(20): 4850–4852. doi: 10.3969/j.issn.1000-7024.2007.20.007 ZHAO Lijiang, HUANG Yongqing, LIU Yulong. Improved clustering algorithm for mixture data sets[J]. Computer engineering and design, 2007, 28(20): 4850–4852. doi: 10.3969/j.issn.1000-7024.2007.20.007 [14] ZHOU Caiying, HUANG Longjun. The improvement of initial point selection method for fuzzy K-Prototype clustering algorithm[C]//2010 2nd International Conference on Education Technology and Computer. Shanghai: IEEE, 2010, 4: 549−552. [15] Knorr E M, NG R T. Algorithms for mining distancebased outliers in large datasets[C]//Proceeding of the 24th International Conference on Very Large Data Bases. San Francisco: IBM Press, 1997: 219−222. [16] HU Qinghua, YU Daren, LIU Jinfu, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information sciences, 2008, 178(18): 3577–3594. doi: 10.1016/j.ins.2008.05.024 [17] HU Qinghua, LIU Jinfu, YU Daren. Mixed feature selection based on granulation and approximation[J]. Knowledge-based systems, 2008, 21(4): 294–304. doi: 10.1016/j.knosys.2007.07.001 [18] HU Qinghua, YU Daren, XIE Zongxia. Neighborhood classifiers[J]. Expert systems with applications, 2008, 34(2): 866–876. doi: 10.1016/j.eswa.2006.10.043 [19] HU Qinghua, ZHANG Lei, ZHANG D, et al. Measuring relevance between discrete and continuous features based on neighborhood mutual information[J]. Expert systems with applications, 2011, 38(9): 10737–10750. doi: 10.1016/j.eswa.2011.01.023 [20] DOLATSHAH M, HADIAN, MINAEI-BIDGOLI B. Ball*-tree: efficient spatial indexing for constrained nearest-neighbor search in metric spaces[EB/OL]. (2015−11−02)[2022−03−17].https://arxiv.org/abs/1511.00628. [21] 徐章艳, 刘作鹏, 杨炳儒, 等. 一个复杂度为max(O(| C| | U| ), O(| C^2| U/C| ))的快速属性约简算法[J]. 计算机学报, 2006, 29(3): 391–399. doi: 10.3321/j.issn:0254-4164.2006.03.006 XU Zhangyan, LIU Zuopeng, YANG Bingru, et al. A quick attribute reduction algorithm with complexity of max(O(| C| | U| ), O(| C2| | U/C| ))[J]. Chinese journal of computers, 2006, 29(3): 391–399. doi: 10.3321/j.issn:0254-4164.2006.03.006 [22] Bache K, Lichman M. UCI machine learning repository[EB/OL]. (2013−04−04) [2022−03−17]. http://archive.ics.uci.edu/ml. [23] SAJIDHA S A, CHODNEKAR S P, DESIKAN K. Initial seed selection for K-modes clustering - A distance and density based approach[J]. Journal of king Saud university - computer and information sciences, 2021, 33(6): 693–701. doi: 10.1016/j.jksuci.2018.04.013 [24] CAO Fuyuan, LIANG Jiye, BAI Liang. A new initialization method for categorical data clustering[J]. Expert systems with applications, 2009, 36(7): 10223–10228. doi: 10.1016/j.eswa.2009.01.060 [25] PENG Liwen, LIU Yongguo. Attribute weights-based clustering centres algorithm for initialising K-modes clustering[J]. Cluster computing, 2019, 22(3): 6171–6179. [26] DINH D T, HUYNH V N. k-PbC: an improved cluster center initialization for categorical data clustering[J]. Applied intelligence, 2020, 50(8): 2610–2632. doi: 10.1007/s10489-020-01677-5 [27] WU Shu, JIANG Qiangshan S, HUANG J Z. A new initialization method for clustering categorical data[C]//Proceeding of the 11th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Nanjing: Springer Press, 2007: 972−980. [28] DEMSAR J. Statistical comparisons of classifiers over multiple data sets[J]. Journal of machine learning research, 2006, 7: 1–30.



































































































































































 下载:
下载: