Longitudinal motion control of underwater high-speed vehicles based on reinforcement learning
-
摘要: 水下高速航行体由于空泡特性导致其数学模型存在强非线性和强不确定性，经典控制方法如线性二次型调节控制（linear quadratic regulator, LQR）、切换控制等很难实现有效控制。针对水下高速航行体模型难以准确解耦或线性化处理；经典控制方法难以充分考虑水下环境复杂多变性以及在应对扰动时控制器可能会出现过饱和现象的问题，采用智能控制中的强化学习算法，使用在不基于准确模型的条件下与环境不断探索与交互得到控制策略的策略，完成了深度确定性策略梯度（deep deterministic policy gradient,DDPG）智能体控制器的设计。实验结果证明，设计的控制器能够保证水下高速航行体纵向运动的稳定控制，在执行器不超过饱和范围内能够应对扰动并完成下潜控制任务，具有较强的鲁棒性和更好的适应性。Abstract: Owing to cavitation characteristics, the mathematical model of a high-speed underwater vehicle has strong nonlinearity and uncertainty. Classical methods such as the linear quadratic regulator and switching control cannot achieve effective control. To address problems in the difficulty of decoupling or linearizing the underwater high-speed vehicle model accurately, the classical control method cannot fully consider the complexity and variability of the underwater environment, and the controller may be oversaturated when dealing with disturbances. Thus, the reinforcement learning algorithm in intelligent control was adopted in this study. It continuously explores and interacts with the environment to obtain control despite the absence of an accurate model and thereby completing the design of the deep deterministic policy gradient agent controller. The experimental results show that the designed controller can ensure stable control of the longitudinal motion of the high-speed underwater vehicle. Within the saturation range of the actuator, it can respond to disturbance and complete the diving control task, and the controller has strong robustness and better adaptability.
-
由流体特性可知，在同等条件下，航行体在水下受到的阻力是在空气中的一千倍，因此，水下航行体的运动速度远小于飞机等大气中的航行体，一般难以超过40 m/s[1]。超空泡技术的出现，使得水下航行体速度大幅度提升，在20世纪70年代，俄罗斯成功研制了第一代“暴风”水下高速航行体，其大部分表面被空泡包裹，所受阻力大幅减小，速度达到了100 m/s，目前，其研制的新一代的水下高速航行体的速度甚至可达到200 m/s[2]。但空泡的包裹也给水下航行体带来了控制上的难题，为降低研究的复杂性，目前各国的研究者多数在纵向平面内对水下高速航行体的控制问题进行研究。Dzielski等[3]采用反馈线性化方法设计了控制器；陈超倩等[4]针对航行体的耦合问题通过精确线性化和解耦设计了最优控制器，实现对航行深度的渐进跟踪控制；庞爱平等[5]设计了扰动观测补偿器和H∞控制结合的控制方法以消除滑水现象来实现稳定控制；韩云涛等[6]针对执行器饱和问题，提出一种基于线性变参数的抗饱和控制方法。李洋等[7]对水下高速航行体非全包裹模型中的不确定项利用RBF神经网络进行逼近估计，设计的自适应控制器能够完成较好的信号跟踪。除以上研究成果外，其他国内外学者还采用了很多经典控制方法为水下高速航行体设计控制器，如LQR、滑模控制、切换控制、H2和H∞状态反馈控制等[8-10]。
智能控制近几年应用普遍，以强化学习控制方法为代表，池海红等[11]针对高速飞行器模型参数不确定的情况，利用强化学习设计控制律，具有较好的控制效果。Mu等[12]针对吸气式超高速飞行器的跟踪控制问题，基于强化学习提出了一种具有自适应学习能力的数据驱动补充控制方法，与滑模控制相结合实现了具有参数不确定性和环境干扰的超高速飞行器系统稳定巡航控制。在水下机器人控制方面，许雅筑等[13]介绍了采用强化学习控制水下机器人的优点，能够充分考虑水中环境的不确定性和特殊干扰，总结了强化学习控制算法的挑战和应用研究。Hafner等[14]提出了基于神经网络的连续动作值控制器，应用于水下自主航行器。王日中等[15]在水下环境中基于深度强化学习算法设计了智能体控制器，完成了水下航行器的深度控制，且与传统PID控制算法相比具有更高的精度。通过对传统和智能控制方法的比较可知，相对于经典控制方法，智能控制具有不依赖具体模型信息、有效抗扰等优势，近几年强化学习与神经网络的结合让强化学习能够应用到更多的领域中。通过对以上文献的分析可知，水下高速航行体由于自身流体特性的复杂性，导致其自身模型具有很强的不确定性，因此本文采用基于强化学习的智能控制方法，通过设计合适的奖励函数搭建强化学习环境，从而学习和训练出一个能使水下高速航行体在一定条件下实现稳定运动的控制器，本文的方法较现有的控制方法的优势是不需要对数学模型进行简化处理，能更加有效地做到使水下高速航行体在空化器和尾舵正常偏转范围内完成应对扰动并下潜的控制任务，其适应性和鲁棒性均优于传统控制算法。
1. 水下高速航行体建模
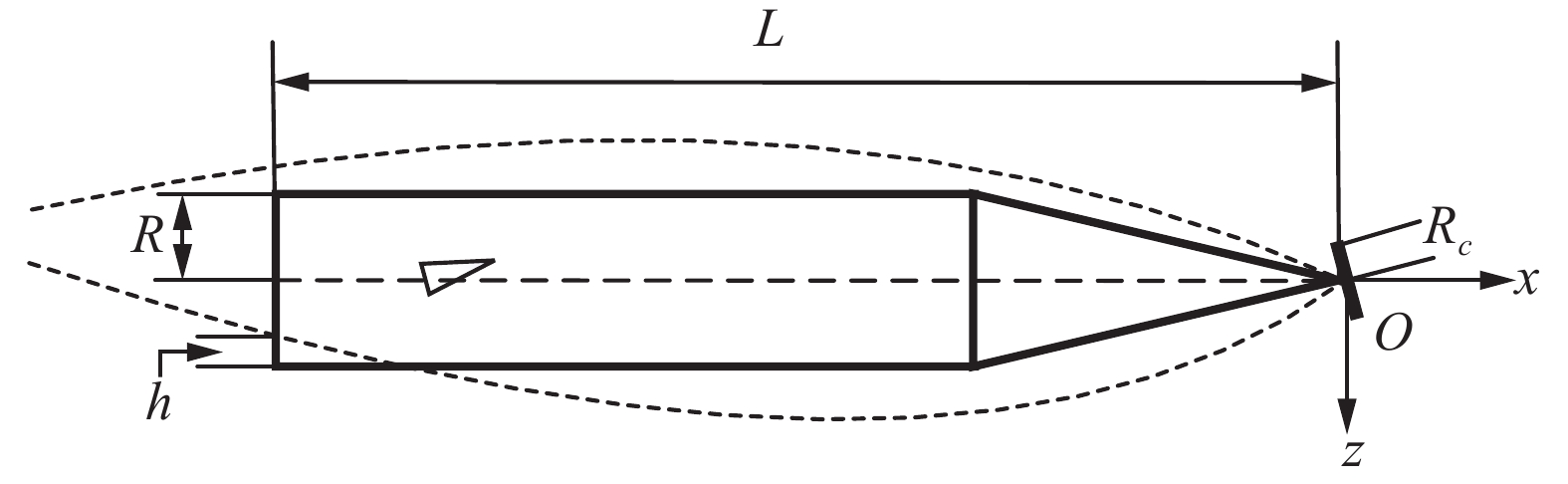
目前在对水下高速航行体运动控制的研究中，Dzielski等[3]提出的模型得到了广泛的应用，这是一个中心建立在航行体头部空化器中心处的纵向平面内的 4 状态 2 自由度模型，该模型结构简单、易于分析，同时又保留了航行体与空泡碰撞时产生的滑行力，本文即在此模型的基础上进行研究。水下高速航行体模型图如图1所示，取空化器中心为参考点,建立体坐标系Oxz，R为航行体半径，Rc为空化器半径，h为航行体尾部浸水深度，L为航行体长度。
图 1 水下高速航行体纵向模型Fig. 1 Supercavitating vehicle longitudinal model
下载:
全尺寸图片
1.1 水下高速航行体运动方程建模及开环仿真
水下高速航行体运动方程参考文献[3]纵向平面运动方程，整理如下：
$$ \begin{array}{c}{m}_{b}\left(\dot{\omega }-{x}_{g}\dot{q}-qV\right)={F}_{{\textit{z}}}\end{array} $$ $$ \begin{array}{c}{I}_{yy}\dot{q}-{m}_{b}{x}_{g}\left(\dot{\omega }-qV\right)=M\end{array} $$ $$ \begin{array}{c}\dot{{\textit{z}}}=\omega\; {\rm{cos}}\;\theta -V\;{\rm{sin}}\;\theta \end{array} $$ $$ \begin{array}{c}\dot{\theta }=q\end{array} $$ 式中：mb为航行体质量，ω为纵向速度，xg为航行体重心到空化器的距离，q为航行体俯仰角速度，Fz为z轴上的合力，Iyy为惯性矩，M为力矩，z为深度，θ为航行体俯仰角。
对运动方程进行简化处理，因航行体俯仰角度为小角度，可近似认为cos θ=1，sin θ=0。其中有：
$$ \begin{array}{c}{m}_{b}={m}_{1}+{m}_{2}=\dfrac{7}{9}L\text{π} {R}^{2}m\rho \end{array} $$ $$ \begin{array}{c}{I}_{\text{yy}}={I}_{1}+{I}_{2}=\dfrac{11}{60}m\rho \text{π} {R}^{4}L+\dfrac{133}{405}m\rho \text{π} {R}^{2}{L}^{3}\end{array} $$ $$ \begin{array}{c}{x}_{g}=-\dfrac{17}{28}L\end{array} $$ $$ \begin{array}{c}{F}_{{\textit{z}}}={F}_{\rm{grav}}^{{\textit{z}}}+{F}_{\rm{fin}}^{{\textit{z}}}+{F}_{\rm{cav}}^{{\textit{z}}}+{F}_{p}^{{\textit{z}}}\end{array} $$ $$ \begin{array}{c}M={M}_{\rm{grav}}+{M}_{\text{fin}}+{M}_{p}\end{array} $$ $$ \begin{array}{c}{F}_{\rm{grav}}={m}_{b}g\;{{\rm{cos}}}\;\theta \approx {m}_{b}g\end{array} $$ $$ \begin{array}{c}{F}_{\rm{cav}}=0.5\text{π} \rho {{R}_{n}}^{2}{V}^{2}{C}_{x0}\left(1+\sigma \right){\alpha }_{c}={C}_{l}{\alpha }_{c}\end{array} $$ $$ \begin{array}{c}{F}_{\rm{fin}}=-n{C}_{l}{\alpha }_{f}\end{array} $$ $$ \begin{array}{c}{M}_{\rm{fin}}={F}_{\rm{fin}}L\end{array} $$ $$ \begin{array}{c}{M}_{\rm{grav}}={F}_{\rm{grav}}\left(-{x}_{g}\right)\end{array} $$ $$ \begin{array}{c}{M}_{p}={F}_{p}L\end{array} $$ $$ \begin{array}{c}{\alpha }_{c}=\dfrac{\omega }{V}+{\delta }_{c}\end{array} $$ $$ \begin{array}{c}{\alpha }_{f}=\dfrac{\omega }{V}+{\dfrac{qL}{V}+\delta_{f} }\end{array} $$ 滑行力Fp是航行体尾部与空泡壁接触产生的强非线性力，是导致水下高速航行体空泡破裂的主要原因，滑行力的计算采用经验公式[16]，受纵向速度ω影响，从图2中可以看出当ω在一定范围内时，滑行力存在死区空间。
图 2 滑行力Fp与纵向速度ω的关系Fig. 2 Relationship between planning force Fp and longitudinal speed ω下载:
全尺寸图片
$$ {F}_{p}=-{V}^{2}\left[\begin{array}{c}\dfrac{1}{mL}\\ \dfrac{1}{m}\end{array}\right]\left(1-\left(\dfrac{{R}{{'}}}{\left({h}{{'}}+{R}{{'}}\right)}\right)^{2}\right)\left(\dfrac{1+{h}{{'}}}{1+2{h}{{'}}}\right)\alpha $$ $$ \begin{array}{c}{R}{{'}}=\dfrac{{R}_{c}-R}{R}\end{array} $$ $$ \begin{array}{c}{h}{{'}}=\left\{\begin{array}{l}\begin{array}{ll}0 , & {R}{{'}} > \dfrac{L}{R}\left|\dfrac{\omega }{V}\right|\end{array}\\ \begin{array}{cc}\dfrac{L}{R}\left|\dfrac{\omega }{V}\right|-{R}{{'}} , & 其他\end{array}\end{array}\right.\end{array} $$ $$ \begin{array}{c}\alpha =\left\{\begin{array}{cc}\dfrac{\omega }{V}-\dfrac{{\dot{R}}_{c}}{V} , & \dfrac{\omega }{V} > 0\\ \dfrac{\omega }{V}+\dfrac{{\dot{R}}_{c}}{V} , & 其他\end{array}\right.\end{array} $$ $$ \begin{array}{c}{\kappa }_{1}=\dfrac{L}{{R}_{n}}\left(\dfrac{1.92}{\sigma }-3\right)^{-1}-1\end{array} $$ $$ \begin{array}{c}{\kappa }_{2}=\left(1-\left(1-\dfrac{4.5\sigma }{1+\sigma }\right){{\kappa }_{1}}^{\frac{40}{17}}\right)^{0.5}\end{array} $$ $$ \begin{array}{c}{R}_{c}={R}_{n}\left(0.82\dfrac{1+\sigma }{\sigma }\right)^{0.5}{\kappa }_{2}\end{array} $$ 1.2 水下高速航行体开环运动仿真
取航行体深度z、纵向速度ω、俯仰角度θ、俯仰角速度q为状态变量x，取航行体尾舵偏转角δf和空化器偏转角δc为控制输入变量u，x=[z w θ q]T，u=[δf δc]T,对方程同时除以πρmR2L进行简化处理，得到水下高速航行体的数学模型的标准公式如下：
$$ \begin{array}{c}\dot{x}={\boldsymbol{Ax}}+{\boldsymbol{Bu}}+{\boldsymbol{C}}+{\boldsymbol{D}}{F}_{p}\end{array} $$ 2. 强化学习
强化学习是一种机器学习方法，通过强化学习智能体与环境不断交互学习训练出一种符合期望的策略。强化学习目前在很多领域都有着成功的应用，如游戏模拟、工业制造、机器控制等[17-19]。利用强化学习训练智能体需要大量的试错与探索，该过程中不需要人为干预，该过程使用的数据来自搭建的动态环境，即不需要事先提供训练集。
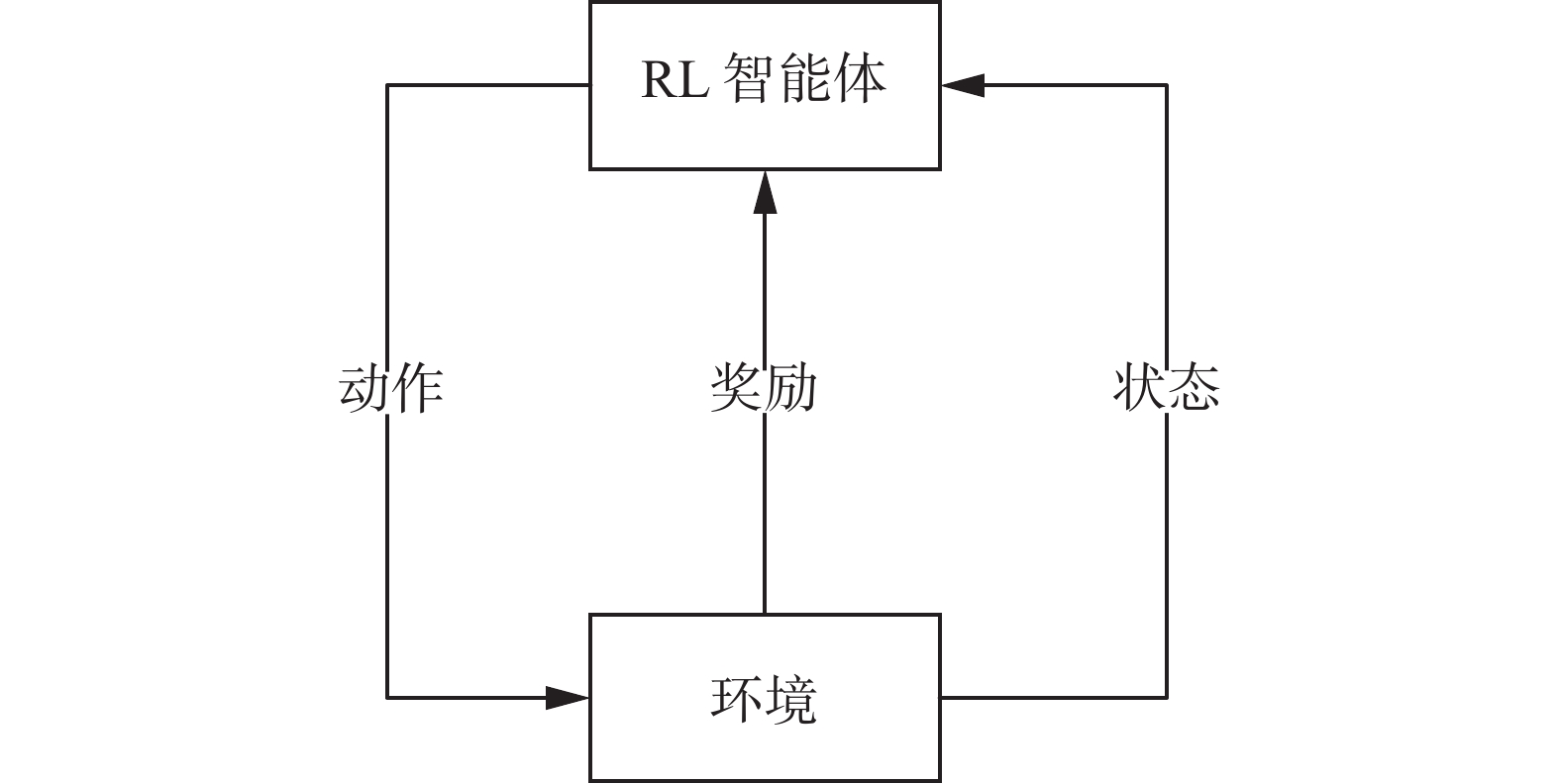
强化学习是一种从环境状态映射到动作的一种学习，目标是使强化学习智能体与环境的交互中获得最大的累计奖励值。如图3所示，强化学习由三部分构成：智能体、奖励函数、环境。环境的初始状态输入给智能体，智能体根据状态等量选取合适的动作，动作输入给环境，环境得到新的状态和该动作产生的奖励值，二者输入给智能体，智能体根据奖励值调整策略，根据新状态输出新的动作，以此循环。强化学习的目标是学得一个策略函数π(x)，π(x)是从状态空间x到动作空间a的一个映射。
图 3 强化学习基本结构Fig. 3 Reinforcement learning basic structure下载:
全尺寸图片
强化学习算法从结构上可以分为3类：基于值函数的强化学习[20]、基于策略的强化学习[21]、执行器−评价器(actor-critic,A-C)结构[22]。
2.1 执行器−评价器(A-C)结构
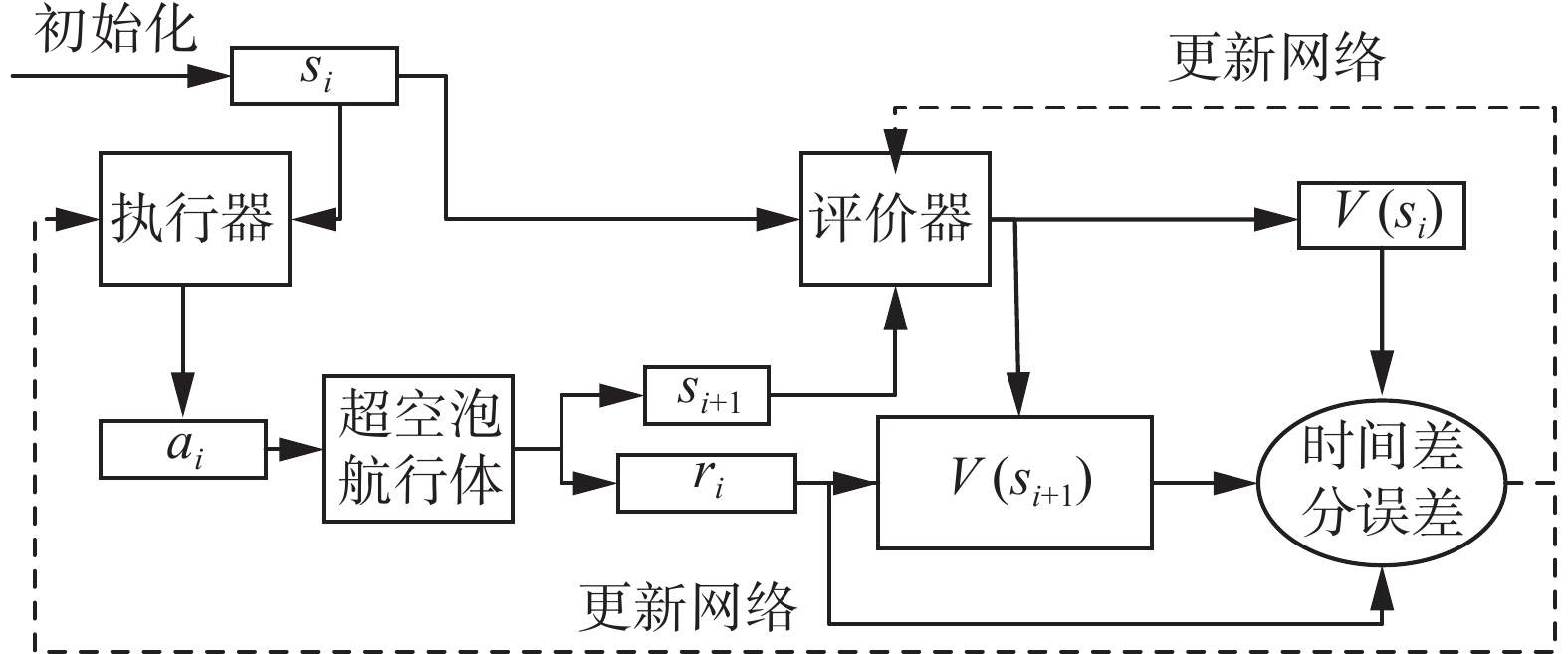
执行器−评价器结构法结合了前两类方法的优点，执行器部分采用策略函数算法方式选择动作给到环境，评价器根据计算出的价值函数和奖励值得到误差，根据误差更新评价器和执行器的权值参数等。如图4所示，执行器actor和评价器critic分别代表策略π和值函数V(s)，各用一个神经网络来逼近。
图 4 A-C结构Fig. 4 A-C structure下载:
全尺寸图片
执行器的输入为水下高速航行体现在的状态，输出为空化器、尾舵的偏转量，评价器输入为水下高速航行体的状态，输出为状态值函数。空化器动作输入给水下高速航行体后得到新状态量并根据奖励函数公式得到即时奖励值。执行器根据使得时间差分误差最小化的方向来迭代更新，评价器同样根据时间差分误差带权重梯度更新。在一次迭代更新中，先更新执行器再更新评价器。最终当训练次数达到最大值或累积奖励值达到目标要求则训练停止。
$$ \begin{array}{c}{E}_{{\rm{TD}}}=r+\gamma V\left({s}_{i+1}\right)-V\left(\mathrm{s}\right)\end{array} $$ $$ \begin{array}{c}w\leftarrow w+E_{\rm{{TD}}}\beta {\nabla }_{w}V\left({s}_{i},w\right)\end{array} $$ $$ \begin{array}{c}\theta \leftarrow \theta +E_{\rm{{TD}}}\alpha {\nabla }_{\theta }\mathrm{log}\;\text{π}\left({a}_{i}|{s}_{i},\theta \right)\end{array} $$ 式中：ETD为时间差分误差,w为执行器网络参数，θ为评价器网络参数，α、β为执行器和评价器的系数。
2.2 DDPG算法
策略梯度算法利用随机性策略在动作空间进行采样，在大的动作空间内计算量相应也变大，Silver等[23]提出确定性策略梯度算法（deterministic policy gradient, DPG），采用确定性方法对动作空间采样。Lillicrap等[24]在深度Q网络（deep Q-network, DQN）的基础上对确定性策略梯度方法进行拓展，提出了一种基于A-C结构的深度确定性策略梯度（DDPG）算法。该算法增加了经验回放池，加快了策略更新速度，加入了噪声，增加了探索空间，执行器和评价器网络各采用两个神经网络，能够解决连续动作空间上的深度强化学习问题，且取得最优解的时间少于DQN。
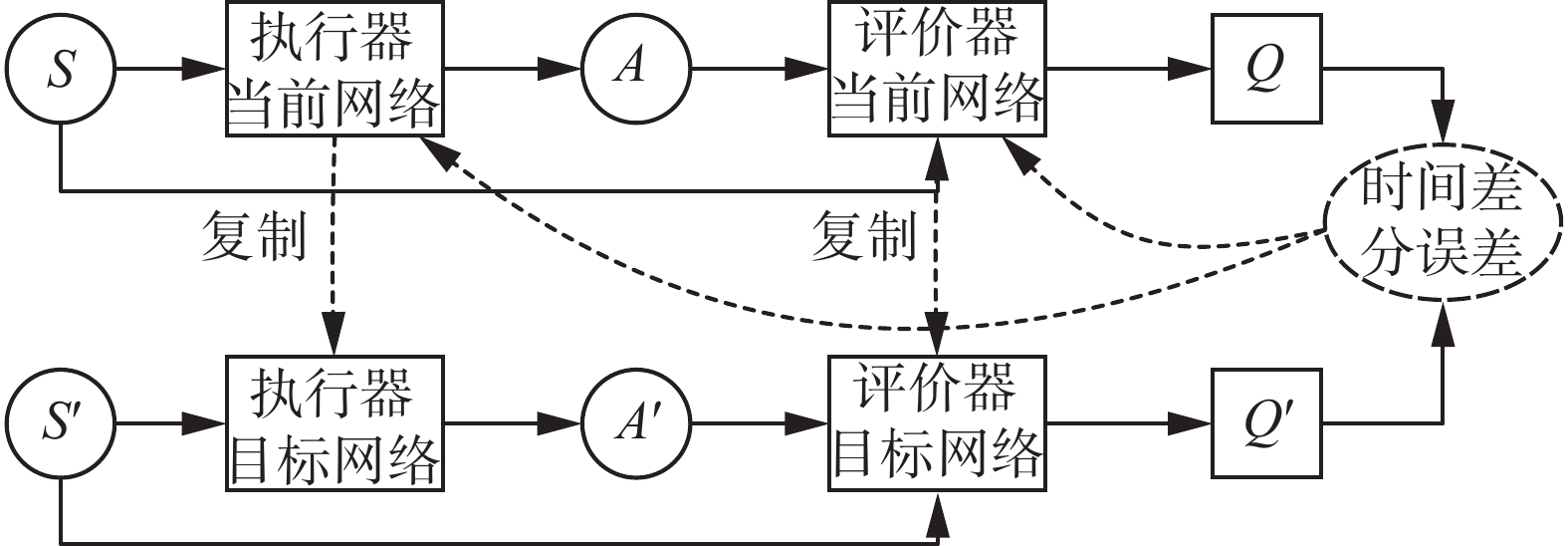
如图5所示，DDPG的核心在于把执行器和评价器都拆分为两个网络：当前网络与目标网络。执行器产生动作给环境后，产生样本(si，ai，si+1，ri)，样本放入经验回放池。评价器的当前网络负责更新参数θQ和计算当前状态动作价值Q(si，ai)，评价器目标网络计算Q'(si+1，ai+1)值。之后根据损失函数对评价器当前网络进行更新，更新后的当前网络会定时把权重θQ'复制给目标网络。
图 5 DDPG结构Fig. 5 DDPG structure下载:
全尺寸图片
执行器当前网络接受状态si根据权重θπ选择最优动作ai，并根据梯度公式更新权重，目标网络根据经验回放池中的状态si+1和权重θπ'选择最优动作ai+1。当前网络会定时把权重复制给目标网络。
$$ \begin{array}{c}{{L}}=\dfrac{1}{N}\displaystyle\sum _{i}({y}_{i}-Q({s}_{i},{a}_{i}|{\theta }^{Q}){)}^{2}\end{array} $$ $$ \begin{array}{c}{y}_{i}={r}_{i}+\gamma \cdot {Q}{{{'}}}({s}_{i+1},{\pi }{{{'}}}({s}_{i+1}\left|{\theta }^{{\pi }{{{'}}}}\right)\left|{\theta }^{{Q}{{{'}}}}\right)\end{array} $$ $$ \begin{array}{c}{\nabla }^{\theta^\pi }J \sim \dfrac{1}{N}\displaystyle\sum _{i}{\nabla }^{ai}Q\left({s}_{i},{a}_{i}|{\theta }^{Q}\right)|{\nabla}^{\theta^\pi }\pi \left({s}_{i}\right|{\theta}^{ \pi })\end{array} $$ $$ \begin{array}{c}{\theta }^{{Q}{{{'}}}}=\tau \cdot{\theta }^{Q}+\left(1-\tau \right){\theta }^{{Q}{{{'}}}}\end{array} $$ $$ \begin{array}{c}{\theta }^{{\pi }{{{'}}}}=\tau \cdot{\theta }^{\pi }+\left(1-\tau \right){\theta }^{{\pi }{{{'}}}}\end{array} $$ 式中：L为根据损失函数计算的损失值；N为选取的样本数；γ∈(0，1)为折扣因子，表示未来奖励的当前价值；τ为软更新系数，一般取0.01或0.001。
3. 基于DDPG算法的强化学习控制器
3.1 控制器及奖励函数设计
设强化学习智能体的观察输入为4维，航行体的状态输出x=[z w θ q]T，智能体的输出作为航行体的控制动作，先令尾舵偏转角为0，仅控制空化器偏转，又因空化器偏转角有限，所以动作信号经饱和处理后再作为航行体的输入，最大偏转角度不超过0.6 rad。由以上标准，设航行体训练条件为
$$ \left\{\begin{array}{c}-300\;{\rm{m}}\leqslant {\textit{z}}\leqslant 300\;{\rm{m}}\\ -1\;{\rm{rad}}\leqslant \theta \leqslant 1\;{\rm{rad}}\end{array}\right. $$ 当超出该范围集则训练终止。该范围若太小，则训练过程中动作的探索空间受到限制，耗费大量时间奖励函数也难以收敛，范围若太大，则不符合实际运行情况，易出现当航行体俯仰角达到80°还可以控制的情况，当航行体俯仰角度超过一定范围时，实际运行中已不可能再调整回稳定状态，因此通过设定训练范围筛出无用的训练样本数据。
设计奖励函数在训练的过程中指导航行体逼近期望的运行状态，奖励函数的设计直接影响最后控制器的控制精度和鲁棒性，为实现水下高速航行体的平稳运行需要保证航行体姿态稳定，航行体的姿态受深度z和俯仰角度θ直接影响，因此当ω和q贴近于期望的状态时对二者给一个较大的奖励值。根据前文可知纵向速度ω影响强非线性滑行力的大小，状态值q反映了航行体俯仰角速度，是俯仰角θ的导数，在航行体偏转的过程中不期望出现反复快速抖动的现象，因此ω、q也作为平稳运行的指标。对于4个状态量，在训练时对实际值与期望值之间的偏差进行奖励。期望稳定运行时航行体状态为头部上翘，尾部周期性拍打空泡壁前进，令期望值xd=[0.1 0 0.05 0]T，因此Δz,ω,θ,q= xd−x。再对其赋以系数以调整影响量的大小，根据经验与试验，对较为直接的两个状态量z和θ的系数设为0.3和0.5，ω和q的系数设为0.04和0.03，同时对上一步的控制动作进行奖励，设其系数为0.005，综上奖励函数为
$$ r_1 = -0.3(\Delta {\textit{z}}{)}^{2} - 0.04(\Delta \omega {)}^{2}-0.5(\Delta \theta {)}^{2}-0.03(\Delta q{)}^{2}-0.005{\delta }_{c} $$ 对航行体状态每0.01 s进行一次采样，每集运行时间为4 s。为增加探索空间，对航行体每集初始状态z设为（−0.5 m，0.5 m）范围内随机选取。
3.2 神经网络结构
图 6 评价器神经网络结构Fig. 6 Critic neural networks下载:
全尺寸图片
图 7 执行器神经网络Fig. 7 Actor neural networks下载:
全尺寸图片
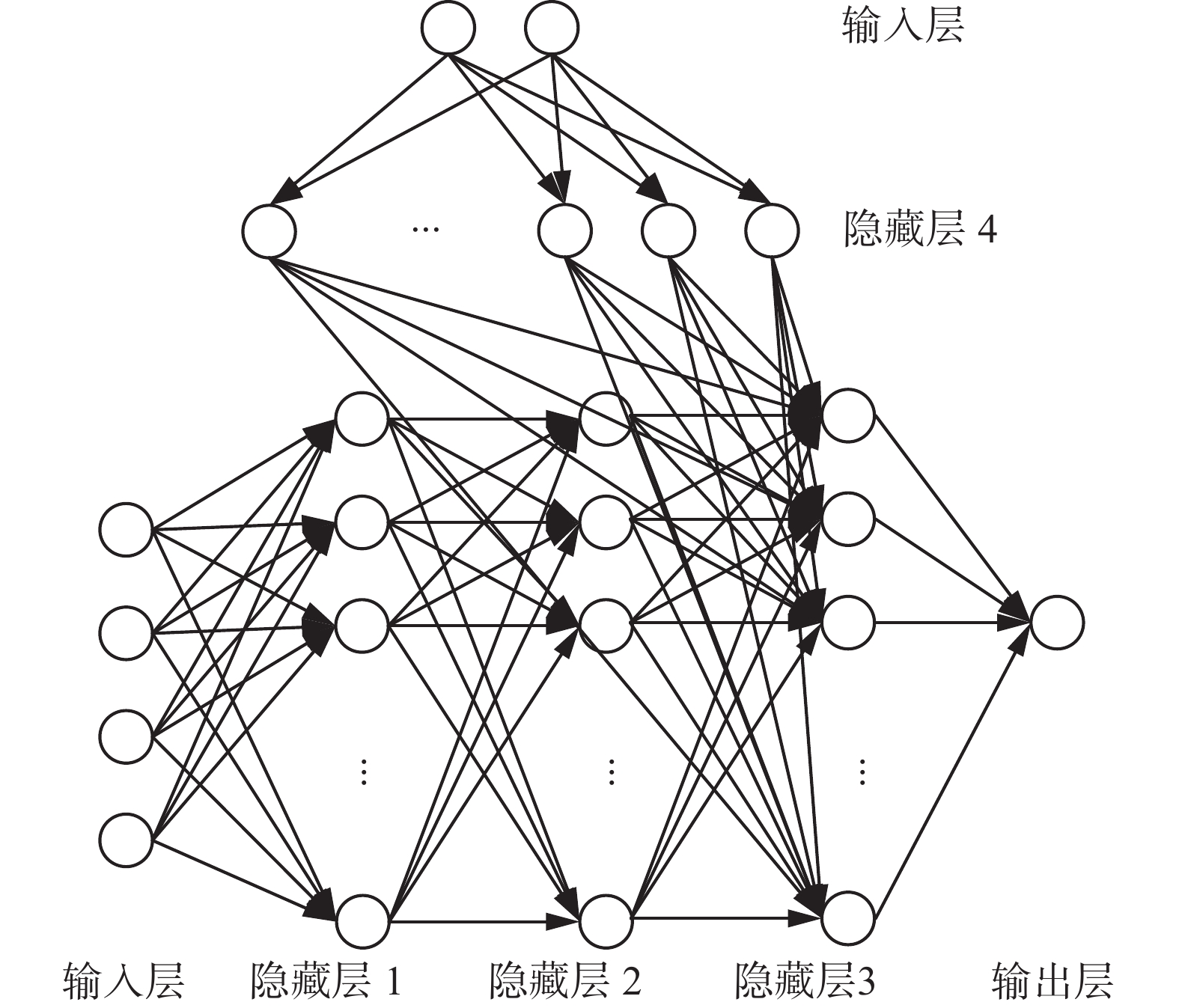
隐藏层大小为100，其中评价器的输入层输入航行体的状态和动作，隐藏层由5个全连接层和3个relu激活函数构成，输出层输出状态动作函数的值，学习率为0.001；执行器的输入层输入航行体的状态，隐藏层由4个全连接层、3个relu激活函数构成，输出层输出控制器的偏转角度，执行器学习率为0.0001，执行器和评价器的梯度阈值均为1。
智能体训练过程的其他参数N、τ、γ分别为128、0.001和0.99。
航行体越靠近期望状态，奖励值越大，令训练目标为在连续5集的奖励函数平均值大于−100。在后续测试中发现因设定训练范围，出现航行体在1 s内状态超出训练范围导致终止该集训练情况，但该集累计奖励值因采样数量少而大于−100，连续5集终止训练后得到的控制器并不能完成航行体稳定控制任务。改变训练完成条件，当在每集采样达到400次且连续5集奖励函数平均值大于−100时为达到目标要求。
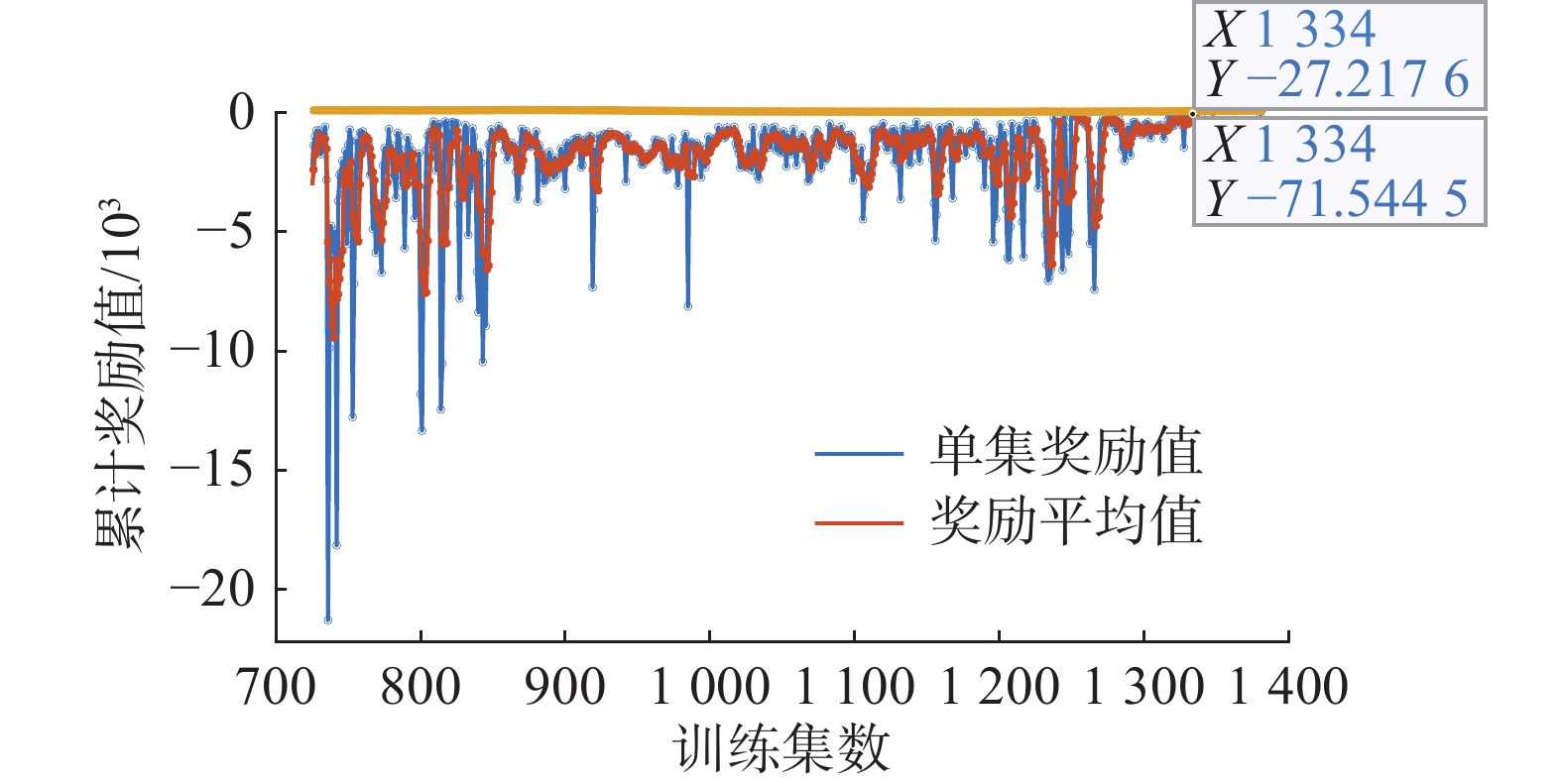
通过建立仿真环境进行训练，当奖励函数收敛且达到要求时终止该次训练。由强化学习得到控制器的过程是一个不断调整和改进的过程，并不存在最优结果，通过该次训练的仿真结果来进一步调整奖励函数和训练要求，逐步达到航行体运行期望状态。图8中横坐标为训练集数，纵坐标为单集内由奖励函数计算得出的累计奖励值。蓝色线表示单集的奖励函数值，橙红色线表示连续5集的奖励函数平均值，根据奖励函数曲线变化可见，在前期的训练中奖励值比较发散，且幅值较大，连续两集累计奖励值差值甚至高达一万，此阶段是因为处于不断地试错与探索，奖励函数反应的状态值都比较大。如图8右上角所示，在第1334集训练中，奖励函数值达到了−27，且包括该集在内的前5集平均奖励值为−71，达到训练要求。
图 8 训练窗口1Fig. 8 Training window 1下载:
全尺寸图片
4. 仿真结果分析及调整
根据表1数据计算，得到标准化公式中各矩阵的值：
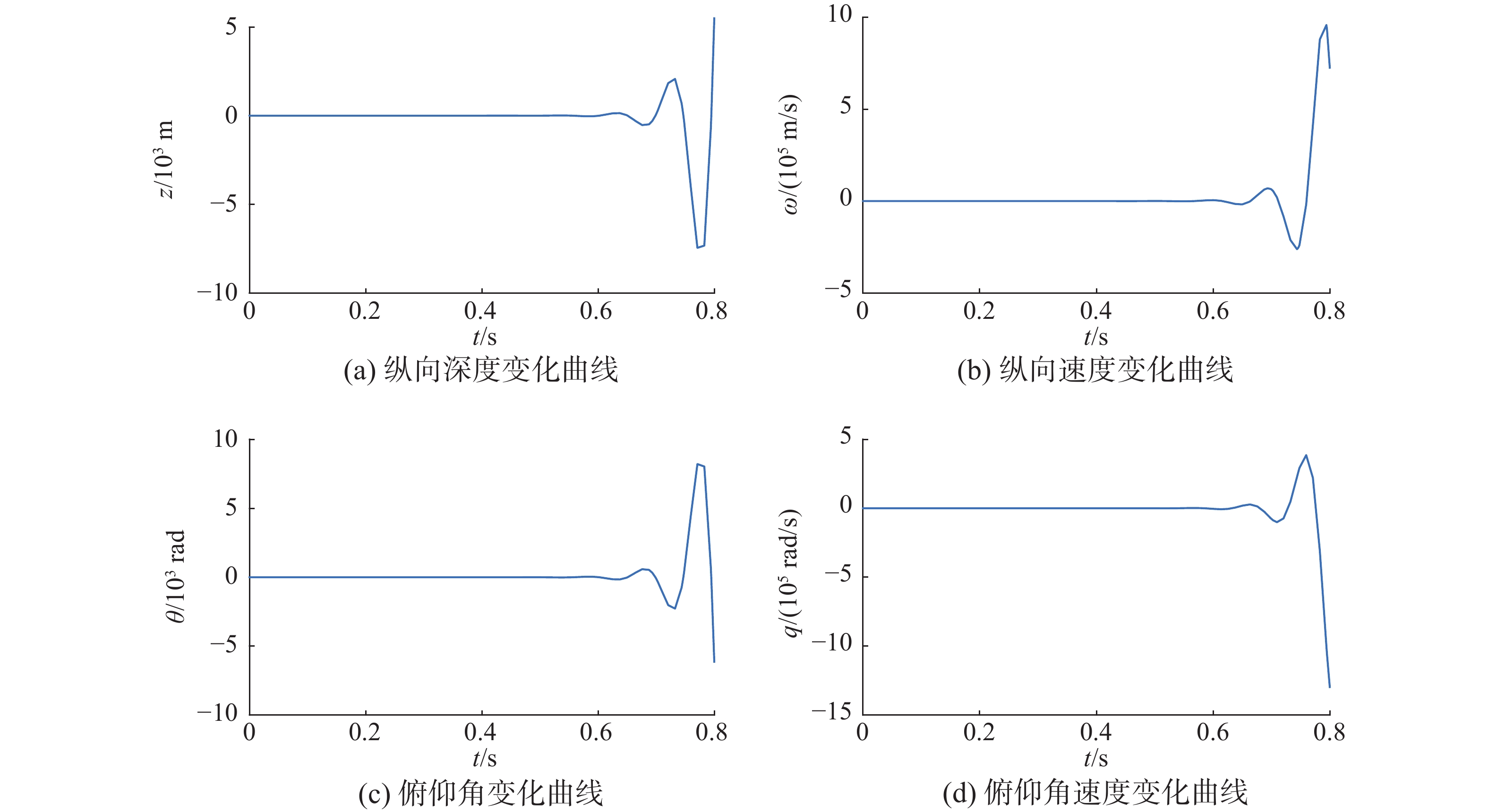
表 1 航行体模型参数Table 1 Supercavitating vehicle model parameters参数 参数数值 航行体长度L/m 1.80 水的密度ρ/(kg/m3) 1000 重力加速度g/(m/s2) 9.81 空化器半径Rn/m 0.0191 航行体半径R/m 0.0508 升力系数Cx0 0.82 空化数σ 0.03 密度比m 2 尾翼相似系数n 0.5 前进速度V/(m/s) 75 空泡半径Rc/m 0.09 空泡半径变化率 $ {\dot{R}}_{c} $ 20 $$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&{ - 75}&0\\ 0&{15.303\;9}&0&{79.942\;8}\\ 0&0&0&1\\ 0&{ - 13.271\;9}&0&{ - 5.839\;6} \end{array}} \right] $$ $$ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ {205.948\;0}&{941.840\;9}\\ 0&0\\ { - 243.318\;7}&{ - 752.061} \end{array}} \right] $$ $$ {\boldsymbol{C}}=\left[\begin{array}{c}0\\ 9.81\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right]D=\left[\begin{array}{c}0\\ -1.226\;6\\ \begin{array}{c}0\\ 1.449\;2\end{array}\end{array}\right] $$ 对航行体模型进行开环仿真，从图9中可以看出水下高速航行体在不加控制的情况下无法保持稳定。
图 9 开环状态下航行体状态Fig. 9 The state of the vehicle in open loop下载:
全尺寸图片
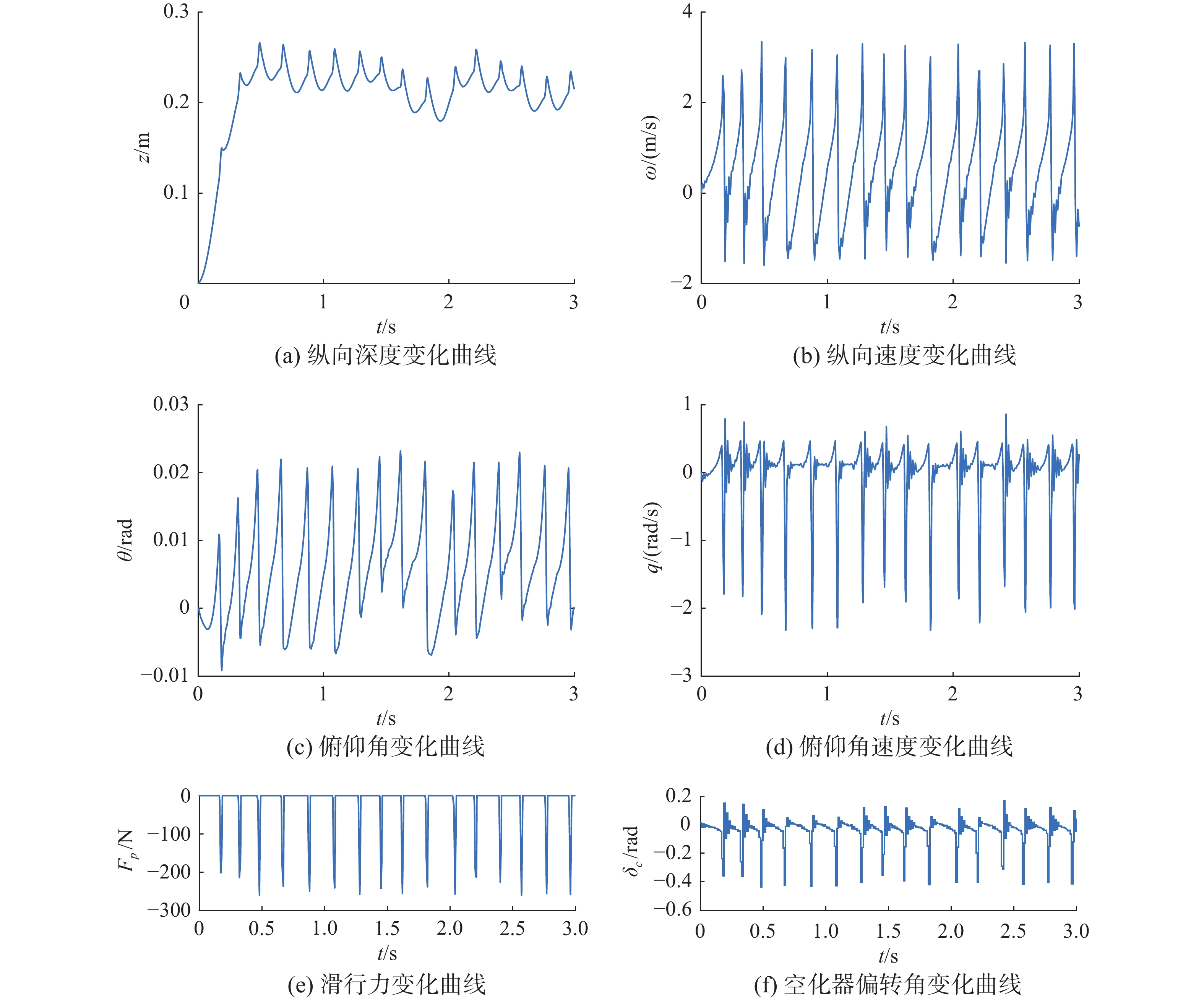
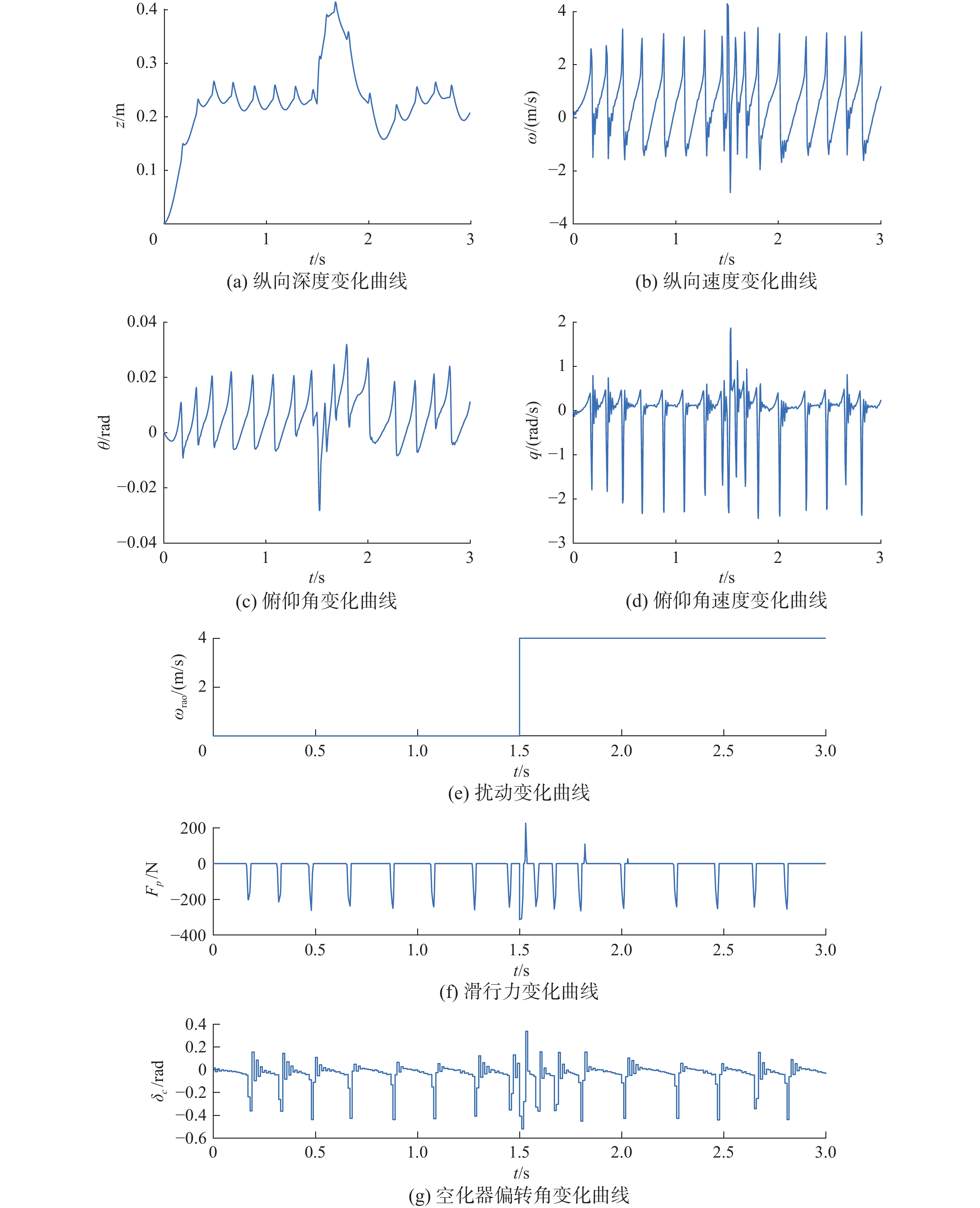
初步训练完成的控制器对航行体的控制效果如图10。观察图10，此时航行体在控制器的控制下，头部向上翘起，尾部不断拍打空泡壁前进，滑行力大小在（200 N，260 N）。由强化学习训练出的控制器具有一定的抗扰性，在1.5 s时加入一个幅值为+4 m/s的纵向速度扰动ωrao，如图11所示，航行体能够在0.5 s内稳定下来且滑行力不超过300 N。
图 10 DDPG控制器1控制下的航行体状态Fig. 10 The state of the vehicle under the control of the DDPG controller 1下载:
全尺寸图片
图 11 DDPG控制器1控制下的航行体状态（加扰动）Fig. 11 The state of the vehicle under the control of the DDPG controller 1(with disturbance)下载:
全尺寸图片
满足了控制航行体在一定范围内稳定下来的情况之后，证明由DDPG算法训练出的控制器可行，但是现在的航行体处于一种震荡状态，且稳定精度不高，需要对奖励函数进一步地调整。
航行体的震荡是由于尾部受重力影响触碰空泡壁产生向上的滑行力，将尾部弹回空泡内后再次受力下落而产生的。滑行力的存在是破坏航行体稳定运行状态的重要原因，消除滑行力需要平衡航行体的重力，仅凭空化器的偏转无法抵消航行体的重力，为消除震荡状态，在控制方面增加尾舵的偏转角，同样经饱和处理后再给到航行体，在奖励函数中加入滑行力的影响，考虑到滑行力数值（200，260），令其系数为0.01，由图2可知滑行力受纵向速度ω的影响，当ω大小约在（−1.65，1.65）范围时滑行力为0，相应的调大ω的系数。
在训练环境中不断调试和训练，设计一个奖励函数为
$$ \begin{array}{c}r_2=-{C}_{{\textit{z}}}(\Delta {\textit{z}}{)}^{2}-{C}_{\omega }(\Delta \omega {)}^{2}-{C}_{\theta }(\Delta \theta {)}^{2}-{C}_{q}(\Delta q{)}^{2}-\\ {C}_{p}\left|{F}_{p}\right|-{\boldsymbol{C}}{u}_{t-1}\end{array} $$ 其中：Cz、Cω、Cθ、Cq、Cp分别为0.3、0.08、0.5、0.03、0.01，C=[0.06 0.08]T，期望状态为x=[0 0 0 0]T。
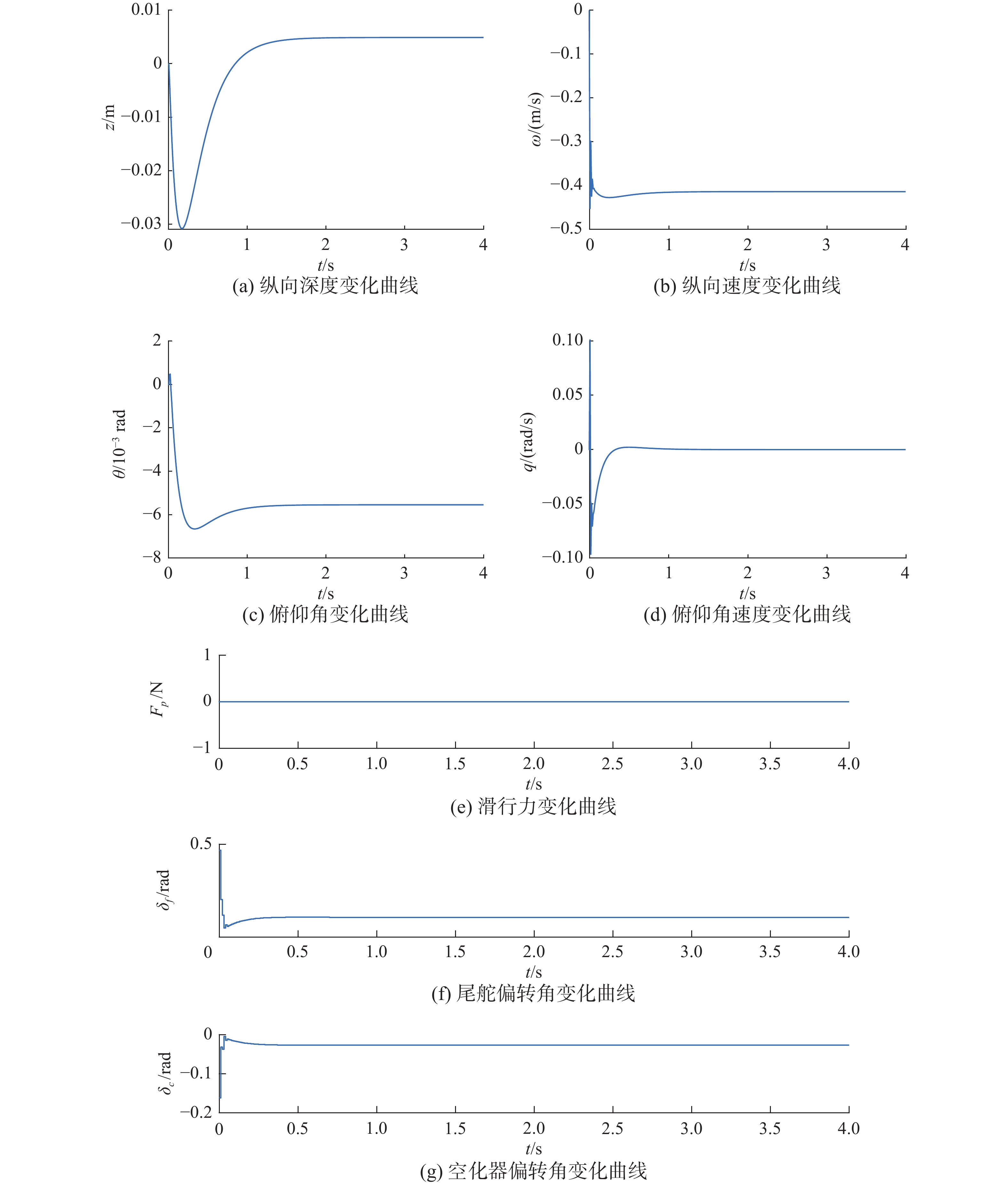
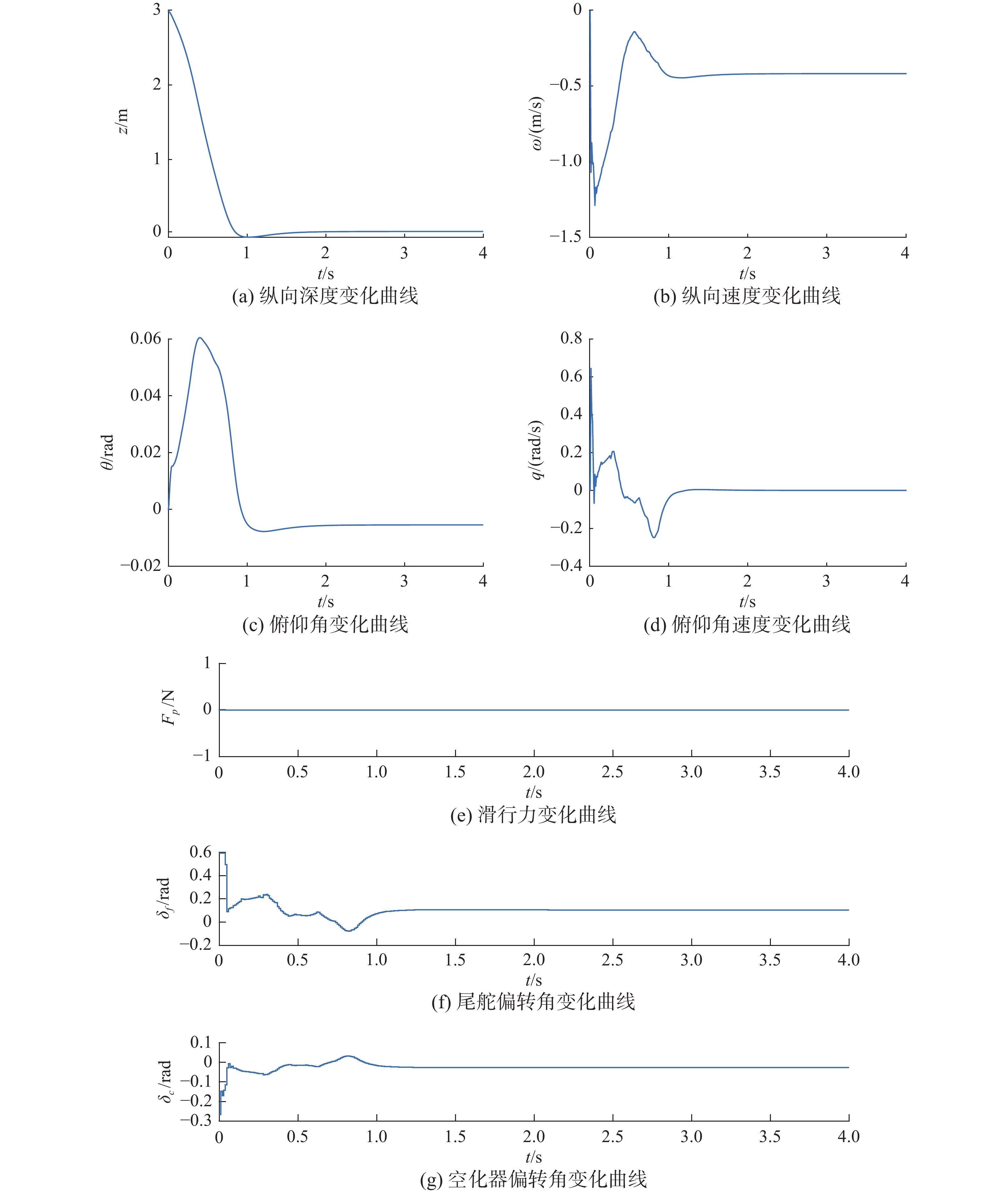
经过3000集的训练后，奖励函数逐渐收敛，停止训练，训练完成的DDPG控制器仿真结果如图12。图12中，在强化学习控制器的控制作用下，航行体的纵向速度与俯仰角分别在0.5 s和1 s内趋于稳定，因深度z需要通过一个积分环节得到，其变化相对于其他变量慢，所以在1.2 s内趋于稳定，纵向速度大小不超过产生滑行力的阈值，因此航行体尾部不与空泡接触，不产生滑行力。在控制过程中，深度变化范围Δz小于0.035 m，俯仰角Δθ小于0.0065 rad，空化器和尾舵偏转角在正常范围内。
图 12 DDPG控制器2控制下的航行体状态Fig. 12 The state of the vehicle under the control of the DDPG controller 2下载:
全尺寸图片
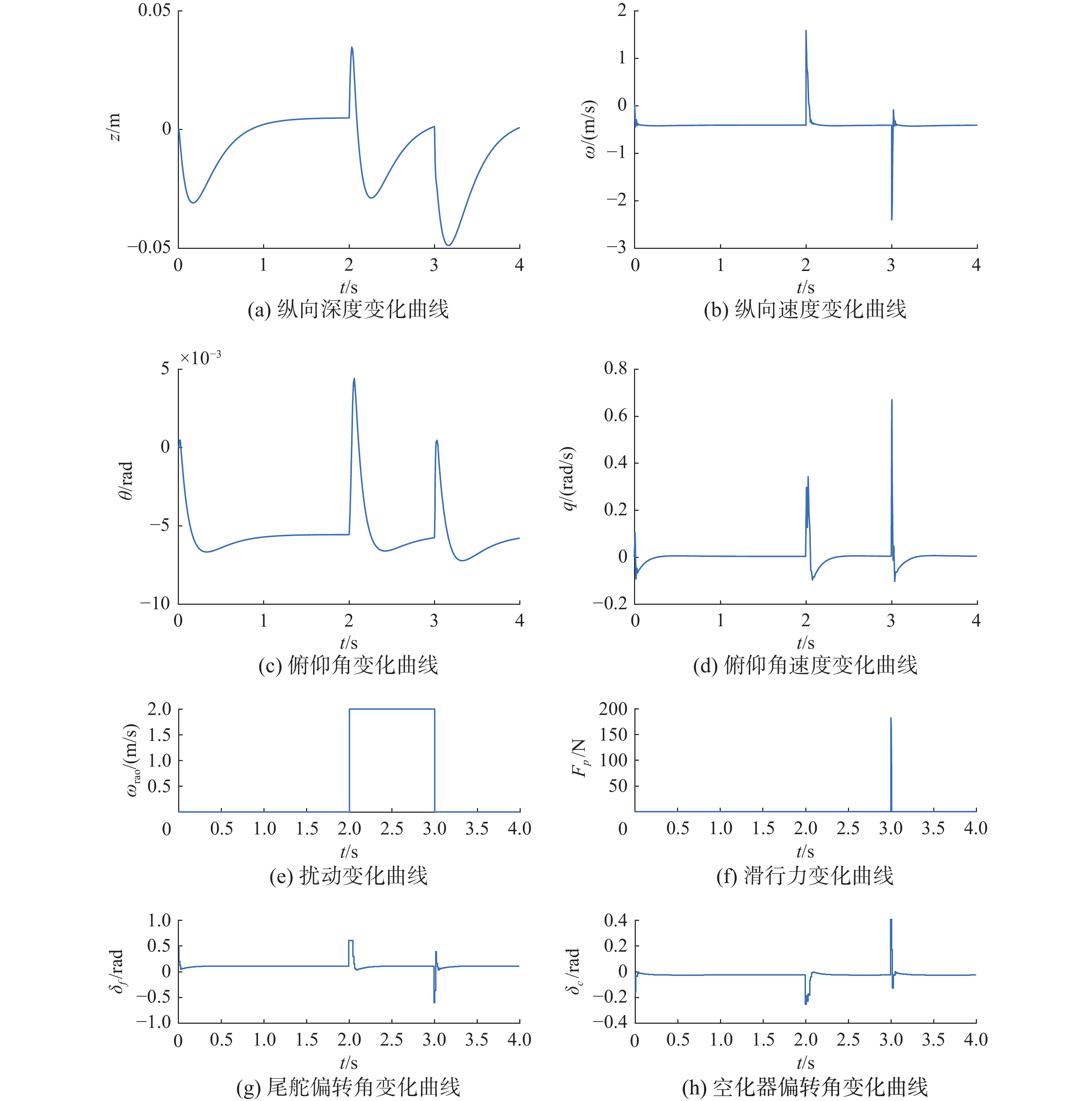
在航行体运行时需要考虑来自环境的扰动，面对扰动影响控制器仍能完成控制也是评价一个控制器的标准。如图13所示，在2~3 s，加入一个幅值为2 m/s纵向速度扰动信号ωrao，控制器在0.2 s内完成反应，深度波动范围为0.06 m，俯仰角度波动范围0.01 rad，对于该扰动带来的影响，航行体在0.5 s内能够恢复到稳定状态。
图 13 DDPG控制器2控制下的航行体状态（加扰动）Fig. 13 The state of the vehicle under the control of the DDPG controller 2(with disturbance)下载:
全尺寸图片
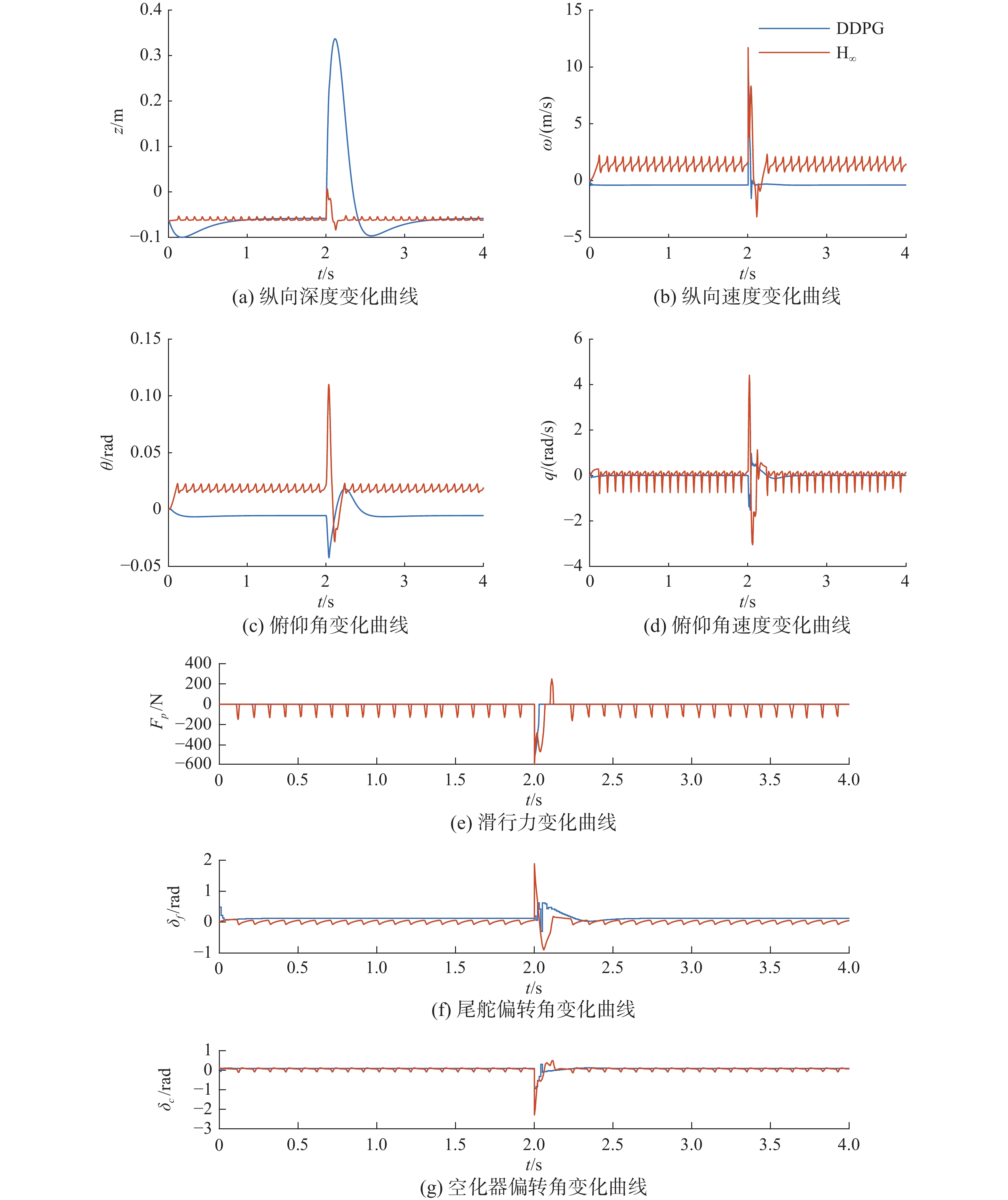
在2 s时加入一个较大的纵向速度扰动，幅值为10 m/s，选取文献[5]中设计的H∞状态反馈控制律进行比较。
由图14可见，当面临较大纵向速度扰动时，与经典控制方法[5]相比，DDPG控制器虽然在反应时间和深度z变化上表现差一些，但也在可接受范围内，而其他状态量变化均优于经典控制方法，且因为在设计DDPG控制器时，限定了动作空间，如在应对该扰动时尾舵偏转角δf最大偏转为0.60 rad，而经典控制方法达到了1.85 rad，且随着扰动的增大，经典控制方法的控制动作会越大，而DDPG控制器能够在尾舵偏转角度δf在(−0.6，+0.6) rad范围内进行稳定控制。也正是因为偏转角度限制到合理范围内，所以深度的变化时间要长于经典控制方法。
图 14 不同控制器控制下的航行体状态（加较大扰动）Fig. 14 The state of the vehicle controlled by different controllers (with large disturbance)下载:
全尺寸图片
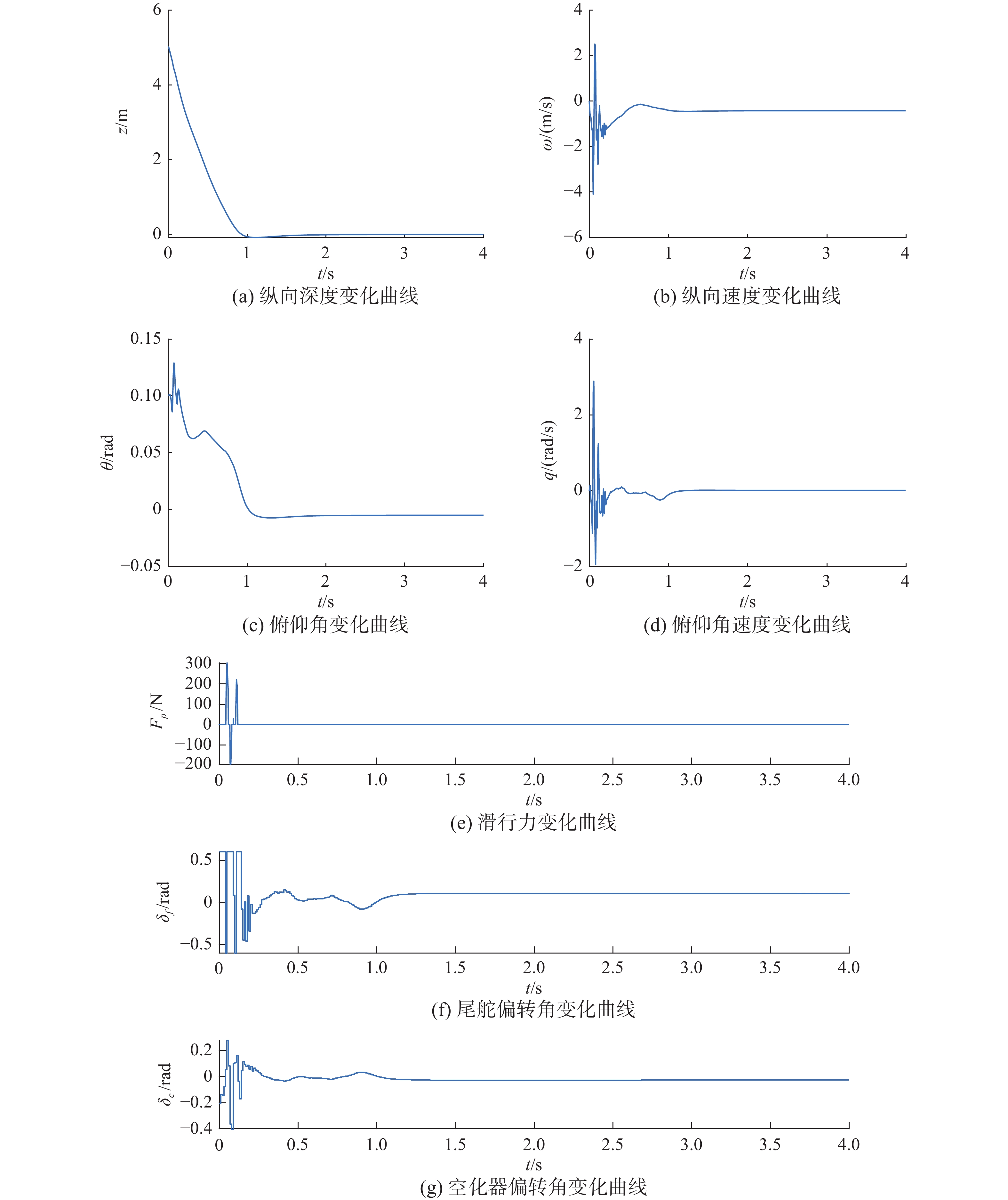
令航行体初始状态为[5 0 0.1 0]，此时纵向深度z偏离期望值较大，奖励值较小，为获得更大的奖励值，航行体的纵向深度会在控制器的联合控制下平滑修正轨迹。
由图15可见航行体的深度z能够在1 s内稳定平滑地下潜5 m并达到稳定运行状态，仅在下降初期航行体尾部与空泡壁接触产生滑行力，滑行力幅值最大不超过300 N，在智能体控制下航行体尾部在与空泡壁碰撞3次后稳定下来。控制过程空化器偏转角度最大幅值为0.4 rad，尾鳍偏转角度最大幅值为饱和的0.6 rad，保证了控制器在正常的工作范围内。
图 15 DDPG控制器2控制下的航行体状态（下潜5 m）Fig. 15 The state of the vehicle under the control of the DDPG controller 1(dive 5 m)下载:
全尺寸图片
若令航行体初始状态为[3 0 0 0]，此时下潜深度相对较小，如图16所示，俯仰角波动范围小于0.06 rad，纵向速度大小不超过阈值，不产生滑行力，所以控制器的偏转角在幅值和角速率上均更小，这也从侧面反应了非线性滑行力对航行体运动的影响是较大的，在产生滑行力的控制反应中，控制器变化更加剧烈。
图 16 DDPG控制器2控制下的航行体状态（下潜3 m）Fig. 16 The state of the vehicle under the control of the DDPG controller 1(dive 3 m)下载:
全尺寸图片
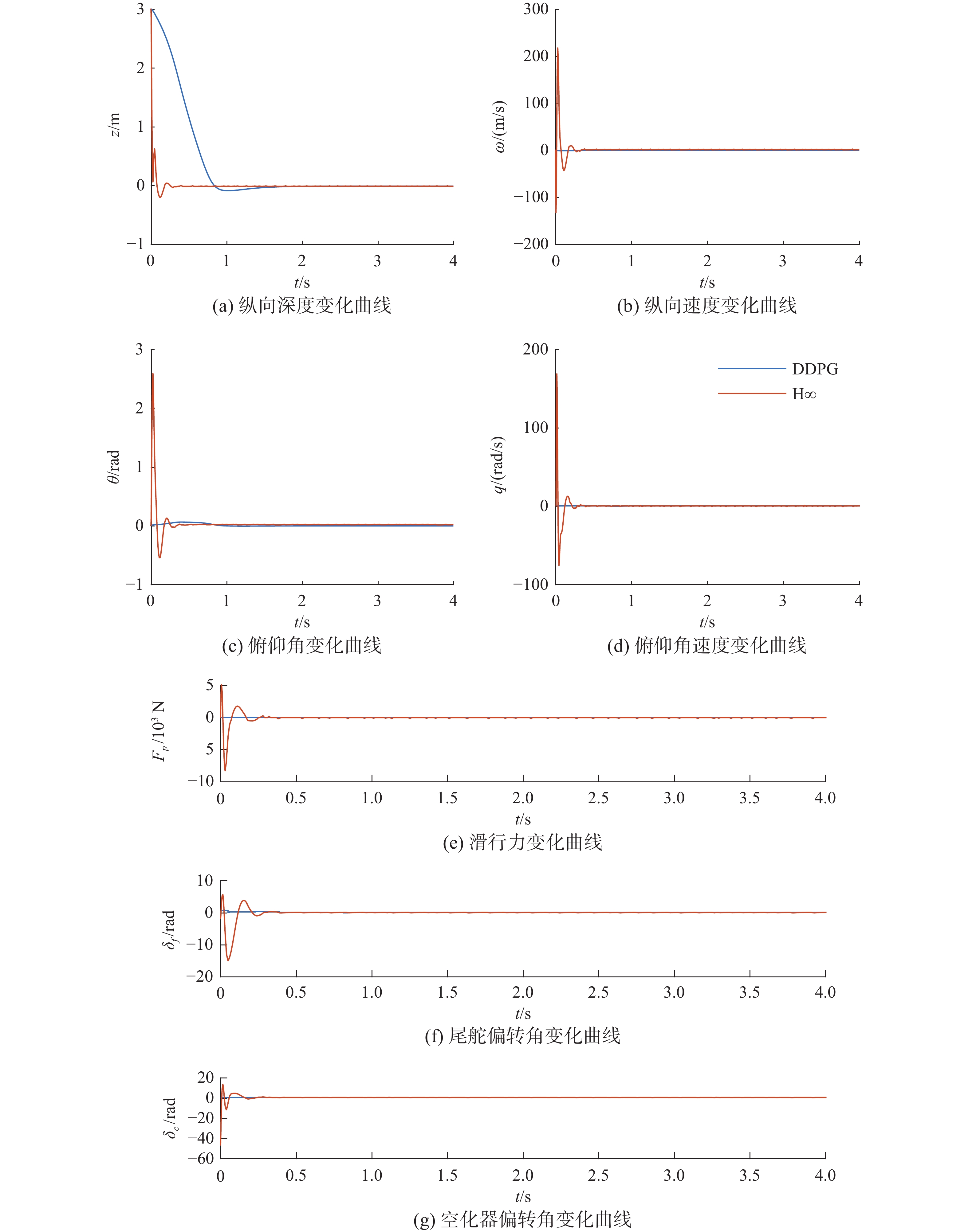
与文献[5]中方法对比初始状态异常情况下的航行体下潜反应，初始状态为[3 0 0 0]，z偏离原点3 m，对比结果如图17，从图17中可以明显看到，DDPG控制器控制下的水下高速航行体虽然在深度上变化缓慢，其原因是因为限定了控制动作δf、δc的最大输出范围，但是该控制器能够实现在合理且有限的偏转范围内快速稳定的目标。文献[5]中的方法控制器偏转角度均超过10 rad，在实际工程中不可能实现。
图 17 不同控制器控制下的航行体状态（下潜3 m）Fig. 17 The state of the vehicle controlled by different controllers (dive 3 meters)下载:
全尺寸图片
综上所述，由强化学习方法训练的DDPG智能体控制器不仅能够实现在无扰动的情况下高精度平稳运行，不产生滑行力，而且在运行过程中应对大小扰动能快速做出反应，消除扰动带来的影响，保持系统稳定。与经典控制方法中用的较多的线性化控制相比，线性控制在处理水下高速航行体的非线性方程组时，大多利用小扰动线性化方法把非线性方程组在设定的平衡点位置线性化，在线性模型的基础上进行控制律的设计，但是在处理航行体偏离平衡点较大的情况时会出现偏转角过大，不符合实际情况等问题，鲁棒性较差。而强化学习控制器在应对较大的纵向速度扰动和下潜运动方面，智能控制器做出的偏转动作更加符合实际情况，适应性更好，强化学习方法在控制精度上甚至更高。但是如强化学习、模糊控制等类的智能控制方法在水下高速航行体控制领域的规则设计比较依赖于人工经验。
5. 结束语
本文主要研究了在无法准确描述水下高速航行体数学模型和对执行器进行物理限制的情况下的水下高速航行体智能控制器设计。文中基于强化学习算法设计了DDPG智能体控制器，通过仿真实验证明了，DDPG控制器在模型主体条件确定时，能够有效解决水下高速航行体的纵向运动控制问题，其既能在实际空化器与尾舵偏转范围内应对突发扰动，又能够快速消除下潜过程出现的滑行力，使深度的过渡过程平滑稳定，相较于传统控制方法来说，其稳定精度较高，并具有更强的鲁棒性。
基于强化学习设计控制器未来还有以下几个点作为继续探索的方向：
1) 通过搭建更加合适的神经网络和优化奖励函数缩短反应时间，如分段奖励函数；
2) 通过不同的强化学习算法训练控制器，如TD3算法、SAC算法等；
3) 强化学习控制器作辅助控制器，先利用经典状态反馈法把航行体稳定在一定范围内，再通过强化学习控制器提升其稳定精度。
-
图 1 水下高速航行体纵向模型
Fig. 1 Supercavitating vehicle longitudinal model
下载:
全尺寸图片
图 2 滑行力Fp与纵向速度ω的关系
Fig. 2 Relationship between planning force Fp and longitudinal speed ω
下载:
全尺寸图片
图 3 强化学习基本结构
Fig. 3 Reinforcement learning basic structure
下载:
全尺寸图片
图 4 A-C结构
Fig. 4 A-C structure
下载:
全尺寸图片
图 5 DDPG结构
Fig. 5 DDPG structure
下载:
全尺寸图片
图 6 评价器神经网络结构
Fig. 6 Critic neural networks
下载:
全尺寸图片
图 7 执行器神经网络
Fig. 7 Actor neural networks
下载:
全尺寸图片
图 8 训练窗口1
Fig. 8 Training window 1
下载:
全尺寸图片
图 9 开环状态下航行体状态
Fig. 9 The state of the vehicle in open loop
下载:
全尺寸图片
图 10 DDPG控制器1控制下的航行体状态
Fig. 10 The state of the vehicle under the control of the DDPG controller 1
下载:
全尺寸图片
图 11 DDPG控制器1控制下的航行体状态（加扰动）
Fig. 11 The state of the vehicle under the control of the DDPG controller 1(with disturbance)
下载:
全尺寸图片
图 12 DDPG控制器2控制下的航行体状态
Fig. 12 The state of the vehicle under the control of the DDPG controller 2
下载:
全尺寸图片
图 13 DDPG控制器2控制下的航行体状态（加扰动）
Fig. 13 The state of the vehicle under the control of the DDPG controller 2(with disturbance)
下载:
全尺寸图片
图 14 不同控制器控制下的航行体状态（加较大扰动）
Fig. 14 The state of the vehicle controlled by different controllers (with large disturbance)
下载:
全尺寸图片
图 15 DDPG控制器2控制下的航行体状态（下潜5 m）
Fig. 15 The state of the vehicle under the control of the DDPG controller 1(dive 5 m)
下载:
全尺寸图片
图 16 DDPG控制器2控制下的航行体状态（下潜3 m）
Fig. 16 The state of the vehicle under the control of the DDPG controller 1(dive 3 m)
下载:
全尺寸图片
图 17 不同控制器控制下的航行体状态（下潜3 m）
Fig. 17 The state of the vehicle controlled by different controllers (dive 3 meters)
下载:
全尺寸图片
表 1 航行体模型参数
Table 1 Supercavitating vehicle model parameters
参数 参数数值 航行体长度L/m 1.80 水的密度ρ/(kg/m3) 1000 重力加速度g/(m/s2) 9.81 空化器半径Rn/m 0.0191 航行体半径R/m 0.0508 升力系数Cx0 0.82 空化数σ 0.03 密度比m 2 尾翼相似系数n 0.5 前进速度V/(m/s) 75 空泡半径Rc/m 0.09 空泡半径变化率 $ {\dot{R}}_{c} $ 20 -
[1] MAO Xiaofeng, WANG Qian. Adaptive control design for a supercavitating vehicle model based on fin force parameter estimation[J]. Journal of vibration and control, 2015, 21(6): 1220–1233. doi: 10.1177/1077546313496263 [2] 赵新华, 孙尧, 安伟光, 等. 超空泡航行体控制问题研究进展[J]. 力学进展, 2009, 39(5): 537–545. doi: 10.3321/j.issn:1000-0992.2009.05.003 ZHAO Xinhua, SUN Yao, AN Weiguang, et al. Advances in supercavitating vehicle control technology[J]. Advances in mechanics, 2009, 39(5): 537–545. doi: 10.3321/j.issn:1000-0992.2009.05.003 [3] DZIELSKI J, KURDILA A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J]. Journal of vibration and control, 2003, 9(7): 791–804. doi: 10.1177/1077546303009007004 [4] 陈超倩, 曹伟, 王聪, 等. 超空泡航行体最优控制建模与仿真[J]. 北京理工大学学报, 2016, 36(10): 1031–1036. doi: 10.15918/j.tbit1001-0645.2016.10.009 CHEN Chaoqian, CAO Wei, WANG Cong, et al. Modeling and simulating of supercavitating vehicles based on optimal control[J]. Transactions of Beijing Institute of Technology, 2016, 36(10): 1031–1036. doi: 10.15918/j.tbit1001-0645.2016.10.009 [5] 庞爱平, 何朕, 王京华, 等. 超空泡航行体H∞状态反馈设计[J]. 控制理论与应用, 2018, 35(2): 146–152. doi: 10.7641/CTA.2017.70139 PANG Aiping, HE Zhen, WANG Jinghua, et al. H-infinity state feedback design for supercavitating vehicles[J]. Control theory & applications, 2018, 35(2): 146–152. doi: 10.7641/CTA.2017.70139 [6] 韩云涛, 强宝琛, 孙尧, 等. 基于LPV的超空泡航行体H∞抗饱和控制[J]. 系统工程与电子技术, 2016, 38(2): 357–361. doi: 10.3969/j.issn.1001-506X.2016.02.18 HAN Yuntao, QIANG Baochen, SUN Yao, et al. H∞ anti-windup control for a supercavitating vehicle based on LPV[J]. Systems engineering and electronics, 2016, 38(2): 357–361. doi: 10.3969/j.issn.1001-506X.2016.02.18 [7] 李洋, 刘明雍, 张小件. 基于自适应RBF神经网络的超空泡航行体反演控制[J]. 自动化学报, 2020, 46(4): 734–743. doi: 10.16383/j.aas.2018.c170387 LI Yang, LIU Mingyong, ZHANG Xiaojian. Adaptive RBF neural network based backsteppting control for supercavitating vehicles[J]. Acta automatica sinica, 2020, 46(4): 734–743. doi: 10.16383/j.aas.2018.c170387 [8] KIRSCHNER I N, KRING D C, STOKES A W, et al. Control strategies for supercavitating vehicles[J]. Journal of vibration and control, 2002, 8(2): 219–242. doi: 10.1177/107754602023818 [9] ZHAO Xinhua, ZHANG Xiaoyu, YE Xiufen, et al. Sliding mode controller design for supercavitating vehicles[J]. Ocean engineering, 2019, 184: 173–183. doi: 10.1016/j.oceaneng.2019.04.066 [10] 范辉, 张宇文. 超空泡航行器稳定性分析及其非线性切换控制[J]. 控制理论与应用, 2009, 26(11): 1211–1217. FAN Hui, ZHANG Yuwen. Stability analysis and nonlinear switching controller design for supercavitating vehicles[J]. Control theory & applications, 2009, 26(11): 1211–1217. [11] 池海红, 于馥睿, 郭泽会. 基于强化学习的高速飞行器巡航段高度控制[J]. 哈尔滨工程大学学报, 2021, 42(9): 1340–1346,1362. CHI Haihong, YU Furui, GUO Zehui. Altitude control for high-speed vehicles in the cruise phase based on reinforcement learning[J]. Journal of Harbin Engineering University, 2021, 42(9): 1340–1346,1362. [12] MU Chaoxu, NI Zhen, SUN Changyin, et al. Air-breathing hypersonic vehicle tracking control based on adaptive dynamic programming[J]. IEEE transactions on neural networks and learning systems, 2017, 28(3): 584–598. doi: 10.1109/TNNLS.2016.2516948 [13] 许雅筑, 武辉, 游科友, 等. 强化学习方法在自主水下机器人控制任务中的应用[J]. 中国科学:信息科学, 2020, 50(12): 1798–1816. doi: 10.1360/SSI-2020-0065 HSU Yachu, WU Hui, YOU Keyou, et al. A selected review of reinforcement learning-based control for autonomous underwater vehicles[J]. Scientia sinica (informationis), 2020, 50(12): 1798–1816. doi: 10.1360/SSI-2020-0065 [14] HAFNER R, RIEDMILLER M. Reinforcement learning in feedback control[J]. Machine learning, 2011, 84(1): 137–169. [15] 王日中, 李慧平, 崔迪, 等. 基于深度强化学习算法的自主式水下航行器深度控制[J]. 智能科学与技术学报, 2020, 2(4): 354–360. WANG Rizhong, LI Huiping, CUI Di, et al. Depth control of autonomous underwater vehicle using deep reinforcement learning[J]. Chinese journal of intelligent science and technology, 2020, 2(4): 354–360. [16] LOGVINOVICH G V. Some Problems of supercavitating flows[C]// Proceedings of NATO-AGARD, [S. l. : s. n. ] , 1997: 36−44. [17] 刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1–27. LIU Quan, ZHAI JianWei, ZHANG Zongzhang, et al. A survey on deep reinforcement learning[J]. Chinese journal of computers, 2018, 41(1): 1–27. [18] 袁兆麟, 何润姿, 姚超, 等. 基于强化学习的浓密机底流浓度在线控制算法[J]. 自动化学报, 2021, 47(7): 1558–1571. YUAN Zhaolin, HE Runzi, YAO Chao, et al. Online reinforcement learning control algorithm for concentration of thickener underflow[J]. Acta automatica sinica, 2021, 47(7): 1558–1571. [19] 严家政, 专祥涛. 基于强化学习的参数自整定及优化算法[J]. 智能系统学报, 2022, 17(2): 341–347. doi: 10.11992/tis.202012038 YAN Jiazheng, ZHUAN Xiangtao. Parameter self-tuning and optimization algorithm based on reinforcement learning[J]. CAAI transactions on intelligent systems, 2022, 17(2): 341–347. doi: 10.11992/tis.202012038 [20] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236 [21] SUTTON R S, MCALLESTER D, SINGH S, et al. Policy gradient methods for reinforcement learning with function approximation[C]//Proceedings of the 12th International Conference on Neural Information Processing Systems. New York: ACM, 1999: 1057−1063. [22] HAARNOJA T, ZHOU A, ABBEEL P, et al. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor[EB/OL]. (2018−01−04)[2021−01−01]. https://arxiv.org/abs/1801.01290. [23] SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]//Proceedings of the 31st International Conference on International Conference on Machine Learning-Volume 32. New York: ACM, 2014: I−387. [24] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL]. (2015−09−09)[2021−01−01]. https://arxiv.org/abs/1509.02971
