Prediction model of theft crime based on the dynamic fusion of multiscale perspective characteristics
-
摘要: 针对盗窃犯罪时空预测特征融合不精、时序动态适应性不足问题，提出自注意力和多尺度多视角特征动态融合的预测模型。首先，以盗窃发案的位置信息为基础，将数据投射到地图栅格内，通过构建一种可将不同时序长度案件数据匹配为自适应长度数据的方法，并组合向量映射后的天气、作案时间、地理位置等属性，构造多维度特征融合的输入向量；其次，采用自注意力机制生成多视角特征动态融合的向量；最后，通过采用多尺度窗口CNN对多视角特征动态融合向量进行编码后送入分类器，预测出每个地图栅格内的发案态势。在某市盗窃数据集上验证，本文方法在3种地理栅格尺度下，预测准确率最高可达到0.899，显著优于其他对比模型。Abstract: A prediction model combining self-attention and dynamic fusion of multiscale and multiview features is proposed to solve the problems of inaccurate fusion of spatiotemporal prediction features and insufficient temporal dynamic adaptability of theft crime. Initially, data are processed by constructing a method that can match case data with different lengths of time series to an adaptive length by projecting the crime data onto the map grid based on local longitude and latitude information. After word vector mapping, the weather, crime time, and location are used to construct the input vector of multidimensional feature fusion. In addition, a self-attention mechanism is introduced to generate the vector of a dynamic fusion of multiview features. The final step involves encoding the dynamic fusion vector of perspective features and sending it to the classifier to predict the crime situation in each map grid. By validating the method on a real dataset of theft crimes in a city, the proposed model can achieve a maximum prediction precision of 0.899 at three different geographic grid divisions, which is significantly better than other comparable models.
-
盗窃犯罪是始终困扰社会治安稳定的一大难题，它是犯罪人以非法占有为目的，从而实施严重影响社会秩序、侵犯他人人身财产安全的犯罪行为[1]。根据中国统计年鉴关于公安机关立案的刑事案件统计情况，近20年来，中国盗窃类案件数始终占到案件总数的一半以上[2]，给人民的财产和隐私安全带来巨大威胁。特别是近几年来，盗窃案件呈现出作案手段隐蔽、案件线索难寻的特点，所以在此类案件的防控中主动预防优于被动响应。“实现对犯罪空间内的发案趋势进行预测”是开展主动预防的最优路径，也是公安机关实现“智慧警务”运作模式的必然选择。如果能够实现对犯罪空间内发案趋势的有效预测，则可以较为准确地研判各个犯罪空间内的发案情况，从而锁定犯罪热点地区，为公安机关提前防控、合理布警提供科学依据。
在实战工作中，盗窃犯罪发案趋势的预测多依靠公安办案经验或人工统计规律给出定性的结论[3]。如今伴随着大数据环境的数据挖掘和人工智能技术的崛起，该类犯罪的发案趋势便可依赖智能技术得到更为科学精准的定量结论，为打防工作提供科学量化指导。
目前，借助智能算法进行盗窃犯罪预测研究主要是从时空角度入手，依托历史发案数据，融合地理空间特征构建数学模型，预测犯罪的高发区域和时段[4]。颜靖华等[5]以天为犯罪预测时间尺度，应用LSTM记忆盗窃犯罪案件的长期或短期特征，得到每日盗窃犯罪案件数量的预测结果。沈寒蕾等[6]构建二值化长短期记忆模型BD-LSTM和频数统计长短期记忆模型RD-LSTM,对入室盗窃案件发生概率及案件发生数量进行预测。朱小波等[7]引入粒子群PSO优化算法，构建改进后的PSO-BP神经网络模型,对一般盗窃犯罪数量进行预测。陈笛[8]应用ARIMA 模型和指数平滑模型对盗窃犯罪发案数量进行预测，从时序维度的犯罪预测上取得了一定效果。石拓等[9]基于Bagging算法，提出了基于特征选择准确度和差异性双重考量的集成学习算法,通过对影响盗窃犯罪发生因子的有效选择,利用更少维度的特征数据集提升盗窃犯罪预测效率和准度。翟一鸣等[10]基于Prophet算法将节假日因素纳入时序分析模型中，对现有的犯罪预测模型进行多重优化,丰富了犯罪预测方法的体系。
虽然上述时空视角下的盗窃犯罪预测方法已有一定的研究积累，但现有预测方法主要存在两方面问题：1)空间维度下的多视角特征融合度不够，仅以空间区域内已发案件数据为单一输入特征开展预测，缺乏其他视角下的特征融入；2)时间序列维度下的预测动态适应性不足，即若采用不同历史天数预测未来发案情况，需要重新构造相应天数的样本数据训练模型，不能实现天数的动态调整来预测发案，致使时空视角下盗窃犯罪预测的准确率、鲁棒性及灵活性无法兼顾，限制了现有模型预测的效能。
鉴于以上问题，本文提出一种基于自注意力和多尺度视角特征动态融合的盗窃犯罪预测模型(a theft crime prediction model based on the dynamic fusion of self attention and multi-scale perspective features, DF-SAMS）。首先，以盗窃发案的经纬度位置信息为基础，将犯罪数据投射到一定大小地图栅格内，并在数据预处理中构建了一种面向不同时间长度的动态自适应数据预处理方法（one for all），将不同时序长度的已发盗窃案件数据，匹配为预期时序长度的训练数据，采用Glove模型映射后进一步拼接天气、时间、区域位置属性情况特征向量，构造出多维度特征融合的输入向量；其次，采用自注意力机制动态计算出自定义时间范围内各天内发案数据的依赖关系，生成多视角特征动态融合的向量；随后，在CNN卷积模块采用多尺度窗口信息融合方式，捕获高层次特征，最终实现盗窃犯罪输入信息的多维高阶特征编码，送入分类器，预测出每个地图栅格内的发案态势。通过引入本文所提算法，能够显著提升盗窃案件预测的准确率和灵活性，为公安部门在盗窃犯罪防控甚至更多类型犯罪预测场景中，提供新的技术思路和研究范式。
1. 模型框架
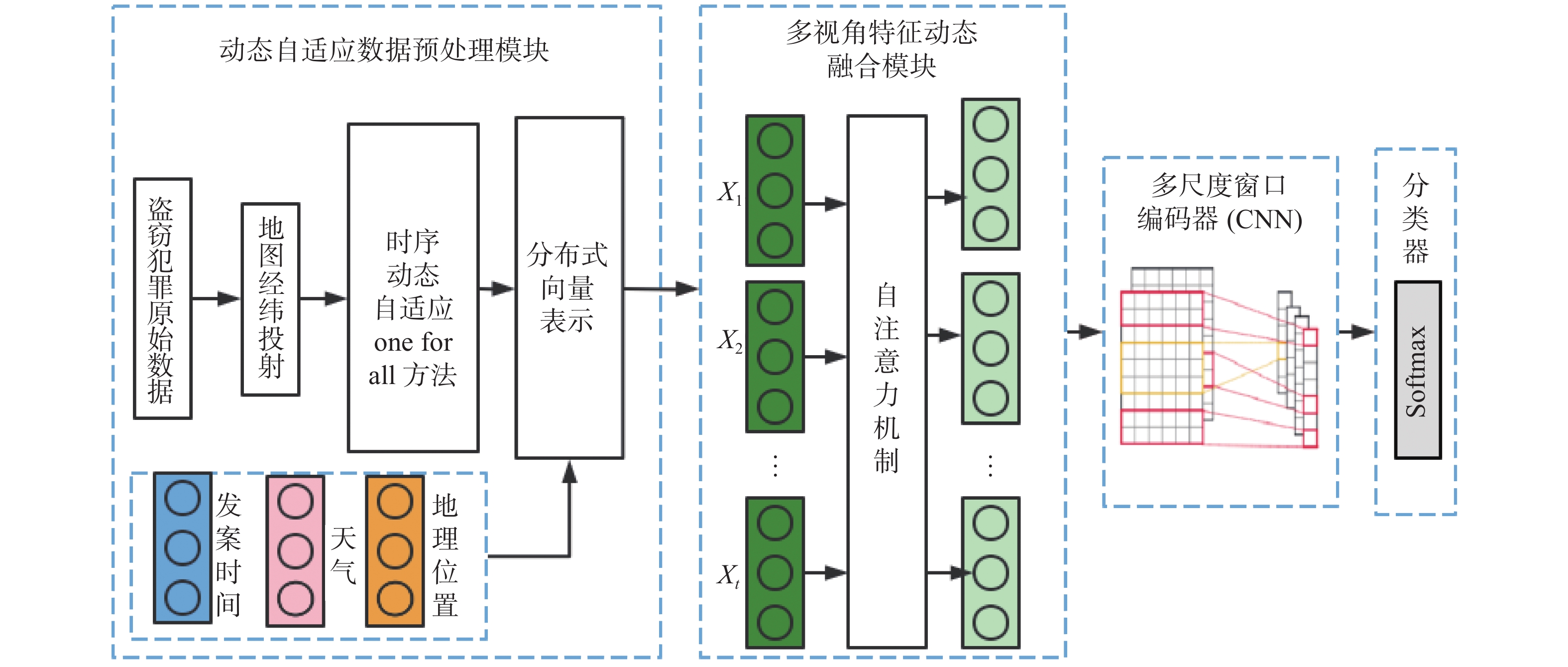
本文所提出的基于自注意力和多尺度视角特征动态融合（DF-SAMS）的盗窃犯罪预测模型结构如图1所示。该DF-SAMS模型主要由4个模块组成：动态自适应数据预处理模块、多视角特征动态融合、多尺度窗口编码器模块以及分类器模块。
图 1 多尺度视角特征动态融合的盗窃犯罪预测模模型Fig. 1 Prediction model of theft crime based on DF-SAMS
下载:
全尺寸图片
1.1 动态自适应数据预处理
盗窃犯罪案件原始数据只包含发案位置的文本描述信息，需要应用地址信息编码，将盗窃犯罪发案区位投射于对应地图经纬度位置上。随后将数据进一步处理为预期长度的特征序列表示，实现时序数据的动态自适应处理。具体可以分为地图经纬投射、时序动态自适应处理和分布式向量表征三步。
1.1.1 地图经纬投射
采用百度地图地址解析，抽取犯罪案件发生地的经纬度信息。将对应研究区域的矢量地图进行预设数量（
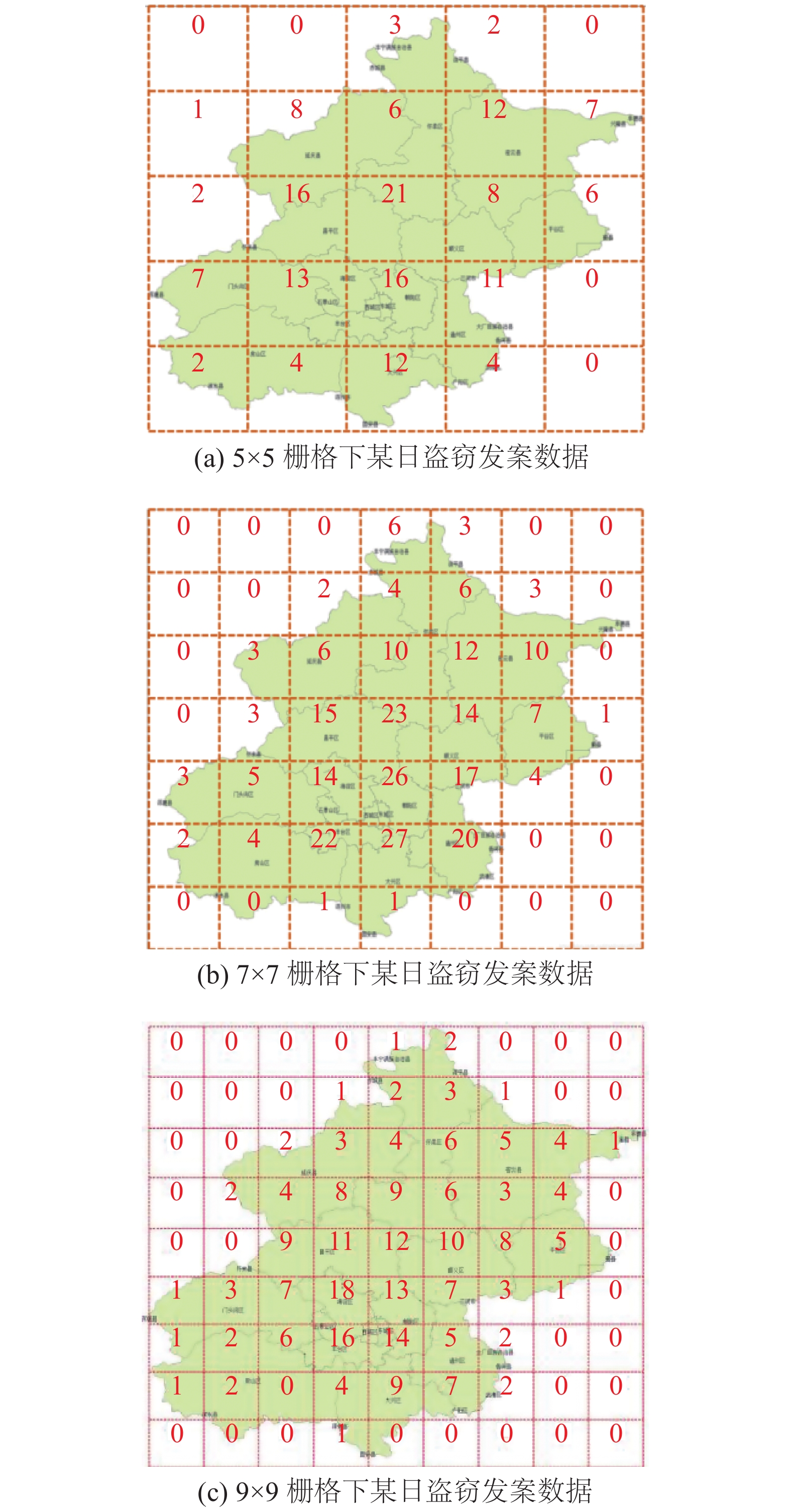
$5 \times 5$ 、$7 \times 7$ 、$9 \times 9$ ）的栅格划分，得到每一网格的经纬度范围，而后将发案地点以经纬度为依据，按照日期投射到对应的栅格地图上，统计获得每一网格内每天的盗窃犯罪发案个数，数据处理样例如图2所示。
图 2 不同栅格尺度下盗窃发案数据地图投射处理样例Fig. 2 Example of map projection processing of theft data under different grid divisions下载:
全尺寸图片
1.1.2 时序动态自适应处理
由以上的数据预处理过程，可以得到每个网格在每天的盗窃犯罪发案统计信息，随后将数据送入时序动态自适应处理步骤。在传统方法中，假设采用m天的盗窃发案历史数据进行预测，就需要将训练数据统一构造为序列长度为m的形式，即
${{\rm{ID}}_k} =$ $\left[ {{d_{k1}}\;{d_{k2}}\; \cdots \;{d_{km}}} \right]$ ，其中${\text{I}}{{\text{D}}_k}$ 表示第$k$ 个栅格区域的标号，${d_{kl}},l \in [1,m]$ 表示第$k$ 个栅格区域内的第$l$ 天的盗窃犯罪发案历史记录。当模型需要采用不同时序长度的发案历史数据，即m取不同数值时，则每次都需要重新将数据整理成对应长度为不同数值m的序列来从头训练对应模型，大大增加了模型训练的数据预处理工作量。为解决上述问题，本文在数据处理模块中提出一种可以将不同时序长度的发案数据补齐为预期长度序列（one for all）的方法，假设拟利用时序长度为m天的历史数据训练模型进行预测，只需要在生成训练数据时，将所有训练数据统一构造成长度为预期长度为
$n$ 的序列。当$ m<n $ 时，从列表左侧扩充$\left( {n - m} \right)$ 天的历史数据，用特殊标签“UNK”代替；当$m \geqslant n$ 时，将会从列表左侧将数据截断成长度为$n$ 的序列，如此就可以实现发案数据时序动态自适应处理的目标。由于采用该方法生成的模型训练数据包含不同时间范围的历史数据，所以只需一次性处理数据，就可以得到自适应利用不同范围天数的历史发案数据预测犯罪趋势的能力，大幅降低了重复处理和训练的工作量。1.1.3 多视角特征分布式表征
根据公安实践经验可知，盗窃犯罪的发案态势与案发当天的天气、作案时间和地理位置属性有极强相关性[11-13]，为此本文进一步引入多视角特征作为输入以提升盗窃犯罪预测精度。将发案数据、天气、作案时间、地理位置共4种特征向量进行融合作为模型输入。具体做法是对4种输入特征均采用分布式向量表示。由于每天的发案是离散数据，因此可以对于每个栅格区域中的盗窃案件预设历史天数的发案序列
${{\rm{ID}}_k}$ 通过预训练Glove embedding模型，将其映射为维度$s$ 维的分布式向量。针对天气、作案时间和地理位置3类特征则通过构建特征词表，随机初始化为固定维度分别为
$i、j、o$ 维的向量，随后在模型训练过程中不断更新向量参数，对此3种特征进行分布式向量表征。最后将案件个数、天气、作案时间和地理位置这4种向量的序列矩阵，直接拼接构成
$n (s + i + j + o)$ 维的矩阵${\boldsymbol{X}} = {[{\boldsymbol{X}}_1\;{\boldsymbol{X}}_2\; \cdots \;{{\boldsymbol{X}}_n}]^{\rm T}}$ ，其中$n$ 表示样本的容量。进一步用${{\boldsymbol{X}}_t},t \in [1,n]$ 表示样本集${\boldsymbol{X}}$ 中的某个样本元素。然后将此时获得的${\boldsymbol{X}}$ 作为输入向量，送入到多视角特征动态融合模块，以进一步捕获时序依赖特征信息。1.2 多视角特征动态融合
在时间序列预测任务中，常常基于CNN编码器[14-16]或是LSTM编码器对输入特征间的依赖关系进行提取[17-19]。CNN特征编码器只能捕获窗口范围内的特征依赖关系，缺乏更多尺度下的关系考量；而基于LSTM的特征编码器虽然能捕获较大范围的特征信息，但该编码器仍存在长距离依赖捕获能力不足的问题。为了解决上述问题，本文引入自注意力（self-attention）机制，动态融合一段时间范围内各天盗窃发案数据的历史信息依赖关系，以进一步提取更大范围的潜在时序关联信息。
在将各类别特征向量化表示形成特征输入矩阵
${\boldsymbol{X}}$ 后，给每天的数据向量${{\boldsymbol{X}}_t}$ 随机初始化一个${\bf{ke}}{{\bf{y}}_t}$ 值，${\mathbf{ke}}{{\mathbf{y}}_t}$ 值是一个用户可自己设置的维度为$p$ 的向量，取值将会在算法模型的不断训练中通过学习获得。然后利用点积模型计算自注意力层输入${{\boldsymbol{X}}_t}$ 与各个天数向量表征之间的相似度，通过相似度对比得出该天与各发案天数${X_{{\mathbf{key}}}}$ 的重要程度，得到注意力得分${\rm Score}({\mathbf{ke}}{{\mathbf{y}}_t},{X_{{\mathbf{key}}}})$ ，再利用softmax函数将注意力得分转换为[0,1]之间的概率分布[20]，得到权重系数${\alpha _t}$ ，根据权重系数对输入${\boldsymbol{X}}$ 序列元素进行加权求和，得到自注意力模块计算的更新向量${\boldsymbol{X}}_t',t \in [1,n]$ ，具体计算如下：$$ {\rm Score}({\bf key}_{t},{X}_{\bf key})={\bf key}_{t}^{\rm{T}}\cdot{X}_{\bf key} $$ (1) $$ {\alpha _t} = \dfrac{{\exp ({\rm Score}({\bf{ke}}{{\bf{y}}_t},{X_{{\bf{key}}}}))}}{{\displaystyle\sum_{{t}} {\exp ({\rm Score}({\bf{ke}}{{\bf{y}}_t},{X_{{\bf{key}}}}))} }} $$ (2) $$ {\boldsymbol{X}}_t' = \displaystyle\sum_t {{\alpha _t}{{\boldsymbol{X}}_t}} ,\quad t \in [1,n] $$ (3) 1.3 多尺度窗口编码器
经过多视角特征动态融合模块计算后，就得到了各历史天数之间的依赖关系。为了捕获更高层次的特征，本文采用多尺度窗口CNN特征编码器，对盗窃犯罪发案的高阶信息采取进一步融合编码，如图3所示。
图 3 基于CNN的多尺度窗口编码器Fig. 3 Multi-scale window encoder based on CNN下载:
全尺寸图片
采用3种不同尺度大小的卷积窗口捕获2-gram、3-gram、4-gram的特征，通过该模块模型将获得更多尺度的犯罪发案依赖信息，多窗口的卷积操作计算公式为
$$ {U_{a{\text{\_gram}}}} = w {\boldsymbol{X}}_{n \times d}',\quad a = 2,3,4 $$ (4) 式中：
${U_{a{\text{\_gram}}}}$ 表示输入数据经过不同尺度卷积核操作后的计算结果；$a$ 表示采用的卷积核尺寸。然后叠加偏置$c$ ，再使用激活函数$f$ 激活得到所需的特征，进一步更新公式为$$ {U_{a{\text{\_gram}}}} = w {\boldsymbol{X}}_{n \times d}' + c,\quad a = 2,3,4 $$ (5) 上述不同尺寸的卷积窗口得到的特征大小也是不一样的，因此对每个计算后的特征向量再使用池化函数，使它们的维度相同，此处采用K-max pooling方法[21]进一步提取特征，计算公式为
$$ {U_{a{\text{\_gram}}}} = \max ({K_{{\text{top}}}}({U_{a{\text{\_gram}}}})) $$ (6) 式（6）表示保留
${U_{a{\text{\_gram}}}}$ 中前$K$ 个信息值的最大值，最后将3种窗口编码后的特征进行拼接形成融合向量${\boldsymbol{v}}$ ，送入后续分类器模块进行犯罪发案态势预测。1.4 分类器
在公安实际工作中，盗窃犯罪的打防工作更多关注未来时段内发案情况的高低态势[22]，进而可根据发案态势寻得犯罪热点区域进行布防[23]，实现针对盗窃犯罪的提前预警和警力部署。为此本文立足实践需求，将发案态势分为高发、中发、低发3个热度等级，把模型的最后模块设计为分类器，将前期模块计算处理后的特征向量用softmax函数进行分类，得到当前输入样本条件下的未来目标天数发案预测分布
$P$ 。Softmax 函数是深度学习中常用且有效的分类器，计算公式为$$ P = {\text{soft}}\max (W{\boldsymbol{v}} + b) $$ (7) 经过以上各模块的处理计算，实现了应用预期时序长度的盗窃犯罪发案数据预测未来的发案态势。本文采用模型计算得到的预测结果所对应目标日期发案数量的概率分布情况，与真实发案数量概率分布情况的接近程度作为模型的交叉熵损失函数，计算公式为
$$ H(p,q) = - \sum\nolimits_x {p(x)\log q(x)} $$ (8) 式中：
$p$ 表示真实发案概率分布情况；$q$ 为预测得到的发案概率分布情况，该值越小表明模型越优。在模型参数求解过程中，采用Adam梯度下降法[24]更新计算参数，最终获得使交叉熵损失函数取值最小的对应参数即为模型最优参数，最优模型也随之确定。2. 实验结果及分析
2.1 实验数据集及评价标准
本实验以“天”为研究的时间粒度，采用我国北方某大型城市B市2014—2018年，共1862天的实际盗窃犯罪案件情况为数据集，应用气象局发布的包括晴天、下雨、下雪等气象数据作为天气维度的特征描述；采用盗窃案件发案地点所属的栅格区域数据为地理位置维度的特征描述。由于盗窃犯罪与季节和具体日期等时间特性具有相关性[25]，所以本文就以案发的具体日期作为作案时间维度的特征描述。分别设置样本时间范围为5~15天的发案情况，分别尝试将
$5 \times 5$ 、$7 \times 7$ 和$9 \times 9$ 栅格地图划分下的数据作为训练集来预测未来一天的发案趋态势，如利用2018年1月1日至1月5日的数据预测1月6日的发案态势，某栅格区域内盗窃犯罪输入的原始数据样例如表1所示。表 1 某栅格区域内盗窃犯罪输入的原始数据样例Table 1 Original data sample of theft crime in a grid area作案时间 案件数量 天气 地理位置 目标预测时
间实际发案1月1日 1 晴转多云 IDk — 1月2日 3 阴转多云 IDk — 1月3日 4 多云 IDk — 1月4日 9 阴天 IDk — 1月5日 7 晴天 IDk 高发 盗窃犯罪态势预测问题本质上是一个多分类问题，因此本文选择精确率
$p$ 、召回率$r$ 、${F_1}$ 值作为评价指标。具体计算公式为$$ p = \frac{{{\text{TP}}}}{{{\text{TP}} + {\text{FP}}}} $$ (9) $$ r = \frac{{{\text{TP}}}}{{{\text{TP}} + {\text{FN}}}} $$ (10) $$ {F_1} = \frac{{2rp}}{{r + p}} $$ (11) 式中：
${{\rm{TP}}}$ 表示正类样本被判定正类的数量；${{\rm{FP}}}$ 表示负类样本被判定为正类的数量；${{\rm{FN}}}$ 表示正类样本被判定负类的数量。2.2 实验参数设置
为了兼顾算法模型预测能力的性能和效能，本文分别在
$5 \times 5$ 、$7 \times 7$ 和$9 \times 9$ 栅格的地图划分模式下开展测试实验，3种划分模式的实验过程参数设置保持一致，如表2所示。表 2 实验参数设置Table 2 Experimental parameter setting参数 取值 发案数据预设序列长度n 15 多视角特征融合后的序列长度d 30 卷积核窗口尺寸 2-gram、3-gram、4-gram 池化层 1-max pooling 每个尺寸卷积核数量 2 激活函数 Relu 暂退率 0.3 批量样本尺寸 64 迭代轮次 10 2.3 实验结果分析
为了验证本文所提DF-SAMS模型的性能优劣，分别选取了目前在犯罪预测场景中较为常用的CNN、LSTM、Bi-LSTM、LSTM-CNN四个模型作对比。实验中针对不同的模型编码器，均采用相同的特征向量数据作为输入，分别在
$5 \times 5$ 、$7 \times 7$ 、$9 \times 9$ 栅格地图划分模式下进行测试，对比实验结果如表3~5所示。表 3$ \text{ } $ $5 \times 5$ 栅格地图划分下的模型对比效果Table 3 Model comparison effect under a grid map division of$5 \times 5$ 模型 p r F1 CNN 0.732 0.772 0.751 LSTM 0.785 0.767 0.776 Bi-LSTM 0.798 0.821 0.809 LSTM-CNN 0.856 0.868 0.862 DF-SAMS 0.882 0.896 0.889 表 4$7 \times 7$ 栅格地图划分下的模型对比效果Table 4 Model comparison effect under a grid map division of$7 \times 7$ 模型 p r F1 CNN 0.756 0.732 0.744 LSTM 0.807 0.826 0.816 Bi-LSTM 0.834 0.847 0.840 LSTM-CNN 0.863 0.854 0.858 DF-SAMS 0.897 0.902 0.899 表 5$9 \times 9$ 栅格地图划分下的模型对比效果Table 5 Model comparison effect under a grid map division of$9 \times 9$ 模型 p r F1 CNN 0.758 0.724 0.74 LSTM 0.809 0.819 0.813 Bi-LSTM 0.836 0.849 0.842 LSTM-CNN 0.866 0.861 0.863 DF-SAMS 0.899 0.901 0.9 上述实验结果表明，在不同的地图栅格尺度划分下，5个模型在盗窃犯罪时空预测场景中都表现出较好的性能。但由于CNN和LSTM在时序维度特征的提取上，存在范围受限和长跨度依赖关系捕获不佳的问题，所以各项评价指标都明显逊色于其他3种模型。事实上盗窃犯罪发案在时间维度上也是存在较强依赖关系的，所以Bi-LSTM、LSTM-CNN和本文所提出的DF-SAMS模型都获得了比较好的预测效果。但由于提出的DF-SAMS模型融入多视角特征，并且在时序维度上引入了自注意力机制，同时又采用了多尺度窗口CNN进行特征编码，所以在多样性和高层次信息方面都捕获了更好的特征，使得其实验的各项指标显著优于其他模型，最高精确率达到了0.899，F1值也达到了0.901，这一水平的预测精度能够很好地服务于公安防控实战工作。
通过进一步观察实验结果可以发现，
$7 \times 7$ 栅格地图划分下的各模型预测效果都优于$5 \times 5$ 栅格地图划分下的评价指标，而采用$9 \times 9$ 栅格地图划分下的精确率$p$ 和${F_1}$ 值效果表现更佳，这在一定程度上揭示出在开展盗窃犯罪中，越是细粒度的空间划分，越能够取得较优的预测效果，这也为公安数据警务建设提供了一种思路，即在犯罪时空预测中要尽量做到精细化、科学化分析。为了进一步验证本文在动态自适应数据预处理模块所提出的one for all训练方法在简化数据处理过程中是否牺牲了预测效果，本文又分别在
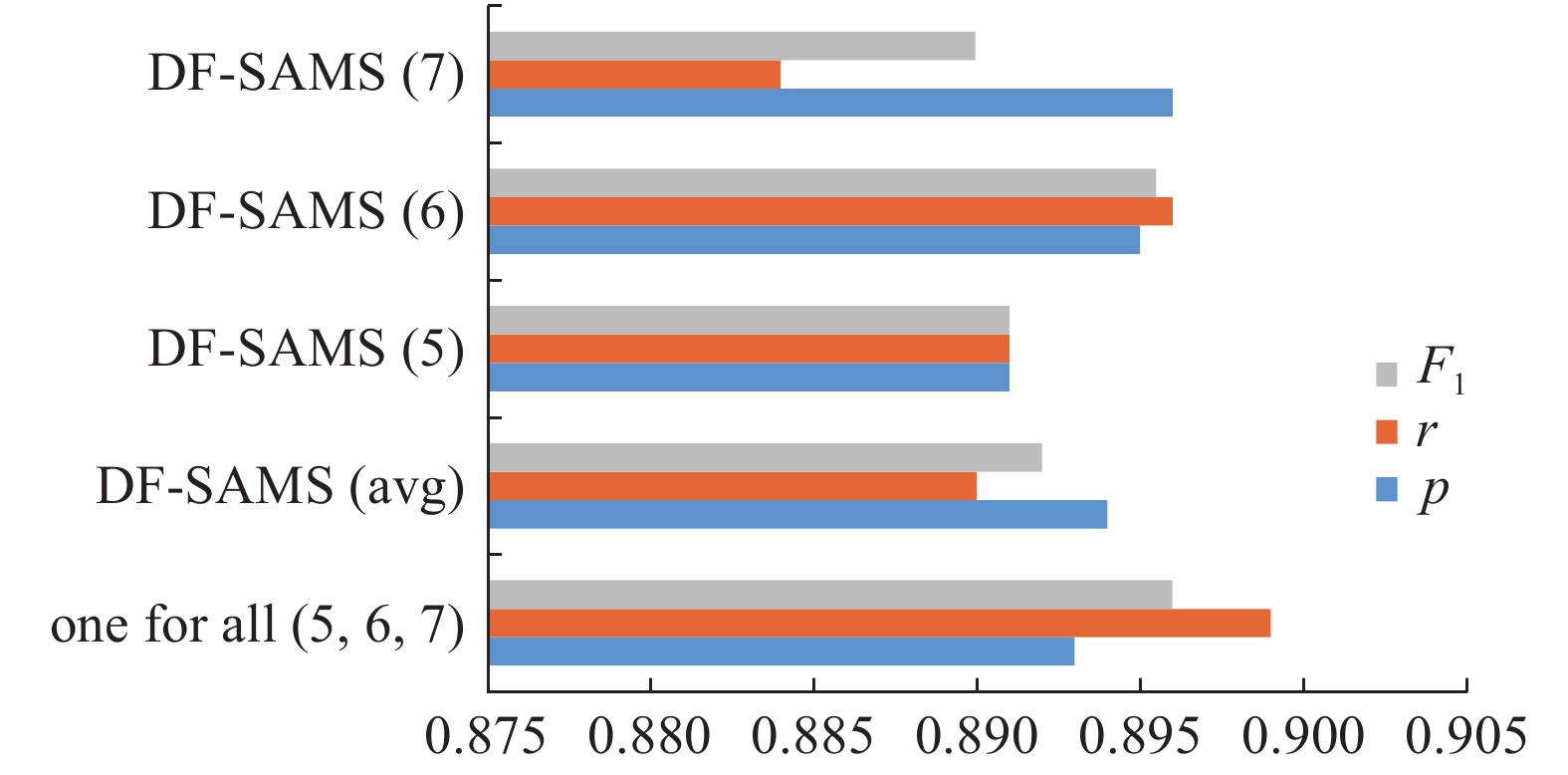
$5 \times 5$ 和$9 \times 9$ 栅格地图划分下作了对比测试，实验选取预测效果较好的5、6、7天作为训练数据时序天数，并对不同数据处理方法下的5、6、7天预测指标求平均值，用DF-SAMS(avg)表示，其测试结果如图4~6所示。
图 4 5×5栅格地图划分下不同数据处理方式的测试对比效果Fig. 4 Test comparison of different data processing methods under a grid division of 5×5下载:
全尺寸图片
图 5 7×7栅格地图划分下不同数据处理方式的测试对比效果Fig. 5 Test comparison of different data processing methods under a grid division of 7×7下载:
全尺寸图片
图 6 9×9栅格地图划分下不同数据处理方式的测试对比效果Fig. 6 Test comparison of different data processing methods under a grid division of 9×9下载:
全尺寸图片
上述实验中，one for all训练方法得到的模型分别对采用历史时间为5、6、7天的数据样本集进行了测试，实验结果表明其在
$5 \times 5$ 栅格地图划分下的预测平均精确率为0.872，而采用传统的数据处理方法，即将训练数据分别构造成长度为5、6、7的向量，再分别训练单独的预测模型，其预测准确率分别为0.867、0.874、0.878，平均精确率为0.873，可见利用本文所提出的动态自适应数据预处理one for all方法得到的预测结果与传统数据处理方法所获结果差距甚微，反而在$r$ 值和${F_1}$ 分值上的表现更优。进一步观察到在$7 \times 7$ $ \text{ } $ 和$9 \times 9$ 栅格地图划分下，one for all训练方法得到的模型分别在采用历史时间范围为5、6、7天时，对应的平均预测精准率分别达到了0.891和0.893，与传统数据处理方法所得预测结果的精度出入十分微小，在值和两个指标上的结果与传统数据处理方法所得预测结果差距也不大。这说明本文所提出的one for all模型数据处理方法不仅能实现采用一个模型预测不同时间范围内的犯罪态势，而且能保证模型与传统处理方法的预测结果基本持平，印证了所提模型在盗窃犯罪发案态势预测上的运算高效性和效果优越性。3. 结束语
本文着眼于公安实战部门对于盗窃犯罪智能化防控的需求，提出了基于自注意力机制和多尺度多视角特征动态融合的预测模型。模型分别从训练数据预处理和深度神经网络结构设计两个角度出发。首先提出了one for all的动态自适应数据的匹配方法，实现了在不损失预测效果的前提下节省模型的训练数据构造工作量；其次，在模型的网络结构设计中通过融入多视角特征提升预测效果，并尝试引入了自注意力机制，以捕获盗窃犯罪发案的时序依赖信息，进一步使用多尺度窗口的CNN编码器提取更高阶的依赖信息，达成了盗窃犯罪时空精准预测的目标。实验表明，本文提出的DF-SAMS模型具有良好的特征提取和发案态势预测性能，相较于实验中另外4种常用的犯罪预测神经网络模型，本文所提模型表现出更好的测试结果。
未来工作中将继续扩充输入特征，如考虑引入警力分布、交通设施等数据，并进一步完善模型网络结构，探索更优的参数设置和数据预处理方法，不断提升模型训练效率和预测性能，以期实现对本文DF-SAMS模型的进一步优化与改进，更好提升公安机关开展盗窃犯罪打防工作的效率和准度。
-
图 1 多尺度视角特征动态融合的盗窃犯罪预测模模型
Fig. 1 Prediction model of theft crime based on DF-SAMS
下载:
全尺寸图片
图 2 不同栅格尺度下盗窃发案数据地图投射处理样例
Fig. 2 Example of map projection processing of theft data under different grid divisions
下载:
全尺寸图片
图 3 基于CNN的多尺度窗口编码器
Fig. 3 Multi-scale window encoder based on CNN
下载:
全尺寸图片
图 4 5×5栅格地图划分下不同数据处理方式的测试对比效果
Fig. 4 Test comparison of different data processing methods under a grid division of 5×5
下载:
全尺寸图片
图 5 7×7栅格地图划分下不同数据处理方式的测试对比效果
Fig. 5 Test comparison of different data processing methods under a grid division of 7×7
下载:
全尺寸图片
图 6 9×9栅格地图划分下不同数据处理方式的测试对比效果
Fig. 6 Test comparison of different data processing methods under a grid division of 9×9
下载:
全尺寸图片
表 1 某栅格区域内盗窃犯罪输入的原始数据样例
Table 1 Original data sample of theft crime in a grid area
作案时间 案件数量 天气 地理位置 目标预测时
间实际发案1月1日 1 晴转多云 IDk — 1月2日 3 阴转多云 IDk — 1月3日 4 多云 IDk — 1月4日 9 阴天 IDk — 1月5日 7 晴天 IDk 高发 表 2 实验参数设置
Table 2 Experimental parameter setting
参数 取值 发案数据预设序列长度n 15 多视角特征融合后的序列长度d 30 卷积核窗口尺寸 2-gram、3-gram、4-gram 池化层 1-max pooling 每个尺寸卷积核数量 2 激活函数 Relu 暂退率 0.3 批量样本尺寸 64 迭代轮次 10 表 3
$ \text{ } $ $5 \times 5$ 栅格地图划分下的模型对比效果Table 3 Model comparison effect under a grid map division of
$5 \times 5$ 模型 p r F1 CNN 0.732 0.772 0.751 LSTM 0.785 0.767 0.776 Bi-LSTM 0.798 0.821 0.809 LSTM-CNN 0.856 0.868 0.862 DF-SAMS 0.882 0.896 0.889 表 4
$7 \times 7$ 栅格地图划分下的模型对比效果Table 4 Model comparison effect under a grid map division of
$7 \times 7$ 模型 p r F1 CNN 0.756 0.732 0.744 LSTM 0.807 0.826 0.816 Bi-LSTM 0.834 0.847 0.840 LSTM-CNN 0.863 0.854 0.858 DF-SAMS 0.897 0.902 0.899 表 5
$9 \times 9$ 栅格地图划分下的模型对比效果Table 5 Model comparison effect under a grid map division of
$9 \times 9$ 模型 p r F1 CNN 0.758 0.724 0.74 LSTM 0.809 0.819 0.813 Bi-LSTM 0.836 0.849 0.842 LSTM-CNN 0.866 0.861 0.863 DF-SAMS 0.899 0.901 0.9 -
[1] 于洪岭. 侵财类犯罪中“非法占有目的”的认定[J]. 中国检察官, 2016(18): 27–30. YU Hongling. Identification of “purpose of illegal possession”in the crime of infringing property[J]. The Chinese procurators, 2016(18): 27–30. [2] 付逸飞. 入户盗窃犯罪的时空分布热点及其机理研究: 以A市CP区警情分析为例[J]. 世界地理研究, 2021, 30(5): 1005–1014. FU Yifei. Study on the temporal-spatial distribution hot-spots and mechanisms in burglary: based on the analysis of policing alert in City A District CP[J]. World regional studies, 2021, 30(5): 1005–1014. [3] 刘熊. 多发性侵财犯罪侦查中的大数据应用研究[D]. 北京: 中国人民公安大学, 2017. LIU Xiong. Study on the application of big data in the frequent property-related crimes investigation[D]. Beijing: Chinese People’s Public Security University, 2017. [4] 石拓. 社会环境数据视角下的犯罪空间情报分析模式研究[J]. 中国人民公安大学学报(社会科学版), 2019, 35(3): 29–36. SHI Tuo. Research on the analysis mode of crime spatial information from the perspective of social environmental data[J]. Journal of People’s public security university of China (social sciences edition), 2019, 35(3): 29–36. [5] 颜靖华, 侯苗苗. 基于LSTM网络的盗窃犯罪时间序列预测研究[J]. 数据分析与知识发现, 2020, 4(11): 84–91. YAN Jinghua, HOU Miaomiao. Predicting time series of theft crimes based on LSTM network[J]. Data analysis and knowledge discovery, 2020, 4(11): 84–91. [6] 沈寒蕾, 张虎, 张耀峰, 等. 基于长短期记忆模型的入室盗窃犯罪预测研究[J]. 统计与信息论坛, 2019, 34(11): 107–115. SHEN Hanlei, ZHANG Hu, ZHANG Yaofeng, et al. Prediction of burglary crime based on LSTM[J]. Statistics & information forum, 2019, 34(11): 107–115. [7] 朱小波, 次晋芳. 基于改进PSO-BP神经网络算法在一般盗窃犯罪预测中的应用[J]. 计算机应用与软件, 2020, 37(1): 37–42, 75. ZHU Xiaobo, CI Jinfang. Application of improved pso-bp neural network algorithm in the prediction of theft crime[J]. Computer applications and software, 2020, 37(1): 37–42, 75. [8] 陈笛. 盗窃类犯罪的时间序列分析: 以H市X区盗窃类报警数据为例[D]. 北京: 中国人民公安大学, 2017. CHEN Di. Time series analysis of theft—a case study base on the police calling data of X district in H city[D]. Beijing: Chinese People’s Public Security University, 2017. [9] 石拓, 蒋伟, 张晶晶, 等. 基于集成特征选择的盗窃案件预测方法[J]. 北京理工大学学报, 2018, 38(9): 958–990. SHI Tuo, JIANG Wei, ZHANG Jingjing, et al. Theft prediction method based on ensemble features selection[J]. Transactions of Beijing Institute of Technology, 2018, 38(9): 958–990. [10] 翟一鸣, 丁宁, 李成龙. 基于节假日因素的多尺度犯罪时序预测方法研究[J]. 中国人民公安大学学报(自然科学版), 2020, 26(3): 78–84. ZHAI Yiming, DING Ning, LI Chenglong. Research on multi-scale crime time series prediction method considering holiday factors[J]. Journal of People’s Public Security University of China (science and technology edition), 2020, 26(3): 78–84. [11] HU Tao, ZHU Xinyan, DUAN Lian, et al. Urban crime prediction based on spatio-temporal Bayesian model[J]. PLoS One, 2018, 13(10): e0206215. [12] 顾海硕, 陈鹏, 李慧波. 犯罪时空预测方法研究综述与展望[J]. 地球信息科学学报, 2021, 23(1): 43–57. GU Haishuo, CHEN Peng, LI Huibo. A review and prospect of the research on space-time prediction methods of crime[J]. Journal of geo-information science, 2021, 23(1): 43–57. [13] LIN Y L, YEN M F, YU L C. Grid-based crime prediction using geographical features[J]. ISPRS international journal of geo-information, 2018, 7(8): 298. doi: 10.3390/ijgi7080298 [14] 邢红涛, 郭江龙, 刘书安, 等. 基于CNN-LSTM混合神经网络模型的NOx排放预测[J]. 电子测量技术, 2022, 45(2): 98–103. XING Hongtao, GUO Jianglong, LIU Shu’an, et al. NOx emission prediction based on cnn-lstm-hybrid neural networkmodel[J]. Electronic measurement techno- logy, 2022, 45(2): 98–103. [15] 刘永乐, 谷远利. 基于CNN-BiLSTM的高速公路交通流量时空特性预测[J]. 交通科技与经济, 2022, 24(1): 9–18. LIU Yongle, GU Yuanli. Prediction of temporal and spatial characteristics of freeway traffic flow based on CNN-BiLSTM[J]. Technology & economy in areas of communications, 2022, 24(1): 9–18. [16] 郭应时, 张瑞宾, 陈元华, 等. 基于观测数据潜在特征与双向长短期记忆网络的车辆轨迹预测[J]. 汽车技术, 2022(3): 21–27. GUO Yingshi, ZHANG Ruibin, CHEN Yuanhua, et al. Vehicle trajectory prediction based on potential features of observation data and bidirectional long short-term memory network[J]. Automobile technology, 2022(3): 21–27. [17] 赵长伟, 骈睿珺, 杜天硕, 等. 基于LSTM的重要用户电能质量趋势预测分析模型[J]. 电力系统及其自动化学报, 2022, 34(7): 26–33. ZHAO Changwei, PIAN Ruijun, DU Tianlei, et al. Power quality trend prediction and analysis model of important users based on LSTM[J]. Proceedings of the CSU-EPSA, 2022, 34(7): 26–33. [18] ZHANG Xu, LIU Lin, XIAO Luzi, et al. Comparison of machine learning algorithms for predicting crime hotspots[J]. IEEE access, 2020(8): 181302–181310. doi: 10.1109/ACCESS.2020.3028420 [19] SAFAT W, ASGHAR S, GILLANI S A. Empirical analysis for crime prediction and forecasting using machine learning and deep learning techniques[J]. IEEE access, 2021(9): 70080–70094. doi: 10.1109/ACCESS.2021.3078117 [20] 李倩玉, 王蓓, 金晶, 等. 基于双向LSTM卷积网络与注意力机制的自动睡眠分期模型[J]. 智能系统学报, 2022(3): 523–530. LI Qianyu, WANG Bei, JIN Jing, et al. Automatic sleep staging model based on the bi-directional LSTM convolutional network and attention mechanism[J]. CAAI transactions on intelligent systems, 2022(3): 523–530. [21] KALCHBRENNER N, GREFENSTETTE E, BLUNSOM P. A convolutional neural network for modelling sentences[EB/OL]. (2014−04−28)[2022−03−14]. https: //arxiv. org/abs/1404.2188.https://arxiv.org/abs/1404.2188. [22] 单勇, 王熠. “建设更高水平的平安中国”的新展开: 犯罪热点稳定性的再验证及其启示[J]. 河南社会科学, 2021, 29(9): 73–81. SHAN Yong, WANG Yi. Some new thoughts on the peaceful China construction—the re-verification and enlightenment of the stability of crime hotspots[J]. Henan social sciences, 2021, 29(9): 73–81. [23] 孙畅, 翟一鸣, 丁宁, 等. 入室盗窃犯罪时空分布与预测研究: 以B市为例[J]. 绥化学院学报, 2021, 41(3): 19–22. SUN Chang, ZHAI Yiming, DING Ning, et al. Research on spatial and temporal distribution and prediction of burglary: a case study of city B[J]. Journal of Suihua University, 2021, 41(3): 19–22. [24] KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. (2014−12−22)[2022−3−14]. https: //arxiv. org/abs/1412.6980https://arxiv.org/abs/1412.6980. [25] 王海林, 陈鹏, 井晓龙. 基于Aoristic方法的多发性案件发案时间特征分析[J]. 中国人民公安大学学报(自然科学版), 2021, 27(3): 93–101. WANG Hailin, CHEN Peng, JING Xiaolong. Analysis of the time characteristic of multiple cases based on the aoristic method[J]. Journal of People’s Public Security University of China (science and technology edition), 2021, 27(3): 93–101.
