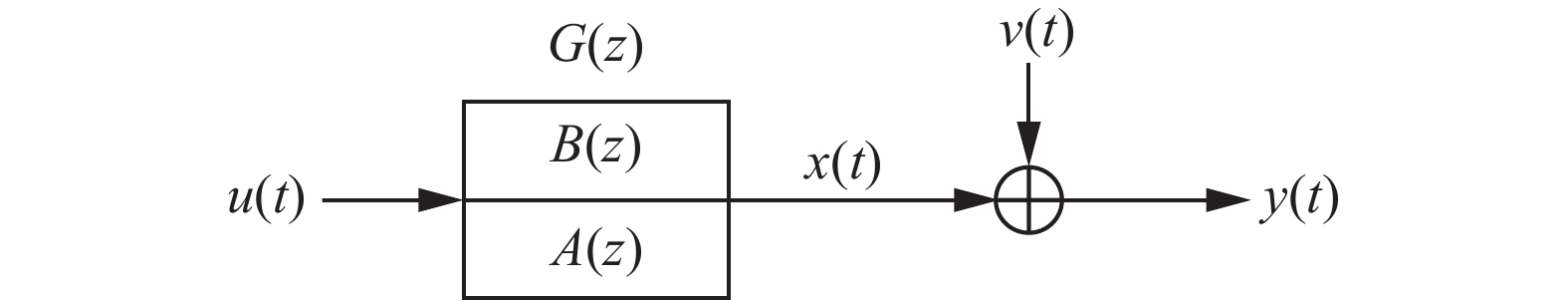Research on deck motion prediction algorithm based on output error model optimization
-
摘要: 本文提出了一种适用于多种复杂海况的大型舰船甲板运动预报方法,目的在于提高算法对不同海域复杂海况的适用性,以及对甲板运动模型的辨识精度与预报精度。该方法通过将量测数据的时间滞后处理引入输出误差模型来描述甲板运动的动力学模型,引入定阶准则确定了模型最优阶数数对。在此基础上应用了辅助模型递推最小二乘算法进行系统参数辨识并估计输出误差模型中的状态变量。实验结果表明,本文所提出的预报方法在系统参数辨识阶段可以将递推最小二乘算法的辨识精度提高5.13%,并且在预报阶段可以有效地将甲板运动的幅值与相位预测精度提高3.17%。该方法在复杂海况下具备良好的预测性能,适用于大型舰船甲板运动预报。Abstract: This paper presents a method for large ship deck motion prediction for many complex sea conditions, with the purpose of improving the applicability to complex sea conditions in different seas, as well as the recognition and prediction accuracy of the deck motion model. The method describes the dynamics of the deck motion by introducing a time lag processing of the measurement data into the output error model. And the order estimation criterion is introduced to determine the optimal order pair of the model. The auxiliary model recursive least squares (AM-RLS) algorithm is applied to identify the system parameters and estimate the state variables in the output error model. The experimental result shows that the proposed prediction method can improve accuracy of the recursive least squares algorithm by 5.13% in the system parameter identification period and can effectively improve the prediction accuracy of the deck motion’s amplitude and phase by 3.17% in the prediction period. The method has good prediction performance under complex sea conditions and is suitable for the large ship deck motion prediction.
-
基于输出误差模型的甲板极短期运动预报采用时间序列分析方法,利用过去时刻的离散时间数据建立甲板运动模型(输出误差模型)并预测未来5~15 s内的甲板运动状态。甲板极短期运动预报技术广泛应用在大型舰船的减摇控制、舰载飞行器着舰系统、船舶航行风险评估等领域,可以有效地提高船舶海上航行以及舰载飞行器着陆的安全性,目前甲板运动预报研究的主流方法有3类:时间序列分析、卡尔曼滤波、机器学习[1]。
时间序列分析方法中,黄礼敏[2]提出了波浪效应自回归模型,在保证预报精度的同时,提高了模型辨识的效率,降低了预报结果对采样频率的敏感性;Duan等[3]提出了一种用于非线性和非平稳海浪波动预测的混合EMD-AR模型,有效地提高了预测的精度;Yang等[4]提出了一种近似预测模型,将当前观测值视为其先前状态和系统输入的函数,描述了船舶的固有动力学特征并提高了纵摇运动的预报精度;Pena等[5]从线性模型、高斯过程等角度研究AR模型,用AR模型模拟波浪时间序列并得到了与理论上最优的波高预测器。
卡尔曼滤波方法中,殷大鹏[6]采用鲁棒状态融合卡尔曼滤波器建立了船舶运动预报模型,增强模型对不确定性影响的鲁棒性,减小了均方误差提高了预报精度;张彪[7]提出了基于改进无迹卡尔曼滤波的船舶运动滤波方法,降低了量测值异常对船舶运动姿态估计的影响,提高了船舶运动姿态估计的精确度和时效性。
机器学习方法中,Duan等[8]提出了用于波高短期预测的EMD-SVR模型,有效地消除了海浪波高短期预测的时间偏移问题,进一步证明了EMD方法对于非线性非平稳海浪的有效性;Mafi等[9]使用支持向量机、人工神经网络和随机森林预测墨西哥湾上空的飓风波高。结果表明在较长的超前时间内使用更多的输入参数可以提高方法的预测性能。Demetriou等[10]提出了一种在有监督机器学习模型训练中联合使用气象和结构数据进行海岸带有效波高短期预报的方法,降低了计算负担和昂贵的仪器成本。
卡尔曼滤波严苛地依赖于精确的船舶运动模型。而在实际工程应用中,很难即时地建立不同海况下的精确运动模型[11],因此会导致卡尔曼滤波方法的预测精度降低;机器学习方法近年来被广泛应用于海洋工程领域。该方法对舰船非线性运动有着很强的学习能力,可以有效地提高局部的预测精度,因此通常应用于固定海域的预测。但在实际工程上甲板运动预报需要即时针对任何海域进行预测,而机器学习方法无法避免对局部海域过度拟合的现象,一旦更换海域预报精度无法保证,因此难以应用到不同海域的不同海况中。目前在工程应用中甲板运动预报的主流方法是时间序列分析方法[12],自2000年左右该方法就被广大学者提出并广泛应用到船舶运动姿态预报中。理论上该方法忽略了高阶谐波,预测出甲板运动基波和低阶谐波,将局部的非线性运动进行线性化拟合降低了信号复杂程度。时间序列分析方法只利用过去时刻的数据[13],回避了卡尔曼滤波需要精确船舶运动模型的问题;并且相比于机器学习方法更适用于广泛的海域。综上所述,本文提出的甲板运动预报建模方法以及系统参数辨识方法是基于时间序列分析[14]方法提出的。
但目前在该领域时间序列分析方法依旧存在不足。首先从大型舰船甲板运动与海浪运动的特性出发考虑以下三点因素:1)在大型舰船航行过程中,只能通过惯性器件测得每一时刻船体的运动数据,无法对海浪的数据进行采集,更难以衡量海浪对船舶运动姿态的影响[15]。2)大型舰船航行过程中垂荡与纵摇运动基波的幅值和频率远小于海浪运动基波的幅值和频率,且难以建立船体运动与海浪运动幅频特性之间的联系。3)由于大型舰船纵向长度较大、体积较大、质量大,舰船甲板运动相对于某一时刻海浪的运动存在一定的滞后性。当前时刻船体的运动状态受到其先前一段时间运动状态与海浪的共同作用。
传统的时间序列分析方法所利用的模型不能在舰船运动的输入输出量之间建立复杂的传递函数进行动力学建模,也不能描述系统真实输出与输入之间的关系,例如:AR、AMRA、CAR、CARMA模型等。因此本文引入了输出误差(OE)模型来描述舰船运动过去时刻与当前时刻运动状态的输入输出关系,并利用估计的真实输出进行反馈来不断校正系统参数[16]。
1. 甲板运动预报算法概述
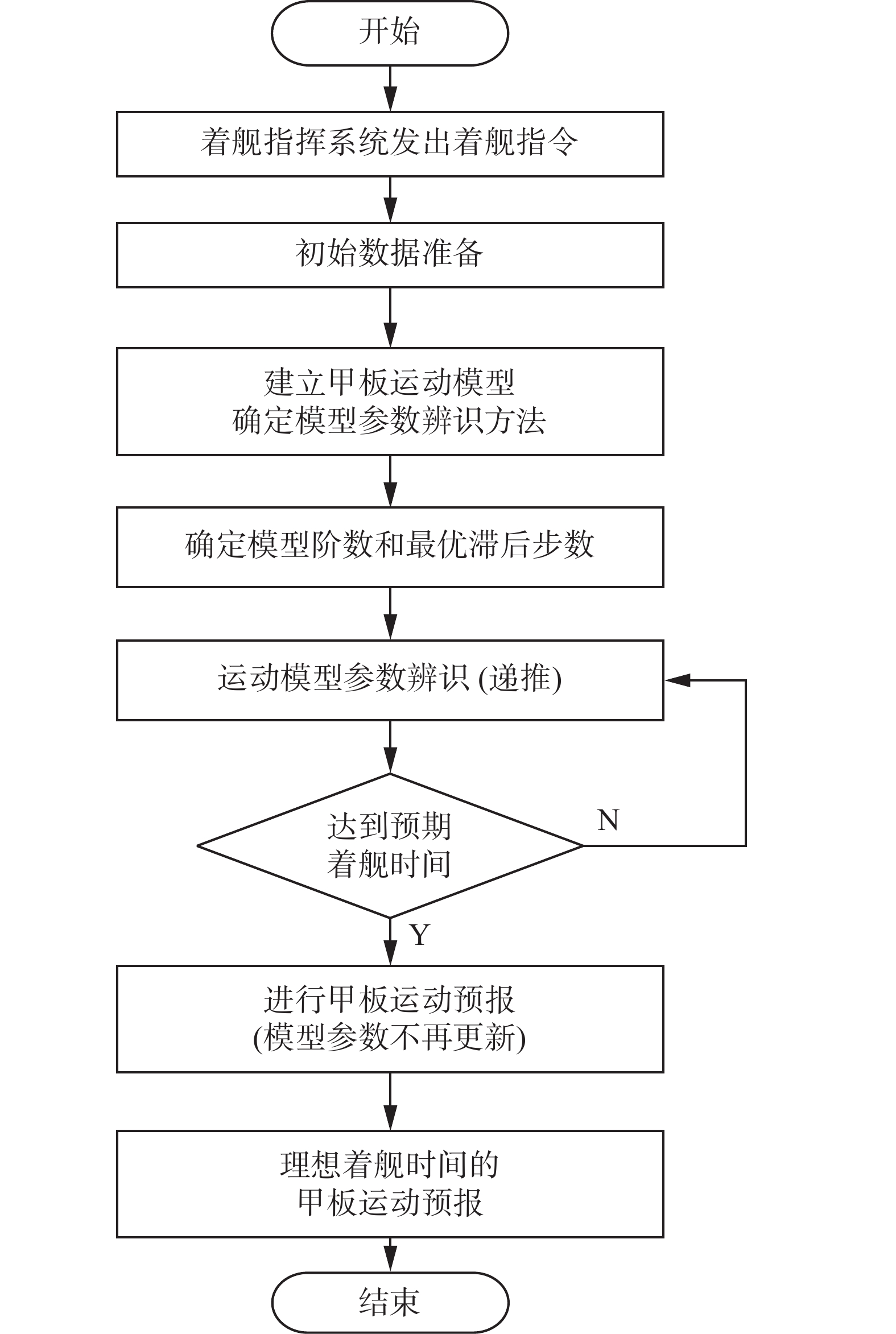
本文提出的甲板运动预报算法主要针对大型舰船的垂荡和纵摇运动进行开发和研究。如图1所示为甲板极短期运动预报的流程图。后文中将按照流程图中所示步骤顺序对基于输出误差模型的甲板运动预报算法展开论述。
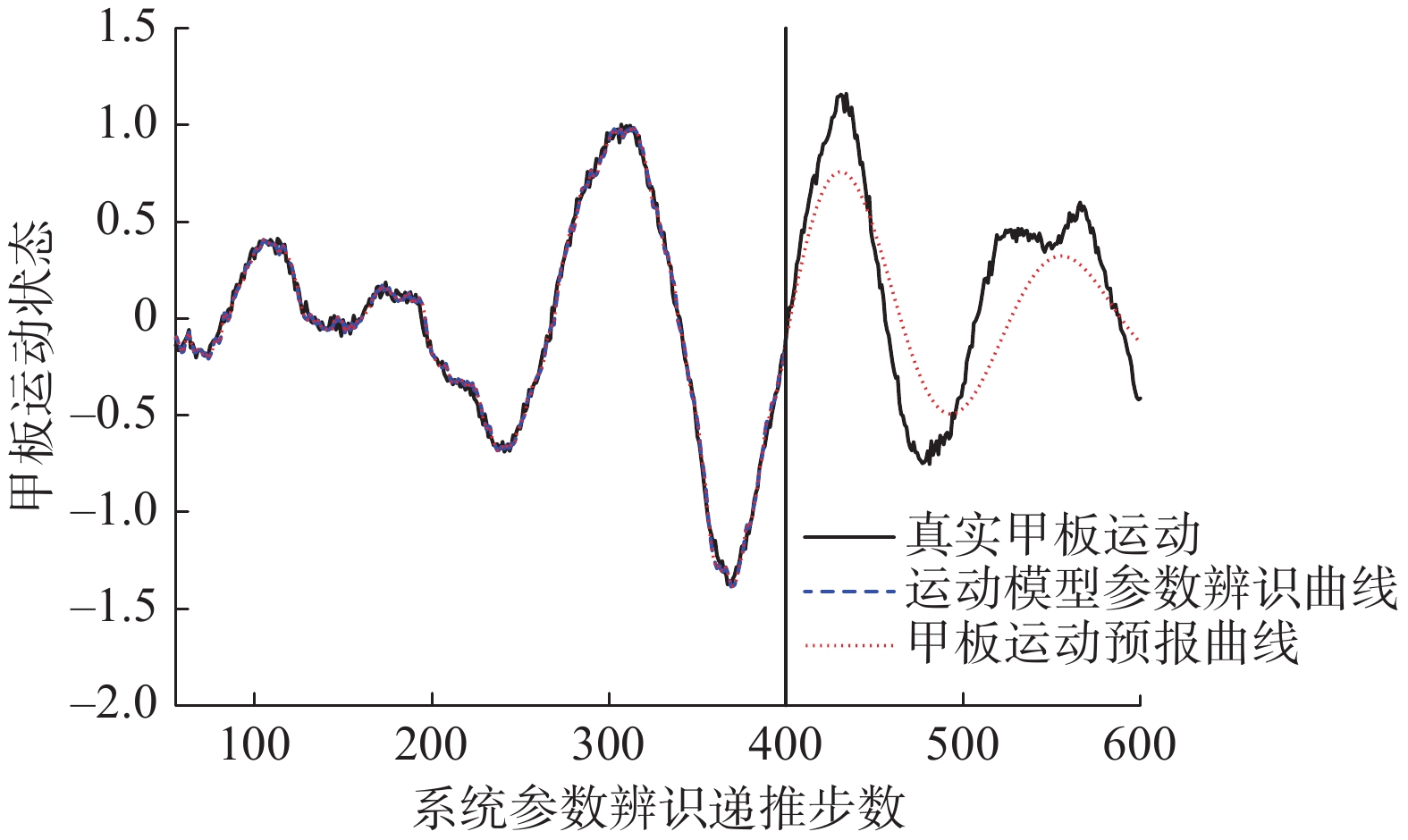
如图2所示,大型舰船甲板运动预报算法主要分为两部分:1)图2中400步处分割线左侧所示为第1部分:首先准备数据,建立基于输出误差模型的最优动力学模型来描述舰船运动模型输入输出之间的传递函数关系,利用辅助模型递推最小二乘算法(AM-RLS)分析甲板运动特征确定模型阶数与最优滞后步数。继续通过AM-RLS算法估计系统真实输出,利用估计的真实输出与量测输出不断校正系统模型参数并计算瞬时扰动直到预期着舰时刻。2)图2中400步处分割线右侧所示为第2部分:根据之前递推过程中确定的最优运动模型进行甲板极短期运动预报。
2. 甲板运动模型的建立
2.1 输出误差动力学模型中的变量关系
文献[4]中的方法中提出了一种具有超前特性的相位预测器,建立了甲板运动真实数据与预测数据之间的近似运动学关系,从而完成了超前相位预测。在此近似预测的思想基础上本文提出的甲板运动预报模型以及系统参数辨识方法旨在描述过去某段特定时间内甲板运动和未来某段特定时间内甲板运动之间的动态关系。
根据前文中大型舰船甲板运动与海浪运动的3点特性,本文的研究中确定:1)甲板运动预报的输入数据来自于惯性器件的量测数据;2)甲板运动预报模型旨在描述大型舰船自身的运动学特征,将海浪的瞬时作用作为当前时刻的扰动处理;3)甲板运动预报模型需要建立过去时刻甲板运动状态与当前时刻甲板运动状态的数学关系。
综上本文使用
$ y(t) = G(z)u(t) + v(t) $ 带有传递函数形式的数学模型来描述甲板运动的动力学特征。其中,当前输入$ u(t) $ 为过去时刻甲板运动的动力学信息,$ y(t) $ 为惯性器件量测得到的甲板运动数据,$ v(t) $ 为不可测的传感器噪声与海浪共同作用产生的变量。$ G(s) $ 为描述甲板运动动力学特征的传递函数,$ G(z) $ 为$ G(s) $ 进行$ {\rm{Z}} $ 变换后的形式。2.2 建立输出误差动力学模型
引入输出误差模型(OE模型)如图3所示。
模型公式为
$$ \begin{gathered} A(z) = 1 + {a_1}{z^{ - 1}} + {a_2}{z^{ - 2}} + \cdots + {a_n}{z^{ - {n_a}}},\quad{A_i} \in R \\ B(z) = {{\text{b}}_1}{z^{ - 1}} + {b_2}{z^{ - 2}} + \cdots + {b_n}{z^{ - {n_b}}},\quad{B_i} \in R \\ y(t) = \frac{{B(z)}}{{A(z)}}u(t) + v(t) \\ \end{gathered} $$ 式中:
$ u(t) $ 、$ y(t) $ 时是系统中可测的输入和输出序列;$G(z) = \dfrac{{B(z)}}{{A(z)}}$ 为系统传递函数${\rm{ Z}}$ 变换后的形式。参数向量${\boldsymbol{ \theta}} $ 和信息向量${\boldsymbol{ \varphi }}(t) $ 的定义分别为$$ \begin{gathered} {\boldsymbol{\varphi}} (t) = [x(t - 1)\;\;x(t - 2)\;\; \cdots \;\;x(t - {n_a}) \\ u(t - 1)\;u(t - 2)\;\; \cdots \;\;u(t - {n_b}){]^{\text{T}}} \in {{\bf{R}}^{{n_a} + {n_b}}} \\ \end{gathered} $$ $$ {\boldsymbol{\theta }}(t) = {\left[ { - {a_1}\;\; - {a_2} \cdots - {a_{{n_{\text{a}}}}}\;\;{b_1}\;\;{b_2} \cdots {b_{{n_b}}}} \right]^{\rm{T}}} \in {{\bf{R}}^{{n_a} + {n_b}}} $$ 式中x(t)为系统的状态变量(中间变量),可以视其为无噪声输出[17]:
$$ \begin{gathered} x(t) = \frac{{B(z)}}{{A(z)}}u(t) \end{gathered} $$ (1) 引入
$ [{z^{ - 1}}x(t) = x(t - 1) $ ,${z^{ - 1}}u(t) = u(t - 1)] $ ,其中${{{z}}^{ - 1}}$ 为单位后移算子。可以将式(1)写为差分方程形式:$$ \begin{gathered} x(t) + {a_1}x(t - 1) + {a_2}x(t - 2) + \cdots + {a_{{n_a}}}x(t - {n_a}) =\\ {b_1}u(t - 1) + {b_2}u(t - 2) + \cdots + {b_{{n_b}}}u(t - {n_b}) \end{gathered} $$ 即可表示为
$x(t) = {{\boldsymbol{\varphi }}^{\rm{T}}}(t){\boldsymbol{\theta}}$ ,从而可以将甲板运动的动力学模型写为最小二乘形式的辨识模型${{y}}(t) = {{\boldsymbol{\varphi}} ^{\rm{T}}}(t){\boldsymbol{\theta}} + v(t)$ 。定义准则函数[18]:
$$ {J_1}({\boldsymbol{\theta}} ) = \sum\limits_{j = 1}^t {{{\left[ {y(j) - {{\boldsymbol{\varphi}} ^{\rm{T}}}(j){\boldsymbol{\theta}} } \right]}^2}} $$ 极小化准则函数,令
$\dfrac{{\partial J_1({\boldsymbol{\theta }})}}{{{{\partial}} {\boldsymbol{\theta }}}} = 0$ 。定义协方差矩阵
$ {\boldsymbol{P}}(t) $ 如下:$$ \begin{gathered} {{\boldsymbol{P}}^{ - 1}}(t) = \sum\limits_{j = 1}^t {{\boldsymbol{\varphi}} (j){{\boldsymbol{\varphi}} ^{\rm{T}}}(j)} = {{\boldsymbol{P}}^{ - 1}}(t - 1) + {\boldsymbol{\varphi }}(t){{\boldsymbol{\varphi}} ^{\rm{T}}}(t) \\ {\boldsymbol{P}}(0) = {p_0}{{\boldsymbol{I}}_{{n_a} + {n_b}}},\quad{p_0} = {10^6} \end{gathered} $$ 式中:
$ {\boldsymbol{P}}(0) $ 为默认情况下$ {\boldsymbol{P}}(t) $ 的初值;$ {p_0} $ 为$ {\boldsymbol{P}}(t) $ 的初始化常数;$ {{\boldsymbol{I}}_{{n_a} + {n_b}}} $ 为对应信息向量维数的单位阵。并按照递推最小二乘算法(RLS)推导可得:$$ \begin{gathered} \hat {\boldsymbol{\theta}} (t) = \hat {\boldsymbol{\theta}} (t - 1) + {\boldsymbol{P}}(t){\boldsymbol{\varphi}} (t)\left[ {y(t) - {{\boldsymbol{\varphi}} ^{\rm{T}}}(t)\hat {\boldsymbol{\theta}} (t - 1)} \right] \\ {\boldsymbol{P}}(t) = {\boldsymbol{P}}(t - 1) - \frac{{{\boldsymbol{P}}(t - 1){\boldsymbol{\varphi}} (t){{\boldsymbol{\varphi}} ^{\rm{T}}}(t){\boldsymbol{P}}(t - 1)}}{{1 + {{\boldsymbol{\varphi}} ^{\rm{T}}}(t){\boldsymbol{P}}(t - 1){\boldsymbol{\varphi}} (t)}} \end{gathered} $$ 设
$ \hat {\boldsymbol{\theta}} (t) $ 代表参数向量$ {\boldsymbol{\theta}} $ 的估计。由于信息向量${\boldsymbol{ \varphi}} (t) $ 中包含了未知的状态变量$ x(t - i),i = 1,2,\cdots ,{n_a} $ ,所以上述算法不可实现。为了解决该问题要引入辅助模型辨识思想。如图4,建立一个与$G(z) = \dfrac{{B(z)}}{{A(z)}}$ 结构相同的辅助模型${G_a}(z) = \dfrac{{{B_a}(z)}}{{{A_a}(z)}}$ ,辅助模型的输出$ {x_a}(t) $ 可以表示为$$ {x_a}(t) = \frac{{{B_a}(z)}}{{{A_a}(z)}}u(t) $$ (2) 仿照式(1)状态变量的写法上式可以表达为:
${x_a}(t) = {{\boldsymbol{\varphi}} _a}^{\rm{T}}(t){{\boldsymbol{\theta}} _a}(t)$ ,其中$ {{\boldsymbol{\theta}} _a}(t) $ 和$ {{\boldsymbol{\varphi}} _a}(t) $ 为$ t $ 时刻辅助模型的参数向量和信息向量。如果利用图4中的$ {x_a}(t) $ 代替系统的真实状态变量$ x(t) $ ,那么信息向量$ {\boldsymbol{\varphi}} (t) $ 中的状态变量就都可以被替代。参数向量${\boldsymbol{ \theta}} $ 的辨识问题可以利用$ u(t) $ 和$ {x_a}(t) $ 得到解决。这就是辅助模型辨识的思想[19]。在系统参数辨识算法的递推过程中,如果$ {x_a}(t) $ 会不断逼近$ x(t) $ ,就可以把辅助模型的输出$ {x_a}(t) $ 作为$ x(t) $ 的一个估计$ \hat x(t) $ 。将
$ \hat {\boldsymbol{\theta}} (t) $ 作为辅助模型的参数向量$ {{\boldsymbol{\theta}} _a}(t) $ ,用$ {x_a}(t - i) $ 代替$ x(t - i) $ 后的信息向量${\boldsymbol{ \varphi}} (t) $ 记作$ \hat {\boldsymbol{\varphi }}(t) $ ,同时将$ \hat {\boldsymbol{\varphi}} (t) $ 作为辅助模型的信息向量$ {{\boldsymbol{\varphi }}_a}(t) $ ,即$$ \begin{gathered} {x_a}(t) = {{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(t)\hat {\boldsymbol{\theta}} (t)\\ \hat {\boldsymbol{\varphi}} (t) = [{x_a}(t - 1)\;\;{x_a}(t - 2)\;\; \cdots \;\;{x_a}(t - {n_a}) \\ u(t - 1)\;\;u(t - 2)\;\;\cdots\;\;u(t - {n_b}){]^{\rm{T}}} \in {{\bf{R}}^{{n_a} + {n_b}}} \end{gathered} $$ (3) 在
$ t $ 时刻,$\hat {\boldsymbol{\varphi }}(t)$ 是已知的。极小化准则函数:$$ {J_2}(\theta ) = \sum\limits_{j = 1}^t {{{\left[ {y(j) - {{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(j){\boldsymbol{\theta}} } \right]}^2}} $$ (4) 可以得到估计参数向量
$\hat {\boldsymbol{\theta}}$ 的辅助模型最小二乘算法(AM-RLS):$$ \begin{gathered} \hat {\boldsymbol{\theta}} (t) = \hat {\boldsymbol{\theta }}(t - 1) + {\boldsymbol{L}}(t)\left[ {y(t) - {{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(t)\hat {\boldsymbol{\theta}} (t - 1)} \right]\\ {\boldsymbol{L}}(t) = {\boldsymbol{P}}(t - 1)\hat {\boldsymbol{\varphi}} (t){\left[ {1 + {{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(t){\boldsymbol{P}}(t - 1)\hat {\boldsymbol{\varphi}} (t)} \right]^{ - 1}} \\ {\boldsymbol{P}}(t) = {\boldsymbol{P}}(t - 1) - \frac{{{\boldsymbol{P}}(t - 1){\boldsymbol{\varphi}} (t){{\boldsymbol{\varphi}} ^{\rm{T}}}(t){\boldsymbol{P}}(t - 1)}}{{1 + {{\boldsymbol{\varphi}} ^{\rm{T}}}(t){\boldsymbol{P}}(t - 1){\boldsymbol{\varphi}} (t)}} =\\ \left[ {{\boldsymbol{I}} - {\boldsymbol{L}}(t){{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(t)} \right]{\boldsymbol{P}}(t - 1),{\boldsymbol{P}}(0) = {p_0}{\boldsymbol{I}} \\ \hat {\boldsymbol{\varphi}} (t) = [{x_a}(t - 1)\;{x_a}(t - 2) \cdots {x_a}(t - {n_a}) \\ u(t - 1)\;u(t - 2)\; \cdots \;u(t - {n_b}){]^{\rm{T}}} \in {{\bf{R}}^{{n_a} + {n_b}}} \\ {x_a}(t) = {{\hat {\boldsymbol{\varphi}} }^{\rm{T}}}(t)\hat {\boldsymbol{\theta}} (t) \end{gathered} $$ (5) AM-RLS算法中辅助模型为
$$ {x_a}(t) = {{\boldsymbol{\varphi}} _a}^{\rm{T}}(t){{\boldsymbol{\theta}} _a}(t) = {\hat {\boldsymbol{\varphi}} ^{\rm{T}}}(t)\hat {\boldsymbol{\theta}} (t) $$ 2.3 基于AM-RLS算法的模型参数更新
由于状态变量
$ {x_a}(t) $ 的引入,导致参数估计过程当中,算法的每一步递推计算都需要采集系统输出数据、系统输入数据并递推计算状态变量。相比于传统递推最小二乘算法(RLS)的区别是在运算的过程中对状态变量进行不断地修正,RLS算法只在递推过程中修正了参数估计向量$ \hat {\boldsymbol{\theta}} (t) $ 。相比之下算法的数据计算量有所增加以谋求更高的辨识精度。算法具体计算流程如图5所示。算法具体计算过程:
1)数据初始化,首先令
$ t = 1 $ 。确定初值${\boldsymbol{ P}}(0) = {p_0}{\boldsymbol{I}}$ ,$\hat \theta (0) = \dfrac{1}{{{p_0}}}$ ,$x(t) = \dfrac{1}{{{p_0}}}$ ,$ {p_0} = {10^6} $ ,采集足够长度的$ x(t),u(t) $ 以构造设定好维数的$\hat {\boldsymbol{\varphi }}(t)$ ,时刻采集$ y(t) $ 准备用于递推计算。2)确定初始时刻
$ {t_0} $ 以及递推拍数$ N $ 。实际工程上,当指挥系统向舰载飞行器发出着舰指令时甲板运动预报算法便开始启动,此时$ t = 0 $ 。待到数据准备阶段结束时递推开始,此时$ t = {t_0} $ 。递推拍数$ N $ 为舰载飞行器预期着舰时间段开始时刻所对应的步数,模型参数更新阶段结束时$ t = N $ 。考虑到海浪运动的复杂程度不同,理论上着舰指挥系统从$ {t_0} $ 到$ N $ 之间预留的时间跨度至少为5 s。3)进入递推的参数更新阶段,用最新的输入输出量测数据刷新
$ u(t)、y(t) $ ,利用上一步中保存的辅助模型变量$ {x_a}(t - i) $ 结合式(3)更新信息向量$ \hat {\boldsymbol{\varphi}} (t) $ 。4)利用式(5)计算最新的协方差矩阵
${\boldsymbol{P}}(t)$ 与矩阵${\boldsymbol{L}}(t)$ 。5)利用步骤4)中最新的
${\boldsymbol{P}}(t)$ 与${\boldsymbol{L}}(t)$ 刷新本次递推中参数估计$\hat {\boldsymbol{\theta}} (t)$ 。6)利用更新的参数估计
$\hat {\boldsymbol{\theta}} (t)$ 与信息向量$\hat {\boldsymbol{\varphi}} (t)$ 通过公式(3)计算变量$ {x_a}(t - i) $ 并准备用于下一时刻的递推计算,其中$ i = 0,1, \cdots ,{n_a} - 1 $ 。7)判断是否继续进行递推,是的话
$ t = t + 1 $ 转到步骤3),否则结束递推,并保存参数估计数据[20]。3. 基于输出误差模型的甲板运动预报算法实现
在确定了运动模型和模型参数辨识算法的基础上,本节展开介绍了在甲板运动预报阶段开始前的模型定阶方式、预报阶段的原理以及数据处理过程。
3.1 输出误差模型的输入输出数据定阶
通常基于AR模型的甲板运动预报模型只需要确定输出
$ y(t) $ 阶数。但本文中输出误差模型的辨识过程中引入了辅助模型辨识方法,因此需要为状态变量$ x(t) $ 和系统输入$ u(t) $ 定阶。难点在于如何同时确定模型中两个阶数$ {n_a} $ 与$ {n_b} $ ,可以在保证运动学模型最接近真实运动状态的基础上同时兼顾递推算法的计算效率。定阶的意义在于较低阶的模型难以拟合复杂信号,而较高阶模型会产生较大的峰值误差,为了能最大程度的提高系统模型参数辨识的精度,需要以合理的方式确定模型的最佳阶数。将OE模型写成最小二乘格式:
$$ y(t) = {{\boldsymbol{\varphi}} ^T}(t){\boldsymbol{\theta}} + v(t) $$ 考虑到模型阶数
$ {n_a} $ 、$ {n_b} $ 均不确定,定义估计残差与方差:$$ \begin{gathered} e({n_a},{n_b},t) = y(t) - {{\boldsymbol{\varphi}} ^{\rm{T}}}({n_a},{n_b},t)\hat {\boldsymbol{\theta }}({n_a},{n_b},t - 1) \\ {{\hat \sigma }^2}({n_a},{n_b},T) = \frac{1}{{T - {n_a} - {n_b}}}\sum\limits_{t = {n_a} + {n_b} + 1}^{{T}} {{e^2}({n_a},{n_b},t)} \\ \end{gathered} $$ 式中:
$ {\hat \sigma ^2}({n_a},{n_b},T) $ 为估计方差;$ e({n_a},{n_b},t) $ 为估计残差;$ T $ 为定阶递推的总步数。由于模型定阶阶段发生在图2所示的参数辨识过程中,并且不涉及预报过程。通常取$ {t_0} \leqslant T < N $ 。本文将以$ {\hat \sigma ^2}({n_a},{n_b},T) $ 作为重要指标衡量选取定阶准则。一些可用的指定系统顺序的方法有AIC准则(Akaike,1974)、BIC准则(Schwarz,1978)、反馈控制系统信息标准(CIC)以及预计最小二乘准则(PLS)。
本文考虑如下定阶准则[21]:
$$ \begin{gathered} {S_{{\rm{AIC}}}}({n_a},{n_b},T) = \ln {{\hat \sigma }^2}({n_a},{n_b},T) + \frac{{2({n_a} + {n_b})}}{T} \\ {S_{{\rm{BIC}}}}({n_a},{n_b},T) = \ln {{\hat \sigma }^2}({n_a},{n_b},T) + \frac{{({n_a} + {n_b})\ln T}}{T} \\ {S_{{\rm{CIC}}}}({n_a},{n_b},T) = \sum\limits_{t = {n_a} + {n_b} + 1}^T {{e^2}({n_a},{n_b},t)} + ({n_a} + {n_b}){(\ln T)^2} \\ {S_{{\rm{PLS}}}}({n_a},{n_b},T) = {{\hat \sigma }^2}({n_a},{n_b},T) \\ \end{gathered} $$ 式中:
$ {S_{{\rm{AIC}}}} $ 表示AIC准则衡量算法拟合程度的评定值,$ {S_{{\rm{AIC}}}} $ 越小说明算法拟合精度越高;$ {S_{{\rm{BIC}}}} $ 表示BIC准则的评定值;$ {S_{{\rm{CIC}}}} $ 表示CIC准则的评定值;$ {S_{{\rm{PLS}}}} $ 表示PLS准则的评定值,且评定值越小拟合精度越高;状态变量阶数为$ {n_a} $ ,系统输入阶数为$ {n_b} $ ,$ T $ 为定阶递推的总步数。对于本文的输出误差模型,不推荐使用AIC准则,因为不能保证AIC的一致性特征;对于CIC准则,式中后一项通常远大于前一项,从而导致在定阶过程中辨识误差的数据特征无法充分体现。CIC准则还需要初始情况下充分的系统阶数信息,而在甲板运动模型定阶过程中无法获得初始阶数;PLS准则的原理与AM-RLS算法的原理一致,在模型定阶中不具备指导意义。
根据BIC准则的强一致性[22],当BIC值达到最小值时,可以获得唯一的系统阶数。但输出误差模型需要联合确定系统状态变量阶数
$ {n_a} $ 和系统输入阶数$ {n_b} $ 。理论上来说最小$ {S_{{\rm{BIC}}}} $ 值对应于已经给定的系统输入阶数的最佳状态变量阶数,在此模型定阶过程中目的是选取一个最优的数对$ ({n_a}^*,{n_b}^*) $ 使得BIC值最小[4]。定阶的步骤如下:1)在保证计算量的范围内确定最大系统状态变量阶数
$ {n_{{a_{\max }}}} $ 和最大系统输入阶数$ {n_{{b_{\max }}}} $ 。2)对于任意的状态变量阶数
$ {n_a} $ 选取一个最优的系统输入阶数$ {n_{{b_j}}}^* $ 。${n_{{b_j}}}^* = \arg \min \left\{ {{S_{{\rm{BIC}}(i,j,T)}}} \right\},j = 1,2, \cdots ,{n_{{b_{\max }}}}$ 对于任意的$i = 1,2, \cdots ,{n_{{a_{\max }}}}$ 。3)确定最优系统输入阶数
$ {n_b}^* $ ,$ {n_b}^* = \max \left\{ {{n_{{b_j}}}^*} \right\} $ 。4)对于最优系统输入阶数
$ {n_b}^* $ ,可能会存在多个对应的状态变量阶数$ {n_{a1}},{n_{a2}}, \cdots ,{n_{ar}}, $ $ {n_{ar}} \leqslant {n_{{a_{\max }}}} $ ,为了权衡模型参数辨识精度与计算效率之间的关系,在长时间预测中降低模型的复杂度与存储负担,选取$ {n_a}^* = \min \left\{ {{n_{{a_k}}}} \right\},k = 1,2, \cdots ,r $ 。3.2 最优滞后步数的确定
基于引言中提到的甲板运动的3个特性考虑,OE模型所需要数据中系统输出的
$ y(t) $ 为量测得到的甲板运动数据,$ x(t) $ 为算法递推过程中的估计值,系统输入$ u(t) $ 的确定是运动模型是否符合实际运动规律的关键。考虑到当前时刻甲板运动的状态会对之后的运动产生滞后的影响[23],在不同海况下这种滞后影响的时间和效果不同。因此本文在确定了模型最优阶数数对
$ ({n_a}^*,{n_b}^*) $ 的基础上,针对不同海况下甲板的运动特征实时建立对应的时间滞后关系[13]。引入滞后步数
$ L $ (lag step),考虑前文中的动力学模型在$ t $ 时刻满足:$$ \begin{gathered} y(t) = \frac{{B(z)}}{{A(z)}}u(t) + v(t) \\ u(t) = y(t - L) \end{gathered} $$ 引入状态变量
$x(t) = \dfrac{{B(z)}}{{A(z)}}u(t)$ 后写成差分方程形式得到:$$ \begin{gathered} x(t) + {a_1}x(t - 1) + {a_2}x(t - 2) + \cdots + \\ {a_{{n_a}}}x(t - {n_a}^*) = {b_1}y(t - L - 1) + \\ {b_2}y(t - L - 2) + \cdots + {b_{{n_b}}}y(t - L - {n_b}^*) \end{gathered} $$ 首先通过甲板运动真实数据确定符合当前海况运动学特征的
$ {L_{\max }} $ ,考虑到AM-RLS算法基于最小二乘原理,因此利用PLS准则确定最优的滞后步数$ {L^*} $ :$$ \begin{gathered} {\rm{PLS}}(L,T) = {{\hat \sigma }^2}({n_a},{n_b},L,T) \\ {n_a} = {n_a}^*,{n_b} = {n_b}^* \\ {L^*} = \arg \min \left\{ {{S_{{\rm{PLS}}}}(L,T)} \right\} \\ L = 1,2, \cdots ,{L_{\max }} \\ \end{gathered} $$ 如图1所示,在确定最优阶数数对
$ ({n_a}^*,{n_b}^*) $ 与最优滞后步数$ {L^*} $ 后,此时$ t = T,{t_0} \leqslant T < N $ 。甲板运动模型参数辨识阶段尚未结束,因此在$ T \leqslant t < N $ 的时间内继续通过AM-RLS算法递推估计系统真实输出并利用估计残差校正系统模型参数来提高之后甲板运动预报部分的预测精度。3.3 实现基于输出误差模型的极短期预报
在预报阶段继续沿用3.1和3.2中确定的模型最优阶数数对与最优滞后步数
$ {L^*} $ ,从甲板运动模型参数辨识阶段到预报阶段模型的参数更新与数据的处理方式会有较大的区别。截至参数辨识阶段结束时刻$ t $ ,此时$ t = N $ 。OE模型在甲板运动预报开始时刻
$ t $ 变为如下形式[24]:$$ \begin{gathered} y(t + W\left| t \right.) = \frac{{B(z)}}{{A(z)}}u(t + W) + v(t + W) \\ t = N,W = 1,2, \cdots ,{W_{\max }} \end{gathered} $$ 式中:
$ u(t + W) $ 为未来时刻系统估计输入;$ y(t + W) $ 为未来时刻的系统估计输出;$ v(t + W) $ 为未来时刻系统状态变量,$ W = 1,2, \cdots ,{W_{\max }} $ ;$ {W_{\max }} $ 为甲板运动预报阶段的总步数。将参数辨识阶段结束时刻
$ t $ 引入$x(t + W) = \dfrac{{B(z)}}{{A(z)}}u(t + W)$ 。写成差分方程形式得:$$ \begin{gathered} x(t + W) + {a_1}x(t + W - 1) + {a_2}x(t + W - 2) + \cdots + \\ {a_{{n_a}}}x(t + W - {n_a}) = {b_1}u(t + W - 1) + \\ {b_2}u(t + W - 2) + \cdots + {b_{{n_b}}}u(t + W - {n_b}) \\ t = N,W = 1,2, \cdots ,{W_{\max }} \end{gathered} $$ (6) 但是式(6)在实际过程中无法实现,这是由于参数辨识阶段结束时刻
$ t = N $ 之后无法估计未来采样时刻不可测的传感器噪声与海浪共同作用产生的变量$ v(t + W) $ ,所以导致$ x(t + W) $ 与$ y(t + W) $ 无法获得。因此为了预测的进一步实现,使预报算法能输出未来时刻甲板运动估计值,忽略变量
$ v(t+W), W=1,2,\cdots ,{W}_{\mathrm{max}} $ ,则有[25]:$$ \begin{gathered}y(t+W|t)+{a}_{1}y(t+W-1|t)+{a}_{2}y(t+W-2|t)+\cdots +\\ {a}_{{n}_{a}}y(t+W-{n}_{a}|t)={b}_{1}u(t+W-1)+\\ {b}_{2}u(t+W-2)+\cdots +{b}_{{n}_{b}}u(t+W-{n}_{b})\\ t=N\text{,}W=1,2,\cdots ,{W}_{\mathrm{max}}\end{gathered} $$ 忽略变量
$ v(t + W) $ 后,预报阶段系统输出为模型的状态变量,即$ x(t + W) = y(t + W\left| t \right.) $ 成立,并代入最优滞后步数$ {L^*} $ 得:$$ \begin{gathered}x(t+W)+{a}_{1}x(t+W-1)+{a}_{2}x(t+W-2)+\cdots +\\ {a}_{{n}_{a}}x(t+W-{n}_{a})={b}_{1}y(t+W-{L}^{*}-1)+\\ {b}_{2}y(t+W-{L}^{*}-2)+\cdots +{b}_{{n}_{b}}y(t+W-{L}^{*}-{n}_{b})\\ t=N\text{,}W=1,2,\cdots ,{W}_{\mathrm{max}}\end{gathered} $$ 整理后可写成最小二乘格式:
$$ \begin{gathered}x(t+W)={\widehat{{\boldsymbol{\phi}} }}^{\;{\rm{T}}}(t+W)\widehat{{\boldsymbol{\theta }}}(t+W)\\ \widehat{{\boldsymbol{\phi}} }(t+W)=[x(t+W-1),x(t+W-2),\cdots ,\\ x(t+W-{n}_{a}),y(t+W-{L}^{*}-1),y(t+W-{L}^{*}-2),\cdots ,\\ y(t+W-{L}^{*}-{n}_{b}){]}^{{\rm{T}}}\in {{\rm{R}}}^{{n}_{a}+{n}_{b}}\\ \widehat{{\boldsymbol{\theta}} }(t+W)={\left[-{a}_{1},-{a}_{2},\cdots ,-{a}_{{n}_{\text{a}}},{b}_{1},{b}_{2}\cdots{b}_{{n}_{b}}\right]}^{{\rm{T}}}\in {{\rm{R}}}^{{n}_{a}+{n}_{b}}\\ t=N\text{,}W=1,2,\cdots ,{W}_{\mathrm{max}}\end{gathered} $$ 4. 对比仿真实验及分析
4.1 多海况垂荡/纵摇测试
为了验证OE模型以及AM-RLS算法能够完成各种复杂海况下的甲板运动预报,实验中考虑了某典型舰船在不同海况下的运动特性并对算法的性能进行了验证。如下为不同海况下该舰船甲板运动的幅频特性:
3级海况垂荡赋幅值为0.909 m,速率为0.53 rad/s。纵摇赋幅值为1.08°,速率为0.58 rad/s。
4级海况垂荡赋幅值为1.641 m,速率为0.55 rad/s。纵摇赋幅值为1.725°,速率为0.6 rad/s。
5级海况垂荡赋幅值为2.181 m,速率为0.42 rad/s。纵摇赋幅值为2.595°,速率为0.57 rad/s。
多海况实验通过甲板运动信号叠加和离散傅里叶变换的方式合成不同海况下的信号发生器。将大型舰船运动幅频特性作为基波,适当引入高次谐波模拟真实的甲板运动,并引入白噪声作为传感器噪声进行叠加,然后通过离散傅里叶变换确定符合甲板运动特性的信号发生器[26]。
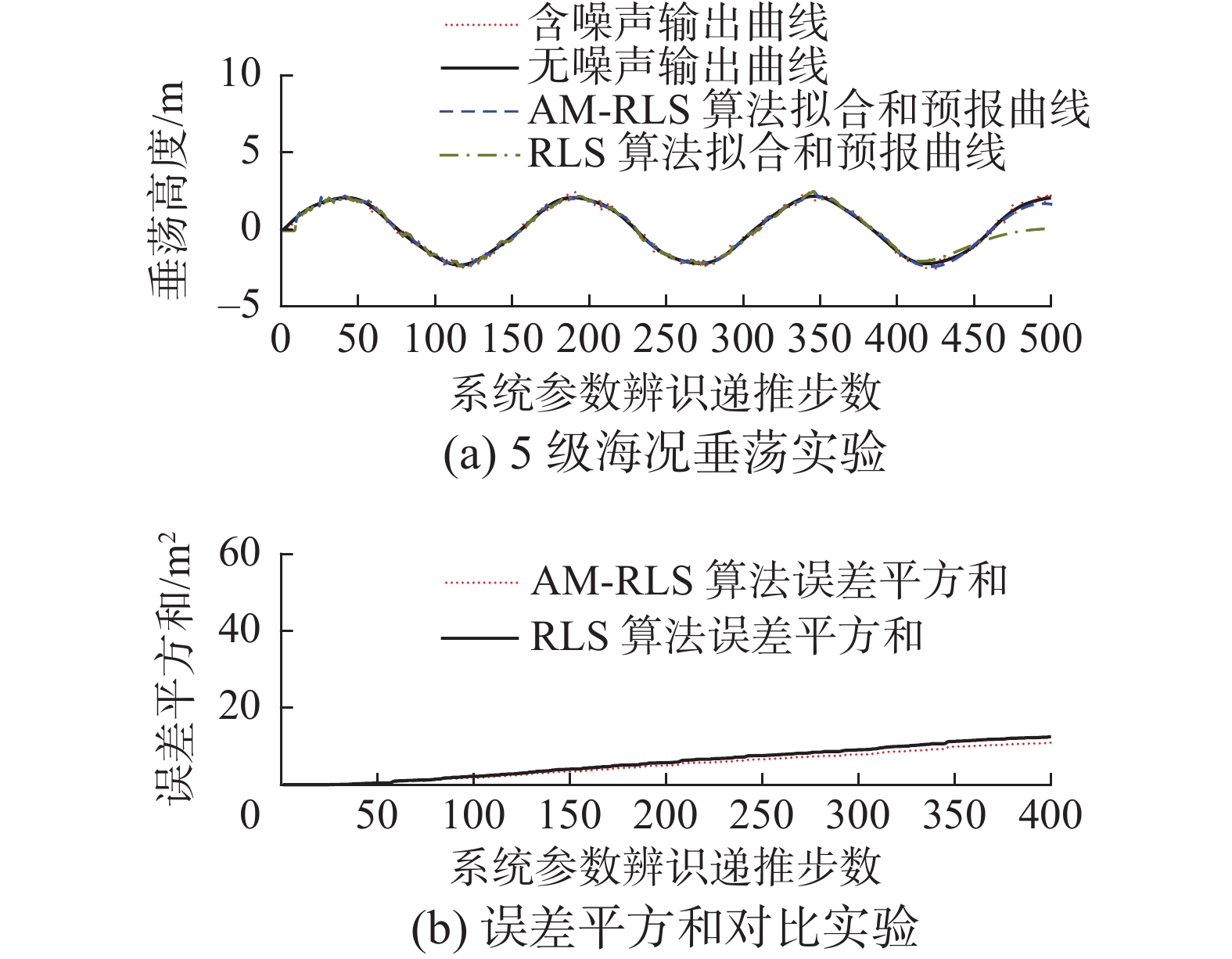
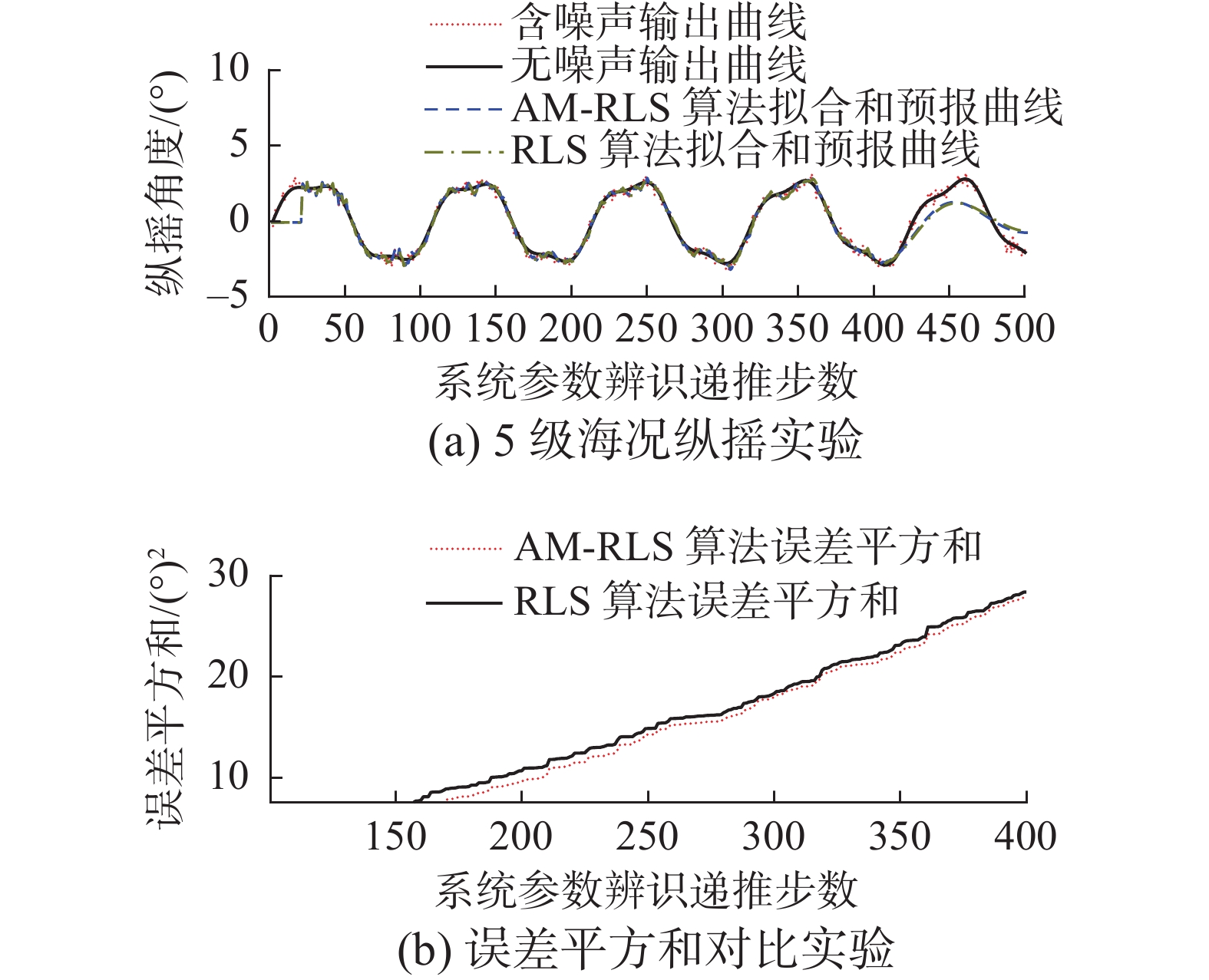
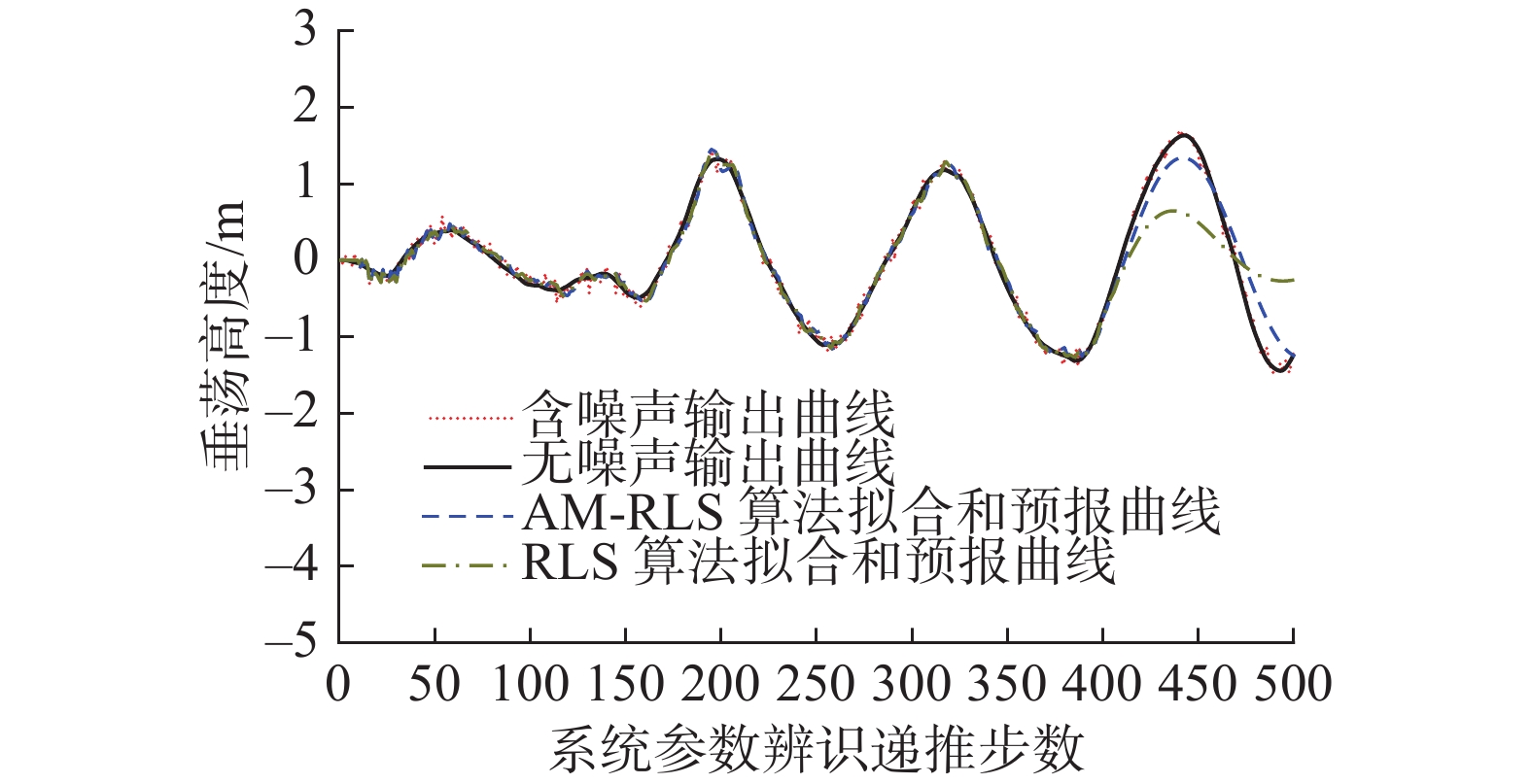
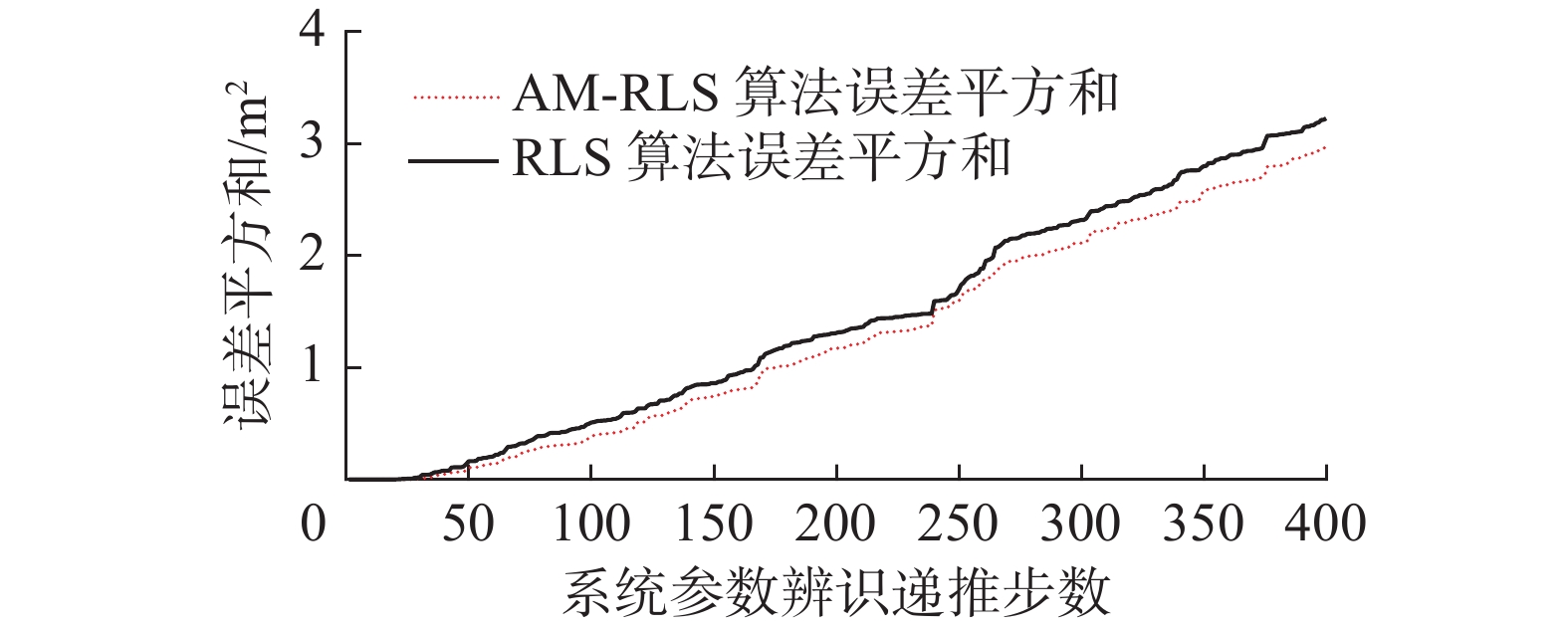
由于目前在甲板运动预报领域精度最高的系统参数辨识算法是RLS算法。而接近OE模型中表现最优秀的甲板运动模型为CAR模型。因此多海况实验中的对比实验组为基于OE模型的AM-RLS算法和基于CAR模型的RLS算法。因为以上两种算法在系统模型参数辨识阶段产生的误差平方和相比于预报阶段产生的误差平方和较小,在预报阶段的误差对比较为明显。为了突出体现两种算法在系统模型参数辨识阶段的性能差异,下文实验中误差平方和对比图的横轴坐标只截止到递推阶段结束时刻。多海况垂荡实验结果如图6~8和表1所示。
表 1 多海况垂荡实验结果对比Table 1 Comparison of heave test results in different sea states% 海况 3级 4级 5级 t0后5 s内辨识误差 2.65 3.43 4.41 递推阶段提高的辨识精度 4.04 5.32 2.18 预报阶段最大误差 8.62 34.57 13.91 预报阶段提高的预测精度 3.88 3.61 17.38 从3、4、5级海况垂荡实验图中可以看出,使用基于OE模型的AM-RLS的算法进行甲板垂荡预报可以将5 s内的系统参数辨识误差控制在4.5%以内,并且在不同海况下系统参数辨识的精度都有所提高。在4级海况下垂荡预测的误差最大,主要是由于甲板运动预测曲线幅值较小导致的。但3、4、5级海况下甲板垂荡运动的相位预测都十分准确,接近真实运动曲线,误差主要来源于垂荡运动预测的幅值偏小。实验结果表明本文的预测方法相比于基于CAR模型的RLS算法在不同海况下的垂荡预测精度都有所提高。
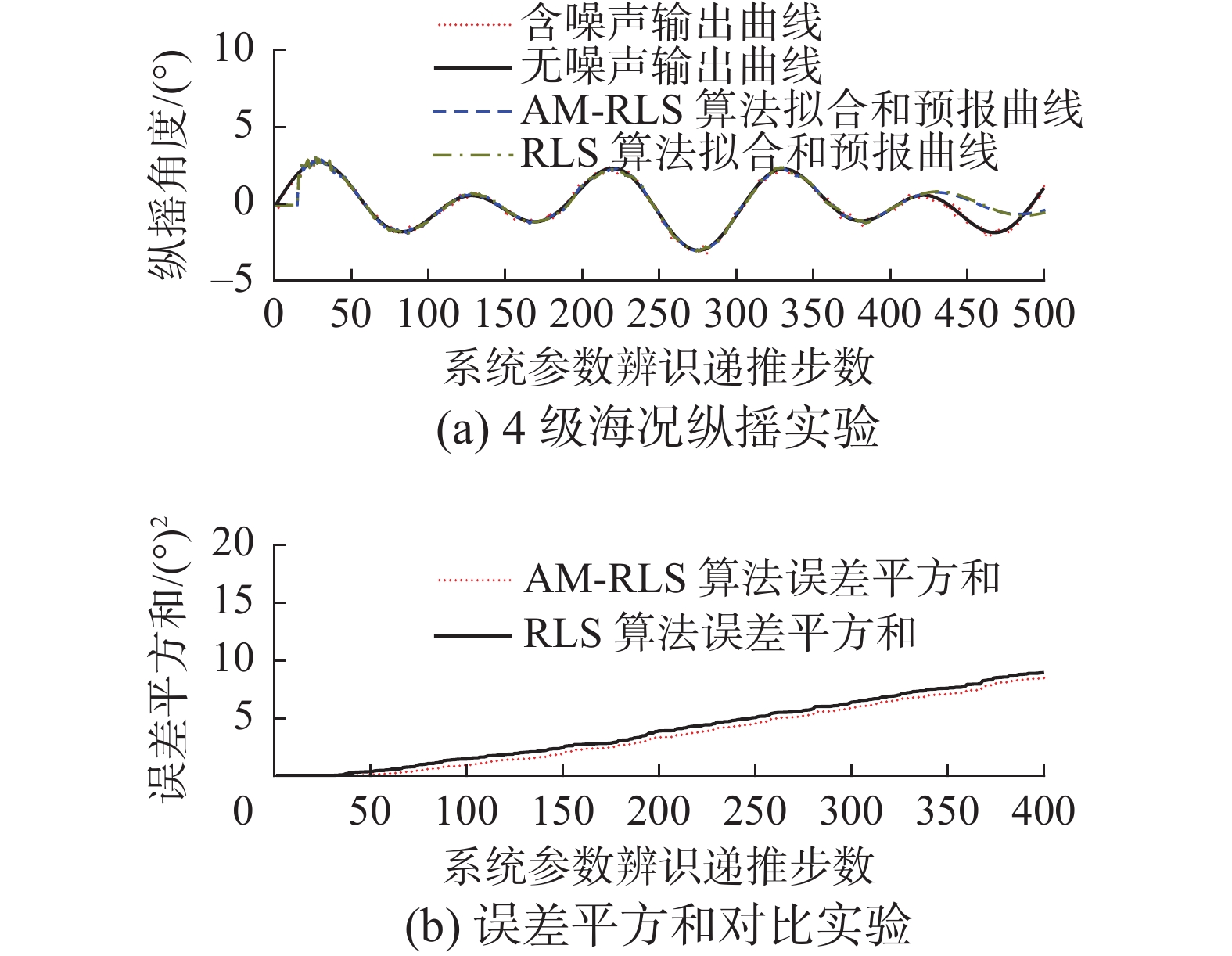
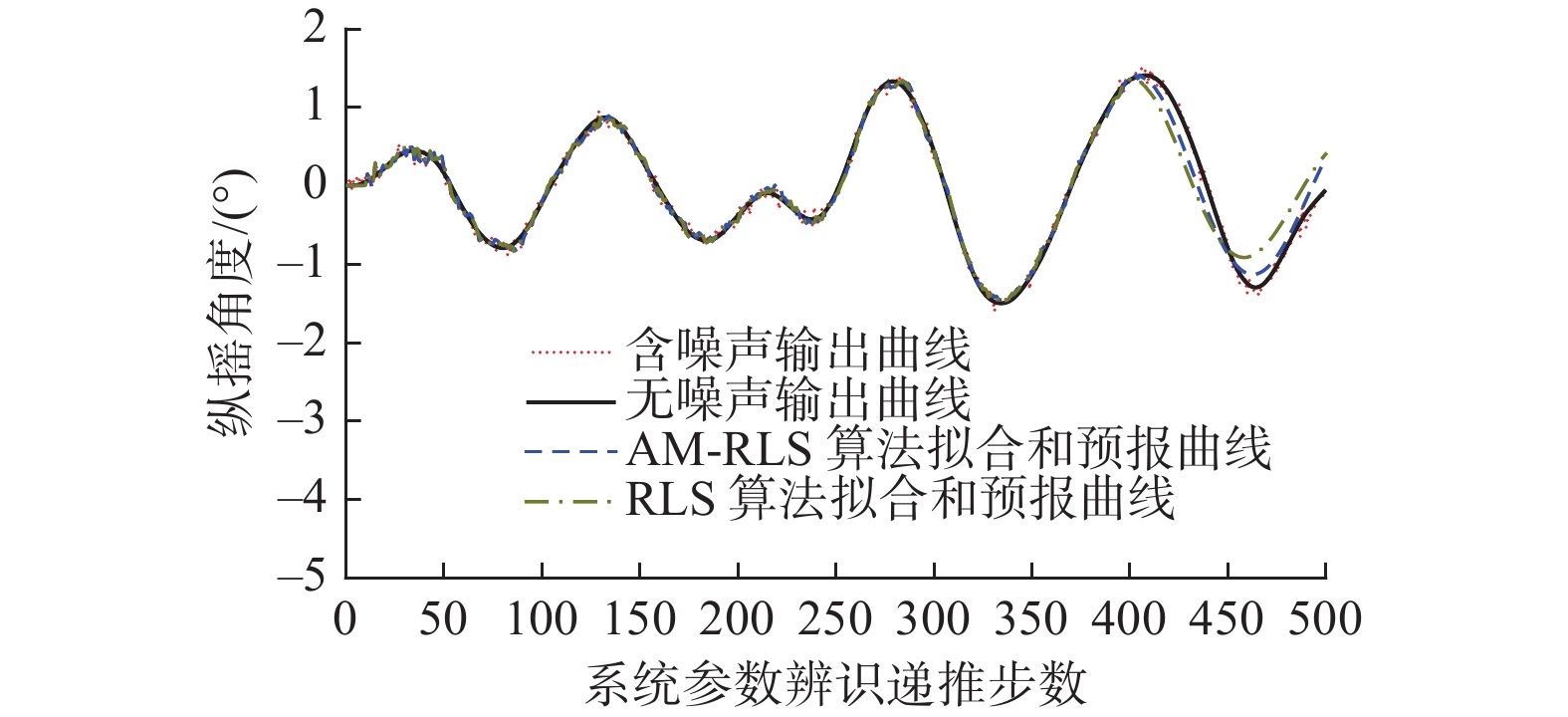
从3、4、5级海况纵摇实验图中可以看出,使用基于OE模型的AM-RLS算法进行甲板纵摇预报可以将5 s内的系统参数辨识误差控制在7.5%以内,并且在不同海况下系统参数辨识的精度都有所提高。在3级海况下基于OE模型的AM-RLS算法提高的预测精度最大。在4级海况下纵摇预测的误差最大,主要是由于纵摇预测曲线相比于真实曲线相位滞后导致的。在5级海况下,本文提出方法的预测曲线幅值较小,但相位预测较为准确。实验结果表明本文的预测方法相比于基于CAR模型的RLS算法在不同海况下的纵摇预测精度都有所提高。
表 2 多海况纵摇实验结果对比Table 2 Comparison of pitch test results in different sea states% 海况 3级 4级 5级 t0后5 s内辨识误差 6.24 7.16 7.39 递推阶段提高的辨识精度 14.97 4.73 2.65 预报阶段最大误差 28.09 52.19 32.84 预报阶段提高的预测精度 45.81 2.76 3.28 4.2 传函形式信号发生器垂荡/纵摇测试
为了进一步提高甲板运动信号的复杂度,使仿真结果更接近实际情况。实验引入了文献[27]中的传递函数形式舰船垂荡/纵摇信号发生器。以白噪声为系统输入模拟真实情况下复杂多变的海浪,为了提高仿真实验的真实性,在该信号上叠加了噪声来模拟真实预报过程中传感器的误差。该垂荡信号发生器传递函数为
$$ \begin{gathered} Z(s) = \frac{{0.353\;568s(s + 0.04)}}{{({s^2} + 0.16s + 0.16)({s^2} + 0.22s + 0.3025)}} \end{gathered} $$ (7) 式中:
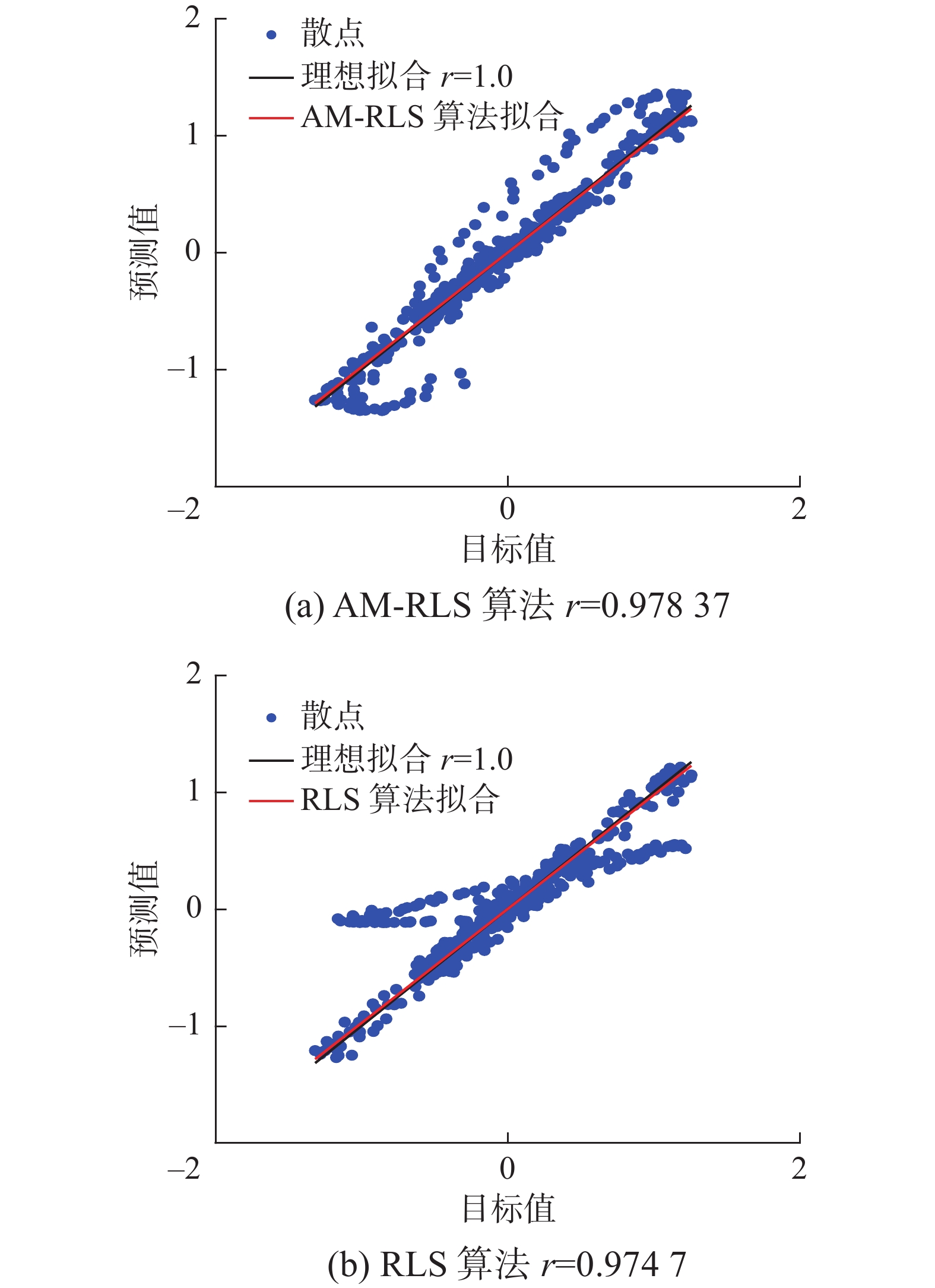
$ s ={\rm{ j}}\omega $ 为复频域信号的表示方法,$ \omega $ 为信号频率(本文只有在表示传递函数时$s ={\rm{ j}}\omega$ )。本节实验中的对比实验组为基于OE模型的AM-RLS算法和基于CAR模型的RLS算法。实验中引入了系统参数辨识递推过程中的误差平方和以及相关系数$ r $ 作为算法的评价标准[28]。实验结果如图12~14所示。舰船纵摇垂荡信号发生器传递函数为
$$ \begin{gathered} \theta (s) = \frac{{0.334\;059s}}{{({s^2} + 0.22s + 0.302\;5)({s^2} + 0.384s + 0.409\;6)}} \end{gathered} $$ (8) 其中
$ \omega $ 、$ s $ 与式(1)中定义相同。结果如图15~17和表3所示。表 3 复杂海况实验结果对比Table 3 Comparison of test results in complex sea states% 复杂海况垂荡 复杂海况纵摇 $ {t_0} $后5 s内辨识误差 4.67 4.59 递推阶段提高的辨识精度 4.26 8.41 预报阶段最大误差 6.93 9.56 预报阶段提高的预测精度 49.87 26.73 从本节中垂荡实验图12和纵摇实验图15中可以看出本文提出的甲板运动预报方法得到的预报曲线幅值和相位都与真实运动曲线较为接近。从散点图14和图17中可以看出本文提出的预测方法所得到的相关系数更接近1,与真实运动曲线的拟合程度最高。预报方法可以将5 s内参数辨识误差控制在4.7%以内,并且将复杂海况下的预测误差控制在10%以内。相比于基于CAR模型的预测算法有了明显的提高。
5. 结束语
本文将输出误差模型引入甲板运动动力学建模,提出了将惯性器件的量测数据进行最优时间滞后处理的思想,并结合辅助模型递推最小二乘算法设计了一种预测舰船甲板真实运动状态的预报算法。该方法在传统甲板运动预报的AR和CAR模型的研究基础上做出了改进:1)首次应用了传递函数形式的动力学模型来描述舰船过去时刻运动状态与当前运动状态的输入输出关系。2)同时结合了最优输入输出定阶准则确定了最接近真实甲板运动的模型最优阶数数对
$ ({n_a}^*,{n_b}^*) $ ,以及使用PLS准则确定最优滞后步数$ {L^*} $ 。3)数据递推过程中采用了抗扰动能力更强的辅助模型递推最小二乘算法来降低传感器量测误差和环境扰动对动力学模型参数辨识精度的影响,同时提高了预报算法对复杂海况的适应能力。结论表明:1)在运动模型参数辨识阶段AM-RLS算法与基于CAR模型的RLS算法相比,无论是在多种确定海况下,还是在复杂的混合海况下,AM-RLS算法基本上可以将5 s内的系统参数辨识误差控制在4.8%以内,将系统参数辨识精度提高5.13%。2)在甲板运动预报预报阶段,基于AM-RLS的预报方法可以获得与真实运动幅值和相位更加接近的预报结果。可以将甲板垂荡预报的精度提高3.81%,将甲板纵摇预报的精度提高3.17%。3)基于AM-RLS的预报方法在提高精度的基础上可以保证该方法具备与基于CAR模型预报方法相当的实时性。 -
表 1 多海况垂荡实验结果对比
Table 1 Comparison of heave test results in different sea states
% 海况 3级 4级 5级 t0后5 s内辨识误差 2.65 3.43 4.41 递推阶段提高的辨识精度 4.04 5.32 2.18 预报阶段最大误差 8.62 34.57 13.91 预报阶段提高的预测精度 3.88 3.61 17.38 表 2 多海况纵摇实验结果对比
Table 2 Comparison of pitch test results in different sea states
% 海况 3级 4级 5级 t0后5 s内辨识误差 6.24 7.16 7.39 递推阶段提高的辨识精度 14.97 4.73 2.65 预报阶段最大误差 28.09 52.19 32.84 预报阶段提高的预测精度 45.81 2.76 3.28 表 3 复杂海况实验结果对比
Table 3 Comparison of test results in complex sea states
% 复杂海况垂荡 复杂海况纵摇 $ {t_0} $后5 s内辨识误差 4.67 4.59 递推阶段提高的辨识精度 4.26 8.41 预报阶段最大误差 6.93 9.56 预报阶段提高的预测精度 49.87 26.73 -
[1] HUANG Limin, DUAN Wenyang, HAN Yang, et al. A review of short-term prediction techniques for ship motions in seaway[J]. 船舶力学, 2014, 18(12): 1534–1542. doi: 10.3969/j.issn.1007-7294.2014.12.013 HUANG Limin, DUAN Wenyang, HAN Yang, et al. A review of short-term prediction techniques for ship motions in seaway[J]. Journal of ship mechanics, 2014, 18(12): 1534–1542. doi: 10.3969/j.issn.1007-7294.2014.12.013 [2] 黄礼敏. 海浪中非平稳非线性舰船运动在线预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2016. HUANG Limin. On-line prediction of non-stationary and nonlinear ship motions at sea[D]. Harbin: Harbin Engineering University, 2016. [3] DUAN Wenyang, HUANG Limin, HAN Yang, et al. A hybrid EMD-AR model for nonlinear and non-stationary wave forecasting[J]. Journal of Zhejiang university-SCIENCE A, 2016, 17(2): 115–129. [4] YANG Xilin, POTA H, GARRATT M, et al. Ship motion prediction for maritime flight operations[J]. IFAC proceedings volumes, 2008, 41(2): 12407–12412. doi: 10.3182/20080706-5-KR-1001.02100 [5] PEÑA-SANCHEZ Y, MÉRIGAUD A, RINGWOOD J V. Short-term forecasting of sea surface elevation for wave energy applications: the autoregressive model revisited[J]. IEEE journal of oceanic engineering, 2020, 45(2): 462–471. doi: 10.1109/JOE.2018.2875575 [6] 殷大鹏. 基于鲁棒融合Kalman滤波的船舶运动预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. YIN Dapeng. Research on ship motion prediction based on robust fusion Kalman filter[D]. Harbin: Harbin Engineering University, 2019. [7] 张彪. 船舶运动姿态估计与预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2020. ZHANG Biao. Research on ship motion attitude estimation and prediction methods[D]. Harbin: Harbin Engineering University, 2020. [8] DUAN Wenyang, HAN Yang, HUANG Limin, et al. A hybrid EMD-SVR model for the short-term prediction of significant wave height[J]. Ocean engineering, 2016, 124: 54–73. doi: 10.1016/j.oceaneng.2016.05.049 [9] MAFI S, AMIRINIA G. Forecasting hurricane wave height in gulf of mexico using soft computing methods[J]. Ocean engineering, 2017, 146: 352–362. doi: 10.1016/j.oceaneng.2017.10.003 [10] DEMETRIOU D, MICHAILIDES C, PAPANASTASIOU G, et al. Coastal zone significant wave height prediction by supervised machine learning classification algorithms[J]. Ocean engineering, 2021, 221: 108592. doi: 10.1016/j.oceaneng.2021.108592 [11] 宋蕙慧, 于国星, 曲延滨. 基于扩展卡尔曼滤波算法的船舶姿态监测预报系统设计 (英文)[J]. 中国惯性技术学报, 2018, 26(1): 6–12. SONG Huihui, YU Guoxing, QU Yanbin. Monitoring and forecasting system for ship attitude motion based on extended Kalman filtering algorithm[J]. Journal of Chinese inertial technology, 2018, 26(1): 6–12. [12] 刘世林. 船舶运动姿态短时高精度预测方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. LIU Shilin. Research on the method of high-precision prediction of the movement attitude of the ship within a short time[D]. Harbin: Harbin Engineering University, 2019. [13] WU Mengning, STEFANAKOS C, GAO Zhen, et al. Prediction of short-term wind and wave conditions for marine operations using a multi-step-ahead decomposition-ANFIS model and quantification of its uncertainty[J]. Ocean engineering, 2019, 188: 106300. doi: 10.1016/j.oceaneng.2019.106300 [14] GE Ming, KERRIGAN E C. Short-term ocean wave forecasting using an autoregressive moving average model[C]//2016 UKACC 11th International Conference on Control. Belfast: IEEE, 2016: 1−6. [15] 袁秋梦, 王胜正, 韩冰, 等. 海浪预报不确定下的船舶运动姿态分析方法[J]. 中国航海, 2022, 45(1): 31–36. doi: 10.3969/j.issn.1000-4653.2022.01.006 YUAN Qiumeng, WANG Shengzheng, HAN Bing, et al. A method for analyzing ship motion attitude under the condition of uncertain sea wave forecast[J]. Navigation of China, 2022, 45(1): 31–36. doi: 10.3969/j.issn.1000-4653.2022.01.006 [16] 萧德云. 系统辨识理论及应用[M]. 北京: 清华大学出版社, 2014: 39-41. [17] DING Feng, DING Jie. Least-squares parameter estimation for systems with irregularly missing data[J]. International journal of adaptive control and signal processing, 2010, 24(7): 540–553. [18] 丁锋. 系统辨识新论[M]. 北京: 科学出版社, 2013. [19] DING Feng, CHEN Tongwen. Combined parameter and output estimation of dual-rate systems using an auxiliary model[J]. Automatica, 2004, 40(10): 1739–1748. doi: 10.1016/j.automatica.2004.05.001 [20] DING Feng, CHEN Tongwen. Parameter estimation of dual-rate stochastic systems by using an output error method[J]. IEEE transactions on automatic control, 2005, 50(9): 1436–1441. doi: 10.1109/TAC.2005.854654 [21] FUSCO F, RINGWOOD J V. Short-term wave forecasting with AR models in real-time optimal control of wave energy converters[C]//2010 IEEE International Symposium on Industrial Electronics. Bari: IEEE, 2010: 2475−2480. [22] HUANG Limin, DUAN Wenyang, HAN Yang, et al. Extending the scope of AR model in forecasting non-stationary ship motion by using AR-EMD technique[J]. Journal of ship mechanics, 2015, 19(9): 1033−1049. [23] 刘佳男. 船舶运动姿态测量及预报[D]. 哈尔滨: 哈尔滨工程大学, 2020. LIU Jianan. Measurement and prediction of ship motion attitude[D]. Harbin: Harbin Engineering University, 2020. [24] DING Feng, LIU Guangjun, LIU Xiaoping P. Parameter estimation with scarce measurements[J]. Automatica, 2011, 47(8): 1646–1655. doi: 10.1016/j.automatica.2011.05.007 [25] 彭秀艳, 赵希人, 魏纳新, 等. 大型舰船姿态运动极短期预报的一种AR算法[J]. 船舶工程, 2001, 23(5): 5–7,10. doi: 10.3969/j.issn.1000-6982.2001.05.001 PENG Xiuyan, ZHAO Xiren, Wei Naxinand, et al. AR algorithm for extremely short-term prediction of large ship's motion[J]. Ship engineering, 2001, 23(5): 5–7,10. doi: 10.3969/j.issn.1000-6982.2001.05.001 [26] SHI Shuo, PATTON R J, LIU Yanhua. Short-term wave forecasting using Gaussian process for optimal control of wave energy converters[J]. IFAC-PapersOnLine, 2018, 51(29): 44–49. doi: 10.1016/j.ifacol.2018.09.467 [27] 彭兢. 舰载飞机进舰着舰的自动引导和控制研究[D]. 北京: 北京航空航天大学, 2001. PENG Jing. Research on the Automatic Guide and Control of Carrier-based Airplane Approach and landing. Beijing: Beihang University, 2001. [28] LI Jiangxia, PAN Shunqi, CHEN Yongping, et al. The performance of the copulas in estimating the joint probability of extreme waves and surges along east coasts of the mainland China[J]. Ocean engineering, 2021, 237: 109581. doi: 10.1016/j.oceaneng.2021.109581

 下载:
下载: