视觉目标跟踪作为计算机视觉领域的一个重要研究问题^[1]，结合了数学经典算法^[2]、人工智能、目标检测^[3]等领域的先进思想，已在现实生活中得到广泛应用。近年来，许多学者在相关滤波的速率和精度方面潜心钻研，更优质高效的算法被广泛认可并加以应用。2010年Bolme等^[4]首次将相关滤波（correlation filters, CF）引入目标跟踪，旨在利用相关的概念衡量信号的相似度，将卷积算子由空域转换到频域，提出了最小输出平方和误差滤波跟踪算法（minimum output sum of squared error, MOSSE），因为采用单通道的灰度特征，只能局部提取部分信息，不能跟踪完整的图像。2012年Henriques等^[5]提出核循环结构算法，使用循环矩阵作用于样本区域，对图像进行循环采样，提高了特征信息的完整性。2014年Henriques等^[6]提出了核相关滤波算法（kernelized correlation filters, KCF），采用梯度直方图特征，并在岭回归中加入高斯核，实现非线性到空间线性，提高计算速率。2014年，Danelljan等^[7]提出了判别型尺度空间跟踪算法，利用2个独立的滤波器分别进行位置确定与尺度评估，采用不同的特征种类，自适应地实现目标定位。2016年，Bertinetto等^[8]提出背景直方图目标跟踪算法（Staple算法），该算法结合梯度直方图和颜色直方图2种特征，但非刚性运动效果不好，实用性较弱。综上算法，跟踪目标的运动状态出现速度骤变和快速形变的状况时，边界效应的问题随之产生。为解决上述问题，2015年，Galoogahi等^[9]提出有规定边界的相关滤波器算法，用于训练和检测的图像块过大，且训练样本有限，过度拟和学习模型，导致准确性降低。2015年，Danelljan等^[10]提出固定空间正则化项的相关性过滤器（learning spatially regularized correlation filters for visual tracking, SRDCF），设置空间权重系数，给予目标区域较大权重和边缘区域较小权重，但记录每一帧的样本信息，并不适合实现目标的实时跟踪。2017年，Mueller等^[11]提出上下文感知的相关滤波算法，记录作为正样本的目标与4个方向作为负样本的背景块的信息，实现改进相关滤波算法框架的目的。2018年，Li等^[12]在SRDCF的基础上加入时间正则化，提出了具有固定的时空正则化项的相关性过滤器（learning spatial-temporal regularized correlation filters for visual tracking，STRCF），权重矩阵的引入使得该算法相较于其他跟踪算法，在目标出现快速运动和形变时体现出良好的鲁棒性。

尽管STRCF已经取得了令人满意的性能，但它确实有2个局限性：固定的空间正则化无法适应跟踪场景中的外观变化，不变的时间惩罚强度不适用于非目标区域。因此，本文为解决上述问题，在目标函数中，根据相邻两帧局部变化的可信度判断滤波器学习的像素，运动影响消除后结合空间惩罚缓解边界效应，既可以在边界进行完整的信息采样，又可以明确跟踪学习的特征信息，实现利用局部和全局响应变化进行空间和时间同时正则化的目的，重新设定自适应参数，将跟踪训练得到的响应模型作用于目标区域，从而明确待学习的特征样本，进而得到一个更加强壮的外观模型。在不同数据集上对本文算法进行精确率、成功率和实时性等多方面评估，实验表明，相较于其它主流的跟踪算法，本文算法具有较高的鲁棒性。

1.   时空正则化相关滤波算法原理

时空正则化相关滤波算法通过在目标函数中加入权重矩阵 $ {\boldsymbol{u}} $ 和时间感知项，结合空间和时间正则化，能够在有效处理边界效应的同时，提高跟踪的速度与性能。

通过最小化以下目标函数学习第 $t$ 帧中的最佳滤波器：

式中：符号*表示卷积运算； ${{\boldsymbol{x}}}_{k}^{t} \in {{\bf{R}}^{T \times 1}}\left( {k = 1,2, \cdots ,K} \right)$ 表示在 $ t $ 帧中提取出的特征样本， $ K $ 为每帧图片的通道数； ${\boldsymbol{y}} \in {{\bf{R}}^{T \times 1}}$ 为理想的相关响应值， $ T $ 代表矩阵维度； ${\boldsymbol{H}} = \left[ {{\boldsymbol{h}}_1^t\; {\boldsymbol{h}}_2^t\; \cdots\; {{\boldsymbol{h}}}_{k}^{t}} \right]$ ， ${{\boldsymbol{h}}}_{k}^{t} \in {{\bf{R}}^{T \times 1}}$ 为第 $ t $ 帧训练的第 $ k $ 通道的滤波器。STRCF算法引用SRDCF算法中的空间正则项 $\dfrac{1}{2}\displaystyle\sum\limits_{k = 1}^K {\left\| {{\boldsymbol{u}} \cdot {{\boldsymbol{h}}}_{k}^{t}} \right\|_2^2}$ ，其中 ${{\boldsymbol{u}}}$ 为负高斯形状的空间权重向量，使正则化权重从目标区域平稳地过渡到背景区域，并且增加了权重矩阵在傅里叶域中的稀疏性。引入时间正则项，其中 $ \theta $ 为系数， ${{{\boldsymbol{h}}}^{t}}$ 和 ${{\boldsymbol{h}}^{t - 1}}$ 表示当前帧和上一帧训练的滤波器。

STRCF采用固定的空间权重向量，有效地缓解了边界效应，但负高斯形状忽视了边界区域样本信息的完整性。当跟踪目标被遮挡或者发生较大形变时，是非目标区域无法实现自适应地分配权重，就会导致跟踪失败。因此，本文针对STRCF算法的空间权重问题，提出了自适应时空正则化的相关滤波跟踪算法，通过在目标函数中构造自适应时空正则项，与样本信息建立联系，从而提高算法的跟踪性能。

2.   自适应时空正则化相关滤波算法

2.1   自适应时空正则化

在检测过程中，响应图中的信息至关重要。因为其信息可以反映前一帧所学习到的外观模型和当前帧检测到的实际对象之间的相似性。所以，本文采用响应变化来实现正则化。

首先，本文定义局部响应变化量， $\sigma =({\sigma }_{1},{\sigma }_{2},\cdots, {\sigma }_{i})$ 用于对象边界框中的可视化。其第 $ i $ 个元素 ${\sigma _i}$ 定义为

式中： ${\phi _\Delta }$ 是在两个响应图 ${R^t}$ 和 ${R^{t - 1}}$ 产生的两个峰值的位置差^[13]， $\left[ {{\phi _\Delta }} \right]$ 表示相邻峰值为达到高度相似而移动的距离。局部响应变化显示当前帧搜索区域中每个像素的可信度。当外观发生较大变化时导致 $\left[ {{\phi _\Delta }} \right]$ 的值变大，因相似而移动的距离变大，相似性低，像素可信度低。在学习过程中，应限制学习可信度低的像素，本文通过将局部变化 $ \sigma $ 引入空间正则化参数 $\tilde {\boldsymbol{u}}$ 来实现这一点：

其中 ${P^T} \in {{\bf{R}}^{T \times T}}$ 用于裁剪对象所在滤波器的中心部分，将目标从背景模板中剪切出来，从而提高样本质量并提高计算速度。 $\delta $ 是一个常数，用于调整局部响应变化的权重，而 ${\boldsymbol{u}}$ 是从STRCF中继承来的权重向量，用于缓解边界效应。局部响应变量反应了当前帧局部位置每个像素的可信度， ${\text{log}}\left( {\sigma + 1} \right)$ 作为单调递增函数，与 $ \sigma $ 的增减保持相同趋势，放大 $ \sigma $ 的变化。通过式（3），将其引入到空间正则化参数中，目标发生变化时，滤波器将有选择地进行学习，避免学习响应发生剧烈变化时的样本信息，实现空间自适应。在STRCF中，相邻两帧滤波器的变化率由一个固定参数 $ \theta $ 决定，本文通过自适应确定参数的值，进一步优化目标函数，从而提高滤波器跟踪时的准确性，定义参数 $ \tilde \theta $ 作为目标函数的全局响应：

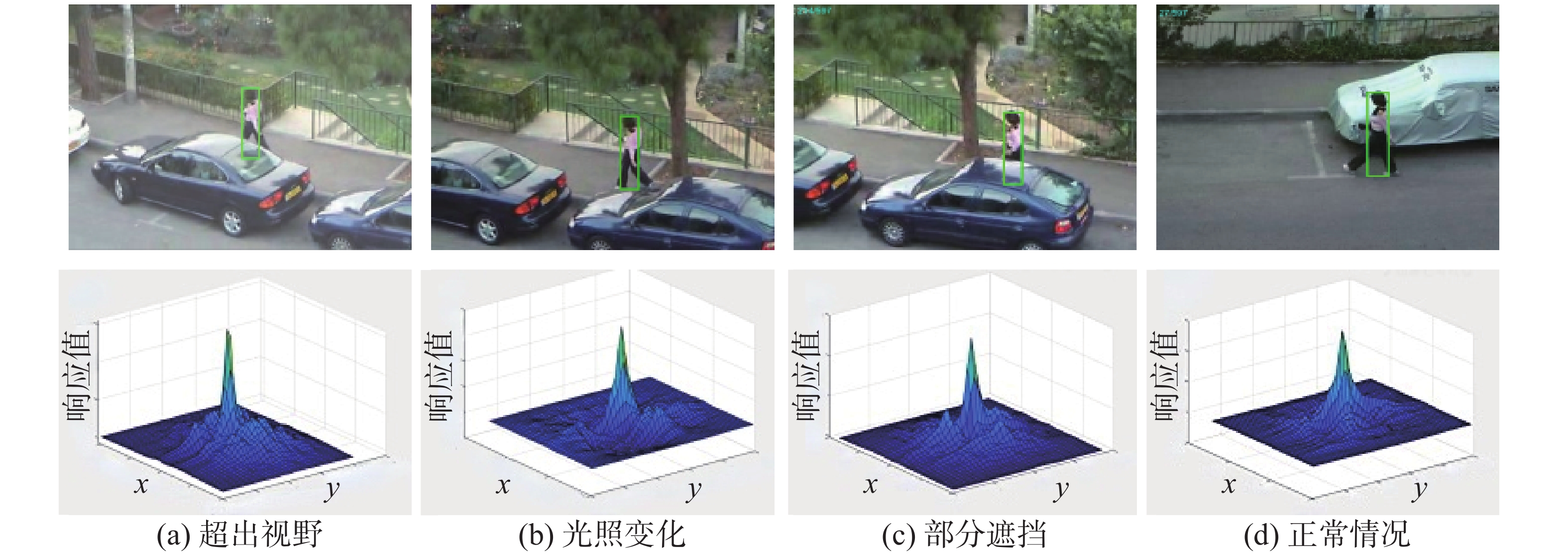
引入欧几里德范数来比较 ${R^t}$ 和 ${R^{t - 1}}$ 两个响应图的差异水平，发生畸变时，相似性会突然下降，则 ${\sigma _i}$ 的值会升高，当全局响应变量高于阈值 ${\phi _{}}$ 时，滤波器将停止学习。而当全局响应变量低于阈值时，响应剧烈程度与 $ \tilde \theta $ 值成负相关，进而判断是否进行滤波器的更新迭代，实现时间自适应。如图1，利用空间局部和全局响应变化，局部变化表示目标边界框中的局部可信度，光照变化、部分遮挡和超出视野均会降低像素的可信度。

图  1  整体响应变化

Fig.  1  Global response variation

下载: 全尺寸图片

2.2   目标函数模型

STRCF的函数模型在进行目标跟踪的过程中，采取逐帧的方式更新外观模型和滤波器，但在进行迭代的过程中，无差别的学习将导致最终跟踪结果的不准确。针对上述问题，本文采用更新后的目标函数模型。

式中： $ \theta $ 和 ${\theta }_{{\text{score}}}^t$ 分别表示参考和优化的时间正则化参数， $ \tilde {\boldsymbol{u}} $ 表示通过式（3）计算得到的新的权重向量，既缓解了边界效应，又明确了样本中的学习区域，实现了空间自适应的目的。外观变化时，前后两帧的滤波器系数差别较大，容易产生漂移，被动地更新滤波器，使其接近前一帧的滤波器系数，达到减少漂移的目的。反之，滤波器系数近乎一致，可忽略最后一项，主动地学习滤波器。本文通过局部响应和全局响应的迭代计算，判断是否进行滤波器的更新，从而实现了时间自适应性。

根据Parseval定理，引入辅助变量， ${{\hat {\boldsymbol{g}}}_{k}} \in {{\bf{R}}^{TK \times 1}}$ ， ${\hat {\boldsymbol{G}}} = \left[ {{{{\hat {\boldsymbol{g}}}}_{1}}\;\;{{{\hat {\boldsymbol{g}}}}_{2}}\;\; \cdots\;\; {{{\hat {\boldsymbol{g}}}}_{k}}} \right]$ ，符号ˆ表示信号的离散傅里叶变换，可将式(5)转化到频域：

式中： ${\hat {\boldsymbol{y}}} = \sqrt T {{\boldsymbol{F}}{\boldsymbol{y}}}$ ， ${{\hat {\boldsymbol{x}}}_{k}} = \sqrt T {{\boldsymbol{F}}}{{{\boldsymbol{x}}}_{k}}$ ， ${{\hat {\boldsymbol{g}}}_{k}} = \sqrt T {{\boldsymbol{F}}}{{{\boldsymbol{g}}}_{k}}$ 为傅里叶变换，其中 ${\boldsymbol{F}} \in {{\bf{R}}^{T \times T}}$ 为正交矩阵。

2.3   目标函数优化

式（6）为凸光滑可微函数，可通过交替方向乘数法（ADMM）迭代求解，降低算法复杂度的同时提高跟踪速度。方程的增广拉格朗日形式为

式中： ${\hat {\boldsymbol{M}}} = \left[ {{{{\hat {\boldsymbol{m}}}}_{1}}\;{{{\hat {\boldsymbol{m}}}}_{2}}\; \cdots \;{{{\hat {\boldsymbol{m}}}}_{k}}} \right] \in {{\bf{R}}^{T \times K}}$ 为拉格朗日乘子^[14]， $\gamma $ 为步长参数，上角标 $\rm{T^z}$ 表示矩阵的共轭转置。

引入 ${\boldsymbol{v}}_k^t = \dfrac{1}{\gamma }{\boldsymbol{m}}_k^t$ ， ${{\boldsymbol{V}}} = \left[ {{{{\boldsymbol{v}}}_{1}}\;{{{\boldsymbol{v}}}_{2}}\; \cdots \;{{{\boldsymbol{v}}}_{K}}} \right]$ ，式(7)可转化为

通过使用ADMM算法^[15]，等式可被分解为 ${\hat {\boldsymbol{G}}}$ 、 ${\theta }_{{\text{score}}}^t$ 、 ${{\boldsymbol{H}}}$ 等3个子问题，式(5)可通过对这3个子问题进行迭代解出最优解。

1）求解 ${\hat {\boldsymbol{G}}}$ ：假设给定 ${{{\boldsymbol{H}}}_{k}}$ 、 ${\theta }_{{\text{score}}}^t$ 、 ${{\hat {\boldsymbol{V}}}_{k}}$ 、 ${\hat {\boldsymbol{G}}} = [ {{{\hat {\boldsymbol{g}}}}_{1}}\;{{{\hat {\boldsymbol{g}}}}_{2}}\; \cdots\; {{{\hat {\boldsymbol{g}}}}_{k}} ]$ ，目标函数为

由式(9)可以看出，如果直接对 $\hat {\boldsymbol{g}}_k^t$ 求导，第1项的求和运算会增加较大的计算复杂度。由于 ${\hat {\boldsymbol{x}}_k}$ 为稀疏带状变量，并且 $\hat y$ 只依赖于 ${{\hat {\boldsymbol{x}}}_{k}} = [ {\hat {\boldsymbol{x}}}_{k}^{1}\;{\hat {\boldsymbol{x}}}_{k}^{2}\; \cdots {\hat {\boldsymbol{x}}}_{k}^{K} ]^{\text{T}}$ 和 ${{\hat {\boldsymbol{g}}}_{k}} = {\left[ {{\text{conj}}\left( {{\hat {\boldsymbol{g}}}_{k}^{1}} \right)\;{\text{conj}}\left( {{\hat {\boldsymbol{g}}}_{k}^{2}} \right)\; \cdots \;{\text{conj}}\left( {{{\boldsymbol{g}}}_{k}^{K}} \right)} \right]^{\text{T}}}$ 中的元素，其中 ${\text{conj}}\left( \cdot \right)$ 表示复共轭运算，所以可以考虑通过单独计算 $\hat {\boldsymbol{y}}$ 中的元素即 ${\hat {\boldsymbol{y}}_k}\left( {k = 1,2, \cdots ,K} \right)$ 来简化计算。记 ${\zeta _j}\left( {\hat {\boldsymbol{G}}} \right) \in {{\bf{R}}^{K \times 1}}$ ,表示在像素 $j$ 上 $\hat {\boldsymbol{x}}$ 的所有 $ K $ 通道值的向量，解：

式(10)时间复杂度为 $O\left( {T{K^3}} \right)$ ，使用Sherman-Morrison公式推导后，其解可以转化为

其中， ${\boldsymbol{\rho}} = {{\zeta }_{j}}\left( {{{{\hat {\boldsymbol{X}}}}^{t}}} \right){{{\boldsymbol{y}}}_{j}} + {\theta }_{{\text{score}}}^t{\zeta }\left( {{{{\hat {\boldsymbol{G}}}}^{{t - 1}}}} \right) - \gamma {{\zeta }_{j}}\left( {{{{\hat {\boldsymbol{V}}}}^{t}}} \right) + \gamma {{\zeta }_{j}}\left( {\sqrt T {{\boldsymbol{F}}}{{{\boldsymbol{H}}}^{t}}} \right)$ 。此时的时间复杂度为 $O\left( {TK} \right)$ ，显著地缩短了程序计算的时间。

2）求解 ${\boldsymbol{H}}$ ：假设给定 ${\theta }_{{\text{score}}}^t、{{\hat {\boldsymbol{G}}}^{t}}、{{\hat {\boldsymbol{V}}}^{t}}$ 、 ${\boldsymbol{H}} \in {{\bf{R}}^{T \times 1}}$ ，其 ${{\boldsymbol{h}}_k}$ 优化可以表示为

${{\boldsymbol{h}}_k}$ 的封闭解为

式中 $\tilde {\boldsymbol{U}} = {\text{diag}}\left( {\tilde {\boldsymbol{u}}} \right) \in {{\bf{R}}^{T \times T}}$ 。由式(12)可以看出对 ${{\boldsymbol{h}}_k}$ 的求解过程仅需逐元相乘和快速傅里叶^[15]逆变换得到，即 ${{{\boldsymbol{v}}}_{k}} = \dfrac{1}{{\sqrt T }}{{\boldsymbol{F}}^{\rm{T}}}{\hat {\boldsymbol{v}}_k}$ ， ${{\boldsymbol{g}}_k} = \dfrac{1}{{\sqrt T }}{{\boldsymbol{F}}^{\rm{T}}}{\hat {\boldsymbol{g}}_k}$ 。所以，对 ${\boldsymbol{H}}$ 进行求解的时间复杂度为 $O\left( {KT\lg T} \right)$ 。

3）求解优化的时间正则化参数 ${\theta }_{{\text{score}}}^t$ ：

给定式(8)中的其他变量 ${{\boldsymbol{H}}}、{\hat {\boldsymbol{G}}}、{\hat {\boldsymbol{V}}}$ ，对 ${\theta}_{{\text{score}}} ^t$ 采用ADMM算法求 ${\theta }_{{\text{score}}}^t$ 的最优解可确定为

4）拉格朗日乘子更新：

式中： $i$ 和 $i + 1$ 表示迭代次数； ${\hat {\boldsymbol{G}}^{i + 1}}$ 和 ${\hat {\boldsymbol{H}}^{i + 1}}$ 表示在第 $\left( {i + 1} \right)$ 次迭代中，式（6）子问题 $\hat {\boldsymbol{G}}$ 和式(11)子问题 $\hat {\boldsymbol{H}}$ 的解； $\tau$ 为更新参数。

式中： $\beta = 10$ ， ${\tau ^{{\text{max}}}} = 10\;000$ 。

2.4   目标定位

式中： ${R^t}$ 为 $t$ 帧响应图， ${\boldsymbol{Z}}_k^t$ 为 $t$ 帧提取的特征映射的傅里叶^[16]形式， ${\boldsymbol{g}}_k^{t - 1}$ 表示第 $t - 1$ 帧中训练好的相关滤波器的傅里叶形式。跟踪目标的中心所在位置就是响应值数值最大处。

3.   特征提取

针对图像高维特征占用巨大存储空间的问题，由于部分特征本身存在相关性，考虑利用卷积神经网络，获取更多图像信息，但是通过卷积神经网络（convolutional neural network, CNN）^[17]提取的图像特征维数过高，加大了计算难度，所以本文采用一种特殊的方式——主成分分析^[18]（principal component analysis, PCA）来处理提取的CNN^[19-21]特征，从而在降低计算复杂度的同时，保持信息准确性。

原始数据经线性变换，成为一组新的向量，各维度线性无关，只提取主特征分量。在面对图像大量高维数据时，利用数据本身存在的相关性进行降维^[22]操作。在保证主要特征准确性的前提下，虽丢失少量信息，但减少了计算成本，从而提高了速度。

输入　样本集 ${D} = \left\{ {{{x}_{{1}}},{{x}_{2}}, \cdots ,{{x}_{n}}} \right\} \in {{\bf{R}}^{m \times d}}$ ；低维空间维数 $d'$ 。

过程：

1）对所有样本^[23-25]进行中心化： ${{\boldsymbol{x}}} = {{{\boldsymbol{x}}}_{i}} - \dfrac{1}{m}\displaystyle\sum\limits_{i = 1}^m {{{{\boldsymbol{x}}}_{i}}}$ ，为了方便计算投影点的方差，可以通过各点与原点间距离之和来计算。

2）计算样本的协方差矩阵： ${\boldsymbol{E}} = {{\boldsymbol{X}}}{{{\boldsymbol{X}}}^{{\rm{T}}}}$ ，在坐标上点到原点的距离用映射所得点与点间的方差来表示，即对原向量和投影向量两个向量点积的绝对值求和。

3）对协方差矩阵 ${\boldsymbol{E}}$ 的特征值 ${\lambda }_{1},{\lambda }_{2},\cdots, {\lambda }_{m}$ 分解，取最大的 $d'$ 个特征值所对应的特征向量 ${{\boldsymbol{\omega}} }_{1},{{\boldsymbol{\omega}} }_{2},\cdots, {{\boldsymbol{\omega}} }_{{d}'}$ 。

输出　投影矩阵 ${\boldsymbol{W}}=\left[{\boldsymbol{\omega}} _{\text{1}}\;\;{\boldsymbol{\omega}} _{\text{2}}\;\;\cdots\;\; {\boldsymbol{\omega}} _{{d'}}\right]$

将问题转化为求 $\mathop {{\text{max}}}\limits_{{{\boldsymbol{\omega}} _1}} \dfrac{1}{m}{{\boldsymbol{\omega}} _1}^{\text{T}}{{\boldsymbol{X}}}{{{\boldsymbol{X}}}^{\text{T}}}{{{\boldsymbol{\omega}} }_{1}}$ ，求得一个向量 ${{\boldsymbol{\omega }}_1}$ ，使得 $\dfrac{1}{m} {{\boldsymbol{\omega}} _1}^{\text{T}}{{\boldsymbol{X}}}{{{\boldsymbol{X}}}^{\text{T}}}{{{\boldsymbol{\omega}} }_{1}}$ 得到最大化，最大值为 ${\boldsymbol{X}}{{\boldsymbol{X}}^{\text{T}}}$ 的最大特征值，向量 ${{\boldsymbol{\omega}} _1}$ 即为该特征值对应的特征向量，主成分分析后数据保留的成分比例为 ${{\displaystyle\sum_{i = 1}^{d'} {{\lambda _i}} }}\bigg/{{\displaystyle\sum_{i = 1}^d {{\lambda _i}} }}$ ，其中 $d'$ 为主成分个数。降维效果如图2所示。图2(a)中，星号为高维空间的样本点，而圆点是经过降维后的样本点。通过图像可以清晰地看出降维后仍保留了大量的主成分样本特征。图2(b)所示，样本标记可以清楚地看出不同特征在降维后仍保持原样本空间的数据，因此在算法中降维从而保留数据集中有效的信息，对滤波器学习的性能影响甚小。

图  2  PCA降维效果

Fig.  2  PCA dimension reduction effect diagram

下载: 全尺寸图片

4.   算法步骤

自适应时空正则化的相关滤波目标跟踪算法步骤如下：

1）初始帧建模：初始帧中的目标区域经过裁剪得到，使用STRCF算法中负高斯形状的权重对本文算法的空间正则项权重进行初始化。使用CNN提取特征，训练相关滤波器，建立目标模型和响应图模型。

2）目标定位：前一帧经过训练得到的相关滤波器，作用于当前帧的目标区域，提取特征的过程中，使用PCA方法进行降维处理，从而得到响应图，目标中心位置即响应值最大处。

3）权重更新：采用式（3）更新自适应空间正则化，并进行滤波器训练。

4）模型更新：对每一帧进行采样，得到局部像素的可信度，结合式（4）判定目标是否发生畸变，选择是否学习，采用式（6）动态更新目标模型和响应图模型。

5）目标跟踪：执行步骤2），针对下一帧图像进行滤波器训练并进行模型更新，经过算法迭代即循环跟踪，最终得到跟踪结果。

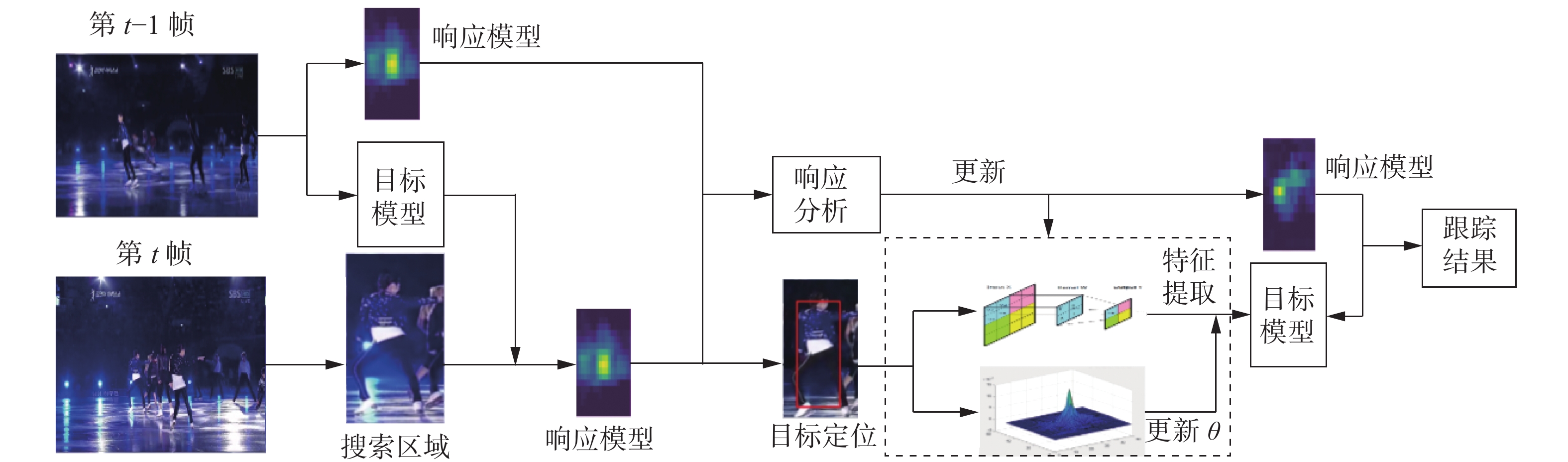
本文算法是基于时空正则化相关滤波算法进行改进，因此选用STRCF算法作为基础框架。本文算法总体框架如图3所示。

图  3  算法总体框架示意

Fig.  3  Overall schematic diagram of the algorithm

下载: 全尺寸图片

5.   实验验证与分析

本文所选用的编程软件为Python.3.10，实验操作系统为mac OS Mojave 10.14.6，处理器为2.9 GHz Intel Core i7 CPU，内存为8 GB。

5.1   自适应时空正则化的相关滤波目标跟踪算法的对比实验

为了客观并且有针对性地验证本文在STRCF基础上所提出的自适应时空正则化相关滤波目标跟踪算法框架的有效性，本文与6种同类型算法进行对比实验，分别是本文在目标函数中使用了预定义的基线算法STRCF（2018），以及引入高斯核提高计算速率并利用循环矩阵进行循环取样的KCF（2014）；提高样本数量但减小搜索区域得到BACF（2017）；引入时间正则项的SRDCF（2016）；对于区域进行约束，从而减少异常的ARCF（2019）；采用局部响应减少对时间和空间限制的AutoTrack（2020）。使用单次评价标准（OPE）综合衡量精确率、成功率和实时性等3项性能指标。在本实验中，搜索区域选定边长为正方形区域，使用ADMM算法进行迭代求解时，迭代次数为4；在对自适应空间正则项权重初始化时，参数 $\delta = 10$ ；在模型更新时，目标模型的学习参数 $\alpha $ 为0.02，响应图模型的阈值 $\varphi = 3\;000$ 。其余参数与本文基线算法STRCF的参数设置相同。

5.2   定性分析

图4为数据集OTB100中具有遮挡和形变（DEF）、光影变化和背景杂乱（BC）、快速运动（FM）等不同属性视频序列的跟踪结果，从图4中可以看出，与其他对比算法相比，本文算法的跟踪性能较优。

图  4  各种算法在部分序列上的跟踪结果对比

Fig.  4  Comparison of tracking results of various algorithms on partial sequences

下载: 全尺寸图片

1）遮挡和形变（DEF）。从图4（a）可以看到，在视频序列Girl2_1中，在第105帧之前各算法均可成功跟踪到目标，在第107~298帧从出现遮挡到遮挡完全消失的过程中，SRDCF、KCF、AutoTrack和ARCF算法均出现不同程度的漂移，到第358帧时，由于本文算法具有自适应的空间正则项，背景区域的权重随目标变化而降低，到第717帧仍可以进行有效跟踪。

2）光照变化（IV）和背景杂乱（BC）。背景杂乱指背景信息与目标信息具有相对较高的相似度，在进行信息特征提取时易混淆，滤波器无法确定目标位置，导致跟踪失败。从图4（b）可以看到，截止到第458帧，7种算法均可正确定位目标位置，但第458~509帧由于背景信息相似度高和光照变化的同时影响，导致SRDCF、KCF、AutoTrack、BACF和ARCF算法陆续跟踪失败。在第517~518帧时，只有本文算法可以继续跟踪，通过空间局部响应和全局响应的变化确定局部响应的可信度，有效地区分目标和背景信息，有较高的精确率。

3）快速运动（fast moition）。快速运动是目标在连续图像中运动区间大于20个像素。从图4（c）序列明显发现，面对跟踪目标快速运动时，采用单一通道的KCF算法无法准确定位目标位置。在第52~82帧时，STRCF出现漂移现象。到第92帧，BACF、ARCF虽然采用多通道特征，但由于跟踪目标在短时间内多次改变运动状态，没有判定滤波器是否更新的权重，导致跟踪失败。由于本文利用相邻两个峰值响应的相似度，通过峰值的移位实现自适应降低目标模型更新率的目的，使得该算法在快速运动的场景下具备较好的鲁棒性。

5.3   定量比较

7种算法在不同数据集上的对比结果如表1所示，加粗字体表示最优对比结果，倾斜和下划线字体表示次优对比结果。

从表1可以看出，在数据集OTB2013和OTB2015中，本文算法的成功率和精确率均高于STRCF算法，在数据集DTB70中，该数据集为无人机拍摄，本文算法的成功率和精确率也较高。本文算法是基于STRCF框架的算法，通过表2和表3可以看出其每种属性的精确率和成功率得分均高于STRCF算法。并且在数据集OTB2013和OTB2015上的平均精确率（0.87）和平均成功率（0.814）相比于STRCF算法的平均精确率（0.823）和平均成功率（0.787）分别提高了4.7%和12.7%。

为了更清晰、更全面地将本文算法与各主流算法的跟踪性能进行比较，表2、表3分别给出了包括本文在内的各种算法在数据集OTB100上各种属性的跟踪成功率与跟踪精确率得分。从表2和表3中可知，本文算法由于具有空间正则项，当跟踪目标与背景颜色相近或模糊时，自适应地分配背景区域的权重大小，实现精准跟踪；减少搜索区域时，因为本文通过空间局部响应和全局响应的变化确定局部响应的可信度，当目标自身形态发生变化或运动状态骤变时，可信度较低，滤波器将停止更新，避免迭代非必要信息导致跟踪失败。由于本文算法选取结合深度特征的提取方式，面对大量样本时，提取特征信息更准确，使得算法在处理光照变化、遮挡时有良好的处理效果。在处理超视野属性时，会成功将目标区域和背景区域区分开，所以本文算法的效果偏好。表4为不同算法在部分实验图像序列上的平均跟踪速度。结合表3，本文算法的整体跟踪效果与6种对比算法相比，能够在实时跟踪的前提下，具有较好的跟踪效果，并且在大多情况下均可以保持稳定的跟踪。

6.   结束语

根据固定的正则化项无法抑制非目标区域学习的问题，本文提出了一种具有空间自适应性的目标跟踪算法。通过对自适应空间正则项权重进行初始化，引入欧几里德范数，结合图像信息为目标和背景区域分配不同的权重，训练相关滤波器。利用局部响应变化表明了像素可信度，当外观变化较大时限制了局部相关滤波器的学习，得到更强壮的外观模型和响应图模型，从而动态地更新学习率。选择PCA来处理提取的CNN特征，确保图像信息的准确性和高效性。通过在不同数据集上与目前主流算法，从精确率、成功率和实时性3项性能指标综合分析可以发现本文算法具有较高的鲁棒性。目标跟踪作为计算机视觉领域中一个颇具挑战性的问题，还需要潜心钻研，下一步将围绕如何构建多个相关滤波器分别进行跟踪而展开深入研究。