Privileged LSSVM for classification and simultaneous importance identification of missing information on incomplete data
-
摘要: 针对直接移除缺失数据的样本可能会导致因样本数量规模的减少从而降低了分类性能的问题,本文基于同时处理缺失数据与构建模式分类模型的策略,提出使用特权信息学习(learning using privileged information, LUPI)的特权最小二乘支持向量机 (privileged least squares support vector machine, P-LSSVM),从而达到既能改进其分类性能,又能在保证无偏的情况下确定缺失特征的重要性。本文的基本思想是将完整数据的训练作为特权信息,以此来引导面向整个不完全数据的最小二乘支持向量机(least squares support vector machine, LSSVM)的学习,通过可加性核表达每个特征(含缺失特征)的重要性,推导完整数据的训练的特权信息,并以此构建P-LSSVM,运用所提出的留一交叉验证方法完成无偏的缺失特征重要性识别。实验结果表明,本文提出的方法不但在平均测试精度上优于对比算法,还能同时确定缺失特征的重要性。Abstract: While handling missing data classification tasks, the commonly-used removal strategy of missing data may perhaps degrade the classifier’s performance, due to very insufficient perfect data. Based on the strategy of processing missing data and constructing classification model simultaneously, we develop a novel privileged LSSVM (P-LSSVM), which learns using privilaged information. It can not only improve its classification performance, but also determines the importance of missing features without bias. The basic idea is to take the trained classifier of the available perfect data as the privileged information to guide the learning of LSSVM for the whole incomplete data, express the importance of each feature including missing features through the additivity kernel, then deduce the privilaged information of complete data after training, based on which P-LSSVM is constructed. Finally, the unbiased missing feature importance recognition is completed by the proposed leaving-one cross-validation method. Experimental results show that the proposed method can achieve better testing accuracies, with the importance identification of missing features.
-
在实际应用中,数据的缺失是一个难以避免的问题。它减少了样本数量,还可能会在研究中引入偏见[1]。数据缺失的原因多且难以有效避免。例如受访者出于保护隐私的目的拒绝提供某些信息、设备在某一时刻出现故障、调查时的失误导致的信息遗漏。缺失数据的修复通常比较困难,对缺失数据的不当处理可能导致分类性能下降。因此,以适当方式处理分类问题中缺失数据是一项基本要求[2]。
机器学习对缺失数据分类的研究一般分为2个部分:缺失数据的处理和分类模型的构建。在目前的机器学习中,已对样本的局部缺失做了很多研究[1]。通常会用3种类型的策略处理缺失数据。最直接的处理策略是直接丢弃不完整的数据,仅使用完整的样本构建分类模型[2]。这种策略会减少样本的数量,只适用于样本足够多且不完整样本占比例较小的情况。当丢失的数据不满足随机分布时,可能引入偏差[2-3]。另一种策略是模式基础法,估计输入数据的分布并将其用于模式分类。例如,使用期望最大化(expectation maximization, EM)算法[4]开发混合模型来估计数据分布,再使用贝叶斯决策理论来分类[5]。但估计值标准误差的计算[6],以及建模协变量联合分布的EM算法的蒙特卡罗实现[7]较复杂,使该方法的适用性差。第3种策略先通过使用估计值填充缺失数据来修复数据集,然后再使用修复后的数据建立分类模型。常用的填充方法有均值填充[1]和基于回归的填充[2]。均值填充法是使用具有完整数据的样本的特征平均值来填充缺失样本缺失的特征值。此方法没有考虑到数据集中样本的其他特征之间的相关性[1]。基于回归的填充使用具有完整数据的样本构建出的回归模型来估计特征的缺失值。该方法高度依赖于数据的质量[2-3]。此外,还可以通过使用机器学习技术构建预测模型来估计缺失值。例如k最邻近填充(k-nearest neighbor, KNN)[8]和神经网络[9]。其中最常被使用的方法是KNN,从完整样本中选出距离含缺失数据的样本最近的k个样本,用它们来估算出缺失的数据。KNN的性能总体上优于其他机器学习方法,如决策树和均值填充方法[3]。在DNA研究中,KNN具有优于均值填充和基于奇异值分解填充的性能[10]。然而,KNN的性能依赖于k值等参数的设置,而这些参数难以使用理论方法确定。
近年来,在处理缺失数据的同时构建模式分类模型的相关研究工作正在发展,不同于前述策略中先处理缺失数据再建立模型的思路,该策略选择将处理缺失数据与构建模式分类模型同时进行。例如,设计神经网络集成用于不完整数据的分类[11-13]。从含有缺失数据的数据集中生成多个完整的子数据集,将其作为神经网络的训练数据集[14]。此外,还有使用模糊规则分类器处理缺失数据的模糊方法,可以通过使用模糊C均值算法[15]实现。该策略最大限度地利用了数据集中的信息,在尽可能地保留原始数据特性的同时,无需对数据分布做任何假设。越来越多的研究用该策略提高模型的性能[1]。
基于教学中教师的角色对学生学习起到的重要作用,Vapnik等[16]提出了使用特权信息学习范式(learning using privileged information, LUPI)方法。LUPI通过提供仅在训练阶段可用的信息帮助提高模型在测试阶段的表现。经典的使用特权信息学习支持向量机(learning using privileged information support vector machine, SVM+),若在校正空间获得了较小的误差,在决策空间中也会得到较小的误差,使用特权信息所定义的校正函数来计算支持向量机(support vector machine, SVM)中的松弛变量[16]。利用这一特性,将LUPI引入到此策略中,将完整数据的训练作为特权信息,保证训练样本中误差和特权信息误差的相似,能得到由不完整特征的局部数据缺失所带来的对整体分类性能的影响。然而,目前还没有将LUPI引入这种策略的研究。大多数机器学习方法侧重于提高缺失数据的总体性能,但很少关注数据集中特征的缺失数据对分类性能的影响。如果能识别其影响,慎重地对待影响更大的特征,依此为数据收集过程提供指导,可以促进数据质量的改善[2]。基于在处理缺失数据的同时构建分类模型的思路,本文提出一种新的引入LUPI的特权最小二乘支持向量机 (privileged least squares support vector machine, P-LSSVM)来处理数据缺失问题[17-18]。将LSSVM与可加性高斯核相结合,用完整数据的训练作为特权信息引导面向含有缺失数据的最小二乘支持向量机(least squares support vector machine, LSSVM)的学习。P-LSSVM可同时完成对不完整样本的分类和对缺失数据特征无偏的重要性识别。P-LSSVM继承了LSSVM的理想特性,即通过最小化基于LSSVM的目标函数,可以得到对应凸优化问题的解[18-19]。
在实验部分,将P-LSSVM与使用了前3种策略处理缺失数据的LSSVM在公开数据集上进行了比较,实验结果证明了P-LSSVM的有效性。此外还介绍了使用P-LSSVM对German数据集进行的案例研究,强调了该方法对该实际应用的贡献。
本文的主要贡献归纳如下:
1)开展了将LUPI引入在处理缺失数据的同时构建模式分类模型这一处理数据缺失策略的研究。
2)提出了一种新的引入了LUPI的可加性LSSVM模型,可直接用于具有缺失数据的数据集的分类任务,不需要提前对不完整数据集进行处理。
3)通过留一交叉验证无偏评估出模型构建过程中特征缺失数据造成的分类误差,提供了其相关重要性,可为数据收集过程提供引导,改善数据质量。
4)在公开数据集的实验结果证明了P-LSSVM的有效性。并针对使用P-LSSVM对指导数据收集进行了案例研究。
1. 相关模型与学习范式
1.1 最小二乘支持向量机
LSSVM将SVM中的不等式约束修改为等式约束,将原来的解二次规划问题变成了解线性方程组的问题,方便了对拉格朗日乘子的求解[17]。
标准LSSVM模型为
$$ \begin{gathered}\underset{{\boldsymbol{w}},{\boldsymbol{b}},{\boldsymbol{e}}}{\mathrm{min}}J({\boldsymbol{w}},{\boldsymbol{e}})=\dfrac{1}{2} \left\langle {\boldsymbol{w}},{\boldsymbol{w}} \right\rangle +\dfrac{\lambda }{2}{\displaystyle \sum _{i=1}^{n}{e}_{i}^{2}}\\ {\rm{s.t.}}\text{ }{y}_{t}= \left\langle {\boldsymbol{w}},\phi ({{\boldsymbol{x}}}_{t}) \right\rangle +{\boldsymbol{b}}+{e}_{t},t=1,2,\mathrm{\cdots},n\text{ }\end{gathered} $$ (1) 式中:
$ {\boldsymbol{w}} $ 、$ {\boldsymbol{b}} $ 为样本特征空间的权重向量和偏置向量;$ \phi (\cdot) $ 为样本特征空间上的由核函数所诱导的特征映射函数,用于非线性可分的训练样本;$ {e_t} $ 为第t个样本$ {{{{\boldsymbol{x}}}}_t} $ 的误差变量,用来处理可能出现特异点的问题;正实数$ \lambda $ 为正则化参数,通过在训练误差和模型复杂度之间进行折衷,可以使函数具有更好的泛化能力[17]。对式(1)求解即可得到LSSVM的决策函数。1.2 可加性核
在本文中,为了能够使模型可以学习包含了缺失信息的样本数据,采用可加性核。可加性核能单独的考虑每一维特征产生的影响,使用在各特征上的影响的组合衡量2个样本的关系。可加性核在多种框架下得到应用。Maji等[20]证明了利用可加性核SVM建立分类器,其运行时和内存复杂度与支持向量的数量无关。在运行时间相同的情况下,与线性SVM相比,可加性核SVM可以显著提高各种任务的精度,使其适用于大规模识别或实时检测任务。Demir等[21]在遥感任务中引入了适合直方图特征的可加性核,提出了基于直方图特征和可加性核SVM的快速准确的分类方法。王旭凤[22]使用随机梯度下降(stochastic gradient descent,SGD)以及一些改进的SGD方法包括异步随机梯度下降(asynchronous stochastic gradient descent , ASGD)、随机方差减少梯度下降(stochastic variance reduced gradient, SVRG)和Katyusha算法来处理基于可加性核的SVM分类问题。Pelckman等[18]将可加性核引入LSSVM,提出分量LSSVM,用于建立由非线性分量和组成的可加性模型。
可加性核定义为
$$ k({{{{\boldsymbol{x}}}}_i},{{{{\boldsymbol{x}}}}_j}) = \sum\limits_{l = 1}^d {{k_g}(x_j^g,x_i^g)} $$ (2) 式中:
$ {{{{\boldsymbol{x}}}}_i} $ 、$ {{{{\boldsymbol{x}}}}_j} $ 为数据集中的任意2个样本,$ d $ 为样本的特征数量,${k_g}({\boldsymbol{*}},{\boldsymbol{*}})$ 为在样本的第$ g $ 维特征上使用的核函数。相比较于传统的核函数,在模型上应用可加性核,不论特征是否具有缺失值,都可以很容易地用于计算核函数的相应值。1.3 特权信息学习
基于老师往往在学习过程中发挥重要作用这一观察,Vapnik等[16]提出了使用特权信息学习的算法。在实际应用中特权信息是常见且有用的。Xue等[23]使用特权信息来控制决策误差,设计出可以有效对抗数据中噪声的鲁棒的SVM+算法。Xu等[24]基于LUPI设计了一种新颖的距离度量学习算法,从图像中分别提取视觉特征和深度特征并将深度特征视为特权信息,改进RGB图像中的人脸验证和人员重新识别。Pal等[25]从数据集中提取特权信息,将特权信息引入校正函数,提出了使用特权信息改进型双支持向量机(improved twin support vector machine using privilege information, I-TWSVMPI)。
本文基于LUPI,以LSSVM为基础,提出了能将缺失数据的处理和分类模型的构建同时进行的特权最小二乘支持向量机(privileged least squares support vector machine, P-LSSVM),可用于缺失数据的分类问题以及缺失数据影响识别问题。
2. P-LSSVM
2.1 数据表示
在引入LUPI的LSSVM模型中,训练数据集的形式和SVM+类似。定义
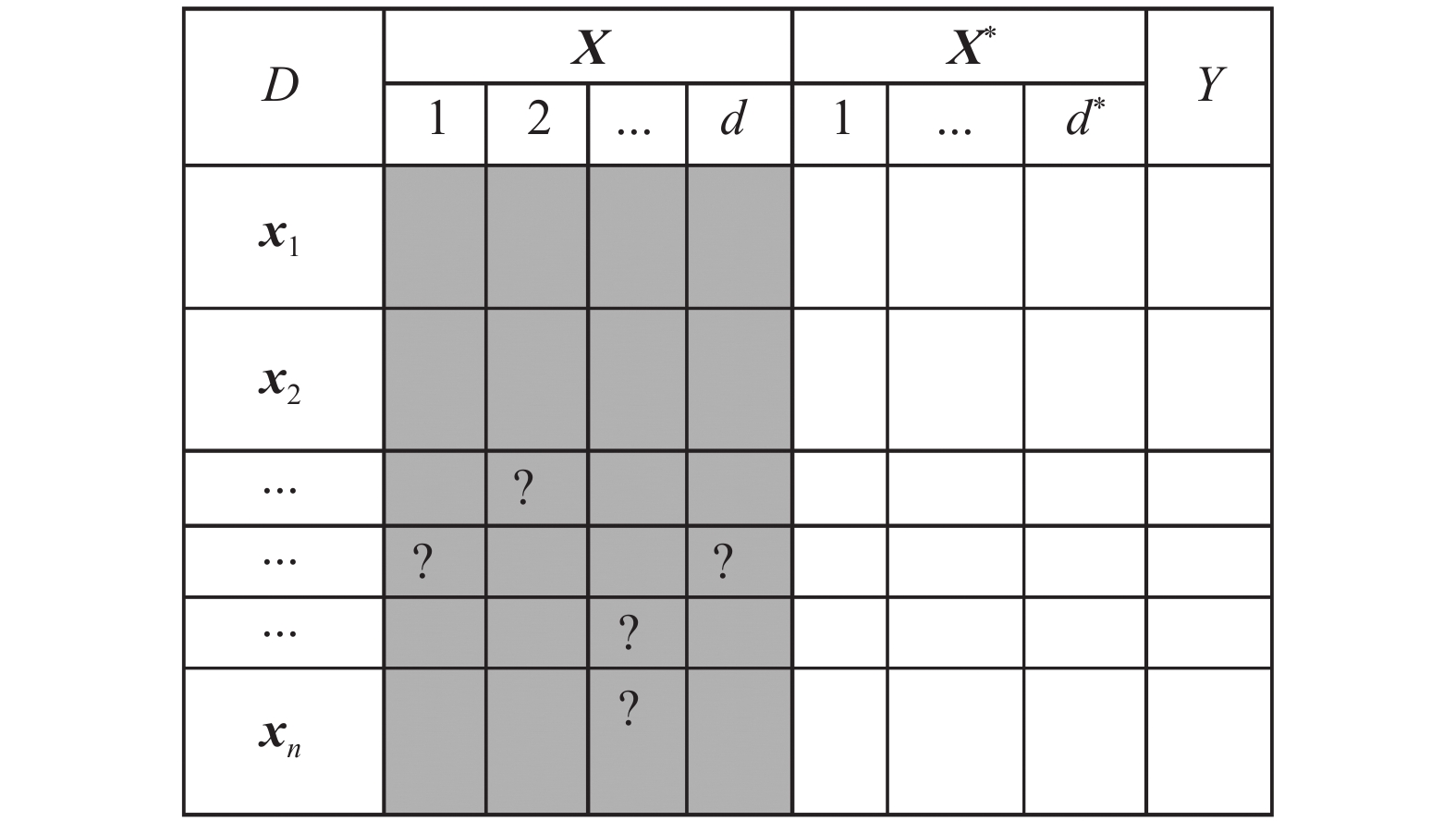
$ D $ 是一个数据集,它具有n个样本和n个样本对应的特权信息,样本有$ d $ 个特征,样本对应的特权信息具有${d*}$ 个特征:$$ \{ ({{{{\boldsymbol{x}}}}_{\mathbf{1}}}{{,{\boldsymbol{x}}}}_1^*,{y_1}),({{{{\boldsymbol{x}}}}_2},{{{\boldsymbol{x}}}}_2^*,{y_2}),\cdots,({{{{\boldsymbol{x}}}}_n},{{{\boldsymbol{x}}}}_n^*,{y_n})\} $$ 式中:第
$ i $ 个样本的特征向量标记为${{{{\boldsymbol{x}}}}_i} = ({{{\boldsymbol{x}}}}_i^1,{{{\boldsymbol{x}}}}_i^2,\cdots, {{{\boldsymbol{x}}}}_i^d)$ ,对应的特权信息标记为${{{\boldsymbol{x}}}}_i^* = ({{{\boldsymbol{x}}}}{_i^{*1}},{{{\boldsymbol{x}}}}_i^{*2},\cdots,{{{\boldsymbol{x}}}}{_i^{*d*}})$ ,其对应的标签为$ {y_i} \in \{ + 1, - 1\} $ ,$i = 1,2,\cdots, n$ 。对于一个包含了缺失数据的数据集,定义$ d $ 为含有缺失数据的特征的个数,可以定义$ {d*} $ 为数据集中完整特征的个数,将原数据集$ D $ 划分为2部分。即原数据集$ D $ 的只含有不完整特征的一个子集${{{\boldsymbol{X}}}} = \{ {{{\boldsymbol{x}}}}_i^1,{{{\boldsymbol{x}}}}_i^2,\cdots,{{{\boldsymbol{x}}}}_i^d| i = 1,2,\cdots,n\}$ 和原数据集$ D $ 的子集${{{{\boldsymbol{X}}}}^{{*}}} = \{ {{{\boldsymbol{x}}}}{_{i}^{*1}},{{{\boldsymbol{x}}}}{_i^{*2}},\cdots, {{{\boldsymbol{x}}}}{_i^{*d*}}| i = 1,2,\cdots,n\}$ ,其中只含有完整信息的特征。图1是对数据集$ D $ 的描述,标记“?”表示此处的数据缺失了。2.2 P-LSSVM算法
在SVM+中使用特权信息定义的校正函数来计算SVM中的误差变量。保证了训练样本中误差以特权信息为上界,即对于LUPI方法,特权信息对决策模型的建立进行了引导,如果在校正空间获得了较小的损失,那么在决策空间中也应该得到较小的损失[23]。在LSSVM中引入LUPI,将完整数据的训练作为特权信息,利用特权信息对LSSVM进行引导,保证不完整特征中误差和特权信息误差的相似,反映出由特征的局部数据缺失所带来的对整体分类性能的影响。在LSSVM中引入LUPI得到的使用特权信息来引导LSSVM中误差变量e的LSSVM+模型,可得到其目标函数和约束为
$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{w}},{{\boldsymbol{w}}^*},{\boldsymbol{b}},{{\boldsymbol{b}}^*}} J({{{\boldsymbol{w}}}},{{{{\boldsymbol{w}}}}^*},{{{\boldsymbol{e}}}},{{{\boldsymbol{\xi}} }}) = \frac{1}{2} \left\langle {{{\boldsymbol{w}}}},{{{\boldsymbol{w}}}} \right\rangle + \frac{\rho }{2} \left\langle {{{{\boldsymbol{w}}}}^*},{{{{\boldsymbol{w}}}}^*} \right\rangle + \\ \frac{\lambda }{2}\sum\limits_{i = 1}^n {e_i^2 + \frac{C}{2}\sum\limits_{i = 1}^n {{{({e_i} - {\xi _i})}^2}} } \\ {\rm{s.t.}}\;\;{{{y}}_t} = \left\langle {{{\boldsymbol{w}}}},\phi ({{{{\boldsymbol{x}}}}_t}) \right\rangle + b + {e_t} \\ {\xi _t} = \left\langle {{{{\boldsymbol{w}}}}^*},\psi ({{{\boldsymbol{x}}}}_t^*) \right\rangle + {b^*} \\ t = 1,2,\cdots,n \\ \end{gathered} $$ (3) 式中:
${\boldsymbol{w}} $ 、$ b $ 和${{{{\boldsymbol{w}}}}^*}$ 、$ {b^*} $ 分别为样本特征空间和特权信息特征空间的权重向量与偏置;$\phi (·)$ 和$\psi (·)$ 分别为2空间上由核所诱导的特征映射函数。$ \lambda $ 和C为正则化参数;$〈 {{{{\boldsymbol{w}}}}^*},{{{{\boldsymbol{w}}}}^*} 〉$ 用来限制校正空间的容量;$ \rho $ 为非负权衡参数。在本文提出的P-LSSVM模型中,定义Vg为由于第$ g $ 维特征数据的缺失所导致的分类误差上界,$g = 1,2,\cdots, d$ 。在构建分类器时,可以同时使用留一交叉验证将Vg求出。定义$ I_g^i $ 为$$ {I}_{g}^{i}=\bigg\{\begin{array}{l}1,\text{ }{{\boldsymbol{x}}}_{i}的第g个特征({{{x}}}_{g}^{i})的值缺失\\ 0,\text{ }其他\end{array}\text{ } $$ (4) 那么对于第
$ i $ 个样本,公式$\displaystyle\sum\limits_{g = 1}^d {{V_g}I_g^i}$ 给出了所有缺失数据特征所导致的误差之和,即总分类误差的上界。$ {V_g} $ 的绝对值越大,说明由第$ g $ 维特征数据缺失造成的误差越大,第$ g $ 维特征对分类性能的影响就越大,第$ g $ 维特征也就越重要。在式(3)中引入
$ {V_g} $ ,可得:$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{w}},{{\boldsymbol{w}}^*},b,{b^*}} J({{{\boldsymbol{w}}}},{{{{\boldsymbol{w}}}}^*},{{{\boldsymbol{e}}}},{{{\boldsymbol{\xi}} }}) = \frac{1}{2} \left\langle {{{\boldsymbol{w}}}},{{{\boldsymbol{w}}}} \right\rangle + \frac{\rho }{2} \left\langle {{{{\boldsymbol{w}}}}^*},{{{{\boldsymbol{w}}}}^*} \right\rangle + \\ \frac{\lambda }{2}\sum\limits_{i = 1}^n {e_i^2 + \frac{C}{2}\sum\limits_{i = 1}^n {{{({e_i} - {\xi _i})}^2}} } \\ {\rm{s.t.}}\;\;{{{y}}_t} = \left\langle {{{\boldsymbol{w}}}},\phi ({{{{\boldsymbol{x}}}}_t}) \right\rangle + b + {e_t} + \sum\limits_{g = 1}^d {{V_g}I_g^t} \\ {\xi _t} = \left\langle{{{{\boldsymbol{w}}}}^*},\psi ({{{\boldsymbol{x}}}}_t^*) \right\rangle + {b^*} \\ t = 1,2,\cdots,n \end{gathered} $$ (5) 式(5)在数学上等价于:
$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{w}},{{\boldsymbol{w}}^*},b,{b^*}} J({{{\boldsymbol{w}}}},{{{{\boldsymbol{w}}}}^*},{{{\boldsymbol{e}}}},{{{\boldsymbol{\xi}} }}) = \frac{1}{2} \left\langle{{{\boldsymbol{w}}}},{{{\boldsymbol{w}}}} \right\rangle + \frac{\rho }{2} \left\langle {{{{\boldsymbol{w}}}}^*},{{{{\boldsymbol{w}}}}^*} \right\rangle + \\ \frac{\lambda }{2}\sum\limits_{i = 1}^n {{{\left({e_i} - \sum\limits_{g = 1}^d {{V_g}I_g^i} \right)^2}} + \frac{C}{2}\sum\limits_{i = 1}^n {{{\left({e_i} - \sum\limits_{g = 1}^d {{V_g}I_g^i} - {\xi _i}\right)^2}}} } \\ {\rm{ s.t.}}\;\;{{{y}}_t} = \left\langle {{{\boldsymbol{w}}}},\phi ({{{{\boldsymbol{x}}}}_t}) \right\rangle + b + {e_t} \\ {\xi _t} = \left\langle {{{{\boldsymbol{w}}}}^*},\psi ({{{\boldsymbol{x}}}}_t^*) \right\rangle + {b^*} \\ t = 1,2,\cdots,n \end{gathered} $$ (6) 不论特征是否具有缺失值,可加性核都能计算出核函数的值。在算法中使用可加性核函数,使算法具有单独计算各维度所带来影响的能力。这样本文提出的算法就可以分别对每一维特征上由于数据缺失所带来的误差进行统计。
$\phi ({{{{\boldsymbol{x}}}}_i}) = (\tilde \phi (x_1^i),\tilde \phi (x_2^i),\cdots,\tilde \phi (x_d^i))$ ,可加性核中$ \tilde \phi (x_g^i) $ 是对样本$ {{\boldsymbol{x}}_i} $ 第$ g $ 个特征进行映射的函数。采用可加性核的样本核函数矩阵${{{\boldsymbol{\varOmega}} }}$ 定义为$$\begin{gathered}{\boldsymbol{\varOmega}} _j^i = \phi ({{{{\boldsymbol{x}}}}_i})\phi {({{{{\boldsymbol{x}}}}_j})^{\rm{T}}} = \sum\limits_{g = 1}^d {\tilde \phi (x_g^i)\tilde \phi (x_g^j) = \sum\limits_{g = 1}^d {{k_g}(x_g^i,x_g^j)} } \end{gathered}$$ (7) 类似的,特权信息的核函数矩阵
${{{{\boldsymbol{\varOmega}} }}^*}$ 为$$\begin{gathered}{\boldsymbol{\varOmega}}_j^{i*} = \psi ({{{{\boldsymbol{x}}}}_i^*})\psi {({{{{\boldsymbol{x}}}}_j^*})^{\rm{T}}} = \sum\limits_{g = 1}^{{d^*}} \tilde {\psi} (x_g^{i*})\tilde {\psi} (x_g^{j*}) = \sum\limits_{g = 1}^{{d^*}} {{k_g}(x_g^{i*},x_g^{j*}) }\end{gathered} $$ (8) 其中,
$$ {k}_{g}({x}_{g}^{i},{x}_{g}^{j})=\left\{\begin{split} &{\tilde{k}}_{g}({x}_{g}^{i},{x}_{g}^{j}),{x}_{g}^{i}和{x}_{g}^{j}都有值\\ &\text{0},其他\end{split} \right. $$ (9) 式中
$ {\tilde k_g}(x_g^i,x_g^j) $ 为核函数。在本文中采用高斯核函数${\tilde k_g}(x_g^i,x_g^j)={\rm{exp}}(-(x_g^j-x_g^i)^2/2 \sigma_g{^2}), \;g=1, 2,\cdots, d$ 。其中$ {\sigma _g} $ 是应用在第$ g $ 维特征的核函数参数。在去除训练数据集中由缺失特征所导致的总分类误差后,式(6)原问题的优化目标本质上可以看作是最小化所有完整特征所导致的总分类误差。即当训练数据集的所有样本中都没有缺失值时,任意的
$ {{{\boldsymbol{I}}}} = 0 $ ,式(6)会简化为式(3)中的LSSVM+模型。为了得到式(6)的解,令
$$ f({{{\boldsymbol{x}}}}) = \sum\limits_{t = 1}^n {{\alpha _t}( \left\langle {{{\boldsymbol{w}}}},\phi ({{{{\boldsymbol{x}}}}_t}) \right\rangle + b + {e_t} - {y_t})}$$ (10) $$g({{{{\boldsymbol{x}}}}^ * }) = \sum\limits_{t = 1}^n {{\beta _t}( \left\langle {{{{\boldsymbol{w}}}}^ * },\psi ({{{\boldsymbol{x}}}}_t^*) \right\rangle + {b^ * } - {\xi _t})} $$ (11) 构造其拉格朗日函数为
$$ L\left( {{{{\boldsymbol{w}}}},{\boldsymbol{w}^*},b,{b^ * },{{{\boldsymbol{\alpha}} }},{{{\boldsymbol{\beta}} }}} \right) = J({{{\boldsymbol{w}}}},{{{{\boldsymbol{w}}}}^ * },b,{b^ * })\; - \;f({{{\boldsymbol{x}}}})\; - \;g({{{{\boldsymbol{x}}}}^ * }) $$ (12) 通过引入拉格朗日乘子
${\alpha _t},{\beta _t},t = 1,2,\cdots,n$ ,根据KKT条件,可以得:$$ \left\{ \begin{gathered} \frac{{\partial L}}{{\partial {{{\boldsymbol{w}}}}}} = 0 \to {{{\boldsymbol{w}}}} = \sum\limits_{i = 1}^n {{\alpha _i}\phi ({{{{\boldsymbol{x}}}}_i})\quad\quad\quad\quad\quad\quad\qquad\qquad\;{\text{ (13)}}} \\ \frac{{\partial L}}{{\partial b}} = 0 \to \sum\limits_{i = 0}^n {{\alpha _i}} = 0\quad\quad\quad\quad\quad\qquad\qquad\qquad\quad\;\;{\text{ (14)}} \\ \frac{{\partial L}}{{\partial {{\boldsymbol{w}}^*}}} = 0 \to {{\boldsymbol{w}}^*} = \sum\limits_{i = 1}^n {{\beta _i}\psi ({{{\boldsymbol{x}}}}_i^*)\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;{\text{ (15)}}} \\ \frac{{\partial L}}{{\partial {b^*}}} = 0 \to \sum\limits_{i = 0}^n {{\beta _i}} = 0\quad\quad\quad\quad\quad\qquad\qquad\qquad\quad\;{\text{ (16)}} \\ \frac{{\partial L}}{{\partial {e_t}}} = 0 \to {e_t} = \frac{1}{\lambda }({\alpha _t} - {\beta _t}) + \sum\limits_{g = 1}^d {{V_g}I_g^t\quad\quad\quad\quad\quad\quad\;\;{\text{ (17)}}} \\ \frac{{\partial L}}{{\partial {\xi _t}}} = 0 \to {\xi _t} = \frac{1}{\lambda }{\alpha _t} - \left(\frac{1}{\lambda } + \frac{1}{C}\right)\;{\beta _t}\quad\quad\quad\quad\quad\quad\quad\;\;{\text{ (18)}} \\ \frac{{\partial L}}{{\partial {\alpha _t}}} = 0 \to \left\langle {{{\boldsymbol{w}}}},\phi ({{{{\boldsymbol{x}}}}_t}) \right\rangle + b + {e_t} - {y_t} = 0\quad\quad\quad\quad\quad\;\;\;\;{\text{ (19)}} \\ \frac{{\partial L}}{{\partial {\beta _t}}} = 0 \to \left\langle {{{{\boldsymbol{w}}}}^*},\psi ({{{\boldsymbol{x}}}}_t^*) \right\rangle + {b^*} - {\xi _t} = 0\quad\quad\quad\quad\quad\quad\;\;\;{\text{ (20)}} \\ t = 1,2,\cdots,n \\ \end{gathered} \right. $$ 结合式(13)、(17)和(19),消去
$ {{{\boldsymbol{w}}}}$ 和${e_t} $ , 结合式(15)、(18)和(20),消去$ {{{{\boldsymbol{w}}}}^*},{\xi _t} $ 后,得到线性等式:$$ \begin{gathered} \sum\limits_{i = 1}^n {\sum\limits_{g = 1}^d {{\alpha _i}\phi (x_g^i)\phi (x_g^t)} } + b + \left(\frac{1}{\lambda }\left({\alpha _t} - {\beta _t}\right) + \sum\limits_{g = 1}^d {{V_g}I_g^t} \right) = {y_t} \end{gathered} $$ $$ \begin{gathered} \frac{1}{\rho }\sum\limits_{i = 1}^n {\sum\limits_{g = 1}^{{d^*}} {{\beta _i}\psi (x{{_g^i}^*})\psi (x{{_g^t}^*})} } + {b^*} -\left(\frac{1}{\lambda }{\alpha _t} - \left(\frac{1}{\lambda } + \frac{1}{C}\right){\beta _t}\right) =0 \\ {{t = 1,2,}}\cdots{{,n}} \end{gathered}$$ (22) 结合式(14)、(16)可进一步将式(21)和式(22)写成紧凑矩阵形式:
$$\begin{gathered} \left[{\begin{array}{*{20}{c}} {{{{\boldsymbol{\varOmega}} }} + \dfrac{1}{\lambda }{{{\boldsymbol{E}}}}}&{\boldsymbol{1}}&{ - \dfrac{1}{\lambda }{{{\boldsymbol{E}}}}}&{{\boldsymbol{0}}} \\ {{{\boldsymbol{1}}^{\rm{T}}}}&{{0}}&{{{\boldsymbol{0}}^{\rm{T}}}}&0 \\ { - \dfrac{1}{\lambda }{{{\boldsymbol{E}}}}}&{\boldsymbol{0}}&{\dfrac{1}{\rho }{{{{\boldsymbol{\varOmega}} }}^{\mathbf{*}}} + \left(\dfrac{1}{\lambda } + \dfrac{1}{C}\right){{{\boldsymbol{E}}}}}&{\boldsymbol{1}} \\ {{{\boldsymbol{0}}^{\rm{T}}}}&0&{{{\boldsymbol{1}}^{\rm{T}}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\alpha}} }} \\ b \\ {{{\boldsymbol{\beta}} }} \\ {{b^*}} \end{array}} \right] = \\ \left[\begin{array}{*{20}{c}} {{{\boldsymbol{y}}}} - \displaystyle \sum\limits_{g = 1}^d {{V_g}{{{\boldsymbol{I}}}}_g^{}} \\ 0 \\ {\mathbf{0}} \\ 0 \end{array} \right]\end{gathered}$$ (23) 式中:
$ {{{\boldsymbol{\alpha }}}} $ 、${{{\boldsymbol{\beta}} }} $ 是拉格朗日乘子组成的向量,${{{\boldsymbol{\alpha}} }} = ({a_1}, {a_2},\cdots, {a_n})^{\rm{T}}$ ,${{{\boldsymbol{\beta}} }} = {({\beta _1},{\beta _2},\cdots,{\beta _n})^{\rm{T}}}$ ;${{{\boldsymbol{y}}}}$ 是样本的标签所组成的向量,${{{\boldsymbol{y}}}} = {({y_1},{y_2},\cdots,{y_n})^{\rm{T}}}$ ;${\boldsymbol{1}} = (1, 1,\cdots, 1)^{\rm{T}}$ ;${\boldsymbol{0}} = (0, 0,\cdots, 0)^{\rm{T}}$ ;${{{{\boldsymbol{I}}}}_g}$ 是矩阵${{{\boldsymbol{I}}}}$ 的第$ {{g}} $ 列,${{{{\boldsymbol{I}}}}_g} = {(I_g^1,I_g^2,\cdots,I_g^n)^{\rm{T}}}$ ;${{{\boldsymbol{E}}}}$ 是单位矩阵;${{{\boldsymbol{\varOmega}} }}$ 和${{{{\boldsymbol{\varOmega}} }}^{\mathbf{*}}}$ 分别是样本特征空间和特权特征空间的核函数矩阵,可用式(7)、(8)求出。$$ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\alpha}} }} \\ b \\ {{{\boldsymbol{\beta}} }} \\ {{b^*}} \end{array}} \right] = {{{\boldsymbol{P}}}}\left[ \begin{array}{*{20}{c}} {{{\boldsymbol{y}}}} - \displaystyle \sum\limits_{g = 1}^d {{V_g}{{{\boldsymbol{I}}}}_g^{}} \\ 0 \\ {\mathbf{0}} \\ 0 \end{array} \right] $$ (24) 式中:
${{{\boldsymbol{P}}}} = {{{{\boldsymbol{Q}}}}^{ - 1}}$ ,${{{\boldsymbol{Q}}}}$ 是式(23)中等号左侧的第1项。依据式(24),若已知所有
$ {V_g} $ 的值,便可求出${{{\boldsymbol{\alpha}} }}$ 、 $b $ ,进而可根据式(13)重构权重向量${{{\boldsymbol{w}}}}$ 。最后可得到P-LSSVM的决策函数为$$ y({{{{\boldsymbol{x}}}}_t}) = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{g = 1}^d {{\alpha _i}} } {k_g}(x_g^i,x_g^t) + b + \displaystyle\sum\limits_{g = 1}^d {{V_g}I_g^t} $$ (25) 式中:
${{{{\boldsymbol{x}}}}_t}$ 是输入的未知样本,$y({{{{\boldsymbol{x}}}}_t})$ 是决策函数的预测值。如果未知样本${{{{\boldsymbol{x}}}}_t}$ 是完整的,那么有$\displaystyle\sum_{g = 1}^d {{V_g}I_g^t} = 0$ ,决策函数就会被简化。令
${\boldsymbol{V}}\text{=}({V}_{1},{V}_{2},\mathrm{\cdots},{V}_{d})$ ,若要得到式(25)中的决策函数,需要得到${{{\boldsymbol{V}}}}$ 的值。本文采用留一交叉验证这一无偏估计方法通过迭代来求出${{{\boldsymbol{V}}}}$ 的最优值。定义:
$$ {\left[ { {{{{{{{\boldsymbol{\alpha}}}} }}'}^{\rm{T}}}\;\;{{{{b}}'}}\;\;{{{{{{{\boldsymbol{\beta}}}} }}'}^{\rm{T}}}\;\;{{{{b}}^*}'} } \right]^{\rm{T}}} = P{\left[ {{{{{{{\boldsymbol{y}}}}}}^{\rm{T}}}}\;\;0\;\;{{{\boldsymbol{0}}^{\rm{T}}}}\;\;0 \right]^{\rm{T}}} $$ (26) $$ {\left[ { {{{{{{{\boldsymbol{\alpha}}}} }}''}^{\rm{T}}}\;\;{{{\boldsymbol{b}}_g''}}\;\;{{{{{{{\boldsymbol{\beta}}}} }}''}^{\rm{T}}}\;\;{{{\boldsymbol{b}}_g^*}''} } \right]^{\rm{T}}} = P{\left[ { {{I_g}^{\rm{T}}}\;\;0\;\;{{{\boldsymbol{0}}^{\rm{T}}}}\;\;0 } \right]^{\rm{T}}}$$ (27) 由式(24)可得:
$$ {{{\boldsymbol{\alpha}} }} = {{{{\boldsymbol{\alpha}} }}'} - \sum\limits_{g = 1}^d {{{{{{V}}}}_g}} {{{\boldsymbol{\alpha}} }}_g'' $$ (28) 结合式(28)和决策函数式(25),有:
$$\begin{gathered} y({x_t}) = \sum\limits_{i = 1}^n {\sum\limits_{l = 1}^d {\left({{a}}_i'- \sum\limits_{g = 1}^d {{{{{{V}}}}_g}{{{\boldsymbol{\alpha}} }}_{gi}''} \right)} } {k_l}(x_l^i,x_l^t) + b + \sum\limits_{g = 1}^d {{V_g}I_g^t} \end{gathered}$$ (29) 从式(28)可以看出,
${{{\boldsymbol{\alpha }}}}$ 和${{{\boldsymbol{V}}}}$ 存在线性关系,只要确定了一组${{{\boldsymbol{V}}}}$ 的值,${{{\boldsymbol{\alpha }}}}$ 的值也可被确定。随后便可使用式(29)作为决策函数求出样本${{{{\boldsymbol{x}}}}_t}$ 的预测值${\tilde y_t} = y({{{{\boldsymbol{x}}}}_t})$ 。$ {y_t} $ 是样本${{{{\boldsymbol{x}}}}_t}$ 的标签值,对于在训练集中所有的样本,能使$ {\tilde y_t}{y_t} $ 取正值的值,即为${{{\boldsymbol{V}}}}$ 的最优值。但是如果在优化${\boldsymbol {V}}$ 时只考虑到$ {\tilde y_t}{y_t} $ 的正负,可能产生具有许多局部极小值的非凸解。因此,本文中使用了一种类似于hinge损失的损失函数:$$ \begin{gathered} l({{\tilde y}_t},{y_t}) = {\left| {1 - {{\tilde y}_t}{y_t}} \right|_ + } = \\ {\left| {1 - {y_t}\left(\sum\limits_{i = 1}^n {\sum\limits_{l = 1}^d {\left({{{\boldsymbol{\alpha}} }}_i' - \sum\limits_{g = 1}^d {{{{{{V}}}}_g}{{{\boldsymbol{\alpha}} }}_{gi}''} \right)} } {k_l}(x_l^i,x_l^t) + b + \sum\limits_{g = 1}^d {{V_g}I_g^t} \right)} \right|_ + } \end{gathered} $$ (30) 式中
$ {\left| l \right|_ + }{\text{ = max\{ 0,}}l{\text{\} }} $ 。式(30)中的损失函数给出了误分类损失的凸上界,它更偏好可使$ {\tilde y_t} $ 绝对值不小于1且与$ {y_t} $ 同号的解。最后可以得到目标函数为
$$ \displaystyle\sum\limits_{t = 1}^n {l({{\tilde y}_t},{y_t})\;\;{\text{ s}}{\text{.t}}{\text{. }}{{\left\| {{{\boldsymbol{V}}}} \right\|}_2}} \leqslant B $$ (31) 在约束条件中,B是一个常数,
$ {\left\| · \right\|_2} $ 是施加在向量${{{\boldsymbol{V}}}}$ 上的L2范数,用来保证${{{\boldsymbol{V}}}}$ 的解存在。本文使用次梯度投影法实现对${{{\boldsymbol{V}}}}$ 的优化。P-LSSVM的伪代码如下所示。先初始化,然后通过次梯度投影法实现对
${{{\boldsymbol{V}}}}$ 的优化,在确定$ {\boldsymbol{V}} $ 的最优值后,可以方便地计算出P-LSSVM的${{{\boldsymbol{\alpha}} }}$ 和$ b $ ,最后可得到P-LSSVM的决策函数$y({{{\boldsymbol{x}}}})$ 。P-LSSVM算法
输入
${ { { {\boldsymbol{\alpha} } } }' },{ { {\boldsymbol{\alpha} } } }_g'',{ { { {{I} } } }_g},g = 1,2,\cdots,d$ 。初始化:
${ { {\boldsymbol{V} } } } \leftarrow {\boldsymbol{0}},t' \leftarrow 1$ Repeat:
For t 1 to n by 1:
${ { {\boldsymbol{x} }\_{\bf{train} } } } \leftarrow \{ { { { {\boldsymbol{x} } } }_m}|m = 1,2,\cdots,t - 1,t + 1,\cdots n\}$ 使用
${{{\boldsymbol{x}}\_{\bf{train}}} }$ ,${{{\boldsymbol{V}}} }$ 及式(28)求出LSSVM+的$ {\mathbf{\alpha }} $ 和$ b $ ,得到其决策函数关于${ {{{\boldsymbol{x}}} }_t}$ 的预测值:${\tilde y_t} = \displaystyle\sum\limits_{i = 1}^{n - 1} {\displaystyle\sum\limits_{l = 1}^d { {\alpha _i} } } k({ { {\boldsymbol{x} }\_{\bf{train} } } }_l^i,x_l^t) + b + \displaystyle\sum\limits_{g = 1}^d { {V_g}I_g^t}$ End
$ {d_t} = 1\{ {\tilde y_t}{y_t} > 0\} $ ,$t = 1,2,\cdots,n$ For g 1 to d by 1:
${ { { {{V} } } }_g} = { { { {{V} } } }_g} - \left\{ \dfrac{1}{ {\sqrt {t'} } }\displaystyle\sum\limits_{t = 1}^n {d_t}{y_t}\left[\displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{l = 1}^d { {\mathbf{\alpha } }_{gi}''} } {k_l}(x_l^i,x_l^t) - { { {\boldsymbol{} }I} }_g^t \right]\right\}$ End
If
$\left\| {{{\boldsymbol{V}}} } \right\| > B{\text{ } }$ then${{{\boldsymbol{V}}} } \leftarrow ({{{\boldsymbol{V}}} }*B)/{\left\| {{{\boldsymbol{V}}} } \right\|_2}{\text{ } }$ End if
$t' = t' + 1$ Until convergence
使用式(28)由
${{{\boldsymbol{V}}} }$ 求出P-LSSVM的${{{\boldsymbol{\alpha}} } }$ 和$ b $ ,得到P-LSSVM决策函数:$y({ { {\boldsymbol{x} } } }) = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{g = 1}^d { {\alpha _i} } } {k_g}(x_g^i,x_g^{}) + b + \displaystyle\sum\limits_{g = 1}^d { {V_g}I_g^{}{\text{ } } }$ ${{{\boldsymbol{V}}} } \leftarrow {\text{norm} }(\left| {{{\boldsymbol{V}}} } \right|)$ 输出
${{{\boldsymbol{V}}} }$ ,$y({{{\boldsymbol{x}}} })$ 。P-LSSVM算法将处理缺失数据与构建分类模型同时进行。首先在LSSVM中引入LUPI,利用特权信息对LSSVM进行引导,可以保证不完整特征中误差和特权信息误差的相似,反映出由特征的局部数据缺失所带来的对整体分类性能的影响。选用可加性核作为算法的核函数,使算法可对每一维特征上由缺失值所带来的误差分别进行统计。利用这一特性,在LSSVM+中的约束条件里引入了分类误差上界
$ {{\boldsymbol{V}}} $ ,最后采用留一交叉验证的无偏估计方法通过迭代来求出$ {{\boldsymbol{V}}} $ 的最优值,对缺失值的处理包含在对$ {{\boldsymbol{V}}} $ 的优化过程中。上述的同时进行指的是在构建分类器的同时,通过对不同特征的缺失值带来的分类误差上界进行优化,改善模型的性能,而无需在建模前先对缺失值进行处理。2.3 包含缺失值的特征的重要性
在本文提出的P-LSSVM中,
${{{V}}_g}$ 被定义为由于第$ g $ 维特征数据的缺失所导致的总分类误差上界,由提出留一交叉验证法迭代求出,${{{{{V}}}}_g}$ 的大小揭示了包含缺失值的第$ g $ 维特征对于分类性能所造成的影响,它提供了在分类模型中第$ g $ 维特征的相对重要性。此相对重要性可以对数据收集过程提供指导。共考虑以下3种情况:1)如果
${{{{{V}}}}_g}$ 等于0,可以将由第$ g $ 维特征数据缺失对分类性能所能造成的影响视为是无关紧要的,其缺失数据造成的影响相对其他特征是最小的。2)如果
${{{{{V}}}}_g}$ 小于一个给定的阈值,由第$ g $ 维特征数据的缺失所带来的分类误差较小,说明第$ g $ 维特征数据的缺失对分类性能所能造成的影响较小,即第$ g $ 维特征相对其他具有较大值的特征是不重要的,在模式分类过程中起到的效果要小于其他特征,在收集数据时不用太过关注。3)如果
${{{{{V}}}}_g}$ 大于一个给定的阈值,由第$ g $ 维特征数据的缺失所带来的分类误差较大,说明第$ g $ 维特征数据的缺失对分类性能所能造成的影响更大,即第$ g $ 维特征相对其他具有较大值的特征是更重要的,在模式分类过程中起到了更大的效果。在收集数据时要比其他特征更慎重的对待,尽量先保证其数据的完整。${{{{{V}}}}_g}$ 是作为衡量第$ g $ 维特征对分类性能影响程度的指标,${{{{{V}}}}_g}$ 的值越大,第$ g $ 维特征的缺失对分类性能造成的影响越大。为了凸显出缺失特征之间的相对重要程度,在本算法中对${{{{\boldsymbol{V}}}}}$ 取绝对值后应用了归一化。${{{{{V}}}}_g}$ 的大小,说明了包含了缺失值的第$ g $ 维特征对分类性能的相对影响的大小。3. 实验结果与分析
为了验证本文提出的P-LSSVM的有效性,将P-LSSVM与4种面向缺失数据的算法分别在German (UCI german credit)、Fire(fire dataset)等公开数据集上的表现进行对比。不同于处理缺失数据和建模同时进行的P-LSSVM,对比算法采用了先处理缺失数据,再对处理后的数据使用LSSVM进行建模这一常用策略。在3.3.1节给出了实验的结果,证明了P-LSSVM的有效性。此外,为了说明P-LSSVM确定的特征相对重要性对于改善数据质量的贡献,在3.3.2节给出了使用P-LSSVM对German数据集进行的案例研究。
表1汇总了数据集的相关信息。所有实验均在同一环境下完成,处理器为AMD Ryzen 74 800U,内存16 GB,在Windows10环境下配置 Python3.9.0。
表 1 数据集相关信息Table 1 Dataset descriptions数据集 样本数 特征数 German 1000 20 Australian 690 14 Fire 243 13 Surgery 470 16 Wine 178 12 Diabetes 1151 19 Fertility 100 9 Pima 769 8 3.1 数据集预处理
为了进行仿真实验,在实验中为所有数据集设置一个缺失信息矩阵I,在样本数据中以随机的方式选取一部分的数据作为缺失的数据,在I中记录缺失情况。此外,为了防止数据的缺失将样本完全破坏,出现无法分类的情况,规定每个数据集最多可缺失10%的信息。German数据集是UCI德国信用数据集。可用来根据个人财务情况来预测贷款客户违约倾向。Fire数据集中前3个特征不使用。Wine数据集将通过划分将第1种葡萄酒设定为正例,将其余2种葡萄酒合并后设定为负例。
3.2 实验设计
本文进行的实验的主要目的是与使用了不同的缺失数据处理策略LSSVM相比,评估所提出的P-LSSVM的性能,对比算法有:1)特征删除LSSVM:把包含了缺失值的特征移除, 再对处理后的数据用标准LSSVM进行建模。2)样本删除LSSVM:把含有缺失值的样本移出数据集, 再对处理后的数据用LSSVM进行建模。3)均值填充LSSVM:若一个样本的某个特征含有缺失值,可使用其余完整样本在此特征的平均值来填充此缺失值,再对处理后的数据用LSSVM进行建模。4)最近邻填充LSSVM:从完整样本中选取距离缺失特征数据的样本最近的样本来估算缺失的特征信息, 再对处理后的数据使用标准LSSVM进行建模。
为了保证公平性,本文提出的P-LSSVM算法与对比方法都采用加性高斯核函数。
$ {\sigma _l} $ 是应用在第$ l $ 维特征的核函数参数,取第$ l $ 维特征的方差[23]。LUPI的超参数
$ \rho $ 在$ \{ {10^{ - 2}},{10^{ - 1}},{10^0},{10^1},{10^2}\} $ 中搜索选取最优值,基于对式(13)的观察,为了保持量纲的一致性,超参数$ C $ 在$ \{ {10^{ - 4}},{10^{ - 3}},{10^{ - 2}},{10^{ - 1}}, {10^0}, {10^1},{10^2},{10^3},{10^4}\} $ [23]搜索选取最优值。所有的算法的正则化参数$ \lambda $ 都在$ \{ {10^{ - 2}},{10^{ - 1}},{10^0},{10^1},{10^2}\} $ 中搜索选取最优值。在实验中使用了五折交叉验证策略,以确保数据集中的每个样本都有机会用于训练集和测试集,减少可能会导致过拟合或欠拟合的偏差的影响。本文将数据集随机分成5个子集。该模型使用4个子集构建,并在剩余的1个子集上进行测试。采用五折交叉验证中准确度的平均值和标准差作为分类性能的评估。
3.3 实验结果分析
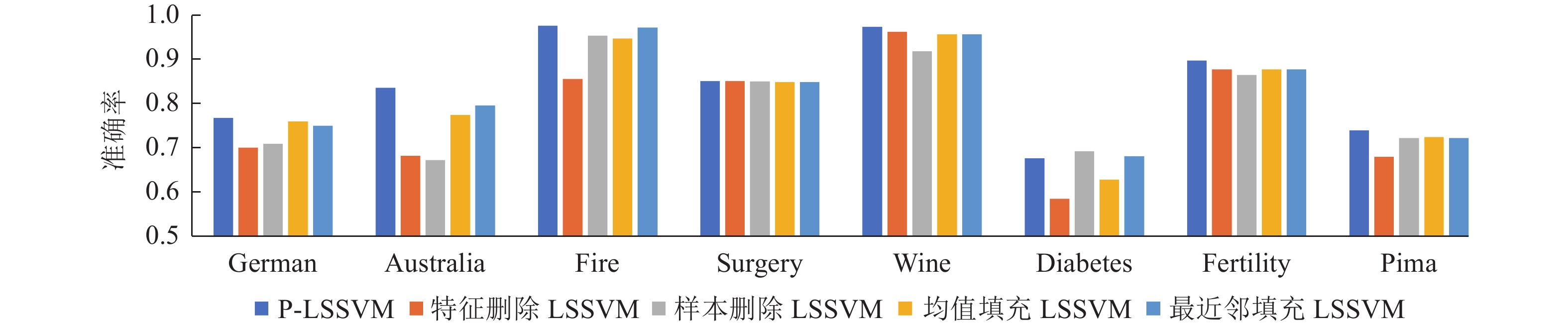
表2和图2给出了P-LSSVM和对比算法的关于平均准确率和标准差的实验结果,接下来将在3.3节对实验结果进行分析和讨论。为了对P-LSSVM还可得到不完整特征的重要性这一优势进行说明,以German数据集为例进行了案例研究,具体说明如何使用P-LSSVM对特征的相关重要性进行分析,区分出更重要的特征,用以指导数据收集。总体而言,本文提出的算法不但在平均测试精度上优于对比算法,而且可以同时获得特征数据的缺失对于分类预测的影响,即特征的相对重要性这一额外成果。
表 2 5种算法在8个数据集上的实验结果Table 2 Performance of the five algorithms on eight datasets数据集 P- LSSVM 对比算法 特征删除LSSVM 样本删除LSSVM 均值填充LSSVM 最近邻填充LSSVM German 0.7690±0.0222 0.7010±0.0278 0.7100±0.0426 0.7610±0.0203 0.7510±0.0208 Australia 0.8376±0.0227 0.6826±0.0353 0.6731±0.0525 0.7753±0.0333 0.7971±0.0270 Fire 0.9791±0.0131 0.8583±0.0847 0.9571±0.0349 0.9500±0.0282 0.9750±0.0242 Surgery 0.8531±0.0206 0.8531±0.0236 0.8526±0.0376 0.8510±0.0242 0.8510±0.0512 Wine 0.9771±0.0114 0.9657±0.0114 0.9215±0.0366 0.9600±0.0387 0.9600±0.0291 Diabetes 0.6765±0.0243 0.5843±0.0231 0.6927±0.0280 0.6286±0.0141 0.6817±0.0181 Fertility 0.9000±0.0774 0.8800±0.0748 0.8666±0.0666 0.8800±0.0748 0.8800±0.0748 Pima 0.7411±0.0253 0.6797±0.0362 0.7230±0.0517 0.7254±0.0184 0.7228±0.0066 3.3.1 分类性能分析
1)在大多数数据集上,与先修复缺失数据,再对处理后的数据使用标准LSSVM建模的算法相比,本文提出的算法取得了更好的分类性能。这表明本文提出的算法能够对缺失数据进行分类,证明了其有效性。2)在Diabetes数据集上,样本删除LSSVM算法的性能比其他算法更好。这可能是因为LSSVM 对噪声的敏感性较高,而被丢弃的样本上具有噪声,即在将缺失数据样本移出数据集时,将较多的异常样本移除了,因此样本删除增强了分类性能。
需要强调的是,P-LSSVM还提供了关于缺少数据的特征的相对重要性信息,具有指导数据收集的优势,这是其他对比方法都无法做到的。
表3列出了P-LSSVM和次优方法最近邻填充LSSVM的训练时间和测试时间。
表 3 P-LSSVM 和 最近邻填充LSSVM模型的计算时间Table 3 Calculation time of P-LSSVM and LSSVM with KNN on each adopted datasets 数据集 P-LSSVM 最近邻填充LSSVM 训练 测试 训练 测试 German 920.413 8.183 221.794 15.707 Australia 209.955 2.072 65.3945 2.465 Fire 32.345 0.172 8.864 0.306 Surgery 144.513 1.186 35.046 1.809 Wine 13.466 0.116 5.305 0.215 Diabetes 846.404 7.013 191.215 12.682 Fertility 5.453 0.030 4.156 0.049 Pima 108.595 1.723 47.571 2.528 由表3可知,对P-LSSVM的训练需要花费更多的时间成本,这是因为训练P-LSSVM时需要额外对特权信息进行训练和确定维度的重要性,但额外的运算也使P-LSSVM在平均测试精度上优于对比算法,还能同时得到缺失特征的重要性这一额外成果。此外,与最近邻填充LSSVM相比,P-LSSVM的测试时间更短。也就是说,一旦训练完成,P-LSSVM在应用时更有优势。所以本文认为时间成本的增加是可以接受的。当然,如何有效地降低P-LSSVM的训练时间也将是本文下一步的研究重点。
3.3.2 German数据集上的案例研究
如2.3节所述,缺失特征对于分类预测的影响可用分类过程中获得的
$ {{\boldsymbol{V}}_g} $ 值表示,$ {{\boldsymbol{V}}_g} $ 的值越大,说明相对于其他特征信息的缺失,第g维特征的信息的缺失对于分类预测的影响更大,所以它更加重要。可以依据此相对重要性来引导数据收集过程。在表4列出了German数据集的所有不完整特征的相对重要性,表4的第1列是特征名(长特征名用首字母缩写),第2列是特征的
$ {{{{\boldsymbol{V}}}}_g} $ 的值。由表4知,在所有缺失数据的特征中,“property”特征的值最高,说明“property”特征比其他特征更重要。因此可推断,“property”对预测客户的贷款违约倾向非常重要,其缺失数据的影响非常显著。反之,如“Credit history”和“purpose”的值较低,表明客户的既往信用历史和贷款目的特征对预测客户的贷款违约倾向不如其他特征重要,缺失数据的影响最小。此外,综合来看,与客户长期资产相关的特征(如“property”、“present residence”)的值要高于与客户流动资产相关的特征(如“savings”、“present employment”、),而它们又都大于无关客户资产信息的特征(如“personal”、“other debtors”)的值。表 4 在German上具有缺失值特征的影响Table 4 Effects of incomplete features on German特征名 相对重要性 property 1.0000 Installment rate 0.8970 present residence
savings
present employment
CAS
Credit amount
duration
personal
other debtors0.8504
0.5225
0.5190
0.4766
0.4710
0.4560
0.3544
0.1917purpose 0.1074 Credit history 0 分析结果表明,为了改善German数据集的质量,在收集数据时,应更多地关注与客户资产相关的特征,资产相关的特征中最值得关注的是与长期资产相关的特征,尽量保证此类特征的完整。表5~11中列出了其他数据集的不完整特征的相对重要性,篇幅所限,仅降序列出了每个数据集中最重要的3个特征和最不重要的2个特征。
表 5 在Australian上具有缺失值特征的影响Table 5 Effects of incomplete features on Australian特征名 相对重要性 A4 1.0000 A6 0.9317 A8 0.6451 A3 0.3835 A10 0 表 6 在Fire上具有缺失值特征的影响Table 6 Effects of incomplete features on Fire特征名 相对重要性 FWI 1.0000 ISI 0.8833 FFMC 0.6754 DC 0.3971 BUI 0 表 7 在Surgery上具有缺失值特征的影响Table 7 Effects of incomplete features on Surgery特征名 相对重要性 PRE25 1.0000 PRE19 0.9754 PRE7 0.9084 PRE17 0.0989 PRE10 0 表 8 在Wine上具有缺失值特征的影响Table 8 Effects of incomplete features on Wine特征名 相对重要性 Malic acid 1.0000 Alcohol 0.6845 Flavanoids 0.5926 Alcalinity of ash 0.0357 Ash 0 表 9 在Diabetes上具有缺失值特征的影响Table 9 Effects of incomplete features on Diabetes特征名 相对重要性 7th 1.0000 6th 0.8776 1th 0.8222 13th 0.1730 3th 0 表 10 在Fertility上具有缺失值特征的影响Table 10 Effects of incomplete features on Fertility特征名 相对重要性 Age 1.0000 Childish 0.6156 Season 0.4868 Surgical 0.2957 Accident 0 表 11 在Pima上具有缺失值特征的影响Table 11 Effects of incomplete features on Pima特征名 相对重要性 Pregnancies 1.0000 Glucose 0.8898 Insulin 0.4424 BMI 0.1353 Blood Pressure 0 4. 结束语
针对机器学习研究中常见的数据缺失问题,本文提出了一种新的基于LUPI的可加性LSSVM(P-LSSVM),以使用特权信息对学习过程进行引导的思路来处理缺失数据。传统的数据处理分类算法会先对数据进行填充后再构建决策模型,在本文提出的算法中,缺失数据的处理过程和决策函数的构建过程都是在特权信息的引导下同时进行的。实验结果证实了P-LSSVM对于具有缺失数据的数据集中分类问题的有效性。此外,P-LSSVM还可同时获得包含缺失数据的特征对于分类性能的影响的评估,可为收集数据提供引导来保证数据质量。尽管P-LSSVM有着令人满意的分类性能,但其训练时间还可以进一步优化,这也是我们下一步的研究方向。此外,P-LSSVM是从特征角度来构建模型,下一步将探索从样本角度出发构建模型的可能性。
-
表 1 数据集相关信息
Table 1 Dataset descriptions
数据集 样本数 特征数 German 1000 20 Australian 690 14 Fire 243 13 Surgery 470 16 Wine 178 12 Diabetes 1151 19 Fertility 100 9 Pima 769 8 表 2 5种算法在8个数据集上的实验结果
Table 2 Performance of the five algorithms on eight datasets
数据集 P- LSSVM 对比算法 特征删除LSSVM 样本删除LSSVM 均值填充LSSVM 最近邻填充LSSVM German 0.7690±0.0222 0.7010±0.0278 0.7100±0.0426 0.7610±0.0203 0.7510±0.0208 Australia 0.8376±0.0227 0.6826±0.0353 0.6731±0.0525 0.7753±0.0333 0.7971±0.0270 Fire 0.9791±0.0131 0.8583±0.0847 0.9571±0.0349 0.9500±0.0282 0.9750±0.0242 Surgery 0.8531±0.0206 0.8531±0.0236 0.8526±0.0376 0.8510±0.0242 0.8510±0.0512 Wine 0.9771±0.0114 0.9657±0.0114 0.9215±0.0366 0.9600±0.0387 0.9600±0.0291 Diabetes 0.6765±0.0243 0.5843±0.0231 0.6927±0.0280 0.6286±0.0141 0.6817±0.0181 Fertility 0.9000±0.0774 0.8800±0.0748 0.8666±0.0666 0.8800±0.0748 0.8800±0.0748 Pima 0.7411±0.0253 0.6797±0.0362 0.7230±0.0517 0.7254±0.0184 0.7228±0.0066 表 3 P-LSSVM 和 最近邻填充LSSVM模型的计算时间
Table 3 Calculation time of P-LSSVM and LSSVM with KNN on each adopted dataset
s 数据集 P-LSSVM 最近邻填充LSSVM 训练 测试 训练 测试 German 920.413 8.183 221.794 15.707 Australia 209.955 2.072 65.3945 2.465 Fire 32.345 0.172 8.864 0.306 Surgery 144.513 1.186 35.046 1.809 Wine 13.466 0.116 5.305 0.215 Diabetes 846.404 7.013 191.215 12.682 Fertility 5.453 0.030 4.156 0.049 Pima 108.595 1.723 47.571 2.528 表 4 在German上具有缺失值特征的影响
Table 4 Effects of incomplete features on German
特征名 相对重要性 property 1.0000 Installment rate 0.8970 present residence
savings
present employment
CAS
Credit amount
duration
personal
other debtors0.8504
0.5225
0.5190
0.4766
0.4710
0.4560
0.3544
0.1917purpose 0.1074 Credit history 0 表 5 在Australian上具有缺失值特征的影响
Table 5 Effects of incomplete features on Australian
特征名 相对重要性 A4 1.0000 A6 0.9317 A8 0.6451 A3 0.3835 A10 0 表 6 在Fire上具有缺失值特征的影响
Table 6 Effects of incomplete features on Fire
特征名 相对重要性 FWI 1.0000 ISI 0.8833 FFMC 0.6754 DC 0.3971 BUI 0 表 7 在Surgery上具有缺失值特征的影响
Table 7 Effects of incomplete features on Surgery
特征名 相对重要性 PRE25 1.0000 PRE19 0.9754 PRE7 0.9084 PRE17 0.0989 PRE10 0 表 8 在Wine上具有缺失值特征的影响
Table 8 Effects of incomplete features on Wine
特征名 相对重要性 Malic acid 1.0000 Alcohol 0.6845 Flavanoids 0.5926 Alcalinity of ash 0.0357 Ash 0 表 9 在Diabetes上具有缺失值特征的影响
Table 9 Effects of incomplete features on Diabetes
特征名 相对重要性 7th 1.0000 6th 0.8776 1th 0.8222 13th 0.1730 3th 0 表 10 在Fertility上具有缺失值特征的影响
Table 10 Effects of incomplete features on Fertility
特征名 相对重要性 Age 1.0000 Childish 0.6156 Season 0.4868 Surgical 0.2957 Accident 0 表 11 在Pima上具有缺失值特征的影响
Table 11 Effects of incomplete features on Pima
特征名 相对重要性 Pregnancies 1.0000 Glucose 0.8898 Insulin 0.4424 BMI 0.1353 Blood Pressure 0 -
[1] GARCÍA-LAENCINA P J, SANCHO-GÓMEZ J L, FIGUEIRAS-VIDAL A R. Pattern classification with missing data: a review[J]. Neural computing and applications, 2010, 19(2): 263–282. doi: 10.1007/s00521-009-0295-6 [2] WANG Guanjin, DENG Zhaohong, CHOI K S. Tackling missing data in community health studies using additive LS-SVM classifier[J]. IEEE journal of biomedical and health informatics, 2016, 22(2): 579–587. [3] BATISTA G E A P A, MONARD M C. An analysis of four missing data treatment methods for supervised learning[J]. Applied artificial intelligence, 2003, 17(5/6): 519–533. [4] MOON T K. The expectation-maximization algorithm[J]. IEEE signal processing magazine, 1996, 13(6): 47−60. [5] DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the royal statistical society series B: statistical methodology, 1977, 39(1): 1−22. [6] HORTON N J, KLEINMAN K P. Much ado about nothing[J]. The American statistician, 2007, 61(1): 79−90. [7] IBRAHIM J G, CHEN M H, LIPSITZ S R. Monte Carlo EM for missing covariates in parametric regression models[J]. Biometrics, 1999, 55(2): 591−596. [8] 仝伯兵, 王士同, 梅向东. 稀疏条件下的两层分类算法[J]. 智能系统学报, 2015, 10(1): 27–36. TONG Bobing, WANG Shitong, MEI Xiangdong. Sparsity-inspired two-level classification algorithm[J]. CAAI transactions on intelligent systems, 2015, 10(1): 27–36. [9] GARCÍA-LAENCINA P J, SERRANO J, FIGUEIRAS-VIDAL A R, et al. Multi-task neural networks for dealing with missing inputs[M]. Berlin: Springer Berlin Heidelberg, 2007: 282−291. [10] TROYANSKAYA O, CANTOR M, SHERLOCK G, et al. Missing value estimation methods for DNA microarrays[J]. Bioinformatics (Oxford, England), 2001, 17(6): 520−525. [11] JUSZCZAK P, DUIN R P W. Combining one-class classifiers to classify missing data[M]. Berlin: Springer Berlin Heidelberg, 2004: 92−101. [12] JIANG Kai, CHEN Haixia, YUAN Senmiao. Classification for incomplete data using classifier ensembles[C]//2005 International Conference on Neural Networks and Brain. Piscataway: IEEE, 2006: 559−563. [13] KRAUSE S, POLIKAR R. An ensemble of classifiers approach for the missing feature problem[C]//Proceedings of the International Joint Conference on Neural Networks. Piscataway: IEEE, 2003: 553−558. [14] CHOUDHURY S J, PALN R. Imputation of missing data with neural networks for classification[J]. Knowledge-based systems, 2019, 182: 104838 [15] 卞则康, 王士同. 基于混合距离学习的鲁棒的模糊C均值聚类算法[J]. 智能系统学报, 2017, 12(4): 450–458. doi: 10.11992/tis.201607019 BIAN Zekang, WANG Shitong. Robust FCM clustering algorithm based on hybrid-distance learning[J]. CAAI transactions on intelligent systems, 2017, 12(4): 450–458. doi: 10.11992/tis.201607019 [16] VAPNIK V, VASHIST A. A new learning paradigm: learning using privileged information[J]. Neural networks, 2009, 22(5/6): 544−557. [17] SUYKENS J A K, VANDEWALLE J. Chaos control using least-squares support vector machines[J]. International journal of circuit theory and applications, 1999, 27(6): 605−615. [18] PELCKMANS K, GOETHALS I, BRABANTER J D, et al. Componentwise least squares support vector machines[M]. Berlin: Springer Berlin Heidelberg, 2005: 77−98. [19] 李欢, 王士同. 支持向量机的多观测样本二分类算法[J]. 智能系统学报, 2014, 9(4): 392–400. LI Huan, WANG Shitong. Binary-class classification algorithm with multiple-access acquired objects based on the SVM[J]. CAAI transactions on intelligent systems, 2014, 9(4): 392–400. [20] MAJI S, BERG A C, MALIK J. Efficient classification for additive kernel SVMs[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 66−77. [21] DEMIR B, BRUZZONE L. Fast and accurate image classification with histogram based features and additive kernel SVM[C]//2015 IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE, 2015: 2350−2353. [22] 王旭凤. 基于可加性核的快速支持向量机分类算法的研究[D]. 西安: 西安电子科技大学, 2017. WANG Xufeng. Fast support vector machine classification algorithm with additive kernel [D]. Xi’an: Xi’an University of Electronic Science and technology, 2017. [23] XUE Li. Robust learning with imperfect privileged information[J]. Artificial intelligence, 2020, 282: 103246. [24] XU Xinxing, LI Wen, XU Dong. Distance metric learning using privileged information for face verification and person re-identification[J]. IEEE transactions on neural networks and learning systems, 2015, 26(12): 3150−3162. [25] PAL A, KHEMCHANDANI R R N. Learning TWSVM using privilege information[C]//2018 IEEE Symposium Series on Computational Intelligence Piscataway: IEEE, 2019: 1548−1554.































 下载:
下载: