成对约束被认为是一种弱监督信息^[1]，因为相比于标签信息，成对约束不能提供显式的类信息，而是一种综合的监督信息。具体来说，成对约束不是标记每一个数据样本属于哪一类，而是标记一对数据样本之间的关系，即由必须链接和不能链接两类约束信息来说明两个数据样本是否属于同一类。因此成对约束信息不具备推演传导的特性^[2]，例如，给定3个数据点a、b、c，已知a和b之间存在必须链接，b和c之间存在必须链接，但a和c之间的约束关系并无法推导出。在很多机器学习任务中，成对约束比类标签使用起来更简单。

成对约束可以作为一种先验知识改进模型来提高聚类^[3-7]、降维^[8-10]、特征选择^[11-12]、度量学习^[13-17]和半监督分类^[18]等任务的性能。但是可用的成对约束通常是有限的，因此成对约束的传播就至关重要。成对约束传播就是将有限可用的成对约束关系从已知约束的数据样本对传播到未知约束的数据样本对，从而获得大量可靠的成对约束信息，显著提高机器学习任务的性能。

为了将初始成对约束信息传播到整个数据集中，前人做了大量的工作，提出很多方法。例如，Lu等^[19]通过高斯核函数将已知的约束传播到其他相似的未知约束的数据点，但是该方法做了特定假设，仅针对两个类的聚类问题。Li等^[20]将成对约束传播表示为半定规划(semi-definite programming, SDP)过程，不局限于两个类的问题，但是SDP求解过程会产生极大的开销，计算复杂度达到 $O({n^4})$ 。Yu等^[21]把成对约束传播表示为一个约束优化问题，但只局限于必须链接的优化。Lu 等^[22] 为了克服上述问题，提出一种不限于两类和必须链接，并且能够降低计算复杂度的方法，将成对约束传播分解为一组相互独立的半监督分类子问题。为了增强传播中两种约束的可辨别性，Jia等^[23]提出一种基于对抗流形正则化的成对约束传播模型，将必须链接和不能链接分开传播，并且加入其对抗关系。上述方法都是应用于单模态数据成对约束传播问题的，现实生活中多模态数据已经非常普遍，因此一些扩展方法也研究了多模态数据的成对约束传播问题^[24-25]。

前面提到的很多成对约束传播模型都是利用精确的初始成对约束来传播，而在现实世界中，想要获取精确的成对约束存在一定的困难，很多约束关系来自现实环境，其具有弱关系，所以关系的不确定性是可变的^[26]。很显然只追求精确的初始成对约束时并没有考虑到现实中获取成对约束的精准性，导致在现实情境下的传播会忽略一部分不精确信息。例如当初始成对约束信息是从用户反馈中获得时，就存在很大的不确定性。假设现有两个病例的症状信息，不同个体出现的症状差异和表达能力的偏差等都会成为判断两个病例是否患同一种病的不确定因素，我们不能得出两个病例一定患或不患同一种病的结论，但可以判断二者患或不患同一种病的可能性。

为了解决这个问题，本文提出了不确定成对约束这个新概念，并在其基础上构造出一种双对抗的约束传播模型。这种传播通过已知信息获得两个数据样本属于或不属于同一类的可能性，两种可能性之间形成一个对抗，另外必须链接和不能链接本身存在一个对抗，综合两个对抗并使其作用于判断其他数据样本间的约束类别。不仅较大限度地利用了有限数量初始成对约束的潜力，也增强了成对约束传播的现实应用性。

本文的主要贡献如下：1)关注到从现实场景中推断出成对约束关系时的准确性问题，首次提出不确定成对约束这个新的概念。2)在不确定成对约束的传播过程中，与文献[23]不同，在考虑了约束对抗的基础上，引入了可能性的对抗，形成双对抗的新结构，调整对抗强度。3）本文提出模型的交替迭代算法在理论上保证了收敛性。4）在8个数据集上的实验结果验证了不确定成对约束的双对抗传播效果的有效性，在现实场景的应用中有着明显的优越性。

1.   相关知识

1.1   流形正则化

假设给定一个由n个d维数据样本组成的数据集X，将其第i列记为 ${{\boldsymbol{x}}_i}$ ，那么输入数据表示为 ${\boldsymbol{X}} = \left\{ {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},\cdots,{{\boldsymbol{x}}_n}} \right\}$ 。假定数据分布的几何形状由基础流形支持，可以将其映射为一个无向加权图 $ G = < \nu ,\varepsilon > $ ，每一个数据样本代表一个顶点，所以 $ \nu $ 是由X中所有数据样本组成的顶点集， $ \varepsilon $ 是描述成对的数据样本之间存在约束情况的边集，边的权值大小通过计算相关的两个数据样本之间的相似度获得。k近邻(k-nearest neighbor, k-NN)图通常用来构造相似矩阵，其形成的稀疏图可以带来更好的性能。构造过程如下：首先基于欧氏距离找到与样本 ${{\boldsymbol{x}}_i}$ 最靠近的k个样本，并记录为 ${N_k}({{\boldsymbol{x}}_i})$ ^[27] ，两个顶点之间的边权通常使用径向基核函数(radial basis function, RBF)计算，生成一个位于区间 $[0,1]$ 的真实值 ${{\boldsymbol{W}}_{i,j}}(1 \leqslant i,j \leqslant n)$ ，表示为

其中 $\sigma > 0$ 是高斯核的宽度。因为k-NN图是对称的，需要用公式 ${\boldsymbol{W}} = ({\boldsymbol{W}} + {{\boldsymbol{W}}^{\rm{T}}})/2$ 对初步获得的权值矩阵进行对称处理。

图的正则化将迫使嵌入的数据样本与临近点具有相似的性质，从而保持原来的流形结构。已知上述 $ {{\boldsymbol{W}}_{i,j}} $ 表示 ${{\boldsymbol{x}}_i}$ 和 ${{\boldsymbol{x}}_j}$ 两个数据样本之间在流形结构上的相似度，给定k-NN图，流形正则化表示为

式中： ${\boldsymbol{D}} = {\rm diag} ({{\boldsymbol{d}}_1},{{\boldsymbol{d}}_2},\cdots,{{\boldsymbol{d}}_n})$ 是一个对角矩阵，它的第i个对角元素计算为 ${{\boldsymbol{D}}_{i,i}} = \displaystyle\sum_{j = 1}^n {{{\boldsymbol{W}}_{i,j}}}$ ，也就是相似度矩阵W对应行的元素的和； $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ 是拉普拉斯矩阵； ${\rm{tr}}( \cdot )$ 表示矩阵的迹。

1.2   对抗的PCP

成对约束传播已经被证明是利用有限数量的成对约束的一种有效方法。对于给定的数据集，已知其中一定数量成对的数据样本之间的关系，即初始成对约束信息，将必须链接保存在集合M中，表示为

同理不能链接的集合C表示为

成对约束提供的监督信息被广泛应用于许多机器学习任务中，而在现实环境中，我们可以获得的初始成对约束信息相当有限，因此提出成对约束传播模型。具体来说，就是在基础数据分布的支持下，将初始成对约束关系传播到整个数据集中，使任意一对数据样本之间都产生一个成对约束关系的预测值，以增加成对约束的数量。

在已知的成对约束传播（pairwise constraint propagation，PCP）模型中，Jia等^[23]提出的一种对抗流形正则化的成对约束传播方法，是能够兼顾必须链接和不能链接传播的有效方法之一。它使用相似矩阵和不相似矩阵两个非负矩阵，分别记录传播中的必须链接和不能链接，采用流形正则化，将必须链接和不能链接的传播分别表示为

此外，加入必须链接和不能链接的对抗关系 $ {\left\| {{\boldsymbol{S}} \odot {\boldsymbol{D}}} \right\|_1} $ ，将提出的模型总结为

式中：S是必须链接的传播矩阵；D是不能链接的传播矩阵；L是拉普拉斯矩阵；M和C矩阵分别保存了初始必须链接和不能链接的信息，用来保证S和D均满足初始的成对约束。

该模型利用了必须链接和不能链接之间的对抗关系，从而获得了更加准确的传播结果。然而，模型中所输入的初始成对约束信息都是以必须链接或不能链接理想化存在为前提，即提供的初始约束信息仅包含0和1两个值，但是现实场景中想要确定两个样本之间一定存在必须链接或不能链接并不容易，这导致该PCP模型在实际中的应用能力并不理想。

2.   不确定成对约束的双对抗流形传播模型

如前所述，在现有的成对约束的对抗流形传播方法中，关于精确初始约束信息的要求忽略了其在实际中的应用性，只是在给定精确的初始成对约束的理想假设下得到较好的结果，并未考虑到实际情况下可以获得的初始成对约束信息的精准性。为此，我们提出了一种不确定成对约束的双对抗流形传播方法不确定成对约束传播（uncertain pairwise constraint propagation，UPCP），能够利用两个样本数据之间存在必须链接和不能链接其中一种的可能性来将成对约束信息泛化到整个数据集，不仅可以充分挖掘其在实际应用中的潜力，还能大大减少人工标注监督信息的成本。

2.1   UPCP模型的建立

不同信息对于提高成对约束传播的准确性都至关重要，必须链接和不能链接的传播都不可忽略，因此，给定一个由n个d维数据样本组成的输入数据矩阵，首先根据已获得的初始成对约束信息，将其理想化处理后分为两个矩阵A和B，分别表示理想状态下为必须链接和不能链接的成对约束：

下面，我们定义一个新的概念：

定义1　当两个数据样本 ${{\boldsymbol{x}}_i}$ 和 ${{\boldsymbol{x}}_j}$ 在理想化状态下存在必须链接（或不能链接）时，根据客观经验，判断这个必须链接（或不能链接）实际存在的可能性为 ${p_{i,j}}$ ，以此表示的成对约束称为不确定成对约束。

根据定义1，在用数学公式来表达不确定成对约束时，定义相似可能性矩阵U和不相似可能性矩阵V来分别表示初始必须链接的可能性和初始不能链接的可能性：

其中 $ {u_{i,j}} $ 和 $ {v_{i,j}} $ 都是根据与现实场景相关的知识判断得到，例如用户反馈等途径，其数值范围在 $ (0.5,1] $ 。具体来说， $ {u_{i,j}} $ 或 $ {v_{i,j}} $ 所在位置关联的两个数据样本 ${{\boldsymbol{x}}_i}$ 和 ${{\boldsymbol{x}}_j}$ 之间存在初始成对约束， $ {u_{i,j}} $ 和 $ {v_{i,j}} $ 的大小表示成对约束存在的可能性。因为只有在可能性大于0.5时，两个数据样本之间的约束类型才相对可靠，故其取值设定在 $ (0.5,1] $ 。

为了记录传播过程中的必须链接和不能链接，我们使用两个非负矩阵K和F，在基于数据样本构建的k-NN图指导下，根据流形正则化，将必须链接和不能链接的传播分别表示为

对于同一对样本，其间存在必须链接或不能链接是相对的，从而形成一种对抗关系，数学表示为 $\left\| {{\boldsymbol{K}} \circ {\boldsymbol{F}}} \right\| = \displaystyle\sum\limits_{i,j = 1}^n {{{\boldsymbol{K}}_{i,j}}{{\boldsymbol{F}}_{i,j}}}$ ，其值的大小表示对抗的强弱。当同一对样本之间的 ${{\boldsymbol{K}}_{i,j}}$ 和 ${{\boldsymbol{F}}_{i,j}}$ 差异较大时， ${{\boldsymbol{K}}_{i,j}}{{\boldsymbol{F}}_{i,j}}$ 的值越小，对抗越弱，反之则对抗越强。

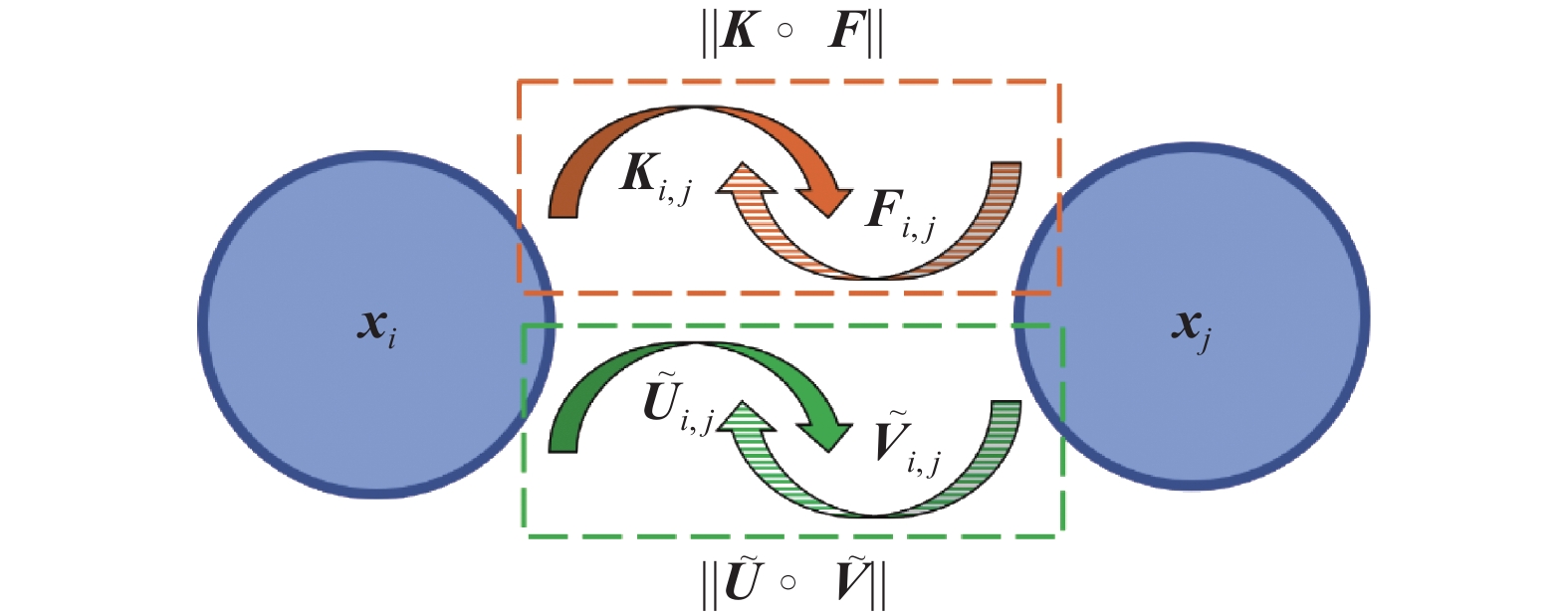
对应地，定义两个非负矩阵 $ {\boldsymbol{\tilde U}} $ 和 $ {\boldsymbol{\tilde V}} $ 分别记录传播过程中的相似可能性和不相似可能性。当一对样本之间的相似可能性越大时，其不相似可能性相应就越小，所以相似可能性和不相似可能性之间也存在对抗关系，同样使用Hadamard乘积可以将二者的对抗表示为 $\left\| {{\boldsymbol{\tilde U}} \circ {\boldsymbol{\tilde V}}} \right\|$ 。

图1是一对样本间双对抗结构的表达。 ${{\boldsymbol{x}}_i}$ 和 ${{\boldsymbol{x}}_j}$ 表示两个数据样本， ${{\boldsymbol{K}}_{i,j}}$ 和 ${{\boldsymbol{F}}_{i,j}}$ 分别记录传播时两个样本间的必须链接和不能链接， $ {{{\tilde {\boldsymbol{U}}}}_{i,j}} $ 和 $ {{{\tilde {\boldsymbol{V}}}}_{i,j}} $ 分别记录传播时两个样本间的相似可能性和不相似可能性。如标注所示，上半部分的对抗流是两种约束的对抗，下半部分则是两种约束可能性的对抗。在数学表达中这种双对抗关系可以有多种形式，而 $ \left\| {{\boldsymbol{\tilde U}} \circ {\boldsymbol{\tilde V}}} \right\| $ $\left\| {{\boldsymbol{K}} \circ {\boldsymbol{F}}} \right\| $ 就是其中的一种，这种形式不仅能够产生更真实的对抗强度，而且便于交替优化求解，可以有效调节成对约束的传播效果。

图  1  双对抗结构

Fig.  1  Doubly adversarial structure

下载: 全尺寸图片

将双对抗过程加入到成对约束的传播过程中，并且使其最小化，可使相近的成对约束具有相似的标记：

其中 $ \alpha $ 和 $ \beta $ 是两个用来控制必须链接和不能链接的传播强度的参数，避免因为数据集潜在成对约束中的必须链接和不能链接的比例差距使传播失衡。

很明显，在成对约束传播的过程中，相似可能性和不相似可能性也在传播，利用初始的两个可能性矩阵U和V中的信息，可以通过添加 $ {\left\| {{\boldsymbol{\tilde U}} - {\boldsymbol{U}}} \right\|^2} $ 和 $ {\left\| {{\boldsymbol{\tilde V}} - {\boldsymbol{V}}} \right\|^2} $ 两项将可能性信息泛化到未知可能性的成对约束中，这样可以将模型表述为

其中 $ {\lambda _1} $ 和 $ {\lambda _2} $ 是调节初始可能性信息贡献权重的参数。

2.2   算法的优化

为了有效地处理模型中的等式约束条件，我们定义了一个矩阵P来协助模型的优化，数学表达如下：

矩阵P记录了初始成对约束的位置，当 ${{\boldsymbol{P}}_{i,j}}$ 的值为1时，表明样本 ${{\boldsymbol{x}}_i}$ 和 ${{\boldsymbol{x}}_j}$ 之间的成对约束已知，否则就是未知。因为已知成对约束很少而未知成对约束很多，为缓解过拟合，利用P将两个等式约束表示成 $ {\left\| {{\boldsymbol{P}} \circ ({\boldsymbol{K}} - {\boldsymbol{A}})} \right\|^2} $ 和 $ {\left\| {{\boldsymbol{P}} \circ ({\boldsymbol{F}} - {\boldsymbol{B}})} \right\|^2} $ 的形式，引入已知初始成对约束信息，迫使预测情况与真实情况尽可能接近，将模型优化为

为求解传播结果矩阵，使用拉格朗日乘子法处理不等式约束条件，将式(17)的拉格朗日函数表示为

其中 ${\boldsymbol{\varPhi}}$ 和 ${\boldsymbol{\varphi}}$ 是两个拉格朗日乘子矩阵。求H关于K和F的一阶偏导，可得

强制 $\partial {\boldsymbol{H}}/\partial {{\boldsymbol{K}}_{i,j}}$ 和 $\partial {\boldsymbol{H}}/\partial {{\boldsymbol{F}}_{i,j}}$ 等于0，并且等式两边分别乘以 ${{\boldsymbol{K}}_{i,j}}$ 和 $ {{\boldsymbol{F}}_{i,j}} $ 矩阵，可得等式：

根据KKT(Karush-Kuhn-Tucker)条件可知 ${{\boldsymbol{\varPhi}} _{i,j}}{{\boldsymbol{K}}_{i,j}} = 0$ 和 ${{\boldsymbol{\varphi}} _{i,j}}{{\boldsymbol{F}}_{i,j}} = 0{\text{ }}$ ，并且依据关系 $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ 将L矩阵替换，可分别得到矩阵K和F的更新规则，如下：

传播后的K和F应该是对称矩阵，需要在每次传播后用公式 $({\boldsymbol{K}} + {{\boldsymbol{K}}^{\rm{T}}})/2$ 和 $({\boldsymbol{F}} + {{\boldsymbol{F}}^{\rm{T}}})/2$ 将其处理以保持对称性。

同样地，求H关于 $ {\boldsymbol{\tilde U}} $ 和 $ {\boldsymbol{\tilde V}} $ 的一阶偏导，可得：

强制 $\partial {\boldsymbol{H}}/\partial {{\boldsymbol{\tilde U}}_{i.j}}$ 和 $\partial {\boldsymbol{H}}/\partial {{\boldsymbol{\tilde V}}_{i.j}}$ 等于0，可以求出相似可能性矩阵 $ {\boldsymbol{\tilde U}} $ 和不相似可能性矩阵 $ {\boldsymbol{\tilde V}} $ 的更新规则为

由于可能性矩阵是非负的对称矩阵，更新后的 $ {\boldsymbol{\tilde U}} $ 和 $ {\boldsymbol{\tilde V}} $ 需要归一化为0~1，并处理成对称矩阵。

优化算法的详细求解过程总结为如下算法：

输入　参数 $ \alpha $ 、 $ \beta $ 、 $ \gamma $ 、 $ {\lambda _1} $ 、 $ {\lambda _2} $ ，数据集的k-NN图结构的边权矩阵W，初始成对约束的位置矩阵P，理想状态下的初始必须链接矩阵A和不能链接矩阵B，初始相似可能性矩阵U和不相似可能性矩阵V

初始化： $ {\boldsymbol{K}} = {\text{ran}}{{\text{d}}^ + }(n,n) $ ， ${\boldsymbol{F}} = {{{\rm{rand}}} ^ + }(n,n)$

　　 　 ${\boldsymbol{\tilde U}} = {{{\rm{rand}}} ^ + }(n,n) ， {\boldsymbol{\tilde V}} = {{{\rm{rand}}} ^ + }(n,n)$

（ $ {\text{ran}}{{\text{d}}^ + }(n,n) $ 返回一个正的 $n \times n$ 的随机矩阵 ）

1）计算对角矩阵D

　　 计算拉普拉斯矩阵 $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ 。

2）迭代更新K、F、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ 矩阵

　　 While不收敛do

　　　　　固定F、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ ，根据式(23)更新K；

　　　　　固定K、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ ，根据式(24)更新F；

　　　　　固定K、F、 $ {\boldsymbol{\tilde V}} $ ，根据式(27)更新 $ {\boldsymbol{\tilde U}} $ ；

　　　　　将 $ {\boldsymbol{\tilde U}} $ 归一化到 $ [0,1] $ ；

　　　　　固定K、F、 $ {\boldsymbol{\tilde U}} $ ，根据式(28)更新 $ {\boldsymbol{\tilde V}} $ ；

　　　　　将 $ {\boldsymbol{\tilde V}} $ 归一化到 $ [0,1] $ ；

　　　　　 $({\boldsymbol{K}} + {{\boldsymbol{K}}^{\rm{T}}})/2$ ；

　　　　　 $({\boldsymbol{F}} + {{\boldsymbol{F}}^{\rm{T}}})/2$ ；

　　　　　 $({\boldsymbol{\tilde U}} + {{\boldsymbol{\tilde U}}^{\rm{T}}})/2$ ；

　　　　　 $({\boldsymbol{\tilde V}} + {{\boldsymbol{\tilde V}}^{\rm{T}}})/2$ ；

　　　end while

输出　 K、F、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ 矩阵

2.3   收敛性分析

定理1　目标函数式(17)在算法下收敛。

定理1的证明可以等价地分解为5个命题:

命题1　式(17)中的目标函数在式(23)中的更新规则下递减，直到到达驻点;

命题2　式(17)中的目标函数在式(24)中的更新规则下递减，直到到达驻点;

命题3　式(17)中的目标函数在式(27)中的更新规则下递减，直到到达驻点;

命题4　式(17)中的目标函数在式(28)中的更新规则下递减，直到到达驻点;

命题5　式(17)是下界。

只要以上5个命题都成立，定理1即可成立。

首先，引入上界辅助函数的定义，辅助命题1的证明。

定义2^[28] 　当同时满足条件 $ g(x,x') \geqslant f(x) $ ， $g(x,x) = f(x)$ 时， $ g(x,x') $ 是 $ f(x) $ 的一个上界辅助函数。

引理1　如果g是f的一个上界辅助函数，那么f在按照 $ {x^{t + 1}} = \arg \mathop {\min }\limits_t g(x,{x^t}) $ 更新时不递增。

引理1的证明:

当F、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ 固定时，如果能够证明式(23)中的更新规则可以降低式(17)的上界函数，则命题1得证。去掉与K无关的项，将式(17)中的目标函数重新表示为

引理2　式(30)关于 $ \boldsymbol{K}_{i, j} $ 的上界辅助函数为

引理2的证明：式(30)在点 $ {\boldsymbol{K}}_{i,j}^t $ 处的泰勒级数表示为

其中 ${\left( {\partial {{\boldsymbol{H}}_{\boldsymbol{K}}}/\partial ({{\boldsymbol{K}}^t})} \right)_{i,j}}$ 和 ${{\boldsymbol{H}}}_{K}''{({{\boldsymbol{K}}}^{t})}_{i,j}$ 分别是 ${{\boldsymbol{H}}_{\boldsymbol{K}}}$ 关于 $ {{\boldsymbol{K}}_{i,j}} $ 的一阶导数和二阶导数，具体表示为

若 $ g({{\boldsymbol{K}}_{i,j}},{{\boldsymbol{K}}_{i,j}}) = {H_{{{\boldsymbol{K}}_{i,j}}}} $ ，根据定义1，要证明 $ g({{\boldsymbol{K}}_{i,j}},{\boldsymbol{K}}_{i,j}^t) $ 为 $ {H_{{{\boldsymbol{K}}_{i,j}}}} $ 的上界辅助函数，就等价于证明 $ g({{\boldsymbol{K}}_{i,j}},{\boldsymbol{K}}_{i,j}^t) \geqslant {H_{{{\boldsymbol{K}}_{i,j}}}} $ ，代入式(31)和式(32)即为

根据推导可知 ${({{\boldsymbol{K}}^t}{\boldsymbol{D}})_{i,j}} = \displaystyle\sum\limits_{k = 1}^n {{\boldsymbol{K}}_{i,k}^t} {{\boldsymbol{D}}_{k,j}} \geqslant {\boldsymbol{K}}_{i,j}^t{{\boldsymbol{D}}_{j,j}}$ ，又因为 $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ ，可推出 $ {\boldsymbol{K}}_{i,j}^t{{\boldsymbol{D}}_{j,j}} \geqslant {\boldsymbol{K}}_{i,j}^t{{\boldsymbol{L}}_{j,j}} $ ，综合可得 $ {({{\boldsymbol{K}}^t}{\boldsymbol{D}})_{i,j}} \geqslant {\boldsymbol{K}}_{i,j}^t{{\boldsymbol{L}}_{j,j}} $ 。同时 ${\left(\left\| {{\boldsymbol{\tilde U}} \circ {\boldsymbol{\tilde V}}} \right\|{\boldsymbol{F}}\right)_{i,j}} \geqslant 0$ ，由此可得式(35)成立。即引理2也成立。

由于式(31)是凸二次函数，其全局最优值在点 ${\boldsymbol{K}}_{i,j}^{t + 1} $ ，其求解过程为

式(36)与必须链接矩阵K的更新规则式(23)相同，所以可证明命题1。

按照同样的流程，式(24)中的更新规则可以在K、 $ {\boldsymbol{\tilde U}} $ 、 $ {\boldsymbol{\tilde V}} $ 固定时降低式(17)的上界函数，由此命题2也可以证明。

对于命题3，当K、F、 $ {\boldsymbol{\tilde V}} $ 固定时 ，去掉与 $ {\boldsymbol{\tilde U}} $ 无关的项，式(17)中的目标函数可表示为

观察可知，式(37)是关于 $ {\boldsymbol{\tilde U}} $ 的凸二次函数，其全局最优值在 ${{\boldsymbol{\tilde U}}_{i,j}} = {{\boldsymbol{U}}_{i,j}} - \dfrac{{{{({\boldsymbol{\tilde V}}\left\| {{\boldsymbol{K}} \circ {\boldsymbol{F}}} \right\|)}_{i,j}}}}{{2{\lambda _1}}}$ 处，与更新规则式(27)相同，所以可证明命题3。同理，命题4也可以证明。

最后，因为已知 $ {\boldsymbol{K}} \geqslant 0 $ 、 $ {\boldsymbol{F}} \geqslant 0 $ 、 $ {\boldsymbol{\tilde U}} \geqslant 0 $ 、 $ {\boldsymbol{\tilde V}} \geqslant 0 $ ，很显然可以判断

所以命题5得到了证明。

综上所述，定理1成立，即可证明算法的收敛性。

3.   实验与结果

3.1   数据集

为了展现UPCP方法传播效果的可靠性，我们将其与没有加入可能性时精确的单对抗PCP方法传播效果进行比较。为了更好地评估传播性能，实验在8个常用的UCI数据集上进行，其都来源于实际的应用问题。如表1所示，表中介绍了实验所用数据集的样本数、特征维度和类别数。其中，Chart数据集是用于测试时间序列数据库中的索引方案。Dermatology数据集是确定红细胞鳞状病变的类型。Glass数据集是根据玻璃的化学成分来判断玻璃类型、确定玻璃用途，多用于犯罪证据的取证。Ionosphere数据集包含了雷达站的信号数据。Libras数据集是对4个天秤座的人在视频中的手部运动路径的映射。Mnist数据集是从70000个初始样本中按照每类样本数相同的原则随机选取500个进行实验。Wine数据集是关于红酒的化学成分分析的数据。Zoo数据集包含了用于动物分类或聚类分析的一些动物特征，例如是否有毛发、是否有腿等布尔值。

3.2   参数设置

对于实验中用到的参数，我们进行了如下设置：首先在正则化部分涉及的k-NN图结构，每个数据集选取k值的大小由公式 $ k = \left\lfloor {{{\log }_2}n} \right\rfloor + 1 $ 来确定^[23]，其中n是数据集的样本数量， $ \left\lfloor \cdot \right\rfloor $ 表示取对数结果的下整数。在用RBF核函数计算已知k-NN图的边权值时，依据斯科特法则设置高斯核的宽度 $\sigma $ ^[29]，公式为 $ \sigma = \sqrt 5 s{n^{ - 1/(d + 4)}} $ ，其中s为数据集的标准差，n为数据集的样本数量，d为数据集的特征维度。另外，为了避免求解过程中出现自增强效应，权值矩阵主对角线上的元素都设定为 ${{\boldsymbol{W}}_{i,i}} = 0$ 。两个约束正则化项的参数 $ \alpha $ 和 $ \beta $ 在 $\left\{ 0.1,\right. \left.0.3,1,3,10 \right\}$ 中选择，可能性矩阵泛化项的参数 $ {\lambda _1} $ 和 $ {\lambda _2} $ 从 $\{ {2^{ - 4}}, {2^{ - 3}},{2^{ - 2}},{2^{ - 1}},{2^0} \}$ 中选择，通过穷举搜索，约束矩阵的泛化项参数 $ \gamma $ 设置为10。

3.3   评价指标

成对约束传播追求的是模型的预测性能。实验中采用F₁值、精确率(precision)和召回率(recall) 作为评价指标。以必须链接为例，precision表示的是在预测为必须链接的成对约束中，有多少是真正的必须链接，追求precision高，目的在“精”，即希望预测的必须链接中为真的比例越高越好，即使还有很多必须链接没有预测到。recall则指的是真正的必须链接有多少被预测准确了，追求recall高，目的在“全”，即希望所有必须链接都被预测到，即使同时有很多约束被预测错误。仅追求precision或recall某一个高，可能会使预测结果走向极端，而F₁值是二者的调和均值，计算公式为 $F_1=\dfrac{{2\cdot{\text{precision}}\cdot{\text{recall}}}}{{{\text{precision}} + {\text{recall}}}}$ ，它不仅能够兼顾“精”和“全”，又可以克服准确率(accuracy)不能解决的两种链接数量不平衡的问题，因此将F₁值作为最重要的衡量指标。

为了方便计算F₁值、precision和recall，对于传播后的约束矩阵K和F，定义两个结果矩阵 ${\boldsymbol{Q}} = {\boldsymbol{K}} - {\boldsymbol{F}}$ 和 ${\boldsymbol{R}} = {\boldsymbol{F}} - {\boldsymbol{K}}$ 分别来辅助必须链接和不能链接的结果统计，对于每个矩阵，采用不同的阈值离散，以Q为例，离散方法为

其中，TH表示阈值大小，变化范围在0.01~0.09，步长为0.01。将离散后的矩阵与ground-truth值比较，计算出99种情况下的F₁值、precision和recall，并且取F₁值最大时的一组数据作为必须链接（或不能链接）最终的评价值。

由于每个数据集中潜在的必须链接和不能链接的比例不同，所以在综合二者的F₁值时需要调节两个F₁值的比重，数学表示为

式中： ${{F}}_{1_m}$ 和 ${{F}}_{1_c}$ 分别表示必须链接和不能链接的F1值， $\mu $ 为所有潜在不能链接占所有潜在成对约束的比值。precision和recall也采用同样的方法计算。

3.4   实验结果

对每一个数据集，首先从ground-truth值中随机选取1000个初始成对约束，作为精确信息，并且在其他条件改变时这1000个成对约束固定不变。为了减少随机抽样的影响，随机选择初始成对约束20次，并计算这20次的平均性能，作为实验结果。在模拟现实场景中获得的不确定成对约束时，我们将初始可能性矩阵U和V进行人工设定，实验设计为两组。

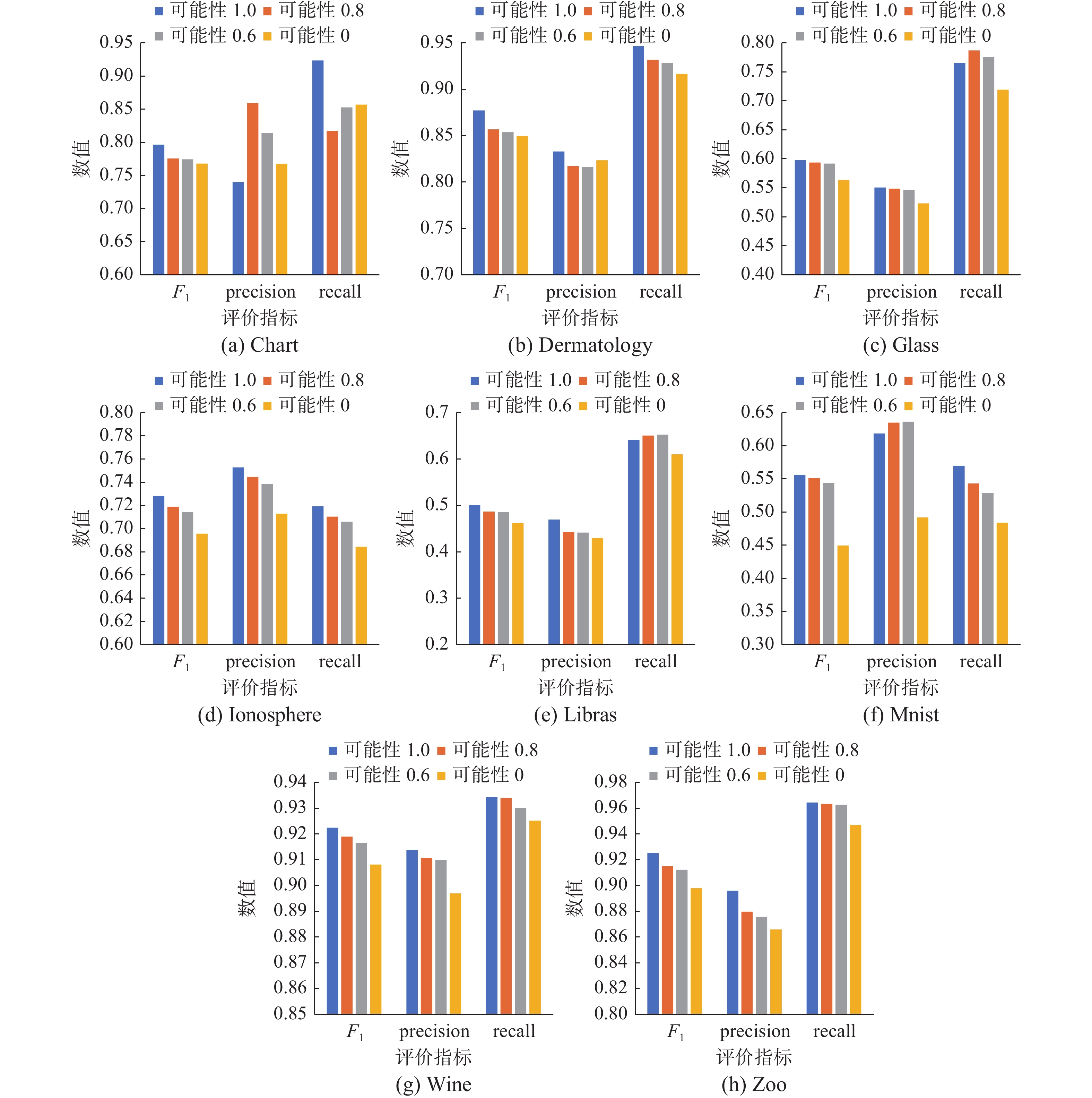
第1组是从已选的1000个精确初始成对约束中随机选取50%为其设定可能性值，这部分成对约束的可能性大小在 $\left\{ {1,0.8,0.6,0} \right\}$ 中变化，观察在不确定成对约束的数量相同时可能性大小对成对约束传播效果的影响。当可能性取1时，实验就简化为这1000个精确的初始成对约束的单对抗传播，如文献[23]中的方法，同样取0时则表示剩下的500个精确的初始成对约束的单对抗传播。实验结果如图2所示。

图  2  可能性大小不同时F₁、precision和recall的值

Fig.  2  F₁, precision and recall against probability

下载: 全尺寸图片

图2直观地展现了在各个数据集上可能性大小对成对约束传播效果的影响。在取50%初始成对约束加入可能性时，不确定成对约束双对抗传播所得到的F₁值虽然略低于1000个精确的初始成对约束单对抗传播的水平，但是通常明显高于去掉这50%初始成对约束的500个精确的初始成对约束单对抗传播的F₁值，在Ionosphere、Libras、Mnist、Wine和Zoo数据集中尤为明显。当赋给这50%的可能性不同时，随着可能性的增大，传播结果的F₁值会升高，并且在超过一半的数据集中呈现较明显的逐步升高趋势。但由于赋值可能性的部分比重较大且为随机，可能会出现一些成对约束的赋值与实际有差距的情况，影响传播效果，导致可能性为0.6~0.8时的F₁值升高不明显。综合来看， UPCP中的可能性信息在成对约束传播时发挥了一定的作用，并且可能性的提升有利于提高传播性能。

另外，实验还选取了两个先进的无对抗的PCP模型进行比较，分别为穷举且有效的约束传播模型(exhaustive and efficient constraint propagation ，E2CP)^[22]和对称图正则化约束传播模型(symmetric graph regularized constraint propagation ，SRCP)^[30]，这两个模型分别选取500和1000个初始成对约束进行测试，并与上述可能性大小为0.6和0.8时的实验结果作比较。E²CP和SRCP都是基于图的方法，其涉及的图构造过程均与UPCP的实验设置相同，两个模型中的 $ \alpha $ 参数均在 $\left\{ {0.2,0.4,0.6,0.8} \right\}$ 中选择。结果矩阵统计方法也与上述实验统一，所得的F₁值如表2所示，最优F₁值加粗标注。同时，讨论UPCP模型自身的鲁棒性，研究在大量给初始成对约束赋可能性值时，随机选取不同的成对约束对传播结果的影响。表2中在UPCP模型的F₁值后添加了随机20次实验的标准差。

表2中，UPCP在可能性为0.6和0.8时的传播性能都明显优于E²CP和SRCP在初始成对约束为500时的传播性能，而当E²CP和SRCP初始成对约束为1000时，除Chart和Dermatology数据集外，UPCP在可能性为0.6和0.8时的F1值也高于E²CP和SRCP模型。由此可见，相对于传统的PCP方法，UPCP在精确的初始成对约束较少的情况下，也能表现出较好的传播性能。另外，UPCP在初始信息大量不确定时的标准差也都比较理想，表现出较好的鲁棒性。

第2组实验是从1000个初始成对约束中，分别随机选取10%、20%、30%、40%和50%加入可能性，设置选到的必须链接对应的 $ {{\boldsymbol{U}}_{i,j}} $ 和不能链接对应的 $ {{\boldsymbol{V}}_{i,j}} $ 大小在 $\left\{ {0.6,0.8} \right\}$ 中变化，并与初始成对约束数量为1000时的精确传播作比较，观察在可能性大小相同时不确定成对约束数量对成对约束传播效果的影响。

从图3可以看到，不确定成对约束的数量也是影响UPCP传播性能的重要因素。以F₁值为观测目标，在每个数据集中，随着不确定成对约束比重的增加，在两种可能性下传播结果的F₁值都逐渐下降，且下降的趋势大致相同。可能性为0.8时的F₁值不会大跨度地下降，总体上，在大部分数据集中，下降的速率存在减缓的趋势。而可能性为0.6时的F₁值会比可能性为0.8时下降得大，同样下降速率也有所减缓。但因为数据集中必须链接和不能链接的不平衡，导致对不确定信息所占比重的敏感度存在差异，下降速率也存在一些波动。由此可以得出结论，当不确定成对约束数量越少时，UPCP的传播效果越好，即便在不确定成对约束数量较多的情况下，UPCP的传播性能也并不会急剧下降，而是尽可能保证传播结果的精准。另外，在8个数据集中，可能性为0.8时的F₁值总是高于可能性为0.6时的F₁值，符合第1组实验的结论。

图  3  加入可能性比重不同时F1值的变化

Fig.  3  Change of F1 value when the proportion of possibility is different

下载: 全尺寸图片

综合以上两组实验，相比于精确的成对约束传播方法的适用范围，UPCP还可用于精确的初始成对约束较少，但存在一定量的不确定初始成对约束的现实场景中，充分挖掘不确定成对约束的潜力，表现出较好传播效果。

4.   结束语

本文提出了一种不确定成对约束的双对抗流形传播模型UPCP，来解决现有PCP模型中仅使用精确的初始必须链接和不能链接进行传播的问题。在已被提出的PCP方法中，通常需要给出一定量的精确的初始成对约束，在这种理想条件下进行传播。考虑到初始成对约束获取过程中受各种客观因素的影响，可获得的精确约束信息很少，我们定义了不确定成对约束这个新概念来表示不精确的初始成对约束。根据现实场景中相关知识的判断，将初始必须链接和不能链接存在的可能性分别保存在两个矩阵中，并让两个可能性矩阵之间形成对抗，同时结合必须链接和不能链接之间的对抗，通过双对抗结构调节对抗强度进行传播，从而有效利用不确定成对约束。实验结果表明，本文提出的方法能够接近于等量初始约束信息情况下的精确传播的效果。接下来，将关注提高不确定成对约束传播的精确度并将其应用于机器学习任务中。