Partial label classification algorithm based on sparse reconstruction disambiguation
-
摘要: 针对现有的大多数方法在消歧过程中缺乏对特征空间潜在有用信息的利用和对候选标签不同置信度水平的考虑的问题，本文提出了一种基于稀疏重构消歧的偏标记学习( partial label learning by sparse reconstruction disambiguation，PL-SRD)的新方法，利用特征空间的结构信息促进标签的消歧过程。本文通过对训练样本进行稀疏重构来刻画特征空间的拓扑结构并将其融入到标签消歧过程中；提出一个统一的框架将标签消歧与训练预测模型同时进行。在人工合成和真实数据集上进行的大量实验表明，本文提出的方法比多个现有的偏标记学习算法取得了更好的性能。Abstract: Most of the existing partial label learning (PLL) methods neither ignores making full use of potentially useful information from feature space, nor considers different labeling confidence levels of the candidate labels in the disambiguation process. In this paper, we propose a novel approach for partial label learning by sparse reconstruction disambiguation (PL-SRD), which facilitates the labeling disambiguation process by leveraging the structural information in feature space. We first characterize the topological structure of feature space by conducting sparse reconstruction among the training examples and integrate it into the label disambiguation process. Then, we present a unified framework, which performs label disambiguation and predictive model training simultaneously. Extensive experimental results on both artificial and real-world datasets demonstrate the superiority of our method to other state-of-the-art PLL methods.
-
偏标记学习（partial label learning, PLL），也被称为模糊标记学习（ambiguous label learning）[1-4]和超级标签学习（superset label learning）[5-6]，是弱监督学习的一个重要分支。在偏标记学习中，每个训练示例分配了一组由一个真实标签和一些噪声标签组成的候选标签集，且训练算法不能直接访问示例的真实标签。由于在许多现实场景中标签完全正确的完美数据难以收集，偏标记学习已经被广泛应用于各个领域，如文本挖掘[7]、自动图像标注[3]、医疗诊断[8]、多媒体内容分析[2,9]、生态信息学[6,10]等。
由于偏标记示例的真实标签信息隐藏在候选标签集中，对于这种带有歧义信息的数据，最常用的方法是消除每个训练示例候选标签的歧义，即在多个候选标签中识别出唯一的正确标签。基于消歧的PLL方法主要有2种，即基于平均的方法和基于辨识的方法。基于平均的方法在模型归纳中对每个候选标签进行同等处理，通过平均所有候选标签的建模输出来进行最终预测[1,11-12]。如果不能充分地将真实标签与无关的噪声标签区分开来，这种简单的方法通常不能获得很好的性能。基于辨识的方法将真实标签视为潜在变量，并通过使用迭代的标签细化过程来识别真实标签[6,13-14]。然而，这些方法在识别过程中多侧重于识别唯一的真实标签，而忽略了其他候选标签做的不同贡献，这可能导致这些方法是次优的。因此，Feng等[15-16]提出了一个新的统一框架将不同的标记置信水平转化为潜在标签分布，并同时训练预测模型。除了消歧的方法外，也有一些方法将偏标记学习问题转化为其他成熟的学习问题来学习[17-18]。近年来，一些研究人员提出了利用特征空间的局部流形结构来帮助候选标签集消歧，并且达到了较好的效果。因此，一个重要的问题是能否从特征空间中提取有用的信息来帮助恢复隐藏的标签分布。
基于上述观察，本文提出了一种基于稀疏重构消歧的偏标记学习( partial label learning by sparse reconstruction disambiguation，PL-SRD)的新方法，具体来说，为了充分利用特征空间的信息，本文基于训练样本之间的稀疏重构关系构造了一个有向图，用以描述特征空间的拓扑结构。然后，根据特征空间的拓扑结构可以通过局部转移到标签空间的平滑假设，利用重构的信息来丰富标签信息的分布，并促进候选标签的消歧过程。此外，为了克服基于辨识的PLL方法通常忽略其他虚假候选标签不同贡献的缺点，将候选标签的不同标签置信度形式化为潜在的标签分布，并提出了一个同时进行标签消歧和预测模型训练的框架，通过交替迭代的方式优化标签置信度矩阵和学习模型。一方面，通过最小化潜在标签分布拟合的最小二乘损失对预测模型进行训练；另一方面，通过建模输出优化潜在的标签分布，借助最优标签分布估计来识别出训练示例的真实标签。在4个人工UCI（University of California Irvine，UCI）数据集和5个真实数据集上的实验上表明，PL-SRD算法比其他现有算法的分类准确率更高。
1. 偏标记学习相关工作
偏标记学习是一个用于从部分标签数据中学习单标签任务的弱监督学习框架，在许多实际应用中得到了广泛的关注。偏标记学习算法中的基本策略是消除候选标签的歧义，也就是从与每个训练示例相关的候选标签集中识别真实标签。现有的策略包括通过平均消除歧义或通过辨识消除歧义。
基于平均的消歧策略是假设每个候选标签的重要性相等，然后通过平均它们的建模输出来进行预测。有不同的方法被用来实例化这个平均过程，其中基于示例的方法对不可见示例的类标签预测是由它的相邻实例的候选标签投票来决定的[1,5,11]。一些参数化方法通过假设一个可以将候选标签和非候选标签的平均建模输出区分开的参数模型来进行消歧[3]。此外，一些研究人员使用参数化模型来描述特征与真实标签之间的函数关系且这些参数是通过训练使得候选标签的平均分数减去非候选标签的平均分数最大化得到的[12]。尽管这个策略是直观且容易实现的，但是它们都存在一些共同的缺点，就是模型的有效性受候选标签集中假阳性标签的影响很大，这可能会降低学习模型的鲁棒性。
基于辨识的消歧策略是假设某一参数化模型，将真实标签作为潜在变量，通过优化某一目标迭代细化。目标函数可以根据不同的方法进行实例化，其中大量方法使用了主要的机器学习技术，如最大似然准则和最大裕度准则。最大似然准则中的似然函数是通过观察每个偏标记训练示例在其候选标签集上的概率来定义的[6,13]。最大裕度准则则是通过最大化每个偏标记训练示例上的候选标签与非候选标签之间的预测差异来定义分类裕度，进一步细化真实标签[14,19-20]。此外，一些研究人员利用增强技术并且通过同时调整训练样本的权值和候选标签的置信度来改进消歧模型[21]。由于不区分地对待标签集中的真实标签，基于辨识的方法识别出的标签可能是假阳性标签而不是潜在的真实标签，并且它们很难在后边的迭代中被纠正，考虑到以上缺点，Chen等[22-23]尝试通过在相应的PLL框架中采用批次标签校正或标签增强过程来改进学习模型。
除了消歧策略外，也有一些方法将偏标记学习问题转换为其他成熟的学习问题来从训练示例中学习。Feng等[15,24]将偏标记问题转换为一个凹凸问题，且证明了凹凸问题的优化等价于一组二次规划（quadratic programming, QP）问题。随着深度神经网络的流行，通过组合不同的网络来提高性能的方法开始崭露头角[25-27]。此外，一些研究者通过对标签空间进行变换，将偏标记学习问题分解为二进制分类[17-18]、多分类[4]或回归问题[12]。近年来，一些研究人员提出了利用特征空间中的图结构对候选标签集产生不同的标签置信，并且取得了相当的效果[28]。
2. PL-SRD方法
偏标记学习框架是假设
${\boldsymbol{\mathcal{X}}} \subset {{\bf{R}}^d}$ 为d维的样本特征空间，$\mathcal{Y} = \{ {l_1},{l_2},\cdots,{l_q}\}$ 表示q个类别标签的标签空间。偏标记学习的目的是从偏标记训练数据集$\mathcal{D} = \{ ({{\boldsymbol{x}}_i},{S_i})|1 \leqslant i \leqslant m\}$ 中推导出一个分类器模型$f:{\boldsymbol{\mathcal{X}}} \to \mathcal{Y}$ ，其中${{\boldsymbol{x}}_i} \in {\boldsymbol{\mathcal{X}}}$ 是d维特征向量$[{x_{i1}} \;\; {x_{i2}}\;\;\cdots \;\; {x_{id}}]^ {\rm{T}}$ ，$ {S_i} \subseteq \mathcal{Y} $ 是与$ {y_i} $ ${{\boldsymbol{x}}_i}$ 相关的候选标签集。此外，每个示例$ {{\boldsymbol{x}}_i} $ 的真实标签存在于其候选标签$ {S_i} $ (即$ {y_i} \in {S_i} $ )中并且在训练阶段不能直接访问。为了便于描述，分别使用${{\boldsymbol{X}}} = {[{x_1}\;\;{x_2}\;\;\cdots\;\;{x_m}]^ {\rm{T}} } \in$ ${{\bf{R}}^{m \times d}}$ 和${{\boldsymbol{Y}}} = {\{ 0,1\} ^{m \times q}}$ 表示偏标记数据集中的特征矩阵和标签矩阵。在这个设置中，$ {Y_{ij}} = 1 $ 表示赋予示例$ {{\boldsymbol{x}}_i} $ 第j个类别标签。PL-SRD的学习过程包括框架形成、模型训练和更新标签置信度3个步骤，以下是这些步骤的技术细节。2.1 框架形成
为了解决PLL问题，本文提出了一个新的统一框架，将标签消歧和预测模型联合优化，以获得较强的泛化性能。此外，在实现消歧的过程中考虑到了特征空间中的多重结构也应保持在标签空间中的光滑性假设，并通过规范的稀疏表示描述特征空间的结构信息。
本文通过构造一个加权有向图
${{{G}}} =$ $(V,E,{{\boldsymbol{W}}})$ 来刻画特征空间的拓扑结构信息，其中顶点集合$V = \{ {{\boldsymbol{x}}_i}|1 \leqslant i \leqslant m\}$ 对应于训练实例集，有向边$E = \{ ({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j})|{w_{ij}} \ne 0,$ $ 1 \leqslant i \ne j \leqslant m\} $ 连接任意一对非零权重的示例$ {{\boldsymbol{x}}_i} $ 和$ {{\boldsymbol{x}}_j} $ ，相似权重矩阵${{\boldsymbol{W}}} = {[{w_i}_j]_{m \times m}}$ 描述所有示例之间的关系，$ {w_i}_j $ 表示示例${{\boldsymbol{x}}_j}$ 对${{\boldsymbol{x}}_i}$ 的影响。为了全面而简洁地利用所有训练示例之间的关系，本文利用稀疏重构的方法来对一个示例与其他示例之间的关系进行建模，从而实现相似权重矩阵${{\boldsymbol{W}}}$ 的实例化。PL-SRD的目标是从训练集中的其他示例(即$ V\backslash \{ {{\boldsymbol{x}}_i}\} $ )中重构出示例$ {{\boldsymbol{x}}_i} $ 。设${{\boldsymbol{A}}_i} = [{x_1}\;\; {x_2}\;\; \cdots \;\; {x_{i - 1}}\;\;{x_{i + 1}}\;\; \cdots \;\;{x_m}] $ ；${\boldsymbol{A}}_i $ 表示除示例${{\boldsymbol{x}}_i}$ 之外的所有示例形成的$d \times (m - 1)$ 维矩阵；${{\boldsymbol{u}}_i} = [{w_{1i}}\;\;{w_{2i}}\;\; \cdots \;\;{w_{(i - 1)i}}\;\; {w_{(i + 1)i}}\;\; \cdots \;\;$ ${w_{mi}}]^{\rm{T}} $ ，${\boldsymbol{u}}_i$ 表示$ (m - 1) $ 维重构系数。在规范的稀疏表示下，重构系数向量通过求解以下优化问题得到：$$ \mathop {\min }\limits_{{{\boldsymbol{u}}_i}} \left\| {{{{\boldsymbol{A}}}_i}{{\boldsymbol{u}}_i} - {x_i}} \right\|_2^2 + \lambda {\left\| {{{\boldsymbol{u}}_i}} \right\|_1} $$ (1) 式中：第1项通过L2范数控制线性重构误差，第2项通过L1范数控制重构系数的稀疏性，正则化参数
$ \lambda $ 用来权衡每一项的相对重要性。为了求解式(1)的优化${{\boldsymbol{u}}_i}$ 问题，本文采用流行的交替方向乘子法（alternating direction method of multiplier，ADMM）[29-30]将上述优化问题重新表述为$$ \begin{array}{c} \mathop {\min }\limits_{\{ {u_i},{v_i}\} } \left\| {{{{\boldsymbol{A}}}_i}{{\boldsymbol{u}}_i} - {{\boldsymbol{x}}_i}} \right\|_2^2 + \lambda {\left\| {{{\boldsymbol{v}}_i}} \right\|_1},\;\; {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{u}}_i} - {{\boldsymbol{v}}_i} = 0 \end{array} $$ (2) 根据ADMM迭代求解过程，式(2)中的约束优化问题可以转化为如下的增广拉格朗日函数：
$$ \begin{array}{c} L({{\boldsymbol{u}}_i},{{\boldsymbol{v}}_i},{{\boldsymbol{\alpha}} _i}) = \displaystyle \frac{1}{2}\left\| {{{{\boldsymbol{A}}}_i}{{\boldsymbol{u}}_i} - {{\boldsymbol{x}}_i}} \right\|_2^2 + \\ {\text{ }}\lambda {\left\| {{{\boldsymbol{v}}_i}} \right\|_1} + {\boldsymbol{\alpha}} _i^ {\rm{T}} ({{\boldsymbol{u}}_i} - {{\boldsymbol{v}}_i}) + \displaystyle \frac{\rho }{2}\left\| {{{\boldsymbol{u}}_i} - {{\boldsymbol{v}}_i}} \right\|_2^2 \\ \end{array} $$ (3) 式中：第4项为添加的平方正则项，用来削弱式(3)第1项严格凸的要求；
$ \rho $ 为惩罚参数；${{\boldsymbol{\alpha}} _i}$ 、${{\boldsymbol{u}}_i}$ 为拉格朗日乘数；变量${{\boldsymbol{v}}_i}$ 和${{\boldsymbol{\alpha}} _i}$ 的最优化解通过ADMM迭代生成：$$ \left\{\begin{split} {\boldsymbol{u}}_i^{(k + 1)} = &{({{\boldsymbol{A}}}_i^ {\rm{T}} {{{\boldsymbol{A}}}_i} + \rho {{\boldsymbol{I}}})^{ - 1}}({{\boldsymbol{A}}}_i^ {\rm{T}} {{\boldsymbol{x}}_i} + \rho {\boldsymbol{v}}_i^{(k)} - {\boldsymbol{\alpha}} _i^{(k)}) \\ {\boldsymbol{ v}}_i^{(k + 1)} = &{({\boldsymbol{u}}_i^{(k + 1)} + {\boldsymbol{\alpha}} _i^{(k)}/\rho - \lambda /\rho )_ + } - \\ &{( - ({\boldsymbol{u}}_i^{(k + 1)} + {\boldsymbol{\alpha}} _i^{(k)}/\rho ) - \lambda /\rho )_ + } \\ {\boldsymbol{\alpha}} _i^{(k + 1)} = &{\boldsymbol{\alpha}} _i^{(k)} + \rho ({\boldsymbol{u}}_i^{(k + 1)} - {\boldsymbol{v}}_i^{(k + 1)}) \\ \end{split}\right. $$ (4) 根据ADMM方法求解式(2)中的稀疏重构问题，最终的相似权重矩阵
${{\boldsymbol{W}}}$ 由重构系数$ {{\boldsymbol{u}}_i}(1 \leqslant i \leqslant m) $ 和零对角元素实例化生成。此外，示例$ {{\boldsymbol{x}}_i} $ 在重构示例$ {{\boldsymbol{x}}_j} $ 时的影响一般不同于示例$ {{\boldsymbol{x}}_j} $ 在重构示例$ {{\boldsymbol{x}}_i} $ 时的影响，所以在大多数情况下$ {w_{ij}} \ne {w_{ji}} $ 。相似权重矩阵${{\boldsymbol{W}}}$ 表征了特征空间中拓扑结构信息，根据特征空间的拓扑结构可以通过局部转移到标签空间的平滑假设，相似权重矩阵在特征空间中指定的结构关系也应保持在标签空间中，即$ {{\boldsymbol{x}}_i} $ 对$ {{\boldsymbol{x}}_j} $ 的影响也传递给了$ {p_i} $ 对$ {p_j} $ 的影响。本文利用相似矩阵${{\boldsymbol{W}}}$ 编码的结构信息生成丰富的标签信息，进而达到对候选标签消歧的目的。标签置信度矩阵${{\boldsymbol{P}}} = {[{p_1}\quad {p_2}\quad\cdots\quad {p_m}]^ {\rm{T}} }\in$ $ {{{\bf{R}}}^{m \times q}}$ 可以通过解决以下问题来确定：$$ \begin{gathered} \mathop {\min }\limits_{\boldsymbol{P}} \sum_{i = 1}^m {\left\| {{p_i} - \sum_{j = 1}^m {{w_{ji}}{p_j}} } \right\|_2^2}, \;\; {\text{s}}{\text{.t}}{\text{. }}\sum_{j = 1}^q {{p_{ij}} = 1,\forall i \in [m]} \\ \end{gathered} $$ (5) 此外，为了缓解训练过程中忽略候选标签的不同标签置信水平这一缺点，在充分考虑平滑假设和模型输出的情况下，本文将真实标签矩阵作为潜在标签置信矩阵，并提出了一个新的统一框架，在训练模型的同时估计潜在标签分布：
$$ \min \sum\limits_{i = 1}^m {L({x_i},{p_i},{f} ) + \mu \varOmega ({f} )} + \beta \varPsi ({{\boldsymbol{P}}}) $$ (6) 式中：
$L(\cdot)$ 为损失函数，本文使用最小二乘损失对预测模型进行优化，即$L({x_i},{p_i},{f} ) = \left\| {{{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{x_i} + {{\boldsymbol{b}}} - {p_i}} \right\|_2^2$ ，其中模型参数为${{\boldsymbol{\varTheta}} }$ $\in {{{\bf{R}}}^{d \times q}}$ ,${{\boldsymbol{b}}}$ $\in {{{\bf{R}}}^{q \times 1}}$ ；$\varOmega ({f} )$ 控制模型复杂度，本文采用常用的平方Frobenius范数；$\varPsi ({{\boldsymbol{P}}})$ 为正则化项，保证标签置信度矩阵${{\boldsymbol{P}}}$ 的最优估计；$ \mu $ 和$ \beta $ 为控制3项平衡的参数。最后，将所提出的正则化项整合到统一的框架中，得到最终的约束优化问题为$$ \left\{\begin{split} & \mathop {\min }\limits_{{{\boldsymbol{P}}},{{\boldsymbol{\varTheta}} },{{\boldsymbol{b}}}} \bigg(\sum\limits_{i = 1}^m {\left\| {{{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{{\boldsymbol{x}}_i} + {{\boldsymbol{b}}} - {p_i}} \right\|_2^2} + \\ & \quad\quad\beta \sum\limits_{i = 1}^m {\left\| {{p_i} - \sum_{j = 1}^m {{w_{ji}}{p_j}} } \right\|_2^2} + \mu \left\| {{\boldsymbol{\varTheta}} } \right\|_F^2 \bigg)\\ & {\text{s}}{\text{.t}}.\sum_{j = 1}^q {{p_{ij}} = 1,\forall i \in [m]} \\ & {0_{m \times q}} \leqslant {{\boldsymbol{P}}} \leqslant {{\boldsymbol{Y}}} \\ \end{split} \right.$$ (7) 式中：第1个约束项保证在标签传播过程分配给每个示例的标签分布是一致的；第2个约束项则保证标签只在候选标签之间传播且真实标签严格地出现在候选标签集中，每个非候选标签的标签置信度必须为0。显然，上述优化问题是一个双凸优化问题[31]，本文采用交替优化方法解决这个问题。首先，通过固定变量
${{\boldsymbol{P}}} $ ，${w_{ij}} \ne {w_{ji}} $ 优化目标函数${{\boldsymbol{\varTheta}} }$ 和${{\boldsymbol{b}}}$ ，然后固定变量${{\boldsymbol{\varTheta}} }$ 和${{\boldsymbol{b}}}$ 优化目标函数${{\boldsymbol{P}}}$ 。不断重复这个过程，直到算法收敛或达到最大迭代次数。2.2 模型训练
在固定变量
${{\boldsymbol{P}}}$ 的基础上，利用简单的线性模型${{f}}({{\boldsymbol{x}}_i},{{\boldsymbol{\varTheta}} }) = {{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{{\boldsymbol{x}}_i} + {{\boldsymbol{b}}}$ 将优化问题式(7)表示为$$ \mathop {\min }\limits_{{{\boldsymbol{\varTheta}} },{{\boldsymbol{b}}}}\left( \sum\limits_{i = 1}^m {\left\| {{{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{{\boldsymbol{x}}_i} + {{\boldsymbol{b}}} - {p_i}} \right\|_2^2} + \mu \left\| {{\boldsymbol{\varTheta}} } \right\|_F^2\right) $$ (8) 式(8)的损失函数是可微的，可以通过标准的梯度下降算法进行优化。为了获得更好的预测模型性能，本文进一步对一般的非线性情况进行内核扩展，即
${z_i} = \varphi ({{\boldsymbol{x}}_i})$ ，其中$\varphi (\cdot):{{\bf{R}}}^{d}\to {{\bf{R}}}^{h}$ 表示特征映射，将特征空间映射到某个具有h维的高维希尔伯特空间。基于核扩展的预测函数可以表示为${{f}}({{\boldsymbol{x}}_i},{{\boldsymbol{\varTheta}} }) = {{{\boldsymbol{\varTheta }}}^{\rm{T}} }{{\text{z}}_i} + {{\boldsymbol{b}}}$ ，可以通过最小化以下目标函数来计算模型参数${{\boldsymbol{\varTheta}} }$ 和${{\boldsymbol{b}}}$ ：$$ \begin{gathered} \mathop {\min }\limits_{{{\boldsymbol{\varTheta}} },{{\boldsymbol{b}}}} \left(\sum\limits_{i = 1}^m {\left\| {{\xi _i}} \right\|_2^2} + \mu \left\| {{\boldsymbol{\varTheta}} } \right\|_F^2\right) \\ {\text{s}}{\text{.t}}{\text{. }}{p_i} = {{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{z_i} + {{\boldsymbol{b}}} - {\xi _i} \end{gathered} $$ (9) 通过定义一个矩阵
${{\boldsymbol{\varXi}} } = {[{\xi _1}\quad{\xi _2}\quad\cdots\quad{\xi _m}]^ {\rm{T}} } \in$ 可以将式(9)重写为$$ \begin{gathered} \mathop {\min }\limits_{{{\boldsymbol{\varTheta}} },{{\boldsymbol{b}}}}\left( [{{\rm{tr}}} ({{{\boldsymbol{\varXi}} }^ {\rm{T}} }{{\boldsymbol{\varXi}} }) ]+ \mu {{\rm{tr}}} ({{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{{\boldsymbol{\varTheta}} }){{{\bf{R}}}^{m \times q}}\right) \\ {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{P}}} = {{\boldsymbol{Z}}{\boldsymbol{\varTheta}} } + {{{\mathbf{1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} } - {{ \boldsymbol{\varXi}} } \\ \end{gathered} $$ (10) 式中：
${{{\mathbf{1}}}_m} = {[1\quad1\quad\cdots\quad1]^ {\rm{T}} }$ $\in {{{\bf{R}}}^m}$ ；$ \mathrm{tr}(\cdot) $ 为矩阵的迹。由于式(10)是一个约束优化问题，可以用拉格朗日乘子来求解，该问题的拉格朗日函数为$$ \begin{gathered} L({{\boldsymbol{\varTheta}} },{{\boldsymbol{b}}},{{\boldsymbol{\varXi}} },{{\boldsymbol{A}}}) = {{\rm{tr}}} ({{{\boldsymbol{\varXi}} }^ {\rm{T}} }{{\boldsymbol{\varXi}} }) + \mu {{\rm{tr}}} ({{{\boldsymbol{\varTheta}} }^ {\rm{T}} }{{\boldsymbol{\Theta}} }) - \\ {{\rm{tr}}} ({{{\boldsymbol{A}}}^ {\rm{T}} }({{\boldsymbol{Z}}{\boldsymbol{\varTheta}} } + {{{{\mathbf1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} } - {{\boldsymbol{\varXi}} } - {{\boldsymbol{P}}})) \end{gathered} $$ (11) 式中：
${{\boldsymbol{A}}} = {[{\alpha _1}\quad{\alpha _2}\quad\cdots\quad{\alpha _m}]^ {\rm{T}} }$ $\in {{{\bf{R}}}^{m \times q}}$ 为拉格朗日乘子矩阵。根据KKT（Karush-Kuhn-Tucker）条件求最优解可导出方程为$$ \left\{\begin{split} &\frac{{\partial L}}{{\partial {{\boldsymbol{\varTheta}} }}} = 2\mu {{\boldsymbol{\varTheta}} } - {{{\boldsymbol{Z}}}^ {\rm{T}} }{{\boldsymbol{A}}} = 0 \\ &\frac{{\partial L}}{{\partial {{\boldsymbol{b}}}}} = {{{\boldsymbol{A}}}^ {\rm{T}} }{{{\mathbf{1}}}_m} = 0\\ &\frac{{\partial L}}{{\partial {{\boldsymbol{\varXi}} }}} = 2{{\boldsymbol{\varXi}} } + {{\boldsymbol{A}}} = 0 \\ &\frac{{\partial L}}{{\partial {{\boldsymbol{A}}}}} = {{\boldsymbol{Z}}{\boldsymbol{\varTheta}} } + {{{\mathbf{1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} } - {{\boldsymbol{\varXi}} } - {{\boldsymbol{P}}} = 0 \end{split} \right.$$ (12) 从式（12）的线性方程可以得到：
$$ {{{\boldsymbol{b}}}^ {\rm{T}} } = \frac{{{{\mathbf{1}}}_m^ {\rm{T}} {{{\boldsymbol{\varGamma}} }^{ - 1}}{{\boldsymbol{P}}}}}{{{{\mathbf{1}}}_m^ {\rm{T}} {{{\boldsymbol{\varGamma} }}^{ - 1}}{{{{1}}}_m}}},{{\boldsymbol{A}}} = {{{\boldsymbol{\varGamma} }}^{ - 1}}({{\boldsymbol{P}}} - {{{\mathbf{1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} }) $$ (13) 式中：
${{\boldsymbol{\varGamma} }} = \displaystyle \frac{1}{{2\mu }}{{\boldsymbol{K}}} - \displaystyle \frac{1}{2}{{{\boldsymbol{I}}}_{m \times m}}$ ，且${{\boldsymbol{K}}} = {{\boldsymbol{Z}}}{{{\boldsymbol{Z}}}^ {\rm{T}} }$ ，根据对应的核函数$ \kappa (\cdot) $ ，其元素$ {k_{ij}} = \kappa ({x_i},{x_j}) = $ ${\boldsymbol{\phi}} ({x_i}){\boldsymbol{\phi}}^ {\rm{T}} {({x_j}) }$ 。对于PL-SRD，核函数使用高斯核函数$ \kappa ({x_i},{x_j}) = $ $\exp \left( - \displaystyle \frac{{\left\| {{x_i} - {x_j}} \right\|_2^2}}{{{\sigma ^2}}}\right)$ ，$ \sigma $ 为每对训练样本之间的平均距离。在固定${{\boldsymbol{P}}}$ 的基础上，建模输出矩阵为$${{\boldsymbol{Q}}} = {{\boldsymbol{Z}}{\boldsymbol{\varTheta}} } + {{{\mathbf{1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} } =\displaystyle \frac{1}{{2\mu }}{{\boldsymbol{KA}}} + {{{\mathbf{1}}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} }。 $$ 2.3 更新置信度
由于观察到的标签矩阵
${{\boldsymbol{Y}}}$ 在偏标记学习中是一个噪声损坏的版本，本文将建模输出矩阵${{\boldsymbol{Q}}}$ $\in {{{\bf{R}}}^{m \times q}}$ 作为每个优化迭代的初始标签矩阵，从而通过迭代调整每个候选标签的置信度。在固定${{\boldsymbol{\varTheta}} }$ 和${{\boldsymbol{b}}}$ 的基础上，式(7)的优化问题可以表述为$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{P}}}\left( \left\| {{{\boldsymbol{Q}} - {\boldsymbol{P}}}} \right\|_F^2 + \beta \displaystyle \sum\limits_{i = 1}^m {\left\| {{p_i} - \displaystyle \sum_{j = 1}^m {{w_{ji}}{p_j}} } \right\|_2^2} \right) \\ {\text{s}}{\text{.t}}.\displaystyle \sum_{j = 1}^q {{p_{ij}} = 1,\forall i \in [m]} \\ {{\boldsymbol{0}}_{m \times q}} \leqslant {{\boldsymbol{P}}} \leqslant {{\boldsymbol{Y}}} \\ \end{gathered} $$ (14) 这个优化问题实际上是一个约束标签传播问题[32]，其中
$ \beta $ 用来平衡来自邻近点的标签信息和建模输出。为了解决式(14)，假设${\tilde {\boldsymbol{p}}} = {\rm{ vec}}({{\boldsymbol{P}}}) \in {[0,1]^{mq}}$ ，${\tilde {\boldsymbol{q}}} = {\rm{vec}}({{\boldsymbol{Q}}})$ $\in {{{\bf{R}}}^{mq}}$ ，${\tilde {\boldsymbol{y}}} = {\rm{vec}}({{\boldsymbol{Y}}}) \in {\{ 0,1\} ^{mq}}$ 且$ {\rm{vec}}(\cdot) $ 为矢量化算子。此外，为了使用${\tilde {\boldsymbol{p}}}$ 处理等式约束，通过定义一个集合$ \varepsilon $ 来获取${\tilde {\boldsymbol{p}}}$ 的下标：$$ \varepsilon = \{ {\varepsilon _0},{\varepsilon _1},\cdots,{\varepsilon _{m - 1}}\} $$ (15) $j \in {\varepsilon _i}$ ，如果$j\% m = i$ ，$ \forall j\in [mq] $ 。为了方便优化目标函数，本文将式(14)重新定义为一个标准的二次规划(QP)问题：$$ \begin{array}{c}\underset{\tilde{p}}{\mathrm{min}}\left(\displaystyle \frac{1}{2}{\tilde{{\boldsymbol{p}}}}^{{\rm{T}} }\tilde{{\boldsymbol{H}}}\tilde{{\boldsymbol{p}}}+{\tilde{{\boldsymbol{c}}}}^{{\rm{T}} }\tilde{{\boldsymbol{p}}}\right)\\ \mathrm{s.t.}\displaystyle\sum_{j\in {\varepsilon }_{i}}{\tilde{p}}_{j}=1\text{，}\forall {\varepsilon }_{i}\subseteq \varepsilon \\ {{{{\mathbf{0}}}}}_{mq}\leqslant \tilde{{\boldsymbol{p}}}\leqslant \tilde{{\boldsymbol{y}}}\end{array} $$ (16) 式中：
${\tilde {\boldsymbol{c}}} = - 2{\tilde {\boldsymbol{q}}}$ ；$\tilde {\boldsymbol{H}}$ $\in {{{\bf{R}}}^{mq \times mq}}$ 定义为$$ \tilde {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{T}}}&{{{\mathbf{0}}_{m \times m}}}& \cdots &{{{\mathbf{0}}_{m \times m}}} \\ {{{\mathbf{0}}_{m \times m}}}&{\tilde {\boldsymbol{T}}}& \ddots & \vdots \\ \vdots & \ddots & \ddots &{{{\mathbf{0}}_{m \times m}}} \\ {{{\mathbf{0}}_{m \times m}}}& \cdots &{{{\mathbf{0}}_{m \times m}}}&{\tilde {\boldsymbol{T}}} \end{array}} \right] $$ (17) 式中：
${\tilde {\boldsymbol{T}}} = 2((\beta + 1){{\boldsymbol{I}}_{m \times m}} + \beta ({{\boldsymbol{W}}^ {\rm{T}} }{\boldsymbol{W}} + ({{\boldsymbol{W}}^ {\rm{T}} }{1_{m \times m}}{{\boldsymbol{W}}})\odot {{\boldsymbol{I}}_{m \times m}} -$ $ 2{\boldsymbol{W}}))$ $\in {{\mathbf{R}}^{m \times m}}$ 为一个方阵，$ \odot $ 为哈达玛积运算，${{\boldsymbol{I}}_{m \times m}}$ 为单位矩阵。这样，借助任何现成的QP工具都可以有效地解决式(16)。在整个优化过程完成后，PL-SRD对测试示例
$ x $ 的预测结果为$$ {y^*} = \mathop {\arg \max }\limits_{k \in \left[ q \right]} \mathop \sum \limits_{i = 1}^m {\alpha _{ik}}\kappa \left( {x,{x_i}} \right) + {b_k} $$ (18) 本文方法的伪代码如下。在整个优化过程中，首先基于稀疏表示构建相似权重矩阵并初始化所需的变量（步骤1）~4）），然后重复（步骤6）~8）），直到算法收敛或达到最大迭代次数。最后，对未见示例进行预测。
算法 PL-SRD伪代码
输入
$\mathcal{D} = \{ ({x_i},{S_i})|1 \leqslant i \leqslant m\} $ 为偏标记训练数据集，$\lambda $ 为稀疏重构的正则化参数，$ \mu $ 、$ \beta $ 为损失函数的权衡参数，$ k $ 为近邻样本数目，$ x $ 为测试样本。训练过程：
1）根据式（4）求解重构系数；
2）根据
${u_i}$ 构建相似权重矩阵${{\boldsymbol{W}}}$ ；3）计算核矩阵
${{\boldsymbol{K}}} = {[\kappa ({x_i},{x_j})]_{m \times m}}$ ；4）根据
${{\boldsymbol{W}}}$ 和式（5）初始化${{\boldsymbol{P}}}$ ；5） repeat；
6）根据式（13）更新
${{\boldsymbol{b}}}$ 和${{\boldsymbol{A}}}$ ；7)更新模型输出矩阵
${\boldsymbol{Q}}={\boldsymbol{Z}} {\boldsymbol{\varTheta}} +{{{{\mathbf{1}}}}}_{m}{{\boldsymbol{b}}}^{\rm{T} }=\displaystyle \frac{{\mathbf{1}}}{{2\mu }}$ ${{\boldsymbol{KA}}} + {\mathbf{\boldsymbol{1}}_m}{{{\boldsymbol{b}}}^ {\rm{T}} }$ ；8)通过常用的QP工具求解式（16）更新
${{\boldsymbol{P}}}$ ；9) until 收敛或达到最大迭代次数。
输出 根据式（18）得到测试样本的预测标记
${y^*}$ 。3. 实验及结果分析
3.1 实验设置
为了验证本文提出方法PL-SRD的性能，本文分别在4组人工合成数据集和6个真实数据集上进行实验。数据集信息分别见表1与表2，包括样本数、特征数和类别数目，真实数据集还给出样本的平均候选标记集合大小。人工数据集包括4个传统的UCI分类数据集，通过控制
$p$ 、$r$ 和$\varepsilon $ 等3个参数将每个UCI数据集合成为偏标记数据集，其中，$p$ 控制合成数据集中偏标记示例所占比例，$r$ 控制候选标签集中假阳性标签的数量，$\varepsilon $ 控制特定的假阳性标签与真标签同时出现的概率。本文实验中的28个(4×7)参数配置见表1。表 1 UCI数据集的数据特征Table 1 Characteristics of UCI data sets数据集 样本数 特征数 类别数目 参数设置 Deter 358 23 6 $r = 1,p \in \{ 0.1,0.2,\cdots,0.7\}$ Vehicle 846 18 4 $r = 2,p \in \{ 0.1,0.2,\cdots,0.7\}$ Segment 2310 18 7 $r = 3,p \in \{ 0.1,0.2,\cdots,0.7\}$ Usps 9298 256 10 $p = 1,r = 1,\varepsilon \in \{ 0.1,0.2,\cdots,0.7\}$ 表 2 真实数据集的数据特征Table 2 Characteristics of real-world data sets数据集 样本数 特征数 类别数目 平均候选标记数 FG-NET 1002 262 78 7.48 Lost 1122 108 16 2.23 MSRCv2 1758 48 23 3.16 Mirflickr 2780 1536 14 2.76 Soccer Player 17472 279 171 2.09 Yahoo! News 22991 163 219 1.91 真实世界的数据集来源于不同的应用领域，例如FG-NET[33]数据集来自于面部年龄估计，Lost[1]、Soccer Player[2]和Yahoo!News[34]数据集来自于图像和视频中的人脸标注，MSRCv2[6]数据集来自于目标检测领域，Mirflickr[35]来自于web图像分类。每个数据集的基本特征见表2。
为了验证提出算法PL-SRD的有效性，本文采用了5种常用的偏标记学习算法进行比较研究。
PL-KNN[1]：一种基于平均的消歧方法，采用
$ k $ 近邻的加权投票对示例进行预测，近邻样本数设置为$k = 10$ 。LSB_CMM[6]：一种基于辨识的消歧方法，通过混合模型进行学习的最大似然方法，其中混合成分个数设置为
$q$ (即类别个数)。PL-ECOC[18]：一种基于非消歧策略的方法，采用纠错输出编码（error-correcting output codes，ECOC）技术将偏标记学习问题分解成若干个二分类学习问题来学习预测模型，编码长度设为
$L = \left\lceil {{{\log }_2}\left( q \right)} \right\rceil $ 。LALO[16]：一种基于辨识的消歧方法，通过参数模型估计候选标签置信度的潜在分布，并采用标签传播的方式来更新置信度，近邻样本数设置为
$k = 10$ ，最大迭代次数设置为$T = 100$ 。PL-AGGD[28]：一种基于辨识的消歧方法，采用自适应图引导的方法实现消歧，并同时进行标签消歧和预测模型的训练，近邻样本数设置为
$k = 10$ ，最大迭代次数设置为$T = 20$ 。3.2 人工数据集实验
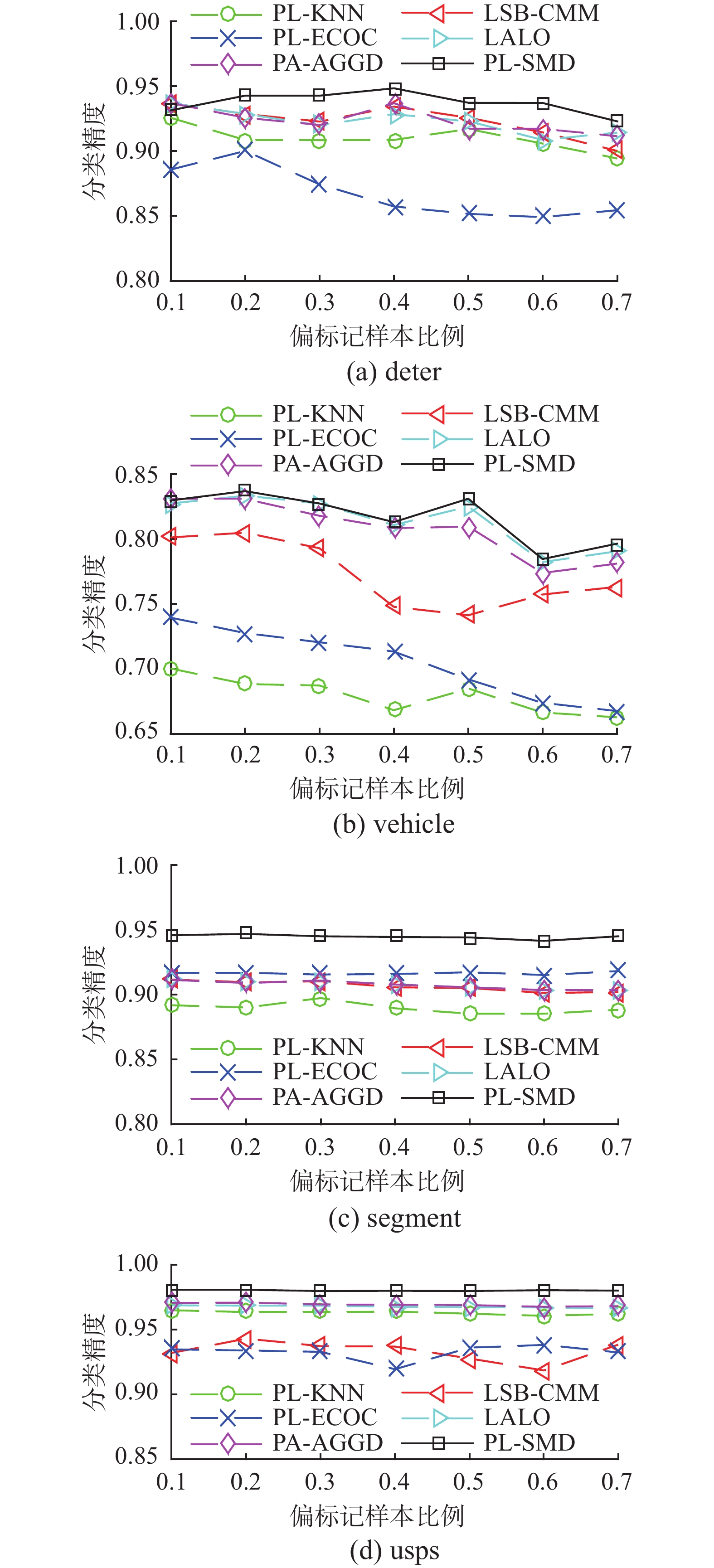
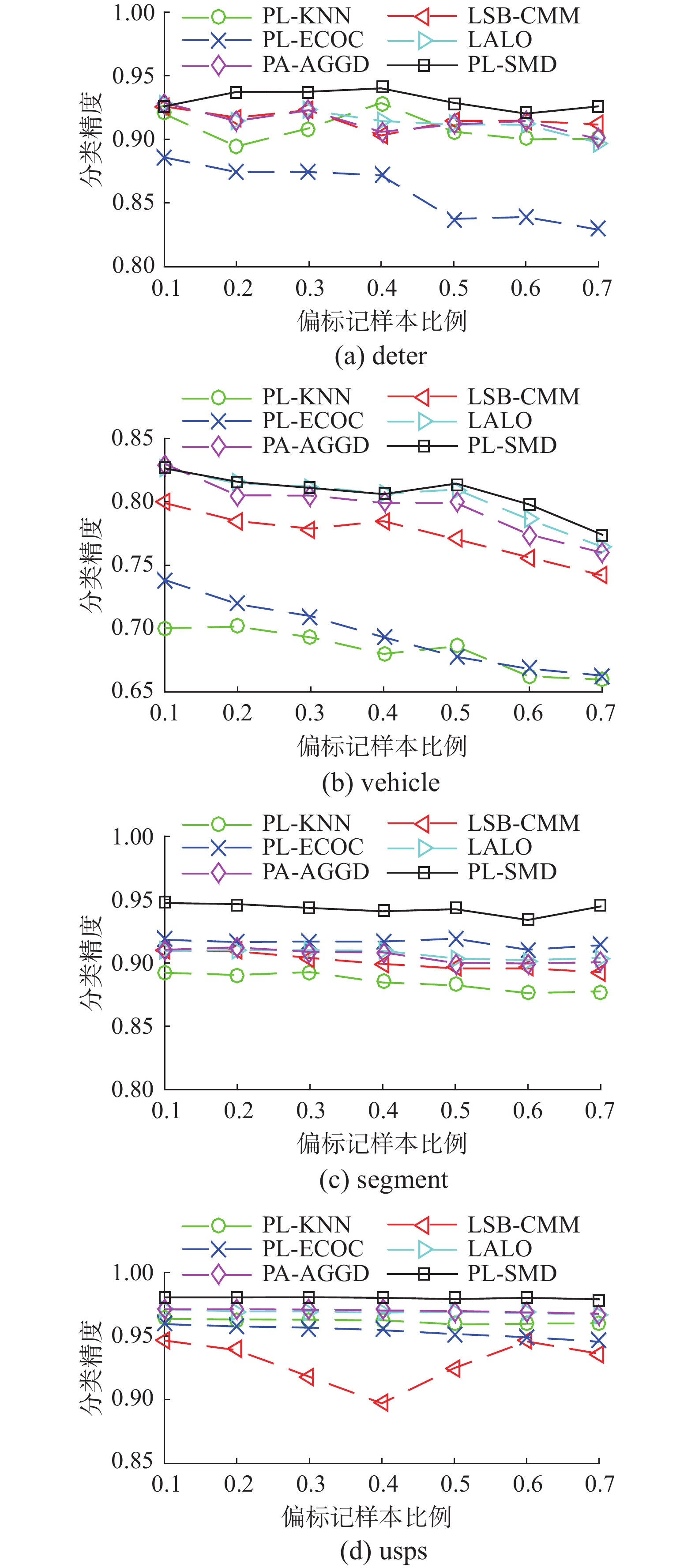
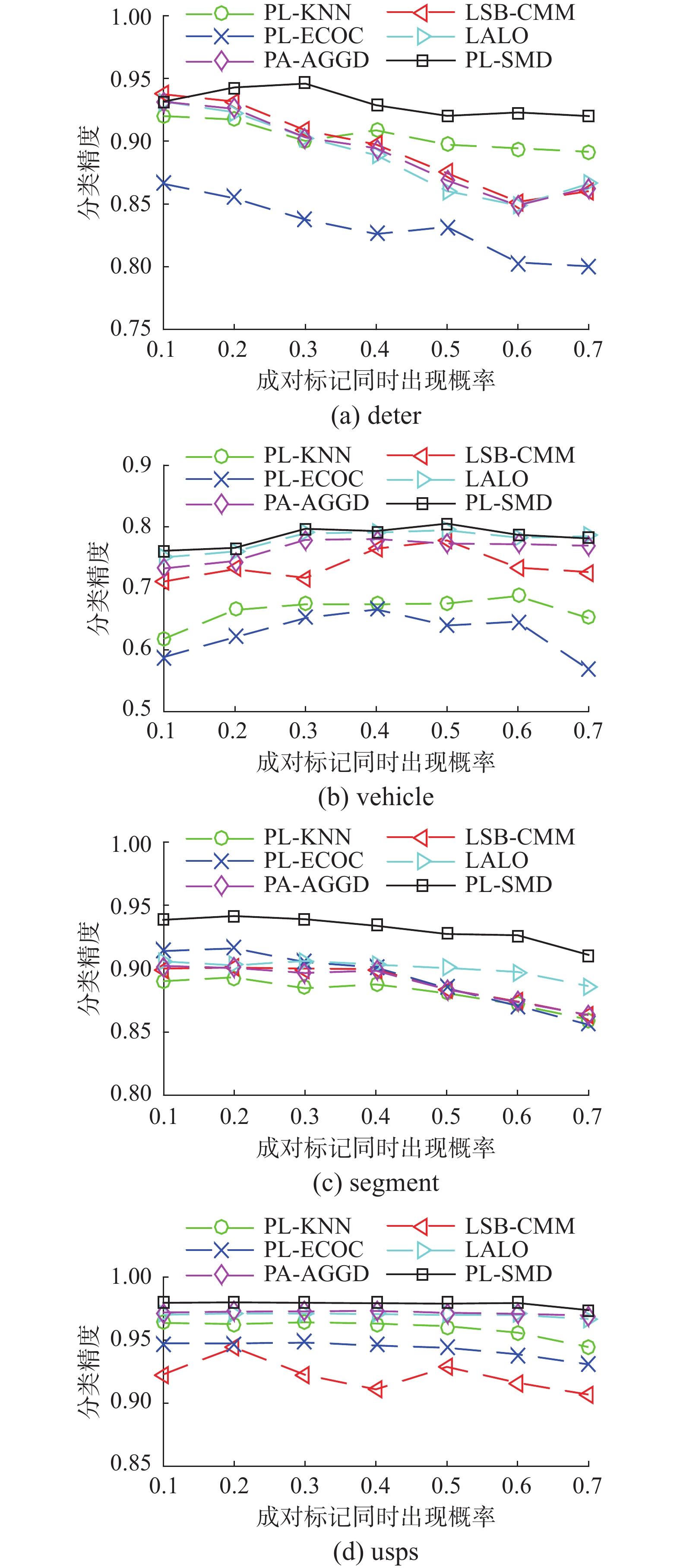
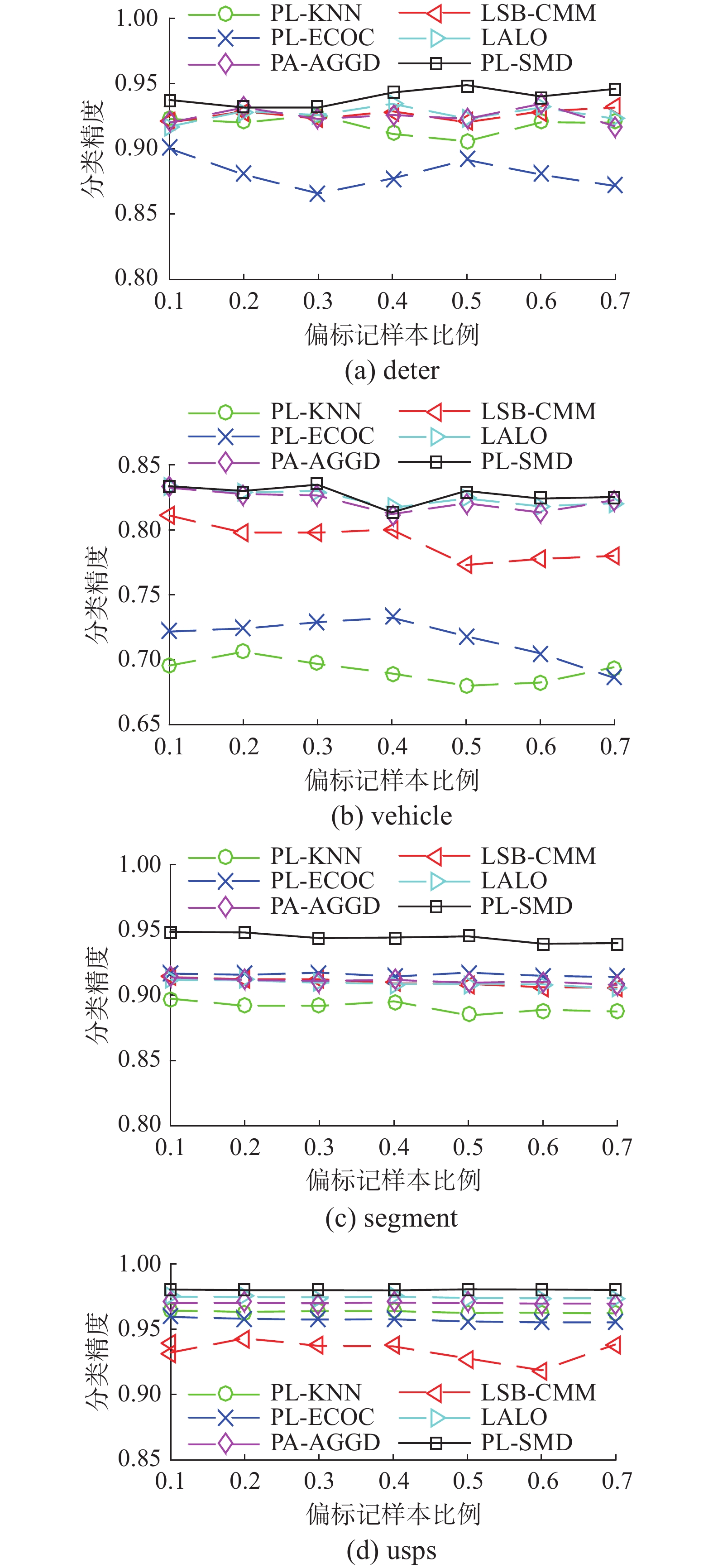
图1~3给出了PL-SRD和其他5种对比算法在4个UCI数据集上的性能表现，分别为假阳性候选标记数目
$r = 1$ ，$r = 2$ 和$r = 3$ 时偏标记样本比例$p$ 从0.1增长到0.7的分类准确率。图4给出了在UCI数据集上，$r = 1$ ，$ p=1 $ 时成对标记同时出现概率$\varepsilon $ 随着步长为0.1，从0.1~0.7变化时各种算法的分类准确率。其中，图4(a)~(d)分别为4个数据集对应的结果图。从图1~4可以发现，PL-SRD在大多数情况下性能优于或持平于其他对比算法，且随着$p$ 或$\varepsilon $ 的增大，deter和vehicle这2个数据集的分类准确率逐渐上升并达到一个峰值，同传统PL-KNN、LSB_CMM、PL-ECOC、PL-AGGD算法相比，PL-SRD的峰值表现更高。此外，由于PL-SRD的分类精度依赖于特征空间中稀疏重构的相似权重矩阵${{\boldsymbol{W}}}$ 的质量，而usps数据集的特征维数远超其他UCI数据集，构造的权重矩阵${{\boldsymbol{W}}}$ 更加全面且准确。因此，随着$p$ 或$\varepsilon $ 的增大，usps数据集上的分类准确率无显著变化。表3总结了基于显著程度为0.05的成对$t$ 检验4个数据集上所有情况下PL-SRD优于/持平/劣于其他比较算法的计数分布。通过112个结果，可以得出以下结论：
图 1$r = 1$ 时各算法在4个数据集上的性能表现Fig. 1 Performance of each algorithm on four datasets with$r = 1$ 
下载:
全尺寸图片
图 2$r = 2$ 时各算法在4个数据集上的性能表现Fig. 2 Performance of each algorithm on four datasets with$r = 2$ 下载:
全尺寸图片
图 3$r = 3$ 时各算法在4个数据集上的性能表现Fig. 3 Performance of each algorithm on four datasets with$r = 3$ 下载:
全尺寸图片
图 4$p = 1,r = 1$ 时各算法在4个数据集上的性能表现Fig. 4 Performance of each algorithm on four datasets with$p = 1,r = 1$ 下载:
全尺寸图片
1)在所有UCI数据集上，PL-SRD的性能均优于对比算法PL-KNN和PL-ECOC。
2)在98.2%和90.2%的配置下，PL-SRD分别优于算法LSB_CMM和PL-AGGD。
3)与算法LALO相比，PL-SRD在78.6%的配置下取得了较好的效果，而仅在一次配置下差于LALO。这些结果验证了PL-SRD对人工合成UCI数据集的有效性。
3.3 真实数据集实验
本文基于十倍交叉验证进行实验，并采用显著程度为0.05的成对
$t$ 检验计算出各算法在真实数据集上的平均分类精度及标准差。结果如表4所示，各数据集上性能最优的算法在表中用粗体表示。表 3 PL-SRD 分类性能优于/持平/劣于其他对比算法的次数统计Table 3 Win/tie/loss counts on the classification performance of PL-SRD against each comparing algorithm表 4 各比较算法在真实数据集上的分类精度Table 4 Classification accuracy of each comparing algorithm on real-world data sets数据集 PL-SRD PL-KNN LSB_CMM PL-ECOC LALO PL-AGGD FG-NET 0.082±0.024 0.037±0.021 0.043±0.022 0.042±0.016 0.073±0.028 0.076±0.029 Lost 0.803±0.032 0.392±0.048 0.703±0.043 0.703±0.022 0.693±0.036 0.711±0.030 MSRCv2 0.513±0.038 0.443±0.030 0.459±0.023 0.505±0.036 0.465±0.030 0.464±0.032 Mirflickr 0.668±0.020 0.550±0.028 0.511±0.032 0.571±0.025 0.645±0.024 0.654±0.020 Soccer Player 0.539±0.013 0.508±0.012 0.491±0.014 0.518±0.011 0.523±0.014 0.524±0.015 Yahoo! News 0.649±0.009 0.468±0.009 0.539±0.012 0.508±0.012 0.613±0.009 0.622±0.008 由表4可看出，PL-SRD算法在数据集FG-NET、Lost、Mirflickr、Soccer Player、Yahoo! News上的性能优于其他所有对比算法。其中，相比算法PL-KNN和PL-AGGD，PL-SRD算法在Lost数据集上的分类精度分别提升了9.2%和41.1%。在Mirflickr、Soccer Player和Yahoo! News数据集上，PL-SRD与其他算法相比，分类精度分别提升了15.7%、4.8%和18.1%。在MSRCv2数据集上，算法PL-SRD与PL-ECOC结果持平且优于其他对比算法。
3.4 算法的参数敏感分析
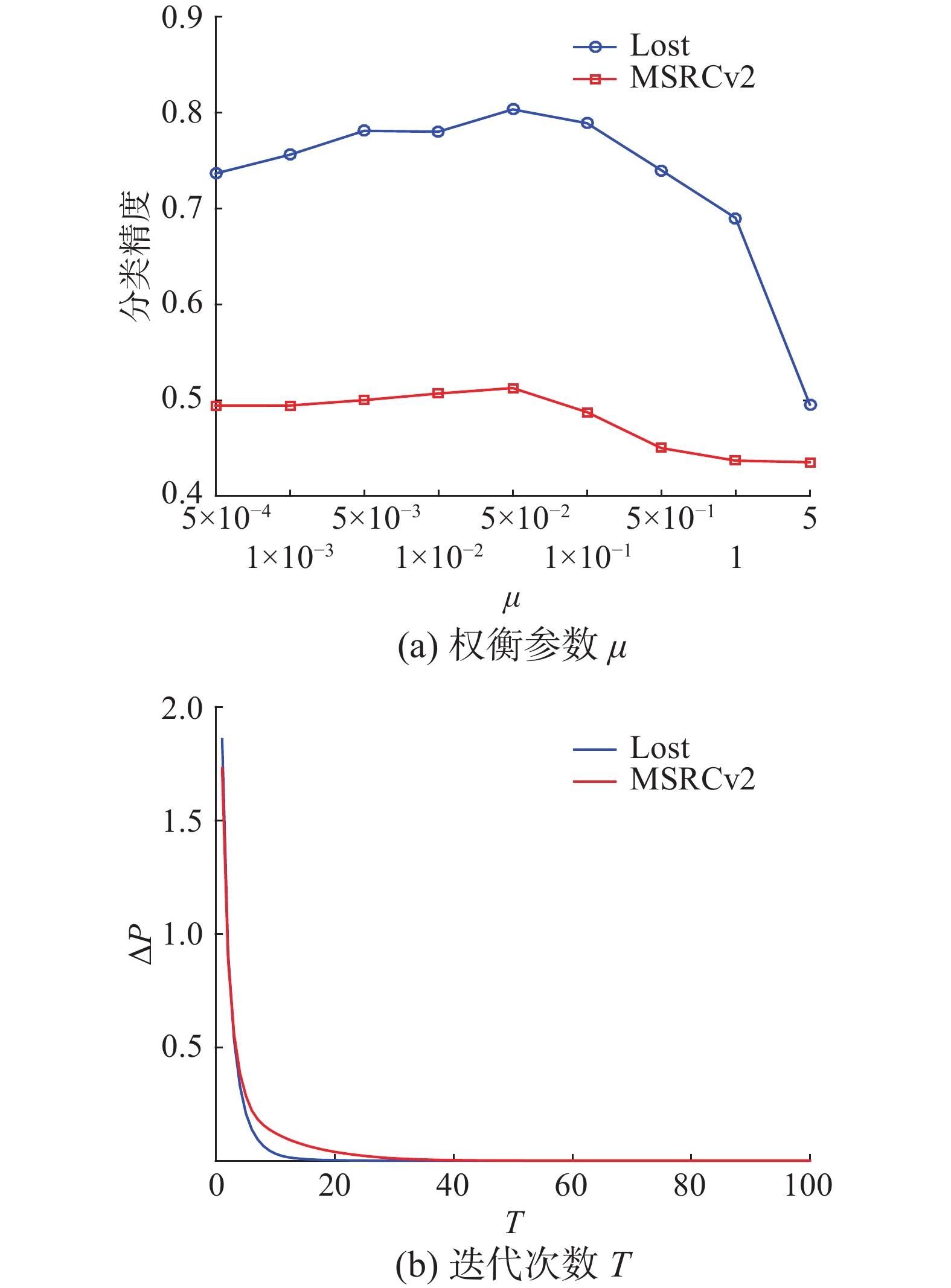
PL-SRD算法有4个参数
$\lambda $ 、$\beta $ 、$\mu $ 和$T$ ，本文对一个参数进行灵敏度分析的同时保持其他参数在最佳设置不变。图5给出了PL-SRD在Lost和MSRCv2 2个数据集上不同参数配置下的性能。图5(a)表示控制模型复杂性的参数$\mu $ 从0.0005~5改变时PL-SRD在2个数据集上分类准确率的变化。图5(b)通过比较2个连续迭代之间标签分布矩阵的差异$\vartriangle {{P}} = \left\| {{{\boldsymbol{P}}^{\left( t \right)}} - {{\boldsymbol{P}}^{\left( {t - 1} \right)}}} \right\|_F^2$ 在2个数据集上进行了收敛性分析，可以发现$\vartriangle {{P}}$ 随着迭代次数$T$ 增加逐渐减少到0，从而证明了PL-SRD算法的收敛性。对于参数$\beta $ 来说，取值较小将导致更新${{\boldsymbol{P}}}$ 使标签空间流形信息利用率低，取值太大又将导致准确度急剧下降。对于$\lambda $ 来说，过大或过小也会导致性能降低。因此，PL-SRD的最佳配置为$\lambda = 1$ ，$\beta = 1$ ，$\mu = 0.05$ 和$T = 20$ 。
图 5 PL-SRD在Lost和MSRCv2上的参数敏感性分析Fig. 5 Parameter sensitivity analysis for PL-SRD on Lost and MSRCV2下载:
全尺寸图片
3.5 算法的复杂度分析
给定具有
$m$ 个示例和$q$ 个标签的偏标记数据。PL-SRD的计算成本主要来自相似权重矩阵计算和每次迭代中参数的更新操作。相似权重矩阵${{\boldsymbol{W}}}$ 的计算复杂度为$O(m \times ({T_1}\times {m^3}))$ ，其中${T_1}$ 是ADMM算法的迭代次数。此外，在更新参数的过程中，更新${{\boldsymbol{b}}}$ 和${{\boldsymbol{A}}}$ 的计算成本主要来自求导计算，其计算复杂度为$O({T_2}\times ({m^2}\times {m^2}q))$ ，其中${T_2}$ 是更新参数的迭代次数。更新置信度矩阵${{\boldsymbol{P}}}$ 的计算复杂度为$O({T_2} \times ({m^3}))$ 。因此，本文方法的整体计算复杂度为$O({T_1}{m^4} + {T_2} \times ({m^4}q + {m^3}))$ ，可以达到$O({m^4}q)$ 。4. 结束语
本文提出了一种新的基于稀疏重构消歧的偏标记学习算法PL-SRD。首次尝试用稀疏重建模型的底层结构信息来刻画特征空间，并利用平滑假设促进标签消歧过程。PL-SRD还通过同时进行标签消歧和预测模型训练从偏标记示例中学习，有效缓解了现有方法忽略每个候选标签作为真实标签可信度的问题。大量的实验结果证明，本文提出的方法可以取得优于其他方法的性能。考虑到PL-SRD的分类精度依赖于构造加权图G的质量，未来我们计划利用深度学习技术构建更精确的图来刻画数据丰富的内在信息。此外，将稀疏重构消歧的思想应用于其他弱监督学习也具有一定的研究价值。
-
图 1
$r = 1$ 时各算法在4个数据集上的性能表现Fig. 1 Performance of each algorithm on four datasets with
$r = 1$ 下载:
全尺寸图片
图 2
$r = 2$ 时各算法在4个数据集上的性能表现Fig. 2 Performance of each algorithm on four datasets with
$r = 2$ 下载:
全尺寸图片
图 3
$r = 3$ 时各算法在4个数据集上的性能表现Fig. 3 Performance of each algorithm on four datasets with
$r = 3$ 下载:
全尺寸图片
图 4
$p = 1,r = 1$ 时各算法在4个数据集上的性能表现Fig. 4 Performance of each algorithm on four datasets with
$p = 1,r = 1$ 下载:
全尺寸图片
图 5 PL-SRD在Lost和MSRCv2上的参数敏感性分析
Fig. 5 Parameter sensitivity analysis for PL-SRD on Lost and MSRCV2
下载:
全尺寸图片
表 1 UCI数据集的数据特征
Table 1 Characteristics of UCI data sets
数据集 样本数 特征数 类别数目 参数设置 Deter 358 23 6 $r = 1,p \in \{ 0.1,0.2,\cdots,0.7\}$ Vehicle 846 18 4 $r = 2,p \in \{ 0.1,0.2,\cdots,0.7\}$ Segment 2310 18 7 $r = 3,p \in \{ 0.1,0.2,\cdots,0.7\}$ Usps 9298 256 10 $p = 1,r = 1,\varepsilon \in \{ 0.1,0.2,\cdots,0.7\}$ 表 2 真实数据集的数据特征
Table 2 Characteristics of real-world data sets
数据集 样本数 特征数 类别数目 平均候选标记数 FG-NET 1002 262 78 7.48 Lost 1122 108 16 2.23 MSRCv2 1758 48 23 3.16 Mirflickr 2780 1536 14 2.76 Soccer Player 17472 279 171 2.09 Yahoo! News 22991 163 219 1.91 表 3 PL-SRD 分类性能优于/持平/劣于其他对比算法的次数统计
Table 3 Win/tie/loss counts on the classification performance of PL-SRD against each comparing algorithm
表 4 各比较算法在真实数据集上的分类精度
Table 4 Classification accuracy of each comparing algorithm on real-world data sets
数据集 PL-SRD PL-KNN LSB_CMM PL-ECOC LALO PL-AGGD FG-NET 0.082±0.024 0.037±0.021 0.043±0.022 0.042±0.016 0.073±0.028 0.076±0.029 Lost 0.803±0.032 0.392±0.048 0.703±0.043 0.703±0.022 0.693±0.036 0.711±0.030 MSRCv2 0.513±0.038 0.443±0.030 0.459±0.023 0.505±0.036 0.465±0.030 0.464±0.032 Mirflickr 0.668±0.020 0.550±0.028 0.511±0.032 0.571±0.025 0.645±0.024 0.654±0.020 Soccer Player 0.539±0.013 0.508±0.012 0.491±0.014 0.518±0.011 0.523±0.014 0.524±0.015 Yahoo! News 0.649±0.009 0.468±0.009 0.539±0.012 0.508±0.012 0.613±0.009 0.622±0.008 -
[1] COUR T, SAPP B, JORDAN C, et al. Learning from ambiguously labeled images[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2009: 919−926. [2] ZENG Zinan, XIAO Shijie, JIA Kui, et al. Learning by associating ambiguously labeled images[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2013: 708−715. [3] COUR T, SAPP B, TASKAR B. Learning from partial labels[J]. Journal of machine learning research, 2011, 12: 1501–1536. [4] CHEN Yichen, PATEL V M, CHELLAPPA R, et al. Ambiguously labeled learning using dictionaries[J]. IEEE transactions on information forensics and security, 2014, 9(12): 2076–2088. doi: 10.1109/TIFS.2014.2359642 [5] GONG Chen, LIU Tongliang, TANG Yuanyan, et al. A regularization approach for instance-based superset label learning[J]. IEEE transactions on cybernetics, 2018, 48(3): 967–978. doi: 10.1109/TCYB.2017.2669639 [6] LIU Liping, DIETTERICH T G. A conditional multinomial mixture model for superset label learning[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems-Volume 1. New York: ACM, 2012: 548−556. [7] LUO Jie, ORABONA F. Learning from candidate labeling sets[J]. Neural information processing systems, 2010, 23(4): 1504−1512. [8] SONG Jingqi, LIU Hui, GENG Fenghuan, et al. Weakly-supervised classification of pulmonary nodules based on shape characters[C]//2016 IEEE 14th Intl Conf on Dependable, Autonomic and Secure Computing. Piscataway: IEEE, 2016: 228− 232. [9] XIE Mingkun, HUANG Shengjun. Partial multi-label learning with noisy label identification[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(7): 3676–3687. [10] 陈鸿昶,谢天,高超,等.候选标记信息感知的偏标记学习算法[J].电子与信息学报, 2019, 41(10):2516−2524. CHEN Hongchang, XIE Tian, GAO Chao, et al. Candidate label-aware partial label learning algorithm[J]. Journal of electronics & information technology, 2019, 41(10): 2516−2524. [11] ZHANG Minling, YU Fei. Solving the partial label learning problem: an instance-based approach[C]//Proceedings of the 24th International Conference on Artificial Intelligence. New York: ACM, 2015: 4048−4054. [12] ZHANG Minling, ZHOU Binbin, LIU Xuying. Partial label learning via feature-aware disambiguation[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1335−1344. [13] GRANDVALETY, BENGIO Y. Semi-supervised Learning by entropy minimization[C]// Advances in Neural Information Processing Systems. Vancouver: MIT Press, 2004: 13−18. [14] NGUYEN N, CARUANA R. Classification with partial labels[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data mining. New York: ACM, 2008: 551−559. [15] FENG Lei, AN Bo. Partial label learning by semantic difference maximization[C]// Proceeding of the 28th International Joint Conference on Artificial Intelligence. MacauL AAAI Press, 2019: 2294−2300. [16] FENG Lei, AN Bo. Leveraging latent label distributions for partial label learning[C]// 27th International Joint Conference on Artificial Intelligence, Stockholm: AAAI Press, 2018: 2107−2113. [17] 周斌斌,张敏灵,刘胥影. 基于三元纠错输出编码的偏标记学习算法[J]. 计算机科学与探索, 2018, 12(9): 1444–1453. ZHOU Binbin, ZHANG Minling, LIU Xuying. Ternary error-correcting output codes based partial label learning algorithm[J]. Journal of frontiers of computer science and technology, 2018, 12(9): 1444–1453. [18] ZHANG Minling, YU Fei, TANG Caizhi. Disambiguation-free partial label learning[J]. IEEE transactions on knowledge and data engineering, 2017, 29(10): 2155–2167. doi: 10.1109/TKDE.2017.2721942 [19] YU Fei, ZHANG Minling. Maximum margin partial label learning[J]. Machine learning, 2017, 106(4): 573–593. doi: 10.1007/s10994-016-5606-4 [20] CHAI Jing, TSANG I W, CHEN Weijie. Large margin partial label machine[J]. IEEE transactions on neural networks and learning systems, 2020, 31(7): 2594–2608. doi: 10.1109/TNNLS.2019.2933530 [21] TANG Caizhi, ZHANG Minling. Confidence-rated discriminative partial label learning[C]//Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. New York: ACM, 2017: 2611−2617. [22] XU Ning, LYU Jiaqi, GENG Xin. Partial label learning via label enhancement[C]// Proceedings of the AAAI conference on artificial intelligence. Honolulu: ACM, 2019: 5557−5564. [23] YAN Yan, GUO Yuhong. Partial label learning with batch label correction[J]. Proceedings of the AAAI conference on artificial intelligence. New York: ACM, 2020: 6575−6582. [24] FENG Lei, AN Bo. Partial label learning with self-guided retraining[C]// Proceedings of the AAAI conference on artificial intelligence. Honolulu: ACM, 2019: 3542−3549. [25] YAO Yao, DENG Jiehui, CHEN Xiuhua, et al. Deep discriminative CNN with temporal ensembling for ambiguously-labeled image classification[C]// Proceedings of the AAAI conference on artificial intelligence. New York: ACM, 2020: 12669−12676. [26] YAO Yao, GONG Chen, DENG Jiehui, et al. Network cooperation with progressive disambiguation for partial label learning[M]. Machine Learning and Knowledge Discovery in Databases. Cham: Springer International Publishing, 2021: 471−488. [27] LYU Jiaqi, XU Miao, FENG Lei, et al. Progressive identification of true labels for partial-label learning[C]//Proceedings of the 37th International Conference on Machine Learning. New York: ACM, 2020: 6500−6510. [28] WANG Dengbao, ZHANG Minling, LI Li. Adaptive graph guided disambiguation for partial label learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(12): 8796–8811. doi: 10.1109/TPAMI.2021.3120012 [29] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and trends in machine learning, 2011, 3(1): 1–122. [30] GABRIEL V, PACHECO, LACIANO C A, et al. Distributed parameterized predictive control for multi-robot curve tracking[J]. IFAC-papersonLine, 2020, 53(2): 3144–3149. doi: 10.1016/j.ifacol.2020.12.1054 [31] GORSKI J, PFEUFFER F, KLAMROTH K. Biconvex sets and optimization with biconvex functions: a survey and extensions[J]. Mathematical methods of operations research, 2007, 66(3): 373–407. doi: 10.1007/s00186-007-0161-1 [32] ZHOU Dengyong, BOUSQUET O, LAL T N, et al. Learning with local and global consistency[C]//Proceedings of the 16th International Conference on Neural Information Processing Systems. New York: ACM, 2003: 321−328. [33] PANIS G, LANITIS A. An overview of research activit ies in facial age estimation using the FG-NET aging data base[C]//European Conference on Computer Vision. Switzerland: Springer, 2014: 737−750. [34] LYU Gengyu, FENG Songhe, LI Yidong, et al. HERA: partial label learning by combining heterogeneous loss with sparse and low-rank regularization[J]. ACM transactions on intelligent systems and technology, 2020, 11(3): 1–19. [35] HUISKES M J, LEW M S. The MIR flickr retrieval evaluation[C]//Proceedings of the 1st ACM international conference on Multimedia information retrieval. New York: ACM, 2008: 39−43.
