Sleep staging model based on multimodal fusion
-
摘要: 针对睡眠多导图中各模态信息在睡眠各阶段存在差异性，而导致特征利用不充分的问题，本文提出了一种基于通道注意力机制和多模态门控机制的睡眠分期模型。首先利用残差收缩网络设计各模态特征提取网络用于提取各模态特征，并在通道维度上进行拼接融合，利用通道注意力机制进一步对融合特征进行重标定得到睡眠多导图的时不变特征；之后提出了一种基于自适应门控机制的多模态门控模块，对各模态特征及时不变特征按照重要程度进行加权融合，实现特征融合；最后利用双向长短时记忆网络提取睡眠多导图的时序特征。实验结果表明，本文提出的睡眠分期模型在欧洲数据格式睡眠数据集(sleep-European data format, sleep-EDF)上准确率为87.6%，
$ {M_{{F_1}}} $ 为82.0%，取得了目前最好的分期效果。Abstract: To solve the problem of insufficient feature use due to the differences in modal information in sleep polygraphs at different stages, this paper proposes a sleep staging method based on the channel attention mechanism and multimodal gating module. First, a residual shrinkage network is used to design each modal feature extraction network to extract the features of all modules, which are spliced and fused in the channel dimension, and the fused features are further recalibrated using the channel attention mechanism to obtain time-invariant polysomnography features. Then, a multimodal gating module based on an adaptive gating mechanism is proposed, which weighs and fuses all modal and time-invariant features according to their importance, thereby realizing the organic fusion of features. Finally, the time sequence characteristics of polysomnography are obtained using a bidirectional long short-term memory network. The experimental result shows that the accuracy of the sleep staging model proposed in this paper is 87.6% on the Sleep-EDF dataset, with an$M_{F_1} $ of 82.0%, thus achieving the best staging effect to date. -
睡眠分期是睡眠监测领域的一项基础研究，通过对睡眠时期进行划分，可以帮助医学专家更好地认识睡眠结构，并为失眠、嗜睡等相关睡眠疾病的诊断与治疗提供依据。AASM标准[1]指出，睡眠可分为清醒期（wake, W）、非快速动眼期（non-rapid eye movements, NREM）和快速动眼期（rapid eye movements, REM）。NREM又被细分为N1、N2、N3期[2]。而睡眠多导图（polysomnogram，PSG）被称为睡眠分期的“黄金标准”，其包含睡眠过程中脑电(electroencephalogram, EEG)、眼电(electrooculogram, EOG)、肌电(electromyography，EMG)等信号的记录。通过综合分析睡眠多导图中的各模态信息，能实现睡眠阶段的划分[1]，但耗费了睡眠专家大量时间和精力，因此睡眠多导图的分期任务成为了热点问题[3]。
通过非线性时域、频域分析等操作可实现睡眠PSG特征的提取[4]，利用支持向量机等技术进行分类，但易出现错分，且模型泛化能力不高[5]。近年来深度学习在图像领域取得突破性进展，结合深度学习利用睡眠PSG进行睡眠分期研究逐渐成为研究的热点。一些在图像领域取得显著效果的模型如VGG[6]、ResNet[7]、膨胀卷积[8]、深度可分离卷积[9]等都被应用到睡眠分期中，取得了较好的效果。但是，由于输入模态的多样性与差异性，如何实现多模态信息的有机融合成为亟待解决的问题。目前睡眠分期领域最常用的模态融合方法分别是从数据[10-14]和特征[15]两个角度进行融合。Phan等[10]从数据融合的角度，将PSG经短时傅里叶变换为含EEG、EOG信息的多通道时频图，然后利用2维卷积神经网络提取时不变特征。除此之外，小波变化[11]、希尔伯特变换[12]等方法也被应用到了睡眠分期中。这种方法虽然综合考虑了多模态的信息，但是转换为时频图时会丢失关键的时域信息[13]。随后，从特征角度进行融合的方法成为主流，其中代表性的有Duan等[15]利用卷积神经网络提取各个模态的时不变特征，利用多模态联合网络实现睡眠分期。
虽然从特征角度进行模态融合的实验效果优于从数据角度融合，但是没有充分考虑各模态在不同时期的差异性，而主要依据了EEG特征，例如在REM期会出现明显的眼球运动，EOG信号更为重要。
本文针对睡眠PSG中各模态特征存在差异性导致的特征融合不充分的问题，主要进行了如下工作：
1）设计了一种基于通道注意力机制的睡眠PSG的不变提取特征网络，根据各通道特征的重要性对模态特征进行重标定，得到睡眠多导图的时不变特征；
2）设计了一种基于自适应门控机制的多模态门控模块，对各模态特征及时不变特征按照重要性程度进行加权融合；
3）利用睡眠分期最常用的Sleep-EDF数据集的多导图数据设计20折交叉验证实验，通过与对比算法比较，证明了算法具有一定的有效性和先进性。
1. 模型框架
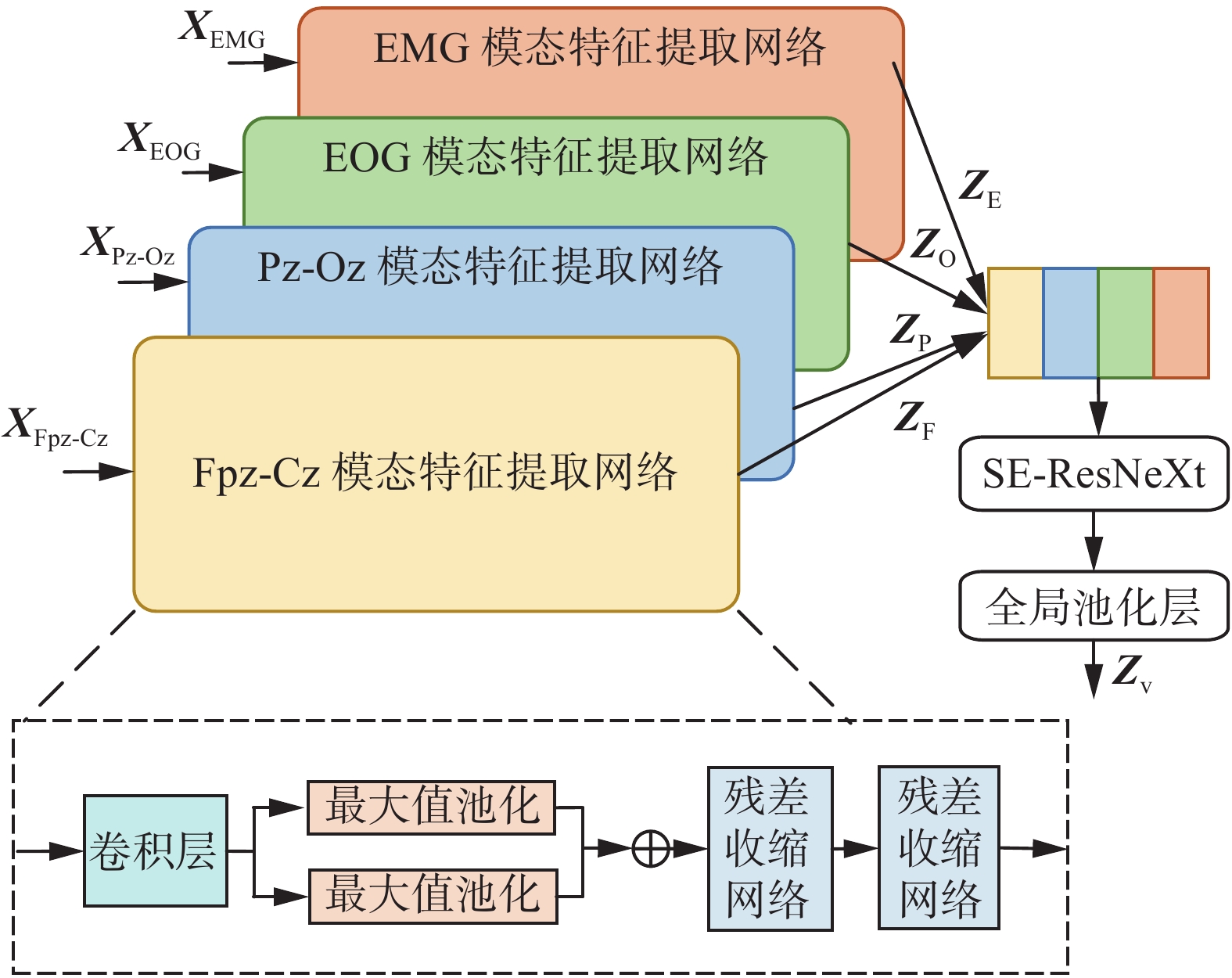
基于通道注意力机制和多模态门控机制的睡眠分期模型如图1所示，首先利用各模态特征提取网络分别提取不同模态的高维特征，并利用通道注意力机制对在通道维度上拼接的各模态高维特征进行重标定，得到睡眠多导图的时不变特征，然后设计多模态门控模块实现不同模态特征的融合，得到能充分表征各模态信息的融合特征，最后，将其输入到时序特征提取网络中，提取信号的时序特征。下面将详细介绍本文所设计的模型框架。
图 1 基于多模态融合的睡眠分期网络结构Fig. 1 Network structure of sleep staging based on multimodal fusion
下载:
全尺寸图片
1.1 时不变特征提取网络
针对PSG中各模态信号中含有噪声的问题，本文首先利用残差收缩网络设计各个模态的特征提取网络，然后利用通道注意力机制学习不同模态特征间的相关性，进而得到睡眠多导图的时不变特征，本文采用的时不变特征提取网络如图2所示。
图 2 时不变特征提取网络Fig. 2 Architecture of time-invariant feature extraction下载:
全尺寸图片
首先利用各模态特征提取网络分别提取不同模态的高维特征，分别将每个模态信息输入到卷积尺度为30，步长为6的1维卷积提取原始信号的低维特征。然后利用2个并行的最大池化层实现下采样，提取不同尺度的关键信息。
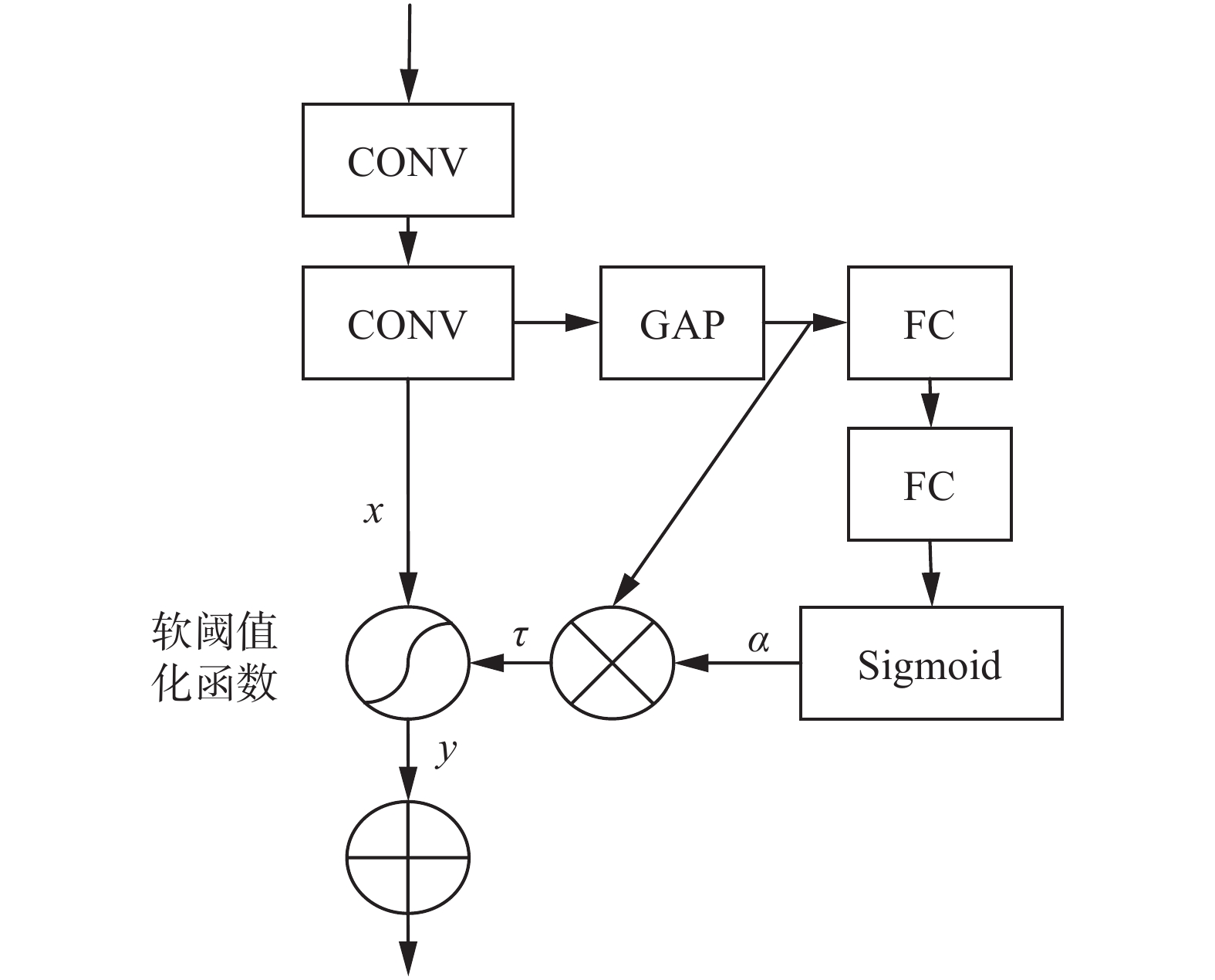
利用残差收缩网络去除融合特征的冗余信息[16]，残差收缩网络结构如图3所示，进而得到每个模态信息的高维抽象特征。
图 3 残差收缩网络Fig. 3 Residual shrinkage network下载:
全尺寸图片
由图3可知，残差收缩网络由ResNet网络(residual neural network)、阈值学习网络和软阈值化函数组成。利用ResNet学习抽象特征表示，然后通过阈值学习网络学习反映信息重要程度的阈值，其中阈值学习网络的表达式为
$$ \tau = {\boldsymbol{\alpha }} \cdot {\text{average|}}{{\boldsymbol{x}}_{i,j,c}}| $$ (1) 式中
$ {\boldsymbol{\alpha }} $ 表示由全连接层和Sigmoid函数得到的权值。通过阈值学习网络可以确保$ \tau $ 是一个很小的正实数。然后利用软阈值化函数将特征中不重要的信息置为0，其中软阈值化函数是小波降噪算法中的核心步骤，其表达式为$$ y=\left\{\begin{aligned} &x-\tau \text{，}x > \tau \\ &0\text{，}-\tau \leqslant x\leqslant \tau \\ &x+\tau \text{，}x < -\tau \end{aligned}\right. $$ (2) 通过软阈值化函数的引入，可以有效地增强有效的信息，抑制冗余的信息，进而消除信号中噪声的影响，得到高效的各模态抽象特征表示。
将各模态的抽象特征在通道维度上进行拼接，如式（3）所示，得到初步融合特征。
$$ {\boldsymbol{Z}} = {\text{Concat}}({{\boldsymbol{Z}}_{\text{F}}},{{\boldsymbol{Z}}_{\text{P}}},{{\boldsymbol{Z}}_{\text{O}}},{{\boldsymbol{Z}}_{\text{M}}}) $$ (3) 式中：
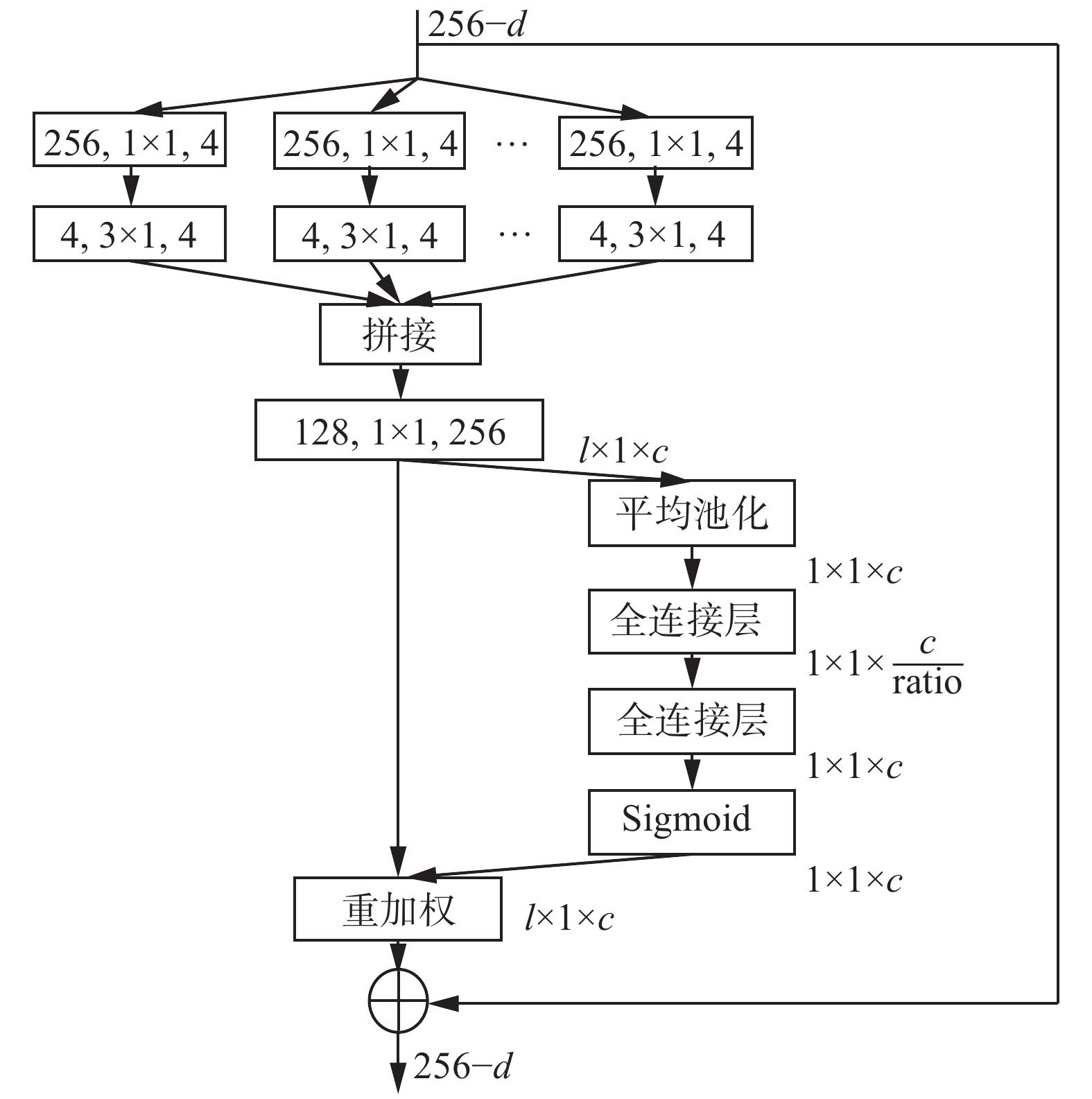
${{\boldsymbol{Z}}_{\text{F}}},{{\boldsymbol{Z}}_{\text{P}}},{{\boldsymbol{Z}}_{\text{O}}},{{\boldsymbol{Z}}_{\text{M}}} \in {{\bf{R}}^{l \times C}}$ ，代表各个模态特征，l为特征图的尺度，C为输出滤波器的个数；Z代表拼接特征，${\boldsymbol{Z}} \in {{\bf{R}}^{l \times nC}}$ ，n代表模态的个数。随后利用通道注意力机制学习不同通道特征间的相关性。本文利用SE-ResNeXt模块[17]根据不同通道特征重要程度对特征进行整合。其中，SE-ResNeXt由ResNeXt和SENet (squeeze and excitation network)两部分组成，如图4所示。残差网络通过增加模型深度和宽度来提高特征提取的质量，但会造成模型参数量增加、计算开销增加的问题，ResNet在此基础上引入了基数的超参数，即卷积支路的个数。通过增加基数，在不增加网络参数量的前提下有效提高了模型的特征提取能力。
图 4 SE-ResNeXt结构Fig. 4 Architecture of SE-ResNeXt下载:
全尺寸图片
SENet通过自适应获得各个通道特征的重要程度，对输出特征进行重标定，进而提升有用的通道特征，抑制重要程度低的特征。图中l为特征图尺度，c为通道数，ratio为特征维度缩放比。SENet分别经过压缩和激励变换，建模各通道特征的重要权重，最后各通道特征逐点相乘的操作将归一化的权重加权到输入特征中，得到含通道重要程度的特征向量。式（4）~（6）分别给出了压缩、激励、加权的公式。
$$ {{\boldsymbol{z}}_c} = {F_{{\rm{sq}}}}({{\boldsymbol{u}}_c}) = \frac{1}{l}\sum\limits_{i = 1}^l {{{\boldsymbol{u}}_c}(i)} $$ (4) $$ {\boldsymbol{s}} = {{\text{F}}_{{\rm{ex}}}}({\boldsymbol{z}},{\boldsymbol{W}}) = \sigma ({{\boldsymbol{W}}_2}\delta ({{\boldsymbol{W}}_1}{\boldsymbol{z}})) $$ (5) $$ {\tilde{x}}_{c}={F}_{{\rm{scale}}}({u}_{c},{s}_{c}）\text={s}_{c}\cdot {u}_{c} $$ (6) 式中：
$ {{\boldsymbol{W}}_1} $ 和$ {{\boldsymbol{W}}_{{2}}} $ 分别代表两个全连接层的权重；$ \delta $ 代表ReLu函数；$ \sigma $ 代表Sigmoid函数；Fsq、Fex、Fscale分别代表压缩、激励和尺度变换的效果。1.2 多模态门控模块
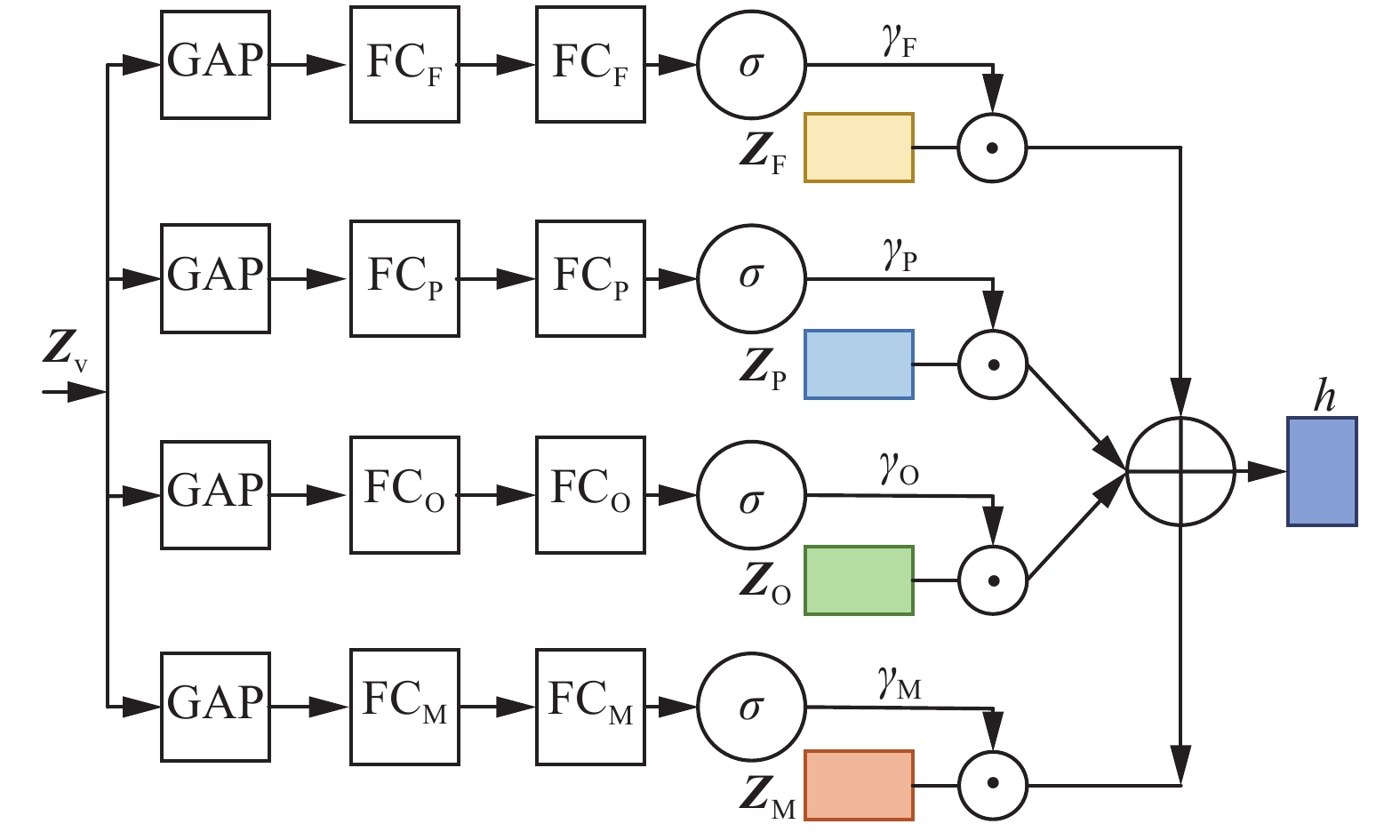
多模态学习中模态融合对模型性能有很大的影响，为了充分发挥不同模态间的差异性[18]，本文模拟人工判读以关键信号为主，其他信号为辅的判读模式，引入了多模态门控模块，建模各个模态特征对于睡眠分期任务的重要程度，通过自适应门控机制[19]对不同模态特征按照重要程度进行加权，根据不同模态特征的组合自适应地找到更适合睡眠分期任务的特征表示。设计的多模态门控模块如图5所示。图中
$ {{\boldsymbol{Z}}_{\text{v}}} $ 为睡眠多导图的时不变特征，$ {{\boldsymbol{Z}}_{\text{F}}} $ 、$ {{\boldsymbol{Z}}_{\text{P}}} $ 、$ {{\boldsymbol{Z}}_{\text{O}}} $ 、$ {{\boldsymbol{Z}}_{\text{M}}} $ 分别为各模态高维抽象特征表示。
图 5 多模态门控模块Fig. 5 Multimodal gating module下载:
全尺寸图片
将睡眠多导图的时不变特征分别首先经过全局平均池化层得到全局信息，然后经过两层全连接层和Sigmoid函数增加特征的非线性，通过式（7）~（10）分别学习各个模态特征的权重，然后通过式（11）得到输出特征的最优组合， 寻找对于输出贡献度最大的各个模态的特征组合，进而得到更丰富的融合特征表示。
$$ {{\boldsymbol{\gamma }}_{\text{F}}}{\text{ = Sigmoid(}}{\boldsymbol{W}}_{\text{F}}^2{\text{(}}{\boldsymbol{W}}_{\text{F}}^1{\text{(GAP(}}{{\boldsymbol{Z}}_{\text{v}}}{\text{))))}} $$ (7) $$ {{\boldsymbol{\gamma }}_{\text{P}}}{\text{ = Sigmoid(}}{\boldsymbol{W}}_{\text{P}}^2{\text{(}}{\boldsymbol{W}}_{\text{P}}^1{\text{(GAP(}}{{\boldsymbol{Z}}_{\text{v}}}{\text{))))}} $$ (8) $$ {{\boldsymbol{\gamma }}_{\text{O}}}{\text{ = Sigmoid(}}{\boldsymbol{W}}_{\text{O}}^2{\text{(}}{\boldsymbol{W}}_{\text{O}}^1{\text{(GAP(}}{{\boldsymbol{Z}}_{\text{v}}}{\text{))))}} $$ (9) $$ {{\boldsymbol{\gamma }}_{\text{M}}}{\text{ = Sigmoid(}}{\boldsymbol{W}}_{\text{M}}^2{\text{(}}{\boldsymbol{W}}_{\text{M}}^1{\text{(GAP(}}{{\boldsymbol{Z}}_{\text{v}}}{\text{))))}} $$ (10) $$ {\boldsymbol{h}} = {{\boldsymbol{\gamma }}_{\text{F}}} \cdot {{\boldsymbol{Z}}_{\text{F}}} + {{\boldsymbol{\gamma }}_{\text{P}}} \cdot {{\boldsymbol{Z}}_{\text{P}}} + {{\boldsymbol{\gamma }}_{\text{O}}} \cdot {{\boldsymbol{Z}}_{\text{O}}} + {{\boldsymbol{\gamma }}_{\text{M}}} \cdot {{\boldsymbol{Z}}_{\text{M}}} $$ (11) 式中：
$ {\boldsymbol{W}}_{\text{F}}^1 $ 、$ {\boldsymbol{W}}_{\text{P}}^1 $ 、$ {\boldsymbol{W}}_{\text{O}}^1 $ 、$ {\boldsymbol{W}}_{\text{M}}^1 $ 、$ {\boldsymbol{W}}_{\text{F}}^2 $ 、$ {\boldsymbol{W}}_{\text{P}}^2 $ 、$ {\boldsymbol{W}}_{\text{O}}^2 $ 、$ {\boldsymbol{W}}_{\text{M}}^2 $ 分别代表相应全连接层的参数向量；$ {{\boldsymbol{\gamma }}_{\text{F}}} $ 、$ {{\boldsymbol{\gamma }}_{\text{P}}} $ 、$ {{\boldsymbol{\gamma }}_{\text{O}}} $ 、$ {{\boldsymbol{\gamma }}_{\text{M}}} $ 分别代表各模态的重要性权值；$ {{\boldsymbol{Z}}_{\text{v}}} $ 代表时不变特征；h代表融合特征。1.3 时序特征提取网络
睡眠PSG是一种时序信号，相邻样本间具有时序相关性。在对t时刻的样本进行分期时，可以利用t−1和t+1时刻的特征或分期结果辅助进行t时刻样本阶段的分类。
本文利用双向长短时记忆网络(bi-directional long short-term memory, Bi-LSTM)[20]设计时序特征提取网络。与长短时记忆网络只能学习序列前向传播规律不同的是Bi-LSTM分别由一个前向传播和一个反向传播的LSTM组成，保证了时序特征提取网络既可以学习前向传播规律，还可以学习序列的反向传播规律。最后将Bi-LSTM学习到的时序特征与多模态特征进行融合得到睡眠PSG的时序特征，得到的时序特征表达式为
$$ {{\boldsymbol{O}}_t} = g({{\boldsymbol{w}}_{\rm{F}}}{\boldsymbol{h}}_{\rm{F}}^t + {{\boldsymbol{w}}_{\rm{B}}}{\boldsymbol{h}}_{\rm{B}}^t) + {{\boldsymbol{w}}_{{\rm{FC}}}}{{\boldsymbol{h}}_t} $$ (12) 式中：
$ {{\boldsymbol{h}}_t} $ 、${{\boldsymbol{O}}_t}$ 分别代表t时刻的输入和输出；${{\boldsymbol{w}}_{\rm{F}}}$ 、$ {{\boldsymbol{w}}_{\text{B}}} $ 、$ {{\boldsymbol{w}}_{{\text{FC}}}} $ 分别代表$ {\text{LST}}{{\text{M}}_{\text{F}}} $ 、$ {\text{LST}}{{\text{M}}_{\text{B}}} $ 的输出权重和全连接的权重；${\boldsymbol{h}}_{\rm{F}}^t$ 、${\boldsymbol{h}}_{\rm{B}}^t$ 分别代表$ {\text{LST}}{{\text{M}}_{\text{F}}} $ 和$ {\text{LST}}{{\text{M}}_{\text{B}}} $ 的输出；g代表拼接操作。2. 实验结果及分析
为了验证本文创新工作的有效性和先进性，进行了3个方面的实验：1）分别利用PSG中不同的模态组合设置相关实验，进而验证本文利用多模态信号进行睡眠分期的有效性，并且得到最优的模态组合；2）设计不同初步融合方式的对比实验，验证本文采用SE-ResNeXt进行特征重标定的有效性；3）将本文提出的MSN算法与4种先进的方法进行对比，验证本文算法的先进性。
2.1 数据集
利用Sleep-EDF数据集[21]设计相关的实验共包括39个完整夜晚的PSG记录。每个PSG包含个两模态的EEG，分别是Fpz-Cz和Pz-Cz，一个模态的EOG和一个模态的EMG[22]。每个样本都已由睡眠专家标记为W、N1、N2、N3、N4、REM，根据AASM标准将N3和N4合并为N3。最后，W、N1、N2、N3、REM各个类别的样本量分别为7927、2804、17799、5703、7717，共41950个样本。
2.2 实验条件
本文所有实验均是在64位的Ubuntu16.04系统中进行，采用的深度学习框架为tensorflow 1.14.0，在训练过程中利用GeForce RTX 980Ti显卡进行加速，并且采用python3.5编程语言完成代码的编写。
优化过程中采用Adam函数，学习率设为0.001，序列学习过程中batch size为25，子序列长度为10，ResNeXt中的基数设置为8，ratio设置为4。利用丢失率为0.5 dropout层来防止过拟合。进行20折交叉验证，按19∶1划分训练集和验证集。
2.3 评价指标
采用
$ {M_{{F_1}}} $ 分数（macro-averaging F1-score,$ {M_{{F_1}}} $ ）、整体准确率（overall-accuracy, ACC）作为评价指标，具体公式为$$ {A_{{\text{CC}}}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^C {{T_P}_{_i}} }}{N} \times 100{\text{%}} $$ (13) $$ {M_{{F_1}}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^C {{F_1}_{_i}} }}{C} \times 100{\text{%}} $$ (14) 式中：N代表样本总数；C代表类别总数；
$ {F_{{1_i}}} $ 代表类别i的F1分数，即$$ {F_{\text{l}}}_{_i} = \dfrac{{2 {P_i} {R_i}}}{{{P_i} + {R_i}}} $$ (15) 式中：
${P_i} = \dfrac{{{T_{{P_i}}}}}{{{T_P}_{_i} + {F_P}_{_i}}}$ ；${R_i} = \dfrac{{{T_P}_i}}{{{T_P}_i + {F_N}_i}}$ ；$ {T_P}_{_i} $ 代表正确分数为i类的样本数；$ {F_P}_{_i} $ 代表被错分为i类的样本数；$ {F_N}_{_i} $ 代表被错分为其他类别的样本数。2.4 多模态信息有效性验证
由于EEG是睡眠分期的主要判读依据，在验证利用多模态信息有效性时选择在EEG的基础上加入不同模态的数据，验证不同模态数据对睡眠分期的影响。得到的结果如表1所示,表中1代表两个模态的EEG组合，2代表两个模态EEG加EOG的组合，3代表两个模态EEG加EOG加EMG的组合。
表 1 多模态信息有效性验证Table 1 Verification of the multimodal information% 模态 $ {A_{{\text{CC}}}} $ $ {M_{{F_1}}} $ 每个类别F1 W N1 N2 N3 REM 1 86.1 80.3 89.7 48.3 88.7 89.2 85.8 2 87.3 81.4 90.7 49.9 90.0 89.1 87.6 3 87.6 82.0 91.9 51.3 89.0 87.3 87.9 从表1中可以看出，仅用两模态EEG进行睡眠研究时平均准确率为86.1%，
$ {M_{{F_1}}} $ 为80.3%，但是当加入眼电信号后平均准确率达到了87.3%，相较于仅利用脑电信号提高了1.4%，$ {M_{{F_1}}} $ 达到了81.4%，提高了1.4%。并且由于快速眼动是REM期的典型特征，在加入眼电信号后，REM期的F1有了较大的提升，提升了2.0%，同时对于W期、N1期、N2期也有了一定的提升，说明眼电的加入可以有效地丰富信息特征，增强模型对于睡眠各阶段的识别能力。在脑电、眼电信号的基础上加入肌电后，平均准确率达到了87.6%，与利用脑电和眼电相比提升了0.3%，$ {M_{{F_1}}} $ 达到了82%，提升了0.7%，说明肌电信号的加入进一步丰富了信息特征，可以让网络模型学习到更丰富的分期特征，特别是肌肉运动明显的时期如W和N1期的识别精度有了明显的提升，其中W期的F1提升了1.3%，N1期的F1提升了2.8%，说明肌电信号的加入有效地增大了W、N1期与其他类别的阶段差异性，进而提高了网络模型的分期性能。综上证明了同时利用EEG、EOG、EMG可以得到更好的睡眠分期结果。2.5 特征融合方式验证实验
本文将各模态特征在通道维度上进行拼接，然后利用通道注意力机制对拼接特征进行重标定的方式实现各模态的初步融合，为了进一步验证该方法的有效性，分别与逐点相加、通道拼接的特征融合方式进行对比，表2分别给出了不同融合方式得到的分期结果。从表2中可以看出，采用各通道特征逐点相加进行特征融合的整体准确率为86.4%，
$ {M_{{F_{\text{1}}}}} $ 为80.4%，但是将特征融合的方式变为在通道维度上拼接后，准确率提高了0.5%，$ {M_{{F_{\text{1}}}}} $ 提高了1.1%，证明利用在通道维度上拼接的方式能够更好地利用不同特征之间的差异性，进而得到更充分的初步融合特征。随后加入通道注意力机制后准确率提高了0.9%，$ {M_{{F_{\text{1}}}}} $ 提高了0.8%，并且各个类别的F1都有了一定的提高，进而证明了本文采用SE-ResNeXt对特征按照通道重要性权重进行重标定，能够让特征融合得更充分，进而验证了本文采用通道维度拼接和SE-ResNeXt对特征进行初步融合的有效性。表 2 特征融合方式有效性验证Table 2 Verification of modal fusion% 融合方法 $ {A_{{\text{CC}}}} $ $ {M_{{F_1}}} $ 每个类别F1 W N1 N2 N3 REM 逐点相加 86.4 80.4 91.9 48.3 88.8 87.4 85.7 通道拼接 86.8 81.3 91.9 50.0 89.3 88.3 87.7 通道拼接+通道注意力 87.6 82.0 91.9 51.3 90.0 89.0 87.9 2.6 算法先进性验证
为了验证本文算法的先进性与目前4种先进的算法进行对比，表3给出了对比结果。
从表3中可以看出，本文提出的模型的平均准确率为87.6%，
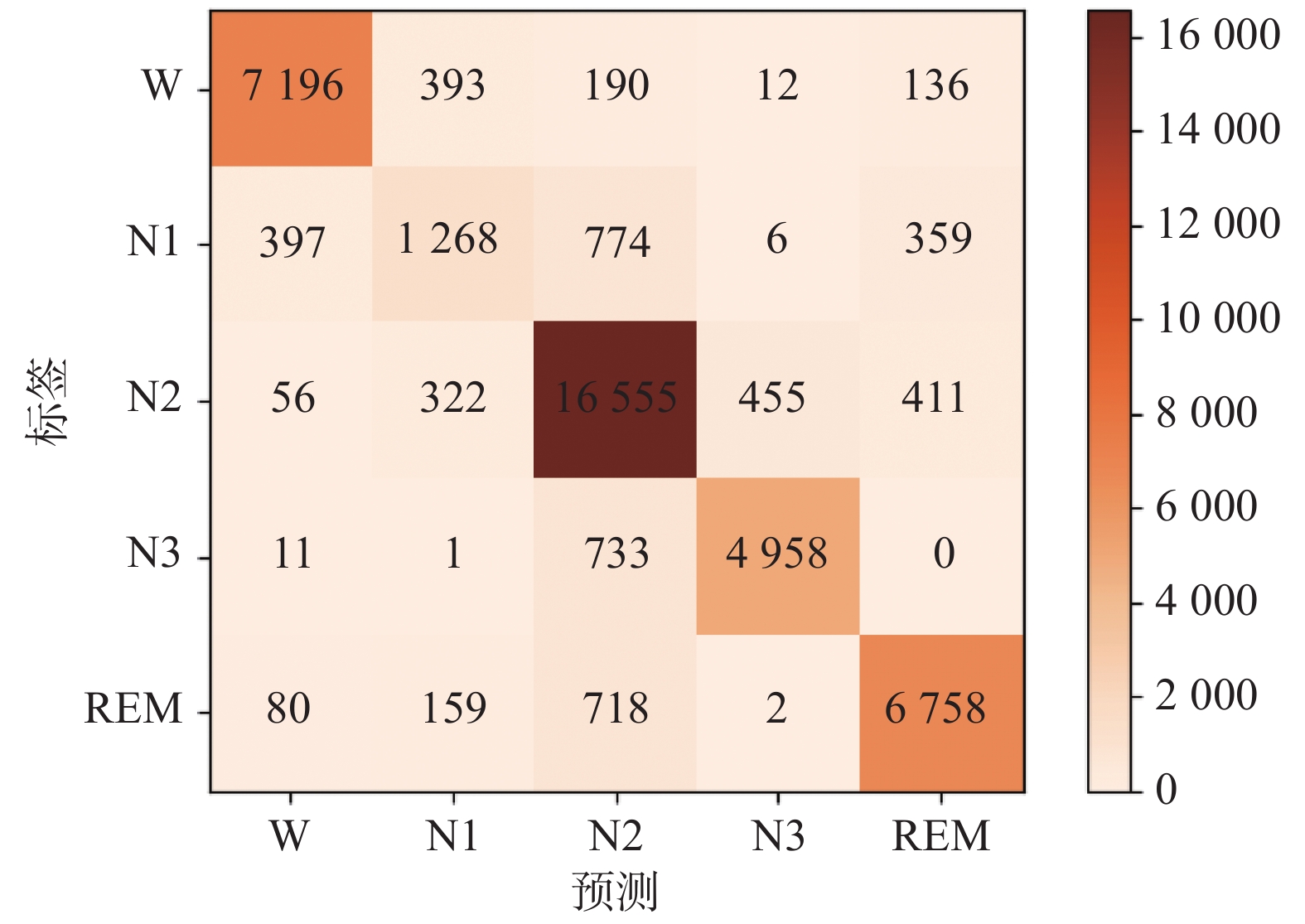
$ {M_{{F_{\text{1}}}}} $ 为82.0%，均高于目前先进的对比算法，并且除N1期外，各个类别的F1分数均取得了最优的水平，证明本文算法能够充分学习不同睡眠阶段的特征，取得了优异的睡眠分期性能，进而证明了本文算法的先进性。采用混淆矩阵对本文提出的算法进行可视化操作。图6给出了本文算法利用两个模态EEG、一个模态EOG和一个模态EMG达到的最好分类效果时的混淆矩阵。图中每一行代表实际标签为该类别的样本数，每一列代表预测为该类别的样本数，并且颜色越深代表预测为该类别的样本数越多。从混淆矩阵中可以看出，本文利用所提出的多模态融合的方法进行睡眠分期研究，大多数样本都能被正确分类，并且主要的错分出现在相邻阶段的样本中，这主要是因为转换阶段的样本特征中存在一定的中和，甚至睡眠专家也无法对转换期的样本进行正确分类，导致模型学到的转换期特征边界较模糊，进而造成了错分主要出现在相邻阶段转换期的样本。由于睡眠本身的特征，N1期存在时间短于其他时期，样本量较小，所以N1期的F1低于其他类别。
图 6 混淆矩阵Fig. 6 Confusion matrix下载:
全尺寸图片
3. 结束语
本文为了充分利用睡眠PSG中各模态信息，利用通道注意力机制和多模态门控机制设计了基于多模态融合的睡眠分期模型。首先利用残差收缩网络设计各模态特征提取网络提取各个模态的高维特征，并将各个模态的高维特征在通道维度上进行融合得到初步融合特征，然后利用SE-ResNeXt根据各通道信息的重要性程度对特征进行重标定，得到睡眠多导图的时不变特征。然后输入到多模态门控模块中，利用全连接层和非线性函数，学习各个模态信息的重要性程度，结合乘法门对各模态特征进行加权，进而找到能充分表示各模态信息的最优组合。随后，利用Bi-LSTM提取相邻样本间的时序相关性。本文利用Sleep-EDF中的Fpz-Cz、Pz-Oz、EOG、EMG模态信息进行了二十折交叉验证实验，并通过与目前先进的4种对比算法进行比较，本文提出的算法无论是整体准确率还是
$M_{F_1} $ 均高于对比算法，进而证明了本文算法的有效性和先进性。 -
图 1 基于多模态融合的睡眠分期网络结构
Fig. 1 Network structure of sleep staging based on multimodal fusion
下载:
全尺寸图片
图 2 时不变特征提取网络
Fig. 2 Architecture of time-invariant feature extraction
下载:
全尺寸图片
图 3 残差收缩网络
Fig. 3 Residual shrinkage network
下载:
全尺寸图片
图 4 SE-ResNeXt结构
Fig. 4 Architecture of SE-ResNeXt
下载:
全尺寸图片
图 5 多模态门控模块
Fig. 5 Multimodal gating module
下载:
全尺寸图片
图 6 混淆矩阵
Fig. 6 Confusion matrix
下载:
全尺寸图片
表 1 多模态信息有效性验证
Table 1 Verification of the multimodal information
% 模态 $ {A_{{\text{CC}}}} $ $ {M_{{F_1}}} $ 每个类别F1 W N1 N2 N3 REM 1 86.1 80.3 89.7 48.3 88.7 89.2 85.8 2 87.3 81.4 90.7 49.9 90.0 89.1 87.6 3 87.6 82.0 91.9 51.3 89.0 87.3 87.9 表 2 特征融合方式有效性验证
Table 2 Verification of modal fusion
% 融合方法 $ {A_{{\text{CC}}}} $ $ {M_{{F_1}}} $ 每个类别F1 W N1 N2 N3 REM 逐点相加 86.4 80.4 91.9 48.3 88.8 87.4 85.7 通道拼接 86.8 81.3 91.9 50.0 89.3 88.3 87.7 通道拼接+通道注意力 87.6 82.0 91.9 51.3 90.0 89.0 87.9 -
[1] BERRY R B, BUDHIRAJA R, GOTTLIEB D J, et al. Rules for scoring respiratory events in sleep: update of the 2007 AASM manual for the scoring of sleep and associated events[J]. Journal of clinical sleep medicine, 2012, 8(5): 597–619. doi: 10.5664/jcsm.2172 [2] 王菡侨. 有关美国睡眠医学学会睡眠分期的最新判读标准指南解析[J]. 诊断学理论与实践, 2009, 8(6): 575–578. doi: 10.16150/j.1671-2870.2009.06.003 WANG Hanqiao. Analysis of the latest guidelines for sleep staging of the american academy of sleep medicine[J]. Journal of diagnostics concepts & practice, 2009, 8(6): 575–578. doi: 10.16150/j.1671-2870.2009.06.003 [3] ZHANG Linda, FABBRI D, UPENDER R, et al. Automated sleep stage scoring of the sleep heart health study using deep neural networks[J]. Sleep, 2019, 42(11): zsz159. doi: 10.1093/sleep/zsz159 [4] ZHAO Dechun, WANG Yi, WANG Qiangqiang, et al. Comparative analysis of different characteristics of automatic sleep stages[J]. Computer methods and programs in biomedicine, 2019, 175: 53–72. doi: 10.1016/j.cmpb.2019.04.004 [5] FAUST O, RAZAGHI H, BARIKA R, et al. A review of automated sleep stage scoring based on physiological signals for the new millennia[J]. Computer methods and programs in biomedicine, 2019, 176: 81–91. doi: 10.1016/j.cmpb.2019.04.032 [6] VILAMALA A, MADSEN K H, HANSEN L K. Deep convolutional neural networks for interpretable analysis of EEG sleep stage scoring[C]//2017 IEEE 27th International Workshop on Machine Learning for Signal Processing. Tokyo: IEEE, 2017: 1−6. [7] HUMAYUN A I, SUSHMIT A S, HASAN T, et al. End-to-end sleep staging with raw single channel EEG using deep residual ConvNets[C]//2019 IEEE EMBS International Conference on Biomedical & Health Informatics. Chicago: IEEE, 2019: 1−5. [8] 贾子钰, 林友芳, 张宏钧, 等. 基于深度卷积神经网络的睡眠分期模型[J]. 浙江大学学报(工学版), 2020, 54(10): 1899–1905. JIA Ziyu, LIN Youfang, ZHANG Hongjun, et al. Sleep stage classification model based on deep convolutional neural network[J]. Journal of Zhejiang University (engineering science edition), 2020, 54(10): 1899–1905. [9] FERNANDEZ-BLANCO E, RIVERO D, PAZOS A. EEG signal processing with separable convolutional neural network for automatic scoring of sleeping stage[J]. Neurocomputing, 2020, 410: 220–228. doi: 10.1016/j.neucom.2020.05.085 [10] PHAN H, ANDREOTTI F, COORAY N, et al. Joint classification and prediction CNN framework for automatic sleep stage classification[J]. IEEE transactions on biomedical engineering, 2019, 66(5): 1285–1296. doi: 10.1109/TBME.2018.2872652 [11] JADHAV P, RAJGURU G, DATTA D, et al. Automatic sleep stage classification using time-frequency images of CWT and transfer learning using convolution neural network[J]. Biocybernetics and biomedical engineering, 2020, 40(1): 494–504. doi: 10.1016/j.bbe.2020.01.010 [12] YÜCELBAŞ C, YÜCELBAŞ Ş, ÖZŞEN S, et al. Effect of the Hilbert-Huang transform method on sleep staging[C]//2017 25th Signal Processing and Communications Applications Conference (SIU). Antalya: IEEE, 2017: 1−4. [13] LOH H W, OOI C P, VICNESH J, et al. Automated detection of sleep stages using deep learning techniques: a systematic review of the last decade (2010–2020)[J]. Applied sciences, 2020, 10(24): 8963. doi: 10.3390/app10248963 [14] SOKOLOVSKY M, GUERRERO F, PAISARNSRISOMSUK S, et al. Deep learning for automated feature discovery and classification of sleep stages[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2020, 17(6): 1835–1845. doi: 10.1109/TCBB.2019.2912955 [15] DUAN Lijuan, LI Mengying, WANG Changming, et al. A novel sleep staging network based on data adaptation and multimodal fusion[J]. Frontiers in human neuroscience, 2021, 15: 727139. doi: 10.3389/fnhum.2021.727139 [16] ZHAO Minghang, ZHONG Shisheng, FU Xuyun, et al. Deep residual shrinkage networks for fault diagnosis[J]. IEEE transactions on industrial informatics, 2020, 16(7): 4681–4690. doi: 10.1109/TII.2019.2943898 [17] HU Jie, SHEN Li, SUN Gang. Squeeze-and-excitation networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 7132−7141. [18] 张峰, 李希城, 董春茹, 等. 基于深度情感唤醒网络的多模态情感分析与情绪识别[J]. 控制与决策, 2022, 37(11): 2984–2992. ZHANG Feng, LI Xicheng, DONG Chunru, et al. Deep emotional arousal network for multimodal sentiment analysis and emotion recognition[J]. Control and decision, 2022, 37(11): 2984–2992. [19] WANG Yansen, SHEN Ying, LIU Zhun, et al. Words can shift: dynamically adjusting word representations using nonverbal behaviors[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Honolulu: Assoc Advancement Artifical Intelligence, 2019: 7216−7223. [20] ABDELHAMEED A M, DAOUD H G, BAYOUMI M. Deep convolutional bidirectional LSTM recurrent neural network for epileptic seizure detection[C]//2018 16th IEEE International New Circuits and Systems Conference. Montreal: IEEE, 2018: 139−143. [21] KEMP B, ZWINDERMAN A H, TUK B, et al. Analysis of a sleep-dependent neuronal feedback loop: the slow-wave microcontinuity of the EEG[J]. IEEE transactions on bio-medical engineering, 2000, 47(9): 1185–1194. doi: 10.1109/10.867928 [22] GOLDBERGER A L, AMARAL L A, GLASS L, et al. PhysioBank, physiotoolkit, and physionet: components of a new research resource for complex physiologic signals[J]. Circulation, 2000, 101(23): E215–E220. [23] ZHANG Lei, CHEN Dan, CHEN Peilu, et al. Dual-CNN based multi-modal sleep scoring with temporal correlation driven fine-tuning[J]. Neurocomputing, 2021, 420: 317–328. doi: 10.1016/j.neucom.2020.08.020 [24] PHAN H, CHÉN O Y, KOCH P, et al. Towards more accurate automatic sleep staging via deep transfer learning[J]. IEEE transactions on biomedical engineering, 2021, 68(6): 1787–1798. doi: 10.1109/TBME.2020.3020381 [25] YAN Rui, LI Fan, ZHOU Dong dong, et al. Automatic sleep scoring: a deep learning architecture for multi-modality time series[J]. Journal of neuroscience methods, 2021, 348: 108971. doi: 10.1016/j.jneumeth.2020.108971
