Adaptive multi-point crossover genetic algorithm for solving continuous distributed constraint optimization problems
-
摘要: 针对连续型分布式约束优化问题(continuous distributed constraint optimization problems, C-DCOPs)求解算法的anytime属性的缺失、约束函数形式的限制和无法保证收敛等局限,本文提出一种求解C-DCOP的自适应多点交叉遗传算法(adaptive multi-point crossover genetic algorithm based C-DCOP, AMCGA)。在AMCGA中,智能体(agent)构建分布式种群和广度优先搜索(breadth first search, BFS)伪树以分布式地计算个体适应度;通过贪婪策略选择精英个体进行自适应多点交叉实现全局搜索,智能体之间协同通信保证分布式种群中解的一致性;利用变异算子完成局部搜索。AMCGA适用于任意形式的约束函数,并被证明具有任意时间属性和全局收敛性。在4类基准问题上的广泛实验结果表明,AMCGA的求解质量优于最先进的C-DCOP求解算法,能有效地打破目前C-DCOP求解算法的局限,并在求解质量方面存在20%~30%的提升。Abstract: Aiming at the limitations of the solving algorithm for continuous distributed constraint optimization problems (DCOPs), such as the lack of anytime property, the limitation of constraints function form and the inability to guarantee convergence, an adaptive multi-point crossover genetic algorithm for solving C-DCOP (AMCGA) is proposed. In AMCGA, the agent firstly builds distributed population and breadth first search (BFS) pseudo-tree to calculate the individual fitness in a distributed way. Secondly, the agent selects elite individuals through greedy strategy for adaptive multi-point crossover, achieving global search; cooperative communication between agents ensures the consistency of solutions in the distributed population. Finally, the agent uses mutation operator to complete local search. AMCGA is suitable for any form of constraint function and is proved to have anytime property and global convergence. Extensive experimental results on four types of benchmark problems demonstrate that the solution quality of AMCGA is superior to the state-of-the-art C-DCOP solving algorithms, it can effectively break through the limitations of current C-DCOP solving algorithms, and improve the solution quality by 20% to 30%.
-
分布式约束优化问题(distributed constraint optimization problems, DCOPs)[1]是解决分布式多智能体系统建模的有效框架。DCOP由一组智能体构成,每个智能体控制一组离散变量,通过与局部的智能体协同通信优化全局目标函数。全局目标函数被定义为约束代价的集合,其中约束代价由变量所定义。相比于传统的集中式优化,DCOP强调通过局部交互使得全局最优,因此DCOP具有更强的容错性和更高的并行度[2]。目前DCOP已经广泛应用于实际生活,如会议调度[3]、微网控制[4]、任务调度[5]、智能家居[6] 、传感器网络[7]和资源分配[8]等。DCOP求解算法主要分为完备算法和非完备算法,完备算法如异步分布式优化(asynchronous distributed optimization, ADOPT)[9]、分布式伪树优化过程(distributed pseudo-tree optimization procedure, DPOP)[10]和基于伪树的前向定界(forward bounding on pseudo-trees, PT-FB)[11]等提供一个全局最优解,但计算开销和内存需求随着问题规模增加而呈现指数级增长;非完备算法如分布式随机算法(distributed stochastic algorithm, DSA)[12]、最大和算法(max-sum algorithm, MS)[13]、最大增益消息(maximal gain message, MGM)[14]和求解DCOP的蚁群优化(ant colony optimization for solving DCOP, ACO-DCOP)[15]等在较低的计算开销和内存需求下提供一个近似解。
然而在一些实际应用中,智能体必须取得一个或者多个连续值参数,比如方向、速度或者传感器激活时间等。DCOP建模连续型变量问题的效果并不理想,因此Stranders等[16]提出了连续型DCOP (continuous DCOP, C-DCOP)来更有效地建模连续型变量应用。与DCOP相比,C-DCOP的变量和值域是连续的,并且约束代价由一组函数所定义。
为了应对C-DOCP中变量、值域和约束代价的变化,研究人员提出了连续最大和算法(continuous max-sum, CMS)。在CMS中,约束代价函数被近似为分段线性函数,通过对比离散最大和和连续最大和算法,由CMS能够得到更高质量的解证明了C-DCOP的必要性。然而只有极少数实际应用可以适用于分段线性函数。混合连续最大和(hybrid continuous max-sum, HCMS)[17]首先通过离散最大和获得一组近似解,通过非线性优化方法提高近似解的精度。虽然HCMS解决了分段线性函数的局限,但由于存在导数计算,使得HCMS不适用于不可微的问题,并且不能保证收敛。精确连续DPOP (exact continuous DPOP, EC-DPOP)、近似连续DPOP (approximate continuous DPOP, AC-DPOP)、聚类近似连续DPOP (clustered AC-DPOP)和连续DSA (continuous DSA)[18]被同时提出以解决函数形式的限制。EC-DPOP、AC-DPOP和CAC-DPOP能够获得高质量的解,但计算开销和内存需求巨大;C-DSA逻辑简单,计算开销小,但解的质量不佳。基于C-DCOP的粒子群优化算法(particle swarm optimization based C-DCOP, PFD)[19]被提出以减少计算开销和内存需求。PFD引入种群思想,通过种群寻优的方式找到近似解,然而搜索能力差和容易陷入局部最优的问题限制了解质量的提升。连续协同约束近似(continuous cooperative constraint approximation, C-CoCoA)[20]是一种非迭代算法,不具备anytime属性,虽然能够以极快的计算速度和极小的计算开销求解C-DCOP,但由于C-CoCoA中的半贪婪局部搜索策略,使得其在复杂的大规模问题上的求解质量不佳。
基于以上分析,求解C-DCOP的自适应多点交叉遗传算法(adaptive multi-point crossover genetic algorithm for C-DCOP, AMCGA)被提出用于解决目前C-DCOP求解算法的缺点与局限。为了将遗传算法(genetic algorithm, GA)[21]扩展到C-DCOP并进一步改进,本文的贡献概括如下:
1) 采用分布式种群[22]和广度优先搜索(breadth first search, BFS)伪树[23]满足分布式特性,使得算法具有anytime属性并适用于任意函数形式。
2) 设计一种自适应的多点交叉方法,增强算法的搜索能力,通过智能体的决策与协同通信保证交叉过程中解的一致性。
3) 设计自适应的种群大小增强算法的鲁棒性并设计自适应的交叉和变异概率平衡算法。
4) 改进的精英筛选与保留策略能够保证算法的收敛。
在4类基准问题上的广泛实验表明,AMCGA的求解质量优于最先进的C-DCOP求解算法并有着20%~30%的提升。
1. 连续型分布式约束优化问题的定义与基础方法
1.1 连续型分布式约束优化问题
在通常情况下,一个C-DCOP可以由一个五元组
$ < A,X,D,F,\alpha > $ 定义,其中,$A = \{ {a_1}, {a_2},\cdots, {a_n}\}$ 是一组智能体的集合,能够控制一个或者多个变量;$X = \{ {x_1},{x_2},\cdots,{x_m}\}$ 是一组由智能体控制的连续变量集合;$D = \{ {D_1},{D_2},\cdots,{D_m}\}$ 是一组连续值域集合,每个变量$ {x_i} $ 能够取得值域${D_i} = [{{L}}{{}_i},{{U}}{{}_i}]$ 中的任意值,其中${{L}}{{}_i}$ 和${{ U}}{{}_i}$ 分别表示值域的下界和上界;$F = \{ {f_1},{f_2},\cdots,{f_l}\}$ 是一组约束代价函数的集合,其中每一个约束代价函数$ {f_i} \in F $ 被变量集合$ X $ 的一组子集${x_i} = \{ {x_{{i_1}}},{x_{{i_2}}},\cdots,{x_{{i_k}}}\}$ 所定义,意味着${f_i}:{D_{{i_1}}} \times {D_{{i_2}}} \times \cdots \times {D_{{i_k}}} \to R$ ,$ {f_i} $ 受$ k $ 个变量的约束。本文仅考虑二元约束,即$ k $ = 2;$ \alpha $ :$ X \to A $ 是一个映射函数,表示将每个变量$ {x_j} \in X $ 的控制权分配给智能体$ {a_i} \in A $ 。为便于理解,假设一个智能体控制一个变量,因此智能体$ {a_i} $ 与变量$ {x_i} $ 可以认为是同一概念,在本文中交替使用。一个C-DCOP的解为一个赋值集合
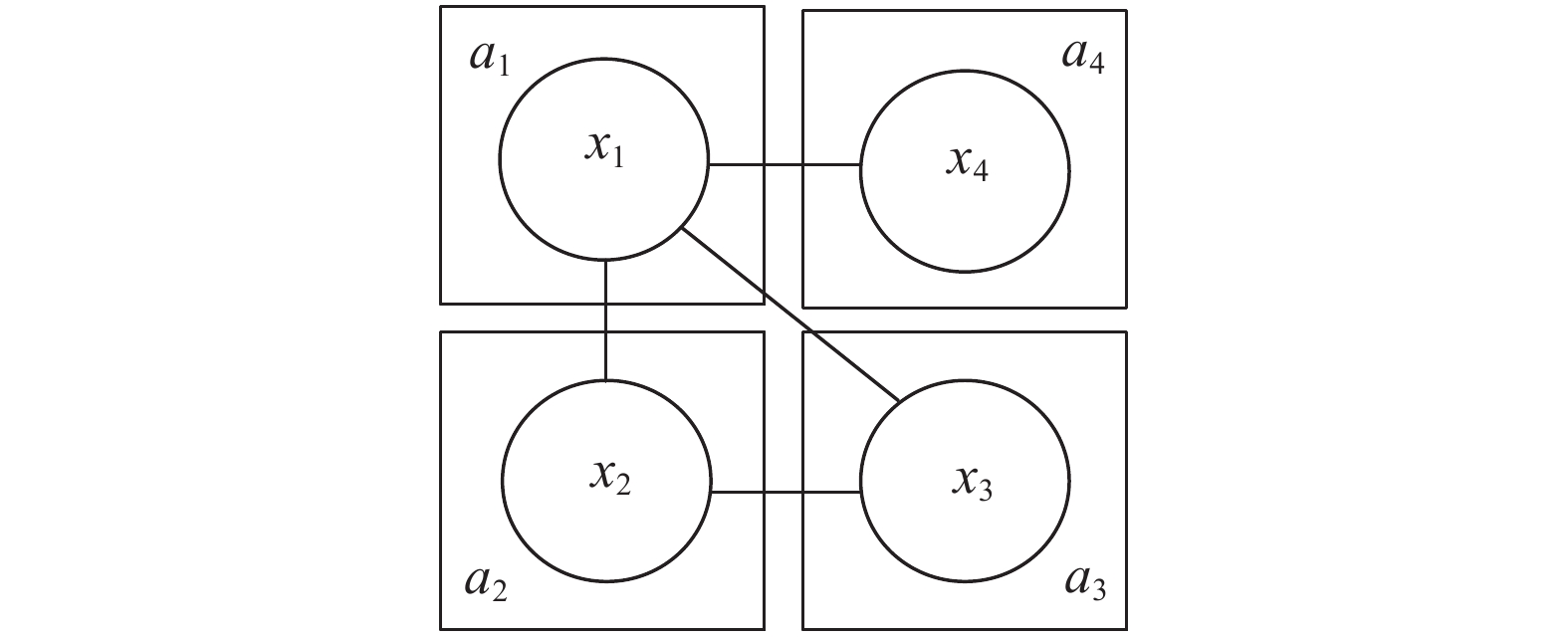
$ {X^*} $ ,使得全部约束代价函数之和最小:$$ {X^*} = \mathop {\arg \min }\limits_X \displaystyle \sum\limits_{i = 1}^l {f({x^i})} $$ (1) 图1为一个C-DCOP的例子,是一个具有4个变量的约束图,每个变量由相应的一个智能体控制,每条边代表一个约束代价函数。变量
$ {x_i} $ 的值域$ {D_i} $ 为[−10,10]。$\forall {x_i} \in X:{D_i} = [ - 10,10],$ $f({x_1}, {x_2}) = 2x_1^2 + 3{x_1}{x_2} - x_2^2,$ $f({x_1},{x_3}) = \exp \sqrt {x_1^2 + x_3^2} ,$ $f({x_1}, {x_4}) = x_1^4 - 2x_1^2{x_4} - 2x_4^3,$ $f({x_2},{x_3}) = 2x_2^2-{\rm{sin}}(\text{π} {x_3})。$ 1.2 分布式种群
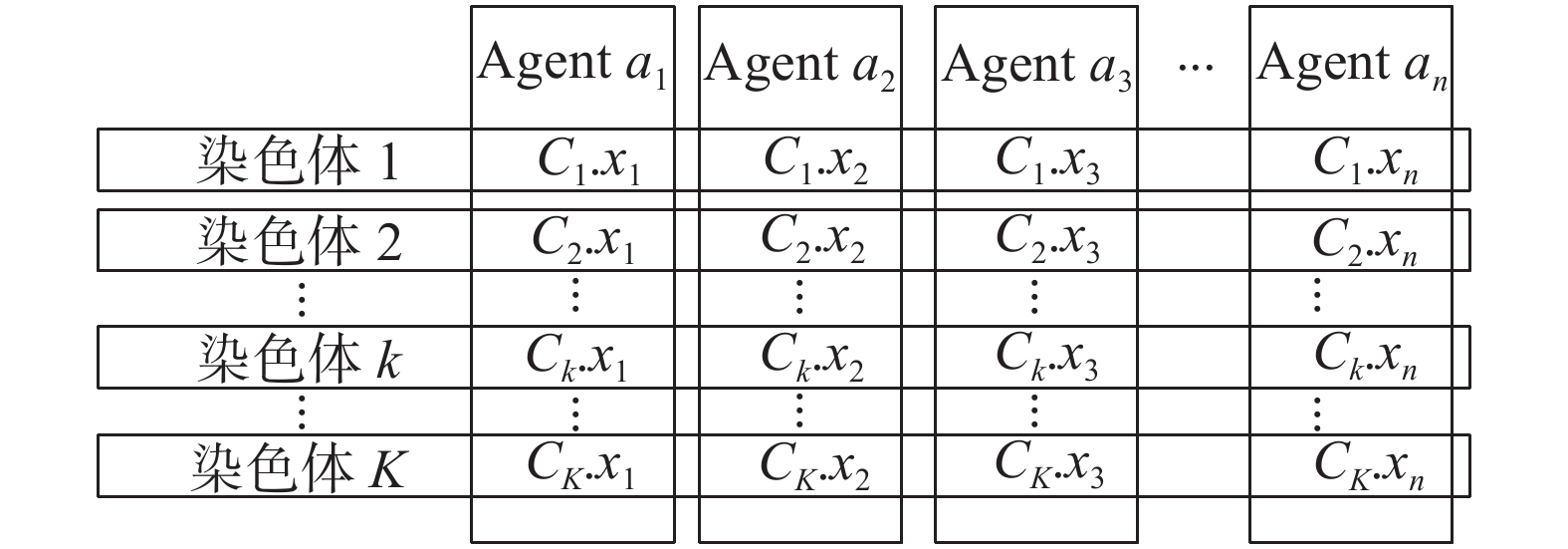
分布式种群是基于种群的C-DCOP求解算法中常用的一种方法,每个智能体持有所有个体一个维度的变量,所有智能体协同持有一个分布式种群,一个个体代表一个解。图2表示一个具有
$ K $ 个染色体、$ n $ 个智能体的分布式种群,使用${C_k}.{x_n}$ 表示第$ k $ 个染色体的第$ n $ 个维度的变量。1.3 广度优先搜索伪树
BFS伪树是DCOP和C-DCOP中常用的一种通信结构,其特点为多个分支并行计算,通信路径和通信时间短。
图3(a)表示以图1为例的一个BFS伪树,图3(b)表示BFS伪树的有序排列。BFS伪树用于智能体之间的通信,有序排列代表消息传递的顺序,深度较小的智能体相比于深度较大的智能体有着更高的优先级,使用
$ {H_i} $ 和$ {L_i} $ 分别表示智能体$ {a_i} $ 的高优先级邻居和低优先级邻居。在图3(b)中,智能体$ {a_1} $ 表示根智能体,智能体$ {a_3} $ 、$ {a_4} $ 为叶智能体;对于智能体$ {a_2} $ ,其邻居$ {N_2} = \{ {a_1},{a_3}\} $ ,高优先级邻居$ {H_2} = \{ {a_1}\} $ ,低优先级邻居$ {L_2} = \{ {a_3}\} $ 。2. 基于连续型分布式约束优化问题的自适应多点交叉遗传算法
AMCGA是一种基于种群的C-DCOP求解算法,种群中的个体被称为染色体,染色体的一个维度称为一个基因。AMCGA包括5个阶段:初始化、评估、选择、交叉和变异阶段。在初始化阶段,AMCGA初始化种群和参数;智能体在评估阶段协同计算染色体的适应度;选择阶段通过贪婪策略选择精英染色体;在交叉阶段,智能体执行多点交叉算子;在变异阶段,智能体执行变异算子并保留精英染色体。具体流程见算法1。
算法1 ACMGA
1)构造有序的广度优先搜索(BFS)伪树;
2)初始化参数:
$ K $ ,$ G $ ,${P_{c_1}}$ ,${P_{c_2}}$ ,$ {S_a} $ ,$ {P_m} $ ;3)
$ C $ $ \leftarrow $ 生成$ K $ 个染色体 // 构造种群4)for
$ {a_i} $ $ \leftarrow $ $ {a_1} $ to$ {a_I} $ do //$ I $ 个智能体5) for
$ {C_k} $ $ \leftarrow $ $ {C_1} $ to$ {C_K} $ do6)
$ {C_k}.{x_i} $ $ \leftarrow $ $ {D_i} $ 7) end for
8) 发送
$C.{x_i}$ 给集合$ {L_i} $ 中的智能体9)end for
10)未达到终止条件,for 每一个智能体
$ {a_i} $ do11)
${\rm{Messaging}}()$ 12) if
$ {a_i} $ $ = = $ $\rm {root}$ do //$ {a_i} $ 为根智能体13)
${\rm{Selection}}(C_{\rm{fitness}})$ 14) end if
15) 等待直到消息被接收
16) if从集合
$ {H_i} $ 中接收到消息 do17)
${C_g}.{x_i} \leftarrow {\rm{CrossList }}\cup {\rm{UncrossList}}$ 18)
${C^{{\rm{cam}}}}.{x_i} \leftarrow {\rm{CrossList}}$ 19) if agent
$ {a_i} $ in${\rm{Agen}}{{\rm{t}}_c}$ do20)
${\rm{Crossover}}({C^{{\rm{cam}}}}.{x_i})$ 21) end if
22)
${C^{{\rm{cam}}}}.{x_i} \leftarrow {\rm{CrossList}} \cup {\rm{UncrossList}}$ 23) 计算
${P_{{\rm{mutation}}}}$ 24) for
$C_g^{{\rm{cam}}}.{x_i} \leftarrow C_1^{{\rm{cam}}}.{x_i}$ to$C_G^{{\rm{cam}}}.{x_i}$ do25)
${\rm{Mutation}}(C_g^{{\rm{cam}}}.{x_i})$ 26) end for
27)
$C.{x_i} \leftarrow {C_g}.{x_i} \cup {C^{{\rm{cam}}}}.{x_i}$ 28) if
$ {L_i} \ne 0 $ do29) 发送
$C.{x_i}$ 给集合$ {L_i} $ 30) 发送信息给
$ {L_i} $ 中的智能体31) end if
32) end if
33)end while
初始化阶段:AMCGA首先构造有序的BFS伪树;然后初始化参数:
$K$ 为染色体的数量;$ G $ 为精英个体的数量;${P_{c_1}}$ ,${P_{c_2}}$ 为共同定义交叉概率;${S_a} $ 为交叉点的数量;$ {P_m} $ 为定义变异概率。最后,智能体协同构造一个分布式种群并对所持有基因赋予一个值域中的随机值,然后将赋值发送给低优先级邻居(算法1:步骤1)~9)。
以图1和图3为例,假设染色体的数量为4,分布式种群可表示为
$ C = \{ {C_1},{C_2},{C_3},{C_4}\} $ ,每条染色体的完整赋值可表示为$$ {C_1}.X = \{ {x_1} = 1,{x_2} = 2,{x_3} = 2.5,{x_4} = 3.1\} $$ $$ {C_2}.X = \{ {x_1} = 2,{x_2} = 4,{x_3} = 0,{x_4} = 5.2\} $$ $$ {C_3}.X = \{ {x_1} = 3,{x_2} = - 3,{x_3} = 6,{x_4} = - 2.5\} $$ $$ {C_4}.X = \{ {x_1} = - 2,{x_2} = 1.4,{x_3} = 7,{x_4} = 0\} $$ 智能体
$ {a_1} $ 发送C.x1 = { 1, 2, 3, −2}给低优先级邻居$ {a_2} $ 、$ {a_3} $ 和$ {a_4} $ ;智能体$ {a_2} $ 向智能体$ {a_3} $ 发送${C_2}.X = \{ {x_1} = 2,{x_2} = 4,{x_3} = - 3,{x_4} = 1.4\}$ 。函数 1)
${\rm{Messaging}}()$ ① for
$C.{x_j}$ received from$ {H_{{i_j}}} \in {H_i} $ do //$ {H_{{i_j}}} $ 表示高优先级邻居$ {H_i} $ 中的一个邻居智能体② for
$ {C_k} $ $ \leftarrow $ $ {C_1} $ to$ {C_K} $ do③
${C}_{k.{\text{fitness}}} \leftarrow {{\rm{Cos}}} {t_{i,j}}({C_k}.{x_i},{C_k}.{x_j})$ ④ end for
⑤ send
$C_{{\text{fitness}}}$ fitness to agent in$ {H_{{i_j}}} $ ⑥ end for
⑦ Wait
$C_{\text{fitness}}$ received from all agents in$ {L_i} $ ⑧ if
$ \left| {{L_i}} \right| \ne 0 $ and$C_{\text{fitness}}$ received from$ {L_i} $ ⑨ for
$ {C_k} $ $ \leftarrow $ $ {C_1} $ to$ {C_K} $ do⑩
${C_{k.{\text{fitness}}}} \leftarrow \sum\nolimits_{j \in {L_i}} {C_{\text{fitness}}}$ ⑪ end for
⑫ if
${a_i} \ne {\rm{root}}$ do // 智能体$ {a_i} $ 不为根智能体⑬ send
$C_{\text{fitness}}$ to an agent$ {H_{{i_j}}} \in {H_i} $ ⑭ end if
⑮ end if
函数 2)
${\rm{ Selection}}(C_{\text{fitness}})$ ①
${C^{{\rm{sort}}}} \leftarrow {\rm{sorted}}(C_{\text{fitness}})$ // 适应度排序②
$C_G^{{\rm{sort}}} \leftarrow$ Select the top$ G $ chromosomes // 选择适应度靠前的$ G $ 条染色体③ information:
${\rm{ CrossList}},\;{\rm{UncrossList}},\;{\rm{Agen}}{{\rm{t}}_c}$ $ \leftarrow $ {} // 创建3个集合④ 计算
${P_{{\rm{cross}}}}$ ⑤ for
$C_g^{{\rm{sort}}} \leftarrow C_1^{{\rm{sort}}}$ to$C_g^{{\rm{cam}}}$ do⑥ if
${r_p} < {P_{{\rm{cross}}}}$ do⑦
${\rm{CrossList}} \leftarrow {\rm{CrossList}} \cup C_g^{{\rm{sort}}}$ ⑧ else
⑨
${\rm{UnCrossList}} \leftarrow {\rm{UnCrossList}} \cup C_g^{{\rm{sort}}}$ ⑩ end if
⑪ end for
⑫ if
$\left| {{\rm{CrossList}}} \right|\% 2 \ne 0$ do // 数量为奇数⑬
${\rm{CrossList}} \leftarrow {\rm{CrossList}}\backslash {\rm{end}}$ //移除
${\rm{CrossList}}$ 中最后一个元素⑭
${\rm{UnCrossList }}\leftarrow {\rm{UnCrossList}} \cup {\rm{end}}$ ⑮ end if
⑯
${\rm{Agen}}{{\rm{t}}_c} \leftarrow$ Select$ {S_a} $ different agents⑰ 发送信息给集合
$ {L_i} $ 中的智能体函数 3)
${\rm{Crossover}}({C^{{\rm{cam}}}}.{x_i})$ ①
${\rm{len}} \leftarrow \left| {{C^{{\rm{cam}}}}.{x_i}} \right|$ // 变量的数量②
${\rm{start }}\leftarrow 1$ ③ while
${\rm{ start}} \leqslant {\rm{len}}/2$ do④
$C_{{\rm{start}}}^{{\rm{cam}}}.{x_i} \leftrightarrow C_{{\rm{len}} - {\rm{start}} + 1}^{{\rm{cam}}}.{x_i}$ // 以中心为对称轴互换前后基因
⑤
${\rm{start}} + +$ ⑥ end while
函数 4)
${\rm{Mutation}}(C_g^{{\rm{cam}}}.{x_i})$ ① if
${r_m} < {P_{{\rm{mutation}}}}$ do②
$C_g^{{\rm{cam}}}.{x_i} \leftarrow$ a random value from$ {D_i} $ ③ end if
评估阶段:当接收到高优先级邻居的赋值后,智能体依次计算与每个高优先级邻居的每条染色体的部分适应度,并发送给相应的高优先级邻居(函数1):①~⑥)。除了叶智能体,每个智能体将从低优先级邻居接收的部分适应度求和,若该智能体不为根智能体,则将求和之后的部分适应度沿着BFS伪树发送给一个高优先级邻居(函数1):⑧~⑮)。
$$ {C_{{k}.{\text{fitness}}}} = \displaystyle \sum\limits_{{f_i} \in F} {{f_i}({C_k}.{x^i})}$$ (2) 每条染色体的适应度通过式(2)计算,其中
${C_k}.{x_i}$ 表示2个具有约束关系的变量赋值。单个智能体不能计算染色体的完整适应度,而是在所有智能体的配合下协同计算染色体的完整适应度。在上述例子中,智能体
$ {a_3} $ 分别计算与智能体$ {a_1} $ 、$ {a_2} $ 的部分适应度$C_{\text{fitness}}({x_1},{x_3})$ 和$C_{\text{fitness}}({x_2},{x_3})$ 并发送给相应的智能体$ {a_1} $ 、$ {a_2} $ 。智能体$ {a_4} $ 计算与$ {a_1} $ 的部分适应度$C_{\text{fitness}}({x_1},{x_4})$ 并发送给$ {a_1} $ 。此外,由于智能体$ {a_2} $ 不是根智能体,因此不仅计算与智能体$ {a_1} $ 的部分适应度$C_{\text{fitness}}({x_1},{x_2})$ 并发送给$ {a_1} $ ,还会将接收的部分适应度$C_{\text{fitness}}({x_2},{x_3})$ 发送给$ {a_1} $ 。计算的部分适应度为$$ C_{\text{fitness}}({x_1},{x_2}) = \{ 4,16, - 18, - 2.36\} $$ $$ C_{\text{fitness}}({x_1},{x_3}) = \{ 14.77,7.39,819.10,1451.15\} $$ $$ C_{\text{fitness}}({x_1},{x_4}) = \{ 54.38,255.62,94.75,16\} $$ $$ C_{\text{fitness}}({x_2},{x_3}) = \{ 7,32,18,3.92\} $$ 选择阶段:由于每个智能体都会将部分适应度发送给高优先级邻居,因此染色体的所有部分适应度都将传递到根智能体。根智能体首先对染色体的适应度排序并选择适应度靠前的
$ G $ 条染色体(函数2):①~②);然后对每一条染色体进行判断,若[0, 1]之间的随机数$ {r_p} $ 小于通过${P_{{\rm{cross}}}} = {P_{c_1}} + \dfrac{{{P_{c_2}}\times({{I}_{\max }} - {I}_{{\rm{cur}}})}}{{{{I}_{\max }}}} $ 计算的交叉概率$ {P_{{\rm{cross}}}} $ ,则将该染色体标记为交叉染色体$ {\rm{CrossList}} $ ,否则标记为非交叉染色体$ {\rm{UnCrossList}} $ ,若交叉染色体为奇数,则将交叉染色体中最后一个染色体移除并添加到非交叉染色体中(函数2):④~⑮);最后,根智能体随机选择$ {S_a} $ 个不同的智能体作为交叉点并将信息发送给低优先级邻居中的智能体(函数2):⑯~⑰)。${{I}}_{\max }$ 和${{I}}_{{\rm{cur}}}$ 分别为最大迭代次数和当前迭代次数。在例子中,假设
$ G = 2 $ 并且智能体$ {a_2} $ 、$ {a_3} $ 被选择为交叉点。智能体$ {a_1} $ 获得染色体的完整适应度$C_{\text{fitness}} = \{ 80.15,311.03,913.85,1\,468.71\}$ 并在排序和选择之后得到$C_2^{{\rm{sort}}} = \{ {C_1},{C_2}\}$ 。最后,$ {a_1} $ 将信息$= \{ {\rm{CrossList}}, \;{\rm{UncrossList}},\;{\rm{Agen}}{{\rm{t}}_c}\}$ 发送给低优先级邻居$ {a_2} $ 、$ {a_3} $ 、$ {a_4} $ 。交叉阶段:当收到高优先级邻居传递的information后,智能体首先复制交叉染色体和非交叉染色体作为父代;若智能体被标记为交叉点,则使用交叉染色体执行交叉算子(算法1:17)~21))。具体来说,智能体将自身持有染色体一个维度的基因前后互换位置(函数3):①~⑥)。
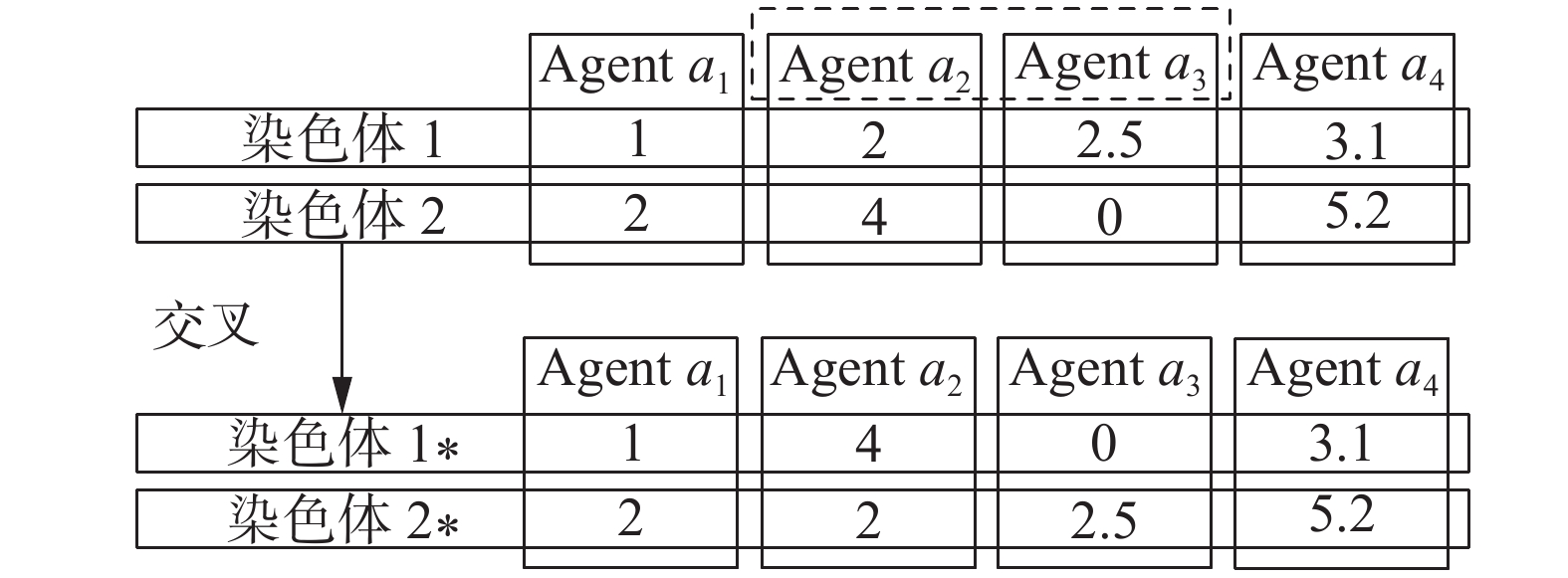
在之前的例子中,
$ {C_1} $ 和$ {C_2} $ 执行交叉算子,智能体$ {a_2} $ 交换${C_1}.{x_2}$ 和${C_2}.{x_2}$ ,智能体$ {a_3} $ 交换${C_1}.{x_3}$ 和${C_2}.{x_3}$ ,如图4所示。$ {C_{1*}}$ 和${C_{2*}}$ 为子代染色体:$$ {C_{1*}}.X = \{ {x_1} = 1,{x_2} = 4,{x_3} = 0,{x_4} = 3.1\} $$ $$ {C_{2*}}.X = \{ {x_1} = 2,{x_2} = 2,{x_3} = 2.5,{x_4} = 5.2\} $$ 变异阶段:在交叉完成之后,子代染色体与非交叉染色体合并,通过
$ {P_{{\rm{mutation}}}} = {P_m}\times \displaystyle \frac{{{{I}}_{\max } - {{I}_{{\rm{cur}}}}}}{{{{I}_{\max }}}} $ 计算变异概率并对每一条染色体执行变异算子(算法1:22)~26))。具体来说,在[0, 1]之间的随机数$ {r_m} $ 若小于变异概率,则智能体$ {a_i} $ 将此染色体的此维度基因重新赋值为值域$ {D_i} $ 里的一个随机值(函数4):①~③)。最后,智能体将子代染色体和父代染色体合并为一个新的种群(算法1:37))。假设只有智能体
$ {a_4} $ 所持有的基因发生变异,$ {C_{1*}} $ 和$ {C_{2*}} $ 变异后的完整赋值为$$ {C_{1*}}.X = \{ {x_1} = 1,{x_2} = 4,{x_3} = 0,{x_4} = 5\} $$ $$ {C_{2*}}.X = \{ {x_1} = 2,{x_2} = 2,{x_3} = 2.5,{x_4} = - 9\} $$ 因此,新种群的完整赋值为
$$ {C_1}.X = \{ {x_1} = 1,{x_2} = 4,{x_3} = 0,{x_4} = 5\} $$ $$ {C_2}.X = \{ {x_1} = 2,{x_2} = 2,{x_3} = 2.5,{x_4} = - 9\} $$ $$ {C_3}.X = \{ {x_1} = 1,{x_2} = 2,{x_3} = 2.5,{x_4} = 3.1\} $$ $$ {C_4}.X = \{ {x_1} = 2,{x_2} = 4,{x_3} = 0,{x_4} = 5.2\} $$ 3. 算法收敛性分析
本节使用通信步骤表示智能体接收邻居智能体发送的消息次数。此外,在本节使用H代表 BFS 伪树的深度。
引理1 根智能体在通信步骤为T+H时获得通信步骤为T时的最优解。
证明:智能体通过BFS伪树传递染色体的部分适应度,根智能体计算染色体的完整适应度需要叶智能体沿着BFS伪树向上传递染色体的部分适应度。由于BFS伪树的高度为H,根智能体需要等待最多H次通信步骤来计算染色体的完整适应度,从而找到最优解。因此,根智能体在通信步骤为T+H时获得通信步骤为T时的最优解。
引理2 所有智能体在通信步骤为T+2H时获得通信步骤为T时的最优解。
证明 通过引理1,根智能体在T+H时获得T时的最优解,最优解通过BFS伪树到达每一个智能体需要等待最多H次通信步骤。因此,所有智能体在通信步骤为T+2H时获得通信步骤为T时的最优解。
命题1 AMCGA是一种任意时间属性算法。
证明 从引理2可得,所有智能体在通信步骤为T+2H+Δ (Δ > 0)时获得通信步骤为 T+Δ时的最优解。只有智能体找到了更好的解,最优解才会更新,通信步骤为T+2H+Δ的最优解不会差于通信步骤为T+2H时最优解。因此,AMCGA中解的质量不会随着时间增加而降低并且在任意时刻都能提供一个最优解,即AMCGA是一种任意时间属性算法。
命题2 AMCGA具有全局收敛性。
证明 设b(m)为第m代种群的最优解,若
$$ {b}_{\text{fitness}}(m) < {{b}}_{\text{fitness}}(m + 1) $$ 则
$$ {{b}}(m + 1) = {{b}}(m) $$ $$ {{b}}_{\text{fitness}}(m + 1) = {{b}}_{\text{fitness }}(m)$$ 从命题1可知,每一代种群产生的最优解组成的序列是一个非递增序列。在AMCGA中,由于精英个体保留策略,最优解以概率1保留到下一代种群,若在第M代种群找到了全局最优解B,则B将一直保留而不会丢失。
若m > M,
${{b}}_{\text{fitness}} (m)= {{B}}_{\text{fitness}}$ 则
$$ \mathop {\lim }\limits_{m \to \infty } P({{b}}_{\text{fitness}}(m) = {{B}}_{\text{fitness}}) = 1 $$ 因此,AMCGA具有全局收敛性。
4. 复杂度分析
本节定义染色体数量为
$ K $ ,智能体的数量为$ n $ ,高优先级邻居的数量为$ H $ ,低优先级邻居的数量为$ L $ ,因此邻居数量为$ N = H + L $ 。此外,图的类型定义为全连接图,即$ N \approx n $ 。一次迭代定义为经过完整的评估、选择、交叉和变异阶段。在AMCGA中,一个智能体在初始化阶段和选择阶段向低优先级邻居发送消息;在评估阶段,智能体向高优先级邻居发送消息,此外,非叶智能体还会传递一次消息(部分适应度)。因此,在最坏情况,即所有邻居为低优先级邻居,一个智能体在一次迭代中发送的消息数量为
$ O(2L + H + 1) = O(N + L + 1) = O(n) $ 。智能体会发送5类消息:
$C.{x_i}$ 、$C_{\text{fitness }}$ 、$\phi$ 、$\varphi$ 、$\gamma$ 。其中第1类和第2类消息分别包含$ K $ 条染色体的信息;第3类和第4类共包含$ G $ 条染色体的信息;最后一类消息远小于$ K $ 。因此,一个智能体在一次迭代中发送的消息大小为$O(2Kn + Gn) = O(Kn)$ 。在一次迭代中,智能体计算每条染色体的适应度。此外还会分别计算一次交叉、变异概率。因此一个智能体在一次迭代中的计算复杂度为
$O(Kn + 1 + 1) = O(Kn)$ 。5. 实验与分析
为了验证ACMGA的有效性,本文在4类基准问题上使用AMCGA与最先进的C-DCOP求解算法C-CoCoA、PFD和HCMS进行实验对比。虽然AMCGA适用于任何函数形式,为了更好地展示对比效果,本文遵循文献[18]中的约束代价函数形式:
$ a{x^2} + bx + cxy + dy + e{y^2} + f $ 。其中$a、b、c、 d、e、f$ 均为区间[−5, 5]中的随机数。智能体$ {a_i} $ 控制的变量值域$ {D_i} $ 设置为[−50, 50],迭代次数设置为500。对于每一种实验配置,每一种算法独立运行30次并取平均值作为最终的结果。5.1 基准问题
随机图 稀疏随机图(密度为0.1)和稠密随机图(密度为0.6)。密度表示在随机图的构造过程中任意2个点的连接概率。智能体的数量为10~100,数量间隔为10。
无尺度网络 无尺度网络由Barabási-Albert模型[24]生成。首先生成一个由10个智能体组成的连通图,在每一次迭代中加入一个新的智能体与当前网络中的7个智能体相连,直到所有智能体加入到该网络,一个智能体被连接的概率与该智能体的度数成正比。设置智能体的数量为60~100,数量间隔为5。
随机树 根据文献[18]将随机树作为一个基准问题并设置智能体的数量为60~100,数量间隔为5。
小世界网络 小世界网络由Watts-Strogatz拓扑模型[25]生成,在多个节点相连的环中,每个节点与最邻近的
$ J $ 个节点相连,顺时针选择一个节点和与其相连的一条边随机与环上的一个节点以概率$ P $ 重连,规定其中不能有重边和自环。设置$ J $ 为6,$ P $ 为0.5,智能体数量为60~100,数量间隔为5。5.2 参数讨论
AMCGA的性能取决参数的选择,在本节对交叉点的数量、交叉概率和变异概率进行讨论并选择合适的参数。选择100个智能体的稠密随机图来进行实验。根据经验,AMCGA的初始系数设置为
$ K = 10n $ ,$ G = 5n $ ,$ {P_{c_1}} = 0.9 $ ,$ {P_{c_2}} = 0.05 $ ,${S_a} = 0.1n$ 和$ {P_m} = 0.01 $ ,$ n $ 表示智能体的数量。5.2.1 交叉点数量
设置8种不同的交叉点数量以对比参数
$ {S_a} $ 对AMCGA性能的影响:$ {S_a} = 0.01n $ ,$ 0.02n $ ,$ 0.05n $ ,$ 0.1n $ ,$ 0.2n $ ,$ 0.3n $ ,$ 0.4n $ 和$ 0.5n $ 。从图5可见,AMCGA的求解质量随着交叉点的增加变得更好。由于$ {S_a} = 0.3n $ 在较快的收敛速度下能够获得更高质量的解,因此选择该参数设置进行接下来的实验。5.2.2 交叉概率
为了对比不同交叉概率对AMCGA性能的影响,设置6种不同的交叉概率进行试验:
${P_{c_1}} = 0.9$ ,0.8,0.7,0.6,0.5,0.4。在图6中,交叉概率越大,算法的收敛速度越快,表示个体之间信息交互越多。由于交叉概率为0.9的算法有着更快的收敛速度并且能够得到一个更高质量的解,因此在接下来的实验中设置交叉概率为0.9。5.2.3 变异概率
图7表示AMCGA在不同变异概率下的求解质量。变异概率影响算法的局部搜索,变异概率越大,局部搜索的概率越大,但算法退化为随机搜索。由于AMCGA在变异概率为0.02时能够得到更高质量的解,因此在接下来的实验中设置变异概率为0.02。
5.3 算法对比实验
通过5.2节的参数讨论,设置AMCGA的参数为:
$ K = 10n $ ,$ G = 5n $ ,$ {P_{c_1}} = 0.9 $ ,$ {P_{c_2}} = 0.05 $ ,$ {S_a} = 0.3n $ ,$ {P_m} = 0.02 $ 。对于AMCGA的竞争算法HCMS、PFD和C-CoCoA的参数设置,通过文献[18]设置HCMS中离散点的个数为3,梯度下降的步长为0.001;遵循文献[19],设置PFD中的$ K = 2\,000 $ ,$ w = 0.9 $ ,$ {c_1} = 0.9 $ ,$ {c_1} = 0.1 $ ,${m _{sc}} = 15$ ,${m _{fc}} = 5$ ;最后,使用文献[20]中C-CoCoA的参数设置:离散点的个数为3,梯度下降的次数为100,步长为0.01。图8、9分别给出了AMCGA、HCMS、PFD和C-CoCoA在稀疏和稠密随机图上的求解质量。可以看出AMCGA在稀疏和稠密配置下均优于其他竞争算法,随着智能体数量的增加,AMCGA的优势程度更加明显。
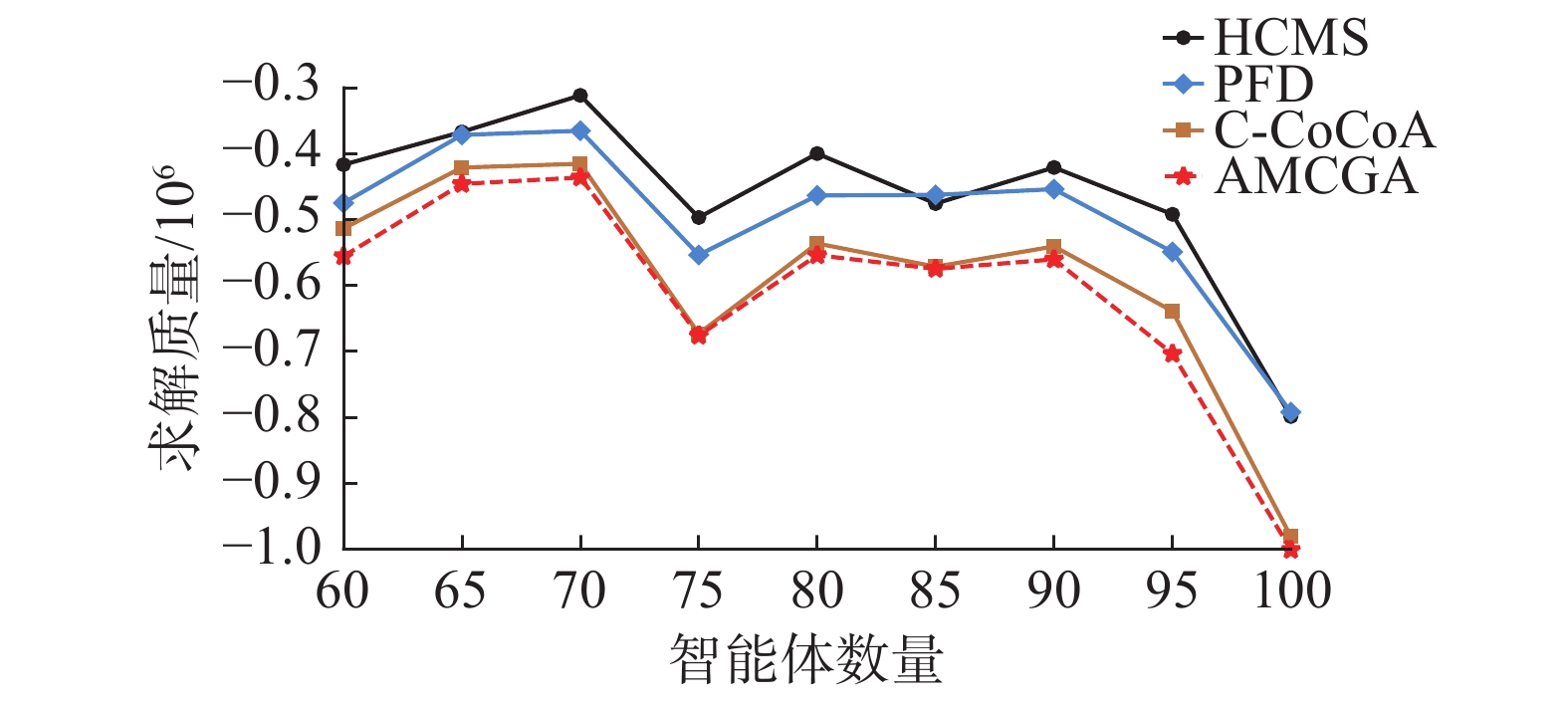
图10表示4种算法在无尺度网络上的求解质量,可以看出AMCGA在每一种智能体数量设置下都明显优于竞争算法。
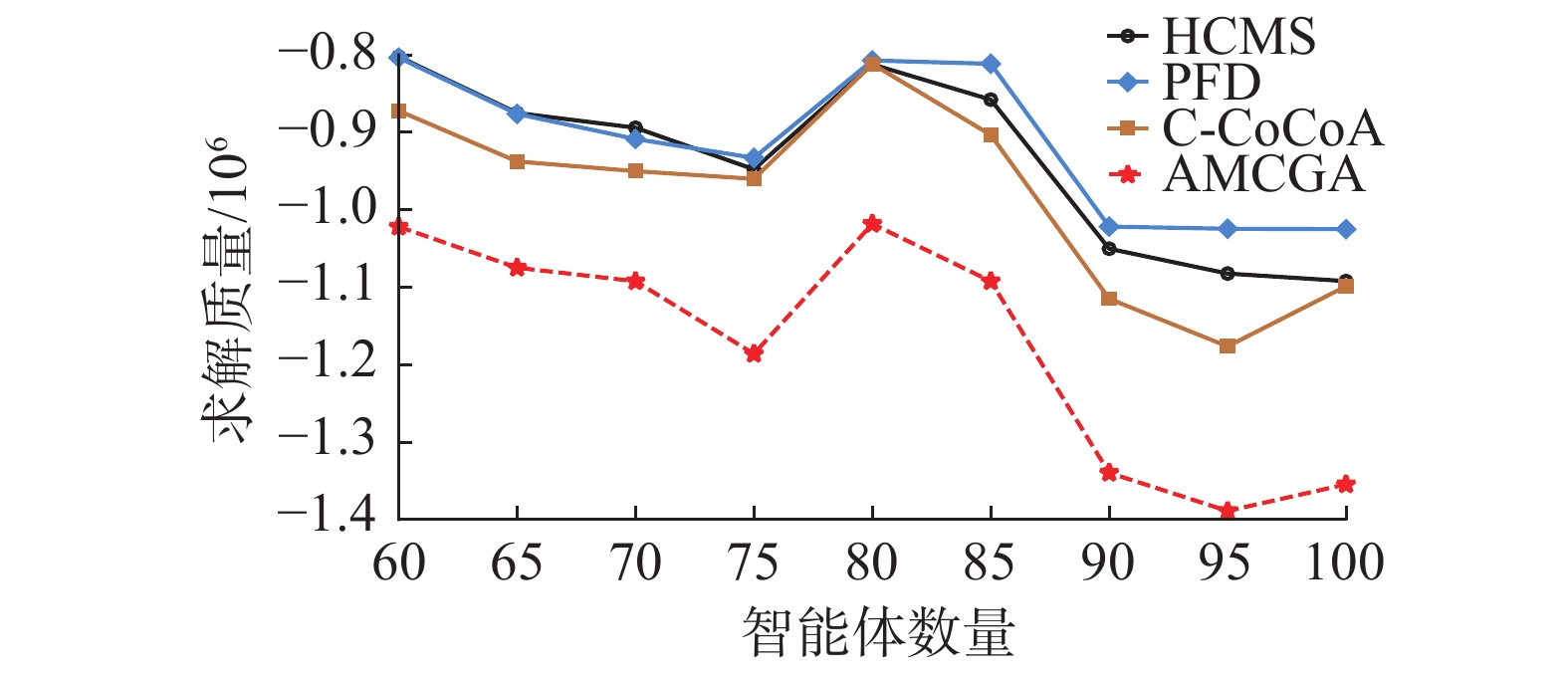
在图11中,AMCGA的求解质量优于竞争算法。但易看出C-CoCoA的求解质量在一些智能体数量设置下接近于AMCGA,这是由于在随机树的拓扑结构中,节点之间的连接较少并且约束关系简单,C-CoCoA中半贪婪的局部搜索策略更容易在简单的约束图中找到较高质量的解。
从图12中可以看出4种算法在小世界网络上不同智能体数量设置下的求解质量。与无尺度网络上的对比实验相似,AMCGA的求解质量优于竞争算法。
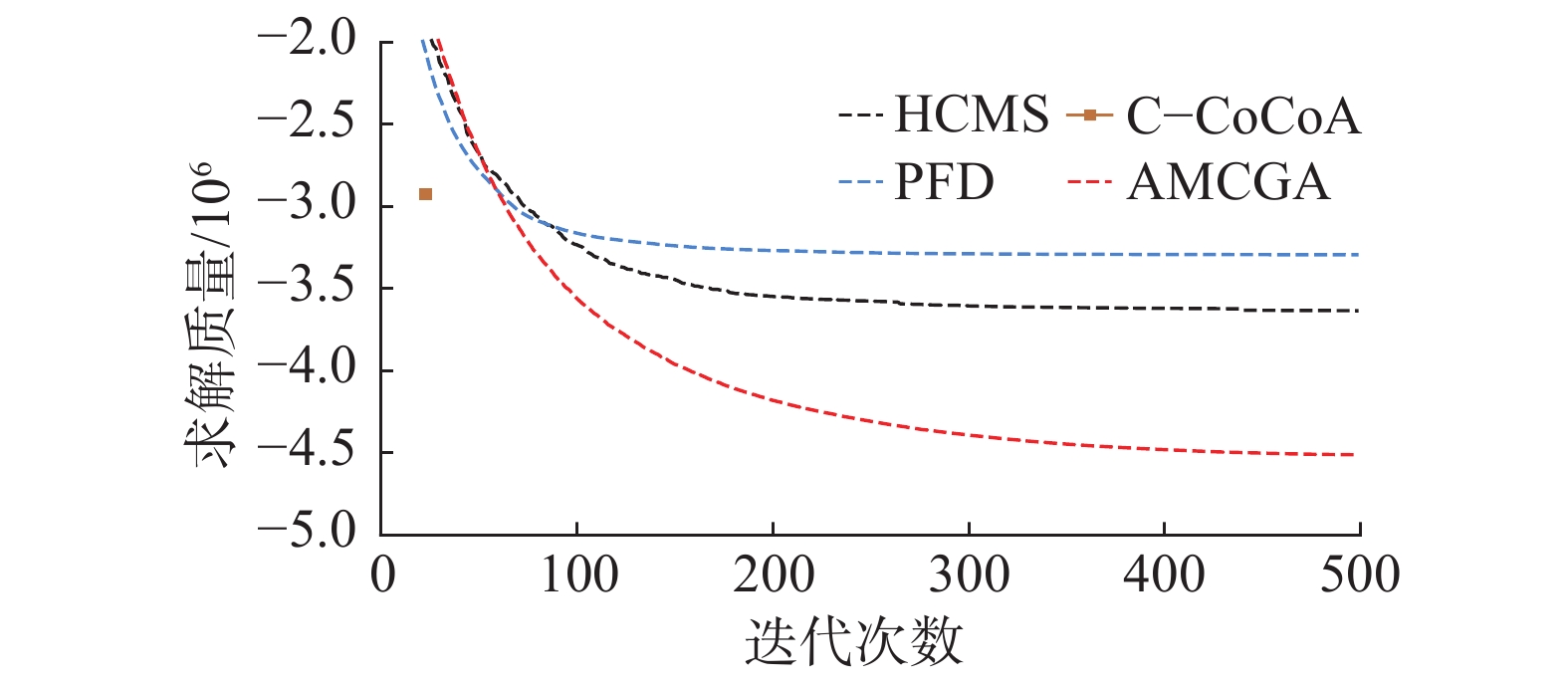
图13进一步给出AMCGA、HCMS、PFD和C-CoCoA在100个智能体的稠密随机图上的收敛曲线。值得一提的是,本文同时运行C-CoCoA和AMCGA,在C-CoCoA运行完成时,记录AMCGA的迭代次数作为C-CoCoA的迭代次数。此外,由于HCMS无法保证收敛,因此使用HCMS的历史最优取值作为结果并显示在图中。
从图13中可以看出,C-CoCoA是第一个完成求解的算法,其他的算法则继续优化。在迭代大约80次之后,AMCGA每一次迭代结果都优于HCMS和PFD。随着迭代次数增加,AMCGA的优势程度变大并且其最终的求解质量优于竞争算法。
表1给出了AMCGA相比于3种竞争算法在不同类型问题上的提升率。其中提升率为不同基准问题下所有智能体数量设置下提升率的平均值,结果保留2位小数。
表 1 AMCGA相比于竞争算法在基准问题上的提升率Table 1 Improvement rates of AMCGA compared to competing algorithms on benchmark problems% 算法 HCMS PFD C-CoCoA 稀疏随机图 30.43 18.99 14.30 稠密随机图 21.74 20.38 45.21 无尺度网络 24.85 28.81 27.40 随机树 34.42 22.26 4.36 小世界网络 25.54 28.50 19.78 AMCGA优于其他竞争算法,对不同大小和密度的基准问题都有着较好的提升率。对比HCMS和PFD,AMCGA在任意问题配置下都有着较高的提升率。尽管C-CoCoA在随机树上能够表现优异的求解性能,但AMCGA仍然存在4.36%的提升率。
6. 结束语
针对现有C-DCOP算法的缺点和局限性,提出一种求解C-DCOP的自适应多点交叉遗传算法。AMCGA通过自适应的交叉、变异概率平衡算法的探索与开发,自适应的多点交叉算子增强种群的搜索能力,智能体之间的协同调度保证了分布式环境中解的一致性。本文证明了AMCGA是一种anytime算法并具有全局收敛性。在4类基准问题上的广泛实验表明AMCGA的求解质量优于HCMS、PFD和C-CoCoA。尽管AMCGA相对于HCMS和PFD的求解质量有着较高的提升,但收敛速度略微落后于HCMS和PFD,因此未来的工作可以概括为2点:1)结合一些策略来提高AMCGA的收敛速度。2)将AMCGA扩展到多目标C-DCOP。
-
表 1 AMCGA相比于竞争算法在基准问题上的提升率
Table 1 Improvement rates of AMCGA compared to competing algorithms on benchmark problems
% 算法 HCMS PFD C-CoCoA 稀疏随机图 30.43 18.99 14.30 稠密随机图 21.74 20.38 45.21 无尺度网络 24.85 28.81 27.40 随机树 34.42 22.26 4.36 小世界网络 25.54 28.50 19.78 -
[1] 段沛博, 张长胜, 张斌. 分布式约束优化方法研究进展[J]. 软件学报, 2016, 27(2): 264–279. doi: 10.1016/j.eswa.2014.02.039 ALLAN R L, FABRICIO E, JEAN P A. Distributed constraint optimization problems: review and perspectives[J]. Expert systems with applications, 2016, 27(2): 264–279. doi: 10.1016/j.eswa.2014.02.039 [2] 邓衍晨. 求解分布式约束优化问题的推理算法研究[D]. 重庆: 重庆大学, 2018. DENG Yanchen. The study on inference-based algorithms for distributed constraint optimization problems[D]. Chongqing: Chongqing University, 2018. [3] SULTANIK E A, MODI P J, REGLI W C. On modeling multiagent task scheduling as a distributed constraint optimization problem[C]//Proceedings of the 20th International Joint Conference on Artifical Intelligence. New York: ACM, 2007: 1531−1536. [4] 马瑞, 金艳, 刘鸣春. 基于机会约束规划的主动配电网分布式风光双层优化配置[J]. 电工技术学报, 2016, 31(3): 145–154. MA Rui, JIN Yan, LIU Mingchun. Bi-level optimal configuration of distributed wind and photovoltaic generations in active distribution network based on chance constrained programming[J]. Transactions of China electrotechnical society, 2016, 31(3): 145–154. [5] 吴玲, 张朱峰, 吴威. 基于分布式约束优化的多UCAV协同任务分配[J]. 海军工程大学学报, 2018, 30(6): 64–68. doi: 10.1016/j.jnca.2011.02.016 BARTHS A, ENEMBRECK F. Distributed constraint optimization with MULBS: a case study on collaborative meeting scheduling[J]. Journal of network and computer applications, 2018, 30(6): 64–68. doi: 10.1016/j.jnca.2011.02.016 [6] FERDINANDO F, ENRICO P, WILLIAM Y. A multiagent system approach to scheduling devices in smart homes[C]// Proceedings of the 16th Conference on Autonomous Agents and Multi-Agent Systems. Paulo: AAMAS Press, 2017: 981–989. [7] MULDOON C, O'HARE G M P, O'GRADY M J, et al. Distributed constraint optimization for resource limited sensor networks[J]. Science of computer programming, 2013, 78(5): 583–593. doi: 10.1016/j.scico.2012.10.005 [8] 雷兴明, 邢昌风, 吴玲. 基于分布式约束优化的武器目标分配问题研究[J]. 计算机工程, 2012, 38(7): 128–130. doi: 10.3233/WIA-140288 CHENG Shanjun, RAJA A, XIE Jiang. Dynamic multiagent load balancing using distributed constraint optimization techniques[J]. Web intelligence and agent systems, 2012, 38(7): 128–130. doi: 10.3233/WIA-140288 [9] JMODI P J, SHEN W M, TAMBE M. Adopt: asynchronous distributed constraint optimization with quality guarantees[J]. Artificial intelligence, 2005, 161(1/2): 149–180. [10] PETCU A, FALTINGS B. A scalable method for multiagent constraint optimization[C]//Proceedings of the 19th International Joint Conference on Artificial Intelligence. New York: ACM, 2005: 266−271. [11] LITOV O, MEISELS A. Forward bounding on pseudo-trees for DCOPs and ADCOPs[J]. Artificial intelligence, 2017, 252: 83–99. doi: 10.1016/j.artint.2017.07.003 [12] ZHANG Weixiong, WANG Guandong, ZHAO Xing, et al. Distributed stochastic search and distributed breakout: properties, comparison and applications to constraint optimization problems in sensor networks[J]. Artificial intelligence, 2005, 161(1/2): 55–87. [13] FARINELLI A, ROGERS A, PETCU A, et al. Decentralised coordination of low-power embedded devices using the max-sum algorithm[C]// Proceedings of the 7th International Joint Conference on Autonomous Agents and Multi-Agent Systems. Estoril: AAMAS Press, 2008: 639–646. [14] MAHESWARAN R T, PEARCE J P, TAMBE M. A family of graphical-game-based algorithms for distributed constraint optimization problems[J]. Coordination of large-scale multiagent systems, 2006: 127–146. [15] CHEN Ziyu, WU Tengfei, DENG Yanchen, et al. An ant-based algorithm to solve distributed constraint optimization problems[C]//Proceedings of the 32th AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press, 2018:4653–4661. [16] STRANDERS R, FARINELLI A, ROGERS A, et al. Decentralised coordination of continuously valued control parameters using the max-sum algorithm[C]// Proceedings of the 8th International Conference on Autonomous Agents and Multi-Agent Systems. Budapest: Springer Press, 2009: 601−608. [17] VOICE T, STRANDERS R, ROGERS A, et al. A hybrid continuous max-sum algorithm for decentralised coordination[C]// Proceedings of the 19th European Conference on Artificial Intelligence. Lison: IOS Press, 2010: 61−66. [18] KHOI D H, WILLIAM Y, MAKOTO Y, et al. New algorithms for continuous distributed constraint optimization problems[C]// Proceedings of the 19th International Conference on Autonomous Agents and Multi-Agent Systems. Auckland: Springer Press, 2020: 502−510. [19] CHOUDHURY M, MAHMUD S, KHAN M M. A particle swarm based algorithm for functional distributed constraint optimization problems[C]// Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI Press, 2020:7111−7118. [20] AMIT S, MOUMITA C, MD M K. A local search based approach to solve continuous DCOPs[C]// Proceedings of the 20th International Conference on Autonomous Agents and Multi-Agent Systems. Richland: Springer Press, 2021: 1127−1135. [21] EIBEN A E, RAUE P E, RUTTKAY Z. Solving constraint satisfaction problems using genetic algorit-hms[C]//Proceedings of the First IEEE Conference on Evolutionary Computation. Orlando: IEEE Press, 1994:542−547. [22] CHEN Ziyu, LIU Lizhen, HE Jingyuan, et al. A genetic algorithm based framework for local search algorithms for distributed constraint optimization problems[J]. Autonomous agents and multi-agent systems, 2020, 34(2): 41. doi: 10.1007/s10458-020-09464-9 [23] CHEN Ziyu, HE Zhen, HE Chen. An improved DPOP algorithm based on breadth first search pseudo-tree for distributed constraint optimization[J]. Applied intelligence, 2017, 47(3): 607–623. doi: 10.1007/s10489-017-0905-4 [24] ALBERT R, BARABASI A L. Statistical mechanics of complex networks[EB/OL]. (2001-06-09)[2022-02-22]. https://arxiv.org/abs/cond-mat/0106096. [25] WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440–442. doi: 10.1038/30918
































 下载:
下载: