Passenger flow prediction in urban areas based on residual networks with split attention mechanism
-
摘要: 客流量预测是城市交通资源和公共安全智能化管理的重要依据。为了综合考虑城市乘客人群流动自身的既有周期性、趋势性和突发性，以及与城市物理和社会空间的耦合关系，在时空残差网络的基础上，本文提出了基于深度时空数据的分割注意力机制残差网络的城市细粒度客流量预测模型。首先以不同时空间隔的区域客流量历史数据为基础，引入分割注意力机制模块，为各模态的数据分配不同的权重，动态捕捉更高相关性的抽象数据特征；在时空数据的基础上，引入城市功能区属性作为联合特征，结合节假日、气候等外部特征，形成deep&wide网络结构，有效记忆重要特征对客流量变化的贡献。基于北京出租车数据的区域客流量对比实验表明，相比于传统的深度时空残差网络和其他经典机器学习模型，引入了分割注意力机制和城市功能区特征的预测模型能够更好地提取数据多元化的特征，预测精度明显优于其他同类别方法。Abstract: Passenger flow prediction is an important basis for intelligent management of urban transportation resources and public safety. In order to comprehensively consider the existing periodicity, trend and suddenness of urban passenger crowd flow itself, as well as the coupling relationship with urban physical and social space, based on the spatio-temporal residual network, this paper proposes an urban fine-grained passenger flow prediction model based on the residual network of split-attention mechanism with deep spatio-temporal data. Firstly, based on the regional passenger flow history data of different spatio-temporal intervals, the segmented attention mechanism module is introduced to assign different weights to the data of each modality to dynamically capture the abstract data features of higher relevance; on the basis of spatio-temporal data, the city functional area attributes are introduced as joint features, which are combined with external features such as holidays and climate to form a deep&wide network structure to effectively remember the contribution of important features to passenger flow changes. The regional passenger flow comparison experiments based on Beijing cab data show that compared with the traditional deep spatio-temporal residual network and other classical machine learning models, [] the prediction model introducing segmented attention mechanism and urban functional area features can better extract the features of data diversity, and the prediction accuracy is significantly better than other methods of the same category.
-
流量预测是实现城市交通智能管理的基石，是构建未来智能交通系统（intelligent transportation system，ITS）的必要技术支撑，其核心是实时准确地预测城市不同尺度区域人流的分布和流向，为城市规划、交通管理、安全防护、个体化服务提供可靠依据，从而减少拥堵，提高交通效率，并为公共安全应急管理提供早期预警，优化城市交通系统的效率和城市居民的出行体验[1-2]。
在城市交通流量预测的相关研究中，乘客流量的预测实质上就是基于人流特征的预测，有些针对人流的预测，根据人流分布空间的不同可以分为主要道路上的人流量[3]预测和整个城市范围的人流量预测。其中，道路上的人流速度、人流量的研究主要面向部分路段，而不是整个城市范围，因此该类研究与交通流量预测更为相关[4]。城市范围[2]的人流量预测又根据预测范围的尺度和形状差异可以分为针对单个区域和针对整个城市的研究。针对单个区域预测的模型[5]，多采用较为复杂的方法以划分出不规则的区域，并借助马尔科夫模型进行预测。针对整个城市的人群预测[6-7]往往采用多源大数据进行分析。
机器学习框架下的客流量预测方法差别在于预测对象和预测依据。有些研究[8-10]只针对短期客流进行预测，不具备迁移能力和普适性。有些研究[11-12]利用了深度学习、迁移学习等手段对不同区域客流进行预测，但没有考虑突发性活动与周期性、趋势性活动的差异。研究[13]考虑了活动的周期性，同时利用起点—终点（origin-destination，OD）客流数据的区域上下文对活动地区进行建模，但是忽略了人群活动中有很大一部分属于突发性活动，同时没有考虑外部因素的影响。
预测客流量也可以建模为时间序列的预测问题。历史平均（historical average，HA）模型[14]比较简单，该模型仅使用历史时间序列的平均值，来预测未来时间序列的平均值。然而，该模型无法对动态事件（如交通事故等突发事件）做出响应。自回归滑动平均模型（autoregressive integrated moving average model，ARIMA）假设未来时间序列的值，是历史值的线性组合与残差，因此，为了获得稳定的结果，非稳定的时间序列在分析之前需要特殊处理[15]。自回归滑动平均模型不适合处理有缺失值的时间序列，因为它依赖于非缺失时间序列数据，随着应用场景复杂度的提高，数据填补技术将不能满足需求[16]。在使用自回归滑动平均模型之前，额外的周期性差异通常应用到周期 性时间序列中以获得稳定的结果，称之为周期性自回归整体滑动平均模型（season autoregressive integrated moving average，SARIMA），其不足之处在于它具有较大的时间复杂度[17]。向量自回归模型（vector autoregressive，VAR）能够捕捉非相关时间序列的线性依赖[18]，但是该模型没有考虑到预测值和残差之间的关系。
Zhang等[19]定义了区域数据的流入量流出量概念，并且把空间依赖性分为长距离空间依赖和短距离空间依赖，将乘客人群流动的时间特性归纳为3类：临近性、周期性和趋势性，利用不同时空特性的三模块时空残差网络和外部特征网络，从多源数据中提取与客流量变化密切相关的抽象特征表示，具有较好的预测性能。但是，该方法忽略了不同城市功能区对客流量变化的显著影响，同时，更为有效的深度学习机制也有助于模型能力的进一步提升。
针对上述问题，本文构建了基于分割注意力机制的残差网络（residual split-attention network, ResNeSt），形成深度时空分割注意力机制残差网络框架(spatio-temporal split-attention networks, ST-SANet），面向整个城市范围内的乘客人群进行流量预测。引入分割注意力模块，实现了跨不同特征图组的注意力机制，进而更深入地发掘城市不同时空区域间多模态数据的特征和关系[20]。同时，除了对小区域客流量的时空关联进行挖掘之外，在城市客流量时空数据中增加了“城市功能区属性”这一新特征，捕捉各区域客流量变化与所处城市功能区之间的关联关系，同时结合外部特征数据形成多模态数据集，进而提升客流量预测模型的准确性。
1. 相关工作
Zhang等[19]提出深度时空残差网络（spatio-temporal residual network, ST-ResNet）的客流量预测，首先定义了区域数据的流入量流出量概念。将每个时间间隔内的流入量和流出量转化成类似于图像的双通道矩阵，并按照时间尺度分为3类：临近时间段、较近时间段和遥远时间段，然后将3个时间段的人流矩阵输入到不同的模块中进行建模，从而提取客流群体活动所具备的邻近性、周期性和趋势性。
在此基础上，Zhang等采用深度时空残差网络模型来进行特征表示学习和预测。该网络包括3个主要的残差网络模块，共享相同网络结构。每个模块的输入都是一个矩阵
$ \boldsymbol X $ 。以邻近性模块为例，一个时间间隔内的数据可以表示为$$ [{X_{t - {l_c}}}\;\;{X_{t - ({l_c} - 1)}}\;\;\cdots\;\;{X_{t - l}}] $$ (1) 式（1）称为邻近性依赖矩阵，其中
$ {l_c} $ 为时间间隔，$ c $ 下标代表了卷积层，然后按照时间轴将其连接为一个矩阵：${\boldsymbol{X}}_c^{(1)} \in {T^{2{l_c} \times I \times J}} $ 。其中$ {T^{2{l_c} \times I \times J}} $ 表示维度为$ 2{l_c} \times I \times J $ 的矩阵的集合，随后输入到一个卷积单元：$$ {\boldsymbol{X}}_c^{(1)} = f(W_c^{(1)} * X_c^{(0)} + b_c^{(1)}) $$ 式中：“ * ”表示卷积操作；
$ f $ 是一个激活函数；$ W_c^{(1)} $ ；$ b_c^{(1)} $ 是需要学习的参数。每一个卷积操作中堆叠
$ L $ 个残差单元，即：$$ {\boldsymbol{X}}_c^{(l + 1)} = {\boldsymbol{X}}_c^{(l)} + F({\boldsymbol{X}}_c^{(l)};\theta _c^{(l)}),\;\;l = 1,2,\cdots,L $$ 式中：
$ F $ 是残差方程（即两个ReLU和卷积的组合），$ {\theta ^{(1)}} $ 包括所有第$ l $ 层需要学习的参数。同样，在ReLu之前，使用批归一化（batch normalization，BN）。在顶端的第L层残差单元输出为$ {\boldsymbol{X}}_c^{(L + 2)} $ 。将3个模块的结果进行拼接，调用Tanh激活函数，结合外部因素模块，最终计算Loss值，训练得到城市区域客流量预测模型。
2. 城市区域客流量预测
本文以城市区域的流入流出量、当前城市功能区域分布、天气节假日等外部特征3类异构数据来源为基础，以Deep&Wide网络为框架，提出包括4个主要网络模块的多源时空客流量预测方法。
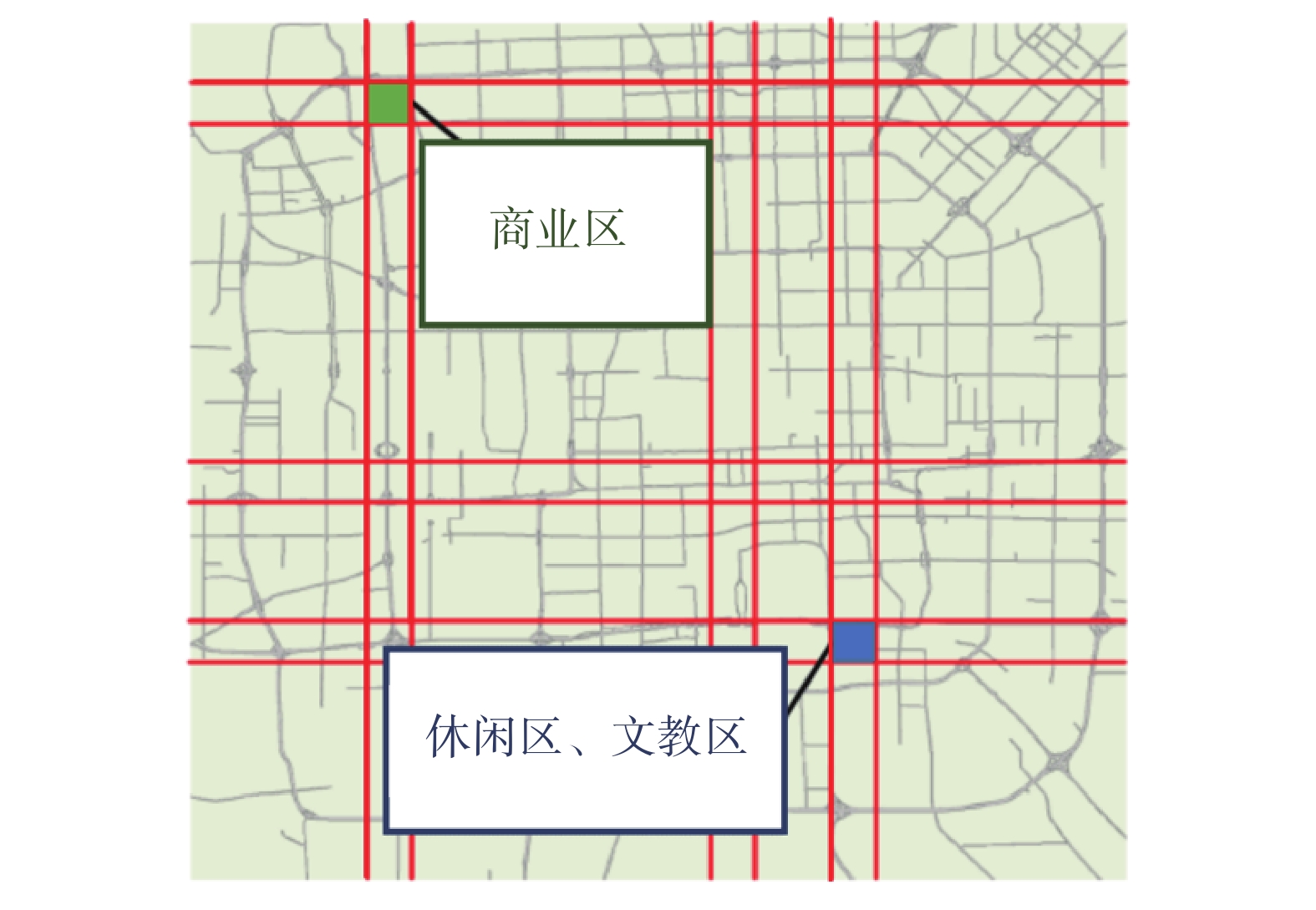
为了更好地提取与城市区域客流量相关的特征，以ST-ResNet框架为基础，在空间依赖性、时间依赖性以及外部因素之上，引入“城市功能区属性”作为重要的特征。其原因在于不同时段的客流量变化与区域功能属性密切相关。如工作日的上班早高峰时间段，住宅区和商业区的人口密度与客流量变化会明显多于其他功能区。同时，以ST-SANet来提取区域客流量的时空抽象特征。
2.1 基于ST-SANet网络的区域客流量预测模块
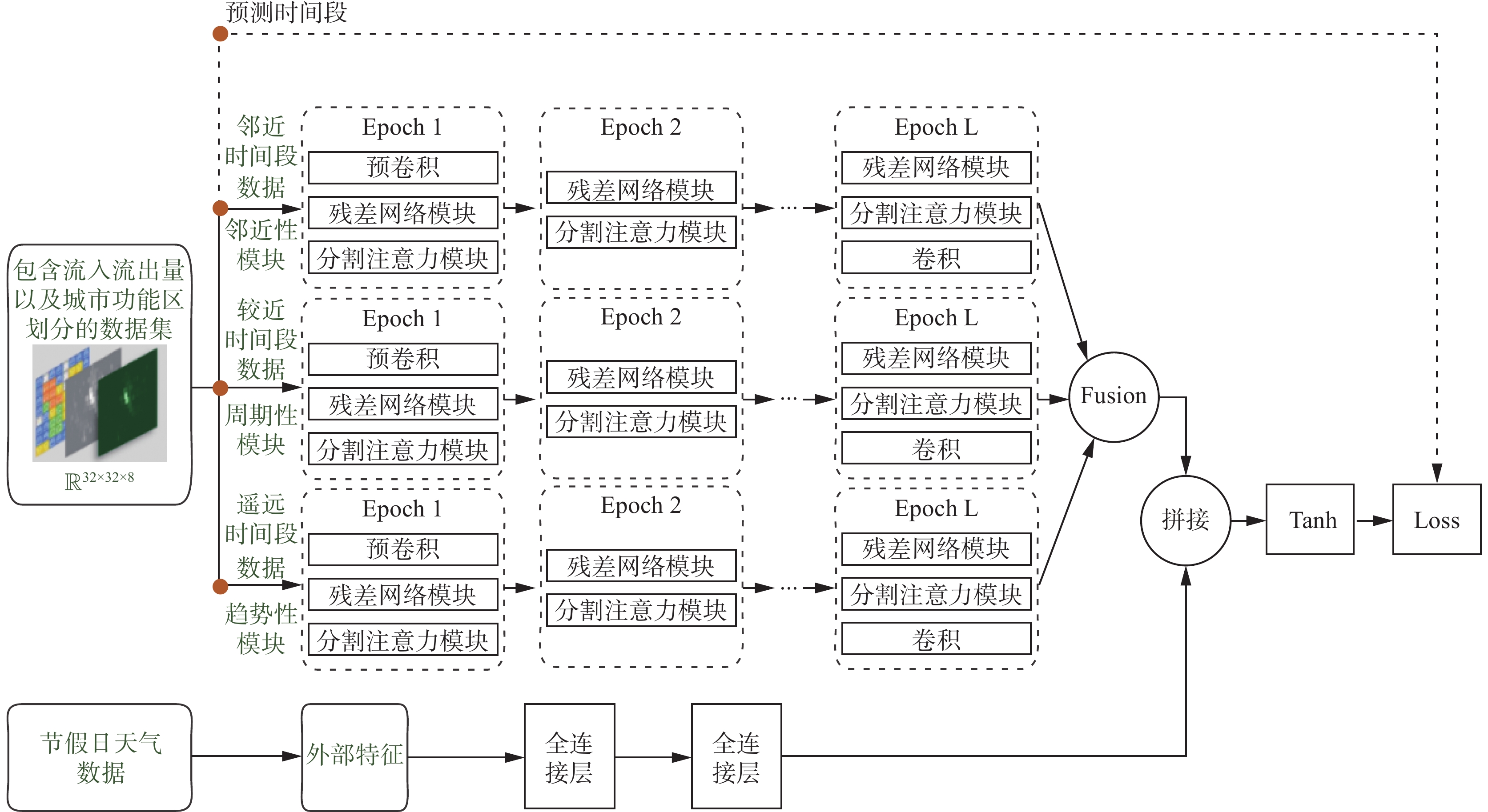
将数据集划分为邻近时段（Xclose）、较近时段（Xperiod）、遥远时段（Xtrend）数据，采用ST-SANet分别对活动邻近性、周期性、趋势性进行建模，动态聚合3个网络模块的输出，为不同模态的特征分配不同的权重。采用全连接网络对节假日、天气等外部影响因子进行建模。最后将得到的特征进行拼接，利用激活函数实现对小区域客流量的预测，整体结构如图1所示。
图 1 分割注意力机制残差网络结构图Fig. 1 Structure diagram of split-attention residual network
下载:
全尺寸图片
2.1.1 带有城市功能区域属性的流入流出矩阵构建
输入为表征小区域流入流出量、功能区域属性的8维向量：
${{\boldsymbol{X}}_t} = ({\rm{fin}}_t,{\rm{fout}}_t,{\boldsymbol{F}}_{{\rm{unc}},t})$ 形成的矩阵，其中${{\rm{fin}}_t}$ 、${{\rm{fout}}_t}$ 分别代表t时刻区域流入量以及流出量，${\boldsymbol{F}}_{{\rm unc},t}$ 为6位one-hot编码向量，表征了功能区域属性。$$ X_{i,j}^t = [{v_{\rm in}},{v_{\rm out}},{v_1},\cdots,{v_6}] $$ 其中
$ X_{i,j}^t(i \in [0,h),j \in [0,w)) $ 表示t时刻第$ i $ 行、第$ j $ 列的栅格区域。本文根据北京市经纬度范围将整个市区划分为32
$ \times $ 32个栅格区域，参考北京市功能区分布将各区域划分为“居住区”、“商业区”、“文教区”、“行政区”、“休闲区”。每个栅格内选取比重较大的一至三类功能区属性作为划分依据，如图2所示。
图 2 城市功能区划分示意图Fig. 2 Schematic diagram of urban functional area division下载:
全尺寸图片
将包含了城市功能区特征和时空流入流出量信息的数据，绘制成流入量流出量热力图[21-22]，按照时间轴分成较近时间段、临近时间段以及遥远时间段3类，然后将3类数据输入到对应的模块中进行建模，从而提取前述的活动邻近性、周期性以及趋势性。3个模块共享相同的网络结构，且彼此相互独立，都采用了卷积神经网络、残差单元序列、分割注意力机制模块结构。相较于原始模型，改进后的结构能够更动态地提取影响程度较大的数据特征，更准确地捕捉数据中的潜在关联性[23]。
为前3个主要模块的输出分配相应的权值后，融合为一个结果矩阵。然后将主要模块的结果矩阵与外部特征模块的结果矩阵进行拼接。最后用Tanh函数将融合后的输出映射到区间[−1,1]中。在反向传播中，Tanh函数比标准逻辑函数收敛得更快[24]。
2.1.2 ST-SANet构架
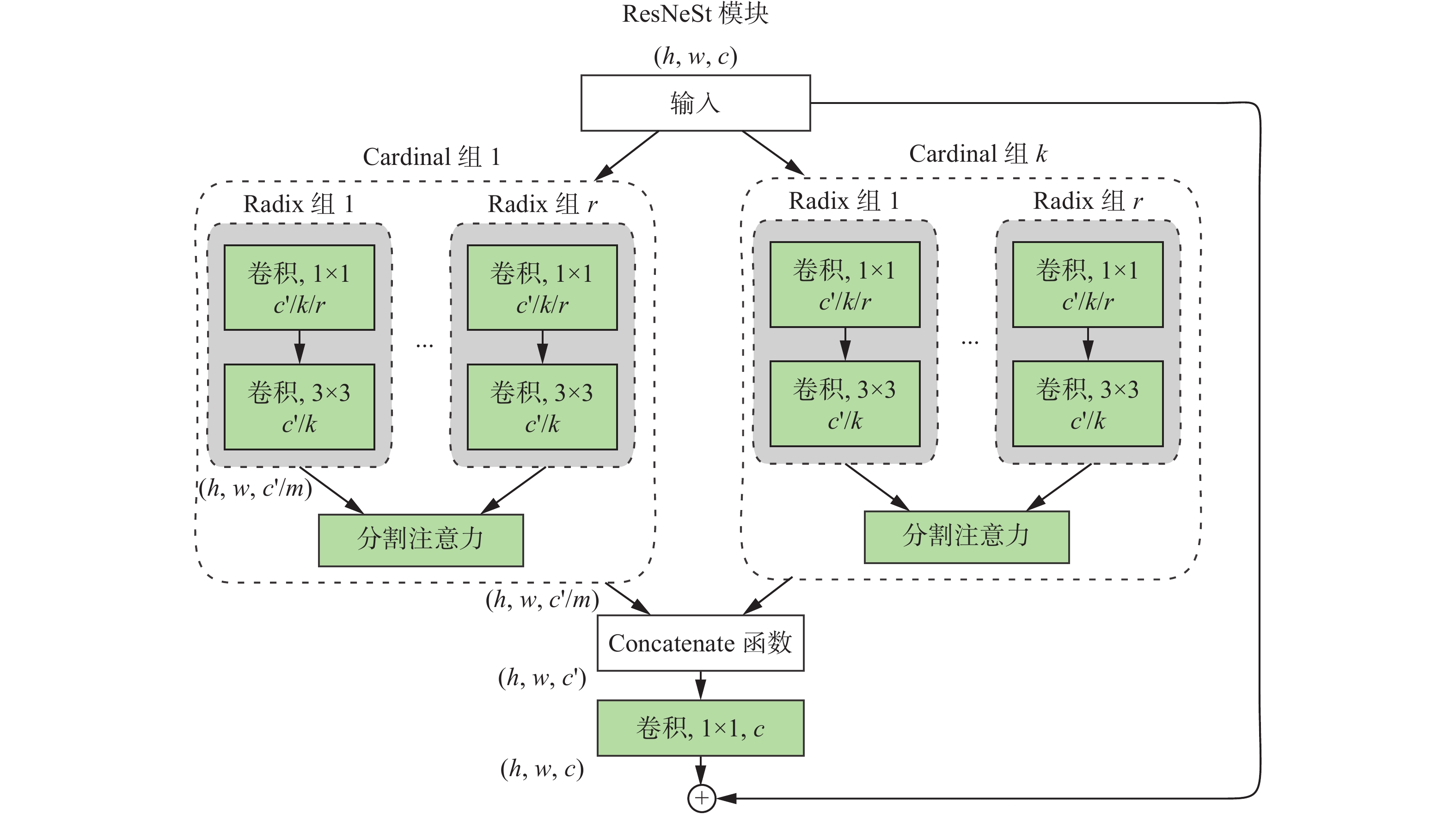
图1展示了ST-SANet的架构，模型的主体为上半部分的3个模块，分别对邻近性、周期性、趋势性进行建模，每个模块由两个主要子模块组成，分别是残差单元和分割注意力机制模块。整个城市范围内的数据量非常庞大，同时包含许多不同属性的区域，使得抽象数据中隐藏了大量多元化的特征信息，本文在残差网络算法（residual network，ResNet）的基础上引入了分割注意力机制，使模型具备了多模态数据特征提取的能力，进而深入地发掘了更多维度数据信息。通过在ResNet结构中堆叠分割注意力机制模块，形成了新的ResNet变体ResNeSt[25]。它保留了整个ResNet结构，以便直接用于下游任务，而不引入额外的计算成本。
分割注意力机制模块中同一层的多个卷积核相互独立，可以各自提取特征，使得模型具有提取多元化信息的特性。
残差模块输出为维度h = 32、w = 32、c = 8的矩阵
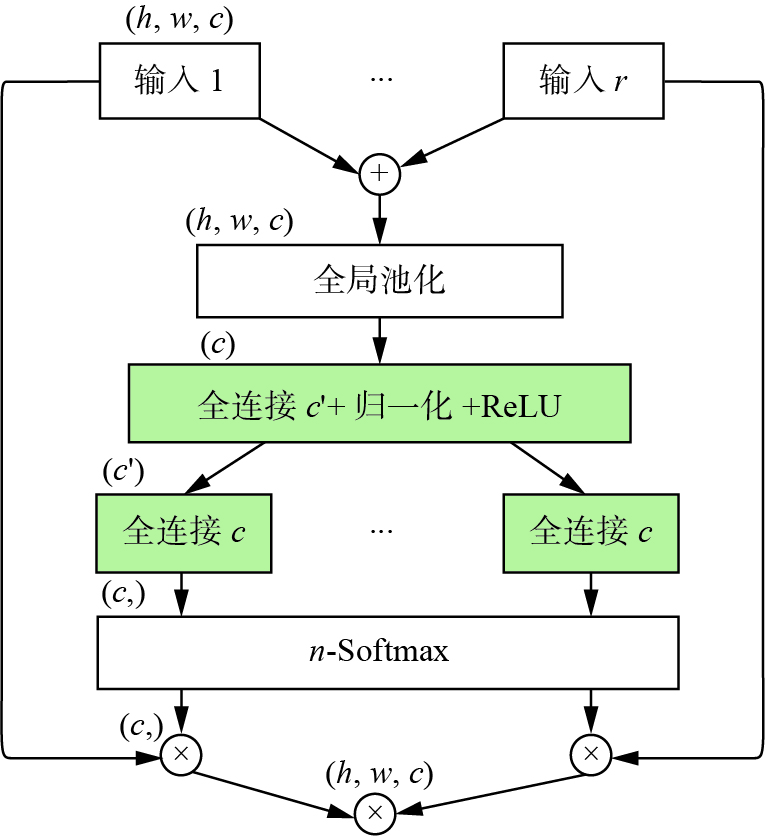
$ {\boldsymbol{X}} \in {T^{h \times w \times c}} $ ，并作为分割注意力机制模块的输入，ResNeSt算法中的特征图组与ResNeXt算法[26]相似，特征可以分为若干组，特征图组的数量由超参数K提供[27-29]，以此种方式将输入的特征分成了若干基组（Cardinal组），如图3所示。
图 3 分割注意力机制模块Fig. 3 Model of split-attention下载:
全尺寸图片
在每个相互独立的基组中，又把输入分成了多个分支，每个分支的注意力层能够提供捕捉特征相关性的网络机制，通过引入自注意力机制实现特征分支间的权重分配，如图4所示。
图 4 组群中的注意力机制分支Fig. 4 Branches of Split-attention in groups下载:
全尺寸图片
此处涉及了第二个超参数R，将特征分成了若干基组的组内分支（Radix分支），后文简称为“组内分支”，使得模型能进一步地提取具有多元化属性的特征。
在组内分支中首先将特征求和并进行全局池化操作，然后使用卷积等操作进行权重系数的分配。第一组卷积的输出维度为4维，作为缩放系数用于减少参数量；第二组卷积的输出维度通道数乘以组内分支数，保持了与组内分支特征层相对应的维度。为了确保组内分支间特征层的权重独立分布，使用n-Softmax对各组内分支的权重分别计算，最后将各组对应的特征层与注意力系数相乘再求和。
上文提到的超参数R描述了基数组内的分支模块数目，因此特征组的总数为
$ G = K \times R $ 并应用一系列变换
$ \{ {F_1},{F_2}, \cdots ,{F_G}\} $ 得到每个单独的组，各组的中间量表示为u：$$ {u_i} = {F_i}(X),i \in \{ 1,2,\cdots,G\} $$ 基组可以通过多个组内分支逐元素求和来获得，其中第 k个基数组表示为
$$ {U^k} = \displaystyle\sum_{i = R(k - 1) + 1}^{Rk} {{u_i}} $$ 超参数R代表了分支数量，h、w和c分别是模块输出特征图的维度参数。可以使用全局平均池化来收集嵌入式通道（embedded channel-wise）中全局上下文信息[30]。第c个分量S的计算公式为
$$ S_c^k = \dfrac{1}{{h \times w}}\displaystyle\sum\limits_{i = 1}^h {\displaystyle\sum\limits_{j = 1}^w {U_c^k} } (i,j) $$ 把每个基数组的输出拼接在一起，又经过一层1×1的卷积层，最终输出一个与输入同为h、w、c维度的特征矩阵
$ {{\boldsymbol{X}}^{w \times h \times c}} $ ，并传递给下一模块。2.1.3 参数矩阵融合
使用下述方法融合图1中3个主要模块的输出：
$$ {X_{{\rm Res}}} = {W_c} \circ X_c^{(L + 2)} + {W_p} \circ X_p^{(L + 2)} + {W_q} \circ X_q^{(L + 2)} $$ 式中：“
$ \circ $ ”是阿达玛乘法（即元素间相乘），参数$ {W_c} $ 、$ {W_p} $ 和$ {W_q} $ 分别表征了邻近性、周期性和趋势性的影响程度。2.2 融合外部特征的客流量预测
在外部因素模块中，本文把与时空数据时间相对应的完整外部数据（天气数据和节假日数据）输入到一个两层的全连接神经网络中，以获取天气和节假日特征对区域客流量的影响[31]。
用
$ {E_t} $ 表示预测时间节点t的外部因素特征向量，包括了天气、节假日、工作日等信息。与时空数据预测方式相似，使用t−1时刻的数据近似预测t时刻的外部因素情况。输出的$ {E_t} $ 需要经过两个全连接层，第一层可以理解为每个子因素的嵌入层，后面连接一个激活函数。第二层则可以理解为是将低维向量映射到高维空间。最终把外部因素模块和主要的模块进行融合，如图1框架图所示。预测得到t时间的区域客流量预测值
$ {\hat X_t} $ ：$$ {\hat X_t} = {\text{Tanh}}({X_{\rm Res}} + {X_{\rm Ext}}) $$ 式中的Tanh为双曲线切线函数，保证了输出的范围在−1到1之间。
2.3 ST-SANet模型训练过程
算法1 ST-SANet模型
输入 流入、流出量数据XRes、预测时间点真实数据XReal，外部特征数据XExt。
输出 经过训练得到各项模型参数。
1)按照距离预测时间点的时间间隔划分数据集；
$$X_{\rm Res} \to X_{\rm close}、X_{\rm period}、X_{\rm trend}$$ 2)将流入流出量数据通过预卷积层：
$$h_{\rm close}= {\rm{conv2d}} (X_{\rm close}, 64, (7, 7), (1, 1))$$ $$h_{\rm period}= {\rm{conv2d}} (X_{\rm period}, (7, 7), (1, 1))$$ $$h_{\rm trend} = {\rm{conv2d}} (X_{\rm trend}, (7, 7), (1, 1))$$ 3)外部特征数据经过两层全连接后得到结果Et ：
$$E_t= {\rm fully_connected} (X_{\rm Ext}))$$ 4)将预卷积层结果输入到ResNeSt模块：
邻近性模块：
$$h_{\rm close}= {\rm{ResInput}} (h_{\rm close})$$ $$g_{\rm close} = {\rm{ResNeStUnit}} (h'_{\rm close} )$$ $$r_{\rm close} = {\rm{ResOutput}} (g_{\rm close})$$ 周期性模块：
$$h_{\rm period}= {\rm ResInput} (h_{\rm period})$$ $$g_{\rm period} = {\rm ResNeStUnit} (h'_{\rm period})$$ $$r_{\rm period} = {\rm ResOutput }(g_{\rm period})$$ 趋势性模块：
$$h_{\rm trend} '= {\rm ResInput} (h_{\rm trend})$$ $$g_{\rm trend} = {\rm ResNeStUnit} (h'_{\rm trend} )$$ $$r_{\rm trend} = {\rm ResOutput }(g_{\rm trend})$$ 5)将邻近性、周期性以及趋势性3个模块的输出进行全连接后生成Xt ；
$${\boldsymbol{X}}_t = {\rm Fusion }(r_{\rm close} ,r_{\rm period} , r_{\rm trend})$$ 6)拼接Xt与Et后，经过Tanh激活函数得到预测结果
${\hat X_t} $ ；${\hat X_t} $ =Tanh (Connection(Xt , Et) )7)按照公式计算loss值：
$${\text{loss}} = \sqrt {\dfrac{{\displaystyle\sum\nolimits_{i = 1}^N {{{(\hat X_t^i - X_{\rm Real}^i)}^2}} }}{{{\rm{shape}}({{\hat X}_t})}}}$$ 反向传播更新网络参数。
本实验在16C32G服务器环境下，平均训练时间为47 h 16 min。
3. 实验设置与结果分析
3.1 数据集
本文以公开的真实数据集—北京出租车数据集（TaxiBJ）[32]以及对应的北京气象信息、节假日等数据（BJ_Meteorology）为基础对客流情况进行预测。TaxiBJ数据集为h5文件，包括“date”和“data”两个字段，分别表示数据集的时间、以及流入流出量数据。该数据集涵盖了4个时间范围的数据，分别是2013年7月1日~10月30日；2014年3月1日~6月30日；2015年3月1日~6月30日；2015年11月1日~2016年4月10日。4年的数据集的形状分别为（4888，2，32，32）、（4780，2，32，32）、（5596，2，32，32）以及（7220，2，32，32），其中数据第一位代表总数据量，第二位的二维数组分别代表了该区域的流入量和流出量，第三、四位代表了32×32的栅格网络区域。时间戳的间隔设定以30 min为单位。
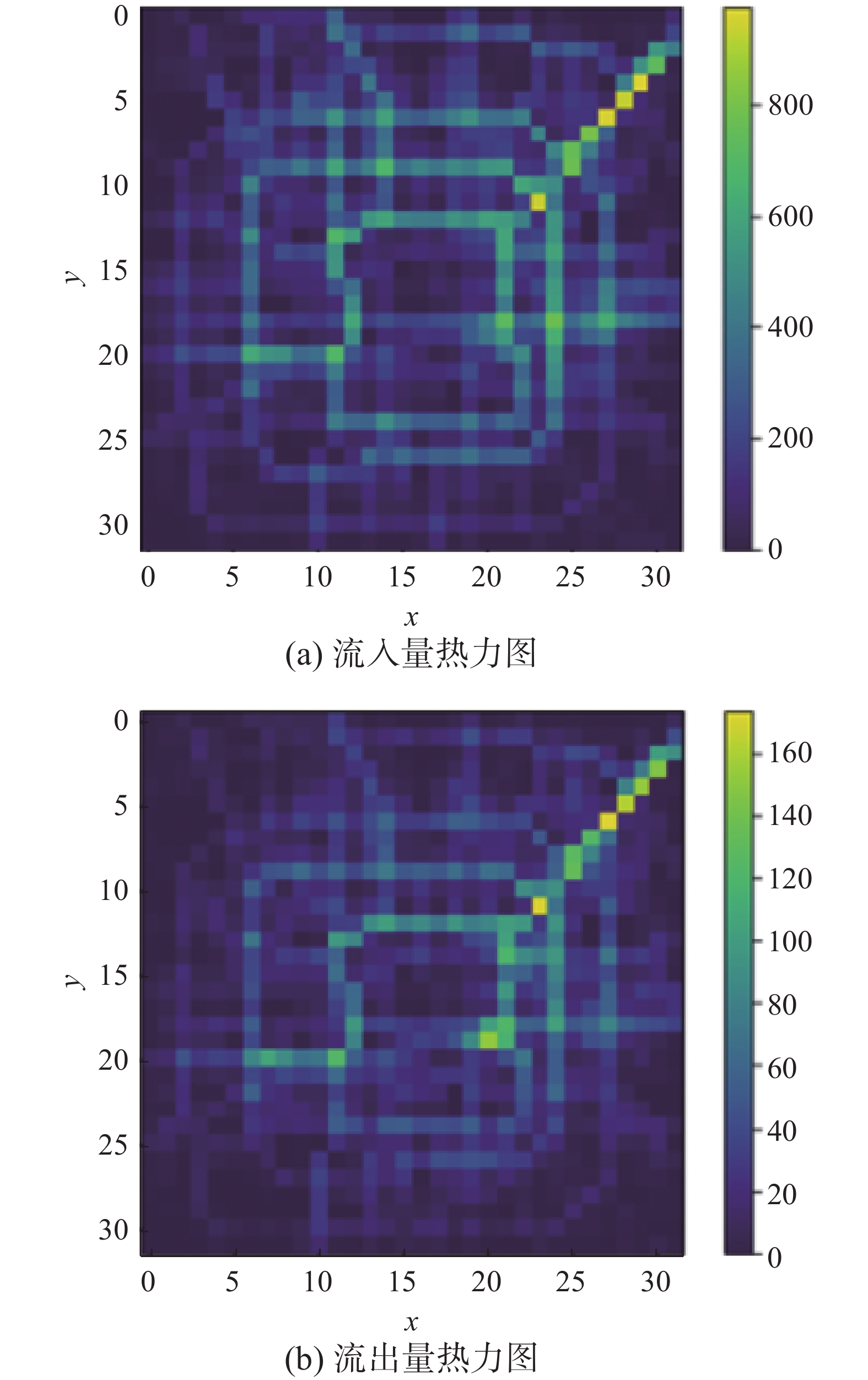
图5为TaxiBJ数据集中某时间节点的流入流出量热力图，其中(a)图为流入量热力图，(b)图为流出量热力图。
图 5 流入流出量数据热力图Fig. 5 Heat map of inflow and outflow data下载:
全尺寸图片
3.2 评估指标
本文选择均方根误差（RMSE）作为框架的衡量标准，从而评估算法预测结果的准确性。均方根误差的公式为
$$ {\text{RMSE}} = \sqrt {\dfrac{{\displaystyle\sum\nolimits_{i = 1}^N {{{({\rm{predicted}}_{i} - {{\rm{actual}}_i})}^2}} }}{N}} $$ 式中predicted为预测量，actual为真实量，分别对应了各时间段、各区域出租车客流量的流入流出量的预测值以及真实值。进而对模型的预测准确度进行评估。
3.3 实验关键参数设置及相关代码
本文提出的新模型经过多次实验的沉淀，最终获得的参数设置如表1所示。论文中代码见文献[33]。
表 1 实验参数表Table 1 Experimental parameters table参数名称 参数值 批次大小（batch_size） 32 特征图宽（map_width） 32 续表 1 参数名称 参数值 特征图高（map_height） 32 邻近性数据长度（closeness_sequence_length） 8 周期性数据长度（period_sequence_length） 8 趋势性数据长度（trend_sequence_length） 8 残差单元数量（num_of_residual_units） 12 学习率 （lr） 0.001 周期数量（num_epochs） 10 过滤器数量（num_of_filters） 64 一阶矩估计的指数衰减因子（beta1） 0.8 二阶矩估计的指数衰减因子（beta2） 0.999 采样数（nb_flow） 2 基组数量（K） 4 组内分支数量（R） 4 3.4 对比实验的设置与分析
3.4.1 对比实验的设置
实验过程中随机选择了数量为8周的数据作为测试集，剩余数据为训练集。选取了ST-ResNet和DeepST[34]两种人流量预测模型和ARIMA、SARIMA、VAR、RNN、LSTM、GRU等主流时间序列预测模型作为对比模型。
HA 计算对应时间区间的所有历史输入流和外出流的平均流量。例如：周二上午9:00~9:30，对应所有历史数据中所有周二上午的9:00~9:30。
ARIMA[35] 自回归滑动平均（ARIMA），著名的预测时间序列的模型。
SARIMA[36] 季节性ARIMA，在ARIMA的基础上，SARIMA考虑了季节特性，能够同时学习时间邻近性和周期性。
VAR 向量自回归模型（VAR）能够捕捉成对乘客流量之间的关系，但由于参数规模十分庞大，致使时间复杂度较高。
ST-ANN 抽取空间（周围8个区域的值）和时间（前8个时间区间）的特征作为模型预测的依据。
DeepST 面向时空数据的深度神经网络（DNN）预测模型，在交通领域数据预测问题上展示了较好的特性。
RNN[37] 递归神经网络是一种深度学习模型，能够较好捕捉时间依赖性，可用于训练不同维度的时间序列数据。本文的实验中，分别选取了长度为3、6、12、24、48、336的输入序列作为对比实验。不同的序列长度预测效果不尽相同，例如当序列长度选取48、时间间隔为30min时，数据的时间依赖性为24 h。因此，有6种RNN的变种：RNN-3、RNN-6、RNN-12、RNN-24、RNN-48和 RNN-336。
LSTM 长短记忆单元网络（LSTM）[38]是一种特殊的RNN，能够学习到较长的时间依赖。与RNN的设置相同，做了6种LSTM的变种实验，即LSTM-3、LSTM-6、LSTM-12、LSTM-24、LSTM-48和LSTM-336。
GRU[39] 门递归单元网络，是一种新的RNN，能够捕捉较长的时间依赖。与RNN 的设置相同，有以下6种GRU变种作为对比实验：GRU-3、GRU-6、GRU-12、GRU-24、GRU-48以及GRU-336。
3.4.2 对比实验的结果与分析
与上述模型的对比实验结果如表2所示。
表 2 TaxiBJ数据集下的各个模型RMSE对比实验Table 2 Comparison of RMSE results of various frameworks under Taxibj dataset模型框架 RMSE评估指标 HA 57.69 ARIMA 22.78 SARIMA 26.88 VAR 22.88 ST-ANN 19.57 DeepST 18.1 RNN-3 23.42 RNN-6 23.80 RNN-12 32.21 RNN-24 38.66 RNN-48 46.41 RNN-336 39.10 LSTM-3 22.90 LSTM-6 20.62 LSTM-12 23.93 LSTM-24 21.97 LSTM-48 23.02 LSTM-336 31.13 GRU-3 22.63 GRU-6 20.85 GRU-12 20.46 GRU-24 20.24 GRU-48 21.37 GRU-336 31.34 ST-ResNet 16.89 ST-SANet 14.27 从表2可以看出，本文提出的ST-SANet准确率明显优于所有的对比方法。含有12个残差单元和分割注意力机制模块的ST-SANet优于DeepST等传统算法约22%以上，优于RNN约40%以上，优于LSTM约31%以上，优于GRU30%以上，优于ST-ResNet约6%。
ST-ANN和VAR也采用了时空数据进行模型训练，但是性能都不及ST-SANet模型，因为它们只是考虑了较近时间段以及邻近时间段信息。对于时间序列模型而言，GRU和LSTM的RMSE性能相似，且均优于RNN，但是都不及ST-SANet模型，其原因在于GRU和LSTM都能够捕捉较长的时间依赖性，但不具备提取多元化特征的能力[40]。
3.5 消融实验
3.5.1 消融实验设置
为了验证分割注意力机制模块以及城市功能区划分对模型的性能影响，本文针对ST-SANet，构造了未引入城市功能区特征的消融版模型ST-SANetRib，未引入分割注意力机制的消融模型ST-ResNet，以及未引入分割注意力机制及城市功能区特征的消融模型ST-ResNetRib。
3.5.2 消融实验的结果与分析
4个模型的预测结果如表3所示。
表 3 消融实验对比结果Table 3 Comparison results of ablation experiments模型框架 RMSE评估指标 ST-ResNet 16.89 ST-ResNetRib 17.11 ST-SANet 14.27 ST-SANetRib 14.51 从消融实验对比结果表中可以看出，首先对于城市功能区划分的消融实验，无论是改进后形成的ST-SANet模型，还是原始的ST-ResNet模型，引入城市功能区划分后的预测效果都有显著提升，说明了城市功能区特征在很大程度上影响着客流量的预测。同时，功能区特征对传统模型ST-ResNet的提升略小，也侧面说明针对多模态特征的数据集，ST-SANet更具有优势。
其次，在分割注意力机制模块的消融实验中，无论是否在多模态数据集下，引入了分割注意力机制的ST-SANet模型的预测精度均明显优于传统的ST-ResNet模型，并且面对复杂数据集时，模型精度的提升更为明显，说明分割注意力模块能够有效提升预测的准确率，同时能够更好的从多模态数据集中提取多元化特征。
3.6 实验结论
引入城市功能区属性的数据集，包含了各时段各区域的客流量变化信息，并且在一定程度上反映了与区域相关的活动语义。不同的人群活动会发生在不同的区域，比如“上班”会发生在工作区，那么引入功能区划分这一特征，就可以提取各时段不同功能区乘客群体的活动规律，从而提升模型的预测精度。实验中相同模型下，引入了城市功能区属性的数据带来的预测结果要优于原始数据的预测结果。
面对多模态数据集，引入分割注意力机制模块能够更好地提取多样化的特征。并且人群活动的成因十分复杂，不同区域、不同类型乘客群体活动的原因和规律具有明显差异，注意力机制模块能够动态地分析各种场景的乘客群体活动，挑选影响程度较高的特征，同时能够更好地捕捉多模态数据间的潜在关系，这无疑是模型性能提升的主要原因。
4. 结束语
针对城市各区域客流量预测问题，本文将城市区域的功能属性作为重要特征，采用分割注意力机制残差网络算法，提取城市中任意两个区域之间的相互关系；采用包含区域功能属性的历史时空数据，以及节假日、天气等外部特征数据进行训练，能够更好地捕捉多模态数据之间的时间依赖、空间依赖、地区属性依赖以及外部因素的影响；在真实数据集上与10种类似算法进行对比，结果充分说明了本模型具有更高的准确性。
在未来的工作中，本文将会基于扩张卷积算法，探究空间上的近距离、远距离数据依赖对于预测的影响程度，以减轻无效数据对模型性能造成的负面影响。
-
图 1 分割注意力机制残差网络结构图
Fig. 1 Structure diagram of split-attention residual network
下载:
全尺寸图片
图 2 城市功能区划分示意图
Fig. 2 Schematic diagram of urban functional area division
下载:
全尺寸图片
图 3 分割注意力机制模块
Fig. 3 Model of split-attention
下载:
全尺寸图片
图 4 组群中的注意力机制分支
Fig. 4 Branches of Split-attention in groups
下载:
全尺寸图片
图 5 流入流出量数据热力图
Fig. 5 Heat map of inflow and outflow data
下载:
全尺寸图片
表 1 实验参数表
Table 1 Experimental parameters table
参数名称 参数值 批次大小（batch_size） 32 特征图宽（map_width） 32 续表 1 参数名称 参数值 特征图高（map_height） 32 邻近性数据长度（closeness_sequence_length） 8 周期性数据长度（period_sequence_length） 8 趋势性数据长度（trend_sequence_length） 8 残差单元数量（num_of_residual_units） 12 学习率 （lr） 0.001 周期数量（num_epochs） 10 过滤器数量（num_of_filters） 64 一阶矩估计的指数衰减因子（beta1） 0.8 二阶矩估计的指数衰减因子（beta2） 0.999 采样数（nb_flow） 2 基组数量（K） 4 组内分支数量（R） 4 表 2 TaxiBJ数据集下的各个模型RMSE对比实验
Table 2 Comparison of RMSE results of various frameworks under Taxibj dataset
模型框架 RMSE评估指标 HA 57.69 ARIMA 22.78 SARIMA 26.88 VAR 22.88 ST-ANN 19.57 DeepST 18.1 RNN-3 23.42 RNN-6 23.80 RNN-12 32.21 RNN-24 38.66 RNN-48 46.41 RNN-336 39.10 LSTM-3 22.90 LSTM-6 20.62 LSTM-12 23.93 LSTM-24 21.97 LSTM-48 23.02 LSTM-336 31.13 GRU-3 22.63 GRU-6 20.85 GRU-12 20.46 GRU-24 20.24 GRU-48 21.37 GRU-336 31.34 ST-ResNet 16.89 ST-SANet 14.27 表 3 消融实验对比结果
Table 3 Comparison results of ablation experiments
模型框架 RMSE评估指标 ST-ResNet 16.89 ST-ResNetRib 17.11 ST-SANet 14.27 ST-SANetRib 14.51 -
[1] GONG Yongshun, LI Zhibin, ZHANG Jian, et al. Network-wide crowd flow prediction of Sydney trains via customized online non-negative matrix factorization[C]//CIKM’18: Proceedings of the 27th ACM International Conference on Information and Knowledge Management. New York: ACM, 2018: 1243−1252. [2] MA Xiaolei, DAI Zhuang, HE Zhengbing, et al. Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors, 2017, 17(4): 818. doi: 10.3390/s17040818 [3] SILVA R, KANG S M, AIROLDI E M. Predicting traffic volumes and estimating the effects of shocks in massive transportation systems[J]. Proceedings of the national academy of sciences of the United States of America, 2015, 112(18): 5643−5648. [4] FLORIO L, MUSSONE L. Neural-network models for classification and forecasting of freeway traffic flow stability[J]. Control engineering practice, 1996, 4(2): 153–164. doi: 10.1016/0967-0661(95)00221-9 [5] XU Yanyan, KONG Qingjie, KLETTE R, et al. Accurate and interpretable Bayesian MARS for traffic flow prediction[J]. IEEE transactions on intelligent transportation systems, 2014, 15(6): 2457–2469. doi: 10.1109/TITS.2014.2315794 [6] CHEN Pota, CHEN Feng, QIAN Zhen. Road traffic congestion monitoring in social media with hinge-loss Markov random fields[C]//2014 IEEE International Conference on Data Mining. Shenzhen: IEEE, 2014: 80−89. [7] ZHENG Yu, YI Xiuwen, LI Ming, et al. Forecasting fine-grained air quality based on big data[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2015: 2267−2276. [8] ZHAO Yi, LI Jianbo, MIAO Xin, et al. Urban crowd flow forecasting based on cellular network[C]//ACM TURC '19: Proceedings of the ACM Turing Celebration Conference - China. New York: ACM, 2019: 1−5. [9] HE Yuxin, LI Lishuai, ZHU Xinting, et al. Multi-graph convolutional-recurrent neural network (MGC-RNN) for short-term forecasting of transit passenger flow[J]. IEEE transactions on intelligent transportation systems, PP(99): 1−20. [10] WEI Yu, CHEN Muchen. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J]. Transportation research part C:emerging technologies, 2012, 21(1): 148–162. doi: 10.1016/j.trc.2011.06.009 [11] LI Yang, WANG Xudong, SUN Shuo, et al. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks[J]. Transportation research part C:emerging technologies, 2017, 77: 306–328. doi: 10.1016/j.trc.2017.02.005 [12] FU Xiao, YU Guanyi, LIU Zhiyuan. Spatial-temporal convolutional model for urban crowd density prediction based on mobile-phone signaling data[J]. IEEE transactions on intelligent transportation systems, 2021, 13(2): 1–13. doi: 10.1109/TITS.2021.3131337 [13] WANG Senzhang, MIAO Hao, LI Jiyue, et al. Spatio-temporal knowledge transfer for urban crowd flow prediction via deep attentive adaptation networks[J]. IEEE transactions on intelligent transportation systems, 2022, 23(5): 4695–4705. doi: 10.1109/TITS.2021.3055207 [14] MA Jiaman, CHAN J, RAJASEGARAR S, et al. Multi-attention 3D residual neural network for origin-destination crowd flow prediction[C]//2020 IEEE International Conference on Data Mining. Sorrento: IEEE, 2020: 1160−1165. [15] EBRAHIMPOUR, WAN, CERVANTES, et al. Comparison of main approaches for extracting behavior features from crowd flow analysis[J]. ISPRS international journal of geo-information, 2019, 8(10): 440. doi: 10.3390/ijgi8100440 [16] SMITH B L, DEMETSKY M J. Traffic flow forecasting: comparison of modeling approaches[J]. Journal of transportation engineering, 1997, 123(4): 261–266. doi: 10.1061/(asce)0733-947x(1997)123:4(261 [17] BOX G, JENKINS G, REINSEL G. Time series analysis: forecasting and control. rev. ed[J]. Journal of marketing research, 1977, 14(2): 269. doi: 10.2307/3150485 [18] SMITH B L, WILLIAMS B M, KEITH OSWALD R. Comparison of parametric and nonparametric models for traffic flow forecasting[J]. Transportation research part C:emerging technologies, 2002, 10(4): 303–321. doi: 10.1016/S0968-090X(02)00009-8 [19] ZHANG Junbo, ZHENG Yu, QI Dekang. Deep spatio-temporal residual networks for citywide crowd flows prediction[J]. Proceedings of the AAAI conference on artificial intelligence, 2017, 31(1): 1655–1661. doi: 10.1609/aaai.v31i1.10735 [20] SONG Xuan, ZHANG Quanshi, SEKIMOTO Y, et al. Prediction of human emergency behavior and their mobility following large-scale disaster[C]//KDD’14: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. New York: ACM, 2014: 5−14. [21] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [22] CHANDRA S R, AL-DEEK H. Predictions of freeway traffic speeds and volumes using vector autoregressive models[J]. Journal of intelligent transportation systems, 2009, 13(2): 53–72. doi: 10.1080/15472450902858368 [23] QIN Tianxiang, LIU Tong, WU Hexiang, et al. RESGCN: RESidual graph convolutional network based free dock prediction in bike sharing system[C]//2020 21st IEEE International Conference on Mobile Data Management. Versailles: IEEE, 2020: 210−217. [24] YAO Huaxiu, WU Fei, KE Jintao, et al. Deep multi-view spatial-temporal network for taxi demand prediction[J]. Proceedings of the AAAI conference on artificial intelligence, 2018, 32(1). [25] ZHANG HANG, WU CHONGRUO, ZHANG ZHONGYUE, et al. ResNeSt: split-attention networks[EB/OL]. (2020−04−30)[2022−02−20]. https://www.researchgate.net/publication/340805846_resnest_split-attention_networks. [26] XIE Saining, GIRSHICK R, DOLLÁR P, et al. Aggregated residual transformations for deep neural networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 5987−5995. [27] YAMAMOTO M, SATO A, KAWADA S, et al. Incremental tracking of human actions from multiple views[C]//Proceedings of 1998 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Santa Barbara: IEEE, 1998: 2−7. [28] LECUN Y A, BOTTOU L, ORR G B, et al. Efficient BackProp[M]//Lecture Notes in Computer Science. Berlin: Springer Berlin Heidelberg, 2012: 9−48. [29] LI Xiang, WANG Wenhai, HU Xiaolin, et al. Selective kernel networks[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 510−519. [30] LI Yexin, ZHENG Yu, ZHANG Huichu, et al. Traffic prediction in a bike-sharing system[C]//SIGSPATIAL '15: Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2015: 1−10. [31] WANG Xiaolong, GIRSHICK R, GUPTA A, et al. Non-local neural networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 7794−7803. [32] ZHANG Junbo, ZHENG Yu, QI Dekang. 北京出租车数据集[EB/OL].[2022−02−20]. https://gitee.com/arislee/taxi-bj. [33] LI Bohan. ST-SANet 算法代码[EB/OL].[2022−02−20]. https://gitee.com/arislee/st-sanet_-code.git [34] ZHANG Junbo, ZHENG Yu, QI Dekang, et al. DNN-based prediction model for spatio-temporal data[C]//SIGSPACIAL’16: Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2016: 1−4. [35] ZHANG G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50: 159–175. doi: 10.1016/S0925-2312(01)00702-0 [36] ZHANG G P, QI Min. Neural network forecasting for seasonal and trend time series[J]. European journal of operational research, 2005, 160(2): 501–514. doi: 10.1016/j.ejor.2003.08.037 [37] ZAREMBA W, SUTSKEVER I, VINYALS O. Recurrent neural network regularization[EB/OL]. (2014−09−08)[2022−02−20]. https: //arxiv. org/abs/1409.2329. [38] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735 [39] CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[EB/OL]. (2014−06−03)[2022−02−20]. https: //arxiv. org/abs/1406.1078. [40] DOUGHERTY M S, COBBETT M R. Short-term inter-urban traffic forecasts using neural networks[J]. International journal of forecasting, 1997, 13(1): 21–31. doi: 10.1016/S0169-2070(96)00697-8
