Mean square couple-group consensus for heterogeneous multiagent systems based on Markov switching and cooperative-competitive relation
-
摘要: 针对马尔可夫切换下离散和连续异质多智能体系统均方二分组一致问题，本文分别构造了2类包含合作竞争关系和马尔可夫切换拓扑结构异质多智能体系统均方二分组一致协议。利用随机不可约非周期矩阵(stochastic indecomposable and aperiodic matrices, SIA) 相关性质、图论代数和矩阵分析等理论，得到相关系统实现均方二分组一致的充分必要条件。仿真实例说明了理论结果的有效性。Abstract: In order to solve the problem of mean square couple-group consensus of discrete and continuous heterogeneous multiagent systems under Markov switching, this paper respectively constructs two kinds of mean square couple-group consensus protocols of heterogeneous multi-agent systems (HMASs), including cooperative competition relationship and Markov switching topology heterogeneous multiagent systems. Based on related properties of stochastic irreducible aperiodic (SIA) matrix, graph theory algebra and matrix analysis, the necessary and sufficient conditions are obtained to realize mean square couple-group consensus. Simulation examples prove effectiveness of the result.
-
因多智能体系统在智能交通控制、智能电网和互联网安全等领域存在巨大的应用价值[1-4]，多智能体系统研究已经成为复杂系统理论研究的一个热点问题。一致性作为多智能体系统研究的首要问题，通过设计合适的分布式控制协议来协调和控制多智能体系统，从而使整个多智能体的状态或速度达到一致。
目前，多智能系统一致性问题的研究已经取得很多成果。根据不同拓扑结构，文献[5]研究了一类一阶连续多智能体系统分组一致控制，且在单积分动力学一致性算法中引入了旋转矩阵，得到系统实现分组一致的充要条件。文献[6]对一类二阶离散多智能体系统二分组一致问题进行讨论，通过线性变换和矩阵变换把系统的二分组一致问题转变为判断误差系统稳定性问题。文献[7]根据智能体之间关系，研究了一类有向二部图的多智能体系统群同步。在这种情况下，信息只能在两部分网络中的不同子组之间交互，不能在同一子组内交互。为克服文献[7]中合作或竞争交互的局限性，文献[8]研究了拓扑结构可分为2个子网的合作−竞争多智能体系统分组一致问题，并假定同一子网络中智能体之间通信权重为正，不同子网络中智能体之间通信权重为负。此外，现有许多有关多智能体系统一致性问题研究中，大多假定研究对象为同质系统[9-11]，即系统中每个智能体具有相同动力学性质。然而，在实际情况下，多智能系统中智能体往往具有不同动力学性质，即多智能体是异质的。因此，有必要研究异质多智能体系统的一致性。目前，有关异质多智能体系统的一致性已取得一些研究成果[12-14]。文献[12]讨论了包含一阶和二阶智能体的离散异质多智能体系统分组一致。 文献[13]讨论了具有时延的竞争网络中异质多智能体系统分组一致。文献[14]研究了具有合作−竞争机制的时滞离散加权异质多智能体系统分组一致，并且采用频域分析法获得了确保多智能体系统能够达到分组一致时通信和输入时延范围。此外，根据系统网络拓扑结构切换方式不同，大部分成果都假定系统拓扑结构是固定的[15-17]。基于牵制控制策略，文献[15]研究了固定拓扑结构下多智能体系统的有限时间达到一致性问题。文献[16-17]分别讨论了多智能体系统具有固定拓扑和时延约束时二分组一致和具有测量噪声二阶延迟多智能体系统一致控制。然而，在很多实际问题中，多智能体系统拓扑结构通常会随着时间变化而发生改变。这就是通常所说的具有切换拓扑结构多智能体系统分组一致[18-20]。针对切换拓扑下多智能系统一致控制，相关成果也取得不少。基于模态平均驻留时间切换拓扑，文献[18-19]分别研究了多智能体系统中领导跟随一致和牵制一致。文献[20]则研究了基于平均驻留时间切换规则在丢包补偿中的应用。此外，在自然界中，多智能体系统往往会受到来自内部或外部一些突发或未知随机因素影响，从而导致系统拓扑结构的改变具有更加不确定和随机性。如何描述这种拓扑的切换随机性是一致性研究的难点。鉴于马尔可夫链可以很好地描述随机切换，因此它被广泛应用到具有不确定事件发生的场景，如图像处理、多模态制造和滤波检测等[21-22]。不仅如此，基于马尔可夫切换多智能体系统一致性研究也越来越引起众多学者关注[23-25]，并取得很多重要成果。文献[23]研究了具有马尔可夫切换的通信拓扑下异质连续时间多智能体系统输出一致性问题。文献[24]讨论了在噪声环境下具有马尔可夫切换连续时间多智能体系统均方一致问题。基于合作关系，文献[25]讨论了具有马尔可夫跳跃离散线性多智能体系统输出调节问题。
综上所述，针对离散或连续异构多智能体系统一致性研究，虽取得很多成果，但这些成果主要基于合作或竞争关系、切换策略给定或整个拓扑结构中存在生成树等强条件下得到。而在许多实际多智能体系统中，合作竞争关系始终存在，且多智能体系统含有多个子拓扑结构，这些拓扑结构之间是随机切换的。因此，在研究多智能体系统一致性问题时，有必要同时考虑合作竞争关系、异构和随机切换等实际因素。本文讨论包含一阶和二阶智能体的异质多智能体系统，分离散和连续2种情况，基于竞争合作关系，结合马尔可夫链，分别提出2种分组一致协议。利用图论代数、马尔科夫链和随机不可约非周期矩阵的相关性质，得到这些系统达成均方二分组一致的充分必要条件，并通过仿真实例说明了所得结论的有效性。
1. 马尔可夫切换多智能体系统
1.1 马尔可夫模型
假定
$ \{ \varOmega ,F,P\} $ 是一个完备概率空间，其中$ \varOmega $ 是样本空间,$ F $ 代表事件代数，$ P $ 表示概率测度。$ \left\{ {\sigma (\kappa ),\kappa \geqslant 0} \right\} $ 是一个有限状态离散时间马尔可夫链，$S = \left\{ {1,2,\cdots,s} \right\}$ 是$ \sigma (\kappa ) $ 的取值范围。该链在时间$ k $ ~$ k + 1 $ 从状态$ i $ 转移到状态$ j $ 的转移概率矩阵${\boldsymbol{\varLambda }} = ({p_{ij}} \in {{\bf{R}}^{s \times s}})$ 为$$ P (\sigma (\kappa + 1) = j|\sigma (\kappa ) = i) = {p_{ij}} $$ 式中：
$ {p_{ij}} \geqslant 0 $ ，且$\displaystyle\sum_{j = 1}^s {{p_{ij}}} = 1$ 。类似地，设
$ \left\{ {o(t),t \geqslant 0} \right\} $ 是一个有限状态连续时间马尔可夫链，$ o(t) $ 的取值范围为$S = \left\{ {1,2,\cdots,s} \right\}$ ，它在时间$t$ ~$ t + T $ 从状态$ i $ 转移到状态$ j $ 的转移概率矩阵${\boldsymbol{\varPsi }} = ({\pi _{ij}} \in {{\bf{R}}^{s \times s}})$ 为$$ {{P}} (o(t + T) = j|o(t) = i) = {\pi _{ij}} $$ 式中：
$ {\pi _{ij}} \geqslant 0 $ ，且$\displaystyle\sum_{j = 1}^s {{\pi _{ij}}} = 1$ 。1.2 图论基础
$G = ({{v}},{{e}},{{A}})$ 表示一个图，${{v}} = \{ {v_1},{v_2},\cdots,{v_n}\}$ 表示图$ G $ 的n个结点构成的集合，图$ G $ 的边集是$ v \times v $ ，其元素${e_{ij}} = ({v_j},{v_i}) \in {{v}} \times {{v}}$ 。矩阵${\boldsymbol{A}} = [{a_{ij}}] \in {{\bf{R}}^{n \times n}}$ 是图G的邻接矩阵，当$({v_i},{v_j}) \in {{e}}$ 时，$ {a_{ij}} = 1 $ ，反之$ {a_{ij}} = 0 $ 。此外，${{{N}}_i} = \{ {v_j} \in {{v}}:({v_j},{v_i}) \in {{e}}\}$ 表示节点$ {v_i} $ 的邻居集。${\boldsymbol{L}}(G) = [{l_{ij}}] \in {{\bf{R}}^{n \times n}}$ 表示图$ G $ 的拉普拉斯矩阵，它的元素取值为$$ {l_{ij}} = \left\{ \begin{gathered} - {a_{ij}},i \ne j \\ \sum\limits_{j = 1,j \ne i}^n {{a_{ij}},i = j} \\ \end{gathered} \right. $$ 1.3 异质多智能体系统
异质多智能体系统是指具有不同动力学性质多智能体构成的系统。下面主要讨论由一阶和二阶多智能体组成的离散和连续异质多智能体系统。离散异质多智能体系统为
$$ \left\{\begin{split} &{{\boldsymbol{\iota }}_i}(\kappa + 1) = {{\boldsymbol{\iota }}_i}(\kappa ) + h{{\boldsymbol{u}}_i}(\kappa ), i \in {\rho _1},i = 1,2,\cdots,m \\ &\left\{ \begin{aligned} &{{\boldsymbol{\iota }}_i}(\kappa + 1) = {{\boldsymbol{\iota }}_i}(\kappa ) + h{{\boldsymbol{\mu }}_i}(\kappa ) \\ &{{\boldsymbol{\mu }}_i}(\kappa + 1) = {{\boldsymbol{\mu }}_i}(\kappa ) + h{{\boldsymbol{u}}_i}(\kappa ) \\ \end{aligned} \right., i \in {\rho _2},i = m + 1,m + 2,\cdots,n \\ \end{split} \right.$$ (1) 连续异质多智能体系统为
$$\left\{\begin{split} & {{{\boldsymbol{\dot \iota }}}_i}(t) = {{\boldsymbol{u}}_i}(t),i \in {\rho _1},i = 1,2,\cdots,m \\ & \left\{ \begin{aligned} &{{{\boldsymbol{\dot \iota }}}_i}(t) = {{\boldsymbol{\mu }}_i}(t) \\ &{{{\boldsymbol{\dot \mu }}}_i}(t) = {{\boldsymbol{u}}_i}(t) \\ \end{aligned} \right.,i \in {\rho _2},i = m + 1,m + 2,\cdots,n \\ \end{split}\right. $$ (2) 式中：
$ {{\boldsymbol{\iota }}_i} $ 和$ {{\boldsymbol{\mu }}_i} $ 分别表示第$ i $ 个智能体位置和速度向量；$ {{\boldsymbol{u}}_i} $ 表示第$ i $ 个智能体输入控制向量；$ {\rho _1} $ 和$ {\rho _2} $ 分别表示一阶和二阶智能体2个分组，$ {\rho _1} $ 为一阶智能体，$ {\rho _2} $ 为二阶智能体。异质多智能系统式 (1) 和 式(2) 的邻接矩阵
$ {\boldsymbol{A}} $ 用分块矩阵表示为$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_{{\rm{ff}}}}}&{{{\boldsymbol{A}}_{{\rm{fs}}}}} \\ {{{\boldsymbol{A}}_{{\rm{sf}}}}}&{{{\boldsymbol{A}}_{{\rm{ss}}}}} \end{array}} \right] $$ 式中：
${{\boldsymbol{A}}_{{\rm{ff}}}}$ 和${{\boldsymbol{A}}_{{\rm{ss}}}}$ 分别表示一阶智能体和二阶智能体之间邻接矩阵；${{\boldsymbol{A}}_{{\rm{fs}}}}$ 表示一阶智能体和二阶智能体邻接矩阵；${{\boldsymbol{A}}_{{\rm{sf}}}}$ 表示二阶智能体到一阶智能体邻接矩阵。易知，异质多智能体系统式 (1) 和式 (2) 的拉普拉斯矩阵为
$$ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{L}}_{{\rm{ff}}}} + {{\boldsymbol{D}}_{{\rm{fs}}}}}&{ - {{\boldsymbol{A}}_{{\rm{fs}}}}} \\ { - {{\boldsymbol{A}}_{{\rm{sf}}}}}&{{{\boldsymbol{L}}_{{\rm{ss}}}} + {{\boldsymbol{D}}_{{\rm{sf}}}}} \end{array}} \right] $$ ${\boldsymbol{D}} = {\rm{diag}}\left\{ {\hat d_1},{\hat d_2},\cdots,{\hat d_n}\right\}$ 是图$ G $ 的入度矩阵，且$$ {{\boldsymbol{D}}_{{\rm{fs}}}} = {\rm{diag}}\left\{ \displaystyle\sum_{j \in {N_{i,s}}} {{a_{ij}},i \in {\rho _1}} \right\} $$ $$ {{\boldsymbol{D}}_{{\rm{sf}}}} = {\rm{diag}}\left\{ \displaystyle\sum_{j \in {N_{i,f}}} {{a_{ij}},i \in {\rho _2}} \right\} $$ 1.4 定义和引理
定义1 离散异质多智能体系统式 (1) 称为均方二分组一致当且仅当如下条件成立：
$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to \infty } E{[|{{\boldsymbol{\iota }}_i}(\kappa ) - {{\boldsymbol{\iota }}_j}(\kappa )|]^2} = 0,i,j \in {\rho _\varOmega },\varOmega = 1,2\\ \mathop {\lim }\limits_{\kappa \to \infty } E{[|{{\boldsymbol{\mu }}_i}(\kappa ) - {{\boldsymbol{\mu }}_j}(\kappa )|]^2} = 0,i,j \in {\rho _1} \end{gathered} $$ 类似地，可给出连续异质多智能体系统均方二分组一致定义，此时，仅需将定义中
$\kappa$ 替换成$ t $ 即可。定义2 以概率为元素且每行元素和为1的矩阵称为随机矩阵。
引理1[26] 若
${\boldsymbol{B}} \in {{\bf{R}}^{n \times n}}$ 是随机矩阵，$ \lambda = 1 $ 是$ {\boldsymbol{B}} $ 的一重代数特征值，$ {\boldsymbol{B}} $ 的其余特征值的模都小于1，那么$ {\boldsymbol{B}} $ 是随机不可约非周期矩阵(stochastic indecomposable and aperiodic matrices, SIA)矩阵。引理2[27] 设s是一个正整数，且
${\boldsymbol{B}} = \{ {{\boldsymbol{B}}_1},{{\boldsymbol{B}}_2},\cdots， {{\boldsymbol{B}}_s}\}$ 是由s个n阶SIA矩阵组成的集合，则${\boldsymbol{B}}$ 中任意j个元素乘积${{\boldsymbol{B}}_{{i_1}}}{{\boldsymbol{B}}_{{i_2}}}\cdots{{\boldsymbol{B}}_{{i_j}}}$ 也是SIA矩阵，且$$ \mathop {\lim }\limits_{j \to \infty } {{\boldsymbol{B}}_{{i_1}}}{{\boldsymbol{B}}_{{i_2}}}\cdots{{\boldsymbol{B}}_{{i_j}}} = {{\boldsymbol{1}}_n}{{\boldsymbol{c}}^{\rm T}} $$ 式中
$ {{\boldsymbol{c}}^{\rm T}} $ 是一个元素值为非负的列向量。推论1 根据引理2和克罗内克积性质，2个SIA矩阵的克罗内克积仍是SIA矩阵。
证明 因为
$({{\boldsymbol{B}}_{{i_1}}} \otimes {{\boldsymbol{B}}_{{i_1}}})({{\boldsymbol{B}}_{{i_2}}} \otimes {{\boldsymbol{B}}_{{i_2}}})\cdots({{\boldsymbol{B}}_{{i_j}}} \otimes {{\boldsymbol{B}}_{{i_j}}}) = ({{\boldsymbol{B}}_{{i_1}}}{{\boldsymbol{B}}_{{i_2}}}\cdots{{\boldsymbol{B}}_{{i_j}}}) \otimes$ $({{\boldsymbol{B}}_{{i_1}}} {{\boldsymbol{B}}_{{i_2}}}\cdots {{\boldsymbol{B}}_{{i_j}}})$ 所以，矩阵$({{\boldsymbol{B}}_{{i_1}}} \otimes {{\boldsymbol{B}}_{{i_1}}})({{\boldsymbol{B}}_{{i_2}}} \otimes {{\boldsymbol{B}}_{{i_2}}})\cdots({{\boldsymbol{B}}_{{i_j}}} \otimes {{\boldsymbol{B}}_{{i_j}}}) $ 也是SIA矩阵。引理3 设s是一个正整数，且
$ \{ {{\boldsymbol{B}}_{ij}}\} _{i,j = 1}^s $ 是一个n阶SIA矩阵集合。$ {\boldsymbol{P}} = ({p_{ij}}) $ 是一个$ s \times s $ 维服从齐次不可约正循环马尔可夫链的转移概率矩阵。定义矩阵${\boldsymbol{Q}} \in {{\bf{R}}^{ns \times ns}}$ ，它第$ i $ 行与第$ j $ 列的矩阵块是$ {{\boldsymbol{Q}}_{ij}} = {p_{ji}}{{\boldsymbol{B}}_{ij}} $ ，则有$ \mathop {\lim }\limits_{\varepsilon \to \infty } {({{\boldsymbol{Q}}^\varepsilon })_{ij}} = p_{ji}^\infty {\boldsymbol{1c}}_{ij}^{\rm T} $ ，$ p_{ji}^\infty $ 是当$ \varepsilon = \infty $ 时，$ {{\boldsymbol{P}}^\varepsilon } $ 第$ j $ 行第$ i $ 列的元素值。$ {\boldsymbol{c}}_{ij}^{\rm T} $ 是一个元素值为非负的列向量。证明 矩阵
$ {{\boldsymbol{Q}}^\varepsilon } $ 第$ i $ 行第$ j $ 列的分块矩阵可以表示为$$ \begin{gathered} {({{\boldsymbol{Q}}^\varepsilon })_{ij}} = \sum\limits_{1 \leqslant {i_1},{i_2},\cdots,{i_{\varepsilon - 1}} \leqslant n} {{p_{j{i_1}}}{{\boldsymbol{B}}_{i{i_1}}}} {p_{{i_1}{i_2}}}{{\boldsymbol{B}}_{{i_1}{i_2}}}\cdots{p_{{i_{\varepsilon - 1}}i}}{{\boldsymbol{B}}_{{i_{\varepsilon - 1}}j}} = \\ p_{ij}^\varepsilon \sum\limits_{1 \leqslant {i_1},{i_2},\cdots,{i_{\varepsilon - 1}} \leqslant n} {{\xi _{1 \leqslant {i_1},{i_2},\cdots,{i_{\varepsilon - 1}} \leqslant n}}{{\boldsymbol{B}}_{i{i_1}}}} {{\boldsymbol{B}}_{{i_1}{i_2}}}\cdots{{\boldsymbol{B}}_{{i_{\varepsilon - 1}}j}} \end{gathered} $$ 如果
$ p_{ji}^\varepsilon > 0 $ ，则：$$ {\xi _{1 \leqslant {i_1},{i_2},\cdots,{i_{\varepsilon - 1}} \leqslant n}} = ({p_{j{i_1}}}{p_{{i_1}{i_2}}}\cdots{p_{{i_{\varepsilon - 1}}i}})/p_{ji}^\varepsilon $$ 否则
$ p_{ji}^\varepsilon = 0 $ 。$ {{\boldsymbol{Q}}^\varepsilon } $ 第$ i $ 行和第$ j $ 列对应的分块矩阵都是$ p_{ji}^\varepsilon $ 和SIA矩阵乘积。根据引理2，随着$ \varepsilon $ 趋于无穷大，乘积${{\boldsymbol{B}}_{i{i_1}}}{{\boldsymbol{B}}_{{i_1}{i_2}}}\cdots{{\boldsymbol{B}}_{{i_{\kappa - 1}}j}}$ 将会收敛到$ {\boldsymbol{1c}}_{ij}^{\rm T} $ 。若马尔可夫链是非周期的，则转移概率矩阵极限将收敛到一组确定值，即该链是遍历的。否则，如果马尔可夫链是周期性的，这将导致$ p_{ji}^\varepsilon $ 不收敛。推论2 设s是一个正整数，且
$ \{ {{\boldsymbol{B}}_j}\} _{j = 1}^s $ 是一个n阶SIA矩阵集合。$ {\boldsymbol{P}} = ({p_{ij}}) $ 是一个$ s \times s $ 维服从齐次不可约正循环马尔可夫链转移概率矩阵。定义矩阵${\boldsymbol{\tilde Q}} \in {{\bf{R}}^{{n^2}s \times {n^2}s}}$ ，且它的第$ i $ 行与第$ j $ 列对应的矩阵块是$ {{\boldsymbol{\tilde Q}}_{ij}} = {p_{ji}}{{\boldsymbol{B}}_j} \otimes {{\boldsymbol{B}}_j} $ ，则有$\mathop {\lim }\limits_{\varepsilon \to \infty } {({{\boldsymbol{\tilde Q}}^\varepsilon })_{ij}} = p_{ji}^\infty {\boldsymbol{1\tilde c}}_{ij}^{\rm{T}}$ ，其中$ p_{ji}^\infty $ 是当$ \varepsilon = \infty $ 时，$ {{\boldsymbol{P}}^\varepsilon } $ 第$ j $ 行与第$ i $ 列对应的元素值。$ {\boldsymbol{\tilde c}}_{ij}^{\rm T} $ 为一个元素值为非负的列向量。证明类似引理3，其余略。
引理4[28] 若矩阵
${\boldsymbol{B}} = [{b_{ij}}] \in {{\bf{R}}^{n \times n}}$ ，其中$ {b_{ii}} \leqslant 0 $ ，且$ \forall i \ne j $ ，$ {b_{ij}} \geqslant 0 $ ，每行元素和为0，那么矩阵${\boldsymbol{B}}$ 有唯一的零特征值，其余特征值具有负实部，且零特征值的特征向量是$ {{\boldsymbol{1}}_n} $ 当且仅当矩阵${\boldsymbol{B}}$ 是一个图的邻接矩阵且该图含有一棵生成树。引理5[28] 如果存在矩阵
${\boldsymbol{B}}$ 满足引理4的条件，则对于$ \forall t \geqslant 0 $ ，矩阵${{\rm{e}}^{ - {\boldsymbol{B}}t}}$ 是一个主对角线元素为正的随机矩阵。此外，若矩阵${\boldsymbol{B}}$ 有一个零特征值，且存在向量${\boldsymbol{v}} = {[{v_1},{v_2},\cdots,{v_n}]^{\rm{T}}} \geqslant 0$ 满足${\boldsymbol{1}}_n^{\rm{T}}{\boldsymbol{\nu }} = 1$ 和${{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{\nu }} = 0$ ，则当$ t \to 0 $ 时，${{\rm{e}}^{ - {\boldsymbol{B}}t}} \to {{\boldsymbol{1}}_n}{{\boldsymbol{\nu }}^{\rm{T}}}$ 。2. 马尔可夫切换多智能体系统分组一致主要研究结果
2.1 离散时间异质多智能体系统均方二分组一致性
这部分主要研究马尔可夫切换下离散时间异质多智能体系统式 (1) 的均方二分组一致性。基于智能体之间合作竞争关系，设计如下均方二分组一致控制协议：
$$ \left\{ \begin{aligned} &{{\boldsymbol{u}}_i}(\kappa ) = \alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa ))} - \right. \\ &\quad \left.\sum\limits_{j \in {\boldsymbol{N}}_{Di}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) + {{\boldsymbol{\iota }}_i}(\kappa ))} \right],i \in {\rho _1} \\ &{{\boldsymbol{u}}_i}(k) = \alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa ))} - \right. \\ &\quad \left.\sum\limits_{j \in {\boldsymbol{N}}_{Di}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) + {{\boldsymbol{\iota }}_i}(\kappa )} \right] - \beta {{\boldsymbol{\mu }}_i}(\kappa ),i \in {\rho _2} \end{aligned} \right. $$ (3) 式中：
$ {\boldsymbol{N}}_{Si}^{\sigma (\kappa )} $ 为智能体$ i $ 同组邻居集合；$ {\boldsymbol{N}}_{Di}^{\sigma (\kappa )} $ 为智能体$ i $ 不同组邻居集合；$ \alpha $ 和$ \beta $ 为相应的耦合系数；$ a_{ij}^{\sigma (\kappa )} $ 是邻接矩阵$ {{\boldsymbol{A}}^{\sigma (\kappa )}} $ 中的元素。定理1 若
$ \{ \sigma (\kappa ),\kappa \geqslant 0\} $ 是一个齐次遍历马尔可夫链，其状态空间为$S = \{ 1,2,\cdots,s\}$ ,若$$ \alpha < \frac{1}{{h{l_{\max }}}} \text{，} \beta < \frac{2}{h} 且 {l_{\max }} < \frac{{{\beta ^2}}}{{4\alpha }} $$ 则在控制协议式 (3) 下，离散异质多智能体系统式 (1)均方二分组一致当且仅当该系统联合拓扑存在有向生成树。
证明 1) 充分性：
假设
$ {G_1} \cup {G_2} \cup \cdots \cup {G_s} $ 具有有向生成树。为简单起见，引进变量
$ {{\boldsymbol{\bar \mu }}_i}(\kappa ) $ ， 且：$$ {{\boldsymbol{\bar \mu }}_i}(\kappa ) = {{\boldsymbol{\iota }}_i}(\kappa ) + \frac{2}{\beta }{{\boldsymbol{\mu }}_i}(\kappa ) $$ 综合式 (1) 和式 (3)，当
$ i \in {\rho _1} $ 时，有：$$ \begin{gathered} {{\boldsymbol{\iota }}_i}(\kappa + 1) = {{\boldsymbol{\iota }}_i}(\kappa ) + \\h\alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa )) - } \sum\limits_{j \in {\boldsymbol{N}}_{Di}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) + {{\boldsymbol{\iota }}_i}(\kappa ))} \right] \end{gathered} $$ (4) 当
$ i \in {\rho _2} $ 时，有：$$ {{\boldsymbol{\iota }}_i}(\kappa + 1) = {{\boldsymbol{\iota }}_i}(\kappa ) + \frac{{\beta h}}{2}({{\boldsymbol{\bar \mu }}_i}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa )) $$ (5) $$ \begin{gathered} {{{\boldsymbol{\bar \mu }}}_i}(\kappa + 1) = {{{\boldsymbol{\bar \mu }}}_i}(\kappa ) - \frac{{\beta h}}{2}({{{\boldsymbol{\bar \mu }}}_i}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa )) + \\ \frac{{2\alpha h}}{\beta }\left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) - {{\boldsymbol{\iota }}_i}(\kappa ))} - \sum\limits_{j \in {\boldsymbol{N}}_{Di}^{\sigma (\kappa )}} {a_{ij}^{\sigma (\kappa )}({{\boldsymbol{\iota }}_j}(\kappa ) + {{\boldsymbol{\iota }}_i}(\kappa ))} \right] \end{gathered} $$ (6) 由式(4)~(6) 可得：
$$ \begin{gathered} {{\boldsymbol{\iota }}_f}(\kappa + 1) = {{\boldsymbol{\iota }}_f}(\kappa ) - \\ h\alpha \left[ - {\boldsymbol{A}}_{fs}^{\sigma (\kappa )}{{\boldsymbol{\iota }}_s}(\kappa ) + ({\boldsymbol{L}}_{ff}^{\sigma (\kappa )} + {\boldsymbol{D}}_{fs}^{\sigma (\kappa )}){{\boldsymbol{\iota }}_f}(\kappa )\right] \end{gathered} $$ (7) $$ {{\boldsymbol{\iota }}_s}(\kappa + 1) = {{\boldsymbol{\iota }}_s}(\kappa ) + \frac{{\beta h}}{2}({{\boldsymbol{\bar \mu }}_s}(\kappa ) - {{\boldsymbol{\iota }}_s}(\kappa )) $$ (8) $$ \begin{gathered} {{{\boldsymbol{\bar \mu }}}_s}(\kappa + 1) = {{{\boldsymbol{\bar \mu }}}_s}(\kappa ) - \frac{{\beta h}}{2}({{{\boldsymbol{\bar \mu }}}_s}(\kappa ) - {{\boldsymbol{\iota }}_s}(\kappa )) - \\ \frac{{2\alpha h}}{\beta }\left[ {({\boldsymbol{L}}_{ss}^{\sigma (\kappa )} + {\boldsymbol{D}}_{sf}^{\sigma (\kappa )}){{\boldsymbol{\iota }}_s}(\kappa ) - {\boldsymbol{A}}_{sf}^{\sigma (\kappa )}{{\boldsymbol{\iota }}_f}(\kappa )} \right] \end{gathered} $$ (9) 其中，
$$ {{\boldsymbol{\iota }}_f}(\kappa ) = [{{\boldsymbol{\iota }}_1}(\kappa ),{{\boldsymbol{\iota }}_2}(\kappa ),\cdots,{{\boldsymbol{\iota }}_m}(\kappa )] $$ $$ {{\boldsymbol{\iota }}_s}(\kappa ) = [{{\boldsymbol{\iota }}_{m + 1}}(\kappa ),{{\boldsymbol{\iota }}_{m + 2}}(\kappa ),\cdots,{{\boldsymbol{\iota }}_n}(\kappa )] $$ $$ {{\boldsymbol{\bar \mu }}_s}(\kappa ) = [{{\boldsymbol{\bar \mu }}_{m + 1}}(\kappa ),{{\boldsymbol{\bar \mu }}_{m + 2}}(\kappa ),\cdots,{{\boldsymbol{\bar \mu }}_n}(\kappa )] $$ 由式 (7)~(9)得到：
$$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\iota }}_f}(\kappa + 1)} \\ {{{\boldsymbol{\iota }}_s}(\kappa + 1)} \\ {{{{\boldsymbol{\bar \mu }}}_s}(\kappa + 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_m} - h\alpha \left({\boldsymbol{L}}_{ff}^{\sigma (\kappa )} + {\boldsymbol{D}}_{fs}^{\sigma (\kappa )}\right)}&{h\alpha {\boldsymbol{A}}_{fs}^{\sigma (\kappa )}}&0 \\ 0&{\left(1 - \dfrac{{\beta h}}{2}\right){{\boldsymbol{I}}_{n - m}}}&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}}} \\ {\dfrac{{2\alpha h}}{\beta }{\boldsymbol{A}}_{sf}^{\sigma (\kappa )}}&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}} - \dfrac{{2\alpha h}}{\beta }\left({\boldsymbol{L}}_{ss}^{\sigma (\kappa )} + {\boldsymbol{D}}_{sf}^{\sigma (\kappa )}\right)}&{\left(1 - \dfrac{{\beta h}}{2}\right){{\boldsymbol{I}}_{n - m}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\iota }}_f}(\kappa )} \\ {{{\boldsymbol{\iota }}_s}(\kappa )} \\ {{{{\boldsymbol{\bar \mu }}}_s}(\kappa )} \end{array}} \right] \end{gathered} $$ (10) 将式 (10) 写为
$$ {\boldsymbol{X}}(\kappa + 1) = {{\boldsymbol{H}}_{\sigma (\kappa )}}{\boldsymbol{X}}(\kappa ) $$ (11) 式中
$ {\boldsymbol{X}}(\kappa ) = {[{\boldsymbol{\iota }}_f^{\rm T}(\kappa ),{\boldsymbol{\iota }}_s^{\rm T}(\kappa ),{\boldsymbol{\bar \mu }}_s^{\rm T}(\kappa )]^{\rm T}} $ 。设离散异质多智能体系统式 (1) 的拉普拉斯矩阵元素最大值为
$$ {l_{\max }} = \max \{ {l_{11}},{l_{12}},\cdots,{l_{nn}}\} $$ 若存在参数
$ \alpha $ 和$ \beta $ 满足$$ \alpha < \frac{1}{h{l}_{\mathrm{max}}},\beta < \frac{2}{h}，{l}_{\mathrm{max}} < \frac{{\beta }^{2}}{4\alpha } $$ 则矩阵
$ {{\boldsymbol{H}}_{\sigma (\kappa )}} $ 是一个非负矩阵，同时$ {{\boldsymbol{H}}_{\sigma (\kappa )}} $ 的行元素和是1，因此，$ {{\boldsymbol{H}}_{\sigma (\kappa )}} $ 是一个随机矩阵。下面证明
${{\boldsymbol{H}}_1}{{\boldsymbol{H}}_2},\cdots,{{\boldsymbol{H}}_s}$ 是SIA矩阵。因为$$ \dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_l}} = \left( {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_m} - \dfrac{{h\alpha }}{s}\displaystyle\sum\limits_{l = 0}^s {\left({\boldsymbol{L}}_{ff}^l + {\boldsymbol{D}}_{fs}^l\right)} }&{\dfrac{{h\alpha }}{s}\displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{fs}^l} }&0 \\ 0&{\left(1 - \dfrac{{\beta h}}{2}\right){{\boldsymbol{I}}_{n - m}}}&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}}} \\ {\dfrac{{2\alpha h}}{{\beta s}}\displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{sf}^l} }&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}} - \dfrac{{2\alpha h}}{{\beta s}}\displaystyle\sum\limits_{l = 0}^s {\left({\boldsymbol{L}}_{ss}^l + {\boldsymbol{D}}_{sf}^l\right)} }&{\left(1 - \dfrac{{\beta h}}{2}\right){{\boldsymbol{I}}_{n - m}}} \end{array}} \right) $$ (12) $$ \dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_l}} - {\boldsymbol{I}} = \left( {\begin{array}{*{20}{c}} { - \dfrac{{h\alpha }}{s}\displaystyle\sum\limits_{l = 0}^s {({\boldsymbol{L}}_{ff}^l + {\boldsymbol{D}}_{fs}^l)} }&{\dfrac{{h\alpha }}{s}\displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{fs}^l} }&0 \\ 0&{ - \dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}}}&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}}} \\ {\dfrac{{2\alpha h}}{{\beta s}}\displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{sf}^l} }&{\dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}} - \dfrac{{2\alpha h}}{{\beta s}}\displaystyle\sum\limits_{l = 0}^s {({\boldsymbol{L}}_{ss}^l + {\boldsymbol{L}}_{sf}^l)} }&{ - \dfrac{{\beta h}}{2}{{\boldsymbol{I}}_{n - m}}} \end{array}} \right) $$ (13) 由矩阵初等变换，得到：
$$ \begin{gathered} \dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_{\boldsymbol{l}}}} - {\boldsymbol{I}} \to \left( {\begin{array}{*{20}{c}} 0&0&{{{\boldsymbol{I}}_{n - m}}} \\ {\displaystyle\sum\limits_{l = 0}^s {({\boldsymbol{L}}_{ff}^l + {\boldsymbol{D}}_{fs}^l)} }&{ - \displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{fs}^l} }&0 \\ { - \displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{A}}_{sf}^l} }&{\displaystyle\sum\limits_{l = 0}^s {({\boldsymbol{L}}_{ss}^l + {\boldsymbol{D}}_{sf}^l)} }&0 \end{array}} \right) \to \left[ {\begin{array}{*{20}{c}} 0&{{{\boldsymbol{I}}_{n - m}}} \\ {\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{L}}^l}} }&0 \end{array}} \right] \end{gathered} $$ (14) 由于
${G_1} \cup {G_2} \cup \cdots \cup {G_s}$ 具有向生成树，因此${\rm{rank}} \left(\displaystyle\sum\limits_{l = 0}^s {{\boldsymbol{L}}^l}\right) = \ n - 1$ ，${\rm{rank}}\left(\dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_l}} - {\boldsymbol{I}}\right) = 2n - m - 1$ ，即$ \lambda = 1 $ 为矩阵$\dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_l}}$ 重数为1的特征值。又因为$\dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_l}}$ 是随机矩阵，故它的其余特征值的模均小于1。由此可知$\dfrac{1}{s}\displaystyle\sum\limits_{l = 0}^s {{{\boldsymbol{H}}_{\boldsymbol{l}}}}$ 是SIA矩阵，由文献[29]结论易知$ {{\boldsymbol{H}}_1}{{\boldsymbol{H}}_2},\cdots,{{\boldsymbol{H}}_s} $ 是SIA矩阵。定义矩阵
${\boldsymbol{Q}} \in {{\bf{R}}^{ns \times ns}}$ 和${\boldsymbol{\tilde Q}} \in {{\bf{R}}^{{n^2}s \times {n^2}s}}$ ，且它们的第$ i $ 行与第$ j $ 列对应的矩阵块分别为$ {{\boldsymbol{Q}}_{ij}} = {p_{ji}}{{\boldsymbol{H}}_j} $ 和${{\boldsymbol{\tilde Q}}_{ij}} = {p_{ji}}{{\boldsymbol{H}}_j} \otimes {{\boldsymbol{H}}_j}$ ，又${{\boldsymbol{H}}_1}{{\boldsymbol{H}}_2},\cdots,{{\boldsymbol{H}}_s}$ 为SIA 矩阵，由引理3，有：$$ \mathop {\lim }\limits_{\varepsilon \to \infty } {({{\boldsymbol{Q}}^\varepsilon })_{ij}} = p_{ji}^\infty {\boldsymbol{1c}}_{ij}^{\rm T} \text{，} \mathop {\lim }\limits_{\varepsilon \to \infty } {({{\boldsymbol{\tilde Q}}^\varepsilon })_{ij}} = p_{ji}^\infty {\boldsymbol{1\tilde c}}_{ij}^{\rm T} $$ 式中
$ {\boldsymbol{c}}_{ij}^{\rm T} $ 和$ {\boldsymbol{\tilde c}}_{ij}^{\rm T} $ 分别为元素为非负的列向量。下面证明多智能体系统式(1) 的均方二分组一致。定义：
$$ {\boldsymbol{\psi }}(\kappa ) = \left({{\boldsymbol{I}}_{2n - m}} - \dfrac{{{{\boldsymbol{1}}_{2n - m}}{\boldsymbol{1}}_{2n - m}^{\rm{T}}}}{{{\boldsymbol{1}}_{2n - m}^{\rm{T}}{{\boldsymbol{1}}_{2n - m}}}}\right){\boldsymbol{\varGamma }}(\kappa ) $$ 且
$$ \begin{gathered} {\boldsymbol{\varGamma }}(\kappa ) = [{\boldsymbol{\iota }}_1^{\rm T}(\kappa ),{\boldsymbol{\iota }}_2^{\rm T}(\kappa ),\cdots,{\boldsymbol{\iota }}_m^{\rm T}(\kappa ),{\boldsymbol{\iota }}_{m + 1}^{\rm T}(\kappa ),{\boldsymbol{\iota }}_{m + 2}^{\rm T}(\kappa ),\cdots,{\boldsymbol{\iota }}_n^{\rm T}(\kappa ), \\ {\boldsymbol{\bar \mu }}_{n + 1}^{\rm T}(\kappa ),{\boldsymbol{\bar \mu }}_{n + 2}^{\rm T}(\kappa ),\cdots,{\boldsymbol{\bar \mu }}_{2n - m}^{\rm T}(\kappa ){]^{\rm T}} \end{gathered} $$ 式中
${\boldsymbol{\bar \mu }}_{n + 1}^{\rm T}(\kappa ) = {\boldsymbol{\bar \mu }}_{m + 1}^{\rm T}(\kappa ) ,{\boldsymbol{\bar \mu }}_{m + 2}^{\rm T}(\kappa ) ,\cdots, {\boldsymbol{\bar \mu }}_n^{\rm T}(\kappa ) = {\boldsymbol{\bar \mu }}_{2n - m}^{\rm T}(\kappa )$ ，由$ {\boldsymbol{\varGamma }}(\kappa ) $ 定义，其意义类似于$ {\boldsymbol{X}}(\kappa ) $ ，只是形式不同。再设$$ \begin{gathered} {\boldsymbol{\psi }}(\kappa ) = [{\boldsymbol{\psi }}_1^{\rm T}(\kappa ),{\boldsymbol{\psi }}_2^{\rm T}(\kappa ),\cdots,{\boldsymbol{\psi }}_m^{\rm T}(\kappa ),{\boldsymbol{\psi }}_{m + 1}^{\rm T}(\kappa ),\cdots, \\ {\boldsymbol{\psi }}_n^{\rm T}(\kappa ),{\boldsymbol{\psi }}_{n + 1}^{\rm T}(\kappa ),\cdots,{\boldsymbol{\psi }}_{2n - m}^{\rm T}(\kappa ){]^{\rm T}} \end{gathered} $$ 以及
$$\begin{array}{c} {\boldsymbol{g}}(\kappa ) = \dfrac{1}{{2n - m}}\displaystyle\sum\limits_{l = 1}^m {{{\boldsymbol{\iota }}_l}} (\kappa ) + \\ \dfrac{1}{{2n - m}}f\displaystyle\sum\limits_{l = m + 1}^n {{{\boldsymbol{\iota }}_l}} (\kappa ) + \dfrac{1}{{2n - m}}\displaystyle\sum\limits_{l = m + 1}^n {{{{\boldsymbol{\bar \mu }}}_l}} (\kappa ) \end{array}$$ 则有：
$$ {{\boldsymbol{\psi }}_i}(\kappa ) = {{\boldsymbol{\iota }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ),i = 1,2,\cdots,m $$ $$\begin{gathered} {{\boldsymbol{\psi }}_i}(\kappa ) = {{\boldsymbol{\iota }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ),i = m + 1, m + 2,\cdots,n \\ {{\boldsymbol{\psi }}_i}(\kappa ) = {{\boldsymbol{\bar \mu }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ),i = n + 1,n + 2,\cdots,2n - m \end{gathered}$$ 状态向量
$ {\boldsymbol{\varGamma }}(\kappa ) $ 的二阶矩为$$ V(\kappa ) ={\rm{ E}}[{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{(\kappa )}] \text{，} $$ 式中
${\rm{E}}$ 表示数学期望。定义：$$ {V_i}(\kappa ) = {\rm{E}}[{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{(\kappa )}{\theta _{\{ \sigma (\kappa ) = i\} }}],i \in S $$ 式中
$ {\theta _{\{ \sigma (\kappa ) = i\} }} $ 为事件$ \{ \sigma (\kappa ) = i\} $ 的示性函数，则：$$ V(\kappa ) = \sum\limits_{i = 1}^s {{V_i}(\kappa )} $$ 根据重期望公式，有：
$$ \begin{gathered} {V_i}(\kappa + 1) = {\rm{E}}[{\boldsymbol{\varGamma }}(\kappa + 1){\boldsymbol{\varGamma }}^{\rm T}{(\kappa + 1)}{\theta _{\{ \sigma (\kappa ) = i\} }}] = \\ \sum\limits_{j = 1}^s {{\rm{E}}[{{\boldsymbol{H}}_{\sigma (\kappa )}}{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{{(\kappa )}}{\boldsymbol{H}}_{\sigma (\kappa )}^{\rm T}{\theta _{\{ \sigma (\kappa + 1) = i\} }}|} \sigma (\kappa ) = j] \times \\ p\{ \sigma (\kappa ) = j\} = \\ \sum\limits_{j = 1}^s {{\rm{E}}[{{\boldsymbol{H}}_j}{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{{(\kappa )}}{\boldsymbol{H}}_j^{\rm T}|\sigma (\kappa ) = j]} {\rm{E}}[{\theta _{\{ \sigma (\kappa + 1) = i\} }}|\sigma (\kappa ) = j] \times \\ p\{ \sigma (\kappa ) = j\} = \end{gathered} $$ $$ \begin{gathered} \sum\limits_{j = 1}^s {{{\boldsymbol{H}}_j}{\rm{E}}[{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{{(\kappa )}}|\sigma (\kappa ) = j]} p\{ \sigma (\kappa ) = j\} {\boldsymbol{H}}_j^{\rm T}{p_{ji}}= \\ \sum\limits_{j = 1}^s {{p_{ji}}{{\boldsymbol{H}}_j}{\rm{E}}[{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{{(\kappa )}}{\theta _{\{ \sigma (\kappa + 1) = i\} }}]} {\boldsymbol{H}}_j^{\rm T} =\\ \sum\limits_{j = 1}^s {{p_{ji}}{{\boldsymbol{H}}_j}{V_j}(\kappa )} {\boldsymbol{H}}_j^{\rm T},i \in S \end{gathered} $$ (15) 初始值为
${V_i} = {q_i}{{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T},{q_i} = P{\rm{r}} (\sigma (0) = i)$ 。将式(15)写为向量形式，可得：
$$ {\boldsymbol{\varsigma }}(\kappa + 1) = {\boldsymbol{\varPhi \varsigma }}(\kappa ) $$ 式中：
$ {\boldsymbol{\varsigma }}(k) $ 是一个$ {n^2}s $ 维向量；${\boldsymbol{\varPhi }} \in {{\bf{R}}^{{n^2}s \times {n^2}s}}$ ，且$$ \begin{gathered} {\boldsymbol{\varPhi }} = \left[ {\begin{array}{*{20}{c}} {{p_{11}}{{\boldsymbol{H}}_1} \otimes {{\boldsymbol{H}}_1}}& \cdots &{{p_{s1}}{{\boldsymbol{H}}_s} \otimes {{\boldsymbol{H}}_s}} \\ \vdots & \ddots & \vdots \\ {{p_{1s}}{{\boldsymbol{H}}_1} \otimes {{\boldsymbol{H}}_1}}& \cdots &{{p_{ss}}{{\boldsymbol{H}}_s} \otimes {{\boldsymbol{H}}_s}} \end{array}} \right] \\ {\boldsymbol{\varsigma }}^{\rm T}{(0)} = [{q_1}{{\rm{col}}_1}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}} \quad {q_2}{{\rm{col}}_1}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}}\quad \cdots \quad{q_1}{{\rm{col}}_n}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}}\quad \\ \cdots \quad {q_s}{{\rm{col}}_1}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}} \quad {q_s}{{\rm{col}}_2}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}}\quad \cdots \quad{q_s}{{\rm{col}}_n}{({{\boldsymbol{\varGamma }}_0}{\boldsymbol{\varGamma }}_0^{\rm T})^{\rm T}}] \end{gathered} $$ 式中
${{\rm{col}}_i}$ 表示相应矩阵的第$ i $ 列。综上所述，得到：
$$ \mathop {\lim }\limits_{\varepsilon \to \infty } {({{\boldsymbol{\varPhi }}^\varepsilon })_{ij}} = p_{ji}^\infty {\boldsymbol{1c}}_{ij}^{\rm T} $$ 式中：
$ {\boldsymbol{1}} $ 是$ {n^2} $ 维单位向量；$ {\boldsymbol{c}}_{ij}^{\rm T} $ 是元素值为非负且和为1的$ {n^2} $ 维向量。因此：$$ \mathop {\lim }\limits_{\kappa \to \infty } {\boldsymbol{\varsigma }}(\kappa ) = {[{\xi _1}{\boldsymbol{1}}\quad{\xi _2}{\boldsymbol{1}}\quad\cdots\quad{\xi _s}{\boldsymbol{1}}]^{\rm T}} $$ $ {p_i} $ 是马尔可夫链的遍历结果，其和为1，即有：$$ \mathop {\lim }\limits_{\kappa \to \infty } V(\kappa ) = \tau {\boldsymbol{1}}{{\boldsymbol{1}}^{\rm T}} \text{，} \tau = \sum\limits_{i = 1}^s {{\xi _i}} $$ 因此：
$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[{\boldsymbol{\psi }}(\kappa ){\boldsymbol{\psi }}^{\rm T}{(\kappa )}] = \left({{\boldsymbol{I}}_{2n - m}} - \frac{{{{\boldsymbol{1}}_{2n - m}}{\boldsymbol{1}}_{2n - m}^{\rm T}}}{{{\boldsymbol{1}}_{2n - m}^{\rm T}{{\boldsymbol{1}}_{2n - m}}}}\right) \times \\ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[{\boldsymbol{\varGamma }}(\kappa ){\boldsymbol{\varGamma }}^{\rm T}{(\kappa )}]\left({{\boldsymbol{I}}_{2n - m}} - \frac{{{{\boldsymbol{1}}_{2n - m}}{\boldsymbol{1}}_{2n - m}^{\rm T}}}{{{\boldsymbol{1}}_{2n - m}^{\rm T}{{\boldsymbol{1}}_{2n - m}}}}\right)=\\ \left({{\boldsymbol{I}}_{2n - m}} - \frac{{{{\boldsymbol{1}}_{2n - m}}{\boldsymbol{1}}_{2n - m}^{\rm T}}}{{{\boldsymbol{1}}_{2n - m}^{\rm T}{{\boldsymbol{1}}_{2n - m}}}}\right)\tau {\boldsymbol{1}}{{\boldsymbol{1}}^{\rm T}}\left({{\boldsymbol{I}}_{2n - m}} - \frac{{{{\boldsymbol{1}}_{2n - m}}{\boldsymbol{1}}_{2n - m}^{\rm T}}}{{{\boldsymbol{1}}_{2n - m}^{\rm T}{{\boldsymbol{1}}_{2n - m}}}}\right) \end{gathered} $$ (16) 所以有：
$$ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[{\boldsymbol{\psi }}(\kappa ){\boldsymbol{\psi }}^{\rm T}{(\kappa )}] = 0 $$ 故
$$ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[{{\boldsymbol{\psi }}_i}(\kappa ){{\boldsymbol{\psi }}_j}(\kappa )] = 0,i,j = 1,2,\cdots,2n - m $$ 因此当
$i,j = 1,2,\cdots,m$ 或$i,j = m + 1,m + 2,\cdots,n$ 且$ i \ne j $ 时，有：$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\iota }}_i}(\kappa ) - {{\boldsymbol{\iota }}_j}(\kappa ))^2} =\\ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\iota }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ) + {\boldsymbol{g}}(\kappa ) - {{\boldsymbol{\iota }}_j}(\kappa ))^2} = \\ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\iota }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ))^2} + \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\iota }}_j}(\kappa ) - {\boldsymbol{g}}(\kappa ))^2} + \\ 2\mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[({{\boldsymbol{\iota }}_i}(\kappa ) - {\boldsymbol{g}}(\kappa ))({{\boldsymbol{\iota }}_j}(\kappa ) - {\boldsymbol{g}}(\kappa ))] =\\ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\psi }}_i}(\kappa ))^2} + \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\boldsymbol{\psi }}_j}(\kappa ))^2} + \\ 2\mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}[{{\boldsymbol{\psi }}_i}(\kappa ){{\boldsymbol{\psi }}_j}(\kappa )] = 0 \end{gathered} $$ (17) 同理：
$$ \begin{gathered} \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{{\boldsymbol{\bar \mu }}}_i}(\kappa ) - {{{\boldsymbol{\bar \mu }}}_j}(\kappa ))^2} = 0 \\ i,j = m + 1,m + 2,\cdots,n,i \ne j \\ \end{gathered} $$ (18) 利用施瓦兹柯西不等式，可得：
$$ \begin{gathered} {\rm{E}}[({{\boldsymbol{\iota }}_i}(\kappa ) - {{\boldsymbol{\iota }}_j}(\kappa ))({{{\boldsymbol{\bar \mu }}}_i}(\kappa ) - {{{\boldsymbol{\bar \mu }}}_j}(\kappa ))] \leqslant \\ {[{\rm{E}}{({{\boldsymbol{\iota }}_i}(\kappa ) - {{\boldsymbol{\iota }}_j}(\kappa ))^2}]^{\tfrac{1}{2}}}[{\rm{E}}{({({{{\boldsymbol{\bar \mu }}}_i}(\kappa ) - {{{\boldsymbol{\bar \mu }}}_j}(\kappa ))^2}]^{\tfrac{1}{2}}} \end{gathered} $$ (19) 根据式 (19)，得到：
$$\begin{gathered} \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\bf{\mu }}_i}(\kappa ) - {{\bf{\mu }}_j}(\kappa ))^2}=\\ \mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{\left[\frac{\beta }{2}({{{\bf{\bar \mu }}}_i}(\kappa ) - {{\bf{\iota }}_i}(\kappa )) - \frac{\beta }{2}({{{\bf{\bar \mu }}}_j}(\kappa ) - {{\bf{\iota }}_j}(\kappa ))\right]^2}=\\ \frac{{{\beta ^2}}}{4}\mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{\left[({{{\bf{\bar \mu }}}_i}(\kappa ) - {{{\bf{\bar \mu }}}_j}(\kappa )) + ({{\bf{\iota }}_j}(\kappa ) - {{\bf{\iota }}_i}(\kappa ))\right]^2}\leqslant\\ \frac{{{\beta ^2}}}{4}\mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{{\bf{\bar \mu }}}_i}(\kappa ) - {{{\bf{\bar \mu }}}_j}(\kappa ))^2} + \frac{{{\beta ^2}}}{4}\mathop {\lim }\limits_{\kappa \to \infty } {\rm{E}}{({{\bf{\iota }}_j}(\kappa ) - {{\bf{\iota }}_i}(\kappa ))^2}+\\ \frac{{{\beta ^2}}}{2}\mathop {\lim }\limits_{\kappa \to \infty } {\left[{\rm{E}}{({{\bf{\iota }}_i}(\kappa ) - {{\bf{\iota }}_j}(\kappa ))^2}\right]^{\tfrac{1}{2}}}\left[{\rm{E}}({({{{\bf{\bar \mu }}}_i}(\kappa ) - {{{\bf{\bar \mu }}}_j}(\kappa ))^2}\right]^{\tfrac{1}{2}} = 0\\ i,j = m + 1,m + 2,\cdots,n,i \ne j \end{gathered}$$ (20) 由式 (17) 和 (20) 即知多智能体系统式 (1) 实现均方二分组一致。
2) 必要性：
反设
$ {G_1} \cup {G_2} \cup \cdots \cup {G_s} $ 不含有向生成树，则当系统经过几次马尔可夫跳变到不含生成树的网络拓扑时，该拓扑中至少有一个智能体信息无法和其他智能体信息进行交换，从而无法实现多智能体系统式 (1) 中多智能体位置和速度的均方二分组一致，矛盾。2.2 连续时间异质多智能体的均方一致性
这部分主要研究马尔可夫切换下连续异质多智能体系统式(2) 的均方二分组一致控制。基于智能体之间的合作竞争关系，设计控制协议为
$$ \left\{ \begin{aligned} &{{\boldsymbol{u}}_i}(t) = \alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) - {{\boldsymbol{\iota }}_i}(t)) - } \right.\\ &\quad \left.\sum\limits_{j \in N_{Di}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) + {{\boldsymbol{\iota }}_i}(t))} \right],i \in {\rho _1} \\ &{{\boldsymbol{u}}_i}(t) = \alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) - {{\boldsymbol{\iota }}_i}(t)) - }\right. \\ &\quad \left.\sum\limits_{j \in {\boldsymbol{N}}_{Di}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) + {{\boldsymbol{\iota }}_i}(t)} \right] - \beta {{\boldsymbol{\mu }}_i}(t),i \in {\rho _2} \end{aligned} \right. $$ (21) 参数与定义2.1相同。
定理2 若
$ \{ o(t),t \geqslant 0\} $ 是一个齐次遍历马尔可夫链，其状态空间为$S = \{ 1,2,\cdots,s\}$ ,若$ {\beta ^2} - 4\alpha {l_{\max }} > 0 $ ，那么在控制协议 (21) 下，连续异质多智能体系统式 (2) 均方二分组一致当且仅当该系统联合拓扑存在有向生成树。证明 类似定理1的证明，设：
$$ {{\boldsymbol{\bar \mu }}_i}(t) = {{\boldsymbol{\iota }}_i}(t) + \frac{2}{\beta }{{\boldsymbol{\mu }}_i}(t)$$ 根据式 (2) 和 (21)，分如下2种情况讨论。
1）当
$ i \in {\rho _1} $ 时，有$$ \begin{gathered} {{{\boldsymbol{\dot \iota }}}_i}(t) = \alpha \left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) - {{\boldsymbol{\iota }}_i}(t)) - } \sum\limits_{j \in {\boldsymbol{N}}_{Di}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) + {{\boldsymbol{\iota }}_i}(t))} \right] \end{gathered} $$ (22) 2）当
$ i \in {\rho _2} $ 时，有$$ {{\boldsymbol{\dot \iota }}_i}(t) = \frac{\beta }{2}({{\boldsymbol{\bar \mu }}_i}(t) - {{\boldsymbol{\iota }}_i}(t)) $$ (23) $$ \begin{gathered} {{{\boldsymbol{\dot{ \bar {\mu} }}}}_i}(t) = - \frac{\beta }{2}({{{\boldsymbol{\bar \mu }}}_i}(t) - {{\boldsymbol{\iota }}_i}(t)) +\\ \frac{{2\alpha }}{\beta }\left[\sum\limits_{j \in {\boldsymbol{N}}_{Si}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) - {{\boldsymbol{\iota }}_i}(t)) - } \sum\limits_{j \in {\boldsymbol{N}}_{Di}^{o(t)}} {a_{ij}^{o(t)}({{\boldsymbol{\iota }}_j}(t) + {{\boldsymbol{\iota }}_i}(t))} \right] \end{gathered} $$ (24) 根据式 (22)~(24)，得到多智能体系统系统式 (2) 一阶和二阶智能体的矩阵形式：
$$ {{\boldsymbol{\dot \iota }}_f}(t) = - \alpha [ - {\boldsymbol{A}}_{fs}^{o(t)}{{\boldsymbol{\iota }}_s}(t) + ({\boldsymbol{L}}_{ff}^{o(t)} + {\boldsymbol{D}}_{fs}^{o(t)}){{\boldsymbol{\iota }}_f}(t)] $$ (25) $$ {{\boldsymbol{\dot \iota }}_s}(t) = \frac{\beta }{2}({{\boldsymbol{\bar \mu }}_s}(t) - {{\boldsymbol{\iota }}_s}(t)) $$ (26) $$ \begin{gathered} {{{\boldsymbol{\dot {\bar{ \mu} }}}}_s}(t) = - \frac{\beta }{2}({{{\boldsymbol{\bar \mu }}}_s}(t) - {{\boldsymbol{\iota }}_s}(t)) - \\ \frac{{2\alpha }}{\beta }\left[({\boldsymbol{L}}_{ss}^{o(t)} + {\boldsymbol{D}}_{sf}^{o(t)}){{\boldsymbol{\iota }}_s}(t) - {\boldsymbol{A}}_{sf}^{o(t)}{{\boldsymbol{\iota }}_f}(t)\right] \end{gathered} $$ (27) 其中，
$$ {{\boldsymbol{\iota }}_f}(t) = [{{\boldsymbol{\iota }}_1}(t),{{\boldsymbol{\iota }}_2}(t),\cdots,{{\boldsymbol{\iota }}_m}(t)] $$ $$ {{\boldsymbol{\iota }}_s}(t) = [{{\boldsymbol{\iota }}_{m + 1}}(t),{{\boldsymbol{\iota }}_{m + 2}}(t),\cdots,{{\boldsymbol{\iota }}_n}(t)] $$ $$ {{\boldsymbol{\bar \mu }}_s}(t) = [{{\boldsymbol{\bar \mu }}_{m + 1}}(t),{{\boldsymbol{\bar \mu }}_{m + 2}}(t),\cdots,{{\boldsymbol{\bar \mu }}_n}(t)] $$ 再由式(25) 和 (26)，得到多智能体系统式 (2) 的矩阵形式为
$$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\dot {\iota} }}}_f}(t)} \\ {{{{\boldsymbol{\dot{ \iota} }}}_s}(t)} \\ {{{{\boldsymbol{\dot {\bar{ \mu}} }}}_s}(t)} \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} {\alpha \left({\boldsymbol{L}}_{ff}^{o(t)} + {\boldsymbol{D}}_{fs}^{o(t)}\right)}&{ - \alpha {\boldsymbol{A}}_{fs}^{o(t)}}&0 \\ 0&{\dfrac{\beta }{2}{{\boldsymbol{I}}_{n - m}}}&{ - \dfrac{\beta }{2}{{\boldsymbol{I}}_{n - m}}} \\ { - \dfrac{{2\alpha }}{\beta }{\boldsymbol{A}}_{sf}^{o(t)}}&{ - \dfrac{\beta }{2}{{\boldsymbol{I}}_{n - m}} + \dfrac{{2\alpha }}{\beta }\left({\boldsymbol{L}}_{ss}^{o(t)} + {\boldsymbol{D}}_{sf}^{o(t)}\right)}&{\dfrac{\beta }{2}{{\boldsymbol{I}}_{n - m}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\iota }}_f}(t)} \\ {{{\boldsymbol{\iota }}_s}(t)} \\ {{{{\boldsymbol{\bar \mu }}}_s}(t)} \end{array}} \right] \end{gathered} $$ (28) 进一步，将式 (28) 简写成微分方程形式：
$$ {\boldsymbol{\dot R}}(t) = - {{\boldsymbol{F}}_{o(t)}}{\boldsymbol{R}}(t) $$ (29) 式中
${\boldsymbol{R}}(t) = {[{\boldsymbol{\iota }}_f^{\rm T}(t)\quad{\boldsymbol{\iota }}_s^{\rm T}(t)\quad{\boldsymbol{\mu }}_s^{\rm T}(t)]^{\rm T}}$ 。根据引理4，若
$ {\beta ^2} - 4\alpha {l_{\max }} > 0 $ ，则矩阵$ - {{\boldsymbol{F}}_{o(t)}} $ 主对角线元素为负，非主对角线元素为正，且$ - {{\boldsymbol{F}}_{o(t)}} $ 的每行元素总和为零。显然，$ - {{\boldsymbol{F}}_{o(t)}} $ 至少有一个零特征值，其对应的特征向量为$ {{\boldsymbol{1}}_n} $ 。将连续异质多智能体系统式 (29) 离散化，设采样时间为
$ \nabla $ ，则其相应的离散化方程为$$ {\boldsymbol{\varXi }}(\kappa + 1) = {{\mathbf {e}}^{ - {{\boldsymbol{F}}_{o(\kappa )}}\nabla }}{\boldsymbol{\varXi }}(\kappa ) $$ 由引理5可知，当采样周期足够小时，有：
$${{\mathbf {e}}^{ - {{\boldsymbol{F}}_{o(\kappa )}}\nabla }}{{\boldsymbol{1}}_n} = {{\boldsymbol{1}}_n}，且{{\mathbf {e}}^{ - {{\boldsymbol{F}}_{o(\kappa )}}\nabla }} \geqslant 0$$ 式中：
${{\mathbf {e}}^{ - {{\boldsymbol{F}}_{o(\kappa )}}\nabla }}$ 为一个随机矩阵，余下证明类似定理1。3. 仿真结果
本节将用3个例子来验证所得结论的有效性。假定离散和连续情况下马尔可夫切换过程对应的转移概率矩阵均为
$$ {\boldsymbol{\varLambda}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{2}{3}}&{\dfrac{1}{6}}&{\dfrac{1}{6}} \\ {\dfrac{1}{4}}&{\dfrac{1}{2}}&{\dfrac{1}{4}} \\ {\dfrac{1}{4}}&{\dfrac{1}{4}}&{\dfrac{1}{2}} \end{array}} \right] $$ 例1先讨论离散情形，验证定理1的有效性。例2分析连续情况，验证定理2的正确性。例3则验证不满足定理1条件时，异质多智能体系统式 (1) 的分组一致将不能实现。
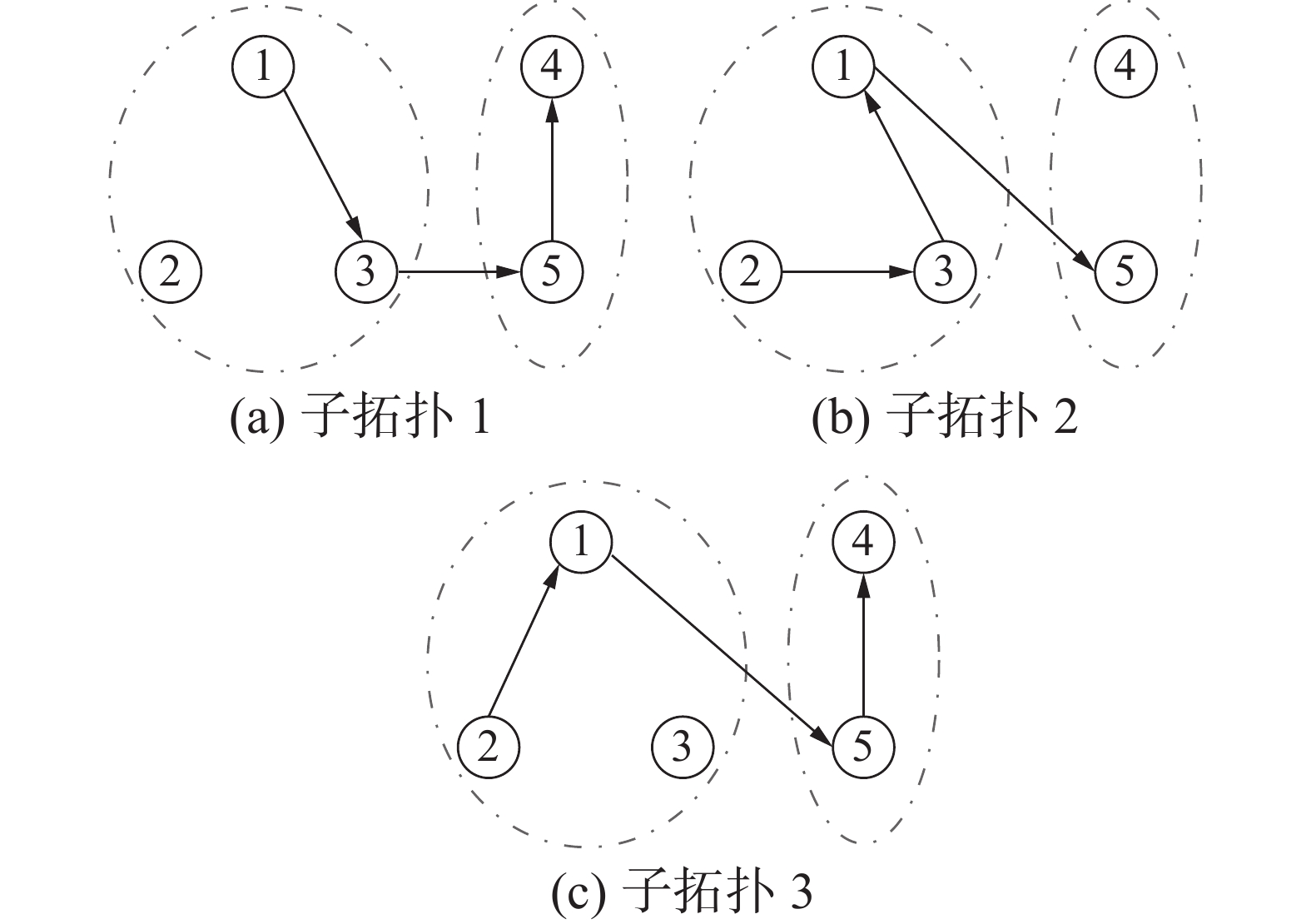
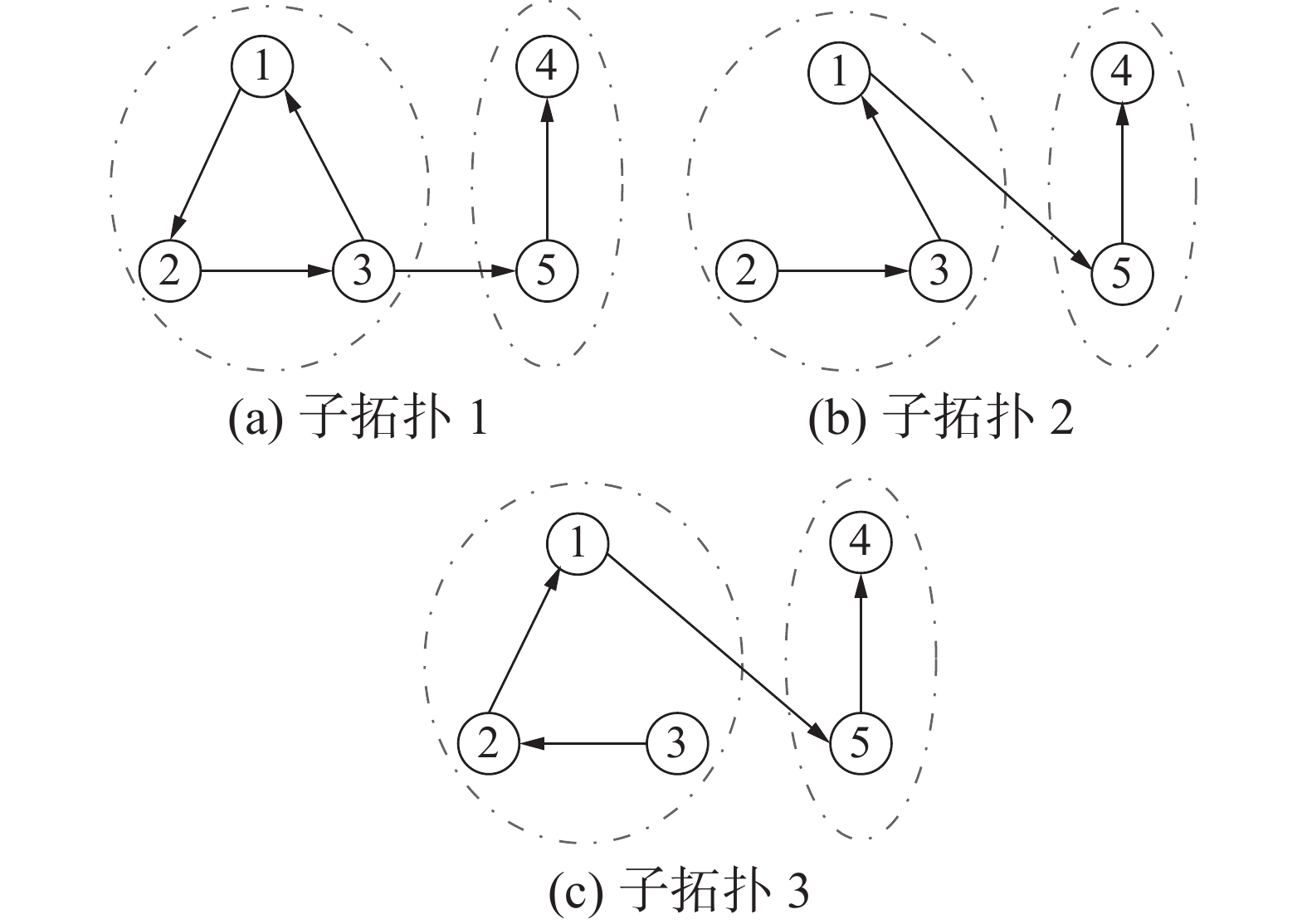
图1 表示多智能体系统式 (1) 和式 (2) 的网络拓扑，图1中包含3个不同的子拓扑，每个子拓扑均包含有一棵生成树。在每个子拓扑中，智能体1~3是二阶智能体，构成第1组；智能体4和5是一阶智能体，构成第2组。同组智能体之间为合作关系，不同组智能体之间为竞争关系。
图 1 含生成树的多智能体系统（1）和（2）切换拓扑Fig. 1 Switching toplogies of the multiagent systems (1) and (2) with spanning tree
下载:
全尺寸图片
例1 在离散异质多智能体系统式(1) 中，采样时间设为
$h = 0.2\;{\rm{s}}$ ，耦合系数设为$\alpha = 1$ 且$\beta = 2.1$ ，易知这些参数满足定理1的要求。此时，智能体初始位置状态向量设为$$ {{\boldsymbol{\iota }}^{\rm T}}[0] = \left[ {3\quad5\quad - 4\quad3\quad6} \right] $$ 初始速度向量设为
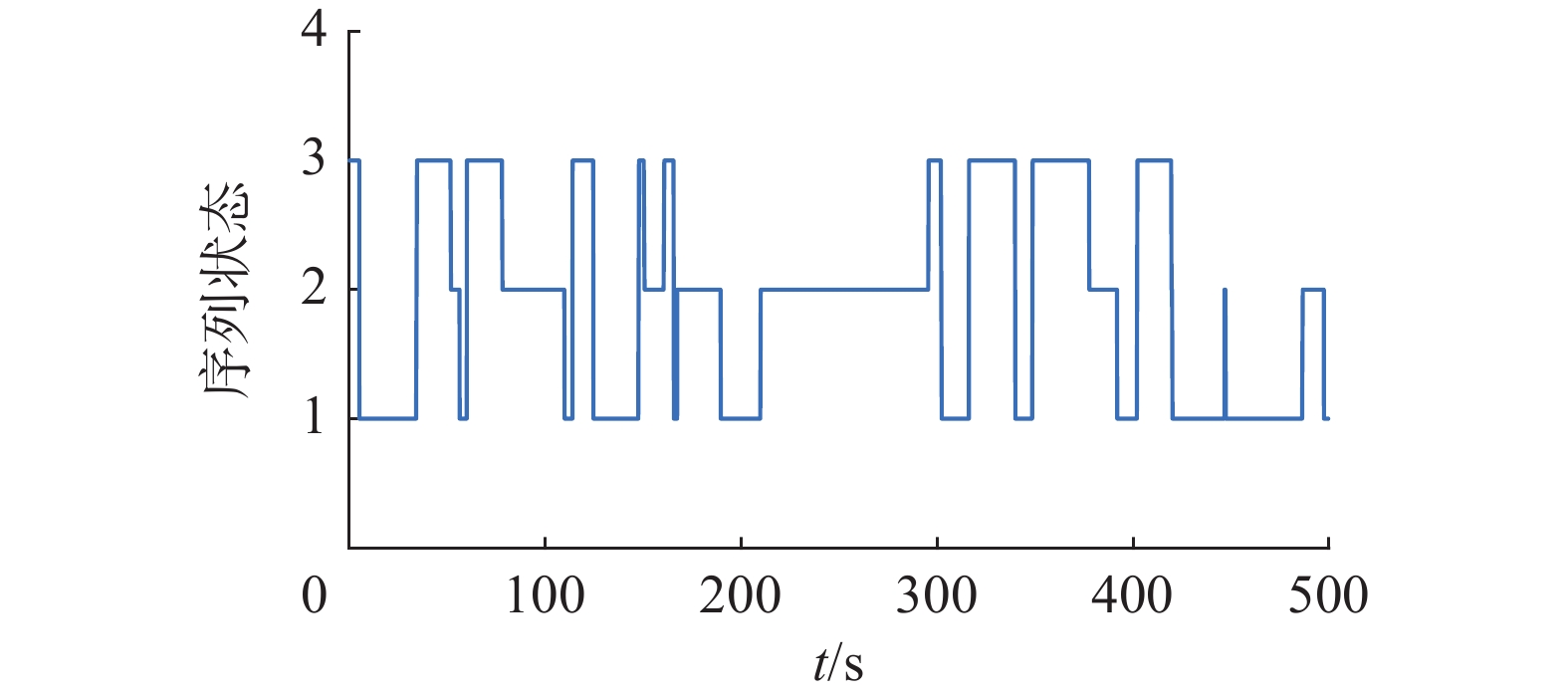
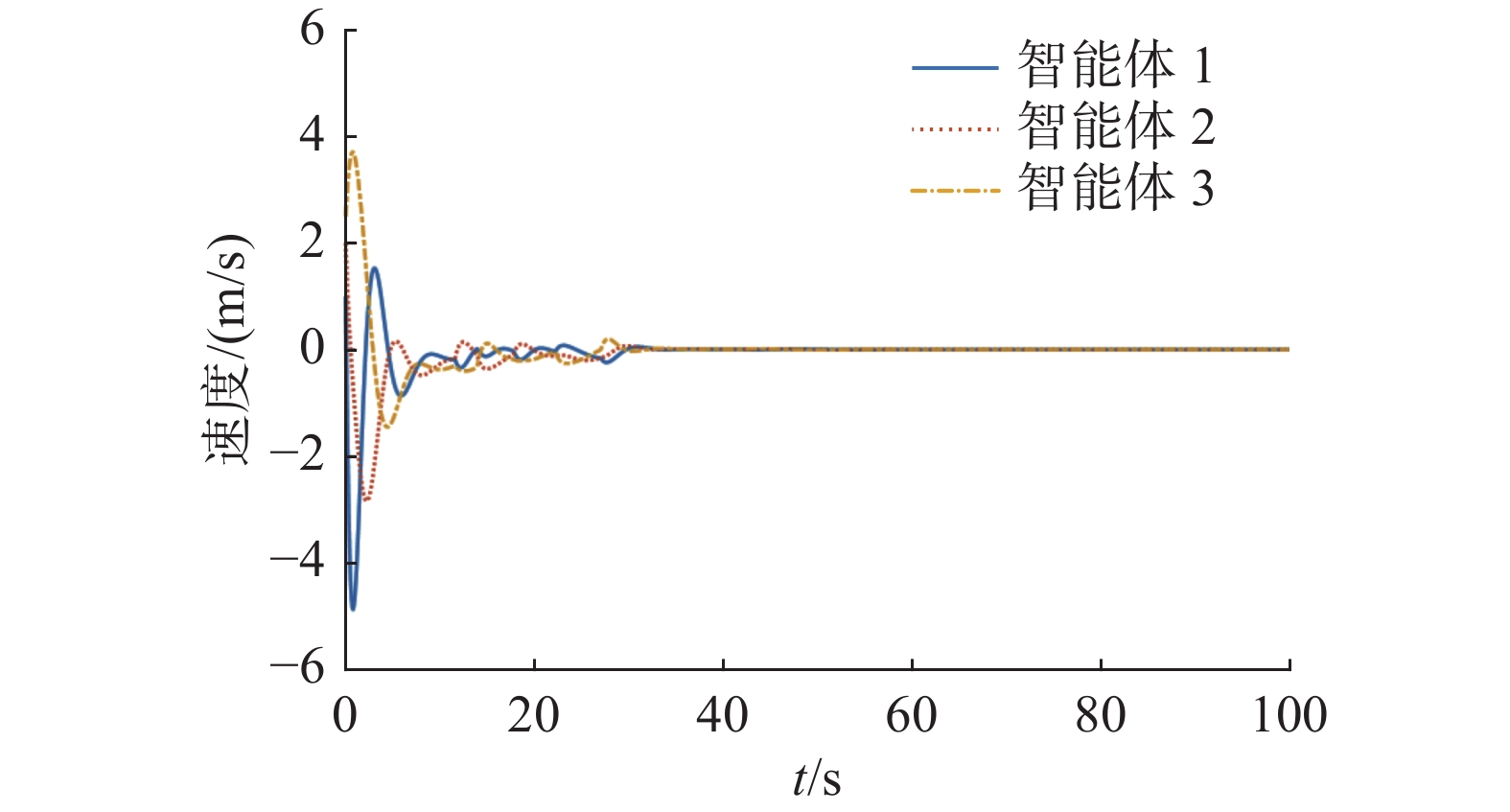
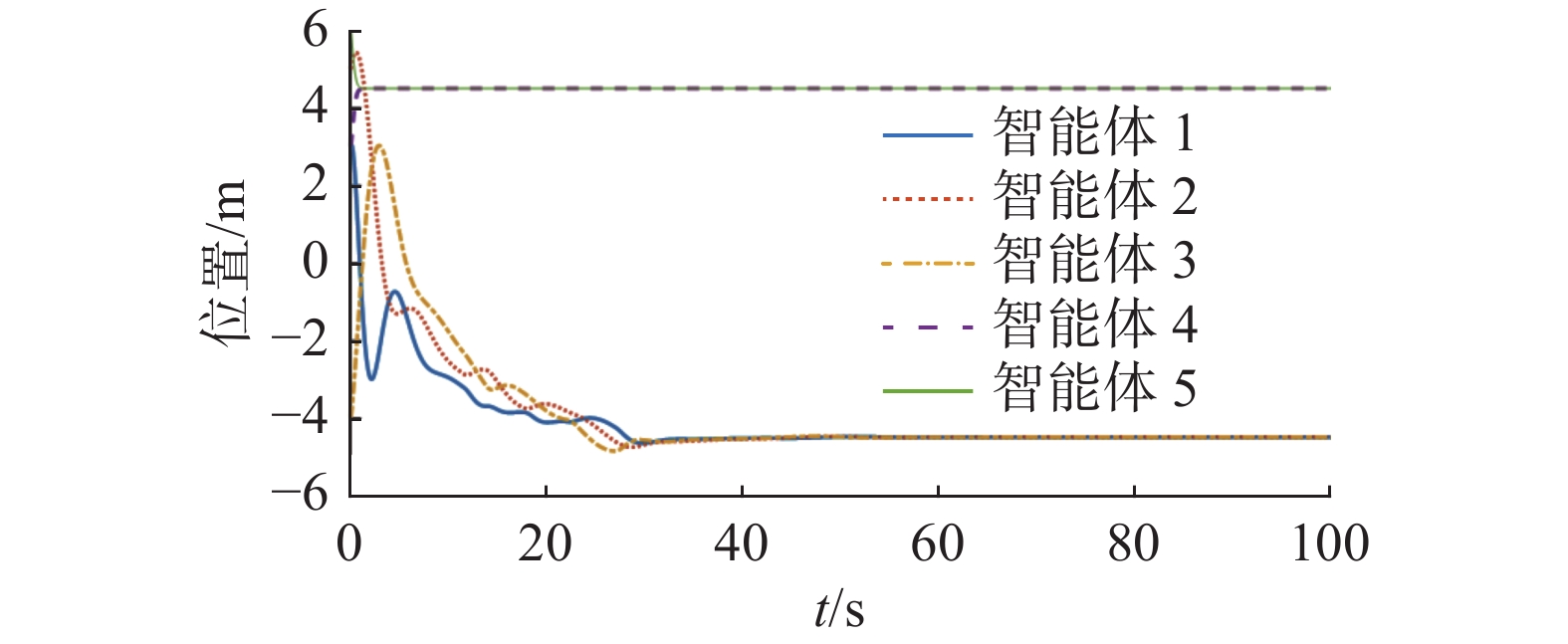
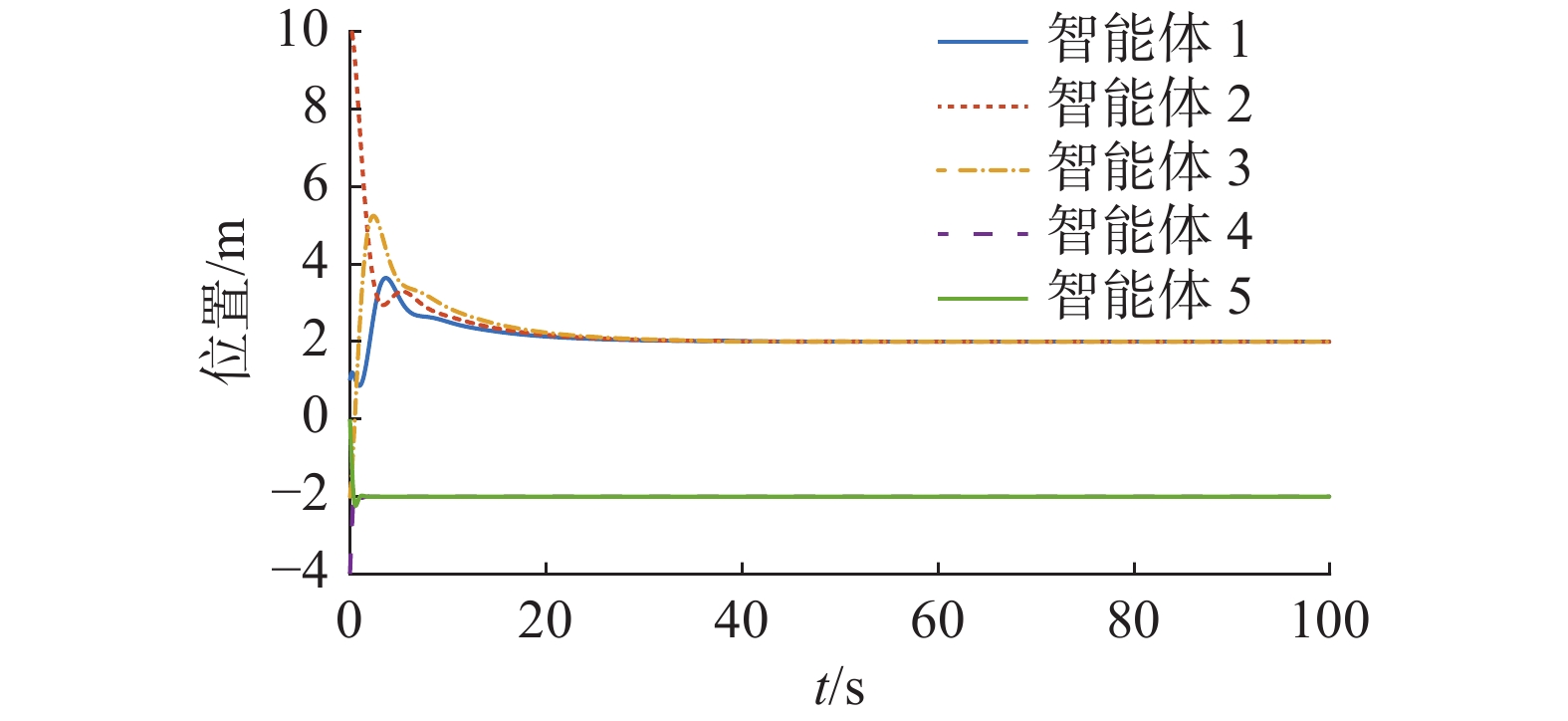
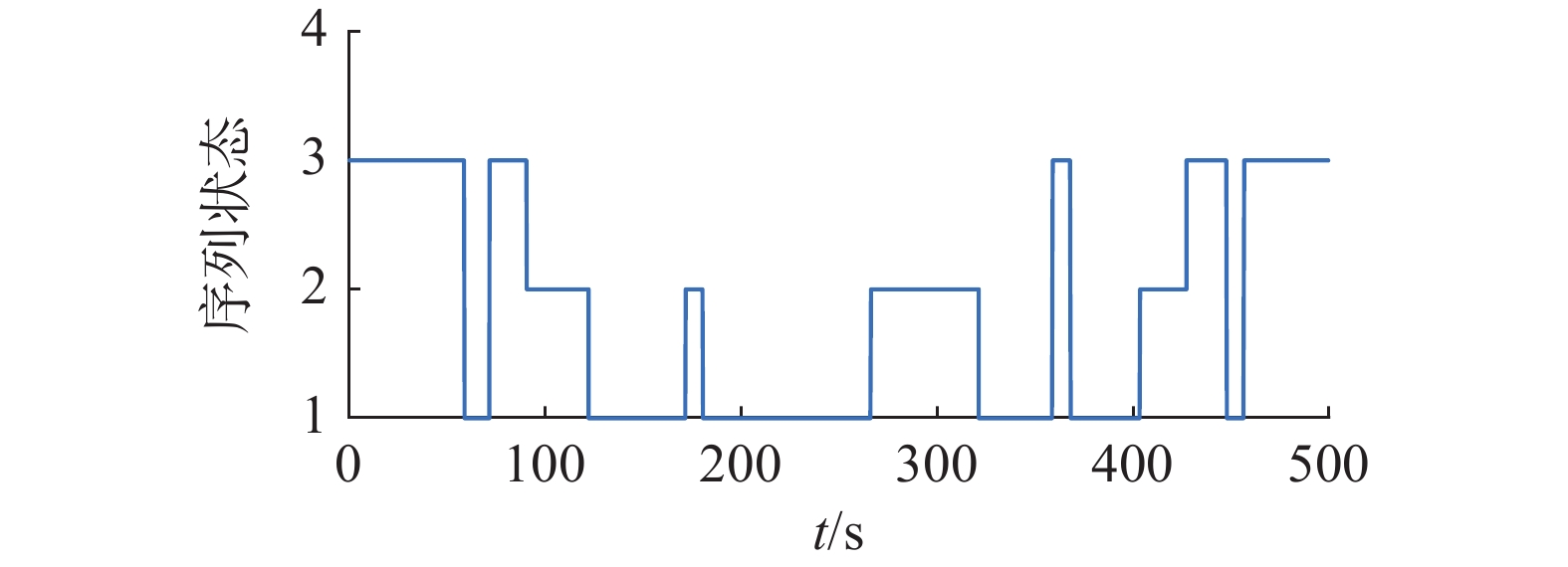
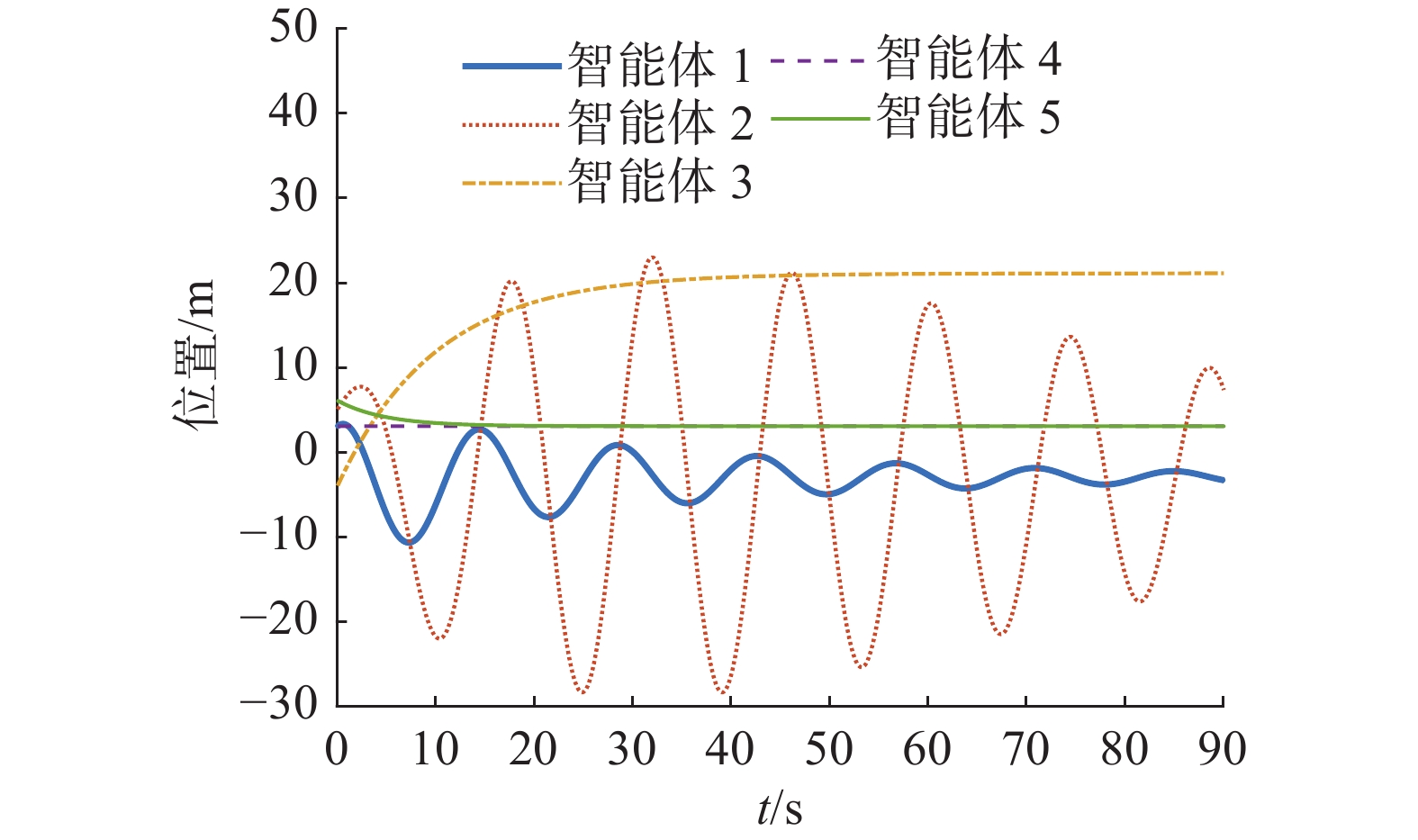
$$ {{\boldsymbol{\mu }}^{\rm T}}[0] = \left[ {1\quad2\quad2.5} \right] $$ 此时，在图2马尔可夫切换信号的作用下，离散异质多智能体系统式 (1) 的位置状态和速度如图3、4。由图3、4可知，当系统拓扑结构和相关系数满足定理1的条件时，离散异质多智能体系统式(1)在控制协议式(3)下能实现均方二分组一致。
图 2 离散马尔可夫切换序列Fig. 2 Discrete sequence with Markov switching signal下载:
全尺寸图片
图 3 离散多智能体系统 (1) 中智能体速度变化曲线Fig. 3 Velocity trajectories of agents in discrete system (1)下载:
全尺寸图片
图 4 离散多智能体系统 (1) 中智能体位置变化曲线Fig. 4 Position trajectories of agents in discrete system (1)下载:
全尺寸图片
例2 在连续异质多智能体系统式 (2) 中，耦合系数设为
$\alpha = 1.5$ 且$\beta = 3$ ，易知这些参数满足定理2的要求。智能体初始位置状态向量设为$$ {{\boldsymbol{\iota }}^{\rm T}}[0] = \left[ {1\quad10\quad - 2\quad - 4\quad0} \right] $$ 初始速度向量设为
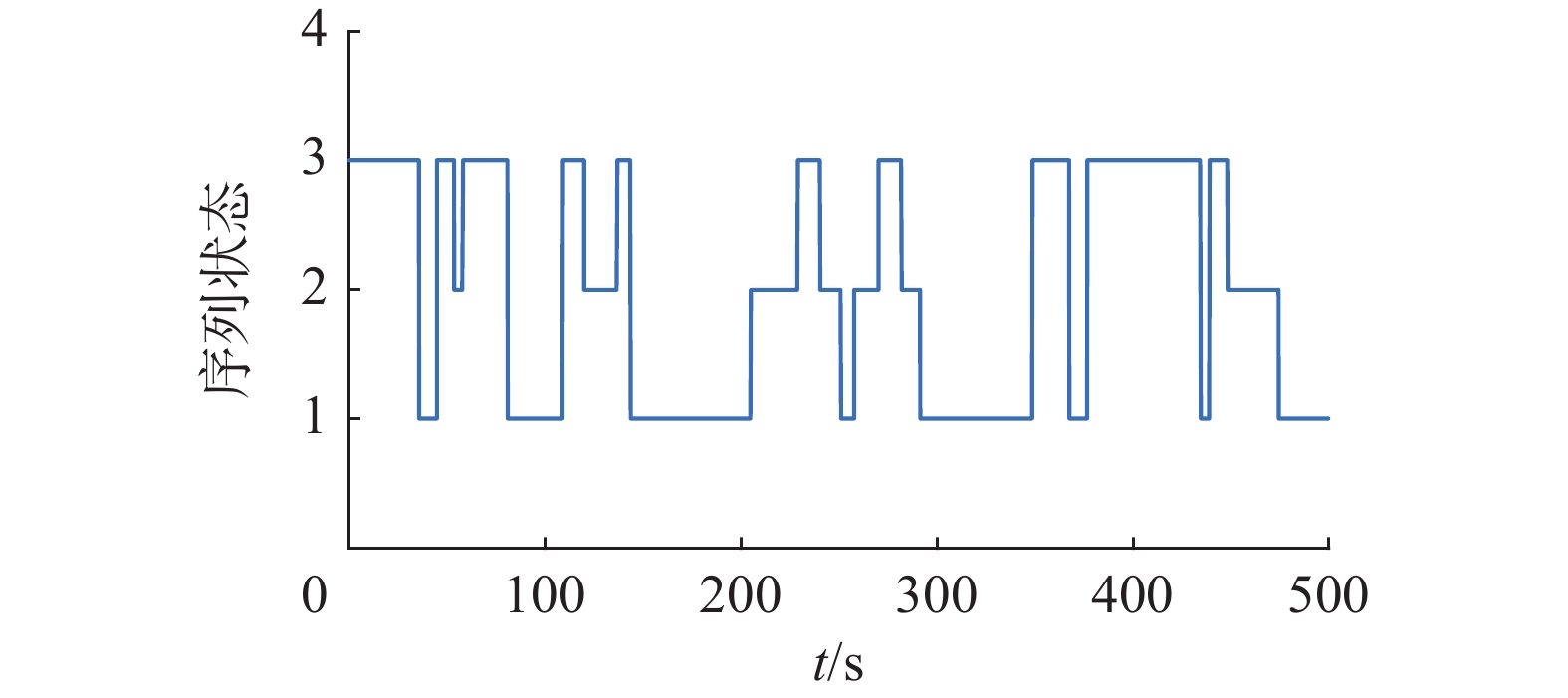
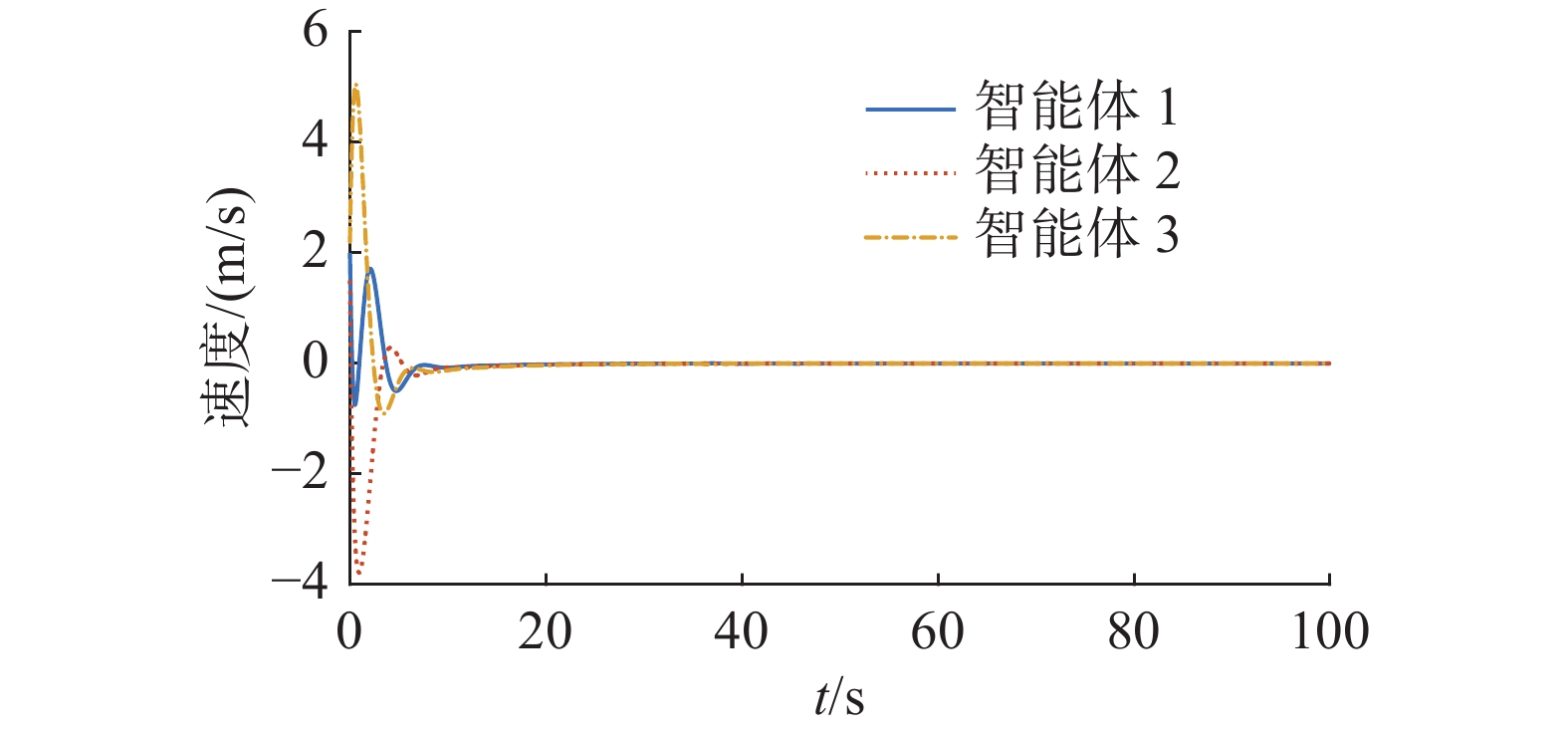
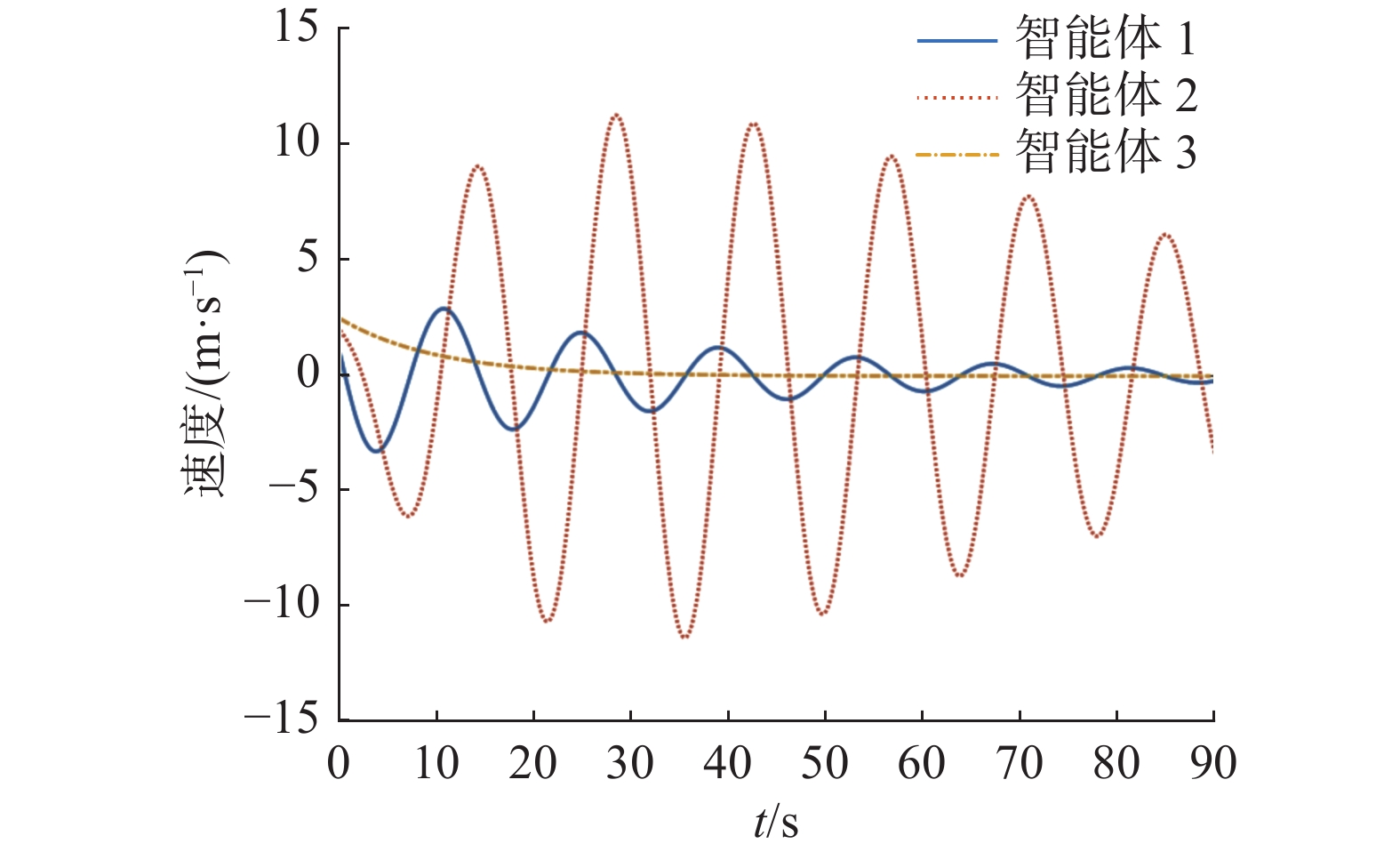
$$ {{\boldsymbol{\mu }}^{\rm T}}[0] = \left[{2\quad1.5\quad2.2} \right] $$ 连续多智能体系统(2)的马尔可夫切换序列如图5所示，连续异质多智能体系统式(2) 的位置状态和速度如图6 和7。由图6 、7可知，当系统拓扑结构和相关系数满足定理2的条件时，连续异质多智能体系统式(2)在控制协议式(21)下能实现均方二分组一致。
图 5 连续多智能体系统(2)的马尔可夫切换序列Fig. 5 Markov switching sequence of continuous multiagent system (2)下载:
全尺寸图片
图 6 连续多智能体系统式 (2) 中智能体速度变化曲线Fig. 6 Velocity trajectories of agents in continuous system (2)下载:
全尺寸图片
图 7 连续多智能体系统式 (2) 中智能体位置变化曲线Fig. 7 Position trajectories of agents in continuous system (2)下载:
全尺寸图片
例3 继续分析离散异质多智能体系统式(1)，在其他参数相同情况下，假设系统有3个如图8所示子拓扑结构，易知每个子拓扑中不包含生成树。
图 8 子拓扑不含生成树的网络拓扑Fig. 8 Switching subtoplogies with no spanning tree下载:
全尺寸图片
图9~11 分别表示切换信号、速度和位置状态随时间变化情况。
图 9 拓扑不含生成树的离散多智能体系统(1)的马尔可夫切换序列Fig. 9 Markov switching sequence of discrete multiagent system (1) with the topology having no spanning tree下载:
全尺寸图片
图 10 离散多智能体系统 式(1) 中智能体速度变化曲线Fig. 10 The velocity trajectories of agents in discrete multiagent system (1) with the topology having no spanning tree下载:
全尺寸图片
图 11 拓扑不含生成树的离散多智能体系统式(1) 中智能体位置变化曲线Fig. 11 The Position trajectories of agents in discrete multiagent system (1) with the topology having no spanning tree下载:
全尺寸图片
由图10~11可以看出，当多智能体系统拓扑结构不包含生成树的时候，多智能体系统式 (1) 不能实现均方二分组一致。
4. 结束语
基于智能体之间合作竞争关系，针对马尔可夫切换下的离散和连续时间异质多智能体系统，提出2种新的控制协议。利用图论、矩阵理论和随机不可约非周期矩阵的相关性质，得到相关系统在马尔可夫切换下实现均方二分组一致的充要条件。数值仿真实验证明了所得结果的有效性。接下来，我们将继续研究概率转移矩阵不完全确定和时滞情况下相应系统的分组一致控制。
-
图 1 含生成树的多智能体系统（1）和（2）切换拓扑
Fig. 1 Switching toplogies of the multiagent systems (1) and (2) with spanning tree
下载:
全尺寸图片
图 2 离散马尔可夫切换序列
Fig. 2 Discrete sequence with Markov switching signal
下载:
全尺寸图片
图 3 离散多智能体系统 (1) 中智能体速度变化曲线
Fig. 3 Velocity trajectories of agents in discrete system (1)
下载:
全尺寸图片
图 4 离散多智能体系统 (1) 中智能体位置变化曲线
Fig. 4 Position trajectories of agents in discrete system (1)
下载:
全尺寸图片
图 5 连续多智能体系统(2)的马尔可夫切换序列
Fig. 5 Markov switching sequence of continuous multiagent system (2)
下载:
全尺寸图片
图 6 连续多智能体系统式 (2) 中智能体速度变化曲线
Fig. 6 Velocity trajectories of agents in continuous system (2)
下载:
全尺寸图片
图 7 连续多智能体系统式 (2) 中智能体位置变化曲线
Fig. 7 Position trajectories of agents in continuous system (2)
下载:
全尺寸图片
图 8 子拓扑不含生成树的网络拓扑
Fig. 8 Switching subtoplogies with no spanning tree
下载:
全尺寸图片
图 9 拓扑不含生成树的离散多智能体系统(1)的马尔可夫切换序列
Fig. 9 Markov switching sequence of discrete multiagent system (1) with the topology having no spanning tree
下载:
全尺寸图片
图 10 离散多智能体系统 式(1) 中智能体速度变化曲线
Fig. 10 The velocity trajectories of agents in discrete multiagent system (1) with the topology having no spanning tree
下载:
全尺寸图片
图 11 拓扑不含生成树的离散多智能体系统式(1) 中智能体位置变化曲线
Fig. 11 The Position trajectories of agents in discrete multiagent system (1) with the topology having no spanning tree
下载:
全尺寸图片
-
[1] WEI Ren. Multi-vehicle consensus with a time-varying reference state[J]. Systems & control letters, 2007, 56(7/8): 474–483. [2] CORTES J. Coverage optimization and spatial load balancing by robotic sensor networks[J]. IEEE transactions on automatic control, 2010, 55(3): 749–754. doi: 10.1109/TAC.2010.2040495 [3] BREZHNEV R V, MAL'TSEV E A. An ontological spatial monitoring system for agricultural land monitoring[J]. Pattern recognition and image analysis, 2015, 25(2): 201–208. doi: 10.1134/S1054661815020054 [4] QU Yi, XU Haopeng, SONG Cheng, et al. Coverage control for mobile sensor networks with time-varying communication delays on a closed curve[J]. Journal of the Franklin Institute, 2020, 357(17): 12109–12124. doi: 10.1016/j.jfranklin.2020.08.005 [5] XIE Dongmei. Necessary and sufficient condition for the group consensus of multi-agent systems[J]. Applied mathematics and computation, 2014, 243: 870–878. doi: 10.1016/j.amc.2014.06.069 [6] ZHAO Huanyu. Couple-group consensus for second-order multi-agent systems with fixed and stochastic switching topologies[J]. Applied mathematics and computation, 2014, 232: 595–605. doi: 10.1016/j.amc.2014.01.018 [7] WANG Qiang, WANG Yuzhen. Cluster synchronization of a class of multi-agent systems with a bipartite graph topology[J]. Science China information sciences, 2014, 57(1): 1–11. [8] HU Hongxiang, YU Wenwu, WEN Guanghui, et al. Reverse group consensus of multi-agent systems in the cooperation-competition network[J]. IEEE transactions on circuits and systems I:regular papers, 2016, 63(11): 2036–2047. doi: 10.1109/TCSI.2016.2591264 [9] 周瑞敏, 司文杰, 耿则勋. 二阶多智能体编队及碰撞避免控制[J]. 控制工程, 2021, 28(11): 2223–2229. doi: 10.14107/j.cnki.kzgc.20210361 ZHOU Ruimin, SI Wenjie, GENG Zexun. Formation control of second-order multi-agent systems with collision avoidance[J]. Control engineering of China, 2021, 28(11): 2223–2229. doi: 10.14107/j.cnki.kzgc.20210361 [10] MA Qian, XU Shengyuan. Consensusability of first-order multiagent systems under distributed PID controller with time delay[J]. IEEE transactions on neural networks and learning systems, 2022, 33(12): 7908–7912. doi: 10.1109/TNNLS.2021.3084366 [11] LENG Hui, WU Zhaoyan, ZHAO Yi. Group consensus in second-order multi-agent systems with nonlinear dynamics[J]. International journal of modern physics C, 2021, 32(5): 2150071. doi: 10.1142/S0129183121500716 [12] JIANG Yiliu. Couple-group consensus for discrete-time heterogeneous multiagent systems with cooperative-competitive interactions and time delays[J]. Neurocomputing, 2018, 319: 92–101. doi: 10.1016/j.neucom.2018.08.048 [13] JI Lianghao, YU Xinghuo, LI Chaojie. Group consensus for heterogeneous multiagent systems in the competition networks with input time delays[J]. IEEE transactions on systems, man, and cybernetics:systems, 2020, 50(11): 4655–4663. doi: 10.1109/TSMC.2018.2858556 [14] PU Xingcheng, ZHAO Longlong, XIONG Chaowen. Weighted group consensus for discrete-time heterogeneous multi-agent systems in the cooperative-competitive network with time delays[J]. IEEE access, 2019, 7: 123679–123688. doi: 10.1109/ACCESS.2019.2934988 [15] 赵玮, 任凤丽. 基于牵制控制的多智能体系统的有限时间与固定时间一致性[J]. 应用数学和力学, 2021, 42(3): 299–307. ZHAO Wei, REN Fengli. Finite time and fixed time consistency of multi-agent system based on containment control[J]. Applied mathematics and mechanics, 2021, 42(3): 299–307. [16] 冀秀坤, 谢广明, 文家燕, 等. 含时延约束的多智能体系统二分一致性[J]. 智能系统学报, 2020, 15(4): 780–786. doi: 10.11992/tis.201908027 JI Xiukun, XIE Guangming, WEN Jiayan, et al. Binary consistency of multi-agent systems with delay constraints[J]. CAAI transactions on intelligent systems, 2020, 15(4): 780–786. doi: 10.11992/tis.201908027 [17] ZONG Xiaofeng, LI Tao, ZHANG Jifeng. Consensus control of second-order delayed multiagent systems with intrinsic dynamics and measurement noises[J]. International journal of robust and nonlinear control, 2018, 28(16): 5050–5070. doi: 10.1002/rnc.4301 [18] SONG Ge, TAO Gang. Adaptive leader-following state consensus of multiagent systems with switching topology[J]. International journal of adaptive control and signal processing, 2018, 32(10): 1508–1528. doi: 10.1002/acs.2926 [19] PU Xingcheng. Couple-group consensus for heterogeneous MASs under switched topologies in cooperative-competitive systems: a hybrid pinning and delta operator skills[J]. Neurocomputing, 2021, 441: 335–349. doi: 10.1016/j.neucom.2020.11.013 [20] MA Dan. Switching scheme based on ADT for packet dropout compensating[C]//Proceedings of 2013 IEEE International Conference on Service Operations and Logistics, and Informatics. Piscataway: IEEE, 2013: 576−580. [21] CHENG Peng. Asynchronous fault detection filtering for piecewise homogenous Markov jump linear systems via a dual hidden Markov model[J]. Mechanical systems and signal processing, 2021, 151: 107353. doi: 10.1016/j.ymssp.2020.107353 [22] EICKELER S, MÜLLER S, RIGOLL G. Recognition of JPEG compressed face images based on statistical methods[J]. Image and vision computing, 2000, 18(4): 279–287. doi: 10.1016/S0262-8856(99)00055-4 [23] MENG Min, LIU Lu, FENG Gang. Output consensus for heterogeneous multiagent systems with Markovian switching network topologies[J]. International journal of robust and nonlinear control, 2018, 28(3): 1049–1061. doi: 10.1002/rnc.3918 [24] LI Mengling, DENG Feiqi. Necessary and sufficient conditions for consensus of continuous-time multiagent systems with Markovian switching topologies and communication noises[J]. IEEE transactions on cybernetics, 2020, 50(7): 3264–3270. doi: 10.1109/TCYB.2019.2919740 [25] LIU Zili. Cooperative output regulation problem of discrete-time linear multi-agent systems with Markov switching topologies[J]. Journal of the Franklin Institute, 2020, 357(8): 4795–4816. doi: 10.1016/j.jfranklin.2020.02.020 [26] XIE Dongmei, CHENG Yongli. Bounded consensus tracking for sampled-data second-order multi-agent systems with fixed and Markovian switching topology[J]. International journal of robust and nonlinear control, 2015, 25(2): 252–268. doi: 10.1002/rnc.3085 [27] WOLFOWITZ J. Products of indecomposable, aperiodic, stochastic matrices[J]. Proceedings of the American mathematical society, 1963, 14(5): 733–737. doi: 10.1090/S0002-9939-1963-0154756-3 [28] REN Wei, BEARD R W. Distributed consensus in multi-vehicle cooperative control: theory and applications[M]. London: Springer, 2008. [29] REN Wei, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE transactions on automatic control, 2005, 50(5): 655–661. doi: 10.1109/TAC.2005.846556
