Vehicle trajectory prediction method based on modeling of multi-agent interaction behavior
-
摘要: 预测周围智能体的运动轨迹是实现自动驾驶行为决策规划的关键。面对复杂的车辆交互影响和多模态驾驶意图所带来的难题，本文提出一种基于车辆多目标交互行为建模的轨迹预测方法。该方法采用条件变分自编码器生成轨迹终点的多模态结果，结合自注意力机制和多头注意力机制来捕捉车辆之间的群体交互影响，最终使用逆强化学习输出多模态轨迹的最优决策，实现了同步预测多个目标轨迹。在高速公路数据集NGSIM上的实验结果证明该模型的有效性，并且预测效果整体优于现有方法。Abstract: Predicting trajectories of surrounding agents is critical to realize the decision-making planning of autonomous driving behaviors. Facing the difficulties brought by complex vehicle interaction and multimodal driving intention, this paper proposes a trajectory prediction method based on vehicle multi-agent interaction behavior modeling. The method uses conditional variational autoencoder to generate multi-modal results of the trajectory endpoints. By combination with the self-attention mechanism and multi-head attention mechanism, the influence of group interaction between vehicles is captured. Finally, the inverse reinforcement learning is used to output the optimal decision of multi-modal trajectory, realizing synchronous prediction of multi-agent trajectory. An experiment has been carried out on the NGSIM, which is a real-world trajectory prediction dataset on the highway traffic scene. The results prove effectiveness of the model, and the prediction effect is better than existing methods as a whole.
-
在复杂的道路交通场景中，自动驾驶汽车需要做出安全高效的决策规划，如更换车道、超车或者减速。现有的路径规划算法[1]大多依赖于对周围车辆未来轨迹的估计预测。因此，自动驾驶汽车需要对周围车辆的行为做出合理的推测，从而避免碰撞事故。
车辆轨迹预测是指在给定一段历史时期的车辆运动轨迹和场景信息的情况下，对一段未来时期的车辆运动位置进行推断。该问题的难点主要包括：1）车辆之间的动态交互会对车辆行驶轨迹产生影响，需要对其交互模式进行建模；2）目前车辆行驶主要由驾驶员操控，受诸多因素影响，如驾驶风格、状态、意图、道路条件等，同一条历史轨迹可能存在多条合理的未来轨迹。因此车辆轨迹预测是一个存在空间、时间以及车辆交互等多种依赖关系的多模态问题。为了解决上述问题，本文提出了一种结合注意力机制和生成模型的多模态轨迹预测方法，并在高速公路数据集NGSIM上进行了实验对比。本文的主要贡献主要分为以下3个部分：
1）采用结合自注意力机制的条件变分自编码器（conditional variational auto encoder，CVAE）作为模型的主体结构。使用CVAE仅学习目标终点的潜在分布，再联系历史轨迹以及未来终点轨迹的上下文信息推理出剩余轨迹序列的分布，解决了误差累积导致的终点位置偏差大的问题。
2）关注多目标间的双向交互过程，利用自注意力机制与多头注意力机制建模不同车辆之间的交互影响，结合个体轨迹特征与全局轨迹特征，实现道路场景下车辆之间的交互行为建模。
3）相较于一般的多模态预测评价方法，利用逆强化学习方法，通过回归奖励函数的方式获取多模态决策校正，从而获得预测结果。
1. 相关工作
相关工作涉及以下3个方向，包括交互建模方法、注意力机制方法以及多模态轨迹预测方法。
1.1 交互建模方法
关于预测运动轨迹行为，传统方法引入社会力模型[2]建模研究对象交互过程，但大量的参数设置和规则设定使该模型无法建模复杂场景下的运动轨迹。高斯混合模型[3-4]用于计算不同运动模式的概率分布，但模型构造复杂使其无法应用于大型数据集。卡尔曼滤波方法[5-6]利用前一时刻的估计值和当前时刻的观测值更新状态估计，实现对下一时刻的轨迹位置预测，但该方法受数据集噪声影响明显，不适用于长时间序列预测。近年来，受益于基于深度学习的序列处理结构，如seq2seq[7]，以及表征学习方法的发展，基于深度学习的轨迹预测模型最初应用于行人轨迹预测[8]，基于递归神经网络(recurrent neural network， RNN)、生成对抗网络（generative adversarial networks，GAN）的方法被接连提出，其中作为RNN变体的长短期记忆模型(long short-term memory，LSTM)善于保存和处理长期信息依赖，故常用于建模时序数据[9-10]。
由于独立运行的LSTM编码器无法模拟个体相关性，因此为了泛化局部个体交互过程，多种社交池化机制应用于轨迹预测方法[11]。Alahi等[12]提出了Social LSTM模型，引入社交池化层建模行人交互，允许特定网格空间内相关序列共享特征。Deo等[13]提出了CS-LSTM模型用于车辆轨迹预测，用卷积的方式改进社交池化层，可处理网格空间内可变数目的输入车辆。Messaoud等[14]对卷积社交池化层进行扩展，在空间网格的基础上引入非局部多头注意力机制来捕捉序列长距离依赖性，进一步提升精度。然而，社交池化层的核心是用统一共享的方式处理网格空间内周车行为对目标车辆的单向交互影响，但实际的群体交互会随着个体轨迹时空特征的不同而发生变化，模型需要为多目标的双向交互提供不同的关注度。因此，为建模高度动态的群体互动影响，注意力机制成为近期轨迹预测模型研究的一种建模方法。
1.2 注意力机制方法
注意力机制可以建模个体之间有选择性的交互作用，因此最初注意力机制被应用于轨迹的空间特征，意图捕捉动态变化的道路场景中不同个体之间距离变化带来的影响[15]。注意力机制常辅助LSTM模型[16-17]、GAN网络[18-19]以及图网络[20]，学习符合社会规范的行为影响，提升模型的精确度和可解释性。
得益于自然语言处理领域中Transformer模型[21]的提出，自注意力机制和多头注意力机制可以应用于时间域特征，捕捉当前时刻与历史时刻数据之间的非线性相关性。Jean等[22]使用多头注意力机制结合多智能体的空间位置来建模交互。Giuliari等[23]直接采用完整的Transformer模型结构处理行人轨迹的时间序列，在没有考虑交互过程的情况下得到了较好的预测结果。但Transformer模型的解码结构导致其不断迭代循环并逐帧输出预测结果，无法一次性得到全部位置点的预测信息，存在时效性不足以及误差累积的缺点。因此本文模型仅在编码结构中使用自注意力机制和多头注意力机制建模车辆互动信息，获取多车之间的双向交互影响，从而更新个体车辆轨迹特征以及群体交互场景的全局信息，实现道路场景下多车辆对多车辆的轨迹预测。并通过在解码器应用CVAE的方法，以目标终点为预测条件输出多模态结果，大幅度降低了目标终点的误差，从而在输出剩余轨迹序列的过程中结合历史轨迹与目标终点的上下文信息，优化了预测轨迹的实验结果。
1.3 多模态轨迹预测方法
由于轨迹预测受个体的行进目标和环境因素的影响，所以同一条历史轨迹都可能存在多条合理的未来轨迹。即多模态轨迹预测模型认为如Social LSTM等输出确定性轨迹的单模态模型，无法捕捉运动过程的动态随机性，需要利用生成模型来学习历史轨迹到未来轨迹的一对多映射，进而从未来轨迹的分布中采样得到输出结果。生成模型主要包括条件变分自编码器CVAE[24]和生成式对抗网络GAN[25]等方法。Gupta等[26]提出的Social GAN处理行人轨迹的多模态问题，采用平均池化的方式处理交互过程。Sadeghian等[27]提出的Sophie模型也基于GAN的框架，添加场景上下文信息辅助预测。Lee等[28]提出的DESIRE模型采用CVAE为基础结构，结合场景语义信息生成多个未来轨迹。上述模型在实验过程中会存在如下问题，即误差会随着预测时间的增加而不断累积，对此Mangalam等[29]提出的PECNET模型采用以目标为条件的预测方法，该方法先用CVAE确定个体的意图目标端点，再对剩余轨迹进行反向规划，意图模拟人的决策过程，大大降低端点的预测误差，这也启发了本文模型采用以预测目标端点为条件的CVAE模型作为主体架构。
除此之外，处理多模态轨迹的模型在实验评价过程中仍存在不足。由于多模态轨迹预测表征未来轨迹的多种可能性，而数据集的未来轨迹真值只是多模态分布下的一种可能性，如果多模态结果的每一条轨迹都贴近真值，那么这个结果就会变为单模态，所以多模态模型尚未有一个两全的评价方法。多模态轨迹预测模型大多使用多模态结果中与真值误差最小的轨迹，作为模型输出的最优策略来计算结果的评价指标，这与无法提供未来轨迹真值的实际应用场景存在出入。由于逆强化学习（inverse reinforcement learning，IRL）可以依据真值示例学习得到最接近最佳策略结果的奖励函数作为评价手段，因此本文添加基于逆强化学习的决策校正模块，在不引入轨迹真值的情况下，通过学习奖励函数的方式获取多模态结果的最佳策略。
2. 模型结构
本文提出一种基于车辆多目标交互建模的轨迹预测模型，结合自注意力机制与CVAE方法（vehicle trajectory prediction model based on self-attention mechanism and CVAE，SAC）处理道路交通场景下的车辆轨迹预测问题。
假设存在
${{N}}$ 个车辆进入交通场景，给定过去${t_{\rm{p}}}$ 时间的历史轨迹${{X}} = {{X}}_{k = 1: N}^{t = 1 : {t_{\rm{p}}}} = \{ ({x_k},{y_k})\} _{k = 1: N}^{t = 1 : {t_{\rm{p}}}}$ ，需要预测接下来$\delta $ 时间车辆的未来轨迹位置为${{Y}} = {{Y}}_{k = 1{\kern 1pt} :{\kern 1pt} N}^{t = {t_{\rm{p}}} + 1{\kern 1pt} :{\kern 1pt} {t_{\rm{p}}} + \delta } = \{ ({x_k},{y_k})\} _{k = 1{\kern 1pt} :{\kern 1pt} N}^{t = {t_{\rm{p}}} + 1{\kern 1pt} :{\kern 1pt} {t_{\rm{p}}} + \delta }$ ，其中轨迹真值用${{Y}}$ 表示，预测结果用${{\hat Y}}$ 表示。由于本文使用的生成模型以目标端点为条件，故设定${{Y}}$ 的最后一个轨迹端点为${{G}} = {{Y}}_{k = 1{\kern 1pt} :{\kern 1pt} N}^{t = {t_{\rm{p}}} + \delta }$ ，用${{R}} = {{Y}}_{k = 1{\kern 1pt} :{\kern 1pt} N}^{t = {t_{\rm{p}}} + 1{\kern 1pt} :{\kern 1pt} {t_{\rm{p}}} + \delta - 1}$ 表示剩下的其他预测轨迹点，即${{Y}} = \{ {{R}},{{G}}\}$ 。2.1 基于条件变分自编码器的端点生成模块
本文使用条件变分自编码器CVAE[30]作为预测的主体结构，意图在预测整个轨迹之前先确定个体运动的最终目标。主要思想是构建一个从隐变量
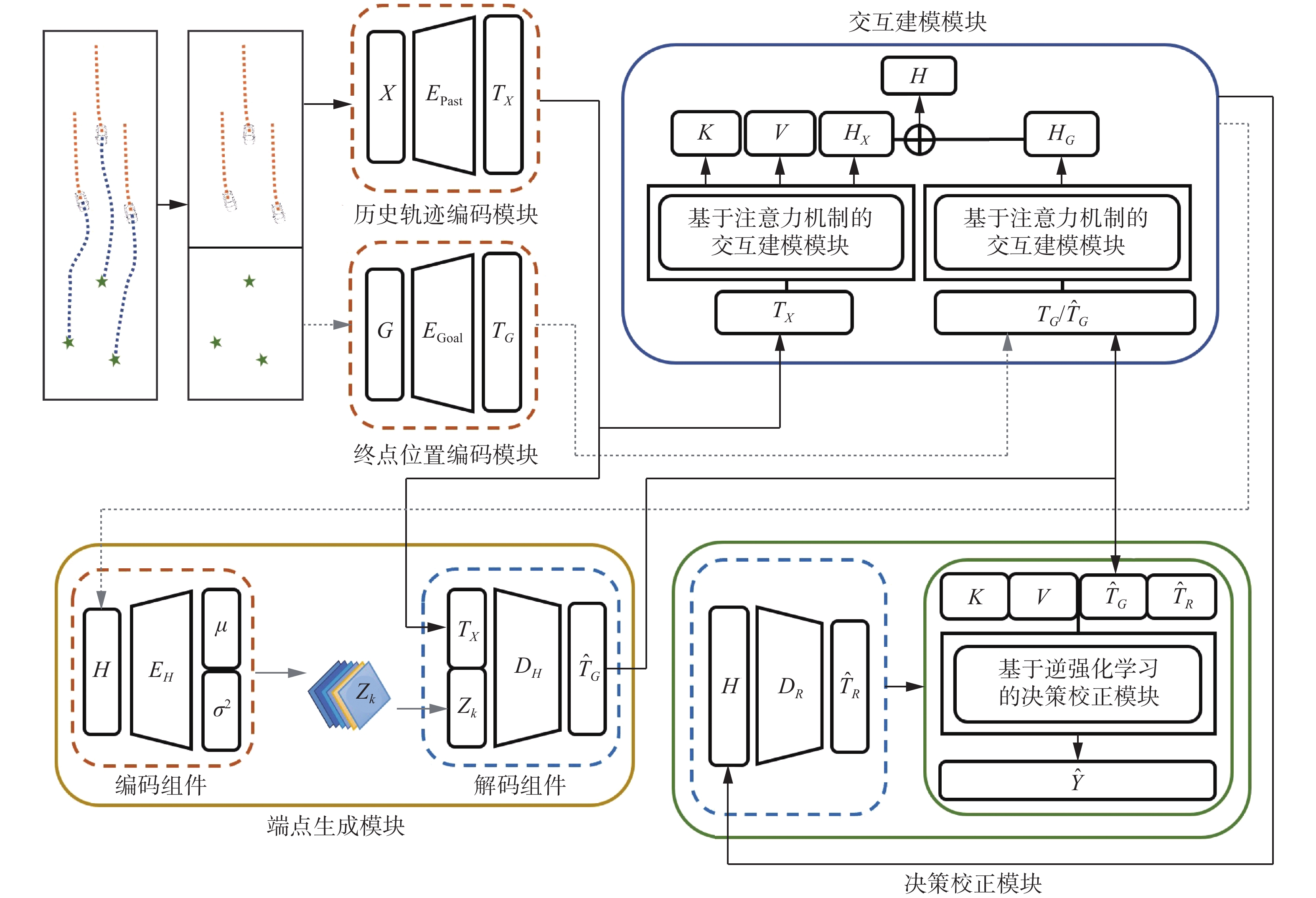
${{Z}}$ 到生成目标数据${{G}}$ 的模型，假设后验分布$p{\kern 1pt} ({{Z}}|{{{G}}_k})$ 是正态分布，这样就可以训练一个终点位置的生成器，把从$p{\kern 1pt} ({{Z}}|{{{G}}_k})$ 采样得到的${{{Z}}_k}$ 还原为${{{G}}_k}$ ，通常使用神经网络拟合得到该分布的均值$\mu $ 和方差${\sigma ^2}$ ，并使${{{Z}}_k}\sim\mathcal{N}(\mu ,{\sigma ^2})$ 无限接近$\mathcal{N}(0,1)$ 。通过这种方式训练好的生成模型可以直接从标准正态分布$\mathcal{N}(0,1)$ 采样${{{Z}}_k}$ ，生成多个符合车辆终点位置分布的端点${{{\hat G}}_k}$ ，从而满足多模态需求。具体结构细节如图1所示。图1主要由3部分构成，分别代表交互建模模块、端点生成模块、决策校正模块。其中模块之间传递向量的灰色虚线表示仅发生于训练过程，实线表示模块在训练和测试过程中均有参与。
图 1 基于车辆多目标交互行为建模的轨迹预测模型整体结构Fig. 1 Structure of the vehicle trajectory prediction method based on modeling of multi-agent
下载:
全尺寸图片
首先训练过程会从数据集中获取同场景中全部车辆的历史轨迹
${{X}}$ 和需要预测的终点真值${{G}}$ ，并通过历史轨迹编码模块${{{E}}_{{{\rm{Past}}}}}$ 和终点位置编码模块${{{E}}_{{{\rm{Goal}}}}}$ 独立编码得到张量${{{T}}_{{{X}}}}$ 和${{{T}}_{{{G}}}}$ ，二者经过交互建模模块可以学习到场景内车辆之间隐式交互带来的影响，从而得到带有交互特征的${{{H}}_{{{X}}}}$ 和${{{H}}_{{{G}}}}$ ，并通过级联的方式得到${{H}}$ 传入编码器${{{E}}_{{{H}}}}$ 中学习终点的分布${{Z}}\sim\mathcal{N}(\mu ,{\sigma ^2})$ 。通过联系上下文的方式，将历史轨迹特征${{{T}}_{{{X}}}}$ 和从终点分布中采样得到隐变量${{{Z}}_k}$ 进行级联，通过终点解码网络${{{D}}_{{{H}}}}$ 得到生成模型的终点位置预测结果${{{\hat T}}_{{{G}}}}$ 。接下来需要对预测轨迹的其他位置补齐，于是将${{{\hat T}}_{{{G}}}}$ 回传到互动建模编码模块，通过学习交互影响与${{{H}}_{{{X}}}}$ 得到新的上下文特征${{H}}$ ，经由剩余轨迹解码模块${{{D}}_{{{R}}}}$ 输出预测轨迹除终点外的剩余轨迹，即可得到初步轨迹预测结果$\{ {{{\hat T}}_{{{R}}}},{{{\hat T}}_{{{G}}}}\}$ ，后续传入决策校正模块得到优化后的最优策略轨迹${{\hat Y}}$ 作为最终轨迹输出。由于评估期间只获取历史轨迹${{X}}$ ，因此测试过程从$\mathcal{N}(0,1)$ 采样得到${{{Z}}_k}$ 开始，按照图1中实线所示步骤生成多模态轨迹结果。2.2 基于注意力机制的交互建模模块
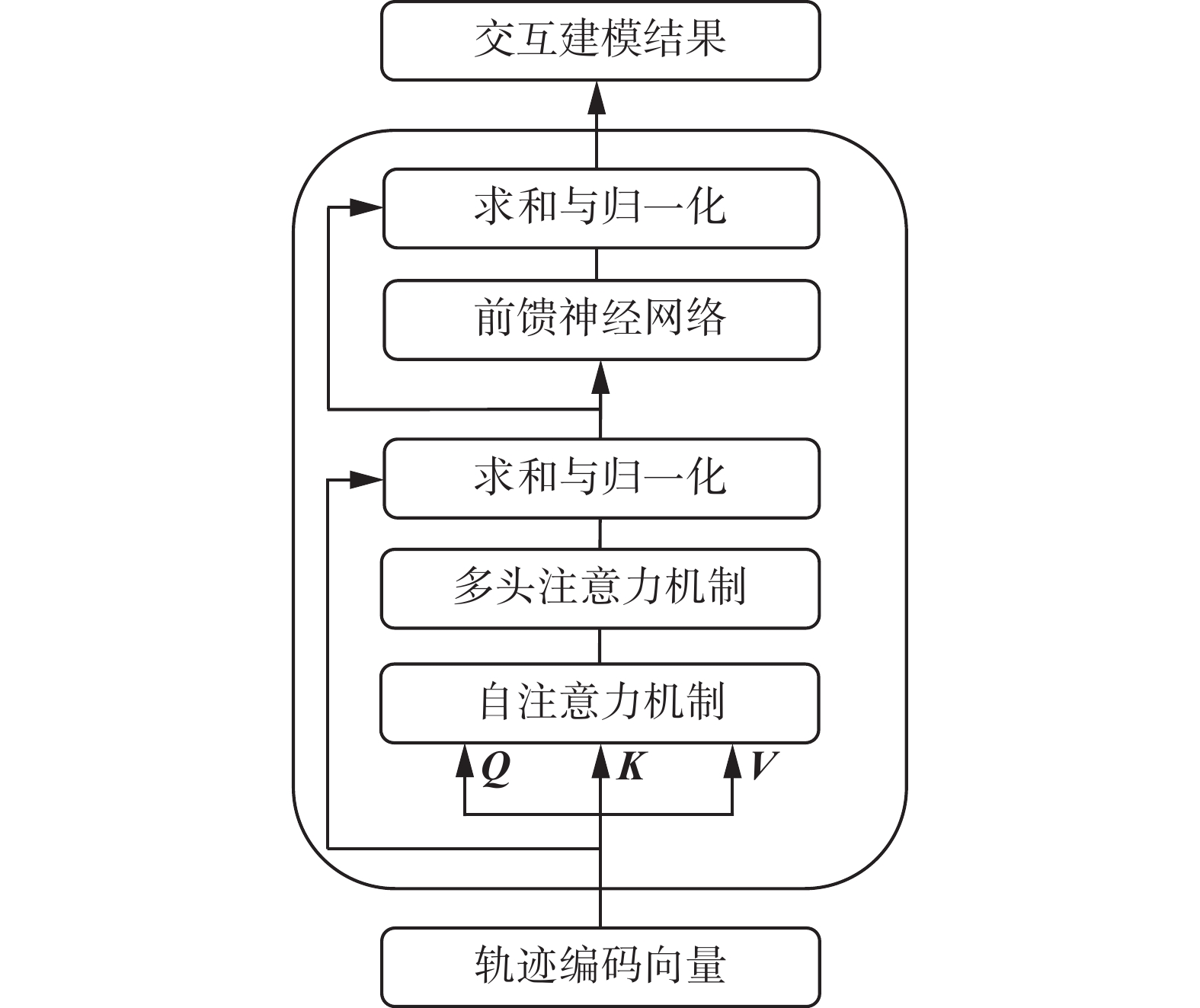
交互建模模块主要使用自注意力机制（self-attention）、多头注意力机制（multi-head attention）以及前馈神经网络（feed-forward network）、求和与归一化操作组成，具体实现细节如图2所示。其中，自注意力机制实现动态赋权，捕捉场景内每个车辆和其他个体之间的相互依赖关系，并分配不同的关注度权重。交互建模模块以轨迹编码特征向量为输入，对每个车辆的轨迹特征都通过3个全连接层生成查询向量Q、键向量K和值向量V，计算车辆之间的交互权重公式为
图 2 基于注意力机制的交互建模模块结构Fig. 2 Structure of the interaction modeling module下载:
全尺寸图片
$$ {\text{Self-Attention}}({{\boldsymbol{Q}}},{{\boldsymbol{K}}},{{\boldsymbol{V}}}) = {\rm{softmax}}\left(\frac{{{{\boldsymbol{Q}}}{{{\boldsymbol{K}}}^{\rm{T}}}}}{{\sqrt{d_k}} }\right){{\boldsymbol{V}}} $$ 因此获取交通场景中其他车辆对某一个车辆的影响可以用该车辆轨迹特征的查询向量
${\boldsymbol{Q}}$ 与其他车辆的键向量${\boldsymbol{K}}$ 逐个相乘得到初始权值。softmax函数提供将权值归一化的方法，通过除以维度大小$\sqrt {{{{d}}}_k}$ ，防止点积得到过大的初始权值而导致梯度趋近于零。最后将得到的权值与每个车辆的值向量${\boldsymbol{V}}$ 进行加权求和，即可得到建模交互影响后的车辆轨迹特征。多头注意力机制为每个车辆提供了多种不同的自注意力结果：
$$ \begin{gathered} {\rm{MHead(}}{{\boldsymbol{Q}}},{{\boldsymbol{K}}},{{\boldsymbol{V}}}{\rm{) = Concat(}}{{{{h}}}_1},{{{{h}}}_2}, \cdots ,{{{{h}}}_n}{\rm{)}}{{{\boldsymbol{W}}}^O} \\ \quad \quad {{{\boldsymbol{h}}}_i} = {\text{Self-Attention(}}{{{\boldsymbol{Q}}}^i},{{{\boldsymbol{K}}}^i},{{{\boldsymbol{V}}}^i}{\rm{)}} \\ \end{gathered} $$ 式中：多头注意力机制使模型从
$n$ 个不同特征子空间$\{ {{{{h}}}_1}{\rm{,}}\;{{{{h}}}_2}{\rm{,}}\; \cdots {\rm{,}}\;{{{{h}}}_n}\}$ 学习车辆交互影响；Concat表示将不同子空间捕捉到的特征级联，通过全连接层的权重$ {{\boldsymbol{W}}^O} $ 将不同特征空间的互动影响进行概括归纳，从而增强了模型的拟合能力以及对不同场景的适应能力。此外，前馈神经网络由2个具有ReLU激活的全连接层组成，并应用于每个注意子层，加快收敛速度。求和与归一化部分使用了残差结构，可以提高网络的效率，使用归一化模块是为了解决梯度消失的问题。
2.3 基于逆强化学习的决策校正模块
强化学习通常适用于可以明确定义个体行为奖励函数的场景，从而学习出个体最大收益的行为。但面对道路场景不断变化的复杂交通流信息，很难根据具体的路况给定一个明确的奖励函数。而IRL可以依据教学示例学习得到接近最佳策略结果的奖励函数[31]。因此，根据轨迹预测结果真值作为示例，逆强化学习提供了一个学习多模态轨迹结果中最接近真值分布的奖励函数的方法，从而决策输出预测结果中的最佳策略。
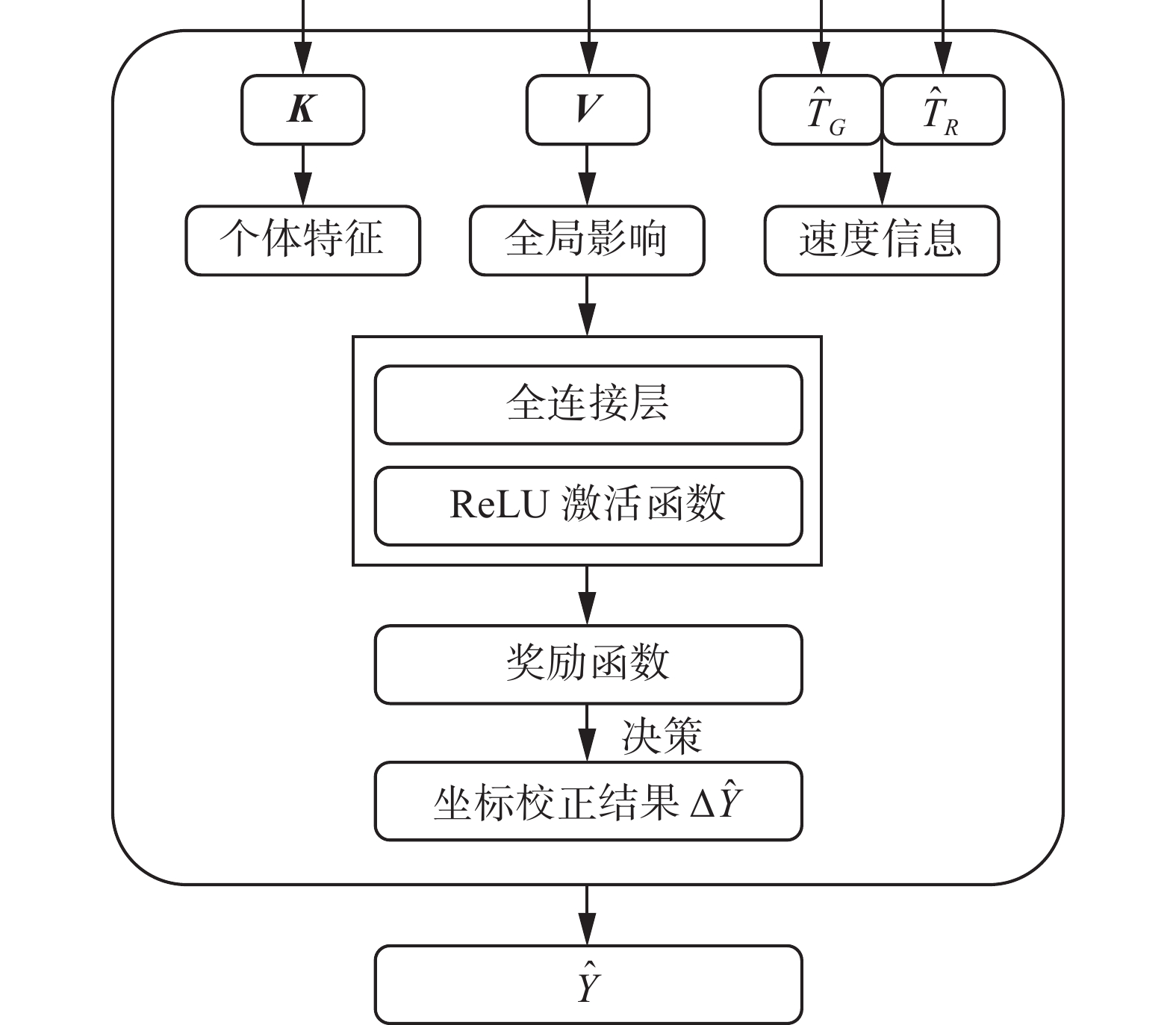
由于决策校正模块具备评分细化功能，需要结合全局特征和局部特征，联系车辆运动特征的上下文信息。因此选用历史轨迹特征和初步的多模态预测结果作为模块的输入，由键向量
${\boldsymbol{K}}$ 、值向量${\boldsymbol{V}}$ 以及初步预测结果$ \{ {{{\hat T}}_{{{R}}}},{{{\hat T}}_{{{G}}}}\} $ 构成。历史轨迹特征由自注意力机制学习得到3个向量${\boldsymbol{Q}}$ 、${\boldsymbol{K}} $ 、${\boldsymbol{V}} $ 。其中，${\boldsymbol{Q}}$ 主要用于查询向量之间的注意力权重，${\boldsymbol{K}}$ 作为权重索引涵盖了历史轨迹的个体特征，${\boldsymbol{V}}$ 可以理解为在原有历史轨迹特征的基础上，根据当前场景互动关系得到的全局信息轨迹特征，因此选择键向量${\boldsymbol{K}}$ 、值向量${\boldsymbol{V}}$ 提供历史轨迹特征，由初步轨迹预测结果$\{ {{{\hat T}}_{{{R}}}},{{{\hat T}}_{{{G}}}}\}$ 提供未来轨迹的动态速度信息。决策校正模块的具体结构如图3所示，该模块的输入结合了每个时间步的动态速度信息、轨迹的个体特征与全局交互特征，由全连接层和ReLU激活函数构成的评分细化模块学习奖励函数，在决策过程将评分值最大的轨迹作为多模态结果的最优策略。并充分联系上下文信息，通过另一个全连接层学习位置偏差
$\Delta {{\hat Y}}$ ，进一步优化轨迹结果。
图 3 决策校正模块结构Fig. 3 Structure of the decision refinement module下载:
全尺寸图片
2.4 损失函数
整个模型的损失函数由4个部分组成，首先是CVAE生成模块的2个损失项，包括重构损失
${L_{{{\rm{recon}}}}}$ 以及KL散度${L_{{{\rm{KL}}}}}$ 。重构损失用于计算初步预测结果$ \{ {{{\hat T}}_{R}},{{{\hat T}}_{{{G}}}}\} $ 与真值的L2距离，意图为决策校正模块提供更准确的初始预测轨迹。KL散度用于衡量端点后验分布$\mathcal{N}(\mu ,{\sigma ^2})$ 与标准正态分布$\mathcal{N}(0,1)$ 的相似度，意图学习多模态轨迹的端点潜在分布。具体公式如下：$$ {L_{\rm{recon}}} = \frac{1}{N}\sum\limits_{i \in N} {||{{{\boldsymbol{Y}}}_i}} - {{\hat {\boldsymbol{Y}}}_i}|{|_{\rm{2}}}{\kern 1pt} {\kern 1pt} $$ $$ \begin{gathered} {L_{\rm{KL}}} = {{\rm{KL}}}(N(\mu ,{\sigma ^2})||N(0,1))\;\,= \\ \quad {\kern 1pt} \frac{1}{2}( - \ln {\sigma ^2} + {\mu ^2} + {\sigma ^2}{\rm{ - 1}}) \\ \end{gathered} $$ 决策校正模块引出另外2个损失项，包括交叉熵损失
${L_{{{\rm{ce}}}}}$ 和偏差回归损失${L_{{{\rm{reg}}}}}$ 。交叉熵损失衡量真值轨迹分布$p$ 和多模态预测轨迹结果$q$ 的相似度，用于决策多模态轨迹结果的最优策略。偏差回归损失用于校正初始轨迹结果，从而得到更准确的最终轨迹输出。$$ {L_{{{\rm{ce}}}}} = H(p,q) = - \sum\limits_{i = 1}^N {p({{{{Y}}}_i})} \ln (q({{\hat {{Y}}}_i})) $$ $$ {L_{{{\rm{reg}}}}} = \frac{1}{N}\sum\limits_{i \in N} {||{{{{Y}}}_i}} - {{\hat {{Y}}}_i} - \Delta {{\hat {{Y}}}_i}|{|_{\rm{2}}} $$ 总损失函数
$L$ 的计算公式为$$ L = \alpha {L_{{{\rm{recon}}}}} + \beta {L_{{{\rm{KL}}}}} + \lambda {L_{{{\rm{ce}}}}} + \gamma {L_{{{\rm{reg}}}}} $$ 其中各损失项系数可根据实验过程进行调整。本文实验设定
$\alpha = \beta = \lambda = \gamma = 1$ 。3. 实验分析
3.1 数据集与评价指标
实验部分基于公开的NGSIM US-101数据集[32]和I-80数据集[33]进行开展，该数据集由摄像机采集，可以获取高速公路车道指定路段和时间段内全部车辆轨迹的数据。每个数据集由简单、中度和复杂拥堵的交通条件进行15 min的分割。本文参照CS-LSTM[13]的工作，将完整的数据集划分为训练集、验证集和测试集。利用每个数据集提供的坐标数据，本文将轨迹分割为8 s的片段，包括3 s的历史观测轨迹和接下来5 s的未来真值轨迹。其中，8 s片段的原始采样频率为10 Hz，为了降低模型的复杂性，本文设置下采样系数为2，即通过15帧的历史轨迹来预测未来25帧的轨迹位置。
本文实验使用以下性能指标来评价车辆轨迹预测模型的定量结果。首先是最小平均位移误差（minimum average displacement error，mADE）EmAD，EmAD用于衡量在时间累积条件下k条多模态预测轨迹点与真值轨迹点的最小平均欧氏距离：
$$ E_{\rm{mAD}} = \min {\left\{ \frac{{\displaystyle \sum\limits_{i \in N} {\displaystyle \sum\limits_{t \in {t_f}} {||{\hat {{Y}}}_t^i - {{{Y}}}_t^i|{|_2}} } }}{{N \times {t_f}}}\right\} _k} $$ (1) 本文实验中，k均取值为20，即输出20条多模态轨迹结果，
${t_f}$ 代表预测时间。其次是最小终点位移误差（minimum final displacement error，mFDE）EmFD，EmFD用于衡量k条多模态预测结果具体到某一时刻的终点预测位置和终点真值之间的最小欧氏距离：$$ E_{\rm{mFD}} = \min {\left\{ \frac{{\displaystyle \sum\limits_{i \in N} {||{\hat {{Y}}}_t^i - {{{Y}}}_t^i|{|_2}} }}{N}\right\} _k},t = {t_f} $$ (2) 3.2 定量结果与分析
本文选择以下模型与SAC模型进行对比实验：1）Social GAN[26]，最初用于行人轨迹预测研究，以GAN网络为基础架构，使用空间网格建模交互过程；2）DESIRE[28]，采用CVAE网络作为基础架构，以全部轨迹预测点为预测条件，结合场景语义信息辅助学习优化结果；3）PECNET[29]，提出以目标终点为条件的CVAE网络模型预测行人轨迹，以空间网格建模行人交互过程；4）SAC（A），不使用决策校正模块的本文模型，以车辆目标终点为条件的CVAE网络模型，采用自注意力机制和多头注意力机制作为交互建模方法；5）SAC（A+R），本文模型的完整结构，使用决策校正模块对轨迹预测结果进行优化更新。
实验过程采用测试集的历史轨迹数据作为输入，以测试集的未来轨迹数据作为真值，通过各模型输出多模态轨迹结果中的最优策略，并依据式（1）和式（2）进行mADE和mFDE指标的计算。其中基线模型的预测结果评价过程是选取多模态结果中具备最小平均位移误差mADE的轨迹作为最优策略。本文模型SAC（A+R）采取决策校正模块后得到奖励函数最高奖励的轨迹结果作为最优策略进行mADE以及mFDE指标的计算。
上述5个对比模型在NGSIM数据集上的mADE和mFDE表现结果如表1所示，给出了各模型在预测时间1~5 s的指标变化，评价指标以m为单位。
表 1 在5 s预测时间内SAC模型与其他基线模型的mADE/mFDE表现结果Table 1 The mADE/mFDE performance of SAC over 5 s for prediction compared with baseline models时间/s Social GAN DESIRE PECNET SAC(A) SAC (A+R) 1 0.19/0.33 0.15/0.28 0.22/0.41 0.20/0.38 0.17/0.31 2 0.34/0.71 0.33/0.67 0.49/0.87 0.41/0.79 0.29/0.62 3 0.57/1.23 0.54/1.22 0.90/1.55 0.62/1.36 0.53/1.15 4 0.83/1.79 0.89/2.06 1.47/2.59 1.09/2.23 0.79/1.64 5 1.21/2.55 1.33/2.72 1.63/1.22 1.31/0.97 1.17/1.06 根据表1的结果，首先Social GAN和DESIRE作为以全部轨迹为预测条件的生成模型，可以看到其误差在时间上的不断累积。而PECNET以端点为预测条件，在终点的mFDE表现结果明显优于其他2个模型，但其他时刻的指标并没有更好的表现。同样的问题也在SAC（A）的结果上体现，SAC（A）具备最优的终点mFDE值，其他指标也优于PECNET，可以证明注意力机制的使用在车辆交互建模过程中带来一定的优化效果。但实验过程中仍存在无法权衡其他轨迹点和终点的预测结果的问题。在引入决策校正模块以后，通过联系上下文的方式，结合全局和个体特征来训练校正偏移量，增加了损失函数的损失项做进一步训练。虽然SAC（A+R）在终点mFDE表现有所下降，但优化作用在轨迹其他时刻的mADE和mFDE结果上得以体现，证明了本文模型的有效性。
3.3 定性结果与分析
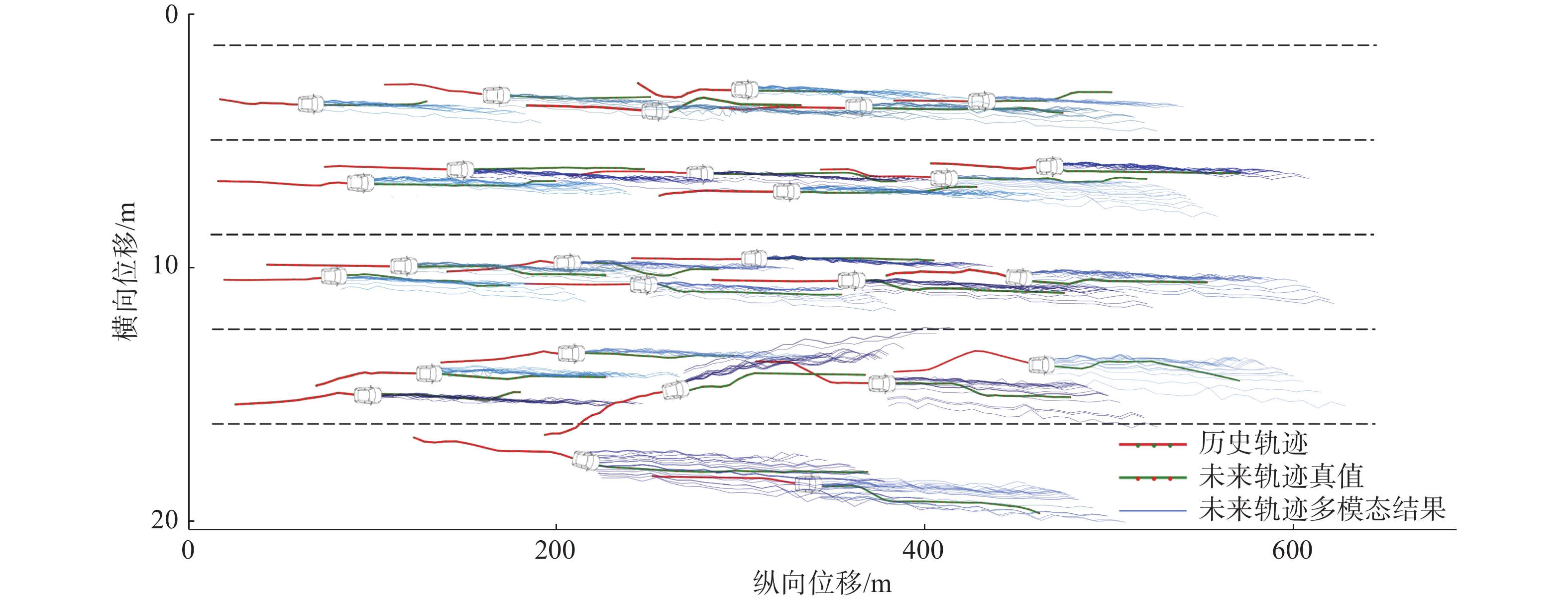
本文模型旨在解决轨迹预测的多模态问题，多模态轨迹的评价指标不仅在于包含更接近真值的轨迹，还在于提供更加全面的轨迹可能性。SAC模型的多模态结果如图4所示。其中红色线条代表历史轨迹，绿色线条代表未来轨迹的真值，蓝色线条描绘了本文模型输出的未来轨迹多模态结果。从图4中可以看到本文模型输出的大部分多模态结果形成了覆盖真值的区域，既存在接近真值的轨迹结果，也提供了车辆未来行驶的其他可能轨迹。但面对车辆临时变道的突发性动作，本文模型仍存在适应性不足的问题，这也成为未来进一步工作的发展方向。
图 4 多模态轨迹结果可视化图Fig. 4 The visualization of multimodal trajectory results下载:
全尺寸图片
4. 结束语
本文提出一种结合注意力机制的多模态车辆轨迹预测方法，以轨迹的潜在端点为预测目标，在条件变分自编码器的基础上引入注意力机制建模车辆交互过程，并利用逆强化学习方法输出多条轨迹的最优策略。区别于一般的单模态输出，本文关注于群体交互行为预测，充分利用上下文信息，融合个体轨迹特征和全局轨迹特征，生成未来轨迹的多模态结果，适用于多车交互关系建模。根据在NGSIM数据集上开展的实验结果，本文对比其他基线模型提高了轨迹预测结果的精确度。在未来的工作中将尝试引入额外的场景信息来学习驾驶场景对车辆轨迹的潜在影响，从而进一步提升预测结果。
-
图 1 基于车辆多目标交互行为建模的轨迹预测模型整体结构
Fig. 1 Structure of the vehicle trajectory prediction method based on modeling of multi-agent
下载:
全尺寸图片
图 2 基于注意力机制的交互建模模块结构
Fig. 2 Structure of the interaction modeling module
下载:
全尺寸图片
图 3 决策校正模块结构
Fig. 3 Structure of the decision refinement module
下载:
全尺寸图片
图 4 多模态轨迹结果可视化图
Fig. 4 The visualization of multimodal trajectory results
下载:
全尺寸图片
表 1 在5 s预测时间内SAC模型与其他基线模型的mADE/mFDE表现结果
Table 1 The mADE/mFDE performance of SAC over 5 s for prediction compared with baseline models
时间/s Social GAN DESIRE PECNET SAC(A) SAC (A+R) 1 0.19/0.33 0.15/0.28 0.22/0.41 0.20/0.38 0.17/0.31 2 0.34/0.71 0.33/0.67 0.49/0.87 0.41/0.79 0.29/0.62 3 0.57/1.23 0.54/1.22 0.90/1.55 0.62/1.36 0.53/1.15 4 0.83/1.79 0.89/2.06 1.47/2.59 1.09/2.23 0.79/1.64 5 1.21/2.55 1.33/2.72 1.63/1.22 1.31/0.97 1.17/1.06 -
[1] SIVARAMAN S, TRIVEDI M M. Dynamic probabilistic drivability maps for lane change and merge driver assistance[J]. IEEE transactions on intelligent transportation systems, 2014, 15(5): 2063–2073. doi: 10.1109/TITS.2014.2309055 [2] HELBING D, MOLNÁR P. Social force model for pedestrian dynamics[J]. Physical review E, statistical physics, plasmas, fluids, and related interdisciplinary topics, 1995, 51(5): 4282–4286. [3] 乔少杰, 金琨, 韩楠, 等. 一种基于高斯混合模型的轨迹预测算法[J]. 软件学报, 2015, 26(5): 1048–1063. doi: 10.13328/j.cnki.jos.004796 QIAO Shaojie, JIN Kun, HAN Nan, et al. Trajectory prediction algorithm based on Gaussian mixture model[J]. Journal of software, 2015, 26(5): 1048–1063. doi: 10.13328/j.cnki.jos.004796 [4] 高建, 毛莺池, 李志涛. 基于高斯混合−时间序列模型的轨迹预测[J]. 计算机应用, 2019, 39(8): 2261–2270. doi: 10.11772/j.issn.1001-9081.2019010030 GAO Jian, MAO Yingchi, LI Zhitao. Trajectory prediction based on Gauss mixture time series model[J]. Journal of computer applications, 2019, 39(8): 2261–2270. doi: 10.11772/j.issn.1001-9081.2019010030 [5] 乔少杰, 韩楠, 朱新文, 等. 基于卡尔曼滤波的动态轨迹预测算法[J]. 电子学报, 2018, 46(2): 418–423. doi: 10.3969/j.issn.0372-2112.2018.02.022 QIAO Shaojie, HAN Nan, ZHU Xinwen, et al. A dynamic trajectory prediction algorithm based on Kalman filter[J]. Acta electronica sinica, 2018, 46(2): 418–423. doi: 10.3969/j.issn.0372-2112.2018.02.022 [6] SCHULZ J, HUBMANN C, LÖCHNER J, et al. Multiple model unscented Kalman filtering in dynamic Bayesian networks for intention estimation and trajectory prediction[C]//2018 21st International Conference on Intelligent Transportation Systems. Maui: IEEE, 2018: 1467−1474. [7] SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems - Volume 2. Montreal: ACM, 2014: 3104–3112. [8] 孔玮, 刘云, 李辉, 等. 基于深度学习的行人轨迹预测方法综述[J]. 控制与决策, 2021, 36(12): 2841–2850. doi: 10.13195/j.kzyjc.2020.1841 KONG Wei, LIU Yun, LI Hui, et al. Survey of pedestrian trajectory prediction methods based on deep learning[J]. Control and decision, 2021, 36(12): 2841–2850. doi: 10.13195/j.kzyjc.2020.1841 [9] JEONG Y, KIM S, YI K. Surround vehicle motion prediction using LSTM-RNN for motion planning of autonomous vehicles at multi-lane turn intersections[J]. IEEE open journal of intelligent transportation systems, 2020, 1: 2–14. doi: 10.1109/OJITS.2020.2965969 [10] ZHANG Pu, XUE Jianru, ZHANG Pengfei, et al. Social-aware pedestrian trajectory prediction via states refinement LSTM[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(5): 2742–2759. [11] PSALTA A, TSIRONIS V, KARANTZALOS K, et al. Social pooling with edge convolutions on local connectivity graphs for human trajectory prediction in crowded scenes[C]//2020 IEEE 23rd International Conference on Intelligent Transportation Systems. Rhodes: IEEE, 2020: 1−6. [12] ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: human trajectory prediction in crowded spaces[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 961−971. [13] DEO N, TRIVEDI M M. Convolutional social pooling for vehicle trajectory prediction[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Salt Lake City: IEEE, 2018: 1549−15498. [14] MESSAOUD K, YAHIAOUI I, VERROUST-BLONDET A, et al. Non-local social pooling for vehicle trajectory prediction[C]//2019 IEEE Intelligent Vehicles Symposium (IV). Paris: IEEE, 2019: 975−980. [15] VEMULA A, MUELLING K, OH J. Social attention: modeling attention in human crowds[C]//2018 IEEE International Conference on Robotics and Automation. New York: ACM, 2018: 1–7. [16] MESSAOUD K, YAHIAOUI I, VERROUST-BLONDET A, et al. Attention based vehicle trajectory prediction[J]. IEEE transactions on intelligent vehicles, 2021, 6(1): 175–185. doi: 10.1109/TIV.2020.2991952 [17] LIN Lei, LI Weizi, BI Huikun, et al. Vehicle trajectory prediction using LSTMs with spatial-temporal attention mechanisms[J]. IEEE intelligent transportation systems magazine, 2022, 14(2): 197–208. doi: 10.1109/MITS.2021.3049404 [18] 孙亚圣, 姜奇, 胡洁, 等. 基于注意力机制的行人轨迹预测生成模型[J]. 计算机应用, 2019, 39(3): 668–674. doi: 10.11772/j.issn.1001-9081.2018081645 SUN Yasheng, JIANG Qi, HU Jie, et al. Attention mechanism based pedestrian trajectory prediction generation model[J]. Journal of computer applications, 2019, 39(3): 668–674. doi: 10.11772/j.issn.1001-9081.2018081645 [19] 李琳辉, 周彬, 连静, 等. 基于社会注意力机制的行人轨迹预测方法研究[J]. 通信学报, 2020, 41(6): 175–183. doi: 10.11959/j.issn.1000-436x.2020100 LI Linhui, ZHOU Bin, LIAN Jing, et al. Research on pedestrian trajectory prediction method based on social attention mechanism[J]. Journal on communications, 2020, 41(6): 175–183. doi: 10.11959/j.issn.1000-436x.2020100 [20] HUANG Yingfan, BI Huikun, LI Zhaoxin, et al. STGAT: modeling spatial-temporal interactions for human trajectory prediction[C]//2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2020: 6271−6280. [21] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all You need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017: 6000–6010. [22] MERCAT J, GILLES T, EL ZOGHBY N, et al. Multi-head attention for multi-modal joint vehicle motion forecasting[C]//2020 IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020: 9638−9644. [23] GIULIARI F, HASAN I, CRISTANI M, et al. Transformer networks for trajectory forecasting[C]//2020 25th International Conference on Pattern Recognition. Milan: IEEE, 2021: 10335−10342. [24] FENG Xidong, CEN Zhepeng, HU Jianming, et al. Vehicle trajectory prediction using intention-based conditional variational autoencoder[C]//2019 IEEE Intelligent Transportation Systems Conference. Auckland: IEEE, 2019: 3514−3519. [25] ROY D, ISHIZAKA T, MOHAN C K, et al. Vehicle trajectory prediction at intersections using interaction based generative adversarial networks[C]//2019 IEEE Intelligent Transportation Systems Conference. Auckland: IEEE, 2019: 2318−2323. [26] GUPTA A, JOHNSON J, LI Feifei, et al. Social GAN: socially acceptable trajectories with generative adversarial networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 2255−2264. [27] SADEGHIAN A, KOSARAJU V, SADEGHIAN A, et al. SoPhie: an attentive GAN for predicting paths compliant to social and physical constraints[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2020: 1349−1358. [28] LEE N, CHOI W, VERNAZA P, et al. DESIRE: distant future prediction in dynamic scenes with interacting agents[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 2165−2174. [29] MANGALAM K, GIRASE H, AGARWAL S, et al. It is not the journey but the destination: endpoint conditioned trajectory prediction[C]//Computer Vision – ECCV 2020: 16th European Conference. Glasgow: ACM, 2020: 759–776. [30] KINGMA D P, MOHAMED S, REZENDE D J, et al. Semi-supervised learning with deep generative models[C]//Advances in Neural Information Processing Systems. Montreal: NIPS, 2014: 3581−3589. [31] 陈希亮, 曹雷, 何明, 等. 深度逆向强化学习研究综述[J]. 计算机工程与应用, 2018, 54(5): 24–35. doi: 10.3778/j.issn.1002-8331.1711-0289 CHEN Xiliang, CAO Lei, HE Ming, et al. Overview of deep inverse reinforcement learning[J]. Computer engineering and applications, 2018, 54(5): 24–35. doi: 10.3778/j.issn.1002-8331.1711-0289 [32] COLYAR J, HALKIAS J. Us highway 101 dataset: federal highway administration research and technology fact sheet [EB/OL]. (2007−09−08)[2022−05−20].https://www.fhwa.dot.gov/publications/research/operations/07030/index.cfm. [33] COLYAR J, HALKIAS J. Us highway 80 dataset, federal highway administration[EB/OL]. (2006−12−01) [2022−05−20].https://rosap.ntl.bts.gov/view/dot/38708.
