Multi-objective evolutionary algorithm for optimal scheduling of dynamic maintenance resources
-
摘要: 为解决维修资源调度过程中出现的维修资源预测不准、资源冲突的问题，本文建立了不同作战阶段的多供应中心−多需求点的的动态维修资源优化调度模型，使得多个供应中心可以及时、高效地对需求点进行维修资源调度，减少了资源调度时间和每个需求点的维修资源不满足量。为了更好地求解提出的模型，本文提出了一种改进的多目标进化算法，在经典的多目标进化算法的基础上，使用正态分布交叉算子、全局探索增强型差分进化算子和自适应变异算子的协同进化策略，提高了算法的局部搜索能力和种群的多样性。仿真实验表明，本文提出的算法具有良好的收敛性和分布均匀性，并且具有较高的求解效率。Abstract: This paper establishes a dynamic maintenance resource optimization scheduling model of multi-supply centers and multi-demand points in different combat stages to solve the problems of inaccurate prediction and resource conflict in the process of maintenance resource scheduling. Therefore, multiple supply centers can timely and efficiently schedule maintenance resources at demand points. The model reduces the resource scheduling time and the unsatisfying amount of maintenance resources at each demand point. An improved multi-objective evolutionary algorithm is proposed in this paper to solve the proposed model effectively. The co-evolution strategy of the normal distribution crossover operator, global exploration enhanced differential evolution operator, and adaptive mutation operator is used to improve the local search capability and population diversity of the algorithm based on the classical MOEA/D algorithm. Simulation results show that the proposed algorithm has good convergence and distribution uniformity and has high solution efficiency.
-
车辆、飞机、舰船等装备是进行作战的重要物质基础，由于作战损坏或者随机故障，会出现多个维修资源需求，维修保障资源的优化调度将会帮助解决协同维修过程中出现的维修保障资源分配不均、计划不周、预测不准等问题，能够充分利用现有资源缩短待修装备的平均等待时间，在较短的时间内恢复装备的战斗力，最大限度地保持和恢复装备的完好性，提高装备的快速、高强度出动能力[1-2]。在维修保障资源短缺、时间紧迫的情况下，制定合理的维修保障资源调度优化方案[3]。以有效解决紧急维修资源调度问题，使战斗的顺利进行，确保最终作战的胜利[4]。
目前研究资源调度问题常见的有工序调度和应急式资源调度问题。针对工序调度[5-6]问题，关键在于如何有效的利用维修资源，合理高效地进行各种维修项目，保证多工序、多项目能够交叉有序推进，解决好维修保障过程中出现的资源分配不合理而导致资源冲突的问题。针对应急式资源调度[7-8]问题，关键在于如何在维修资源有限、资源需求不确定的情况下，合理地分配维修资源，提供及时的应急资源优化配置。张鑫等[9]考虑舰船维修任务具有高并发性和关键资源的约束的特殊性质，考虑了工序的紧前约束关系，建立了以维修任务工期最短的资源优化调度模型，并利用蚁群算法求解，可以有效地解决资源冲突的问题。陈盖凯等[10]认为在维修保障过程中资源保障点的数目应尽可能的少一点，能够减少资源调度中存在的风险，在考虑了维修任务优先顺序的基础上，建立了以资源调度时间最短、保障点个数最少、维修保障效益最大的源优化调度模型，能够充分发挥飞机的作战性能。Zheng等[11]以最大完成时间最小和人力资源成本最小为目标函数，建立了装甲装备维修资源优化调度模型，并利用NSGA-II算法[12]求解该模型，提高了装备的维修效率，缩短了设备的维修周期，具有较高的应用价值。另外，可将一些算子混合到算法中以提高算法全局搜索能力。如，张敏等[13]将应用正态分布交叉算子提高了
$ \varepsilon {\text{-MOEA}} $ 的全局搜索能力，白芸等[14]采用差分进化很好地解决了旅行商问题的优化。但是资源调度问题并不是一个静态的过程，而是一个动态的调度过程，在作战期间，所处作战阶段不同，所需的维修资源也是不一样的。目前针对维修资源的优化调度的研究较多的是考虑单个维修资源的需求，并且没有分具体的作战阶段去研究，并不符合实际需求，并不能很好地解决战时资源需求不确定、资源预测不准等问题。本文根据作战期间所处不同的阶段，考虑每个需求点的优先级，构建了多供应中心−多需求点的动态维修资源优化调度模型，并设计改进的MOEA/D算法[15]进行求解。
1. 问题描述
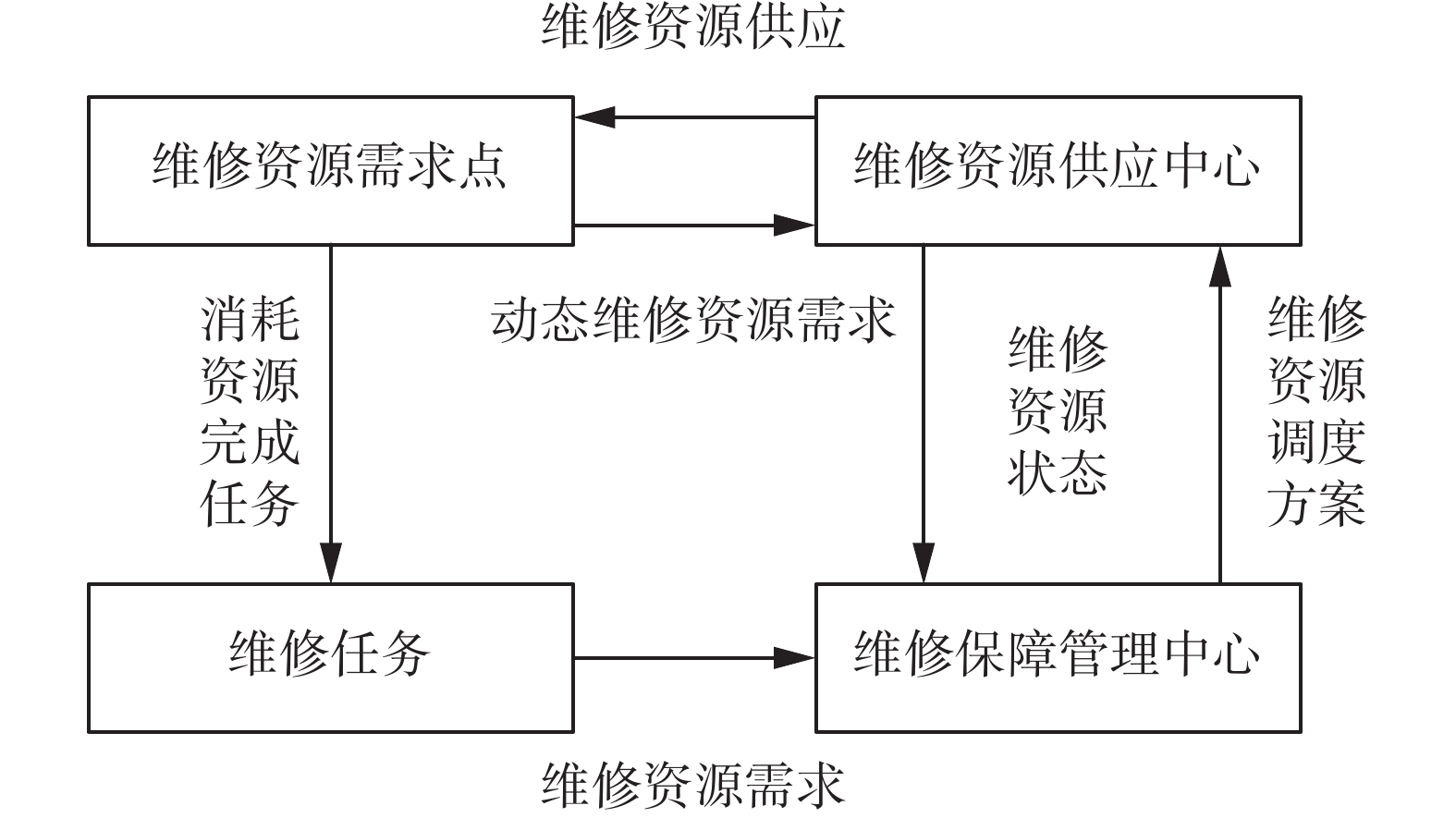
在作战过程中，会产生一系列的损伤，根据具体的维修任务会向维修保障管理系统提出维修资源供应需求，根据各维修点的预测资源需求量和供应中心相应维修资源的存储量，制定对应的维修资源优化调度方案，采用科学的分配原则合理地对需求点分配维修资源，以确保供应中心可以及时、高效地将维修资源调配到各需求点中。维修资源供应中心集合
$A = \{ {A_i}|i = 1,2, \cdots, I\}$ ，维修资源需求点集合$A = \{ {A_i}|i = 1,2, \cdots, I\}$ ，$ t = 1,2, \cdots ,T $ 表示调度阶段，$k = 1,2, \cdots, K$ 表示维修资源种类。本文求解不同的作战阶段，动态的维修资源优化调度方案。图1为维修资源调度示意图。
图 1 维修资源调度示意图Fig. 1 Schematic diagram of maintenance resourcescheduling
下载:
全尺寸图片
2. 动态维修资源调度优化模型
2.1 模型假设与模型符号表示
1)维修资源运输车辆数量充足；
2)供应中心到需求点之间的道路由于作战原因受到损坏，运输效率降低；
3)资源调度过程中，不考虑中转，直接由供应中心运输到需求点；
4)一辆车可以运输多种维修资源；
5)在每个阶段，需求点的维修资源需求量是可以预测得到。
对所建模型的符号定义如下：
${\rm{ forecast}}_{j,t,k} $ 表示$ t $ 阶段需求点$ {\overline A _j} $ 维修资源$ k $ 的预测需求量；$ {\rm{SC}}_{i,k,t} $ 表示$ t $ 阶段供应中心$ {A_i} $ 维修资源$ k $ 的存储量；${\rm{ RSC}}_{i,k,t} $ 表示$ t $ 阶段初始调度结束，供应中心$ {A_i} $ 维修资源$ k $ 剩余存储量；$ {\rm{SR}}_{j,k,t} $ 表示需求动态变化后，$ t $ 阶段需求点$ {\overline A _j} $ 维修资源$ k $ 的需求量；$ {r_{i,j,k,t}} $ 表示$ t $ 阶段供应中心$ {A_i} $ 实际分配维修资源$ k $ 到需求点$ {\overline A _j} $ 的资源量；$ {\rm{short}}_{j,t,k} $ 表示在$ t $ 阶段需求点$ {\overline A _j} $ 维修资源$ k $ 未满足的数量；$ {h_{i,j,t}} $ 表示$ t $ 阶段供应中心$ {A_i} $ 到需求点$ {\overline A _j} $ 资源运输时间效率降低参数；$ \beta $ 表示$ t $ 阶段供应中心$ {A_i} $ 到需求点$ {\overline A _j} $ 延误的处罚系数；$ {\rm{time}}_{i,j} $ 表示$ t $ 阶段供应中心$ {A_i} $ 到需求点$ {\overline A _j} $ 的时间；$ {\gamma _j} $ 为第$ j $ 个需求点的重要度。2.2 模型构建
1)延误成本
在作战期间，为了能够及时有效地发挥作战效能，资源调度成本往往不会考虑，但是由于战斗的进行，从供应中心到需求点运输的时间效率会降低，为了能够迅速运输维修资源，应该尽可能地减少延误成本。延误成本可以表示为
$$ \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {\beta ({\rm{time}}_{i,j}{h_{i,j,t}} - {\rm{time}}_{i,j}){r_{i,j,k,t}}} } } } $$ (1) 2)需求点优先级
由于维修资源是有限的，在作战期间，在总体需求满足均衡的条件下，应尽可能地满足优先级高需求点的资源需求，需求点的重要度在本文中基于多个指标的加权总和，作战紧急程度指标(
${\xi _1}$ )、故障装备的可维修性指标(${\xi _2}$ )、故障装备维修及时性指标(${\xi _3}$ )和设备维修的贡献进行运算装备维修对作战贡献度指标(${\xi _4}$ )。需求点的重要度计算如下：$$ {\gamma _j} = \sum\limits_{l = 1}^4 {{\varepsilon _l}{\xi _{jl}}} $$ (2) 式中：第
$j$ 个需求点的重要度指数由${\gamma _j}$ 表示；第$j$ 个需求点的第$l$ 个指标因素用${\gamma _{jl}}$ 表示；${\varepsilon _l}$ 表示第第$l$ 个指标的权重，$\displaystyle \sum\limits_{l = 1}^4 {{\varepsilon _l}} {\text{ = }}1$ 。3)资源不满足量
在维修资源调度中，应该尽可能满足每个需求点的资源需求，资源不满足量计算如下：
$$ \sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {{\gamma _j} \cdot {\rm{short}}_{j,t,k}} } } $$ (3) 综上所述，本文所研究的动态多阶段维修资源优化调度模型分为两步：
第1步：
$$ \min \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {\beta ({\rm{time}}_{i,j}{h_{i,j,t}} - {\rm{time}}_{i,j}){r_{i,j,k,t}}} } } } $$ (4) $$ \min \sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {{\gamma _j} \cdot {\rm{short}}_{j,t,k}} } } $$ (5) 第2步：
$$ \min \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\beta ({\rm{time}}_{i,j}{h_{i,j,t}} - {\rm{time}}_{i,j})({r_{i,j,k,t}} + r_{i,j,k,t}^ * )} } } $$ (6) $$ \min \sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {{\gamma _j} \cdot {\rm{short}}_{j,t,k}^ * } } } $$ (7) 约束条件：
$$ \forall i = 1, 2,\cdots, I;j = 1,2,\cdots, J;k = 1,2, \cdots, K;t = 1,2, \cdots, T $$ $$ 0 \leqslant \sum\limits_{j = 1}^J {{r_{i,j,k,t}}} \leqslant {\rm{SC}}_{i,k,t} $$ (8) $$ 0 \leqslant \sum\limits_{j = 1}^J {r_{i,j,k,t}^ * } \leqslant {\rm{RSC}}_{i,k,t} $$ (9) $$ {\rm{RSC}}_{i,k,t} = {\rm{SC}}_{i,k,t} - \sum\limits_{j = 1}^J {{r_{i,j,k,t}}} $$ (10) $$ {\rm{short}}_{j,t,k} = \max \left\{ {0,{\rm{forecast}}_{j,t,k} - \sum\limits_{i = 1}^I {{r_{i,j,k,t}}} } \right\} $$ (11) $$ {\rm{short}}_{j,t,k}^ * = \max \left\{ {0,{\rm{SR}}_{j,t,k}- \sum\limits_{i = 1}^I {({r_{i,j,k,t}} + r_{i,j,k,t}^ * )} } \right\} $$ (12) 动态的维修资源优化调度第1步是根据供应中心每种维修资源的预测量和实际存储量，求解出一组优化调度方案，目标函数是式(4)确保维修资源延误成本最小和式(5)确保各需求点维修资源不满足量最小;第2步只有在第1步最优的初始调度后，才能继续动态地调整资源需求，根据增加的维修资源需求量和剩余存储量，为各需求点提供动态的资源需求，目标函数是调整后的式(6)资源调度成本最小和式(7) 各需求点维修资源不满足量最小。约束条件式(8)表示每一阶段，每一个供应中心各种维修资源的运输量非负且不超过实际存储量；约束条件式(9)表示每一阶段，每一个供应中心各种维修资源的补充运输量非负且不超过剩余存储量；约束条件式(10)表示初始调度后，供应中心各种维修资源的剩余存储量；约束条件式(11)表示优化调度第1步未满足资源量的计算；约束条件式(12)表示初始调度后未满足资源量的计算。
3. 改进的MOEA/D算法
多目标进化算法[16-17](multiobjective evolutionary algorithm based on decomposition, MOEA/D)解决多目标优化问题的核心思想是，将多目标优化问题转化为一系列的单目标优化子问题或多个多目标的子问题。利用这些子问题的邻域关系，通过协作的方式对这些子问题同时进行优化。
首先利用切比雪夫分解策略[18]将维修资源调度延误成本最少和需求点资源不满足量最少的多目标问题分解成
$ N $ 个子问题，其中第$ w $ 个子问题的目标函数是$$ {g^{te}}(v\_{{\rm{var}}} |{{\boldsymbol{\lambda}} ^w},{z^*}) = \mathop {\max \limits_{1 \leqslant u \leqslant n}}\left\{ {\lambda _u^w|{f_u}(v\_{{\rm{var}}} ) - z_u^*} \right\} $$ (13) 式中：
${{\boldsymbol{\lambda}} ^1},{{\boldsymbol{\lambda}} ^2}, \cdots ,{{\boldsymbol{\lambda}} ^N}$ 是一组均匀分布的权重向量，${{\boldsymbol{\lambda}} ^w} = {({{\lambda}} _1^w,{{\lambda}} _2^w, \cdots ,\lambda _n^w)^{\rm{T}}}$ ，根据改进权重向量，可以得到不同的Pareto最优解，${z^*} = \left\{ {z_1^*, z_2^*\cdots, z_n^*} \right\}$ 为参考点，$ n $ 为决策空间的维度。3.1 染色体表示和种群初始化
采用实数编码的方式，每个染色体表示一个维修资源调度方案，每一个调度方案有供应中心、需求点、资源种类、调度阶段4部分组成，表示为每个调度阶段，由每个供应中心到各个需求点的每种维修资源的运输量。解的表示形式为
$$ \begin{gathered} r = \{ {r_{1,1,1,1}},{r_{1,1,1,2}} ,\cdots, {r_{1,1,1,T}}|{r_{1,1,2,1}}, \cdots, {r_{1,1,2,T}}, \cdots ,{r_{1,1,K,T}} \\ |{r_{1,2,1,1}}, \cdots, {r_{1,2,K,T}}, \cdots, {r_{1,J,K,T}}|{r_{2,1,1,1}}, \cdots, {r_{2,J,K,T}}, \cdots ,{r_{I,J,K,T}}\} \\ \end{gathered} $$ (14) {15,5,6|3,…,12,…,8|14,…,22,…,9|34,…,25,…,0|22,…,35,…,18}，假设有3个供应中心，3个需求点，3种维修资源，3个调度阶段，那么上面式子表示的含义为：第1部分是供应中心1在第1个阶段给需求点1运输的维修资源1的量为15，供应中心1在第2个阶段给需求点1运输的维修资源1的量为5，供应中心1在第3个阶段给需求点1运输的维修资源1的量为6；第2部分是供应中心1在第1个阶段给需求点1运输的维修资源2的量为3，供应中心1在第3个阶段给需求点1运输的维修资源2的量为12，供应中心1在第3个阶段给需求点1运输的维修资源31的量为8；第3部分是供应中心1在第1个阶段给需求点2运输的维修资源1的量为34，供应中心1在第3个阶段给需求点2运输的维修资源3的量为25，供应中心1在第3个阶段不给需求点3运输的维修资源3；第4部分是供应中心2在第1个阶段给需求点1运输的维修资源1的量为22，供应中心2在第3个阶段给需求点3运输的维修资源3的量为35，供应中心3在第3个阶段给需求点3运输的维修资源3的量为18。
3.2 进化算子
本文使用正态分布交叉算子(normal distribution crossover, NDX)[13]和全局探索增强型差分进化算子(population-based global exploration of enhanced differential evolution, PEEDE)[19]和自适应变异算子的协同进化策略。
1) NDX算子：本文采用实数编码的方式，以往采用模拟二进制交叉算子(simulated binary crossover, SBX)来进行协同进化,但是SBX算子的局部搜索能力较差，容易产生局部最优的问题，最优解的选取往往会存在一定的偏差。NDX算子最早是由张敏等[13]提出的，将正态分布引入到SBX算子中，父代个体
$ {R}_{1}和{R}_{2} $ ，通过式(15)和式(16)进行离散重组操作，使得每个子代个体$ {R}_{1}^{'}和{R}_{2}^{'} $ 在每一维中都具有2个等概率的取值，则对$ n $ 维的搜索空间而言,每个子个体的取值共有2种,且每种取值概率均为1/ 2，使得种群多样性增加，扩大了搜索范围。若不采用该重组操作，则每个子个体的取值只有1种,且包含在前面的2种之中，搜索范围较小。$$ \begin{gathered} R_{1,i}'(t) = [({R_{1,i}}(t) + {R_{2,i}}(t)) \pm 1.481 \cdot ({R_{1,i}}(t) - {R_{2,i}}(t)) \cdot \\ \left| {N(0,1)} \right|]/2,\;{\mu _i} \leqslant 0.5 \end{gathered} $$ (15) $$ \begin{gathered} R_{2,i}'(t) = [({R_{1,i}}(t) + {R_{2,i}}(t)) \pm 1.481 \cdot ({R_{1,i}}(t) - {R_{2,i}}(t)) \cdot \\ \left| {N(0,1)} \right|]/2,{\mu _i} > 0.5 \end{gathered} $$ (16) 其中
$ {\mu _i} $ 为(0,1)区间上均匀分布的随机数。2) PEEDE算子
传统的差分进化算子[20]忽略了个体进化中的信息，在进化过程中，常常希望个体朝着更有希望的方向进化，并增强种群的全局探索能力，因此这里引进了PEEDE算子。对于解
$ {r_{i,j,k,t}} $ 、$ r_{i,j,k,t}^1 $ 是$ {r_{i,j,k,t}} $ 邻域内随机挑选的个体，$ r_{i,j,k,t}^{1p} $ 是$ r_{i,j,k,t}^1 $ 的父代，$ r_{i,j,k,t}^{np1} $ 和$ r_{i,j,k,t}^{np2} $ 是根据NDX算子重组操作得到的两个不同的解，根据式(17)得到新的解${R_{{\rm{new}}}} = \{ r_{1,1,1,1}^{{\rm{new}}}, r_{1,1,1,2}^{{\rm{new}}}, \cdots r_{i,j,k,t}^{{\rm{new}}}, \cdots \}$ ，如果求得的子代解不满足公式(8)，则用父代解来替换子代解：$$ {r}_{i,j,k,t}^{{\rm{new}}}=\left\{\begin{split} &{r}_{i,j,k,t}+\theta \left({r}_{i,j,k,t}^{1}-{r}_{i,j,k,t}^{1p}\right)+\theta \left({r}_{i,j,k,t}^{np1}-{r}_{i,j,k,t}^{np2}\right),\quad{c}_{e} < {p}_{c}\\ &{r}_{i,j,k,t}\quad{其他}\end{split} \right.$$ (17) 式中：
$ \theta $ 是控制参数，本文设为0.5，$ {p_c} $ 是执行PEEDE算子的概率，$ {c_e} $ 是[0,1]区间内的随机数。3)自适应变异算子
对于新的子代解
$ {R_{{\rm{new}}}} $ ，如果满足变异概率$ {p_m} $ ，那么根据式(18)来执行自适应变异算子，如果变异后的解满足式(8)，那么用变异前的解来代替。$$ r_{i,j,k,t}^{{\rm{new}}} = \left\{ {\begin{split} &{r_{i,j,k,t}^{{\rm{new}}}(1 - {\rm{ck}}), \sum\limits_{i = 1}^I {r_{i,j,k,t}^{{\rm{new}}} > {\rm{forecast}}_{j,t,k}} } \\ &{r_{i,j,k,t}^{{\rm{new}}}(1 + {\rm{ck}}), \sum\limits_{i = 1}^I {r_{i,j,k,t}^{{\rm{new}}} < {\rm{forecast}}_{j,t,k}} } \\ &{r_{i,j,k,t}^{{\rm{new}}}, \sum\limits_{i = 1}^I {r_{i,j,k,t}^{{\rm{new}}} = {\rm{forecast}}_{j,t,k}}} \end{split}} \right. $$ (18) 式中：
$ {\rm{ck}} $ 是(0,1)区间内的一个小数，${\rm{ ck}} = U{(0,1)^{1 + \delta }} $ ，$ \delta $ 是取值范围为[0,9]的变异分布指数。3.3 外部存档更新策略
外部存档 EP将算法迭代过程中产生的非支配解存储起来，外部存档更新机制决定了算法输出值的好坏。本文引用个体之间的拥挤距离[21]，当非支配解的总数超出容量的限制时，删除拥挤距离最小的个体，直至非支配解的数量不超过最大容量。
3.4 调整策略
在维修资源调度中，当出现动态的维修资源需求变化时，并不是在任何时候都可以补充运送的，并且运输的时间也是不相同的，会出现3种情况，第1种情况是当动态的维修资源需求变化出现的时间较早，所有的供应中心均可以继续为其进行维修资源供应；第2种情况是仅有部分供应中心可以提供新的维修资源供应；第3种情况是没有供应中心可以提供新的维修资源供应。当出现情况3时，动态的维修资源需求变化无法满足。因此本文做了相应的调整策略。
策略1：动态的维修资源需求则由所有供应中心剩余的维修资源提供。新产生的需要供应的维修资源由式(19)得出，如果调整后资源调度方案的剩余存储量能满足初始调度方案剩余阶段的资源需求，则继续执行初始的调度方案，如果不满足的话，则需要重新规划剩余阶段的资源调度方案。
$$ {\hat r_{i,j,k,t = }}\left\{ {\begin{split} &{{\rm{add}}_{j,k,t}, \quad {\rm{RSC}}_{i,k,t} \geqslant {\rm{add}}_{j,k,t}} \\ &{\alpha \cdot {\rm{RSC}}_{i,k,t},\quad{\rm{RSC}}_{i,k,t} < {\rm{add}}_{j,k,t}} \end{split}} \right. $$ (19) 式中：
$ {\rm{add}}_{j,k,t} $ 是动态的维修资源需求增加的量，$ \alpha $ 是(0,1)之间的随机数。策略2：动态的维修资源需求则由部分的供应中心共同提供，如果调整后资源调度方案的剩余存储量能满足初始调度方案剩余阶段的资源需求，则继续执行初始的调度方案，如果不满足的话，则需要重新规划剩余阶段的资源调度方案。
3.5 改进的MOEA/D算法流程
算法 改进的MOEA/D算法
输入
$ N $ ：多目标问题利用切比雪夫分解策略分解子问题的数量；${{{\boldsymbol{\lambda}} ^1}, {\boldsymbol{\lambda}} ^2},\cdots ,{{\boldsymbol{\lambda }}^N}$ ：一组均匀分布的权重向量；$ H $ ：每个权重的邻域权重的数量；$ {p_c} $ ：交叉概率；$ {p_m} $ ：变异概率；Popsize：种群规模；
gen：迭代次数
输出 最优解集
初始化：
1) 初始化每个权重的邻域：
$ \forall w = 1, 2, \cdots ,N $ ，从任意两个权重之间的欧氏距离，找到$ {{\boldsymbol{\lambda }}^w} $ 的$ H $ 个最近的权重向量，并将邻域中的权重向量索引保存在$ B(w) = \{ {w_1}, {w_2},\cdots ,{w_H}\} $ 中，其中${{\boldsymbol{\lambda}} ^{{w_1}}},{{\boldsymbol{\lambda}} ^{{w_2}}}, \cdots ,{{\boldsymbol{\lambda}} ^{{w_H}}}$ 是$ {{\boldsymbol{\lambda}} ^w} $ 的$ H $ 个最近的权重向量；2) 按步骤1）方法随机初始化种群
$ v\_{{var} _1}, v\_{{var} _2}, \cdots , v\_{{var} _N} $ ；3) 初始化参考点，分配给
$ z = \{ {z_1}, {z_2}\cdots ,{z_n}\} $ $ n $ 个足够大的数；种群更新：
1) 对于
$ B(w) $ 中的个体，两两执行NDX算子，得到新的子代种群，与$ B(w) $ 合并为新的子代种群；2) 从新的子代种群里选择合适的个体，满足交叉概率，执行PEEDE算子，生成新的个体
$ y $ ，如果不满足交叉概率，相应的解保持不变；3) 若满足变异概率，在解
$ y $ 执行自适应变异算子，产生新的解；4) 如果
$ {z_o} > {f_o}(\hat y) $ ，那么$ {z_o} = {f_o}(\hat y) $ ，其中，$ o = 1, 2, \cdots ,n $ ；5) 如果
${g^{te}}(\hat y|{\lambda ^p},z) < {g^{te}}({v_p}|{\lambda ^p},z)$ ，那么$ {v_p} = \hat y $ ，其中，$ p \in B(w) $ ；调度调整策略：
1) 如果初次调度后剩余的时间大于每一个供应点到需求点的时间，则对最优解集执行策略1得到新的调度方案；
2) 如果初次调度后剩余的时间大于一部分供应点到需求点的时间，则对最优解集执行策略2得到新的调度方案；
3) 如果初次调度后剩余的时间小于每一个供应点到需求点的时间，则不进行重新调度，保留初始调度方案。
4. 仿真与分析
以某军队作战期间维修保障活动为例，将作战阶段分为作战初期、作战中期和作战后期3个阶段，本文考虑短时间作战，每个调度周期将持续5个小时，3个供应中心，4个需求点，对3类维修资源进行优化调度调度。表1是供应中心向需求点运输的时间，资源运输时间效率降低参数3个阶段分别为0.9, 0.8, 0.6，重要度指标权重为
表 1 供应中心向需求点运输时间Table 1 Transportation time from supply center to demand pointh 供应中心 B1 B2 B3 B4 A1 1 1 3 4 A2 3 4 2 1 A3 4 2 2 2 $$ {{\boldsymbol{\varepsilon}} _l} = \left[ {0.3\;\;0.2\;\;0.2\;\;0.3} \right] 。 $$ 4个需求点的重要参数为
$$ {{\boldsymbol{\xi }}_{jl}} = \left[ {\begin{array}{*{20}{c}} {0.65}&{0.47}&{0.83}&{0.86} \\ {0.85}&{0.53}&{0.63}&{0.92} \\ {0.76}&{0.73}&{0.74}&{0.50} \\ {0.56}&{0.88}&{0.63}&{0.72} \end{array}} \right] $$ 4.1 参数设置
在MATLAB2018b仿真平台对数值案例进行仿真分析。选取NSGA-II、MOEA/D-DE和MOEA/D-SBX与本文算法进行对比。选取算法的参数提前调优以确保对比实验的公平性，交叉概率
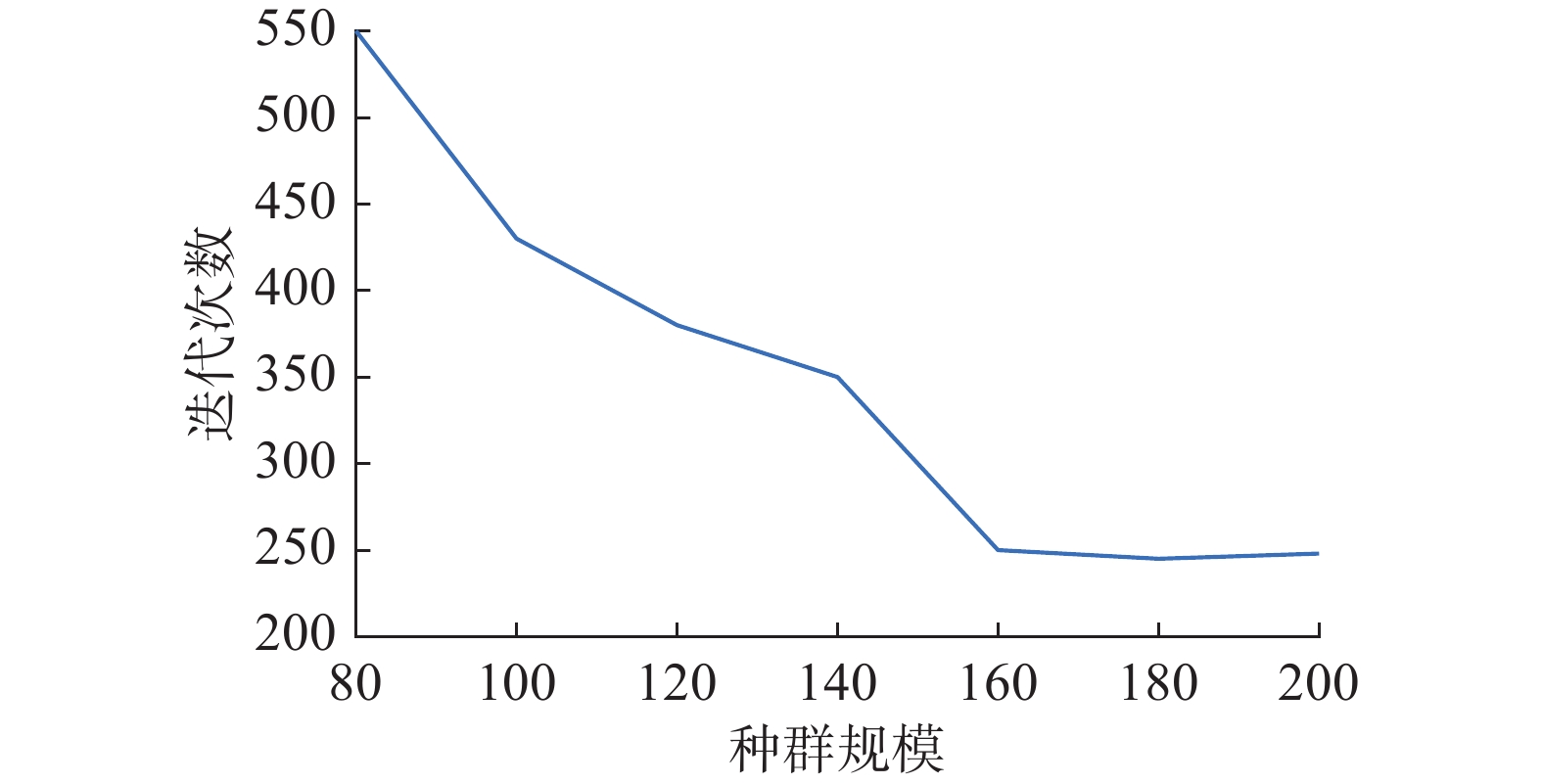
$ {p_c} $ 为0.8，变异概率$ {p_m} $ 为0.2，邻域大小为$ N/10 $ ，经过大量的实验分析可以发现，种群规模和算法的迭代次数都会影响算法的收敛性。虽然迭代次数越多，算法的精确度就越高，但是会造成计算资源的浪费，因此合适的种群规模十分重要。由于C系列算例的已知最优解集只有一个非支配解，方便我们观察迭代过程中最优解的收敛情况，因此本文使用C101算例仿真测试种群规模对算法收敛的影响情况，独立运行20次求获得最优解时迭代次数的平均值。由表2和图2可以知道，当种群规模达到180左右时，求得最优解的迭代次数趋于稳定。因此仿真实验时选取的种群规模为180，迭代次数为250。
表 2 种群规模对本文算法的收敛性影响Table 2 The influence of population size on the convergence of this algorithm种群规模 20 40 60 80 100 迭代次数 >550 >550 >550 550 421 种群规模 120 140 160 180 200 迭代次数 386 352 253 248 251 
图 2 种群规模对本文算法的收敛性影响Fig. 2 The influence of population size on the convergence of this algorithm下载:
全尺寸图片
4.2 评价指标
本文选用GD(generational distance)[22]指标和Spacing[23]指标和HV(hypervolume)[24]指标来评价和比较算法的收敛性和多样性。此外，还有众多评价指标[25]，本文不再赘述。
1) GD衡量了从
$ P $ 上各点到$ {P^{\text{*}}} $ 的平均最短距离，GD值越小，算法收敛性越好，计算公式为$$ {\rm{GD}}(P,{P^{\text{*}}}) = \dfrac{{\sqrt {\displaystyle\sum\limits_{y \in P} {\mathop {\min }\limits_{x \in {P^*}} {\rm{dis}}(x,y)} } }}{{\left| P \right|}} $$ 式中：
$ P $ 从算法求得的解集，$ {P^*} $ 为从PF上采样的一组均匀分布的参考点。2) Spacing:度量每个解到其他解的最小距离的标准差，体现解集中个体分布的均匀程度，Spacing值越小，解集分布越均匀。计算公式为
$$ {\rm{Spacing}}(P) = \sqrt {\dfrac{{\displaystyle\sum\limits_{i \in P} {{{(\overline d - {d_i})}^2}} }}{{\left| P \right| - 1}}} $$ 式中：
$ {d_i} $ 表示第$ i $ 个解到$ P $ 中其他解的最短距离，$ \overline d $ 表示所有$ {d_i} $ 的均值。3) HV为算法在目标空间中获得的与参照点围成区域的超体积，HV值越大表示算法的收敛性就越好，计算公式为
$$ {\rm{HV}} = {\rm{volume}}(\mathop \cup \limits_{y \in P} [{y_1},y_1^*] \times [{y_2},y_2^*]\times \cdots [{y_m},y_m^*]) $$ 其中
${y^*} = (y_1^*,y_2^*, \cdots, y_m^*)$ 是选择的参考点。4.3 算法性能分析
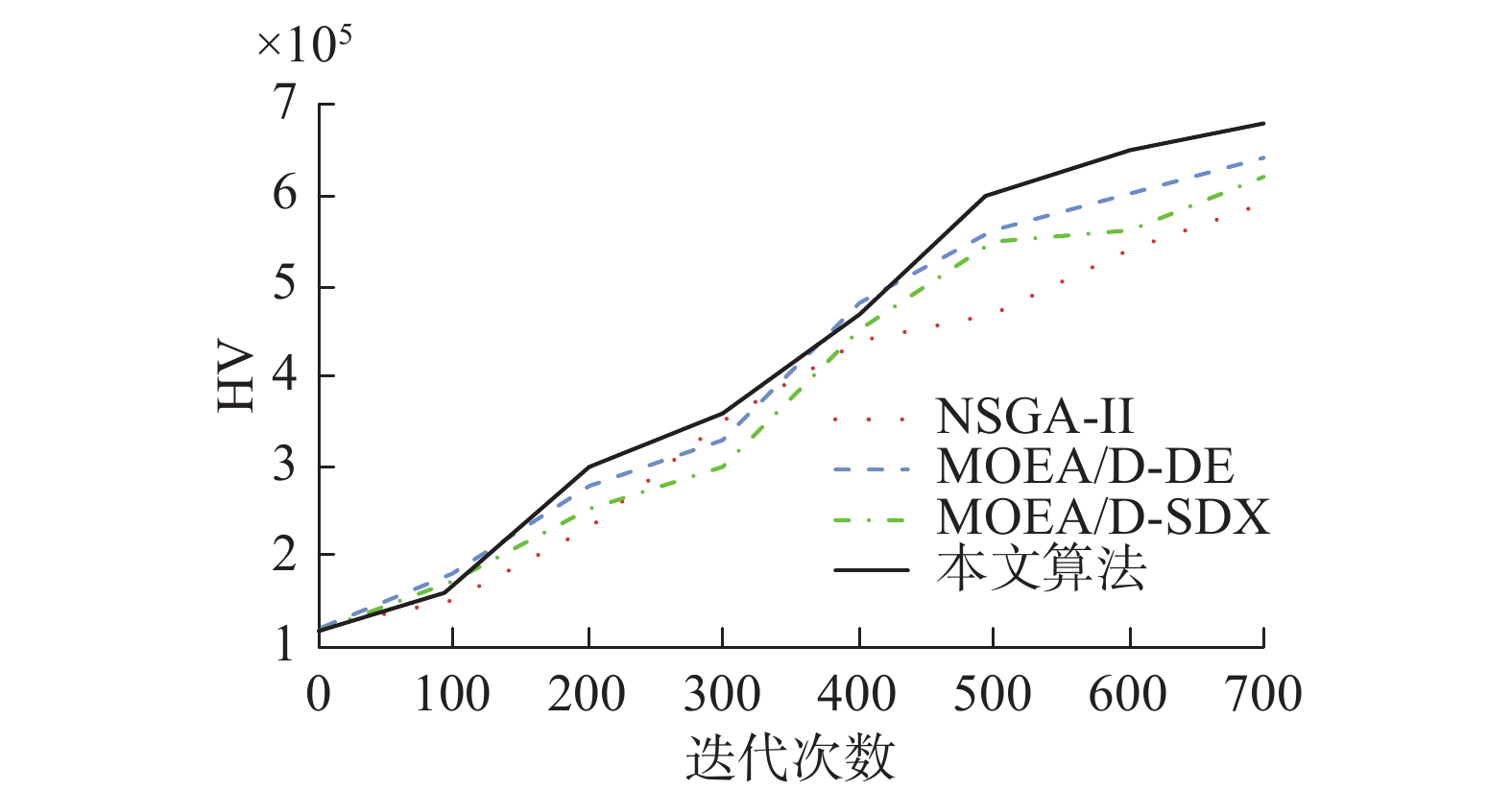
由图3和图4可知NSGA-II算法在收敛性和分布均匀性都较差；MOEA/D-DE算法收敛性较好，但是其分布均匀性与MOEA/D-SBX和本文算法相比都较差，MOEA/D-SBX分布均匀性较好，但是收敛性不如MOEA/D-DE算法和本文算法；本文算法在收敛性和分布均匀性都有较大的优势。
图 3 GD指标分布箱式图Fig. 3 Box diagram of GD index distribution下载:
全尺寸图片
图 4 Spacing指标分布箱式图Fig. 4 Box diagram of Spacing index distribution下载:
全尺寸图片
在作战过程中，战场指挥者需要根据候选的调度方案，选择出最为合理的维修资源调度方案，以便快速处理，保证作战的顺利进行。迭代250次，每个算法分别进行20次独立运行，可以得到超体积值、CPU运行时间和函数评价次数的平均值。
图5、表3结果显示，本文的算法相比于3种算法，收敛性能更好，运行时间较快。
图 5 HV指标图Fig. 5 HV indicatrix下载:
全尺寸图片
表 3 实验数值结果比较Table 3 Comparison of experimental and numerical results算法 HV CPU运行/s 评价次数 NSGA-II 5.9656 $ \times {10^5} $ 15.23 6.5236 $ \times {10^5} $ MOEA/D-DE 6.4562 $ \times {10^5} $ 8.65 5.2365 $ \times {10^5} $ MOEA/D-SDX 6.2956 $ \times {10^5} $ 9.23 5.6523 $ \times {10^5} $ 本文算法 6.8567 $ \times {10^5} $ 3.25 4.9689 $ \times {10^5} $ 4.4 优化调度结果
表4为供应中心维修资源存储量，表5为各需求点不同阶段维修资源预测需求量，由于内容过多，我们仅给出了一个供应中心的最终调度结果。如表6所示，针对供应中心A1，需求动态变化发生在作战的中期，且发生在调度周期的一个小时之内，由于一整个调度周期为5 h，因此所有的供应中心均可以为需求点提供动态的资源调度，根据调整策略1 进行动态的调整。对结果进行分析，供应中心A1向需求点B1在作战前期提供维修资源1的量为6.5，作战中期提供维修资源1的量是10.8，在作战中期发生动态需求变化时，由10.8变为了14.6，在作战后期提供维修资源1的量是4.5，发生动态需求变化后，剩余的维修资源量依旧可以完成剩余的初始调度方案，因此，作战后期维修资源1的供应量不变。如表7，针对供应中心A2，需求动态变化发生在作战的前期，且发生在调度周期的一半的时间点内，由于一整个调度周期为5 h，因此只有供应中心到需求点时间为2.5 h以下的供应中心可以提供动态的资源调度，根据调整策略2 进行动态的调整。对结果进行分析，供应中心A2向需求点B3在作战前期提供维修资源1的量为8.5，在作战前期发生动态需求变化时，由10.8变为了14.6，但是剩余的维修资源无法满足剩余的调度方案，因此根据种群初始化的方式为剩余的作战阶段产生新的调度方案，作战中期提供维修资源1的量由12.3变为了10.5，作战后期提供维修资源1的量由20.6变为了18.4。
表 4 供应中心维修资源存储量Table 4 Maintenance resource storage of supply center供应中心 A1 A2 A3 1 2 3 1 2 3 1 2 3 存储量 300 500 800 600 400 700 500 560 420 表 5 需求点不同阶段维修资源预测需求量Table 5 Forecast demand of maintenance resources at different stages of demand point需求点 B1 B2 B3 B4 1 2 3 1 2 3 1 2 3 1 2 3 前期 35 50 100 60 80 80 30 40 120 40 50 60 中期 30 45 80 28 40 120 45 60 60 20 30 50 后期 25 30 60 8 20 60 20 15 80 35 50 60 表 6 根据策略1的资源调度调整方案Table 6 Resource scheduling adjustment scheme according to strategy 1A B T 初始调度方案 调整后的调度方案 前期 中期 后期 前期 中期 后期 A1 B1 1 6.5 10.8 4.5 6.5 14.6 4.5 2 10.6 8.9 6.2 10.6 10.2 6.2 3 18.5 15.2 8.9 18.5 18.6 8.9 B2 1 4.0 6.5 2.2 4.0 8.2 2.2 2 16.5 9.8 3.5 16.5 16.2 3.5 3 12.8 20.6 10.3 12.8 28.6 10.3 B3 1 9.6 10.2 5.6 9.6 10.2 5.6 2 8.8 10.8 4.8 8.8 10.8 4.8 3 20.6 12.8 20.5 20.6 12.8 20.5 B4 1 9.5 0 0 9.5 0 0 2 10.2 12.6 8.8 10.2 12.6 8.8 3 0 0 12.5 0 0 12.5 表 7 根据策略2的资源调度调整方案Table 7 Resource scheduling adjustment scheme according to strategy 2A B T 初始调度方案 调整后的调度方案 前期 中期 后期 前期 中期 后期 A2 B1 1 9.2 15.6 10.8 9.2 15.6 10.8 2 12.5 14.2 9.6 12.5 14.2 9.6 3 8.2 12.3 10.0 8.2 12.3 10.0 B2 1 12.5 9.6 18.0 12.5 9.6 18.0 2 10.2 20.5 11.6 10.2 20.5 11.6 3 9.5 12.6 8.8 9.5 12.6 8.8 B3 1 8.5 12.3 20.6 14.2 10.5 18.4 2 10.6 20.3 15.3 16.8 15.8 14.3 3 18.2 15.6 9.6 22.6 12.6 8.8 B4 1 12.0 15.6 15.6 18.6 13.9 10.6 2 16.6 8.9 20.9 24.2 6.6 15.9 3 15.4 22.3 21.3 19.6 18.2 12.6 5. 结束语
考虑作战期间维修资源预测信息不准确，根据作战所处阶段的不同，本文建立了动态的维修资源调度优化模型。根据建立的模型，设计了改进的MOEA/D算法，利用正态分布交叉算子、全局探索增强型差分进化算子和自适应变异算子的协同进化策略，提高了算法的全局搜索能力，避免算法早熟，通过仿真对比实验，结果表明本文算法具有良好的收敛性和均匀分布性，并且适用于作战期间各阶段维修资源优化调度。
-
图 1 维修资源调度示意图
Fig. 1 Schematic diagram of maintenance resourcescheduling
下载:
全尺寸图片
图 2 种群规模对本文算法的收敛性影响
Fig. 2 The influence of population size on the convergence of this algorithm
下载:
全尺寸图片
图 3 GD指标分布箱式图
Fig. 3 Box diagram of GD index distribution
下载:
全尺寸图片
图 4 Spacing指标分布箱式图
Fig. 4 Box diagram of Spacing index distribution
下载:
全尺寸图片
图 5 HV指标图
Fig. 5 HV indicatrix
下载:
全尺寸图片
表 1 供应中心向需求点运输时间
Table 1 Transportation time from supply center to demand point
h 供应中心 B1 B2 B3 B4 A1 1 1 3 4 A2 3 4 2 1 A3 4 2 2 2 表 2 种群规模对本文算法的收敛性影响
Table 2 The influence of population size on the convergence of this algorithm
种群规模 20 40 60 80 100 迭代次数 >550 >550 >550 550 421 种群规模 120 140 160 180 200 迭代次数 386 352 253 248 251 表 3 实验数值结果比较
Table 3 Comparison of experimental and numerical results
算法 HV CPU运行/s 评价次数 NSGA-II 5.9656 $ \times {10^5} $ 15.23 6.5236 $ \times {10^5} $ MOEA/D-DE 6.4562 $ \times {10^5} $ 8.65 5.2365 $ \times {10^5} $ MOEA/D-SDX 6.2956 $ \times {10^5} $ 9.23 5.6523 $ \times {10^5} $ 本文算法 6.8567 $ \times {10^5} $ 3.25 4.9689 $ \times {10^5} $ 表 4 供应中心维修资源存储量
Table 4 Maintenance resource storage of supply center
供应中心 A1 A2 A3 1 2 3 1 2 3 1 2 3 存储量 300 500 800 600 400 700 500 560 420 表 5 需求点不同阶段维修资源预测需求量
Table 5 Forecast demand of maintenance resources at different stages of demand point
需求点 B1 B2 B3 B4 1 2 3 1 2 3 1 2 3 1 2 3 前期 35 50 100 60 80 80 30 40 120 40 50 60 中期 30 45 80 28 40 120 45 60 60 20 30 50 后期 25 30 60 8 20 60 20 15 80 35 50 60 表 6 根据策略1的资源调度调整方案
Table 6 Resource scheduling adjustment scheme according to strategy 1
A B T 初始调度方案 调整后的调度方案 前期 中期 后期 前期 中期 后期 A1 B1 1 6.5 10.8 4.5 6.5 14.6 4.5 2 10.6 8.9 6.2 10.6 10.2 6.2 3 18.5 15.2 8.9 18.5 18.6 8.9 B2 1 4.0 6.5 2.2 4.0 8.2 2.2 2 16.5 9.8 3.5 16.5 16.2 3.5 3 12.8 20.6 10.3 12.8 28.6 10.3 B3 1 9.6 10.2 5.6 9.6 10.2 5.6 2 8.8 10.8 4.8 8.8 10.8 4.8 3 20.6 12.8 20.5 20.6 12.8 20.5 B4 1 9.5 0 0 9.5 0 0 2 10.2 12.6 8.8 10.2 12.6 8.8 3 0 0 12.5 0 0 12.5 表 7 根据策略2的资源调度调整方案
Table 7 Resource scheduling adjustment scheme according to strategy 2
A B T 初始调度方案 调整后的调度方案 前期 中期 后期 前期 中期 后期 A2 B1 1 9.2 15.6 10.8 9.2 15.6 10.8 2 12.5 14.2 9.6 12.5 14.2 9.6 3 8.2 12.3 10.0 8.2 12.3 10.0 B2 1 12.5 9.6 18.0 12.5 9.6 18.0 2 10.2 20.5 11.6 10.2 20.5 11.6 3 9.5 12.6 8.8 9.5 12.6 8.8 B3 1 8.5 12.3 20.6 14.2 10.5 18.4 2 10.6 20.3 15.3 16.8 15.8 14.3 3 18.2 15.6 9.6 22.6 12.6 8.8 B4 1 12.0 15.6 15.6 18.6 13.9 10.6 2 16.6 8.9 20.9 24.2 6.6 15.9 3 15.4 22.3 21.3 19.6 18.2 12.6 -
[1] 宋建社, 曹小平, 曹耀钦, 等. 装备维修信息化工程[M]. 北京: 国防工业出版社, 2005: 1−8. [2] 曹小平, 路广安. 装备维修器材保障[M]. 北京: 国防大学出版社, 2008: 10-15. [3] 王涛. 基于混合进化算法的军用车辆维修保障资源调度优化研究[D]. 北京: 北京理工大学, 2013. WANG Tao. Research on maintenance resource scheduling optimization for military vehicles based on hybrid evolutionary algorithm[D]. Beijing: Beijing Institute of Technology, 2013. [4] 张柳, 聂成龙, 张伟. 装备作战单元维修保障建模与仿真[M]. 北京: 国防工业出版社, 2015. [5] JAIN N N, R S K, AKRAM S. Improvising process scheduling using machine learning[C]//2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology. Bangalore: IEEE, 2018: 1379−1382. [6] 孙笑, 宋卫星, 班利明, 等. 复杂人力资源约束下的抢占式维修工序调度[J]. 控制与决策, 2022, 37(2): 393–400. SUN Xiao, SONG Weixing, BAN Liming, et al. Preemptive maintenance process scheduling under complex human resource constraints[J]. Control and decision, 2022, 37(2): 393–400. [7] WANG Yadong, SHI Quan, HU Qiwei. Dynamic multi-objective optimization for multi-period emergency logistics network[J]. Journal of intelligent & fuzzy systems, 2019, 37(6): 8471–8481. [8] WANG Feiyue, PEI Zhongwei, DONG Longjun, et al. Emergency resource allocation for multi-period post-disaster using multi-objective cellular genetic algorithm[J]. IEEE access, 2020, 8: 82255–82265. [9] 张鑫, 赵金超, 张勇明. 基于蚁群算法的舰船维修资源优化调度[J]. 兵工自动化, 2011, 30(11): 31–35. doi: 10.3969/j.issn.1006-1576.2011.11.009 ZHANG Xin, ZHAO Jinchao, ZHANG Yongming. Optimized dispatching of warship maintenance resources based on ant colony algorithm[J]. Ordnance industry automation, 2011, 30(11): 31–35. doi: 10.3969/j.issn.1006-1576.2011.11.009 [10] 陈盖凯, 李海瑞. 基于应急模式的飞机维修资源优化调度方法[J]. 空军预警学院学报, 2016, 30(1): 9–12,16. doi: 10.3969/j.issn.2095-5839.2016.01.003 CHEN Gaikai, LI Hairui. Optimal scheduling method of aircraft maintenance resources in emergency mode[J]. Journal of air force early warning academy, 2016, 30(1): 9–12,16. doi: 10.3969/j.issn.2095-5839.2016.01.003 [11] ZHENG Junxi, CAO Junhai, AN Binlai. Optimization modeling and decision making of equipment maintenance resource scheduling based on NSGA-2 algorithm[C]//Proceedings of the 2019 3rd International Conference on Innovation in Artificial Intelligence-ICIAI 2019. New York: ACM Press, 2019: 253−257. [12] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017 [13] 张敏, 罗文坚, 王煦法. 一种基于正态分布交叉的ε-MOEA[J]. 软件学报, 2009, 20(2): 305−314. ZHANG Min, LUO Wenjian, WANG Xufa. A normal distribution crossover for ε-MOEA[J]. Journal of software, 2009, 20(2): 305−314. [14] 白芸, 高玉渊. 差分进化算法在旅行商问题中的应用[J]. 科学技术创新, 2022(23): 23–26. doi: 10.3969/j.issn.1673-1328.2022.23.007 BAI Yun, GAO Yuyuan. Application of differential evolution algorithm in traveling salesman problem[J]. Scientific and technological innovation, 2022(23): 23–26. doi: 10.3969/j.issn.1673-1328.2022.23.007 [15] ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712–731. doi: 10.1109/TEVC.2007.892759 [16] KANG Qi, SONG Xinyao, ZHOU Mengchu, et al. A collaborative resource allocation strategy for decomposition-based multiobjective evolutionary algorithms[J]. IEEE transactions on systems, man, and cybernetics:systems, 2019, 49(12): 2416–2423. doi: 10.1109/TSMC.2018.2818175 [17] WANG Jiahai, WENG Taiyao, ZHANG Qingfu. A two-stage multiobjective evolutionary algorithm for multiobjective multidepot vehicle routing problem with time windows[J]. IEEE transactions on cybernetics, 2019, 49(7): 2467–2478. doi: 10.1109/TCYB.2018.2821180 [18] QI Yutao, MA Xiaoliang, LIU Fang, et al. MOEA/D with adaptive weight adjustment[J]. Evolutionary computation, 2014, 22(2): 231–264. doi: 10.1162/EVCO_a_00109 [19] 耿焕同, 许可, 戴中斌, 等. 基于双重贡献分配的多目标混合算子进化算法[J]. 控制与决策, 2022, 37(5): 1195–1202. GENG Huantong, XU Ke, DAI Zhongbin, et al. Multi-objective evolutionary algorithm with multiple operators based on double credit assignment[J]. Control and decision, 2022, 37(5): 1195–1202. [20] DAS S, ABRAHAM A, CHAKRABORTY U K, et al. Differential evolution using a neighborhood-based mutation operator[J]. IEEE transactions on evolutionary computation, 2009, 13(3): 526–553. doi: 10.1109/TEVC.2008.2009457 [21] 温泽宇, 谢珺, 谢刚, 等. 基于新型拥挤度距离的多目标麻雀搜索算法[J]. 计算机工程与应用, 2021, 57(22): 102–109. doi: 10.3778/j.issn.1002-8331.2011-0468 WEN Zeyu, XIE Jun, XIE Gang, et al. Multi-objective sparrow search algorithm based on new crowding distance[J]. Computer engineering and applications, 2021, 57(22): 102–109. doi: 10.3778/j.issn.1002-8331.2011-0468 [22] VAN VELDHUIZEN D A, LAMONT G B. On measuring multiobjective evolutionary algorithm performance[C]//Proceedings of the 2000 Congress on Evolutionary Computation. CEC00 (Cat. No. 00TH8512). La Jolla: IEEE, 2000: 204−211. [23] BANDYOPADHYAY S, PAL S K, ARUNA B. Multiobjective GAs, quantitative indices, and pattern classification[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2004, 34(5): 2088–2099. doi: 10.1109/TSMCB.2004.834438 [24] BADER J, ZITZLER E. HypE: an algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary computation, 2011, 19(1): 45–76. doi: 10.1162/EVCO_a_00009 [25] 李密青, 郑金华. 一种多目标进化算法解集分布广度评价方法[J]. 计算机学报, 2011, 34(4): 647–664. doi: 10.3724/SP.J.1016.2011.00647 LI Miqing, ZHENG Jinhua. An indicator for assessing the spread of solutions in multi-objective evolutionary algorithm[J]. Chinese journal of computers, 2011, 34(4): 647–664. doi: 10.3724/SP.J.1016.2011.00647
