融合经验反思机制的教与学优化算法

吴迪; 贾鹤鸣; 刘庆鑫; 齐琦; 王爽

doi:10.11992/tis.202112043

融合经验反思机制的教与学优化算法

doi: 10.11992/tis.202112043

吴迪¹,
贾鹤鸣^2, ,,
刘庆鑫³,
齐琦³,
王爽²

1.
三明学院教育与音乐学院，福建三明 365004;
2.
三明学院信息工程学院，福建三明 365004;
3.
海南大学计算机科学与技术学院，海南海口 570228

基金项目: 全国教育科学规划教育部重点课题(DIA220374).

详细信息

作者简介:
吴迪，副教授，博士，主要研究方向为元启发式优化算法、现代教育技术;

贾鹤鸣，教授，主要研究方向为群体智能优化算法与工程应用。主持福建省自然科学基金等项目10余项。发表学术论文60余篇;

刘庆鑫，硕士研究生，主要研究方向为智能优化算法及现实应用.

通讯作者:
贾鹤鸣. E-mail： jiaheminglucky99@126.com.

中图分类号: TP301.6
出版历程
- 收稿日期: 2021-12-30
- 网络出版日期: 2023-03-24

Teaching and learning optimization algorithm based on empirical reflection mechanism

1.
School of Education and Music, Sanming University, Sanming 365004, China;
2.
School of Information Engineering, Sanming University, Sanming 365004, China;
3.
School of Computer Science and Technology, Hainan University, Haikou 570228, China

摘要

摘要: 针对传统教与学算法存在易陷入局部最优、收敛速度慢和求解精度低等问题，提出一种融合经验反思机制的教与学优化算法(empirical reflection teaching learning based optimization, ERTLBO)。首先在教学阶段引入经验反思机制，遴选精英个体引导普通个体向教师靠近，提高班级整体水平，从而提高算法全局探索能力。其次在学习阶段引入动态自适应权重，能够根据学生的适应度值对位置进行自适应扰动，进而实现个体位置的动态更新，提高算法跳出局部最优的能力。仿真实验选取23个基准测试函数对ERTLBO同其他变体和流行算法进行性能测试。实验结果表明，ERTLBO算法具有更好的寻优性能和求解稳定性。最后，通过2个工程设计问题进一步验证ERTLBO解决实际问题的有效性和优越性。
- 教与学优化算法 /
- 经验反思机制 /
- 动态自适应权重 /
- 元启发式算法 /
- 基准函数 /
- 压力容器设计问题 /
- 焊接梁设计问题 /
- Wilcoxon秩和检验
Abstract: In this paper, an empirical reflection teaching learning based optimization (ERTLBO) algorithm is proposed to solve the problems of easy falling into local optimum, slow convergence speed and low accuracy in traditional teaching-learning-based optimization. Firstly, the empirical reflection mechanism is introduced in the teaching stage to select elite individuals, guide ordinary individuals to approach teachers, and improve the overall level of the class, so as to improve the overall exploration ability of the algorithm. Secondly, the dynamic adaptive weight is introduced in the learning stage, which can adaptively disturb the position according to the fitness value of students, so as to realize dynamic updating of individual position and improve the ability of the algorithm to jump out of local optimum. In the experiment, 23 benchmark functions are selected to test the performance of ERTLBO, variant, and popular algorithms. Experimental results show that ERTLBO has better optimization performance and solution stability. Finally, the effectiveness and superiority of ERTLBO in solving practical problems are further verified through two engineering design problems.
- teaching and learning-based optimization /
- empirical reflection mechanism /
- dynamic adaptive weight /
- meta-heuristic algorithm /
- benchmark functions /
- pressure vessel design problem /
- welded beam design problem /
- Wilcoxon rank-sum test

HTML全文

近年来不同学科和工程领域中的优化问题日益复杂与多样化，诸如牛顿法、梯度下降法和共轭梯度法等传统优化方法已经不能满足实际需求。因此，许多研究者受自然启发，通过模仿生物或物理现象提出了各种元启发式优化算法。与传统优化算法不同，元启发式优化算法概念简单，不需要梯度信息，灵活且易于实现，可广泛应用于不同领域下的各类优化问题^[1-3]。其中，教与学优化算法(teaching-learning-based optimization, TLBO)^[4]是印度学者Rao等于2011年提出的一种以班级内教师教学和学生学习为设计思想的群体智能优化算法，该算法将优化求解空间模拟为一个班级，而班级里的每位学生就对应于解空间中的搜索个体，每个学生的成绩对应于解的适应度值，教师则代表当前整个群体中适应度值最好的解。该算法思想清晰，来源于基本的教育理论和教育方法，原理简单且参数较少，具有较快的收敛速度，已被成功应用于多个学术或工业领域，如：天线优化设计^[5]、电力系统优化调度^[6]、结构可靠性分析^[7]、手势识别技术^[8]等。然而，无免费午餐理论^[9]指出没有一种算法能独立解决所有的优化问题，即每种优化算法都具有其自身的优势和局限性，只能在某些领域中表现出较好的效果。因此，不断有学者提出各种新颖或改进的优化算法试图解决不同的优化问题。

李丽荣等^[10]提出了一种基于头脑风暴策略的改进教与学优化算法，在学习阶段选择优秀的学生个体与当前个体进行头脑风暴式学习，提高算法开发能力。欧阳城添等^[11]提出一种改进天牛须搜索的教与学优化算法，在教学阶段引入天牛须搜索，提高解的精度，学习阶段利用混合变异，提高算法跳出局部最优能力。李丽荣等^[12]为克服算法易出现早熟收敛和搜索精度差的问题，在教学部分引入自适应因子，提高教师自身学习能力，很好的保持了种群的多样性。Lakshmi等^[13]提出一种鲸鱼与教与学混合优化算法，在23个基准测试函数表现出一定求解能力，并将其应用于面部情绪识别领域。Xu等^[14]提出基于动态反向学习的教与学优化算法，利用非对称搜索空间显著提高了种群获得全局最优解的概率，整体上提高了种群的开发能力。Tsai等^[15]在教学和学习阶段引入不同的突变策略来提高算法探索与开发能力。Shukla等^[16]引入混沌映射与动态自适应权重提高种群多样性与收敛能力，并应用于目标分类中。Taheri等^[17]提出一种平衡教与学优化算法，引入辅导阶段和重启阶段平衡算法探索和开发能力。

上述研究方法对TLBO的收敛速度与收敛精度均有改善，但上述诸多研究思想都是从数学公式的改进或者融入一些生物机制角度进行算法效果的提升，往往与原算法作者提出的教育学理论不一致，忽视了元启发式算法的设计初衷。本文的主旨在于吸收学习教育学的基本理论和思想，从教育学原理角度对教师的教和学生的学进行改进，利用当下主流的教育思想来设计算法的改进公式，提出一种融合经验反思机制的教与学优化算法。在教学阶段引入经验反思策略，鼓励精英个体引导普通个体向最优位置靠近，使得不同类型个体之间具有更强的联系，从而提升班级整体水平。学习阶段引入动态自适应权重，根据个体适应度值进行位置扰动，实现动态位置更新，提升算法避免早熟收敛能力，提高收敛精度。通过23个测试函数、Wilcoxon秩和检验、焊接梁设计问题以及压力容器设计问题进行测试实验，实验结果表明改进算法具有更优越的寻优性能和鲁棒性，解决实际工程问题时效果显著。

1. 教与学优化算法

教与学优化算法主要灵感来源于课堂上教师教学行为与学生的学习行为。TLBO将种群集合称为班级，种群中个体称为学生，当前适应度值最佳的个体称为教师。该算法具体过程分为教师教学阶段与学生学习阶段。

1.1 教学阶段

在教学阶段，教师向学生传授知识，以提高班级的整体水平。考虑到教学成果受到班级平均成绩影响，因此位置更新方式表达为

$$ {\boldsymbol{X}}_i^{{\text{new}}}(t + 1) = {{\boldsymbol{X}}_i}(t) + {\text{rand}} \times ({{\boldsymbol{X}}_{{\text{teacher}}}}(t) - {T_F} \times {{\boldsymbol{X}}_{{\text{mean}}}}(t)) $$

(1)

式中：X_i^new(t+1)与X_i(t)分别学习后的个体与学习前的个体；rand表示均匀分布在0~1的随机数；X_teacher(t)代表种群内最佳个体，称为教师；T_F称为教学因子，随机确定为1或2；X_mean(t)是种群平均位置。

1.2 学习阶段

在学习阶段，学生之间相互交流，来提高自己的成绩。具体来说，学生X_r1(t)随机选择X_r2(t)进行交流学习，比较学习成绩，选出学习优秀的学生引导另一位学习，其数学表达式为

$$ {{\boldsymbol{X}}}_{i}^{\text{new}}(t+1)=\left\{\begin{array}{l}{{\boldsymbol{X}}}_{i}^{\text{old}}(t)+\text{rand}\times ({{\boldsymbol{X}}}_{r1}(t)-{{\boldsymbol{X}}}_{r2}(t)),\\ f({X}_{r1}(t)) > f({X}_{r2}(t))\\ {{\boldsymbol{X}}}_{i}^{\text{old}}(t)+\text{rand}\times ({{\boldsymbol{X}}}_{r2}(t)-{{\boldsymbol{X}}}_{r1}(t)),\;\;其他\end{array}\right. $$

(2)

其中，f(·)表示需要优化的目标函数；X_r1(t)与X_r2(t)代表2个随机个体。TLBO算法伪代码如下所示。

1) 设置种群规模N，当前迭代次数t，最大迭代次数T

2) 初始化种群位置

3)While t < T

4)计算个体适应度值并选取最佳个体为教师

5) For i = 1 to N

6)教学阶段：通过式(1)更新种群位置

7)学习阶段：通过式(2)更新种群位置

8) End For

9) t = t+1

10) End While

2. 融合经验反思机制的教与学优化算法

2.1 经验反思教学模式

教与学算法在教学阶段强调学生从教师的授课中获得知识。依据教学相长理论，教师需要不断提升自身素养才能促进学生不断学习。原算法中的策略是教师依据学生的平均成绩进行教学，然而这种教学模式没有获得学生反馈，无法根据学生所学情况进行教学模式的调整。同时，该模式也没有考虑更多学生个体不同的个性情况，容易以点盖面片面地对学生进行教授。这种情况是由于当下缺少一种教师对学生学习情况经验反思的机制导致的。现有的机制并不能够保障将获得的成功的教学经验或者失败的经验吸收转化，忽视了持续改进的作用，从而无法进一步提升教学质量（水平）。因此本文改进思想正是在教学阶段加入一个基于经验反思的机制，通过反思教师可以对学生的学习行为进行及时监控，根据学生学习情况对自身进行有效调整，从而可以保证教学效果的持续改进，因此融入反思机制的教与学算法，相比于其他算法，具有循环增强和持续改进的特点。

在标准教与学算法的教学阶段中，教师向学生传授知识，希望整体平均位置向教师靠近，从而提高全班的平均成绩。然而，该模式下可能会导致算法探索能力不强，影响实际寻优效果。针对这一问题，提出一种经验反思策略，根据不同学生的学习情况调整教学方式，提高整体教学质量，具体描述如下：

$$ \begin{gathered} {\boldsymbol{X}}_i^{{\text{new}}}(t + 1) = {\boldsymbol{X}}_i^{{\text{old}}}(t) + {{\text{e}}^{\frac{{ - 10 t}}{T}}} \times ({{\boldsymbol{X}}_{{\text{teacher}}}}(t) - {{\boldsymbol{X}}_{r3}}(t)) + \\ {\text{rand}} \times ({{\boldsymbol{X}}_{{\text{bp}}}}(t) - {{\boldsymbol{X}}_{{\text{np}}}}(t)) \end{gathered} $$

(3)

式中：T为最大迭代次数；X_r3(t)代表随机个体位置；X_bp(t)与X_np(t)分别代表成绩排名前30%与后70%的随机个体（即适应度排名前30%和后70%的个体）。

由上述可知，在完成教学阶段后，教师会对学生成绩（适应度值评估）进行观测并收集反馈意见，记录成绩没有提升的学生个体数量。若学生数量没有超过该班级学生总数量的60%（反思阈值R），即大部分个体适应度值均不理想。此时教师对自己的教学行为进行反思，依据不同层次的学生来调整教学模式，对剩下的个体进行经验反思式教学，选拔优秀适应度值个体辅导普通个体，使整体种群位置朝最优点靠近，进而提高整体的学习质量。

2.2 动态自适应学习模式

在学习阶段中，学生之间互相学习，与其他同学交流知识，从而提高对知识的理解程度。TLBO随机选择2个学生，比较其适应度值，将优秀学生的位置减去次优学生，以提高次优学生知识水平。然而，仅通过随机选取的2个体无法有效提高学生成绩，容易在局部最优值附近停止，导致算法收敛速度慢。合适的选择动态权值能够加速算法寻优效果，提高算法收敛速度^[18]。因此，提出一种动态自适应学习模式，提升算法避免早熟收敛能力，数学表达式如下：

$$ {w_i}(t) = \left\{ \begin{split} & k \times {\text{sin(rand}} \times {\text{π }}) \times \left( {\frac{{{f_i}(t) - {f_{{\text{min}}}}(t)}}{{{f_{{\text{avg}}}}(t) - {f_{{\text{min}}}}(t)}}} \right),{f_i}(t) \leqslant {f_{{\text{avg}}}}(t) \\ & k,{\text{ }}{f_i}(t) > {f_{{\text{avg}}}}(t) \end{split} \right. $$

(4)

式中：k为常量；f_i(t)为第i个个体所获适应度值；f_min(t)为全局最优适应度值（以求极小值为例）；f_avg(t)为种群平均适应度值。

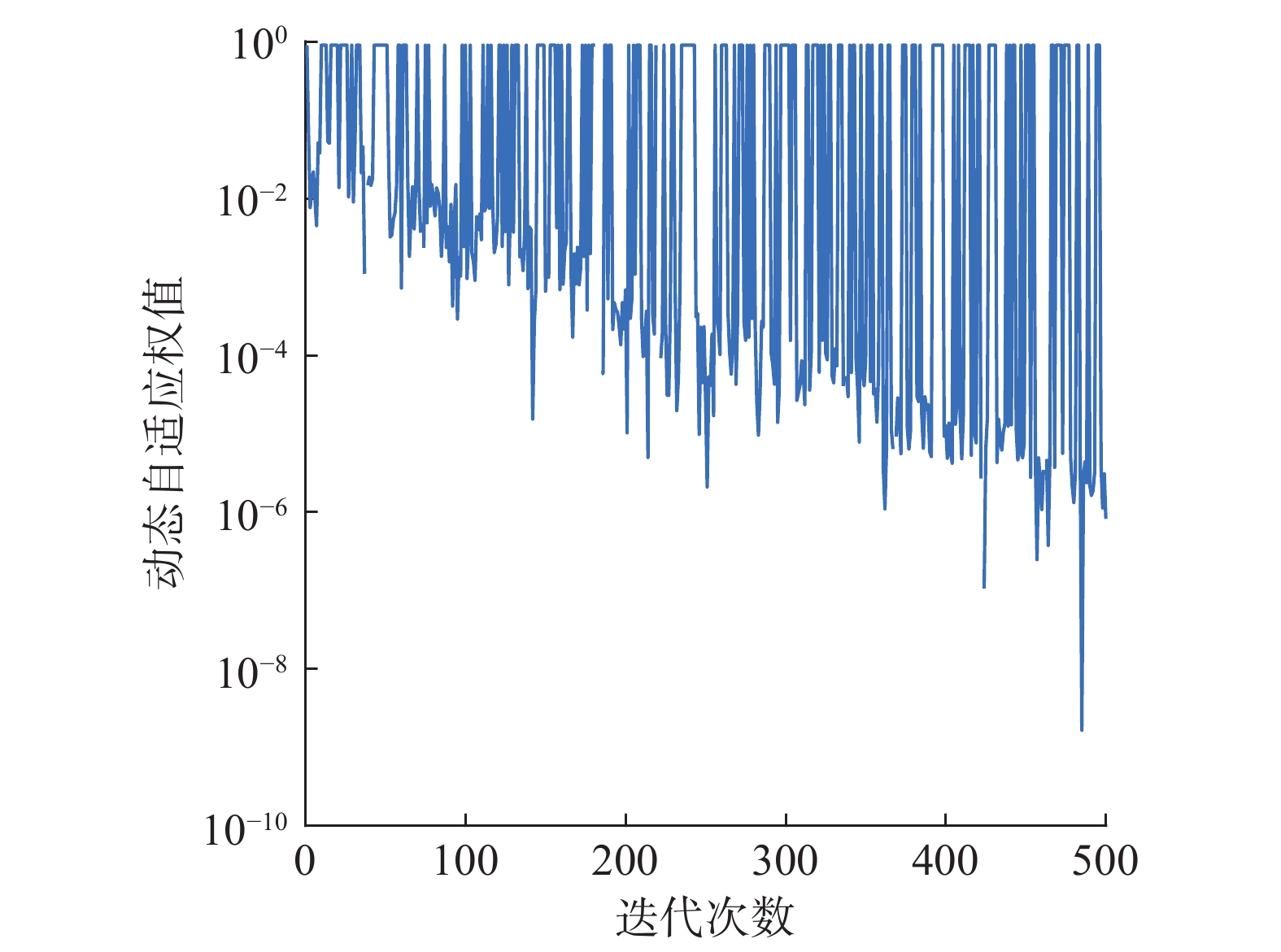
根据式(4)可知，若当前个体适应度值小于种群平均适应度，惯性权值将较小，对算法的扰动减小，允许当前个体充分开发邻近区域，提升局部寻优能力。反之，若当前个体适应度值大于种群平均适应度时，借助扰动因子k可有效扩大搜索范围，明显增强其全局探索能力。图1代表某个体基于式(4)所得自适应权值曲线图，图中自适应权值呈振荡下降趋势。结合式(4)可以看出，个体适应度值时常小于种群平均适应度值，因此产生一个较小的权值对位置进行扰动，可令种群充分开发邻近区域，提升求解精度。为了帮助个体选择最佳搜索模式，本文经过大量实验分析，将扰动因子k设置为0.5最为合适。

图 1 动态自适应权值曲线

Fig. 1 Dynamic adaptive weight curve

下载: 全尺寸图片

基于上述分析，本文将动态自适应权重与学习阶段相结合，提出了改进的动态自适应学习模式，改进更新公式为

$$\begin{gathered} {\boldsymbol{X}}_i^{{\text{new}}}(t + 1) = \\ \left\{ \begin{split} & {w_i}(t) \times {{\boldsymbol{X}}_i}(t) + {\text{rand}} \times ({{\boldsymbol{X}}_{r1}}(t) - {{\boldsymbol{X}}_{r2}}(t)), f({{\boldsymbol{X}}_{r1}}(t)) > f({{\boldsymbol{X}}_{r2}}(t)) \\ & {w_i}(t) \times {{\boldsymbol{X}}_i}(t) + {\text{rand}} \times ({{\boldsymbol{X}}_{r2}}(t) - {{\boldsymbol{X}}_{r1}}(t)), {\text{其他}} \end{split} \right.\end{gathered} $$

(5)

综上两节，将经验反思机制融合到教学模式中，允许教师在教学环境中参考不同层次学生的知识掌握情况，进而调整教学模式。与此同时，鼓励学习成绩不好的学生(适应度值排名位于后40%个体)向成绩好的学生学习(适应度值排名位于前60%个体)，进而提升班级整体成绩，提升算法的全局探索能力。此外，式(3)中的 $ {{\rm{e}}^{\tfrac{{ - 10 t}}{T}}} $ 是从1到0线性递减的参数，迭代前期主要依靠老师完成教学任务，但随着迭代次数的增加，一些成绩好的学生能够与老师互相配合，提升整体适应度值水平。学习阶段引入动态自适应系数，根据个体适应度值进行位置扰动，帮助个体调整最佳搜索模式，从而增加个体找到最优解的几率，同时有效避免算法易陷入局部最优，提升算法收敛精度。上述改进策略分别增强了算法的全局探索与局部开发能力，利用经验反思提升了算法整体探索能力，迭代前期主要由教师完成教学活动，当班级整体学习效果不佳时，教师利用经验反思策略引导学生学习，提升班级整体水平。利用动态自适应学习系数令个体进行适当扰动，提升了局部开发能力，避免算法陷入局部极值，使得算法在全局和局部的能力上达到有效平衡。

2.3 算法实现

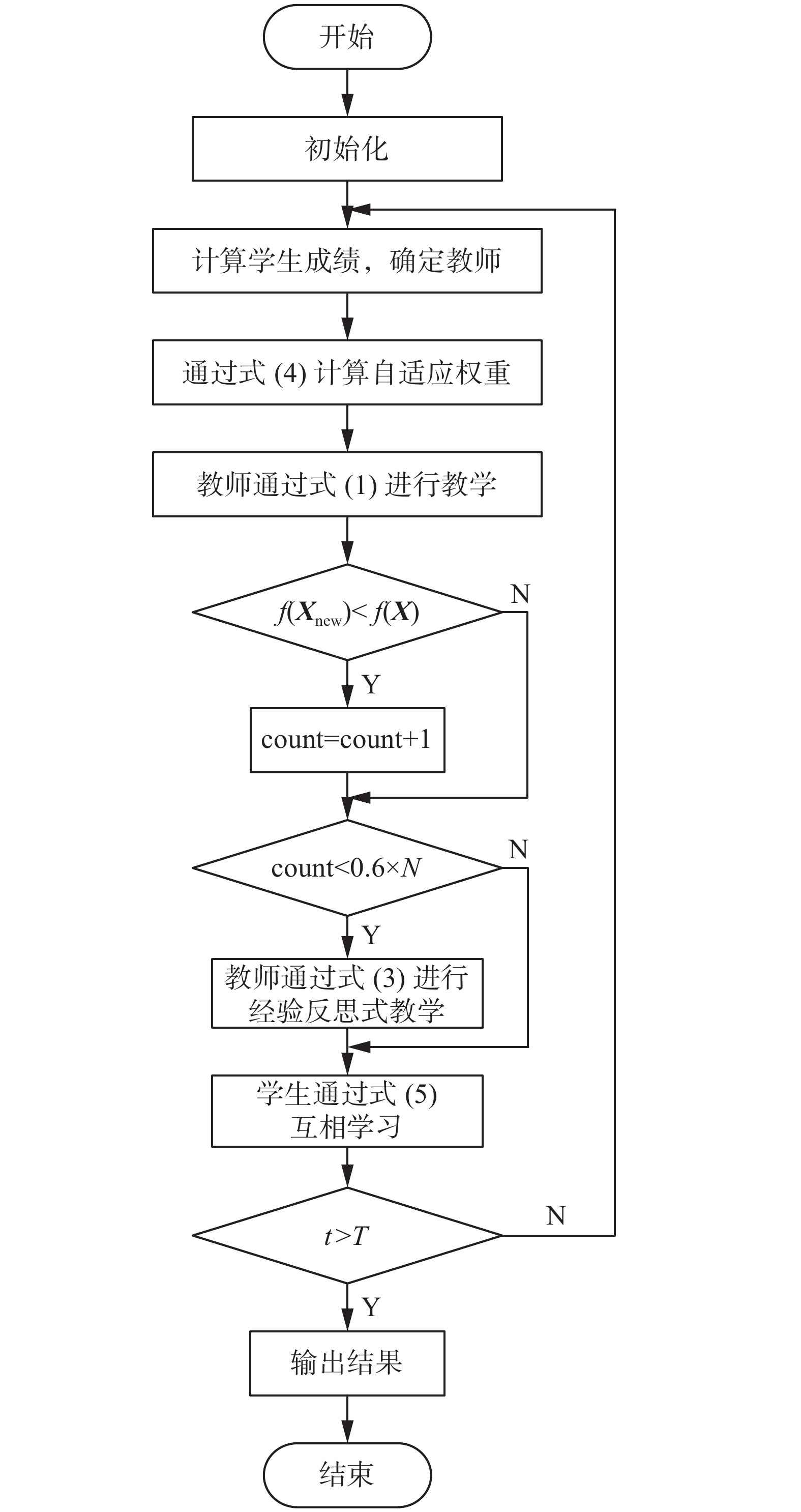
将经验反思机制与动态自适应权重加入到教与学优化算法中，改进传统教与学优化算法的寻优能力。ERTLBO算法伪代码如下，执行流程如图2所示。

图 2 ERTLBO算法实现流程图

Fig. 2 Flowchart of ERTLBO algorithm

下载: 全尺寸图片

ERTLBO算法如下：

1)初始化种群规模N,当前迭代t，最大迭代次数T，反思阈值count

2)初始化种群位置

3) While t < T

4)计算个体适应度值并选取最佳个体为教师

5)根据式(4)计算权重因子w

6) For i = 1 to N

7)通过式(1)计算种群位置

8) If f(X_new)<f(X)

9) count=count+1

10) End If

11) If count < 0.6 × N

12)通过经验反思机制（式(3)）更新种群位置

13) End If

14)通过式(4)计算种群位置

15) End For

16) t = t+1

17) End While

2.4 运算复杂度分析

由1、2节内容可知，TLBO算法运算复杂度主要取决于以下过程：初始化阶段、适应度值评估以及种群位置更新阶段。定义种群规模N、问题维度D、最大迭代次数T。则初始化阶段复杂度为O(N×D)，适应度值评估部分复杂度为O(N×T)。种群位置更新分为教师教学阶段及学生学习阶段，运算复杂度为O(N×D×T)。因此TLBO算法运算复杂度为O(N×D×T)。同理，ERTLBO算法运算复杂度取决于初始化阶段、适应度值评估以及种群位置更新阶段。初始化阶段复杂度为O(N×D)，适应度值评估部分复杂度为O(N×T)。种群位置更新分为教学阶段、经验反思教学模式以及学生相互学习阶段，因此该部分运算复杂度为O(N×D×T)。综上所述，ERTLBO运算复杂度为O(N×D×T)，可知改进算法与原始算法运算复杂度相同，并未对算法产生负面影响。

3. 实验仿真与分析

3.1 仿真环境

本次实验环境为64位Windows 10系统，处理器型号Intel(R) Core(TM) i5-9500 CPU,主频为3.00 GHz，内存24 GB，使用基于R2018b版MATLAB实现。为验证本文提出改进算法的有效性，采用23个标准测试函数对ERTLBO进行性能测试^[19]。标准测试函数包括7个单峰函数，6个多峰测试函数与10个固定维多峰测试函数。其中函数F1~F7只有一个全局最优解，验证算法的局部开发能力与收敛速度。函数F8~F23具有多个局部最优值与一个全局最优值，可验证算法跳出局部最优与全局搜索能力。因此，通过不同类型的测试函数，可充分验证算法的寻优性能。

3.2 对比算法与参数设置

为了更好地验证ERTLBO算法性能，本文采用两组优化算法进行对比。其中一组为TLBO改进算法，如BASTLBO、ITLBOBSO与DSLTLBO。另一组为目前主流优化算法如SSA^[20]、WOA^[21]、GWO^[22]以及GA^[23]。这些算法被证实具有良好的寻优能力。为确保实验结果有效性，统一设定种群规模N=30，维度D=100，最大迭代次数T=500，各算法独立运算100次进行统计分析。算法参数设置如表1所示。选取平均值、标准差与Wilcoxon秩和检验作为评价指标。在解决极小值问题中，平均值可以反映算法收敛精度与寻优能力，标准差可以反映算法搜索结果鲁棒性，Wilcoxon秩和检验可反映两种算法的显著性差异。

表 1 各算法参数设置

Table 1 Parameter setting of algorithms

算法	参数设置
ERTLBO	k=0.5; R=0.6
ITLBOBSO^[10]	α= [0.5,1); k=[0.3, 0.6]
BASTLBO^[11]	δ=1; d=2
DSLTLBO^[12]	k=3
TLBO^[4]	T_F=[1,2]∈N
SSA^[20]	c₁∈[0,1]; c₂∈[0,1]
WOA^[21]	a₁=[2,0]; a₂=[−2,1]; b=1
GWO^[22]	a=[2,0]
GA^[23]	P_c=0.7; P_m=0.3

3.3 收敛精度分析

实验结果如表2和表3所示，其中Mean代表平均值，Std为标准差，最优结果用粗体标出。从表2数据可以看出，ERTLBO在求解单峰测试函数F1~F4和F7时均达到了全局最优值，收敛精度分别达到了10⁻¹⁹⁹、10⁻¹⁰⁶、10⁻⁷⁶、10⁻⁸⁸和10⁻⁵量级，明显强于其他改进TLBO和原始算法。从标准差上看ERTLBO的求解稳定性也强于其他算法，说明动态自适应学习模式对局部寻优效果有显著增强。对于F5与F6函数，ERTLBO并未收敛至全局最优值，但平均值和标准差数据仅次于ITLBOBSO和BASTLBO。从单峰测试函数结果可以看出，动态自适应学习模式可根据适应度值对个体位置进行动态自适应调整，提高算法避免早熟收敛能力，增强算法求解精度。在多峰测试函数F8~F13中，ERTLBO仍能取得不错的效果。对于函数F9~F11，ERTLBO收敛精度达到理论最优值且标准差最小。但在求解F9和F11测试函数时，有些对比算法同样取得了理论最优值，此时结合图3的收敛曲线可以看出ERTLBO更快收敛速度，说明ERTLBO的搜索性能更佳。对于函数F10，仅有ERTLBO收敛到理论最优值。对于函数F12~F13，ERTLBO效果不及BASTLBO和ITLBOBSO。在固定维多峰测试函数中，对于函数F14、F16、F17~F21，ERTLBO取到理论最优值，仅有个别函数测试时的稳定性不如对比算法，体现出ERTLBO算法在全局探索上的稳定性。对于函数F15，虽未取到理论最优值，但收敛到了更接近的全局最优值，并且稳定性高。对于函数F22和F23，虽未达到理论最优，但相比基本算法TLBO，ERTLBO还是有进步的趋势。综上所述，经验反思机制与动态自适应权重策略能够有效提升TLBO算法求解精度，赋予算法不错的稳定性，搜索效率得到提升。

表 2 ERTLBO及其对比算法在单峰测试函数实验结果

Table 2 Experimental results of ERTLBO and compared algorithms in unimodal benchmark functions

函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	Mean	4.86×10⁻¹⁹⁹	1.93×10⁻¹⁷	1.35×10⁻¹⁰⁰	2.29×10⁻⁷⁸	3.52×10⁻⁷¹	1.38×10³	2.34×10⁻⁷¹	1.57×10⁻¹²	3.45×10⁴
F1	Std	0.00	5.66×10⁻¹⁸	4.54×10⁻¹⁰⁰	4.87×10⁻⁷⁸	4.69×10⁻⁷¹	3.70×10²	1.21×10⁻⁷⁰	1.33×10⁻¹²	7.87×10³
F2	Mean	8.93×10⁻¹⁰⁶	5.23×10⁻⁸	9.10×10⁻⁵⁰	4.88×10⁻⁴⁰	2.81×10⁻³⁶	4.73×10¹	5.15×10⁻⁴⁹	4.24×10⁻⁸	1.60×10²
F2	Std	2.13×10⁻¹⁰⁵	5.57×10⁻⁹	2.56×10⁻⁴⁹	2.76×10⁻⁴⁰	1.89×10⁻³⁶	7.79	2.88×10⁻⁴⁸	1.55×10⁻⁸	6.94×10¹
F3	Mean	9.54×10⁻⁷⁶	1.12×10⁻¹⁶	2.71×10⁻⁵³	2.45×10⁻³⁴	1.44×10⁻⁶	5.14×10⁴	1.07×10⁶	5.78×10²	1.43×10⁵
F3	Std	7.68×10⁻⁷⁵	1.05×10⁻¹⁶	8.95×10⁻³⁷	8.85×10⁻³⁴	4.52×10⁻⁶	2.44×10⁴	3.26×10⁵	6.51×10²	5.89×10⁴
F4	Mean	2.18×10⁻⁸⁸	1.21×10⁻⁵	8.09×10⁻⁵⁰	1.03×10⁻³⁵	3.01×10⁻²⁹	2.75×10¹	7.55×10¹	1.01	3.96×10¹
F4	Std	4.80×10⁻⁸⁸	1.39×10⁻⁵	2.70×10⁻⁴⁹	7.32×10⁻³⁶	2.31×10⁻²⁹	3.18	2.58×10¹	1.28	4.67
F5	Mean	9.61×10¹	1.47	4.88×10⁻²	9.75×10¹	9.63×10¹	1.76×10⁵	9.82×10¹	9.80×10¹	2.65×10⁷
F5	Std	1.03×10⁻¹	9.17×10⁻¹	2.38×10⁻²	7.24×10⁻¹	8.27×10⁻¹	8.36×10⁴	1.93×10⁻¹	5.66×10⁻¹	1.26×10⁷
F6	Mean	1.92×10¹	5.14×10⁻⁷	5.08	6.89	2.18	1.47×10³	4.07	1.00×10¹	3.61×10⁴
F6	Std	9.95×10⁻¹	3.52×10⁻⁷	1.09	1.01	5.37×10⁻¹	4.87×10²	1.16	1.00	8.79×10³
F7	Mean	2.38×10⁻⁵	7.99×10⁻⁴	3.37×10⁻⁴	2.28×10⁻⁴	1.47×10⁻³	2.82	3.84×10⁻³	6.87×10⁻³	3.99×10¹
F7	Std	2.14×10⁻⁵	3.47×10⁻⁴	2.23×10⁻⁴	1.30×10⁻⁴	4.92×10⁻⁴	6.88×10⁻¹	4.39×10⁻³	2.58×10⁻³	1.88×10¹

表 3 ERTLBO及其对比算法在多峰测试函数实验结果

Table 3 Experimental results of ERTLBO and compared algorithms in multimodal benchmark functions

函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F8	Mean	−7.49×10³	−2.31×10⁴	−9.59×10³	−1.83×10⁴	−1.72×10⁴	−2.17×10⁴	−3.49×10⁴	−1.64×10⁴	−7.49×10³
F8	Std	6.57×10²	3.93×10³	7.17×10²	3.13×10³	3.92×10³	1.72×10³	5.95×10³	2.58×10³	1.11×10³
F9	Mean	0.00	2.03×10²	1.59×10¹	0.00	8.69	2.34×10²	2.27×10⁻¹⁵	8.73	8.57×10²
F9	Std	0.00	3.35×10¹	3.67×10¹	0.00	3.40×10¹	4.42×10¹	2.27×10⁻¹⁴	7.38	4.87×10¹
F10	Mean	8.88×10⁻¹⁶	1.04×10⁻⁸	9.24×10⁻¹⁶	4.44×10⁻¹⁵	6.71×10⁻²	1.02×10¹	3.98×10⁻¹⁵	1.29×10⁻⁷	1.54×10¹
F10	Std	0.00	6.36×10⁻⁹	3.55×10⁻¹⁶	0.00	6.71×10⁻¹	1.23	2.46×10⁻¹⁵	5.12×10⁻⁸	8.04×10⁻¹
F11	Mean	0.00	5.70×10⁻⁷	0.00	0.00	0.00	1.42×10¹	3.64×10⁻³	4.74×10⁻³	3.33×10⁺²
F11	Std	0.00	5.70×10⁻⁶	0.00	0.00	0.00	4.00	3.64×10⁻²	1.04×10⁻²	7.52×10¹
F12	Mean	7.11×10⁻¹	3.11×10⁻⁴	1.51×10⁻¹	9.22×10⁻²	2.08×10⁻²	3.56×10⁺¹	5.29×10⁻²	2.94×10⁻¹	7.80×10⁺⁶
F12	Std	8.94×10⁻²	3.11×10⁻³	4.29×10⁻²	2.64×10⁻²	7.26×10⁻³	1.14×10⁺¹	2.61×10⁻²	8.10×10⁻²	7.53×10⁺⁶
F13	Mean	9.97	2.09×10⁻³	6.09×10⁻³	9.74	5.25	6.55×10⁺³	2.90	6.74	5.00×10⁺⁷
F13	Std	9.51×10⁻³	4.33×10⁻³	3.24×10⁻⁵	8.01×10⁻¹	7.35×10⁻¹	1.29×10⁺⁴	1.25	4.09×10⁻¹	3.23×10⁺⁷
F14	Mean	9.98×10⁻¹	9.98×10⁻¹	1.63	1.04	9.98×10⁻¹	1.29	2.79	4.12	4.00
F14	Std	1.81	7.06×10⁻¹⁷	1.30	2.79×10⁻¹	0.00	6.65×10⁻¹	3.11	3.85	2.91
F15	Mean	3.14×10⁻⁴	3.90×10⁻⁴	3.20×10⁻⁴	3.29×10⁻⁴	5.67×10⁻⁴	2.44×10⁻³	7.38×10⁻⁴	6.26×10⁻³	3.70×10⁻³
F15	Std	8.56×10⁻⁵	1.50×10⁻⁴	7.67×10⁻⁴	1.15×10⁻⁴	2.01×10⁻³	5.33×10⁻³	5.09×10⁻⁴	1.01×10⁻²	6.06×10⁻³
F16	Mean	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03
F16	Std	6.03×10⁻¹⁶	2.10×10⁻⁵	1.01×10⁻⁵	6.68×10⁻¹⁶	6.56×10⁻¹⁶	2.27×10⁻¹⁴	1.19×10⁻⁹	2.18×10⁻⁸	5.48×10⁻⁹
F17	Mean	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹
F17	Std	1.03×10⁻³	0.00	1.07×10⁻⁶	0.00	0.00	7.54×10⁻¹⁵	9.95×10⁻⁶	9.24×10⁻⁷	6.97×10⁻¹³

续表 3
函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F18	Mean	3.00	3.00	3.00	3.00	3.00	3.00	3.00	3.00	3.00
F18	Std	8.13×10⁻⁴	1.24×10⁻¹⁵	8.01×10⁻⁴	6.45×10⁻¹⁶	6.44×10⁻¹⁶	2.21×10⁻¹³	2.70	4.44×10⁻⁵	1.88×10⁻¹¹
F19	Mean	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86
F19	Std	9.45×10⁻³	2.14×10⁻¹⁵	1.08×10⁻⁴	2.20×10⁻¹⁵	2.23×10⁻¹⁵	6.35×10⁻¹¹	9.45×10⁻³	4.58×10⁻³	9.93×10⁻³
F20	Mean	−3.32	−3.16	−3.28	−3.31	−3.30	−3.22	−3.19	−3.26	−3.17
F20	Std	5.54×10⁻¹²	8.98×10⁻²	7.11×10⁻²	3.09×10⁻²	4.68×10⁻²	5.75×10⁻²	2.78×10⁻¹	7.29×10⁻²	1.09×10⁻¹
F21	Mean	−1.02×10¹	−5.06	−5.75	−5.81	−1.00×10¹	−7.75	−8.29	−9.27	−7.16
F21	Std	3.72×10⁻¹	8.73×10⁻¹⁴	1.33	1.59	6.68×10⁻¹	3.29	2.58	2.07	3.21
F22	Mean	−7.03	−1.04×10¹	−5.61	−6.05	−1.01×10¹	−7.66	−7.00	−1.02×10¹	−8.10
F22	Std	9.09×10⁻¹	3.59×10⁻¹⁵	1.20	1.86	1.36	3.40	3.20	1.18	3.09
F23	Mean	−7.93	−1.05×10¹	−6.01	−7.24	−9.97	−8.60	−7.37	−1.03×10¹	−8.23
F23	Std	6.24×10⁻³	2.27×10⁻¹⁵	1.56	2.42	1.82	3.18	3.45	1.26	3.12

3.4 收敛曲线

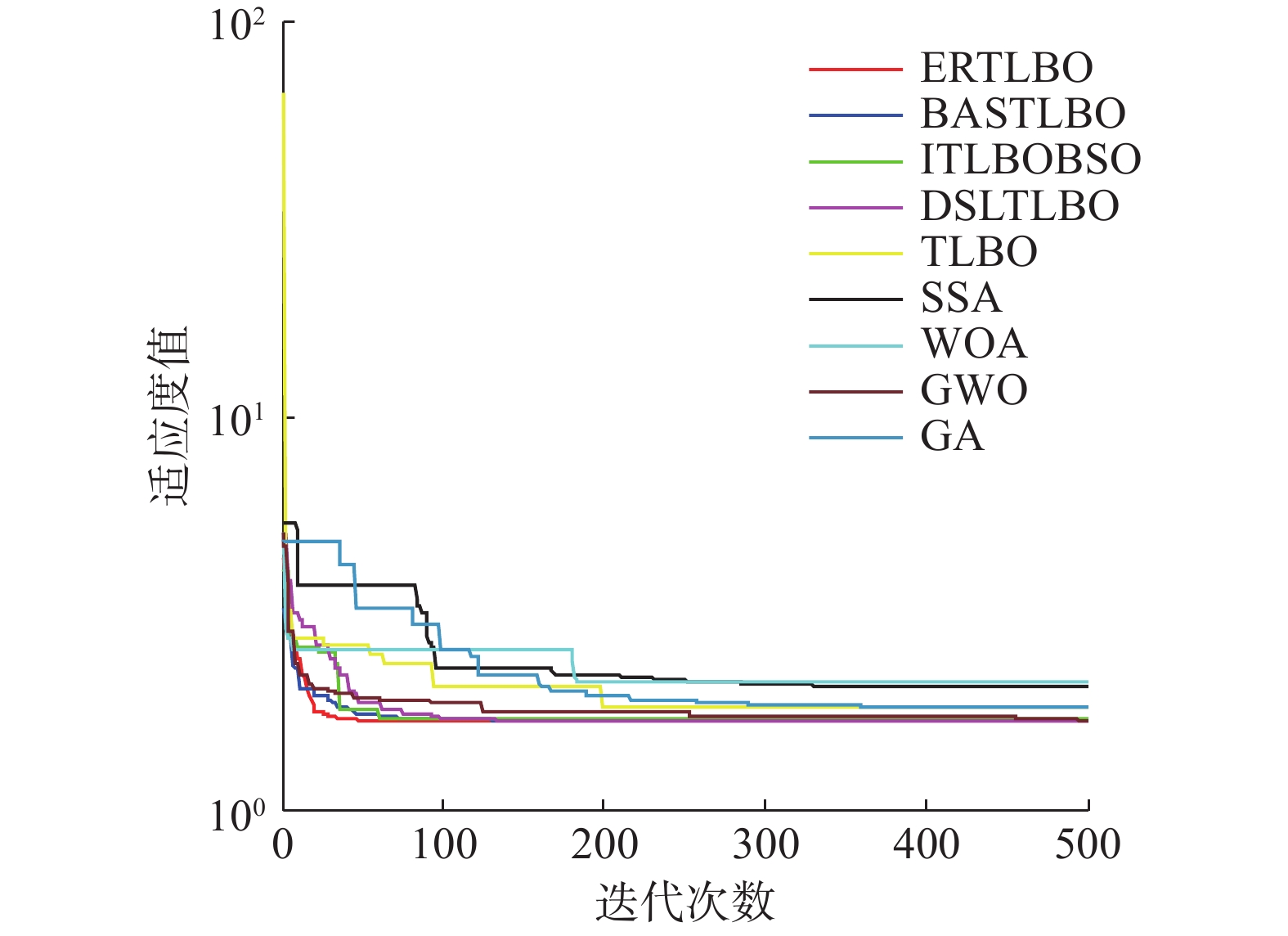
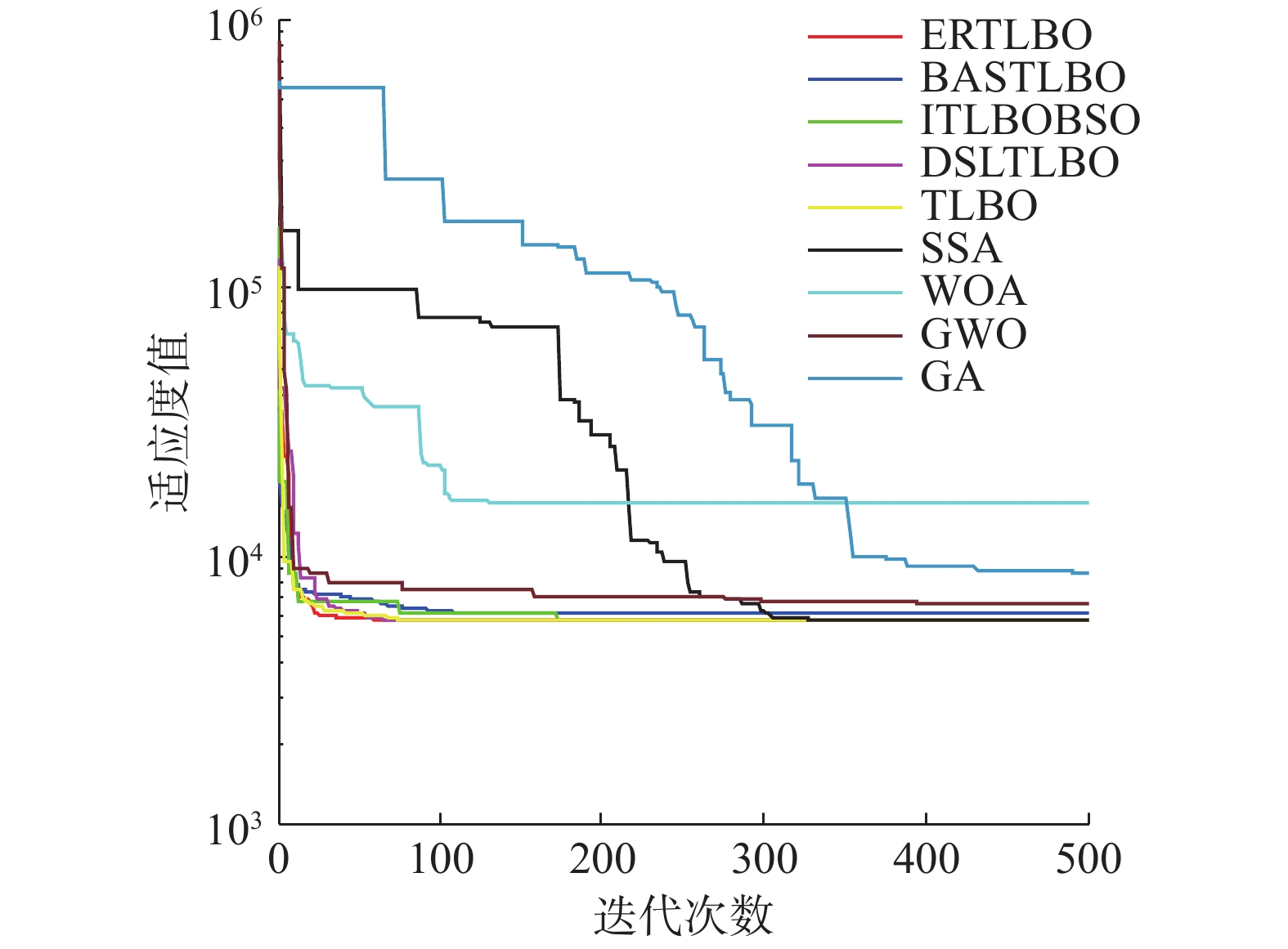
为了更直观地对比各算法寻优性能，图3为9种算法在不同测试函数上进行测试的结果。对于单峰测试函数F1和F4，迭代初期ERTLBO和DSLTLBO收敛速度相当。然而随着迭代次数的增加，ERTLBO收敛能力逐渐增强，并于迭代后期收敛到全局最优解，从收敛精度上看明显强于其他对比算法。对于函数F6，除BASTLBO外其他算法均陷入不同程度的局部最优值。对于函数F7，从收敛曲线可以看出ERTLBO具有多个梯度下降，表明算法有效跳出局部最优值，更接近理论最优值。从多峰测试函数收敛曲线可以看出ERTLBO的全局搜索能力同样得到提高。对于函数F8，ERTLBO收敛到全局最优值。对于函数F9和F11，ERTLBO不仅找到了理论最优值，且收敛速度最快。对于F15，ERTLBO不仅收敛到全局最优值，且收敛速度也保持最佳水平。对于函数F16~F19，虽然各算法均收敛到理论最优值，但ERTLBO所需迭代次数更少，表现出优越的收敛速度。对于函数F20、F22和F23，ERTLBO均保持最快的收敛速度。综上分析，ERTLBO算法整体收敛速度快于大部分改进TLBO算法以及流行算法，表现出更好的收敛性能。结合收敛精度分析，可以得出结论：在求解单峰测试函数中，动态自适应学习模式有效提升了算法的收敛精度，提高算法跳出局部极值点能力。对于多峰测试函数和固定维多峰测试函数，经验反思机制提升了整体搜索性能，在迭代前期就能表现出优秀的收敛速度，可以看出本文提出的改进策略对算法的收敛速度和跳出局部最优能力有积极影响。

图 3 各算法求解部分测试函数收敛曲线

Fig. 3 Convergence curve behavior obtained by algorithms on some benchmark functions

下载: 全尺寸图片

3.5 Wilcoxon秩和检验

上述实验仅采用了平均值与标准差进行评价，为了进一步验证改进算法有效性，本文采用Wilcoxon秩和检验进行统计检验^[24]。显著性水平设置为5%，若p值小于5%，则拒绝零假设，说明两种算法之间具有显著性差异，否则说明两种算法性能相差不大。Wilcoxon秩和检验p值结果如表4所示，因为算法无法与自身对比，故表中不再列出ERTLBO的p值。表中p值大于0.05已用粗体展示，NaN表示数据无效，即实验样本数据相同，算法性能相当。

表 4 各算法得到的Wilcoxon秩和检验结果

Table 4 Statistical results of Wilcoxon rank sum test obtained by algorithms

函数	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F2	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F3	2.56×10⁻³⁴	1.63×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F4	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F5	2.56×10⁻³⁴	2.56×10⁻³⁴	6.48×10⁻³⁴	3.46×10⁻³⁴	2.56×10⁻³⁴	2.70×10⁻³³	2.19×10⁻³³	2.56×10⁻³⁴
F6	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F7	2.56×10⁻³⁴	2.26×10⁻³³	6.54×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴	2.13×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴

由表4可知，大部分p值均小于5%，表明ERTLBO算法优越性在统计检验上是显著的。可以认为ERTLBO算法相比于对比算法，表现出更高的收敛性能。

续表 4
函数	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F8	2.56×10⁻³⁴	3.74×10⁻³³	2.56×10⁻³⁴	4.27×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	4.38×10⁻²⁶	7.37×10⁻¹
F9	5.64×10⁻³⁹	7.58×10⁻⁷	NaN	3.22×10⁻¹	5.64×10⁻³⁹	3.22×10⁻¹	5.64×10⁻³⁹	5.64×10⁻³⁹
F10	5.79×10⁻³⁸	1.70×10⁻³⁹	7.30×10⁻³	6.97×10⁻⁴¹	5.79×10⁻³⁸	9.51×10⁻¹	5.79×10⁻³⁸	5.79×10⁻³⁸
F11	NaN	NaN	NaN	NaN	5.64×10⁻³⁹	1.58×10⁻¹	5.64×10⁻³⁹	5.64×10⁻³⁹
F12	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.89×10⁻³⁴	2.56×10⁻³⁴
F13	2.56×10⁻³⁴	2.56×10⁻³⁴	1.25×10⁻³²	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F14	1.78×10⁻³⁷	6.12×10⁻¹²	8.10×10⁻³⁹	5.64×10⁻³⁹	1.11×10⁻²³	1.08×10⁻⁴	4.52×10⁻¹	8.93×10⁻⁵
F15	2.47×10⁻¹	7.71×10⁻²²	2.43×10⁻²⁹	3.00×10⁻⁶	9.00×10⁻³²	1.84×10⁻²⁴	1.32×10⁻¹¹	1.91×10⁻³⁰
F16	3.33×10⁻³⁶	3.85×10⁻⁶	1.62×10⁻³⁸	1.03×10⁻³⁷	2.56×10⁻³⁴	2.72×10⁻³⁴	2.11×10⁻³²	2.80×10⁻³⁴
F17	5.64×10⁻³⁹	4.24×10⁻³²	5.64×10⁻³⁹	5.64×10⁻³⁹	2.09×10⁻³⁴	6.99×10⁻²⁶	1.47×10⁻³¹	2.40×10⁻³⁴
F18	1.28×10⁻³⁴	1.79×10⁻¹	1.47×10⁻³⁵	9.85×10⁻³⁷	2.56×10⁻³⁴	8.81×10⁻¹⁶	9.61×10⁻¹⁵	2.56×10⁻³⁴
F19	2.01×10⁻³⁶	1.90×10⁻³¹	4.27×10⁻³⁸	8.10×10⁻³⁹	2.56×10⁻³⁴	3.93×10⁻¹	1.61×10⁻¹³	1.65×10⁻³¹
F20	2.33×10⁻³⁷	3.96×10⁻²²	1.03×10⁻³²	4.46×10⁻²⁸	8.00×10⁻⁶	7.81×10⁻⁹	2.28×10⁻¹³	3.16×10⁻²
F21	5.79×10⁻³⁸	1.08×10⁻²⁰	3.60×10⁻²¹	2.50×10⁻³⁵	1.26×10⁻⁹	1.52×10⁻²²	1.61×10⁻²⁷	2.78×10⁻⁸
F22	1.62×10⁻³⁸	7.35×10⁻¹⁸	5.74×10⁻²⁰	9.83×10⁻³³	2.45×10⁻¹³	2.01×10⁻⁹	2.56×10⁻³⁴	1.83×10⁻³
F23	2.31×10⁻³⁷	4.97×10⁻²³	6.75×10⁻²⁶	6.97×10⁻²⁸	2.40×10⁻¹⁴	1.62×10⁻⁸	3.89×10⁻²⁹	3.77×10⁻¹¹

通过分析算法收敛精度、收敛性和统计性检验结果，可以得出结论：经验反思机制与动态自适应权重策略有效增强了TLBO收敛能力，表现出更优秀的收敛性能及稳定性。

3.6 仿真时间

本节对ERTLBO和其他算法在23个测试函数上的运行时间进行分析，如表5所示，其中最佳结果用粗体展示。从实验数据上看，对于大部分测试函数，WOA、GWO、GA、TLBO、SSA相较于其他算法所需的运行时间更少。但结合表2、表3的实验数据，上述算法并不能获得一个较好的解。尽管ERTLBO运行时间不是最快的，但从收敛精度上看ERTLBO相较于其他算法具有显著优势。此外，考虑到无免费午餐定理，适当增加一些运行时间来获得更高精度的解是可接受的。

表 5 各算法所需运行时间

Table 5 Statistical results of runtime obtained by algorithms s

函数	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	0.2397	0.3548	0.1199	0.2249	0.1256	0.1450	0.0948	0.1902	0.0702
F2	0.2499	0.3831	0.1482	0.2383	0.1496	0.1401	0.1181	0.2333	0.0937
F3	1.8536	3.2118	0.8565	1.1293	0.7901	0.5252	0.4308	0.5524	0.0142
F4	0.1983	0.3187	0.0952	0.2167	0.1302	0.1305	0.1007	0.2159	0.0709
F5	0.2476	0.4192	0.1244	0.2552	0.1490	0.1367	0.1279	0.2506	0.1236
F6	0.1924	0.3519	0.0913	0.2308	0.1041	0.1328	0.0915	0.2012	0.0442
F7	1.0536	1.7270	0.4365	0.6911	0.4548	0.3126	0.2557	0.3643	0.5991
F8	0.3519	0.5840	0.2023	0.3099	0.1994	0.1650	0.1110	0.2427	0.1540
F9	0.2646	0.5725	0.1327	0.2557	0.1187	0.1648	0.0978	0.2206	0.1650
F10	0.2328	0.4602	0.1335	0.2379	0.1419	0.1689	0.0872	0.2246	0.1642
F11	0.3166	0.5420	0.1485	0.2863	0.1420	0.2067	0.1654	0.3346	0.8134
F12	2.7467	4.8544	4.1141	1.6169	2.9185	1.1044	2.1335	0.7198	3.3038
F13	2.6362	4.8122	1.1436	1.5587	5.1400	4.1887	0.6731	2.0365	5.8029
F14	1.6302	10.9205	0.7577	3.6405	2.6188	0.4010	0.3176	0.2700	0.8149
F15	0.1012	0.2646	0.0832	0.1501	0.0956	0.0462	0.0340	0.0447	0.0578

4. 工程设计问题

为了验证ERTLBO算法解决工程问题的性能和有效性，选用焊接梁设计问题^[25]与压力容器问题^[26]进行测试。上述工程设计问题是约束优化问题的具体应用。以优化最小值问题为例，约束优化问题可以描述为

$$最小化 f({\boldsymbol{X}}),{\boldsymbol{X}} = [{x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_n}] $$

(6)

$$ 约束条件 \begin{gathered} {g_j}({\boldsymbol{X}}) \leqslant 0,j = 1,2, \cdots,q \\ {h_j}({\boldsymbol{X}}) = 0,j = q + 1,q + 2, \cdots,m \\ \end{gathered} $$

(7)

式中：f(X)为目标函数；X为满足边界条件的决策变量；g_j(X)为不等式约束；h_j(X)为等式约束。

对于这类问题，除了考虑目标函数外，还要考虑约束条件，其中罚函数是最常用的约束处理技术之一，其思想为：基于个体的约束违反程度构造罚数项，通过对目标函数增加罚数项来构造惩罚目标函数，从而将约束优化问题转为无约束优化问题^[27]。具体的数学模型如下：

$$ 最小化 F({\boldsymbol{X}}) = f({\boldsymbol{X}}) + \omega \times \sum\limits_{i = 1}^q {\max (0,{g_i}({\boldsymbol{X}}))} $$

(8)

式中：F(X)为惩罚目标函数；f(X)为原目标函数；ω为惩罚因子。下节将使用ERTLBO求解惩罚目标函数下的焊接梁设计问题和压力容器设计问题。

4.1 焊接梁设计问题

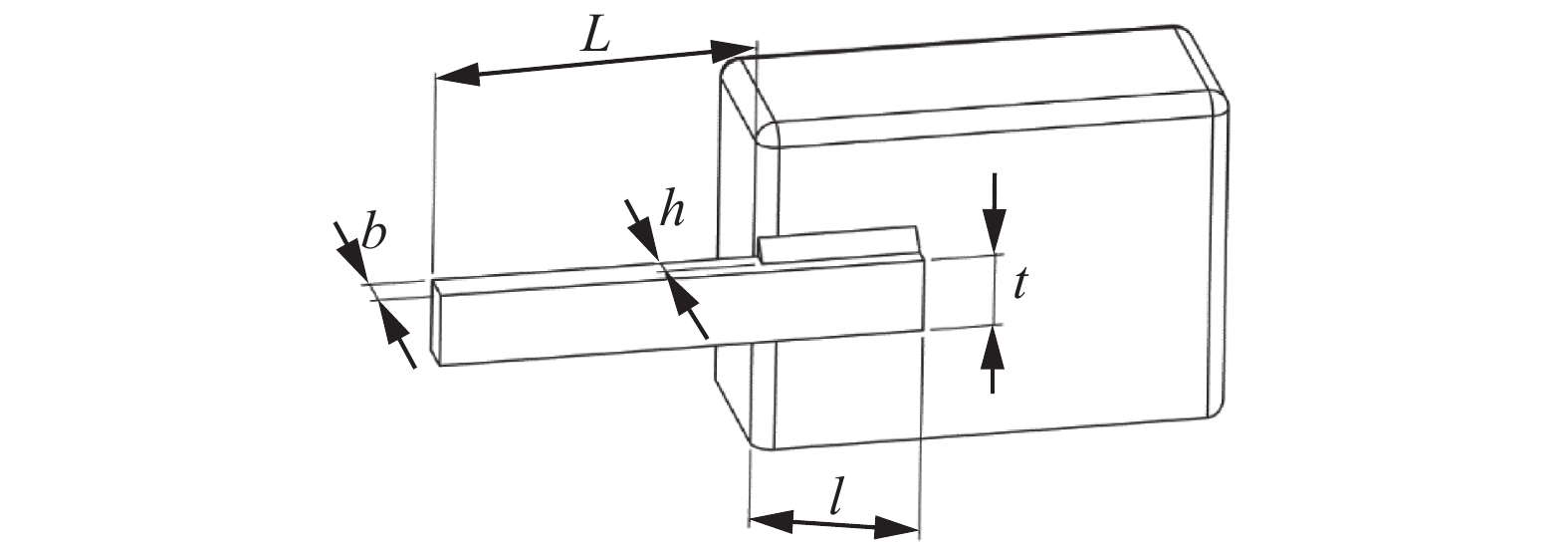
焊接梁设计（如图4）是一个著名的约束工程设计问题^[25]，目标使其设计成本最小化。该问题的决策变量为：焊缝宽度h(z₁)、焊接梁厚度b(z₂)、焊接梁长度l(z₃)以及焊接梁高度t(z₄)。

图 4 焊接梁设计问题

Fig. 4 Welded beam design problem

下载: 全尺寸图片

目标函数f(·)、约束条件g以及变量范围如下所示：

优化参数及目标函数如下：

$$ \begin{gathered} {\boldsymbol{z}} = [{{{z}}_1}\;{{{z}}_2}\;{{{z}}_3}\;{{{z}}_4}] = [h\;l\;t\;b], \\ f({{z}}) = 1.104\;71{{z}}_1^2{{{z}}_2} + 0.048\;11{z_3}{z_4}(14.0 + {z_2}) \\ \end{gathered} $$

(9)

问题的约束条件为

$$ \left\{ \begin{gathered} {g_1}({\boldsymbol{z}}) = \tau ({\boldsymbol{z}}) - {\tau _{\max }} \leqslant 0 \\ {g_2}({\boldsymbol{z}}) = \sigma ({\boldsymbol{z}}) - {\sigma _{\max }} \leqslant 0 \\ {g_3}({\boldsymbol{z}}) = \delta ({\boldsymbol{z}}) - {\delta _{\max }} \leqslant 0 \\ {g_4}({\boldsymbol{z}}) = {{\boldsymbol{z}}_1} - {{\boldsymbol{z}}_4} \leqslant 0, \\ {g_5}({\boldsymbol{z}}) = P - {P_c}({\boldsymbol{z}}) \leqslant 0 \\ {g_6}({\boldsymbol{z}}) = 0.125 - {{{z}}_1} \leqslant 0 \\ {g_7}({\boldsymbol{z}}) = 1.104\;71{{z}}_1^2 + 0.048\;11{{{z}}_3}{{{z}}_4}(14.0 + {{{z}}_2}) - 5.0 \leqslant 0 \\ \end{gathered} \right.$$

取值范围：

$$ 0.05 \leqslant {z_1} \leqslant 2.00,0.25 \leqslant {z_2} \leqslant 1.30,2.00 \leqslant {z_3} \leqslant 15.0 $$

其中

$$ \left\{ \begin{split} &\tau ({\boldsymbol{z}}) = \sqrt {{{\tau '}^2} + 2\tau '\tau ''\frac{{{{{z}}_2}}}{{2R}} + {{\tau ''}^2}} ,\tau ' = \frac{P}{{\sqrt 2 {{{z}}_1}{{{z}}_2}}} \\ &\tau '' = \frac{{MR}}{J},M = P\left(L + \frac{{{{{z}}_2}}}{2}\right) \\ &R = \sqrt {\frac{{{{z}}_2^2}}{4} + {{\left(\frac{{{{{z}}_1} + {{{z}}_3}}}{2}\right)}^2}} ,J = 2\left\{ \sqrt 2 {{{z}}_1}{{{z}}_2}\left[\frac{{{{z}}_2^2}}{{12}} + {\left(\frac{{{{{z}}_1} + {{{z}}_3}}}{2}\right)^2}\right]\right\} \\ & \sigma ({\boldsymbol{x}} ) = \frac{{6PL}}{{{{{z}}_4}{{z}}_3^2}} \\ & \delta ({\boldsymbol{z}}) = \dfrac{{4P{L^3}}}{{E{{z}}_3^3{{{z}}_4}}},{P_c}({\boldsymbol{z}}) = \frac{{4.013E\sqrt {\dfrac{{{{z}}_3^2{{z}}_4^6}}{{36}}} }}{{{L^2}}}\left(1 - \frac{{{{{z}}_3}}}{{2L}}\sqrt {\frac{E}{{4G}}} \right) \\ &P=2\;721.55 \;{\rm{kg}},{\rm{L}}=35.56 \;{\rm{cm}},E=2.07\times10^8\; {\rm{kPa}}\\ &G=8.27\times10^7 \;{\rm{kPa}} \end{split} \right.$$

图5给出了各算法求解焊接梁设计问题所得收敛曲线，可以看出ERTLBO收敛速度快于其他算法。表6统计了8种算法求解焊接梁设计问题实验结果，其中较好结果用粗体展示。从中可以看出，ERTLBO在h=0.20573、l=3.253、t=9.0366、b=0.20573处得到的最小代价为1.6952，说明本文算法对于求解此类工程问题具有良好的性能。

图 5 焊接梁问题收敛曲线

Fig. 5 Convergence curve of welded beam design problem obtained by algorithms

下载: 全尺寸图片

表 6 8种算法求解焊接梁设计问题实验结果

Table 6 Experimental results of eight algorithms for solving welding beam design problems

算法	h	l	t	b	f (x)
ERTLBO	0.2057	3.253	9.0366	0.20573	1.6952
BASTLBO	0.2085	3.2204	8.9964	0.20871	1.7102
ITLBOBSO	0.1970	3.4227	9.0342	0.20588	1.7058
DSLTLBO	0.1937	3.4874	9.0275	0.20625	1.7111
TLBO	0.2089	3.2319	9.0003	0.20976	1.7210
SSA	0.1937	3.4011	9.3469	0.2052	1.7468
WOA	0.2057	3.2530	9.0366	0.2057	1.7185
GWO	0.2046	3.2797	9.0327	0.2060	1.6988
GA	0.2331	2.6193	9.9920	0.2427	2.0964

4.2 压力容器设计问题

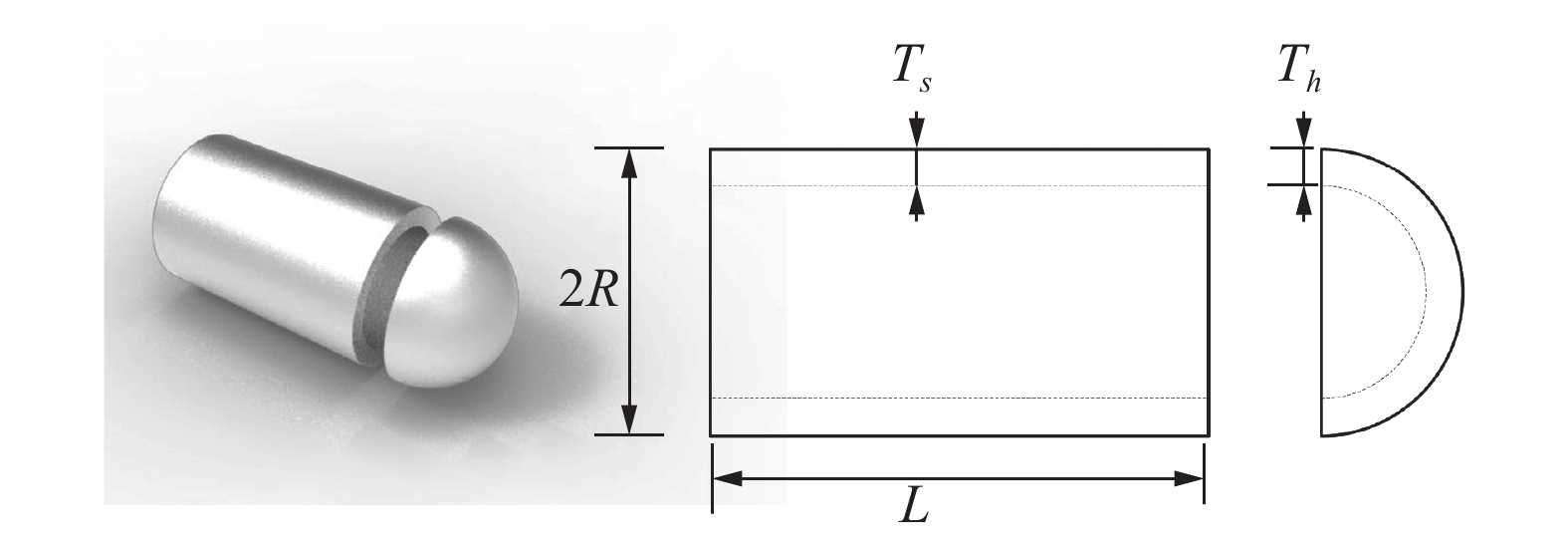
压力容器设计问题^[26]试图在满足压力要求下使设计总成本最小化，如图6所示。该问题的决策变量为：壳体厚度T_s(x₁)、封头厚度T_h(x₂)、壳体半径R(x₃)、圆柱形截面长度L(x₄)。

图 6 压力容器设计问题

Fig. 6 Pressure vessel problem

下载: 全尺寸图片

优化参数及目标函数为

$$ \begin{array}{c} {\boldsymbol{x}} = [{{{x}}_1}\;{{{x}}_2}\;{{{x}}_3}\;{{{x}}_4}] = [{T_s}\;{T_h}\;R\;L], \\ f\left( {\boldsymbol{x}} \right) = 0.622\;4{{{x}}_1}{{{x}}_3}{{{x}}_4} + 1.778\;1{{{x}}_2}{{x}}_3^2 + \\ 3.166\;1{{x}}_1^2{{{x}}_4} + 19.84{{x}}_1^2{{{x}}_3} \end{array} $$

(10)

问题的约束条件为：

$$ \left\{ \begin{gathered} {g_1}\left( {\boldsymbol{x}} \right) = - {{{x}}_1} + 0.019\;3{{{x}}_3} \leqslant 0 \\ {g_2}\left( {\boldsymbol{x}} \right) = - {{{x}}_3} + 0.009\;54{{{x}}_3} \leqslant 0 \\ {g_3}\left( {\boldsymbol{x}} \right) = - {\text{π}} {{x}}_3^2{{{x}}_4} - \frac{4}{3}{\text{π}} {{x}}_3^3 + 1\;296\;000 \leqslant 0 \\ {g_4}\left( {\boldsymbol{x}} \right) = {{{x}}_4} - 240 \leqslant 0 \\ \end{gathered} \right. $$

取值范围：

$$ 0 \leqslant {x_1} \leqslant 99,{\text{ }}0 \leqslant {x_2} \leqslant 99 , 10 \leqslant {x_3} \leqslant 200,{\text{ }}10 \leqslant {x_4} \leqslant 200 $$

图7为各算法求解压力容器设计问题所得收敛曲线，可以看出ERTLBO于迭代初期便取得了较高的收敛精度，并于迭代后期收敛到全局最优值。表7统计了8种算法在求解压力容器问题时得到的最佳解决方案数据。可以看出ERTLBO取得了最低设计方案，设计成本远低于原始TLBO算法，充分说明了ERTLBO对压力容器设计问题优良可信的求解能力。

图 7 压力容器设计问题收敛曲线

Fig. 7 Convergence curve of pressure vessel design problem obtained by algorithms

下载: 全尺寸图片

表 7 各算法应用压力容器设计问题优化结果

Table 7 Optimization results of pressure vessel design problem by algorithms

算法	T_s(x₁)	T_h(x₂)	R(x₃)	L(x₄)	f (x)
ERTLBO	0.7527	0.4138	42.2128	176.8576	5984.622
BASTLBO	0.8827	0.4310	47.2537	121.7488	6027.769
ITLBOBSO	0.8828	0.4311	47.2707	121.5889	6028.433
DSLTLBO	0.8202	0.3841	45.1290	142.5473	6054.547
TLBO	0.9015	0.4390	48.2043	113.2618	6072.663
SSA	0.8759	0.4279	46.9243	124.7872	6043.665
WOA	0.7942	0.4064	44.5199	150.4761	6057.799
GWO	0.7371	0.3555	41.6434	186.6832	6050.765
GA	0.9008	0.4344	48.0603	115.3819	6092.908

续表 5
函数	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F16	0.1042	0.2681	0.0813	0.1393	0.1017	0.0404	0.0366	0.0349	0.0829
F17	0.0815	0.2210	0.0797	0.1320	0.0649	0.0348	0.0265	0.0342	0.0517
F18	0.0799	0.2533	0.0913	0.1215	0.0656	0.0436	0.0293	0.0310	0.0497
F19	0.1178	0.1888	0.1198	0.1629	0.0837	0.0614	0.0358	0.0406	0.0901
F20	0.1233	0.3223	0.1118	0.1556	0.1173	0.0595	0.0411	0.0576	0.0667
F21	0.1297	0.3612	0.1384	0.1681	0.1237	0.0545	0.0493	0.0496	0.0999
F22	0.1470	0.4036	0.1366	0.1792	0.1139	0.0632	0.0470	0.0649	0.1126
F23	0.1705	0.2779	0.1281	0.1776	0.1292	0.0810	0.0597	0.0756	0.1135

通过对上述典型著名工程设计问题的测试，可以看出本文改进算法ERTLBO具有较强的局部开发能力，在求解工程优化设计问题具有较好的应用潜力，能够提供优秀的解决方案。

5. 结束语

为了改善传统TLBO算法存在收敛速度慢、收敛精度低，易陷入局部最优等问题，本文提出一种融合经验反思机制的教与学优化算法(ERTLBO)。ERTLBO源于教育学原理的思想，运用教育学基本理论设计策略对原算法进行改进，有效地增强并平衡了全局探索和局部开发过程。具体表现为：教学阶段引入经验反思机制，提升班级整体水平，增强算法全局探索性能。学习阶段引入动态自适应权重，实现学生的动态位置更新，提升种群多样性，避免算法陷入局部最优，进而在探索和开发之间取得较好的平衡。

仿真实验采用较高维度的基准函数对改进算法的优化性能进行测试，同时选取了其他改进TLBO算法和流行算法作为对比，实验结果发现针对不同类型测试函数，ERTLBO均具有更佳的收敛速度和精度，具有一定的竞争性和稳定性。最后通过2个经典工程设计问题验证改进算法解决实际问题能力，结果表明ERTLBO可用于解决实际问题并具有良好的工程应用前景。然而ERTLBO也不可避免地提高了运行时间，因此未来的工作方向是在现有基础上继续改进，保证优化性能的同时减少运行时间开销，提高计算效率。其次，可将ERTLBO应用到多目标优化中，并结合实际问题作进一步探究。

图 1 动态自适应权值曲线

Fig. 1 Dynamic adaptive weight curve

下载: 全尺寸图片

图 2 ERTLBO算法实现流程图

Fig. 2 Flowchart of ERTLBO algorithm

下载: 全尺寸图片

图 3 各算法求解部分测试函数收敛曲线

Fig. 3 Convergence curve behavior obtained by algorithms on some benchmark functions

下载: 全尺寸图片

图 4 焊接梁设计问题

Fig. 4 Welded beam design problem

下载: 全尺寸图片

图 5 焊接梁问题收敛曲线

Fig. 5 Convergence curve of welded beam design problem obtained by algorithms

下载: 全尺寸图片

图 6 压力容器设计问题

Fig. 6 Pressure vessel problem

下载: 全尺寸图片

图 7 压力容器设计问题收敛曲线

Fig. 7 Convergence curve of pressure vessel design problem obtained by algorithms

下载: 全尺寸图片

表 1 各算法参数设置

Table 1 Parameter setting of algorithms

算法	参数设置
ERTLBO	k=0.5; R=0.6
ITLBOBSO^[10]	α= [0.5,1); k=[0.3, 0.6]
BASTLBO^[11]	δ=1; d=2
DSLTLBO^[12]	k=3
TLBO^[4]	T_F=[1,2]∈N
SSA^[20]	c₁∈[0,1]; c₂∈[0,1]
WOA^[21]	a₁=[2,0]; a₂=[−2,1]; b=1
GWO^[22]	a=[2,0]
GA^[23]	P_c=0.7; P_m=0.3

表 2 ERTLBO及其对比算法在单峰测试函数实验结果

Table 2 Experimental results of ERTLBO and compared algorithms in unimodal benchmark functions

函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	Mean	4.86×10⁻¹⁹⁹	1.93×10⁻¹⁷	1.35×10⁻¹⁰⁰	2.29×10⁻⁷⁸	3.52×10⁻⁷¹	1.38×10³	2.34×10⁻⁷¹	1.57×10⁻¹²	3.45×10⁴
F1	Std	0.00	5.66×10⁻¹⁸	4.54×10⁻¹⁰⁰	4.87×10⁻⁷⁸	4.69×10⁻⁷¹	3.70×10²	1.21×10⁻⁷⁰	1.33×10⁻¹²	7.87×10³
F2	Mean	8.93×10⁻¹⁰⁶	5.23×10⁻⁸	9.10×10⁻⁵⁰	4.88×10⁻⁴⁰	2.81×10⁻³⁶	4.73×10¹	5.15×10⁻⁴⁹	4.24×10⁻⁸	1.60×10²
F2	Std	2.13×10⁻¹⁰⁵	5.57×10⁻⁹	2.56×10⁻⁴⁹	2.76×10⁻⁴⁰	1.89×10⁻³⁶	7.79	2.88×10⁻⁴⁸	1.55×10⁻⁸	6.94×10¹
F3	Mean	9.54×10⁻⁷⁶	1.12×10⁻¹⁶	2.71×10⁻⁵³	2.45×10⁻³⁴	1.44×10⁻⁶	5.14×10⁴	1.07×10⁶	5.78×10²	1.43×10⁵
F3	Std	7.68×10⁻⁷⁵	1.05×10⁻¹⁶	8.95×10⁻³⁷	8.85×10⁻³⁴	4.52×10⁻⁶	2.44×10⁴	3.26×10⁵	6.51×10²	5.89×10⁴
F4	Mean	2.18×10⁻⁸⁸	1.21×10⁻⁵	8.09×10⁻⁵⁰	1.03×10⁻³⁵	3.01×10⁻²⁹	2.75×10¹	7.55×10¹	1.01	3.96×10¹
F4	Std	4.80×10⁻⁸⁸	1.39×10⁻⁵	2.70×10⁻⁴⁹	7.32×10⁻³⁶	2.31×10⁻²⁹	3.18	2.58×10¹	1.28	4.67
F5	Mean	9.61×10¹	1.47	4.88×10⁻²	9.75×10¹	9.63×10¹	1.76×10⁵	9.82×10¹	9.80×10¹	2.65×10⁷
F5	Std	1.03×10⁻¹	9.17×10⁻¹	2.38×10⁻²	7.24×10⁻¹	8.27×10⁻¹	8.36×10⁴	1.93×10⁻¹	5.66×10⁻¹	1.26×10⁷
F6	Mean	1.92×10¹	5.14×10⁻⁷	5.08	6.89	2.18	1.47×10³	4.07	1.00×10¹	3.61×10⁴
F6	Std	9.95×10⁻¹	3.52×10⁻⁷	1.09	1.01	5.37×10⁻¹	4.87×10²	1.16	1.00	8.79×10³
F7	Mean	2.38×10⁻⁵	7.99×10⁻⁴	3.37×10⁻⁴	2.28×10⁻⁴	1.47×10⁻³	2.82	3.84×10⁻³	6.87×10⁻³	3.99×10¹
F7	Std	2.14×10⁻⁵	3.47×10⁻⁴	2.23×10⁻⁴	1.30×10⁻⁴	4.92×10⁻⁴	6.88×10⁻¹	4.39×10⁻³	2.58×10⁻³	1.88×10¹

表 3 ERTLBO及其对比算法在多峰测试函数实验结果

Table 3 Experimental results of ERTLBO and compared algorithms in multimodal benchmark functions

函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F8	Mean	−7.49×10³	−2.31×10⁴	−9.59×10³	−1.83×10⁴	−1.72×10⁴	−2.17×10⁴	−3.49×10⁴	−1.64×10⁴	−7.49×10³
F8	Std	6.57×10²	3.93×10³	7.17×10²	3.13×10³	3.92×10³	1.72×10³	5.95×10³	2.58×10³	1.11×10³
F9	Mean	0.00	2.03×10²	1.59×10¹	0.00	8.69	2.34×10²	2.27×10⁻¹⁵	8.73	8.57×10²
F9	Std	0.00	3.35×10¹	3.67×10¹	0.00	3.40×10¹	4.42×10¹	2.27×10⁻¹⁴	7.38	4.87×10¹
F10	Mean	8.88×10⁻¹⁶	1.04×10⁻⁸	9.24×10⁻¹⁶	4.44×10⁻¹⁵	6.71×10⁻²	1.02×10¹	3.98×10⁻¹⁵	1.29×10⁻⁷	1.54×10¹
F10	Std	0.00	6.36×10⁻⁹	3.55×10⁻¹⁶	0.00	6.71×10⁻¹	1.23	2.46×10⁻¹⁵	5.12×10⁻⁸	8.04×10⁻¹
F11	Mean	0.00	5.70×10⁻⁷	0.00	0.00	0.00	1.42×10¹	3.64×10⁻³	4.74×10⁻³	3.33×10⁺²
F11	Std	0.00	5.70×10⁻⁶	0.00	0.00	0.00	4.00	3.64×10⁻²	1.04×10⁻²	7.52×10¹
F12	Mean	7.11×10⁻¹	3.11×10⁻⁴	1.51×10⁻¹	9.22×10⁻²	2.08×10⁻²	3.56×10⁺¹	5.29×10⁻²	2.94×10⁻¹	7.80×10⁺⁶
F12	Std	8.94×10⁻²	3.11×10⁻³	4.29×10⁻²	2.64×10⁻²	7.26×10⁻³	1.14×10⁺¹	2.61×10⁻²	8.10×10⁻²	7.53×10⁺⁶
F13	Mean	9.97	2.09×10⁻³	6.09×10⁻³	9.74	5.25	6.55×10⁺³	2.90	6.74	5.00×10⁺⁷
F13	Std	9.51×10⁻³	4.33×10⁻³	3.24×10⁻⁵	8.01×10⁻¹	7.35×10⁻¹	1.29×10⁺⁴	1.25	4.09×10⁻¹	3.23×10⁺⁷
F14	Mean	9.98×10⁻¹	9.98×10⁻¹	1.63	1.04	9.98×10⁻¹	1.29	2.79	4.12	4.00
F14	Std	1.81	7.06×10⁻¹⁷	1.30	2.79×10⁻¹	0.00	6.65×10⁻¹	3.11	3.85	2.91
F15	Mean	3.14×10⁻⁴	3.90×10⁻⁴	3.20×10⁻⁴	3.29×10⁻⁴	5.67×10⁻⁴	2.44×10⁻³	7.38×10⁻⁴	6.26×10⁻³	3.70×10⁻³
F15	Std	8.56×10⁻⁵	1.50×10⁻⁴	7.67×10⁻⁴	1.15×10⁻⁴	2.01×10⁻³	5.33×10⁻³	5.09×10⁻⁴	1.01×10⁻²	6.06×10⁻³
F16	Mean	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03	−1.03
F16	Std	6.03×10⁻¹⁶	2.10×10⁻⁵	1.01×10⁻⁵	6.68×10⁻¹⁶	6.56×10⁻¹⁶	2.27×10⁻¹⁴	1.19×10⁻⁹	2.18×10⁻⁸	5.48×10⁻⁹
F17	Mean	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹
F17	Std	1.03×10⁻³	0.00	1.07×10⁻⁶	0.00	0.00	7.54×10⁻¹⁵	9.95×10⁻⁶	9.24×10⁻⁷	6.97×10⁻¹³

续表 3
函数	统计值	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F18	Mean	3.00	3.00	3.00	3.00	3.00	3.00	3.00	3.00	3.00
F18	Std	8.13×10⁻⁴	1.24×10⁻¹⁵	8.01×10⁻⁴	6.45×10⁻¹⁶	6.44×10⁻¹⁶	2.21×10⁻¹³	2.70	4.44×10⁻⁵	1.88×10⁻¹¹
F19	Mean	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86	−3.86
F19	Std	9.45×10⁻³	2.14×10⁻¹⁵	1.08×10⁻⁴	2.20×10⁻¹⁵	2.23×10⁻¹⁵	6.35×10⁻¹¹	9.45×10⁻³	4.58×10⁻³	9.93×10⁻³
F20	Mean	−3.32	−3.16	−3.28	−3.31	−3.30	−3.22	−3.19	−3.26	−3.17
F20	Std	5.54×10⁻¹²	8.98×10⁻²	7.11×10⁻²	3.09×10⁻²	4.68×10⁻²	5.75×10⁻²	2.78×10⁻¹	7.29×10⁻²	1.09×10⁻¹
F21	Mean	−1.02×10¹	−5.06	−5.75	−5.81	−1.00×10¹	−7.75	−8.29	−9.27	−7.16
F21	Std	3.72×10⁻¹	8.73×10⁻¹⁴	1.33	1.59	6.68×10⁻¹	3.29	2.58	2.07	3.21
F22	Mean	−7.03	−1.04×10¹	−5.61	−6.05	−1.01×10¹	−7.66	−7.00	−1.02×10¹	−8.10
F22	Std	9.09×10⁻¹	3.59×10⁻¹⁵	1.20	1.86	1.36	3.40	3.20	1.18	3.09
F23	Mean	−7.93	−1.05×10¹	−6.01	−7.24	−9.97	−8.60	−7.37	−1.03×10¹	−8.23
F23	Std	6.24×10⁻³	2.27×10⁻¹⁵	1.56	2.42	1.82	3.18	3.45	1.26	3.12

表 4 各算法得到的Wilcoxon秩和检验结果

Table 4 Statistical results of Wilcoxon rank sum test obtained by algorithms

函数	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F2	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F3	2.56×10⁻³⁴	1.63×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F4	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F5	2.56×10⁻³⁴	2.56×10⁻³⁴	6.48×10⁻³⁴	3.46×10⁻³⁴	2.56×10⁻³⁴	2.70×10⁻³³	2.19×10⁻³³	2.56×10⁻³⁴
F6	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F7	2.56×10⁻³⁴	2.26×10⁻³³	6.54×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴	2.13×10⁻³³	2.56×10⁻³⁴	2.56×10⁻³⁴

续表 4
函数	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F8	2.56×10⁻³⁴	3.74×10⁻³³	2.56×10⁻³⁴	4.27×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	4.38×10⁻²⁶	7.37×10⁻¹
F9	5.64×10⁻³⁹	7.58×10⁻⁷	NaN	3.22×10⁻¹	5.64×10⁻³⁹	3.22×10⁻¹	5.64×10⁻³⁹	5.64×10⁻³⁹
F10	5.79×10⁻³⁸	1.70×10⁻³⁹	7.30×10⁻³	6.97×10⁻⁴¹	5.79×10⁻³⁸	9.51×10⁻¹	5.79×10⁻³⁸	5.79×10⁻³⁸
F11	NaN	NaN	NaN	NaN	5.64×10⁻³⁹	1.58×10⁻¹	5.64×10⁻³⁹	5.64×10⁻³⁹
F12	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.89×10⁻³⁴	2.56×10⁻³⁴
F13	2.56×10⁻³⁴	2.56×10⁻³⁴	1.25×10⁻³²	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴	2.56×10⁻³⁴
F14	1.78×10⁻³⁷	6.12×10⁻¹²	8.10×10⁻³⁹	5.64×10⁻³⁹	1.11×10⁻²³	1.08×10⁻⁴	4.52×10⁻¹	8.93×10⁻⁵
F15	2.47×10⁻¹	7.71×10⁻²²	2.43×10⁻²⁹	3.00×10⁻⁶	9.00×10⁻³²	1.84×10⁻²⁴	1.32×10⁻¹¹	1.91×10⁻³⁰
F16	3.33×10⁻³⁶	3.85×10⁻⁶	1.62×10⁻³⁸	1.03×10⁻³⁷	2.56×10⁻³⁴	2.72×10⁻³⁴	2.11×10⁻³²	2.80×10⁻³⁴
F17	5.64×10⁻³⁹	4.24×10⁻³²	5.64×10⁻³⁹	5.64×10⁻³⁹	2.09×10⁻³⁴	6.99×10⁻²⁶	1.47×10⁻³¹	2.40×10⁻³⁴
F18	1.28×10⁻³⁴	1.79×10⁻¹	1.47×10⁻³⁵	9.85×10⁻³⁷	2.56×10⁻³⁴	8.81×10⁻¹⁶	9.61×10⁻¹⁵	2.56×10⁻³⁴
F19	2.01×10⁻³⁶	1.90×10⁻³¹	4.27×10⁻³⁸	8.10×10⁻³⁹	2.56×10⁻³⁴	3.93×10⁻¹	1.61×10⁻¹³	1.65×10⁻³¹
F20	2.33×10⁻³⁷	3.96×10⁻²²	1.03×10⁻³²	4.46×10⁻²⁸	8.00×10⁻⁶	7.81×10⁻⁹	2.28×10⁻¹³	3.16×10⁻²
F21	5.79×10⁻³⁸	1.08×10⁻²⁰	3.60×10⁻²¹	2.50×10⁻³⁵	1.26×10⁻⁹	1.52×10⁻²²	1.61×10⁻²⁷	2.78×10⁻⁸
F22	1.62×10⁻³⁸	7.35×10⁻¹⁸	5.74×10⁻²⁰	9.83×10⁻³³	2.45×10⁻¹³	2.01×10⁻⁹	2.56×10⁻³⁴	1.83×10⁻³
F23	2.31×10⁻³⁷	4.97×10⁻²³	6.75×10⁻²⁶	6.97×10⁻²⁸	2.40×10⁻¹⁴	1.62×10⁻⁸	3.89×10⁻²⁹	3.77×10⁻¹¹

表 5 各算法所需运行时间

Table 5 Statistical results of runtime obtained by algorithms s

函数	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F1	0.2397	0.3548	0.1199	0.2249	0.1256	0.1450	0.0948	0.1902	0.0702
F2	0.2499	0.3831	0.1482	0.2383	0.1496	0.1401	0.1181	0.2333	0.0937
F3	1.8536	3.2118	0.8565	1.1293	0.7901	0.5252	0.4308	0.5524	0.0142
F4	0.1983	0.3187	0.0952	0.2167	0.1302	0.1305	0.1007	0.2159	0.0709
F5	0.2476	0.4192	0.1244	0.2552	0.1490	0.1367	0.1279	0.2506	0.1236
F6	0.1924	0.3519	0.0913	0.2308	0.1041	0.1328	0.0915	0.2012	0.0442
F7	1.0536	1.7270	0.4365	0.6911	0.4548	0.3126	0.2557	0.3643	0.5991
F8	0.3519	0.5840	0.2023	0.3099	0.1994	0.1650	0.1110	0.2427	0.1540
F9	0.2646	0.5725	0.1327	0.2557	0.1187	0.1648	0.0978	0.2206	0.1650
F10	0.2328	0.4602	0.1335	0.2379	0.1419	0.1689	0.0872	0.2246	0.1642
F11	0.3166	0.5420	0.1485	0.2863	0.1420	0.2067	0.1654	0.3346	0.8134
F12	2.7467	4.8544	4.1141	1.6169	2.9185	1.1044	2.1335	0.7198	3.3038
F13	2.6362	4.8122	1.1436	1.5587	5.1400	4.1887	0.6731	2.0365	5.8029
F14	1.6302	10.9205	0.7577	3.6405	2.6188	0.4010	0.3176	0.2700	0.8149
F15	0.1012	0.2646	0.0832	0.1501	0.0956	0.0462	0.0340	0.0447	0.0578

表 6 8种算法求解焊接梁设计问题实验结果

Table 6 Experimental results of eight algorithms for solving welding beam design problems

算法	h	l	t	b	f (x)
ERTLBO	0.2057	3.253	9.0366	0.20573	1.6952
BASTLBO	0.2085	3.2204	8.9964	0.20871	1.7102
ITLBOBSO	0.1970	3.4227	9.0342	0.20588	1.7058
DSLTLBO	0.1937	3.4874	9.0275	0.20625	1.7111
TLBO	0.2089	3.2319	9.0003	0.20976	1.7210
SSA	0.1937	3.4011	9.3469	0.2052	1.7468
WOA	0.2057	3.2530	9.0366	0.2057	1.7185
GWO	0.2046	3.2797	9.0327	0.2060	1.6988
GA	0.2331	2.6193	9.9920	0.2427	2.0964

表 7 各算法应用压力容器设计问题优化结果

Table 7 Optimization results of pressure vessel design problem by algorithms

算法	T_s(x₁)	T_h(x₂)	R(x₃)	L(x₄)	f (x)
ERTLBO	0.7527	0.4138	42.2128	176.8576	5984.622
BASTLBO	0.8827	0.4310	47.2537	121.7488	6027.769
ITLBOBSO	0.8828	0.4311	47.2707	121.5889	6028.433
DSLTLBO	0.8202	0.3841	45.1290	142.5473	6054.547
TLBO	0.9015	0.4390	48.2043	113.2618	6072.663
SSA	0.8759	0.4279	46.9243	124.7872	6043.665
WOA	0.7942	0.4064	44.5199	150.4761	6057.799
GWO	0.7371	0.3555	41.6434	186.6832	6050.765
GA	0.9008	0.4344	48.0603	115.3819	6092.908

续表 5
函数	ERTLBO	BASTLBO	ITLBOBSO	DSLTLBO	TLBO	SSA	WOA	GWO	GA
F16	0.1042	0.2681	0.0813	0.1393	0.1017	0.0404	0.0366	0.0349	0.0829
F17	0.0815	0.2210	0.0797	0.1320	0.0649	0.0348	0.0265	0.0342	0.0517
F18	0.0799	0.2533	0.0913	0.1215	0.0656	0.0436	0.0293	0.0310	0.0497
F19	0.1178	0.1888	0.1198	0.1629	0.0837	0.0614	0.0358	0.0406	0.0901
F20	0.1233	0.3223	0.1118	0.1556	0.1173	0.0595	0.0411	0.0576	0.0667
F21	0.1297	0.3612	0.1384	0.1681	0.1237	0.0545	0.0493	0.0496	0.0999
F22	0.1470	0.4036	0.1366	0.1792	0.1139	0.0632	0.0470	0.0649	0.1126
F23	0.1705	0.2779	0.1281	0.1776	0.1292	0.0810	0.0597	0.0756	0.1135

参考文献(27)

[1]	贾鹤鸣, 李瑶, 孙康健. 基于遗传乌燕鸥算法的同步优化特征选择[J]. 自动化学报, 2022, 48(6): 1601–1615. JIA Heming, LI Yao, SUN Kangjian. Simultaneous feature selection optimization based on hybrid sooty tern optimization algorithm and genetic algorithm[J]. Acta automatica sinica, 2022, 48(6): 1601–1615.
[2]	贾鹤鸣, 姜子超, 李瑶. 基于改进秃鹰搜索算法的同步优化特征选择[J]. 控制与决策, 2022, 37(2): 445–454. JIA Heming, JIANG Zichao, LI Yao. Simultaneous feature selection optimization based on improved bald eagle search algorithm[J]. Control and decision, 2022, 37(2): 445–454.
[3]	贾鹤鸣, 刘宇翔, 刘庆鑫, 等. 融合随机反向学习的黏菌与算术混合优化算法[J]. 计算机科学与探索, 2022, 16(5): 1182–1192. JIA Heming, LIU Yuxiang, LIU Qingxin, et al. Hybrid algorithm of slime mould algorithm and arithmetic optimization algorithm based on random opposition-based learning[J]. Journal of frontiers of computer science and technology, 2022, 16(5): 1182–1192.
[4]	RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information sciences, 2012, 183(1): 1–15. doi: 10.1016/j.ins.2011.08.006
[5]	杨闰. 改进TLBO算法及其在天线优化设计中的应用[D]. 杭州: 杭州电子科技大学, 2019: 44−54. YANG Run. Improved TLBO algorithm and its application in antenna optimization design[D]. Hangzhou: Hangzhou Dianzi University, 2019: 44−54.
[6]	麻利新. 基于教与学算法的风−火−蓄电力系统优化调度[D]. 银川: 宁夏大学, 2020: 31−38. MA Lixin. Optimal dispatching of wind power-thermal power-pumped storage power system based on teaching and learning algorithm[D]. Yinchuan: Ningxia University, 2020: 31−38.
[7]	曾恋捷. 基于教与学优化算法的结构可靠性分析方法[D]. 广州: 暨南大学, 2020: 59−71. ZENG Lianjie. Reliability analysis method based on teaching and learning optimization algorithm[D]. Guangzhou: Jinan University, 2020: 59−71.
[8]	李木子. 基于神经网络的手势识别技术研究[D]. 石家庄: 河北地质大学, 2021: 35−46. LI Muzi. Research on gesture recognition technology based on neural network[D]. Shijiazhuang: Hebei GEO University, 2021: 35−46.
[9]	WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE transactions on evolutionary computation, 1997, 1(1): 67–82. doi: 10.1109/4235.585893
[10]	李丽荣, 杨坤, 王培崇. 融合头脑风暴思想的教与学优化算法[J]. 计算机应用, 2020, 40(9): 2677–2682. doi: 10.11772/j.issn.1001-9081.2020010087 LI Lirong, YANG Kun, WANG Peichong. Improved teaching & learning based optimization with brain storming[J]. Journal of computer applications, 2020, 40(9): 2677–2682. doi: 10.11772/j.issn.1001-9081.2020010087
[11]	欧阳城添, 周凯. 融合改进天牛须搜索的教与学优化算法[J]. 计算机工程与应用, 2022, 58(4): 91–99. OUYANG Chengtian, ZHOU Kai. Teaching-learning based optimization algorithm with improved beetle antennae search[J]. Computer engineering and applications, 2022, 58(4): 91–99.
[12]	李丽荣, 李木子, 李崔灿, 等. 具有动态自适应学习机制的教与学优化算法[J]. 计算机工程与应用, 2020, 56(19): 62–67. LI Lirong, LI Muzi, LI Cuican, et al. Teaching and learning based optimization with dynamic self-adaptive learning[J]. Computer engineering and applications, 2020, 56(19): 62–67.
[13]	LAKSHMI V A, MOHANAIAH P. WOA-TLBO: whale optimization algorithm with Teaching-learning-based optimization for global optimization and facial emotion recognition[J]. Applied soft computing, 2021, 110: 107623. doi: 10.1016/j.asoc.2021.107623
[14]	XU Yunlang, YANG Zhile, LI Xiaoping, et al. Dynamic opposite learning enhanced teaching–learning-based optimization[J]. Knowledge-based systems, 2020, 188: 104966. doi: 10.1016/j.knosys.2019.104966
[15]	TSAI H C. Confined teaching-learning-based optimization with variable search strategies for continuous optimization[J]. Information sciences, 2019, 500: 34–47. doi: 10.1016/j.ins.2019.05.065
[16]	SHUKLA A K, SINGH P, VARDHAN M. An adaptive inertia weight teaching-learning-based optimization algorithm and its applications[J]. Applied mathematical modelling, 2020, 77: 309–326. doi: 10.1016/j.apm.2019.07.046
[17]	TAHERI A, RAHIMIZADEH K, RAO R V. An efficient balanced teaching-learning-based optimization algorithm with Individual restarting strategy for solving global optimization problems[J]. Information sciences, 2021, 576: 68–104. doi: 10.1016/j.ins.2021.06.064
[18]	LI Yu, ZHAO Yiran, LIU Jingsen. Dynamic sine cosine algorithm for large-scale global optimization problems[J]. Expert systems with applications, 2021, 177: 114950. doi: 10.1016/j.eswa.2021.114950
[19]	贾鹤鸣, 刘庆鑫, 刘宇翔, 等. 融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法[J]. 智能系统学报, 2023, 18(1): 104–116. JIA Heming, LIU Qingxin, LIU Yuxiang, et al. Hybrid Aquila and Harris Hawks optimization algorithm with dynamic opposition-based learning[J]. CAAI transactions on intelligent systems, 2023, 18(1): 104–116.
[20]	MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in engineering software, 2017, 114: 163–191. doi: 10.1016/j.advengsoft.2017.07.002
[21]	MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008
[22]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007
[23]	吕冰垚, 姜志翱, 宁春玉. 基于PSO和GA混合优化的FCM算法[J]. 长春理工大学学报(自然科学版), 2021, 44(6): 125–130. LYU Bingyao, JIANG Zhiao, NING Chunyu. FCM algorithm based on hybrid optimization of PSO and GA[J]. Journal of Changchun University of Science and Technology (natural science edition), 2021, 44(6): 125–130.
[24]	LIU Qingxin, LI Ni, JIA Heming, et al. Modified remora optimization algorithm for global optimization and multilevel thresholding image segmentation[J]. Mathematics, 2022, 10(7): 1014. doi: 10.3390/math10071014
[25]	ABUALIGAH L, YOUSRI D, ABD ELAZIZ M, et al. Aquila Optimizer: a novel meta-heuristic optimization algorithm[J]. Computers & industrial engineering, 2021, 157: 107250.
[26]	LIU Qingxin, LI Ni, JIA Heming, et al. A hybrid arithmetic optimization and golden sine algorithm for solving industrial engineering design problems[J]. Mathematics, 2022, 10(9): 1567. doi: 10.3390/math10091567
[27]	汪逸晖, 高亮. 乌鸦搜索算法的改进及其在工程约束优化问题中的应用[J]. 计算机集成制造系统, 2021, 27(7): 1871–1883. WANG Yihui, GAO Liang. Improvement of crow search algorithm and its application in engineering constrained optimization problems[J]. Computer integrated manufacturing systems, 2021, 27(7): 1871–1883.

点击查看大图

图(7) / 表(10)

摘要

融合经验反思机制的教与学优化算法

doi: 10.11992/tis.202112043

通讯作者: 贾鹤鸣. E-mail： jiaheminglucky99@126.com.

出版历程

Teaching and learning optimization algorithm based on empirical reflection mechanism

1. 教与学优化算法

1.1 教学阶段

1.2 学习阶段

2. 融合经验反思机制的教与学优化算法

2.1 经验反思教学模式

2.2 动态自适应学习模式

2.3 算法实现

2.4 运算复杂度分析

3. 实验仿真与分析

3.1 仿真环境

3.2 对比算法与参数设置

3.3 收敛精度分析

3.4 收敛曲线

3.5 Wilcoxon秩和检验

3.6 仿真时间

4. 工程设计问题

4.1 焊接梁设计问题

4.2 压力容器设计问题

5. 结束语

出版历程

目录

通讯作者:
贾鹤鸣. E-mail： jiaheminglucky99@126.com.