云制造是指对制造资源系统采用集中式云计算来支持分布式、动态的协同制造方式的一种新概念^[1]。基于面向服务的特征，云制造系统将物理资源层中的制造资源映射到虚拟层的资源池中，由平台层中的运营方按照资源供需方的制造要求，集中调度制造资源，实现制造资源与需求的匹配^[2-3]。然而，这种集中式的云制造平台架构在遭受单点故障，譬如云平台运营节点宕机时，难以保障云制造系统的可用性。其次，云制造系统中需要保障所有有关制造的数据信息能够被准确无误的存储，避免黑客攻击或者内部人员篡改，降低云制造参与方的信任成本。因此，如何提高云制造系统的可靠度和可信度是一个值得研究的问题。

虚拟货币的长期可靠安全运行，已经证明了作为其底层技术的区块链在数据安全方面的可靠性。其去中心化、共同维护、数据安全可信等特性，受到学术界和工业界的广泛关注^[4-9]。区块链底层融合密码学、分布式共识 、智能合约等技术，实现在弱信任环境下的安全可信。依托非对称加密技术，保证区块链参与者的匿名性；依托高效可靠的共识机制，实现各个节点的数据状态的一致；依托智能合约，保障区块链网络功能的灵活性和可拓展性。目前，区块链技术已经在制造业^[10]、医疗^[11]、供应链^[12]、物联网^[13]等领域获得深入研究。然而，其在智能制造中的应用刚刚起步，仍有待在理论方法上展开深入研究。

作为一种分析系统性能和服务质量的数学方法，排队论在分析区块链性能方面受到广泛关注^[14-15]。文献[16]提出了一种基于队列网络的联盟区块链协议一致性分析方法，主要用于评估区块链共识阶段的性能，并将该方法应用到Hyperledger Fabric系统中。为了研究区块链工作原理，文献[17]提出了一个基于排队论的模型，并通过比特币和以太坊的统计数据来验证该模型。文献[18]建立了一个具有批处理服务和门控服务的离散时间非穷载休假队列。该模型将事务初始化、挖矿和块验证分别视为到达、休假和服务期，并结合嵌入马尔可夫链方法和再生周期方法，最终得到了事务的平均响应时间。文献[19]利用节点连通性随机分布的网络分支过程对数据分布算法进行建模，提出了一个针对比特币分析模型。上述的研究证明了排队论在区块链网络的建模的可行性，但是研究的对象局限于比特币、以太坊和超级账本等区块链项目。目前，极少有研究关注云制造系统中区块链的排队时延问题。

作为面向服务的制造模式，云制造系统将所有与制造生产相关的对象封装成具体的服务，以满足制造资源需求方的各种任务需求。这就要求云制造系统在运行时，能够快速地响应制造需求方的任务请求，给云制造系统的使用者带来良好的体验感。为此，本文着重研究了云制造系统中区块链的排队时延问题，并探索降低云制造系统中区块链排队时延的因素。

综上，本文创新性的用排队论分析云制造系统中区块链节点的排队时延，探索云制造系统中区块链节点排队时延的影响因素，以期提高云制造系统的响应速度。主要的工作内容为：

首先阐述了云制造系统中区块链技术的应用现状，提出一种新的云制造系统中区块链应用框架。在该框架下结合云制造用户向云制造系统发送制造服务请求为场景，基于 $M/M/1$ 排队模型，剖析了服务请求在交易缓冲池阶段和共识阶段的排队过程。结合云制造系统特征，给出平均队长(average length, AL)、平均排队长(average queue length, AQL)、平均逗留时间(average stay time, AST)、平均排队时间(average queue time, AQT)、服务强度(service intensity, SI)等指标的定义与表达式。针对影响云制造系统性能指标的区块链因素，提过了一种共识环节的自适应难度值的机制，以及研究了挖矿激励对提高该系统性能的影响。最后，采用实验仿真的方式，在MATLAB上多次运行仿真程序，模拟云制造资源服务记录在交易缓冲池阶段和共识阶段时延过程，统计AL、AQL、AST、AQT及SI的平均结果。并对自适应难度值机制和挖矿激励对区块链节点服务率的影响做出实验验证和分析。研究结果表明，这两种措施对提高区块链节点的服务率有正作用，进而降低该系统处理云制造用户的服务请求时间，提高用户的体验感。

1.   云制造系统中区块链排队时延

1.1   基于区块链的云制造系统架构

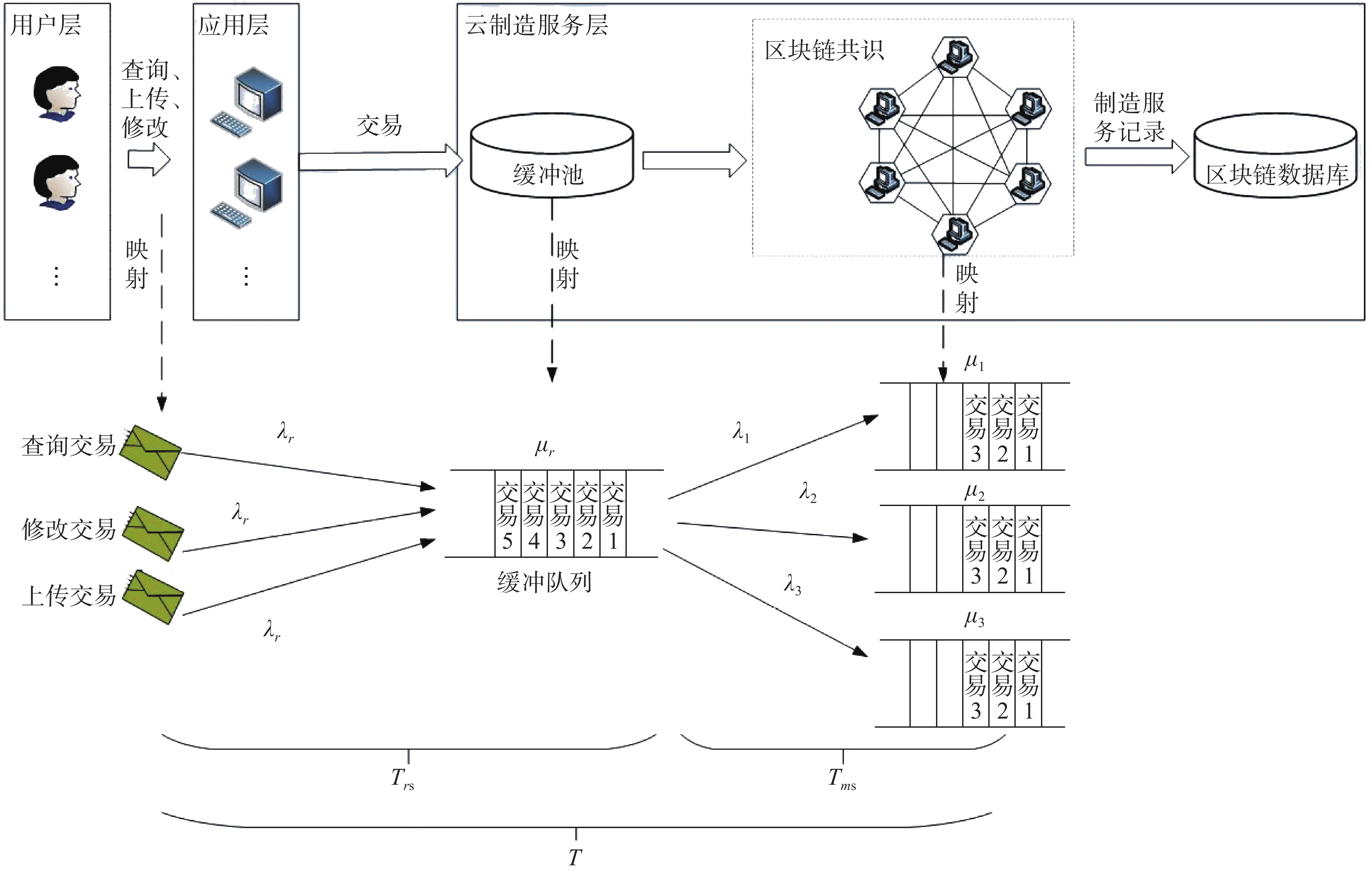
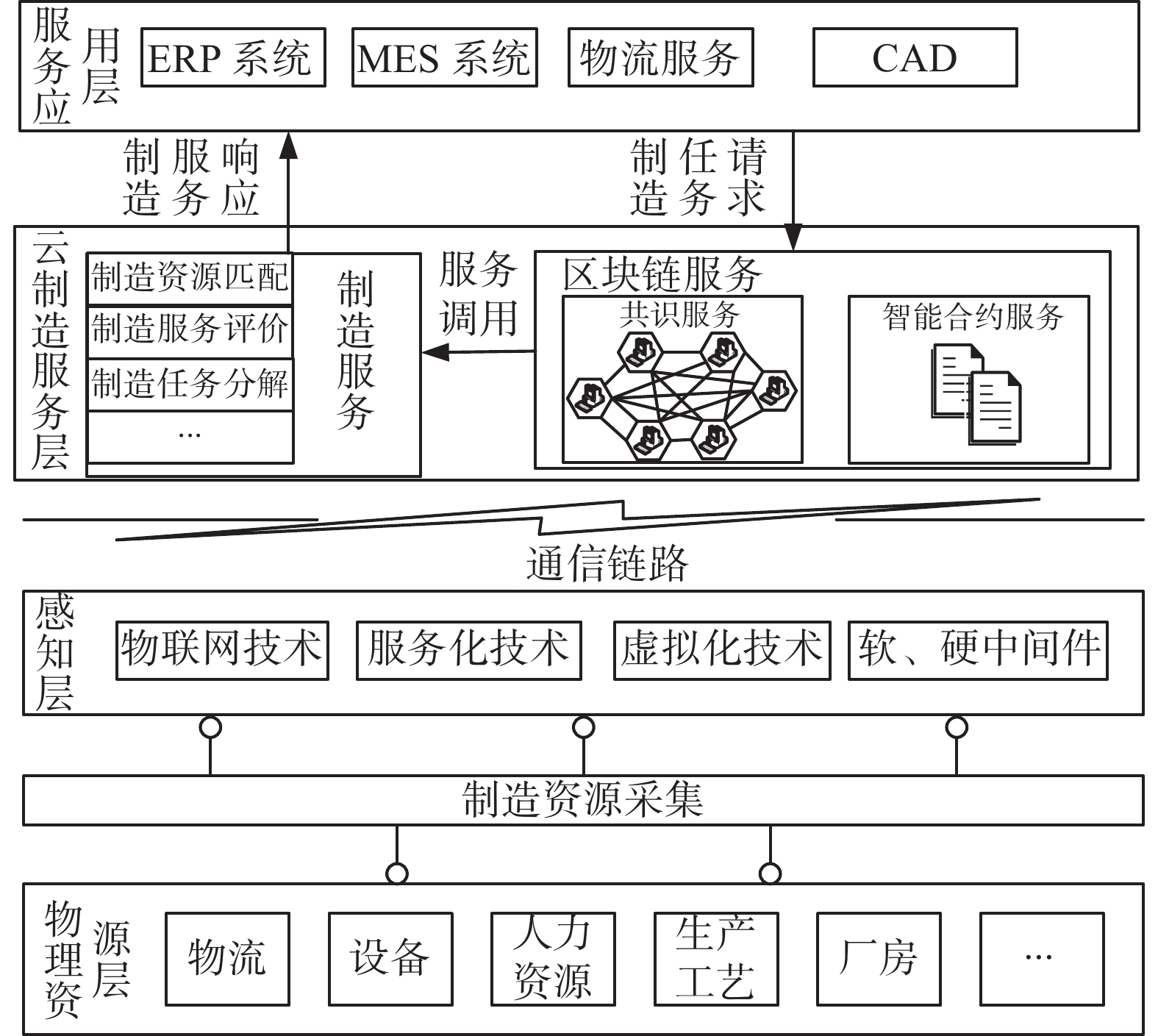
现阶段取得的研究成果表明，利用区块链的去中心以及安全可信等特性，是解决云制造平台集中化和数据安全问题的有效途径。文献[20-21]基于区块链技术开发了一种分布式点对点网络架构，以提高云制造系统的安全性、可信性和可扩展性。文献[22]基于以太坊公有链，研究了智能合约在云制造中的应用，保证了制造资源供应商和需求方之间的协议不被篡改。文献[23]提出了一种基于区块链的云制造架构，以增强信息透明度和去中心化。其中，区块链用于中介服务组合和记录事务结果。在上述研究的基础上，为了研究云制造系统中区块链节点的排队时延问题，本文提出一种基于区块链的云制造框架(blockchain-based cloud manufacturing framework, BCMF)，如图1所示。

图  1  基于区块链的云制造框架

Fig.  1  Blockchain-based cloud manufacturing framework

下载: 全尺寸图片

和已有研究不同的是，本文提出的区块链在云制造框架的服务层。该框架在满足对外提供制造服务的相关功能外，兼顾系统的去中心化和数据的安全可靠。该框架由物理资源层(physical resource layer, PRL)、感知层(perception layer, PL)、云制造服务层(cloud manufacturing service layer, CMSL)和服务应用层(service application layer, SAL)组成。PRL主要涵盖制造生产过程中的制造资源和制造能力，包括加工原料、厂房、设备、资金、人力、加工工艺等。PL通过各种物联网设备、虚拟化技术、服务化技术、软硬中间件等将制造资源虚拟化，组建虚拟资源池。CMSL是系统的核心层，处于该层的服务器组建区块链节点，提供区块链服务、制造任务分解、制造资源匹配、制造服务评价等服务。其中，区块链服务的核心是提供区块链共识服务和智能合约服务。针对云制造用户的制造任务请求，由各云制造节点组建的区块链网络进行共识，并通过智能合约服务对制造服务的相关方自动执行制造服务，记录在各自的本地数据库中，避免了制造服务请求的丢失，同时也可追溯到云制造用户的制造服务历史记录。SAL作为应用层，提供各种具体的制造服务，如MES系统、ERP系统等。

1.2   BCMF中节点排队时延分析

考虑以下云制造系统应用场景，如图2所示。

图  2  服务请求处理过程

Fig.  2  Service request processing flow

下载: 全尺寸图片

云制造资源需求方或者供应方需要了解平台中的制造资源情况，用户可以查询相关制造资源，也可以上传或者修改某种制造资源。这些请求经过云制造应用层的服务终端后被封装成对应的服务交易。这些服务交易是需要被云制造服务器节点组成的区块链网络处理的。首先需要对所有未处理的服务交易暂存在交易缓冲池中，如果此时交易缓冲池没有服务交易，则该交易会被立即处理，否则将在交易缓冲池中排队等待。进入到区块链网络的服务交易将由云制造服务节点运行共识算法，譬如工作量证明算法(proof of work, POW)，将相关服务交易记录打包成区块并发布，最终形成服务交易记录的区块链。之后云制造服务层在调用对应的制造服务，如制造资源查询等，将查询结果反馈到应用层，并响应到用户端。其中耗时比较严重的环节是服务层中的区块链服务。

定义1　排队时延 $T$ 为服务交易在交易缓冲池的平均逗留时间 ${T_{r{\rm{s}}}}$ 和共识阶段的平均逗留时间 ${T_{m{\rm{s}}}}$ 之和。

在POW共识过程中，节点通过消耗硬件设备提供的算力，找到一个满足难度值的随机数，从而将其打包的区块广播到网络中，获得对应的奖励。其弊端是需要消耗大量的硬件资源和算力^[24]。且导致系统挖矿的吞吐量难以匹配资源服务交易的请求增长速度。从而导致云制造用户需要等待一段时间才能获得云制造系统的响应结果。为避免服务交易在排队中丢失，需要在打包挖矿阶段之前，将资源服务记录进行缓存。

云制造服务节点向制造服务需求方提供相关服务后，需要在由云制造服务节点组成的区块链网络中广播服务记录。广播服务交易记录的数量取决于该区块链网络的性质和业务需求量，一般情况下，公有链中的节点数远高于联盟链，因而，产生的服务交易记录量也远高于联盟链。有研究表明^{[17, 19, 25]}，以比特币为代表的区块链系统，其交易记录的到达数量服从泊松分布。因此，本文做出如下假设：随着系统的长期无故障运行，系统中的服务交易记录量为无穷多个。由于各个服务节点相互独立的广播服务交易记录，因此，被广播的资源服务交易记录也是相互独立的到达记录缓冲池，记服务交易记录数量为随机变量 $X(t)$ ,令 $X(t) = k$ 则构建公式为

式中： ${P_k}(t)$ 表示在时刻 $t$ 有 $X(t) = k$ 条服务交易记录到达交易缓冲池的概率，服从参数为 ${\lambda _r}$ 的泊松分布。

由式（1）可知相邻两条记录的到达间隙 ${T_r}$ ，服从参数为 ${\lambda _r}$ 的指数分布。记分布函数为 $F(t)$ ：

交易缓冲池根据资源服务交易记录到达的先后顺序，按照先到先服务的规则(first come first service, FCFS)接收资源交易服务记录。假设交易缓冲池的容量足够大，则资源服务交易记录进入交易缓冲池的过程可以用 $M/M/1$ 模型进行描述，该模型适用于资源服务交易记录到达时间和记录服务时间服从泊松分布，参数分别为 ${\lambda _r}$ 和 ${\mu _r}$ ，缓冲服务队列为1的场景。

缓存在交易缓冲池的云制造资源服务交易记录，需要通过矿工节点打包、验证，最终形成记录区块。由于在交易缓冲池处理阶段，交易缓冲池的服务时间服从参数为 ${\mu _r}$ 的泊松分布。假设在每一轮的服务交易记录处理流程中，参与打包挖矿的节点数为 $s$ 。由于每条服务交易记录最终都会被各节点打包，且各节点有相同的机会打包服务记录，则到达各节点的服务记录也服从泊松分布，且服务记录的到达率相等，即 ${\lambda _1} = {\lambda _2} = \cdots = {\lambda _s} = \lambda $ 。

各节点对到达的服务交易记录根据POW共识和FCFS规则进行挖矿，假设挖矿时间服从泊松分布，挖矿时间的长短受节点算力影响，记节点 $i$ 的泊松参数为 ${\mu _i}$ ， $i = 1,2, \cdots ,s$ 。各节点彼此竞争挖矿，因此，该过程可视为 $s$ 个节点并行运行，所以将节点共识阶段用 $s$ 个 $M/M/1$ 模型描述。

1.3   BCMF排队时延指标

为定量研究BCMF系统性能，结合排队论的相关理论，做出如下系统指标定义：

定义2　服务强度 ${\rho _s}$ 用以表征BCMF系统处理服务交易的能力，是单位时间内服务交易到达的数量 ${\lambda _s}$ 与BCMF系统能够处理的服务交易数量 ${\mu _s}$ 的比值。

定义3　平均队长 $Q$ 用以表征BCMF系统正常运行时任意时刻处于排队状态或者正在被服务层处理的制造服务交易的数量。

定义4　平均排队长 ${Q_q}$ 用以表征BCMF系统正常运行时任意时刻处于排队状态的制造服务交易的数量。

定义5　平均逗留时间 ${T_s}$ 用以表征BCMF系统正常运行时每条制造服务交易从进入排队开始到被服务层处理结束所消耗的时间。

定义6　平均排队时间 ${T_w}$ 用以表征BCMF系统正常运行时每条制造服务交易处于排队状态所消耗的时间。

假设在资源服务交易进入交易缓冲池阶段，只有1个缓冲队列。记 ${p_n} = P\{ N = n\} ,n = 1,2, \cdots$ 为BCMF系统长期稳定运行后服务交易的数量 $N$ 的概率分布，记服务强度为 $\rho = \dfrac{{{\lambda _r}}}{{{\mu _r}}}$ ， $\rho < 1$ 。由生灭过程可以得到：

所以，该阶段的平均队长 ${Q_r}$ 可表示为

平均排队长 ${Q_{r{\rm{q}}}}$ 为

根据服务强度 $\rho = \dfrac{{{\lambda _r}}}{{{\mu _r}}}$ ，式(2)~ (3)以及little定律可得平均逗留时间 ${T_{r{\rm{s}}}}$ 为

平均排队时间 ${T_{r{\rm{w}}}}$ 为

在共识阶段，假设存在 $s$ 个节点打包服务记录。任何一笔待处理记录均由 $s$ 个节点并行处理服务记录，且处理过程相互独立。记节点 $i$ 的服务率为 ${\mu _i}$ ，记该阶段服务时间为服从参数为 ${\mu _m}$ 的泊松分布，则服务强度 ${\rho _m}$ 可表示为

平均队长 ${Q_m}$ 可表示为

平均排队长 ${Q_{m{\rm{q}}}}$ 为

根据little定律可得平均逗留时间 ${T_{m{\rm{s}}}}$ 为

平均排队时间 ${T_{m{\rm{w}}}}$ 为

2.   基于BCMF排队时延的共识机制设计

在云制造系统服务交易记录到达率一定的情况下，根据式（4）~（9）可知，随着系统的服务率升高，该阶段的AL、AQL、AST、AQT均降低。由式（4）可知，系统的服务率为该阶段参与打包节点的服务率之和。由此可以得到2条重要的结论：

1) 单个节点服务率的增加与系统的服务率增加有正影响作用。

2) 系统中参与服务的节点数量的增加将有效提高系统服务率。

因此，如果能采取一定措施提高云制造系统中节点的服务率，必然会缩短BCMF的排队时延，缩短系统处理用户的制造请求的响应时间，给用户带来更好的体验感。

2.1   共识难度改进

在基于区块链的云制造系统中，节点通过消耗算力进行哈希运算，找到满足系统难度值的随机数，通过共识机制共同维护该系统的数据的一致性。然而，以比特币为代表的区块链网络，通过控制区块生成时间来调节系统的难度值。该难度调整策略导致系统的吞吐量及交易确认时间无法进一步提升，同时也引发节点不断提高算力以提高挖矿胜率的恶性循环，降低了算力较弱的节点的参与机会。为解决该问题，本文在BCMF系统中引入针对节点的自适应难度值的概念。

云制造系统在运行之前，一般根据经验设置系统的初始难度值 $D$ ，为避免算力竞赛造成的资源浪费，本文通过自适应难度值机制调节每个节点各自的难度值。

定义7　记系统的初始难度值为 $D$ ，若系统中共有 $s$ 个节点参与挖矿，节点 $i$ 的算力为 ${\alpha _i}$ 。则节点 $i$ 的自适应难度值 ${d_i}$ 为

系统在每轮挖矿之前统计参与挖矿节点的算力，根据节点的算力调整各节点的挖矿难度。

2.2   节点挖矿激励

云制造系统需要给挖矿成功的节点高额的奖励，用以刺激节点参与挖矿的积极性。若缓冲池中存在 $x$ 条服务记录，服务交易记录 $j$ 的大小为 ${m_j}$ , $j = 1,2, \cdot \cdot \cdot ,x$ 。记服务记录 $j$ 对节点 $i$ 的价值为 ${v_{i,j}}$ ，本文中的BCMF系统奖励由两部分组成，一部分是挖矿成功的固定奖励 $r$ ，另一部分奖励取决于打包的服务交易记录的价值和 $\sum\limits_{j = 1}^z {{v_{i,j}}} $ ， $z \leqslant x$ 。则节点 $i$ 的奖励 ${R_i}$ 为

式中 ${p_{mi}}$ 表示云制造服务节点 $i$ 在一次挖矿过程中获得记账权的概率。 ${p_{mi}}$ 与节点的算力成正比，因此 ${p_{mi}}$ 为

为刺激节点打包信息量大的服务交易记录，本文取 ${\Delta _j}$ 与服务记录 $j$ 的大小的平方成正比，比例系数为 $a$ 。相同条件下，服务记录的容量越大，被节点打包的可能性越高。则：

一般情况下，区块的容量是有限的，记区块容量上限为 ${M_c}$ ，则：

记节点 $i$ 在单位时间单位算力的成本为 ${c_i}$ ，则节点 $i$ 在提供算力 ${\alpha _i}$ 的条件下，处理服务记录 $j$ 的成本 ${e_{i,j}}$ 为

则：

节点通过消耗算力获取服务能力，记算力与服务率的比值为 ${\gamma _i}$ ：

在区块容量的约束下，节点需要有选择的确定被打包的服务记录，从而获取最大的打包收益 $V$ 。即：

为获取节点打包收益的全局最优解，对上述问题使用动态规划求解。

算法1　节点 $i$ 动态规划打包记录

输入　 ${M}_{c}、{m}_{j},\;\;j=1,2,\cdots,n$

输出　 $\max \displaystyle\sum\limits_{j = 1}^z {{v_{i,j}}} , \;\;z \leqslant n$

1) $\forall {m_j}$ ，根据式（11）计算 ${v_{i,j}}$

2) While $j \leqslant n$

3) $v_{\text{ol}} = 1$ // $v_{\text{ol}} $ 表示区块容量的中间变量

4) While $v_{\text{ol}} < {M_c}$

5) 　If $j = = 1\& \& v_{\text{ol}} \geqslant {m_j}$

6) 　　 ${V_{j,{\text{vol}}}} = {v_{i,j}}$

7) 　Else

8)　　 $V{\text{ = }}\max ({V_{j - 1,{\text{vol}}}},{v_{i,j}} + {v_{j - 1,{\text{vol}} - {m_j}}})$

9)　 $v_{\text{ol}} $ ++

3.   实验仿真

为验证上文理论结果的准确性，本文采用实验仿真模拟云制造服务交易在交易缓冲池和共识阶段的排队时延过程，

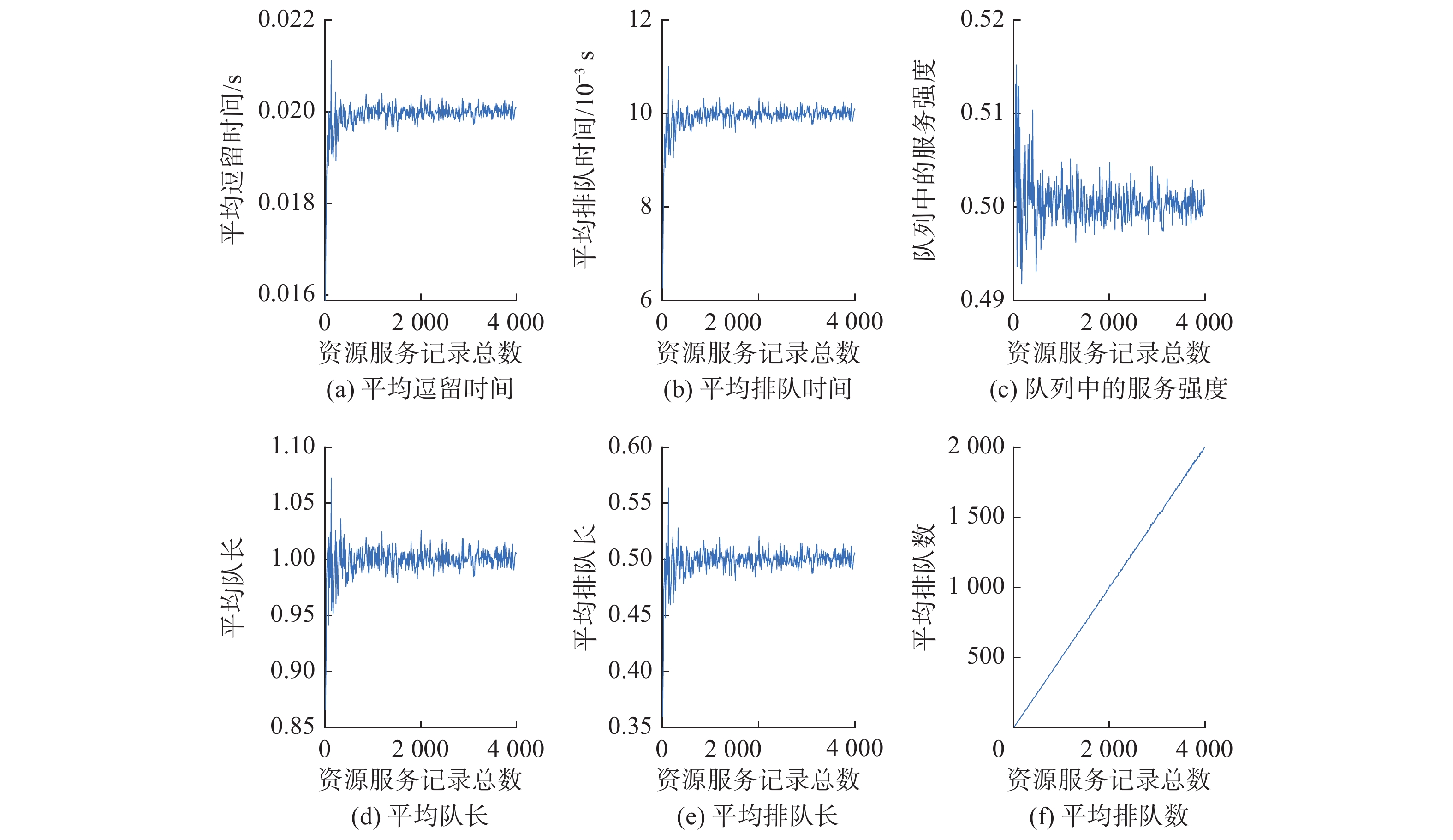
将服务交易记录进入交易缓冲池阶段模拟为一个 $M/M/1$ 队列，设置服务交易记录到达率 ${\lambda _r} = 50$ ，交易缓冲池服务率 ${\mu _r} = 100$ 。统计AL、AQL、AST、AQT、SI以及平均排队数，实验模拟云制造系统正常运行时，用户不断向云制造系统发送服务请求。请求数从0开始，每次增加10条请求，重复试验400次，每次重复试验100次，取100次的平均值作为本次统计结果，仿真工具采用MATLAB R2016b，操作系统为windows10 x64，AMD A8-7100 Radeon R5，4核，1.80 GHz，12 RAM。仿真结果见图3，理论计算结果和仿真统计结果见表1。

图  3  交易缓冲池阶段各指标仿真结果

Fig.  3  Simulation results of each index in the transaction buffer pool stage

下载: 全尺寸图片

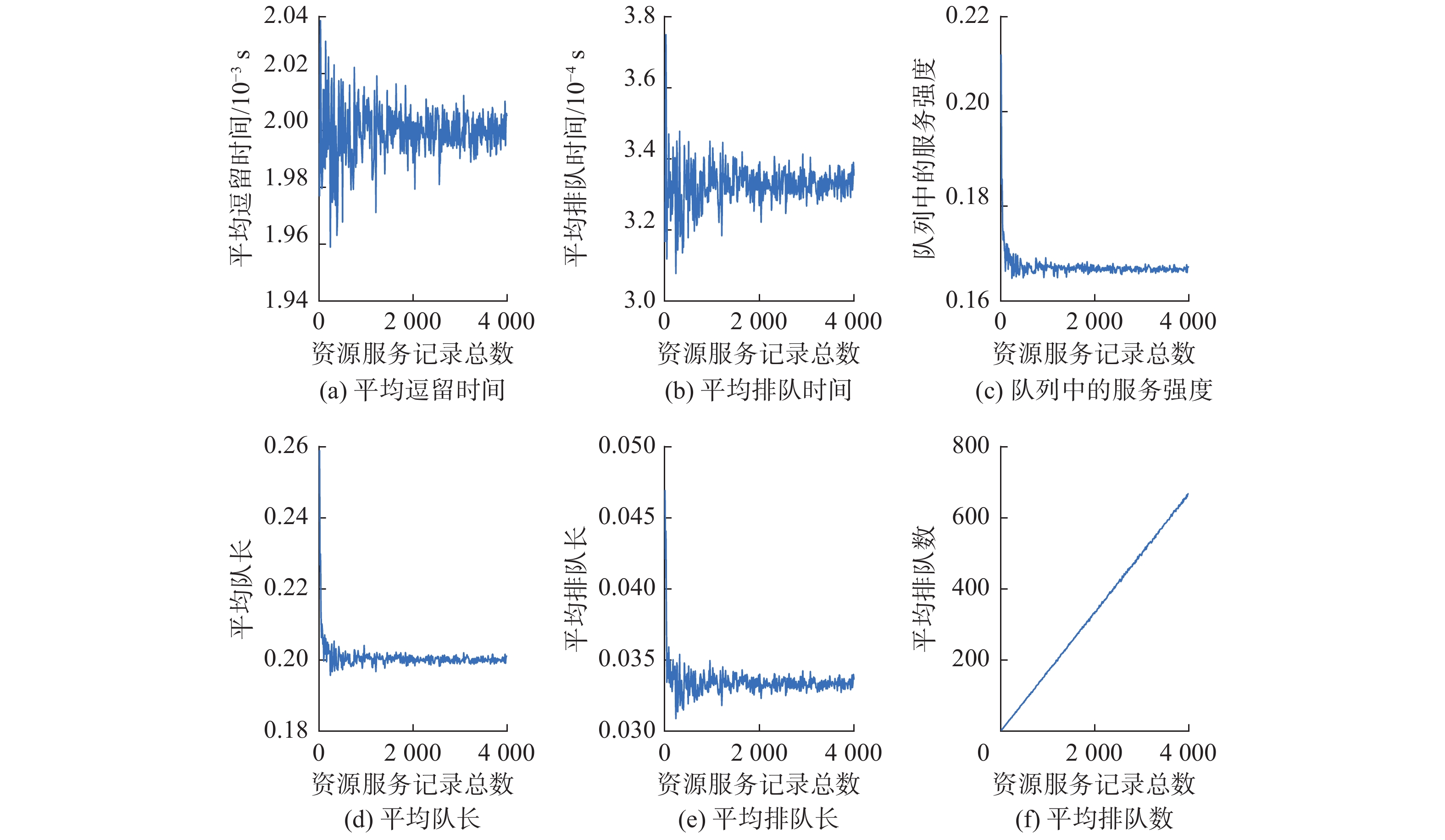
在共识阶段，每个云制造服务器节点被视为一个 $M/M/1$ 队列，实验采取3个节点进行仿真。因此，该阶段可视为3个 $M/M/1$ 队列组成的系统。取待打包服务交易记录的到达率取 ${\lambda _{m1}} = {\lambda _{m2}} = {\lambda _{m3}} = 100$ ，各节点的服务率取 ${\mu _{m1}} = {\mu _{m2}} = {\mu _{m3}} = 200$ 。统计AL、AQL、AST、AQT、SI以及平均排队数，实验模拟云制造系统正常运行时，用户不断向云制造系统发送服务请求。请求数从0开始，每次增加10条请求，重复试验400次，每次重复试验100次，取100次的平均值作为本次统计结果，仿真工具采用MATLAB R2016b，操作系统为windows10 x64，AMD A8-7100 Radeon R5，4核，1.80 GHz，12 RAM。仿真结果见图4，理论计算结果和仿真统计结果见表2。

图  4  共识阶段各指标仿真结果

Fig.  4  Simulation results of each index in the consensus stage

下载: 全尺寸图片

由表1和表2可知，理论值和仿真值近似一致，由图3和图4可以明确看到，仿真的实时结果在理论值附近波动，并收敛于理论值，通过大量重复试验得到的频率结果近似趋近于概率值，这表明基于 $M/M/1$ 排队模型的请求仿真，在一定程度上能代表云制造系统中云制造用户的制造请求的排队时延特征。

为研究具有不同服务率的节点对共识阶段平均挖矿时间和系统平均挖矿时间的影响，取服务率不同的3个节点， $ {\mu }_{m1}=50、{\mu }_{m2}=100、 {\mu }_{m3}=200 $ 。统计系统与各个节点的平均挖矿时间，请求数从0开始，每次增加10条请求，重复试验400次，每次重复试验100次，取100次的平均值作为本次统计结果，仿真工具采用MATLAB R2016b，操作系统为windows10 x64，AMD A8-7100 Radeon R5，4核，1.80 GHz，12 RAM。仿真结果见图5。仿真结果表明系统的挖矿时间为各节点挖矿时间之和，不同节点的挖矿时间与其服务率成正比。服务率越高，节点在系统中挖矿时间越长。因此，可通过提高节点的服务率或者增加服务节点的数量来增加系统的服务能力和吞吐量，从而降低云制造系统对用户请求的响应时间。

图  5  服务率对挖矿时间的影响

Fig.  5  Influence of service rate on mining time

下载: 全尺寸图片

由图5可知，随着节点贡献的服务率的提升，系统整体的服务率将增加，最终系统在处理云制造客户端的任务请求时间将会有所改善，缩短系统的排队时延。

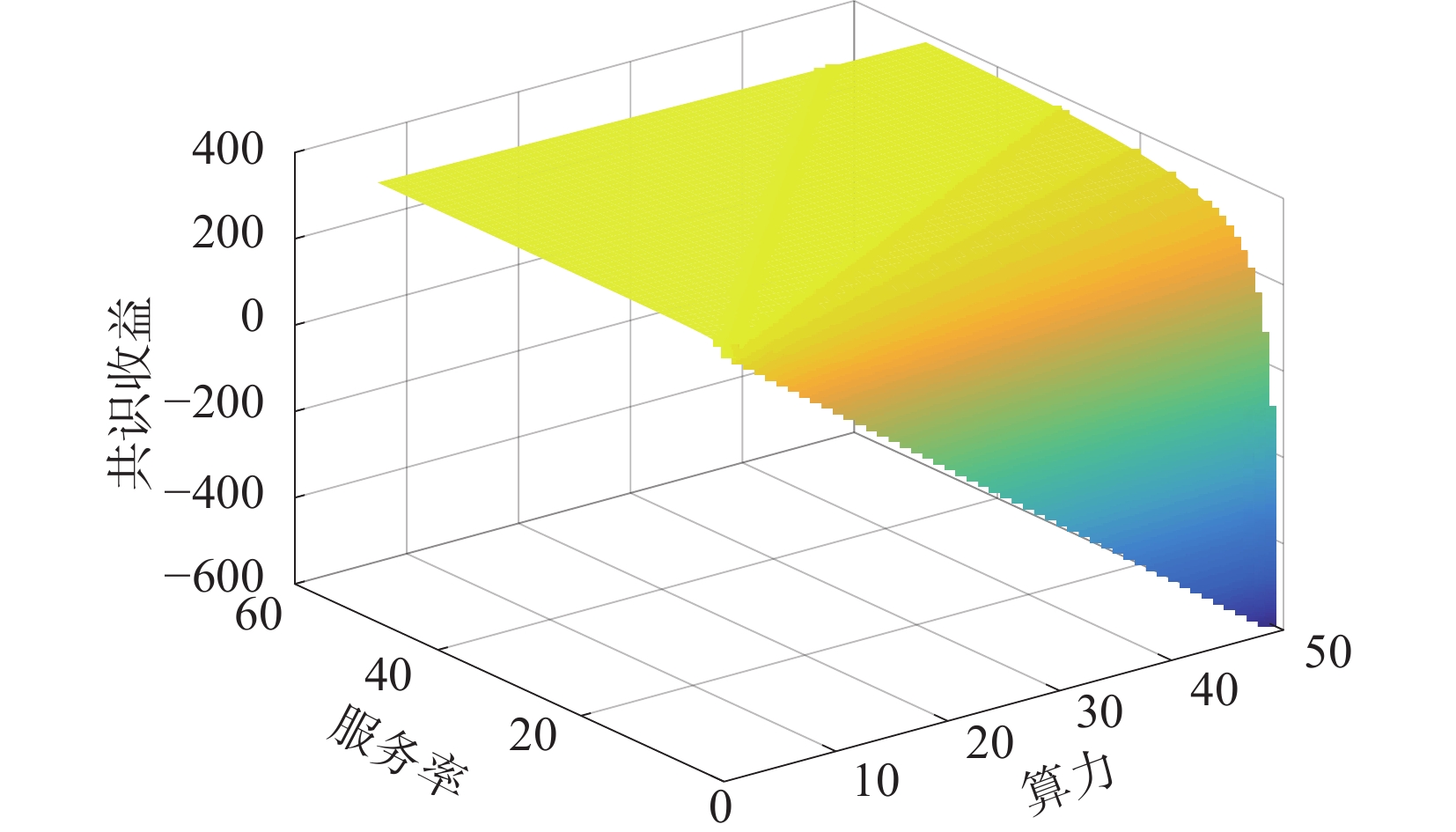
为验证节点服务率、算力与节点收益之间的关系，选取参数如下：系统中两个节点算力固定 ${\alpha _1}{\text{ = }}{\alpha _2}{\text{ = }}30$ ，服务交易记录的系数 $a = 1$ ，服务交易记录的容量 $m = 20$ ，挖矿成功的奖励 $r = 1$ ，单位时间算力的成本 $c = 1$ 。则收益与节点3服务率、算力的关系见图6。由图6可知，节点3的收益与服务率呈正相关，与投入的算力呈负相关。在节点服务率较低的情况下，其收益随着投入算力的增大，而大幅缩减；在服务率较高的情况下，收益相对稳定。因此，对于想要获得收益的节点而言，提高自己的服务率不仅能带来较高的收益，还能对抗算力成本对收益的影响。

图  6  收益与服务率、算力的关系

Fig.  6  Relationship between revenue and service rate and computing power

下载: 全尺寸图片

为验证自适应难度在节点共识阶段对云制造系统排队时延的影响。本文使用Java语言实现POW共识算法，仿真工具采用IntelliJ IDEA，操作系统为windows10 x64，AMD A8-7100 Radeon R5，4核，1.80 GHz，12 RAM。模拟3个节点的算力大小分别为15、20、25。分别在系统初始难度 $D = 4$ 和自适应难度的情况下运行共识算法20、50、100次，每种情况运行10次，统计各自的平均耗时情况，见表3。

由于仿真设备资源限制，在统计初始难度共识耗时时，本文只对算力为20的节点进行统计。根据算力与耗时成反比的关系，计算算力为15和25的初始难度耗时。在统计自适应难度时，根据式(10)计算各节点算力，可知其对应的自适应难度值为3、4、5。各节点的共识排队时延数据见表3。由表3可知，自适应难度耗时近似与节点的算力成正相关。即算力小的节点在运行共识算法的排队时延较小，算力大的节点在运行共识算法的排队时延较大。

这是由于系统采用自适应难度后，各节点的难度值跟节点算力在系统中的占比一致。而难度值在共识排队时延中的影响是指数级别的，从而削弱算力对共识时延的影响。相比较初始难度，采用自适应难度，算力小的节点有更多的机会参与共识，甚至有机会花费更少的排队时延完成共识，从而提升BCMF系统的用户请求响应速度，提高用户的满意度。

4.   结束语

本文主要研究了云制造系统中的区块链排队时延问题的仿真与分析。在分析了区块链在云制造系统应用的基础上，提出一种基于区块链的云制造框架。以云制造用户向云制造系统发送任务请求为场景，剖析了该系统的工作流程。并使用 $M/M/1$ 排队模型对该系统中的服务交易记录进入资源缓冲池阶段和云制造节点共识阶段进行理论分析，给出平均排队长、平均队长、平均逗留时间和平均排队时间等云制造系统指标的定义与表达。研究表明该系统的排队时延与单位时间系统的服务率有密切的关系。具体而言，若节点的服务率提高或者增加参与共识的节点将有助于缩短系统的排队时延。为此，本文在节点共识阶段,提出一种难度自适应机制，改善POW共识过程中的算力竞赛，同时提高了算力较小节点的参与机会，降低系统在共识阶段的排队延迟。利用奖励机制刺激节点参与共识的积极性，研究结果表明，当节点贡献出更大的服务率时，其收益也会增加。两种方式均有助于提高云制造系统处理用户任务请求的排队时延。

鉴于目前研究云制造系统中区块链排队时延问题的研究相对匮乏，本文在该方向上提供了一定的研究基础。基于该时延模型，设计一种低延迟、高吞吐量的共识策略将是一个有价值的研究目标，也是本文后续的着力点。