为面对不断加剧的市场竞争压力，企业除了改进现有制造工艺和生产设备技术水平，还可以通过引入基于人工智能的排产优化算法来缩短加工时间、降低能耗、制定出更契合企业实际生产运作规律的生产计划，进一步挖掘企业现有的生产潜力。对新的投产任务进行排产优化过程中，基于常规群体进化算法或数学规划算法的排产优化算法每次都需要复杂的迭代寻优计算才能获得较好的优化结果，如果排产优化过程较慢，会增加计划人员的排产工作时间，特别是当生产计划进行调整或是重排时，车间工况随着时间也在不断变化，更需要快速给出排产优化结果。同时，对于复杂的生产优化问题很难构建精准的生产优化模型，并且这些问题求解过程比较复杂，因此更需要探索一种充分依托历史生产数据，并可以快速给出合理排产结果的方法来解决上述问题。深度学习方法具有无需人工建模、快速提取数据潜在特征以及并行计算等特点，近年来在语言处理和回归分析领域都有比较成功的应用案例，因此将深度学习算法引入到生产优化领域中，利用深度学习算法挖掘历史排产数据中隐含的排产知识，获取排产数据与排产结果的映射关系网络，从而指导柔性流水车间的实时生产。

本文针对制造业典型的柔性流水车间^[1-2]排产优化问题进行研究，将深度学习方法应用于求解这类排产优化问题。在柔性流水生产车间优化方向上，当前学者都进行了深入的探索。文献[3]结合遗传算法和模拟退火算法的优点，提出一种改进混合遗传模拟退火算法，提高了算法自身的收敛速度和寻优能力。文献[4]提出一种混合蛙跳算法，通过对全解空间禁忌搜索，扩大了算法解空间，提高了算法的有效性和优越性。文献[5]通过设计一种改进的蝙蝠算法来解决部分设备维护时的车间调度问题，并通过验证证明了方法的有效性。上述文献的方法侧重于对智能排产优化算法^[6-9]的改进，但当需求产能出现变动导致需要快速重新编制生产计划的时候，常用的群体进化算法和数学规划算法都需要重新进行耗时的迭代寻优计算过程，难以快速给出较好的优化结果。

深度学习算法^[10-12]可以充分利用历史数据^[13]，找到数据之间的关联关系，快速给出智能决策结果，在图像分类、场景建模、网络安全、自然语言处理等领域得到广泛，但在生产优化领域的应用研究目前还处于起步阶段，并且学者多侧重于研究生产调度和局部指派问题，文献[14]提出基于BP神经网络的数据驱动实时调度方法，神经网络通过对历史样本数据进行挖掘学习，形成生产系统状态与调度规则的映射关系网络，最后将其应用在生产在线实时调度，其性能指标良好。文献[15]提出一种嵌入指针网络的长短期记忆(long short-term memory, LSTM)深度学习模型，模型通过对实际生产数据进行挖掘训练，利用指针网络来选择工件优先进入缓冲区，提高了模型的有效性和可靠性。文献[16]使用BP神经网络对历史生产信息进行分析，将数据归一化之后进行计算，预测产品完工时间。文献[17]针对柔性作业车间调度问题，提出一种改进的多阶段优化调度方法和结合了遗传算法与神经网络的小范围竞争择优策略，通过仿真实验证明了该算法的优良性。

上述文献表明深度学习算法在局部指派和工时预测方面已经得到了一定程度的应用，但多数情况下还是将其用以解决智能决策问题，为了进一步扩展和探索深度学习算法在生产优化领域的应用，本文将深度学习算法引入到求解排产优化优化问题中。工件加工上线序实质上是多个工件互有关联的工件序列，在目前主流的深度学习体系中，序列到序列(Seq2Seq)方法具有良好的处理和生成序列的能力，其在许多领域已经得到了应用，文献[18]提出一种基于改进Seq2Seq的短时自动识别系统(automatic identification system, AIS)轨迹序列预测模型，选取两类典型河段的数据对模型进行训练，最终验证了该模型能够有效提高短时轨迹序列预测的准确性和效率。文献[19]提出一种新的台风等级预测模型SeqTyphoon，模型结合了Seq2Seq与卷积神经网络，通过对历史台风图像进行训练预测，利用卷积神经网络对预测的台风图像进行评级，提高了预测的精度和速率。

基于上述研究成果，本文提出了一种基于深度学习的智能排产优化方法，重点研究生产数据中生产任务信息、工艺信息与排产结果的相关性，通过对历史生产数据的学习，训练能够快速给出有效的排产结果的智能优化模型。提出面向排产优化问题的基于门控循环单元(gated recurrent unit, GRU)构建的Seq2Seq深度学习模型(sequence-to-sequence deep learning model based on gated recurrent unit, SeqGRU)，该模型神经元采用门控循环单元，构建序列到序列模型的编码器和解码器，模型解码器输出为工件上线序，并进一步引入注意力机制提高寻优的精度和速率。

1.   柔性流水车间排产优化问题概述

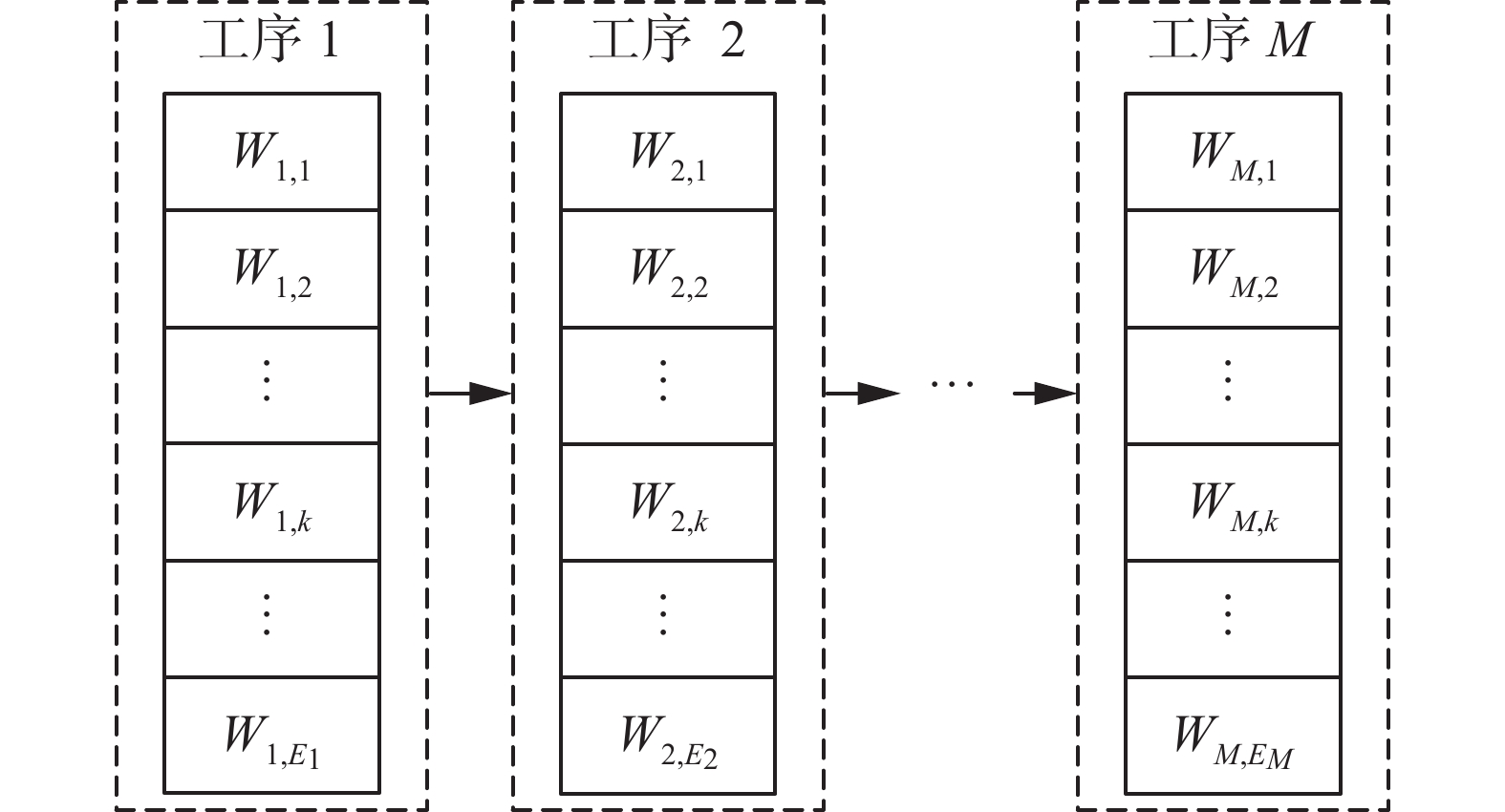
柔性流水车间排产优化问题描述为： $ N $ 个工件按照同一加工顺序在 $ M $ 道工序上进行加工， $ M $ 道工序之中至少有一道工序的并行机器数多于一台( $ {E_j} \geqslant 2 $ )。同一工件的同一工序，所有机器上的加工时间相同，工件在各工序的加工顺序一致。加工时间为已知量。柔性流水车间如图1所示。优化目标是找到 $ N $ 个工件进入车间加工的上线序，最小化最大完工时间。并在其生产过程中存在多种假设条件包括：同一时刻同一台机器只能加工一道工序；每个工件在某一时刻只能在一台机器上加工；同一工件的工序有先后约束，不同工件的工序之间没有先后约束；不同工件具有相同的优先级；任何操作在加工过程中不能中断。

图  1  柔性流水车间示意

Fig.  1  Schematic of flexible flow workshop

下载: 全尺寸图片

模型中主要参数包括： $ N $ 表示工件总数， $ M $ 表示工序总数， $ i $ 表示工件的序号， $ j $ 表示第 $ j $ 道工序的序号， $ {E_j} $ 表示第 $ j $ 道工序的设备数目,其中 $ j \in \{ 1,2, \cdots ,M\} $ ， $ {W}_{j,k} $ 表示第 $ j $ 道工序的第 $ k $ 个设备工位， ${S}_{i,j}$ 表示工件 $ i $ 在第 $ j $ 道工序的开工时间，其中 $ i \in \{ 1,2, \cdots ,N\} $ ， ${F}_{i,j}$ 表示工件 $ i $ 在第 $ j $ 道工序的完工时间， ${T}_{i,j}$ 表示工件 $ i $ 在第 $ j $ 道工序的加工时间， $ {F_{\max }} $ 表示最大完工时间。

针对柔性流水车间生产过程的约束条件主要约束开工时间、完工时间关系，连续加工工序间的关系。

式(1)表示工件 $ i $ 在第 $ j $ 道工序的完工时间与开工时间的关系；式（2）表示工件 $ i $ 需要在上一道工序完工之后才可以进入下一道工序进行加工。

在求解柔性流水车间排产优化问题过程中，最常用的评价指标是最小最大完工时间，即最小化全部工件在最后一道工序加工完工时间中的最大值。

式(3)表示最大完工时间为所有工件完成最后一道工序 $ M $ 的完工时间集合中的最大值，式（4）为最小化最大完工时间。

2.   基于深度学习的智能排产方法设计

本文提出一种针对柔性流水车间排产优化问题的深度学习方法，该方法主要是运用SeqGRU深度学习模型来解决生产优化问题，该方法的主要步骤和处理流程如图2所示。

图  2  基于深度学习的智能排产优化方法整体流程图

Fig.  2  Overall flow chart of the intelligent scheduling optimization method based on deep learning

下载: 全尺寸图片

该方法首先对历史生产数据进行预处理，再将预处理后的数据集划分为训练集、验证集和测试集输入到模型中；数据经过模型的编码层转化为向量，并通过引入注意力机制增强模型输入信息与排产结果相关性；在训练阶段，模型解码层利用历史已优化上线序的先验经验生成上线序，再通过该上线序与已优化上线序进行对比分析，调整模型参数；待训练完成后，模型输入工件信息，模型解码层可输出有效的排产结果。

2.1   构造仿真数据

仿真数据来源于某制造企业柔性流水生产车间历史生产加工数据，从中随机选取4 185组历史生产数据构建实验数据集。该数据集每组数据都包含了若干工件和若干道工序，每个工件包括了工件各工序加工时间，工件开工时间，工件完工时间和工件基本信息等属性，数据集输出为该4 185组数据对应的已优化上线序和最小最大完工时间。数据集数据的类型主要分为浮点型和字符串型。

2.2   数据集的预处理

深度学习模型在训练时，输入数据多采用数值型数据，而该数据集的数据具有多样性和类型复杂性，因此需要对该数据集进行预处理。对数据集的预处理过程分为3步：数值化处理、归一化处理和编码处理。

1）数值化处理

数据集的数据具有多样性和类型复杂性，例如每组数据对应的已优化上线序有起止符号start和end，使用独热编码可以将字符型数据转换为以0和1表示的二进制数据，通过独热编码转换后，1代表start，0代表end。

2）归一化处理

由于某些工件的工序加工时间过长，数值化处理后的数据特征属性差异相对较大，导致模型训练速度减缓。因此需要将数据进行归一化处理，标准化值全部分类到[0,1]区间之中。进行归一化处理的计算公式为

式中： $ G $ 是归一化前的一组生产数据， $ {G_i} $ 是一组生产数据中第 $ i $ 位数据， $ {G_{\min }} $ 是这组生产数据中的最小值， $ {G_{\max }} $ 是这组生产数据中的最大值， $ {G}' $ 是归一化之后的生产数据。

3）编码处理

由于SeqGRU模型的输入需为向量形式，因此需要对历史生产数据进行相应的变化。历史生产数据在输入到深度学习模型前可以通过Tensorflow的Embedding函数实现对数据编码处理，将输入数据映射成向量。每一次迭代训练提取64组生产数据，将数据编码成三维的向量，数据编码处理维度变化见表1。

2.3   针对排产优化问题的深度学习模型设计

本文针对排产优化问题，提出了基于深度学习的柔性流水车间排产优化方法，该方法核心为基于门控循环单元构建的序列到序列深度学习模型SeqGRU。模型中的Seq2Seq可以实现2个不同序列之间的转化，通过历史生产数据对SeqGRU深度学习模型进行训练，研究生产数据中生产任务信息、工艺信息与排产结果的相关性，生成工件信息与排产结果的映射关系网络，快速输出有效的排产结果，实时指导生产。

2.3.1   序列到序列模型

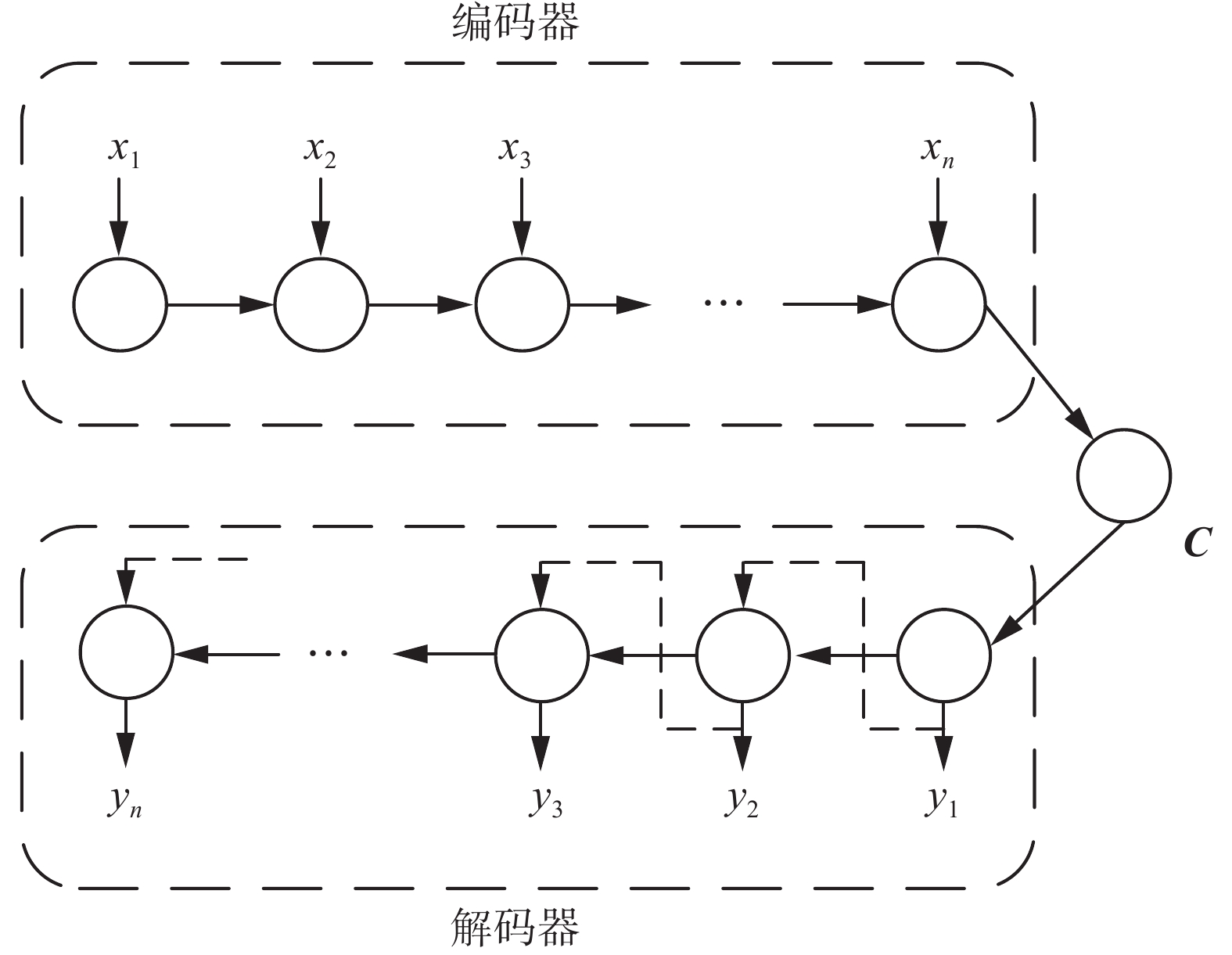
序列到序列模型(Seq2Seq)是一个编码器−解码器结构的神经网络，模型结构如图3所示。

图  3  Seq2Seq结构

Fig.  3  Seq2Seq structure

下载: 全尺寸图片

编码器和解码器一般都是由循环神经网络RNN构成，其中编码器按照输入序列的顺序读取信息 $\left\{ {{x_1},{x_2},\cdots ,{x_n}} \right\}$ ，读取信息时，编码器自身网络的参数也会发生相应的变化，最后编码器将一个可变长度的信息序列变成了一个固定长度的向量 ${\boldsymbol{C}}$ ，紧接着解码器在给定隐藏状态条件下，将固定长度的向量 ${\boldsymbol{C}}$ 变成可变长度的目标信息序列 $\{ {y_1}, {y_2}, \cdots ,{y_n} \}$ 。

2.3.2   序列到序列模型应用与改进

Seq2Seq模型中的递归神经网络(recursive neural network, RNN)在处理数据时易发生梯度消失和梯度爆炸，因此本文使用GRU构建Seq2Seq模型的编码器和解码器，门控循环单元神经网络利用自身循环反馈结构来存储历史信息，保证了信息的远距离传输。模型的解码器生成工件上线序指导实际生产，并进一步引入注意力机制提高模型的寻优精度和速率。最终将模型应用在实际企业柔性流水生产车间场景，实现模型与实际工程项目相结合。深度学习模型结构如图4所示。

图  4  深度学习模型结构

Fig.  4  Structure of deep learning model

下载: 全尺寸图片

1) 门控循环单元

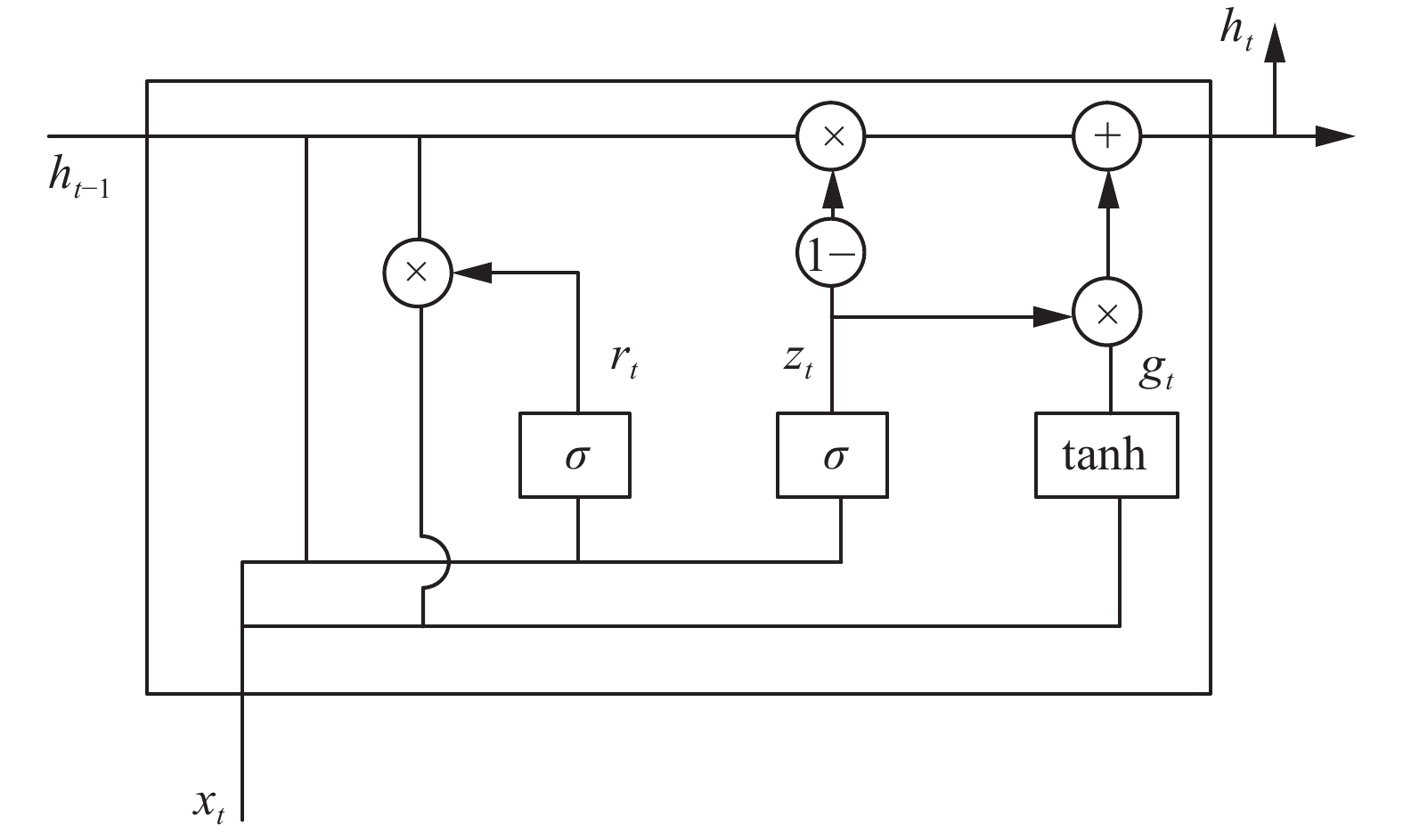
门控循环单元是对循环神经网络研究的较新成果，门控循环单元有更新门、重置门和候选隐藏状态，相比于循环神经网络简化了自身结构，重置门和更新门的设计分别有助于捕捉时序数据中的短期和长期依赖关系，在提取历史生产数据时序特征的同时还保证了信息的远距离传递。模型的编码层和解码层都是采用单层的门控循环单元组成的循环神经网络，在编码层中，GRU通过读取工件的生产信息，改变自身神经元参数，再将抽取到的信息特征通过注意力机制聚合成语义向量C；在解码层中，GRU对语义向量C进行解码，再通过贪婪策略选取当前时间步下概率最大的工件。GRU结构如图5所示。

图  5  门控循环单元

Fig.  5  Gated loop unit

下载: 全尺寸图片

$ {z_t} $ 代表更新门， $ {r_t} $ 代表重置门， $ {g_t} $ 代表候选隐藏状态， $ \sigma $ 是激活函数，在当前时间 $ t $ 下， $ {x_t} $ 代表第 $ t $ 时间步的输入工件信息， $ {h_{t - 1}} $ 和 $ {h_t} $ 分别代表前一个时间步 $ t - 1 $ 和当前时间步 $ t $ 的记忆。

2) 注意力机制

注意力机制可以通过分析输入与输出之间的联系，对输入数据进行不同的权重分配，使得模型更加侧重某些信息，做出更精准的判断。注意力机制按照权重取值、编码长度和模型深度3种分类标准可划分出不同的注意力机制模型^[20-21]。从权重取值可分成软注意和硬注意，软注意的权值在[0, 1]之间；硬注意力的每个权值要么为0要么为1。从模型深度可分成单层注意和多层注意，多层注意是在单层注意的基础上对其再进行新的一次权重分配。从编码长度来说，注意力机制可分为全局注意力和局部注意力。全局注意力不限制输入数据的长度，可以自动根据输入数据长度来适配，读取输入数据的所有信息；局部注意力限制了注意力机制读取输入数据的范围，有一个特定大小的区间，当输入数据在区间外，注意力机制自动进行舍弃。注意力机制可以通过上述3种分类标准中的模型任意组合，但由于本文深度学习模型在解决排产优化问题需要读取所有的数据信息且每个数据对排产结果都有所影响，因此本文使用的注意力机制为单层全局软注意力机制。

鉴于每条历史生产数据的工件信息对排产结果的贡献不同，引入注意力机制来对信息赋予不同的权重。注意力机制的计算公式为

式中： $ n $ 是一组生产数据中包含的工件数目， $ {h_i} $ 是门控循环单元抽取的第 $ i $ 个工件特征， $ {a_i} $ 是第 $ i $ 个工件特征在语义向量中所占的权重，C是聚合而成的向量。模型通过注意力机制对各个工件信息进行合理的权重分配，提高模型寻优的精度。

3) teacher forcing机制

GRU有2种训练模型，一种是自由振荡模式，即上一时间步的输出作为下一时间步的输入；另一种是teacher forcing机制，即每一时间步的输入都是前一时间步的正确输出结果^[22-23]。对于本文的深度学习模型来说，在训练阶段引入teacher forcing机制不仅可以加快模型的训练速率，还可以避免模型解码层受个别参数影响导致第一个时间步输出错误后，之后的时间步输出连错，加强了模型的稳定性。

4)贪婪层

贪婪策略将求解整个时间步长内最优工件上线序问题分解成在各个时间步下寻求最优解工件，最后按照时间步先后顺序将对应的工件进行排列，得到排产结果。通过引入贪婪策略，增加了模型的寻优稳定性。贪婪策略的原理如图6所示，在每一时间步下，选取概率最大的结果，如概率最大的结果在之前已被选取，则取用第2大概率的结果，以此类推。

图  6  贪婪策略原理

Fig.  6  Schematic of greedy strategy

下载: 全尺寸图片

2.3.3   模型评估方法

本文选取了均方根误差、寻优精度、最小最大完工时间和模型计算时间作为衡量模型的评价指标。

1)均方根误差。深度学习模型通过训练不断优化输入数据与输出上线序之间关联性的过程实质是预测回归。均方根误差适用于回归问题，因此引入均方根误差作为评价指标，均方根误差越小，说明模型拟合效果越好，生成的排产结果也越好。本文使用均方根误差来对模型进行评估：

式中： $ {R_i} $ 是真实值， $ {y_i} $ 是预测值， $ n $ 表示工件数量。

2)寻优精度。引入寻优精度评价指标来验证模型的寻优效果。模型每训练完一代，从验证集中抽取适量数据输入到模型中进行计算，检测模型输出的上线序是否与数据集中已优化上线序相同。

式中： $ D $ 表示抽取的生产数据数量， $ {D_t} $ 表示输出的上线序与数据集中已优化上线序相同的生产数据数量。

3)最小最大完工时间。在求解柔性流水车间排产优化问题过程中，最常用的评价指标是最小最大完工时间。为体现本文深度学习模型在求解问题的有效性，引入最小最大完工时间评价指标。

4)计算时间。求解排产优化问题的深度学习模型只需进行一次初始的迭代训练，之后每次只需输入新的生产任务信息，便能快速得到优化结果。为体现本文深度学习模型在求解问题实时性上的优势，引入模型计算时间评价指标。

3.   实验结果与分析

为了验证基于深度学习的柔性流水车间排产优化方法的有效性，分析基于门控循环单元构建的序列到序列深度学习模型SeqGRU在生产优化问题应用效果，进行多组仿真实验。实验在Windows10操作系统下进行，使用的CPU为I7-9750H六核处理器，使用的显卡为英伟达RTX2060显卡，运行内存为16 GB。软件平台基于Pycharm和Tensorflow1.14神经网络框架。

3.1   仿真实验数据准备与参数设置

本实验数据源自调研所在企业的柔性流水生产车间，由于企业车间已经具备完善的工件生产追踪和工件数据记录系统，企业保留有大量的工件生产加工数据记录，将这些记录进行整理，按照6∶2∶2的比例将其分为训练集、验证集和测试集，并在仿真实验过程中将数据进行预处理用于深度学习模型的训练。

数据经过编码层、解码层等模型结构自身维度会发生改变，设模型的神经元个数为256，工件数为10，预处理编码维度为16，注意力层深度为20，数据在模型中每层的输出形状如表2所示。

3.2   多组方案对排产优化方法评估分析

为了验证基于深度学习的柔性流水车间排产优化方法的应用效果，深入研究SeqGRU模型的执行效率和性能，分别从模型中配置的神经元个数、学习率和神经元类型等方面进行仿真实验，并进一步分析引入注意力机制等改进方法对SeqGRU模型的影响，构建了5组仿真方案，由于基于深度学习的柔性流水车间排产优化方法核心是SeqGRU模型，因此前3组方案是对模型进行分析，仿真方案1，设置不同的神经元个数和学习率，分析SeqGRU模型参数对其训练过程中损失值的影响，并评估该模型的执行效率；仿真方案2，SeqGRU模型的神经元分别采用LSTM和GRU的门机制神经元，分析采用不同类型神经元对该模型在训练过程中精度和损失值的影响，进一步评估该模型的执行效率；仿真方案3，通过在SeqGRU模型引入注意力机制，增强模型输入信息与排产结果相关性。建立仿真方案4和5，对基于深度学习的柔性流水车间排产优化方法进行整体性能评估。仿真方案4，基于深度学习的柔性流水车间排产优化方法有效性验证；仿真方案5， 基于深度学习的柔性流水车间排产优化方法快速性验证。

3.2.1   SeqGRU模型中神经元个数和学习率参数分析

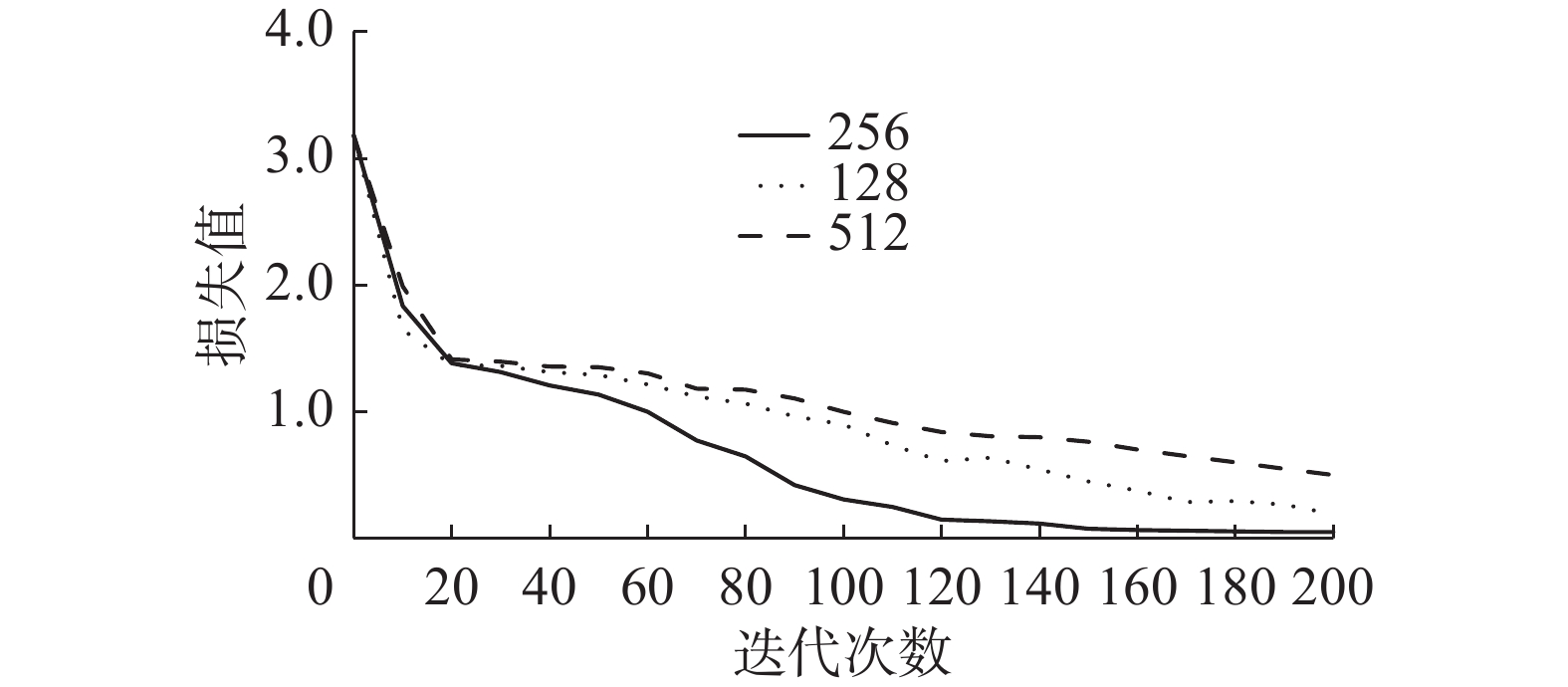
对于深度学习模型来说，模型的相关参数会影响模型最终的效果。SeqGRU模型的神经元个数和学习率对最终结果影响较大，因此需要设置不同的神经元个数和学习率来验证最优参数。为了验证门控循环单元中最合适的神经元个数，分别设置了神经元个数为128、256、512这3种情况进行实验。实验共训练200代，模型损失值与迭代次数关系如图7所示。

图  7  不同神经元个数下损失值与迭代次数关系

Fig.  7  Relationship between the loss value and the number of iterations under different numbers of neurons

下载: 全尺寸图片

从图7中可以看出，模型训练200代，3种神经元个数的损失值都发生了收敛，其中神经元个数为256的损失值图像最好，收敛速度最快且最后的损失值可以达到0.05。相比于神经元个数256来说，神经元个数128、512的图像收敛速度慢，需要更长的训练迭代次数才可以达到一个优秀的损失值，综上，当门控循环单元神经元个数为256时，SeqGRU模型的效果最好。为了验证模型的最优学习率，设置神经元个数为256且分别设置了学习率为0.05、0.01、0.005这3种情况进行实验。实验共训练200代，模型损失值与迭代次数关系如图8所示。

图  8  不同学习速率下损失值与迭代次数关系

Fig.  8  Relationship between the loss value and the number of iterations under different learning rates

下载: 全尺寸图片

学习率会影响深度学习模型的训练速度，学习率过大会使模型无法收敛，学习率过小会导致模型收敛速度变慢。从图8中可以看出，当学习率为0.01时，SeqGRU模型的损失值图像最好，收敛速度最快。综上2个实验，设置门控循环单元神经元个数为256，模型的学习率为0.01。

3.2.2   SeqGRU模型采用不同类型神经元分析

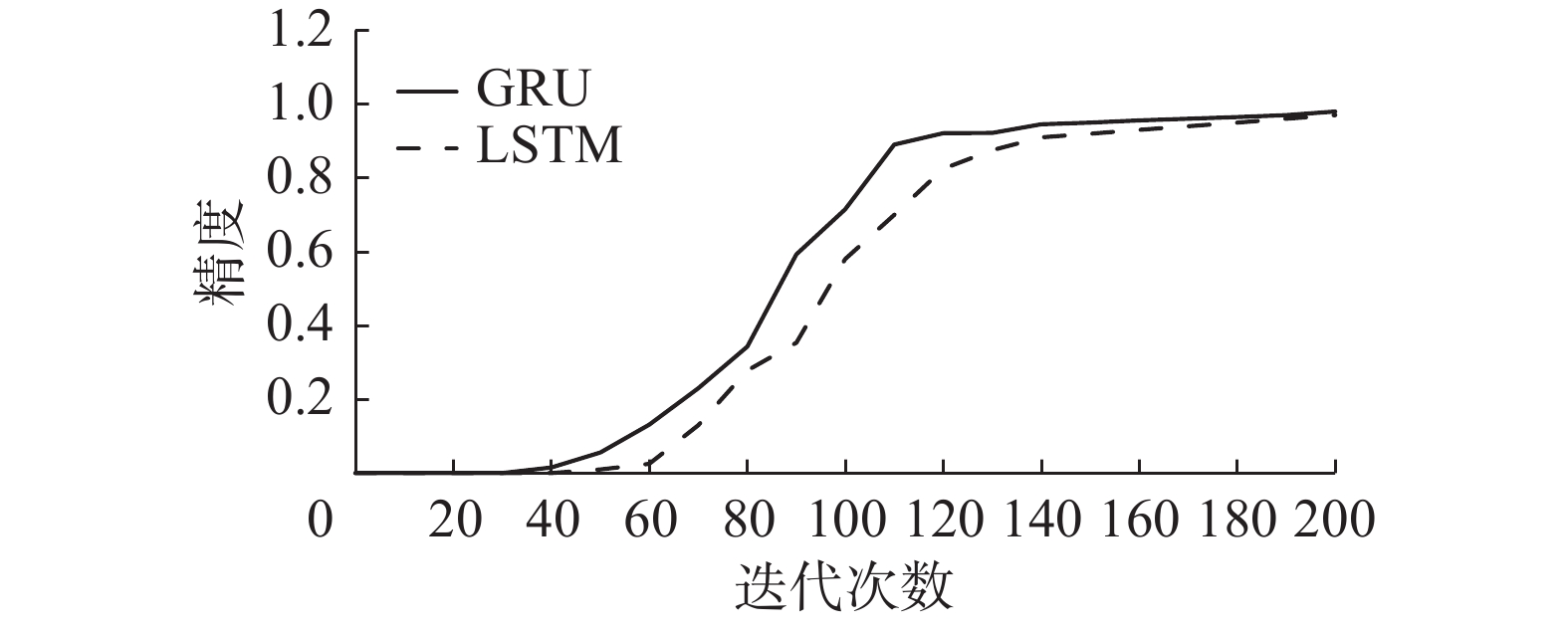
本文使用GRU构建Seq2Seq模型的编码器和解码器，为了验证门控循环单元神经元对模型的有效性，本文设置了2组不同类型的智能决策网络进行了对比实验，分别为：1)编码器和解码器为LSTM^[24]的Seq2Seq模型；2)编码器和解码器为GRU的Seq2Seq模型。两者神经元个数设为256，模型学习率设为0.01，模型的精度和损失值与迭代次数关系如图9、10所示。

图  9  不同类型的智能决策网络对SeqGRU模型损失值与迭代次数的关系

Fig.  9  Relationship between the loss value of the SeqGRU model and the number of iterations by different types of intelligent decision-making networks

下载: 全尺寸图片

图  10  不同类型的智能决策网络对SeqGRU模型精度与迭代次数的关系

Fig.  10  Relationship between the accuracy of the SeqGRU model and the number of iterations by different types of intelligent decision-making networks

下载: 全尺寸图片

从图9、10可以看出，编解码器为GRU和LSTM都可以生成有效的排产结果。LSTM训练时长为950 s，GRU训练时长为640 s，GRU相比于LSTM训练时间更短，且在相同迭代次数下，GRU的损失值和精度总是优于LSTM，这是因为GRU结构比LSTM结构更简单，GRU相比于LSTM少了一个记忆细胞，参数变少，处理时间也相应变短。综上，当编码器和解码器为GRU网络时，模型的效果最好且消耗的计算资源最少。

3.2.3   SeqGRU模型中引入注意力机制分析

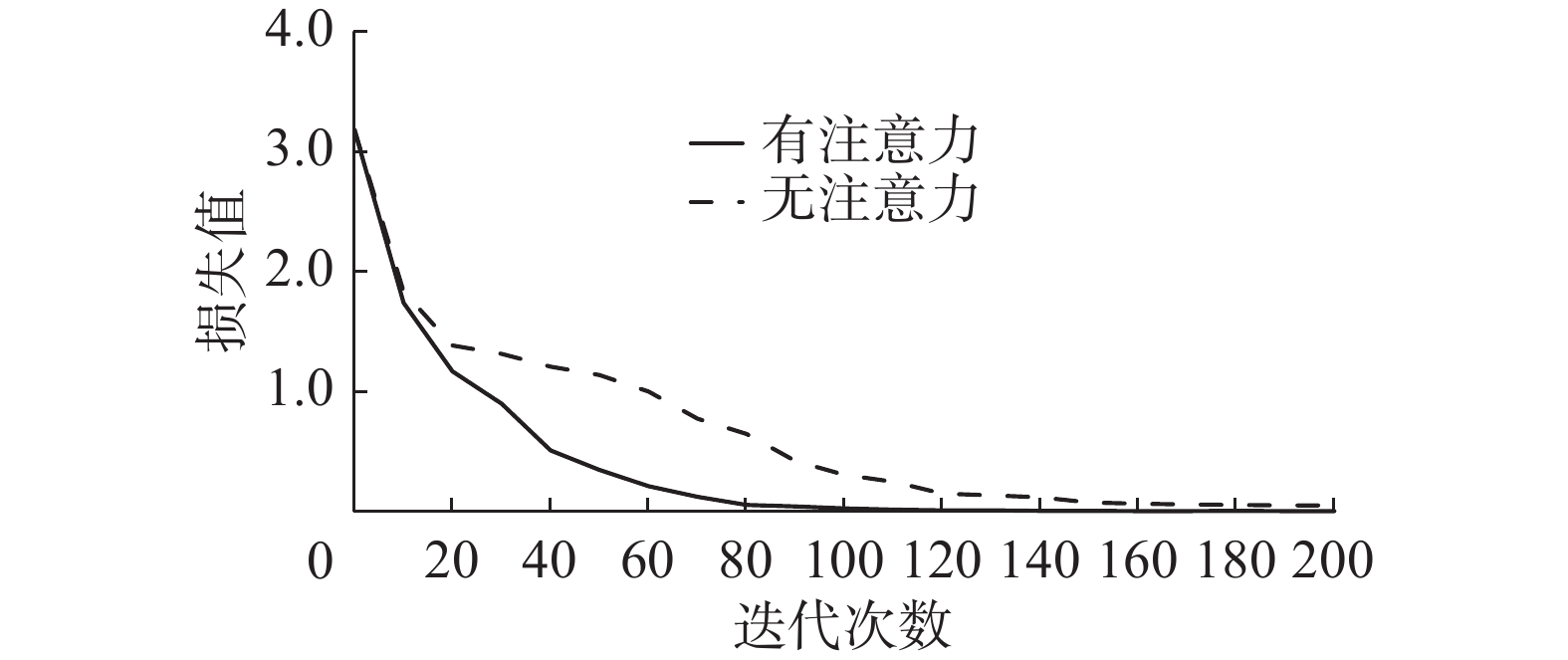
注意力机制根据历史生产数据中的工件信息重要程度赋予不同的权值，直接评估哪些输入是解码器的首选输入，提高模型的精度和运行速度。注意力机制在模型的编码层与解码层之间，设置模型GRU的神经元个数为256，模型的学习率为0.01，模型的精度和损失值图像如图11、12。

图  11  引入注意力机制后损失值与迭代次数的关系

Fig.  11  Relationship between the loss value and the number of iterations after the introduction of the attention mechanism

下载: 全尺寸图片

图  12  引入注意力机制后精度与迭代次数的关系

Fig.  12  Relationship between the accuracy and the number of iterations after the introduction of the attention mechanism

下载: 全尺寸图片

从图11、12可以看出，注意力机制可以加快SeqGRU模型的训练速度，并且在相同的迭代次数下，总可以达到更优的结果。同时模型每迭代训练一次，便会从验证集中抽取若干组生产数据放入模型中进行计算，再将得到的排产结果与数据集中的最优上线序进行比对，最终当模型收敛时，精度可以达到98%，验证了该模型对于解决排产优化问题具有良好的效果。

上述SeqGRU深度学习模型中的注意力机制为单层全局软注意力机制，对于排产优化问题，每个输入数据对排产结果或多或少都有所影响，因此注意力机制必须选用全局软注意力机制，确保注意力机制可以读取到所有数据并给每个数据赋予一个精确的值。为验证SeqGRU深度学习模型中的单层全局软注意力机制更适用于解决排产优化问题，本文将单层全局软注意力机制与多层全局软注意力机制进行对比实验，实验结果如表3所示。

从表3可以看出，随着全局软注意力机制层数的增多，注意力机制每一层都需要对上一层输出的数据重新进行分析并赋予权重，从而导致SeqGRU深度学习模型的运算量不断增加，因此模型收敛时间越来越长，并且由于注意力机制层数不断增加，模型对数据的过度分析导致了过拟合问题，模型的精度反而下降，因此SeqGRU深度学习模型需引入单层全局软注意力机制。

3.2.4   基于深度学习的智能排产优化方法验证

本文以柔性流水车间为应用对象的基于深度学习的智能排产优化方法利用历史生产数据进行学习训练，在训练完成后，只需要输入工件信息，便可直接输出有效的工件上线序指导实际生产。为验证本文排产优化方法在求解问题的有效性，引入最小最大完工时间作为评价指标，并将本文的排产优化方法与遗传算法(genetic algorithm, GA)和狼群算法(wolf pack algorithm, WPA)进行对比实验。

针对小规模数据，测试数据来自于Carlier和Neron针对柔性流水车间提出的标准算例，从中选取3组易解数据j₁、j₂、j₃和3组难解数据j₄、j₅、j₆，将本文的排产优化方法与GA、WPA算法进行对比实验，实验结果如表4所示。 $ B_s $ 表示Carlier和Neron算例的最优解并在文献[25]中给出，为 $ \min {F_{\max }} $ 为算法求解的最小最大完工时间，通过偏差 $ d $ 来衡量模型的有效性，偏差 $ d $ 越小，模型的性能越好，偏差 $ d $ 的公式为

从表4可以看出，本文的排产优化方法和GA、WPA在求解易解数据时都可以达到最优的效果。对于难解数据来说，本文的排产优化方法偏差比其他2种算法要小很多。显然，对于小规模数据来说，本文的排产优化方法求解柔性流水车间排产优化问题具有有效性且比其他2种算法有更好的表现。

针对大规模数据，从测试集中选取50、100、200、400组数据进行测试， $ \overline {{B_{\text{s}}}} $ 为这些数据已优化的最小最大完工时间平均值， $ \overline {\min {F_{\max }}} $ 为算法求解的最小最大完工时间的平均值，通过偏差 $ d $ 来衡量模型的有效性，实验结果如表5所示。

从表5可以看出，本文的排产优化方法和GA、WPA随着数据规模不断扩大，偏差都增大，但GA和WPA的增长幅度更明显，且本文的排产优化方法在数据规模增长到一定规模后，偏差增长幅度变缓。由上述仿真结果可知，基于深度学习的柔性流水车间排产优化方法在处理大规模数据时比其他2种算法具有更好的效果。

3.2.5   基于深度学习的智能排产优化方法快速性验证

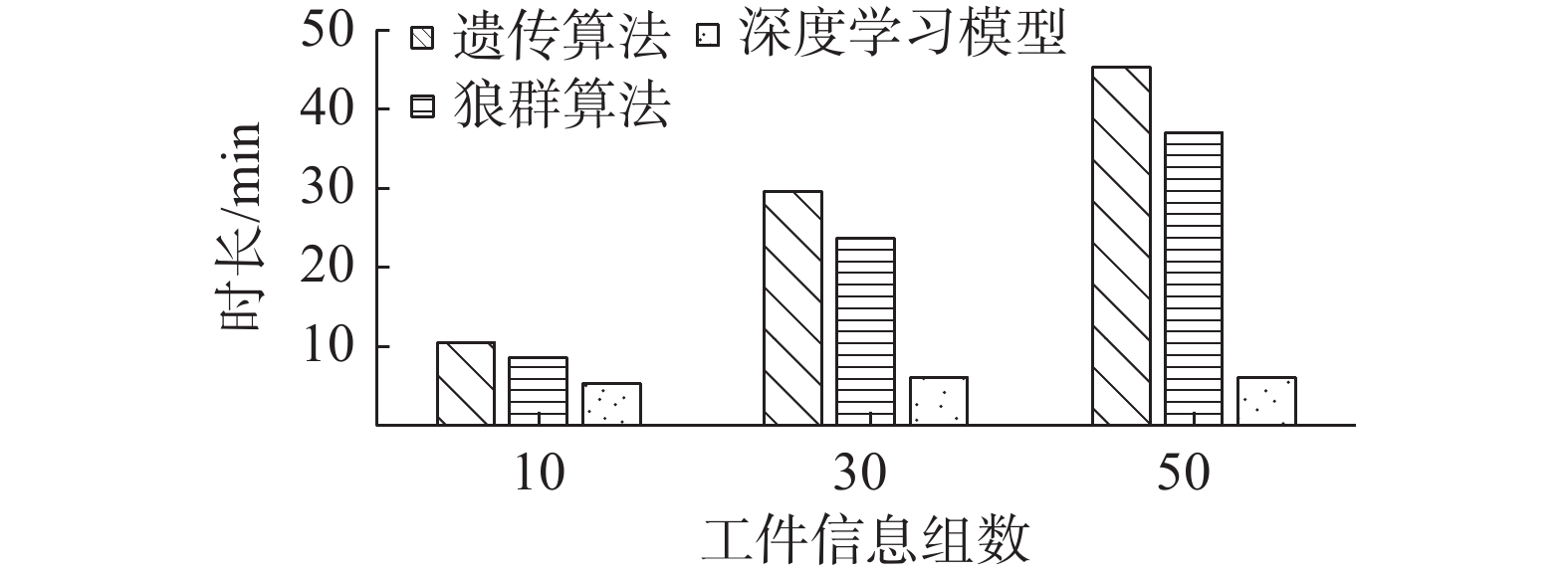
用于求解排产优化问题的SeqGRU深度学习模型只需进行一次初始的迭代训练，之后每次只需输入生产任务信息，便能快速得到优化结果。为了验证本文排产优化方法在求解问题实时性上的优势，引入计算时间作为评价指标，将深度学习模型与GA、WPA进行了比较。随机抽取若干组工件信息输入到深度学习模型和GA、WPA中进行计算，横坐标为工件数据组数，纵坐标为模型计算时间，3组模型的对比如图13所示。

图  13  深度学习模型与遗传算法、狼群算法的对比

Fig.  13  Comparison of deep learning model with genetic algorithm and wolf pack algorithm

下载: 全尺寸图片

由图13可以看出，GA和WPA随着组数不断增多，模型计算时间大幅度增加，且遗传算法增加幅度大于狼群算法，而本文的排产优化方法在训练一次之后，便可快速输出任意组新任务的优化结果，且随着组数增多，模型计算时间增加的并不明显，由此可以看出本文的排产优化方法在实时性上的优势。

4.   结束语

本文提出的基于深度学习的智能排产优化方法通过对历史生产数据学习训练能够快速给出有效的排产结果。SeqGRU模型采用GRU构建Seq2Seq模型的编码器和解码器，模型解码器输出工件上线序，并引入注意力机制提高了寻优的精度和速率。最后通过实验验证了所提方法对解决全局排产优化问题的有效性和实时性。本模型填补了深度学习解决全局排产优化问题的空缺，下一步将对该模型进行扩展优化，引入更复杂的排产优化问题进行研究，并将该模型部署至实际的生产管理系统中，以测试模型的实际应用效果。