当代社会，随着信息技术的突飞猛进，高等学校的教育教学改革的深入化也受到了深刻的影响。尤其处于大数据时代，数据挖掘的各种方法被应用到教育行业^[1-6]，为寻找更好的教育教学方法提供了新思路。学生成绩在高等学校里不但是衡量学校人才培养水平的一个重要指标，同时也是教育大数据中的一个重要内容。由于学生成绩具有数据类型相对统一，数据量较大，相对容易获取等特点，因此依据恰当的数据挖掘技术，对学生成绩进行不同角度的深入挖掘和分析，从而得到指导教学的新方法或新理论的研究成为高等学校教学改革的一个研究热点。丁智斌等^[7]利用决策树中的ID3算法对学生成绩进行分析，从而得出了影响学生成绩的内部原因及一些其他相关结论。喻铁朔等^[8]是基于支持向量机（support vector machine, SVM）等4种数据挖掘的方法对学生成绩进行预测，从不同角度对4种模型进行对比，得出不同模型适用于不同课程的结论，对高校学生课程成绩预测。钟文精等^[9]基于k-means聚类算法，对学生成绩进行聚类分析，为进行深入的教学改革和设计提供数据依据。本文依据可拓数据挖掘中的几种重要算法及皮尔逊相关系数，对北京某高校经管类学生的数学课程相关成绩进行多角度深入分析，从而得到一些和教学相关的重要结论，为改进教学方法，提高教学质量给出合理化建议。

1.   基础知识与算法

1.1   可拓支持向量机

可拓学是由广东工业大学蔡文研究员创立的一门原创学科。在众多专家学者的不懈努力下，历经30余年的潜心研究，建立了可拓论体系和可拓创新方法体系^[10-18]。可拓数据挖掘^[19-20]是将可拓学的理论和方法与挖掘数据的方法技术相结合的一门新技术，可拓支持向量机^[21]就是其中一种经典机器学习算法与可拓理论深入结合而产生的新算法。与标准的支持向量分类机不同，可拓支持向量机是解决可拓分类问题的，其在进行标准分类问题预测的同时，更注重于找到那些通过变化分量（特征）的值而转换类别的样本，这样的样本称为可拓样本，而相应的变量称为可拓变量。

算法　可拓支持向量分类机算法（ESVM）

1)给定训练集：其中 ${x_i} \in {{\mathbf{R}}^n}$ ， ${y_i} \in {\mathbf{Y}} = \left\{ {1, - 1} \right\}$ ， $ i=1,2，\cdots ,l $ 。给定可拓样本 ${x_k}$ 的可拓变量 $j$ 的可拓区间 $a_j^k$ 和 $b_j^k$ ， $ j=1,2，\cdots ,n $ ；选择合适的惩罚参数 $C > 0$ ;

2)构造并求解最优化问题：

得最优解 $\alpha _i^*$ ；

3)计算 ${b^*}$ ：

4)构造决策函数：

5)对于输入 ${x_k}$ ，首先用决策函数 $f({x_k})$ 得到其对应的预测类别 ${y_k}$ ，然后用其可拓变量对应的可拓区间 $a_j^k$ 和 $b_j^k$ 分别代替 ${[{x_k}]_j}$ ，这样对 $\left| E \right|$ 个可拓变量，就得到 ${2^{\left| E \right|}}$ 个不同的组合值。相应的，基于 ${x_k}$ 得到了 ${2^{\left| E \right|}}$ 个新的输入，分别用决策函数来判断，若有一个被判断为 $ - {y_k}$ ，则认为该输入是可变换的。

1.2   基于可拓距的k-means聚类算法

可拓k-means^[22]基于可拓学中点 $x$ 与区间 ${X_0} = \; < a,b > $ 的距离定义，提出了一种选取k-means算法初始聚类中心的新方法，算法描述如下：

1)计算出两两样本间距离及等效密集距离区间 $Z = [A,B] = [\min (D),\max (D)]$ ，其中 $\Bigg\{ D = d \left| d = \left. \sqrt {\displaystyle\sum\nolimits_{p = 1}^m {{{(x_i^p - x_j^p)}^2}} } \right. \right\}$ 为两两样本间距离集合；

2)按照两样本的距离 $Z$ 对区间的左右测距的距离和左、右侧距^[9]的定义，将距离映射为左侧距 $\rho _i^{(i,j)}$ $\rho_{{i}}^{\left({i},{j}\right)}$ 及可拓右侧距 $\rho _j^{(i,j)}$ $\rho_{{r}}^{\left({i},{j}\right)}$ ，将 $\rho _i^{(i,j)}$ $\rho_{{i}}^{\left({i},{j}\right)}$ 按从小到大顺序依次排序，同 $S = \left\{ \left( {{x_1},{y_1}} \right),\left( {{x_{\text{2}}},{y_{\text{2}}}} \right), \cdots ,\left( {{x_l},{y_l}} \right) \right\}$ 时计算样本间可拓平均左侧距 $\overline {{\rho _l}} $ 及可拓平均右侧距 $\overline {{\rho _r}} $ ；

3)遍历排序好的可拓距，将其中首个大于样本间可拓平均左侧距 $\overline {{\rho _l}} $ 的可拓距对应中心点坐标作为第一个初始聚类中心；

4)计算排好序可拓距中下一个值对应中心点坐标并依次计算出其与已确定的初始聚类中心的可拓距，将其与样本平均可拓右测距 $\overline {{\rho _r}} $ 进行比较，若其均大于 $\overline {{\rho _r}} $ ，则该中心点坐标作为下一个初始聚类中心；否则重新执行步骤4；

5)如果遍历一次后，初始聚类中心未达到 $K$ ，则按式（1）计算出缩小因子 $\eta $ ，动态缩小样本平均可拓右侧距 $\overline {{\rho _r}} $ ，重新回到步骤3；

式中： $k'$ 为每次遍历后所获得的初始聚类中心个数； $K$ 为指定聚类中心数

6)若聚类中心数达到 $K$ 时，则完成初始聚类中心的选取。

1.3   皮尔逊（Pearson）相关系数

Pearson相关系数^[23]用于分析定量数据，当数据满足正态分布时可用Pearson相关系数查看变量间相关性。其公式为

式中：相关系数 $r$ 的取值范围为 $ - 1 \leqslant r \leqslant 1$ 。 $r > 0$ 为正相关， $r < 0$ 为负相关， $0 < \left| r \right|{\text{ < 1}}$ 表示相关程度。

2.   高校学生成绩特点分析

2.1   数据描述

收集了北京联合大学2018—2019学年包括旅游学院、管理学院和商务学院3个学院共计929名学生的数据，包括经管类概率论与数理统计（I）课程的平时作业、期中和期末考试成绩等。根据期末试卷的5道客观题（记为kg_1~kg_5）和10道主观题（记为zg_6~zg15）共15道题目，总结出15个主要的知识点。为便于分析，我们把每个学生的知识点掌握描述成一个15维向量，向量的每个分量即为该生在某个知识点上的掌握程度。而知识点的掌握程度则根据学生的平时作业成绩、期中和期末试卷上考核相应知识点的得分，综合计算得到。最后根据每个学生期末试卷的考试总成绩的及格与否把学生分成正负两类，及格为正类，不及格为负类。这样把所有学生组成一个大小为929的两类分类问题的数据集1，记为S₁。

收集了我北京联合大学2018—2019学年包括旅游学院、管理学院和商务学院3个学院共计841名学生的数据，包括微积分（II）课程的平时作业、期中和期末考试成绩等。根据期末试卷的6道客观题（记为kg_1~kg_6）和12道主观题（记为zg_7~zg_18）共18道题目，总结出18个主要的知识点。同上述S₁数据处理类似，我们把每个学生的知识点掌握描述成一个18维向量，根据每个学生期末试卷的考试总成绩的及格与否把学生分成正负两类。这样把所有学生组成一个大小为841的两类分类问题的数据集2，记为S₂。

下面将基于S₁和S₂进行学生成绩特点的挖掘分析。

2.2   基于可拓SVM的试卷题目影响力分析

基于成绩数据集1，探索哪些知识点是影响学生及格与否的主要因素，从而检测试卷是否满足出题意愿；进一步，对每个学生，可以给出决定其及格与否的某个或某几个具体题目，以便学生以后有所侧重学习。

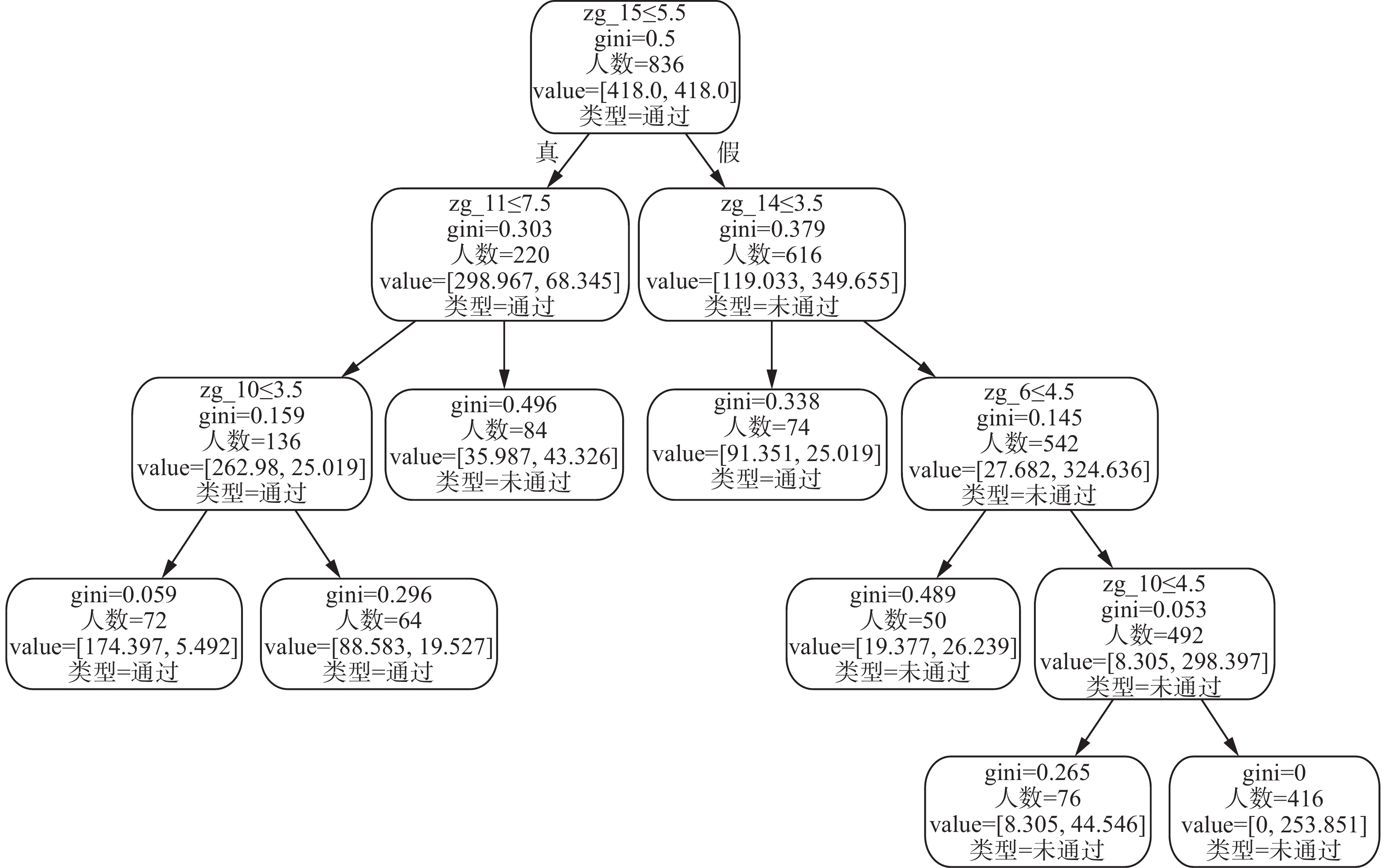
首先，对建立的训练集 ${S}_{1}=\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\cdots , \left({x}_{l},{y}_{l}\right)\right\}\in ({\bf R}^{n}\times {\bf{Y}}{)}^{l}$ ，其中 ${x_i} \in {{\mathbf{R}}^{15}}$ ， ${y_i} \in {\mathbf{Y}} = \left\{ {1, - 1} \right\}$ ， $i=1, 2,\cdots ,929$ ， 利用5–折交叉验证方法，选取最优的参数 $C$ 和径向基核函数参数，并用最优参数对整个训练集进行训练，得到最终的决策函数。利用此决策函数进行规则抽取^[24]，可以得到基本的分类规则，我们这里将分类规则按照决策树的形式表示如图1所示。

图  1  分类规则图

Fig.  1  Classification rule diagram

下载: 全尺寸图片

由图1可以看出，据此规则得到的节点数为 13，叶子节点数为 7，树的最大深度为 5，最基本的区分规则是选择那些对学生是否及格判断起主要作用的题型及题号。从树中可以看出在众多规则中zg_15，zg_14，zg_11，zg_6都被作为分枝的因素。从根节点带有特征取值范围来看，根节点的两个分支分别代表两类学生成绩分布，一类是zg_15的得分大于5.5分，另一类是zg_15得分小于5.5分。

从根节点的左分支中关于zg_11得分是否大于7.5的分支对比观察中可以发现，即便学生对zg_11得分小于8.5，学生的及格率依然很高，由此可见，对该分支的进一步挖掘，可以找出更加具备辨识度的特征以及取值范围。

从根节点的右分支出发，我们可以发现，第个二分支节点判断的特征为zg_14的得分是否小于等于3.5。从选择人数上看，zg_14的得分大于3.5的学生比相应得分小于3.5的人数高出468人，但是在zg_14得分超过3.5的同学不及格的概率更高。由此可见，在众多主观题中，zg_15对学生的成绩及格影响更高，而zg_14对是否成绩及格的概率呈现出较低的相关性，所以导致在14号主观题得分高的同学在最后的及格率分析中影响度不高。

将上述分析进一步总结到规则表1，从中可以看出，影响学生对概率统计及格率的主要因素有以下3点：

1）第15号主观题：从5条分支规则中可以发现，将第15号主观题得分作为根节点分支范围的合计人数最多，由此可以推断第15号主观题是影响学生对于概率统计课程及格率的主要因素。

2）第14号主观题：在所有的规则中同样也对第14号主观题的得分范围进行了划分，基于前面的第15题的分支背景，第14号主观题的取值范围也有了相应的调整。

3）第11号主观题：在规则表中，存在前馈规则一致的两条规则。第11号主观题的得分是否超过7.5分是区分他们的关键。

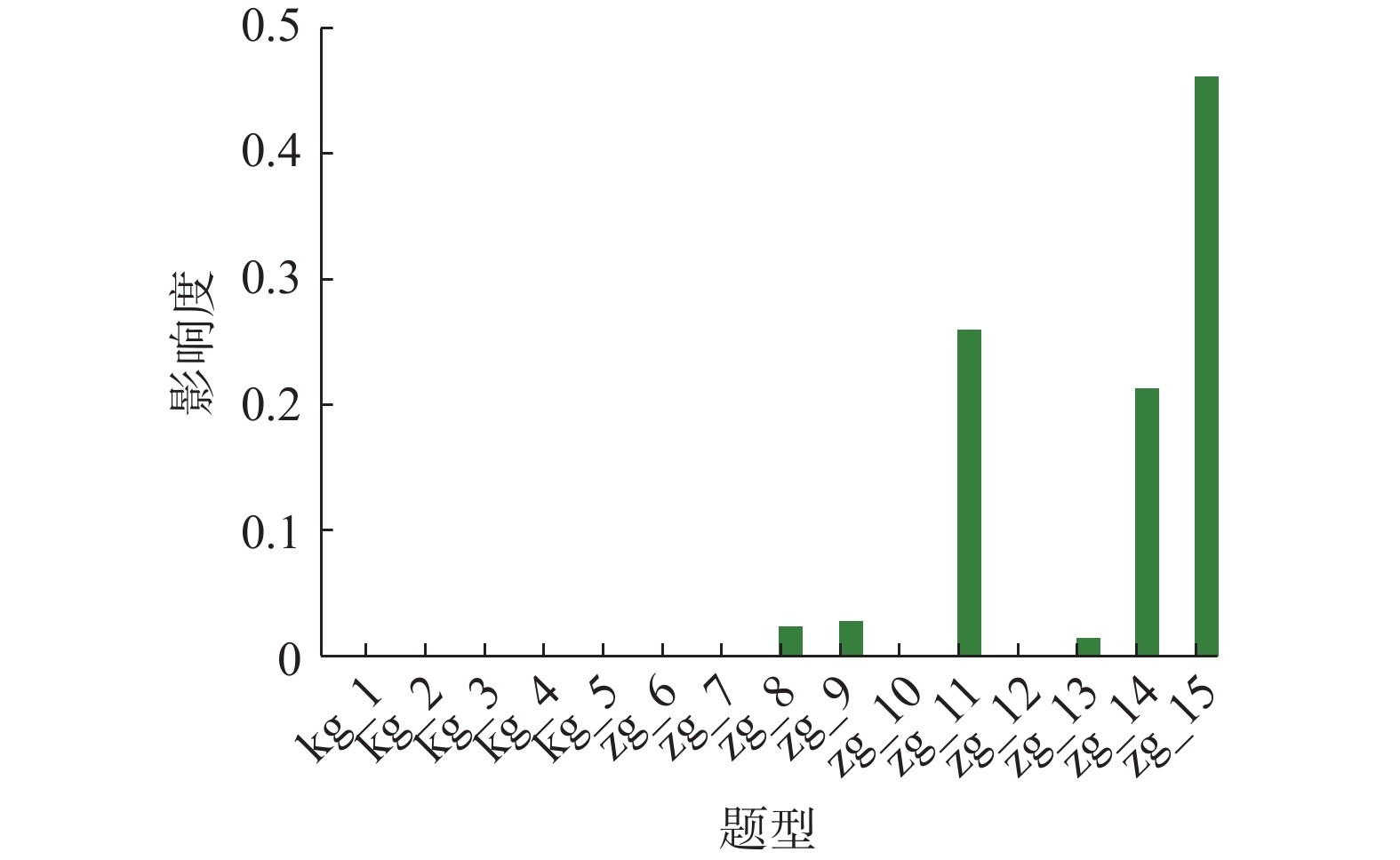
另外，从结果上看，对规则主要的考虑因素也集中在主观题型中，而客观题影响度较低。为了进一步探究一张试卷中各个题型之间的重要性，我们对概率统计试卷上的题型进行了影响度可视化操作，可视化结果如图2所示。

图  2  各题影响度可视化图

Fig.  2  Impact of each question

下载: 全尺寸图片

主观题第15题zg_15作为影响学生概率统计及格的重要因素，该现象在管理学院、旅游学院尤为明显。主要原因在于zg_15得分难度低，导致该题得高分的同学较多；对于其他的主观题，例如zg_14和zg_11也有类似的趋势。而反观客观题的影响比例，可以看到影响力几乎为0，原因在于客观题题型分值较小，且相对得分容易获得，所以导致客观题所占的影响力整体较低。结合上述表1的分析研究，绝大多数及格学生的提分关键在于第11、14和15号主观题。

在上面已得到普遍规律的前提下，进一步分析影响每个学生是否及格的关键知识点：

因每个题目学生得分都有不同，所以每个题目对应的变量都是可拓变量。首先定义所有题目 $j( j=1,2,\cdots ,15)$ 的可拓区间，即 $[{a_j},{b_j}]$ 。 这里将每个题目不得分和得最高分设为可拓区间上下界，即 ${a_j}{\text{ = }}0$ ， ${b_j}$ 为该题目的得分。针对每个学生 ${x_k}$ 的每个题目对应的变量，用其可拓变量对应的可拓区间 $a_j^k$ 和 $b_j^k$ 分别代替 ${[{x_k}]_j}$ 和 ${[{y_k}]_j} $ ，这样对 $\left| E \right|{\text{ = }}15$ 个可拓变量，就得到 ${2^{15}}$ 个不同的组合值。相应的，基于 ${x_k}$ ，利用决策函数得到了 ${2^{15}}$ 新的输入，分别用决策函数来判断，若有一个被判断为 $-{{y}}_{{k}}$ ，则认为该输入是可变换的。

以学生t₁为例，我们得到kg_4，zg_13是影响其及格与否的2个关键题目，即如果学生t₁在kg_4和zg_13对应的知识点掌握程度从最低变为最高的情况下，其将由不及格而变成及格；而对于学生t₂，同理可知学生对kg_2， zg_13，zg_15对应的知识点掌握程度是影响其及格与否的关键。

2.3   基于可拓距的k-means聚类算法成绩特定分析

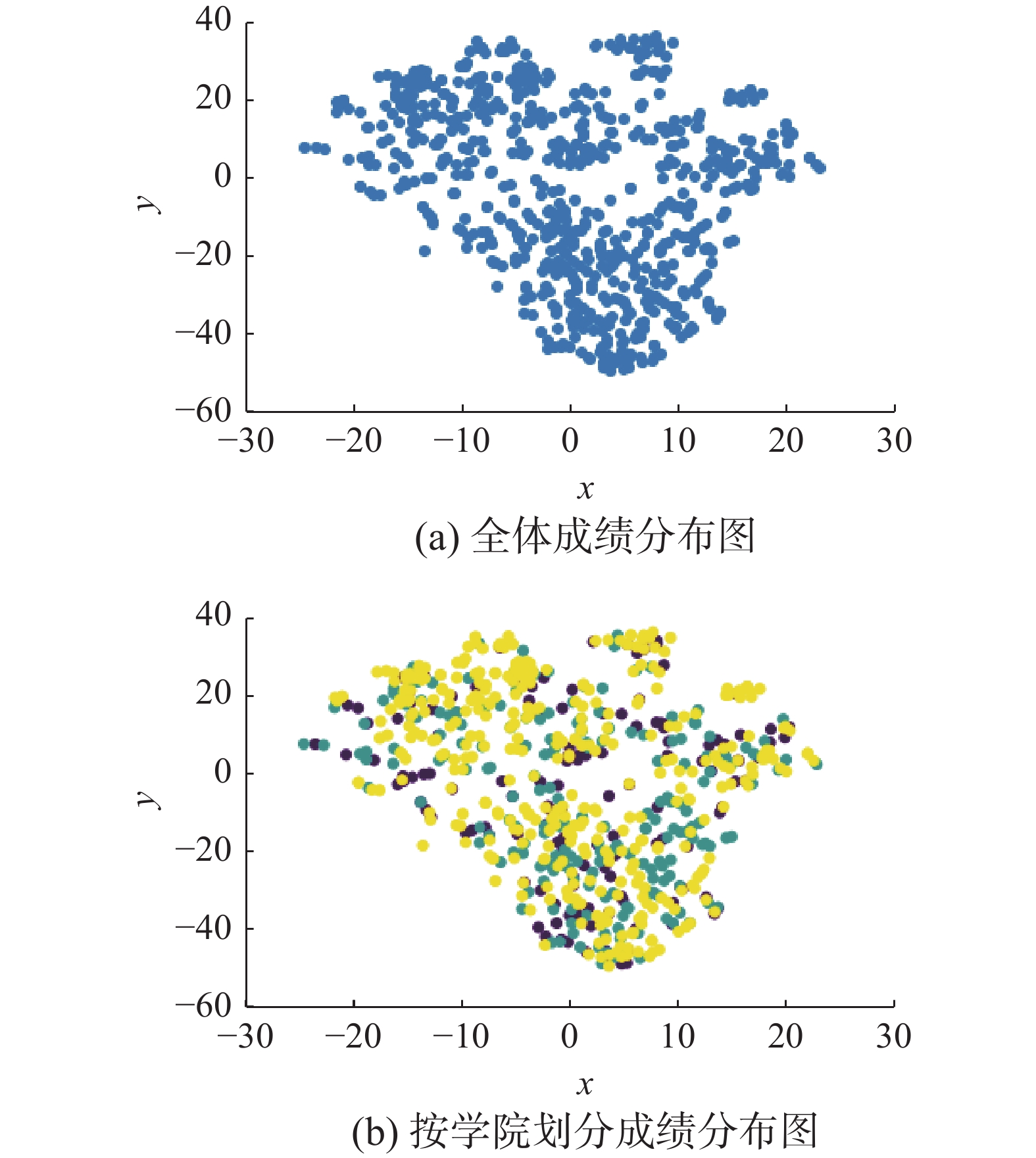
基于成绩数据集S₂，我们拟分析学生成绩分布的整个规律.首先建立数据集 ${S_2} = \left\{ \left( {{x_1},{y_1}} \right),\right. \left.\left( {{x_{\text{2}}},{y_{\text{2}}}} \right), \cdots ,\left( {{x_l},{y_l}} \right) \right\}$ ，其中 ${x_i} \in {{\mathbf{R}}^{18}}$ ， ${y_i} \in {\mathbf{Y}} = \left\{ {1, - 1} \right\}$ ， $i=1, 2,\cdots ,841$ 。为了对数据有整体的了解和把握，以便于进一步从不同角度进行分析。首先，我们对数据利用t-SNE方法进行降维和可视化展示，图3(a)是微积分(II)课程的全体成绩分布图。可以发现，图中的成绩数据分布较为紧密，紧密的样本分布为数据聚类添加了难度。同时，为了验证“同一学院的学生，该门课程的总体水平较为接近”这一设想，我们按照学院划分，将管理学院、旅游学院和商务学院的学生成绩作为不同类别的数据，利用t-SNE方法进行降维和可视化展示，如图3(b)所示。很明显看出，结果和我们预期吻合。（可视化图均为示意图，坐标无实际意义。）

图  3  整体数据可视化图

Fig.  3  Visualization of the overall data

下载: 全尺寸图片

对于具有上述特征的数据，采用上述1.2节中所阐述的基于可拓距的k-means聚类算法，把k分别取为3、4、5，并利用t-SNE方法进行降维和可视化展示得到如下结果（如图4），可以看出k=3时效果比较好。

图  4  k-means可视化图

Fig.  4  Visualization of k-means

下载: 全尺寸图片

进一步，我们对聚类的3类进行分析，对每一类中所有点的每个分量求均值，探索每类的特点，得到表2。可以看出类别2与1，3在各个题目对应的知识点掌握程度都有明显区别，也就是类别2的学生，几乎对所有知识点掌握都较差，这些学生需要全面补习；而类别1和3之间只在某些知识点上取值差别稍大，比如zg_18。

2.4   基于Pearson相关系数的试卷题目相关性分析

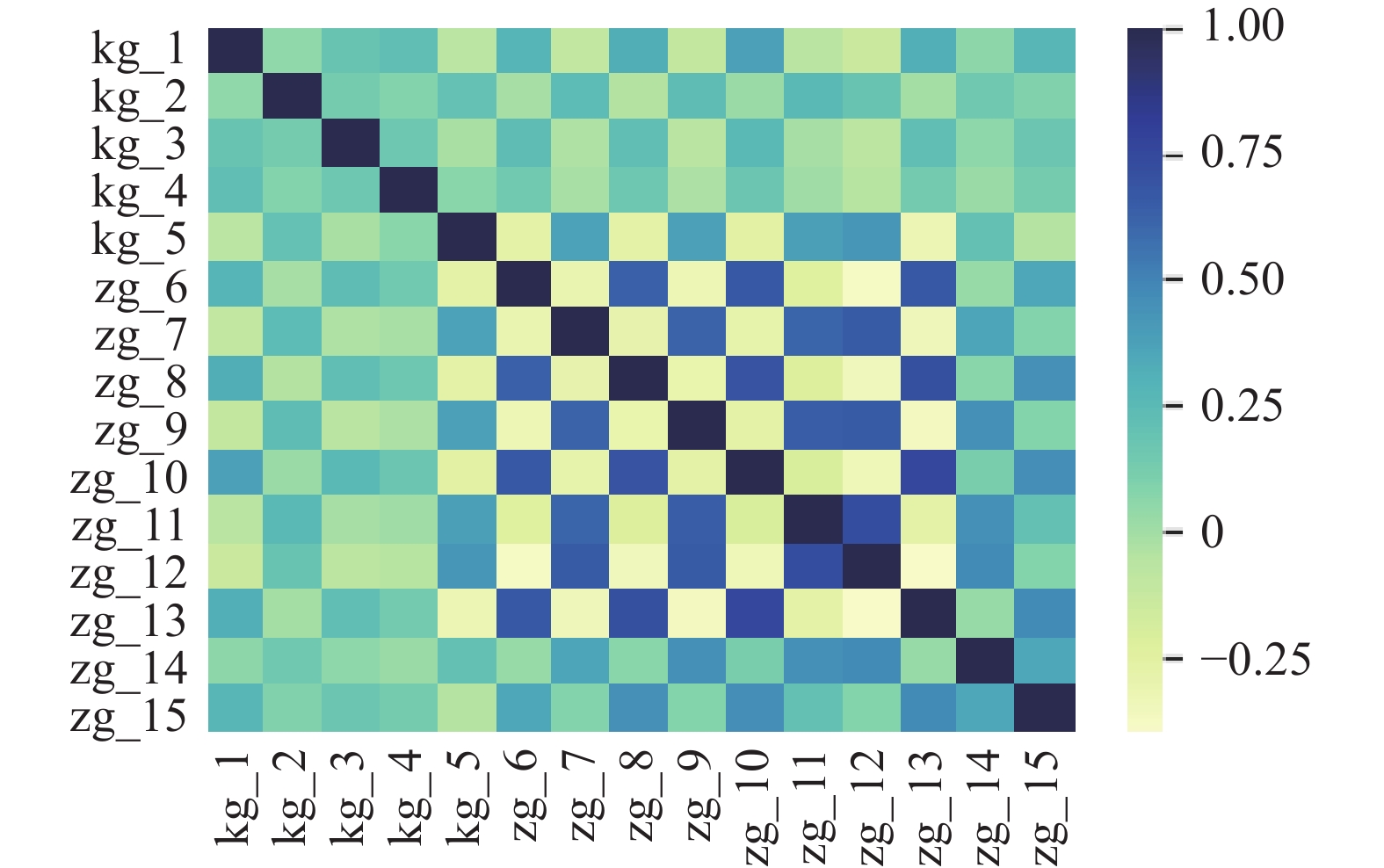
基于数据集S₁，利用Pearson相关系数进行相关性分析，结果如图5所示，其中颜色越深代表着相关性越大。可以发现：正对角线代表着当前特征与特征自身的相关性计算值，正对角线上的值均为1，颜色最深。其余部分代表着当前特征与其他特征的相关性计算，颜色的深浅代表着相关性的强弱。具体而言：客观题kg_1,kg_2,kg_3,kg_4,kg_5之间相关性热力图颜色为浅绿色，说明它们之间相关性较弱，但是总体保持着正相关的关系。据此可以推断，客观题一道题的得分情况对另外一题的得分情况影响较低，或者说题目本身考查的知识点不相关。而主观题之间的相关性则更加复杂。根据主观题之间的相关性热力图分布，它们之间存在负相关和正相关两种相关关系。相关性的数值越接近1 或−1，说明两组数据之间正向或反向线性关联越强。例如， zg_6与zg_7、zg_7与zg_8，zg_8与zg_9之间的相关性热力图颜色为黄色，说明它们之间的相关性为负相关。与之相反的情况为：zg_7与zg_9、zg_11与zg_12之间的相关性热力图颜色为蓝色，说明具有很强的正相关性，两个特征的相关密切程度比较高。此时就要引起注意，试卷中zg_7与zg_9、zg_11与zg_12之间是否考察知识点重合，还是题目难易程度相近引起的高度相关。如果出现命题知识点重合，是否符合我们考核的目的，从而对考试后试卷命题合理性分析给出提示。

图  5  题目相关性热力图

Fig.  5  Correlation map

下载: 全尺寸图片

3.   结束语

本文主要基于可拓数据挖掘的几种重要方法及皮尔逊相关系数，对高校学生成绩利用不同模型，从不同角度进行分析，从而分析影响学生成绩的主要题目，探索学生对知识点的掌握程度。进一步，对每个学生，可以给出决定其及格与否的某个或某几个具体知识点，以便学生以后有所侧重学习。试卷中各题目相关性强弱分析的结论，也对课程考核等方面给出合理化指导和建议。将不断发展的、前沿的科学技术、科研方法应用于不断深化改革的教育教学中，同时也对长期沉睡的庞大的学生成绩数据加以充分利用，教学促进科研，科研反哺教学，起到了示范作用。采用的相关算法是我们精心选取的算法，针对相关成绩数据分析有一定的优势。将来我们可以进一步深入研究，探讨如何将解决矛盾问题的可拓学和机器学习的相关算法深度融合，起到如虎添翼的作用。深究如何进一步将科研的方法应用到教育大数据中，从而对推进教学改革，进一步提高高校教学质量做出贡献。同时也希望上述分析能起到抛砖引玉的作用。