Extension knowledge representation of geometric effects
-
摘要: 科学效应中蕴含庞大的科学知识，是面向功能矛盾问题求解的重要基础。为了建立科学效应的可拓知识库，实现面向功能问题的可拓智能设计，提出了一种以几何效应为例的面向实际应用的可拓知识表示方法，利用该方法对实际问题中几何效应的输入与输出关系所蕴含的可拓知识进行形式化表示。首先根据几何效应，建立基元模型；根据领域知识和可拓学中的相关规则，建立基元间的相关关系；根据主动变换、传导变换知识和基元的发散规则，对相关网中某基元实施主动变换；再根据可拓变换的蕴含系和传导变换规则，得到一系列的传导变换，进而建立可拓知识表达式，实现输入与输出的转换关系的表达；最后以双曲面搅拌器设计为例进一步拓展相应的可拓知识以解决领域问题。本研究可以使设计人员更加全面地理解几何效应实现的机理，以便更准确地选择应用几何效应解决实际问题，也为其他类型科学效应的可拓知识表示研究打下良好基础。Abstract: Scientific effect contains huge scientific knowledge, which is an essential basis for solving functional contradiction problems. To establish an extension knowledge base of scientific effect and realize extension intelligent design for function problems, we propose an extension knowledge representation approach for practical application based on geometric effect. With the help of this technique, extension knowledge found in the input-output relationship of geometric effects in real-world issues can be formally represented. First, the basic-element model is developed according to the geometric effect. Domain knowledge and correlation rules in Extenics are used to establish the relationship between basic-elements. According to the knowledge of active transformation, conductive transformation, and the divergence rules of basic-elements, active transformation is performed on basic-elements in the correlation network, and then a series of conductive transformations are obtained based on the extension transformation implication system and conductive transformation rules, and then the extension knowledge expression is established to realize the expression of transformation relationship between input and output. Finally, the hyperbolic mixer design is taken as an example to further expand corresponding extension knowledge to address the field problems. This study can help designers better understand how geometric effects are realized, enabling them to select them more precisely to solve real-world problems. It can also serve as a solid foundation for the extension knowledge representation to include other types of scientific effects.
-
知识表示、知识获取和知识处理是知识工程的三大支柱，而其核心是知识表示。知识表示是对知识的一种描述或者一种约定，是计算机可以接受的用于描述知识的数据结构。目前人工智能常用的知识表示方法有谓词逻辑、产生式知识表示、语义网络知识表示、框架表示、模糊逻辑知识表示等，但是它们也有各自的局限性[1-2]。
可拓学是以矛盾问题为研究对象，以形式化的模型，探讨事物拓展的可能性以及开拓创新的规律与方法的一门新学科[3-4]。可拓学建立了能够描述物、事和关系的可拓模型，该模型可以作为可拓知识表示的基础。可拓学的逻辑基础是可拓逻辑，研究了矛盾问题转化和推理的规律[4]。文献[5]提出了一种基于事元理论的机械运动系统行为知识表示；文献[6]针对现有计算机辅助工艺过程设计（computer aided process planning, CAPP）系统知识化表示不足，运用可拓学理论，建立了一种成衣制造可拓知识表达模式；文献[7]提出了可拓知识作为元知识的一种新表现形式；文献[8]基于可拓学中的规则，提出了一种可拓规则的知识表示方法；文献[9]提出了可拓信息—知识—策略的形式化表示体系，为计算机生成解决问题的策略提供了基础理论和方法；文献[10]运用可拓模型表示机械概念结构的特征信息、连接约束信息、拓扑结构变换信息；文献[11]将可拓本体理论与知识库技术相融合，构建面向复杂产品方案设计及推理的可拓本体知识库系统；文献[12]提出一种面向生命周期的低碳设计可拓知识建模方法。
科学效应是阿奇舒勒通过对世界范围内的专利分析总结得出的一种解决问题的科学原理，是将效应中有关的量互相联系起来的各领域定律，主要面向功能问题的求解[13]。求解过程中，人们从具体的问题抽象出解决该问题的功能；根据实现功能查询科学效应库，找出解决问题的一个或者多个科学效应，再筛选出合适的科学效应，并将科学效应具体化得到功能原理解。目前，已经总结出的科学效应超过10000条，每条科学效应的具体应用又多种多样。为了高效地使用科学效应知识，快速获得解决矛盾问题的创新解，构建科学效应知识库是十分必要的，而科学效应的知识表示是构建科学效应知识库的基础。针对科学效应的知识表示已经有较多的研究，文献[14]以化学领域为例，提出了基于领域本体科学效应的知识表示；文献[15]提出基于Prolog的科学效应知识表示；文献[16]提出了一种形式化表达物理效应知识的方法；文献[17]提出了基于本体的科学效应知识表达；文献[18-19]建立了基于本体论方法的物理效应知识表示模型，并且提出了一种用于更新物理效应数据库的多智能模型；文献[20]提出了基于知识粒度的科学效应；文献[21-22]基于知识图谱，提出一种科学效应知识库的构建方法。但是这些知识表示对科学效应中输入与输出的变换关系均未详细探讨，也没有对输入与输出进行形式化和定量化的知识表示。
本文从可拓学角度对科学效应中的几何效应机理进行分析，认为几何效应的输入与输出具有相关关系，输入的变换会导致输出的变换。因此根据可拓学中的可拓模型、发散规则、相关规则、可拓变换的蕴含规则、传导变换规则以及相关型知识，提出了一种新的几何效应的可拓知识表示方法，并以双曲面搅拌器设计为例，验证该方法的可行性。
1. 可拓知识表示与科学效应
1.1 基于拓展规则的知识表示
一些简单的知识，可以直接用基元表示，但是一些相对复杂的知识包含基元之间的关系，因此需要用基于可拓规则的基元关系式来表达。可拓规则包括拓展规则、共轭规则、传导规则、基元的逻辑运算规则、变换的运算规则等[1]。基于拓展规则的知识表示，包括发散型知识、相关型知识、蕴含型知识和可扩型知识，统称为拓展型知识[23]。由于科学效应中几何效应的输入与输出具有相关关系，输入的变换会导致输出的变换，主动变换与传导变换之间具有蕴含关系。在实施主动变换前，首先要对待实施主动变换的基元进行发散分析，以获取变换的各种可能途径。但是限于篇幅，本文重点介绍相关型知识，其他类型的知识请参考文献[23]。
相关型知识是根据可拓逻辑中的相关规则得到的表示基元间相关关系的知识，主要包括如下类型：
1）两个基元
${B}_{1}=\left({O}_{1}, \;{c}_{1},\; {v}_{1}\right)$ 与${B}_{2}=\left({O}_{2}, \;{c}_{2},\; {v}_{2}\right)$ 双向（互为）相关的相关型知识的一般表达式为$ {B_1} \sim {B_2} $ 。2）两个基元
${B}_{1}=\left({O}_{1}, \;{c}_{1},\; {v}_{1}\right)$ 与${B}_{2}=\left({O}_{2},\; {c}_{2},\; {v}_{2}\right)$ 为单向相关的相关型知识的一般表达式为$ {B_1}\tilde \to {B_2} $ 。3）一个基元
$B = \left( {O,}{c,}\;v \right)$ 与多个基元${B_1} = \left( {{O_1},}\;\right. \left.{{c_1},}\;{{v_1}} \right)$ ,${B_2} = \left( {{O_2},}\;{{c_2},}\;{{v_2}} \right),\;\cdots$ ,${B_n} = \left( {{O_n},}\;{{c_n},}\;{{v_n}} \right)$ 的“单向与相关”的相关型知识的一般表达式为$$ B\mathop \to \limits^ \wedge \left\{ \begin{aligned} & {B_1} \\ &{B_2} \\[-5pt] &\; \vdots \\ & {B_n} \\ \end{aligned} \right. $$ 也可表示为
$B\tilde \to \mathop \wedge \limits_{i = 1}^n {B_i}$ 。4）多个基元
${B_1} = \left( {{O_1},}\;{{c_1},}\;{{v_1}} \right),$ ${B_2} = \left( {{O_2},}\;{{c_2},}\;{{v_2}} \right),$ $\cdots ， {B_n} = \left( {{O_n},}\;{{c_n},}\;{{v_n}} \right)$ 与一个基元$B = \left( {O,}\;{c,}\;v \right)$ 的“单向与相关”的相关型知识的一般表达式为$$ \left. \begin{aligned} &{B_1} \\ &{B_2} \\[-5pt] & \;\vdots \\ &{B_n} \\ \end{aligned} \right\}\mathop \to \limits^ \wedge B $$ 也可表示为
$\mathop \wedge \limits_{i = 1}^n {B_i}\tilde \to B$ 。5）一个基元
$B = \left( {O,}\;{c,}\;v \right)$ 与多个基元${B_1} = \left( {{O_1},}\;\right. \left.{{c_1},}\;{{v_1}} \right),$ ${B_2} = \left( {{O_2},}\;{{c_2},}\;{{v_2}} \right),$ …,${B_n} = \left( {{O_n},}\;{{c_n},}\;{{v_n}} \right)$ 的“单向或相关”的相关型知识的一般表达式为$$ B\mathop \to \limits^ \vee \left\{ \begin{aligned} &{B_1} \\ &{B_2} \\[-5pt] & \;\vdots \\ &{B_n} \\ \end{aligned} \right. $$ 也可表示为
$B\tilde \to \mathop \vee \limits_{i = 1}^n {B_i}$ 。6）多个基元
${B_1} = \left( {{O_1},}\;{{c_1},}\;{{v_1}} \right),$ ${B_2} = \left( {{O_2},}\;{{c_2},}\;{{v_2}} \right),$ $ \cdots , $ ${B_n} = \left( {{O_n},}\;{{c_n},}\;{{v_n}} \right)$ 与一个基元$B = \left( {O,}\;{c,}\;v \right)$ 的“单向或相关”的相关型知识的一般表达式为$$ \left. \begin{aligned} &{B_1} \\ &{B_2} \\[-5pt] & \;\vdots \\ &{B_n} \\ \end{aligned} \right\}\mathop \to \limits^ \vee B $$ 也可表示为
$\mathop \vee \limits_{i = 1}^n {B_i}\tilde \to B$ 。1.2 可拓知识表示
可拓数据挖掘的目的是获取基于可拓变换的知识，包括基于数据库的可拓分类知识、变换的传导知识、可拓聚类知识以及基于知识库的其他有关变换的知识，简称可拓知识[23]。本文旨在研究对科学效应的知识表示，即对已有的知识进行形式化表示研究，属于变换的传导知识和基于知识库的可拓知识。可拓知识的基础是拓展型知识，本节重点介绍本文研究所使用的基于相关型知识的可拓知识表示。
基于相关型知识的可拓知识是一种传导知识，是在相关型知识的基础上，对相关规则的前件实施某主动可拓变换时，其后件就会发生传导变换，变换后获得的传导规则知识。由于相关型知识包含很多类型，根据不同类型的相关型知识，依据发散规则实施不同的主动变换，根据可拓变换的蕴含规则和传导变换规则，相应的传导变换也不相同，因此可拓知识的表示方法也不相同。
1）基于两个基元间的单向相关型知识的可拓知识表示
设基元
${B_1} = \left( {{O_1},}\;{{c_1},}\;{{v_1}} \right)$ 与${B_2} = \left( {{O_2},}\;{{c_2},}\;{{v_2}} \right)$ 单向相关，即存在单向相关型知识$ {B_1}\tilde \to {B_2} $ 。根据基元的发散规则[1-4]，若对该规则知识的前件基元实施某一主动变换$ {\varphi _1} $ ，使${\varphi _1}{B_1}{\text{ = }}\left( {{O'_1},}\;{{c'_1},}\;{{v'_1}} \right) = {B'_1}$ ，则根据传导变换规则和可拓变换的蕴含规则，必有传导变换$ {}_{{\varphi _1}}{T_2} $ ,使${}_{{\varphi _1}}{T_2}{B_2} = \left( {{O'_2} ,}\;{{c'_2},}\;{{v'_2}} \right) = {B'_2}$ 。基于该单向相关型知识的可拓知识表示为$$ \left( {{B_1} \sim {B_2}} \right) \wedge \left( {{\varphi _1}{B_1}{\text{ = }}{B'_1}} \right)\models \left( {{}_{{\varphi _1}}{T_2}{B_2} = {B'_2}} \right) $$ 同理，对于多个两两相关的基元形成的相关链（网）型知识的某一前件基元实施主动变换，会获得相关链（网）型知识的可拓知识链（网）[23]，此不详述。
2）基于多个基元与一个基元的“单向与相关”型知识的可拓知识表示
设基元
$ {B_1},{B_2}, \cdots ,{B_n} $ 满足条件$ L $ ：$ \mathop \wedge \limits_{i = 1}^n {B_i}\tilde \to B $ ，根据基元的发散规则，若对$ {B_1},{B_2}, \cdots ,{B_n} $ 同时实施主动变换$ \mathop \wedge \limits_{i = 1}^n {\varphi _i} $ ，即$ \mathop \wedge \limits_{i = 1}^n {\varphi _i}{B_i} = \mathop \wedge \limits_{i = 1}^n {B_i}^\prime $ ，则根据传导变换规则和可拓变换的蕴含规则，必有传导变换$ {}_{\left( { \wedge {\varphi _i}} \right)}TB = B' $ 。基于该“单向与相关”型知识的可拓知识表示为$$ \left( {\mathop \wedge \limits_{i = 1}^n {B_i}\tilde \to B} \right) \wedge \left( {\mathop \wedge \limits_{i = 1}^n {\varphi _i}{B_i} = \mathop \wedge \limits_{i = 1}^n {B_i'}} \right)\models\left( {{}_{\left( { \wedge {\varphi _i}} \right)}TB = B'} \right) $$ 同理，对于一个基元与多个基元的“与相关”、多个基元与多个基元的“与相关”的可拓知识，也有类似的表示方法，此不赘述。
3）基于多个基元与一个基元的“单向或相关”型知识的可拓知识表示
设基元
$ {B_1},{B_2}, \cdots ,{B_n} $ 满足条件$ L $ ：$ \mathop \vee \limits_{i = 1}^n {B_i}\tilde \to B $ ，根据基元的发散规则，若对$ {B_1},{B_2}, \cdots ,{B_n} $ 中的至少一个基元实施主动变换$ \mathop \vee \limits_{i = 1}^n {\varphi _i} $ ，即$ \mathop \vee \limits_{i = 1}^n {\varphi _i}{B_i} = \mathop \vee \limits_{i = 1}^n {B_i}^\prime $ ，则根据传导变换规则和可拓变换的蕴含规则，必有传导变换$ {}_{\left( { \vee {\varphi _i}} \right)}TB = B' $ 。基于该“单向或相关”型知识的可拓知识表示为$$ \left( {\mathop \vee \limits_{i = 1}^n {B_i}\tilde \to B} \right) \wedge \left( {\mathop \vee \limits_{i = 1}^n {\varphi _i}B = \mathop \vee \limits_{i = 1}^n {B_i'}} \right)\models\left( {{}_{\left( { \vee {\varphi _i}} \right)}TB = B'} \right) $$ 同理，对于一个基元与多个基元的“或相关”，多个基元与多个基元的“或相关”的可拓知识表示，也有类似的表示方法，此不赘述。
1.3 科学效应
科学效应是各领域定律，它描述在科学原理和系统属性控制下输入与输出的转换关系，以实现相应的功能，包括几何效应、物理效应、化学效应和生物效应等[24]。在不同的理论体系，对科学效应输入与输出有着不同形式的表达。发明问题解决理论（theory of the solution of inventive problems，TRIZ）中认为，输入与输出形成效应；统一结构创新思维（unified structured inventive thinking，USIT）中认为，输入与输出经过转换形成效应；统一的TRIZ（Unified-TRIZ, U-TRIZ）中认为，两个属性相互作用形成效应[25]。上述对科学效应的这些研究，都没有形式化定量化地表述效应中输入与输出间的相关关系，也没有详细说明输入与输出之间的转换机理与转换过程，也没有提出利于计算机表示科学效应的知识表示模型。本文中研究的部分几何效应的输入与输出的关系，如表1所示。
表 1 部分几何效应表达Table 1 Expression of partial geometric effect几何效应 输入 输出 双曲面
效应旋转轴、旋转角度、所选旋转轴长度、双曲线与旋转轴上端距离、双曲线与旋转轴下端距离 形状、体积、双曲
面上下端面半径抛物面
效应焦距、旋转轴、旋转角度、所选旋转轴长度、抛物线与旋转轴上端距离、抛物线与旋转轴下端距离 形状、焦距、体积、抛
物面上下端面半径莫比乌斯
带效应扭转角度 表面个数、扭转圈数 2. 几何效应的可拓知识表示方法
在TRIZ中，科学效应主要面向功能问题求解，是对系统输入输出间转换过程的描述，它是一种变化的知识，一个效应可以有多个输入、输出或控制流，即一个效应可能实现多个功能，一个问题的解也可能对应多个科学效应。目前对科学效应知识表示的研究，大都基于功能到效应的映射的知识表达，并没有详细地形式化表达出输入与输出之间的转换关系。而从可拓学的角度看，输入与输出之间是相关的，存在一定的函数关系，即具有相关关系的基元之间，若一个基元发生主动变换将导致另一个基元发生传导变换。本文运用可拓知识表示方法表示几何效应中输入与输出的变换关系，形成几何效应的可拓知识。几何效应的可拓知识表示方法流程如图1所示。
图 1 几何效应的可拓知识表示方法流程Fig. 1 Process of extension knowledge representation of geometric effects
下载:
全尺寸图片
具体步骤如下：
1）根据几何效应内容和工程技术领域应用需求，建立输入几何对象、输出几何对象的基元模型；
2）根据领域知识和基元的相关规则，建立基元间的相关关系，形成相关链（网）；
3）根据主动变换、传导变换知识和基元的发散规则，对相关网中某基元实施主动变换，再根据可拓变换蕴含系和传导变换规则，会得到一系列的传导变换，进而建立可拓知识表达式，实现输入与输出的转换关系的知识表示。
2.1 双曲面效应的可拓知识表示
双曲面效应是指双曲线绕某条选定的直线或其对称轴（作为旋转轴）旋转而生成的曲面[25]。在实际应用双曲线生成双曲面时，一般步骤是：首先根据实际问题的要求选取双曲线的类型，然后选择该双曲线的一侧图形，确定对应于要使用的旋转轴的长度及双曲线与旋转轴的最小距离和最大距离，再选定某条直线作为旋转轴并设定旋转角度进行旋转，生成所需的双曲面。
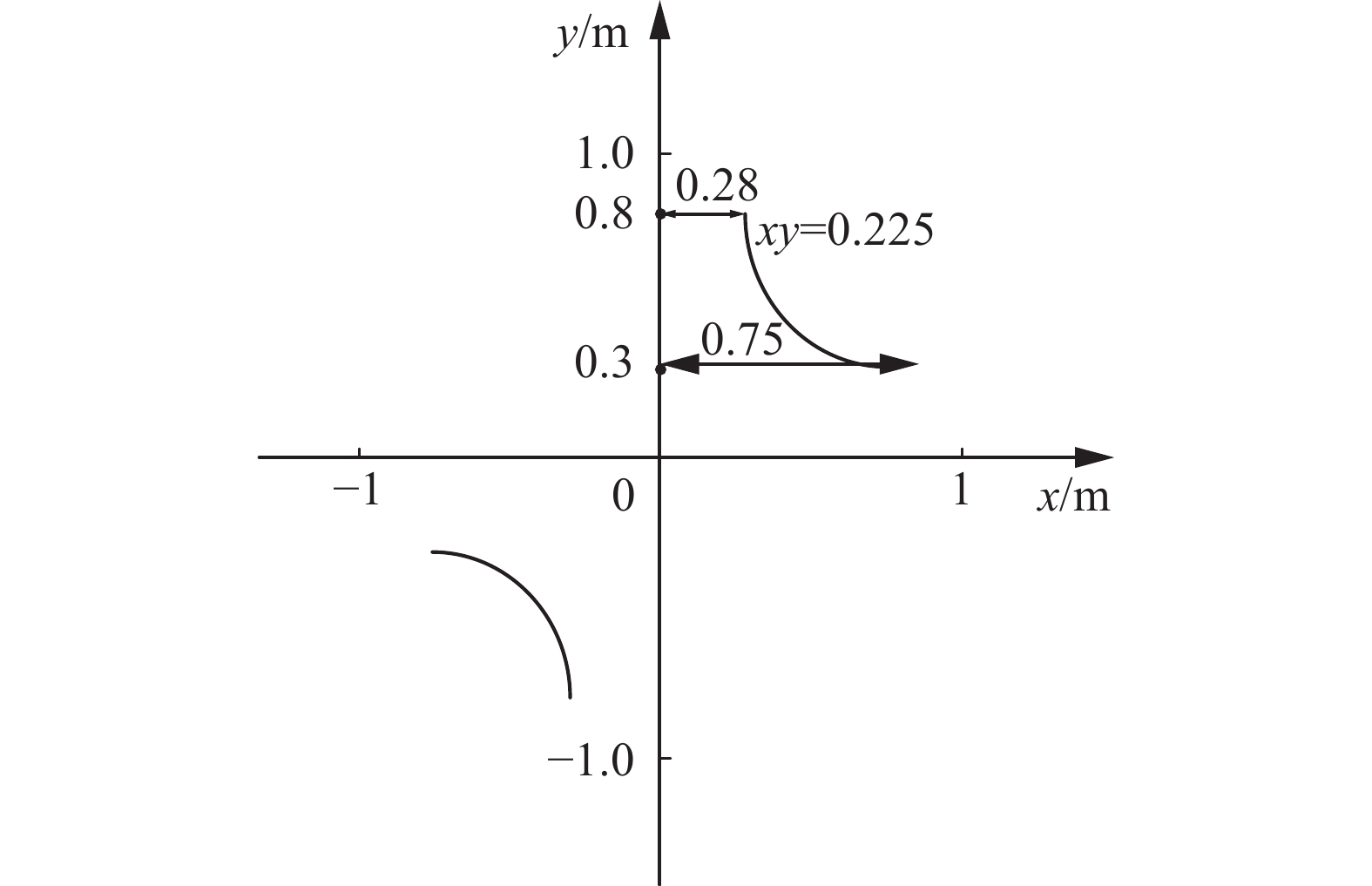
当工程技术领域应用该效应研制相应的产品时，一般是应用该效应产生解决技术领域相应问题的技术特征和相应的符合要求的范围。以图2的右侧图形为例，介绍双曲面效应的可拓知识表示。
图 2 双曲线Fig. 2 Hyperbola下载:
全尺寸图片
设
$ {O_s} $ 为图2中双曲线的右侧图形，选定某条直线$ {v_{s1}} $ 作为生成双曲面的旋转轴$ {c_{s1}} $ ，旋转角度$ {c_{s2}} $ 的量值为$ {v_{s2}} $ ，所使用的旋转轴的两个端点坐标$ {c_{s3}} $ 的量值为图2中没有：$ {v_{s3}} $ ，所使用的双曲线与旋转轴上端的距离$ {c_{s4}} $ 和下端距离$ {c_{s5}} $ 的量值分别为$ {v_{s4}} $ 和$ {v_{s5}} $ 。设$ {O_d} $ 为由双曲线$ {O_s} $ 绕其对称轴y轴旋转而成的双曲面，建立物元模型:$$ {M}_{s}=\left[\begin{aligned} {O}_{s},\;{c}_{s1},\;{v}_{s1}\\ {c}_{s2}, \;{v}_{s2}\\ {c}_{s3},\;{v}_{s3}\\ {c}_{s4},\; {v}_{s4}\\ {c}_{s5},\;{v}_{s5}\end{aligned}\right]= \left[\begin{gathered}{M}_{s1}\\ {M}_{s2}\\ {M}_{s3}\\ {M}_{s4}\\ {M}_{s5}\end{gathered}\right] $$ $$ {M}_{d}=\left[\begin{aligned} {O}_{d},\;&形状,\;&{v}_{d1}\\ &体积,\; &{v}_{d2}\\ &上端面半径,\;&{v}_{d3}\\ &下端面半径,\;&{v}_{d4}\\ \end{aligned}\right]= \left[\begin{aligned} {M}_{d1}\\ {M}_{d2}\\ {M}_{d3}\\ {M}_{d4}\end{aligned}\right] $$ 其中
$ {v_{s3}} = \left( {0,a} \right) \wedge \left( {0,b} \right) $ ，$ {v_{d2}} = {\text{π }}{\int_a^b {\left[ {f\left( y \right)} \right]} ^2}{\text{d}}y $ ，$ {v_{d3}} = {v_{s4}} $ ，$ {v_{d4}} = {v_{s5}} $ 。根据领域知识和可拓学中的相关规则可知: 物元
${M_{s1}}、{M_{s2}}、{M_{s3}}、{M_{s4}}、{M_{s5}}、 {M_{d1}}、 {M_{d2}}、{M_{d3}}、{M_{d4}}$ 具有的单向或相关关系为$$ \left. \begin{gathered} {M_{s1}} \\ {M_{s2}} \\ {M_{s3}} \\ {M_{s4}} \\ {M_{s5}} \\ \end{gathered} \right\}\mathop \to \limits^ \vee \left\{ \begin{gathered} {M_{d1}} \\ {M_{d2}} \\ {M_{d3}} \\ {M_{d4}} \\ \end{gathered} \right. $$ (1) 再根据主动变换、发散规则、相关关系式（1）及传导变换可知，若实施主动变换
$$ \varphi {\text{ = }}{\varphi _{s1}} \vee {\varphi _{s2}} \vee {\varphi _{s3}} \vee {\varphi _{s4}} \vee {\varphi _{s5}}{\text{ = }}\mathop \vee \limits_{i = 1}^5 {\varphi _{si}} $$ 使
$$ {\varphi _{s1}}{M_{s1}} = \left( {{{O'}_s},{c_{s1}},{{v'}_{s1}}} \right){\text{ = }}{M'_{s1}} $$ $$ {\varphi _{s2}}{M_{s2}} = \left( {{{O'}_s},{c_{s2}},{{v'}_{s2}}} \right){\text{ = }}{M'_{s2}} $$ $$ {\varphi _{s3}}{M_{s3}} = \left( {{{O'}_s},{c_{s3}},{{v'}_{s3}}} \right){\text{ = }}{M'_{s3}} $$ $$ {\varphi _{s4}}{M_{s4}} = \left( {{{O'}_s},{c_{s4}},{{v'}_{s4}}} \right){\text{ = }}{M'_{s4}} $$ $$ {\varphi _{s5}}{M_{s5}} = \left( {{{O'}_s},{c_{s5}},{{v'}_{s5}}} \right){\text{ = }}{M'_{s5}} $$ 则必有一阶一次传导变换
$ \mathop \vee \limits_{m = 1}^4 {}_\varphi {T_{dm}} $ ，使$$ {}_{\varphi }T{}_{d1}{M}_{d1}=\left({O'_{d}},\;形状,\;{v'_{d1}}\right)={M'_{d1}} $$ $$ {}_{\varphi }T{}_{d2}{M}_{d2}=\left({O'_{d}},\;体积,\;{v'_{d2}}\right)={M'_{d2}} $$ $$ {}_{\varphi }T{}_{d3}{M}_{d3}=\left({O'_{d}},\;上端面半径,\;{v'_{d3}}\right)={M'_{d3}} $$ $$ {}_{\varphi }T{}_{d4}{M}_{d4}=\left({O'_{d}},\;下端面半径,\;{v'_{d4}}\right)={M'_{d4}} $$ 则双曲面效应的可拓知识表示为
$$ \begin{gathered} \left( {\mathop \vee \limits_{i = 1}^5 {M_{si}}\tilde \to \mathop \vee \limits_{m = 1}^4 {M_{dm}}} \right) \wedge \left( {\mathop \vee \limits_{i = 1}^5 {\varphi _{si}}{M_{si}} = {{M'}_{si}}} \right) \models \\ \left( {\mathop \vee \limits_{m = 1}^4 {}_\varphi {T_{dm}}{M_{dm}} = {{M'}_{dm}}} \right) \end{gathered} $$ (2) 式中
$ \varphi {\text{ = }}\mathop \vee \limits_{i = 1}^5 {\varphi _{si}} $ 。说明：以上双曲面效应的可拓知识表示，是在不考虑领域应用的情况下的通用可拓知识，当在实际领域中应用该可拓知识时，还需要考虑该可拓知识的输出与领域问题的相关性，并在此可拓知识的基础上进一步拓展，获得面向领域应用的领域可拓知识。
2.2 抛物面效应的可拓知识表示
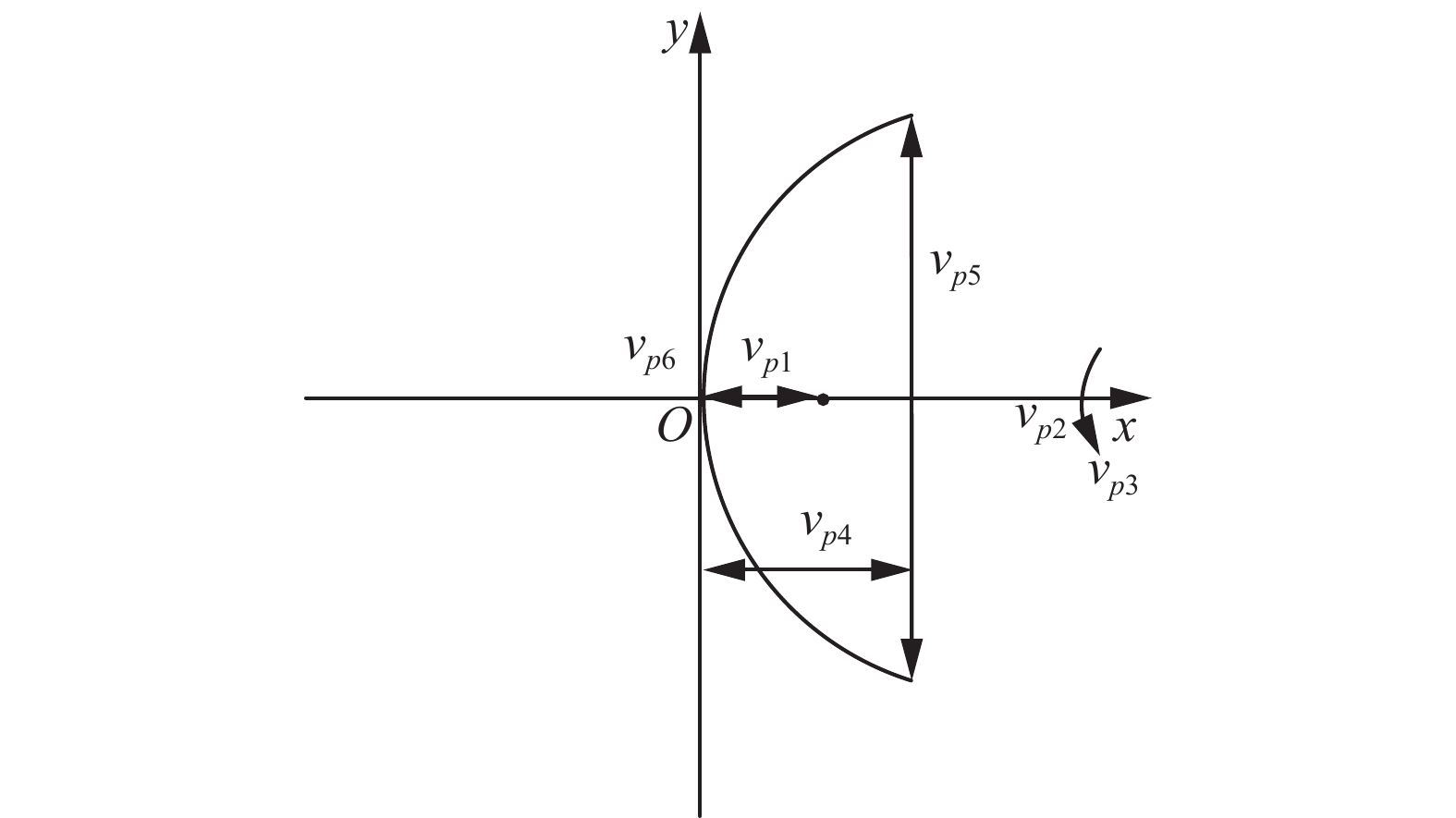
抛物面效应是指抛物线绕对称轴旋转所得到的曲面[25]。以图3所示的抛物面为例，介绍抛物面效应的可拓知识表示。
图 3 抛物线Fig. 3 Parabola下载:
全尺寸图片
设
$ {O_p} $ 为抛物线，其焦距$ {c_{p1}} $ 的量值为$ {v_{p1}} $ ，其对称轴$ {v_{p2}} $ 作为生成抛物面的旋转轴$ {c_{p2}} $ ，旋转角度$ {c_{p3}} $ 的量值为$ {v_{p3}} $ ，所使用的旋转轴的长度$ {c_{p4}} $ 的量值为$ {v_{p4}} $ ，所使用抛物线与旋转轴上端的距离$ {c_{p5}} $ 和下端距离$ {c_{p6}} $ 的量值分别为$ {v_{p5}} $ 和$ {v_{p6}} $ 。设$ {O_t} $ 为抛物线$ {O_p} $ 绕其对称轴x轴旋转而成的椭圆抛物面，建立物元模型：$$ {M_p} = \left[ \begin{aligned} {O_p}, \;{c_{p1}},\; & {v_{p1}}\\ {c_{p2}},\; & {v_{p2}} \\ {c_{p3}},\;& {v_{p3}}\\ {c_{p4}},\; & {v_{p4}}\\ {c_{p5}},\;&{v_{p5}} \\ {c_{p6}}, \;&{v_{p6}}\\ \end{aligned} \right] = \left[ \begin{aligned} {M_{p1}} \\ {M_{p2}} \\ {M_{p3}} \\ {M_{p4}} \\ {M_{p5}} \\ {M_{p6}} \\ \end{aligned} \right] $$ $$ {M}_{t}=\left[\begin{aligned} {O}_{t},\;&形状,\;&{v}_{t1}\\ &体积,\;&{v}_{t2}\\ &焦距,\;&{v}_{t3}\\ &上端面半径,\;&{v}_{t4}\\ &下端面半径,\;&{v}_{t5}\end{aligned}\right]= \left[\begin{aligned} {M}_{t1}\\ {M}_{t2}\\ {M}_{t3}\\ {M}_{t4}\\ {M}_{t5}\end{aligned}\right] $$ 根据领域知识和可拓学中的相关规则可知：物元
${M_{p1}}、{M_{p2}}、{M_{p3}}、{M_{p4}}、{M_{p5}}、 {M_{p6}}、{M_{t1}}、{M_{t2}}、{M_{t3}}、 {M_{t4}}、 {M_{t5}}$ 具有单向或相关关系：$$ \left. \begin{gathered} {M_{p1}} \\ {M_{p2}} \\ {M_{p3}} \\ {M_{p4}} \\ {M_{p5}} \\ {M_{p6}} \\ \end{gathered} \right\}\mathop \to \limits^ \vee \left\{ \begin{gathered} {M_{t1}} \\ {M_{t2}} \\ {M_{t3}} \\ {M_{t4}} \\ {M_{t5}} \\ \end{gathered} \right. $$ (3) 再根据主动变换、发散规则、相关关系式（3）及传导变换可知，若实施主动变换
$$ \varphi {\text{ = }}{\varphi _{p1}} \vee {\varphi _{p2}} \vee {\varphi _{p3}} \vee {\varphi _{p4}} \vee {\varphi _{p5}} \vee {\varphi _{p6}}{\text{ = }}\mathop \vee \limits_{i = 1}^6 {\varphi _{pi}} $$ 使
$$ {\varphi _{p1}}{M_{p1}} = \left( {{O'_p},}\;{{c_{p1}},}\;{{v'_{p1}}} \right)= {M'_{p1}} $$ $$ {\varphi _{p2}}{M_{p2}} = \left( {{O'_p},}\;{{c_{p2}},}\;{{v'_{p2}}} \right) = {M'_{p2}} $$ $$ {\varphi _{p3}}{M_{p3}} = \left( {{O'_p},}\;{{c_{p3}},}\;{{v'_{p3}}} \right) = {M'_{p3}} $$ $$ \begin{gathered}{\varphi _{p4}}{M_{p4}} = \left( {{O'_p},}\;{{c_{p4}},}\;{{v'_{p4}}} \right)= {M'_{p4}} \end{gathered}$$ $$ \begin{gathered} {\varphi _{p5}}{M_{p5}}= \left( {{O'_p},}\;{{c_{p5}},}\;{{v'_{p5}}} \right) = {M'_{p5}} \end{gathered}$$ $$ \begin{gathered} {\varphi _{p6}}{M_{p6}}= \left( {{O'_p},}\;{{c_{p6}},}\;{{v'_{p6}}} \right)= {M'_{p6}} \end{gathered}$$ 则必有一阶一次传导变换
$ \mathop \vee \limits_{m = 1}^5 {}_\varphi {T_{tm}} $ ，使$$ {}_{\varphi }T_{t1}{M}_{t1}\text=\left({O'_{t}},\; 形状,\; {v'_{t1}}\right)={M'_{t1}} $$ $$ {}_{\varphi }T{}_{t2}{M}_{t2}\text=\left({O'_{t}},\; 体积,\; {v'_{t2}}\right)={M'_{t2}} $$ $$ {}_{\varphi }T_{t3}{M}_{t3}=\left({O'_{t}},\; 焦点,\; {v'_{t3}}\right)={M'_{t3}} $$ $$ {}_{\varphi }T{}_{t4}{M}_{t4}=\left({O'_{t}},\; 上端面半径,\; {v'_{t4}}\right)={M'_{t4}} $$ $$ {}_{\varphi }T{}_{t5}{M}_{t5}=\left({O'_{t}},\; 下端面半径,\; {v'_{t5}}\right)={M'_{t5}} $$ 则抛物面效应的可拓知识表示为
$$ \begin{gathered} \left( {\mathop \vee \limits_{i = 1}^6 {M_{pi}}\tilde \to \mathop \vee \limits_{m = 1}^5 {M_{tm}}} \right) \wedge \left( {\mathop \vee \limits_{i = 1}^6 {\varphi _{pi}}{M_{pi}} = {{M'}_{pi}}} \right) \models\\ \left( {\mathop \vee \limits_{m = 1}^5 {}_\varphi {T_{tm}}{M_{tm}} = {{M'}_{tm}}} \right) \\ \end{gathered} $$ (4) 式中
$ \varphi = \mathop \vee \limits_{i = 1}^6 {\varphi _{pi}} $ 。2.3 莫比乌斯带效应的可拓知识表示
莫比乌斯带效应是指将一条带的一端扭转180°，然后两端粘起来组成的只有一个表面和一个边界的带圈[25]，如图4所示。
图 4 莫比乌斯带Fig. 4 Mobius belt下载:
全尺寸图片
设
$ {O_z} $ 为某纸带的一端，$ {O_q} $ 为由该纸带的两端粘起来组成的纸带圈，建立物元模型：$$ {M}_{z}=\left({O}_{z},\; 扭转角度,\; {v}_{z}\right) $$ $$ {M}_{q}\text=\left[\begin{aligned} {O}_{q},\;&表面个数,\;{v}_{q1}\\ &扭转圈数,\;{v}_{q2} \end{aligned}\right]=\left[\begin{aligned}{M}_{q1}\\ {M}_{q2}\end{aligned}\right] $$ 根据领域知识和可拓学中的相关规则可知：物元
$ {M_z}、{M_q} $ 具有单向与相关关系，即$$ {M_z}\mathop \to \limits^ \wedge \left\{ \begin{gathered} {M_{q1}} \\ {M_{q2}} \\ \end{gathered} \right. $$ (5) 再根据主动变换、发散规则、相关关系式（5）及传导变换可知，若实施主动变换
$ {\varphi _z} $ ，使$$ {\varphi }_{z}{M}_{z}=\left({O'_{z}},\; 扭转角度,\; 180^\circ n \right)={M'_{z}} $$ 其中
$ n = 1,3, \cdots ,2n - 1 $ ，则必有传导变换$ \mathop \wedge \limits_{m = 1}^2 {}_{{\varphi _z}}{T_{qm}} $ ，使$$ {}_{{\varphi }_{z}}T{}_{q1}{M}_{q1}=\left({O'_{q}},\; 表面个数,\; 1\right)={M'_{q1}} $$ $$ {}_{{\varphi }_{z}}T{}_{q2}{M}_{q2}=\left({O'_{q}},\; 扭转圈数,\; \dfrac{n}{2}\right)={M'_{q2}} $$ 其中
$ n = 1,3, \cdots ,2n - 1 $ 。则莫比乌斯带效应的可拓知识表示为$$ \begin{gathered} \left( {{M_z}\tilde \to \mathop \wedge \limits_{m = 1}^2 {M_{qm}}} \right) \wedge \left( {{\varphi _z}{M_z}={{M'}_z}} \right) \models\\ \left( {\mathop \wedge \limits_{m = 1}^2 {}_{{\varphi _z}}{T_{qm}}{M_{qm}} = {{M'}_{qm}}} \right) \\ \end{gathered} $$ (6) 3. 实例分析
城市污水处理工艺中，搅拌是关键工序之一，而搅拌器则是搅拌工艺中最重要的设备。目前主要有桨叶式、推进器式和双曲面式3类。其中双曲面搅拌器是一种新型的搅拌器，它的叶轮体上表面是由双曲线
$ xy = c $ 绕叶轮体轴线旋转形成的双曲面，适用于污水处理中的厌氧池、缺氧池和选择池[26]。某污水处理厂的正方形污水处理池，边长为9 m，水深为6 m。现有的双曲面搅拌器是由图5所示的双曲线
$ xy = 0.225 $ 绕y轴旋转360°而形成的双曲面，其叶轮半径$ v_{d4}^0 $ 为0.75 m，搅拌体积为216 m3。在目前的污水池中该双曲面搅拌器搅拌范围较小，可能会导致局部流速低、混合不充分以及搅拌池底有污泥沉积的现象。
图 5 双曲线$ O_s^0 $ Fig. 5 Hyperbola$ O_s^0 $ 下载:
全尺寸图片
对上述的问题进行分析，发现需要通过增大搅拌器的体积来增大搅拌范围，再通过查询科学效应率，最终采用双面效应来实现。根据2.1节的双曲面效应的可拓知识可知，选择不同的双曲线
$ {O_s} $ ，可以获得不同形状和体积的双曲面$ {O_d} $ 。设
$ O_j^0 $ 为由$ O_d^0 $ 形成的解决相应技术领域问题的待改进双曲面搅拌机产品，建立形成原有的双曲面搅拌机的双曲线$ O_s^0 $ 、双曲面$ O_d^0 $ 和双曲面搅拌机$ O_j^0 $ 的初始物元模型为$$ {M}_{s}^{0}= \left[\begin{aligned} {O}_{s}^{0},\;&{c}_{s1},\; y\\ & {c}_{s2}, \;{360}^\circ\\ &{c}_{s3},\;\left(0,0.3\right)\wedge \left(0,0.8\right)\\ &{c}_{s4},\;0.75\text{ m}\\ & {c}_{s5},\;0.28\text{ m}\end{aligned}\right]= \left[\begin{aligned} {M}_{s1}^{0}\\ {M}_{s2}^{0}\\ {M}_{s3}^{0}\\ {M}_{s4}^{0}\\ {M}_{s5}^{0}\end{aligned}\right] $$ $$ {M}_{d}^{0}= \left[\begin{aligned} {O}_{d}^{0},\;&形状,\;\quad\quad\quad 喇叭状\\ &体积,\;\quad\quad\quad 0.33{\text{ m}}^{3}\\ &上端面半径,\;0.28\text{ m}\\ &下端面半径,\;0.75\text{ m}\end{aligned}\right]= \left[\begin{aligned} {M}_{d1}^{0}\\ {M}_{d2}^{0}\\ {M}_{d3}^{0}\\ {M}_{d4}^{0}\end{aligned}\right] $$ $$ {M}_{j}^{0}=\left[ \begin{aligned} {O}_{j}^{0},\;&形状, \quad\quad\;喇叭状\\ &服务范围,\; < 3,6 > \text{ m}\\ &搅拌体积,\; < 54,216 >{\text{ m}}^{\text{3}}\end{aligned}\right]= \left[\begin{aligned} {M}_{j1}^{0}\\ {M}_{j2}^{0}\\ {M}_{j3}^{0}\end{aligned}\right] $$ 为了将搅拌池内的污水充分混合均匀，就需要将该问题中搅拌器的搅拌体积增大到486 m3。
设与初始的双曲线、双曲面和双曲面搅拌机的物元模型对应的一般物元模型为
$$ {M_s} = \left[ \begin{gathered} {M_{s1}} \\ {M_{s2}} \\ {M_{s3}} \\ {M_{s4}} \\ {M_{s5}} \\ \end{gathered} \right] \text{，} {M_d}{\text{ = }}\left[ \begin{gathered} {M_{d1}} \\ {M_{d2}} \\ {M_{d3}} \\ {M_{d4}} \\ \end{gathered} \right] \text{，} {M_j}{\text{ = }}\left[ \begin{gathered} {M_{j1}} \\ {M_{j2}} \\ {M_{j3}} \\ \end{gathered} \right] $$ 再根据双曲面效应的相关关系式（1），在旋转轴和旋转角度的量值不需要改变的情况下，结合实例应用的领域知识，以相关关系式（1）为基础，进一步分析得到结合领域应用的相关关系为
$$ \left. \begin{gathered} {M_{s3}} \\ {M_{s4}} \\ {M_{s5}} \\ \end{gathered} \right\}\mathop \to \limits^ \wedge \left\{ \begin{gathered} {M_{d1}} \\ {M_{d2}} \\ {M_{d3}} \\ {M_{d4}} \\ \end{gathered} \right.\mathop \to \limits^ \wedge \left\{ \begin{gathered} {M_{j1}} \\ {M_{j2}} \\ {M_{j3}} \\ \end{gathered} \right. $$ (7) 相应的可拓知识表示为
$$ \begin{gathered} \left( {\mathop \wedge \limits_{i = 3}^5 {M_{si}}\tilde \to \mathop \wedge \limits_{m = 1}^4 {M_{dm}}\tilde \to \mathop \wedge \limits_{l = 1}^3 {M_{jl}}} \right) \wedge \left( {\mathop \wedge \limits_{i = 3}^5 {\varphi _{si}}{M_{si}} = {M_{si}'}} \right)\models\\ \left( {\mathop \wedge \limits_{m = 1}^4 {}_\varphi {T_{dm}}{M_{dm}} = {{M}_{dm}'}} \right)| = \left( {\mathop \wedge \limits_{l = 1}^3 {}_d{T_{jl}}{M_{jl}} = {M_{jl}'}} \right) \end{gathered} $$ (8) 其中
${\varphi}=\mathop \wedge \limits_{i = 3}^5 \varphi _{si}^1$ 根据可拓知识式（8），通过对
$ \mathop \wedge \limits_{i = 3}^5 {M_{si}} $ 同时实施主动变换$ {\varphi ^1}{\text{ = }}\mathop \wedge \limits_{i = 3}^5 \varphi _{si}^1 $ ，使$$\begin{gathered}\varphi _{s3}^1{M_{s3}} = \left( {O_s^1,{c_{s3}},\left( {0,0.5} \right) \wedge \left( {0,1.3} \right)} \right) = M_{s3}^1 \\ \varphi _{s4}^1{M_{s4}} =\left( {O_s^1,{c_{s4}},{\text{1 m}}} \right)= M_{s4}^1 \\ \varphi _{s5}^1{M_{s5}} = \left( {O_s^1,{c_{s5}},{\text{0.38 m}}} \right) = M_{s5}^1 \end{gathered}$$ 根据相关关系式（7）可知，上述主动变换必导致一阶一次传导变换
$ {T_d}^1{\text{ = }}\mathop \wedge \limits_{m = 1}^4 T_{dm}^1 $ 发生，使$$ {}_{{\varphi }^{1}}T{}_{d1}^{1}{M}_{d1}=\left({O}_{d}^{1},\; 形状,\; 大喇叭状\right)={M}_{d1}^{1} $$ $$ {}_{{\varphi }^{1}}T{}_{d2}^{1}{M}_{d2}=\left({O}_{d}^{1},\; 体积,\; 0.97{\text{m}}^{3}\right)={M}_{d2}^{1} $$ $$ {}_{{\varphi }^{1}}T{}_{d3}^{1}{M}_{d3}=\left({O}_{d}^{1},\; 上端面半径,\; 0.38\text{ m}\right)={M}_{d3}^{1} $$ $$ {}_{{\varphi }^{1}}T{}_{d4}^{1}{M}_{d4}=\left({O}_{d}^{1},\; 下端面半径,\; 1\text{ m}\right)={M}_{d4}^{1} $$ 再根据相关关系式（7）可知，必导致一阶二次传导变换同时发生，使
$$ {}_{{d}^{1}}T{}_{j1}^{1}{M}_{j1}=\left({O}_{j}^{1},\; 形状,\; 大喇叭状\right)={M}_{j1}^{1} $$ $$ {}_{{d}^{1}}T{}_{j2}^{1}{M}_{j2}=\left({O}_{j}^{1},\; 服务范围,\; < 6,14 > \text{m}\right)={M}_{j2}^{1} $$ $$ {}_{{d}^{1}}T{}_{j3}^{1}{M}_{j3}=\left({O}_{j}^{1},\; 搅拌体积,\; < 216,1176 > {\text{m}}^{3}\right)={M}_{j3}^{1} $$ 经上述可拓变换，得到双曲面的下端面半径为1m的双曲面搅拌器，其物元模型为
$$ {M}_{s}^{1}=\left[\begin{aligned} {O}_{s}^{1},\;&{c}_{s1},\;y\\ &{c}_{s2},\;{360}^{\circ }\\ &{c}_{s3},\;\left(0,0.5\right)\wedge \left(0,1.3\right)\\ & {c}_{s4},\;\text{1 m}\\ & {c}_{s5},\;0.38\text{ m}\end{aligned}\right]= \left[\begin{aligned} {M}_{s1}^{1}\\ {M}_{s2}^{1}\\ {M}_{s3}^{1}\\ {M}_{s4}^{1}\\ {M}_{s5}^{1}\end{aligned}\right] $$ $$ {M}_{d}^{1}=\left[\begin{aligned} {O}_{d}^{1},\;&形状,\quad\quad\quad{大喇叭}状\\ &体积,\quad\quad\quad\; \text{{0.97 m}}^{3}\\ &上端面半径,\;0.38\text{ m}\\ &下端面半径,\;1\text{ m}\end{aligned}\right]= \left[\begin{aligned} {M}_{d1}^{1}\\ {M}_{d2}^{1}\\ {M}_{d3}^{1}\\ {M}_{d4}^{1}\end{aligned}\right] $$ $$ {M}_{j}^{1}=\left[\begin{aligned} {O}_{j}^{1},\;&形状,\quad\quad\;大喇叭状\\ &服务范围,\;< 6,14 > \text{m}\\ &搅拌体积,\;< 216,1176 > {\text{m}}^{\text{3}}\end{aligned}\right]= \left[\begin{aligned} {M}_{j1}^{1}\\ {M}_{j2}^{1}\\ {M}_{j3}^{1}\end{aligned}\right] $$ 同理，根据可拓知识式（8），通过对
$ \mathop \wedge \limits_{i = 3}^5 {M_{si}} $ 同时实施主动变换$ {\varphi ^2}{\text{ = }}\mathop \wedge \limits_{i = 3}^5 \varphi _{si}^2 $ ，使$$\begin{gathered} \varphi _{s3}^2{M_{s3}} = \left( {O_s^2,{c_{s3}}{\text{,}}\left( {0,0.8} \right) \wedge \left( {0,1.8} \right)} \right){\text{ = }}M_{s3}^2 \\ \varphi _{s4}^2{M_{s4}} = \left( {O_s^2,{c_{s4}},{\text{1.25 m}}} \right){\text{ = }}M_{s4}^2 \\ \varphi _{s5}^2{M_{s5}} = \left( {O_s^2,{c_{s5}},0.{\text{56 m}}} \right){\text{ = }}M_{s5}^2 \end{gathered}$$ 根据相关关系式（7）可知，上述主动变换必导致如下一阶一次传导变换
$ {T_d}^2{\text{ = }}\mathop \wedge \limits_{j = 1}^4 T_{dj}^2 $ 发生，使$$ {}_{{\varphi }^{2}}T{}_{d1}^{2}{M}_{d1}=\left({O}_{d}^{2},\; 形状,\; 长喇叭状\right)={M}_{d1}^{2} $$ $$ {}_{{\varphi }^{2}}T{}_{d2}^{2}{M}_{d2}=\left({O}_{d}^{2},\; 体积,\; {\text{2.18 m}}^{3}\right)={M}_{d2}^{2} $$ $$ {}_{{\varphi }^{2}}T{}_{d3}^{2}{M}_{d3}=\left({O}_{d}^{2},\; 上端面半径,\; {\text{0.56 m}}\right)={M}_{d3}^{2} $$ $$ {}_{{\varphi }^{2}}T{}_{d4}^{2}{M}_{d4}=\left({O}_{d}^{2},\; 下端面半径,\; 1.25\text{ m}\right)={M}_{d4}^{2} $$ 再根据相关关系式（7）可知，必导致一阶二次传导变换同时发生，使
$$ {}_{{d}^{2}}T{}_{j1}^{2}{M}_{j1}=\left({O}_{j}^{2},\; 形状,\; 长喇叭状\right)={M}_{j1}^{2} $$ $$ {}_{{d}^{2}}T{}_{j2}^{2}{M}_{j2}\text=\left({O}_{j}^{2},\; 服务范围,\; < 10,18 > \text{m}\right)={M}_{j2}^{2} $$ $$ {}_{{d}^{2}}T{}_{j3}^{2}{M}_{j3}\text=\left({O}_{j}^{2},\; 搅拌体积,\; < 600,1944 > {\text{m}}^{3}\right)={M}_{j3}^{2} $$ 经上述可拓变换，得到双曲面的下端面半径为1.25m的双曲面搅拌器，其物元模型为
$$ {M}_{s}^{2}=\left[\begin{aligned} {O}_{s}^{2},\;&{c}_{s1},\;y\\ &{c}_{s2},\;{360}^{\circ }\\ &{c}_{s3},\;\left(0,0.8\right)\wedge \left(0,1.8\right)\\ &{c}_{s4},\;\text{1.25 m}\\ &{c}_{s5},\;\text{0.58 m}\end{aligned}\right]= \left[\begin{aligned} {M}_{s1}^{2}\\ {M}_{s2}^{2}\\ {M}_{s3}^{2}\\ {M}_{s4}^{2}\\ {M}_{s5}^{2}\end{aligned}\right] $$ $$ {M}_{d}^{2}=\left[\begin{aligned} {O}_{d}^{2},\;&形状,\quad\quad\;\;\;\;\;长喇叭状\\ &体积,\;\quad\quad\quad\text{2}{\text{.18 m}}^{3}\\ &上端面半径,\;0.58\text{ m}\\ &下端面半径,\;1.25\text{ m}\end{aligned}\right]= \left[\begin{aligned} {M}_{d1}^{2}\\ {M}_{d2}^{2}\\ {M}_{d3}^{2}\\ {M}_{d4}^{2}\end{aligned}\right] $$ $$ {M}_{j}^{2}=\left[\begin{aligned} {O}_{j}^{2},\;&形状,\quad\quad\;长喇叭状\\ &服务范围,\;< 10,18 > \text{m}\\ &搅拌体积,\;< 600,1944 > {\text{m}}^{\text{3}}\end{aligned}\right]= \left[\begin{aligned} {M}_{j1}^{2}\\ {M}_{j2}^{2}\\ {M}_{j3}^{2}\end{aligned}\right] $$ 对上述的两种双曲面搅拌器仿真分析可得，选取叶轮半径
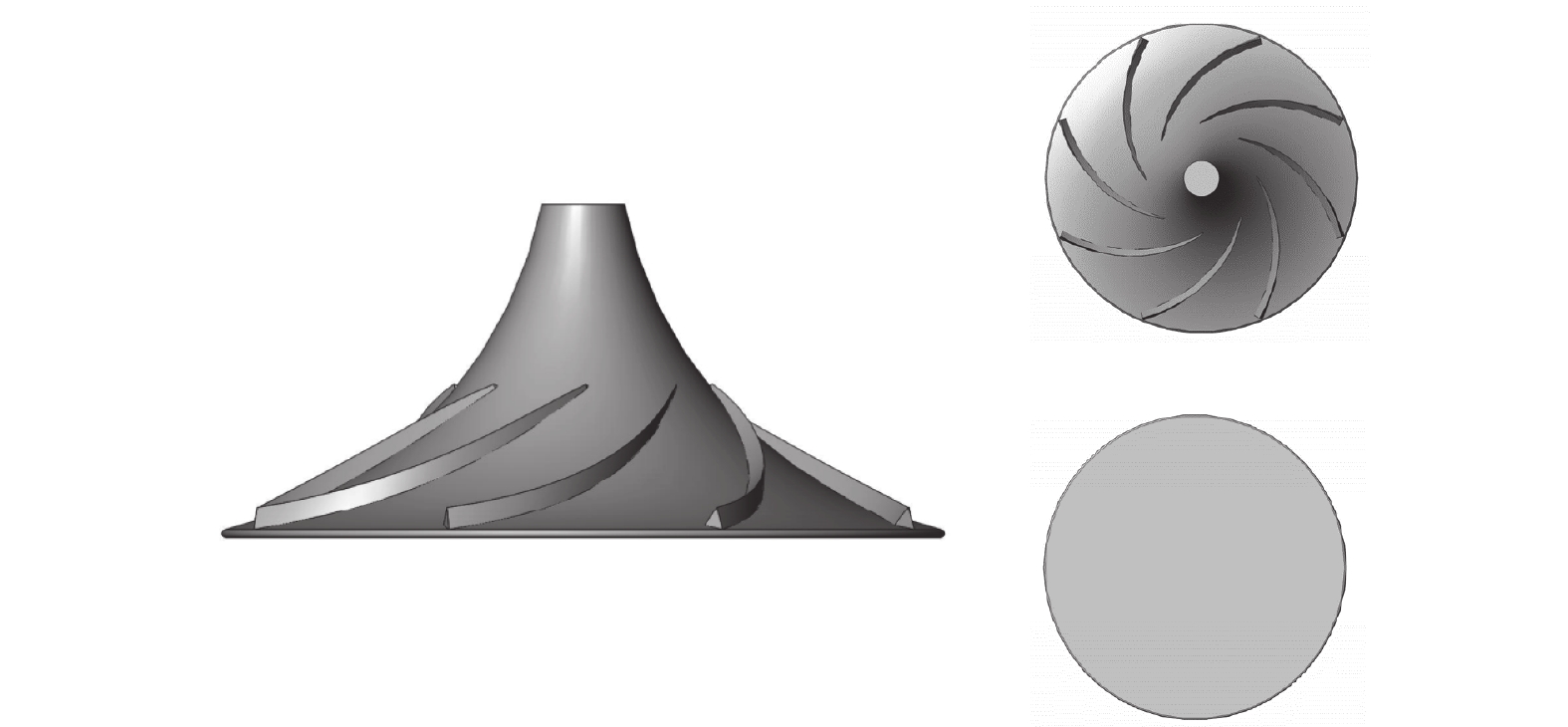
$ {v_{d4}} $ 为1 m的双曲面搅拌器能获得更佳的搅拌效果，还能有效防止污水池底部污泥的沉积。因此，利用可拓知识式（8），改良了原有的双曲面搅拌叶轮，通过改变双曲面搅拌机的母线双曲线，改变了双曲面的形状和体积，从而提高了双曲面型搅拌机的服务范围和搅拌体积。经过改良后的叶轮能够搅拌得更均匀，其结构如图6所示。
图 6 双曲面搅拌机的叶轮及府视图Fig. 6 Impeller and top view of hyperboloid mixer下载:
全尺寸图片
4. 结束语
科学效应对于解决产品创新、技术创新中的矛盾问题具有非常重要的作用。可拓学中的基元是形式化、定量化描述事物及其关系的基本元，可拓变换则是形式化解决矛盾问题的重要工具，可拓知识是基于可拓变换的知识。本文针对科学效应中的几何效应，结合可拓学中的发散规则、相关规则、可拓变换的蕴含规则、传导规则以及相关型知识，提出了一种面向实际应用的通用可拓知识表示方法，利用该方法能对实际应用中几何效应的输入与输出关系中所蕴含的可拓知识进行形式化表示，并通过双曲面搅拌器设计案例，介绍了结合领域知识进一步拓展相应的可拓知识以解决领域问题的方法，验证了该方法的可行性。对科学效应的可拓知识表示研究，可以使设计人员更加全面地理解几何效应实现的机理，为工程技术领域相关矛盾问题的求解提供知识依据，以便更准确地选择应用几何效应解决实际问题，也为其他类型科学效应如物理效应、化学效应和生物效应等的可拓知识表示研究打下良好基础，并可为进一步建立面向可拓智能设计的可拓知识库系统提供一种参考依据和可操作方法。
-
图 1 几何效应的可拓知识表示方法流程
Fig. 1 Process of extension knowledge representation of geometric effects
下载:
全尺寸图片
图 2 双曲线
Fig. 2 Hyperbola
下载:
全尺寸图片
图 3 抛物线
Fig. 3 Parabola
下载:
全尺寸图片
图 4 莫比乌斯带
Fig. 4 Mobius belt
下载:
全尺寸图片
图 5 双曲线
$ O_s^0 $ Fig. 5 Hyperbola
$ O_s^0 $ 下载:
全尺寸图片
图 6 双曲面搅拌机的叶轮及府视图
Fig. 6 Impeller and top view of hyperboloid mixer
下载:
全尺寸图片
表 1 部分几何效应表达
Table 1 Expression of partial geometric effect
几何效应 输入 输出 双曲面
效应旋转轴、旋转角度、所选旋转轴长度、双曲线与旋转轴上端距离、双曲线与旋转轴下端距离 形状、体积、双曲
面上下端面半径抛物面
效应焦距、旋转轴、旋转角度、所选旋转轴长度、抛物线与旋转轴上端距离、抛物线与旋转轴下端距离 形状、焦距、体积、抛
物面上下端面半径莫比乌斯
带效应扭转角度 表面个数、扭转圈数 -
[1] 杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014. [2] YANG Chunyan. Extension innovation method[M]. New York: CRC Press, 2019. [3] 杨春燕. 可拓创新方法[M]. 北京: 科学出版社, 2017. [4] 蔡文, 杨春燕, 何斌. 可拓逻辑初步[M]. 北京: 科学出版社, 2003. [5] 郑震霆, 杨春燕. 基于事元理论的机械运动系统行为知识表示研究[J]. 广东工业大学学报, 2019, 36(6): 1–8,23. doi: 10.12052/gdutxb.190113 ZHENG Zhenting, YANG Chunyan. Behavior knowledge representation of mechanical motion system based on affair-element theory[J]. Journal of Guangdong University of Technology, 2019, 36(6): 1–8,23. doi: 10.12052/gdutxb.190113 [6] 祝勇仁. 成衣制造工艺知识可拓表示与实例推理应用研究[J]. 北京服装学院学报(自然科学版), 2021, 41(2): 56–63. doi: 10.16454/j.cnki.issn.1001-0564.2021.02.009 ZHU Yongren. Research on extension representation of garment manufacturing process knowledge and case-based reasoning application[J]. Journal of Beijing Institute of Fashion Technology(natural science edition), 2021, 41(2): 56–63. doi: 10.16454/j.cnki.issn.1001-0564.2021.02.009 [7] 陈文伟, 黄金才, 毕季明. 适应变化环境的元知识的研究[J]. 智能系统学报, 2009, 4(4): 331–334. doi: 10.3969/j.issn.1673-4785.2009.04.008 CHEN Wenwei, HUANG Jincai, BI Jiming. A study on meta-knowledge suitable for a changing environment[J]. CAAI transactions on intelligent systems, 2009, 4(4): 331–334. doi: 10.3969/j.issn.1673-4785.2009.04.008 [8] YANG Chunyan, CAI Wen. Knowledge representations based on extension rules[C]//2008 7th World Congress on Intelligent Control and Automation. Chongqing: IEEE, 2008: 1455−1459. [9] 杨春燕, 蔡文. 可拓信息−知识−智能形式化体系研究[J]. 智能系统学报, 2007, 2(3): 8–11. YANG Chunyan, CAI Wen. A formalized system of extension information-knowledge-intelligence[J]. CAAI transactions on intelligent systems, 2007, 2(3): 8–11. [10] FENG Yixiong, HAO He, TAN Jianrong, et al. Variant design for mechanical parts based on extensible logic theory[J]. International journal of mechanics and materials in design, 2010, 6(2): 123–134. doi: 10.1007/s10999-010-9114-6 [11] 方磊磊. 面向复杂产品方案设计及推理的可拓本体知识库系统研究[D]. 南京: 南京航空航天大学, 2020. FANG Leilei. Research on extension ontology knowledge base system for complex product scheme design and reasoning[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020. [12] 任设东. 面向产品低碳设计的可拓知识演化方法研究[D]. 杭州: 浙江工业大学, 2018. REN Shedong. Research on methodology of extension knowledge evolution for product low-carbon design[D]. Hangzhou: Zhejiang University of Technology, 2018. [13] 成思源, 周金平, 郭钟宁. 技术创新方法: TRIZ理论及应用[M]. 北京: 清华大学出版社, 2014. [14] 杨政国, 马建红. 基于领域本体科学效应知识语义检索的研究[J]. 计算机系统应用, 2014, 23(2): 209–213. doi: 10.3969/j.issn.1003-3254.2014.02.038 YANG Zhengguo, MA Jianhong. Reseach of semantic retrieval of science effect based on domain ontology[J]. Computer systems & applications, 2014, 23(2): 209–213. doi: 10.3969/j.issn.1003-3254.2014.02.038 [15] 高常青, 杨波, 许佳立, 等. 科学效应及其知识表示与推理方法研究[J]. 机械设计, 2014, 31(10): 4–8. doi: 10.13841/j.cnki.jxsj.2014.10.002 GAO Changqing, YANG Bo, XU Jiali, et al. Research on methodology of knowledge representation and reasoning for effect[J]. Journal of machine design, 2014, 31(10): 4–8. doi: 10.13841/j.cnki.jxsj.2014.10.002 [16] YAN W, ZANNI-MERK C, CAVALLUCCI D, et al. An ontology-based approach for using physical effects in inventive design[J]. Engineering applications of artificial intelligence, 2014, 32: 21–36. doi: 10.1016/j.engappai.2014.02.017 [17] 张星, 马建红, 肖国玺. 基于本体的科学效应知识表达和语义推理[J]. 计算机工程与设计, 2015, 36(7): 1992–1996. doi: 10.16208/j.issn1000-7024.2015.07.060 ZHANG Xing, MA Jianhong, XIAO Guoxi. Scientific effect knowledge representation and semantic reasoning based on ontology[J]. Computer engineering and design, 2015, 36(7): 1992–1996. doi: 10.16208/j.issn1000-7024.2015.07.060 [18] FOMENKOV S, KOROBKIN D, KOLESNIKOV S. Method of ontology-based extraction of physical effect description from russian text[C]// 11th Joint Conference on Knowledge-Based Software Engineering, JCKBSE 2014. Cham: Springer, 2014: 321−330. [19] KOROBKIN D, FOMENKOV S, KAMAEV V, et al. Multi-agent model of ontology-based extraction of physical effects descriptions from natural language text[C]//Proceedings of the 2016 Conference on Information Technologies in Science, Management, Social Sphere and Medicine. Paris: Atlantis Press, 2016: 498−501. [20] 李迅, 王凯, 于翔麟. 基于知识粒度的科学效应库系统构建[J]. 组合机床与自动化加工技术, 2016(7): 96–98. doi: 10.13462/j.cnki.mmtamt.2016.07.027 LI Xun, WANG Kai, YU Xianglin. Construction of scientific effect knowledge base system based on knowledge granularity[J]. Modular machine tool & automatic manufacturing technique, 2016(7): 96–98. doi: 10.13462/j.cnki.mmtamt.2016.07.027 [21] 唐昊. 基于知识图谱的科学效应库研究和开发[D]. 成都: 四川大学, 2021. TANG Hao. Research and development of scientific effect database based on knowledge graph[D]. Chengdu: Sichuan University, 2021. [22] 乔晓东. 基于TRIZ的科学效应知识库系统构建[D]. 郑州: 郑州大学, 2021. QIAO Xiaodong. Construction of scientific effects knowledge database system based on TRIZ[D]. Zhengzhou: Zhengzhou University, 2021. [23] 杨春燕, 李小妹, 陈文伟, 等. 可拓数据挖掘方法及其计算机实现[M]. 广州: 广东高等教育出版社, 2010. [24] 王立新, 乔晓东, 刘晟杰, 等. TRIZ中科学效应库的研究综述[J]. 现代制造工程, 2021(5): 154–160. doi: 10.16731/j.cnki.1671-3133.2021.05.024 WANG Lixin, QIAO Xiaodong, LIU Shengjie, et al. A summary of research on the scientific effect database in TRIZ[J]. Modern manufacturing engineering, 2021(5): 154–160. doi: 10.16731/j.cnki.1671-3133.2021.05.024 [25] 赵敏, 张武城, 王冠殊. TRIZ进阶及实战: 大道至简的发明方法[M]. 北京: 机械工业出版社, 2016. [26] 王斌帆. 双曲面搅拌器反应池内流态分布及其影响因素分析[D]. 西安: 西安建筑科技大学, 2015. WANG Binfan. The analysis of flow regime and affecting factors of reaction tank with hyperboloid stirrer[D]. Xi’an: Xi’an University of Architecture and Technology, 2015.
