A mobile robot path planning method based on adaptive DWA and an improved bacteria algorithm
-
摘要: 针对移动机器人在复杂环境下的路径规划问题,提出一种新的自适应动态窗口改进细菌算法,并将新算法应用于移动机器人路径规划。改进细菌算法继承了细菌算法与动态窗口算法(dynamic window algorithm, DWA)在避障时的优点,能较好实现复杂环境中移动机器人静态和动态避障。该改进算法主要分三步完成移动机器人路径规划。首先,利用改进细菌趋化算法在静态环境中得到初始参考规划路径。接着,基于参考路径,机器人通过自身携带的传感器感知动态障碍物进行动态避障并利用自适应DWA完成局部动态避障路径规划。最后,根据移动机器人局部动态避障完成情况选择算法执行步骤,如果移动机器人能达到最终目标点,结束该算法,否则移动机器人再重回初始路径,直至到达最终目标点。仿真比较实验证明,改进算法无论在收敛速度还是路径规划精确度方面都有明显提升。Abstract: To solve the problem of mobile robot path planning in complex environments, a novel path planning method based on enhanced bacterial chemotaxis and an adaptive dynamic window algorithm is proposed. In addition to inheriting the benefits of bacterial chemotaxis and the dynamic window algorithm in avoiding obstacles, the novel method can also be used to avoid static or dynamic obstacles for mobile robots. It is typically divided into three steps when employed for mobile robot path planning. First, an initial referential planning path in a static environment is determined using the enhanced bacterial chemotaxis algorithm. Next, based on the reference path, the robot detects and avoids dynamic obstacles using its own sensors and completes path planning for local dynamic obstacle avoidance using adaptive DWA. Ultimately, the mobile robot chooses the next execution step based on the outcome of avoiding dynamic obstacles. If the robot is able to reach the final object point, the algorithm stops. Otherwise, the robot will return to the initial path until the final object point is reached. The comparison of simulation and experiment results demonstrates that the algorithm's convergence speed and accuracy of path planning have been significantly enhanced.
-
近年来,随着移动机器人在工业[1]、农业、医疗业和服务业等领域越来越广泛应用,移动机器人技术成为了研究热点。路径规划技术作为移动机器人研究的一个核心内容,已经引起众多科研人员关注并得到深入研究[1-25]。在路径规划时,如何得到高效的路径规划算法,是众多研究者考虑的重点。群智能算法因在未知和信息不完整环境中具有求解优势,被广泛应用于复杂环境中移动机器人路径规划[2],如蚁群、粒子群、鱼群、细菌趋化以及基于这些算法的改进策略等[1-13]。
最近几年,基于改进群智能算法的移动机器人路径规划已经取得诸多研究成果。如文献[3]中,针对蚁群算法收敛速度慢,易陷入局部最优等问题,罗强等按梯度设置初始信息素、优化信息素更新策略、在启发式函数中添加阻尼系数、改进状态转移概率,达到降低死锁概率的目的,从而改善其全局搜索能力和收敛速度。文献[4]中,针对蚁群算法易发生障碍死锁和自死锁现象,孙功武等提出基于全局和局部禁忌表的防死锁策略和自适应启发函数,这样能增强蚁群算法在复杂度较高静态环境中机器人路径规划收敛速度和精度。文献[5]中,Gao等提出一种增强型启发式蚁群改进算法,该算法从信息素更新、扩散、回溯和路径合并等4个方面对蚁群算法进行优化,从而达到改善算法性能的目的。文献[6]中,Miao等基于标准蚁群算法,在状态转移概率中加入障碍排除和角度引导因子,并在信息素更新策略中增加启发式信息素自适应调节和挥发因子,以平衡该算法收敛速度和精度,得到了具有较高实时和稳定性路径。文献[7]中,曹新亮等针对蚁群算法收敛速度慢的问题,通过建立新的初始信息素浓度模型改进蚁群算法,以此在栅格地图中划定优选区域,提高了蚁群算法收敛速度。文献[8]中,李鹏等利用细菌算法优化蚁群算法参数,为蚁群算法快速、准确和有效地选择最优参数提供了一种新的思路。文献[9]中,蒲兴成等结合蚁群和粒子群算法,通过引入反向学习策略去改进粒子群算法惯性权重和学习因子,从而克服了经典粒子群算法易陷入早熟的缺陷,优化了粒子群算法在路径规划中的寻优能力、收敛速度和稳定性。文献[10]中,张毅等基于人工鱼群算法引入衰减函数,提高了鱼群算法全局和局部搜索能力。文献[11]中,Muni等将细菌算法用于机器人导航,实现机器人在复杂环境中路径规划。文献[12]中,梁晓丹等提出一种基于细菌算法的移动机器人路径规划方法,该方法规划的路径可以在不同环境下具有较高的精度和稳定性。文献[13]中,Pang等从自适应步长、搜索方向和全局最优解等几个方面综合考虑,以此改进标准细菌算法,从而改善细菌算法收敛速度和精度。
值得一提的是,上述各种群智能算法及其改进策略大多应用于静态环境中的移动机器人路径规划。而在许多实际问题中,移动机器人基本上处于动态环境下,相关的障碍物也多具有运动特征。此时,如果还采用静态路径规划策略必将产生诸多问题。因此,研究动态障碍物下移动机器人路径规划问题不仅有一定的理论意义,更具有较高的实际应用价值。如今,基于动态障碍物的机器人避障已经成为机器人路径规划的一个热点问题[14-19]。文献[14]中,Lian等提出了基于三次样条插值的混沌自适应粒子群算法,并验证了该模型在不同动态环境下的可行性。但这种算法时间复杂度较高,在线实现比较困难。文献[15]中,李元等将ORB-SLAM算法、GMapping算法、改进人工势场法和二次规划相结合,虽能成功实现移动机器人在复杂环境中定位、避障和路径规划,但这种方案同样存在着计算时间过长和收敛速度慢的问题。文献[16]中,Chang等以标准动态窗口算法为基础,对评价函数进行扩展,从而实现移动机器人在复杂环境的动态避障。但该方法依然存在时间复杂度高和收敛速度较慢的问题。文献[17]中,Henkel等考虑了路径规划过程中能耗情况,在标准动态窗口算法中加入表示能量消耗的代价函数,解决了特殊约束条件下动态避障问题。文献[18]中,Jin等将蚁群算法与动态窗口算法结合,提出一种全局滚动策略。该策略以蚁群算法规划的初始路径为参考,通过动态窗口算法产生初始路径局部目标点,并不断更新局部目标点直至达到最终目标点。该算法能成功实现移动机器人行进途中的动态避障。文献[19]中, Chen等结合A*与动态窗口算法,提出一种全局滚动策略,并将其应用于水面无人船路径规划,以此实现无人船在水面上的避障前行。
综上所述,目前针对移动机器人动态避障问题,大多采用全局滚动策略和动态窗口算法。全局滚动策略和动态窗口算法虽然能在一定程度上解决移动机器人动态避障问题,依然存在着算法计算量大和收敛时间过长的缺陷。为克服这些缺陷,紧贴实际问题,本文提出一种基于自适应动态窗口的改进细菌算法,并将其应用于静态和动态障碍物并存的复杂环境下移动机器人路径规划。本文研究成果主要有4点。1)通过加入一个与目标朝向相关的子函数优化标准细菌算法中的适应度函数,引导细菌在全局寻优过程中能始终向目标点运动,提高算法路径规划精度。2)针对细菌算法中因步长固定导致收敛速度慢的问题,提出一种分阶段选择步长策略。在此过程中,机器人分阶段选择合适步长,即在路径规划前期选择较大步长,中期选择一般步长,后期选择较小步长,最终达到提高收敛速度与精度的目的。3)基于动态窗口适应度函数,加入能影响heading子函数的权重自适应控制,进一步提高DWA收敛精度。4)结合细菌与动态窗口算法,提出一种新的局部滚动策略。该策略基于移动机器人感知动态障碍物进行自主避障,当机器人感知到动态障碍时,立即启动局部滚动策略进行动态避障;当动态障碍物离开机器人感知范围时,机器人重回初始规划路径。通过这些改进方式,该算法不仅能保证移动机器人在复杂环境中实现动态避障,还能提高路径规划效率。
1. 自适应动态窗口改进细菌算法及其应用
本节主要讨论基于自适应动态窗口改进细菌算法及其在移动机器人路径规划方面的性能。
1.1 改进细菌算法的静态路径规划
细菌算法作为群智能算法之一,有着较强全局搜索能力和较快收敛速度。该算法通过模拟细菌在觅食过程中的运动趋化行为求出最优解。实际上,细菌在觅食过程中,会向着营养物质浓度高的区域运动,同时避开存在有害物质区域[21]。在该运动过程中,细菌通过游动和翻滚两种方式实现自身运动。游动使细菌沿着某一方向做直线运动,而翻滚运动则改变细菌运动方向。细菌通过不断地游动和翻滚来避开有害物质,趋向营养物质。这一趋化行为由细菌所在环境的营养物质和有害物质浓度所决定,即细菌总是由食物浓度低的区域游向食物浓度高的区域。当前方出现有害物质时,细菌通过翻滚改变其运动方向,找出最佳区域并向其游动。根据这一原理,不少学者将细菌趋化行为应用于移动机器人路径规划[12-13]。基于细菌算法的路径规划,一般定义营养物质浓度最高位置为路径规划目标点,细菌需要避开的有害物质为环境中障碍物。环境中营养物质与有害物质浓度由适应度函数表示。细菌
$ i $ 从$ t $ 时刻到$ t + 1 $ 时刻的位置更新函数表示为$$ p_i^{t + 1} = p_i^t + c(i)\frac{{{\boldsymbol{\varDelta}} (i)}}{{\sqrt {{{\boldsymbol{\varDelta}} ^{\rm{T}}}(i){\boldsymbol{\varDelta }}(i)} }} $$ (1) 式中:
$ p_i^t $ 为当前位置;$ p_i^{t + 1} $ 为下一时刻位置;$ c(i) $ 为细菌$ i $ 的运动步长,$ {\boldsymbol{\varDelta}} (i) $ 为随机向量。文献[21]提出将细菌算法用于移动机器人路径规划,相应的移动机器人位置更新函数设置为$$ \left\{ \begin{gathered} {x_{{\rm{robot}}}}(t + 1) = {x_{{\rm{robot}}}}(t) + {c_{{\rm{robot}}}}(t) \times \cos ({\theta _{{\rm{robot}}}}(t)) \\ {y_{{\rm{robot}}}}(t + 1) = {y_{{\rm{robot}}}}(t) + {c_{{\rm{robot}}}}(t) \times \sin ({\theta _{{\rm{robot}}}}(t)) \\ \end{gathered} \right. $$ (2) 式中
${c_{{\rm{robot}}}}(t)$ 为t时刻移动机器人步长。在标准细菌算法中,当细菌
$ i $ 完成一次运动后,相关的适应度函数采用式(3)完成更新:$$ F_i^{t + 1} = F_i^t + {F_{{\rm{cc}}}} $$ (3) 式中:
$ F_i^t $ 为细菌$ i $ 在$ t $ 时刻适应度值;$ F_i^{t + 1} $ 为$ t + 1 $ 时刻适应度值;${F_{{\rm{cc}}}}$ 则表示细菌“趋向或排斥”的变量。鉴于移动机器人运动约束为目标点和障碍物,给出细菌算法适应度函数如下:$$ F = {\omega _1}{F_{{\rm{goal}}}} + {\omega _2}{F_{{\rm{obs}}}} $$ (4) 式中:
$ {\omega _1} $ 和$ {\omega _2} $ 分别为目标和避障函数的权重,$ {F_{{\rm{goal}}}} $ 表示移动机器人倾向于目标点运动的适应度子函数。为提高机器人路径规划精度,本文对原适应度子函数$ {F_{{\rm{goal}}}} $ 进行优化,即在原算法基础上增加表示机器人在$ t + 1 $ 时刻位置与目标点倾向角的子函数$ {F_{{\rm{angle}}}} $ ,其表达式为$$ {F_{{\rm{angle}}}} = \left|\arctan \left(\dfrac{{({y_g} - {y^{t{{ + }}1}})}}{{({x_g} - {x^{t{{ + }}1}})}}\right) - \arctan \left(\dfrac{{({y_{{g}}} - {y_{{\rm{start}}}})}}{{({x_g} - {x_{{\rm{start}}}})}}\right)\right| $$ (5) 由此得到新的适应度子函数
${F_{{\rm{goal}}}}$ 表达式:$$ \begin{gathered} {F_{{\rm{goal}}}} = \left[{({x^{t{{ + }}1}} - {x_g})^2} + {({y^{t{{ + }}1}} - {y_g})^2}\right]{{ + }}{F_{{\rm{angle}}}}= \\ \left[{({x^{t{{ + }}1}} - {x_g})^2} + {({y^{t{{ + }}1}} - {y_g})^2}\right]{{ + }} \\ \left|\arctan \left(\dfrac{{({y_g} - {y^{t{{ + }}1}})}}{{({x_g} - {x^{t{{ + }}1}})}}\right) - \arctan \left(\dfrac{{({y_{{g}}} - {y_{{\rm{start}}}})}}{{({x_g} - {x_{{\rm{start}}}})}}\right)\right| \end{gathered} $$ (6) 由式(6)不难看出,
${F_{{\rm{goal}}}}$ 的值与$ t + 1 $ 时刻机器人位置距目标点的距离成正比。${F_{{\rm{goal}}}}$ 值越小,移动机器人在$ t + 1 $ 时刻的位置距离目标点越近,该位置与目标点构成的倾向角越小,说明$ t + 1 $ 时刻位置更优。此外,在式(4)中,
${F_{{\rm{obs}}}}$ 为适应度函数$ F $ 的子函数,其大小可用来评价障碍物位置优劣。距离障碍物越远,${F_{{\rm{obs}}}}$ 函数值越小,机器人位置越优。其具体表达式如下:$$ {F_{{\rm{obs}}}} = \displaystyle\sum\limits_{i = 1}^n {\exp \left[ - \dfrac{{{{({x^{{{t}} + 1}} - x_{{\rm{obs}}}^k)}^2} + {{({y^{t + 1}} - y_{{\rm{obs}}}^k)}^2}}}{{\delta _k^2}}\right]} $$ (7) 式中:
${F_{{\rm{obs}}}}$ 为障碍物高斯轮廓信息;$(x_{{\rm{obs}}}^k,y_{{\rm{obs}}}^k)$ 为第$ k $ 个障碍物中心坐标;$ {\delta _k} $ 表示第$ k $ 个障碍物作用范围。式(7)表明,若$ t + 1 $ 时刻位置距障碍物越远,则${F_{{\rm{obs}}}}$ 值越小,安全性越高。由式(4)、(6)和(7)可知,适应度函数$ F $ 最小值对应位置应作为$ t + 1 $ 时刻的最优位置。此外,在细菌算法中,不同步长会影响移动机器人在路径规划中的收敛速度和精度。基于细菌算法[21],表1给出不同步长对移动机器人路径规划精度和耗时影响。
表 1 不同步长下机器人路径规划精度和收敛速度比较Table 1 Comparison of accuracy and convergence speed in path planning of robots under different length步长/m 路径长度/m 消耗时间/s 迭代步数 0.05 55.1499 0.5143 1180 0.1 55.2645 0.4382 771 0.15 55.3486 0.3042 484 0.2 55.4288 0.2358 390 0.25 55.4381 0.2227 361 0.3 55.4839 0.2181 294 0.35 55.7528 0.2161 280 0.4 55.7692 0.2088 219 表1表明,步长越大,机器人路径规划精确度越低,但收敛速度更快,迭代次数也减少。由此可知,较大步长能让机器人有着较强全局搜索能力,能促使移动机器人快速向目标点运动,但会损失一定的路径搜索精度;反之,较小步长能使机器人有着较强局部搜索能力,从而提高路径搜索精度,但会牺牲搜索时间[19]。受此启发,本文提出一种分阶段选择步长策略以提高路径规划效率。在算法运行前期,采用较大步长,促使移动机器人快速向目标点运动,保证算法有着较强全局搜索能力;在算法运行中期,适当降低算法步长以增强算法局部搜索能力;在算法运行后期,为避免过大步长造成越过目标点现象,采用较短步长进一步强化局部搜索能力。该策略的数学描述如式(8)所示:
$$ {c_{{\rm{robot}}}}(t) = \left\{ {\begin{aligned} &{{\rm{long}},\;\;\;\;\;\quad t \in {\rm{prophase}}} \\ &{{\rm{middle}},\quad t \in {\rm{metaphase}}} \\ &{{\rm{short}},\;\;\;\quad t \in {\rm{anaphasis}}} \end{aligned}} \right. $$ (8) 式中:prophase、metaphase和anaphasis分别表示改进细菌算法在寻路阶段的前期、中期和后期。
1.2 基于自适应动态窗口算法的动态避障
动态窗口算法(dynamic window algorithm, DWA)是一种针对动态障碍物避障的局部路径规划方法,其基本思路是在特定速度约束范围内进行多组采样,并将采样速度引入所建立的运动学模型,模拟在一定时间内移动机器人的运动轨迹[20];然后,通过评价函数选择最优轨迹,得到移动机器人的最优线速度和角速度;最后,控制机器人以该速度沿模拟轨迹运动。在DWA中,速度约束条件如下:
$$ \left\{ \begin{gathered} 0 \leqslant v(t) \leqslant {v_{\max }} \\ v(t) - {a_{l\max }}\Delta t \leqslant v(t + 1) \leqslant v(t) + {a_{l\max }}\Delta t \\ - {\omega _{\max }} \leqslant \omega (t) \leqslant {\omega _{\max }} \\ \omega (t) - {a_{j\max }}\Delta t \leqslant \omega (t + 1) \leqslant \omega (t) + {a_{j\max }}\Delta t \\ \end{gathered} \right. $$ (9) 式中:
$ v(t) $ 和$ \omega (t) $ 分别为$ t $ 时刻移动机器人的线速度和角速度值;$ v(t + 1) $ 和$ \omega (t + 1) $ 分别为$ t + 1 $ 时刻线速度和角速度值;$ {a_{l\max }} $ 和$ {a_{j\max }} $ 分别为线加速度和角加速度;$ \Delta t $ 为向前模拟轨迹时间。现有研究表明,适应度函数的设置是DWA获得最优轨迹的关键[16]。DWA通过适应度函数对机器人
$ t + 1 $ 时刻位置进行评价,选出最优$ v $ 和$ \omega $ ,并产生最优路径轨迹。DWA的标准适应度函数为$$ \begin{gathered} J(v,w) = \sigma [a \cdot {\rm{heading}}(v,w) + \\ b \cdot {\rm{obstacle}}(v,w) + c \cdot {\rm{velocity}}(v,w)] \\ \end{gathered} $$ (10) 由式(10)可知,DWA的标准适应度函数包含heading,obstacle和velocity 3个子评价函数。其中,heading函数表示移动机器人朝向目标点子函数,该子函数表示预测轨迹末端方向角与目标方向角的角度差,角度差越小,函数值越大,说明预测轨迹末端越倾向目标点,此时全局搜索能力越强;obstacle函数表示预测轨迹距障碍物的最小距离,obstacle函数值越大则距离越大,说明机器人若沿该轨迹运动,则它与障碍物发生碰撞的概率越低,安全系数越高;velocity函数为评价机器人前进线速度和角速度的子函数,当线速度越高,角速度越小时,该子函数值越大,机器人更能快速和直线运动。其中
$ a、b $ 和$ c $ 分别为上述3个子函数所占权重,$ \sigma $ 表示归一化过程[16]。根据具体要求,可以对各个子函数设置合适权重。当对机器人有较强全局搜索要求时,则权重$ a $ 设置较大一些;若要求机器人有较强的避障能力,则权重$ b $ 设置较大一些;类似地,若要求机器人所规划的轨迹更平滑,则权重$ c $ 设置较大一些。最后,再通过对这些权值的归一化处理,完全可以确保机器人以较优线速度和角速度朝目标点运动并实现避碍。通过对权重
$ a $ 的取值变化进行分析,经过多次测试,DWA的收敛速度和精度变化曲线如图1所示。由图1可以看出,当权重位于0.05~0.08,DWA的收敛速度较好,但精确度会有所降低;当权重小于0.06或大于 0.12时,DWA路径规划精度较好,但收敛速度会变慢。由此可见,固定权值
$ a $ 无法使DWA同时兼顾收敛速度和精度。针对这一问题,本文提出一种基于自适应权重$ a $ 的改进DWA。改进DWA也是受实际生活经验启发,为迅速到达目的地,当人距离目标位置较远时,需要时刻保持朝向目标点方向运动;当人距离目标位置较近的时候,需要有较强局部搜索能力。基于这种逻辑思维,将影响heading子函数权重
$ a $ 的自适应控制加到标准DWA适应度函数上。在路径规划前期, 自适应控制权重$ a $ 的值较大,机器人就能保持向目标点运动,故能提高机器人全局路径搜索能力;在路径规划后期,自适应控制权重$ a $ 较小,以增强机器人路径规划局部搜索能力。下面具体介绍基于权重$ a $ 的自适应控制器设计思路。首先,分别计算机器人当前位置和初始位置距离目标点的欧氏距离:
$$ \left\{ {\begin{split} &{{d_i} = \sqrt {{{({x_{{\rm{target}}}} - {x_i})}^2} + {{({y_{{\rm{target}}}} - {y_i})}^2}} } \\ &{{d_{{\rm{all}}}} = \sqrt {{{({x_{{\rm{target}}}} - {x_{{\rm{start}}}})}^2}+ {{({y_{{\rm{target}}}} - {y_{{\rm{start}}}})}^2}} } \end{split}} \right. $$ (11) 其次,结合式(11),构造权重a的自适应控制器:
$$ a = k \cdot \frac{{{d_i}}}{{{d_{{\rm{all}}}}}} $$ (12) 式中:k为一个正常数。
$ {d_i} $ 和${d_{{\rm{all}}}}$ 分别为机器人当前和初始位置距离目标点的欧氏距离。(${x_{{\rm{start}}}}$ ,${y_{{\rm{start}}}}$ )、($ {x_i} $ ,$ {y_i} $ )和(${x_{{\rm{target}}}}$ ,${y_{{\rm{target}}}}$ )分别为机器人的起点、当前位置和终点坐标。由式(12)可知,权重$ a $ 与距离$ {d_i} $ 成正比例。这就从理论上解释了权重$ a $ 在前期和后期设置大小的合理性。此外,在动态障碍物干扰的复杂环境中如何实现移动机器人避障,首先要解决的是动态障碍物建模问题。本文参考文献[23]的方法,采用如式(13)的动态障碍物模型:
$$ \left\{ \begin{gathered} {x_{{\rm{obs}}}}(t + 1) = {x_{{\rm{obs}}}}(t) + {v_{{\rm{obs}}}}(t) \cdot \cos ({\theta _{{\rm{obs}}}}(t)) \\ {y_{{\rm{obs}}}}(t + 1) = {y_{\rm{{obs}}}}(t) + {v_{{\rm{obs}}}}(t) \cdot \sin ({\theta _{{\rm{obs}}}}(t)) \\ \end{gathered} \right. $$ (13) 式中:
$ ({x}_{{\rm{obs}}}(t),{y}_{{\rm{obs}}}(t)) $ 为t时刻动态障碍物中心坐标,$ ({x}_{{\rm{obs}}}(t+1),{y}_{{\rm{obs}}}(t+1)) $ 为t+1时刻动态障碍物中心坐标,$ {v_{{\rm{obs}}}}(t) $ 为t时刻动态障碍物移动速度,$ {\theta _{{\rm{obs}}}}(t) $ 为t时刻障碍物与x坐标轴夹角。该模型建立了动态障碍物位置与速度的关系,可直接用于复杂环境下动态障碍物建模。1.3 自适应动态窗口改进细菌算法的移动机器人路径规划分析及步骤
图2和表2从定性和定量角度分别比较分析了DWA与细菌算法在移动机器人全局路径规划中的收敛能力。
表 2 DWA与BF算法的定量比较Table 2 Quantitative comparison between DWA and BF algorithms算法 收敛精度/m 收敛速度/s DWA 55.8380 73.117048 细菌算法 55.1051 0.24071 根据图2和表2,易知细菌算法比DWA在移动机器人全局路径规划方面有较好的收敛精度和速度,即细菌算法具备较强全局路径规划能力。当然,细菌算法也有自身的一些缺点,如该算法缺乏实时避障能力,很难完全消除各种干扰因素。而在实际环境中,各种不确定因素,如动态障碍物,地图非结构化和噪声等是无法避免的。而DWA的良好动态避障和抗干扰性能刚好可以弥补这种不足,因此,在移动机器人路径规划中引入DWA为其动态避障和提高抗干扰能力提供了一种可能。然后,进行实验验证DWA在具有高斯白噪声图3环境下的局部抗干扰能力。经过对比实验发现,DWA和存在噪声干扰的DWA在静态环境下的路径规划长度分别为16.39 m和16.37 m。易知,DWA具备良好的抗干扰性能。
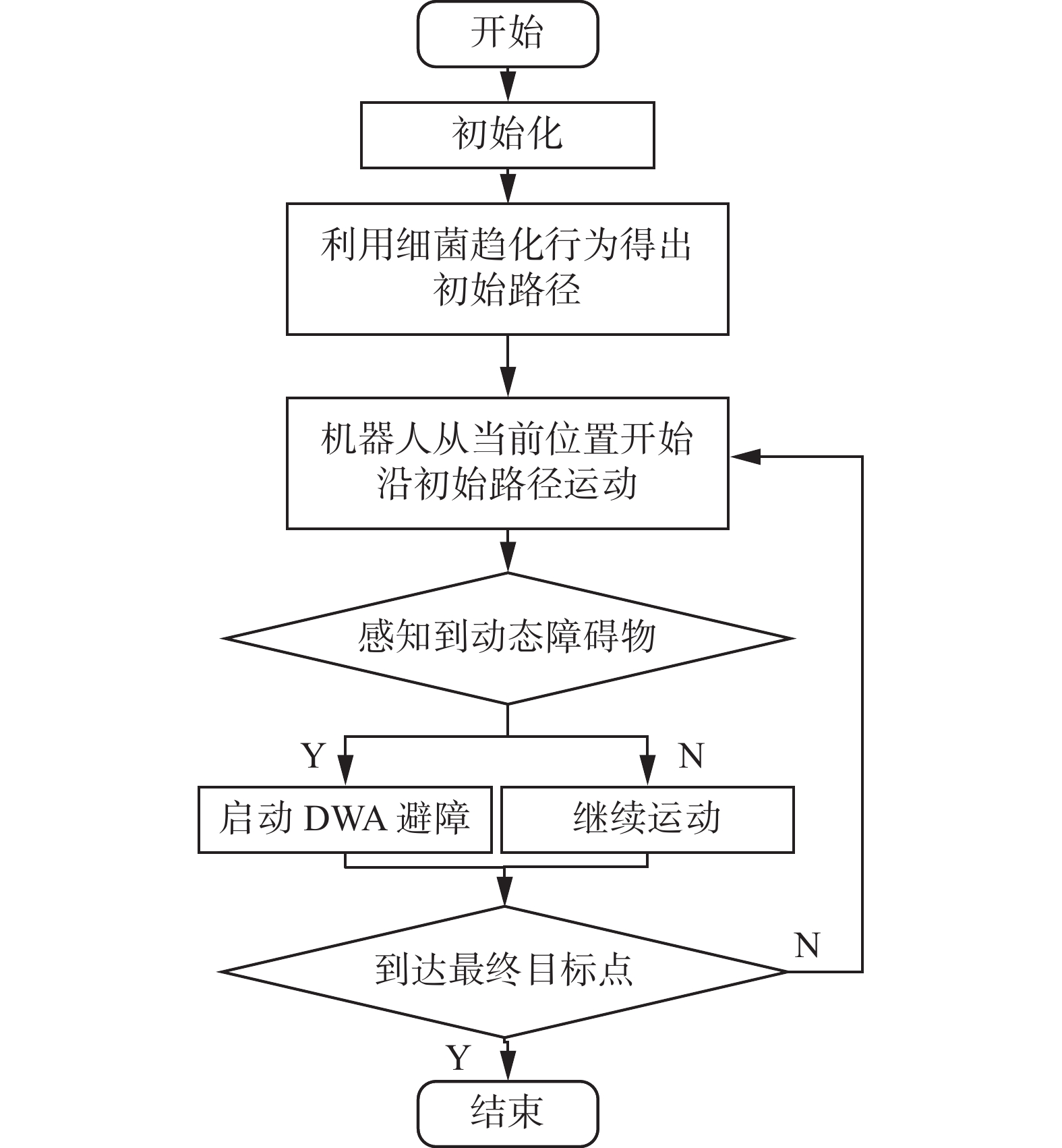
综合以上分析,本文提出一种新的基于自适应动态窗口的改进细菌算法。该算法既继承了改进细菌算法良好的全局收敛能力又具备较强的自适应DWA局部抗干扰动态避障功能。该改进算法主要包括如下5步。
1)各类数值初始化:主要包括移动机器人参数、细菌算法、动态窗口算法和环境信息等初始数据。例如:
$ {\omega _1} $ 、$ {\omega _2} $ 、$ k、b、c $ 、局部目标点${\rm{localgoal}}$ 和障碍物作用半径$ {\delta _k} $ 等。2)在静态环境中,基于改进细菌趋化算法确定初始参考路径
${\rm{ planpath }}$ 。3)基于自身传感器,机器人感知半径为
$ r $ 的周边环境信息,并沿着${\rm{ planpath }}$ 运动。4)移动机器人执行局部滚动策略实现动态避障,产生局部路径。当机器人感知到动态障碍物时,启动DWA开始动态抗干扰避障,将planpath上离机器人当前位置距离为
$ r $ 的点设置为localgoal,滚动前进,直至动态障碍脱离机器人传感范围r。5)确定目标点:以当前局部目标点作为DWA的目标点,当机器人到达目标点后,若该点不是最终目标点,则跳转到步骤3);反之,输出路径结果,算法结束。该算法流程如图4所示。
2. 实验比较分析
2.1 改进细菌算法的仿真
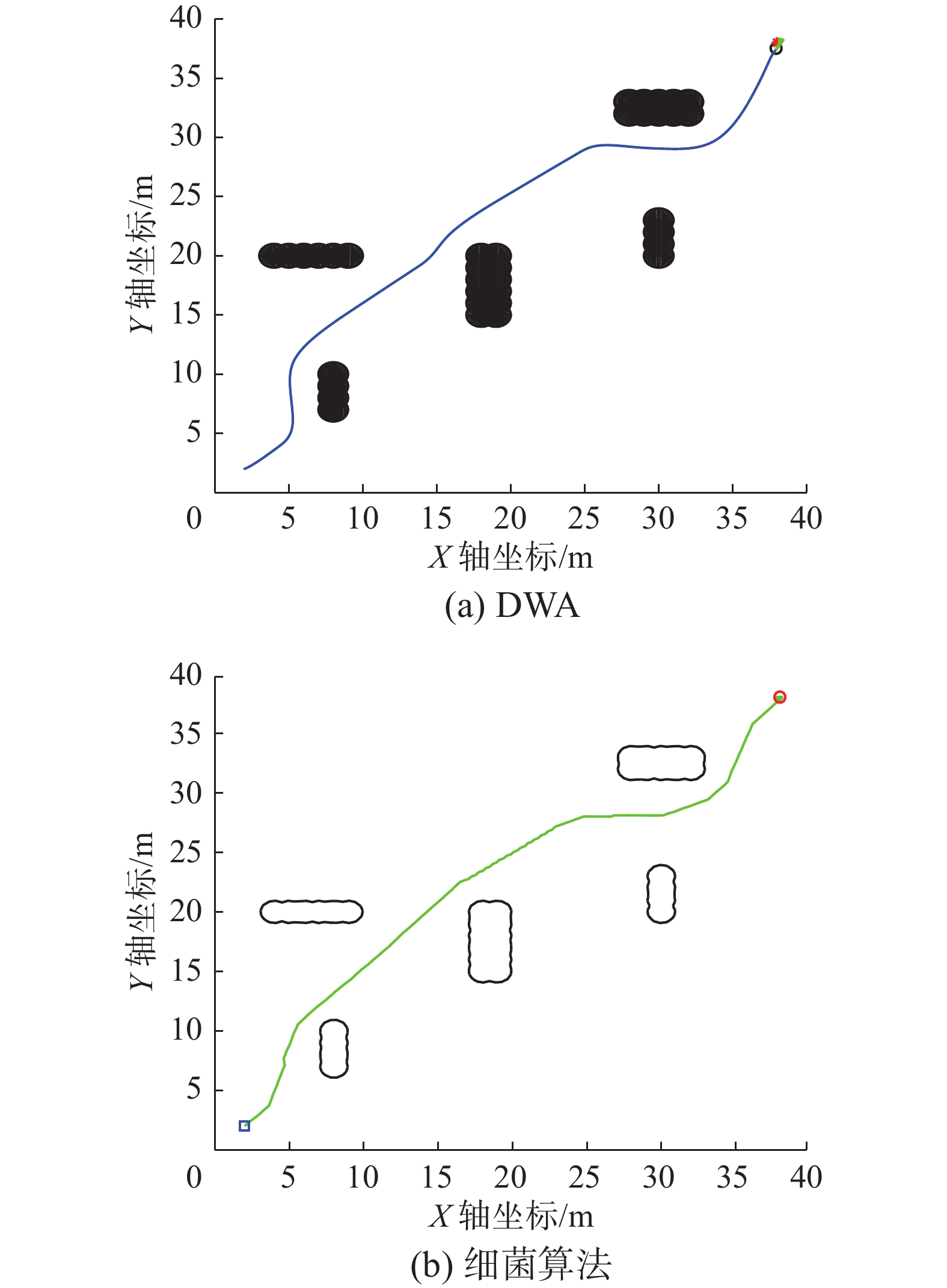
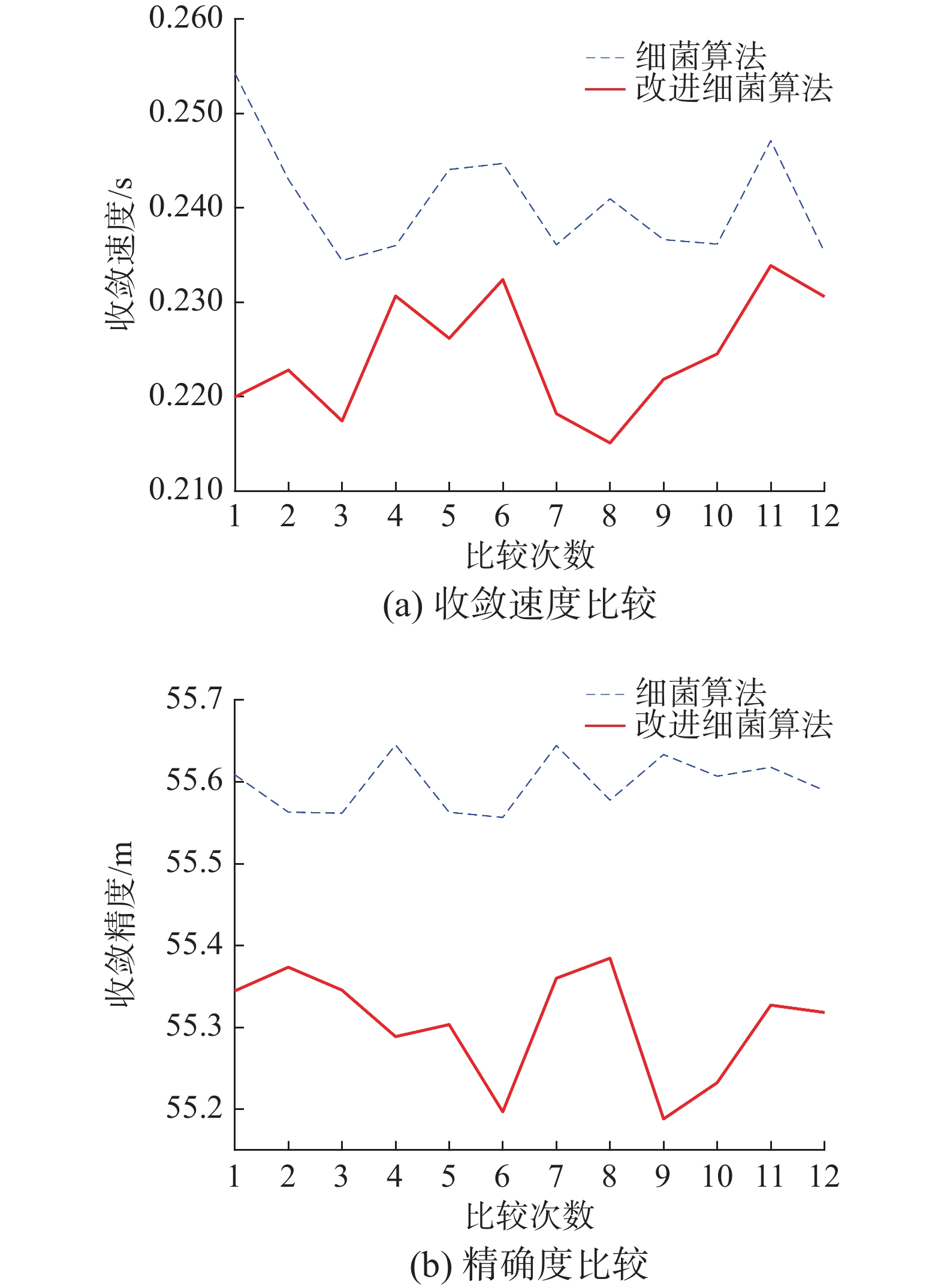
为验证改进算法在移动机器人路径规划中的性能,将改进细菌趋化算法与文献[21]中提出的细菌趋化算法进行比较。路径起点和终点坐标分别设为(2,2)和(38,38)。根据表1,long、middle和short等分段步长分别设为0.3、0.15和0.1。同时,为避免单次实验偶然性,重复进行12次对比实验,实验结果如图5。
图5表明,将改进细菌算法应用于移动机器人路径规划,路径计算速度和精度均优于文献[21]。为突出这种比较效果,定义如下优化率
$ \xi $ :$$ \xi = \frac{{{\text{|}}{\tau _m} - {\tau _o}{\text{|}}}}{{{\tau _o}}} = \frac{{\Delta \tau }}{{{\tau _o}}} $$ (14) 式中:
$ \xi $ 为优化率,$ {\tau _m} $ 为利用改进细菌算法后计算出来的路径长度、消耗时间或迭代次数,$ {\tau _o} $ 为使用标准细菌算法计算出的路径长度、消耗时间或迭代次数。因此,式(14)能直接反映改进算法的优化程度。表3给出了改进细菌算法在路径长度、消耗时间和迭代次数上的优化率。表 3 细菌趋化算法与改进细菌算法的定量比较结果Table 3 Quantitative comparison between the bacterial chemotaxis and the improved bacterial algorithm算法 路径长度/m 消耗时间/s 迭代步数 细菌算法 55.5972 0.24071 545 改进细菌算法 55.3051 0.22445 183 优化率/% 0.53 6.6 66.4 根据表3,与标准细菌算法相比,改进细菌算法在路径规划精度、速度和迭代次数方面分别提高0.53%,6.6%和66.4%。由此可知,改进细菌算法在路径规划精度、速度和迭代次数等方面均有改善,尤其在迭代次数方面提升效果明显。
2.2 基于自适应动态窗口算法移动机器人路径规划
本节将讨论自适应DWA在静态和静动态障碍物并存环境下移动机器人路径规划性能。为简单起见,对障碍物按一定尺寸做膨化处理,即将移动机器人抽象成一质点。设置移动机器人路径规划的起点和终点坐标分别为(0, 0)和(10, 10),动态窗口算法的初始权重设置如表4。
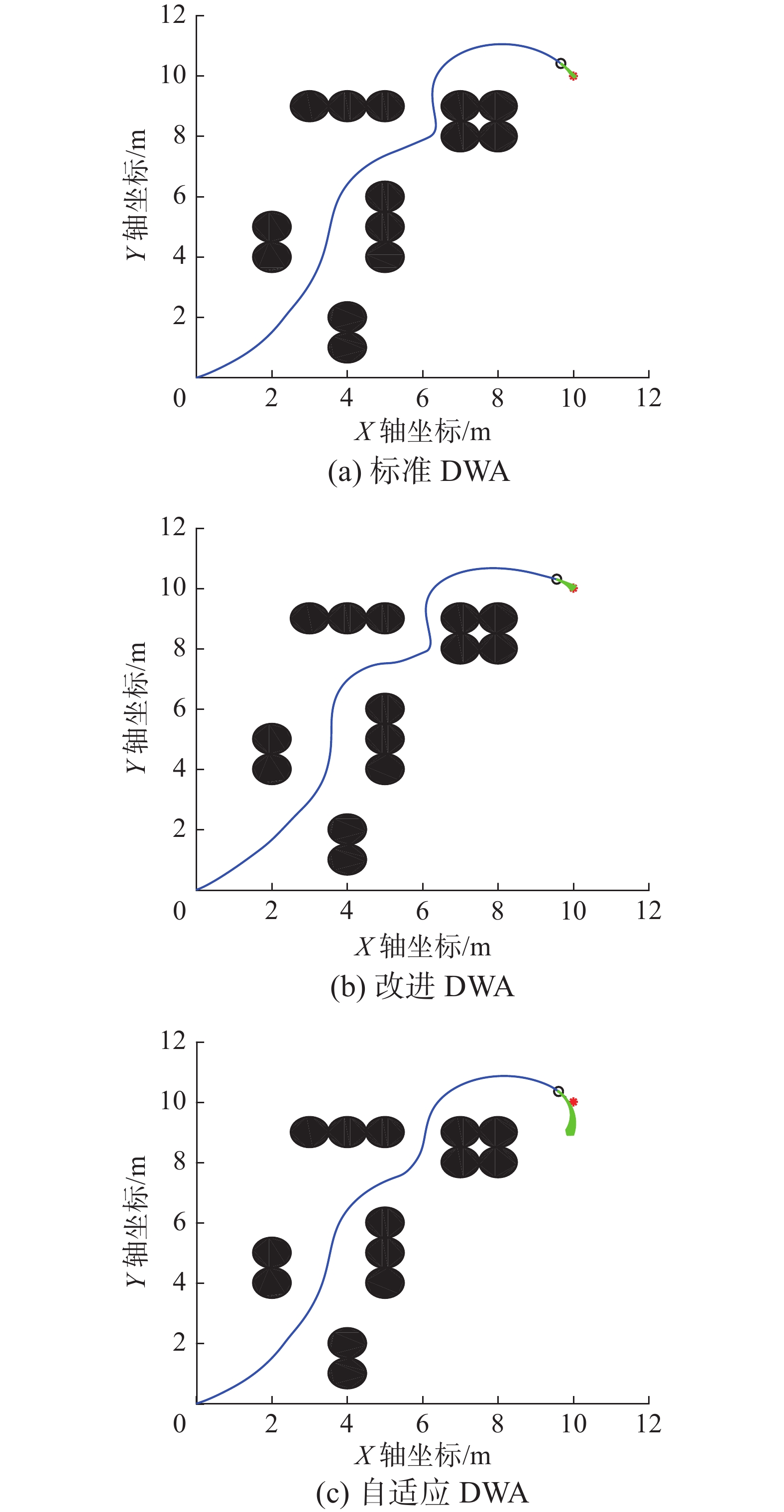
表 4 初始化参数Table 4 Initialization parameter参数名 权重 a 0.1 b 0.4 c 0.1 k 0.1 向前模拟时间/s 3 图6分别表示基于标准DWA、文献[22]改进DWA和自适应DWA 3种算法在静态环境下移动机器人路径规划效果。
由图6可知,与其他两种算法相比,在静态环境中,基于自适应DWA的移动机器人规划出的路径更为平滑。表5给出了移动机器人在3种不同算法下路径规划长度、时间消耗和迭代次数等结果。
表 5 静态环境3种算法下移动机器人路径规划比较Table 5 Comparisons of three algorithms for mobile robot path planning in static environment算法 路径长度/m 消耗时间/s 迭代次数 标准DWA 16.3980 59.7888 463 文献[22]DWA 16.6360 65.8568 514 自适应DWA 16.1200 46.3964 358 为更直观说明问题,根据式(14)中优化率定义,表6给出了自适应DWA相对于标准DWA和文献[22]中DWA在收敛精度、速度和迭代次数等3个方面的优化率。
表 6 自适应DWA机器人路径规划的相对优化率比较Table 6 Comparative optimization rates of path planning for adaptive DWA robots% 算法 路径长度 消耗时间 迭代次数 标准DWA 1.6 22.4 22.7 文献[22]DWA 3.1 29.5 30.3 根据表5~6,在静态环境中,文献[22]中DWA相对于标准DWA在移动机器人路径规划精度和收敛速度方面均不存在明显优势;而自适应DWA相对于标准DWA和文献[22]中DWA在移动机器人路径规划精度上分别提高了1.6%和3.1%,收敛速度分别提高了22.4%和29.5%,迭代次数分别提升了22.7%和30.3%。由此可知,基于自适应DWA的移动机器人路径规划性能在收敛速度、精度和迭代次数方面都有改善,尤其在时间消耗和迭代次数方面优势明显。
实际上,在动态环境下,自适应DWA在移动机器人路径规划方面优势也比较突出。图7分别给出标准DWA、文献[22]中DWA和自适应DWA 3种算法在有动态障碍干扰的复杂环境下移动机器人路径规划效果。
图7表明,移动机器人基于自适应DWA在有动态障碍物干扰复杂环境中得到的路径比标准DWA和文献[22]中DWA得到的路径更为平滑。图7(a)、(b)和(c)也进一步说明,移动机器人基于自适应DWA规划出的路径距离障碍物最小距离比基于标准DWA和文献[22]中DWA得到的相应距离更大一些,此时机器人与障碍物发生碰撞概率更低,因而安全性更好。
表7统计了图7中移动机器人在3种算法下路径长度、时间消耗和迭代次数等数据。
表 7 静态和动态环境下3种算法的比较Table 7 Comparison of three algorithms in static and dynamic environments算法 路径长度/m 消耗时间/s 迭代次数 标准DWA 15.7820 104.7974 748 文献[22]DWA 15.7820 100.4746 748 自适应DWA 15.6400 61.6035 480 类似表6,在有动态障碍物干扰的复杂环境中,得到移动机器人基于自适应DWA相对于其他两种DWA在路径长度、时间消耗和迭代次数等方面的优化率,如表8所示。
表 8 自适应DWA相对优化率的比较Table 8 Comparison of relative optimization rate of self-adaptive DWA% 算法 路径长度 消耗时间 迭代次数 标准DWA 0.9 41.2 35.8 文献[22]DWA 0.9 38.7 35.8 表7~8表明,在有动态障碍物干扰的复杂环境中,文献[22]中DWA相对于标准DWA在路径计算精度上无明显提高,但在收敛时间上有一定优势;而自适应DWA相对于标准DWA和文献[22]中DWA在路径规划精度上均提高0.9%,收敛速度分别提高41.2%和38.7%,迭代次数均提升了35.8%。这就说明即使有动态障碍物干扰,自适应DWA的移动机器人路径规划算法无论在计算精度、收敛速度和迭代次数方面都优于标准DWA和文献[22]中DWA,尤其在时间消耗和迭代次数方面优势比较突出。
综上所述,无论是在静态还是静动态障碍物存在的复杂环境中,自适应DWA的移动机器人路径规划性能比标准DWA和文献[22]中DWA在收敛速度和精度方面都有改善,尤其在收敛速度和迭代次数方面优势明显,并表现出良好的安全性能。
2.3 基于自适应动态窗口改进细菌算法的路径规划效果比较
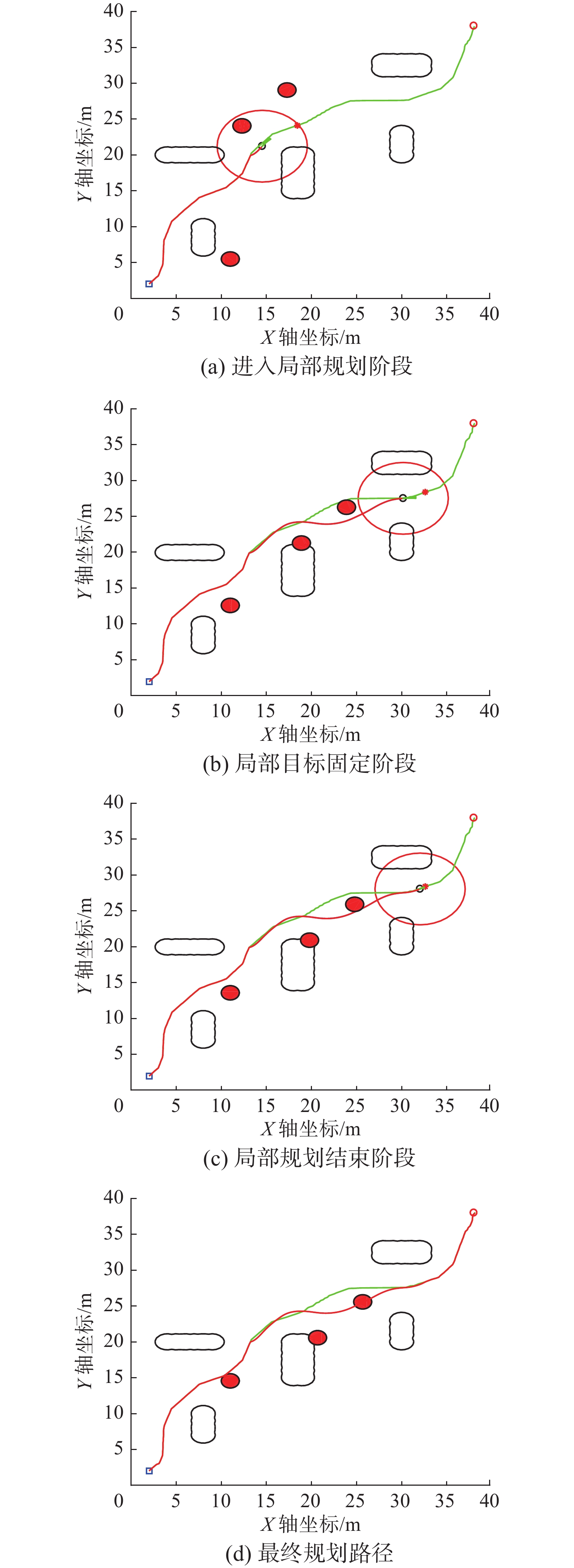
根据图4自适应动态窗口改进细菌算法的流程图,得到机器人避障过程如图8所示。
图8给出基于自适应动态窗口改进细菌算法(local improved window dynamic algorithm and bacteria algorithm,LIDWABA)在各个阶段避障情况。图8(a)表明,当动态障碍物进入机器人感知范围时,移动机器人将启动DWA实现局部滚动避障;图8(b)给出机器人在局部滚动阶段基于DWA的避障效果。图8(c)表明,当动态障碍物脱离机器人传感范围时,局部滚动避障结束,并确定局部目标点。此后,移动机器人向该目标点运动,直至达到该局部目标点,结束DWA。继续重复上述过程,最后得到如图8(d)中红色标注路径。
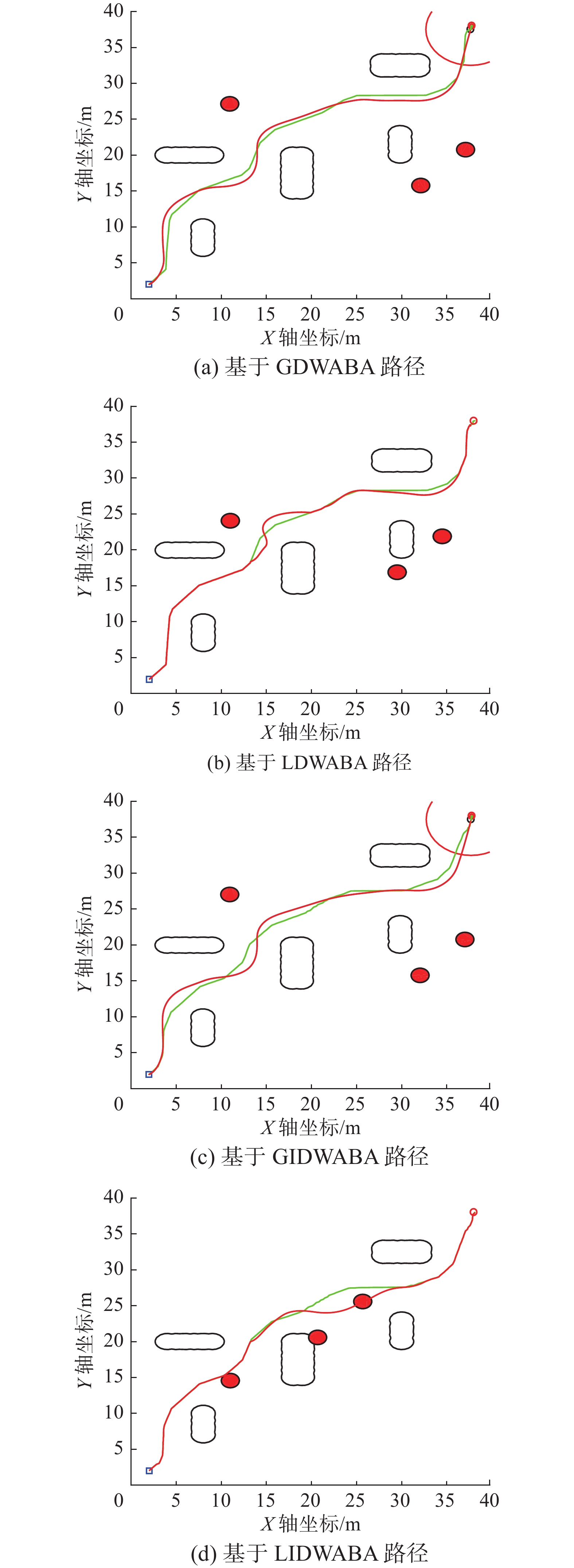
为验证基于自适应动态窗口改进细菌算法(LIDWABA)在机器人路径规划中的良好性能,将该算法与标准动态窗口细菌全局滚动策略(global window dynamic algorithm and bacteria algorithm, GDWABA)、标准动态窗口细菌局部滚动策略(local window dynamic algorithm and bacteria algorithm, LDWABA)和自适应动态窗口改进细菌全局滚动策略(global improved window dynamic algorithm and bacteria algorithm, GIDWABA)算法进行比较。实验结果如图9所示。
表9给出了图9中各种算法下所得路径长度和时间消耗。表9表明,在移动机器人路径规划时,GIDWABA比GDWABA的收敛速度稍慢,但计算精度有一定提高。而LIDWABA与LDWABA相比,路径规划速度和精度都有显著提高。LDWABA与GDWABA相比,虽然精度上有所牺牲,但收敛优势突出。LIDWABA相比GIDWABA,在精度和收敛速度方面都得到了提高,尤其在收敛速度方面优势更为突出。通过GIDWABA、GDWABA、LIDWABA和LDWABA的对比结果可知,在复杂环境中使用基于自适应动态窗口改进细菌算法(LIDWABA)在移动机器人路径规划的速度和精度方面均有明显提高。
表 9 4种算法的路径规划精度与收敛速度对比Table 9 Comparison of path planning precision and convergence speed of four algorithms算法 路径长度/m 消耗时间/s GDWABA 59.0260 166.4868 LDWABA 59.1223 147.5070 GIDWABA 58.7120 168.4537 LIDWABA 55.9108 76.7417 3. 结束语
本文提出一种基于自适应动态窗口的改进细菌算法,该改进算法从分阶段选择步长、使用局部滚动策略和自适应权重确定等方面解释了改进算法的合理性,并用来解决移动机器人在复杂环境中路径规划问题。仿真验证了其可行和优越性。下一阶段,我们将继续研究细菌算法的改进及其在障碍物不规则和三维随机环境中的移动机器人路径规划问题。
-
表 1 不同步长下机器人路径规划精度和收敛速度比较
Table 1 Comparison of accuracy and convergence speed in path planning of robots under different length
步长/m 路径长度/m 消耗时间/s 迭代步数 0.05 55.1499 0.5143 1180 0.1 55.2645 0.4382 771 0.15 55.3486 0.3042 484 0.2 55.4288 0.2358 390 0.25 55.4381 0.2227 361 0.3 55.4839 0.2181 294 0.35 55.7528 0.2161 280 0.4 55.7692 0.2088 219 表 2 DWA与BF算法的定量比较
Table 2 Quantitative comparison between DWA and BF algorithms
算法 收敛精度/m 收敛速度/s DWA 55.8380 73.117048 细菌算法 55.1051 0.24071 表 3 细菌趋化算法与改进细菌算法的定量比较结果
Table 3 Quantitative comparison between the bacterial chemotaxis and the improved bacterial algorithm
算法 路径长度/m 消耗时间/s 迭代步数 细菌算法 55.5972 0.24071 545 改进细菌算法 55.3051 0.22445 183 优化率/% 0.53 6.6 66.4 表 4 初始化参数
Table 4 Initialization parameter
参数名 权重 a 0.1 b 0.4 c 0.1 k 0.1 向前模拟时间/s 3 表 5 静态环境3种算法下移动机器人路径规划比较
Table 5 Comparisons of three algorithms for mobile robot path planning in static environment
算法 路径长度/m 消耗时间/s 迭代次数 标准DWA 16.3980 59.7888 463 文献[22]DWA 16.6360 65.8568 514 自适应DWA 16.1200 46.3964 358 表 6 自适应DWA机器人路径规划的相对优化率比较
Table 6 Comparative optimization rates of path planning for adaptive DWA robots
% 算法 路径长度 消耗时间 迭代次数 标准DWA 1.6 22.4 22.7 文献[22]DWA 3.1 29.5 30.3 表 7 静态和动态环境下3种算法的比较
Table 7 Comparison of three algorithms in static and dynamic environments
算法 路径长度/m 消耗时间/s 迭代次数 标准DWA 15.7820 104.7974 748 文献[22]DWA 15.7820 100.4746 748 自适应DWA 15.6400 61.6035 480 表 8 自适应DWA相对优化率的比较
Table 8 Comparison of relative optimization rate of self-adaptive DWA
% 算法 路径长度 消耗时间 迭代次数 标准DWA 0.9 41.2 35.8 文献[22]DWA 0.9 38.7 35.8 表 9 4种算法的路径规划精度与收敛速度对比
Table 9 Comparison of path planning precision and convergence speed of four algorithms
算法 路径长度/m 消耗时间/s GDWABA 59.0260 166.4868 LDWABA 59.1223 147.5070 GIDWABA 58.7120 168.4537 LIDWABA 55.9108 76.7417 -
[1] 杜永浩, 邢立宁, 蔡昭权. 无人飞行器集群智能调度技术综述[J]. 自动化学报, 2020, 46(2): 222–241. doi: 10.16383/j.aas.c170681 DU Yonghao, XING Lining, CAI Zhaoquan. Survey on intelligent scheduling technologies for unmanned flying craft clusters[J]. Acta automatica sinica, 2020, 46(2): 222–241. doi: 10.16383/j.aas.c170681 [2] 盛亮, 包磊, 吴鹏飞. 启发式方法在机器人路径规划优化中的应用综述[J]. 电光与控制, 2018, 25(9): 58–64. doi: 10.3969/j.issn.1671-637X.2018.09.013 SHENG Liang, BAO Lei, WU Pengfei. Application of heuristic approaches in the robot path planning and optimization: a review[J]. Electronics optics & control, 2018, 25(9): 58–64. doi: 10.3969/j.issn.1671-637X.2018.09.013 [3] LUO Qiang, WANG Haibao, ZHENG Yan, et al. Research on path planning of mobile robot based on improved ant colony algorithm[J]. Neural computing and applications, 2020, 32(6): 1555–1566. doi: 10.1007/s00521-019-04172-2 [4] 孙功武, 苏义鑫, 顾轶超, 等. 基于改进蚁群算法的水面无人艇路径规划[J]. 控制与决策, 2021, 36(4): 847–856. doi: 10.13195/j.kzyjc.2019.0839 SUN Gongwu, SU Yixin, GU Yichao, et al. Path planning for unmanned surface vehicle based on improved ant colony algorithm[J]. Control and decision, 2021, 36(4): 847–856. doi: 10.13195/j.kzyjc.2019.0839 [5] GAO Wenxiang, TANG Qing, YE Beifa, et al. An enhanced heuristic ant colony optimization for mobile robot path planning[J]. Soft computing, 2020, 24(8): 6139–6150. doi: 10.1007/s00500-020-04749-3 [6] MIAO Changwei, CHEN Guangzhu, YAN Chengliang, et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm[J]. Computers & industrial engineering, 2021, 156: 107230. [7] 曹新亮, 王智文, 冯晶, 等. 基于改进蚁群算法的机器人全局路径规划研究[J]. 计算机工程与科学, 2020, 42(3): 564–570. doi: 10.3969/j.issn.1007-130X.2020.03.025 CAO Xinliang, WANG Zhiwen, FENG Jing, et al. Global path planning of robots based on improved ant colony algorithm[J]. Computer engineering & science, 2020, 42(3): 564–570. doi: 10.3969/j.issn.1007-130X.2020.03.025 [8] LI Peng, ZHU Hua. Parameter selection for ant colony algorithm based on bacterial foraging algorithm[J]. Mathematical problems in engineering, 2016, 2016: 6469721. [9] 蒲兴成, 李俊杰, 吴慧超, 等. 基于改进粒子群算法的移动机器人多目标点路径规划[J]. 智能系统学报, 2017, 12(3): 301–309. doi: 10.11992/tis.201606046 PU Xingcheng, LI Junjie, WU Huichao, et al. Mobile robot multi-goal path planning using improved particle swarm optimization[J]. CAAI transactions on intelligent systems, 2017, 12(3): 301–309. doi: 10.11992/tis.201606046 [10] ZHANG Yi, GUAN Guolun, PU Xingchen. The robot path planning based on improved artificial fish swarm algorithm[J]. Mathematical problems in engineering, 2016, 2016: 3297585. [11] MUNI M K, PARHI D R, KUMAR P B. Improved motion planning of humanoid robots using bacterial foraging optimization[J]. Robotica, 2021, 39(1): 123–136. doi: 10.1017/S0263574720000235 [12] LIANG Xiaodan, LI Liangyu, WU Jigang, et al. Mobile robot path planning based on adaptive bacterial foraging algorithm[J]. Journal of Central South University, 2013, 20(12): 3391–3400. doi: 10.1007/s11771-013-1864-5 [13] PANG Bao, SONG Yong, ZHANG Chengjin, et al. Bacterial foraging optimization based on improved chemotaxis process and novel swarming strategy[J]. Applied intelligence, 2019, 49(4): 1283–1305. doi: 10.1007/s10489-018-1317-9 [14] LIAN Jianfang, YU Wentao, XIAO Kui, et al. Cubic spline interpolation-based robot path planning using a chaotic adaptive particle swarm optimization algorithm[J]. Mathematical problems in engineering, 2020, 2020: 1849240. [15] 李元, 王石荣, 于宁波. 基于RGB-D信息的移动机器人SLAM和路径规划方法研究与实现[J]. 智能系统学报, 2018, 13(3): 445–451. doi: 10.11992/tis.201702005 LI Yuan, WANG Shirong, YU Ningbo. RGB-D-based SLAM and path planning for mobile robots[J]. CAAI transactions on intelligent systems, 2018, 13(3): 445–451. doi: 10.11992/tis.201702005 [16] CHANG Lu, SHAN Liang, JIANG Chao, et al. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment[J]. Autonomous robots, 2021, 45(1): 51–76. doi: 10.1007/s10514-020-09947-4 [17] HENKEL C, BUBECK A, XU Weiliang. Energy efficient dynamic window approach for local path planning in mobile service robotics[J]. IFAC-papersonline, 2016, 49(15): 32–37. doi: 10.1016/j.ifacol.2016.07.610 [18] JIN Qibing, TANG Chuning, CAI Wu. Research on dynamic path planning based on the fusion algorithm of improved ant colony optimization and rolling window method[J]. IEEE access, 2021, 10: 28322–28332. [19] CHEN Zheng, ZHANG Youming, ZHANG Yougong, et al. A hybrid path planning algorithm for unmanned surface vehicles in complex environment with dynamic obstacles[J]. IEEE access, 2019, 7: 126439–126449. [20] 黄辰. 基于智能优化算法的移动机器人路径规划与定位方法研究[D]. 大连: 大连交通大学, 2018: 1−123. HUANG Chen. Study on path planning and location of mobile robot based on intelligent optimization algorithm[D]. Dalian: Dalian Jiaotong University, 2018: 1−123. [21] 蒲兴成, 赵红全, 张毅. 细菌趋化行为的移动机器人路径规划[J]. 智能系统学报, 2014, 9(1): 69–75. PU Xingcheng, ZHAO Hongquan, ZHANG Yi. Mobile robot path planning research based on bacterial chemotaxis[J]. CAAI transactions on intelligent systems, 2014, 9(1): 69–75. [22] 封硕, 吉现友, 程博, 等. 融合动态障碍物运动信息的路径规划算法[J]. 计算机工程与应用, 2021, 1(1): 1–8. doi: 10.3778/j.issn.1002-8331.2008-0025 FENG shuo, JI xianyou, CHENG bo, et al. Path planning algorithm based on dynamic obstacle movement information[J]. Computer engineering and application., 2021, 1(1): 1–8. doi: 10.3778/j.issn.1002-8331.2008-0025 [23] AJEIL F H, IBRAHEEM I K, AZAR A T, et al. Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments[J]. Sensors (Basel, Switzerland), 2020, 20(7): 1880. doi: 10.3390/s20071880 [24] WANG Lanfei, KAN Jiangming, GUO Jun, et al. 3D path planning for the ground robot with improved ant colony optimization[J]. Sensors (Basel, Switzerland), 2019, 19(4): 815. doi: 10.3390/s19040815 [25] TULLU A, ENDALE B, WONDOSEN A, et al. Machine learning approach to real-time 3D path planning for autonomous navigation of unmanned aerial vehicle[J]. Applied sciences, 2021, 11(10): 4706. doi: 10.3390/app11104706









































































 下载:
下载: