Knowledge graph representation learning model combining entity description and path information
-
摘要: 知识图谱表示学习方法是将知识图谱中的实体和关系通过特定规则表示成一个多维向量的过程。现有表示学习方法多用于解决单跳知识图谱问答任务，其多跳推理能力无法满足实际需求，为提升多跳推理能力，提出一种融合实体描述与路径信息的知识图谱表示学习模型。首先通过预训练语言模型RoBERTa得到融合实体描述的实体、关系表示学习向量；其次利用OPTransE将知识图谱转化成融入有序关系路径信息的向量。最后构建总能量函数，将针对实体描述和路径信息的向量进行融合。通过实验分析与对比该模型在链路预测任务上与主流知识图谱表示学习模型的性能，验证了该模型的可行性与有效性。Abstract: Knowledge graph representation learning is a process of representing knowledge graph entities and relations in a multidimensional vector through specific rules. Existing representation learning methods are mostly used to solve the single-hop knowledge graph question-and-answer task, but their multi-hop reasoning ability cannot meet the actual demand. To improve the multi-hop reasoning ability, a knowledge graph representation learning model combining entity description and path information is proposed. First, the learning vector of entity and relation representation is obtained using the pre-training language model RoBERTa. Second, OPTransE is used to transform the knowledge graph into a vector integrating the path information of an ordered relation. Finally, the total energy function is constructed to fuse the vectors of entity description and path information. The feasibility and validity of the model are verified by comparing its performance in a link prediction task with that of the mainstream knowledge graph representation learning model.
-
2012年，谷歌公司正式提出知识图谱的概念。作为人工智能应用的关键技术，知识图谱具有清晰的三元组结构，在一个三元组中包含头实体、关系和尾实体，令
$ G $ 表示知识图谱，有$ G \in(E, R, S) $ ，其中$E=\left\{e_{1}, e_{2}, \cdots, e_{\mid{E}\mid}\right\}$ 表示所有实体集合，$R=\left\{r_{1}, r_{2}, \cdots, r_{\mid R\mid}\right\}$ 表示所有关系集合，采用三元组的形式来存储大型知识库的知识信息，可以更方便地融合各个领域的知识[1]。目前，已经出现了众多大规模的知识图谱，诸如Freebase、Wordnet、中文知识图谱OpenKG等。然而，与客观世界相比，这些构建的知识图谱往往是不够完整的，缺失了大量的事实[2]。为缓解数据的稀疏性问题，研究人员提出了知识图谱表示学习，其目的就是将知识图谱中的实体和关系投影到连续低维的向量空间[3]，提升知识图谱上的推理能力 。知识图谱表示学习可以分成三类：几何模型、矩阵分解模型和深度学习模型。几何模型中，最经典的知识图谱表示学习模型是TransE模型[4]，Lin等[5]为了在Trans系列模型的基础之上融入路径信息，提出PTransE[5]模型。矩阵分解模型中，DistMult模型[6]将所有关系强制表示成对角矩阵，这减少了要学习的参数空间，从而使模型更容易训练；CompIEx模型[7]是一种基于复数的知识图谱表示学习，把握了知识图谱中的对称和非对称关系。深度学习模型中，ConvE模型[8]首次引入2D卷积操作来执行链接预测任务，且将该模型扩展用于复杂知识图谱中；ConvKB模型[9]使用了卷积神经网络，将每个三元组表示为三列矩阵并输入进卷积层，最后通过点积将特征向量与权重向量相乘得到分数。
目前，上述大多数知识图谱表示学习及推理模型都仅考虑知识图谱中单一三元组信息[10]，然而，针对复杂问题，一般需要包含多个三元组的长路径进行多跳推理。本文针对如何增强知识图谱表示学习模型的多跳推理能力的问题，研究利用RoBERTa[11]模型对知识图谱及对应的实体描述进行向量映射，结合使用OPTransE[12]获取基于路径信息表示的实体和关系路径向量，最后将二者融合进行知识图谱表示学习模型的构建，提升基于多跳知识图谱的推理能力。
1. 表示学习模型架构
知识图谱最重要的缺陷之一是它们往往不是完整的，不完整的知识图谱造成长路径中大量三元组的缺失，所以多数模型只能解决单跳任务，极大降低了模型在大型知识图谱中的有效性与可移植性。研究发现，实体通常都有对应的实体描述信息，并且实体间也存在大量的路径信息，其中包含丰富的语义，这些额外信息，能够显著改善长路径下建模难的问题，提升推理能力。
因此，为了提升知识图谱表示学习模型的多跳推理能力，模型应做到以下两点：
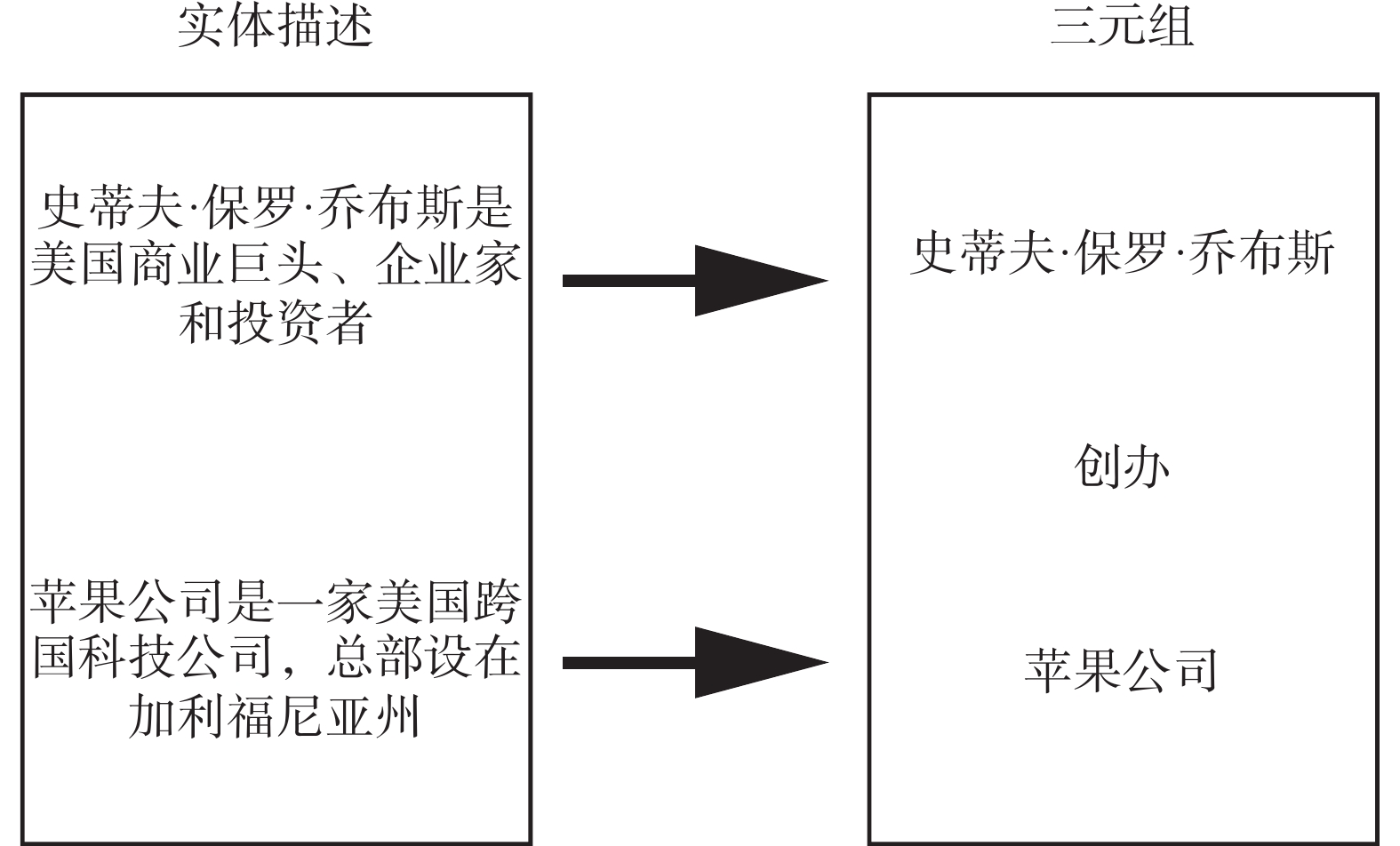
1)充分利用实体描述信息。在执行多跳推理的过程中，仅从知识图谱的结构信息来学习推理是不够的。很多知识图谱中都存在对实体的简洁描述，如图1是一个三元组（史蒂夫·保罗·乔布斯，创办，苹果公司）中两个实体的简要描述。通过在知识图谱表示学习中融入实体描述信息，让实体向量的表征更加符合事实，增加了多跳推理的信息来源。
图 1 知识图谱实体描述Fig. 1 Entity description of knowledge graph
下载:
全尺寸图片
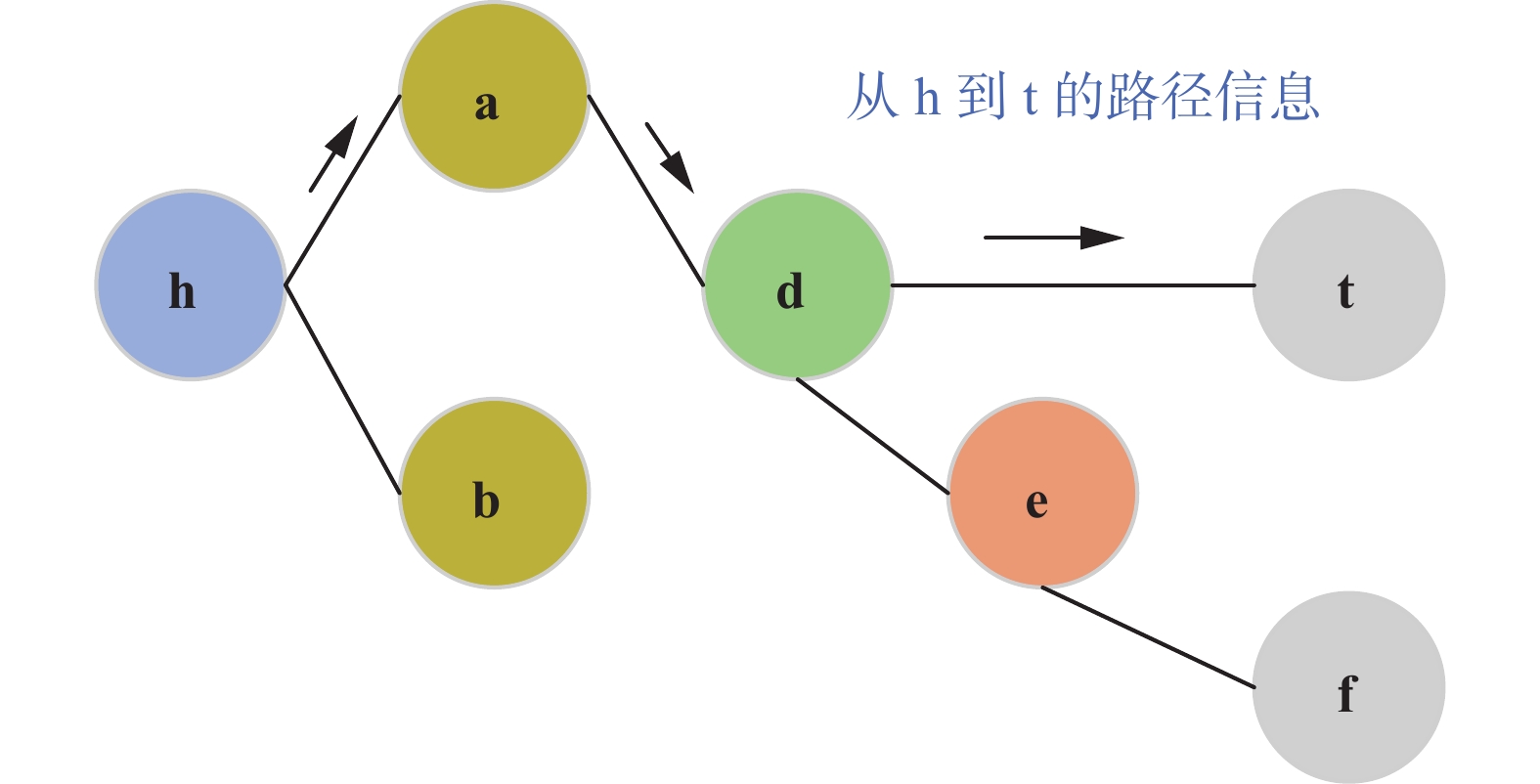
2)多跳推理是长路径问题，表示学习模型不能只考虑直接关系，还应可表征多个三元组的长路径信息，如图2所示。
图 2 知识图谱路径信息Fig. 2 Knowledge graph path information下载:
全尺寸图片
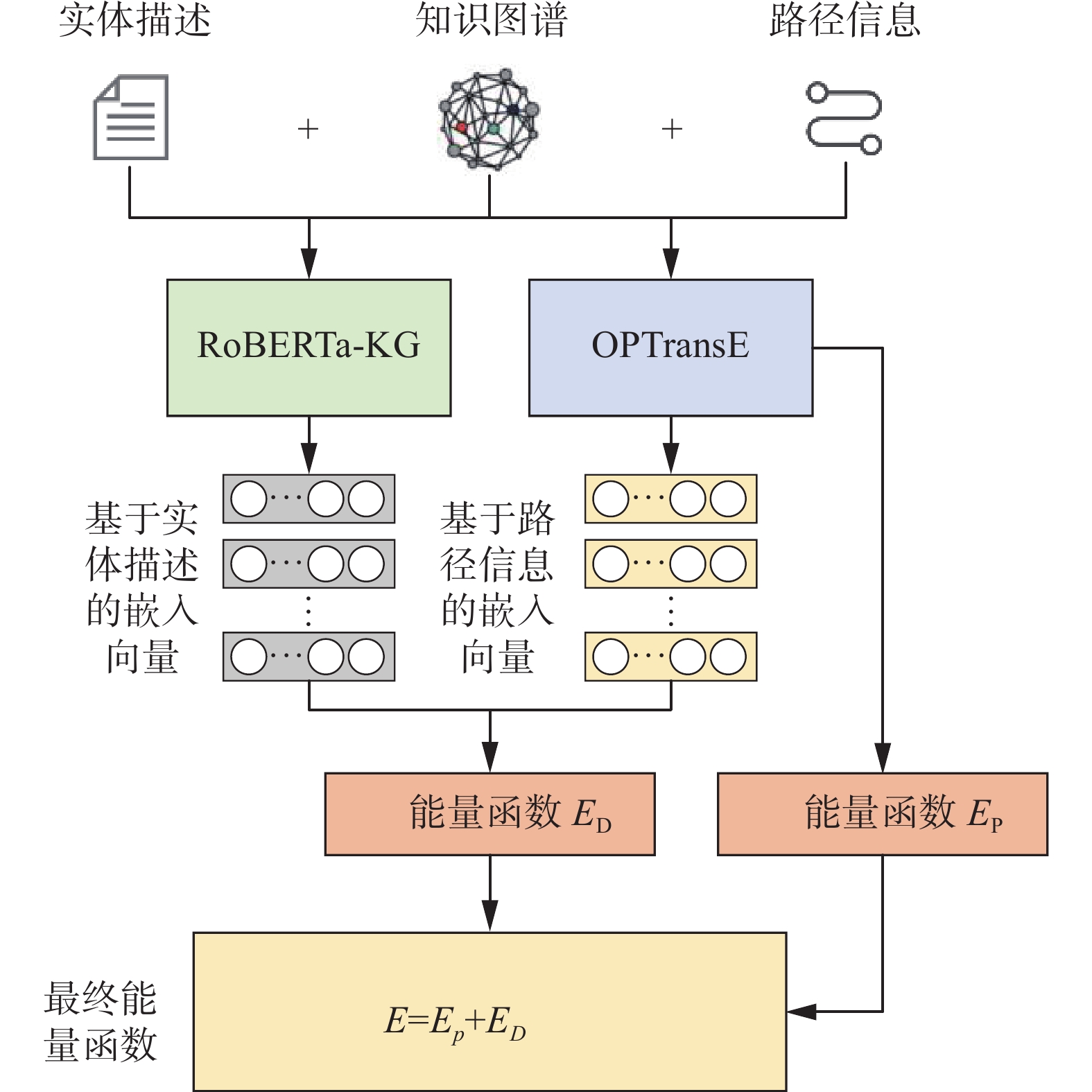
知识图谱是由多个实体与实体间的连接关系组合而成，两个相距较远的实体会通过一条包含多个关系的长路径相连，这条长路径中隐含了非常多的语义信息。在知识图谱表示学习中融入路径信息正是提升多跳推理能力的关键。本文知识图谱表示的学习模型如图3所示。通过设计两个Encoder端实现基于实体描述与路径信息的知识图谱表示学习的融合，第一个Encoder端用于执行基于实体描述的知识图谱表示学习，第二个Encoder端用于训练模型融合路径信息，最后将二者通过构建总能量函数进行融合。
图 3 融合实体描述与路径信息的知识图谱表示学习模型架构Fig. 3 Architecture of knowledge graph representation learning model combining entity description and path information下载:
全尺寸图片
模型训练过程如下：
1)将知识图谱与实体描述输入进微调过的预训练语言模型RoBERTa[11]中，通过自注意力机制和前馈神经网络训练学习，在最后一层输出融合实体描述的实体、关系表示学习向量。
2)同样利用OPTransE[12]将知识图谱转化成融入有序关系路径信息的向量，输出所有训练集三元组的能量值
$ E_{P} $ 。3)结合步骤1)、2)输出的训练向量，计算出能量值
$ E_{D} $ ，与$ E_{P} $ 相加，每个三元组的总能量值定义为$ E_{P} $ +$ E_{D} $ ，然后采用梯度下降来优化三元组的向量表示，目标是最小化总能量值。2. 基于实体描述的表示学习方法
为充分利用实体描述信息进行表示学习，选择预训练语言模型RoBERTa[11]来模拟三元组之间的合理性，由于RoBERTa初始模型并不支持三元组文本序列的直接输入，需要对模型进行微调后，再作为第一个Encoder。
2.1 三元组建模
为减少输入过程中的语义损失，选择直接将三元组
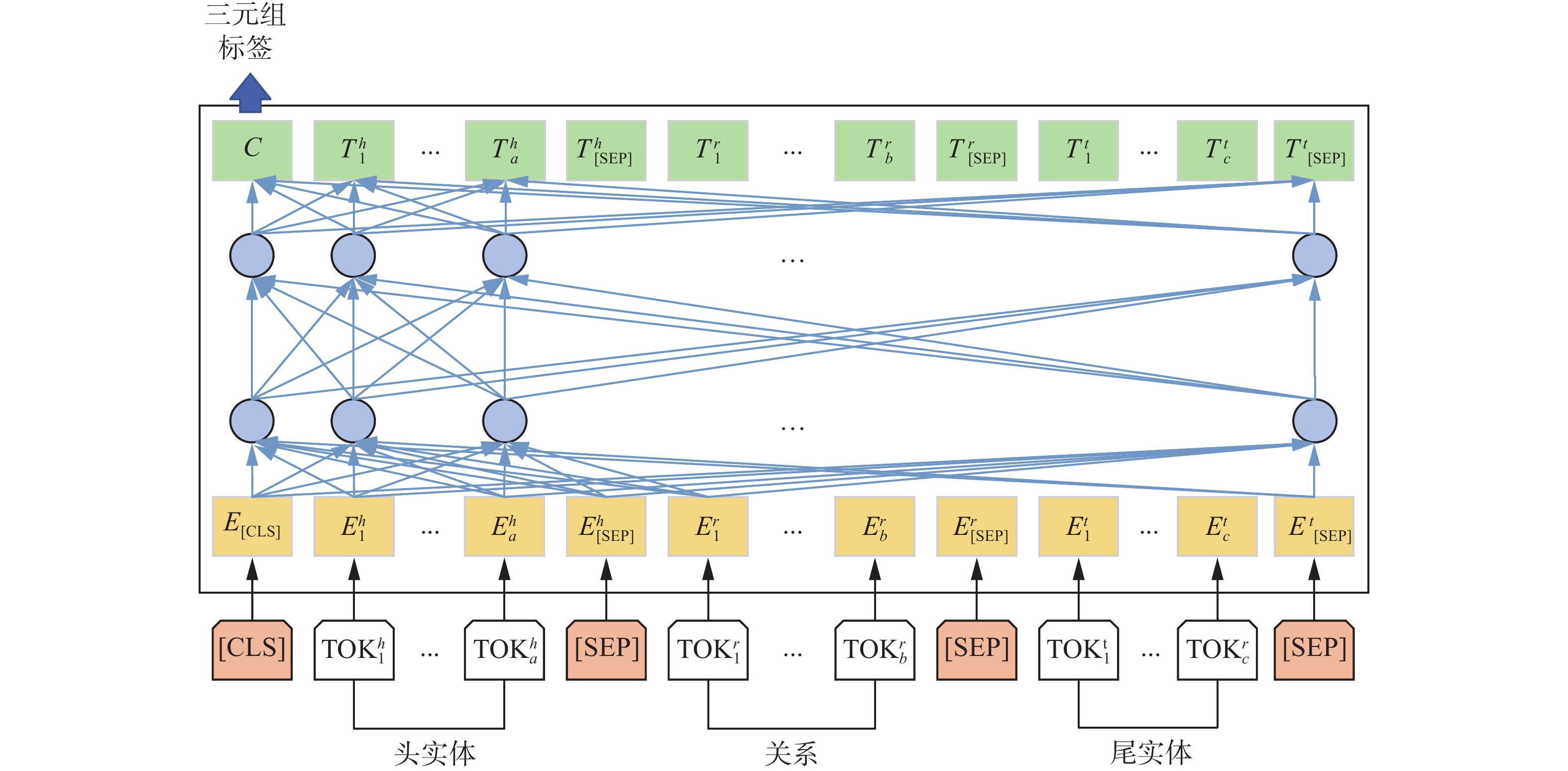
$ (h, r, t) $ 打包成一个输入序列导入RoBERTa模型中，最后利用特殊分类标签[CLS]的隐态输出向量$ {\boldsymbol{C}} $ 来预测三元组是否正确。微调后的RoBERTa结构如图4所示。
图 4 微调后的RoBERTa结构Fig. 4 Fine-tuned structure of RoBERTa下载:
全尺寸图片
使用[CLS]分类标签和[SEP]分割标签，将模型调整为可以接收（头实体–关系–尾实体）形式的文本序列输入。调整后的模型输入具体如下：
1)假定三元组（头实体–关系–尾实体），在每个输入序列的头部位置设置一个特殊的分类标签[CLS]；
2)将头实体或者是对应的实体描述表示成一个包含a个token的句子
${\rm{T O K}}_{1}^{h},\;{\rm{T O K}}_{2}^{h},\; \cdots, {\rm{T O K}}_{a}^{h}$ ；3)将关系表示成一个包含b个token的句子
${\rm{T O K}}_{1}^{r} ,\; {\rm{T O K}}_{2}^{r} ,\cdots,{\rm{T O K}}_{b}^{r}$ ；4)将尾实体或者是对应的实体描述同样表示成一个包含c个token的句子
${\rm{T O K}}_{1}^{t},\;{\rm{T O K}}_{2}^{t},\cdots,{\rm{T O K}}_{a}^{t}$ ；5)在实体与关系之间加入特殊分割标签[SEP]。
分割后的token是自然语言输入进RoBERTa模型的最小单位，对于中文，可以理解为中文的字；对于英文，由于存在时态等表示，所以在输入模型前还需要将英文词汇切分为更细粒度的单位。token是自然语言的形式，在输入模型前需要将其转化成一个计算机能够识别的向量，由三部分组成：①从预训练模型中找到各个token的初始嵌入Tokend Embedding；②由于[SEP]分隔的不同元素具有不同的Segment Embedding，头实体和尾实体同属于实体类别，采用相同的类型嵌入
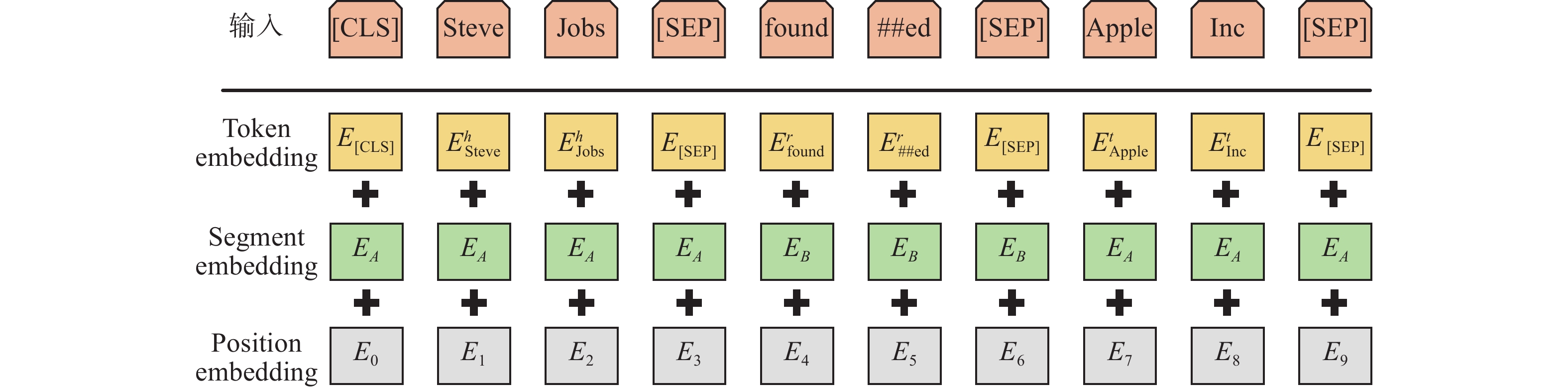
$ e_{A} $ ，而关系选用另一种类型嵌入$ e_{B} $ ；③同一位置的不同token具有相同的位置嵌入Position Embedding。用
$ E $ 表示Input embedding，模型输入过程如图5所示。每个输入的向量表征都是由初始嵌入、类型嵌入和位置嵌入三部分相加构成。在完成三元组建模后，下一步需要对RoBERTa模型内部进行微调。
图 5 模型输入过程Fig. 5 Model input process下载:
全尺寸图片
2.2 RoBERTa模型内部微调
RoBERTa是一个典型的双向编码模型，采用多个双向的Transformer Encoder block[11]进行连接，Transformer能彻底地提取上下文关系，基于多头自注意力机制对文本进行建模，使得每个词都能融合整个句子的信息。自注意力机制的定义如下：
从每个编码器的输入向量（每个单词的词向量）中生成3个向量：查询向量
$ \boldsymbol{Q}_i $ 、键向量$ \boldsymbol{K}_{i} $ 和值向量${\boldsymbol{V}}_{i}$ 。令在第$ i $ 个头的自注意力机制向量为$ \boldsymbol{X}_{i} $ ，$ W^{Q} $ 、$ W^{K} $ 与$ W^{V} $ 为权重值，分别根据按照式（1）、（2）和（3）计算出${\boldsymbol{V}}_{i}、{{\boldsymbol{K}}}_{i}$ 与$ \boldsymbol{Q}_i $ ，即$$ \boldsymbol{V}_{i}=W^{V} \boldsymbol{X}_{i} $$ (1) $$ \boldsymbol{K}_{i}=W^{K} \boldsymbol{X}_{i} $$ (2) $$ {\boldsymbol{Q}}_{i}=W^{Q} X_{i} $$ (3) 最后根据
${\boldsymbol{ V}}_{i}、{{\boldsymbol{K}}}_{i}$ 与$ \boldsymbol{Q}_i $ ，得出表示学习向量$ \boldsymbol{X}_{i} $ 的归一化指数函数：$$ \begin{aligned} \boldsymbol{Y}_{i}=A\left({\boldsymbol{Q}}_{i}, {\boldsymbol{K}}_{i}, {\boldsymbol{V}}_{i}\right) =S_{o}\left(\frac{{\boldsymbol{Q}}_{i} \boldsymbol{K}_{i}^{\mathrm{T}}}{\sqrt{{d}_{{k}}}}\right) {\boldsymbol{V}}_{i} \end{aligned} $$ 式中：A表示自注意力Attention，
$ S_{o} $ 表示归一化指数函数softmax；$ d_{k} $ 为$ \boldsymbol{Q}_i $ 维数；$\boldsymbol{K}_{i}^{{\rm{T}}}$ 为$ \boldsymbol{K}_{i} $ 的转置。在多头注意机制下，在每一个注意力头上都重复上述操作，通过不同的注意力头得到多个特征表示。将这些多头的输出特征向量进行拼接，乘上一个权重矩阵，再通过一个全连接层来降维。
通过多头注意机制后，在每个编码器中的每个子层（自注意力、前馈网络）的周围都有一个残差连接，并且都跟随着一个层标准化函数步骤。层归一化的操作如为
$$ Y=L\left(\left[\boldsymbol{Y}_{1} \boldsymbol{Y}_{2} \cdots \boldsymbol{Y}_{h}\right] W^{Y}+X\right) $$ $$ O=L\left(r\left(Y W_{1}^{o}+b_{1}^{o}\right) W_{2}^{o}+b_{2}^{o}+Y\right) $$ 式中：Y为注意力头输出；L为层标准化函数LayerNormalize；r为激活函数Relu；
$ W $ 和$ b $ 为可调参数；$\left[\boldsymbol{Y}_{1} \boldsymbol{Y}_{2} \cdots \boldsymbol{Y}_{h}\right]$ 表示对多头输出进行拼接；$O= [\boldsymbol{o}_{1} \boldsymbol{o}_{2} \cdots \boldsymbol{o}_{n}]$ 为一个编码块的输出，这个输出同样作为下个编码块的输入，之后以此类推，直到最后一个编码块的输出结果作为整个Transformer的输出。为了执行三元组合理性预测任务，本文在原RoBERTa模型的基础之上加入了一个新的参数，即分类变换矩阵
${\boldsymbol{W}}^{\prime}$ ，令特殊标签[CLS]的最终隐态输出向量为${\boldsymbol{C}}$ 。三元组$ \tau=(h, r, t) $ 的得分函数为$$ S_{\tau}=f(h, r, t)=S_{I}\left({\boldsymbol{C W}}^{\top}\right) $$ 式中：
$ S_{I} $ 为激活函数Sigmoid，$ S_{\tau} \in[0,1] $ 是一个一维向量，用于存放当前批次的三元组正确的概率。通过公式（8）设计出优化用的损失函数，损失函数的类型选用交叉熵损失函数。给定正样本（正确三元组）集合${D}^{+}$ 与负样本（错误三元组）集合$ {D}^{-} $ ，计算三元组与$ S_{\tau} $ 的损失函数如下：$$ \mathcal{L}=-\sum_{\tau \in\left({D}^+\cup {D}^-\right)}\left(y_{{r}} \ln \left(S_{\tau}\right)+\left(1-y_{\tau}\right) \ln \left(1-S_{\tau}\right)\right) $$ 式中：
$y_{\tau} \in\{0,1\}$ 为三元组的标号，标志着该三元组为正样本还是负样本。负样本的产生是通过简单地替换法，随机用知识库中的某个实体$ h^{\prime} $ 或者$ t^{\prime} $ 来替换正确的三元组$(h, r, t) \in {{D}}^{+}$ ：$$ \begin{aligned} {{D}}^{-}=\left\{\left(h', r, t\right) \mid h' \in {{E}} \wedge h' \neq h \wedge\left(h', r, t\right) \notin {{D}}^+\right\} \\ \cup\left\{\left(h, r, t'\right) \mid t' \in {{E}} \wedge t' \neq t \wedge\left(h, r, t'\right) \notin {{D}}^+\right\} \end{aligned} $$ 式中
${E}$ 为知识图谱的实体集合。3. 融合方法
在知识图谱表示学习中融入关系路径信息可以很好提升多跳推理能力，本文基于OPTransE[12]方法实现了基于路径信息的知识图谱表示学习。
基于路径信息的表示学习模型分为两个步骤：
1)输入模型前，考虑到关系路径的顺序关系，分别将关系
$ r $ 对应的头实体$ { h } $ 和尾实体$ t $ 投影到由两个不同的投影矩阵${\boldsymbol{W}}_{r,1}$ 与${\boldsymbol{W}}_{r,2}$ 确定的超平面上。2)通过两层池化策略融合来自不同路径的信息，第一层的池化策略目标是在所有
$ {i} $ 步路径中选择与$ r $ 最匹配的路径；第二层是为了融合来自不同长度路径的信息，从不同长度的路径中提取非线性特征，构造出三元组的总能量函数$ E_{P} $ 。通过2步得到第2节中的实体、关系表示学习向量与本节中的三元组总能量函数。下面通过联合学习二者的能量函数将三元组信息与路径信息和实体描述中的丰富信息相结合[13]。定义总体能量函数：
$$ E=E_{P}+E_{D} $$ (4) 式中：
$ E_{p} $ 是基于OPTransE得出的基于路径信息表示的总能量函数；$ E_{D} $ 是基于实体描述的能量函数。为了通过融合方法相互促进两个编码端的表示学习，需要将它们都嵌入到同一向量空间中。$ E_{D} $ 定义为$$ E_{D}=E_{D D}+E_{D P}+E_{P D} $$ 式中：
$E_{{DD}}=\left\|h_{d} {\boldsymbol{M}}_{r}+r-t_{d} {\boldsymbol{M}}_{r}\right\|$ ，$ E_{{DD}} $ 中的$ h_{d} $ 与$ t_{d } $ 都是基于实体描述的头尾实体表示，r表示关系；$E_{{DP}}= \left\|h_{d} {\boldsymbol{M}}_{r}+r-t_{r}\right\|$ ，$ E_{D P} $ 中的$ h_{d} $ 是基于实体描述的头实体表示，$ t_{r} $ 是基于路径信息的尾实体表示；$E_{P D}= \left\|h_{r}+r-t_{d} {\boldsymbol{M}}_{r}\right\|$ ；${\boldsymbol{M}}_{r}$ 是转置矩阵；$ E_{P D} $ 中的$ h_{r} $ 是基于实体描述的头实体表示，$ t_{d } $ 是基于路径信息的尾实体表示。最后选用基于边际的损失函数进行模型训练，其定义为
$$ L=\sum_{\substack{\left(h, r, t\right) \in T \\\left(h', {r'}, t'\right) \in T'}} \max \left(\gamma+E(h, r, t)-E\left({h'}, {r'}, {t'}\right), 0\right) $$ 式中：
$ \gamma $ 是正负样本集的边界参数，$ E(h, r, t) $ 是式(4)定义的总能量函数；$ T $ 是由正确的三元组集合$ (h, r, t) $ 构成的训练集。$ T'$ 是由错误的三元组集合$ \left(h^{\prime}, r^{\prime}, t^{\prime}\right) $ 构成的负样本集[13]，R表示全体关系集合，$ T^{\prime} $ 定义为$$ \begin{gathered} T^{\prime}=\left\{\left(h^{\prime}, r, t\right) \mid h^{\prime} \in E\right\} \cup\left\{\left(h, r, t^{\prime}\right) \mid t^{\prime} \in E\right\} \cup\\ \left\{\left(h, r^{\prime}, t\right) \mid r^{\prime} \in R\right\} ,\quad (h, r, t) \in T \end{gathered} $$ 4. 实验对比与分析
4.1 实验环境与参数
1)数据集
本文在基准知识图谱数据集FB15K、FB15k-237和WN18RR进行实验。WN18RR、FB15K和FB15k-237的测试集中都只包含正确的三元组，可用于进行链路预测。在实体描述方面，WN18RR使用WordNet的synsets定义作为实体描述。对于FB15k-237和FB15K，使用了Xie等[14]所做的实体描述。表1是相关数据集统计数据信息。
表 1 各数据集的统计数据信息Table 1 Statistical data information for each dataset数据集 #Ent #Rel #Train #Dev #Test FB15K 14951 1345 483142 50000 59071 WN18RR 40943 11 86835 3034 3134 FB15k-237 14541 237 272115 17535 20466 2)对比基准模型
本文将融合实体描述与路径信息的知识图谱表示学习模型与多种知识图谱表示学习方法进行对比，根据实现方法分成3类：①几何模型，包括TransE、PtransE、RotatE、OPTransE和HAKE；②矩阵分解模型，包括DistMult、SimplE、ComplEx、TuckER和RPJE；③深度学习模型，包括ConvE、ConvKB、ConvR、R-GCN、VR-GCN、R-GCN+、KBGAN和InteractE。这些对比模型以2018年之后提出的新模型为主。通过与基准模型在WN18RR、FB15K和FB15k-237数据集上进行实验对比，保证实验结果的可靠性与严谨性。
3)参数设置
针对模型的两个Encoder分别做了不同的参数设置。①融合实体描述的Encoder1使用具有12个layer、12个self attention 头和表示学习维度768的RoBERTa预训练语言模型作为方法的基础。微调过程中设置的参数如下：batch size=32，learning rate=5×10−5，dropout rate=0.1，本文也尝试了这些超参数的其他组合，但没有太大差异。②融合路径信息的Encoder2参考了OPTransE[15]中的最优参数配置，learning rate=0.0001，余量γ=5.0，γ1= 5.0，γ2= 5.5，平衡因子λ= 0.01。链路预测过程中，参数选择为对1个正样本（正确三元组）采样5个负样本（错误三元组），实验结果最优。
4）实验环境
实验软件环境为：操作系统 Ubuntu 18.04 LTS 64Bit，Python，Pytorch。硬件环境：AMD Ryzen 5 3600 6-Core Processor，内存大小为16 GB，显卡NVIDIA Geforce GTX 1660 Ti。
4.2 单跳链路预测对比实验结果及分析
4.1节介绍了经典的用于评估知识图谱表示学习模型的链路预测任务。单跳链路预测指的是，通过头实体
$ h $ 和关系$ r $ ，来预测与头实体$ h $ 直接通过关系$ r $ 相连的尾实体$ t $ ，即仅选用单跳数据对模型进行学习训练和测试。本文将在FB15K、FB15k-237和WN18RR 3个数据集上对比分析本文模型与其他基准模型的表现。具体实验结果分别如表2、3和4所示。表 2 WN18RR单跳链路预测结果对比Table 2 Comparison of WN18RR single-hop link prediction results模型 Mean Rank MMR Hits@10 TransE[16] 3384 0.226 0.505 DistMult[6] 5110 0.43 0.49 ComplEx[7] 5261 0.44 0.51 KBGAN[17] 3542 0.214 0.472 ConvE[8] 4187 0.43 0.52 ConvKB[9] 3324 0.249 0.524 RotatE[18] 3340 0.476 0.571 ConvR[19] 4237 0.475 0.537 TuckER[20] — 0.470 0.526 HAKE[21] 4619 0.497 0.582 InteractE[22] 5203 0.463 0.528 本文模型 3351 0.482 0.583 表 4 FB15K单跳链路预测结果对比Table 4 Comparison of FB15K single-hop link prediction results表2、3和4分别给出了在WN18RR、FB15k-237和FB15K数据集上的多个知识图谱表示学习模型的链路预测结果。表中的“—”为缺少相关实验结果。从表2~4可以观察到：
1)本文提出的融合实体描述与路径信息的知识图谱表示学习模型，在单跳链路预测实验中均取得了较好的结果。3个指标中Hits@10表现最好，在3个数据集上均达到最优。Mean Rank与MMR指标表现稍差，仅次于较新的HAKE、InteractE和RPJE。
2)引入外部信息辅助表示学习的模型均比经典的TransE模型效率高。其原因是，外部信息可以作为对知识图谱的有利补充，无论是实体描述等文本信息、图像信息、路径信息还是逻辑规则都可以从别的方面对知识图谱进行完善，使表示学习向量对知识的学习程度更深更精确。
3)本文模型、PtransE、OPTransE和RPJE等融合了路径信息的方法，在Hits@10指标上的都表现良好。这些模型通过融合了路径结构信息，会根据路径找到预测实体，为它们和附近的邻居实体都赋予较低的能量值，说明在知识图谱中，融入路径信息也是提升正确预测实体的准确率的可行方法。
4.3 多跳链路预测对比实验结果及分析
为了评估模型的多跳推理能力，本节参考PtransE[5]，在FB15K知识图谱中遍历所有的头实体
$ e_1 $ ，存储所有对应的关系和尾实体$ e_{2} $ ，再以$ e_{2} $ 为头实体开始遍历、存储，就能得到2-hop的数据，3-hop的关系路径同理。获取相应的多跳数据之后，接下来开始进行多跳链路预测实现。具体实验结果如表5和6所示。表 5 FB15K-2hop多跳链路预测结果对比Table 5 Comparison of FB15K-2Hop multi-hop link prediction results数据集 评估指标 Mean Rank Hits@10 PTransE (ADD, 2-hop) 54 0.834 PTransE (MUL, 2-hop) 67 0.777 PTransE (RNN, 2-hop) 92 0.822 OPTransE (2-hop) 47 0.859 本文模型 (2-hop) 41 0.871 表 6 FB15K-3hop多跳链路预测结果对比Table 6 Comparison of FB15K-3Hop multi-hop link prediction results数据集 评估指标 Mean Rank Hits@10 PTransE (ADD, 3-hop) 58 0.846 OPTransE (3-hop) 50 0.855 本文模型 (3-hop) 47 0.886 表5和6分别展示了PTransE、OPTransE和本文模型在FB15K数据集上的2-hop和3-hop链路预测结果。粗体数字表示在所有方法中最好的结果。其中PTransE的评估结果来自它的原始论文，ADD、MUL和RNN表示3种合并路径关系的方法；OPTransE的结果是由多次实验后得出的平均结果。
1）OPTransE和本文模型都比PTransE模型的效果好。这是由于PTransE模型在进行路径信息融合时，只是对路径上的关系做向量计算，没有考虑到关系顺序这个隐态信息。本文模型和OPTransE考虑到关系路径的顺序，并得到较优结果。说明路径中的关系顺序对推理的重要性，学习有序关系路径的表示可以提升链路预测的准确性。
2）本文提出的融合实体描述与路径信息的知识图谱表示学习模型，在2-hop和3-hop实验上的指标得分均优于PtransE和OPTransE。这是因为本文模型同时使用了实体描述和路径信息两个外部信息对原图谱进行补充，扩展了知识来源。实体描述可以帮忙捕捉知识图谱中隐藏的细节，例如，单纯的从“苹果公司”这个实体名称中是无法判断出“苹果”这家公司的性质的，但是通过实体描述中的信息，就可以得到它是一家高科技公司这样一个事实。同时，选用RoBERTa对实体进行表示学习，可以更好地表示实体描述的语义，并区分多义词。
因此，融合实体描述与路径信息的知识图谱表示学习模型能全面地提升多跳推理能力。
5. 结束语
本文针对长路径建模难的问题，提出融合实体与路径信息的知识图谱表示学习模型。将实体描述和路径信息融入向量表示学习，通过设计两个Encoder端分别使用RoBERTa和OPTransE来实现实体描述和路径信息的知识图谱表征，最后将二者融合进行知识图谱表示学习模型的构建，显著提升链路预测的准确性，更好地支撑知识推理任务。下一步研究中，将考虑结合中文的数据集与语料库对模型进行改进，使其同样适应于中文文本任务。
-
图 1 知识图谱实体描述
Fig. 1 Entity description of knowledge graph
下载:
全尺寸图片
图 2 知识图谱路径信息
Fig. 2 Knowledge graph path information
下载:
全尺寸图片
图 3 融合实体描述与路径信息的知识图谱表示学习模型架构
Fig. 3 Architecture of knowledge graph representation learning model combining entity description and path information
下载:
全尺寸图片
图 4 微调后的RoBERTa结构
Fig. 4 Fine-tuned structure of RoBERTa
下载:
全尺寸图片
图 5 模型输入过程
Fig. 5 Model input process
下载:
全尺寸图片
表 1 各数据集的统计数据信息
Table 1 Statistical data information for each dataset
数据集 #Ent #Rel #Train #Dev #Test FB15K 14951 1345 483142 50000 59071 WN18RR 40943 11 86835 3034 3134 FB15k-237 14541 237 272115 17535 20466 表 2 WN18RR单跳链路预测结果对比
Table 2 Comparison of WN18RR single-hop link prediction results
模型 Mean Rank MMR Hits@10 TransE[16] 3384 0.226 0.505 DistMult[6] 5110 0.43 0.49 ComplEx[7] 5261 0.44 0.51 KBGAN[17] 3542 0.214 0.472 ConvE[8] 4187 0.43 0.52 ConvKB[9] 3324 0.249 0.524 RotatE[18] 3340 0.476 0.571 ConvR[19] 4237 0.475 0.537 TuckER[20] — 0.470 0.526 HAKE[21] 4619 0.497 0.582 InteractE[22] 5203 0.463 0.528 本文模型 3351 0.482 0.583 表 3 FB15k-237单跳链路预测结果对比
Table 3 Comparison of fB15K-237 single-hop link prediction results
表 4 FB15K单跳链路预测结果对比
Table 4 Comparison of FB15K single-hop link prediction results
表 5 FB15K-2hop多跳链路预测结果对比
Table 5 Comparison of FB15K-2Hop multi-hop link prediction results
数据集 评估指标 Mean Rank Hits@10 PTransE (ADD, 2-hop) 54 0.834 PTransE (MUL, 2-hop) 67 0.777 PTransE (RNN, 2-hop) 92 0.822 OPTransE (2-hop) 47 0.859 本文模型 (2-hop) 41 0.871 表 6 FB15K-3hop多跳链路预测结果对比
Table 6 Comparison of FB15K-3Hop multi-hop link prediction results
数据集 评估指标 Mean Rank Hits@10 PTransE (ADD, 3-hop) 58 0.846 OPTransE (3-hop) 50 0.855 本文模型 (3-hop) 47 0.886 -
[1] XIE Ruobing, LIU Zhiyuan, JIA Jia, et al. Representation learning of knowledge graphs with entity descriptions[J]. Proceedings of the AAAI conference on artificial intelligence, 2016, 30(1): 2659–2665. [2] 刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247–261. doi: 10.7544/issn1000-1239.2016.20160020 LIU Zhiyuan, SUN Maosong, LIN Yankai, et al. Knowledge representation learning: a review[J]. Journal of computer research and development, 2016, 53(2): 247–261. doi: 10.7544/issn1000-1239.2016.20160020 [3] 李涛, 王次臣, 李华康. 知识图谱的发展与构建[J]. 南京理工大学学报, 2017, 41(1): 22–34. doi: 10.14177/j.cnki.32-1397n.2017.41.01.004 LI Tao, WANG Cichen, LI Huakang. Development and construction of knowledge graph[J]. Journal of Nanjing University of Science and Technology, 2017, 41(1): 22–34. doi: 10.14177/j.cnki.32-1397n.2017.41.01.004 [4] 张正航, 钱育蓉, 行艳妮, 等. 基于TransE的表示学习方法研究综述[J]. 计算机应用研究, 2021, 38(3): 656–663. doi: 10.19734/j.issn.1001-3695.2020.02.0028 ZHANG Zhenghang, QIAN Yurong, XING Yanni, et al. Survey of representation learning methods based on TransE[J]. Application research of computers, 2021, 38(3): 656–663. doi: 10.19734/j.issn.1001-3695.2020.02.0028 [5] LIN Yankai, LIU Zhiyuan, LUAN Huanbo, et al. Modeling relation paths for representation learning of knowledge bases[C]//Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. Lisbon, Portugal. Stroudsburg: Association for Computational Linguistics, 2015: 705−714. [6] YANG Bishan, YIH W T, HE Xiaodong, et al. Embedding entities and relations for learning and inference in knowledge bases[EB/OL]. (2014−12−20) [2021−12−01].https://arxiv.org/abs/1412.6575. [7] TROUILLON T, WELBL J, RIEDEL S, et al. Complex embeddings for simple link prediction[C]//ICML’16: Proceedings of the 33rd International Conference on International Conference on Machine Learning-Volume 48. New York: ACM, 2016: 2071−2080. [8] DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2D knowledge graph embeddings[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press, 2018, 32(1): 1811−1818. [9] NGUYEN D Q, NGUYEN T D, NGUYEN D Q, et al. A novel embedding model for knowledge base completion based on convolutional neural network[C]//Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers). New Orleans: Association for Computational Linguistics, 2018: 327−333. [10] 王智悦, 于清, 王楠, 等. 基于知识图谱的智能问答研究综述[J]. 计算机工程与应用, 2020, 56(23): 1–11. doi: 10.3778/j.issn.1002-8331.2004-0370 WANG Zhiyue, YU Qing, WANG Nan, et al. Survey of intelligent question answering research based on knowledge graph[J]. Computer engineering and applications, 2020, 56(23): 1–11. doi: 10.3778/j.issn.1002-8331.2004-0370 [11] LIU Yinhan, OTT M, GOYAL N, et al. RoBERTa: a robustly optimized BERT pretraining approach[EB/OL]. (2019−7−26)[2021−12−01].https://arxiv.org/abs/1907.11692. [12] ZHU Yao, LIU Hongzhi, WU Zhonghai, et al. Representation learning with ordered relation paths for knowledge graph completion[EB/OL]. (2019−09−26) [2021−12−01].https://arxiv.org/abs/1909.11864. [13] 缴霖境, 闫威. 融合实体概念描述与图像特征的知识图谱表示学习研究[J]. 计算机应用研究, 2021, 38(6): 1759–1764. doi: 10.19734/j.issn.1001-3695.2020.06.0164 JIAO Linjing, YAN Wei. Research on knowledge graph representation learning combining entity concept description and image features[J]. Application research of computers, 2021, 38(6): 1759–1764. doi: 10.19734/j.issn.1001-3695.2020.06.0164 [14] XIE Ruobing, LIU Zhiyuan, SUN Maosong. Representation learning of knowledge graphs with hierarchical types[C]//IJCAI’16: Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence. New York: ACM, 2016: 2965−2971. [15] SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks[M]//The Semantic Web. Cham: Springer International Publishing, 2018: 593−607. [16] BORDES A, USUNIER N, GARCIA-DURÁN A, et al. Translating embeddings for modeling multi-relational data[C]//NIPS’13: Proceedings of the 26th International Conference on Neural Information Processing Systems-Volume 2. New York: ACM, 2013: 2787−2795. [17] CAI Liwei, WANG W Y. KBGAN: adversarial learning for knowledge graph embeddings[C]//Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers). New Orleans: Association for Computational Linguistics, 2018: 1470−1480. [18] SUN Zhiqing, DENG Zhihong, NIE Jianyun, et al. RotatE: knowledge graph embedding by relational rotation in complex space[EB/OL]. (2018−09−27)[2021−12−01].https://www.semanticscholar.org/paper/RotatE%3A-Knowledge-Graph-Embedding-by-Relational-in-Sun-Deng/8f096071a09701012c9c279aee2a88143a295935. [19] JIANG Xiaotian, WANG Quan, WANG Bin. Adaptive convolution for multi-relational learning[C]//Proceedings of the 2019 Conference of the North. Minneapolis: Association for Computational Linguistics, 2019: 978−987. [20] BALAZEVIC I, ALLEN C, HOSPEDALES T. TuckER: tensor factorization for knowledge graphcompletion[C]//Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing. Hong Kong: Association for Computational Linguistics, 2019: 5184−5193. [21] ZHANG Zhanqiu, CAI Jianyu, ZHANG Yongdong, et al. Learning hierarchy-aware knowledge graph embeddings for link prediction[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New York: AAAI Press, 2020, 34(3): 3065−3072. [22] VASHISHTH S, SANYAL S, NITIN V, et al. InteractE: improving convolution-based knowledge graph embeddings by increasing feature interactions[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New York: AAAI Press, 2020, 34(3): 3009−3016. [23] YE Rui, LI Xin, FANG Yujie, et al. A vectorized relational graph convolutional network for multi-relational network alignment[EB/OL]. (2019−08−01)[2021−12−01].https://www.semanticscholar.org/paper/A-Vectorized-Relational-Graph-Convolutional-Network-Ye-Li/d6adbd838cb69d3694659bde7c1bf464a8438caf. [24] KAZEMI S M, POOLE D. SimplE embedding for link prediction in knowledge graphs[EB/OL]. (2018−02−13)[2021−12−01].https://www.semanticscholar.org/paper/SimplE-Embedding-for-Link-Prediction-in-Knowledge-Kazemi-Poole/70af3ee98c53441d9090119f7b76efb1b6d03edd. [25] NIU Guanglin, ZHANG Yongfei, LI Bo, et al. Rule-guided compositional representation learning on knowledge graphs[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New York: AAAI Press, 2020, 34(3): 2950−2958.
