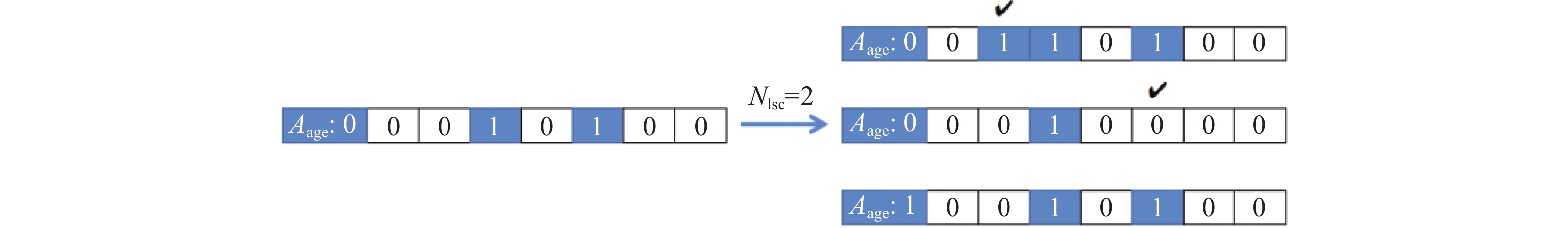Feature selection using forest optimization algorithm based on duplication analysis
-
摘要: 森林优化算法是一种基于森林中树木播种思想的演化算法,其具有良好的特征空间搜索能力,且实现难度低。但该算法在森林整体的收敛速度和寻优能力上仍存在提升空间,而且对高维数据集的适应度较差。本文针对上述问题提出了基于重复度分析的森林优化特征选择算法(feature selection using forest optimization algorithm based on duplication analysis, DAFSFOA)。该算法提出了基于信息增益的自适应初始化策略、森林重复度分析机制、森林重启机制、候选最优树生成策略、综合考虑特征选择数量和分类正确率的适应度函数。实验结果表明,DAFSFOA在大部分数据集上达到了最高的分类准确率。同时,对于高维数据集SRBCT,在维度缩减率和分类准确率方面,DAFSFOA对比森林优化特征选择算法(feature selection using forest optimization algorithm, FSFOA)都有较大提升。DAFSFOA 比FSFOA具有更强的特征空间探索能力,而且能够适应不同维度的数据集。Abstract: The forest optimization algorithm is an evolutionary algorithm based on the concept of forest tree planting. It has a strong capability for searching for feature space and low implementation difficulty. However, the algorithm still has room for improvement in the convergence speed and merit-seeking ability of the forest as a whole, and it is not well-suited to high dimensional data sets. In this paper, we propose to use a forest optimization algorithm based on duplication analysis (DAFSFOA) to address the above problems. The algorithm proposes an adaptive initialization strategy based on information gain, a forest repetition analysis mechanism, a forest restart mechanism, a candidate optimal tree generation strategy, and an adaptation function that integrates the number of feature selections and the correct classification rate. The experimental results show that DAFSFOA achieves the highest classification accuracy on most datasets. Meanwhile, for the high dimensional dataset SRBCT, DAFSFOA has a large improvement over feature selection using a forest optimization algorithm (FSFOA) in terms of dimensionality reduction rate and classification accuracy. DAFSFOA has a stronger feature space exploration capability than FSFOA and can adapt to datasets with different dimensions.
-
大数据和物联网技术的发展,使得越来越多的数据被采集、存储和分析[1]。目前的数据不仅数量巨大,而且维度高,但并不是全部的数据都是有用的。数据的规模在变大的同时也包含了大量的冗余、不相关或者弱相关特征,这些特征与数据的主要基本结构没有关联,或者只有松散的弱关联。如果特征不进行处理就输入机器学习模型,不仅会增大模型的时间开销,而且干扰特征的存在还会降低算法的预测精度。通过对数据原特征空间分析,过滤掉冗余和不相关特征,保留相关特征,这就是特征选择。特征选择以提高模型精度和减少模型运算时间为目标,以保持模型原始精度为底线,选择极小特征子集。此外,大量的特征也会导致模型过拟合,在项目实施时模型性能不佳,特征选择可以预防这种现象的发生,使模型更加适应现实环境[2]。
特征选择是一个复杂的组合优化问题,这是因为随着特征维度的增加特征搜索空间将会呈指数型增加,一个具有
$n$ 维特征的数据集,特征子集(不包含空集)的总数为${2^n} - 1$ [3]。因此采用完全搜索策略的计算成本巨大。近几年基于演化算法的启发式搜索策略常用于特征选择领域,因为其不需要有关领域专业知识、强大寻优能力和较为理想的时间成本。森林优化算法(forest optimization algorithm,FOA)[4],是一种基于森林中树木播种的演化算法。Ghaemi等[5]于2016年,通过改变局部播种和全局播种两个算子,使FOA适应于离散向量,并应用于特征选择,验证了 FSFOA (feature selection using forest optimization algorithm)在特征选择领域的可行性。对比粒子群算法(particle swarm optimization, PSO)和蚁群算法(ant colony optimization, ACO),FSFOA更容易实现,而且需要更少的时间代价就能得出使学习模型性能更好的特征子集。虽然FSFOA已经在低、中、高3个特征维度的数据集中进行了实验取得了较好的效果,但仍然存在以下问题:1)FSFOA在初始化森林的阶段采用随机初始化的策略进行盲目特征选择,特征被选中的概率均为
$1/n$ ,$n$ 为总特征数[6]。因此森林树木初始质量较差,森林收敛速度较慢。而且对高维数据集的适应度较差。2)FSFOA未对候选种群的数量进行限制。随着演化过程的进行,候选种群的数量将过于庞大,算法空间成本过高。
3)随着演化的进行种群趋于收敛,森林中会出现大量相同的树木(特征选择向量相同的树木)。重复树木的适应度计算增加了时间成本,降低了算法的搜索能力。
4)实验表明,在仅考虑准确率作为适应度的情况下,会出现多个适应度相同的最优树。而且只考虑分类准确率为优化目标过于单一,不利于提高维度缩减率。
因此,为了提升森林整体的收敛速度、增强森林整体的空间搜索寻优能力,本文提出了基于重复度分析的森林优化特征选择算法(feature selection using forest optimization algorithm based on duplication analysis,DAFSFOA) 。
近年来,信息论与演化算法相结合的研究工作越来越多[7-10],信息增益(information gain,IG)可用于初步衡量特征的重要性。通过应用IG,可以提高森林树木的初始质量,过滤掉与分类毫无关系的特征,有利于加速森林整体的演化进程。Xu等[11]于2021年提出重复度分析的概念,旨在增加种群多样性,调高算法的全局寻优能力和减少重复计算。受以上内容启发,本文设计了基于信息增益和特征维度的自适应森林初始化策略,加快了森林的收敛速度,且适应于不同类型的数据。同时加入了森林树木分析去重机制、森林种群重启机制、候选森林规模限制和候选最优树生成策略,降低了算法的空间和时间成本,并且增强了算法的空间搜索能力。最后改进适应度函数,提升了算法对于高维数据集的寻优能力。在11个数据集上测试DAFSFOA的性能,对比经典的和近几年提出的特征选择算法,DAFSFOA在分类准确率和特征维度缩减率上都具有很强的竞争力,同时对高维小样本数据也有很好的适应力。
1. 相关工作
特征选择作为一种数据降维手段,能在不改变原始特征物理信息的情况下选择尽量小的特征子集。特征选择常作为数据处理工具,去除干扰特征和选择核心特征。因此许多学者已经对特征选择进行了系统的研究。通常将特征选择方法分为3种类型:过滤式 (filter)、包裹式 (wrapper)和嵌入式 (embedding)[1]。对于过滤式特征选择算法,特征子集的选择与机器学习模型之间没有交互,模型的输出结果不会影响特征子集的选择。在包裹式特征选择算法中,模型的结果例如分类准确率,会直接作为特征子集的适应度函数,评价特征子集的优劣。嵌入式特征选择算法将分类算法或者回归算法的学习过程与特征选择过程合并同时进行,算法学习过程结束的同时产生特征选择结果。包裹式方法往往能取得比过滤式方法更好的效果,但同时也需要付出更大的计算代价。而过滤式方法的计算成本较低,而且通用性更好[12]。随着研究的进展,也产生了越来越多的混合式特征选择算法(hybrid method),混合式特征选择方式结合了过滤式和包裹式方法的优点。
特征子集搜索技术是特征选择的核心,搜索技术的选择往往会直接影响特征选择算法的效果。子集搜索技术一般分为3种:完全搜索、启发式搜索、基于演化算法的搜索[13]。完全搜索能够保证寻找到最优特征子集,但是特征选择是个 NP难问题,当面对高维数据时,完全搜索需要的时间代价过大,因此特征选择中较少采用完全搜索策略[14]。启发式搜索常用于特征选择,例如贪婪搜索。贪婪搜索的典型例子是:序列正向选择(sequential forward selection, SFS)[15]、序列反向选择(sequential backward selection, SBS)[16]。但是这两种搜索方式都存在明显的局限,都存在“嵌套效应”,缺少搜索的灵活性,之前添加或者去除的特征,在之后步骤中不能从特征子集中去除或者重新加入特征子集。为了克服这个问题,提出了加L减R法[17]、顺序反向浮动选择(sequential backward floating selection, SBFS)[18]和顺序正向浮动选择(sequential forward floating selection, SFFS)[18]等。加L减R法通过运行L次SFS算法,R次SBS来达到平衡,但是很难确定L和R的值。演化算法的灵感来源于自然演化中的生物智慧、群体智慧和群体行为,其具有强大的搜索能力。近年来,以粒子群算法(PSO)、遗传算法(genetic algorithm, GA)、蚁群算法(ACO)等经典演化算法为基础的变种算法广泛应用于超参数优化[19]、特征选择[20]和路径规划[21]等领域。同时也出现了大量新型演化算法,如模拟座头鲸气泡网狩猎的鲸鱼算法(whale optimization algorithm, WOA)[22]、受森林中树木播种启发的森林优化算法(FOA)[4]。虽然演化算法的应用领域广泛,但要应用于特征选择也必须进行一系列的改进,形成针对特征选择领域的演化算法。Dong等 [23]结合信息论知识和粒子群算法,并舍弃粒子群更新公式中的速度参数,提出了一种混合特征选择方法:基于PSO的双全局最优的高维特征选择方法。Agrawal等 [24]结合量子计算的概念提出了基于量子的鲸鱼优化算法(quantum based whale optimization algorithm, QWOA)进行特征选择。该方法利用种群个体的量子位表示法和量子旋转门算子,提高了经典WOA的特征空间探索和利用能力,全局寻优能力更强、种群多样性更高。Li等 [25]提出了一种改进的黏性二进制粒子群算法(improved binary particle swarm optimization , ISBPSO)。ISBPSO采用了基于互信息(MI)种群初始化策略获得优质初始种群,并将遗传算法作为PSO的子算子用于交换种群信息避免种群过早收敛,提高了算法跳出局部最优的能力。
本文提出的DAFSFOA主要目标为增加森林中树木的多样性,扩大森林对特征空间的覆盖,同时降低算法的计算成本。为达到以上目的,DAFSFOA添加了基于信息增益的自适应森林初始化策略、森林去重和重启机制、候选森林规模限制策略、候选最优树生成策略,并改进了适应度函数。
2. 森林优化特征选择算法
FSFOA是在FOA的基础上改进而来的,可以看作二进制离散向量的森林优化算法。FOA的灵感来自于森林中树木种群的演化过程。在森林中,参天大树往往在水源和阳光充足的地方。树木种子寻找最佳栖息地的过程,也正是一个搜索寻优的过程。通过对这一过程的建模,最终Ghaemi[4]等于2014年提出了FOA。之后,Ghaemi等[5]提出了针对离散空间搜索的FOA,并应于特征选择。FSFOA主要由初始化森林、局部播种、森林规模限制候选森林生成、全局播种、更新全局最优树五部分组成。FSFOA采用
${X_i} = ({x_{i0}},{x_{i1}}, {x_{i2}}, \cdots ,{x_{iD}})$ ,表示森林中索引值为i的树木。其中${x_{i0}} \geqslant0$ ,${x_{i,j>0}} \in \{ 1,0\}$ ,D表示数据集的维度。树木向量的第0维表示树木的年龄,第1~D维表示特征选择情况,0代表未选中该特征,1代表选中。FSFOA的主要流程如图1所示。2.1 初始化森林
在FSFOA中,森林中每一棵树木都被表示为如图2所示的长度为
$D + 1$ 的离散向量。与常规特征选择算法中选择结果表示方法不同的是,FSFOA中添加了年龄Aage这一维。树木的年龄这一重要的参数在后续局部播种和森林规模限制阶段有重要的作用。初始化森林就是生成一定数目的初始树木向量,树木年龄全部设置为0,其余位置随机初始化为0或1。因此,在初始化森林的阶段每个特征被选中和被删除的概率相同。对于中低维数据集,这种随机的初始化策略s缺点并不明显,但对于高维数据集,完全随机初始化森林将给后续种群寻优带来极大困难。2.2 局部播种
局部播种代表了FSFOA对特征空间的深度搜索,模拟了树木在自身附近播种的行为。局部播种算子只针对Aage=0的树木。Nlsc参数代表了Aage=0的父代树木可产生的子树数目。进行局部播种的树木随机选中Nlsc个不同的位置进行单点翻转突变,也即对选中的位置进行取反操作,选中位置为0的置为1,为1的置为0。每进行1次单点取反将产生1棵子树,并重置父树继续下次单点突变。Nlsc个突变位置将产生Nlsc棵子树,子树Aage=0,森林中其他所有树木的Aage增加1。具体过程如图2所示。图2中
 代表了选中的突变位置。
代表了选中的突变位置。
2.3 森林规模限制
随着演化的进行,森林中树木会越来越多。因此需要对森林中的总容量进行限制,森林的容量为Sarea。Aage>Tlife(年龄限制)的树木将会老死,被森林淘汰,移除到候选森林。如果森林中树木总数仍大于Sarea,FSFOA将会根据适应度值对森林中的树木进行降序排序,排名超过Sarea的树木也将移除到候选森林。FSFOA中的适应度值为分类器的分类准确率,也即树木选择的特征子集的分类能力。
2.4 全局播种
全局播种代表了FSFOA对特征空间的广度搜索。对比局部播种,全局播种产生的子树与父树的差距更大。全局播种操作可在森林陷入局部最优的时候,使森林跳出局部最优。候选森林中的树木以Ptransfer的概率被选中进行全局播种。1棵父树只产生1棵子树,父树随机选择Ngsc个位置进行多点取反,并置Aage=0,加入森林中参与演化,具体如图3所示。
2.5 更新最优树
根据适应度值对森林中的树木进行降序排列,适应度最高的树被选为最优树,并将该树的Aage字段置为0,参与后续的森林演化。将最优树的Aage每次都重置为0,也即优秀的树木不会被淘汰,保证了森林中优秀的树木能够一直参与森林的演化。
3. DAFSFOA算法
针对引言中提出的FSFOA的缺陷,以提升森林的收敛速度和算法的搜索能力为目标,本文提出了DAFSFOA算法。为了加快森林收敛速度,DAFSFOA引入了信息增益对特征进行初筛,提升了初始种群的质量,而且针对不同维度的数据集采用了不同的初始化策略缩小了高维数据集的搜索空间。同时,采用森林树木重复度分析机制和候选森林规模限制策略降低了算法的时间与空间成本。为了提升算法的搜索能力,DAFSFOA设计了森林重启机制,防止森林过早收敛陷入局部最优,同时提出了候选最优解生成策略进一步提升树木多样性,并且改进了适应度函数,大大提高了算法的寻优能力。
3.1 基于信息增益的自适应初始化策略
近年来,特征选择领域常用信息论知识对特征进行初步筛选。信息增益(IG)能够反应特征与分类标签的相关度。信息增益越大,该特征对于分类的帮助越大。信息增益的定义如式(1)~(4)所示:
$$ P(X = {x_i}) = {p_i},i = 1,2, \cdots ,n $$ (1) $$ H(X) = - \sum\limits_{i = 1}^n {{p_i}\log {p_i}} $$ (2) $$ H(Y|X) = \sum\limits_{i = 1}^n {{p_i}H(Y|X = {x_i})} $$ (3) $$ {\text{IG}}(Y,X) = H(Y) - H(Y|X) $$ (4) H(X)为随机变量的熵,H(Y|X)为条件熵,两者之差就是信息增益。但信息增益并不能反应特征与特征之间的关系,因此不能全凭信息增益选择特征。本文提出增1减1法来初始化森林树木。在计算数据集中每个特征的IG后,对森林进行随机初始化,对初始化后的初代森林中前50%的树木,添加信息增益最大的特征,并删除信息增益最小的特征。并且对于高纬度小样本的数据集采用不同的初始化策略。当D(特征维度)
$\gg $ N(样本数量)时,无法覆盖整个特征空间,因为样本数量太少此时在初始化森林时选择较少的特征更利于后续收敛。当D>3N时,初始森林中的树木选择的特征数目应小于等于3N。3.2 候选森林规模的限制策略
FSFOA中随着森林演化的进行,森林中越来越多的树被转移到候选森林。候选森林的规模将越来越大,但保存巨大的候选森林会带来较大的内存开销,而且劣质树木对于森林的寻优帮助不大。较大的候选森林也会导致在全局播种阶段有过多的新生树木加入到森林中,也间接加大了算法的计算消耗。因此,在DAFSFOA中的森林规模限制阶段,本文对候选森林同样进行规模限制。因为候选森林均为较劣质的树木,所以无需在计算适应度进行排序筛选。本文将候选森林的规模限制设为森林规模限制的两倍,即2Sarea。当候选森林中树木数量超过限制时,随机删除树木直到树木数量等于2Sarea。
3.3 重复度分析及森林重启机制
随着演化的进行森林逐渐收敛,森林中产生大量Aage不同,但是所选特征相同的树木。大量重复的树木的存在对森林演化寻优并无帮助,反而因此消耗了大量的计算资源。因此,我们需要对森林中的树木进行重复度分析,每种树木只保留一个个体,极大地提高了森林中树木的多样性,有利于算法的全局寻优。如果经过去重操作森林中剩余的树的数量只有森林初始种群数量Sinitial的一半,此时认为森林种群的多样性过低不利于后续搜索寻优,因此采用森林重启机制,采用初始化森林的方法补充森林中的树木,使森林树木的数量重新达到Sinitial。
3.4 候选最优树生成策略
FSFOA每轮演化只产生1棵最优树,忽略了森林中树木的统计信息。为了充分利用森林演化过程中的统计信息,在DAFSFOA中提出候选最优树概念,即统计目前森林中出现过的全部特征,并根据统计结果生成候选最优树,将候选最优树的年龄置为0,并加入森林参与后续的森林演化。候选最优树的加入不仅增加了森林树木多样性,而且充分利用了森林演化过程中的统计信息。
3.5 改进的适应度函数
适应度值表现了算法所选择的特征子集的好坏。FSFOA中的适应度函数设计考虑较为片面,仅考虑分类准确率(AC),AC的定义如式(5)所示:
$$ {\text{AC}} = \frac{{{N_{{\text{acc}}}}}}{M} $$ (5) 式中:
$N_{{\rm{acc}}} $ 为分类正确的实例数;M为实例总数。在只考虑AC的情况下实验结果中出现了很多适应度值相同的树,不利于最优树的挑选,而且不利于森林朝着增大DR的方向演化,DR为维度缩减率,如式(6)所示:$$ {\text{DR}} = \frac{{{F_{{\text{notSelected}}}}}}{{{F_{{\text{all}}}}}} $$ (6) 式中:
$F_{{\rm{notSelected}}} $ 为对应树未选择的特征数;$F_{\rm{all}} $ 为特征总数。式(7)为DAFSFOA中采用的适应度函数,为AC和DR的加权,避免了不同树适应度值相同的情况。$\alpha + \beta = 1$ 而且$\alpha \gg \beta $ ,因为特征选择算法的主要目的为提高分类准确率。$$ {\text{Fitness}} = \alpha \times {\text{AC}} + \beta \times {\text{DR}} $$ (7) 3.6 DAFSFOA流程图
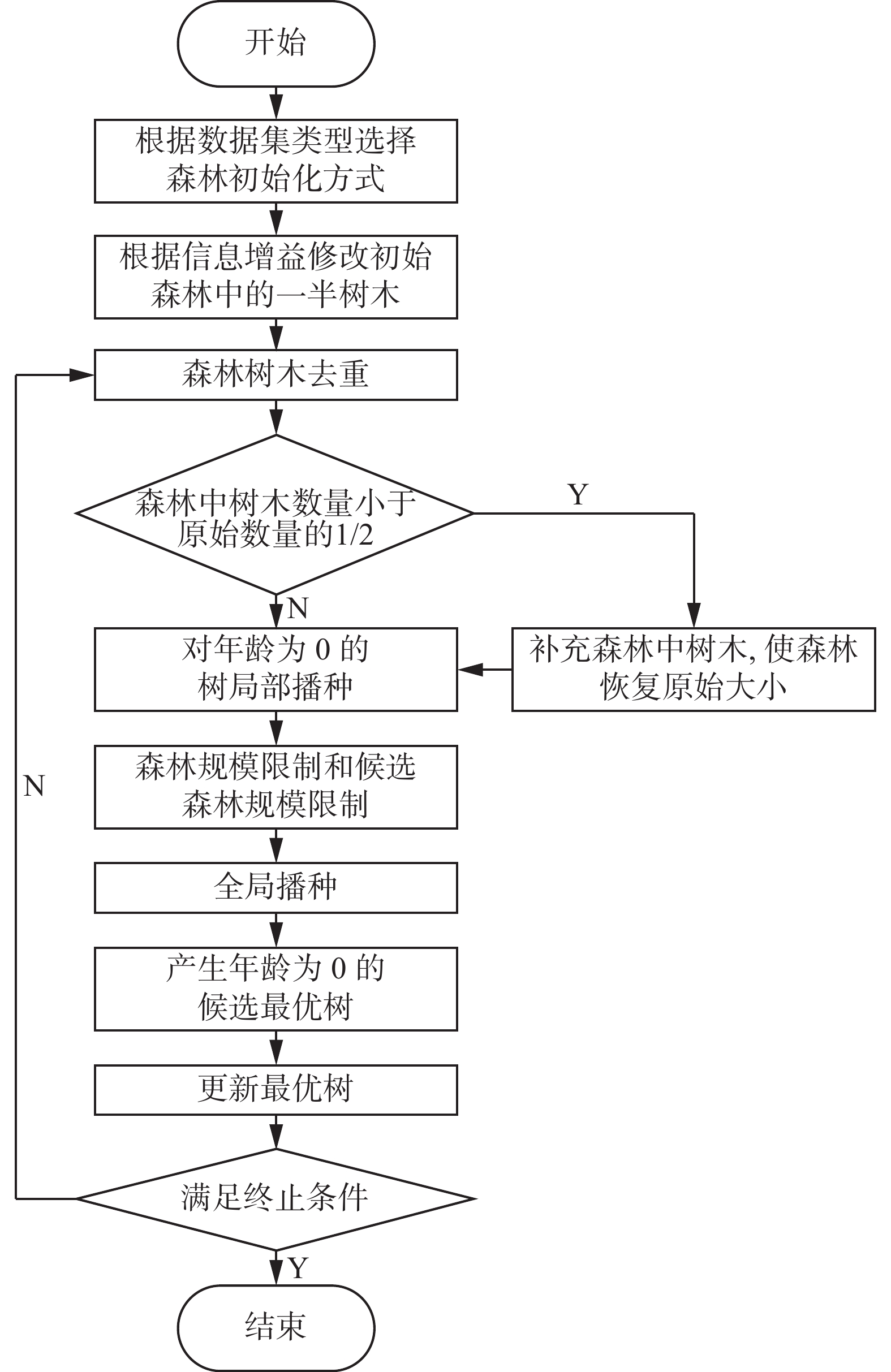
图4为DAFSFOA的算法流程图。DAFSFOA的演化终止条件为迭代50次,当演化次数超过限制,则结束算法,输出森林中目前的最优树也即最优特征子集。
4. 实验和结果分析
实验中代码运行环境为python3.8。硬件环境为CPU Ryzen7 5800H,16 GB内存。
4.1 数据集及对比算法
FSFOA中使用了10个UCI数据集和1个高维微阵列数据集。数据集的维度和实例数如表1所示。
表 1 数据集简介及Nlsc和NgscTable 1 Dataset introduction and corresponding Nlsc and Ngsc values数据集 特征数 样本数 类数 Nlsc Ngsc Heart-statlog 13 270 2 3 6 Vehicle 18 846 4 4 9 Cleveland 13 303 5 3 6 Dermatology 34 366 6 7 15 Ionosphere 34 351 2 7 15 Sonar 60 208 2 12 30 Glass 9 214 7 2 4 Wine 13 178 3 3 6 Segmentation 19 2310 7 4 9 SRBCT 2308 83 4 460 700 Hepatitis 19 155 2 4 10 为了对比显示DAFSFOA算法的性能,本文采用与FSFOA相同的11个数据集。除了与FSFOA进行实验对比,本文也与几种经典的特征选择算法和近年提出的新算法进行了对比。表2列出了文中对比算法的简介。
表 2 文中对比算法Table 2 Comparative algorithms in the paper算法名称 数据集划分方式 算法描述 NFSFOA 70%~30%,10-fold,2-fold 新的森林优化特征选择算法[26] FSFOA 70%~30%,10-fold,2-fold 森林优化特征选择算法[5] SFS,SBS,SFFS 70%~30% 前向选择、后向选择、序列浮动前向选择[27] NSM 10-fold 基于软紧邻间隔的特征选择算法[28] SVM-FuzCoc 70%~30% 基于SVM的模糊互补准则的新型特征选择算法[27] HGAFS 2-fold 一种基于互信息的混合遗传算法的包裹式特征选择算法[29] FS-NEIR 10-fold 基于邻域有效信息比率的特征选择算法[30] UFSACO 70%~30% 一种基于蚁群优化的无监督特征选择算法[31] PSO(4-2) 10-fold 改进的粒子群优化特征选择算法[32] 注:10-fold为十折交叉验证,2-fold为两折交叉验证 4.2 具体参数设置
为了突出DAFSFOA对于FSFOA改进的有效性。除了改进部分,其他参数保持与FSFOA一致。Tlife设为15,Ptransfer设为0.05,Sarea设为50,以上3个参数与FSFOA的设置相同,Sinitial在FSFOA中未提及具体值,本文中设为50[5]。Nlsc和Ngsc 也保持和FSFOA相同。FSFOA中指出Nlsc和Ngsc 与数据集维度有关,同时实验得出当Nlsc=D/5, Ngsc=D/2时,能达到计算成本和寻优效果的最佳平衡[5]。参数设置具体如表1所示。
4.3 分类器和验证方式
本文采用KNN、rbf-svm、C4.5三种分类器计算AC,其中KNN采用了n=1、n=3和n=5这3种不同的参数。C4.5采用J48参数。同时采用70%~30%的数据集划分、10折交叉验证、2折交叉验证这3种不同的数据集划分方式。实验中采用相同的实验条件计算得出森林中每棵树的AC和DR,得出最优树,AC和DR的计算公式如式(5)、(6)所示。
4.4 实验结果分析
DAFSFOA与其他算法对比的结果如表3所示。对于最高正确率和最高维度缩减率均加粗处理。在Dermatology、Sonar、Cleveland、Heart-statlog、Hepatitis、SRBCT、Segmentation这7个数据集上,采用不同的数据集划分方式和分类器,DAFSFOA都取得最高的准确率。
表 3 DAFSFOA与对比算法的实验结果Table 3 Experimental results of DAFSFOA and comparison algorithms数据集 算法 AC/% DR/% 分类器 数据集 算法 AC/% DR/% 分类器 Wine DAFSFOA 98.89(10-fold) 61.15 J48 Ionosphere DAFSFOA 98.05(10-fold) 70.59 J48 NFSFOS 97.25(10-fold) 53.85 J48 NFSFOS 96.62(10-fold) 61.76 J48 FSFOA 96.06(10-fold) 21.42 J48 FSFOA 93.16(10-fold) 68.57 J48 FS-NEIR 95.04(10-fold) 61.53 J48 FS-NEIR 92.59(10-fold) 82.35 J48 DAFSFOA 98.33(10-fold) 53.85 3nn DAFSFOA 95.28(10-fold) 77.06 3nn NFSFOA 95.61(10-fold) 61.54 3nn NFSFOA 93.83(10-fold) 76.47 3nn FSFOA 98.87(10-fold) 42.58 3nn FSFOA 92.30(10-fold) 61.76 3nn NSM 98.00(10-fold) 53.84 3nn NSM 92.00(10-fold) 88.23 3nn DAFSFOA 98.16(70%~30%) 69.23 1nn DAFSFOA 95.00(10-fold) 79.70 5nn NFSFOA 95.61(70%~30%) 61.54 1nn NFSFOA 93.23(10-fold) 79.41 5nn FSFOA 98.07(70%~30%) 50.00 1nn FSFOA 89.43(10-fold) 54.28 5nn SFS 97.69(70%~30%) 35.38 1nn DAFSFOA 97.27(2-fold) 67.65 rbf-svm SBS 94.77(70%~30%) 46.15 1nn NFSFOA 95.16(2-fold) 58.82 rbf-svm SFFS 96.56(70%~30%) 36.92 1nn FSFOA 94.58(2-fold) 57.14 rbf-svm DAFSFOA 98.61(70%~30%) 68.46 J48 HGAFS 92.76(2-fold) 82.35 rbf-svm NFSFOA 96.73(70%~30%) 61.54 J48 DAFSFOA 98.44(70%~30%) 74.56 1nn FSFOA 96.00(70%~30%) 57.14 J48 NFSFOA 95.16(70%~30%) 58.82 1nn UFSACO 95.08(70%~30%) 61.53 J48 FSFOA 89.52(70%~30%) 54.28 1nn DAFSFOA 97.69(70%~30%) 70.00 5nn SVM-FuzCoc 89.46(70%~30%) 88.23 1nn NFSFOA 95.70(70%~30%) 38.46 5nn DAFSFOA 96.60(70%~30%) 73.82 J48 FSFOA 99.20(70%~30%) 30.76 5nn NFSFOA 99.06(70%~30%) 67.65 J48 DAFSFOA 96.07(2-fold) 53.85 rbf-svm FSFOA 95.12(70%~30%) 47.05 J48 NFSFOA 96.06(2-fold) 37.17 rbf-svm UFSACO 88.61(70%~30%) 11.17 J48 HGAFS 98.31(2-fold) 53.85 rbf-svm Cleveland DAFSFOA 62.64(70%~30%) 69.23 1nn Dermatology DAFSFOA 98.26(10-fold) 71.18 J48 NFSFOA 62.22(70%~30%) 61.54 1nn NFSFOA 97.81(10-fold) 73.53 J48 FSFOA 55.55(70%~30%) 71.42 1nn FSFOA 96.99(10-fold) 21.42 J48 SVM-FuzCoc 61.01(70%~30%) 46.10 1nn FS-NEIR 93.95(10-fold) 70.58 J48 SFS 51.79(70%~30%) 47.70 1nn DAFSFOA 99.40(70%~30%) 67.06 1nn SBS 54.80(70%~30%) 38.50 1nn NFSFOA 99.07(70%~30%) 58.82 1nn SFFS 49.55(70%~30%) 53.80 1nn FSFOA 97.27(70%~30%) 45.71 1nn Vehicle DAFSFOA 78.00(10-fold) 33.33 J48 续表 3 数据集 算法 AC/% DR/% 分类器 数据集 算法 AC/% DR/% 分类器 Dermatology SFS 94.02(70%~30%) 44.70 1nn Vehicle NFSFOA 77.74(10-fold) 44.44 J48 SBS 91.78(70%~30%) 58.23 1nn FSFOA 73.04(10-fold) 31.57 J48 SFFS 93.70(70%~30%) 62.35 1nn FS-NEIR 70.98(10-fold) 50.00 J48 SVM-FuzCoc 94.11(70%~30%) 64.70 1nn DAFSFOA 77.17(70%~30%) 51.11 5nn DAFSFOA 98.95(70%~30%) 77.21 J48 NFSFOA 76.77(70%~30%) 55.56 5nn NFSFOA 98.15(70%~30%) 70.59 J48 FSFOA 73.98(70%~30%) 50.00 5nn FSFOA 90.09(70%~30%) 44.11 J48 PSO(4-2) 85.30(70%~30%) 68.40 5nn UFSACO 95.28(70%~30%) 26.47 J48 DAFSFOA 69.38(2-fold) 66.67 rbf-svm Sonar DAFSFOA 88.51(2-fold) 62.83 rbf-svm NFSFOA 69.03(2-fold) 66.67 rbf-svm NFSFOA 75.94(2-fold) 78.33 rbf-svm FSFOA 62.41(2-fold) 47.22 rbf-svm FSFOA 65.86(2-fold) 54.09 rbf-svm Heart-statlog DAFSFOA 85.22(10-fold) 69.23 J48 HGAFS 87.02(2-fold) 75.00 rbf-svm NFSFOA 84.07(10-fold) 61.54 J48 DAFSFOA 92.06(10-fold) 72.22 J48 FSFOA 85.15(10-fold) 48.07 J48 NFSFOA 85.18(10-fold) 65.00 J48 FS-NEIR 79.86(10-fold) 46.15 J48 FSFOA 82.69(10-fold) 52.45 J48 DAFSFOA 85.92(10-fold) 60.00 3nn FS-NEIR 75.97(10-fold) 91.66 J48 NFSFOA 83.33(10-fold) 53.85 3nn DAFSFOA 98.33(70%~30%) 76.58 1nn FSFOA 85.18(10-fold) 35.71 3nn NFSFOA 76.19(70%~30%) 76.67 1nn NSM 84.00(10-fold) 69.23 3nn FSFOA 85.43(70%~30%) 57.37 1nn DAFSFOA 85.22(2-fold) 53.85 rbf-svm DAFSFOA 95.40(70%~30%) 75.67 5nn NFSFOA 84.81(2-fold) 76.92 rbf-svm NFSFOA 74.60(70%~30%) 68.33 5nn FSFOA 84.07(2-fold) 50.00 rbf-svm FSFOA 86.98(70%~30%) 44.26 5nn HGAFS 82.59(2-fold) 76.92 rbf-svm PSO(4-2) 78.16(70%~30%) 81.26 5nn — — — — Glass DAFSFOA 79.90(10-fold) 37.22 J48 Segmentation DAFSFOA 97.10(10-fold) 68.16 3nn NFSFOA 78.13(10-fold) 33.33 J48 NFSFOA 96.88(10-fold) 52.63 3nn FSFOA 75.70(10-fold) 50.00 J48 FSFOA 96.20(10-fold) 30.00 3nn FS-NEIR 68.53(10-fold) 22.22 J48 NSM 95.00(10-fold) 63.15 3nn DAFSFOA 77.23(70%~30%) 42.77 1nn Hepatitis DAFSFOA 91.56(10-fold) 64.21 J48 NFSFOA 75.38(70%~30%) 55.56 1nn FSFOA 86.45(10-fold) 55.00 J48 FSFOA 71.88(70%~30%) 40.00 1nn FS-NEIR 81.11(10-fold) 68.42 J48 SFS 72.24(70%~30%) 26.66 1nn DAFSFOA 91.68(10-fold) 63.68 3nn SBS 71.77(70%~30%) 37.77 1nn FSFOA 87.09(10-fold) 42.10 3nn SFFS 71.77(70%~30%) 37.77 1nn NSM 90.00(10-fold) 15.78 3nn DAFSFOA 66.83(2-fold) 55.55 rbf-svm DAFSFOA 92.23(70%~30%) 66.57 J48 NFSFOA 68.69(2-fold) 33.33 rbf-svm FSFOA 84.40(70%~30%) 45.00 J48 FSFOA 68.22(2-fold) 60.00 rbf-svm UFSACO 78.87(70%~30%) 75.00 J48 HGAFS 65.51(2-fold) 44.44 rbf-svm — — — — SRBCT DAFSFOA 99.99(70%~30%) 92.33 1nn — — — — NFSFOA 94.73(70%~30%) 61.48 1nn — — — — FSFOA 94.73(70%~30%) 49.06 1nn — — — — SVM-FuzCoc 98.88(70%~30%) 98.57 1nn — — — — DAFSFOA在高维数据集SRBCT上算法性能有巨大的提升,对比FSFOA,其准确率提升了5.26%,而且维度缩减率的提升更为巨大。FSFOA在对应数据集上的准确率高达94.73%,但是维度缩减率只有49.06%,而SRBCT数据集的特征维度有2308维,FSFOA得到的最优树仍然包含了大量特征。而DAFSFOA得到的最优树维度缩减率高达92.33%。对比FSFOA,DAFSFOA能够更好地处理高维特征选择问题,这得益于DAFSFOA特殊设计的高维数据集初始化策略。对于同样是高维数据集的Sonar,DAFSFOA的表现也要远远好于FSFOA,平均AC为93.57%,最高AC为98.33%,而FSFOA的平均AC为80.24%,其最高AC为86.98%,也低于DAFSFOA的平均值。当采用rbf-svm分类器并采用2-fold验证的时候,DAFSFOA的准确率比FSFOA高了22%,同时维度缩减率提高了8%。同时,对比2020年提出的NFSFOA,DAFSFOA也具有明显的优势,在同样条件下,DAFSFOA得出的最优特征子集分类准确率最高达98.33%,而相应的NFSFOA只有74.6%,但NFSFOA产生的最优树的维度缩减率只高出DAFSFOA算法0.09%,DAFSFOA只牺牲了0.09%的DR,就达到了98.33%的准确率,可见DAFSFOA的性能优势。在维度缩减率方面,DAFSFOA并不像在分类正确率上表现得如此出众,但对于大部分数据集DAFSFOA都优于FSFOA。对于一部分数据集,虽然DAFSFOA没有取得最高的维度缩减率,但在分类准确率上仍有较大优势。例如,NSM算法在Ionosphere数据集上,采用10折交叉验证和KNN(k=1)分类器取得了88.23%的维度缩减率,高于DAFSFOA。但是NSM算法的分类准确率比DAFSFOA低了3.2%。
在大部分数据集中,DAFSFOA的维度缩减率排行第二,并且与第一相差很小,但分类准确率远超其他算法。通过DAFSFOA在不同数据集的实验,可以得出DAFSFOA在AC和DR上对比原始的FSFOA,均有巨大提升,而且在大部分数据集中的表现也超过了其他经典的算法和近年来提出的新型特征选择算法。
5. 结束语
本文通过对FSFOA的深入分析,提出了FSFOA的4处不足。以提高森林中个体的多样性、降低树木重复度和提高算法的全局寻优能力为目的,本文对FSFOA算法提出了5点改进意见,即基于信息增益的自适应初始化策略、候选森林规模限制策略、森林重复度分析及重启机制、候选最优树生成策略、结合维度缩减率的适应度函数,最终形成了基于重复度分析的森林优化特征选择算法。并通过实验在不同维度的数据集上验证了DAFSFOA改进的有效性。DAFSFOA在AC和DR两个方面的表现普遍超过了FSFOA,尤其是对于高维数据集,DAFSFOA的表现优于FSFOA。
-
表 1 数据集简介及Nlsc和Ngsc
Table 1 Dataset introduction and corresponding Nlsc and Ngsc values
数据集 特征数 样本数 类数 Nlsc Ngsc Heart-statlog 13 270 2 3 6 Vehicle 18 846 4 4 9 Cleveland 13 303 5 3 6 Dermatology 34 366 6 7 15 Ionosphere 34 351 2 7 15 Sonar 60 208 2 12 30 Glass 9 214 7 2 4 Wine 13 178 3 3 6 Segmentation 19 2310 7 4 9 SRBCT 2308 83 4 460 700 Hepatitis 19 155 2 4 10 表 2 文中对比算法
Table 2 Comparative algorithms in the paper
算法名称 数据集划分方式 算法描述 NFSFOA 70%~30%,10-fold,2-fold 新的森林优化特征选择算法[26] FSFOA 70%~30%,10-fold,2-fold 森林优化特征选择算法[5] SFS,SBS,SFFS 70%~30% 前向选择、后向选择、序列浮动前向选择[27] NSM 10-fold 基于软紧邻间隔的特征选择算法[28] SVM-FuzCoc 70%~30% 基于SVM的模糊互补准则的新型特征选择算法[27] HGAFS 2-fold 一种基于互信息的混合遗传算法的包裹式特征选择算法[29] FS-NEIR 10-fold 基于邻域有效信息比率的特征选择算法[30] UFSACO 70%~30% 一种基于蚁群优化的无监督特征选择算法[31] PSO(4-2) 10-fold 改进的粒子群优化特征选择算法[32] 注:10-fold为十折交叉验证,2-fold为两折交叉验证 表 3 DAFSFOA与对比算法的实验结果
Table 3 Experimental results of DAFSFOA and comparison algorithms
数据集 算法 AC/% DR/% 分类器 数据集 算法 AC/% DR/% 分类器 Wine DAFSFOA 98.89(10-fold) 61.15 J48 Ionosphere DAFSFOA 98.05(10-fold) 70.59 J48 NFSFOS 97.25(10-fold) 53.85 J48 NFSFOS 96.62(10-fold) 61.76 J48 FSFOA 96.06(10-fold) 21.42 J48 FSFOA 93.16(10-fold) 68.57 J48 FS-NEIR 95.04(10-fold) 61.53 J48 FS-NEIR 92.59(10-fold) 82.35 J48 DAFSFOA 98.33(10-fold) 53.85 3nn DAFSFOA 95.28(10-fold) 77.06 3nn NFSFOA 95.61(10-fold) 61.54 3nn NFSFOA 93.83(10-fold) 76.47 3nn FSFOA 98.87(10-fold) 42.58 3nn FSFOA 92.30(10-fold) 61.76 3nn NSM 98.00(10-fold) 53.84 3nn NSM 92.00(10-fold) 88.23 3nn DAFSFOA 98.16(70%~30%) 69.23 1nn DAFSFOA 95.00(10-fold) 79.70 5nn NFSFOA 95.61(70%~30%) 61.54 1nn NFSFOA 93.23(10-fold) 79.41 5nn FSFOA 98.07(70%~30%) 50.00 1nn FSFOA 89.43(10-fold) 54.28 5nn SFS 97.69(70%~30%) 35.38 1nn DAFSFOA 97.27(2-fold) 67.65 rbf-svm SBS 94.77(70%~30%) 46.15 1nn NFSFOA 95.16(2-fold) 58.82 rbf-svm SFFS 96.56(70%~30%) 36.92 1nn FSFOA 94.58(2-fold) 57.14 rbf-svm DAFSFOA 98.61(70%~30%) 68.46 J48 HGAFS 92.76(2-fold) 82.35 rbf-svm NFSFOA 96.73(70%~30%) 61.54 J48 DAFSFOA 98.44(70%~30%) 74.56 1nn FSFOA 96.00(70%~30%) 57.14 J48 NFSFOA 95.16(70%~30%) 58.82 1nn UFSACO 95.08(70%~30%) 61.53 J48 FSFOA 89.52(70%~30%) 54.28 1nn DAFSFOA 97.69(70%~30%) 70.00 5nn SVM-FuzCoc 89.46(70%~30%) 88.23 1nn NFSFOA 95.70(70%~30%) 38.46 5nn DAFSFOA 96.60(70%~30%) 73.82 J48 FSFOA 99.20(70%~30%) 30.76 5nn NFSFOA 99.06(70%~30%) 67.65 J48 DAFSFOA 96.07(2-fold) 53.85 rbf-svm FSFOA 95.12(70%~30%) 47.05 J48 NFSFOA 96.06(2-fold) 37.17 rbf-svm UFSACO 88.61(70%~30%) 11.17 J48 HGAFS 98.31(2-fold) 53.85 rbf-svm Cleveland DAFSFOA 62.64(70%~30%) 69.23 1nn Dermatology DAFSFOA 98.26(10-fold) 71.18 J48 NFSFOA 62.22(70%~30%) 61.54 1nn NFSFOA 97.81(10-fold) 73.53 J48 FSFOA 55.55(70%~30%) 71.42 1nn FSFOA 96.99(10-fold) 21.42 J48 SVM-FuzCoc 61.01(70%~30%) 46.10 1nn FS-NEIR 93.95(10-fold) 70.58 J48 SFS 51.79(70%~30%) 47.70 1nn DAFSFOA 99.40(70%~30%) 67.06 1nn SBS 54.80(70%~30%) 38.50 1nn NFSFOA 99.07(70%~30%) 58.82 1nn SFFS 49.55(70%~30%) 53.80 1nn FSFOA 97.27(70%~30%) 45.71 1nn Vehicle DAFSFOA 78.00(10-fold) 33.33 J48 续表 3 数据集 算法 AC/% DR/% 分类器 数据集 算法 AC/% DR/% 分类器 Dermatology SFS 94.02(70%~30%) 44.70 1nn Vehicle NFSFOA 77.74(10-fold) 44.44 J48 SBS 91.78(70%~30%) 58.23 1nn FSFOA 73.04(10-fold) 31.57 J48 SFFS 93.70(70%~30%) 62.35 1nn FS-NEIR 70.98(10-fold) 50.00 J48 SVM-FuzCoc 94.11(70%~30%) 64.70 1nn DAFSFOA 77.17(70%~30%) 51.11 5nn DAFSFOA 98.95(70%~30%) 77.21 J48 NFSFOA 76.77(70%~30%) 55.56 5nn NFSFOA 98.15(70%~30%) 70.59 J48 FSFOA 73.98(70%~30%) 50.00 5nn FSFOA 90.09(70%~30%) 44.11 J48 PSO(4-2) 85.30(70%~30%) 68.40 5nn UFSACO 95.28(70%~30%) 26.47 J48 DAFSFOA 69.38(2-fold) 66.67 rbf-svm Sonar DAFSFOA 88.51(2-fold) 62.83 rbf-svm NFSFOA 69.03(2-fold) 66.67 rbf-svm NFSFOA 75.94(2-fold) 78.33 rbf-svm FSFOA 62.41(2-fold) 47.22 rbf-svm FSFOA 65.86(2-fold) 54.09 rbf-svm Heart-statlog DAFSFOA 85.22(10-fold) 69.23 J48 HGAFS 87.02(2-fold) 75.00 rbf-svm NFSFOA 84.07(10-fold) 61.54 J48 DAFSFOA 92.06(10-fold) 72.22 J48 FSFOA 85.15(10-fold) 48.07 J48 NFSFOA 85.18(10-fold) 65.00 J48 FS-NEIR 79.86(10-fold) 46.15 J48 FSFOA 82.69(10-fold) 52.45 J48 DAFSFOA 85.92(10-fold) 60.00 3nn FS-NEIR 75.97(10-fold) 91.66 J48 NFSFOA 83.33(10-fold) 53.85 3nn DAFSFOA 98.33(70%~30%) 76.58 1nn FSFOA 85.18(10-fold) 35.71 3nn NFSFOA 76.19(70%~30%) 76.67 1nn NSM 84.00(10-fold) 69.23 3nn FSFOA 85.43(70%~30%) 57.37 1nn DAFSFOA 85.22(2-fold) 53.85 rbf-svm DAFSFOA 95.40(70%~30%) 75.67 5nn NFSFOA 84.81(2-fold) 76.92 rbf-svm NFSFOA 74.60(70%~30%) 68.33 5nn FSFOA 84.07(2-fold) 50.00 rbf-svm FSFOA 86.98(70%~30%) 44.26 5nn HGAFS 82.59(2-fold) 76.92 rbf-svm PSO(4-2) 78.16(70%~30%) 81.26 5nn — — — — Glass DAFSFOA 79.90(10-fold) 37.22 J48 Segmentation DAFSFOA 97.10(10-fold) 68.16 3nn NFSFOA 78.13(10-fold) 33.33 J48 NFSFOA 96.88(10-fold) 52.63 3nn FSFOA 75.70(10-fold) 50.00 J48 FSFOA 96.20(10-fold) 30.00 3nn FS-NEIR 68.53(10-fold) 22.22 J48 NSM 95.00(10-fold) 63.15 3nn DAFSFOA 77.23(70%~30%) 42.77 1nn Hepatitis DAFSFOA 91.56(10-fold) 64.21 J48 NFSFOA 75.38(70%~30%) 55.56 1nn FSFOA 86.45(10-fold) 55.00 J48 FSFOA 71.88(70%~30%) 40.00 1nn FS-NEIR 81.11(10-fold) 68.42 J48 SFS 72.24(70%~30%) 26.66 1nn DAFSFOA 91.68(10-fold) 63.68 3nn SBS 71.77(70%~30%) 37.77 1nn FSFOA 87.09(10-fold) 42.10 3nn SFFS 71.77(70%~30%) 37.77 1nn NSM 90.00(10-fold) 15.78 3nn DAFSFOA 66.83(2-fold) 55.55 rbf-svm DAFSFOA 92.23(70%~30%) 66.57 J48 NFSFOA 68.69(2-fold) 33.33 rbf-svm FSFOA 84.40(70%~30%) 45.00 J48 FSFOA 68.22(2-fold) 60.00 rbf-svm UFSACO 78.87(70%~30%) 75.00 J48 HGAFS 65.51(2-fold) 44.44 rbf-svm — — — — SRBCT DAFSFOA 99.99(70%~30%) 92.33 1nn — — — — NFSFOA 94.73(70%~30%) 61.48 1nn — — — — FSFOA 94.73(70%~30%) 49.06 1nn — — — — SVM-FuzCoc 98.88(70%~30%) 98.57 1nn — — — — -
[1] LI Jundong, CHENG Kewei, WANG Suhang, et al. Feature selection: a data perspective[J]. ACM computing surveys, 2018, 50(6): 94. [2] XUE Bing, ZHANG Mengjie, BROWNE W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE transactions on evolutionary computation, 2016, 20(4): 606–626. doi: 10.1109/TEVC.2015.2504420 [3] DASH M, LIU H. Feature selection for classification[J]. Intelligent data analysis, 1997, 1(1/2/3/4): 131–156. [4] GHAEMI M, FEIZI-DERAKHSHI M R. Forest optimization algorithm[J]. Expert systems with applications, 2014, 41(15): 6676–6687. doi: 10.1016/j.eswa.2014.05.009 [5] GHAEMI M, FEIZI-DERAKHSHI M R. Feature selection using Forest Optimization Algorithm[J]. Pattern recognition, 2016, 60: 121–129. doi: 10.1016/j.patcog.2016.05.012 [6] 初蓓, 李占山, 张梦林, 等. 基于森林优化特征选择算法的改进研究[J]. 软件学报, 2018, 29(9): 2547–2558. doi: 10.13328/j.cnki.jos.005395 CHU Bei, LI Zhanshan, ZHANG Menglin, et al. Research on improvements of feature selection using forest optimization algorithm[J]. Journal of software, 2018, 29(9): 2547–2558. doi: 10.13328/j.cnki.jos.005395 [7] UNLER A, MURAT A, CHINNAM R B. mr2PSO: a maximum relevance minimum redundancy feature selection method based on swarm intelligence for support vector machine classification[J]. Information sciences, 2011, 181(20): 4625–4641. doi: 10.1016/j.ins.2010.05.037 [8] CERVANTE L, BING Xue, ZHANG Mengjie, et al. Binary particle swarm optimisation for feature selection: a filter based approach[C]//2012 IEEE Congress on Evolutionary Computation. Brisbane, 2012: IEEE, 2012: 1−8. [9] KANNAN S S, RAMARAJ N. A novel hybrid feature selection via Symmetrical Uncertainty ranking based local memetic search algorithm[J]. Knowledge-based systems, 2010, 23(6): 580–585. doi: 10.1016/j.knosys.2010.03.016 [10] SONG Xianfang, ZHANG Yong, GONG Dunwei, et al. Feature selection using bare-bones particle swarm optimization with mutual information[J]. Pattern recognition, 2021, 112: 107804. doi: 10.1016/j.patcog.2020.107804 [11] XU Hang, XUE Bing, ZHANG Mengjie. A duplication analysis-based evolutionary algorithm for biobjective feature selection[J]. IEEE transactions on evolutionary computation, 2021, 25(2): 205–218. doi: 10.1109/TEVC.2020.3016049 [12] JOHN LU Z Q. The elements of statistical learning: data mining, inference, and prediction[J]. Journal of the royal statistical society:series A (statistics in society), 2010, 173(3): 693–694. doi: 10.1111/j.1467-985X.2010.00646_6.x [13] SUN Zehang, BEBIS G, MILLER R. Object detection using feature subset selection[J]. Pattern recognition, 2004, 37(11): 2165–2176. doi: 10.1016/j.patcog.2004.03.013 [14] DAVIES S, RUSSELL S. NP-completeness of searches for smallest possible feature sets[C]//AAAI Symposium on Intelligent Relevance. Menlo Park: AAAI Press, 1994: 37−39. [15] MARCANO-CEDEO A, QUINTANILLA-DOMÍNGUEZ J, CORTINA-JANUCHS M G, et al. Feature sele-ction using Sequential Forward Selection and classify-cation applying Artificial Metaplasticity Neural Netwo-rk[C]// IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society. Glendale: IEEE, 2010: 2845−2850. [16] PENG Hongyi, JIANG Chunfu, FANG Xiang, et al. Variable selection for Fisher linear discriminant analysis using the modified sequential backward selection algorithm for the microarray data[J]. Applied mathematics and computation, 2014, 238: 132–140. doi: 10.1016/j.amc.2014.03.141 [17] IŞıK Ş. Dominant point detection based on suboptimal feature selection methods[J]. Expert systems with applications, 2020, 161: 113741. doi: 10.1016/j.eswa.2020.113741 [18] SETIAWAN D, KUSUMA W A, WIGENA A H. Sequential forward floating selection with two selection criteria[C]//2017 International Conference on Advanced Computer Science and Information Systems (ICACSIS). Bali: IEEE, 2017: 395−400. [19] SINGH P, CHAUDHURY S, PANIGRAHI B K. Hybrid MPSO-CNN: multi-level particle swarm optimized hyperparameters of convolutional neural network[J]. Swarm and evolutionary computation, 2021, 63: 100863. doi: 10.1016/j.swevo.2021.100863 [20] ZHOU Yu, ZHANG Wenjun, KANG Junhao, et al. A problem-specific non-dominated sorting genetic algorithm for supervised feature selection[J]. Information sciences, 2021, 547: 841–859. doi: 10.1016/j.ins.2020.08.083 [21] LI Yongbo, SOLEIMANI H, ZOHAL M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives[J]. Journal of cleaner production, 2019, 227: 1161–1172. doi: 10.1016/j.jclepro.2019.03.185 [22] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008 [23] DONG Hongbin, PAN Yuyao, SUN Jing. High dimensional feature selection method of dual gbest based on PSO[C]//2020 IEEE Congress on Evolutionary Computation. Glasgow: IEEE, 2020: 1−8. [24] AGRAWAL R K, KAUR B, SHARMA S. Quantum based Whale Optimization Algorithm for wrapper feature selection[J]. Applied soft computing, 2020, 89: 106092. doi: 10.1016/j.asoc.2020.106092 [25] LI Anda, XUE Bing, ZHANG Mengjie. Improved binary particle swarm optimization for feature selection with new initialization and search space reduction strategies[J]. Applied soft computing, 2021, 106: 107302. doi: 10.1016/j.asoc.2021.107302 [26] XIE Qi, CHENG Gengguo, ZHANG Xiao, et al. Feature selection using improved forest optimization algorithm[J]. Information technology and control, 2020, 49(2): 289–301. doi: 10.5755/j01.itc.49.2.24858 [27] MOUSTAKIDIS S P, THEOCHARIS J B. SVM-FuzCoC: a novel SVM-based feature selection method using a fuzzy complementary criterion[J]. Pattern recognition, 2010, 43(11): 3712–3729. doi: 10.1016/j.patcog.2010.05.007 [28] HU Qinghua, CHE Xunjian, ZHANG Lei, et al. Feature evaluation and selection based on neighborhood soft margin[J]. Neurocomputing, 2010, 73(10/11/12): 2114–2124. [29] HUANG Jinjie, CAI Yunze, XU Xiaoming. A hybrid genetic algorithm for feature selection wrapper based on mutual information[J]. Pattern recognition letters, 2007, 28(13): 1825–1844. doi: 10.1016/j.patrec.2007.05.011 [30] ZHU Wenzhi, SI Gangquan, ZHANG Yanbin, et al. Neighborhood effective information ratio for hybrid feature subset evaluation and selection[J]. Neurocomputing, 2013, 99: 25–37. doi: 10.1016/j.neucom.2012.04.024 [31] TABAKHI S, MORADI P, AKHLAGHIAN F. An unsupervised feature selection algorithm based on ant colony optimization[J]. Engineering applications of artificial intelligence, 2014, 32: 112–123. doi: 10.1016/j.engappai.2014.03.007 [32] XUE Bing, ZHANG Mengjie, BROWNE W N. Particle swarm optimisation for feature selection in classification: novel initialisation and updating mechanisms[J]. Applied soft computing, 2014, 18: 261–276. doi: 10.1016/j.asoc.2013.09.018









 下载:
下载: