ERP detection of multi-feature embedding in the low-dimensional subspace for cross-subject RSVP
-
摘要: 基于快速序列视觉呈现（rapid serial visual presentation, RSVP）范式的目标图像检索借助于人脑在看到目标图像时产生的事件相关电位（event-related potentials, ERP）来完成复杂目标图像检索。在应用RSVP范式进行复杂目标图像检索时存在跨时段甚至跨被试的问题。对此，本文提出了一种面向跨被试RSVP的多特征低维子空间嵌入的ERP检测方法，首先采用迁移学习方法中的欧式空间对齐对不同被试的数据进行对齐，其次将来自不同空间的特征分别进行有监督降维、重构。最终采用留一被试法作为检验方法、平衡准确率作为评价指标，在PhysioNetRSVP数据集以及清华RSVP数据集下共计14个长度分段中，有12个长度分段达到最优分类结果。结果表明本文提出的多特征低维子空间嵌入方法能够有效提升ERP检测时的稳定性。Abstract: The rapid serial visual presentation (RSVP)-based target image retrieval method finishes complex target image retrieval by relying on the event-related potentials (ERP) generated by the human brain when noticing a target image. When applying the RSVP paradigm to complex target image retrieval, the problems of cross-period and even cross-subjects often arise. To solve these problems, this paper proposes an ERP detection method of multi-feature embedding in a low-dimensional subspace for cross-subject RSVP. First, the Euclidean space data alignment in the transfer learning method is used to align the EEG data. Then, supervised dimensionality reduction and reconstruction are conducted on features from different spaces, respectively. Finally, the leave-one-subject-out method is used as the test method and the balanced classification accuracy rate as the evaluation indicator. Consequently, out of 14 length segments under the PhysioNetRSVP dataset and the Tsinghua RSVP dataset, 12 length segments achieve optimal classification results. Experimental results show that multi-feature embedding in the low-dimensional subspace proposed in this paper can effectively improve the stability of ERP detection.
-
基于计算机视觉的目标图像检索应用广泛，然而有些目标具有伪装、遮挡、环境变化以及不确定等特性，机器识别由于场景泛化能力弱、本征抽象难导致它对这类复杂目标难以准确识别[1-3]。而基于快速序列视觉呈现（rapid serial visual presentation, RSVP）的目标图像检索借助于人脑在看到目标图像时产生的ERP来完成目标图像检索。RSVP实验范式是通过快速呈现给被试一系列图像，使得被试在发现目标图像后脑电信号中产生事件相关电位（event-related potentials, ERP）。通过检测ERP来判断当前被试是否发现目标图像。得益于人脑强大的泛化能力，其能够对存在伪装、遮挡的复杂目标图像进行识别。ERP是脑电图(electroencephalogram, EEG)中的一个诱发电位，其包含P300、N170、N200等成分，可以通过听觉或者视觉等刺激来进行诱发[4]。
值得注意的是，在经典的RSVP范式中ERP是基于单试次的，相比于基于多试次叠加检测ERP的拼写器范式，存在较大的难度。此外，在应用RSVP范式进行在线的目标图像检测时往往存在跨时段甚至跨被试的问题。跨时段检测会受到被试个人精神状态变化、脑电帽电极位置偏移、外部环境变化等因素的干扰，跨被试检测还会受到被试间个体差异的影响[5]。
为了寻求更好的方法来提高单试次ERP检测的准确率。Solis-Escalante等[6]提出了基于经验模态分解的单试次检测方法，从P300的训练集中分解平均事件响应，在事件响应分解上提供了一个很好的方向；Krusienski等[7]使用逐步线性判别分析(stepwise linear discriminant analysis, SWLDA)来对P300进行判别，在判别器层面提供了一个改进方向；Rivet等[8-9]提出了一种通过构造一个空间滤波器来提高EEG数据信噪比的xDAWN算法，在EEG数据信噪比提升的方法改善上做出了贡献；Lawhern等[10]提出了一个紧凑的卷积神经网络模型架构EEGNet，为EEG数据的模式识别提供了一个优秀的神经网络模型基线。然而这些模型都没有对跨被试情况下的模式识别进行专门的优化设计。
为了增强模型的跨被试性能，迁移学习被引入到EEG数据的模式识别当中,其思路是利用源域的信息来提高目标域的学习性能。Zanini等[11]提出了一种迁移学习方法，称为RA-MDRM，通过利用来自其他被试的辅助数据来提高MDRM分类器的准确率。值得注意的是，该方法还需要用到来自新被试的少量有标签的EEG数据。何赫等[12]提出了一种欧式空间EEG数据对齐的方法，通过将每个试次EEG数据的平均协方差矩阵映射到单位矩阵上来达到数据对齐的目的，这个方法无需用到来自新被试的标签。但是这些方法只使用了单一特征来进行分类，可以考虑使用多特征方法来整合它们，从而进一步提高模型稳定性[13]。
本文在以往研究者对RSVP、ERP检测以及跨被试研究的基础上，提出了一种面向跨被试RSVP的多特征低维子空间嵌入的ERP检测方法。
1. 欧式空间对齐的多特征低维子空间嵌入方法
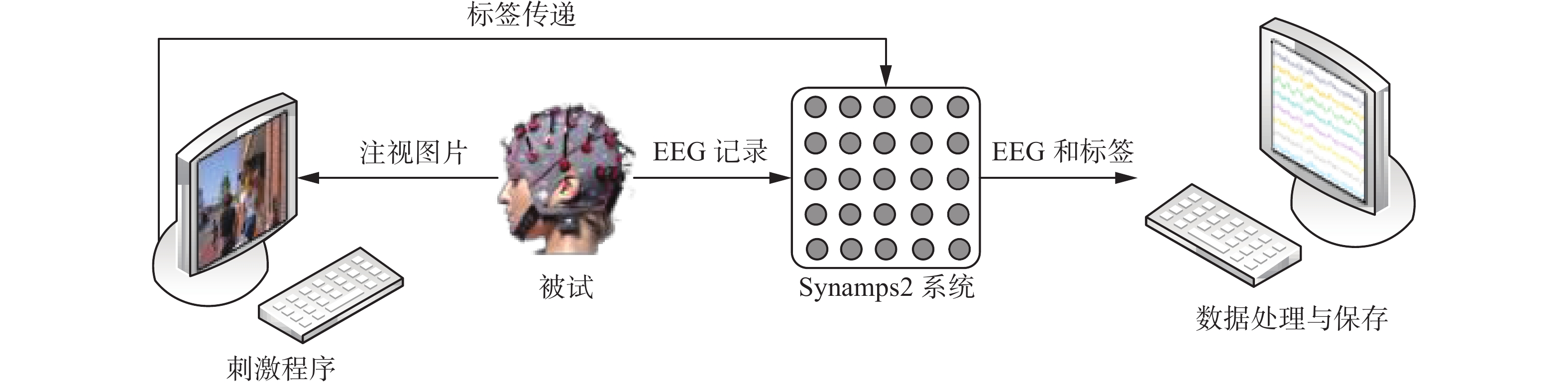
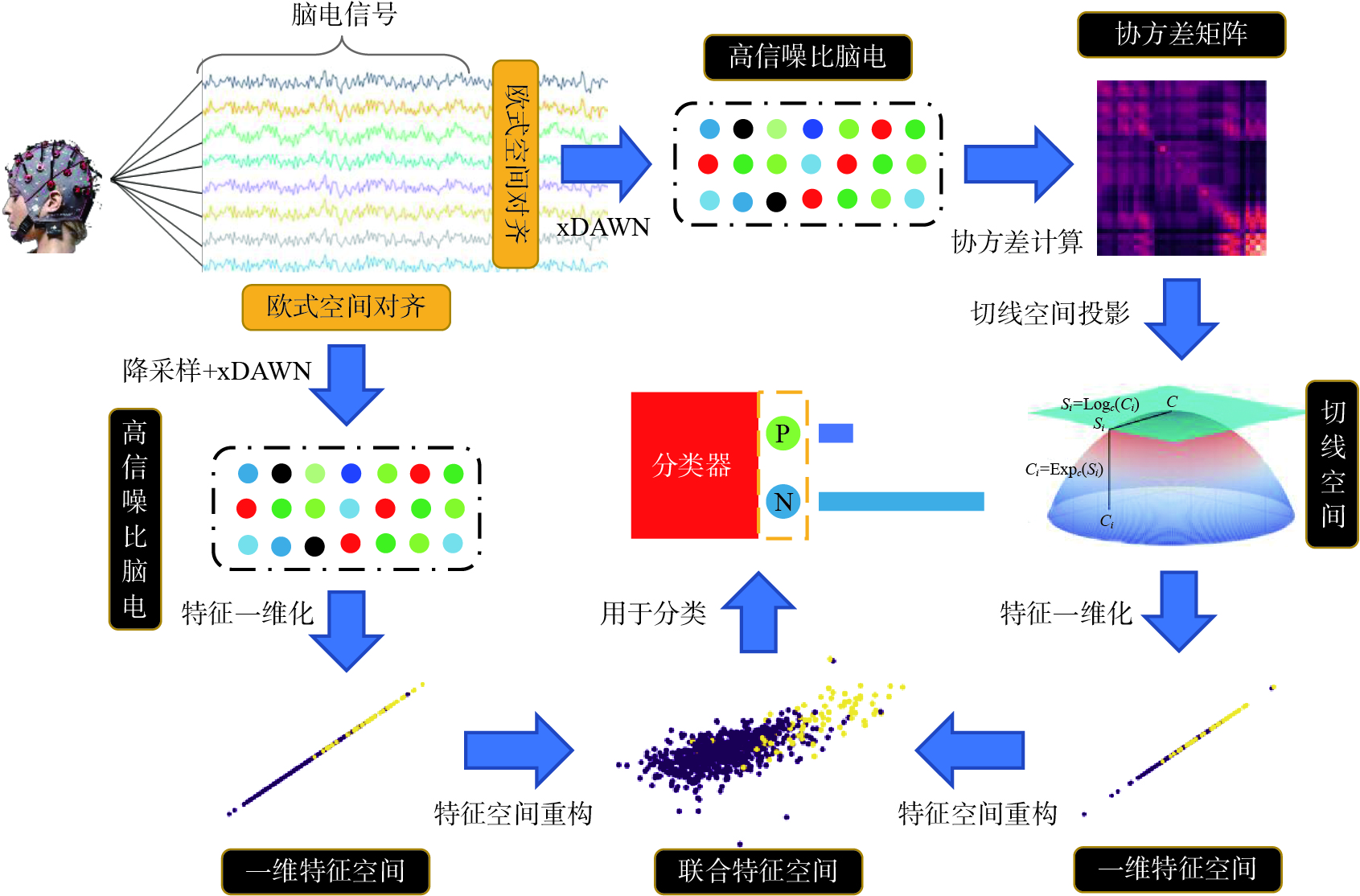
图1给出了使用本文多特征低维子空间嵌入方法这一特征联合方法对脑电信号数据处理的整个流程。
图 1 脑电信号处理流程图Fig. 1 Flowchart of EEG signal processing
下载:
全尺寸图片
首先需要对脑电信号进行欧式空间对齐，将不同被试的脑电信号都对齐到同一个欧式空间，使得数据层面上各被试的数据表征更接近。
1.1 欧式空间对齐
欧式空间对齐(euclidean space data alignment, EA)是一种迁移学习方法。其可以在不需要任何来源于新被试的EEG数据标签的情况下，使得来自不同被试的EEG数据分布更加接近，即在欧式空间内对齐被试的EEG数据[12]。目的在于通过这种方法来使得在原数据集上训练的分类器，在新的被试上同样具有较优表现。
假设一个被试有
$ n $ 个试次的EEG数据,其中第$ i $ 个试次的EEG数据为$ {X_i} $ ，可以通过这$ n $ 个试次计算参考矩阵$\overline {\boldsymbol{R}}$ 。$$ \overline {\boldsymbol{R}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\boldsymbol{X}}_i}} {\boldsymbol{X}}_i^{\rm{T}} $$ (1) 参考矩阵
$\overline {\boldsymbol{R}}$ 的实际意义是当前被试每个试次协方差矩阵的平均矩阵。计算出参考矩阵$\overline {\boldsymbol{R}}$ 后就可以使用式(2)来对齐样本。$$ {\tilde {\boldsymbol{X}}_i} = {\overline {\boldsymbol{R}} ^{ - \frac{1}{2}}}{{\boldsymbol{X}}_i} $$ (2) 其中
${\tilde {\boldsymbol{X}}_i}$ 表示对齐后的样本${{\boldsymbol{X}}_i}$ 。1.2 基于双路并行构建多特征
接下来分为两路对脑电信号进行处理，以此构建脑电信号的多特征，防止单一特征在跨被试时对脑电信号的评价存在偏见。
1.2.1 脑电信号表层特征提取
第一路，负责提取脑电信号中人类能够识别的表层特征，即其信号幅值。ERP在原始的时域上形成的波形具备一定的辨识度，因此对其信号幅值的观察中会包含一些重要信息。由于直接使用信号幅值作为特征，易出现对训练集被试过拟合的问题。为了防止对训练集被试过度拟合，本文在此路中对信号进行了降采样操作，并且采用xDAWN空域滤波器来提升ERP响应的信噪比。
xDAWN是一种空域滤波的方法，旨在提高ERP响应的信噪比。xDAWN最初是为 P300 诱发电位设计的，通过参照非目标响应来增强目标响应，后来被推广到ERP的检测中。
xDAWN依据诱发电位的特点揭示了一个响应模式
$$ {\boldsymbol{S}} = {\boldsymbol{DA}} + {\boldsymbol{N}} $$ (3) 式中：
${\boldsymbol{S}} \in {{\bf{R}}^{{N_t} \times {N_s}}}$ 表示脑电信号，其中$N_t$ 表示采样点个数，$N_s$ 表示通道个数；${\boldsymbol{D}} \in {{\bf{R}}^{{N_t} \times {N_e}}}$ 是一个托普利兹矩阵(Toeplitz matrix)，当存在刺激时其第一列的值被固定为1,${\boldsymbol{A}} \in {{\bf{R}}^{{N_e} \times {N_s}}}$ 表示目标刺激的同步响应，$N_e$ 表示包含ERP的样本数量；${\boldsymbol{N}}$ 表示大脑的持续活动及伪影。1.2.2 脑电信号深层特征提取
第二路，负责提取脑电信号中深层的特征。由于被试间存在一定的个体差异，本文对由信号得到的特征多次使用标签进行检验，以此让特征中包含更多跨被试且ERP相关的信息。首先使用xDAWN空域滤波器提高信号信噪比；其次计算信号的协方差矩阵作为特征，减少跨被试时电极位置偏移的影响；最后将信号投影到切线空间，获取其深层信息。
切线空间投影能够将一组协方差矩阵投影到它们的切线空间，该操作可以看成一个核操作[14-15]。切线空间投影可以看成是一个局部近似的流形学习，在转换样本协方差矩阵的同时保留了流形的内部结构。
首先得到样本的协方差矩阵
${{\boldsymbol{C}}_i} = \dfrac{1}{{n - 1}}{{\boldsymbol{X}}_i}{\boldsymbol{X}}_i^{\text{T}}$ (值得注意的是，样本协方差矩阵对于异常值很敏感，可以使用协方差矩阵估计或正则化技术来进行优化[16])。其次需要计算出参考矩阵${{\boldsymbol{C}}_{\rm ref}}$ ，其计算公式为$$ {{\boldsymbol{C}}_{\rm ref}} = {\rm argmin} \left(\displaystyle\sum\limits_{i = 1}^n {\delta _R^2} ({{\boldsymbol{C}}_{\rm ref}},{{\boldsymbol{C}}_i})\right) $$ (4) 式中：
$ {\delta _R} $ 表示协方差矩阵在黎曼空间距离的度量，可以采用梯度下降的方法求解出${{\boldsymbol{C}}_{\rm ref}}$ 。下一步计算出
${{\boldsymbol{C}}_i}$ 在切线空间的投影$$ {{\boldsymbol{S}}_i} = {\rm upper} \left({\boldsymbol{C}}_{\rm ref}^{ - 1/2}{\log _{{{\boldsymbol{C}}_{\rm ref}}}}\left( {{{\boldsymbol{C}}_i}} \right){\boldsymbol{C}}_{\rm ref}^{ - 1/2}\right) $$ (5) 其中，upper表示取矩阵的上三角矩阵，并将其向量化。在向量化的过程中，对主对角线的元素保持不变，非主对角线的元素乘
$ \sqrt 2 $ 。1.3 特征一维化
在采用不同的特征提取方法获得特征集
${\boldsymbol{F}} = \{ {{\boldsymbol{f}}_1},{{\boldsymbol{f}}_2}, \cdots ,{{\boldsymbol{f}}_n}\}$ 后,本文借用线性判别分析的思想来对数据进行有监督降维，其主要目的是使得类内离散度尽可能低，类间离散度尽可能高[17]。首先借助标签将特征集分成两个集合
${{\boldsymbol{F}}_1},{{\boldsymbol{F}}_2}$ ，分别表示0类和1类的特征集合。接着在原特征空间内计算两个集合的均值向量：$$ {{\boldsymbol{\mu}} _i} = \dfrac{1}{{{n_i}}}\displaystyle\sum\limits_{{{\boldsymbol{f}}_j} \in {{\boldsymbol{F}}_i}} {{{\boldsymbol{f}}_j}} ,i = 1,2 $$ (6) 计算这两类的类内离散度矩阵：
$$ {{\boldsymbol{M}}_i} = \displaystyle\sum\limits_{{{\boldsymbol{f}}_j} \in {{\boldsymbol{F}}_i}} {({{\boldsymbol{f}}_j} - {{\boldsymbol{\mu}} _i}){{({{\boldsymbol{f}}_j} - {{\boldsymbol{\mu}} _i})}^{\text{T}}}} ,i = 1,2 $$ (7) 总类内离散度矩阵：
$$ {{\boldsymbol{S}}_{{w}}} = {{\boldsymbol{M}}_{\text{1}}} + {{\boldsymbol{M}}_{\text{2}}} $$ (8) 类间离散度矩阵定义是
$$ {{\boldsymbol{S}}_{{b}}} = ({{\boldsymbol{\mu}}_1} - {{\boldsymbol{\mu }}_2}){({{\boldsymbol{\mu }}_1} - {{\boldsymbol{\mu }}_2})^{\text{T}}} $$ (9) 接着计算
${\boldsymbol{S}}_{{w}}^{ - {{1}}}{{\boldsymbol{S}}_{{b}}}$ 最大特征值对应的特征向量$\boldsymbol \omega$ ，该特征向量即为特征一维化的投影方向。最终得到一维化后的特征
$$ {\boldsymbol{f}}_i' = {{\boldsymbol{\omega }}^{\text{T}}}{{\boldsymbol{f}}_i} $$ (10) 其中
${{\boldsymbol{f}}_i}$ 表示第$ i $ 个样本对应的特征。1.4 基于多特征构建的联合特征空间
由于两路特征采用不一样的提取方法，位于不同的特征空间，如何将其联合是一个关键点。
传统方法中，直接将处于不同特征空间的特征合并到一个高维的混合的特征空间。其特征既存在相同部分（来源于一个特征空间的特征），也存在差异部分（来源于两个特征空间的特征），而分类器本身不知道当前特征来源于哪一个特征空间，这会对分类器的分类任务增加困难，信息量的增加反而可能导致识别精度下降。
本文提出的方法是先将两路得到的特征进行有监督的降维，分别投影到两个一维特征空间，再将两个一维特征空间的特征合并看成两个维度，重构出二维的联合特征空间，每一维的特征都是对先前提取的特征的高度凝练，不同的特征位于不同的维度，互不干扰。
设来源于两个特征空间的特征集分别为
${{\boldsymbol{F}}_a} \in {{\bf{R}}^{{t_a} \times n}}$ 和${{\boldsymbol{F}}_b} \in {{\bf{R}}^{{t_b} \times n}}$ ，通过特征一维化技术计算得到的两个特征空间的投影方向分别为${{\boldsymbol{\omega}} _a} \in {{\bf{R}}^{{t_a} \times 1}}$ 和${{\boldsymbol{\omega}} _b} \in {{\bf{R}}^{{t_b} \times 1}}$ ，则转换后的特征：$$ {{\boldsymbol{F}}_c} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\omega}} _a^{\text{T}}\;\;{{\boldsymbol{F}}_a}} \\ {{\boldsymbol{\omega}} _b^{\text{T}}\;\;{{\boldsymbol{F}}_b}} \end{array}} \right] $$ (11) 得到转换后的特征集
${{\boldsymbol{F}}_c} \in {{\bf{R}}^{2 \times n}}$ 位于新构建的联合特征空间。2. 数据集
在PhysioNetRSVP数据集和清华RSVP数据集下进行测试。数据集均为RSVP范式下的数据集，RSVP实验过程如图2所示。
图 2 RSVP实验范式图Fig. 2 RSVP experiment diagram下载:
全尺寸图片
2.1 PhysioNetRSVP数据集
该数据集来自PhysioNet，包含来自11个健康被试的EEG数据[18]。每个被试都被要求坐在屏幕前接受快速序列视觉呈现，视觉呈现的频率分别为5、6和10 Hz。用于刺激呈现的图像是来自谷歌地图的卫星影像，可以分为包含飞机的目标图像和没有飞机的非目标图像两类。以2048 Hz频率记录的8通道的脑电信号。通道分布遵循10-20国际标准导联系统(PO8, PO7, PO3, PO4, P7, P8, O1 和 O2)，最终采用记录的脑电信号来识别图像是否为目标图像。
本文选取了其中视觉呈现频率为5 Hz （1 s 5张图像）版本的脑电信号，经过[0.15,28] Hz滤波，并将来源于该数据集的脑电信号降采样到256 Hz，其中目标和非目标的比例为1∶9。
2.2 清华RSVP数据集
该数据集来自清华脑机接口研究组，其包含来自64个健康被试的EEG数据。每个被试同样被要求坐在屏幕前接受快速序列视觉呈现，刺激频率为10 Hz (1 s 10张图像)。刺激图片从麻省理工大学计算机科学与人工智能图书馆下载。刺激图像是两类街景图像：包含人类的目标图像和没有人类的非目标图像。以1000 Hz频率记录的64通道的脑电信号，通道分布遵循10-20国际标准导联系统，最终采用记录的脑电信号来识别图像是否为目标图像。
本文选取了其中前10位被试的EEG数据来检验模型，EEG数据已降采样到250 Hz,并且经过[2,30]Hz滤波，根据数据集原文建议删除了第33个、第43个信号较差的通道[19]，其中目标和非目标的比例约为1∶49。
3. 实验与结果
3.1 评价方法
本文采用留一被试法来对结果进行交叉验证，即每次选定一个被试的脑电数据作为测试集，其他被试的数据作为训练集。分类器均固定为收缩协方差矩阵的线性判别分析[20].
由于目标图像和非目标图像的比例较为悬殊，存在样本不均衡的现象。单纯的准确率指标无法有效体现不均衡数据集的真实表现，而平衡准确率(balanced classification accuracy，BCA)能较好的对不平衡样本的识别结果进行评价，因此本文采用平衡准确率来作为评价指标。
$$ {\rm{BCA}} = \dfrac{{\dfrac{{{\text{TP}}}}{{{\text{TP + FP}}}}{\text{ + }}\dfrac{{{\text{TN}}}}{{{\text{FN + TN}}}}}}{2} $$ (12) 将标签为1的样本称为正样本，标签为0的样本称为负样本。TP表示正样本预测正确，FP表示负样本预测错误，FN表示正样本预测错误，TN表示负样本预测正确。
3.2 欧式空间对齐前后对比
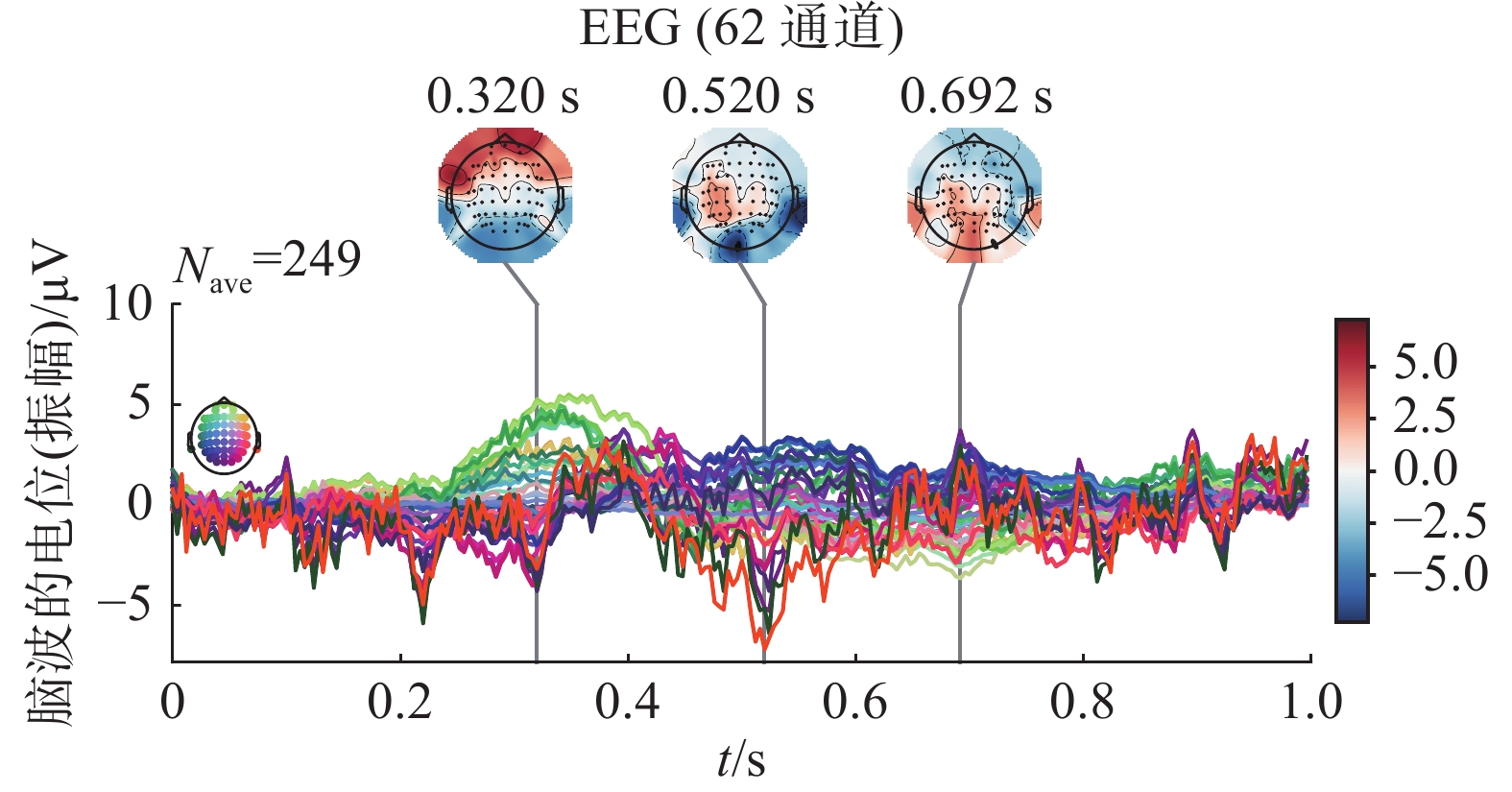
将清华RSVP数据集中的第一位被试看到目标图像时的脑电信号叠加，如图3所示。可以看到其在约300 ms时脑前区的信号幅值较大，属于ERP中的P300成分，说明了该被试确有P300被诱发。
图 3 被试1对齐前目标脑电信号图Fig. 3 The EEG signal of target before alignment of S1下载:
全尺寸图片
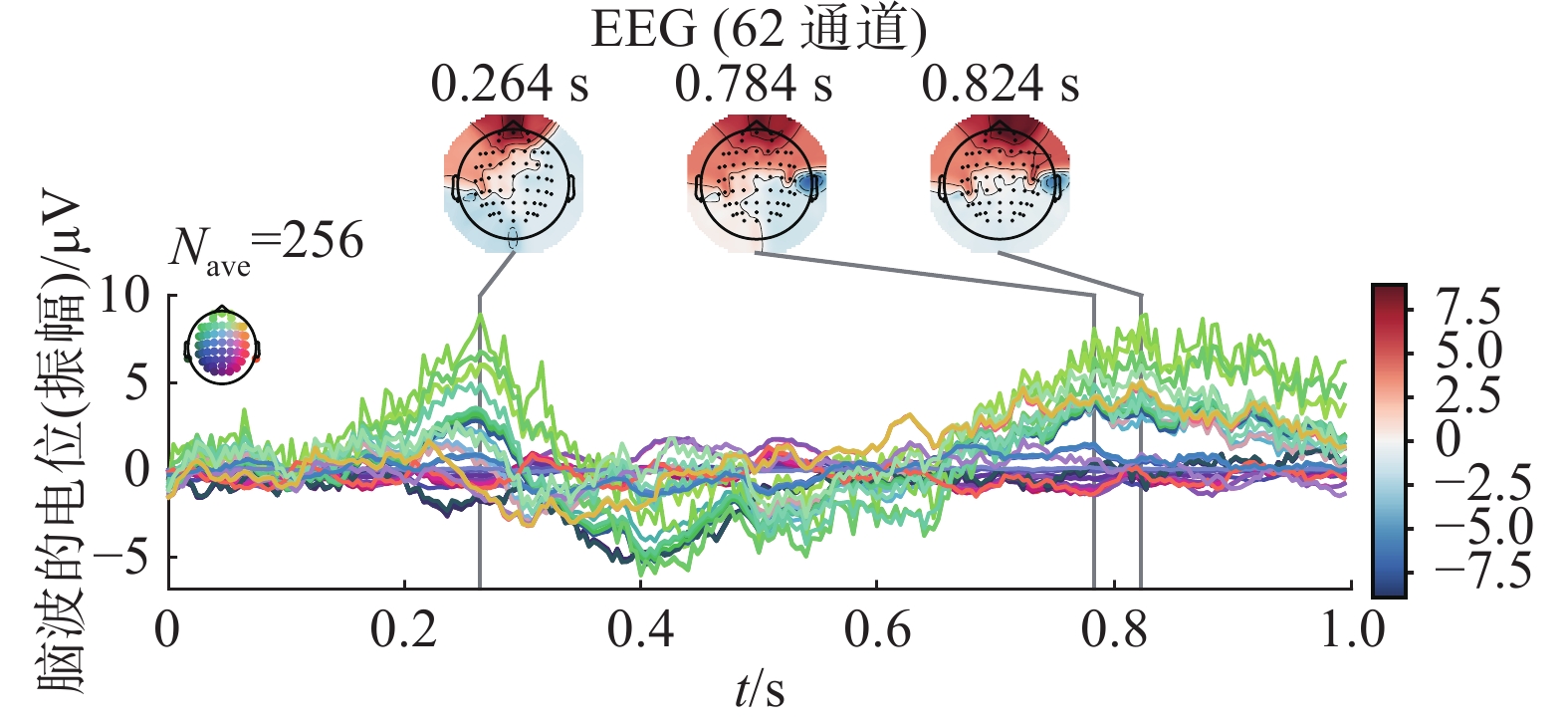
从图4可以看到对齐后目标脑电信号图相比对齐前，多数通道信号的变化更为平稳、均匀，这有助于缩小被试间的差异。通过观察图3、4、5、6，对比被试1和被试10对齐前后的脑电信号可以发现，欧式空间对齐使得原本来源于不同被试的差异较大的脑电信号更为接近。
图 4 被试1对齐后目标脑电信号图Fig. 4 The EEG signal of target after alignment of S1下载:
全尺寸图片
图 5 被试10对齐前目标脑电信号图Fig. 5 The EEG signal of target before alignment of S10下载:
全尺寸图片
图 6 被试10对齐后目标脑电信号图Fig. 6 The EEG signal of target after alignment of S10下载:
全尺寸图片
3.3 特征联合前后的对比
本文在此处对不同方法提取到的特征采用t-sne进行降维可视化[21]。
从图7中可以仅采用一种特征提取方法对于在使用t-sne降维到二维空间后仅有小范围的目标样本聚集，目标样本的类内离散度较高，其与非目标样本直接的类间离散度较低。
图 7 联合前特征降维Fig. 7 Feature dimensionality reduction before union下载:
全尺寸图片
从图8对比直接特征联合和本文特征联合方法之间的差别，直接特征联合由于切线空间投影的数据尺度相比xDAWN的数据尺度较大，xDAWN包含的信息被忽视，使得降维后的样本分布与切线空间投影相似。而本文特征联合方法重构得到的二维空间下的样本，由于预先采用了标签数据进行学习，相比于直接特征联合能够更清晰地区分正负样本。
图 8 联合后特征降维Fig. 8 Feature dimensionality reduction after union下载:
全尺寸图片
3.4 不同长度分段下的对比
在这里本文展现了不同特征提取方法在采用不同长度分段的情况下跨被试分类的平衡准确率。长度分段是指在对脑电数据进行分割时采用的时长t，以当前试次开始点为时间零点，截取时间间隔[0,t]的脑电数据作为当前试次对应脑电样本。
表1给出了其在 PhysioNetRSVP 数据集下的表现，从中可以看出以下几点现象。首先，使用欧式空间对齐数据的分类效果普遍比不对齐数据要好。验证了本文在特征联合的同时使用对齐数据策略的正确性。其次，在7个不同长度分段下，本文的特征联合方法在其中5个长度分段下达到了最好的分类效果，而直接联合只在1个长度分段下达到最优。最后，本文特征联合方法在7个长度的分段下，没有遇到过分类效果最差的情况。
表 1 PhysioNetRSVP下的平衡准确率Table 1 Balanced classification accuracy under PhysioNetRSVP特征提取方法 对齐数据 采用的长度分段 0.4 s 0.5 s 0.6 s 0.7 s 0.8 s 0.9 s 1 s 切线空间投影 是 0.643±0.081 0.704±0.094 0.705±0.095 0.704±0.088 0.696±0.089 0.694±0.090 0.698±0.088 否 0.627±0.092 0.686±0.109 0.690±0.102 0.685±0.093 0.696±0.092 0.690±0.095 0.692±0.096 xDAWN 是 0.627±0.066 0.697±0.100 0.700±0.091 0.702±0.095 0.695±0.093 0.691±0.094 0.690±0.094 否 0.619±0.081 0.677±0.108 0.677±0.099 0.676±0.095 0.676±0.097 0.684±0.097 0.682±0.094 直接联合 是 0.632±0.072 0.706±0.097 0.697±0.100 0.703±0.099 0.692±0.110 0.696±0.100 0.688±0.096 否 0.629±0.089 0.692±0.111 0.693±0.103 0.692±0.096 0.697±0.096 0.697±0.096 0.693±0.089 本文联合 是 0.652±0.078 0.702±0.100 0.703±0.092 0.713±0.091 0.701±0.099 0.701±0.094 0.699±0.096 否 0.634±0.093 0.692±0.108 0.695±0.103 0.693±0.104 0.694±0.104 0.691±0.105 0.685±0.097 表2给出了其在清华 RSVP 数据集下的表现，同样可以发现使用欧式空间对齐数据策略的正确性，本文特征联合方法在7个不同长度分段下，均达到了最优效果。其标准差相较于其他方法也更低，即具备更优的稳定性。
表 2 清华RSVP下的平衡准确率Table 2 Balanced classification accuracy under Tsinghua RSVP特征提取方法 对齐数据 采用的长度分段 0.4 s 0.5 s 0.6 s 0.7 s 0.8 s 0.9 s 1 s 切线空间投影 是 0.700±0.044 0.749±0.048 0.762±0.055 0.767±0.056 0.770±0.064 0.771±0.070 0.775±0.074 否 0.658±0.046 0.713±0.063 0.724±0.072 0.725±0.073 0.717±0.085 0.72±0.093 0.718±0.096 xDAWN 是 0.701±0.039 0.746±0.046 0.761±0.047 0.764±0.049 0.764±0.056 0.767±0.067 0.768±0.068 否 0.655±0.049 0.699±0.061 0.711±0.061 0.711±0.062 0.710±0.068 0.704±0.075 0.710±0.076 直接联合 是 0.698±0.049 0.751±0.055 0.763±0.054 0.765±0.062 0.765±0.068 0.765±0.072 0.770±0.071 否 0.663±0.053 0.708±0.075 0.719±0.079 0.717±0.077 0.721±0.079 0.719±0.085 0.721±0.082 本文联合 是 0.706±0.042 0.752±0.049 0.768±0.051 0.777±0.054 0.777±0.060 0.778±0.067 0.779±0.066 否 0.665±0.053 0.717±0.065 0.725±0.069 0.721±0.077 0.719±0.084 0.718±0.094 0.718±0.097 3.5 不同被试下的对比
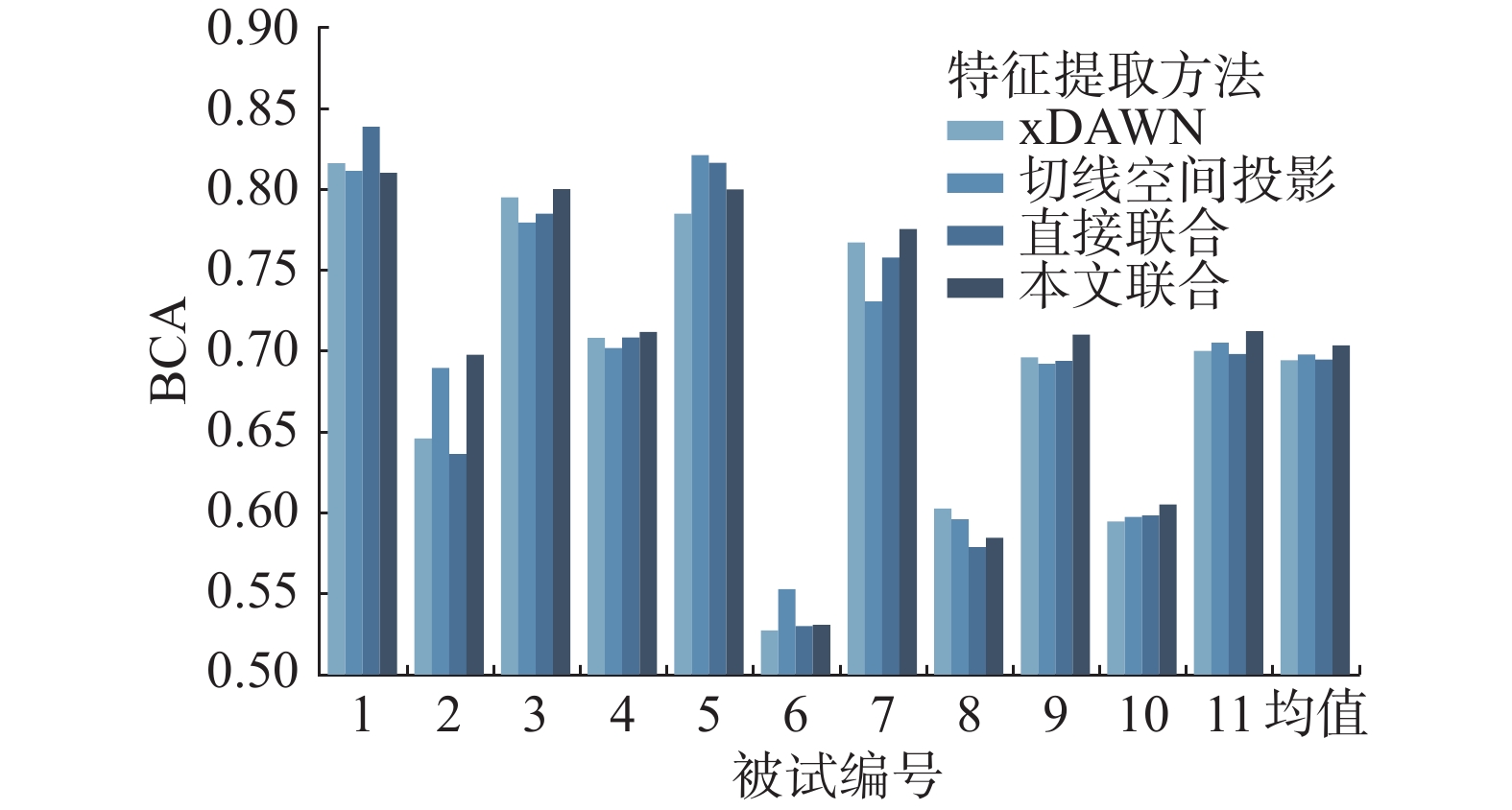
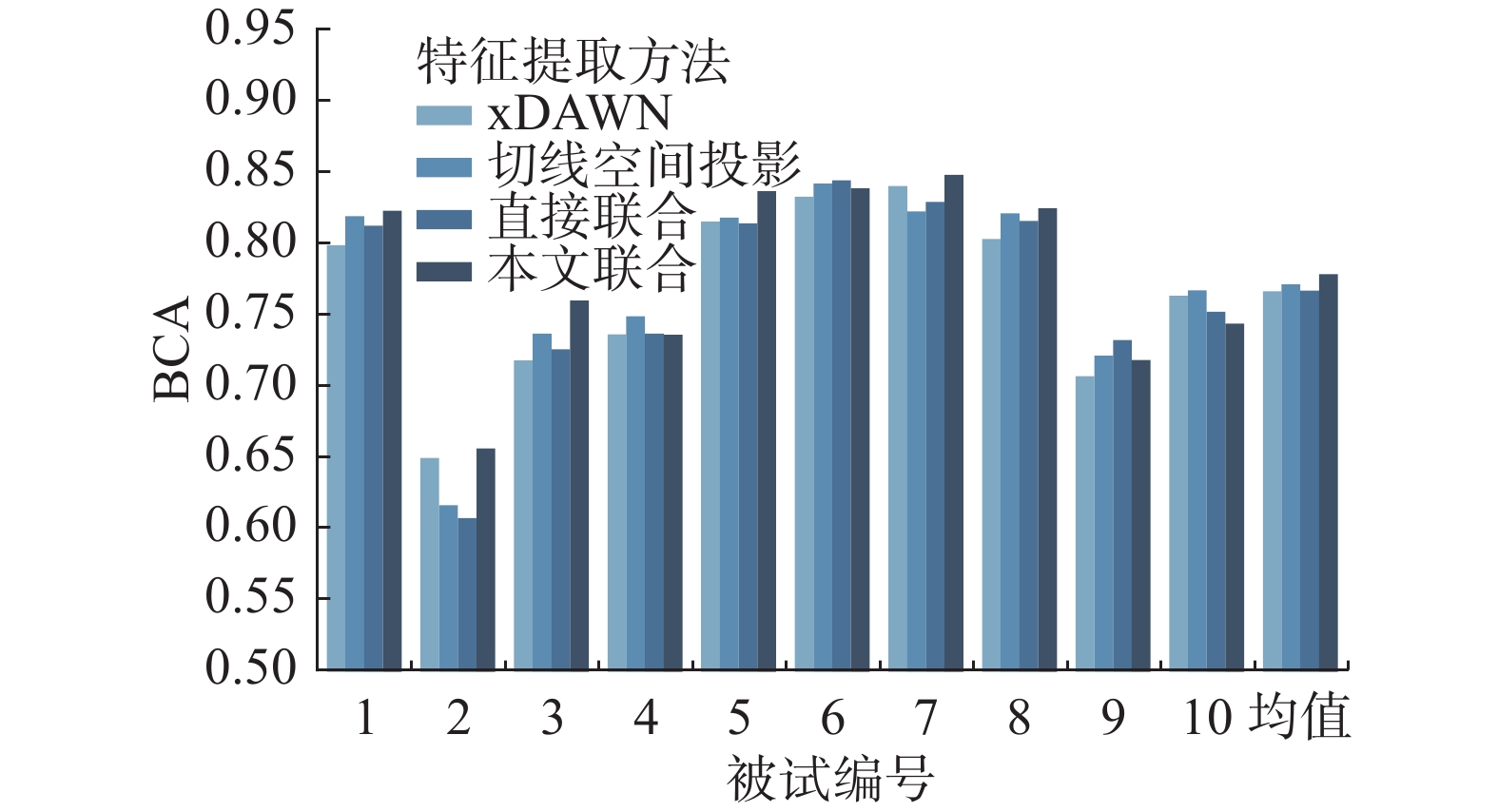
值得注意的是，由于被试间个体差异较大[22-23]，需要对同一模型在不同被试上的表现进行观察。在这里，本文选用每个被试长度分段在0.7 s及以上且采用数据对齐的实验结果做平均值，可以从图9、10观察各特征提取方法在不同被试上分类效果的表现。
图 9 PhysioNetRSVP不同被试的平衡准确率Fig. 9 BCA of different subjects under PhysioNetRSVP下载:
全尺寸图片
图 10 清华RSVP不同被试的平衡准确率Fig. 10 BCA of different subjects under Tsinghua RSVP下载:
全尺寸图片
在 PhysioNetRSVP 数据集的11个被试中, 本文特征联合方法在7个被试上达到了最优；在清华 RSVP 数据集的10个被试中，本文特征联合方法在6个被试上达到了最优。本文特征联合方法在两个数据集上的均值都达到了最优。
4. 结束语
本文提出了一种面向跨被试RSVP的多特征低维子空间嵌入的ERP检测方法。采用欧式空间对齐作为迁移方法，平衡准确率作为评价指标，留一被试法作为检验方法，分别在PhysioNetRSVP数据集和清华RSVP数据集下，探索了该方法在不同脑电长度分段以及不同被试下的表现，并且与切线空间投影特征提取方法、xDAWN特征提取方法以及直接特征联合方法进行了对比。本文特征联合方法在两个数据集共计14个长度分段下，有12个长度分段达到最优分类效果。在两个数据集的超过半数被试上达到了最优的分类效果。实验结果表明，本文提出的特征联合方法能够有效整合来自两个不同空间的特征，使得分类结果更具可靠性。
-
图 1 脑电信号处理流程图
Fig. 1 Flowchart of EEG signal processing
下载:
全尺寸图片
图 2 RSVP实验范式图
Fig. 2 RSVP experiment diagram
下载:
全尺寸图片
图 3 被试1对齐前目标脑电信号图
Fig. 3 The EEG signal of target before alignment of S1
下载:
全尺寸图片
图 4 被试1对齐后目标脑电信号图
Fig. 4 The EEG signal of target after alignment of S1
下载:
全尺寸图片
图 5 被试10对齐前目标脑电信号图
Fig. 5 The EEG signal of target before alignment of S10
下载:
全尺寸图片
图 6 被试10对齐后目标脑电信号图
Fig. 6 The EEG signal of target after alignment of S10
下载:
全尺寸图片
图 7 联合前特征降维
Fig. 7 Feature dimensionality reduction before union
下载:
全尺寸图片
图 8 联合后特征降维
Fig. 8 Feature dimensionality reduction after union
下载:
全尺寸图片
图 9 PhysioNetRSVP不同被试的平衡准确率
Fig. 9 BCA of different subjects under PhysioNetRSVP
下载:
全尺寸图片
图 10 清华RSVP不同被试的平衡准确率
Fig. 10 BCA of different subjects under Tsinghua RSVP
下载:
全尺寸图片
表 1 PhysioNetRSVP下的平衡准确率
Table 1 Balanced classification accuracy under PhysioNetRSVP
特征提取方法 对齐数据 采用的长度分段 0.4 s 0.5 s 0.6 s 0.7 s 0.8 s 0.9 s 1 s 切线空间投影 是 0.643±0.081 0.704±0.094 0.705±0.095 0.704±0.088 0.696±0.089 0.694±0.090 0.698±0.088 否 0.627±0.092 0.686±0.109 0.690±0.102 0.685±0.093 0.696±0.092 0.690±0.095 0.692±0.096 xDAWN 是 0.627±0.066 0.697±0.100 0.700±0.091 0.702±0.095 0.695±0.093 0.691±0.094 0.690±0.094 否 0.619±0.081 0.677±0.108 0.677±0.099 0.676±0.095 0.676±0.097 0.684±0.097 0.682±0.094 直接联合 是 0.632±0.072 0.706±0.097 0.697±0.100 0.703±0.099 0.692±0.110 0.696±0.100 0.688±0.096 否 0.629±0.089 0.692±0.111 0.693±0.103 0.692±0.096 0.697±0.096 0.697±0.096 0.693±0.089 本文联合 是 0.652±0.078 0.702±0.100 0.703±0.092 0.713±0.091 0.701±0.099 0.701±0.094 0.699±0.096 否 0.634±0.093 0.692±0.108 0.695±0.103 0.693±0.104 0.694±0.104 0.691±0.105 0.685±0.097 表 2 清华RSVP下的平衡准确率
Table 2 Balanced classification accuracy under Tsinghua RSVP
特征提取方法 对齐数据 采用的长度分段 0.4 s 0.5 s 0.6 s 0.7 s 0.8 s 0.9 s 1 s 切线空间投影 是 0.700±0.044 0.749±0.048 0.762±0.055 0.767±0.056 0.770±0.064 0.771±0.070 0.775±0.074 否 0.658±0.046 0.713±0.063 0.724±0.072 0.725±0.073 0.717±0.085 0.72±0.093 0.718±0.096 xDAWN 是 0.701±0.039 0.746±0.046 0.761±0.047 0.764±0.049 0.764±0.056 0.767±0.067 0.768±0.068 否 0.655±0.049 0.699±0.061 0.711±0.061 0.711±0.062 0.710±0.068 0.704±0.075 0.710±0.076 直接联合 是 0.698±0.049 0.751±0.055 0.763±0.054 0.765±0.062 0.765±0.068 0.765±0.072 0.770±0.071 否 0.663±0.053 0.708±0.075 0.719±0.079 0.717±0.077 0.721±0.079 0.719±0.085 0.721±0.082 本文联合 是 0.706±0.042 0.752±0.049 0.768±0.051 0.777±0.054 0.777±0.060 0.778±0.067 0.779±0.066 否 0.665±0.053 0.717±0.065 0.725±0.069 0.721±0.077 0.719±0.084 0.718±0.094 0.718±0.097 -
[1] 周燕, 潘丽丽, 陈蓉玉, 等. 结合自适应融合网络与哈希的图像检索算法[J]. 计算机工程与科学, 2021, 43(9): 1616–1622. doi: 10.3969/j.issn.1007-130X.2021.09.012 ZHOU Yan, PAN Lili, CHEN Rongyu, et al. A novel image retrieval algorithm with adaptive fusion network and hash[J]. Computer engineering & science, 2021, 43(9): 1616–1622. doi: 10.3969/j.issn.1007-130X.2021.09.012 [2] 毛莺池, 唐江红, 王静, 等. 基于Faster R-CNN的多任务增强裂缝图像检测方法[J]. 智能系统学报, 2021, 16(2): 286–293. doi: 10.11992/tis.201910004 MAO Yingchi, TANG Jianghong, WANG Jing, et al. Multi-task enhanced dam crack image detection based on Faster R-CNN[J]. CAAI transactions on intelligent systems, 2021, 16(2): 286–293. doi: 10.11992/tis.201910004 [3] 丁斌. 基于非线性哈希的图像与视频检索算法研究[D]. 北京: 北京邮电大学, 2020. DING Bin. Research on image and video retrieval algorithm based on nonlinear hashing[D]. Beijing: Beijing University of Posts and Telecommunications, 2020. [4] WOODMAN G F. A brief introduction to the use of event-related potentials in studies of perception and attention[J]. Attention, perception & psychophysics, 2010, 72(8): 2031–3046. [5] LIU Shuang, WANG Wei, SHENG Yue, et al. Improving the cross-subject performance of the ERP-based brain-computer interface using rapid serial visual presentation and correlation analysis rank[J]. Frontiers in human neuroscience, 2020, 14–296. [6] SOLIS-ESCALANTE T, GENTILETTI G G, YANEZ-SUAREZ O. Single trial P300 detection based on the empirical mode decomposition[C]//2006 International Conference of the IEEE Engineering in Medicine and Biology Society. New York, IEEE, 2006: 1157−1160. [7] KRUSIENSKI D J, SELLERS E W, MCFARLAND D J, et al. Toward enhanced P300 speller performance[J]. Journal of neuroscience methods, 2008, 167(1): 15–21. doi: 10.1016/j.jneumeth.2007.07.017 [8] RIVET B, SOULOUMIAC A, ATTINA V, et al. xDAWN algorithm to enhance evoked potentials: application to brain-computer interface[J]. IEEE transactions on bio-medical engineering, 2009, 56(8): 2035–2043. doi: 10.1109/TBME.2009.2012869 [9] RIVET B, CECOTTI H, SOULOUMIAC A, et al. Theoretical analysis of xDAWN algorithm: application to an efficient sensor selection in a p300 BCI[C]//2011 19th European Signal Processing Conference. Barcelona, IEEE, 2011: 1382−1386. [10] LAWHERN V J, SOLON A J, WAYTOWICH N R, et al. EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces[J]. Journal of neural engineering, 2018, 15(5)–056013. [11] ZANINI P, CONGEDO M, JUTTEN C, et al. Transfer learning: a Riemannian geometry framework with applications to brain–computer interfaces[J]. IEEE transactions on biomedical engineering, 2018, 65(5): 1107–1116. doi: 10.1109/TBME.2017.2742541 [12] HE He, WU Dongrui. Transfer learning for brain-computer interfaces: a euclidean space data alignment approach[J]. IEEE transactions on bio-medical engineering, 2020, 67(2): 399–410. doi: 10.1109/TBME.2019.2913914 [13] WON K, KWON M, JANG S, et al. P300 speller performance predictor based on RSVP multi-feature[J]. Frontiers in human neuroscience, 2019, 13–261. [14] BARACHANT A, BONNET S, CONGEDO M, et al. Classification of covariance matrices using a Riemannian-based kernel for BCI applications[J]. Neurocomputing, 2013, 112: 172–178. doi: 10.1016/j.neucom.2012.12.039 [15] BARACHANT A, BONNET S, CONGEDO M, et al. Multiclass brain–computer interface classification by Riemannian geometry[J]. IEEE transactions on biomedical engineering, 2012, 59(4): 920–928. doi: 10.1109/TBME.2011.2172210 [16] CHEN Yilun, WIESEL A, ELDAR Y C, et al. Shrinkage algorithms for MMSE covariance estimation[J]. IEEE transactions on signal processing, 2010, 58(10): 5016–5029. doi: 10.1109/TSP.2010.2053029 [17] IZENMAN A J. Linear discriminant analysis[M]//Springer Texts in Statistics. New York: Springer New York, 2013: 237−280. [18] MATRAN-FERNANDEZ A, POLI R. Towards the automated localisation of targets in rapid image-sifting by collaborative brain-computer interfaces[J]. PLoS one, 2017, 12(5)–e0178498. [19] ZHANG Shangen, WANG Yijun, ZHANG Lijian, et al. A benchmark dataset for RSVP-based brain-computer interfaces[J]. Frontiers in neuroscience, 2020, 14–568000. [20] LEDOIT O, WOLF M. Honey, I shrunk the sample covariance matrix[J]. Journal of portfolio management, 2004, 30(4): 110–119. doi: 10.3905/jpm.2004.110 [21] VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(11): 2579–2605. [22] 狄洋. 基于脑电个体差异性的身份识别方法研究[D]. 天津: 天津大学, 2019. DI Yang. Research on individual identification approaches based on EEG signals[D]. Tianjin: Tianjin University, 2019. [23] 刘晶. 基于事件相关电位的跨个体脑—机接口研究[D]. 天津: 天津大学, 2014. LIU Jing. Research on subject-independent BCI based on event-related potential[D]. Tianjin: Tianjin University, 2014.
