在传统的分类学习中，每个实例只属于一个类别标记。但在现实世界中，一个样本可能涉及多个语义信息，这种情况符合多标记学习中单个样本多义性的特征。因此，多标记学习更贴近实际应用场景，可以更准确地描述和解决现实世界中的问题。例如，一幅图像往往同时包含“天空”“湖泊”“建筑”等多种重要的语义概念，一种蛋白质可能同时具有多个功能，一篇新闻报道可能同时与“体育”“社会”“娱乐”“财经”等多个话题相关。这类复杂数据很难用单一的语义标记进行描述，合理的处理方式是为每个样本赋予一个标记集合，进而建模和学习。在多标记学习框架下，样本由特征集和相关的标记集构成，学习的目标是将由特征集描述的样本映射到多个类别标记，现已被广泛应用在机器学习、数据挖掘、模式识别等领域^[1-4]。

在多标记学习中，数据特征的高维性容易导致维度灾难，特征选择技术是解决该问题的有效工具。其解决思路之一是通过问题转换的方法来处理多标记数据的特征选择问题，例如，利用二元关系（binary relevance ，BR）^[5]、 标记幂集（label powerset ，LP）^[6]、剪枝问题转换（pruned problem transformation，PPT）等将多标记问题转换为单标记问题。其中，BR将多标记数据转化为多个二分类数据，运用单标记特征选择算法对每个二分类数据进行特征排序。LP将多标记数据中的每种标记组合看作一种类别，进而将多标记数据转化为多类别单标记数据。在剪枝问题转换方法的基础上，Read等^[7]运用卡方检验方法对转换后的数据做特征选择，Doquire等^[8]结合互信息提出了一种多标记数据特征选择算法，避免了LP中类别指数增加及类别不平衡的问题。然而，基于问题转化的特征选择算法往往导致转化后的数据不能真正反映多标记数据之间的真实分布，普遍存在转化过程繁琐耗时，转化后类别数量巨大，忽略标记相关性等问题。

为了避免转化数据带来的信息丢失，基于算法自适应的特征选择算法成为近年来的研究热点。Lee等^[9]运用互信息度量特征与标记的相关性，使用多元互信息近似计算高维联合熵，大大降低了高维信息熵的计算复杂度。在此基础上，Lee等^[10]从理论上分析了为何考虑低阶交叉信息的得分函数能获得有效的特征子集，并提出了新的得分函数以考虑任何程度的交叉信息。由于算法的相关性度量和冗余性度量是独立计算的，在处理大规模多标记数据时，冗余性不能得到很好地体现进而引入冗余特征，为此Lee等^[11]在冗余性度量计算中融合相关性度量，提出了新的特征度量准则。考虑到一些多标记特征选择算法^[12-15]中运用互信息来评估特征的相关性，忽略了已选特征对于相关性度量的影响和标记关系对特征相关性度量的影响，Zhang等^[16]引入条件互信息综合考虑已选特征和标记关系的影响，使用基于两种条件互信息的双条件相关度量特征的相关性。Zhang等^[17]提出了标记依赖、标记冗余、标记互补3种标记关系，通过对3种标记关系和标记关系随着不同特征变化的分析为多标记特征选择提供了新的视角。Qian等^[18]认为在处理多标记数据的特征选择问题时还应该考虑特征之间的互补关系，并结合标签分布学习和特征互补关系提出了一种多标签特征选择算法。

多标记数据往往是高维的连续型数据，以上提到的方法处理连续型数据需要先对数据进行离散化，由此会造成部分信息丢失。邻域粗糙集^[19]通过距离公式和邻域半径来进行信息粒化，可以直接处理连续型数据，已被广泛应用于单标记数据的特征选择^[20-23]。为将邻域粗糙集应用于多标记数据，段洁等^[24]在现有邻域粗糙集基础上重新定义了下近似和依赖度，设计了基于邻域粗糙集的多标记特征选择算法。Lin等^[25]引入大间隔来粒化样本空间，从3种不同的认知观点构造多标记邻域信息系统及其不确定性度量，为多标记特征选择提供了新的邻域粗糙集模型。Long等^[26]和黄锦涛等^[27]使用标记增强方法，将逻辑标记转化为标记分布作为辅助监督信息，由此构建面向标记分布数据的代价敏感特征选择算法。Jorge等^[28]提出了一种分布式模型来计算评估特征的指标和多个标记间的互信息，为大规模多标记数据特征选择提供了方法。

上述研究均假定同一实例的相关标记重要程度相同，并且忽略了特征空间是标记重要程度可能存在差异的内在因素。然而，现实应用中多标记数据的标记间存在潜在的语义关系，不同标记的重要程度也有所不同，并且同一特征与不同标记的相关程度也存在差异，也就是说每个标记都存在相关性高的专属特征。因此，不能区分每个标记对样本的分辨能力，也忽略了每个特征对于不同标记所提供分类信息的差异，进而影响特征选择算法的性能。为此，本文使用谱聚类挖掘标记集中潜在的结构信息，量化标记的重要性和特征权重，进而提出了一种基于加权信息粒化的多标记特征选择算法（multi-label feature selection based on weighted information granulation，MFWIG）。最后，实验结果表明，本文通过融合标记的重要性和特征权重，能有效选择出重要特征，同时避免了高维联合熵的复杂运算，验证了本文算法的有效性。

1.   多标记邻域熵

1.1   大间隔

一个单标记决策系统可以表示为 $ < U,F,D > $ ，其中， $ U=\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\} $ 表示样本集合， $F= \left\{{f}_{1},{f}_{2},\cdots , {f}_{m}\right\}$ 为描述样本的一组特征， $ D $ 是类别标记。

定义 1^[19] 　设 $ U $ 是非空样本集合，若存在 $ U $ 上的距离函数 $ \Delta $ ，使得 $ \forall {x}_{i},{x}_{j},{x}_{k}\in U $ 满足：

1） $\Delta \left({x}_{i},{x}_{j}\right)\geqslant 0$ ，当且仅当 $ {x}_{i}={x}_{j} $ 时， $ \Delta \left({x}_{i},{x}_{j}\right)=0 $ ；

2） $ \Delta \left({x}_{i},{x}_{j}\right)=\Delta \left({x}_{j},{x}_{i}\right) $ ;

3） $\Delta \left({x}_{i},{x}_{k}\right)+\Delta \left({x}_{k},{x}_{j}\right)\geqslant \Delta \left({x}_{i},{x}_{j}\right)$ 。

则称 $ < U,\Delta > $ 是一个度量空间。

在 $ m $ 维特征空间中，给定样本 $ {x}_{i}=({f}_{1i},{f}_{2i},{\cdots ,f}_{mi}) $ 和 $ {x}_{j}=({f}_{1j},{f}_{2j},{\cdots ,f}_{mj}) $ ,样本间的闵可夫斯基距离定义为

当 $ P=1 $ 时， $ \Delta $ 函数表示曼哈顿距离；当 $ P=2 $ 时， $ \Delta $ 函数表示欧氏距离；当 $ P\to \mathrm{\infty } $ 时， ${\Delta _p}({x_i},{x_j}) = {\max _k}\left| {{x_{ki}} - {x_{kj}}} \right|$ 。

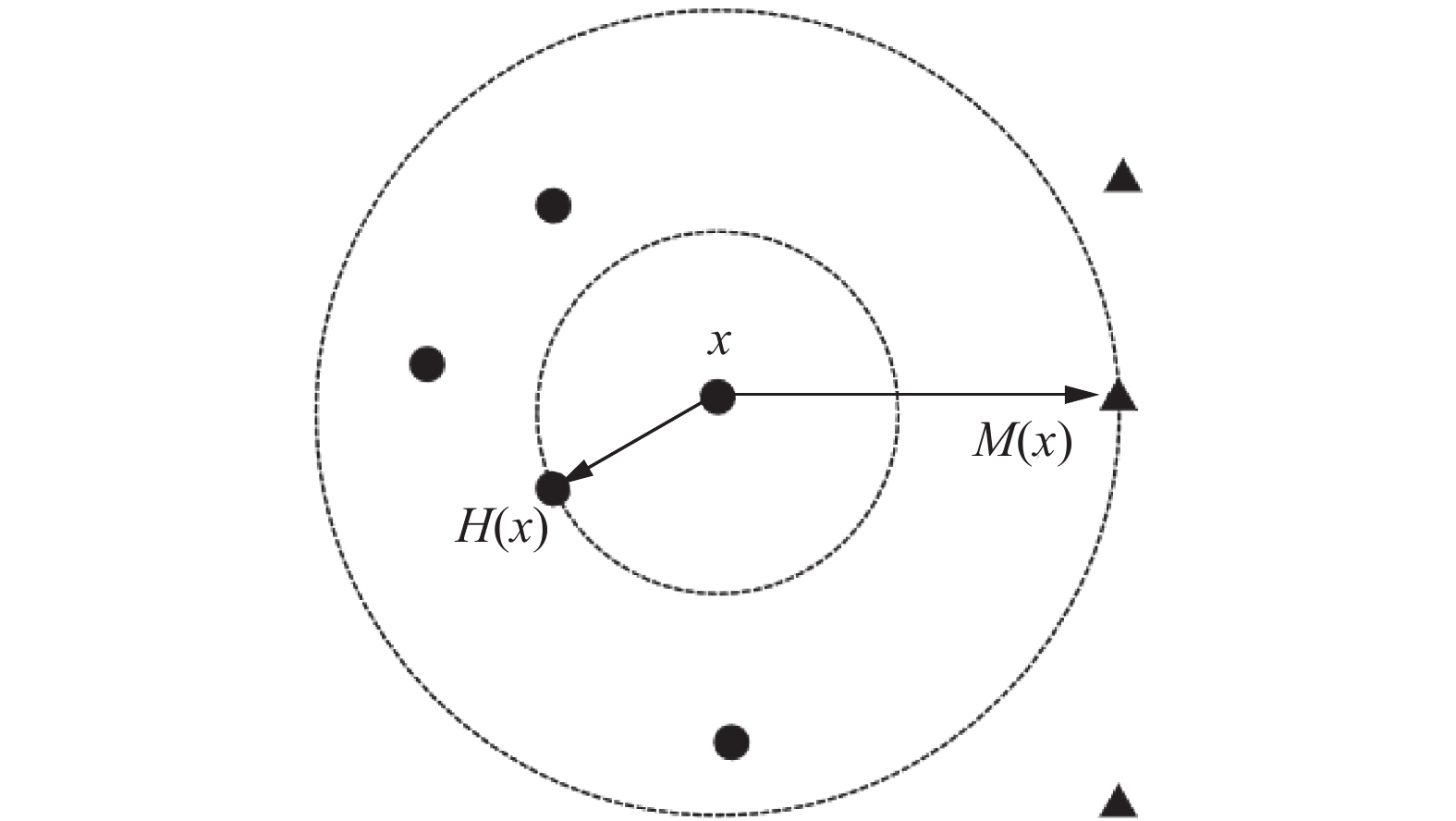
定义2^[25] 　设 $ U $ 是单标记下的非空样本集合， $ \forall x\in U $ ，则样本 $ x $ 的类间隔定义为

式中： $ H\left(x\right) $ 表示样本空间 $ U $ 中距离样本 $ x $ 最近的同类样本， $ M\left(x\right) $ 表示样本空间 $ U $ 中距离样本 $ x $ 最近的异类样本， $ \mathrm{\Delta }\left(x,M\left(x\right)\right) $ 表示样本 $ x $ 到 $ M\left(x\right) $ 的距离， $ \mathrm{\Delta }\left(x,H\left(x\right)\right) $ 表示样本 $ x $ 到 $ H\left(x\right) $ 的距离。分类间隔为样本 $ x $ 到 $ M\left(x\right) $ 和 $ H\left(x\right) $ 的距离之差，如图1所示。

图  1  样本 ${x}$ 的分类间隔 ${m}\left({x}\right)$

Fig.  1  The $ m\left(x\right) $ of sample $ x $

下载: 全尺寸图片

单标记系统中一个样本只有一个类别标记，但在一些实际问题中一个样本可能存在多个类别标记，即多标记系统。一个多标记决策系统可以表示为 $ < U,F,L > $ ，其中, $U=\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\}$ 表示样本集合， $F=\{{f}_{1},{f}_{2},\cdots {,f}_{m}\}$ 为描述样本的一组特征， $L= \{{l}_{1},{l}_{2},\cdots ,{l}_{k}\}$ 代表标记集合。 $ \forall x\in U $ ， $ \forall {l}_{i}\in L $ ，则样本 $ x $ 在标记 $ {l}_{i} $ 下的分类间隔为

式中： $ {H}_{{l}_{i}}\left(x\right) $ 和 $ {M}_{{l}_{i}}\left(x\right) $ 分别表示在标记 $ {l}_{i} $ 下样本空间 $ U $ 中距离样本 $ x $ 最近的同类样本和异类样本。

1.2   多标记邻域熵

给定一个多标记决策系统 $ < U,F,L > $ ，根据式（2）可知， $ {m}_{{l}_{i}}\left(x\right) $ 表示样本 $ x $ 在单个标记 $ {l}_{i} $ 下的分类间隔，则样本 $ x $ 在标记集 $ L $ 下的分类间隔根据3种不同的认知观点可分为3类^[25]，以下给出中立观点下多标记邻域定义。

定义3^[25] 　给定多标记决策系统 ${\rm{MDT}}= < U, F,L >$ ， $ \forall x\in U $ ，样本 $ x $ 在中立观点下的多标记邻域定义为

式中： ${m}^{\mathrm{n}\mathrm{e}\mathrm{u}}\left(x\right)=\displaystyle \frac{1}{\left|L\right|}\displaystyle \sum _{i=1}^{L}{m}_{{l}_{i}}\left(x\right)$ 表示在中立观点下的分类间隔。

定义4^[25] 　设 $ U=\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\} $ 表示多标记下的非空样本集合， $ F $ 为样本的特征集合，设 $ f\subseteq F $ 为任意的特征子集， $ \forall {x}_{i}\in U $ ，样本 $ {x}_{i} $ 由 $ f $ 导出的邻域表示为 $ {\delta }_{f}^{\mathrm{n}\mathrm{e}\mathrm{u}}\left({x}_{i}\right) $ ,则 $ f $ 的邻域熵定义为

定义5^[25] 　设 $ {f}_{1}\subseteq F $ ， $ {f}_{2}\subseteq F $ 为任意两组特征， $ \forall {x}_{i}\in U $ ，样本 $ {x}_{i} $ 由 $ {f}_{1}\cup {f}_{2} $ 导出的邻域表示为 $ {\delta }_{{f}_{1}\cup {f}_{2}}^{\mathrm{n}\mathrm{e}\mathrm{u}}\left({x}_{i}\right) $ ，则 $ {f}_{1} $ 、 $ {f}_{2} $ 的联合熵定义为

定义6^[25] 　设 $ {f}_{1}\subseteq F $ ， $ {f}_{2}\subseteq F $ 为任意两组特征，在已知特征 $ {f}_{1} $ 的条件下， $ {f}_{1} $ ， $ {f}_{2} $ 的条件熵定义为

定理1^[28] 　设 $ {f}_{1}\in F,{f}_{2}\in F $ 为样本 $ {x}_{i} $ 的两组特征， ${\rm{NMI}}$ 为特征 $ {f}_{1} $ 和特征 $ {f}_{2} $ 的互信息，那么有：

由定理1可得， $ \forall {f}_{1}\subseteq F $ ， $ {f}_{2}\subseteq F $ ， $ {f}_{1} $ ， $ {f}_{2} $ 的邻域互信息为

2.   多标记特征选择算法

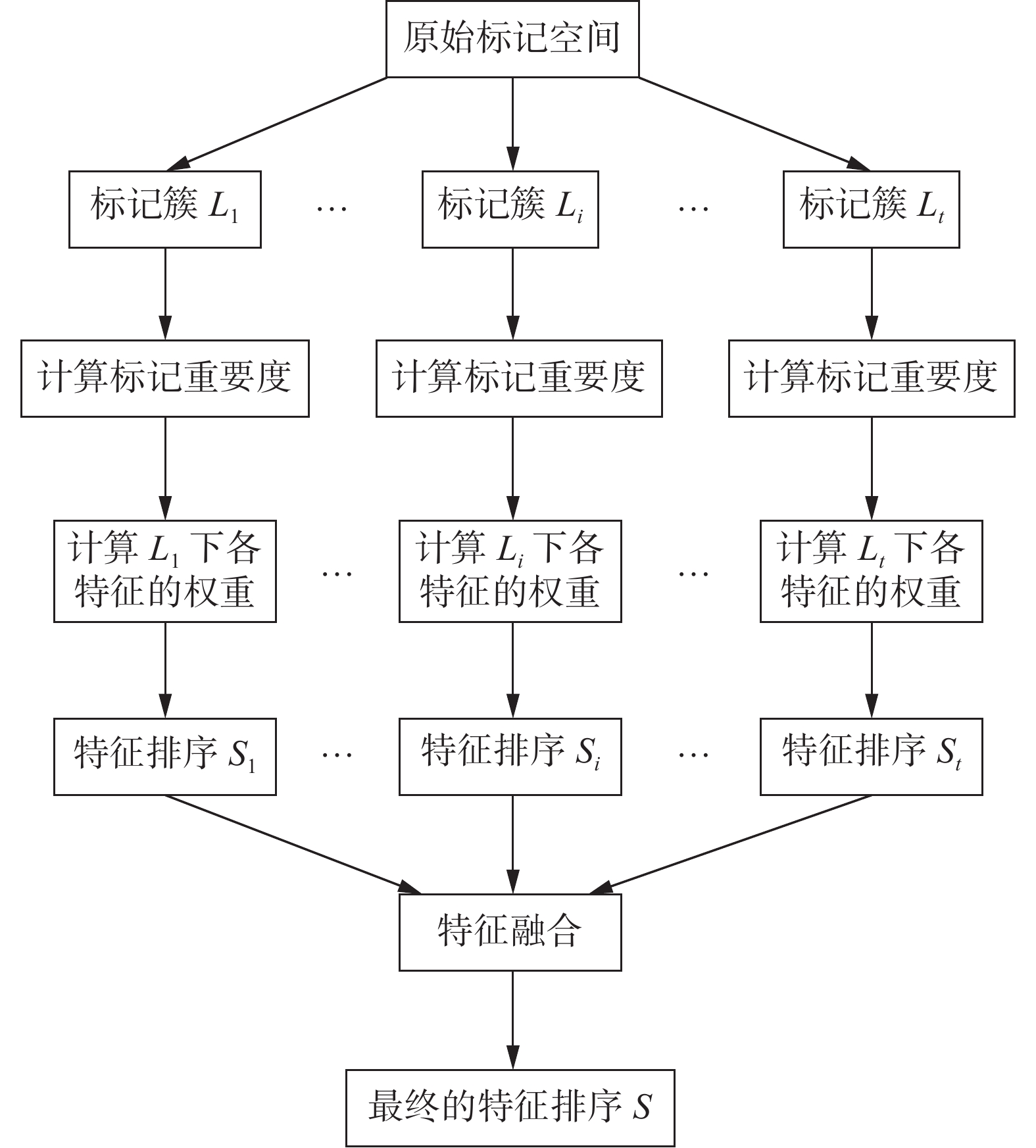
目前多数多标记特征选择方法都假定每个样本的相关标记的重要性相同，并且忽略了特征空间对标记重要性的影响，不能区分每个标记对样本的分辨能力，也忽略了每个特征对于不同标记所提供分类信息的差异，进而影响特征选择算法的性能。此外，多标记特征选择算法大多都考虑在标记全集下进行特征选择，这往往包含大量高维信息熵的计算，高维信息熵的计算复杂，并且从分类性能的方面看，考虑标记全集得出的特征子集对于某个标记或某些标记可能并不重要，即忽略了某些标记的专属特征。为此，本节利用标记空间中潜在的标记关系将标记集划分以简化计算和选择专属特征，使选择的特征提供更全面的分类信息；并在此基础上构造融合标记重要性和特征权重的多标记加权邻域关系，提出了一种基于加权信息粒化的多标记数据特征选择算法MFWIG。图2给出了算法的基本框架。首先，运用谱聚类挖掘标记集划分为标记簇。其次，利用标记间互信息度量簇中各标记的重要性，并根据特征与标记的相关性赋予特征相应的权重。最后结合标记重要度和特征权重设计新的特征选择度量标准，并在该标准的基础上构造特征选择算法。

图  2  MFWIG算法框架

Fig.  2  Framework of MFWIG

下载: 全尺寸图片

2.1   标记簇的划分

为了得到合适的标记划分，本文使用谱聚类来挖掘标记空间中潜在的语义信息将标记空间划分为若干标记簇。相较于传统的聚类方法谱聚类更能适应数据的分布，聚类过程更高效，更适合处理标记集这样的稀疏数据。

设图 $ G=(V,E) $ ，其中节点集合 $ V $ 由标记集 $ L= \{{l}_{1},{l}_{2},\cdots ,{l}_{k}\} $ 构成，边集合 $ E $ 中的每条边 $ e $ 连接的两个标记，表示为两个标记间的权重。谱聚类通过对图进行切割，让切割后的不同子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到划分标记簇的目的。

2.2   多标记加权邻域

给定一个多标记决策系统 ${\rm{ MDT}}= < U,F,L >$ ，通过谱聚类获得若干簇，令得到的标记划分为 $ {{L}^{P}=\{L}_{1},{L}_{2},\cdots ,{L}_{t}\} $ 。

定义7　设 $ \forall {L}_{c}\in {L}^{P} $ ， $ \forall {l}_{i}\in {L}_{c} $ ，标记 $ {l}_{i} $ 的重要度定义为

式中： $ I({l}_{i},{l}_{j}) $ 为标记 $ {l}_{i} $ 和标记 $ {l}_{j} $ 之间互信息^[29]。

给定标记 $ {l}_{i} $ ，设单标记决策系统为 $ < U,F,{l}_{i} > $ ， $\forall f\in F,\forall x\in U,\phi (x,a)$ 为样本 $ x $ 的特征值， ${\boldsymbol{A}}$ 为特征矩阵，决策向量 ${\boldsymbol{Y}}={{[}}{{\phi}} \left({{{x}}}_{{{1}}},{{{l}}}_{{{i}}}\right)\;{{\phi}} \left({{{x}}}_{{{2}}},{{{l}}}_{{{i}}}\right)\;\cdots \;{{\phi}} ({{{x}}}_{{{n}}},{{{l}}}_{{{i}}}){{{]}}}^{{\rm{T}}}$ ，特征的分配系数 ${\boldsymbol{v}}=\left[{{v}}\right({{{f}}}_{{{1}}})\;{{v}}({{{f}}}_{{{2}}})\;\cdots \;{{v}}({{{f}}}_{{{m}}}){]}^{{\rm{T}}}$ 。特征分配系数越大特征与标记 $ {l}_{i} $ 的相关性越高，则赋予其更高的权重。为了得到最优的特征分配系数，求解以下最优问题^[22]：

其中 ${\boldsymbol{A}}=\left[\begin{array}{ccc}{{\phi}} ({{{x}}}_{{{1}}},{{{f}}}_{{{1}}})& \cdots & {{\phi}} ({{{x}}}_{{{1}}},{{{f}}}_{{{m}}})\\ \vdots & \ddots & \vdots \\ {{\phi}} ({{{x}}}_{{{n}}},{{{f}}}_{{{1}}})& \cdots & {{\phi}} ({{{x}}}_{{{n}}},{{{f}}}_{{{m}}}) \end{array} \right]$ 。

定义8^[22] 　设 $ \forall {L}_{c}\in {L}^{P} $ ， $ \forall {l}_{i}\in {L}_{c} $ ，,则单标记决策系统可以表示为 $ < U,F,{l}_{i} > $ ， $ \forall f\in F $ ，特征 $ f $ 关于类别标记 $ {l}_{i} $ 的权重定义为

定理2^[22] 　设 $ \forall {L}_{t}\in {L}^{P} $ ， $ \forall {l}_{i}\in {L}_{t} $ ，单标记决策系统可以表示为 $ < U,F,{l}_{i} > $ ，特征权重向量为 ${\boldsymbol{\omega }}=[{\omega }\left({{f}}_{1}\right)\; {\omega }\left({{f}}_{2}\right)\;\cdots \;{\omega }\left({{f}}_{{m}}\right)]^{\rm{T}}$ ， $ \forall f\in F $ 有：

1） $\omega \left(f\right)\geqslant 0$ ；

2） $ \sum _{{f}_{i}}\omega \left({f}_{i}\right)=\left|F\right| $ 。

定义9　设 $ \forall {L}_{c}\in {L}^{P} $ ， $ {L}_{c}=\{{l}_{s},{l}_{s+1},\cdots ,{l}_{h}\} $ ，则多标记决策系统可以表示为 $ < U,F,{L}_{c} > $ ， $ \forall f\in F $ ，特征 $ f $ 关于标记簇 $ {L}_{c} $ 的权重定义为

式中： $L_{\rm{sig}}\left({l}_{i}\right)$ 表示标记 $ {l}_{i} $ 的重要度， $ {{v}_{l}}_{i}\left(f\right) $ 表示特征 $ f $ 在标记 $ {l}_{i} $ 下的特征分配系数。在此基础上， $ \forall {x}_{1} $ ， $ {x}_{2}\in U $ ，样本间的加权距离为

对于标记 $ {l}_{i} $ ，样本 $ x $ 的加权分类间隔 ${m}_{{l}_{i}}'\left(x\right)$ 为

定义10　设 $ \forall {L}_{c}\in {L}^{P} $ ， $ {L}_{c}=\{{l}_{s},{l}_{s+1},\cdots ,{l}_{h}\} $ ，则多标记决策系统可以表示为 $ < U,F,{L}_{c} > $ ， $ \forall x\in U $ ，样本 $ x $ 在标记簇 $ {L}_{c} $ 下的加权分类间隔定义为

$ \forall {L}_{c}\in {L}^{P} $ ， $ {L}_{c}=\{{l}_{s},{l}_{s+1},\cdots ,{l}_{h}\} $ ,则多标记决策系统可以表示为 $ < U,F,{L}_{c} > $ ， $ \forall x\in U $ ，根据式（6）和式（7）样本 $ x $ 在标记簇 $ {L}_{c} $ 下的加权邻域为

若 ${m}_{{L}_{c}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left(x\right)\leqslant 0$ ，则令 $ {m}_{{L}_{c}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left(x\right)=0 $ 。

2.3   多标记加权邻域熵

定义11　设 $ U=\{{x}_{1},{x}_{2},\cdots ,{x}_{n}\} $ 表示多标记下的非空样本集合， $ F $ 为样本的特征集合，设 $ f\subseteq F $ 为任意的特征子集， $ \forall x\in U $ ，样本 $ {x}_{i} $ 在融合标记重要度和特征权重下由 $ f $ 导出的邻域表示为 $ {\delta }_{f}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right) $ ,那么 $ f $ 的邻域熵定义为

定义12　设 $ {f}_{1}\in F,{f}_{2}\in F $ 为样本 $ {x}_{i} $ 的两组特征， $ {\delta }_{{f}_{1}\cup {f}_{2}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right) $ 表示样本 $ {x}_{i} $ 在 $ {f}_{1}\cup {f}_{2} $ 的特征空间下的邻域，则融合标记重要度和特征权重下的联合熵定义为

当 $ {f}_{1} $ 为输入特征 $ f $ ， $ {f}_{2} $ 为类别标记 $ l $ 时， $ {\delta }_{{f}_{1}\cup {f}_{2}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right) $ 改写为 ${\delta '}_{{f}_{1}\cup {f}_{2}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right)={\delta }_{f}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right)\cap {l}_{{x}_{i}}$ , $ {l}_{{x}_{i}}={\delta }_{l} =\left\{y\right|\Delta (x,y)= 0, y\in U\} $ ，由此，特征 $ f $ 和类别标记 $ l $ 的联合熵可定义为

定义13　设 $ {f}_{1}\in F,{f}_{2}\in F $ 为样本 $ {x}_{i} $ 的两组特征，其中 $ {f}_{1} $ 为已知特征，则 $ {f}_{2} $ 在已知特征 $ {f}_{1} $ 下的条件熵定义为

由定理1可得， $ \forall {f}_{1}\in F,{f}_{2}\in F $ ， $ {f}_{1} $ 、 $ {f}_{2} $ 的加权邻域互信息定义为

当 $ {f}_{1} $ 为输入特征 $ f $ ， $ {f}_{2} $ 为类别标记l时， $ {\delta }_{{f}_{1}\cup {f}_{2}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right) $ 改写为 ${\delta '}_{{f}_{1}\cup {f}_{2}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right)={\delta }_{f}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left({x}_{i}\right)\cap {l}_{{x}_{i}}$ ， ${l}_{{x}_{i}}={\delta }_{l}=\left\{y\right|\Delta (x,y)= 0, y\in U\}$ ，此时，特征 $ f $ 和类别标记 $ l $ 的互信息可定义为

2.4   算法描述

给定标记簇 $ {L}_{i} $ ，特征 $ f $ 与标记簇 $ {L}_{i} $ 之间的相关性通常使用互信息 ${\rm{ NMI}}(f,{L}_{i})$ 来度量，然而，当标记数量巨大时 ${\rm{NMI(}}f,{L}_{i})$ 计算复杂度指数增加且很难精确计算。由于同标记簇中的标记彼此高度相关，使用 $\underset{l\in {L}_{i}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\rm{NM{I}}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\right(f,l\left)\right\}$ 能够有效度量与标记簇 $ {L}_{i} $ 最相关的候选特征，并且避免高维信息熵的复杂计算。选择的候选特征要具有对标记簇 $ {L}_{i} $ 的分辨信息，并且已选择的特征没有提供这些分辨信息，即使选择的候选特征与已选特征间的冗余性尽可能小。条件互信息 ${\rm{NM{I}}}^{\mathrm{w}\mathrm{e}\mathrm{i}}(f,{l}_{{\rm{max}}}|{f}_{j})$ 可以用来度量候选特征 $ f $ 和已选特征 $ {f}_{j} $ 冗余性，若存在已选特征 $ {f}_{j} $ 提供了 ${l}_{{\rm{max}}}$ 相关的分辨信息， ${\rm{NM{I}}}^{\mathrm{w}\mathrm{e}\mathrm{i}}(f,{l}_{{\rm{max}}}|{f}_{j})$ 的值会很小，表示特征 $ {f}_{j} $ 和特征 $ f $ 对于 ${l}_{{\rm{max}}}$ 是存在冗余的。因此，使用 $\underset{l\in {L}_{i}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\rm{NM{I}}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\right(f,l\left)\right\}$ 来确保特征与标记的相关性， $\underset{{f}_{j}\in S}{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{{\rm{NM{I}}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\right(f,{l}_{{\rm{max}}}\left|{f}_{j}\right)\}$ 来度量候选特征 $ f $ 和已选特征集 $ S $ 冗余性，候选特征评估准则可定义为

多标记数据往往存在类别标记不平衡的问题，此时与标记 ${l}_{{\rm{max}}}$ 相关的特征不能很好地描述整个标记簇，为此，结合标记的重要度将式（4）中的评估标准改写为

由文献[11,30]得，式（8）中的条件互信息可由下式近似计算:

根据式（9）提出基于加权邻域粗糙集的多标记特征选择算法：

算法1　基于加权信息粒化的多标记特征选择算法（MFWIG）

输入　多标记决策系统 ${\rm{MDT}}= < U,F,L >$ ，选择特征数 $ N $

输出　特征子集 $ S $

1）谱聚类将标记集 $ L $ 划分为若干标记簇 ${L}^{P}= \{{L}_{1},{L}_{2},\cdots ,{L}_{t}\}$ ；

2）for each ${{L}}_{{i}}{{\in}} {{L}}^{{P}}$ :

3）根据式（4）计算每个标记 $ l{\in L}_{i} $ 的重度 $L_{\rm{sig}}\left(l\right)$ ；

4）根据式（5）计算每个特征 $ f\in F $ 的权重 $ {w}_{m}\left(f\right) $ ；

5） $ \forall x\in U $ ，根据式（7）计算样本 $ x $ 的加权分类间隔 $ {m}_{{L}_{i}}^{\mathrm{w}\mathrm{e}\mathrm{i}}\left(x\right) $ ；

6） $ \forall x\in U $ ，根据式（8）计算样本 $ x $ 的加权邻域 $ {\delta }^{\mathrm{w}\mathrm{e}\mathrm{i}}\left(x\right) $ ;

7）初始化 $ {S}_{i}=\varnothing $ ；

8） while $\left|{{S}}_{{i}}\right|\leqslant {N}{\times}\displaystyle \frac{\left|{{L}}_{{i}}\right|}{\left|{L}\right|}$ :

根据式（9）计算特征得分，选择特征 ${f}_{{\rm{max}}}= \underset{f}{\mathrm{m}\mathrm{a}\mathrm{x}}J'\left(f\right)$ ； ${S}_{i}={S}_{i}\cup \{{f}_{{\rm{max}}}$ }； $F=F-\{{f}_{{\rm{max}}}$ }；

end while

end for

9）将每个专属特征子集按基数大小排列得, ${{S}^{P}=\{S}_{p1},{S}_{p2},\cdots ,{S}_{pt}\}$ ；

10）每次从每个特征子集 $ {S}_{pi} $ 中依次选择一个新的特征加到 $ S $ 中，直到遍历完所有子集；

11） 返回特征子集 $ S $ 。

其中， 8）中分别对每个标记簇选择专属特征，主簇中包含的标记更多，其相关的特征在最终选择的特征子集也应该占更大比重。

算法复杂度分析：标记聚类的复杂度是 $ O\left({k}^{3}\right) $ ，对于每个标记簇，标记重要度的复杂度 $ O\left(\right|{L}_{i}{|}^{2}) $ ，特征权重的复杂度是 $ O\left(m\right|{L}_{i}\left|\right) $ ，计算加权分类间隔的复杂度是 $ O\left({n}^{2}\right|{L}_{i}\left|\right) $ ，特征排序的计算复杂度是 $ O\left({m}^{2}\right) $ 。由此可知算法的时间复杂度为 $O\left(\displaystyle \sum _{i=1}^{t}{n}^{2}\left|{L}_{i}\right|+{m}^{2}+{k}^{3}\right)$ 。

3.   实验及结果分析

3.1   实验数据

为了验证本文所提算法的有效性，选取6个Mulan平台中的真实多标记数据集上进行对比实验。这些数据集涵盖了不同领域的多标记分类问题，包括国家标志、音乐标签、情感分类、鸟类识别等。各数据集的相关信息如表1所示。

3.2   评价指标

本文采用平均精度（average precision, AP) P_A、排序损失（ranking loss, RL) L_R、汉明损失（hamming loss, HL) L_H和覆盖率（coverage, CV) C_V作为算法性能的评价指标。令测试集为 $Z=\left\{\right({x}_{i}, {Y}_{i}){\}}_{i=1}^{m}\subset {R}^{d}\times \{+1,-1{\}}^{\left|L\right|}$ ，根据预测函数 $ {f}_{l}\left(x\right) $ 可定义排序函数 ${\rm{ran{k}}}_{f}(x,l)\in \{1,2,\cdots ,|L\left|\right\}$ 。

AP：表示所有标记的预测集合中，位置排在相关标记前面的标记且仍是相关标记的平均概率，定义为

式中： $ {R}_{i}=\left\{l\right|{Y}_{il}=+1\} $ 表示与样本 $ {x}_{i} $ 相关标记构成的集合。

RL：表示所有样本的不相关标记的排序在其相关标记前面的平均概率，定义为

式中： $ \overline{{R}_{i}}=\left\{l\right|{Y}_{il}=-1\} $ 表示与样本 $ {x}_{i} $ 不相关标记构成的集合。

HL：表示所有样本的预测标记与真实标记的平均差异值，定义为

式中： $\oplus$ 表示异或运算， $ {Y}_{il} $ 表示与样本 $ {x}_{i} $ 相关标记的真实值。

CV：表示所有样本实际包含的标记所需的最大排序距离的平均值，定义为

4种指标中，AP取值越大表示算法性能越好，其他指标则取值越小表示算法性能越好。

3.3   结果分析

实验中选择了5种不同的对比方法，包括PPT-CHI、PPT-MI、PMU、SCLS和CFSM^[26]。采用的多标记分类器为ML-KNN（multi-label learning based on k-nearest neighbors classifier）^[31]，平滑参数 $ s $ 设置为1，近邻个数 $ k $ 设置为10，对分类指标采用10折交叉验证法。

实验首先对比各种算法诱导出的特定特征子集的分类效果，由于以上5种对比算法和本文算法均是对特征进行排序，为确保实验对比的公平性，将所有算法取特征排序的前 $ N $ 个特征作为特征子集，然后分析各算法的分类性能随特征数目的变化情况。其中，为了选择合适比例的特征数量^[32]，本实验按以下规则设定选取比例： $m\leqslant 100$ ，取前 $ 40\mathrm{\%} $ ， $100 < m\leqslant 500$ ，取前 $ 30\mathrm{\%} $ 。各个数据集最终所选取的特征子集的特征个数分别为：Flag 8个，Emotions 28个，CAL 50027个，Birds 78个，Yeast 30个，Scene 88个。表2~5给出了各算法分别在4种评价指标上的实验结果。

于给定的评价指标斜体加粗表示个算法中性能最优的结果。根据表2~5的结果可得出：

1）对于AP指标和RL指标，MFWIG在6个数据集上都明显优于其他5种算法，即分类性能均取得最优；对于HL指标和CV指标，MFWIG分别在4个数据集和5个数据集上均取得最优值。

2）从6个数据集、4个评价指标的24项对比结果可知，PPT-CHI、PPT-MI和CFSM没有取得最优值的情况，PMU、SCLS和CFSM取得最优值的情况均仅占4.1667%，而对比5种算法MFWIG明显优于其他5种对比算法，取得最优值的情况占87.5%。

3）从各评价指标平均性能的对比发现，相对AP指标、RL指标、CV指标和HL指标，MFWIG均取得最优值。

综上，在多数情况下MFWIG算法在各评价指标上优于对比算法，其原因在于MFWIG考虑了标记间潜在的语义关系和标记的不同重要度，在构造邻域关系时融合了特征权重，使得算法选择的特征能更好地描述标记集合，有效提升分类能力和减少标记预测时的损失，并且MFWIG采用条件互信息更好地度量特征间的冗余性。

以上实验是根据指定特征数得到最终特征子集来进行静态的对比分析，图3为不同数据集上6种算法的4个评价指标随特征数目的变化趋势。

图  3  各算法4个评价指标随特征数在3个数据集上的变化趋势

Fig.  3  Variation of 4 evaluation indicators of different algorithms with the number of selected features on 3 datasets

下载: 全尺寸图片

从实验结果可知，选择的特征比例不同算法的性能也不同，并且比例在30%~40%时各算法性能曲线都趋于平稳，验证了之前实验设定的合理性。此外，MFWIG在各数据集上的4个评价指标均取得较优的性能表现，尤其在Emotions数据集上，4个评价指标的性能曲线都明显优于其他算法。最后，MFWIG在选择特征比例过小时性能相对较差，这是由于不同标记簇的专属特征间存在交集，使得最终融合得到的子集数相较于其他算法更小。

4.   结束语

针对现实应用场景中每个实例的相关标记的重要程度不同，并且对于不同标记同一个特征的分类信息也存在差异的问题，本文提出了一种基于加权信息粒化的多标记特征选择算法。该方法首先利用谱聚类挖掘标记间的相关性来划分标记集，然后使用标记间的互信息度量标记的重要性，并在构造邻域关系前融合特征权重，最后利用标记簇内的高度相似性和条件互信息提出了新的特征选择度量标准，避免了高维信息熵的计算，并且构造了一种新的多标记特征选择算法。通过6个真实数据集上基于4种不同的评价指标的实验对比，本文提出的算法相较其他对比方法能取得较优的性能表现，验证了其有效性和可行性。此外，本文未深入分析算法所得特征子集的内部结构与原特征集间的关系，下一步将从多标记数据质量的角度来完善此研究。