街区是城市规划和设计中的重要部分。街区通常指城市中被道路包围的区域，或借助其他自然特征或人文特征进行划分的区域，是城市结构的基本组成部分。街区的品质评估方法能够以统一规范对各街区的品质进行客观评估，其结果可以作为街区品质的提升工作和后期街区建设规划工作的基础。因此，街区的品质评价有着重要价值和意义。在有关城市街区品质评估方法的众多研究中，以图像数据构建评估模型是其中重要的分支。相比于非图像数据，图像数据易于获取且无需考虑多源数据的融合问题。

街景图像被广泛应用于与建筑规划相关的研究中。在目前已有的成果中，Rundle^[1]利用街景图像对纽约37个步行街区进行街区环境美感与其他物质空间指标进行评价。Naik^[2]通过街景图像的智能评价计算2007—2014年间的streetscore指数，以此评价美国21个城市街道空间的安全度。Ewing^[3]则基于已有的指标体系从不同维度对街景图像的空间围合度、意象性等量化评价进行打分。韩君伟^[4]将视觉熵引入到量化商业步行街道景观视觉复杂性的研究中，并借助数字摄像和计算机图像处理技术进行分析。龙瀛等^[5]将大数据与街景数据结合，对北京和成都的街道空间进行品质分析，并提出评价指标：人口密度、城市活力、界面特征、交通特征、开发强度、可达性等。唐婧娴等^[6]通过计算机图像识别、图像分割技术和人口访问调查方法研究北京和上海的中心区街道品质，得出街道环境设计要素为：绿化率、街道高宽比、街道尺度、街道活力、街道围合度、人性化尺度、通透性、整洁度、意象化等。樊钧等^[7]在对苏州古城区街道空间慢行品质的研究中，通过空间网络分析、聚类算法技术分析等提出评价指标：兴趣点、位置服务数据、街道尺度、组织结构、绿化率、空间活力、设施均好性、街道五感等。

上述研究多采用以行人视角拍摄的街景图像进行评估，但不同图像采集点的拍摄角度和高度等标准不统一，易造成图像内容偏差，进而影响街区特征的表达效果。卫星图像相对于街景图像更易获取，基于卫星图的街区品质评估可操作性强，适用范围广。此外卫星图像采集方式和角度统一，可有效减少街景图像的视角偏差带来的模型误差。

卫星图可以解决街区图像在采集和表达上的偏差问题且能够更加快速地采集并扩充数据集，但建筑师人工标注的高成本仍然使得数据集中带标签图像的数量远低于常规方法中训练深度学习模型所需。在研究中经常会遇到带有专家标注的数据量无法达到模型训练需求的情况，研究者为了更好应对带标注数据量小的问题，结合人类可从少量例子中学习新对象的特点，提出了可从有限样本中学习的方法——小样本学习（few shot learning, FSL）。小样本学习从训练集中随机抽取数据组成不同批次用于模型训练，最大化模型训练的充分程度。通过本文对算法的改进，模型可以继承训练过程中生成子空间的参数与各类子空间均值，并在测试过程中快速完成分类。这种继承参数的方法可以减少类别特性弱的数据对小样本数据集的影响，使得分类结果更具泛化性。

本文在街区品质评估中做了如下贡献：

1）本文将计算机领域中的图像分类技术引入到建筑领域对街区品质的评估中，证明了计算机代替人工评估的可行性；

2）提出将卫星图像用于数据采集，通过矢量数据对卫星图中各街区进行比对和截取。此方法可以避免街景图像因采集角度和时间等的不确定性造成图像内容偏差，并可以提高图像数据采集效率，节约成本；

3）提出继承参数的自适应子空间方法，使得模型具有记忆性，对训练过程中出现过的类别更快速直接地分类。继承参数有助于降低类别特性弱的样本对类别整体特性表征的负面影响，避免模型学习效率和分类准确度的降低。

1.   相关工作

小样本学习算法根据模型对先验知识的利用方式可分为3个类别：基于模型、基于优化、基于度量^[8]。基于度量的小样本学习方法先使用先验知识增强数据扩充监督信息，然后通过距离计算进行分类。其中匹配网络（matching nets）^[9]和Samos^[10]样本间距离的度量确定新对象的标签。而原型网络（prototypical nets）^[11]将样本度量扩展到类度量，即来自特定类的所有样本的特征将被认为是该类别的类原型。关系网络（relation nets）^[12]则在孪生网络和原型网络的线性关系分类器基础上，提供了可学习的非线性关系分类器。另外，Ren等^[13]表明未标记的图像有助于提高小样本学习模型的性能，并在研究中成功使用未标记图像细化原型网络。

Simon^[14] 、Yoon^[15]和Devos^[16]在各自的研究中均使用了子空间描述的小样本学习（few-shot learning, FSL）。其中Yoon提出的任务自适应映射网络（task-adaptive projection net ,Tap Net）^[15]中的投影是特定于任务的，而Simon的方法中投影是特定于类别的。本文方法是基于Simon等^[17]于2020年提出以自适应子空间作为分类器进行小样本学习方法的改进。Simon通过深度神经网络提取图像特征矩阵，然后用奇异矩阵分解方法生成子空间，通过计算数据点到各类子空间上投影距离完成分类，具体内容如下。

Simon使用四层卷积神经网络提取街区卫星图像的特征。卷积神经网络由4个卷积模块组成，每个卷积层模块所包含层的数量和类别相同，激活层选用线性整流函数（rectified linear unit, RELU）作为激活函数。

子空间的基础向量由矩阵奇异值分解（singular value decomposition ,SVD）获得。奇异值分解方法将减去该类别均值的图像特征矩阵分解为3个小矩阵（如图1），本文方法取左矩阵作为该类别子空间的基础。假设矩阵 ${\boldsymbol{A}} $ 为 $m \times n$ 矩阵，则定义矩阵 $ \boldsymbol{A} $ 的SVD为

图  1  奇异值分解

Fig.  1  Singular value decomposition

下载: 全尺寸图片

式中： $ {\boldsymbol{U}} $ 为 $m \times n$ 矩阵； ${\boldsymbol{\varSigma }}$ 为 $m \times n$ 矩阵，除主对角线上的元素外全为0，主对角线上每个元素都被称为奇异值； $ {\boldsymbol{V}} $ 是 $n \times n$ 矩阵。 $ {\boldsymbol{U}} $ 和 $ {\boldsymbol{V}} $ 都是酉矩阵，即均满足 ${{\boldsymbol{U}}^{\text{T}}}{\boldsymbol{U}} = {\boldsymbol{I}}$ , ${{\boldsymbol{V}}^{\text{T}}}{\boldsymbol{V}} = {\boldsymbol{I}}$ 。

矩阵 $ {\boldsymbol{V}} $ 和 $ {\boldsymbol{U}} $ 的定义分别为

式中： ${\lambda _i}$ 为特征值； ${{\boldsymbol{v}}_i}$ 和 ${{\boldsymbol{u}}_i}$ 为矩阵V和U中对应的特征向量，其中 ${{\boldsymbol{v}}_i} \in {\boldsymbol{V}}$ ， ${{\boldsymbol{u}}_i} \in {\boldsymbol{U}}$ 。

样本 ${x_{c,i}}\left( {i \in K} \right)$ 且K为该类别数据量，经卷积神经网络 $f\Theta $ 提取特征：

式中类别c的图像均值 ${\mu _{{c}}}$ 为

由 $\widetilde {{X_{{c}}}}$ 计算特定类别c的子空间矩阵即为投影矩阵 ${{\boldsymbol{P}}_{{c}}}$ ，将查询集样本 ${q_j}$ 投影到 ${{\boldsymbol{P}}_{{c}}}$ 上，并计算 ${q_j}$ 到各类别子空间 ${{\boldsymbol{P}}_{c}}$ （原始空间中）的距离，获得距离最近的类别。

子空间分类器的定义为

式中 ${{\boldsymbol{M}}_{{c}}} = {{\boldsymbol{P}}_{{c}}}{\boldsymbol{P}}_{{c}}^{\text{T}}$ ， ${\boldsymbol{P}}$ 为类别c的左奇异矩阵。

查询集所属类别的概率由softmax函数定义（见式(1)）。子空间生成后，生成器随机选取未标记样本经预处理后送入深度神经网络中得到特征矩阵，计算本批次样本与子空间的投影距离，得到描述损失。

子空间方法通过反向传播损失函数和自适应学习率的方式调整卷积神经网络中的各项可调节参数，采用格拉斯曼几何^[18]方法最大化子空间之间的距离，进而得到可以使特征矩阵在奇异值分解后各类别子空间的区分程度最大化的卷积神经网络。假设两个子空间 ${{\boldsymbol{P}}_i}$ 和 ${{\boldsymbol{P}}_j}$ ，其两子空间间的投影度量被定义为

由式(2)可知，最小化 $\left\| {{{\boldsymbol{P}}_i}{{\boldsymbol{P}}_j}^{\text{T}}} \right\|_F^2$ 可以实现投影度量的最大化。因此，模型训练的损失函数定义为 $l = - \dfrac{1}{{{\boldsymbol{MN}}}}\displaystyle\sum_{{c}} {\log \left( {{{\boldsymbol{P}}_{{c}}},q} \right) + \lambda \displaystyle\sum\nolimits_{i \ne j} {\left\| {{{\boldsymbol{P}}_i}^{\text{T}}{{\boldsymbol{P}}_{\boldsymbol{j}}}} \right\|_F^2} }$ 。采用均值细化方法细化每个类别的中心 $\widetilde {{\mu _{{c}}}} = \dfrac{{K{\mu _{{c}}} + \displaystyle\sum_i {{m_i}f\Theta \left( {{r_i}} \right)} }}{{K + \displaystyle\sum_i {{m_i}} }}$ ，未标记样本的软分配分数 ${m_i} = \dfrac{{\exp \left( { - {{\left\| {f\Theta \left( {{r_i}} \right) - {\mu _{{c}}}} \right\|}^2}} \right)}}{{\displaystyle\sum_{{{c}}'} {\exp \left( { - {{\left\| {f\Theta \left( {{r_i}} \right) - {\mu _{{c}}}} \right\|}^2}} \right)} }}$ ， ${r_i}$ 为未标记样本。

以上三步生成的交叉熵损失和描述损失相加，反向传播调节深度神经网络的参数。模型训练过程由以上训练步骤迭代组成，网络结构如图2所示。

图  2  网络结构与奇异值分解

Fig.  2  Network structure and SVD

下载: 全尺寸图片

2.   基于继承自适应子空间的卫星图像小样本学习模型

本文在自适应子空间方法的基础上，针对建筑设计领域传统图像数据难以采集、带标签的街区数据集样本量小且不平衡等特点，提出了从卫星图截取街区图像的数据采集方式和继承参数的自适应子空间方法。

2.1   模型整体结构

本方法将卫星图像经预处理转化为数值矩阵，使用四层卷积神经网络对其进行特征表示输出特征矩阵，将特征矩阵减去该类均值后奇异值分解，得到左奇异矩阵作为该样本类别的子空间，并将特征矩阵到子空间的投影距离和交叉熵损失反向传播回卷积神经网络进行调参。模型的整体结构如图3所示。

图  3  模型整体结构

Fig.  3  Overall structure of the model

下载: 全尺寸图片

2.2   街区卫星图像获取

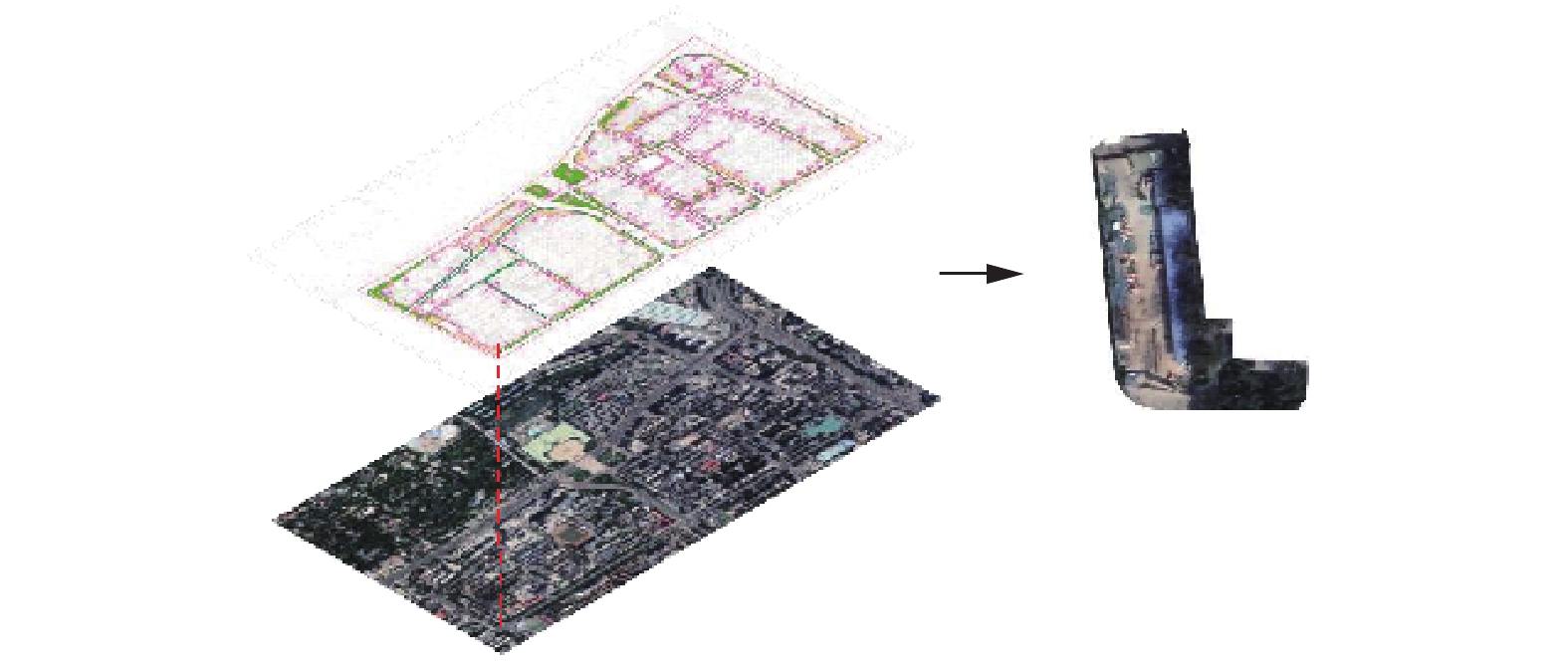
本文通过谷歌卫星地图获取高清卫星图像，并结合街区轮廓矢量数据进行框选和截取，获得严格按照街区轮廓划分的卫星图像并编号。由于卷积神经网络输入图像需为规则图形，故将原街区图像取最小外接矩形并填充白色背景，避免无关内容影响模型训练，如图4所示。

图  4  第8号街区

Fig.  4  Block 8

下载: 全尺寸图片

三通道图像在输入卷机神经网络前需要完成预处理，包括统一调整为 ${\text{84}} \times {\text{84}}$ 尺寸，并依据Imagenet数据集的均值和标准差进行标准化处理，其中均值m=[0.485,0.456,0.406]，标准差s=[0.229,0.224,0.225]。三通道图像在输入卷积神经网络前需要完成预处理，将图像X标准化得到 $X' = \dfrac{{X - \mu }}{s}$ ， $\mu $ 为图像均值。

2.3   分类器子空间参数的继承策略

本文将训练过程中每次训练得出的子空间矩阵和各类别特征矩阵均值传递给街区品质评估过程，与待评估街区的特征矩阵共同完成街区品质评估。子空间参数的继承策略如图5所示。

图  5  继承策略

Fig.  5  Inheritance strategy

下载: 全尺寸图片

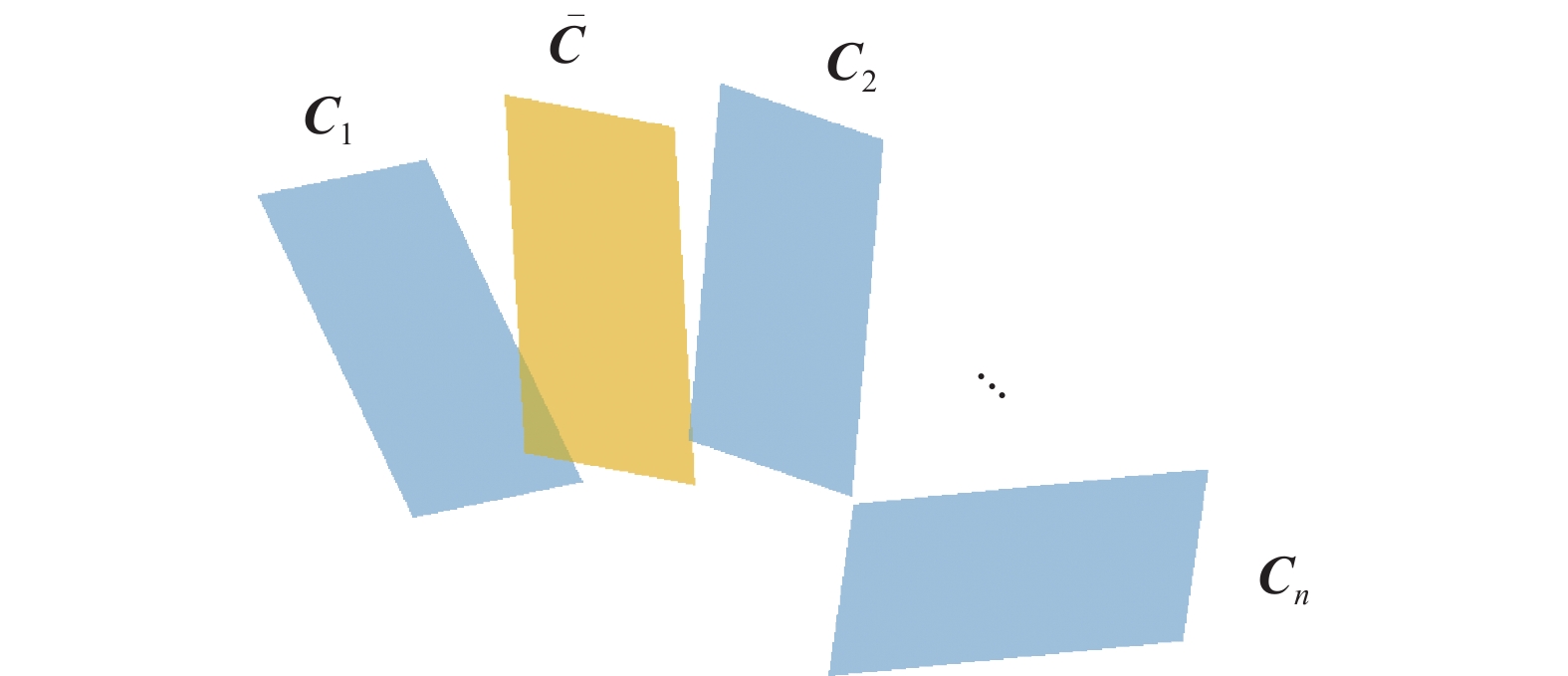
本文数据集中各类别的数据量不等，属于数据失衡。需要注意的是，数据集不平衡会影响继承子空间参数分类器的性能，其原因在于子空间生成过程中，非平衡数据集中数据量小的类别中必然有数据被多次重复使用的情况，在求子空间矩阵均值和类别特征矩阵均值的过程中形成偏差。如图6、7中 ${{\boldsymbol{C}}_1},{{\boldsymbol{C}}_2},\cdots,{{\boldsymbol{C}}_N}$ 分别为不同数据的特征矩阵。

图  6  空间均值

Fig.  6  Mean of spatial

下载: 全尺寸图片

图  7  新空间均值和偏差

Fig.  7  New mean of spatial and deviation

下载: 全尺寸图片

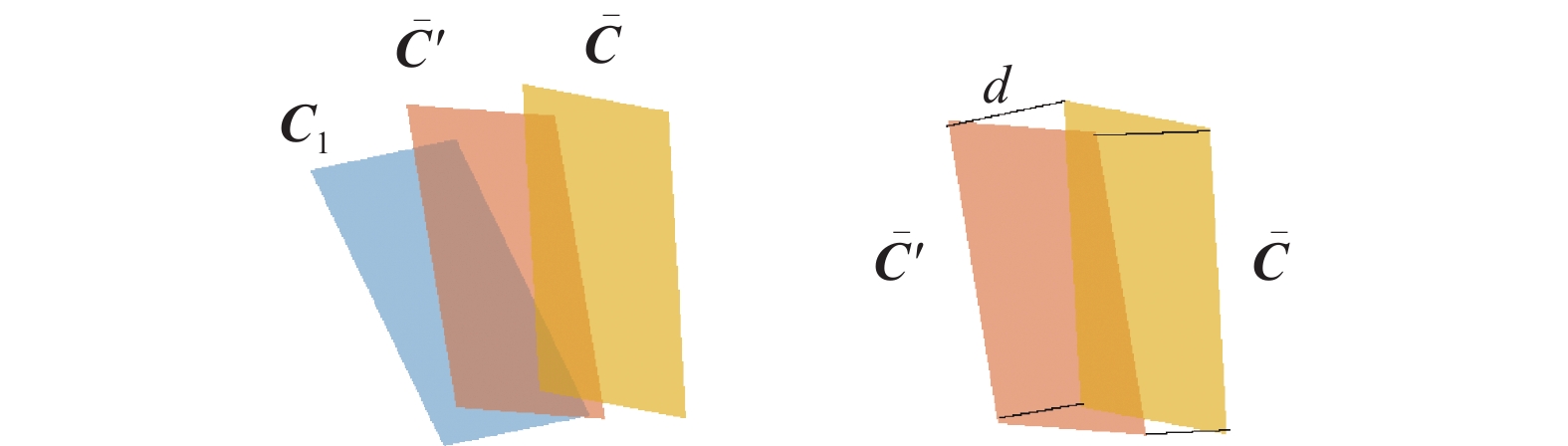
如图6所示， ${{{\boldsymbol{C}}_1}},{{{\boldsymbol{C}}_2}}, \cdots, {{\boldsymbol{C}}_N}$ 的均值为 $\overline {\boldsymbol{C}} = - \dfrac{1}{N}\times \displaystyle\sum_{i = 1}^N {{{\left\| {\left( {{\boldsymbol{I}} - {M_i}} \right)\left( {f\Theta \left( q \right) - {{\boldsymbol{\mu}} _i}} \right)} \right\|}^2}}$ 。在以上特征矩阵基础上，假设 ${{\boldsymbol{C}}_1}$ 被重复使用了一次，则新均值为

图7为各个矩阵的空间关系，可知偏差为新均值与原均值的差值，偏差为 $d = \dfrac{1}{{N + 1}}\left( {\overline {\boldsymbol{C}} ' - \overline {\boldsymbol{C}} } \right)$ 。

训练集的数据被多次使用形成的偏差会影响子空间矩阵均值的计算。因此训练过程中批次生成的方式会使得非平衡数据集的不平衡性直接影响子空间参数，进而造成模型的预测准确性的降低。

本文提出的方法将相关参数进行储存，待所有训练和验证步骤完成后，返回到测试过程中。除深度神经网络模型和相关参数外，继承子空间参数的方法还将训练过程中生成所有子空间矩阵的均值和各类别数据特征矩阵的均值继承到测试过程中，结合测试集样本的各项参数重新计算并完成分类，如算法1所示。

算法1　继承子空间参数的街区品质评估

输入　数据批次 $ {T_i} $ （包括用于生成子空间的S和计算描述损失的Q），随机初始化网络参数 ${\Theta _0}$ 。

输出　预测类别Label。

1） for i in $\left\{ {{{\boldsymbol{T}}_1},{{\boldsymbol{T}}_2}, \cdots ,{{\boldsymbol{T}}_N}} \right\}$ do

2） for k in $\left\{ {1,2, \cdots ,N} \right\}$ do

3） ${{\boldsymbol{X}}_C}$ ← ${{\boldsymbol{S}}_C}$

4） ${\boldsymbol{A}} = \widetilde {{{\boldsymbol{\mu}} _C}} - {{\boldsymbol{X}}_C}$

5） $\left[ {u,{\boldsymbol{\varSigma }},{{\boldsymbol{v}}^{\text{T}}}} \right] = {\text{SVD}}\left( A \right)$

6） ${{\boldsymbol{P}}_C}{{\boldsymbol{\mu}} _k}$

7） for q in Q do

8） ${{\boldsymbol{d}}_C}\left( {{q}} \right)$ ← ${{\boldsymbol{P}}_C}$

9） ${\text{Label = network}}\left( {{\Theta _1},{T_i}} \right)$

3.   实验结果分析

本文以经过专家评估和标注的真实街区卫星图像作为数据集，并设置对比实验验证本文使用方法的可行性和有效性。

3.1   参数学习

本文选取的研究对象为北京市西城区展览馆街道，该街道位于西城区西北部，属于首都功能核心区控制性详细规划（街区层面）的规划范围。其中，展览路街道地块（北京建筑大学所在片区、团结片区）为本文的研究范围，如图8所示，以此进行城市街区品质评估方法的实验探究。

图  8  展览馆街道地块

Fig.  8  Satellite map of the exhibition hall area

下载: 全尺寸图片

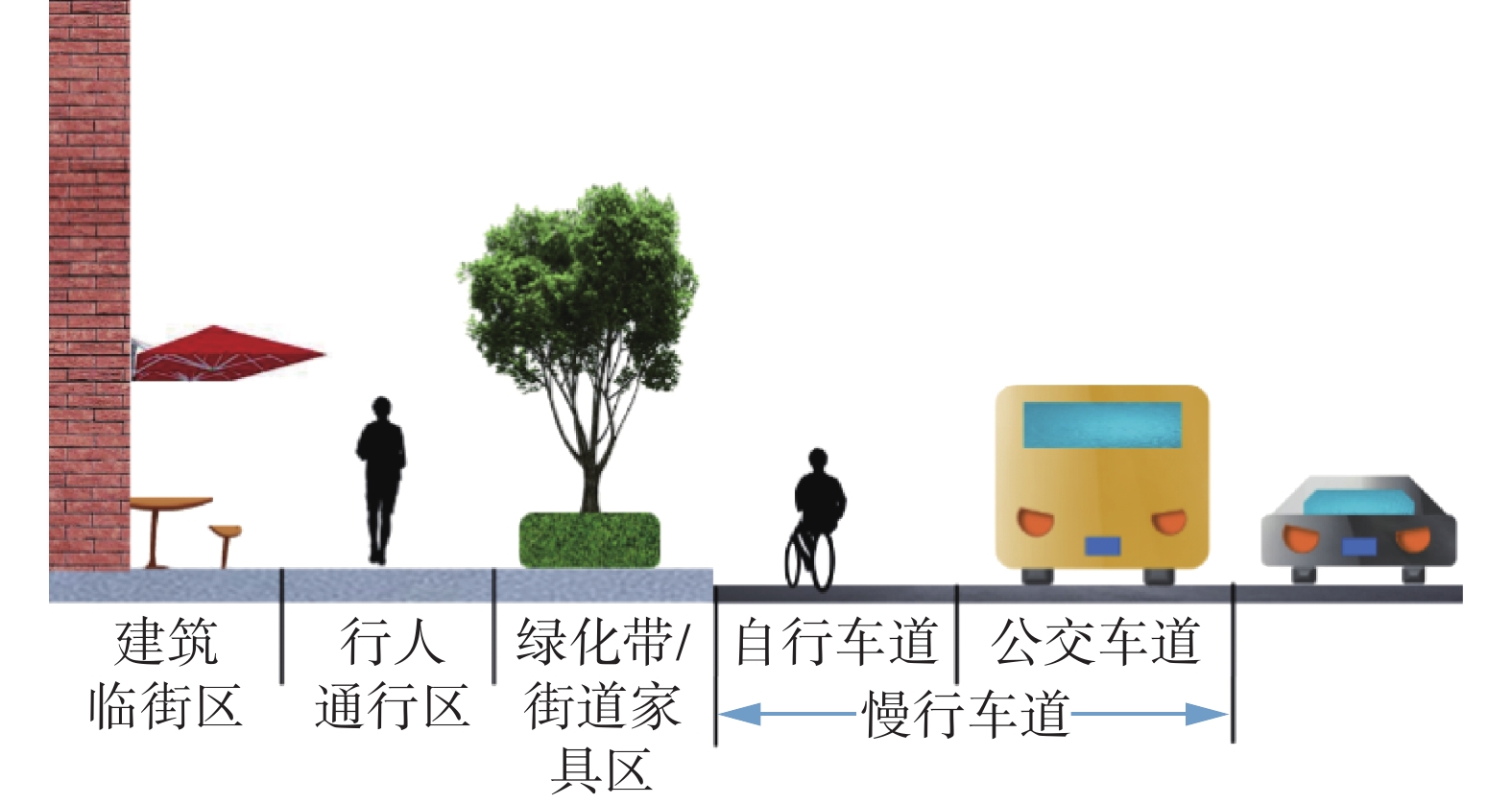
本研究所选街区范围包括：临街步行空间（建筑临街区）、行人通行区（人行道），甚至包括公交车道和自行车道组成的慢行车道^[19-20]，如图9所示。

图  9  评估区域范围

Fig.  9  Scope of the study area

下载: 全尺寸图片

1）数据集1：Jiequ数据集。由5位建筑学专家通过实地调研与考察，按少数服从多数原则确定各街区最终的空间品质等级，将各个街区按空间品质分为A、B、C三个等级。将表1所示样本分布构成的卫星图像真实数据集命名为“Jiequ”。

Jiequ数据集划分为train、validation、test三个子集，划分比例为1∶2∶1。其中：train集用于模型训练；validation集用于在训练过程中分阶段评估和筛选模型；test集用于在输入训练好的模型中进行预测，对模型的分类性能进行最终评估。

2）数据集2：Mini-jiequ数据集。由于Jiequ数据集中样本不均衡，为对比样本均衡性对模型性能的影响，将街区数据集以单类最小样本数为基准，其余类别的样本进行随机削减，创建均衡数据集Mini-jiequ，如表2所示。

Mini-jiequ数据集划分为train、validation、test三个子集，划分比例为1∶1∶1。

以上各数据集的各子集在进入模型前会按照既定的数目a、b随机抽取并打包为一批次，其中a为用于生成子空间的样本个数，b为用于计算样本到子空间的投影距离的样本个数。

3.2   实验参数设置

1）深度神经网络初始设置：深度神经网络由4个卷积模块组成，其中卷积模块中的核函数大小为 $3 \times 3$ ，池化为2，输出通道数为64。

2）数据批次设置：在使用Jiequ数据集训练模型时，样本被随机生成100个批次，每批次中参数a为1，b为2。模型训练总迭代次数为100，每迭代10次进行模型验证并储存模型和相关参数。

在使用Mini-jiequ数据集训练模型时，样本被随机生成为15个批次，各批次组成方式分两类：一类为每批次中参数a为3，b为2；另一类每批次中参数a为1，b为2。

3）对比模型：匹配网络(matching nets)、maml(model-agnostic meta-learning) ^[21]、原型网络(prototypical nets)、关系网络(relation nets)。

3.3   模型评价标准

街区数据集样本数目小且类别间不均衡，故本文选用自助法进行模型评估。按照自助法的特点，使用多次测试取平均的方法进行模型性能度量，其中每项指标随机选取100组数值进行计算并在文中展示。参考文献[22-25]，本文采用的评价指标为正确率、 ${F_1}$ 、加权宏平均和Kappa系数。

正确率 $A{\text{cc }}=\dfrac{T}{{T + F}}$ ，其中， $ T $ 为预测正确的样本数， $ F $ 为预测错误的样本数。 ${F_1} = \dfrac{{2PR}}{{P + R}}$ ，其中，P为精确率 $P = \dfrac{{\rm TP}}{{\rm TP + FP}}$ ，R为召回率 $R = \dfrac{{\rm TP}}{{\rm TP + FN}}$ 。TP为预测为类别P且预测正确的样本数；FP为预测为类别P但预测错误的样本数；FN为预测为非P类别但实际为P类别的样本数。加权宏平均指标是由宏平均指标改进而来的，是所有类别的 ${F_1}$ 加权平均 $W{\text{ = }}\sum {{{w}}{F_1}} $ ，其中w为该类别样本占总样本量的比值。K系数是基于混淆矩阵的检验一致性的指标， $K = \dfrac{{{{P}_a} - {{P}}}}{{1 - {{P}}}}$ ， ${P_a}$ 为总体分类精度，即每一类正确分类的样本数量之和与总样本数的比值；K系数由混淆矩阵计算获得，混淆矩阵越不平衡，K值越小，即偏向性越强的模型K值越低。

3.4   实验结果

由于模型训练过程中批次的组成具有随机性，故采取自助法进行测试，分别计算各模型的 ${F_1}$ 值、加权平均宏、正确率和K值。由表3可知，在使用不平衡Jiequ数据集进行街区品质评估时继承子空间参数，反而使得性能较不继承子空间参数有所下降，其原因在于前文分析得出的数据集的不平衡性会造成包含数据少的类别在模型训练过程中被过度学习，产生偏差。

重新划分后，数据集Mini-jiequ的训练结果明显优于非平衡数据集。由表3可知，在参数a=1，b=2时继承子空间参数的方法相比原方法的 ${F_1}$ 值和加权平均宏值均提高0.02，K值提高0.03，正确率提高了1.7%。

模型使用Mini-jiequ数据集训练的情况下，参数a最大可取为3，表中继承子空间参数的方法较原方法的 ${F_1}$ 值和加权平均宏值均提高0.05，K值提高0.08，正确率提高5.4%。

参数a代表用于生成子空间的图像数量，b代表用于计算描述损失并预测类别的图像数量。

模型训练时，各类别均有a个数据用来计算均值、偏差，进行均值细化，然后经过SVD得到各类子空间；各类别中有b个数据用来计算分到各类别的概率，进行类别预测。反向传播的损失值来自于以上两个过程之和，分别为a个数据生成子空间时的交叉熵损失，b个数据预测类别时的交叉熵损失和描述损失。

当a增大时，每一批次送入模型的数据增多，有更多数据用于计算均值、偏差和各类子空间，理论上来讲综合了各类别中更多数据的信息，更接近该类别整体数据的信息量，不易受劣质数据影响；当b增大时，用于计算描述损失、验证分类性能的数据增多，起到了更好地判断、调参的作用。损失值由a、b生成子空间和预测过程生成，但b在反向传播调参时发挥了更大作用。a、b的取值需要结合数据情况进行设置，当a、b增大使得每一批次包含的数据增多，学习效率和分类效果均会有所提升。

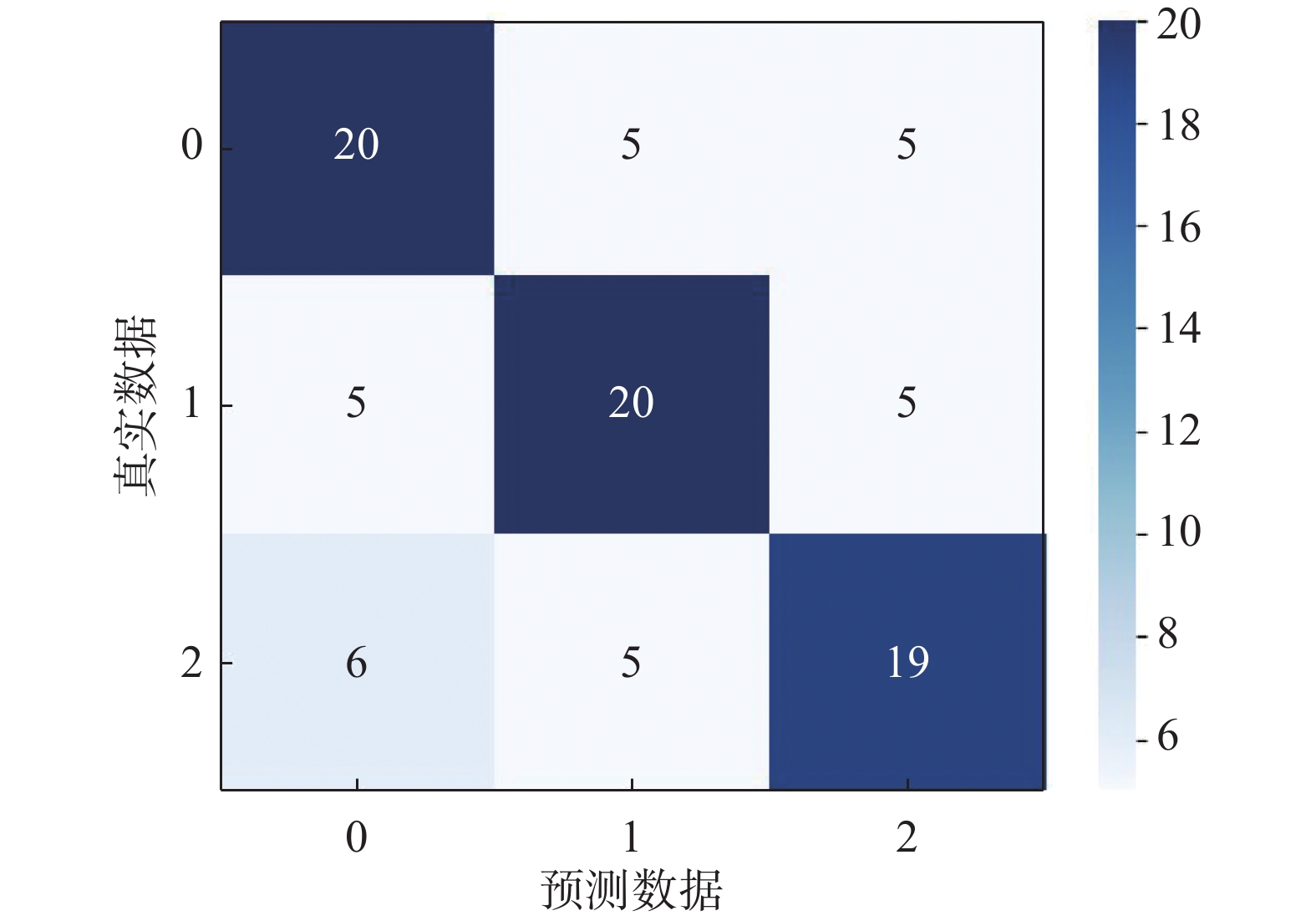
图10是继承子空间参数模型的混淆矩阵，每一次测试过程中形成的批次大小为6，批次个数为20，经自助法多次测试后取平均值生成混淆矩阵用于展示说明。

图  10  继承子空间方法在Mini-Jiequ数据集下的混淆矩阵（a=3, b=2）

Fig.  10  Confusion matrix of inheritance subspace method on the Mini-Jiequ dataset（a=3, b=2）

下载: 全尺寸图片

从混淆矩阵中发现类别A、B、C的正确识别个数分别为20、20、19，识别准确度接近，且错误识别的个数均为5。出现这一情况的原因从数据上分析是因为数据集中各类别仅有15张图片，训练出的模型在样本不明显属于某一类时缺乏更精细的区分，使得识别出错。所以，在条件允许的情况下应尽量获取更多样本，并在训练模型之前对样本进行分析。通过对比实验，本文引用Simon^[17]使用奇异矩阵分解生成自适应子空间分类器的方法具有更好的分类效果，本文提出的继承子空间参数的改进方案在一定程度上具有更高的分类准确度。在街区品质评估中，卫星图像因其易取得和视角统一的特性，在数据获取和模型训练过程中均具有优势，但由于目前带标签的数据集仅有141张图片，模型的识别正确率仅为65.9%，对于数据集的补充和模型的优化将有利于街区品质的评估。

4.   结束语

本研究采用小样本学习中的子空间分类方法，并在原有基础上进行了改进，通过从训练集继承的子空间参数赋予模型记忆性。子空间分类起初用于不固定类别的小样本分类问题，其通过卷积神经网络提取特征，并通过SVD将其进行奇异值分解，并与均值、偏差等数值结合进行均值细化，然后使用其他数据进行投影距离计算、类别预测，将描述损失回传调参。该方法不再关注各图像在视觉上的联系，而是关注图像所属类别本身（类别子空间）之间的关系，通过最大化各类别子空间之间的距离，矫正类别子空间，得到最具有该类别代表性的子空间。当使用这样的子空间进行类别预测时，不易出现边界数据难以分类或分类错误的问题，进而提高了小样本学习的分类性能。

本文在原方法最大化各子空间距离的基础上，结合本任务品质类别固定的特点，继承了训练集构造的子空间特征和基于卷积网络提取图像的特征表示网络参数，相比于只使用特征表示参数的原方法，充分挖掘了训练集中的有效信息。减轻了小样本学习因样本不足导致模型训练效果差的问题，提升了模型性能。

同时本文摒弃了使用街景图作为街区表征的传统数据采集方法，换用拍摄视角统一的卫星图像，并结合矢量数据精确裁剪的方法。以上创新使得自适应子空间的分类方法能够应用于少量街区卫星图像数据集的训练中，并实现轻量级街区品质评估。该方法具有以下优势：

1）区别于街景图存在取景位置和角度不统一导致的误差问题，卫星图在低人力和时间成本下可保证取景角度一致，且数据获取方式简单，应用范围广，更适宜应用到未来大规模的设计和规划工作中。

2）本方法选用卷积神经网络作为卫星图像的特征矩阵提取器，并将训练好的子空间参数用于街区品质评估，相较于传统的定性研究和定量分析，可避免专家在人工评估中由于个体主观差异对评估结果造成的影响，可更科学地实现问题导向下的城市分析，助力于城市规划与设计分析的科学性和创新性。

3）通过对城市街道公共空间进行科学、精确的评价后，可更好地发现城市街道公共空间中的“消极空间”和“剩余空间”，激活并实现对城市街道公共空间的科学、高效、合理的利用，从而达到功能优先、文化传承、场所打造、环境品质提升的目标。

由于数据集存在数据不平衡的问题，模型会产生偏差从而导致性能降低。因此，下一步的研究方向为减弱不平衡数据对于模型训练的不良影响，增强模型性能。