随着信息战、算法战等新型作战样式的出现，人们意识到取得作战胜利的关键之一在于获取信息优势并做出准确合理决策。指挥人员通过对战场数据进行准确实时地分析，可以辅助处理包括预警侦察、实体识别、跟踪监视、指挥决策、效果评估等问题。其中，实体识别^[1]作为确定敌方身份、属性、型号的关键步骤，成为了后续跟踪监视和战术决策的基础。

实体识别问题离不开对预警侦察阶段的数据分析。目前，预警侦察主要手段包括雷达探测^[2]、辐射源侦测^[3]、航天侦察、水声对抗侦察等技术手段。技术人员通过对各种手段获取的目标特征数据分析比对来识别实体目标。相比航天侦察、水声对抗侦察等应用场景有限的技术手段，雷达目标识别技术^[4-5]在战场环境中具有更广泛的应用。该技术通过探测回波提取目标高度、速度、P显轮廓、分辨率起伏等特征进行目标类型的识别，或根据目标的ISAR成像信息获取其几何特征和形状特性开展目标识别^[6-7]。但由于雷达信号强度与目标距离相关，远距离的目标识别率较低，目前通常借助深度学习^[8]手段对获取的特征进行分析来提高这些目标的识别率。但是，仅仅通过分析单目标特征识别目标的范围相比能够发现目标的范围要小很多。

而实际作战场景中，雷达探测设备实时获取的战场态势数据，包含了大量紧密交互的动态实体数据，如坦克、轰炸机、导弹等。它们的共同特点是空间位置和属性信息通常都随着战场态势的变化而变化，如飞机、导弹在飞行过程中空间位置、速度方向的改变。在指挥信息系统的控制下，这些作战实体构成的节点间存在着紧密的联系，充分利用作战实体间的联系将有助于扩大雷达识别范围。

作战实体数据的交互关系一般可以用图数据来表示。图数据是一类广泛存在于各领域的非结构化的数据，譬如社交网络^[9]、交通预测^[10]、生物分子^[11-12]网络等。针对图数据的处理，目前已经有了许多图机器学习算法，特别是近些年兴起的图神经网络，包括图卷积神经网络^[13-14]（graph convolutioanl networks, GCNs）、图注意力神经网络^[15]（graph attention networks, GATs）等。这些方法可以有效地处理这类图数据并取得很好的表现。

但是将图神经网络直接运用到战场态势数据面临特殊的挑战。首先，运用图上的神经网络方法的前提是需要通过已有的信息构建出反映敌方作战实体连接的图模型，而雷达等侦查系统探测到的敌方数据大多是各个作战实体独立的状态属性信息，作战实体之间的连接关系并不能够直接获取到；其次，由于电磁干扰等手段的存在，构建的作战实体关系图模型存在一定的误差，用于处理战场数据的图神经网络的模型必须具有很强的鲁棒性，而当前常见的图神经网络抗干扰能力不强，面对带噪声的图数据时效果不佳，难以直接应用。

因此，本文提出了一类用于预测战场作战实体的类型的图神经网络模型，主要包括基于战场态势数据的图模型构建以及鲁棒图神经网络的应用预测2个方面。基于战场态势数据的图模型构建为在该类场景中运用各种图网络分析方法奠定了基础；搭建的鲁棒图神经网络，可运用到战场环境的态势数据中，提前探知并识别作战实体类型，从而提高了目标识别的范围，更有助于指挥员实时决策。就我们所知，本论文是首次通过轨迹相似度关系从战场态势数据中抽取出了图模型，同时是首次将图鲁棒神经网络用于战场态势数据的分析。

1.   作战实体关系图抽取

以兵棋仿真系统中雷达探测设备获取的战场态势数据为例，其包括一段时间内多个观测时刻{ $ t_{0}, t_{1}, \cdots, t_{m} $ }的敌方各个作战实体的状态数据 $ K_{i} $ ，即 $ \left\{K_{0}, K_{1}, \cdots, K_{{m}}\right\} $ 。某一时刻 $ t_{{i}} $ 捕获到的态势数据 $ K_{i} $ ，其结构表示如表1所示。

表  1  某时刻 $ t_{{i}} $ 获取到的战场态势数据 $ K_{i} $

Table  1  Situation data of battlefield $ K_{i} $ in $t_{{i}}$

编号 $ i $	位置 $L_{{i} }$	速度/(m/s)	航向/(°)	类型
1	(−3151，−12556，100)	166	187	歼击机
2	(−4751，−2816，743)	187	216	歼击机
3	(3869，−2111，673)	193	189	未知
4	(−3151，−5367，118)	80	156	未知
5	(4651，−3576，23)	68	142	轰炸机
…	…	…	…	…

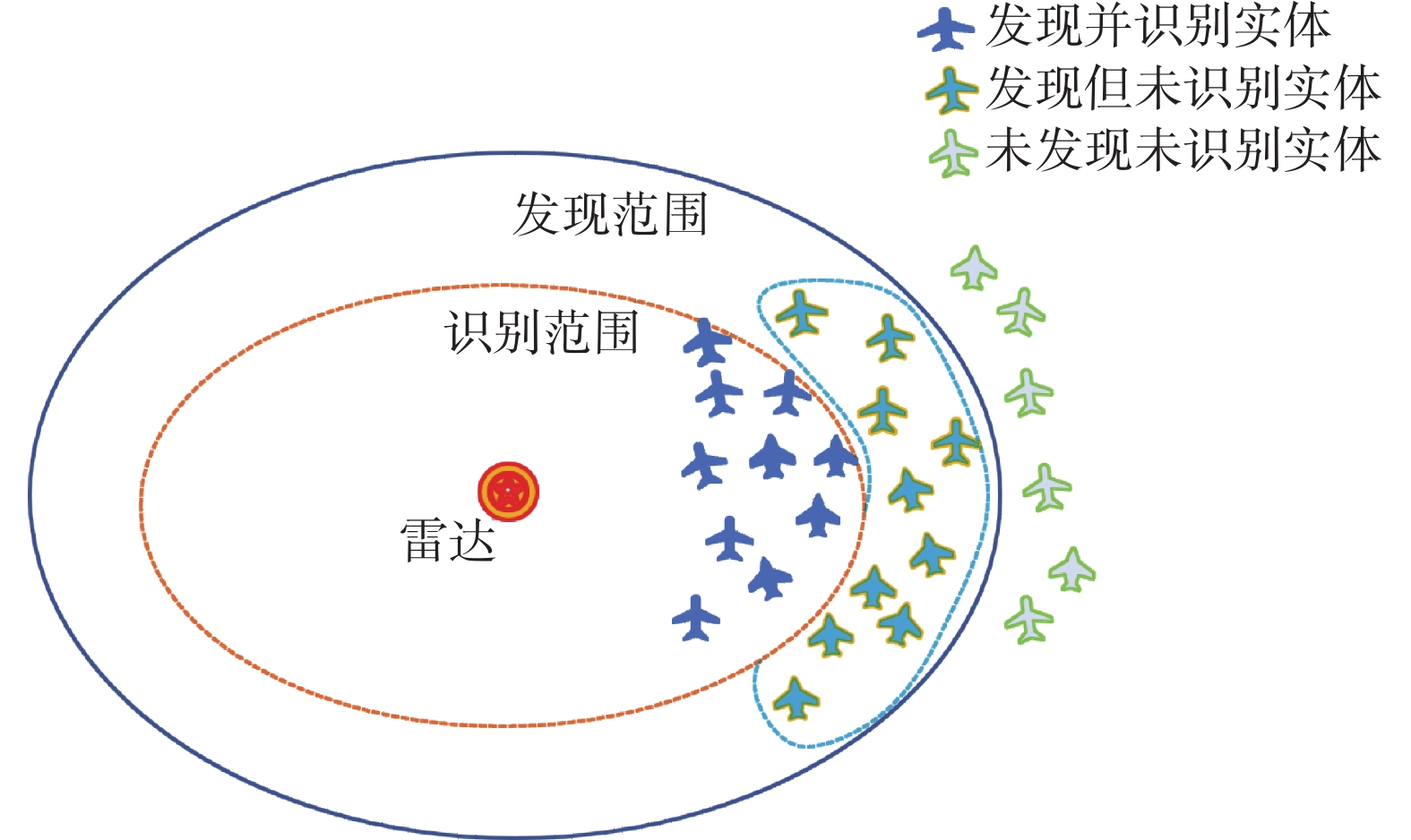
如表1所示， $t_{i}$ 时刻可获取的态势数据，包括发现范围内敌方实体的位置、速度、航向信息以及识别范围内实体的类型信息。由于发现范围内、识别范围之外的实体类型通常不能直接获取，这将一定程度限制了决策。如果能借助数据分析的手段挖掘实体间的紧密关系，并通过已经识别的实体类型较为准确地预测出未知作战实体类型将有助于扩大目标识别半径，辅助决策。

由图1中离散的目标点构建出作战实体间的连接关系，常用方法是依据当前时刻作战实体的距离或属性构建，但这样的图模型构造简单，但是忽略了作战实体的大量历史数据信息，构建的图模型可能存在很大误差。另外，由于飞机航向速度等信息随时间变化扰动较大，仅仅根据当前时刻实体的属性来构建连接关系则会产生较大的误差。而一般而言，同一类型的作战实体倾向于执行同一任务。例如轰炸机群往往会对特定目标点执行轰炸任务，歼击机群会执行护航歼敌等任务。因此，与一般构造图关系方法不同，本文借助敌方作战实体轨迹的相关性来构建出敌方作战关系网络。

图  1  红方雷达探测到态势信息

Fig.  1  Battlefield situation information of red flag

下载: 全尺寸图片

如何衡量两个作战实体位置轨迹的相关性成为了衡量作战实体连接程度的关键因素。假设某一时间段内，总共侦查到 $ N $ 个敌方作战实体。在 $ \left\{t_{0}, t_{1}, \cdots, t_{m}\right\} $ 内，每一个实体在其中的某段时间内被探测到，记第 $ n $ 个实体的观测到的位置序列 $L_{{i}}$ 构成的轨迹为 $ R(n) $ 。由于不同实体进入探测范围内时间不一致，不同实体的轨迹长度是不完全一致的。

本文根据 $ R(n) $ 计算敌方各个作战实体之间轨迹的相似度，采用动态时间规整(dynamic time warping， DTW)^[16-17]算法，来计算不同实体间轨迹的相关度。该算法早期被用于判别两段语音相似度，其优势在于可以对时间序列的延展或压缩具有一定的适应能力。DTW方法同样可以应用到战场作战实体轨迹的相似度衡量。在战场环境中，同一类型的实体可能存在起飞先后顺序、执行任务次序、飞行速度等差别，但其不同长度的轨迹只与其执行任务紧密相关。以先后出发，相同路径的3个作战实体 $ x、 y、 z $ 的轨迹序列为例。这三者的实际轨迹在空间上是一致的，只是在时间上存在先后差异，动态规整算法计算出距离 $ {d}(x, y)=0 $ , 从而可以消除时延，识别出它们之间很高的相似度。由此，DTW距离可以很好的表示作战实体的轨迹序列相似度。

综上，任意两个节点之间的DTW距离均可以根据轨迹 $ R(n) $ 计算出，再通过Min-Max归一化方法，将节点之间的距离调整到 $ [0,1] $ 之内，通过设置合理的阈值 $ \alpha $ ，连接DTW距离小于 $ \alpha $ 的边节点，则可构建出相应的图 $G=(V, E, \boldsymbol{X})$ 。 $ \alpha $ 一般可选取为型号类别数的倒数，可使得生成的边数目接近真实情况。各个作战实体构成节点集 $ V $ ，DTW算法构建的边形成了边集合 $ E $ ,当前时刻作战实体的速度、航向等属性构成了图上节点的属性 $\boldsymbol{X}$ 。算法1描述了图模型建立的过程。

算法1　 DTW图模型抽取算法

输入　态势数据 $ \left\{K_{0}, K_{1}, \cdots, K_{{m}}\right\} $

参数　调节连接边数量的阈值 $ \alpha $

输出　图数据结构 $ G=(V, E, \boldsymbol{X}) $

1) 从态势数据中提取当前时刻所有节点的轨迹时间序列 $ R(n) $ , $ n=1,2, \cdots, N $ 以及特征矩阵 $ \boldsymbol{X} $ ；

2) 借助DTW算法，计算所有节点间的DTW距离 ${d}(i, j) $ , $ i, j=1,2, \cdots, N $ ，记DTW距离构成集合为 $ \mathcal{K} $ ；

3) 对所有节点DTW距离进行Min-Max归一化

4) 连接节点归一化距离小于 $ \alpha $ 的节点，即令 $E(i, j)= $ $\varDelta_{d(4, j) < a}$ ，输出图 $G = \left( {V,E,{{{\boldsymbol{X}}}}} \right)$ 。

根据算法1，从战场中的时序态势数据提取出节点之间的连接关系，并构建图模型 $ G $ ,可用于下一步的图神经网络算法。

2.   基于鲁棒GCN的实体识别算法

在提取了图模型 $ G $ 之后，态势数据中的实体型号识别问题转化成了图上的节点分类问题。给定图结构数据 $G=(V, E, \boldsymbol{X})$ ，其中 $ V=\left\{v_{1}, v_{2}, \cdots, v_{N}\right\} $ 表示 $ N $ 个节点（实体）, $ E $ 表示边构成的集合（提取的连接关系）， $\boldsymbol{X}=\left[ \begin{array}{llll}x_{1} & x_{2} & \cdots & x_{N}\end{array} \right]^{\mathrm{T}} \in \mathbf{R}^{N \times d}$ 表示 $ N $ 个节点属性（实体属性）构成的矩阵， $ \boldsymbol{A} \in \mathbf{R}^{N \times N} $ 表示图的邻接矩阵。 设共有标签（型号种类） $ F $ 种，给定部分有标签的节点 $ V_{\text {train }}=\left\{v_{1}, v_{2}, \cdots, v_{p}\right\} $ ，其对应的标签为 ${ \mathcal{Y}}_{\text {trand }}=\left\{Y_{1}, Y_{2}, \cdots, Y_{p}\right\}$ ，一般采用one-hot表示 $ Y_{i} \in \mathbf{R}^{F} $ 。我们的目标是预测出其余未知的节点 $ V_{\text {test }} $ 的标签。

2.1   图卷积神经网络

由于一般的深度学习框架对图结构数据表示能力有限，人们将深度学习拓展到了图数据上，提出了图神经网络^[18-19]。图神经网络模型可以很好地处理包括节点分类、链路预测等图上的机器学习任务，其模型通常由两类函数复合而成，包括：领域聚合（combination）函数以及输出(readout)函数。领域聚合函数通过聚合其领域节点的特征来更新每一个对应节点的表示；而输出函数通过进一步处理图上各节点表示来获得整幅图的节点表示。这两个步骤可以用GraphSage^[20]框架概括。GCNs^[13]、GATs^[15]都是这类的结构。其中Kipf提出的GCN定义了图谱域上的卷积算子，在图上的各项任务，特别是节点分类任务表现良好。

GCN模型定义了函数 $f: \mathbf{R}^{N \times d_{0}} \rightarrow \mathbf{R}^{N \times F}$ ，借助 $ L $ 层的神经网络来更新各个节点特征。 每层之间的特征矩阵 ${\boldsymbol{X}}^{l}$ 更新规则如下：

其中： $\boldsymbol{X}^{0} \in \mathbf{R}^{N \times d_{0}}$ 表示初始输入的特征矩阵，一般选取为节点属性矩阵 $ \boldsymbol{X} $ ； $\boldsymbol{\theta}^{l} \in \mathbf{R}^{N \times d_{t}}$ 是需要学习的参数； $ d_{L}=F $ ； $ \sigma $ 是激活函数； $ \tilde{\boldsymbol{A}}=\boldsymbol{A}+\boldsymbol{I} $ ， $ \boldsymbol{I} $ 表示单位矩阵；对角阵 $ \tilde{\boldsymbol{D}} $ 为 $ \tilde{\boldsymbol{A}} $ 的度矩阵，其对角元素 $\tilde{\boldsymbol{D}}_{ii}= {\Sigma}_{{j}} \tilde{\boldsymbol{A}}_{{ij}}$ 。令 $\theta=\bigcup\nolimits_{i = 1}^L {\left\{ {{{\boldsymbol{\theta}} ^l}} \right\}}$ 表示所有待训练参数，那么对于节点分类的问题。GCN 通过极小化已知标签的节点上的损失函数：

来更新参数学习映射 $ f_{\theta} $ ，这里 $f_{\theta}\left(\boldsymbol{X}^{0}, \boldsymbol{A}\right)_{i} \in \mathbf{R}^{F}$ 表示输出矩阵的第 $ i $ 行。一般采用已知标签上的交叉熵作为损失函数，即

其中 $Y_{l} \in \mathbf{R}^{F}$ 是标签的one-hot表示。当 $\theta^{*} = \arg \min \mathcal{L}_{\mathrm{GGN}}$ 时，对 $\upsilon _{i} \in V_{\text {text }}$ ， $f_{\theta }(\boldsymbol{X}, \boldsymbol{A})_i$ 即为在未知节点 $\upsilon _{i}$ 上的预测标签概率。

2.2   鲁棒图卷积神经网络

由于本文构建的图模型源自侦查数据的轨迹信息，一方面，仅仅依靠实体轨迹信息而忽略实体属性信息易产生构建图的偏差；另一方面当存在敌方干扰或者欺骗时，轨迹测量数据将不可避免地存在误差，进而导致目标类型的误判。同时文献[21-22]指出，图数据在受到噪声干扰时，GCN准确率会明显下降。因此借助实体属性修正所构建的图结构，提高GCN的鲁棒性对于作战节点类型的正确识别是十分必要的。

为了提高GCN的鲁棒性，文献[23]借助真实世界中网络的低秩性和稀疏性的先验性假设对图结构进行了修正，构建了基于图预处理技术的图鲁棒神经网络模型。但是对于作战实体网络，低秩性和稀疏性假设并不适用。因此，我们需要找到更加适合军事数据的先验信息来修正图结构，提高模型鲁棒性。注意到，属性相似的节点更有可能具有紧密的关系。例如飞行速度和方向接近的作战实体性能更加接近，更可能执行同一任务，因此这些节点更可能为同一类型的实体。所以节点属性信息可以用来对图结构进行修正，使得属性相近的节点具有更大的相似度。

因此，本文提出鲁棒图卷积神经网络（robust GCN, RoGCN），通过对节点属性添加光滑性假设，使得模型同时更新优化图结构 $ {\boldsymbol{A}} $ 和GCN参数 $ \theta $ ，即极小化以下目标函数：

式中： $\operatorname{tr}\left(\boldsymbol{X}^{{\rm{T}}} \bar{\boldsymbol{L}} \boldsymbol{X}\right)$ 表示整个图上各节点属性差异带来的损失， $ \mathcal{L}_{\mathrm{GCN}}\left(\theta, \bar{\boldsymbol{A}}, \boldsymbol{X}^{0}, \mathcal{Y}_{\text {train }}\right) $ 构建了标签带来的损失， $ \lambda $ ， $ \beta $ 是超参数用于平衡这两项的权重。而 $ \bar{\boldsymbol{L}}=\bar{\boldsymbol{D}}-\bar{\boldsymbol{A}} $ ， $\bar{D}_{ii}=\Sigma_{j} \bar{\boldsymbol{A}}_{t f}$ 为度矩阵 $ \bar{{\boldsymbol{D}}} $ 的对角元素， $ \bar{\mathcal{A}} $ 表示邻接矩阵的定义域，即 $ \bar{{\boldsymbol{A}}} $ 中元素限制在0~1之间。通过添加 $\operatorname{tr}\left(\boldsymbol{X}^{{\rm{T}}} \bar{\boldsymbol{L}} \boldsymbol{X}\right)$ 损失使得节点速度航向相近的节点连接更多，而 $ \mathcal{L}_{\mathrm{GCN}}\left(\theta, \bar{\boldsymbol{A}}, \boldsymbol{X}^{0}, \mathcal{Y}_{\text {train }}\right) $ 使得图连接关系尽可能满足标签损失最小^[23-24]。与GCN采用速度与航向矩阵 $ {\boldsymbol{X}} $ 作为初始特征矩阵 $ \boldsymbol{X}^{0} $ 相比，这里RoGCN模型选取初始的特征矩阵 $ \boldsymbol{X}^{0}=\boldsymbol{I} $ ，这使得初始维数更大且避免了速度与航向中的噪声对GCN传播函数的干扰。优化目标(1)将图结构也作为训练的一部分，可以在训练过程中不断更新结构，起到对抗干扰和噪声的作用。优化目标(1)的求解可以分为两部分，分别是图结构的修正和参数 $ \theta $ 的更新。

1）图结构的修正

首先固定参数 $ \theta $ ，借助投影梯度下降方法，求解以下问题：

更新步骤为

其中 $\nabla_{\bar{\boldsymbol{A}}}$ 表示将梯度下降后的 $\bar{\boldsymbol{A}}$ 所有元素投影至0~1之间。这一步骤通过更新图结构矩阵获得修正后的图结构 $\bar{\boldsymbol{A}}$ 。

2）迭代求解新的模型

通过上述方法修正了图结构之后，固定结构 $ \bar{A} $ , 图标签损失极小化模型如下：

通过梯度下降方法优化参数： $\theta \leftarrow \theta-\eta_{2} \nabla_{\theta} \mathcal{L}_{\mathrm{GCN}}$ $\left(\theta, \bar{\boldsymbol{A}}, \boldsymbol{X}^{0}, \mathcal{Y}_{\rm{train}}\right)$

整体过程为：首先选取合适的初始特征矩阵 $ \boldsymbol{X}^{0}=\boldsymbol{I} $ ，并用 ${\boldsymbol{A}}$ 初始化参数 $\bar{\boldsymbol{A}}$ ，随机初始化GCN的参数 $ \theta $ ，选取总的迭代次数 $ T_{1} $ ，通过投影梯度法，对结构 $\bar{\boldsymbol{A}}$ 进行一次修正,再借助梯度下降法，迭代 $ T_{2} $ 次优化神经网络参数。

3.   实验及结果分析

3.1   实验场景设置

本文的实验采用指控学会组织的兵棋推演大赛的数据，该推演场景为：A、B两岛主权存在争议，目前为红方占有，蓝方一直企图收回被占岛屿。双方围绕主权争夺日益激烈，蓝方组织大量空中力量对红方进行攻击，红方强化海域军事力量，进行防御。

兵力设置：蓝方兵力共47个作战单位，完成侦查、预警、干扰、制空、突击等任务，包括轰炸机18架和歼击机24架。

目标识别任务：在实际推演场景具有目标探测的作战单位（预警机、地面雷达、驱逐舰、地面防空）具有目标发现距离和识别距离。在推演的进行过程中，红方发现范围内存在未识别的敌方飞机，且数量随推演时间变化。红方希望可以推断出未识别的敌方飞机类型，判断出是轰炸机还是歼击机。

实验数据及实验配置：每一次仿真实验持续时间约为4 000 s，探测设备每隔20 s左右收集一次数据。因此，所有作战单元轨迹序列最长包含200个元素左右，某一时刻探测到的作战单元的数量最大为42左右。由于该军事应用场景的节点规模很小，计算复杂度小，所有模型均在个人笔记本运行，CPU配置为Intel(R)Core(TM)I7-10710u。

3.2   模型参数设置

目前关于鲁棒图神经网络在兵棋推演的实体识别问题上的模型还很少。而基于低秩性以及稀疏性假设的模型^[23] 不符合我们对该军事网络的一般假设。因此，为了比较本文构建图模型的有效性，以及鲁棒图神经网络模型的效果，我们选择两类经典的深度学习以及图神经网络方法，分别比较了基于多层感知机（multilayer perceptron, MLP）^[25]的分类器、基于欧氏距离建立的GCN^[13]、RoGCN以及基于DTW算法建立的GCN、RoGCN共5类算法。我们分别用MLP、GCN-Dist、 RoGCN-Dist、 GCN-DTW、 RoGCN-DTW算法表示。

MLP：多层感知机，通过多层的线性映射对输入特征进行变换，可以用于处理经典的各类监督问题。

GCN：经典的图卷积神经网络方法，通过定义谱域上的卷积实现了图上的卷积网络，可以用来解决图上的节点分类问题。

RoGCN：本文提出的优化算法，具有更强的鲁棒性。

本文模型和对比模型的实验参数设置如下：

在MLP模型中，我们构造了输入为位置（3维向量）、速度、航向构成的5维输入，隐藏层维数为16，输出层维数为2的多层感知机模型。

对于GCN模型，选取的初始特征矩阵 $ \boldsymbol{X}^{0}=\boldsymbol{X} $ ，为节点速度、航向构成的矩阵，其余参数按照文献[13]中设置；对于RoGCN模型， 选取初始特征矩阵 $ \boldsymbol{X}^{0}=\boldsymbol{I} \in \mathbf{R}^{N \times N} $ 。选取内外训练步数 $ T_{1}=200 $ 、 $ T_{2}=2 $ ，内外训练率 $ \eta_{1} $ 和 $ \eta_{2} $ 均为0.01，权重参数 $ \beta=1, \quad \lambda=1 $ 用于平衡各项损失函数。其余参数同GCN一致。

对于基于欧氏距离(Dist)的模型，选取构造边的阈值为40 km；对于基于DTW相似度的模型，选取阈值 $ \alpha=0.5 $ 。以上参数均是根据验证集上实验选取的阈值。

3.3   实验1：基于DTW构造的图数据

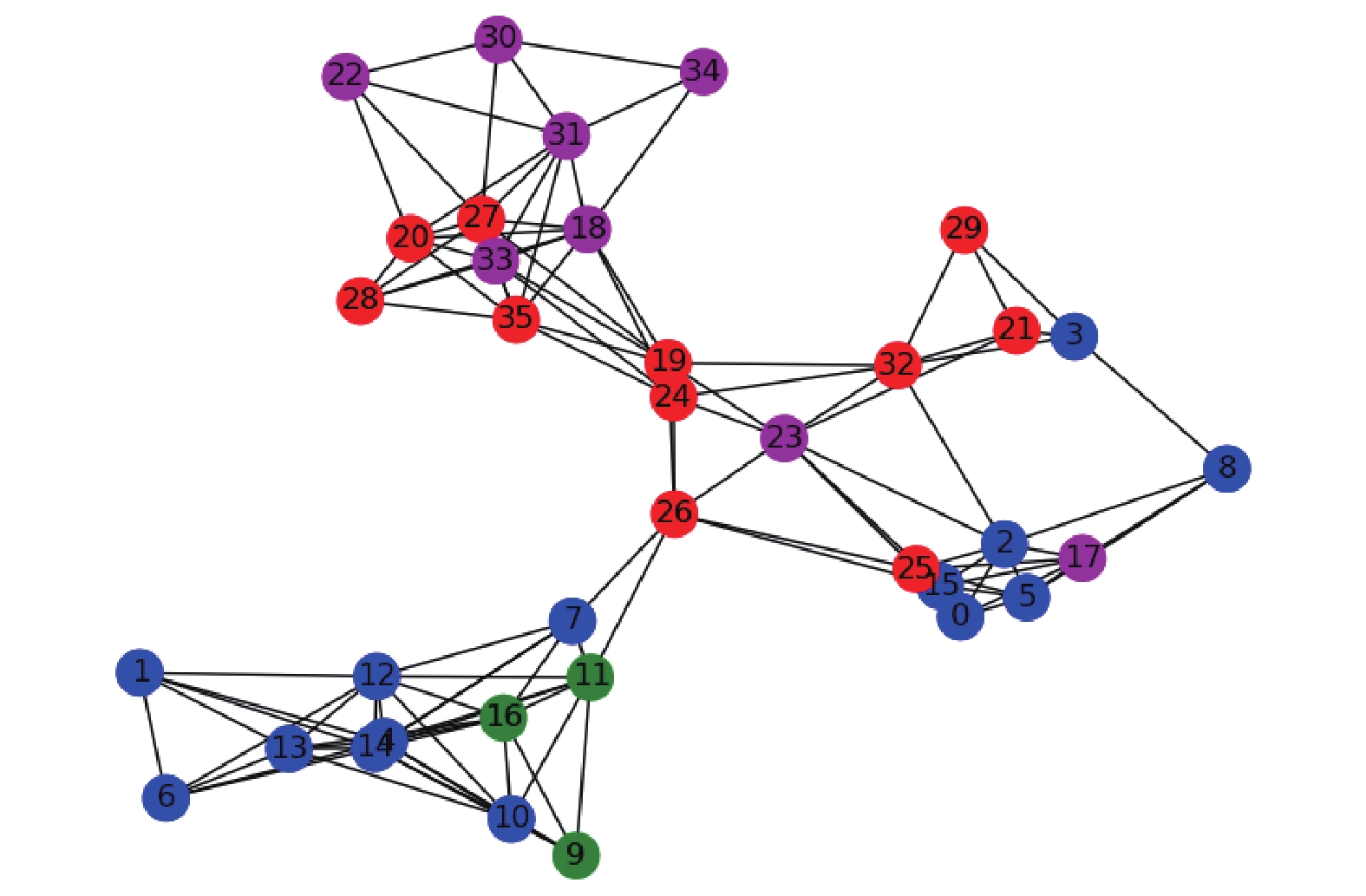
选取某时刻 $ t_{0}=3\;690 $ s，图2和图3分别给出了基于DTW及Dist得到的图 $ G $ 。如图2和图3构造的作战实体网络中，红色节点代表识别出的轰炸机，紫色节点代表未识别出的轰炸机；蓝色节点代表识别出的歼击机，绿色节点代表未识别出的歼击机。可以看出，基于Dist构造的图，只有当节点的欧氏距离较小时，才存在边相连；而基于DTW构造的图，即使两个相同类型的作战实体当前时刻相距很远，但仍可能存在边相连。由此可见，基于DTW构建的图更加符合型号相同的节点连接更加紧密的要求。

图  2  基于DTW构造的图

Fig.  2  The graph based on DTW

下载: 全尺寸图片

图  3  基于欧氏距离构造的图

Fig.  3  The graph based on Dist

下载: 全尺寸图片

3.4   实验2：模型鲁棒性测试

在实际战场数据中，敌方可能存在电子干扰，这使得雷达获取的态势数据存在一定噪声。因此，比较不同模型的抗干扰能力是重要的。为了对比RoGCN与GCN在噪声干扰下的识别准确率，对当前时刻获取到的所有历史态势数据添加一定的高斯分布噪声干扰，噪声模型为

其中 $\overline{L}_{{{k}}}、 \overline\upsilon _{{{k}}}、 \overline{{f}}_{{{k}}}$ 分别表示 $ k $ 时刻下作战单元的位置、速度和航向。

由于兵器推演前期，雷达还未能探测到敌方相应的作战实体，因此选取3个中间时刻，此时仅有部分实体进入识别范围。算法识别准确率如表2，所有结果均为10次实验结果的平均值。表2给出了不同噪声水平下的准确率。由表2可以看出在3个时刻下，RoGCN-DTW方法都要好于其他方法。

MLP模型忽略节点之间相关性，并且只用到当前时刻的信息，所构建模型在不同噪声水平下的准确率相比其他方法要低，相比RoGCN-DTW等模型更是显著得低。

而GCN-Dist与RoGCN-Dist模型仅仅依赖当前节点的位置信息提取节点关系，由于当前节点的位置在干扰之下可能会发生较大改变，不同噪声情况下波动结果准确率波动较大。特别是GCN-Dist方法，存在噪声为0的情况下，但准确率却不如存在噪声的情况。但采用特征信息对图结构进行修正的RoGCN-Dist方法，相比GCN-Dist的准确率和鲁棒性还是要高。

GCN-DTW和RoGCN-DTW两种方法采用了DTW距离计算相似度，整体准确率更高。由于通过该方法采用所有的历史信息计算相似度，即使节点的位置信息存在噪声，但归一化计算后，整体噪声对节点之间的相似度影响不大。同时，RoGCN-DTW方法通过进一步修正构成的图，准确率相比GCN-DTW更高。可以看出RoGCN-DTW在存在噪声水平的情况下，准确率要优于GCN-DTW，这验证了RoGCN-DTW相比GCN-DTW具有更强的鲁棒性，在噪声干扰下可以较为准确的预测出未知作战实体的类型。

3.5   实验3：消融实验

首先，对比设置 $\operatorname{tr}\left(\boldsymbol{X}^{{\rm{T}}} \overline{\boldsymbol{L}} \boldsymbol{X}\right)$ 的影响，实验结果见表3，是否通过特征对图结构修正在低噪声时影响不大，这个时候节点之间的轨迹信息已经准确地确定节点之前的连接关系了，但是在高噪声情况下，缺少特征信息用于修正图结构会导致准确率降低。其次，比较采用标签损失 $\mathcal{L}_{\mathrm{GCN}}\left(\theta, \bar{\boldsymbol{A}}, \boldsymbol{X}^{0}, \mathcal{Y}_{\text {train }}\right)$ 来修正图结构的影响，实验结果见表4，是否通过标签对图结构修正在低噪声时影响不大，但在高噪声情形下，标签本身的信息对图结构的准确重构存在一定的帮助作用。

表  3  不同噪声情况下结构修正参数 $ \lambda $ 对模型的影响

Table  3  The recognition accuracy with respect to $ \lambda $ under different algorithm noise %

当前态势时间	方法	噪声方差
		0	10	20	30	40
$t_{0}=3\;605 \mathrm{~s}$	RoGCN-DTW( $ \lambda=0 $)	100	100	100	99.2	90.7
	RoGCN-DTW( $ \lambda=1 $)	100	100	100	100	99.2
$t_{0}=3\;690 \mathrm{~s}$	RoGCN-DTW( $ \lambda=0 $)	100	100	100	100	97.2
	RoGCN-DTW( $ \lambda=1 $)	100	100	100	100	97.2
$t_{0}=3\;796 \mathrm{~s}$	RoGCN-DTW( $ \lambda=0 $)	100	100	100	100	90.0
	RoGCN-DTW( $ \lambda=1 $)	100	100	100	100	96.3

表  4  不同噪声情况下结构修正参数 $ \alpha $ 对模型的影响

Table  4  The recognition accuracy with respect to $ \alpha $ under different algorithm noise %

当前态势时间	方法	噪声方差
		0	10	20	30	40
$t_{0}=3\;605 \mathrm{~s}$	RoGCN-DTW( $ \alpha=0 $)	100	100	100	100	98.2
	RoGCN-DTW( $ \alpha=1 $)	100	100	100	100	99.2
$t_{0}=3\;690 \mathrm{~s}$	RoGCN-DTW( $ \alpha=0 $)	100	100	100	100	95.1
	RoGCN-DTW( $ \alpha=1 $)	100	100	100	100	97.2
$t_{0}=3\;796 \mathrm{~s}$	RoGCN-DTW( $ \alpha=0 $)	100	100	100	100	96.0
	RoGCN-DTW( $ \alpha=1 $)	100	100	100	100	96.3

经过RoGCN算法分析后，对于原来发现范围内的实体，算法可以准确地识别，因此RoGCN可以有效地扩大目标识别范围。

4.   结束语

目标识别是战争数据分析与决策中的一个重要问题。当前基于特征分析的雷达探测技术存在着识别范围有限的问题。由于作战目标间存在紧密联系，本文首次借助DTW算法从时序态势数据中抽取出相应的图模型，并建立了鲁棒图卷积网络用于推测未知的作战实体类型。实验表明本文算法相比经典的多层感知机及GCN准确率更高。

除了雷达探测技术中识别范围比发现范围小，其他辐射源技术和水声技术获取的数据同样存在识别半径有限的问题。鲁棒GCN方法同样可以推广到其他探测技术获取的特征数据中，辅助战场目标识别问题。另外，基于当前实战需求，本文从战场仿真态势数据所构建的图模型是基于相同类型实体的轨迹相似所确立的。随着战争模式的发展，未来可能出现一些混合编组作战的任务场景，则本文基于作战实体轨迹建立的图模型也适用于进行无监督的编组预测等任务。总而言之，只要作战实体间的关联同作战实体间的轨迹存在紧密联系，本文提出的模型便可以用于提取出作战单元之间的关联，并挖掘出更多信息辅助决策。