A new deeplabv3+ semantic segmentation model of edge gradient interpolation with double branch structure
-
摘要: 针对deeplabv3+解码器采用双线性插值的单一分支结构易导致图像的高频分量损失、语义分割精度不高的问题，采用索伯(Sobel)算子计算各像素点沿不同方向的边缘梯度值并结合双三次插值算法，提出一种边缘梯度插值方法；在此基础上，对1/8输入图像与编码器输出采用边缘梯度2倍上插值再经特征融合和边缘梯度2倍上插值操作，并与1/4输入图像经特征融合后再进行边缘梯度4倍上插值操作，从而提出一种边缘梯度插值的双分支deeplabv3+意义分割模型。对比实验结果表明，本文方法在VOC2012数据集上较原分割模型平均交并比指标有2.2%的提升，且对图像边缘细节分割有较好的视觉效果。Abstract: Aiming at the problem that the single branch structure of deeplabv3 + decoder with bilinear interpolation is easy to lead to the loss of high-frequency components of an image and the low accuracy of semantic segmentation, the Sobel operator is used to calculate the edge gradient values of each pixel along different directions, and by combination with bicubic interpolation algorithm, an edge gradient interpolation method is proposed. On this basis, the 1/8 input image and the encoder output are interpolated up to twice the edge gradient, then interpolated up to twice the edge gradient through feature fusion and edge gradient interpolation, and then interpolated up to four times the edge gradient after feature fusion with the 1/4 input image, thereby a double branch deeplabv3 +semantic segmentation model with edge gradient interpolation is established. The comparative experimental results show that the proposed method has improved MIOU indicator by 2.2% on the VOC2012 dataset compared with the original model, and has a better visual effect on image edge detail segmentation.
-
图像语义分割就是利用深度学习模型从像素级分割出图片中的不同对象并对每个像素进行类别标注，高准确率语义分割是自主移动机器人视觉理解的基础。目前deeplab[1-4]系列网络模型广泛应用于语义分割，最早的deeplab语义分割模型由文献[1]于2014年提出，它通过全连接条件随机场实现像素间的结构化预测，采用空洞卷积来保证所获取的感受野；文献[2]在deeplab语义分割模型的基础上，通过空间金字塔池化(spatial pyramid pooling, SPP)[5]方案提出一种空洞空间金字塔池化(atrous spatial pyr-amid pooling, ASPP)的deeplab语义分割模型——deeplabv2。ASPP能有效获取图像的多尺度特征信息[2]，文献[2]获得比文献[1]更高的分割精度，但文献[2]的空洞率依赖人为经验选取，采用不恰当的、固定的空洞率进行空洞卷积操作不能有效提取不同场景的对象特征，从而导致语义分割精度下降[3]；文献[3]对ASPP模块分别采用级联和并联组合方式，自适应获得多样性的空洞率进行空洞卷积操作提取场景对象特征，从而提出deeplabv3语义分割模型；文献[4]将文献[3]的deeplabv3模型作为编码器，并把编码器输入的图像与编码器输出的高层语义特征子图分别进行1×1卷积和4倍上插值操作成相同尺寸，再把它们进行拼接、3×3卷积和双线性插值操作，得到最终的语义分割结果。编码器之后的这一系列称之为解码器，由编码器和解码器构成了deeplabv3+语义分割模型。
目前在图像的边缘优化语义分割方法中，文献[6]采用deeplabv3+语义分割模型与超像素的相结合的方法来进行边缘优化；文献[7]则提出利用边缘切向流使得图像在恢复大体轮廓线条上有一定程度的改善，但未从图像插值方面进行研究；图像插值的主要任务是恢复图像边缘和纹理并尽可能抑制模糊，在传统线性图像插值方法中，相比于最邻近插值[8]和双线性插值[9]，双三次插值算法[10]能使图像在变换过程中边缘部分更平滑、细节质量保留更完好；deeplabv3+网络的解码器则使用双线性插值[8]进行上插值，而双线性插值仅考虑了4个直接邻点灰度值忽略了各邻点间的影响导致图像物体边缘部分丢失像素点信息[11]，致使物体边缘语义分割精度受损；文献[12]通过计算图像梯度比率从而改进图像插值方法，但没有对物体边缘的分割做进一步研究；文献[13]中使用拉普拉斯滤波器锐化边缘图像从而提高插值后的图像质量，但图像物体仍存在模糊边缘的情况；在deeplabv3+的解码器中，仅仅只是将骨干网络产生的一个低级特征图作为单分支来与经过ASPP模块后的高级特征图进行拼接融合，然而这样会导致图像中边缘等部分像素的不连续性[14]，从而降低图像语义分割精度；针对上述未解决的问题，本文基于deeplabv3+语义分割模型，提出一种边缘梯度插值算法来替代原网络解码器中双线性插值改善插值后物体边缘部分的图像质量，并在其解码器中提出双分支结构来获取图像的多尺度信息以获得更多容易被忽略的图像物体边缘特征信息，从而形成一种边缘梯度插值的双分支deeplabv3+语义分割模型。
1. deeplabv3+网络结构
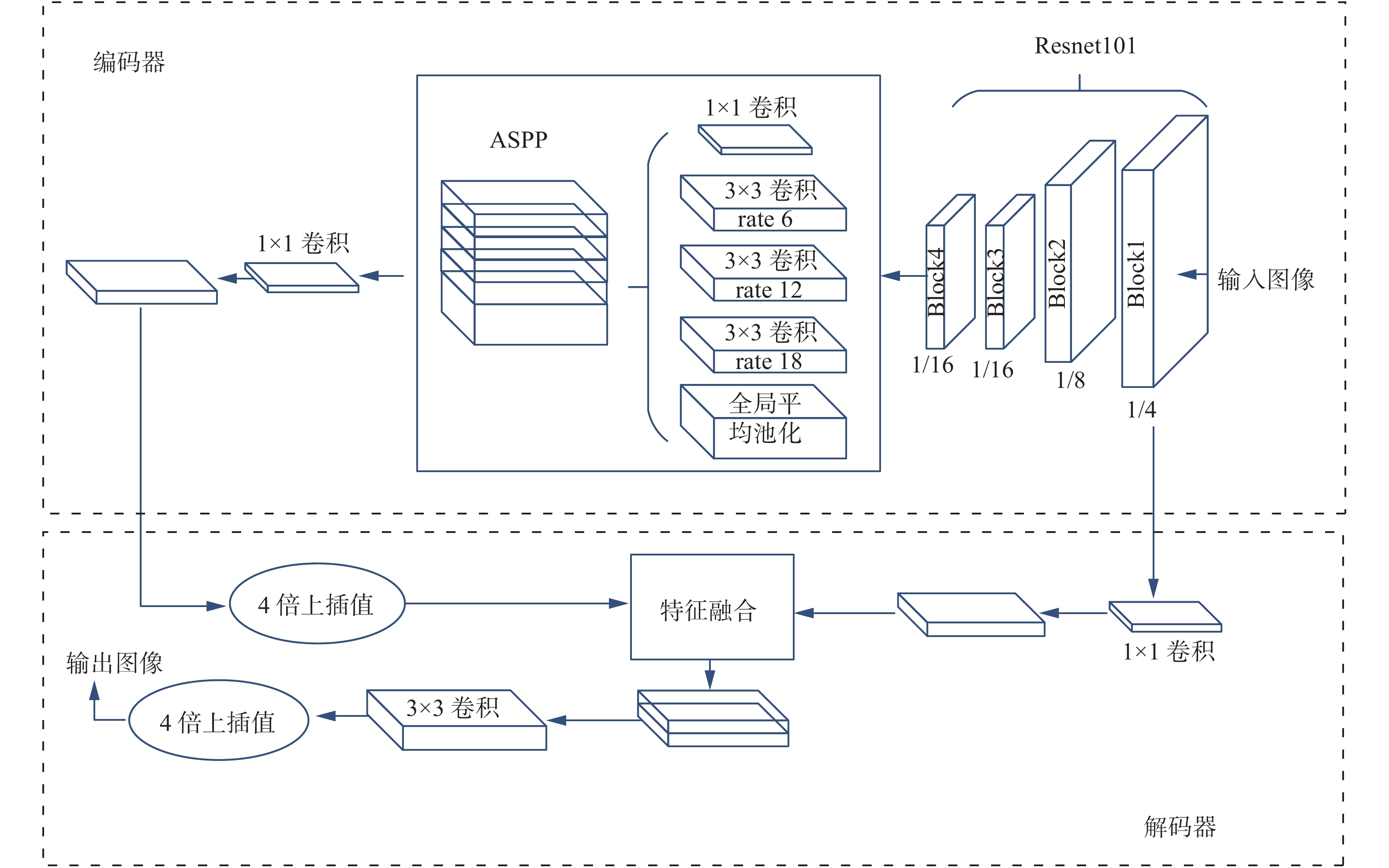
deeplabv3+[4]的网络结构如图1所示，主要包括编码器和解码器。在编码器中，通过骨干网络进行原图的1/4、1/8、1/16下采样提取特征信息得到低级特征图，其中在Block4中是空洞率为2、4、8的空洞卷积，然后经过ASPP特征融合模块得到高级特征图；在解码器中，将经过特征融合后的高级特征图使用双线性插值[9]进行4倍上插值，与特征提取网络后产生的一个低级特征图进行concat操作，最后经过
$ 3 \times 3 $ 卷积使用双线性插值[9]进行4倍上插值将图像恢复至原有大小。
图 1 deeplabv3+网络结构Fig. 1 Deeplabv3+ network structure
下载:
全尺寸图片
空洞卷积可以在减少运算量的同时保证获取的感受野[15]。对于输出信号y和输入信号x，空洞卷积[5]的操作可描述为
$$ y(i) = \sum_k^K {x(i + r \cdot k)} \cdot u(k) $$ 式中：r表示空洞率；
$ u(k) $ 表示滤波器第k个位置的参数；K表示滤波器的尺寸。空洞卷积能够增大感受野，其大小为$$ {R_j} = (r - 1) \times (k - 1){\text{ + }}k,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j = 1,2, \cdots ) $$ 式中
$ {R_j} $ 为第j层的空洞卷积层所提供的感受野大小。2. 边缘梯度插值算法
由于双线性插值具有低通滤波的性质，从而导致缩放后的图像的高频分量收到损失、图像边缘在一定程度上变得较为模糊[16]。本文提出边缘梯度插值算法，以此替换deeplabv3+的解码器中上插值时采用的双线性插值算法。本文的边缘梯度插值算法主要有以下几个步骤。
首先使用高斯模糊降噪，在进行边缘检测之前先对原图像进行高斯滤波，减少噪声对边缘检测的影响，这里使用的是一个
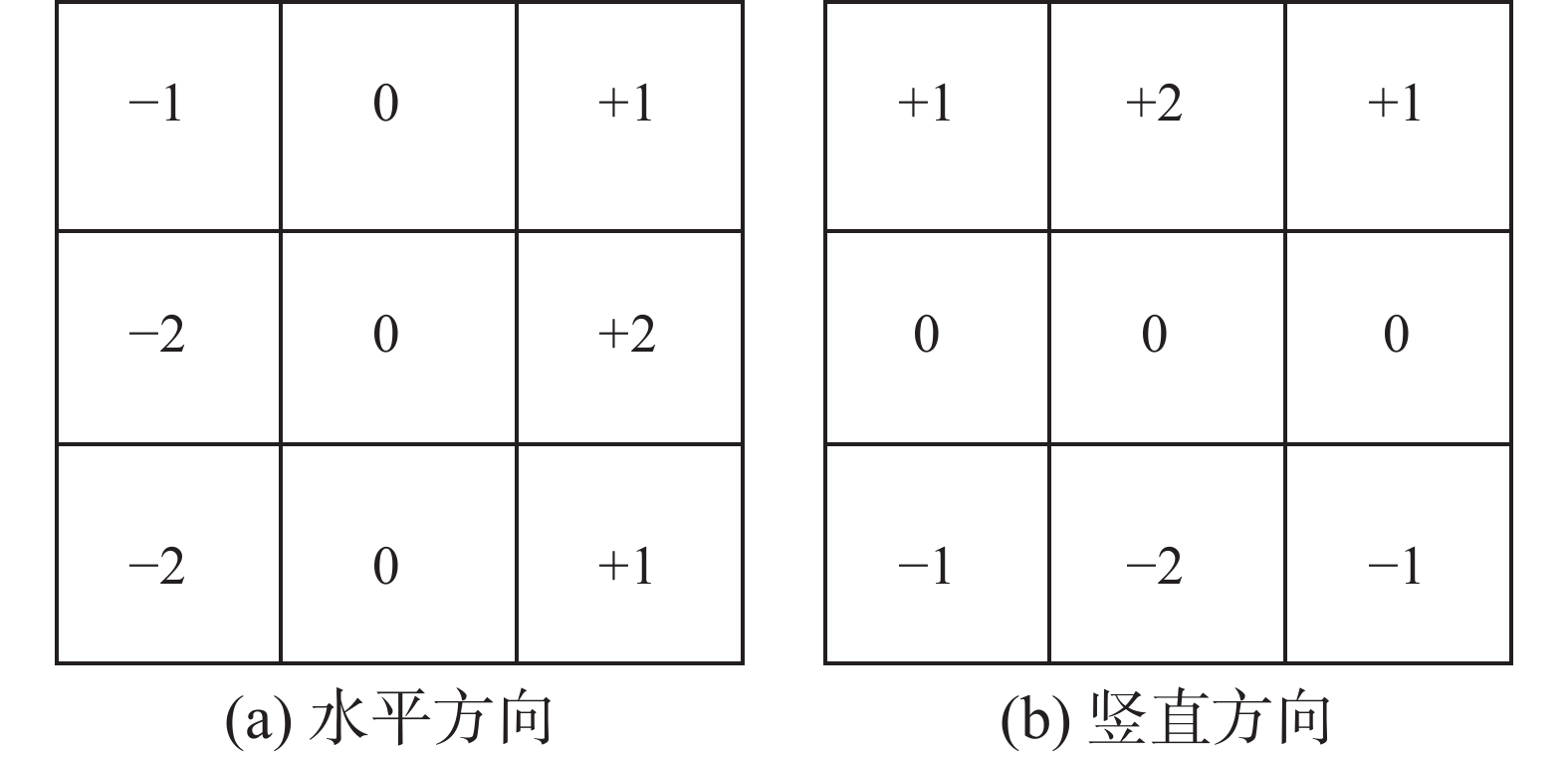
$5 \times 5$ 的滤波窗对图像进行处理，滤波窗口为$$ \frac{1}{{159}} \left[ \begin{array}{*{20}{c}} 2& 4& 5& 4 &2 \\ 4& 9 &12& 9 &4\\ 5 &12 &15 &12& 5 \\ 4 &9 &12 &9 &4 \\ 2 &4 &5& 4 &2 \end{array} \right] $$ 接下来采用索伯（Sobel）算子[17]对模糊后的图像分别求x方向与y方向的梯度，可以得到总的梯度图像即检测到的边缘图。
记真实图像为函数
$f(x,y)$ ，则在像素点$(x,y)$ 的梯度为${{\boldsymbol{G}}_{{\text{rad}}}}{\text{ }}f\left( {x,y} \right) = {\boldsymbol{\nabla}} f\left( {x,y} \right)$ ，用${G_x}$ 、${G_y}$ 分别表示水平方向和垂直方向的梯度分量，则有：$$ {\boldsymbol{\nabla}} f\left( {x,y} \right){\text{ = }}{[{G_x},{G_y}]^{\text{T}}} = {\left[ {\frac{{\partial f}}{{\partial x}},\frac{{\partial f}}{{\partial y}}} \right]^{\text{T}}} $$ 图像梯度的幅值记为
$M({\boldsymbol{\nabla}} f)$ ，计算公式为$$ \left| {{\boldsymbol{\nabla}} f} \right| = M({\boldsymbol{\nabla}} f) = {\left[{\left(\frac{{\partial f}}{{\partial x}}\right)^2} + {\left(\frac{{\partial f}}{{\partial y}}\right)^2}\right]^{\tfrac{1}{2}}} $$ 可以简化为
$$ \left| {{\boldsymbol{\nabla}} f} \right|{\text{ = }}\left| {{G_x}} \right| + \left| {{G_y}} \right| $$ 图像中，梯度矢量的方向角
$\theta (x,y)$ $$ \theta (x,y) = \arctan \left(\frac{{{G_y}}}{{{G_x}}}\right) $$ 对于数字图像
$f(x,y)$ 其像素点都是离散分布的，因此可以表示为数据集合可以表示为$$ \hat {\boldsymbol{f}}(x,y) = \left[ \begin{array}{*{20}{c}} \hat f(0,0)&\hat f(0,1)& \cdots&\hat f(0,n - 1) \\ \hat f(1,0)&\hat f(1,1)&\cdots &\hat f(1,n - 1) \\ \vdots & \vdots & \;&\vdots \\ \hat f(m - 1,0)&\hat f(m - 1,1)&\cdots &\hat f(m - 1,n - 1) \end{array} \right] $$ 在像素点
$(i,j)$ 处，沿着x和y方向的一阶差分计算公式为$$ \left\{ \begin{gathered} {\Delta _x}\hat {\boldsymbol{f}}(i,j){\text{ = }}\hat {\boldsymbol{f}}(i{\text{ + }}1,j) - \hat {\boldsymbol{f}}(i,j) \\ {\Delta _y}\hat {\boldsymbol{f}}(i,j){\text{ = }}\hat {\boldsymbol{f}}(i,j{\text{ + }}1) - \hat {\boldsymbol{f}}(i,j) \\ \end{gathered} \right. $$ 
图 2 梯度模板Fig. 2 Gradient template下载:
全尺寸图片
根据计算各个点的梯度方向，得到低分辨率图像的梯度
${{\boldsymbol{G}}_{\rm{L}}}$ 。$$ {\boldsymbol{G}}_{\rm{L}}=\sqrt {G_x^2 + G_y^2} $$ 最后分别对x和y方向实行双三次插值，从而得到高分辨率图像的初始梯度
${{\boldsymbol{G}}_{\rm{H}}}$ [19]。双三次插值同时考虑了4个相邻的像素图像的强度的影响和图像强度变化率的影响[10]，以待估计点所在位置为中心，已知像素数目为
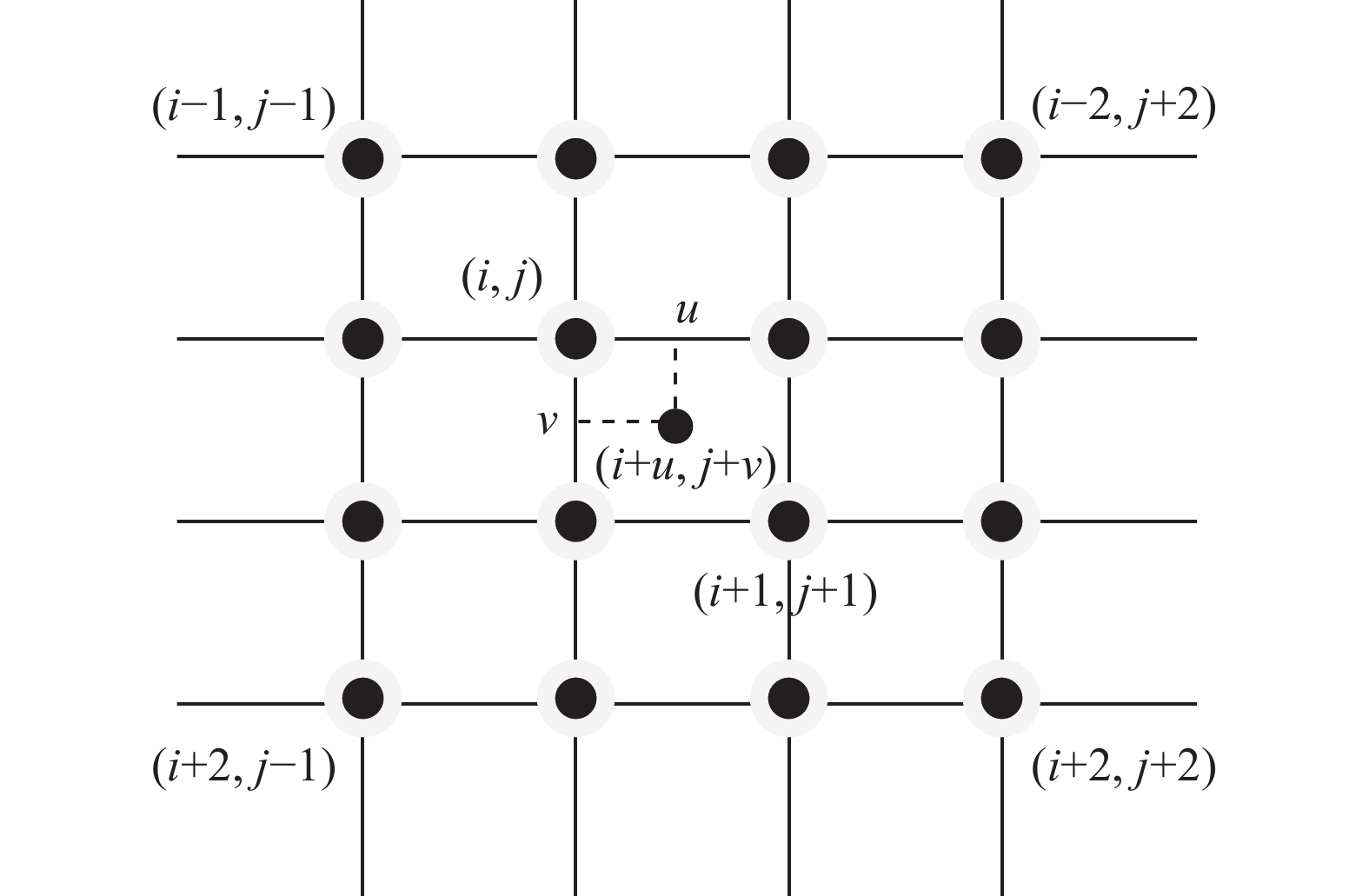
$4 \times 4$ 的邻域窗口内容的16个像素图像强度完成插值计算，最后插值图像的质量比较高，三次多项式$G(t)$ 的数学表达式为$$ G(t) = \left\{ \begin{split} & 0,\quad\left| t \right| \geqslant 2 \\ & 2 - 4\left| t \right| + 2.5{\left| t \right|^2} - 0.5{\left| t \right|^3},\quad1 \leqslant \left| t \right| \leqslant 2 \\ & 1 - 2.5{\left| t \right|^2} + 1.5{\left| t \right|^3},\quad0 \leqslant \left| t \right| \leqslant 1 \end{split} \right. $$ 其中t为自变量。由图3双三次插值基本原理可得：
图 3 双三次插值示意图Fig. 3 Schematic diagram of bicubic interpolation下载:
全尺寸图片
$$\begin{gathered} {\boldsymbol{A}} = [G(1 + u)\;\;G(u)\;\;G(1 - u)\;\;G(2 - u)] \\ {\boldsymbol{B}} = \left[\begin{array}{*{20}{c}} f(i - 1,j - 1) & f(i - 1,j) & f(i - 1,j + 1) & f(i - 1,j + 2) \\ f(i,j - 1) & f(i,j) & f(i,j + 1) & f(i,j - 1) \\ f(i + 1,j - 1) & f(i + 1,j) & f(i + 1,j + 1) & f(i + 1,j + 2) \\ f(i + 2,j - 1) & f(i + 2,j) & f(i + 2,j + 1) & f(i + 2,j + 2) \\ \end{array} \right] \\ {\boldsymbol{C}} = \left[ \begin{gathered} G(1 + v) \\ {\text{ }}G(v)\\ G(1 - v) \\ G(2 - v) \\ \end{gathered} \right]\end{gathered} $$ 式中：B为邻域窗口内的16个相邻像素点组成的图像像素矩阵。因此双三次插值的具体插值计算方法可定义为
$$ f(i + u,i + v) = {\boldsymbol{A}} * {\boldsymbol{B}} * {\boldsymbol{C}} $$ 边缘梯度插值算法流程如下所示。
输入 输入低分辨率图像
输出 输出高分辨率图像
1) 用高斯滤波进行图像的降噪处理；
2) 用Sobel算子求解该图像的一阶导数
${f}_{i,j}'(x,y)$ ，获得图像的水平方向梯度信息Gx与竖直方向梯度信息Gy，分别检测纵向边缘和横向边缘的信息；3) 结合图像中两个方向的梯度信息得到低分辨率图像的梯度
${{\boldsymbol{G}}_{\rm{L}}}$ ；4) 采用双三次插值的方式对
${{\boldsymbol{G}}_{\rm{L}}}$ 实行插值计算，获得高分辨率图像的初始梯度值${{\boldsymbol{G}}_{\rm{H}}}$ 。3. 基于边缘梯度插值的双支deeplabv3+解码器
由于deeplabv3+[4]网络中的解码器仅利用原始图像的1/4高级语义特征信息与池化后的特征图直接进行拼接融合，导致图像中会丢失部分像素的细节信息，本文在其解码器中新增加一个特征融合分支，将经过ASPP特征融合模块的高级特征图先进行1×1卷积然后上插值2倍，然后与特征提取网络中下采样后的1/8图像进行一个1×1卷积后得到的低级特征图进行拼接融合后进行2倍上插值，此时将得到通道数为512的特征图，再经过1×1卷积将通道数降维至256与Block1得到的高分辨率的低级像方差。原始图像、待评价图像的结构分量表示为特征图进行拼接融合，这种小幅度逐层上插值的方式能够增强物体边缘像素信息的连续性，最后叠加2个3×3卷积进行高分辨率特征的精细提取进行4倍上插值后恢复图像大小输出，其中上插值的方式使用本文所提出的边缘梯度插值算法。
最终本文所设计的解码结构如图4所示。
图 4 边缘梯度插值的双分支 deeplabv3+解码器Fig. 4 Double branch deeplabv3+ decoder for edge gradient interpolation下载:
全尺寸图片
4. 实验分析
4.1 边缘梯度插值算法实验
4.1.1 评价指标
本文对于此部分实验的评价指标包括，峰值信噪比(peak signal to noise ratio, PSNR)[20]、结构相似性(structural similarity index measure, SSIM)[21]。
1) 峰值信噪比(PSNR)：
$$ {R_{{\text{PSNR}}}}{\text{ = }}10\frac{{{L^2}}}{{{S_{{\text{MSE}}}}}} $$ 式中：L是像素点值的动态变化范围，即灰度值，通常为255；
${S_{{\text{MSE}}}}$ 为$$ {S_{{\text{MSE}}}}{\text{ = }}\frac{1}{{m \times n}}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{{({x_{i,j}} - {y_{i,j}})}^2}} } $$ 其中：m、n为图像数据行列数；
${x_{i,j}}$ 为原始图像的第i行第j列的像素点值；${y_{i,j}}$ 为待评价图像的第i行第j列的像素点值。2) 结构相似性(SSIM)：
$$ {R_{{\text{SSIM}}}}{\text{ = }}\frac{{(2{\gamma _x}{\gamma _y} + {c_1})(2{\sigma _{xy}} + {c_2})}}{{(\gamma _x^2 + \gamma _y^2 + {c_1})(\sigma _x^2 + \sigma _y^2 + {c_2})}} $$ 式中：
${\gamma _x}$ 、${\gamma _y}$ 、$\sigma_x^2$ 、$\sigma_y^2$ 分别表示原始图像均值、待评价图像的均值，原始图像方差、待评价图像方差；c1和c2均为很小的常数，用于误差修正。PSNR反映了待评价图像的逼真度，PSNR越高，图像失真越小；SSIM是依据待评价图像与原始图像的亮度，对比度之间的相似性，在[0,1]之间，越大表示两张图像之间的结构相似性越高[22]。
4.1.2 实验结果分析
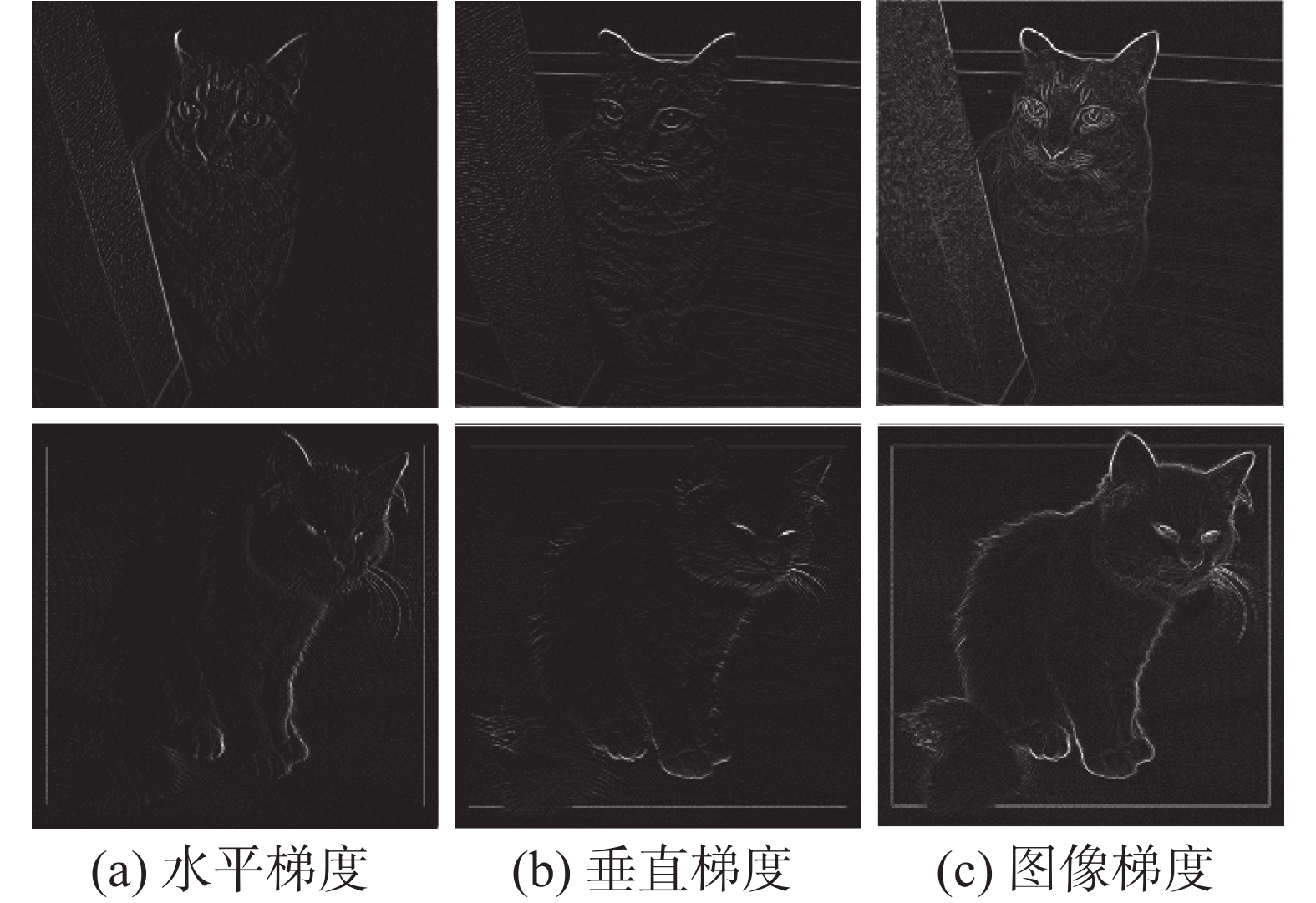
本文选择了几种经典插值方式来进行实验对比分析，包括最近邻插值[8]、双线性插值[9]、双三次插值[10]。首先使用Sobel算子进行边缘不同方向的梯度计算，得到低分辨率的梯度图。如图5所示是两幅示例图的梯度图。
图 5 边缘梯度图像Fig. 5 Edge gradient image下载:
全尺寸图片
然后根据x方向的边缘梯度和y方向的边缘梯度使用双三次插值后得到最后的高分辨率图像。图6是使用不同插值方法对原图进行2倍放大的整体结果，其中第1行与第3行为插值后的图像，第2行与第4行是ssim_map结果，即表示加窗后得到的SSIM组成的映射矩阵，其中颜色越深则表示插值效果越差，颜色越亮表示插值效果越好。可以看出两幅示例图，使用最近邻插值时，边缘部分有明显的锯齿状，并且SSIM结果颜色最深效果最差，使用双线性插值两幅图的整体以及边缘部分都插值效果都有较为明显的提升，双三次插值方法在整个效果图与双线性插值效果相比仍有细微的差别包括猫咪的眼睛以及身上的纹路，但对于边缘平滑方面还是有所欠缺，而本文算法插值后的图像在整体和边缘部分都有更好的表现力，如图6中第1行的柱子纹理、猫咪身上的纹路边缘部分更加清晰，图6中第3行的猫咪胡须以及尾巴各个部分有更好的呈现效果。
图 6 不同插值方法放大 2 倍整体结果Fig. 6 Overall result of different interpolation methods magnify by two times下载:
全尺寸图片
为了能够更加清晰地看出本文插值算法的有效性，本文选取两幅示例图的局部放大4倍来进行对比实验，具体结果如图7所示，图7中第1行为示例图1，第2行为示例图2。可以看出示例图1中的眼睛部分和示例图2中的胡须部分，最邻近插值方法的结果存在明显锯齿状，双线性插值方法虽然有一定的改善但示例图中的轮廓边缘部分较为模糊，双三次插值法能够达到较好的插值效果，但由于区域插值的不确定性，示例图1的眼珠部分以及示例图2的猫咪胡须存在人造细节，本文所提出的算法在边缘细节部分插值效果表现力更好，图的纹理部分更加清晰。
图 7 不同插值方法放大4倍局部结果Fig. 7 Local results of different interpolation methods magnify by four times下载:
全尺寸图片
图8是两幅示例图使用不同插值算法的傅里叶幅度谱，通过对比使用插值算法后图像与原图的傅里叶幅度谱的图像频谱变化强度来衡量图像质量。可以看出与原图的傅里叶幅度谱相比，使用最邻近插值算法的图像频谱变化比较大更加发散，使用双线性插值算法和双三插值算法后的图像频谱变化强度有着明显缓和，本文算法所得到的图像傅里叶幅度谱与原图的频谱最为贴近，其变化强度是几种插值算法中最小的，插值后图像质量更好。
图 8 不同插值方法的傅里叶幅度谱Fig. 8 Fourier amplitude spectrum of different interpolation methods下载:
全尺寸图片
表1和表2分别是2幅示例图使用不同的插值方法最后的PSNR结果和SSIM结果。从表1可以看出2幅示例图使用最邻近插值方法的PSNR最低，其次是双线性插值、双三次插值，本文算法的PSNR值为34.24 dB，是几种插值算法中效果最好的；其SSIM值本文算法在示例图1中达到了0.920 6，在示例图2中达到了0.915 6。
4.2 双分支结构deeplabv3+解码器实验
4.2.1 评价指标和数据集
本文对于此部分的实验采用平均交并比(mean intersection over union, MIOU)作为评价指标，其计算公式为
$$ {S_{{\text{MIOU}}}} = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\dfrac{{{p_{ii}}}}{{\displaystyle\sum_{j = 1}^N {{p_{ij}} + \displaystyle\sum_{j = 1}^k {{p_{ji}} - {p_{ii}}} } }}} $$ 式中：
$ N $ 代表图像中像素的类别数；$ {p_{ii}} $ 表示预测正确的像素数；$ {p_{ij}} $ 为假正例；$ {p_{ji}} $ 表则为假负例,表示实际为i；预测为j的像素总数。PASCAL VOC2012数据集[23]是语义分割任务中具有代表性的数据集之一，总共包含20个前景对象类和1个背景类，其中训练集有1 464张图像，验证集有1 449张图像，测试集有1 456张图像。
本文的实验环境主要为GPU2080Ti、操作系统64-bit、Ubuntu 16.04、CUDA10.1、Data processing为Python3.6，采用主流深度学习框架Pytorch来实现。训练过程中学习率衰减采用“Poly”[24]，损失函数为逐像素的加权交叉熵损失函数(focal loss)[25]。
4.2.2 实验结果分析
本文以Resnet101作为骨干网络，先采用不同空洞率进行实验对比分析，实验结果如表3所示，可以看出当卷积核为3时，空洞率组合为(8, 14, 20)，最大感受野为85时，其MIOU的值达到73.53%，当空洞率组合为(6, 12, 18, 24)，最大感受野为121时，其MIOU的值达到最高为70.75%，因此在本文中将空洞率设置为具有3个卷积核的(8, 14, 20)进行解码器的对比实验分析。
表 3 不同空洞率实验结果Table 3 Experimental results of different atrous ratios卷积核数 空洞率 最大感受野 MIOU/% 3 （4, 10, 16） 61 72.94 3 （6, 12, 18） 73 73.27 3 （8, 14, 20） 85 73.53 4 （4, 10, 16, 22） 105 69.12 4 （6, 12, 18, 24） 121 70.75 4 （8, 14, 20, 26） 137 69.76 为验证本文方法的有效性，采用训练步幅为16，验证步幅为16，空洞率组合为(8,14,20)对本文提出解码器进行对比实验。实验结果如表4所示，插值方法表示在deeplabv3+中所使用的插值方法，解码器代表deeplabv3+中所使用的解码器。当使用deeplabv3+原有网络时，即插值方式及其解码器均未改变，MIOU值为73.53%，当使用本文所提出的边缘梯度插值算法时，解码器未改变其MIOU值为74.09%，表明本文所提出的插值算法能够有效提高最后的图像语义分割精度，而deeplabv3+保持原本网络中使用的双线性插值算法，双支结构解码器时其MIOU值为74.36%，而当使用本文所提出的插值算法，解码器中使用双支结构时，其MIOU值达到75.73%，相比于原有网络有2.2%的提升。
表 4 Deeplabv3+原有网络与本文方法对比实验Table 4 Comparative experiment between the deeplabv3+ original network and the method in this article插值方法 解码器 MIOU/% 原插值
方法边缘梯
度插值原解
码器双分支
解码器√ √ 73.53 √ √ 74.09 √ √ 74.36 √ √ 75.73 为更加直观地证明本文所提出的基于边缘梯度插值算法的双分支结构deeplabv3+的有效性，将本文方法与原deeplabv3+网络在PASCAL VOC2012数据集上进行对比实验并可视化，其结果如图9所示，可以看出原语义分割网络无论是过分割还是欠分割的效果都有一定程度的欠缺，使用本文方法过分割情况包括马的耳朵、鹤嘴的边缘轮廓都更加细化精确，牛角以及腿部的边缘分割情况更好，欠分割部分包括麻雀的嘴和脚，狗的耳朵、腿，鸟的嘴及脚部也能有更好的表现力，可视化的结果能更加直观地观察到本文方法在图像语义分割精度上的提高，由此可证本文方法具有一定的可靠性。
图 9 原有网络与本文方法对比实验可视化Fig. 9 Visualization of the comparison experiment between the original network and our method下载:
全尺寸图片
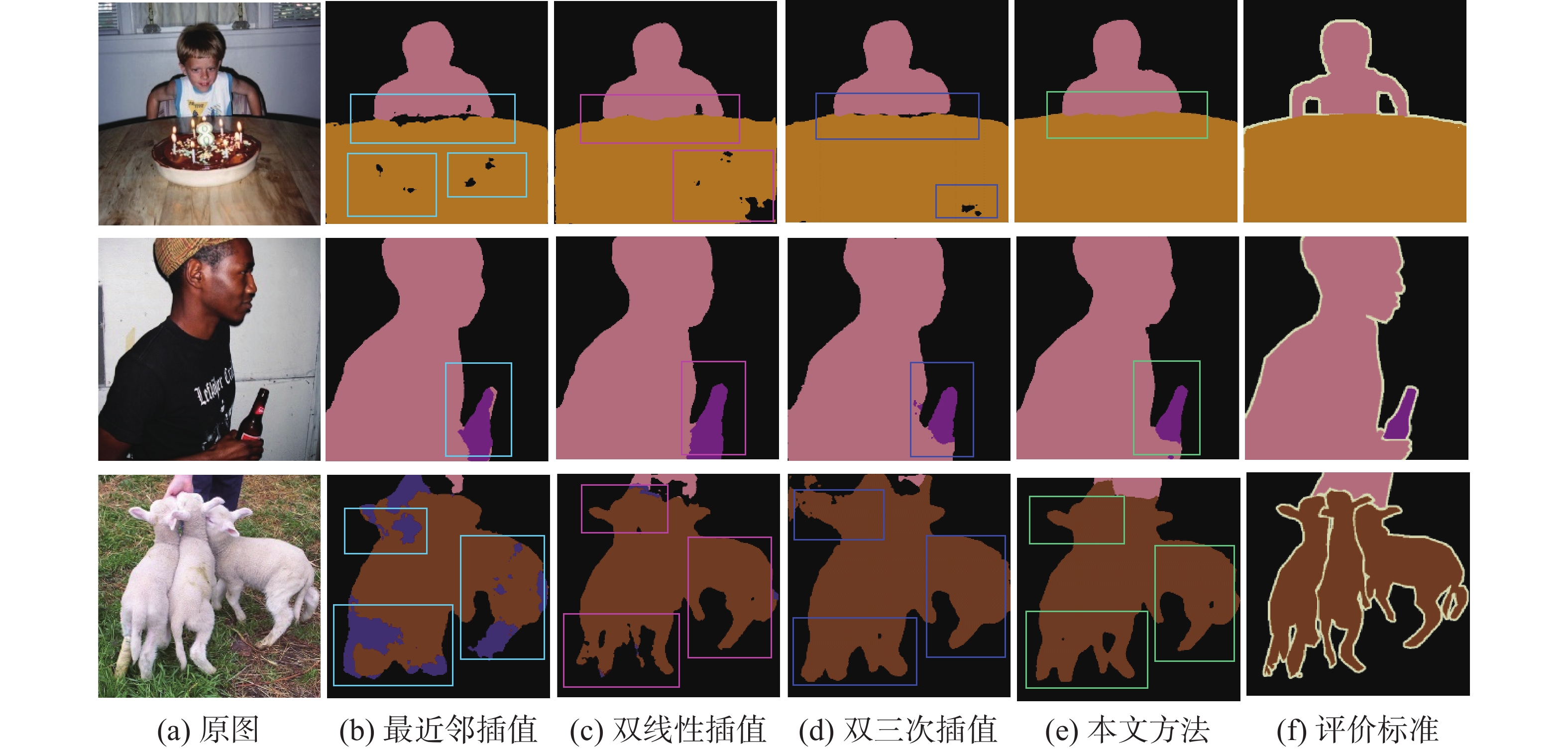
图10是在deeplabv3+的双分支解码器的条件下分别使用不同插值方式的可视化对比，图10中的第1行表示图例1，第2行表示图例2，第3行表示图例3。在图例1中，使用最近邻插值方法时，小男孩与桌子的边缘部分以及整个桌子部分都有欠分割的情况，使用双线性插值和双三次插值方法有明显的改善，而使用本文所提出的插值算法边缘部分分割效果最佳；在图例2中，使用本文所提出的边缘梯度插值算法时，男孩手中的瓶子边缘部分分割效果更加精细，与评价标准图最为贴近；在图例3中，羊的角和腿边缘部分使用最近邻插值方法分割有明显间断的地方，还存在将背景分割成物体的情况，使用双线性插值和双三次插值方法时，其分割效果有明显改善，而本文插值算法图像语义分割效果最佳，尤其是物体的边缘部分更加平滑与具有连续性，由此可证本文所提出的边缘梯度插值算法能够有效改善物体边缘部分的分割效果，从而提高图像整体的分割精度。
图 10 双分支deeplabv3+使用不同插值方法可视化对比Fig. 10 Visual comparison using different interpolation methods under the double branch deeplabv3+ decoder下载:
全尺寸图片
5. 结束语
本文提出一种新的双支边缘梯度插值的deeplabv3+语义分割模型。用边缘梯度插值算法代替原有网络中的双线性插值，即通过Sobel算子计算像素点不同方向的边缘梯度得到低分辨率的梯度图，再使用双三次插值进行图像的插值计算得到高分辨率图像；为获得更多易忽略的图像物体边缘特征信息，在解码器中提出用双分支结构获取图像多尺度信息。实验结果表明本文方法能有效改善图像边缘部分的分割从而提高图像语义分割精度，且在VOC2012数据集上MIOU提高了2.2%。虽然本文方法在物体边缘分割上的效果有所改善，但对于微小目标仍然有所欠缺，因此在未来研究中将以提高微小目标的分割精度为目的进行研究。
-
图 1 deeplabv3+网络结构
Fig. 1 Deeplabv3+ network structure
下载:
全尺寸图片
图 2 梯度模板
Fig. 2 Gradient template
下载:
全尺寸图片
图 3 双三次插值示意图
Fig. 3 Schematic diagram of bicubic interpolation
下载:
全尺寸图片
图 4 边缘梯度插值的双分支 deeplabv3+解码器
Fig. 4 Double branch deeplabv3+ decoder for edge gradient interpolation
下载:
全尺寸图片
图 5 边缘梯度图像
Fig. 5 Edge gradient image
下载:
全尺寸图片
图 6 不同插值方法放大 2 倍整体结果
Fig. 6 Overall result of different interpolation methods magnify by two times
下载:
全尺寸图片
图 7 不同插值方法放大4倍局部结果
Fig. 7 Local results of different interpolation methods magnify by four times
下载:
全尺寸图片
图 8 不同插值方法的傅里叶幅度谱
Fig. 8 Fourier amplitude spectrum of different interpolation methods
下载:
全尺寸图片
图 9 原有网络与本文方法对比实验可视化
Fig. 9 Visualization of the comparison experiment between the original network and our method
下载:
全尺寸图片
图 10 双分支deeplabv3+使用不同插值方法可视化对比
Fig. 10 Visual comparison using different interpolation methods under the double branch deeplabv3+ decoder
下载:
全尺寸图片
表 1 不同插值方法的PSNR结果
Table 1 PSNR results of different interpolation methods
dB 表 2 不同插值方法的SSIM结果
Table 2 SSIM results of different interpolation methods
表 3 不同空洞率实验结果
Table 3 Experimental results of different atrous ratios
卷积核数 空洞率 最大感受野 MIOU/% 3 （4, 10, 16） 61 72.94 3 （6, 12, 18） 73 73.27 3 （8, 14, 20） 85 73.53 4 （4, 10, 16, 22） 105 69.12 4 （6, 12, 18, 24） 121 70.75 4 （8, 14, 20, 26） 137 69.76 表 4 Deeplabv3+原有网络与本文方法对比实验
Table 4 Comparative experiment between the deeplabv3+ original network and the method in this article
插值方法 解码器 MIOU/% 原插值
方法边缘梯
度插值原解
码器双分支
解码器√ √ 73.53 √ √ 74.09 √ √ 74.36 √ √ 75.73 -
[1] CHEN L C, PAPANDREOU G, KOKKINOS I, et al. Semantic image segmentation with deep convolutional nets and fully connected CRFs[EB/OL]. (2014−12−22)[2021−11−12].https://arxiv.org/abs/1412.7062. 2014. [2] CHEN L C, PAPANDREOU G, KOKKINOS I, et al. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(4): 834–848. doi: 10.1109/TPAMI.2017.2699184 [3] CHEN L C, PAPANDREOU G, SCHROFF F, et al. Rethinking atrous convolution for semantic image segmentation[EB/OL]. (2017−06−17) [2021−11−12].https://arxiv.org/abs/1706.05587. [4] CHEN L C, ZHU Yukun, PAPANDREOU G, et al. Encoder-decoder with atrous separable convolution for semantic image segmentation[C]//European Conference on Computer Vision. Cham: Springer, 2018: 833−851. [5] HE K, ZHANG X, REN S, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(9): 1904–1916. doi: 10.1109/TPAMI.2015.2389824 [6] 任凤雷, 何昕, 魏仲慧, 等. 基于DeepLabV3+与超像素优化的语义分割[J]. 光学精密工程, 2019, 27(12): 2722–2729. doi: 10.3788/OPE.20192712.2722 REN Fenglei, HE Xin, WEI Zhonghui, et al. Semantic segmentation based on DeepLabV3+ and superpixel optimization[J]. Optical precision engineering, 2019, 27(12): 2722–2729. doi: 10.3788/OPE.20192712.2722 [7] 吴涛, 董肖莉, 孟伟, 等. 基于语义分割的简洁线条肖像画生成方法[J]. 智能系统学报, 2021, 16(1): 134–141. WU Tao, DONG Xiaoli, MENG Wei, et al. Concise line portrait generation method based on semantic segmentation[J]. CAAI transactions on intelligent systems, 2021, 16(1): 134–141. [8] RUKUNDO O, CAO HANQIANG. Nearest neighbor value interpolation[EB/OL]. (2012−11−08)[2021−11−12].https://arxiv.org/abs/1211.1768. [9] KIRKLAND E J. Bilinear interpolation[M]// Advanced Computing in Electron Microscopy. Boston: Springer, 2010: 261−263. [10] HUANG Zhengzhong, CAO Liangcai. Bicubic interpolation and extrapolation iteration method for high resolution digital holographic reconstruction[J]. Optics and lasers in engineering, 2020, 130: 106090. [11] RUKUNDO O. Effects of improved floor function on the accuracy of bilinear interpolation algorithm[EB/OL]. (2021−04−08)[2021−11−12].https://arxiv.org/abs/2104.03646. [12] 王庆, 唐涛, 项德良, 等. 基于梯度比率的SAR图像局部特征提取方法研究[J]. 智能系统学报, 2017, 12(3): 286–292. WANG Qing, TANG Tao, XIANG Deliang, et al. Research on local feature extraction of SAR images based on gradient ratio[J]. CAAI transactions on intelligent systems, 2017, 12(3): 286–292. [13] 伍锡如, 凌星雨. 基于改进的Faster RCNN面部表情检测算法[J]. 智能系统学报, 2021, 16(2): 210–217. WU Xiru, LING Xingyu. Facial expression recognition based on improved Faster RCNN[J]. CAAI transactions on intelligent systems, 2021, 16(2): 210–217. [14] 徐聪, 王丽. 基于改进DeepLabv3+网络的图像语义分割方法[J]. 激光与光电子学进展, 2021, 58(16): 1610008. XU Cong, WANG Li. Image semantic segmentation method based on improved DeepPlabv 3+Network[J]. Laser & optoelectronics progress, 2021, 58(16): 1610008. [15] 王兴武, 雷涛, 王营博, 等. 基于多模态互补特征学习的遥感影像语义分割[J]. 智能系统学报, 2022, 17(6): 1123–1133. WANG Xingwu, LEI Tao, WANG Yingbo, et al. Semantic segmentation of remote sensing image based on multimodal complementary feature learning[J]. CAAI transactions on intelligent systems, 2022, 17(6): 1123–1133. [16] PANDA J, MEHER S. An efficient image interpolation using edge-error based sharpening[C]//2020 IEEE 17th India Council International Conference. New Delhi: IEEE, 2021: 1−6. [17] VINCENT O, FOLORUNSO O. A descriptive algorithm for sobel image edge detection[C]//Proceedings of the 2009 InSITE Conference. Washington: Informing Science Institute. 2009, 40: 97−107. [18] HOUBRECHTS K, DAS R, KEUPERS M, et al. A complete procedure to prepare virtual clinical trials in digital breast tomosynthesis[C]//Proceedings Volume 12463, Medical Imaging 2023: Physics of Medical Imaging. San Diego: SPIE. 2023, 12463: 267−274. [19] HUANG Zhengzhong, CAO Liangcai. Bicubic interpolation and extrapolation iteration method for high resolution digital holographic reconstruction[J]. Optics and lasers in engineering, 2020, 130: 106090. [20] HORÉ A, ZIOU D. Image quality metrics: PSNR vs. SSIM[C]//2010 20th International Conference on Pattern Recognition. Istanbul: IEEE, 2010: 2366−2369. [21] HAENDEL A, ANDERSON J G, PILZ M, et al. A frequency-dependent model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies[J]. Bulletin of the seismological society of America, 2020, 110(6): 2743–2754. doi: 10.1785/0120200118 [22] YU Lei, DENG Qiuyue, LIU Bin, et al. Dual-branch feature learning network for single image super-resolution[J]. Multimedia tools and applications, 2023: 1−18. [23] EVERINGHAM M, ALI ESLAMI S M, VAN GOOL L, et al. The pascal visual object classes challenge: a retrospective[J]. International journal of computer vision, 2015, 111(1): 98–136. doi: 10.1007/s11263-014-0733-5 [24] LI YUANZHI, WEI C, MA TENGYU. Towards explaining the regularization effect of initial large learning rate in training neural networks[EB/OL]. (2019−07−10)[2021−11−12].https://arxiv.org/abs/1907.04595. [25] LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection[C]//2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 2999−3007.
