Semi-supervised soft sensor modeling method under the help-training framework
-
摘要: 为了充分利用工业过程中大量无标签样本信息，并减少过程的不确定因素对无标签样本质量的影响，提出一种助训练框架下的半监督孪生支持向量回归软测量建模方法。采用孪生支持向量回归机构建主学习器，对高置信度无标签样本添加伪标签；同时，基于K近邻算法构建辅学习器，最大化学习器在近邻样本集上的均方误差，经过此项指标筛选后的待处理样本集包含了更多的数据信息；主、辅学习器二者相辅相成，一定程度上提高了模型的泛化性；再利用所构建的助训练框架提高样本利用率后得到预测模型，实现对无标签样本信息的充分挖掘。通过对脱丁烷塔工业过程中的实际数据进行建模仿真，所得结果表明此模型具有良好的预测性能。Abstract: A semi-supervised twin support vector regression soft sensor modeling method under the help-training framework is proposed to maximize a large number of unlabeled sample information in industrial processes and reduce the impact of process uncertainties on the quality of unlabeled samples. The twin support vector regression is used to build the main learner and add pseudo labels to the unlabeled samples with the highest confidence. Simultaneously, the auxiliary learner is constructed on the basis of the K-nearest neighbor algorithm to maximize the root mean square error of the learner on the nearest neighbor sample set. The candidate sample set screened by this index contains additional data information. The main and auxiliary learners complement each other, which improves the generalization of the model to a certain extent. The prediction model is then obtained by using the help-training framework to improve the sample utilization to mine the unlabeled sample information. Results show that the model has good prediction performance based on the modeling and simulation of the real data in the industrial process of debutanizer.
-
Keywords:
- soft sensor modeling /
- semi-supervised /
- help-training /
- twin support vector regression /
- K-nearest neighbor /
- confidence /
- learner /
- debutanizer
-
在许多复杂工业生产过程中，有一些过程变量往往与最终产品的质量息息相关。但是，由于受到检测技术水平、经济成本和环境因素等条件的制约，导致这些关键过程变量的在线测量成本高、耗时长[1]。软测量技术通过构建准确的数学模型，可以实现对质量指标的实时预测[2]，近年来取得了许多成功的应用。常见的数据驱动软测量模型有：偏最小二乘(partial least squares, PLS)[3]、人工神经网络(artificial neural network, ANN)[4]、高斯过程回归(Gaussian process regression, GPR)[5]、支持向量机(support vector machine, SVM)[6]等。
软测量技术一般需要大量有标签样本进行模型训练，而实际工业过程中的大多数情况是有标签样本少，而且获取样本标签的成本高或者时间滞后。在这种条件下，如何利用少量有标签样本和大量无标签样本来提升模型性能成为软测量建模的一个关键问题[7]。能够同时利用有标签和无标签样本的半监督学习方法得到了广泛的应用。传统的半监督学习算法有：自训练、生成式方法、基于分歧的方法和基于图的方法等[8]。其中，仝小敏等[9]将自训练思想与回归算法结合,充分利用了无标签样本所含信息，提高了模型的预测性能；助训练作为自训练方法的改进形式，由Adankon等[10]提出并将Parzen窗估计引入了助训练SVM分类器，通过在数据分类前预先筛选，大幅提高了分类器性能；Cheriet等[11]扩展了助训练思想，不再使用同类型的学习器训练数据，而是根据样本规模进行选取，与传统半监督方法相比提高了模型的精确度。但是传统自训练模型在针对无标签样本筛选时容易引入误差样本从而导致模型退化，且原始助训练的模型精度不够，泛化性能也需要进一步提升，从而导致预测结果不准确。
综上所述，通过助训练方法构建主、辅学习器，提出一种基于孪生支持向量回归(twin support vector regression, TSVR)的半监督软测量方法。该方法在助训练框架下，构建一种新的主辅协同学习器，将少量有标签样本和大量无标签样本结合进行训练和回归建模。采用TSVR构造主学习器，K近邻(K-nearest neighbor，KNN)构造辅学习器，并设计两种学习器的置信度评估策略，通过辅学习器来协助和优化无标签样本筛选过程，使得筛选出的无标签样本包含更多的全局信息。最后将基于主和辅学习器建立的软测量模型应用于脱丁烷塔浓度的预测，验证了所提方法的有效性和建模精度。
1. 预备知识
1.1 助训练算法
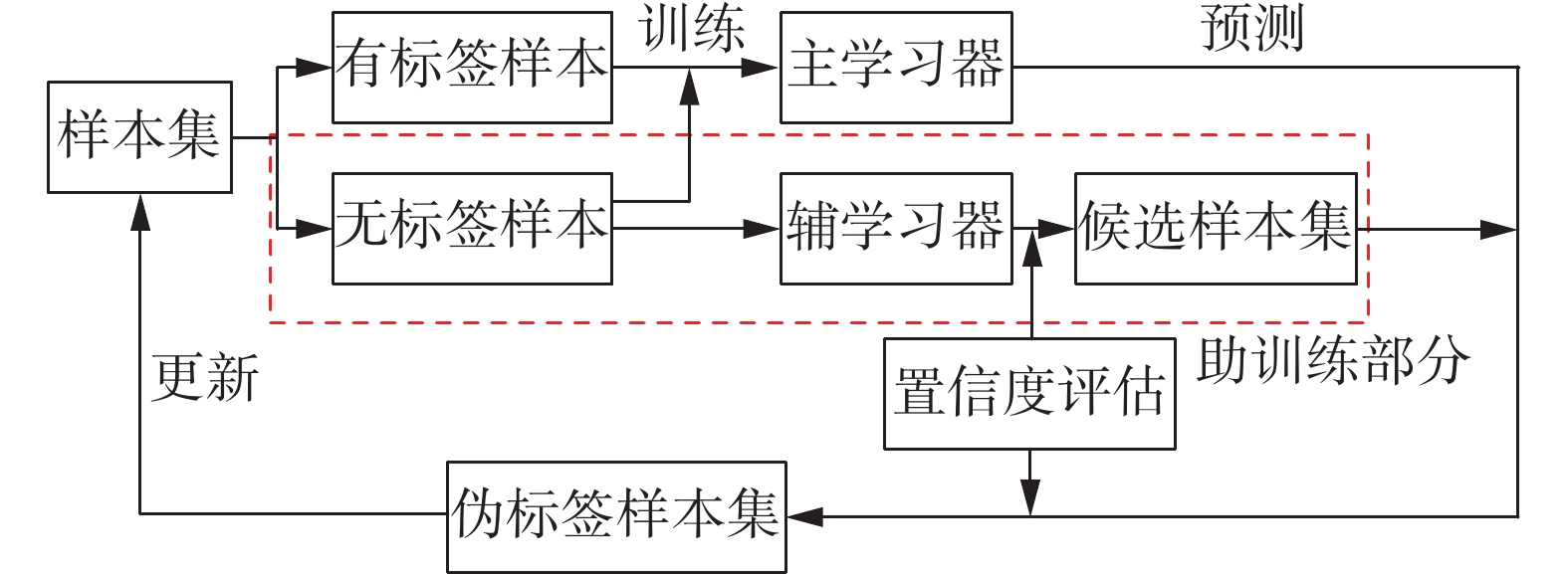
助训练算法是一种新型半监督学习方法，核心是引入辅学习器，通过主学习器和辅学习器的协同训练，增强自训练策略的学习效果。传统的自训练过程是通过有标签样本训练得到的初始学习器对无标签样本添加伪标签，然后筛选部分伪标签样本加入原来的有标签样本集以更新学习器[12-13]。不同于传统自训练只利用样本集不断地训练一个学习器，助训练引入辅学习器对无标签样本进行预筛选组成待处理样本集，协助主学习器选取最高置信度的无标签样本并添加伪标签，最后更新有标签样本集。助训练算法在传统自训练算法的基础上做出了改进，不仅可以依靠相似度自动地学习，而且具有更高的泛化性。其算法基本思想如图1所示。
图 1 助训练基本思想Fig. 1 Basic concept of help-training
下载:
全尺寸图片
1.2 孪生支持向量回归机
TSVR是一种基于统计学习理论的回归模型，适合解决高维度问题，且计算复杂度较低，具有低泛化误差的优点，其需要在训练样本两侧构造一对不平行的超平面[14-15]，使得每个超平面尽可能地与本类样本距离更近，并且尽可能的远离另一类样本[16]。TSVR算法流程：给定训练样本集
${L} = \{ ({{\boldsymbol{x}}_1},{{y}_1}),({{\boldsymbol{x}}_2},{{y}_2}), \cdots ,({{\boldsymbol{x}}_n},{{y}_n})\}$ ，其中${{\boldsymbol{x}}_i} \in {{\bf{R}}^d}$ (d为样本维度)代表数据输入，${y_i} \in {\rm{R}}$ 代表数据输出，i=1,2,···,n为训练样本个数。TSVR算法的核心是利用核函数方法，产生一对不敏感上界和下界[17]：
$$ {f_1}\left( {\boldsymbol{x}} \right){ = }K\left( {{{\boldsymbol{x}}^{\rm{T}}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _1}{ + }{b_1} $$ (1) $$ {f_2}\left( {\boldsymbol{x}} \right){ = }K\left( {{{\boldsymbol{x}}^{\rm{T}}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _2}{ + }{b_2} $$ (2) 式中：
${{\boldsymbol{\omega }}_1}{,}{{\boldsymbol{\omega}} _2} \in {{\bf{R}}^d}$ 代表权重向量；${b_1}{,}{b_2}$ 代表偏置；$K({\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} {\kern 1pt} {,} \cdot {\kern 1pt} {\kern 1pt} {\kern 1pt} )$ 表示核函数。非线性情况下，TSVR的回归模型由不敏感上下界函数的平均值确定：$$ \begin{gathered} f\left( {\boldsymbol{x}} \right){ = }\frac{1}{2}\left( {{f_1}\left( {\boldsymbol{x}} \right){ + }{f_2}\left( {\boldsymbol{x}} \right)} \right){ = }\frac{1}{2}K\left( {{{\boldsymbol{x}}^{\rm{T}}}{,}{\boldsymbol{A}}} \right) \left( {{{\boldsymbol{\omega}} _1}{ + }{{\boldsymbol{\omega}} _2}} \right){ + }\frac{1}{2}\left( {{b_1}{ + }{b_2}} \right) \\ \end{gathered} $$ (3) 此回归函数可以转换为一个二次规划问题，令
${\boldsymbol{A}}{ = }{\left[ {{{\boldsymbol{x}}_1}\;{{\boldsymbol{x}}_2}\; \cdots \;{{\boldsymbol{x}}_{n}}} \right]^{\rm{T}}} \in {{\bf{R}}^{n \times d}}$ ，${\boldsymbol{Y}}{ = }{\left[ {{{{y}}_1}\;{{{y}}_2}\; \cdots \;{{{y}}_n}} \right]^{\rm{T}}} \in {{\bf{R}}^n}$ ，即：$$ \begin{gathered} {\rm min} \frac{1}{2}{\left\| {{\boldsymbol{Y}}{ - }{\boldsymbol{e}}{{\varepsilon }_1}{ - }\left( {K\left( {{\boldsymbol{A}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _1}{ + }{\boldsymbol{e}}{b_1}} \right)} \right\|^{2}}{ + }{{C}_1}{{\boldsymbol{e}}^{\rm{T}}}\xi \\ {\rm s.t.}\;\; {\boldsymbol{Y}}{ - }\left( {K\left( {{\boldsymbol{A}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _1}{ + }{\boldsymbol{e}}{b_1}} \right) \geqslant {\boldsymbol{e}}{{{{\varepsilon }}}_1}{ - }\xi {,}\;\;\xi \geqslant {{\bf{0}}} \\ \end{gathered} $$ (4) $$ \begin{gathered} {\rm min} \frac{1}{2}{\left\| {{\boldsymbol{Y}}{ + }{\boldsymbol{e}}{{\varepsilon }_2}{ - }\left( {K\left( {{\boldsymbol{A}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _2}{ + }{\boldsymbol{e}}{b_2}} \right)} \right\|^{2}}{ + }{{C}_2}{{\boldsymbol{e}}^{\rm{T}}}{\boldsymbol{\eta }} \\ {\rm s.t.}\;\; {\boldsymbol{Y}}{ - }\left( {K\left( {{\boldsymbol{A}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right){{\boldsymbol{\omega}} _2}{ + }{\boldsymbol{e}}{b_2}} \right) \geqslant {\boldsymbol{e}}{{\varepsilon }_2}{ - }{\boldsymbol{\eta}} {,}\;\;{\boldsymbol{\eta}} \geqslant {{\bf{0}}} \end{gathered} $$ (5) 式中，
$\left\| {{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} {\kern 1pt} } \right\|$ 表示2范数，${{C}_{1}}{,}{{C}_{2}}{ > 0}$ ，${{\varepsilon }_{1}}{,}{{\varepsilon }_{2}}{ > 0}$ 为常数，$\xi ,{\boldsymbol{\eta }} \in {{\bf{R}}^d}$ 为松弛变量，${\boldsymbol{e}},{{\bf{0}}} \in {{\bf{R}}^d}$ 表示向量值为1和0的列向量。引入非负拉格朗日乘子
$\alpha ,\gamma \in {{\bf{R}}^d}$ 之后，再结合KKT条件，可以化为式(6)和(7)的对偶问题[18]：$$ \begin{gathered} {\rm max} { - }\frac{1}{2}{{\boldsymbol{\alpha}} ^{\rm{T}}}{\boldsymbol{H}}{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{\alpha}} { + }{{\boldsymbol{f}}^{\rm{T}}}{\boldsymbol{H}}{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}\alpha { - }{{\boldsymbol{f}}^{\rm{T}}}{\boldsymbol{\alpha}} \\ {\rm s.t.}\;\; {{\bf{0}}} \leqslant {\boldsymbol{\alpha}} \leqslant {{C}_{1}}{\boldsymbol{e}} \\ \end{gathered} $$ (6) $$ \begin{gathered} {\rm max}{ - }\frac{1}{2}{{\boldsymbol{\gamma}} ^{\rm{T}}}{\boldsymbol{H}}{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{\gamma}} { + }{{\boldsymbol{h}}^{\rm{T}}}{\boldsymbol{H}}{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{\gamma }}{ - }{{\boldsymbol{f}}^{\rm{T}}}{\boldsymbol{\gamma }} \\ {\rm s.t.}\;\;{{\bf{0}}} \leqslant {\boldsymbol{\gamma }} \leqslant {{C}_{2}}{\boldsymbol{e}} \\ \end{gathered} $$ (7) 式中：
${\boldsymbol{ H}}{ = }\left[ {K\left( {{\boldsymbol{A}}{,}{{\boldsymbol{A}}^{\rm{T}}}} \right) {\boldsymbol{e}}} \right]$ ，${\boldsymbol{f}}{ = }{\boldsymbol{Y}}{ - }{{\varepsilon }_{1}}{\boldsymbol{e}}$ 和${\boldsymbol{h}}{ = }{\boldsymbol{Y}}{ + }{{\varepsilon }_{2}}{\boldsymbol{e}}$ 。求解式(6)和(7)可以得到拉格朗日乘子
${\boldsymbol{\alpha }}$ 和${\boldsymbol{\gamma}}$ 的最优解，从而可以得到：$$ \begin{gathered} {\left[ {{{\boldsymbol{\omega}} _1}^{\rm{T}} {b_1} } \right]^{\rm{T}}}{ = }{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}\left( {{\boldsymbol{f}}{ - }{\boldsymbol{\alpha }}} \right) \\ {\left[ {{{\boldsymbol{\omega}} _2}^{\rm{T}} {b_2}} \right]^{\rm{T}}}{ = }{\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}\left( {{\boldsymbol{h}}{ + }{\boldsymbol{\gamma}} } \right) \\ \end{gathered} $$ (8) 2. 基于助训练的半监督软测量建模
2.1 基于助训练的半监督学习模型
助训练作为一种半监督学习算法可以有效地提高所建回归模型的精度及泛化能力。半监督学习指的是学习器在不受到外界影响的情况下，充分利用无标签样本来提升自身性能，以用来对无标签样本进行预测；而助训练算法既不需要构造复杂多变的图模型，也不需基于特定的假设条件，只需要结合给定的少量有标签样本和大量的无标签样本，构造出一对协同运作的学习器，就可以精准地建立软测量模型，完成复杂的半监督回归学习任务[19-21]。
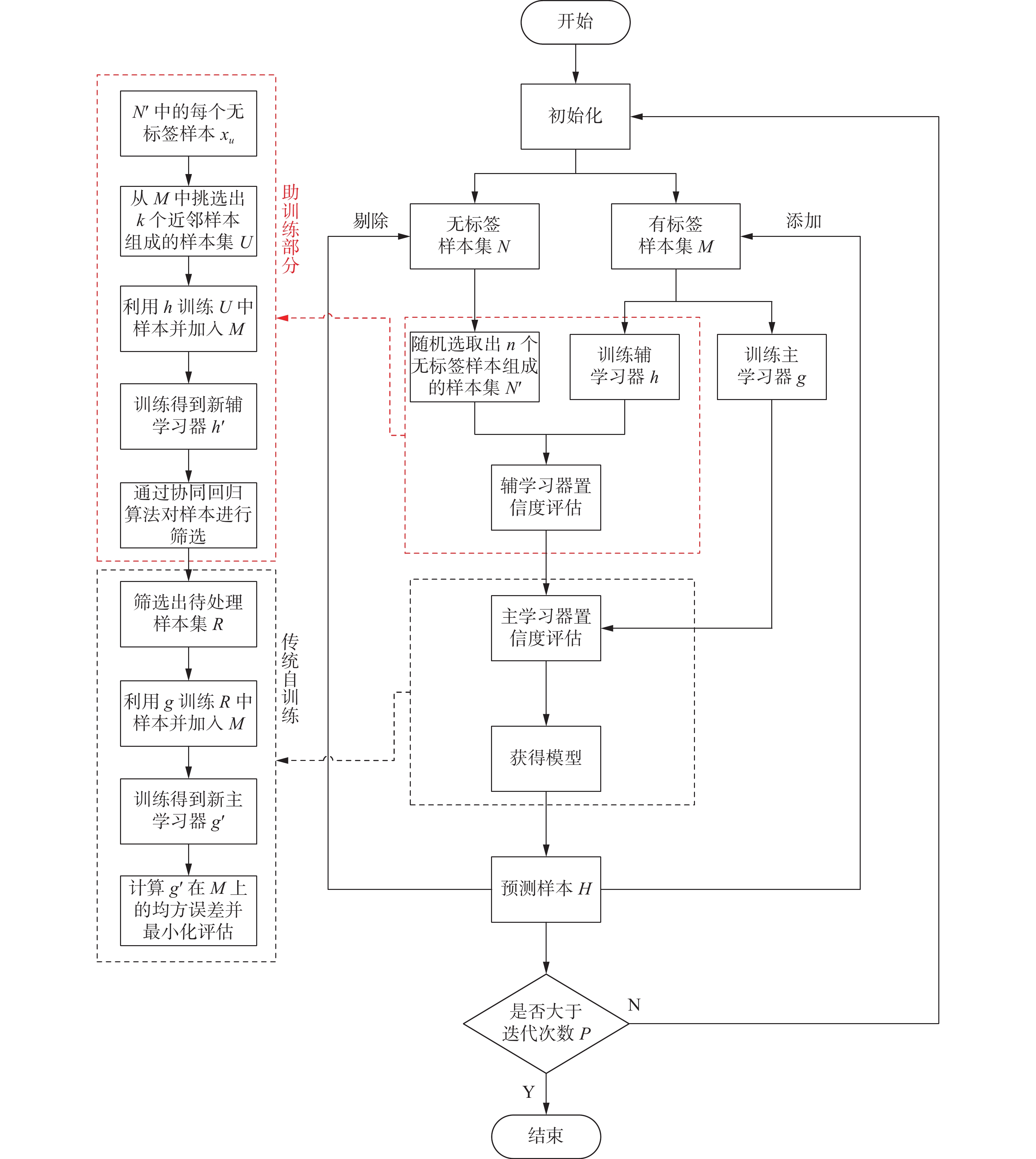
所提基于助训练的半监督学习算法，主要思想是在助训练框架下，首先进行学习器的训练，其次对无标签样本筛选后进行置信度评估，最后把加上伪标签的样本重新加入训练样本，更新原样本集并得到最终模型。
该算法包括两类学习器：基于TSVR的主学习器和基于KNN的辅学习器。TSVR的原始形式与支持向量回归相近，但是TSVR只需要求解两个较小的二次规划问题，同时每个问题的约束条件仅为SVR的一半，而且TSVR的约束条件中没有等式约束，提高了算法运行速度。因此，选用TSVR构建主学习器不仅提高了效率，还具有更好的泛化能力，可以获得更好的预测结果。在有标签样本数量偏少的情况下，为了实现无标签样本的精准预测，需要根据数据的原有特征进行预筛选，选取最能体现原数据特征的无标签样本；又因为有标签样本可能存在离群点等影响因素，所以辅学习器的建立主要是通过设置合适的置信度评估策略，实现对无标签样本的筛选。相比于传统的支持向量机或神经网络算法，KNN的回归模型不需要单独的训练阶段，可以利用马氏距离度量相似度，保证了输出的局部平滑性，故选用KNN构建辅学习器。
在本文算法的流程中，首先利用有标签样本集M来训练基于TSVR的主学习器和基于KNN的辅学习器；同时，从无标签样本集N中随机选择出部分无标签样本组成新的无标签样本集
$N'$ ，辅学习器通过找出对应的近邻样本并对其进行置信度评估，筛选出$N'$ 中置信度最高的无标签样本组成待处理样本集R；经筛选后的待处理样本集R由主学习器对其中样本进行置信度评估，以筛选出置信度最高的样本添加伪标签，将其加入并更新原有标签样本集M。该过程的循环迭代增加了有标签样本的数量，以提高主学习器的学习精度和泛化性能。2.2 置信度评估
置信度评估是半监督回归问题中不可或缺的一部分，它与能否筛选出可信的无标签样本并添加伪标签密不可分[22]。本文所提算法需要对主和辅两个学习器进行样本置信度评估方法设计。
本文所采用的筛选策略借鉴了协同回归算法的思想，不是单一利用学习器筛选出新的有标签样本集，而是在充分挖掘样本信息的基础上，综合考虑全部样本，通过主学习器和辅学习器两者协同评估筛选，尽可能地避免误差累积。设计主辅学习器协同筛选策略的优势在于：训练辅学习器时利用了置信度最高的样本，那么最后再通过主学习器训练更新后的模型将更加精确。因此，使用本策略进行筛选可以有效防止模型退化，减弱离群点影响。以下是具体的置信度筛选策略：
基于KNN的辅学习器通过筛选无标签样本集
$N'$ 得到待处理样本集R时，需要先对无标签样本集$N'$ 中的每一个无标签样本xu，从有标签样本集M中找到xu的k个近邻样本组成的近邻样本集U；然后把$\left( {{x_u},{y_u}} \right)$ 加入有标签样本集M训练得到新的辅学习器$h'$ ，最后计算初始辅学习器$h$ 与新的辅学习器$h'$ 在近邻样本集U上的均方误差的差值$ {\Delta _U} $ ；其中，${x_u} \in N'$ 为无标签样本，yu为初始辅学习器h对xu的预测值，${y_u} = h\left( {{x_u}} \right)$ ，计算出最大$ {\Delta _U} $ 值所对应的xu，也就是置信度最高的样本，并将其加入待处理样本集R中。置信度最高的无标签样本可由式(9)最大化取得：$$ {\Delta _U}{ = }\sqrt {\sum\limits_{{x_{i}} \in U} {{{\left( {{y_{i}}{ - }h\left( {{x_{i}}} \right)} \right)}^{2}}{/}} k} { - }\sqrt {\sum\limits_{{x_{i}} \in U} {{{\left( {{y_{i}}{ - }h'\left( {{x_{i}}} \right)} \right)}^{2}}{/}} k} $$ (9) 式中：U是xu在有标签样本集M中的近邻样本集，k为近邻数；h为初始辅学习器，
$h'$ 为xu和${y_u} = h\left( {{x_u}} \right)$ 加入有标签样本集M后得到的新学习器；yi表示输入xi的真实标签值。基于TSVR的主学习器的任务是对待处理样本集R中的样本进行第二次筛选，选取置信度最高的样本加入有标签样本集M中。相比于辅学习器的筛选策略，不需要再寻找近邻样本，直接利用有标签样本集M训练后得到的初始主学习器g，给待处理样本集R中的样本xv加上伪标签yv，即
${y_v} = g\left( {{x_v}} \right)$ ；然后把带有伪标签的样本加入有标签样本集M中得到新样本集$M'$ ；最后，利用新的样本集$M'$ 训练主学习器，得到新的主学习器$g'$ ，计算新的主学习器$g'$ 在有标签样本集M上的均方误差${\mu _i}$ ；置信度最高的样本就是${\mu _i}$ 值最小时所对应的样本，可通过式(10)最小化评估：$$ {\mu _i}{ = }\sqrt {\sum\limits_{i{ = 1}}^{\left| M \right|} {{{\left( {{y_i}{ - }{y_i}^\prime } \right)}^{2}}{/}\left| M \right|} } $$ (10) 式中：
$\left( {{x_i},{y_i}} \right)$ 为有标签样本集M中的样本，yi表示输入xi的真实标签值；$ {y_i}^\prime $ 为新的主学习器对xi添加的伪标签，即$ {y_i}' = g'\left( {{x_i}} \right) $ 。2.3 算法
基于助训练的半监督孪生支持向量回归算法步骤如下：
1）参数的初始化，其中包括有标签样本集M，无标签样本集N，迭代次数P以及主、辅学习器的各项参数。
2）从无标签样本集N中随机选取n个样本组成新的无标签样本集
$N'$ ；再利用有标签样本集M训练主、辅学习器，得到初始主学习器g和辅学习器h。3）利用初始辅学习器h确定样本集
$N'$ 中的样本xu在有标签样本集M中的近邻样本集U；把近邻样本$\left( {{x_u}{,}{y_u}} \right)$ 加入有标签样本集M后训练初始辅学习器h得到新的辅学习器$h'$ ；再根据式(9)计算出n个无标签样本所对应的$ {\Delta _U} $ 值。4）选取最大
$ {\Delta _U} $ 值所对应的无标签样本xu，将此样本作为置信度最高的样本组成待处理样本集R。5）利用初始主学习器g对于待处理样本集R中的每一个无标签样本xv加上伪标签yv，并将样本
$ \left( {{x_v}{,}{y_v}} \right) $ 加入有标签样本集M训练得到新的主学习器$g'$ ；最后根据式(10)计算R中每一个样本对应的${\mu _i}$ 值。6）选取最小
${\mu _i}$ 值所对应的伪标签样本$ \left( {{x_v}{,}{y_v}} \right) $ ，将此样本作为置信度最高的样本加入到有标签样本集M中，并从无标签样本集N中剔除xv；最后，返回2），循环P次。7）不断迭代更新后建立最终的主、辅学习器模型，对新样本H进行预测和评估。
总体算法步骤如图2。
图 2 助训练算法流程Fig. 2 Help-training algorithm flow下载:
全尺寸图片
3. 仿真实验
3.1 数值仿真
为验证本文所提方法的有效性，对式(11)所表示的非线性函数进行仿真实验：
$$ y = \frac{{{\rm{sin}}\left( x \right)}}{x} + \varepsilon {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \in \left[ { - 5,5} \right] $$ (11) 式中：x为输入,自变量x的取值在[−5,5]上均匀分布；y为x相对应的输出；ε为均值为0，方差为0.1的高斯白噪声。随机产生500个样本，其中一半作为模型训练，一半作为模型测试。训练集中的有标签样本比例分别取10%、30%、50% 3种比例进行仿真。所有涉及TSVR的学习器核函数均选择高斯核函数，正则化参数c1=c2=0.5，核宽度σ2=3。
针对半监督HTSVR算法，每一代选择20个无标签样本进行训练，总共进行20次迭代。KNN算法中的距离度量选用马氏距离，近邻样本k=3。为体现本文算法的性能，对3个模型效果进行比较：
1) 有监督TSVR(supervised TSVR)。利用所有有标签样本建立TSVR学习器的简单模型。
2) 基于自训练的半监督TSVR(self-training semi-supervised TSVR, STSVR)。利用有标签样本建模得到基于TSVR的学习器，然后利用学习器对无标签样本添加伪标签，再利用伪标签样本更新初始样本集来建模。
3) 本文算法——基于助训练的半监督TSVR(help-training semi-supervised TSVR, HTSVR)。利用有标签样本建模得到基于TSVR的主学习器和基于KNN的辅学习器，然后利用主学习器、辅学习器对样本进行置信度评估，选取置信度最高的样本添加伪标签，最后利用伪标签样本更新初始样本集来建模。
仿真结果采用均方根误差(root mean square error, RMSE)作为评估回归模型精度的指标，定义为
$$ {{\rm{RMSE}} = }\sqrt {\sum\limits_{i{ = 1}}^n {{{\left( {{{\hat y}_i}{ - }{y_i}} \right)}^{2}}{/}n} } $$ (12) 式中：
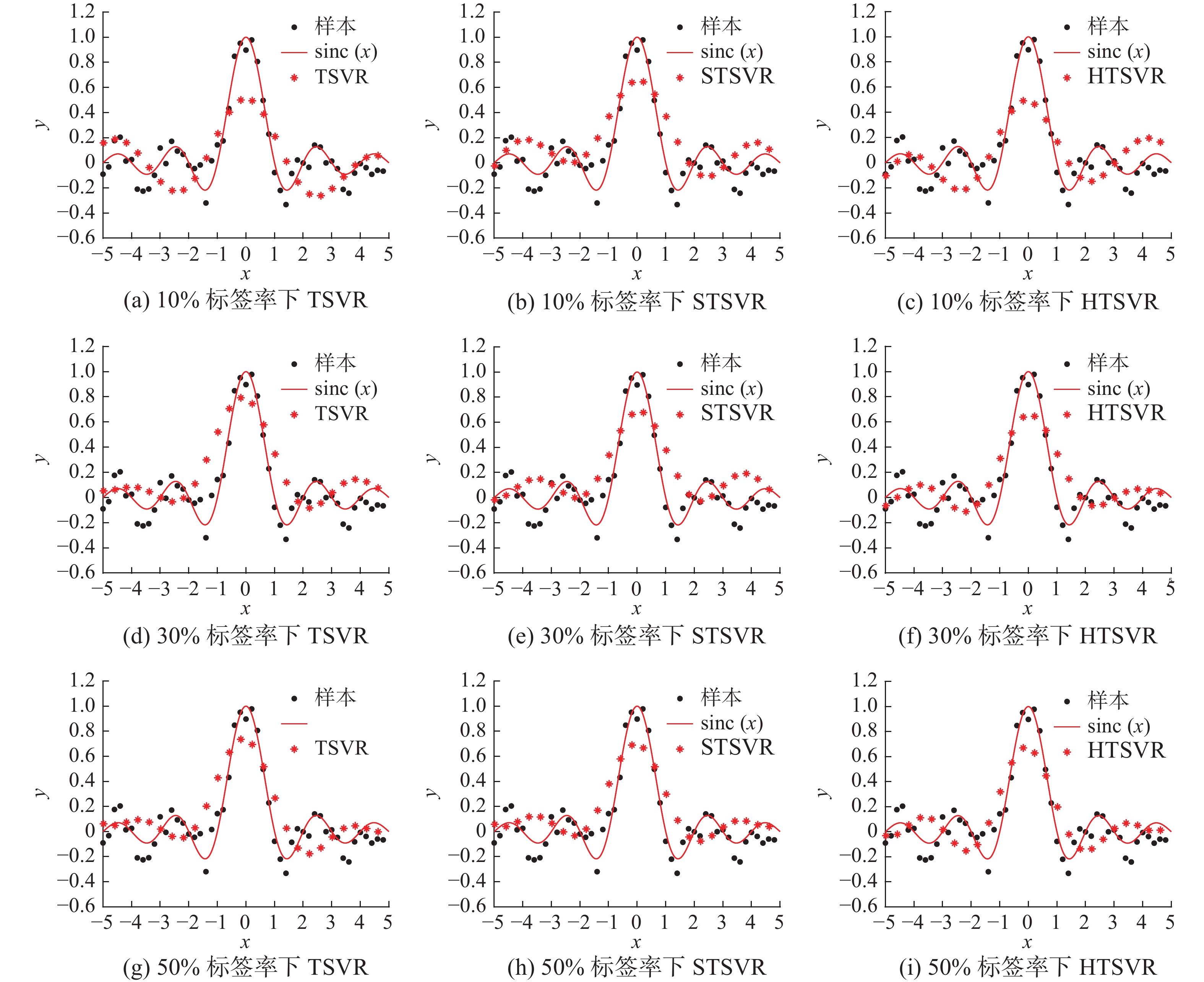
$ {\hat y_i} $ 为实际样本的预测值；$ {y_i} $ 为实际样本的真实值；n为实际样本个数。图3是使用3种不同算法在人工数据集上的跟踪效果图。黑色点是人工数据集的样本点，星号点是测试集经过预测后的样本点，红色曲线是真实的函数曲线。由图3和表1可知，半监督算法STSVR和HTSVR的预测效果在整体上明显优于有监督算法TSVR且更加接近真实的函数曲线，说明无标签样本所包含的信息也是至关重要的。当标签率不断增大，STSVR的预测效果并不明显，此时HTSVR算法相比于STSVR算法，均方根误差均有明显减小，说明本文算法能够有效提高模型的预测效果。
图 3 在3种标签率下数值仿真预测效果Fig. 3 Numerical simulation of prediction under three label rates下载:
全尺寸图片
表 1 3种模型在3种标签率下的均方根误差Table 1 RMSEs of three models under three kinds of label rates模型 标签率 10% 20% 50% TSVR 0.2412 0.2323 0.2110 STSVR 0.2323 0.2243 0.2089 HTSVR 0.2283 0.2095 0.1965 3.2 脱丁烷塔仿真
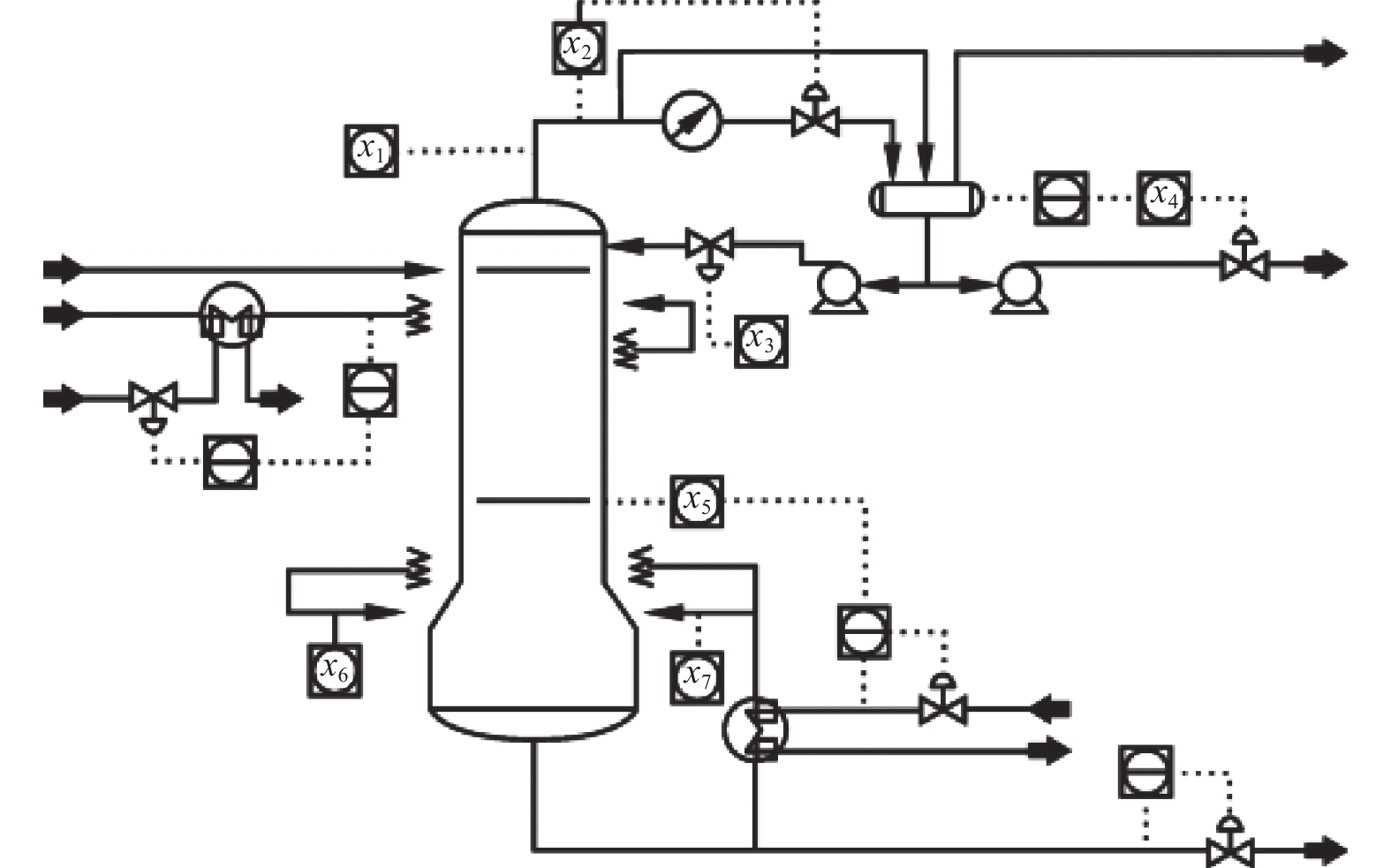
脱丁烷塔是石油炼制过程的重要组成部分，用于脱硫和石脑油裂解[23-24]。图4为脱丁烷塔的工艺流程示意图。在工业过程中，需要从石脑油中去除丁烷，也就是使塔底的丁烷含量最小，因此需要对丁烷浓度实时测量。但丁烷浓度通常很难直接检测并会产生一定的测量延迟，需建立软测量模型预测丁烷浓度。模型及所选取的输入辅助变量如图4和表2[25]。
图 4 脱丁烷塔工艺流程Fig. 4 Process flow of debutanizer下载:
全尺寸图片
表 2 辅助变量选择Table 2 Selection of auxiliary variables主要变量 变量名称 x1 顶层温度 x2 顶层压力 x3 回流流量 x4 流向下个过程的流量 x5 第六塔板温度 x6 塔底温度1 x7 塔底温度2 工业过程数据来源于石脑油裂解过程中的实时采样，共2394组样本，选择数据总数的50%作为模型训练，另外50%作为模型测试。训练集中的有标签样本比例从10%开始，以10%的比例增加到70%，取7种比例进行仿真。针对半监督HTSVR，每一代选择100个无标签样本进行训练，总共进行50次迭代，其他参数选择同数值仿真实验。
为了进一步体现本文算法性能，分别对有监督TSVR方法、基于自训练的半监督STSVR和基于助训练的半监督HTSVR的进行回归性能评估。
由表3可以看出，在标签率高于50%的情况下，两种半监督算法对样本的预测效果优于仅利用有标签样本的有监督TSVR算法。这是因为工业过程中存在大量没有被利用的无标签样本，而半监督算法不仅利用了其中少量的有标签样本，而且加入了大量无标签样本并通过进行分类、筛选出携带有全局信息的无标签样本来构建模型。大量无标签建模样本的加入，改良了模型的预测性能，使其具有更好的泛化性。
表 3 3种模型在7种标签率下的均方根误差结果Table 3 RMSEs of three models under seven kinds of label rates模型 标签率 10% 20% 30% 40% 50% 60% 70% TSVR 0.1557 0.1447 0.1412 0.1362 0.1323 0.1294 0.1270 STSVR 0.1449 0.1393 0.1374 0.1346 0.1340 0.1311 0.1278 HTSVR 0.1417 0.1389 0.1371 0.1331 0.1319 0.1287 0.1255 为了更直观地展示这3种模型的预测效果，图5为10%、30%、50%、70% 4种标签率下，使用3种方法预测的丁烷浓度散点。纵坐标是测试数据的预测值，横坐标是测试数据的真实值，数据点越靠近基准线，预测效果就越好。图6给出了3种方法下对测试数据的预测误差，横坐标是测试数据点，纵坐标是预测值与真实值之差。
图 5 丁烷浓度预测散点图Fig. 5 Scatter plot of butane concentration prediction下载:
全尺寸图片
图 6 丁烷浓度预测误差Fig. 6 Predicted error of butane concentration下载:
全尺寸图片
由图5可以看出，本文所提方法效果最好。再结合图6得到在4种不同的标签率下，半监督方法STSVR与HTSVR方法均优于传统的有监督TSVR方法；而STSVR方法虽然利用了大量无标签样本，但是由于没有经过有效筛选，引入的样本不包含重要的全局信息或误差较大，甚至可能包含了离群点；本文的HTSVR方法则做了进一步改善，筛选后的无标签样本包含了更多的全局数据特征，可以尽可能地减弱误差所带来影响。
综上所述，在正常情况下半监督算法的学习性能强于传统的有监督算法，但对于标签率高于50%的情况，半监督算法STSVR的预测效果却不如有监督算法STSVR。这是因为在传统的自训练算法框架下，模型的预测精度是否准确主要取决于有限的训练样本的多少；由于未经有效筛选，大量无标签训练样本的加入在提高了模型的信息量的同时，也引入了大量的误差，使得模型复杂度提升；如果模型对离群点或较大误差样本发生了过拟合，就会导致模型的预测精度受到影响。所以，对于半监督算法来说，适量增加有效样本会在一定程度上提升模型的预测精度，但当样本总数超过一定的比例后，误差不断累积，模型就可能发生退化。
在标签率递增的情况下，半监督HTSVR算法在任何情况下的预测效果都是最好的。这是因为加入的辅助学习器可以筛选出携带全局信息的无标签样本添加伪标签，协助主学习器更有效地进行样本选择，尽可能地避免大误差样本的加入，削弱特殊工况的影响，提升模型精度，使得模型泛化性更强。
4. 结束语
本文针对工业过程中大量无标签样本的信息利用问题，兼顾样本信息的全局性与准确性，提出了基于助训练的半监督孪生支持向量回归算法。所提方法引入辅助学习器构建助训练框架来协助筛选无标签样本，使得筛选出的样本包含大量的全局信息并尽可能地剔除误差较大样本，避免了数据信息缺失、引入误差样本导致模型不准确等问题，防止模型退化，提高了软测量模型的泛化能力。通过在测试函数和脱丁烷塔数据集上的仿真实验表明，所提方法能够在保证模型准确性的情况下，充分提取工业过程中无标签样本所包含的全局信息与数据特征并对无标签样本进行预测，有效地避免特殊工况影响，具有很好的预测性能和泛化能力。
-
图 1 助训练基本思想
Fig. 1 Basic concept of help-training
下载:
全尺寸图片
图 2 助训练算法流程
Fig. 2 Help-training algorithm flow
下载:
全尺寸图片
图 3 在3种标签率下数值仿真预测效果
Fig. 3 Numerical simulation of prediction under three label rates
下载:
全尺寸图片
图 4 脱丁烷塔工艺流程
Fig. 4 Process flow of debutanizer
下载:
全尺寸图片
图 5 丁烷浓度预测散点图
Fig. 5 Scatter plot of butane concentration prediction
下载:
全尺寸图片
图 6 丁烷浓度预测误差
Fig. 6 Predicted error of butane concentration
下载:
全尺寸图片
表 1 3种模型在3种标签率下的均方根误差
Table 1 RMSEs of three models under three kinds of label rates
模型 标签率 10% 20% 50% TSVR 0.2412 0.2323 0.2110 STSVR 0.2323 0.2243 0.2089 HTSVR 0.2283 0.2095 0.1965 表 2 辅助变量选择
Table 2 Selection of auxiliary variables
主要变量 变量名称 x1 顶层温度 x2 顶层压力 x3 回流流量 x4 流向下个过程的流量 x5 第六塔板温度 x6 塔底温度1 x7 塔底温度2 表 3 3种模型在7种标签率下的均方根误差结果
Table 3 RMSEs of three models under seven kinds of label rates
模型 标签率 10% 20% 30% 40% 50% 60% 70% TSVR 0.1557 0.1447 0.1412 0.1362 0.1323 0.1294 0.1270 STSVR 0.1449 0.1393 0.1374 0.1346 0.1340 0.1311 0.1278 HTSVR 0.1417 0.1389 0.1371 0.1331 0.1319 0.1287 0.1255 -
[1] GE Zhiqiang, SONG Zhihuan, GAO Furong. Review of recent research on data-based process monitoring[J]. Industrial & engineering chemistry research, 2013, 52(10): 3543–3562. [2] 曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3): 788–800. doi: 10.3969/j.issn.0438-1157.2013.03.003 CAO Pengfei, LUO Xionglin. Modeling of soft sensor for chemical process[J]. CIESC journal, 2013, 64(3): 788–800. doi: 10.3969/j.issn.0438-1157.2013.03.003 [3] ZHANG Yingwei, TENG Yongdong, ZHANG Yang. Complex process quality prediction using modified kernel partial least squares[J]. Chemical engineering science, 2010, 65(6): 2153–2158. doi: 10.1016/j.ces.2009.12.010 [4] RANI A, SINGH V, GUPTA J R P. Development of soft sensor for neural network based control of distillation column[J]. ISA transactions, 2013, 52(3): 438–449. doi: 10.1016/j.isatra.2012.12.009 [5] RANJAN R, HUANG Biao, FATEHI A. Robust Gaussian process modeling using EM algorithm[J]. Journal of process control, 2016, 42: 125–136. doi: 10.1016/j.jprocont.2016.04.003 [6] YAN Weiwu, SHAO Huihe, WANG Xiaofan. Soft sensing modeling based on support vector machine and Bayesian model selection[J]. Computers & chemical engineering, 2004, 28(8): 1489–1498. [7] 刘建伟, 刘媛, 罗雄麟. 半监督学习方法[J]. 计算机学报, 2015, 38(8): 1592–1617. doi: 10.11897/SP.J.1016.2015.01592 LIU Jianwei, LIU Yuan, LUO Xionglin. Semi-supervised learning methods[J]. Chinese journal of computers, 2015, 38(8): 1592–1617. doi: 10.11897/SP.J.1016.2015.01592 [8] 周志华. 基于分歧的半监督学习[J]. 自动化学报, 2013, 39(11): 1871–1878. doi: 10.3724/SP.J.1004.2013.01871 ZHOU Zhihua. Disagreement-based semi-supervised learning[J]. Acta automatica sinica, 2013, 39(11): 1871–1878. doi: 10.3724/SP.J.1004.2013.01871 [9] 仝小敏, 吉祥. 基于自训练的回归算法[J]. 中国电子科学研究院学报, 2017, 12(5): 498–502. doi: 10.3969/j.issn.1673-5692.2017.05.011 TONG Xiaomin, JI Xiang. Regression algorithm based on self training[J]. Journal of China academy of electronics and information technology, 2017, 12(5): 498–502. doi: 10.3969/j.issn.1673-5692.2017.05.011 [10] ADANKON M M, CHERIET M. Help-Training for semi-supervised support vector machines[J]. Pattern recognition, 2011, 44(9): 2220–2230. doi: 10.1016/j.patcog.2011.02.015 [11] ADANKON M M, CHERIET M. Help-training semi-supervised LS-SVM[C]//2009 International Joint Conference on Neural Networks. Atlanta: IEEE, 2009: 49−56. [12] 程康明, 熊伟丽. 一种自训练框架下的三优选半监督回归算法[J]. 智能系统学报, 2020, 15(3): 568–577. doi: 10.11992/tis.201905033 CHENG Kangming, XIONG Weili. Three-optimal semi-supervised regression algorithm under self-training framework[J]. CAAI transactions on intelligent systems, 2020, 15(3): 568–577. doi: 10.11992/tis.201905033 [13] LI Yuanqing, GUAN Cuntai, LI Huiqi, et al. A self-training semi-supervised SVM algorithm and its application in an EEG-based brain computer interface speller system[J]. Pattern recognition letters, 2008, 29(9): 1285–1294. doi: 10.1016/j.patrec.2008.01.030 [14] 黄华娟. 孪生支持向量机关键问题的研究[D]. 徐州: 中国矿业大学, 2014: 29−30. HUANG Huajuan. Research on the key problems of twin support vector machines[D]. Xuzhou: China University of Mining and Technology, 2014: 29−30. [15] SHAO Yuanhai, ZHANG Chunhua, YANG Zhimin, et al. An ε-twin support vector machine for regression[J]. Neural computing and applications, 2013, 23(1): 175–185. doi: 10.1007/s00521-012-0924-3 [16] 曹杰, 顾斌杰, 熊伟丽, 等. 增量式约简最小二乘孪生支持向量回归机[J]. 计算机科学与探索, 2021, 15(3): 553–563. doi: 10.3778/j.issn.1673-9418.1912005 CAO Jie, GU Binjie, XIONG Weili, et al. Incremental reduced least squares twin support vector regression[J]. Journal of frontiers of computer science and technology, 2021, 15(3): 553–563. doi: 10.3778/j.issn.1673-9418.1912005 [17] 方建文. 孪生支持向量回归机的研究[D]. 无锡: 江南大学, 2020: 2−5. FANG Jianwen. Research on twin support vector regression[D]. Wuxi: Jiangnan University, 2020: 2−5. [18] TANVEER M, SHARMA A, SUGANTHAN P N. General twin support vector machine with pinball loss function[J]. Information sciences, 2019, 494: 311–327. doi: 10.1016/j.ins.2019.04.032 [19] BAO Liang, YUAN Xiaofeng, GE Zhiqiang. Co-training partial least squares model for semi-supervised soft sensor development[J]. Chemometrics and intelligent laboratory systems, 2015, 147: 75–85. doi: 10.1016/j.chemolab.2015.08.002 [20] WU Di, SHANG Mingsheng, LUO Xin, et al. Self-training semi-supervised classification based on density peaks of data[J]. Neurocomputing, 2018, 275: 180–191. doi: 10.1016/j.neucom.2017.05.072 [21] ZHANG Lei, YANG Lin, MA Tianwu, et al. A self-training semi-supervised machine learning method for predictive mapping of soil classes with limited sample data[J]. Geoderma, 2021, 384: 114809. doi: 10.1016/j.geoderma.2020.114809 [22] YAO Le, GE Zhiqiang. Nonlinear Gaussian mixture regression for multimode quality prediction with partially labeled data[J]. IEEE transactions on industrial informatics, 2019, 15(7): 4044–4053. doi: 10.1109/TII.2018.2885363 [23] MENG Yanmei, LAN Qiliang, QIN J, et al. Data-driven soft sensor modeling based on twin support vector regression for cane sugar crystallization[J]. Journal of food engineering, 2019, 241: 159–165. doi: 10.1016/j.jfoodeng.2018.07.035 [24] NIÑO-ADAN I, LANDA-TORRES I, MANJARRES D, et al. Soft-sensor for class prediction of the percentage of pentanes in butane at a debutanizer column[J]. Sensors (Basel, Switzerland), 2021, 21(12): 3991. doi: 10.3390/s21123991 [25] 程康明, 熊伟丽. 一种双优选的半监督回归算法[J]. 智能系统学报, 2019, 14(4): 689–696. doi: 10.11992/tis.201805010 CHENG Kangming, XIONG Weili. A dual-optimal semi-supervised regression algorithm[J]. CAAI transactions on intelligent systems, 2019, 14(4): 689–696. doi: 10.11992/tis.201805010
