Self-adaptive spectral clustering algorithm for ultra-large-scale data
-
摘要: 针对超大规模数据聚类过程中人为设定邻域参数及计算量庞大等问题,提出了一种基于近似自然近邻的自适应超大规模谱聚类算法(approximate natural nearest neighbor based self-adaptive ultra-scalable spectral clustering algorithm, AN3-SUSC)。该算法首先通过混合代表选取缩小数据规模,在此基础上利用近似自然近邻自适应地确定局部邻域参数并构建相似矩阵,最后运用二部图进行迁移分割将数据空间映射到原超大规模数据空间中并完成谱聚类分析。超大规模数据集实验结果表明,该算法对超大规模数据集聚类效果有所提升,并且降低计算规模同时具有较高的鲁棒性和较强的自适应性。Abstract: An approximate natural neighbor-based self-adaptive ultra-scalable spectral clustering algorithm (AN3-SUSC) is proposed to address the problems of artificially set neighborhood parameters and huge calculation amounts in the process of super-large-scale data clustering. First, the data size is reduced by the algorithm through mixed random selection. Then, approximate natural neighbors are used to determine local neighborhood parameters adaptively, and a similarity matrix is constructed. Finally, the bipartite graph is utilized for migration and segmentation to map the data space to the original ultra-large-scale data space, thereby completing the spectral clustering analysis. Experimental results on super-large-scale data sets show that the algorithm improves the clustering effect of super-large-scale data sets and reduces the computational scale while having high robustness and strong adaptability.
-
随着大数据(big data)、人工智能(artificial intelligence)和数据密集型科学的发展,如何充分挖掘大规模数据乃至超大规模数据中潜在的信息及价值,已经成为各界关注的重要领域。随着这些领域研究的飞速发展,研究者针对不同的数据类型和应用场景,提出了不同的聚类模型及算法。其中,在对超大规模数据聚类分析时,由于海量的样本规模和复杂的数据特征,聚类方法和计算模式的选择会对聚类效果产生巨大影响。因此,无论从算法还是应用方面,超大规模数据都对现有聚类分析方法提出了严峻的挑战。
传统的聚类算法一般通过计算对象间相似度或利用对象间的关系进行聚类,主要分为原型聚类、密度聚类和层次聚类等。K-means算法[1]是典型的原型聚类算法,其主要思想在于通过迭代化的确定质心达到最优聚类结果。基于密度的噪声应用空间聚类(density-based spatial clustering of applications with noise,DBSCAN)算法[2]是著名的密度聚类算法,其利用样本分布的紧密程度进行聚类。Chameleon算法[3]是一种两阶段层次聚类算法,更着重于在对两个类簇进行合并的同时考虑簇间的互连性及近似性。SC算法[4]由图论演化而得,在构建数据空间后对数据构成的图进行切割,形成子图间低内聚、子图内高耦合的状态,从而进行聚类。
以上算法虽然在传统数据集上取得了令人满意的效果,但是在面对大规模数据聚类问题时,往往存在时间、内存和参数等限制。这一问题在对超大规模数据分析时限制更加明显,可能会产生聚类消耗时间骤增、出现内存错误导致中断聚类以及由于参数选择导致误差不可控等问题。围绕着上述问题,研究者们提出一系列大规模聚类方法。Wang等[5]利用渐进式抽样降低数据集规模,获取能够有效代表原始数据集的数据子集进行聚类。Chen等[6]提出利用Nyström方法通过对原始数据集进行随机选取,缩小数据集的规模进行谱聚类。为了更好降低计算量,Cai等[7]基于K-means选取代表点构建相似性矩阵,并提出了基于地标的谱聚类(land-mark based spectral clustering,LSC),能够对大规模数据进行聚类。Wu等[8]通过随机装箱特征(random binning features,RB)加速相似图的构建和特征分解,并引入SVD求解器来有效计算特征向量。Yang等[9]提出了基于代表点的大规模谱聚类 (large-scale spectral clustering based on representative points,RPSC)连续生成两层代表点,然后构造层次二部图并进行谱聚类分析。叶茂等[10]提出了基于快速地标采样的大规模谱聚类算法,利用近似奇异值分解获取地标点并降低相似度矩阵的计算复杂度,从而对大规模数据谱聚类分析进行优化。以上算法均通过对大规模数据集进行处理,降低计算复杂度。随着数据规模爆炸式增长,出现超大规模数据,大规模聚类算法已经很难满足超大规模数据的聚类要求。而Huang等[11]提出超大规模谱聚类(ultra-scalable spectral clustering,U-SPEC),有效地解决了对超大规模数据集进行谱聚类的时间、内存等限制。
本文基于自然邻居思想提出近似自然近邻方法。该方法能够不受整体数据特征的影响,根据数据中局部区域特征自适应的确定邻域参数。在此基础之上,本文以超大规模数据集为背景,提出了一种基于近似自然近邻的自适应超大规模谱聚类算法(approximate natural nearest neighbor based self-adaptive ultra-scalable spectral clustering algorithm,AN3-SUSC)。算法能够很好地解决聚类算法在面对超大规模数据集时计算量庞大、聚类效果不理想等问题,且其能够在聚类过程中根据数据之间的特征关系自适应地选择邻域参数。
1. 相关工作
1.1 自然邻居
自然邻居(natural neighbor, NaN)[12-14]是一种自适应的邻居选择方法,它通过自然稳定状态去除了传统最近邻居方法中设置固定参数的问题。自然邻居方法通过数据的分布情况与密度特征反映数据集在稳定状态下的邻居状况,能够突破人为参数的影响,达到邻居自适应的效果。自然邻居思想现已基本形成完整的理论体系,并应用于许多研究领域,如图像检索[15]、聚类分析[16]等。
以下对自然邻居思想中的相关概念进行定义,其中令
$X = \left\{ {{x_1},{x_2}, \cdots ,{x_N}} \right\}$ 表示一个有$N$ 个对象的数据集,其中${x_i} \in {{\rm{R}}^d}$ ,$d$ 是维度:定义1 自然稳定状态(natural stable state)。对数据集
$X$ ,依次获取每个点的$k$ 个最近邻居$(k = 1,2, \cdots ,N)$ 。在查找过程中,若$k = \lambda $ ,数据集$X$ 中的任意点${x_i}$ 均存在另一个数据点${x_{_j}}$ 与其互为邻居,则当前状态为自然稳定状态,即:$$ \begin{gathered} (\forall {x_i})(\exists {x_j})(\lambda \in N) \wedge ({x_i} \ne {x_j}) \Rightarrow \\ ({x_i} \in {{\rm{knn}}_\lambda }({x_j})) \wedge ({x_j} \in {{\rm{knn}}_\lambda }({x_i})) \end{gathered} $$ (1) 式中:
${\rm{knn}}$ 为数据点$x$ 的前$k$ 个最近邻居构成的集合;$\lambda $ 为循环次数。定义2 自然邻居(natural neighbor, NaN)。当数据集
$X$ 处于自然稳定状态时,互为邻居的点同样互为自然邻居,即:$$ {x_i} \in {{\rm{NaN}}} \left( {{x_j}} \right) \Leftrightarrow \left( {{x_i} \in {{\rm{knn}}_\lambda }\left( {{x_j}} \right)} \right) \wedge \left( {{x_j} \in {{\rm{knn}}_\lambda }\left( {{x_i}} \right)} \right) $$ (2) 定义3 自然邻居特征值(natural neighbor eigenvalue, NaNE)。数据集
$X$ 处于自然稳定状态时,搜索循环次数为$\lambda $ ,则$\lambda $ 为当前数据集X的自然邻居特征值。自然邻居思想与聚类算法结合的应用有很多,并且取得了很好的效果,例如基于自然邻居邻域图的无参数离群检测算法[17]、基于快速自然邻居搜索的谱聚类算法[18]、基于改进的自然邻居图生成子簇的Chameleon算法[19]等。
尤其针对超大规模数据集,由于数据规模庞大、数据点邻居众多等原因,传统的自然邻居在选取邻居过程中会导致邻居划分模糊、最近邻居选取过多等问题。
1.2 混合代表选取
为了避免对超大规模数据集进行完整的相似矩阵计算,相关研究提出了利用子矩阵降低计算量及时间和空间复杂度的方法。子矩阵的代表点的选取通常可以用Nyström算法[6]、LSC算法[7]、混合代表点选取算法[11]等。其中混合代表点选取算法能够更加快速、有效地选取具有数据特征的代表点,从而降低时间、空间复杂度。混合代表的选取过程可以分为两步:
1)在超大规模数据集X中随机抽取
$q'$ 个$\left( q' \ll N \right)$ 候选代表点作为候选代表点集$X'$ 。2)对候选代表点集
$X'$ 进行K-means聚类,获取$q$ 个聚类中心$(q \ll q')$ ,并将其作为代表点集$R$ ,从形式可表示为$$ R = \left\{ {{r_1},{r_2}, \cdot \cdot \cdot ,{r_q}} \right\} $$ (3) 1.3 二部图
谱聚类算法[4,20]是一种建立在图理论上的聚类算法,能有效地对稀疏数据进行聚类,具有高效、适应性强等特点,但对大规模数据进行分析时,计算量庞大。针对谱聚类在大规模数据中特征值计算量复杂的缺点,Li等表示可将迁移分割(transfer cut)[21-22]和二部图[21,23]方法应用于谱聚类分析中,使算法的运行效率更高。
稀疏子矩阵反应了数据点和代表点之间的关系,可将其解释为一个二部图
$G = \{ X,R,{{B}}\} $ ,其中$X \cup R$ 是点集,${\boldsymbol{B}}$ 是交叉稀疏矩阵。利用二部图结构,采用迁移分割的方法,将问题转化为求解一个$p \times p$ 矩阵的特征值问题。若将二部图视为一个普通的图$G$ (包含$N + p$ 个节点),则其邻接矩阵可表示为$$ {{{\boldsymbol{E}}}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{ 0}}&{{{{{\boldsymbol{B}}}}^{\rm{T}}}} \\ {{{\boldsymbol{B}}}}&{\boldsymbol{0}} \end{array}} \right] $$ (4) 为对其进行谱聚类,则需求解下列广义特征值:
$$ {{{\boldsymbol{Lu}}}} = \gamma {{{\boldsymbol{Du}}}} $$ (5) 通过构建部分图
${G_R} = \left\{ {R,{{\boldsymbol{E}}_R}} \right\}$ ,其中${{\boldsymbol{E}}_R} = {{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{D}}_x^{ - 1}{\boldsymbol{B}}$ 为邻接矩阵[24],${{\boldsymbol{D}}_x}$ 为对角线矩阵且第$(i,i)$ 项为${\boldsymbol{B}}$ 的第$i$ 行之和。广义特征值可转化为$$ {{\boldsymbol{L}}_R}{\boldsymbol{v}} = \lambda {{\boldsymbol{D}}_R}{\boldsymbol{v}}, $$ (6) 其中:
${{\boldsymbol{D}}_R}$ 为图${G_R}$ 的度矩阵,${\boldsymbol{v}}$ 是图${G_R}$ 的第$i$ 个向量。设前
$k$ 个特征对式(6)表示为$\left\{ {\left( {{\lambda _i},{{{v}}_i}} \right)} \right\}_{i = 1}^k$ ,其中$0 = {\lambda _1} \leqslant {\lambda _2} \leqslant \cdot \cdot \cdot \leqslant {\lambda _k} < 1$ 。设前$k$ 个特征对式(5)表示为$\left\{ {\left( {{\gamma _i},{{\boldsymbol{u}}_i}} \right)} \right\}_{i = 1}^k$ ,其中$0 = {\gamma _1} \leqslant {\gamma _2} \leqslant \cdot \cdot \cdot \leqslant {\gamma _k} < 1$ 。已证明[21]:$$ {\gamma _i}\left( {2 - {\gamma _i}} \right) = {\lambda _i} $$ (7) $$ {{\boldsymbol{u}}_i} = \left[ {\begin{array}{*{20}{l}} {{{\boldsymbol{h}}_i}} \\ {{{\boldsymbol{v}}_i}} \end{array}} \right]{{ }} $$ (8) $$ {{\boldsymbol{h}}_i} = \frac{1}{{1 - {\gamma _i}}}{\boldsymbol{T}}{{\boldsymbol{v}}_i} $$ (9) 其中
${\boldsymbol{T}} = {\boldsymbol{D}}_x^{ - 1}{\boldsymbol{B}}$ 是迁移概率矩阵。2. 本文算法
本文将近似自然近邻与超大规模谱聚类结合,提出了基于近似自然近邻的超大规模谱聚类算法。该方法可以通过降低数据规模和自适应邻域参数,解决参数人为设定易产生误差和超大规模数据谱聚类计算量庞大的问题,进而提高聚类算法的运算效率和聚类结果的准确性。
2.1 近似自然近邻
本文提出的近似自然近邻(approximate natural nearest neighbor, AN3)思想与传统的自然邻居具有较大的差异。传统自然邻居根据数据集的整体特征选取邻域参数,忽略数据集中局部数据点的特征。而近似自然近邻不仅能够根据整体数据集稳定状态确定邻域参数,还能针对局部数据特征确定不同区域的邻域参数。因此,近似自然近邻能够摆脱传统自然邻居中因数据点分布不均而造成的数据点邻居选取一致的不足。
相对于传统的自然邻居根据整体数据集的特征选取,近似自然近邻算法(如图1所示)能根据部分数据的不同特征确定邻居数。近似自然近邻利用K-means算法对自然邻居思想进行扩展,获取不同特征区域的自适应邻域参数,避免参数的限制、邻居模糊等问题。以图1为例,在图1(b)中,数据点
$({x_i},{P_i})$ 与$({x_j},{P_j})$ 所处区域特征不同,其邻居数也互不相同,因此能够更准确地反映数据之间的相关性。定义4 自然邻居特征均值(natural neighbor mean eigenvalue)将数据集
$X$ 进行聚类,得到$C = \left\{ {c_1},{c_2}, \cdots ,{c_n} \right\}$ ,计算各域的自然邻居特征值$\lambda = \left\{ {\lambda _1},\right. \left.{\lambda _2}, \cdots ,{\lambda _n} \right\}$ ,自然邻居特征均值公式定义为$$ \bar \lambda = \dfrac{{\displaystyle\sum\limits_{i = 1}^n \lambda }}{n} $$ (10) 近似自然近邻的算法主要分为3部分:
1)假设存在数据集
$X$ ,计算其自然邻居特征值,利用K-means对其重新进行聚类,并计算自然邻居特征均值。2)对
$X$ 中的任意数据点$ {x_i} $ ,从距离其最近的簇中寻找最近的点$P$ ,并且寻找$P$ 在对应簇中的最近邻居。3)在点
$P$ 的最近邻居中,计算得到${x_i}$ 的自然邻居特征均值个最近邻居。本文提出的近似自然近邻算法的算法流程如算法1所示。
算法1 近似自然近邻(AN3)
输入 数据集
$X\{{x_1},{x_2}, \cdots ,{x_n}\}$ 输出 近似自然邻居点集
$\rm A{N}^{3}\_Points$ ,特征值$\lambda $ //对于给定的数据集
$X$ ,计算特征值$k = {\rm{ FindNaNE}}(X)$ $ {K^\prime } = 3k $ $K\_{\rm{center}},{\rm{NaNE\_list}} = {\text{ K-means }}\left( {X,K'} \right)$ $\bar \lambda = {{\rm{Mean}}} \left( {{\rm{NaNE\_list}}} \right)$ $\lambda = {\rm{Min}}({\rm{NaNE\_list}})$ For all
${x_i} \in X$ do$\varepsilon = {{\rm{Min}}} \left( {{{\rm{Dist}}} \left( {{x_i},K\_{\rm{center}}} \right)} \right)$ //$\varepsilon $ 为${x_i}$ 的最近领域//计算
${x_i}$ 与$\varepsilon $ 中最近点$P$ $P = {{\rm{Min}}} \left( {{{\rm{Dist}}} \left( {{x_i},\varepsilon } \right)} \right)$ //对最近点
$P$ 找到对应簇的$C$ 个最近邻居$C = {\rm{NaNE}}_i^2$ $P\_{\rm{neighbors}} = {{\rm{Find}}} \_{\rm{neighbor}}(P,C,X)$ //计算
${x_i}$ 的前自然邻居特征均值$\bar \lambda $ 个邻居AN3_Points=Find_neighbor(xi,
$\bar \lambda$ , P_neighbors)End for
Return:
${\rm{A{N^3}\_Points}}$ ,$\lambda $ 其中,不同的数据集,有不同的自然邻居特征值。本文根据数据集的特征,利用K-means算法,将数据集划分
$K' = 3k$ 个簇(随数据集规模发生改变),每个簇的中心为聚类中心($K\_{\rm{center}}$ )。数据集中每个数据点${x_i}$ 的邻域$\varepsilon $ 是距离该数据点最近的聚类中心所在的簇。由于本文提出的算法先对数据集进行了划分,寻找最近邻居时会存在对区域的局限性。为了有效地找到最近邻居,算法通过找到距离数据点
${x_i}$ 的最近点$P$ 及其$C$ 个邻居$P\_{\rm{neighbors}}$ 。为保证寻找到数据点${x_i}$ 的$\bar \lambda $ 个最近邻居,$C$ 的取值为点$P$ 所在簇的特征值的平方(${\rm{NaN{E^2} }}$ )。2.2 基于近似自然近邻的超大规模谱聚类算法
谱聚类算法在对超大规模数据集进行聚类分析时,往往会因为相似性矩阵
${\boldsymbol{W}}$ 计算量庞大导致聚类中断。本文利用混合代表选取对数据集进行抽取,降低相似矩阵${\boldsymbol{W}}$ 的计算量。同时,本文通过近似自然近邻获取能够代表数据局部特征的自适邻域参数来代替谱聚类过程中出现的参数,并利用邻域参数缩小谱聚类过程中相似性矩阵的规模,解决超大规模数据谱聚类时产生的庞大计算量和参数选择导致的聚类误差,进而达到提高算法的自适应性、准确性和降低计算规模的目的。在利用近似自然近邻改进相似性矩阵的计算过程中,算法获取每个数据点
${x_i}$ 的自然邻居特征均值$\bar \lambda $ 个邻居,进而利用高斯核函数进行构建相似性矩阵。该过程具体表示为$$ {\bf{BM}} = {\left\{ {{{\rm{bm}}_{ij}}} \right\}_{N \times P}} $$ (11) $$ {{\rm{bm}}}_{ij}=\left\{\begin{array}{l}{\rm{exp}}\left(-\dfrac{\Vert {x}_{i}-{x}_{j}|{|}^{2}}{2{\sigma }^{2}}\right),\quad {r}_{j}\in N\left({x}_{i}\right) \\ 0,\quad{其他} \end{array}{ } \right.$$ (12) 式中:
$N\left( {{x_i}} \right)$ 表示${x_i}$ 的$\bar \lambda $ 个最近代表的集合,$\sigma $ 被设定为对象与其$\bar \lambda $ 最近代表点之间的平均欧几里德距离。${\bf{BM}}$ 是一个$N \times P$ 维的稀疏矩阵,只包含$N \times \bar \lambda $ 个非零项。综上所述,本文提出的基于近似自然近邻的自适应超大规模谱聚类算法主要分为3部分:
1)利用混合代表点选取提取能够代表数据集特征的代表点,使超大规模数据集转换为数据规模可控的代表点集;
2)通过鲁棒的近似自然近邻算法获取代表点集中代表点的邻居对所选取的代表点及其邻居进行稀疏化,并利用高斯核函数与算法获取的局部特征值结合,作为相似核函数进一步降低计算量,优化谱聚类过程中的相似矩阵计算;
3)利用二部图及迁移分割方法,将重新构造的数据空间映射到原有数据空间中,从而完成谱聚类分析。
本文提出的基于近似自然近邻的自适应超大规模谱聚类算法的算法流程如算法2所示。
算法2 基于近似自然近邻的自适应超大规模谱聚类算法(AN3-SUSC)
输入 超大规模数据集
$X\{{x_1},{x_2}, \cdots ,{x_n}\}$ 输出 聚类标签
${\rm{labels }}$ //初始化代表点集
${\rm{R{p_ - }Points}} = \varnothing$ Initialize:
${\rm{R{p_ - }Points}} = \varnothing$ //利用混合随机选取(HRS)选取
$p$ 个代表点集${\rm{R{p_ - }Points }}$ ${\rm{ Rp\_Points}} = {{\rm{HRS}}} (X)$ //利用算法1(近似自然近邻算法(AN3))获取
${x_i}$ 在抽取后的代表点集中的邻居并构建核函数${\rm{ AN3\_Points}},K = {{{\rm{AN}}} ^3}\left( {{x_i},{{\rm{{ Rp\_Points }}}}} \right)$ 计算相似性矩阵
${\bf{BM}}$ 和${{\rm{bm}}_{ij}}$ $G = {{\rm{Bipartite}}} \_{\rm{graph}}\left( {X,{{\rm{Rp}}_ - }{\rm{P}}} \right.{\rm{oints}},\left. {{\bf{BM}}} \right)$ 根据
${{\boldsymbol{E}}_R} = {{{\bf{BM}}}^{\rm{T}}}{{\boldsymbol{D}}_x}^{ - 1}{\bf{BM}}$ 计算${{\boldsymbol{E}}_R}$ ${{\boldsymbol{G}}_R} = {{\rm{Bipartite}}} \_{\rm{graph}}{{(}}{\rm{Rp\_Points}},\left. {{{\boldsymbol{E}}_R}} \right)$ //利用迁移分割方法计算特征值
${\rm{Fea}}$ ${\rm{Fea}} = {{\rm{transfer}}} {{\rm{cut}}} \left( {{{\boldsymbol{G}}_R},{\boldsymbol{G}}} \right)$ ${\rm{labels}} = {{\rm{K}}} {\text{-}} {\rm{means}}{{ }}({\rm{Fea}},K)$ Return:
${\rm{labels}}$ 其中,AN3-SUSC算法首先利用近似自然近邻算法(AN3)获取
${x_i}$ 的对数据集抽取后的代表点集${\rm{Rp\_Points}}$ 中的邻居,其中数据集的局部特征不同,抽取的邻居也不相同。其次,算法利用构建二部图方法(bipartite_graph)通过计算相似性矩阵${\bf{BM}}$ 及邻接矩阵${{\boldsymbol{E}}_R}$ 来构建二部图。最后,算法通过迁移分割计算特征值${\rm{Fea}}$ ,并利用K-means算法完成谱聚类分析过程。该算法的整体时间复杂度为
$O({p^2} + N{p^2} + N{K^2})$ ,主要分为3个部分:1)通过混合代表点选取方法在超大规模数据集中抽取代表点,时间复杂度为
$O({p^2})$ 。2)对代表点集利用近似自然近邻选取最近邻居并构建核函数,其时间复杂度为
$O(N{p^2})$ 。3)利用二部图进行迁移分割,并在此基础上利用K-means离散化获得最终的聚类结果,其时间复杂度为
$O(N{K^2})$ 。相较于传统的谱聚类算法, AN3-SUSC算法主要通过降低超大规模数据集的数据规模,根据近似自然近邻思想达到邻居自适应的效果。与人为设定参数相比,该算法利用近似自然近邻思想在获取数据邻居的过程中,依据数据点的局部特征确定邻域参数,既不增加算法的运行时间也不会增加数据的存储量。该算法能够利用近似自然近邻摆脱聚类过程中参数人为设定的限制,达到参数自适应的目的,从而对谱聚类进行优化,实现对超大规模数据集的有效聚类分析。
3. 实验
本文所提出的AN3-SUSC算法没有使用人为设定的固定邻域参数,而是能够根据数据特征自适应地得到数据点之间的邻居关系。因此,本文通过自适应的算法将代表点迁移到整个超大规模数据集中,从而达到更好的聚类效果。
与之相比,传统的聚类方法、谱聚类算法与超大规模谱聚类算法在对代表点进行选取邻居过程中,存在邻域参数人为设定的问题。在对代表点进行迁移时,迁移过程同样与邻域参数
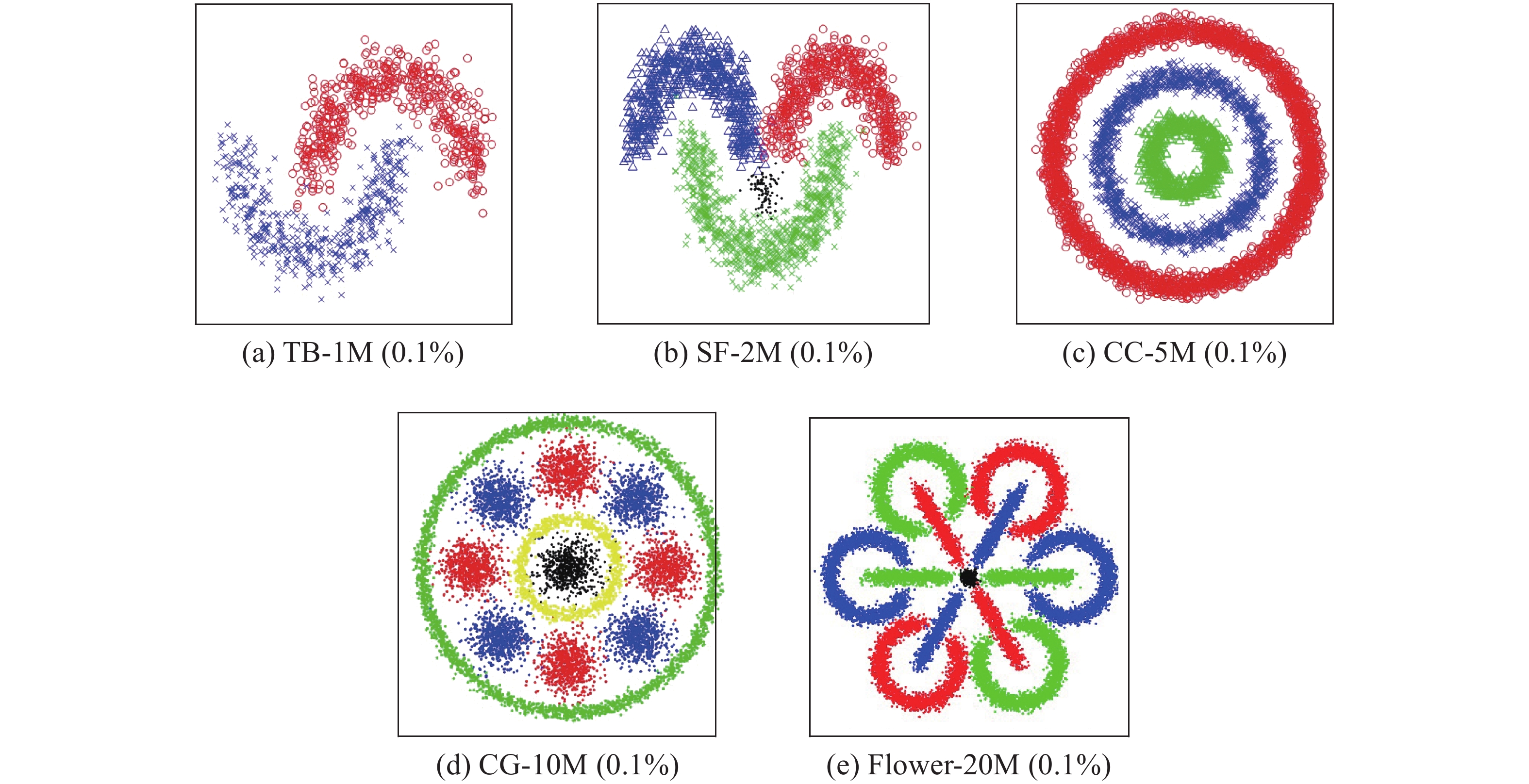
$k$ 有着直接的关系,依然存在参数限制。为了评估基于近似自然近邻的自适应超大规模谱聚类算法更具有优越性,本文选取了5个形状不同、特征不同的超大规模数据集(TB-1M、SF-2M、CC-5M、CG-10M、Flower-20M[11])来进行测试,并将该算法的聚类效果与U-SPEC等算法进行对比。算法实验在具有MATLAB R2018b、硬件配置为Intel(R) Core(TM) i9-10920X CPU @ 3.50GHz、内存64GB的计算机上进行。
3.1 数据集
为保证本实验效果的鲁棒性和准确性,本实验中将在5个超大规模的数据集中进行聚类分析,其数据规模100万~2000万。超大规模的数据集包括:Two Bananas-1M(TB-1M)、Smiling Face-2M(SF-2M)、Concentric Circles-5M(CC-5M)、Circles and Gaussians-10M(CG-10M)和Flower-20M。
数据集的规模、维度等信息如表1所示,其中0.1%数据点的分布趋势如图2所示。
表 1 数据集描述Table 1 Description of the datasets数据集 数据规模 数据维度 数据簇数 TB-1M 1000000 2 2 SF-2M 2000000 2 4 CC-5M 5000000 2 3 CG-10M 10000000 2 11 Flower-20M 20000000 2 13 3.2 实验分析
为了验证本文提出的AN3-SUSC算法效果,实验部分通过利用U-SPEC算法中的超大规模合成数据集进行对比试验。实验选用归一化互信息(NMI)[25]作为评价指标,其计算方法为
$$ {\rm{NMI(labels,gt)}} = \frac{{I({\rm{labels}},{\rm{gt}})}}{{\sqrt {H({\rm{labels}})H({\rm{gt}})} }} $$ (13) 式中:
${\rm{labels}}$ 为算法生成的标签,${\rm{gt}}$ 为数据集原始标签,$I(\cdot)$ 为互信息,$H(\cdot)$ 为信息熵。实验对不同规模的数据集进行20次聚类分析,并将NMI的均值作为衡量标准。同时,为了验证AN3-SUSC算法的自适应性,本文也针对不同数据集中的邻域参数进行对比实验与分析。
在实验过程中,将本文提出的AN3-SUSC算法与经典的K-means算法以及4种谱聚类算法进行对比,具体算法列举如下:
1) K-means算法[1]:K均值算法;
2) SC算法[4]:谱聚类算法;
3) Nyström算法[6]:Nyström谱聚类;
4) LSC算法[7]:基于地标的大规模谱聚类算法;
5) U-SPEC算法[11]:超大规模谱聚类算法;
6) AN3-SUSC算法:基于近似自然近邻的自适应超大规模谱聚类算法。
上述算法中包含部分公共参数和私有参数。为了尽可能准确地评估实验结果,我们在参考其算法论文和实验结果后对参数进行如下设置:
1)在上述算法中,使用高斯核函数构建相似性矩阵的LSC算法、U-SPEC算法以及AN3-SUSC算法有一个共同的参数
$P(P = 1\;000)$ ;2)K-means算法、LSC算法、Nyström算法和U-SPEC算法均含有邻域参数(
$ K = 5 $ )。由于本文进行实验所采用的数据集为超大规模数据集,数据集规模100万~2000万不等,大多数传统的聚类算法在对超大规模数据集进行分析时并不可行。因此本文均选取大规模数据聚类算法进行对比,如表2所示。表2中列举了K-means算法、SC算法和Nyström算法等聚类算法在5个超大规模数据集(TB-1M、SF-2M、CC-5M、CG-10M和Flower-20M)中的NMI聚类评价指标。
表 2 与其他谱聚类算法的平均NMI分数(超过20次运行)的比较Table 2 Comparison with other spectral clustering algorithms with average NMI scores (over 20 runs)% 数据集 K-means SC Nyström LSC U-SPEC AN3-SUSC(本文) TB-1M ${\text{40}}{\text{.16}} \pm {\text{0}}{\text{.00}}$ N ${\text{24}}{\text{.06}} \pm {\text{0}}{\text{.01}}$ 64.83±7.3 ${\text{95}}{\text{.91}} \pm {\text{0}}{\text{.53}}$ ${\bf{96} }.{\bf{86} } \pm {\bf{0} }.{\bf{22} }$ SF-2M ${\text{57}}{\text{.32}} \pm {\text{0}}{\text{.00}}$ N ${\text{46}}{\text{.66}} \pm {\text{0}}{\text{.02}}$ N ${\text{75}}{\text{.14}} \pm {\text{2}}{\text{.36}}$ ${\text{79}}{\text{.60}} \pm {\text{0}}{\text{.04}}$ CC-5M ${\text{25}}{\text{.05}} \pm {\text{0}}{\text{.00}}$ N N N ${\text{99}}{\text{.87}} \pm {\text{0}}{\text{.01}}$ ${\text{99}}{\text{.75}} \pm {\text{0}}{\text{.02}}$ CG-10M ${\text{49}}{\text{.03}} \pm {\text{3}}{\text{.21}}$ N N N ${\text{79}}{\text{.12}} \pm {\text{1}}{\text{.80}}$ ${\text{80}}{\text{.57}} \pm {\text{1}}{\text{.60}}$ Flower-20M $62.32 \pm 3.24$ N N N ${\text{85}}{\text{.98}} \pm {\text{2}}{\text{.10}}$ ${\text{89}}{\text{.70}} \pm {\text{2}}{\text{.30}}$ 注:N表示内存溢出,无法计算 通过表2可以直观地看出, 传统的SC算法在对超大规模数据集进行聚类分析时会产生内存错误,无法进行有效的聚类分析。Nyström 算法只能够对两个较小的数据集进行分析,并且聚类结果较差,并且同样会随着数据集规模逐渐增大产生内存错误。LSC算法只能对TB-1M 数据集进行聚类,当数据集规模继续增大后也会产生内存错误,无法进行更大规模数据集的聚类分析。U-SPEC算法和AN3-SUSC算法均能对5个超大规模数据集进行有效的聚类分析且不存在内存错误的情况。在分析结果中,AN3-SUSC算法对TB-1M 、SF-2M、CG-10M和Flower-20M数据集聚类分析的结果均为最优,超过了U-SPEC算法。尤其在对SF-2M和Flower-20M数据集进行分析时,效果非常明显,NMI评价指标高于U-SPEC算法4%。实验结果表明,AN3-SUSC算法能够有效地选择邻域参数,并对超大规模数据集聚类具有很好效果。
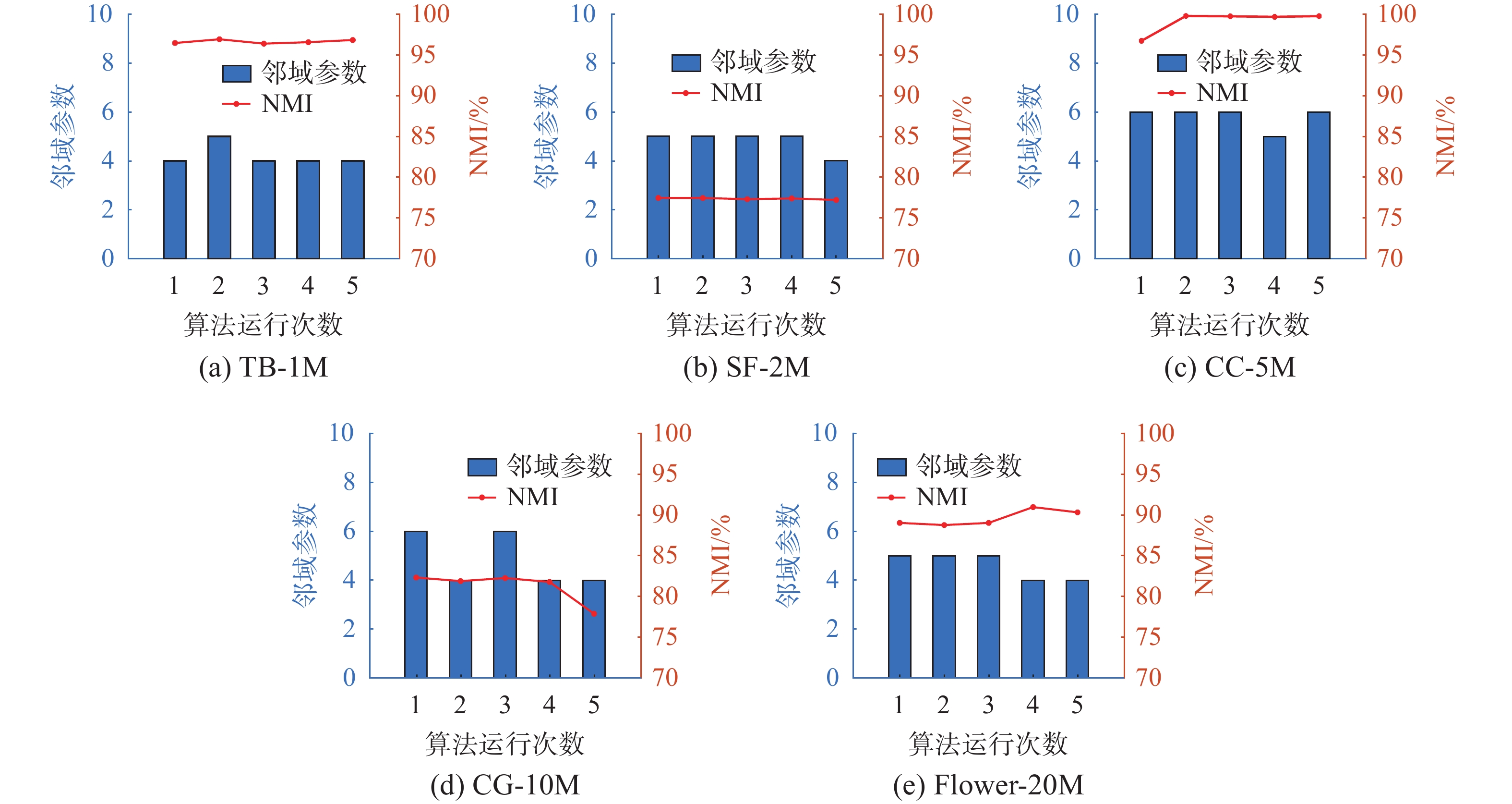
为了证明本文提出的AN3-SUSC算法自适应邻域参数的特性,以及其对LSC、U-SPEC等算法中邻域参数需要人为设定这一不足的改进,我们设定了邻域参数验证实验。改进实验针对5个数据集(TB-1M、SF-2M、CC-5M、CG-10M和Flower-20M),分别进行多轮随机实验,对AN3-SUSC算法的自适应性和稳定性进行验证。实验结果如图3所示,其中柱状图反应在同一数据集下邻域参数在随机5轮实验中的变化情况,折线图表示在随机5轮实验中NMI评价指标的变化趋势。
通过图3可以直观地看出:5个子图的柱状图中,AN3-SUSC算法对5个不同数据集,能够自适应得到大小不同且稳定的邻域参数。而对各个子图中折线图进行观测可以发现,在对任意一个数据集进行随机5轮实验,算法能获得稳定的聚类结果,并且对不同数据集具有较强的鲁棒性。产生这种自适应性和鲁棒性的主要原因则在于算法需要通过混合代表点选取方法在超大规模数据集中抽取数据点,因此具有自适应性的邻域参数对聚类结果的提高将会在超大规模数据集上产生进一步的放大。
3.3 实验结论
为了验证AN3-SUSC算法的自适应性及其聚类效果的准确性,本文在不同规模、不同特征的超大规模数据集上进行了对比试验,并对不同数据集中邻域参数进行了对比分析。
AN3-SUSC算法与SC算法、Nyström 算法和以图3(a)、图3(e)中为例,柱状图体现在随机的5轮实验中,算法根据数据集的特征确定不同的参数,并且邻域参数的选取较为鲁棒,分别为4±1、5±1;
折线图体现在随机5轮实验中,对TB-1M数据集的聚类结果稳定在96.86%±0.22%,对Flower-20M数据集的聚类结果稳定在89.70%±2.3%。以上能够体现出AN3-SUSC算法具有良好的自适应性和鲁棒性。
4. 结束语
本文提出了一种基于近似自然近邻的自适应超大规模谱聚类算法,利用近似自然近邻思想解决了邻域参数选择问题,并提高了聚类分析的效果。实验结果表明,与传统人为设置邻域参数相比,该算法能够在无需邻域参数设置的情况下,根据数据集的特征自适应地确定参数,并能够提高聚类结果。
本文提出的AN3-SUSC算法在不同规模、不同特征的超大规模数据集中都有更好的鲁棒性,能够提高聚类算法的准确性,并且很好地解决了邻域参数依靠实验、经验等人为确定的问题。
随着超大规模数据不断的产生,聚类分析具有更广阔的前景,本文提出的AN3-SUSC算法也具有更大的改进空间。在后续改进中,我们将在更多不同特征、不同维度的超大规模数据集中验证算法聚类效果,并且优化算法的时间、空间复杂度,从而能更好地针对超大规模数据集进行快速、有效的聚类,推动聚类分析方法中自适应邻域参数的算法改进。
-
表 1 数据集描述
Table 1 Description of the datasets
数据集 数据规模 数据维度 数据簇数 TB-1M 1000000 2 2 SF-2M 2000000 2 4 CC-5M 5000000 2 3 CG-10M 10000000 2 11 Flower-20M 20000000 2 13 表 2 与其他谱聚类算法的平均NMI分数(超过20次运行)的比较
Table 2 Comparison with other spectral clustering algorithms with average NMI scores (over 20 runs)
% 数据集 K-means SC Nyström LSC U-SPEC AN3-SUSC(本文) TB-1M ${\text{40}}{\text{.16}} \pm {\text{0}}{\text{.00}}$ N ${\text{24}}{\text{.06}} \pm {\text{0}}{\text{.01}}$ 64.83±7.3 ${\text{95}}{\text{.91}} \pm {\text{0}}{\text{.53}}$ ${\bf{96} }.{\bf{86} } \pm {\bf{0} }.{\bf{22} }$ SF-2M ${\text{57}}{\text{.32}} \pm {\text{0}}{\text{.00}}$ N ${\text{46}}{\text{.66}} \pm {\text{0}}{\text{.02}}$ N ${\text{75}}{\text{.14}} \pm {\text{2}}{\text{.36}}$ ${\text{79}}{\text{.60}} \pm {\text{0}}{\text{.04}}$ CC-5M ${\text{25}}{\text{.05}} \pm {\text{0}}{\text{.00}}$ N N N ${\text{99}}{\text{.87}} \pm {\text{0}}{\text{.01}}$ ${\text{99}}{\text{.75}} \pm {\text{0}}{\text{.02}}$ CG-10M ${\text{49}}{\text{.03}} \pm {\text{3}}{\text{.21}}$ N N N ${\text{79}}{\text{.12}} \pm {\text{1}}{\text{.80}}$ ${\text{80}}{\text{.57}} \pm {\text{1}}{\text{.60}}$ Flower-20M $62.32 \pm 3.24$ N N N ${\text{85}}{\text{.98}} \pm {\text{2}}{\text{.10}}$ ${\text{89}}{\text{.70}} \pm {\text{2}}{\text{.30}}$ 注:N表示内存溢出,无法计算 -
[1] HARTIGAN J A, WONG M A. A K-means clustering algorithm[J]. Journal of the royal statistical society:series C (applied statistics), 1979, 28(1): 100–108. [2] BÄCKLUND H, HEDBLOM A, NEIJMAN N. A density-based spatial clustering of application with noise[J]. Data mining TNM033, 2011, 33: 11–30. [3] KARYPIS G, HAN E H, KUMAR V. Chameleon: hierarchical clustering using dynamic modeling[J]. Computer, 1999, 32(8): 68–75. doi: 10.1109/2.781637 [4] NG A Y, JORDAN M I, WEISS Y. On spectral clustering: analysis and an algorithm[C]//Advances in neural information processing systems. Vancouver: MIT Press, 2002: 849−856. [5] WANG Liang, BEZDEK J C, LECKIE C, et al. Selective sampling for approximate clustering of very large data sets[J]. International journal of intelligent systems, 2008, 23(3): 313–331. doi: 10.1002/int.20268 [6] CHEN Wenyen, SONG Yangqiu, BAI Hongjie, et al. Parallel spectral clustering in distributed systems[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(3): 568–586. doi: 10.1109/TPAMI.2010.88 [7] CAI Deng, CHEN Xinlei. Large scale spectral clustering via landmark-based sparse representation[J]. IEEE transactions on cybernetics, 2015, 45(8): 1669–1680. doi: 10.1109/TCYB.2014.2358564 [8] WU Lingfei, CHEN Pinyu, YEN I E H, et al. Scalable spectral clustering using random binning features[C]//KDD '18: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2018: 2506−2515. [9] YANG Libo, LIU Xuemei, NIE Feiping, et al. Large-scale spectral clustering based on representative points[J]. Mathematical problems in engineering, 2019, 2019: 5864020. [10] 叶茂, 刘文芬. 基于快速地标采样的大规模谱聚类算法[J]. 电子与信息学报, 2017, 39(02): 278–284. YE Mao, LIU Wenfen. A large-scale spectral clustering algorithm based on fast landmark sampling[J]. Journal of electronics and information, 2017, 39(02): 278–284. [11] HUANG Dong, WANG Changdong, WU Jiansheng, et al. Ultra-scalable spectral clustering and ensemble clustering[J]. IEEE transactions on knowledge and data engineering, 2020, 32(6): 1212–1226. doi: 10.1109/TKDE.2019.2903410 [12] ZHU Qingsheng, FENG Ji, HUANG Jinlong. Natural neighbor: a self-adaptive neighborhood method without parameter K[J]. Pattern recognition letters, 2016, 80: 30–36. doi: 10.1016/j.patrec.2016.05.007 [13] 冯骥. 自然邻居思想概念及其在数据挖掘领域的应用[D]. 重庆: 重庆大学, 2016: 25−28. FENG Ji. Natural neighbor: the concepts and applications in data mining[D]. Chongqing: Chongqing University, 2016: 25−28. [14] CHENG Dongdong, ZHU Qingsheng, HUANG Jinlong, et al. Natural neighbor-based clustering algorithm with local representatives[J]. Knowledge-based systems, 2017, 123: 238–253. doi: 10.1016/j.knosys.2017.02.027 [15] 朱庆生, 陈治, 张程. 基于自然邻居流形排序图像检索技术研究[J]. 计算机应用研究, 2016, 33(04): 1265–1268+1276. doi: 10.3969/j.issn.1001-3695.2016.04.068 ZHU Qingsheng, CHEN Zhi, ZHANG Cheng. Research on image retrieval techniques based on natural neighbor stream shape sorting[J]. Computer application research, 2016, 33(04): 1265–1268+1276. doi: 10.3969/j.issn.1001-3695.2016.04.068 [16] 张忠林, 赵昱, 闫光辉. 自然邻居密度极值聚类算法[J]. 计算机工程与应用, 2021, 57(23): 200–210. doi: 10.3778/j.issn.1002-8331.2107-0529 ZHANG Zhonglin, ZHAO Yu, YAN Guanghui. Natural neighborhood density extreme value clustering algorithm[J]. Computer engineering and applications, 2021, 57(23): 200–210. doi: 10.3778/j.issn.1002-8331.2107-0529 [17] 冯骥, 冉瑞生, 魏延. 基于自然邻居邻域图的无参数离群检测算法[J]. 智能系统学报, 2019, 14(5): 998–1006. doi: 10.11992/tis.201809032 FENG Ji, RAN Ruisheng, WEI Yan. A parameter-free outlier detection algorithm based on natural neighborhood graph[J]. CAAI transactions on intelligent systems, 2019, 14(5): 998–1006. doi: 10.11992/tis.201809032 [18] YUAN Mengshi, ZHU Qingsheng. Spectral clustering algorithm based on fast search of natural neighbors[J]. IEEE access, 2020, 8: 67277–67288. doi: 10.1109/ACCESS.2020.2985425 [19] ZHANG Yuru, DING Shifei, WANG Yanru, et al. Chameleon algorithm based on improved natural neighbor graph generating sub-clusters[J]. Applied intelligence, 2021, 51(11): 8399–8415. doi: 10.1007/s10489-021-02389-0 [20] YU Shi. Multiclass spectral clustering[C]//Proceedings Ninth IEEE International Conference on Computer Vision. Nice: IEEE, 2003: 313−319. [21] LI Zhenguo, WU Xiaoming, CHANG S F. Segmentation using superpixels: a bipartite graph partitioning approach[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2012: 789−796. [22] COUR T, BENEZIT F, SHI J. Spectral segmentation with multiscale graph decomposition[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005: 1124−1131. [23] FERN X Z, BRODLEY C E. Solving cluster ensemble problems by bipartite graph partitioning[C]//ICML’04: Proceedings of the Twenty-first International Conference on Machine learning. New York: ACM, 2004: 36. [24] GOLUB G H, VAN LOAN C F. Matrix computations[M]. Baltimore: Johns Hopkins University Press, 2012. [25] STREHL A, GHOSH J. Cluster ensembles: a knowledge reuse framework for combining multiple partitions[J]. J mach learn res, 2003, 3: 583–617.































































 下载:
下载: