Audio detection of transformer partial discharge fault based on SPNCC and one-dimensional dual-channel CNN-LSTM
-
摘要: 变压器运行时产生的声音信号包含了丰富的状态信息，可作为变压器故障诊断的重要依据。为提高变压器故障音频诊断效果，首先将变压器运行时现场采集的声音信号分为工作环境噪声信号、正常工作音频信号以及局部放电故障音频信号；然后通过卷积神经网络分类、小波包分解以及巴特沃斯带通滤波的方法去除原始音频信号中的非稳态环境噪声和短时稳态环境噪声信号；并建立了基于简化版幂律归一化倒谱系数特征的一维双通道卷积神经网络−长短时记忆网络的变压器局部放电故障识别模型。通过现场采集某500 kV变电站不同自然环境下的变压器运行声音信号与故障仿真实验，验证了提出的局部放电故障识别模型的可行性，相较于传统的音频故障诊断方法，提出的模型具有更快的收敛速度，更好的故障识别准确率与故障分类准确率。
-
关键词:
- 变压器局部放电 /
- 变压器故障检测 /
- 智能电网 /
- 小波包分解 /
- 简化版幂律归一化倒谱系数 /
- Gammatone滤波器 /
- 卷积神经网络 /
- 长短时记忆网络
Abstract: The sound signals generated during transformer operation contain abundant state information, which can be used as an important basis for transformer fault diagnosis. In order to improve the audio diagnosis effect of transformer fault, firstly, the sound signals collected in the field during transformer operation are divided into working environment noise signals, normal working audio signals and partial discharge fault audio signals. Then, the non-stationary environmental noise and short-term stationary environmental noise signals in the original audio signals are removed by the methods of convolutional neural network classification, wavelet packet decomposition and Butterworth band-pass filtering. And a one-dimensional two-channel convolutional neural network-long short-term memory (CNN-LSTM) model for transformer partial discharge fault identification is established based on the simple power normalized cepstral coefficient (SPNCC) feature. By collecting sound signals from a 500 kV substation transformer operation under different natural environments and the fault simulation experiments, the feasibility of the proposed partial discharge fault recognition model is verified. Compared with traditional audio fault diagnosis methods, the proposed model has a faster convergence speed, better fault identification accuracy and fault classification accuracy. -
电力变压器是电力系统中十分关键的组成部分，确保电力变压器的正常工作并提高其稳定性，是电网部门极为关切的问题[1]。在此背景下，开展变压器的状态监控与故障诊断研究对确保变压器以及电力系统的安全可靠运行具有深远意义。
变压器局部放电故障诊断中大多使用特高频法(ultra high frequency，UHF)、超声波法、油溶气体分析法(dissolves gas analysis，DGA)和暂态对地电压法（transient earth voltage，TEV）。在UHF诊断方面，文献[2]完成了套管上部局部放电和升高座内部放电的区分，实现了变压器套管局部放电的不停电检测；在超声波诊断方面，文献[3]将局放原始超声信号进行预处理，得到具有代表性的局放特征量，再利用卷积神经网络训练，从而实现了不同类型局部放电的判断；在DGA诊断方面，文献[4]利用Lyapunov指数与零的关系确定油色谱监测装置的有效性，并利用最优时滞判断异常发生的时间点；在TEV诊断方面，文献[5]通过在设备表面安装传感器来实现暂态电压检测，从而检测出电气设备表面局部放电和故障缺陷。
以上几种故障诊断方法都存有缺陷，UHF法局放检测技术的检测频率范围为300~3000 MHz，在如此宽的频带范围内可能存在手机信号、雷达信号、电机碳刷火花干扰等环境电磁干扰信号，从而影响到检测的准确性[6]。超声波法主要用于局部放电的定位，同时由于变压器内部结构复杂，以及超声波的衰减和折反射，使得有些绝缘内部的局部放电可能无法被检测到，导致检测结果的精确度不高[7]。基于DGA的诊断方法诊断周期长，并有特征气体比值界限过于绝对、编码尚未完备、故障特性判别不强等问题，且对于突发故障难以应对，故影响了故障诊断效果[8-9]。TEV法与暂态对地电压传感器参数密切相关，如果不采取补偿措施，即便是相同的放电强度，在不同的参数下也可能会产生差异较大的检测结果，所以单一使用TEV方法进行检测存在一定的局限性，此外TEV法不适用于金属外壳外全封闭的电力设备[10]。
音频信号覆盖范围广，采集时不需要直接接触变压器箱体，属于非接触式测量，采集信号时不产生电磁信号，不会干扰设备的正常运行，经降噪处理后数据分析空间较大，因此逐渐成为了变压器状态监测分析研究的热点。文献[11]利用特征参数GFCC和WA-RF模型实现了变压器机械故障的诊断；文献[12]使用改进的50 Hz倍频倒谱系数和GRU模型实现了变压器直流偏磁声纹识别；文献[13]使用完整人耳集中参数模型提取的听觉特征向量SMVBMDR结合改进的SVM实现了变压器故障诊断。
本文采取音频信号诊断技术实现变压器的故障诊断。首先按噪声特征对原始采集音频中的背景噪声进行分类，然后采用卷积神经网络、小波包分解后再过滤这两种方法实现降噪处理；其次，考虑人耳模型并提取特征表现性更好的特征参数SPNCC(simple power normalized cepstral coefficient)；再次，设计了一维双通道CNN-LSTM(convolutional neural networks-long short-term memory)卷积模型用于完成变压器正常和故障状态的判别；最后将提取到的SPNCC用于模型的训练与测试，检验了本文方法的有效性。
1. 变压器音频信号基本特征
现场采集到的音频信号中可能包括以下3方面成分：
1）变压器正常工作的音频信号
额定工作时，变压器磁密区间通常为1.5~1.8 T，此时的绕组振动相对较小，可以忽略[14]。此外，近年来的铁芯叠积技术有所进度，极大程度地减小了铁芯叠片间的振动[15]，并且采用玻璃丝粘带捆绑技术极大减小硅钢片间的电磁力[16]。因此，铁芯振动是变压器振动发声的关键。
通入交流电后，铁芯内磁场交变引起的磁场力作用在铁芯的硅钢片上，导致磁致伸缩效应产生振动[17]。磁致伸缩力
${F_c}$ 为$$ {F_{\text{c}}} = \frac{1}{2}\nabla \left({H^2}\tau \frac{{\partial \mu }}{{\partial \tau }}\right) = {F_{{\text{c}}\max }}\sin 2\omega t $$ (1) 式中：
${F_{{\text{cmax}}}}$ 为磁致伸缩力幅值；$\omega $ 为交变电磁场的频率；$H$ 为磁场强度；$\mu $ 为铁磁介质磁导率；$\tau $ 为介质的体积密度。电磁场交变周期的1/2为磁致伸缩周期，故铁芯振动的频率为电源基频的2倍。我国的交流电频率是50 Hz，因此铁芯产生100 Hz的振动，发会出连续的、均匀的“嗡嗡”的电磁声，属于工频稳态噪声。
铁芯非线性特点的磁致伸缩使铁芯内外框磁通路不同，导致铁芯内的磁通不是标准的正弦波，存在不同程度的偏离[18]。因此铁芯振动时含有多种基频倍频的高次谐波，如：200、300、400 Hz等。
2）变压器工作环境的背景噪声信号
变压器通常工作在野外环境，所以采集到的变压器音频信号也会包含自然界的背景噪声信号，如：鸟叫声、人说话声、风声、雨声等。这一问题既会给变压器音频的处理和故障诊断带来困扰，又是实际中无法避免的。本文实地采集的变压器运行声音中共包括4类干扰噪声：鸟叫声、人说话声、风声、雨声。经过分析，本文按干扰噪声的特征对其进行了归类，如表1所示
表 1 干扰噪声分类Table 1 Interference noise classification干扰噪声 噪声类型 干扰噪声
时长/s干扰噪声
频率范围/Hz鸟叫声 非工频非稳态噪声 0.7~1.5 2000~8000 人说话声 非工频非稳态噪声 1~5 300~3000 雨声 非工频短时稳态噪声 30以上 50~5000 风声 非工频短时稳态噪声 30以上 20~3000 鸟叫声和人说话声会因个体特征产生差异，这两种声音的持续时间较短，且短时能量变化较快，属于非工频非稳态噪声。雨声指雨滴坠落时，与大地、变压器等产生碰撞所形成的敲击声。由于撞击材质不同，引起的振动频率也不同。风声中也夹杂着风与电线杆、变压器等摩擦撞击的噪声，这两种声音持续时间较长，且在短时间内能量变化并不显著，属于非工频短时稳态噪声。
3）工频下变压器局部放电故障音频信号
局部放电发生在变压器内部电0极间但未击穿电极，多为油与绝缘纸板中的油隙、油中固体绝缘的表面等位置因场强的集中而引起放电。局部放电多出现在工频信号的波峰处，持续时间较短，会发出“噼噼啪啪”的声音，属于工频非稳态噪声。
2. 变压器音频信号获取与预处理
笔者多次前往河北省某500 kV变电站进行实地音频数据采集工作。在采集到的变压器运行音频信号中，包含了上述变压器正常工作声音和自然环境声音信号。为优化采集到的音频数据，在进行特征参数提取或判别训练之前，首先要对变压器的正常工作音频信号实现消噪处理，针对干扰噪声类别的差异使用不同的消噪处理方式。
2.1 变压器音频信号消噪
2.1.1 非工频非稳态噪声消噪处理
对于非工频非稳态噪声干扰使用一维卷积神经网络对采集到的音频数据进行分类，将存在鸟叫声、人说话声的音频片段从中分离出来，剩下的不存在鸟叫声和人说话声的片段用于后续模型的学习。
鸟叫声数据集使用的是百鸟数据和北京智源人工智能研究院联合推出的：birdsdata。将工频下变压器正常运行的声音中混入鸟叫声，作为第1类训练数据，把变压器正常运行的声音和变压器发声局部放电时的声音作为第2类训练数据，使用一维卷积神经网络对其进行训练。人说话声数据集使用的是清华大学语音与语言技术中心的开放式中文语音数据库THCHS30，与鸟叫声类似，将工频下变压器正常运行的声音中混入人说话声，作为第1类训练数据，把变压器正常运行的声音和变压器发声局部放电时的声音作为第2类训练数据。
训练完成后使用训练模型将采集到数据片段中含有鸟叫声和人说话声的片段剔除。原始采集的数据片段共18457条，将含有鸟叫声和人说话声的数据片段剔除后剩下的15980条数据用于后续实验。
2.1.2 非工频短时稳态噪声消噪处理
鉴于变压器声音频率和雨声、风声等非工频短时稳态噪声频率差距比较大，考虑从频率入手，先进行小波包分解，并采用带通滤波器进行过滤，滤波后进行小波重构，以达到消噪目的。
本文对选取db4小波基函数对采集到的含有雨声、风声的数据片段进行小波包分解，分解层数为2层，公式为
$$ \varOmega _0^0 = \varOmega _0^{ - 1} \oplus \varOmega _1^{ - 1} = \varOmega _0^{ - 2} \oplus \varOmega _1^{ - 2} \oplus \varOmega _2^{ - 2} \oplus \varOmega _3^{ - 2} $$ (2) 式中：
$\varOmega _0^0$ 为原信号空间；$\varOmega _{2n + 1}^{j - 1}$ 和$\varOmega _{2n}^{j - 1}$ 为$\varOmega _0^0$ 张成的子空间；$ \oplus $ 为空间直和。根据变压器声音和雨声、风声频率的差异设计100~400 Hz的巴特沃斯带通滤波器。选取巴特沃斯滤波器是为了保证频率响应范围内频率没有波动，实现最大限度平坦。为保证过滤效果，本文将过滤器设置为8阶，带通衰减不超过3 dB，带阻衰减不低于20 dB。巴特沃斯滤波器的幅度平方函数为
$$ {\left| {H(\omega )} \right|^2} = \frac{1}{{1 + {C^{2n}}{{\left(\dfrac{{{\omega _P}}}{{{\omega _c}}}\right)}^{2n}}}} $$ (3) 式中：
${\left| {H(\omega )} \right|^2}$ 为幅值平方响应；$n$ 为滤波器阶数；${\omega _P}$ 为通带截止频率；${\omega _c}$ 为3dB截止频率；$C$ 为常参数。本文对采集的数据使用小波包2层分解，分解后产生的4段音频样本再使用上面设计的8阶巴特沃斯带通滤波器过滤。此处实验采用的是长度为30 s的片段，将这4部分都过滤完以后进行小波包重构，重构之后的结果相较于之前有了较大的提升，相关系数也提高了，如表2所示。
表 2 雨声、风声分离前后相关系数Table 2 Correlation coefficient of rain sound and wind sound before and after separation干扰噪声 变量X 变量Y 相关系数 雨声 变压器正常运行声音 未处理的音频 0.57028571062700707 变压器正常运行声音 处理后的音频 0.98220923850289565 风声 变压器正常运行声音 未处理的音频 0.82028921062726198 变压器正常运行声音 处理后的音频 0.97420261820374065 相关系数定义为
$$ r = \frac{{\displaystyle\sum {(X - \bar X)} (Y - \bar Y)}}{{\sqrt {\displaystyle\sum {{{(X - \bar X)}^2}\displaystyle\sum {{{(Y - \bar Y)}^2}} } } }} $$ (4) 式中：
$r$ 为相关系数；$X$ 为变压器正常运行的一段音频；$Y$ 为未处理的原始音频或经过消噪处理后的音频；$\bar X$ 、$\bar Y $ 分别为对应音频的均值。以上两部分实验分别说明了采用一维卷积神经网络分类和小波包分解后再过滤的方式可以较好的对采集的变压器音频实现降噪处理，处理后与正常运行声音的相关系数有了明显提高，其中含有雨声的变压器音频的相关系数相较于降噪前提升了约0.41，含有风声的变压器音频的相关系数相较于降噪前提升了约0.15。
2.2 变压器音频信号特征提取
将人耳听觉模型的特征参数融入变压器音频信号分析中已有先例[19-20]，目前，mel频率倒谱系数（mel-frequency cepstral coefficients，MFCC）的应用较为普遍，但MFCC中使用的三角滤波器在相邻频带存在能量泄露[21-22]，导致对人耳基底膜分频特性的仿真效果较差。
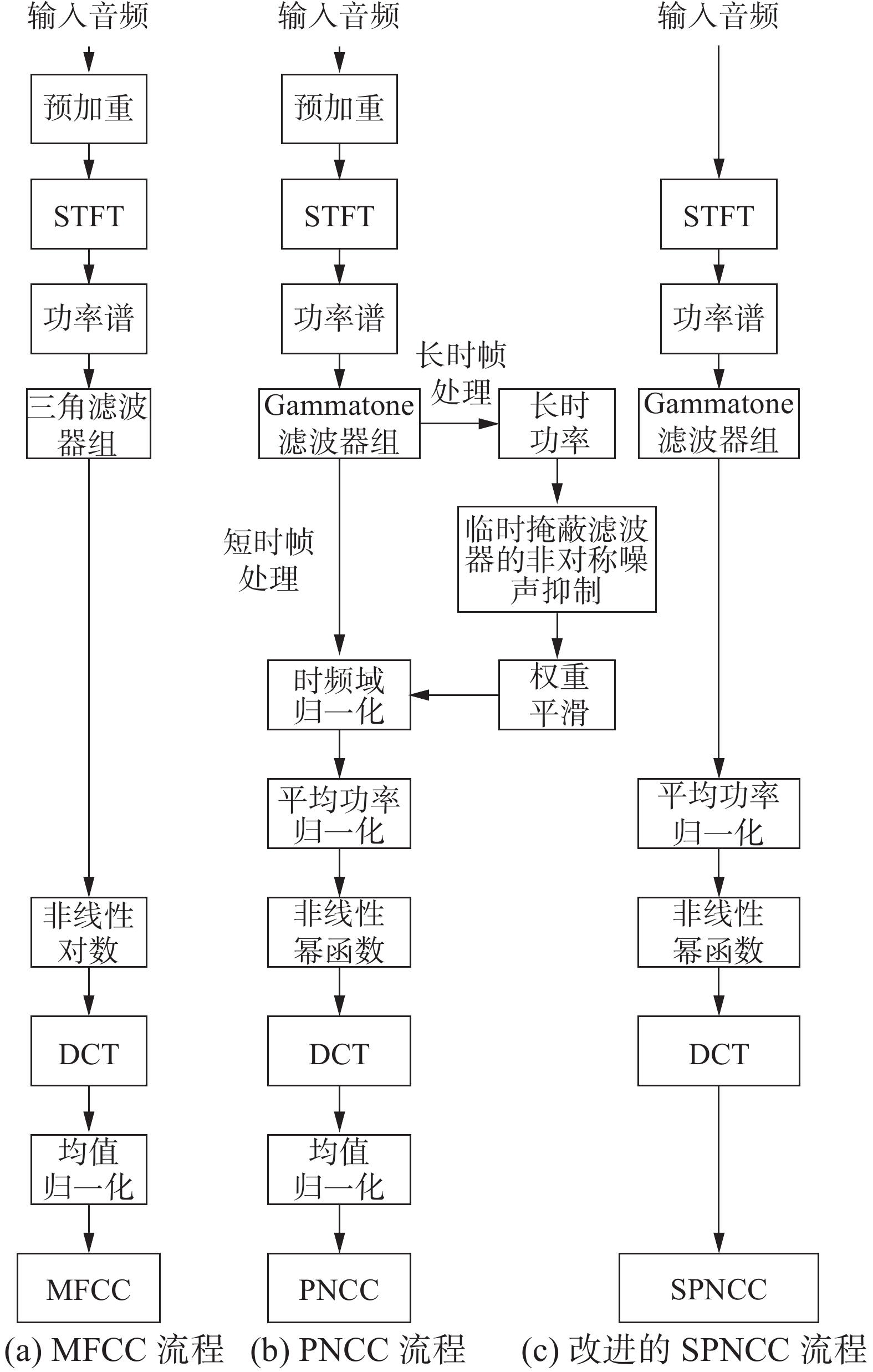
因此本文借鉴MFCC的思路，采用简化版幂律归一化倒谱系数（simple power normalized cepstral coefficient，SPNCC）作为特征参数提取变压器音频信息。改进后的特征参数与之前的特征参数对比如图1所示。
图 1 MFCC、PNCC和改进的SPNCC对比图Fig. 1 Comparison diagram of MFCC，PNCC and improved SPNCC
下载:
全尺寸图片
相较于MFCC，使用SPNCC处理变压器音频信号的优点在于：
1）使用Gammatone滤波器代替三角波滤波器能更好地表现基底膜的分频特性，减少能量泄漏。
2）不同于MFCC所采用的非线性对数，SPNCC先进行功率归一化，再使用非线性幂函数，更符合人耳听觉神经的压缩感知。
SPNCC是Kim等[23]在提出PNCC时提出的简化版，与PNCC相比省略了长时帧处理（medium-time processing），不选用PNCC的原因是考虑到长时帧处理中的临时掩蔽滤波器的非对称噪声抑制和权重平滑不利于变压器的放电信号特征表示，故选取简化版的PNCC-SPNCC作为特征参数。同时对SPNCC进行改进：
1）音频预处理时不采用预加重。因为预加重会抑制声音的低频部分，加重声音高频部分。在语音信号提取中有必要，但是对于变压器声音来说，其大部分频率处于低频，因此不需要预加重。
2）原SPNCC使用的Gammatone滤波器频率为200~8000 Hz，本实验根据变压器音频特征将Gammatone滤波器频率改进为50~8000 Hz。
3）不采用均值归一化。因为均值归一化后的数据不利于放电特征的体现。
3. 改进的一维双通道CNN-LSTM故障诊断模型
CNN通常用来处理二维平面数据[24]。通过采用不同的卷积核与二维数据进行卷积运算达到局部特征提取的目的。本文研究的音频数据属于一维数据，故采用与2D-CNN原理相似的1D-CNN进行卷积运算。
据2.2节说明，每1 s变压器音频信号能生成长度为120的一维向量和长度为40的一维向量，分别表示变压器音频的细节特征和整体特征，为了提高故障识别率需用同时考虑这两部分特征。传统的卷积神经网络为了实现多类型特征提取，通常采用加深网络层数的方法实现，但这会使参数数量急剧增加，导致训练困难，模型收敛速度慢。为此，本文设计了双通道输入结构，同时输入这两部分进行特征提取、共同训练。每个独立的通道只计算一种特征，因此不需要很深的网络层数，提高了模型训练速度同时彼此不会干扰。
由于变压器放电时音频信号会随放电时间发生变化，因此具有时间序列特性，为了提取此特点，在模型中加入LSTM层。LSTM是RNN（recurrent neural network）的改进[25]，它的输出状态与之前的运算结果相关，因此在处理时间序列数据方面具备独特的优势[26]。
本文设计的CNN-LSTM模型层数寻优的过程如表3所示。由于变压器在正常工作状态下的音频长时间保持工频不变，且在出现局部放电故障时时序频率会发生明显变化，故在两个输入通道都设置1层LSTM即可很好的体现局部放电特征。因此该模型层数寻优的主要任务是确定CNN的层数以及全连接层数。
表 3 CNN-LSTM模型层数寻优Table 3 Layer number optimization of CNN-LSTM modelCNN层数 双通道输出连接 故障识别
准确率/%通道1 通道2 CNN层数 Dense层数 1 1 1 2 88.83 2 1 1 2 95.14 2 2 1 2 91.32 3 1 1 2 93.89 3 2 1 2 90.74 2 1 2 2 94.60 2 1 1 3 96.32 2 1 1 4 96.30 首先将2个输入通道的CNN层数都设置为1，在保证双通道输出连接后的后续层数不变的情况下逐步增加输入通道的层数。通道1输入长度为120的一维向量，通道2输入长度为40的一维向量。在通道1 CNN层数为2，通道2 CNN层数为1时的故障识别准确率最高，继续增加模型层数反而出现了识别准确率下降的趋势，推断是由于模型设计过于复杂而导致了过拟合现象。因此选定通道1 CNN层数为2，通道2 CNN层数为1。在确定了输入通道的层数后，继续确定连接后的层数，在反复实验中发现：设置连接后CNN的层数为1，全连接层数为3时能获得最高故障识别准确率。
本文设计的变压器故障音频诊断模型如图2。
图 2 一维双通道CNN-LSTM结构图Fig. 2 One-dimensional two-channel CNN-LSTM structure diagram下载:
全尺寸图片
C1和C2的卷积核大小分别为3和5，卷积核尺寸较小，用于算每帧音频的细节特征，卷积核个数分别为256和128。C3的卷积核大小为8，尺寸较大，用于计算每秒音频的整体特征，卷积核个数为128，步长均为1，使用ReLU作为激活函数。P1、P2、P3的池化大小分别为3、2、3，池化层后设置Dropout层，防止过拟合，丢弃率为0.2。2个LSTM大小都为128，激活函数为tanh，将计算得到的2个结果连接输出，得到长度为256的一维向量。再使用C4卷积，卷积核大小为4，数量为128，步长为1，激活函数为ReLU，P4的池化大小为2。将池化后的结果使用Flatten层展成一维向量，使用3个大小为64、16、2的全连接层计算，D1、D2的激活函数为ReLU，D3的激活函数为Sigmoid，最后输出诊断结果。
整个网络可训练的参数共1455602个，相较于6层卷积3层全连接的网络参数数量大大减少，训练速度明显提高。整个模型使用binary_crossentropy作为损失函数，Adadelta作为模型优化器，F2-Score作为评价函数。选取F2-Score作为评价函数的原因是：本文研究的是故障检测，因此在对实验结果评价时，召回率应占据更高权重，故本文选取F2-Score作为实验的评价函数。F2-Score的公式为
$$ {F_2} = (1 + {2^2}) \times \frac{{{P_{{\rm{precision}}}} \times {R_{{\rm{recall}}}}}}{{({2^2} \times {P_{{\rm{precision}}}}) + {R_{{\rm{recall}}}}}} $$ (5) 4. 实验结果分析
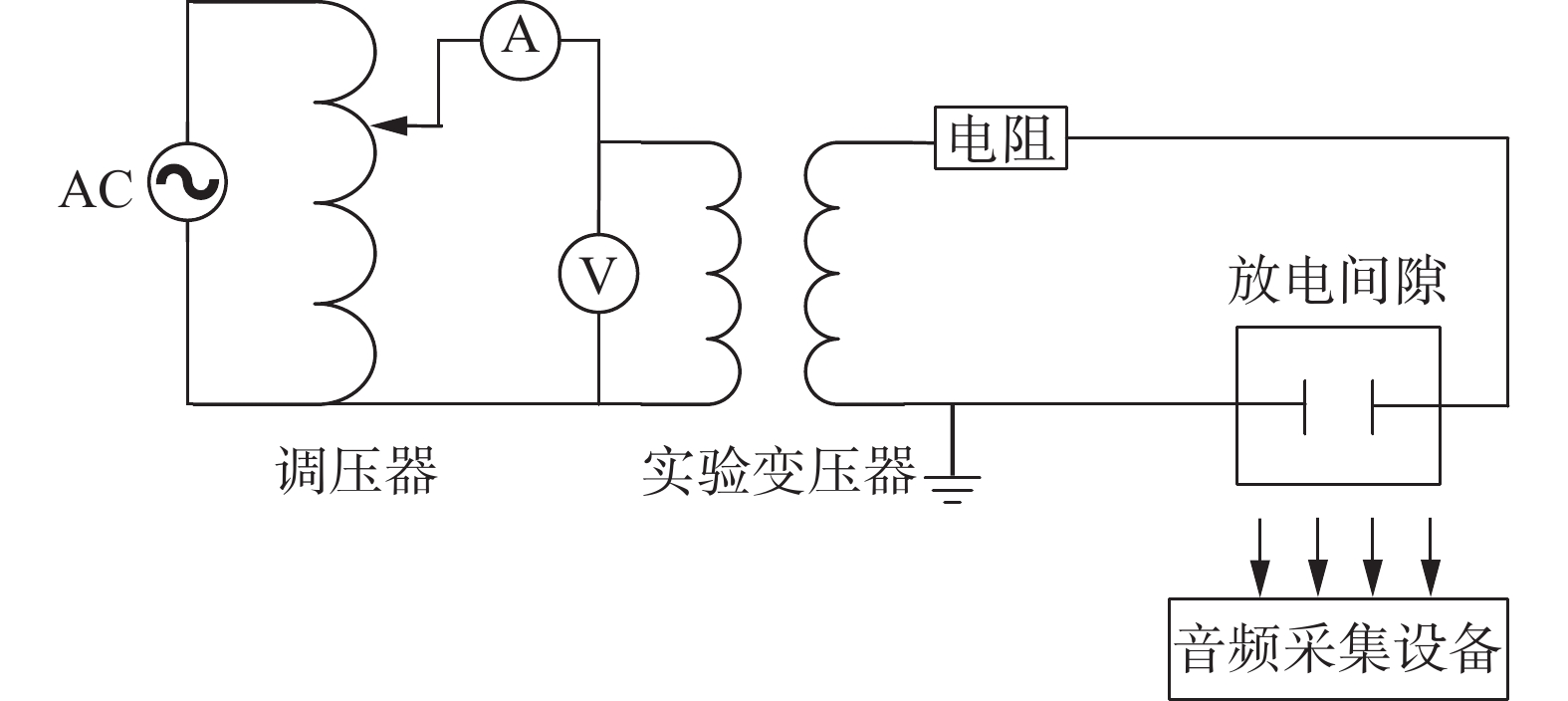
本文采用Intel Core i7-9750H CPU:2.60GHz，内存16 GB，GPU为NVIDIA GTX1650，4 GB显存，操作系统为64位Windows 10系统，使用Keras深度学习框架建模并训练。训练数据共15980条音频，每条音频时长1 s，其中正常音频8196条，故障音频7784条。正常音频数据来源于河北省某变电站正常运行的变压器，并进行了降噪处理，第2节已说明，此处不再赘述。故障音频数据通过变压器局部放电实验采集，实验电路图如图3所示。
图 3 故障实验电路示意Fig. 3 Schematic diagram of fault test circuit下载:
全尺寸图片
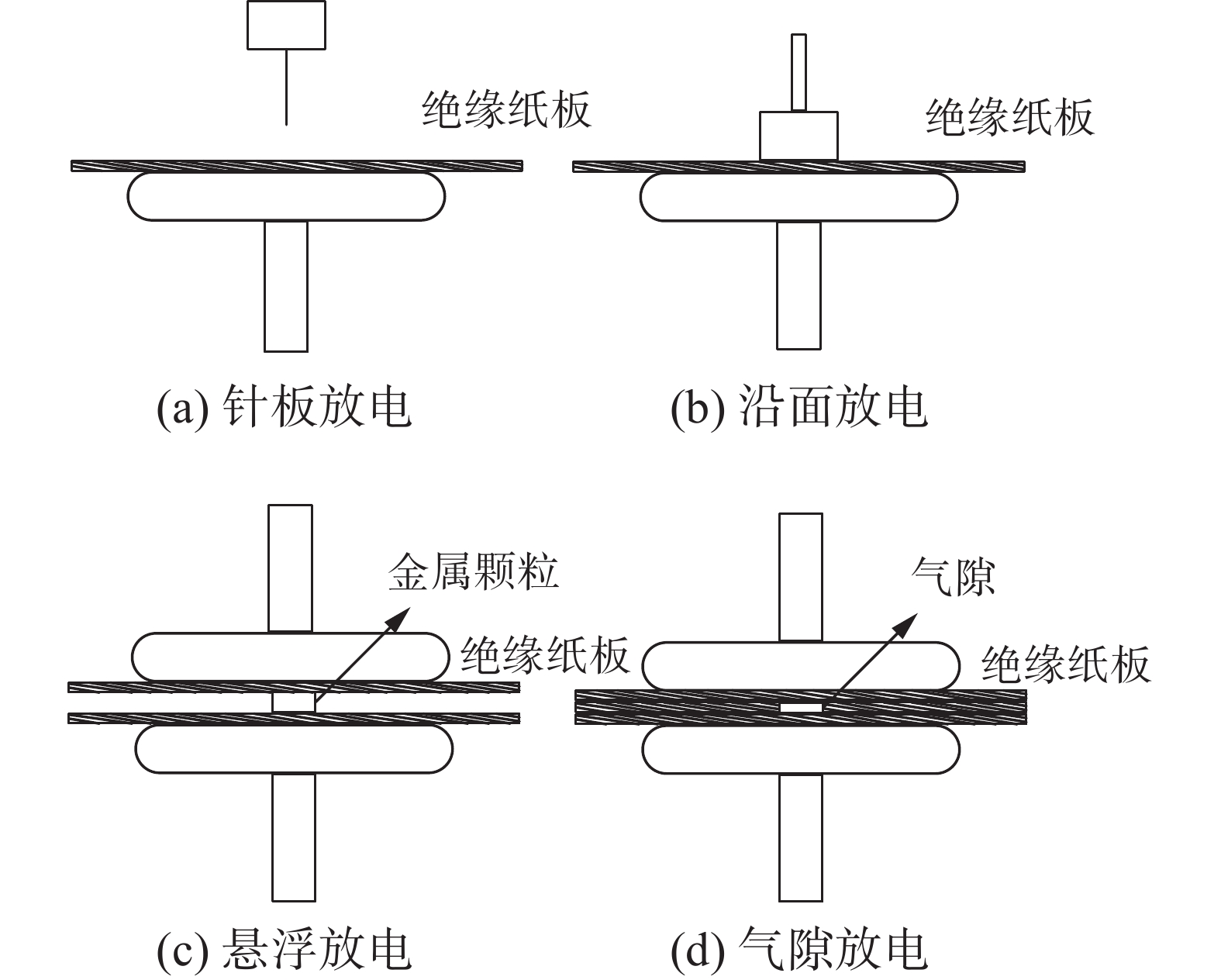
实验在高压大厅屏蔽室进行，根据变压器局部放电的特点设计了针−板放电、沿面放电、悬浮放电、气隙放电这4种放电模型，如图4所示。
图 4 放电模型示意Fig. 4 Schematic diagram of discharge model下载:
全尺寸图片
为保证实验电路正常运行，首先进行耐压与局部放电检测，保证放电量正常。试验过程中采用逐级升压法，每次的升压过程保持一定的恒压时间，分别采集出现的局部放电信号。其中针−板放电、沿面放电、悬浮放电、气隙放电分别在14、25、28、20 kV时开始出现局部放电，继续升高电压，在出现明显的放电声音时保持电压稳定，采集局部放电音频。
本实验基于可听声频率范围20~20000 Hz进行研究，为保证采集到的所有音频信号数据样本具有一致性、采样率固定，每次都使用相同的录音设备进行音频采集。为保证录音的可靠性、灵敏性、抗干扰性这3要素，选取Newsmy公司生产的H12录音笔进行数据采集工作，采样频率为44100 Hz，音频编码格式为16 bit。实验采用GB/T 1094.10-2003中规定的变压器噪声测点位置进行音频信号采集，声传感器布置在离变压器1 m的轮廓线上，并同时设置了4个声传感器同时采集变压器声音。将全部数据按照6∶2∶2的比例划分训练集、验证集、测试集，9588条数据用于训练，3196条数据用于验证，3196条数据用于测试，将正常音频标记为0，故障音频标记为1，其中针−板放电、沿面放电、悬浮放电、气隙放电音频都属于故障音频。
4.1 不同特征参数对故障识别率的影响
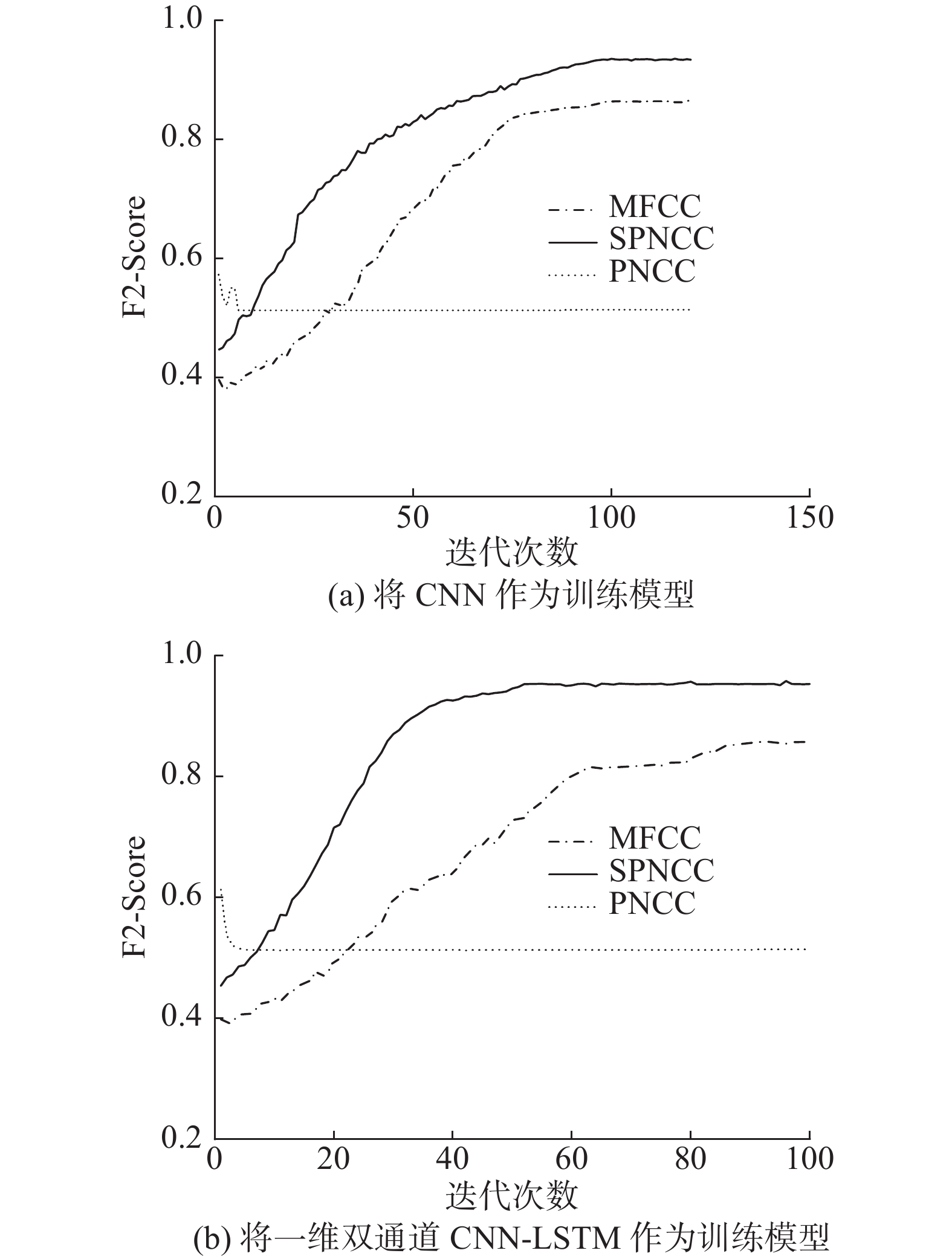
本文选取MFCC、PNCC和改进的SPNCC这3类音频分析中常见的特征参数对变压器放电故障进行识别训练，训练模型采用原始CNN模型和本文第3节介绍过的改进训练模型，训练结果如图5所示。
图 5 不同特征参数的训练结果Fig. 5 Training results of different characteristic parameters下载:
全尺寸图片
图5表明，本文选取的SPNCC相较于MFCC具有更好的故障识别率和收敛速度。PNCC由于使用了长时帧处理将放电声音当做了背景噪声进行平滑，反而不能更好地体现变压器放电特征，但选取SPNCC可以很好的解决这个问题。此外，SPNCC中的Gammatone滤波器在低频部分带宽较窄，而高频部分较宽，且滤波谱峰较MFCC更平缓，因此更能突出局部放电产生的能量，缓解了能量泄露问题，提高了故障识别准确率。收敛后MFCC的F2-Score稳定在87.4%，SPNCC的F2-Score稳定在95.7%。并且，不管是选用CNN作为训练模型还是选用本文设计的一维双通道CNN-LSTM作为训练模型，SPNCC作为特征参数的局部放电故障识别率都高于MFCC，只是在训练速度上有所差异。由此可见SPNCC能较好的用于变压器局部放电故障的音频诊断。
4.2 不同识别模型的故障识别率比较
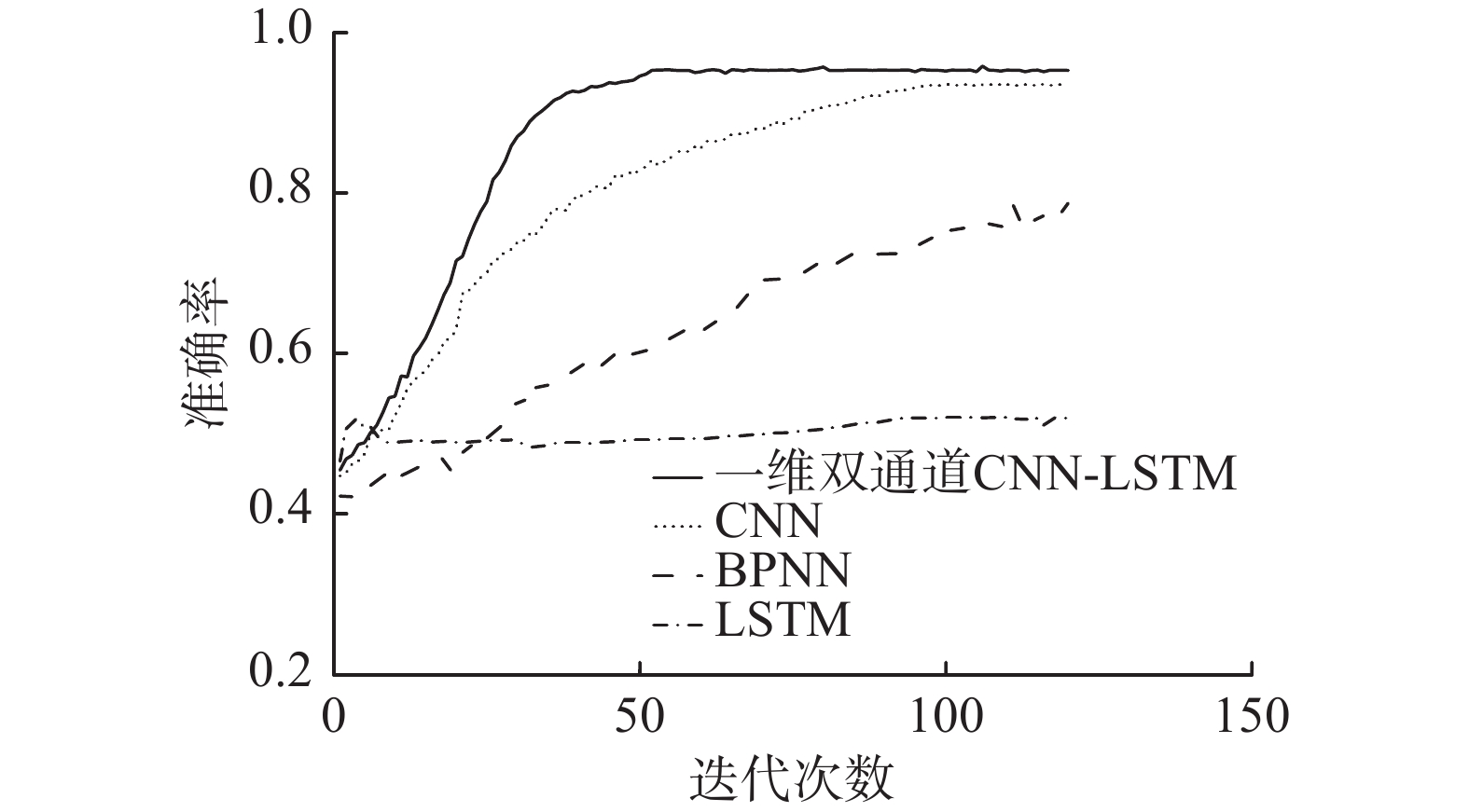
为比较不同分类器模型的性能，本文采用SPNCC作为特征参数，分别使用BPNN（back propagation neural network）、CNN、LSTM以及本文改进的一维双通道CNN-LSTM模型作为分类器进行实验。为保证实验横向对比，BPNN对比模型设置6层全连接层，神经元个数依次为：256、128、128、64、16、2；CNN对比模型设置3个卷积层、3个池化层、3个全连接层，卷积核大小、数量和前面介绍的CNN-LSTM一样，LSTM对比模型设置2层LSTM和3层全连接层。所有模型激活函数除输出层采用Sigmoid外，其余均采用ReLU。Batchsize统一为32，学习率统一为0.01，训练结果如图6所示。
图 6 不同识别模型的训练结果Fig. 6 Training results of different recognition models下载:
全尺寸图片
从图6可以看出使用BPNN作为分类器时算法的收敛速度太慢，即使迭代100次，模型识别率也只能有76%。传统的卷积神经网络相较于BPNN收敛速度有了提高，但依旧很慢，模型收敛的训练次数约为100次。在只使用LSTM作为分类器的情况下训练结果较差，在迭代40次时准确率基本上稳定在81%，后续继续训练的过程中准确率也没有较大幅度提高。
本文改进的一维双通道CNN-LSTM模型相比于以上3种分类器能够达到快速收敛的目的，且收敛后的故障识别率稳定在95.7%以上，较于单纯使用原有的CNN或LSTM来说能得到大幅提升。各模型训练花费时间如表4。
表 4 训练花费时间Table 4 Training takes time训练模型 平均单步
迭代时间/s平均收敛至最高
准确率迭代次数收敛至最高准
确率总时间/sCNN
LSTM4.2921 106 420.62 8.8260 120 1297.42 BPNN
一维双通道
CNN-LSTM2.5980 247 537.79 5.1262 51 174.29 本文设计的CNN-LSTM模型相较于传统的CNN模型融入了LSTM结构，故在单步迭代时间上有所延长，但是由于采用了双通道输入结构，对于两部分输入特征同时训练，提高了模型训练速度同时彼此不会干扰，所以平均单步迭代时间并没有增加很多。并且融入LSTM后对局部放电时序特征能更好的体现，因此达到收敛的总迭代次数更少，故改进的一维双通道CNN-LSTM模型收敛至最高准确率的所需时间较短，在整体收敛速度方面的更有优势。
4.3 不同故障模型分类的准确率比较
为比较不同故障模型分类的准确率，本文采用SPNCC作为特征参数，分别使用BPNN、CNN以及本文改进的一维双通道CNN-LSTM模型作为不同局部放电故障模型的分类器进行实验，将4类放电模型每类取240个音频样本作为训练集，80个音频样本为验证集，80个音频样本为测试集，分类结果如表5所示。
表 5 不同放电模型识别准确率Table 5 Identification accuracy of different discharge models% 训练模型 BPNN CNN 一维双通道CNN-LSTM 针-板放电
沿面放电66.3 85.2 94.7 52.4 79.4 98.4 悬浮放电
气隙放电73.2 89.1 100.0 64.2 88.5 98.4 总体准确率 64.025 85.550 97.875 从表5可以看出传统的BP神经网络对于不同放电模型的分类较差，这是因为传统浅层神经网络在训练维度较高的数据样本时，容易出现陷入局部极小值、过拟合等现象。CNN的分类准确率虽然高于传统BPNN但是明显低于本文改进的一维双通道CNN-LSTM模型。本文在原始CNN模型的基础上融入了LSTM层，捕捉了变压器在发生局部放电时的时序特征并加以训练。同时输入通道2对1 s内时序特征总体概括，更能展现变压器放电时能量的变化，因此在各种放电模型的分类识别中准确率较高，总体正确识别率能达到97%，识别效果最好。
综合分析上述实验结果可得，本文改进的训练模型，能较好地保留了原始的放电数据信息，在样本特征量维数较高时仍具有很好的识别效果。
5. 结束语
变压器正常运行发出的声音中包含了大量状态信息，据此，本文采用基于SPNCC和改进的一维双通道CNN-LSTM模型诊断变压器局部放电故障，得到以下结论：
1）使用卷积神经网络学习鸟叫声、人说话声与变压器声音混合时的特征，将采集的数据中包含鸟叫声、人说话声的片段识别出来从中剔除，只剩下不含非工频非稳态噪声的部分；使用小波包分解和巴特沃斯带通滤波器过滤的方法能将变压器音频中的非工频短时稳态噪声过滤掉，如风声、雨声。降噪后的变压器声音更能凸显变压器正常工作的状态，便于后续深度学习。
2）为解决MFCC三角滤波器能量泄漏的问题，本文采用改进的SPNCC作为特征参数，在保留其主要特征的同时，更准确的描述了变压器是否发生了局部放电故障。
3）在识别变压器故障时使用了改进的一维双通道CNN-LSTM模型，通过对比传统的CNN和LSTM，说明了改进的变压器局部放电故障识别模型具有更快收敛速度和更高准确率的优势，故障识别准确率能够到达95.7%以上。
4）使用改进的一维双通道CNN-LSTM模型还能有效实现不同局部放电故障模型的分类。但考虑到在变压器实际运行时也会出现多种局部放电的混合情况，这会加大局部放电分类的难度，本文将继续对相关内容研究。
变电站运行现场的其他电力设备产生的音频可能与变压器局放音频较为相似，减少此类音频对故障检测的干扰将是本文进一步研究的内容。
-
图 1 MFCC、PNCC和改进的SPNCC对比图
Fig. 1 Comparison diagram of MFCC，PNCC and improved SPNCC
下载:
全尺寸图片
图 2 一维双通道CNN-LSTM结构图
Fig. 2 One-dimensional two-channel CNN-LSTM structure diagram
下载:
全尺寸图片
图 3 故障实验电路示意
Fig. 3 Schematic diagram of fault test circuit
下载:
全尺寸图片
图 4 放电模型示意
Fig. 4 Schematic diagram of discharge model
下载:
全尺寸图片
图 5 不同特征参数的训练结果
Fig. 5 Training results of different characteristic parameters
下载:
全尺寸图片
图 6 不同识别模型的训练结果
Fig. 6 Training results of different recognition models
下载:
全尺寸图片
表 1 干扰噪声分类
Table 1 Interference noise classification
干扰噪声 噪声类型 干扰噪声
时长/s干扰噪声
频率范围/Hz鸟叫声 非工频非稳态噪声 0.7~1.5 2000~8000 人说话声 非工频非稳态噪声 1~5 300~3000 雨声 非工频短时稳态噪声 30以上 50~5000 风声 非工频短时稳态噪声 30以上 20~3000 表 2 雨声、风声分离前后相关系数
Table 2 Correlation coefficient of rain sound and wind sound before and after separation
干扰噪声 变量X 变量Y 相关系数 雨声 变压器正常运行声音 未处理的音频 0.57028571062700707 变压器正常运行声音 处理后的音频 0.98220923850289565 风声 变压器正常运行声音 未处理的音频 0.82028921062726198 变压器正常运行声音 处理后的音频 0.97420261820374065 表 3 CNN-LSTM模型层数寻优
Table 3 Layer number optimization of CNN-LSTM model
CNN层数 双通道输出连接 故障识别
准确率/%通道1 通道2 CNN层数 Dense层数 1 1 1 2 88.83 2 1 1 2 95.14 2 2 1 2 91.32 3 1 1 2 93.89 3 2 1 2 90.74 2 1 2 2 94.60 2 1 1 3 96.32 2 1 1 4 96.30 表 4 训练花费时间
Table 4 Training takes time
训练模型 平均单步
迭代时间/s平均收敛至最高
准确率迭代次数收敛至最高准
确率总时间/sCNN
LSTM4.2921 106 420.62 8.8260 120 1297.42 BPNN
一维双通道
CNN-LSTM2.5980 247 537.79 5.1262 51 174.29 表 5 不同放电模型识别准确率
Table 5 Identification accuracy of different discharge models
% 训练模型 BPNN CNN 一维双通道CNN-LSTM 针-板放电
沿面放电66.3 85.2 94.7 52.4 79.4 98.4 悬浮放电
气隙放电73.2 89.1 100.0 64.2 88.5 98.4 总体准确率 64.025 85.550 97.875 -
[1] 肖飞, 叶康, 邓祥力, 等. 基于最优编码集及智能状态估计的电网故障诊断方法[J]. 电力系统保护与控制, 2021, 49(2): 89–97. doi: 10.19783/j.cnki.pspc.200079 XIAO Fei, YE Kang, DENG Xiangli, et al. A fault diagnosis method of a power grid based on an optimal coding set and intelligent state estimation[J]. Power system protection and control, 2021, 49(2): 89–97. doi: 10.19783/j.cnki.pspc.200079 [2] 肖舒严, 王强钢, 周念成. 基于稳健加权总体最小二乘的变压器局部放电定位[J]. 电力自动化设备, 2020, 40(8): 203–215. doi: 10.16081/j.epae.202007034 XIAO Shuyan, WANG Qianggang, ZHOU Niancheng. Partial discharge location of transformer based on robust weighted total least square[J]. Electric power automation equipment, 2020, 40(8): 203–215. doi: 10.16081/j.epae.202007034 [3] 张重远, 岳浩天, 王博闻, 等. 基于相似矩阵盲源分离与卷积神经网络的局部放电超声信号深度学习模式识别方法[J]. 电网技术, 2019, 43(6): 1900–1907. doi: 10.13335/j.1000-3673.pst.2018.2365 ZHANG Zhongyuan, YUE Haotian, WANG Bowen, et al. Pattern recognition of partial discharge ultrasonic signal based on similar matrix BSS and deep learning CNN[J]. Power system technology, 2019, 43(6): 1900–1907. doi: 10.13335/j.1000-3673.pst.2018.2365 [4] ZHOU Zhengqin, XIAO Li, NIE Dexin, et al. Validity evaluation method of DGA monitoring sensor in power transformer based on chaos theory[C]//2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena. Cancun: IEEE, 2018: 402−405. [5] 李建文. 基于暂态对地电压法的开关柜内部绝缘缺陷检测研究[D]. 镇江: 江苏大学, 2019. LI Jianwen. Research on detection of internal insulation defects of switchgear based on transient earth voltage method[D]. Zhenjiang: Jiangsu University, 2019. [6] 李沐, 冯新岩, 蔄晓琨. 基于TDOA和TS-PSO的变压器特高频局部放电空间定位方法[J]. 中国电机工程学报, 2019, 39(6): 1834–1842,1879. doi: 10.13334/J.0258-8013.PCSEE.181083 LI Mu, FENG Xinyan, MAN Xiaokun. A transformer partial discharge UHF localization method based on TDOA and TS-PSO[J]. Proceedings of the CSEE, 2019, 39(6): 1834–1842,1879. doi: 10.13334/J.0258-8013.PCSEE.181083 [7] 杨壮, 周渠, 赵耀洪, 等. 基于人工神经网络和多频超声波检测技术的变压器油界面张力预测[J]. 高电压技术, 2019, 45(10): 3343–3349. doi: 10.13336/j.1003-6520.hve.20190924036 YANG Zhuang, ZHOU Qu, ZHAO Yaohong, et al. Prediction of interfacial tension of transformer oil based on artificial neural network and multi-frequency ultrasonic testing technology[J]. High voltage engineering, 2019, 45(10): 3343–3349. doi: 10.13336/j.1003-6520.hve.20190924036 [8] 李恩文, 王力农, 宋斌, 等. 基于混沌序列的变压器油色谱数据并行聚类分析[J]. 电工技术学报, 2019, 34(24): 5104–5114. LI Enwen, WANG Linong, SONG Bin, et al. Parallel clustering analysis of dissolved gas analysis data based on Chaotic sequences replacement[J]. Transactions of China electrotechnical society, 2019, 34(24): 5104–5114. [9] GHONEIM S S M. Intelligent prediction of transformer faults and severities based on dissolved gas analysis integrated with thermodynamics theory[J]. IET science, measurement & technology, 2018, 12(3): 388–394. [10] LIU Hongshun, JI Liang, HAN Mingming, et al. Analysis on amplitude frequency characteristics of GIS shell TEV in substation with HRPC[C]//2018 China International Conference on Electricity Distribution. Tianjin: IEEE, 2018: 1572−1575. [11] 耿琪深, 王丰华, 金霄. 基于Gammatone滤波器倒谱系数与鲸鱼算法优化随机森林的干式变压器机械故障声音诊断[J]. 电力自动化设备, 2020, 40(8): 191–196,224,197. doi: 10.16081/j.epae.202007022 GENG Qishen, WANG Fenghua, JIN Xiao. Mechanical fault sound diagnosis based on GFCC and random forest optimized by whale algorithm for dry type transformer[J]. Electric power automation equipment, 2020, 40(8): 191–196,224,197. doi: 10.16081/j.epae.202007022 [12] 刘云鹏, 王博闻, 岳浩天, 等. 基于50Hz倍频倒谱系数与门控循环单元的变压器偏磁声纹识别[J]. 中国电机工程学报, 2020, 40(14): 4681–4694,4746. doi: 10.13334/J.0258-8013.PCSEE.191922 LIU Yunpeng, WANG Bowen, YUE Haotian, et al. Identification of transformer bias voiceprint based on 50Hz frequency multiplication cepstrum coefficients and gated recurrent unit[J]. Proceedings of the CSEE, 2020, 40(14): 4681–4694,4746. doi: 10.13334/J.0258-8013.PCSEE.191922 [13] 邵宇鹰, 王枭, 彭鹏, 等. 基于声场听觉感知的变压器故障诊断方法研究[J]. 中国测试, 2021, 47(3): 92–97. SHAO Yuying, WANG Xiao, PENG Peng, et al. Research on transformer fault diagnosis method based on auditory perception of sound field[J]. China measurement & test, 2021, 47(3): 92–97. [14] 李正明, 钱露先, 李加彬. 基于统计特征与概率神经网络的变压器局部放电类型识别[J]. 电力系统保护与控制, 2018, 46(13): 55–60. doi: 10.7667/PSPC170962 LI Zhengming, QIAN Luxian, LI Jiabin. Type recognition of partial discharge in power transformer based on statistical characteristics and PNN[J]. Power system protection and control, 2018, 46(13): 55–60. doi: 10.7667/PSPC170962 [15] 吴晓文, 周年光, 彭继文, 等. 电力变压器噪声特性与相关因素分析[J]. 电力科学与技术学报, 2018, 33(3): 81–85,146. doi: 10.3969/j.issn.1673-9140.2018.03.013 WU Xiaowen, ZHOU Nianguang, PENG Jiwen, et al. Noise characteristic and relevant factors analysis of power transformers[J]. Journal of electric power science and technology, 2018, 33(3): 81–85,146. doi: 10.3969/j.issn.1673-9140.2018.03.013 [16] 翟海清, 陈敏懋. 新型铁心绑扎机的研制[J]. 变压器, 2013, 50(1): 23–24. doi: 10.19487/j.cnki.1001-8425.2013.01.006 ZHAI Haiqing, CHEN Minmao. Development of a new type of iron core binding machine[J]. Transformer, 2013, 50(1): 23–24. doi: 10.19487/j.cnki.1001-8425.2013.01.006 [17] 高沛, 王丰华, 苏磊, 等. 直流偏磁下电力变压器的振动特性[J]. 电网技术, 2014, 38(6): 1536–1541. doi: 10.13335/j.1000-3673.pst.2014.06.018 GAO Pei, WANG Fenghua, SU Lei, et al. Analysis on vibration characteristics of power transformer under DC bias[J]. Power system technology, 2014, 38(6): 1536–1541. doi: 10.13335/j.1000-3673.pst.2014.06.018 [18] 王格万, 潘超, 郑迤丹, 等. 变压器直流扰动下励磁谐波与铁心饱和失稳研究[J]. 电力系统保护与控制, 2019, 47(9): 49–55. doi: 10.7667/PSPC180645 WANG Gewan, PAN Chao, ZHENG Yidan, et al. Research on excitation harmonics and core saturation instability of transformer under DC disturbance[J]. Power system protection and control, 2019, 47(9): 49–55. doi: 10.7667/PSPC180645 [19] 张重远, 罗世豪, 岳浩天, 等. 基于Mel时频谱−卷积神经网络的变压器铁芯声纹模式识别方法[J]. 高电压技术, 2020, 46(2): 413–423. doi: 10.13336/j.1003-6520.hve.20200131005 ZHANG Zhongyuan, LUO Shihao, YUE Haotian, et al. Pattern recognition of acoustic signals of transformer core based on mel-spectrum and CNN[J]. High voltage engineering, 2020, 46(2): 413–423. doi: 10.13336/j.1003-6520.hve.20200131005 [20] 刘云鹏, 罗世豪, 王博闻, 等. 基于Mel时频谱−卷积神经网络的变压器铁芯夹件松动故障声纹模式识别[J]. 华北电力大学学报(自然科学版), 2020, 47(6): 52–60,67. LIU Yunpeng, LUO Shihao, WANG Bowen, et al. Voiceprint recognition of transformer core clamp looseness fault by mel-spectrum and convolutional neural network[J]. Journal of North China electric Power University (natural science edition), 2020, 47(6): 52–60,67. [21] BAIG F, BEG S, KHAN M F. Speaker recognition based appliances remote control for severely disabled, low vision and old aged persons[J]. INAE letters, 2018, 3(1): 1–9. doi: 10.1007/s41403-017-0032-x [22] SHI Xiaoyuan, YANG Haiyan, ZHOU Ping. Robust speaker recognition based on improved GFCC[C]//2016 2nd IEEE International Conference on Computer and Communications. Chengdu: IEEE, 2017: 1927-1931. [23] KIM C, STERN R M. Power-normalized cepstral coefficients (PNCC) for robust speech recognition[C]//2012 IEEE International Conference on Acoustics, Speech and Signal Processing. Kyoto: IEEE, 2012: 4101−4104. [24] 翟永杰, 杨旭, 赵振兵, 等. 融合共现推理的Faster R-CNN输电线路金具检测[J]. 智能系统学报, 2021, 16(2): 237–246. doi: 10.11992/tis.202012023 ZHAI Yongjie, YANG Xu, ZHAO Zhenbing, et al. Integrating co-occurrence reasoning for Faster R-CNN transmission line fitting detection[J]. CAAI transactions on intelligent systems, 2021, 16(2): 237–246. doi: 10.11992/tis.202012023 [25] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735 [26] 张勇, 高大林, 巩敦卫, 等. 用于关系抽取的注意力图长短时记忆神经网络[J]. 智能系统学报, 2021, 16(3): 518–527. doi: 10.11992/tis.202008036 ZHANG Yong, GAO Dalin, GONG Dunwei, et al. Attention graph long short-term memory neural network for relation extraction[J]. CAAI transactions on intelligent systems, 2021, 16(3): 518–527. doi: 10.11992/tis.202008036
