Automatic identification of metallographic structure based on convolutional neural network
-
摘要: 为了降低人工分辨金相组织图像类别的误差率，提高分辨效率，采用卷积神经网络模型对金相组织图像进行自动辨识。对制备金相样块所得铁素体与马氏体两种金相组织图像进行分析，提出符合金相组织图像分布特征的预处理方案。通过采用图像尺寸归一化、灰度值归一化以及高斯平滑处理等方法，对原始金相组织图像进行预处理，建立金相组织图像数据集。针对建立的铁素体和马氏体金相组织图像数据集，提出了适合金相组织图像辨识的改进模型，分别记为LeNet-MetStr模型、AlexNet-MetStr模型和VGGNet-MetStr模型。对3种改进卷积神经网络进行模型训练及分析，结果表明VGGNet-MetStr模型对2种金相组织图像自动辨识具有更高的准确度。
-
关键词:
- 卷积神经网络 /
- 金相组织 /
- 图像处理 /
- 网络模型 /
- 自动辨识 /
- LeNet神经网络 /
- AlexNet神经网络 /
- VGGNet神经网络
Abstract: The convolutional neural model was used to automatically identify metallographic structure images to reduce the error rate of manual resolution of metallographic structure image categories and improve the resolution efficiency. Two kinds of metallographic structure images of ferrite and martensite obtained from metallographic sample blocks were analyzed, and a preprocessing scheme conforming to the distribution characteristics of the metallographic structure image was proposed. Image size normalization, gray value normalization, and Gaussian smoothing are used to establish the metallographic image sample set and training set. Aiming at the established image data sets of two types of metallographic structures such as ferrite and martensite, the improved models suitable for metallographic structure image recognition are proposed, which are named the LeNet-MetStr model, AlexNet-MetStr model, and VGGNet-MetStr model, respectively. Three improved convolutional neural networks were trained and analyzed. The results show that the VGGNet-MetStr model has higher accuracy for the automatic identification of two kinds of metallographic structure images. -
钢铁材料是目前工业中应用最广、用量最大的金属材料[1]。钢铁材料受加热条件、轧制工艺、冷却速度、热处理工艺等因素的影响，其显微组织类型及形貌特征等呈现出多样性和复杂性，也决定着材料的性能，因此对钢铁材料显微组织进行正确分类尤其重要[2]。其中铁素体和马氏体的结构和性能差别较大。铁素体[3]显微组织呈明亮的多边形晶粒组织，各晶粒位向不同，受腐蚀程度略有差异，因而稍显明暗不同。铁素体组织具有良好的塑性和韧性，但强度和硬度很低。铁素体不锈钢因性价比高而应用广泛。430铁素体不锈钢[3]可作为洗衣机滚筒制造材料，洗碗机内壁材料等。439铁素体不锈钢[3]具有焊接性和成型性佳的特点，在制糖和能源产业中作为热交换管使用。马氏体[3]的立体组织有片状和板条状，在金相中多为针状组织。相比铁素体而言马氏体具有高强度和硬度，但塑性几乎为零。420马氏体不锈钢[3]用作外壳手术刀具。铁素体和马氏体组织对钢铁材料的工艺性能和使用性能有着重要影响，区分与辨识二者尤为关键。
不同材料元素在一定条件下可以制备出相应的金属材料，每种金属材料由于各组份呈现不同的分布状态和具有特定形态的金相组织图像。通过金相组织图像可以观察该材料的宏观组织形貌。金相组织主要是通过光学显微镜拍摄相应图像，通过人工观察与分析金相图片可获得材料信息，如通过确定金相组织可推测该材料的力学性能、评判工艺措施是否合理等，是最常规的一种材料表征方法[4]。该表征方法需要技术人员具有较高的专业知识储备以及丰富的实践经验。现实中往往由于从业人员专业水平不高、人工观察不细致，导致分析的结果不准确，效率较低。因此，利用自动辨识技术对金相组织图像进行计算机辅助鉴别，将有效提高评判的准确度和效率，对金相组织相关的科研分析、生产检测以及相关教学工作都具有重要意义。
计算机图像识别技术是人工智能技术的重要领域之一，在许多领域都有成熟的应用，对金属材料领域也有一定的应用。张勇等[5]改进BP神经网络对AZ91镁合金晶粒尺寸进行预测，使误差降低5%。张鹏等[6]提出了一种预测Gd2O3/6061Al中子屏蔽材料力学性能的卷积神经网络模型，捕捉晶粒并统计晶粒大小、数目等信息。曹卓等[7]研究发现卷积神经网络模型中梯度与材料性能之间有一定的关联性，并进一步验证了卷积神经网络具有较好的材料性能预测能力。李维刚等[8]采用扫描电子显微镜（scanning electron microscope，SEM）获得钢铁材料微观组织图片进行自动辨识，取得了较好的效果，然而训练样本数量过小，容易造成模型过拟合现象，对于不同尺度的微观组织图并未做深入研究。目前针对金属表面形貌的自动识别研究主要集中于通过SEM扫描电镜得到清晰度较高的某种特定微观组织图像，采用传统的数字图像处理方法，拟合晶粒边界，实现晶粒分割[9]；获取晶粒尺寸信息、对晶粒尺寸及性能预测[5-7]；采取手动提取图像特征，利用数据挖掘或机器学习实现图像分类或结构性能分析等[10-13]。然而利用卷积神经网络技术对金相组织图像自动识别的研究却非常少，有效研究成果更是寥寥无几。
本文建立金相组织图像数据集，改进LeNet-5、AlexNet、VGGNet 3种不同卷积神经网络模型，实现自动辨识铁素体与马氏体的金相组织。通过实验结果分析改进卷积神经网络模型特点，使卷积神经网络算法可在金属材料组织的自动辨识领域推广应用。该技术可在工业原材料检测、材料制备检测、成本检测及教学科研等领域实现铁素体与马氏体金属材料组织的自动辨识，不受人为因素影响，有效提高二者的识别率，为后续材料性能分析、工艺研究以及材料的使用等奠定理论依据。
1. 金相组织图像获取与数据集创建
数据集是影响卷积神经网络准确度的重要因素之一，数据集的整理也是本文需要解决的首要问题。卷积神经网络等算法模型要得到高的准确度，需要大量的样本训练，然而实验数据有限，很难获得大量相同材料的金相组织图像。通过标准金相样块，利用奥林巴斯BX系列正置金相显微镜获取金相图像。图1为收集的金相显微组织图像。
图 1 金相组织图像Fig. 1 Metallographic structure images
下载:
全尺寸图片
虽然在同一平面内晶粒大小不同，但金相组织分布相对均匀，整体特征与局部特征相似，分割后的图像也具有较高的辨识度。训练卷积神经网络模型需要大量样本集，如果输入的图像尺寸较大，则训练过程中会产生较大的计算量和大量的参数，这会影响模型训练的速度，甚至对计算机硬件提出很高的要求，实验室无法实现其模型训练过程。小尺寸图像样本有助于提高模型的训练速度，对计算机的硬件要求相对较低。有些图像的局部特征不明显或清晰度不高，影响模型训练的准确度，采用图像分割可以将其去除，避免不必要的影响。因此，本文采用金相组织图像分割的方法增大样本数量。
图2为采集的金相组织图像经过改变分辨率和分割的方法获得大小为(32×32) dpi的对比图像。
图 2 金相组织图像分辨率统一及分割图像对比Fig. 2 Resolution unification of metallographic structure images and image segmentation comparison下载:
全尺寸图片
图2中(a)图为将图1中(a)图铁素体的金相组织图像分辨率归一化为(128×128) dpi，将(a)图分割成(64×64) dpi的四分图像得到图2中的(b)图，(c)图为将(a)图分割成16份(32×32) dpi的图像，(d)图中将(b)图(64×64) dpi的图像缩小成(32×32) dpi的图像。由所得图像可以观察到，(c)图中大部分晶粒被分割，图像中信息无法反映晶粒特征，(d)图中的晶粒特征被保留下来，本文采用此类图像建立样本数据集。
金相组织图像的清晰度受光线等影响，在参与模型训练前需进行图像预处理。本文运用归一化[14]方法将图像灰度值范围扩大以提高图像的对比度。实验发现该方法同时会产生一定的干扰点，本文通过高斯平滑处理[15-17]进行降噪，得到较理想的图像，如图3所示。因金相组织图像放大倍数不同，在分割成相同尺寸的图像时，放大倍数较大的金相组织晶粒较少，有些图像甚至只有某个晶粒的一部分，为使模型具有一定的实用性，本文将一些图像进行缩小处理，从而替代无法反应晶粒真实特征的图像。
图 3 金相组织图像灰度值归一化、平滑处理对比Fig. 3 Comparison of normalization and smoothing of gray value of metallographic structure image下载:
全尺寸图片
图3中(a)和(d)分别是铁素体和马氏体经过分割后的图像，(b)和(e)分别是(a)与(d)经过灰度值归一化后所得的图像，晶粒特征更加清晰，但同时产生一些噪点，干扰图像信息，(c)和(f)分别是(b)与(e)经过高斯平滑处理后所得图像，可看出图像降噪处理后，其特征信息同时得到保留。本文所建数据集为原图像经过上述图像预处理操作。
综上所述，本文的数据集图像分为两类：铁素体和马氏体，每类图像的训练样本集有1000张，测试集为150张，分辨率为(32×32) dpi，均为1通道灰度图像。
2. 卷积神经网络结构
人工神经网络[18-19]是模拟动物神经网络连接方式处理数据的一种算法模型，它由多个神经元结构连接组成。神经网络的学习，是通过计算机自主学习找到一组权重，使得神经网络的输出与目标越来越接近[18]。
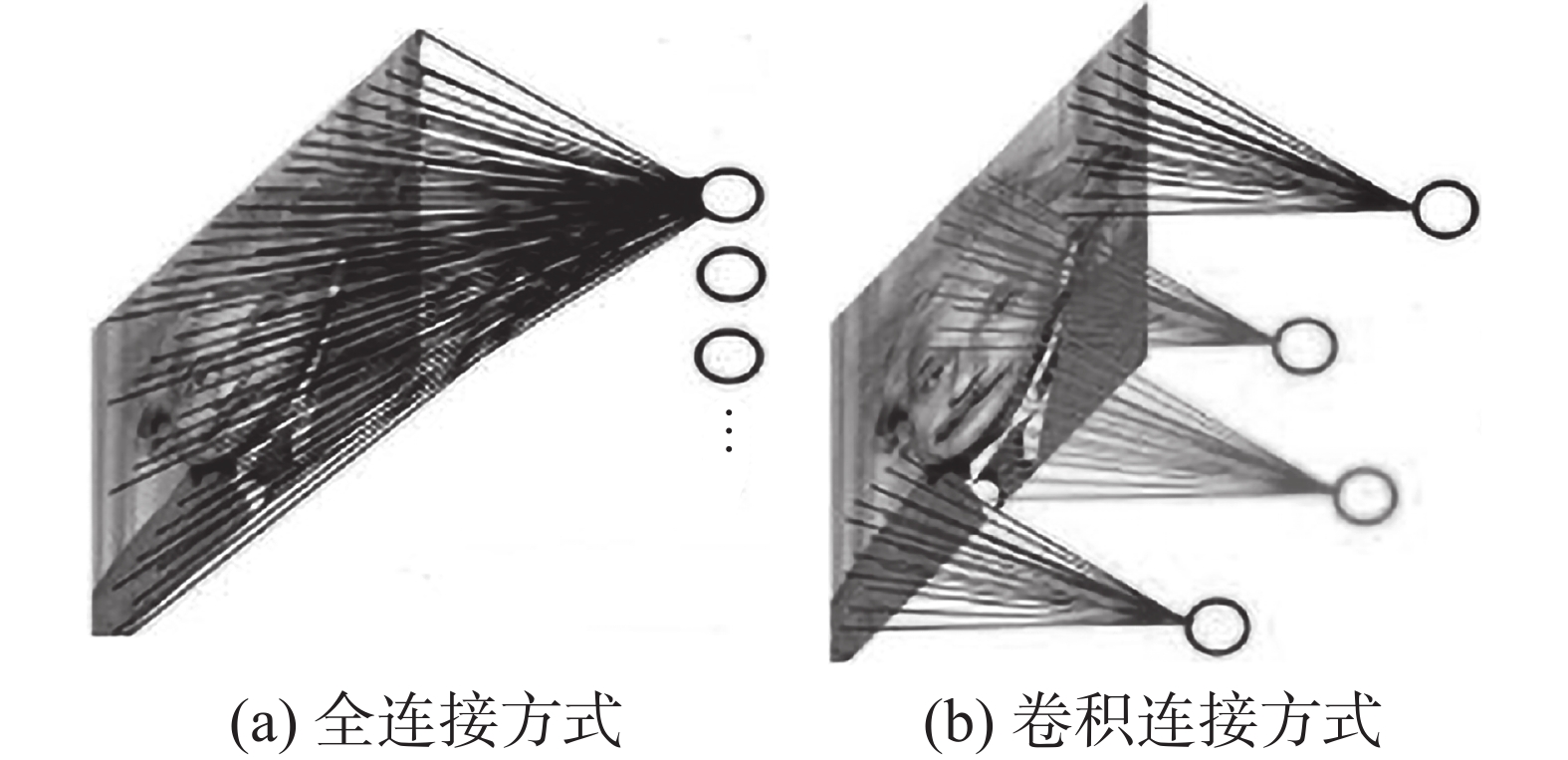
卷积神经网络（convolutional neural network, CNN）[20-22]的层与层之间通过卷积计算的方式连接。图4反应了全连接与卷积连接的区别。
图 4 全连接与卷积连接方式比较Fig. 4 Comparison of fully connection and convolutional connection下载:
全尺寸图片
卷积神经网络主要包含卷积层、池化层和全连接层。输入数据经过卷积层的卷积计算后，得到特征图像，具体计算为
$$ {y_{mn}} = f\left(\sum\limits_{j = 0}^{J - 1} {\sum\limits_{i = 0}^{I - 1} {\mathop x\nolimits_{m + i,n + j} {w_{ij}} + b} } \right), 0 \leqslant m < M,0 \leqslant n < N $$ 式中：
${w_{ij}}$ 为权重值，${x_{m + i,n + j}}$ 为输入值，$b$ 为偏置，${y_{mn}}$ 为特征值。特征图像经过池化层[24-25]后可缩小尺度。池化层的采样方式有均匀采样、最大下采样等。最大下采样（max pooling）是在采样区域取最大值作为输出。如果进行S1×S2的均匀采样，取S1×S2内输入值
$x$ 的平均值为该区域的输出值$y$ ，具体计算为$$ {y_{mn}} = \dfrac{1}{{{S_1}{S_2}}}\sum\limits_{j = 0}^{{S_2} - 1} {\sum\limits_{i = 0}^{{S_1} - 1} {{x_{m \times {S_1} + i,n \times {S_2} + j}}} } $$ 式中：
${y_{mn}}$ 为S1×S2区域的输出值，$ {x_{m \times {S_1} + i,n \times {S_2} + j}} $ 为S1×S2区域内的任意输入值。全连接层是一个浅层感知机，起到分类的作用。输出层采用softmax分类器，通过计算概率来判别样本种类，可完成多种类别的分类，具体计算为
$$ \begin{gathered} f({x^{(i)}}|{\boldsymbol{\theta}} ) = \left[ {\begin{array}{*{20}{c}} {p({y^{(i)}} = 1|{x^{(i)}},{\boldsymbol{\theta}} )} \\ {p({y^{(i)}} = 2|{x^{(i)}},{\boldsymbol{\theta}} )} \\ \vdots \\ {p({y^{(i)}} = k|{x^{(i)}},{\boldsymbol{\theta}} )} \end{array}} \right] = \dfrac{1}{{\displaystyle\sum\nolimits_{j = 1}^k {{{\rm{e}}^{{\boldsymbol{\theta}} _j^{\rm T}{x^{(i)}}}}} }}\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\boldsymbol{\theta}} _1^{\rm T}{x^{(i)}}}}} \\ {{{\rm{e}}^{{\boldsymbol{\theta}} _2^{\rm T}{x^{(i)}}}}} \\ \vdots \\ {{{\rm{e}}^{{\boldsymbol{\theta}} _k^{\rm T}{x^{(i)}}}}} \end{array}} \right] \\ \end{gathered} $$ 式中：
$ k $ 表示某个分类，${\boldsymbol{\theta}} _j^{\rm T}{x^{(i)}}$ 表示该分类的值，$p({y^{(i)}} = k|{x^{(i)}},{\boldsymbol{\theta}} )$ 表示第$ k $ 类的概率，${\boldsymbol{\theta}}$ 为权重。通过训练集样本的学习，softmax分类器学习最优参数，使得损失函数的损失值达到最小，最常用的为交叉熵函数，具体计算为
$$ J({\boldsymbol{\theta}} ) = - \dfrac{1}{m}\left[ {\displaystyle\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {1\{ {y^{(i)}} = j\} {\rm{lg}} \dfrac{{{{\rm{e}}^{{\boldsymbol{\theta}} _j^{\rm T}{x^{(i)}}}}}}{{\displaystyle\sum\nolimits_{l = 1}^k {{{\rm{e}}^{{\boldsymbol{\theta}} _l^{\rm T}{x^{(i)}}}}} }}} } } \right] $$ 式中：
$1\{ {y^{(i)}} = j\} $ 表示若样本i的真实分类为j，则取值为1。训练的过程中损失函数的值逐渐减小，准确度逐渐增高，卷积神经网络模型逐渐收敛，当损失函数小于允许的范围，即得到训练模型。
3. 不同卷积神经网络对比及改进
3.1 LeNet-5网络结构及改进
LeNet-5网络[26]结构中使用BP算法训练模型，采用Sigmoid作为激活函数，提取原始图像上的有效表征。Sigmoid激活函数具体计算为
$$ f(x) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $$ 该函数平滑、易与求导，将输入值映射到[0,1]。
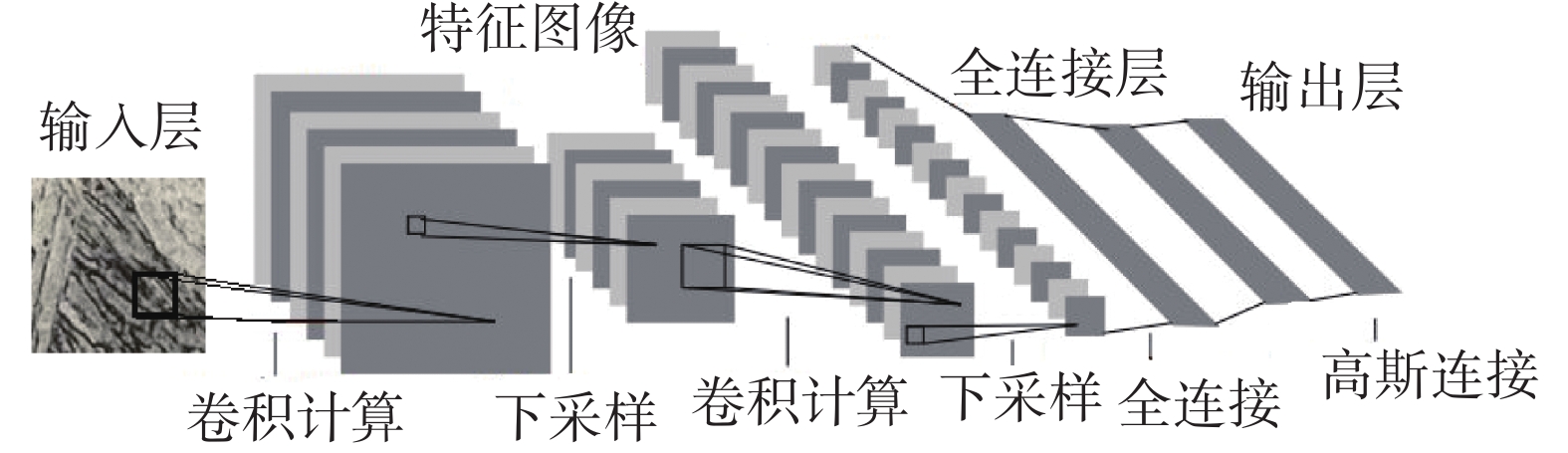
本文改进LeNet-5网络模型记为LeNet-MetStr，输入层为(32×32) dpi的1通道灰度图像，第1层为卷积层，包含6个5×5的卷积核，步长为1，与输入图像进行卷积计算，得到6个(28×28) dpi的特征图像；第2层为池化层，池化核尺寸为2×2步长为2，采用均值下采样方式得到6个(14×14) dpi特征图像；第3层为卷积层，16个5×5的卷积核，步长为1，采用局部连接的方式得到16个(10×10) dpi的特征图像；第4层为池化层，池化核尺寸为2×2，步长为2，采用均值下采样方法得到16个(5×5) dpi的特征图像；第5层为全连接层，使用120个神经元做全连接；第6层为全连接层，含有84个隐藏单元；最后的输出层为2个，用以实现铁素体和马氏体的自动识别。图5为本文运用LeNet-MetStr网络结构训练金相组织模型示意图。
图 5 LeNet- MetStr网络结构Fig. 5 LeNet- MetStr network structure下载:
全尺寸图片
3.2 AlexNet网络结构及改进
AlexNet网络[27-28]结构采用了Relu激活函数；池化尺寸比步长大，产生覆盖的池化操作，使结果更准确；引入Dropout随机删除网络中的一些隐藏神经元，有效避免过拟合现象，模型训练时间也相对缩短。
Relu激活函数[29]的具体计算为
$$ f(x) = \max (0,x) $$ 该函数为非零线性函数，有效克服梯度消失，加快训练速度。
AlexNet网络输入的图像是能反应颜色特征的三通道彩色图像，且分辨率是(224×224) dpi。而本文所研究的金相组织图像并不需要彩色来反应其特征，所以输入图像仍为(32×32) dpi的单通道灰度图像。
本文将AlexNet改进网络记为AlexNet-MetStr，网络结构共6层，其中2层卷积层，2层池化层，2层全连接层。第1层为卷积层，采用7×7的96个卷积核，步长为1，得到(26×26) dpi的96个特征图像；第2层为池化层，采用3×3的池化核，步长为2的最大值下采样法进行池化；第3层为卷积层，采用5×5×256的卷积核，步长为1，得到(9×9) dpi的256个特征图像；第4层为池化层，采用3×3的池化核，步长为1最大值下采样法进行池化；第5层和第6层为全连接层，全连接层采用Dropout (丢弃概率rate=0.5)来随机删除一些隐藏神经元以提高效率，降低过拟合现象。
3.3 VGGNet网络结构及改进
VGGNet[29]通过采用3×3，步长为1的小卷积核多次扫描的方法，加深了网络的深度，其优点是有较好的泛化能力，良好的迁移学习能力。
本文根据所研究图像特性对VGG16网络结构进行改进，记为VGG-MetStr。该模型中采用的激活函数为ELU函数[30]，具体计算为
$$ f(x)=\left\{\begin{aligned} &x,\quad x > 0\\ &\alpha ({\rm e}^{x}-1),\quad 其他\end{aligned} \right.$$ 式中：
$\alpha $ 为可调节的参数。ELU函数将Sigmoid函数和Relu函数相结合，有效解决Relu函数在负数时不被激活、梯度消失的情况，更具鲁棒性，收敛速度更快。VGG-MetStr网络结构共有17层，分为6段，前5段每段由两层卷积层和一层池化层组成，卷积层采用3×3，步长为1的卷积核进行卷积，池化层采用大小为2×2，步长为1的池化核进行池化计算。最后一段为2层全连接层。
4. 实验结果与分析
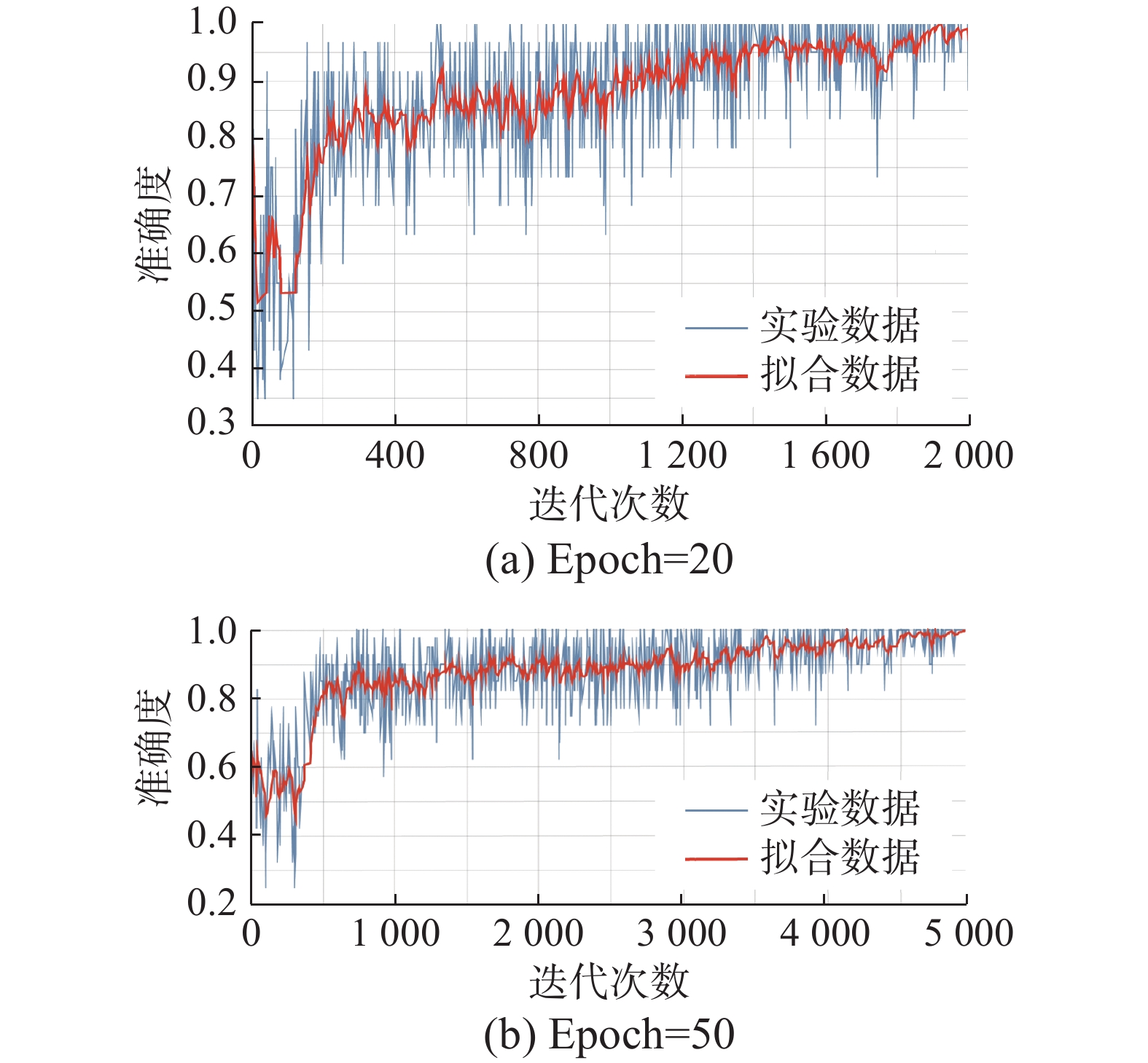
本实验的硬件支持CPU为intel i7-9750H，GPU为NVIDIA GTX1650，内存8 GB，操作系统为Unbuntu18，环境为Pycharm，平台使用Tensorflow与keras，语言使用Python。网络模型的参数采用随机生成，实验所得数据结果采用TensorBoard可视化。经过预处理后的数据集图像作为输入，经过3种改进网络结构训练，得到本文主要统计的2个指标，准确度(acc)和损失函数(loss)。图6为LeNet-MetStr网络模型在不同迭代次数训练样本模型时所得的准确度。
图 6 LeNet-MetStr网络模型在不同迭代次数训练样本模型所得的准确度Fig. 6 Accuracy of LeNet-Metstr network model in training sample model with different iteration times下载:
全尺寸图片
图6(a)为采用LeNet-MetStr网络模型在训练次数为20时所得训练样本准确度，图6(b)为采用LeNet-MetStr网络模型在训练次数为50时所得训练样本准确度。由图6可以看出，随着训练次数及迭代次数增多，模型收敛速度加快，准确度也有所增长。后续的模型训练中，本文均采用训练次数为50。
本文将3种改进网络训练模型的准确度与损失函数值做对比得出结果如表1所示，其中LeNet-MetStr网络和VGG-MetStr网络训练模型的准确度均可达到最高值100%，AlexNet-MetStr网络训练模型的准确度可达到97%；对比损失函数值，AlexNet-MetStr网络训练模型的损失函数值最大，LeNet-MetStr网络训练模型的损失函数值其次，VGG-MetStr网络训练模型的损失函数值最小。
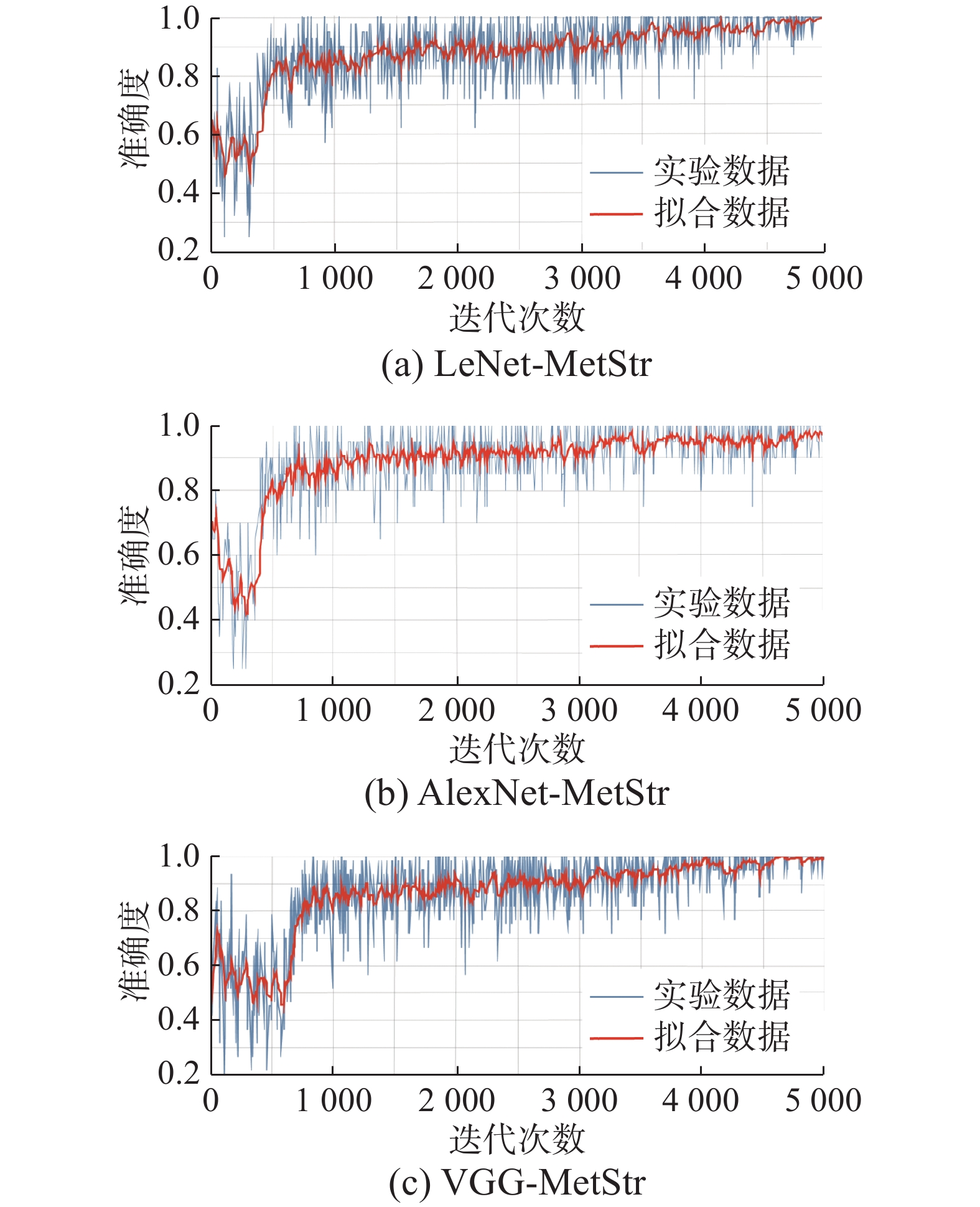
表 1 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr训练模型准确度和损失值对比Table 1 Comparison of accuracyand loss value of LeNet-MetStr,AlexNet-MetStr and VGG-MetStr training models性能 LeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 1.0000 0.9700 1.0000 损失值 0.0057 0.0131 0.0035 图7为3种改进网络模型训练过程所得准确度的变化过程。
图 7 3种改进网络模型训练所得准确度变化过程Fig. 7 Change process of accuracy obtained from training of three improved network models下载:
全尺寸图片
对比图7中3种模型训练过程中准确度的变化过程，可以观察到LeNet-MetStr网络模型在迭代约300次后，准确度开始快速上升，迭代次数至500次左右，准确度达到约0.8，能较快的趋于收敛，随后准确度缓慢上升；AlexNet-MetStr网络模型在迭代次数约500次之前，训练过程与LeNet-MetStr网络模型训练过程相似，其后收敛效果较优，准确度提升相对较慢；VGG-MetStr网络模型在迭代约600次后，准确度开始快速上升，迭代次数至500次左右，准确度达到约0.8，训练过程稍长，迭代次数在4500至5000次左右时，收敛效果更优，准确度更高。该结果与网络结构设置及相关参数设置相符。
本文将测试集数据传入3种网络训练好的模型，得到测试集的准确度如表2所示。
表 2 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr模型测试集准确度Table 2 Test accuracy of LeNet-MetStr,AlexNet-MetStr and VGG-MetStr models性能 LeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 0.9499 0.9499 1.0000 由表2可以看出，VGG-MetStr网络所得训练模型能够100%识别测试集的图像，LeNet-MetStr网络和AlexNet-MetStr网络所得的训练模型识别测试集图像的准确度均为94.99%。VGG-MetStr网络模型要优于LeNet-MetStr网络模型和AlexNet-MetStr网络模型。
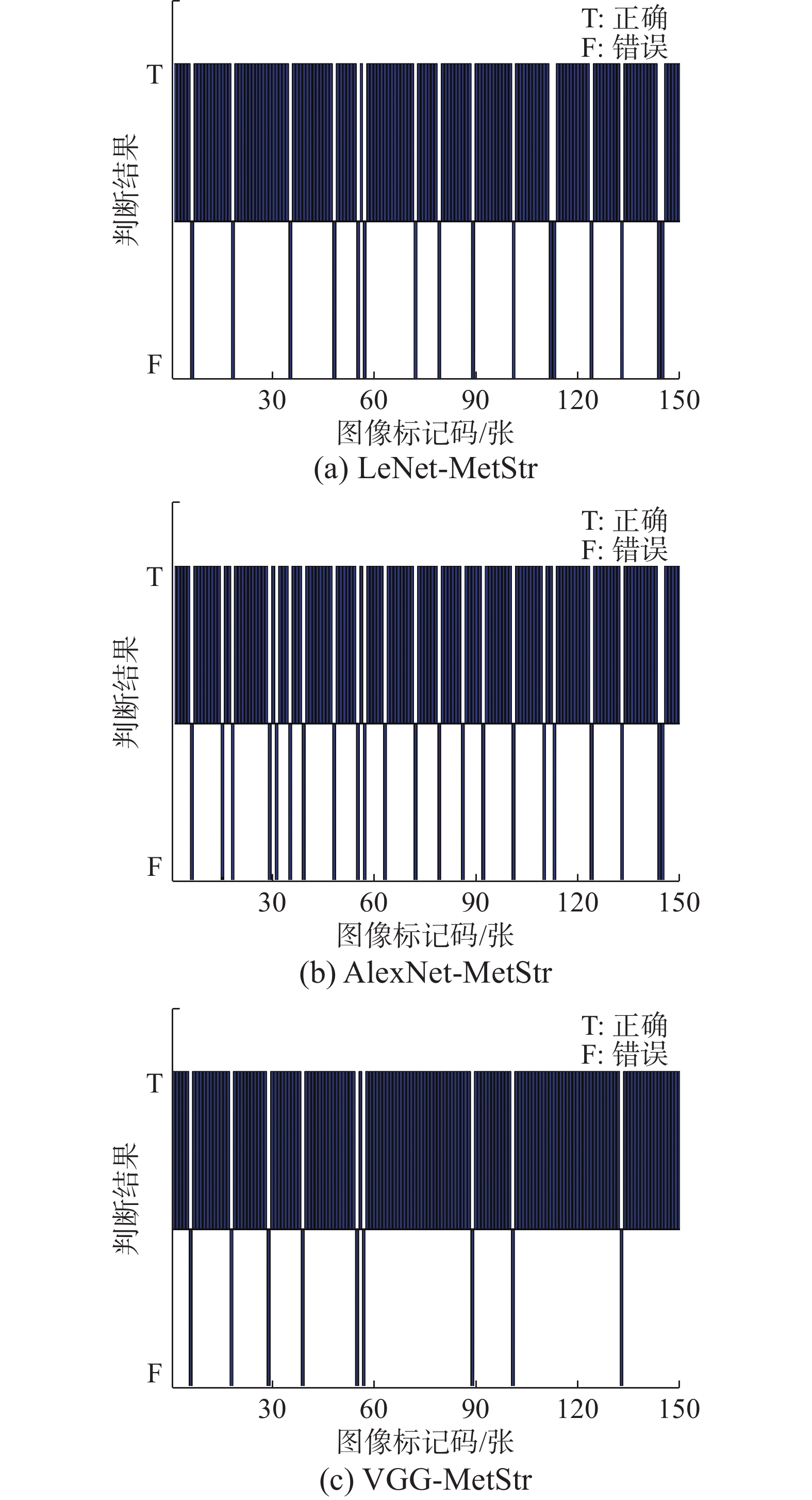
在实际使用中，会出现未经过预处理的图像作为输入，检测材料类别。为此，将未经预处理的150张测试集图像进行测试，所得结果如图8所示。
图 8 3种改进网络模型对未经预处理测试集判断结果Fig. 8 Judgment results of three improved network models on non preprocessed test sets下载:
全尺寸图片
由结果可见，150个测试图像中，LeNet-MetStr网络模型可以准确识别134个，AlexNet-MetStr网络模型可以准确识别128个，VGG-MetStr网络模型可以准确识别141个。表3为3种模型未经预处理测试集准确度对比。
表 3 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr模型未经预处理测试集准确度Table 3 Unprocessed Test accuracy of LeNet-MetStr, AlexNet-MetStr and VGG-MetStr modelsLeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 0.8933 0.8533 0.9400 由此可见，对未经预处理的图像测试，VGG-MetStr网络模型仍可得到较高的准确度。
本文对3种改进网络层级进行比较，如表4所示。可以看出LeNet-MetStr和AlexNet-MetStr的网络层级相同，AlexNet-MetStr比LeNet-MetStr的卷积核和池化尺寸较大，VGG-MetStr网络的卷积核小，层级比LeNet-MetStr和AlexNet-MetStr两种网络模型更深。
表 4 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr网络层级比较Table 4 Comparison of network levels of LeNet-MetStr,AlexNet-MetStr,VGG-MetStrLeNet-MetStr AlexNet-MetStr VGG-MetStr 输入图像(32×32) dpi，单通道 输入图像(32×32) dpi，单通道 输入图像(32×32) dpi，单通道 卷积层：卷积核6个5×5，步长=1 卷积层：卷积核96个7×7，步长=1 卷积层：卷积核64个3×3，步长=1;
卷积核64个3×3，步长=1;
池化层：2×2，步长=1池化层：2×2，步长=2 池化层：3×3，步长=2 卷积层：卷积核128个3×3，步长=1;
卷积核128个3×3，步长=1;
池化层：2×2，步长=1卷积层：卷积核16个5×5，步长=1 卷积层：卷积核256个5×5，步长=1 卷积层：卷积核256个3×3，步长=1;
卷积核256个3×3，步长=1;
池化层：2×2，步长=1池化层：2×2，步长=2 池化层：3×3，步长=1 卷积层：卷积核512个3×3，步长=1;
卷积核512个3×3，步长=1;
池化层：2×2，步长=1— — 卷积层：卷积核512个3×3，步长=1;
卷积核512个3×3，步长=1;
池化层：2×2，步长=12层全连接层 2层全连接层 2层全连接层 经过实验数据对比可以看出，LeNet-MetStr网络结构简单，由于卷积核尺寸较小，网络层级较深，对本文所研究的小尺寸图像训练有很好的效果。AlexNet-MetStr网络模型卷积核尺寸相对较大，对大数量样本和大尺寸彩色图像有很快的计算速度和很高的准确度，而本文由于样本数量有限，输入的图像尺寸相对较小，AlexNet-MetStr网络在训练过程中会丢失图像部分细节特征，从而没有得到较好的准确度。VGG-MetStr网络模型采用更深的层和更小的卷积核计算特征图像，能提取图像中细小的特征，VGG-MetStr比LeNet-MetStr和AlexNet-MetStr具有更高的准确度，更好的收敛效果。
5. 结束语
本文通过对金相组织图像特征分析，改进卷积神经网络实现铁素体和马氏体两种金相组织图的自动识别，模型训练及测试准确度最高均可达到100%。结论总结如下：
1）分析铁素体与马氏体的金相组织图像特点，采用图像增强、图像裁剪、尺寸缩放等方法进行图像预处理，得到能够反映铁素体和马氏体金相组织特征的训练样本集和测试集。
2）提出金相组织自动识别卷积网络模型。结合金相组织训练样本图像特征，优化卷积神经网络模型，对各层网络结构和参数进行调整，获得训练模型准确度优异的LeNet-MetStr、AlexNet-MetStr、VGG-MetStr 3种改进网络模型。
3）通过对比3种改进卷积神经网络模型，分析其性能，得出VGG-MetStr网络模型优于LeNet-MetStr、AlexNet-MetStr网络模型的结论，与理论相符。本文验证了使用卷积神经网络实现金相组织图像自动识别的可行性和准确性，为今后更多金相组织种类的自动识别奠定基础，笔者今后将对双相金相组织图像分析及自动辨识做进一步研究。
-
图 1 金相组织图像
Fig. 1 Metallographic structure images
下载:
全尺寸图片
图 2 金相组织图像分辨率统一及分割图像对比
Fig. 2 Resolution unification of metallographic structure images and image segmentation comparison
下载:
全尺寸图片
图 3 金相组织图像灰度值归一化、平滑处理对比
Fig. 3 Comparison of normalization and smoothing of gray value of metallographic structure image
下载:
全尺寸图片
图 4 全连接与卷积连接方式比较
Fig. 4 Comparison of fully connection and convolutional connection
下载:
全尺寸图片
图 5 LeNet- MetStr网络结构
Fig. 5 LeNet- MetStr network structure
下载:
全尺寸图片
图 6 LeNet-MetStr网络模型在不同迭代次数训练样本模型所得的准确度
Fig. 6 Accuracy of LeNet-Metstr network model in training sample model with different iteration times
下载:
全尺寸图片
图 7 3种改进网络模型训练所得准确度变化过程
Fig. 7 Change process of accuracy obtained from training of three improved network models
下载:
全尺寸图片
图 8 3种改进网络模型对未经预处理测试集判断结果
Fig. 8 Judgment results of three improved network models on non preprocessed test sets
下载:
全尺寸图片
表 1 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr训练模型准确度和损失值对比
Table 1 Comparison of accuracyand loss value of LeNet-MetStr,AlexNet-MetStr and VGG-MetStr training models
性能 LeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 1.0000 0.9700 1.0000 损失值 0.0057 0.0131 0.0035 表 2 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr模型测试集准确度
Table 2 Test accuracy of LeNet-MetStr,AlexNet-MetStr and VGG-MetStr models
性能 LeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 0.9499 0.9499 1.0000 表 3 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr模型未经预处理测试集准确度
Table 3 Unprocessed Test accuracy of LeNet-MetStr, AlexNet-MetStr and VGG-MetStr models
LeNet-MetStr AlexNet-MetStr VGG-MetStr 准确度 0.8933 0.8533 0.9400 表 4 LeNet-MetStr、AlexNet-MetStr、VGG-MetStr网络层级比较
Table 4 Comparison of network levels of LeNet-MetStr,AlexNet-MetStr,VGG-MetStr
LeNet-MetStr AlexNet-MetStr VGG-MetStr 输入图像(32×32) dpi，单通道 输入图像(32×32) dpi，单通道 输入图像(32×32) dpi，单通道 卷积层：卷积核6个5×5，步长=1 卷积层：卷积核96个7×7，步长=1 卷积层：卷积核64个3×3，步长=1;
卷积核64个3×3，步长=1;
池化层：2×2，步长=1池化层：2×2，步长=2 池化层：3×3，步长=2 卷积层：卷积核128个3×3，步长=1;
卷积核128个3×3，步长=1;
池化层：2×2，步长=1卷积层：卷积核16个5×5，步长=1 卷积层：卷积核256个5×5，步长=1 卷积层：卷积核256个3×3，步长=1;
卷积核256个3×3，步长=1;
池化层：2×2，步长=1池化层：2×2，步长=2 池化层：3×3，步长=1 卷积层：卷积核512个3×3，步长=1;
卷积核512个3×3，步长=1;
池化层：2×2，步长=1— — 卷积层：卷积核512个3×3，步长=1;
卷积核512个3×3，步长=1;
池化层：2×2，步长=12层全连接层 2层全连接层 2层全连接层 -
[1] KHEDKAR P, MOTAGI R, MAHAJAN P, et al. A review on advance higu strength steels[J]. International journal of current engineering and technology, 2016, 6: 240. [2] HONEYCOMBE R W K. Steels: microstructure and properties[M]. Fourth edition, Oxford: Butterworth-Heinemann, 2017. [3] KRAUSS G. Steels: processing, structure, and performance[M]. 2nd edition. Materials Park: ASM International, 2015. [4] OHSER J, MÜCKLICH F. Statistical analysis of microstructures in materials science[J]. Practical metallography, 2001, 38(9): 538–539. doi: 10.1515/pm-2001-380907 [5] 张勇, 李恒灿, 梁明亮. 基于PSO-BP神经网络的汽车用铸造AZ91镁合金晶粒尺寸的预测[J]. 热加工工艺, 2019, 48(3): 105–107,111. doi: 10.14158/j.cnki.1001-3814.2019.03.025 ZHANG Yong, LI Hengcan, LIANG Mingliang. Prediction of grain size of cast AZ91 magnesium alloy for automobile based on PSO-BP neural network[J]. Hot working technology, 2019, 48(3): 105–107,111. doi: 10.14158/j.cnki.1001-3814.2019.03.025 [6] 张鹏, 李靖, 王文先, 等. 基于卷积神经网络模型的Gd2O3/6061Al中子屏蔽材料的力学性能预测[J]. 原子能科学技术, 2020, 54(8): 1513–1518. doi: 10.7538/yzk.2020.youxian.0208 ZHANG Peng, LI Jing, WANG Wenxian, et al. Prediction of mechanical property of Gd2O3/6061Al neutron shielding material based on convolutional neural network model[J]. Atomic energy science and technology, 2020, 54(8): 1513–1518. doi: 10.7538/yzk.2020.youxian.0208 [7] 曹卓, 但雅波, 李想, 等. 基于卷积神经网络模型中梯度与特征分析的材料性能优化与预测机理研究[J]. 中国材料进展, 2020, 39(5): 385–390. doi: 10.7502/j.issn.1674-3962.201905008 CAO Zhuo, DAN Yabo, LI Xiang, et al. Research on optimization and prediction mechanism of material properties based on gradient and feature analysis in convolution neural network[J]. Materials China, 2020, 39(5): 385–390. doi: 10.7502/j.issn.1674-3962.201905008 [8] 李维刚, 谌竟成, 范丽霞, 等. 基于卷积神经网络的钢铁材料微观组织自动辨识[J]. 钢铁研究学报, 2020, 32(1): 33–43. doi: 10.13228/j.boyuan.issn1001-0963.20190147 LI Weigang, CHEN Jingcheng, FAN Lixia, et al. Automatic identification of microstructure of iron and steel material based on convolutional neural network[J]. Journal of iron and steel research, 2020, 32(1): 33–43. doi: 10.13228/j.boyuan.issn1001-0963.20190147 [9] 雷涛, 李云彤, 周文政, 等. 数据与模型联合驱动的陶瓷材料晶粒分割[J]. 自动化学报, 2022, 48(4): 1137–1152. doi: 10.16383/j.aas.c200277 LEI Tao, LI Yuntong, ZHOU Wenzheng, et al. Grain segmentation of ceramic materials using data-driven jointing model-driven[J]. Acta automatica sinica, 2022, 48(4): 1137–1152. doi: 10.16383/j.aas.c200277 [10] GOLA J, BRITZ D, STAUDT T, et al. Advanced microstructure classification by data mining methods[J]. Computational materials science, 2018, 148: 324–335. doi: 10.1016/j.commatsci.2018.03.004 [11] WEBEL J, GOLA J, BRITZ D, et al. A new analysis approach based on Haralick texture features for the characterization of microstructure on the example of low-alloy steels[J]. Materials characterization, 2018, 144: 584–596. doi: 10.1016/j.matchar.2018.08.009 [12] TSUTSUI K, TERASAKI H, MAEMURA T, et al. Microstructural diagram for steel based on crystallography with machine learning[J]. Computational materials science, 2019, 159: 403–411. doi: 10.1016/j.commatsci.2018.12.003 [13] GOLA J, WEBEL J, BRITZ D, et al. Objective microstructure classification by support vector machine (SVM) using a combination of morphological parameters and textural features for low carbon steels[J]. Computational materials science, 2019, 160: 186–196. doi: 10.1016/j.commatsci.2019.01.006 [14] 邹耀斌, 雷帮军, 臧兆祥, 等. 归一化互信息量最大化导向的自动阈值选择方法[J]. 自动化学报, 2019, 45(7): 1373–1385. doi: 10.16383/j.aas.2018.c170284 ZOU Yaobin, LEI Bangjun, ZANG Zhaoxiang, et al. Automatic threshold selection guided by maximizing normalized mutual information[J]. Acta automatica sinica, 2019, 45(7): 1373–1385. doi: 10.16383/j.aas.2018.c170284 [15] WU Tingfan, MOVELLAN J. Semi-parametric Gaussian process for robot system identification[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura Algarve: IEEE, 2012: 725−731. [16] VAN DER WILK M, RASMUSSEN C E, HENSMAN J. Convolutional Gaussian processes[C]//NIPS'17: Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 2845−2854. [17] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. London: MIT, 2006 [18] 张若非, 付强, 高斌. 深度学习模型及应用详解[M]. 北京: 电子工业出版社, 2019: 2−6. [19] MITCHELL Tom M. 机器学习[M]. 曾华军, 张银奎译. 北京: 机械工业出版社, 2012: 60−63. [20] LECUN Y, BOSER B, DENKER J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural computation, 1989, 1(4): 541–551. doi: 10.1162/neco.1989.1.4.541 [21] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791 [22] BOUVRIE J. Notes on convolutional neural networks[J]. In practice, 2006: 47–60. [23] DUDA Richard O, HART Peter E, STORK David G. 模式分类[M]. 李宏东, 姚天翔译. 北京: 机械工业出版社, 2004. [24] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(9): 1904–1916. doi: 10.1109/TPAMI.2015.2389824 [25] ZEILER M D, FERGUS R. Stochastic pooling for regularization of deep convolutional neural networks[EB/OL]. New York: arXiv, 2013. (2013−01−16)[2021−10−29].https://arxiv.org/abs/1301.3557. [26] LE CUN Y, BOSER B, DENKER J S, et al. Handwritten digit recognition with a back-propagation network[C]//NIPS'89: Proceedings of the 2nd International Conference on Neural Information Processing Systems. New York: ACM, 1989: 396−404. [27] KIM H, NAM H, JUNG W, et al. Performance analysis of CNN frameworks for GPUs[C]//2017 IEEE International Symposium on Performance Analysis of Systems and Software. New York: IEEE, 2017: 55−64. [28] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of Advances in Neural Information Processing Systems 25. Nevada: Curran Associates, 2012: 1097−1105. [29] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. New York: arXiv, 2014. (2014−09−04)[2021−10−29].https://arxiv.org/abs/1409.1556. [30] CLEVERT D A, UNTERTHINER T, HOCHREITER S. Fast and accurate deep network learning by exponential linear units[EB/OL]. New York: arXiv, 2015. (2015−11−23) [2021−10−29].https://arxiv.org/abs/1511.07289.
