Unmanned aerial vehicles object tracking based on illumination adaptive dynamic consistency
-
摘要: 无人机跟踪任务经常面临各种光线变化场景，然而无人机跟踪方法主要在光线充足下实现鲁棒跟踪。提出一种具有光照自适应性和跨帧语义感知动态一致性评估的无人机跟踪方法，实现光线不足下的无人机目标跟踪。首先构建光照自适应模块对昏暗场景进行识别，对视频图像的光照强度进行补偿；其次构建目标模板训练具有目标感知能力的滤波器进行相关运算，并利用跨帧之间的响应信息进行一致性评估；最后构建动态约束策略并对响应差异进行约束，使跟踪器保持时间平滑。在UAVDark135和UAV123数据集上，与9种先进算法进行对比实验，结果表明该算法具有较好的跟踪性能。Abstract: The tracking of unmanned aerial vehicles (UAVs) is often confronted with illumination change scenes. However, UAV tracking methods mainly achieve robust tracking under sufficient illumination. In this study, a UAV tracking method that uses dynamic consistency evaluation based on illumination adaptability and cross-frame semantic perception is proposed to realize efficient UAV object tracking under insufficient illumination. First, an adaptive illumination module was designed to recognize dim scenes and compensate for the illumination intensity of the dim image. Subsequently, aobject template was built to train a filter with object perception to perform correlation operations; furthermore, the consistency evaluation was performed using the response information between the cross-frames. Finally, a dynamic constraint strategy was developed, and the response difference of the tracker was constrained to maintain temporal smoothness. When the tracking performance of this method was compared to that of nine state-of-the-art algorithms on the UAVDark135 and UAV123 datasets, the results indicated that the algorithm had better tracking performance.
-
得益于无人机强大的机动性和便携性，无人机平台搭载视觉跟踪技术在路径规划、自主着陆、飞行避障等方面受到了广泛关注[1-3]。无人机工作过程不可避免地面临光线变化甚至光线条件恶劣的情况，这影响无人机目标跟踪对视频信息的提取与处理。因此，高效、准确地应对光线不足场景的目标跟踪方法对于无人机应用具有重要意义[4]。
基于相关滤波(correlation filter，CF)的目标跟踪算法由Bolme等[5]提出，经过Henriques[6]、Danelljan[7]、戴煜彤[8]和卢湖川等[9-10]学者的不懈努力，跟踪性能不断提高。BACF算法[11]提出具有背景感知能力的相关滤波器，充分利用背景信息增强算法的判别能力。SRDCF和ASRCF跟踪算法[12-13]构建空间或时空正则化，以缓解相关滤波跟踪器的边界效应。同时，刘威等[14]则尝试将特征融合与模板更新相结合，自适应学习场景信息。这些工作使基于相关滤波的跟踪器能够更好适应目标跟踪场景变化的要求。
随着无人机应用的发展，一些学者将相关滤波方法应用于无人机目标跟踪，取得了较好的进展[15]。AMCF[16]通过保持多帧信息构建更加鲁棒的目标模型，解决相关滤波跟踪器丢失历史信息的问题。OMFL[17]提取了更适应无人机跟踪场景的目标特征，通过融合多特征线索进行精确跟踪。王耀南等[18]结合多特征融合进一步提高跟踪精度。针对无人机相关滤波跟踪中边界效应显著的问题，AutoTrack[19]、BEVT[20]和SASR[21]等算法分别提出自适应时空正则化、在线增强背景信息学习策略和具有背景感知的选择性空间正则化。此外，针对无人机跟踪过程中可用信息较少的情况，ARCF[22]、CPCF[23]和BICF[24]算法探索跟踪过程响应映射中的隐藏信息，解决了无人机跟踪过程出现模型漂移的问题。
然而，当光照条件不充分时，无人机捕捉到的图像目标纹理和轮廓不清晰，颜色失真，且背景干扰严重。这些因素影响了跟踪方法对目标信息的提取与利用，降低了滤波器对目标模型的学习能力。因此目前无人机跟踪方法在光线不足场景中容易发生模型漂移，导致跟踪失败。
针对上述问题，本文提出一种基于光照自适应动态一致性的无人机目标跟踪算法（based on illumination adaptive dynamic consistent tracker for UAV，LADCT），利用跨帧响应构建具有目标感知的动态一致性评估，以实现在光照条件恶劣情况下进行准确跟踪。首先，构建一个光照自适应处理模块，通过光照检测技术识别跟踪场景的光照条件，对光照条件恶劣的视频图像进行光线增强。其次，构建目标掩码提取目标显著性特征，从而训练出具有目标语义感知能力的滤波器。此外，在使用目标感知滤波器进行相关运算时，利用跨帧之间的信息产生一致性评估以保证相邻帧目标一致。通过限制实际响应和理想化响应的误差、平滑跨帧之间的响应变化幅度，保证当前帧响应稳定，降低因为颜色失真，背景干扰带来的影响。最后，引入动态约束策略，随时间变化动态调整理想化响应及一致性响应评估，使一致性约束策略符合目标外观变化，进一步增强LADCT跟踪方法在无人机场景的适应性。在UAVDark135数据集和UAV123数据集上与其他9种先进跟踪算法进行对比实验，LADCT算法获得0.739和0.756的中心位置误差精度以及0.641和0.648的重叠率精度，表明算法在大多数挑战环境下都取得了较好的跟踪性能。
1. 光照自适应模块
为了使无人机在各种恶劣环境下准确地跟踪任务，构建了基于光照自适应动态一致性的无人机目标跟踪方法，具体流程如图1所示。首先构建光照自适应模块分析场景信息，对光线恶劣场景进行光照增强。由此，构建一种有效的光照表达算法计算图像中的光照信息。对于一张长宽为
$w \times h$ 的RGB图像${\boldsymbol{I}} \in {{\bf{R}}^3}^{wh}$ ，图像每个像素的光照值通过式（1）计算：
图 1 LADCT跟踪算法示意Fig. 1 Pipeline of LADCT tracking algorithm
下载:
全尺寸图片
$$ \mathcal{G}(x,y,{\boldsymbol{I}}) = \sum\limits_c {{\alpha _c}} {V_c}({{{ \boldsymbol I}}}(x,y)),c \in \{ {\text{R}},{\text{G}},{\text{B}}\} $$ (1) 式中：
${V_c}({\boldsymbol{I}}(x,y))$ 是坐标$ (x,y) $ 在图像${\boldsymbol{I}}$ 中颜色通道$ c $ 的强度值；$\alpha_c$ 为通道权重参数，且$\displaystyle\sum\limits_c {{\alpha _c}} = 1$ 。通过式（2）获得图像全局对数平均亮度$\tilde{\mathcal{G}}({\boldsymbol{I}})$ ：$$ \tilde{\mathcal{G}}({\boldsymbol{I}}) = \exp \left( {\frac{1}{{wh}}\sum\limits_{x,y} {\log } \left( {\delta + \mathcal{G}(x,y,{\boldsymbol{I}})} \right)} \right) $$ (2) 式中
$\delta $ 是一个用来避免出现零值的极小值。引入阈值$\theta $ 和$\tilde{\mathcal{G}}({\boldsymbol{I}})$ 进行对比，有效判断图像的光照条件：$$ D({\boldsymbol{I}})=\left\{\begin{aligned} &1,\quad{\tilde{\mathcal{G}}}(I) < \theta \\ &0,\quad{\tilde{\mathcal{G}}}(I)\geqslant \theta \end{aligned}\right. $$ (3) 当
$D({\boldsymbol{I}}) = 1$ 表示光线不足的场景。针对光线不足的恶劣场景，需要对其进行光照弥补。为了实现该目的，首先计算基于原始图像的全局光照自适应因子：
$$ \rho (x,y,{\boldsymbol{I}}) = \frac{{\log \left( {\mathcal{G}(x,y,{\boldsymbol{I}})/ {\tilde{\mathcal{G}}}({\boldsymbol{I}}) + 1} \right)}}{{\log \left( {\max (\mathcal{G}(x,y,{\boldsymbol{I}}))/{\tilde{\mathcal{G}}}({\boldsymbol{I}}) + 1} \right)}} $$ 通过计算所得的自适应因子，改变每个像素中3个强度通道的像素值实现图像光照增强：
$$ {{\boldsymbol{I}}_e}(x,y) = {{\boldsymbol{\varPsi}} _m}({\boldsymbol{I}}(x,y)) = {V_c}({{{\boldsymbol I}}}(x,y)) \cdot \frac{{\rho (x,y,{\boldsymbol{I}})}}{{\mathcal{G}(x,y,{\boldsymbol{I}})}} $$ (4) 式中：
${{\boldsymbol{I}}_{\text{e}}}$ 表示基于原始${\boldsymbol{I}}$ 的增强图像；$\mathcal{G}(x,y,{\boldsymbol{I}})$ 表示不同区域的光照值。式(4)可以在保持3个颜色通道比例不变的情况下，调整整个图像亮度，尽可能保持图像颜色不变。2. 跨帧语义感知一致性评估
图像的语义信息在目标跟踪中起着至关重要的作用，而通过光照增强后的图像语义信息存在退化，容易导致跟踪失败发生。因此提出一种对光照增强后目标语义信息显著性增强的滤波器。通过增强跟踪器对被跟踪对象区域的显著性感知能力，进一步提高跟踪性能。
首先，在训练过程中，构建一个目标掩码
$m$ ，加强跟踪器对目标和背景的判别能力：$$ m(x,y)=\left\{\begin{aligned} &1,\quad \mu -3\sigma < {\boldsymbol{M}}(x,y) \\ &0,\quad \text{ }其他\text{ } \end{aligned}\right. $$ 式中：
$ {\boldsymbol{M}} $ 为对输入图像中目标区域设置为1，其他区域设置为0的目标显著性图像；（x，y）表示每个像素的坐标；$ \mu $ 和$ \sigma $ 是显著图$ {\boldsymbol{M}} $ 中目标区域的均值和方差。根据图像信息的概率分布特征，使用阈值$ \mu - 3\sigma $ 过滤噪声信息。通过得到的掩码$m$ ，得出目标特征$f'(x) = f(x) \odot m$ ，其中$x$ 是目标检测样本。此外，为减少光照自适应模块增强图像过程中带来的噪声干扰问题，构建跨帧动态一致性评估。首先研究相邻帧目标响应之间的相似性：
$$ \left\{ {\begin{aligned} &{{{\boldsymbol{R}}_{t - 1}} = \displaystyle\sum\limits_{d = 1}^D {{\boldsymbol{w}}_{t - 1}^d} \star {\boldsymbol{z}}_{t - 1}^d} \\ &{{\boldsymbol{R}}_t^\prime = \displaystyle\sum\limits_{d = 1}^D {{\boldsymbol{w}}_t^d} \star {\boldsymbol{x}}_t^d} \end{aligned}} \right. $$ 式中：
${\boldsymbol{w}}_{t - 1}^d$ 和${\boldsymbol{w}}_t^d$ 表示目标感知第$t-1 $ 帧和第t帧的相关滤波器；下标$ t - 1 $ 和$ t $ 分别表示第$ t - 1 $ 帧和第$ t $ 帧；上标$ d $ 表示第$ d $ 个通道；${\boldsymbol{z}}_{t - 1}^d$ 和${\boldsymbol{x}}_t^d$ 分别表示目标样本和检测样本；操作符$\star$ 为循环相关运算。第
$ t - 1 $ 帧的目标响应${{\boldsymbol{R}}_{t - 1}}$ 和第$ t $ 帧的检测响应$ {\boldsymbol{R}}_t^\prime $ 之间具有很强的时间序列相关性，在帧间一致性中隐藏了大量的时间信息。为了利用这些时间信息，采用循环相关运算对响应之间的一致性进行评估，计算公式为$$ {{\boldsymbol{C}}_t} = {\boldsymbol{R}}_t^\prime \star {{\boldsymbol{R}}_{t - 1}}\left[ {\Delta {\tau _{u,v}}} \right] $$ (5) 式中：
${{\boldsymbol{C}}_t} \in {{\bf{R}}^N}$ 为一致性映射；下标$ u $ 和$ v $ 分别表示目标响应${{\boldsymbol{R}}_{t - 1}}$ 与检测响应$ {\boldsymbol{R}}_t^\prime $ 之间的峰值位置的空间差异；运算符$\left[ {\Delta {\tau _{u,v}}} \right]$ 表示将${{\boldsymbol{R}}_{t - 1}}$ 的峰值位移到与检测响应的峰值对应的位置。理想情况下，响应
$ {\boldsymbol{R}}_t^\prime $ 和${{\boldsymbol{R}}_{t - 1}}$ 等于理想响应${{\boldsymbol{y}}_t}$ 和${{\boldsymbol{y}}_{t - 1}}$ 。一个理想的一致性映射应该由两个理想的响应${\boldsymbol{y}}$ 来生成。将理想一致性映射作为实际一致性映射${{\boldsymbol{C}}_t}$ 的约束标签，设计一个约束标签${{\boldsymbol{l}}_t}$ ，如式（6）:$$ {{\boldsymbol{l}}_t} = {{\boldsymbol{y}}_t} \star {{\boldsymbol{y}}_{t - 1}} $$ (6) 通过标签
${{\boldsymbol{l}}_t}$ 可以对${{\boldsymbol{C}}_t}$ 施加最大的一致性约束:$$ \left\| {{{\boldsymbol{l}}_t} - {{\boldsymbol{C}}_t}} \right\|_2^2 $$ (7) 最小化
${{\boldsymbol{l}}_t}$ 和${{\boldsymbol{C}}_t}$ 之间的平方误差，从而使响应$ {\boldsymbol{R}}_t^\prime $ 和${{\boldsymbol{R}}_{t - 1}}$ 具有较高的一致性，有效提取时间信息。由于不同的跟踪场景，物体的外观变化速率不同，标签
${{\boldsymbol{l}}_t}$ 应该适应目标外观的变化速率，而不是强制执行固定的一致性约束。因此，在式(5)约束标签的基础上，进一步提出动态约束标签:$$ {{\boldsymbol{l}}_t} = {h_t}{{\boldsymbol{l}}_t'} $$ 式中
$ {h_t} $ 为调整约束强度一致性的动态调节因子。跟踪器的一致性约束强度需要符合不同的场景需求，如在快速运动、视觉变化等场景跟踪器会降低约束强度，从而更好学习到目标的外观变化。另一方面，如果外观变化是平滑的，则需要一个较高的一致性约束来增强跟踪器的鲁棒性。因此，根据目标响应
${{\boldsymbol{R}}_t}$ 的质量，计算其质量分数：$$ \Theta = \frac{{\max ({{\boldsymbol{R}}_{t - 1}}) - {\mu _{s1}}}}{{{\sigma _{s1}}}} + \beta \max ({{\boldsymbol{R}}_{t - 1}}) $$ 式中：第1项和第2项分别表示响应图中的峰值旁瓣比和峰值；
${\mu _{s1}}$ 和${\sigma _{s1}}$ 分别表示旁瓣的均值和标准差；$ \beta $ 是平衡两个评价指标的权重系数。引入的动态调节因子$ {h_t} $ 为$$ {h_t} = \min ({{\boldsymbol{l}}_t}) + \frac{\Theta }{\varsigma }\left( {\max ({{\boldsymbol{l}}_t}) - \min ({{\boldsymbol{l}}_t})} \right) $$ 式中：
$ \min ({{\boldsymbol{l}}_t}) $ 和$ \max ({{\boldsymbol{l}}_t}) $ 分别表示${{\boldsymbol{l}}_t}$ 的最小值和最大值；$ \varsigma $ 是一个归一化的系数。3. 总体跟踪框架
为了实现基于光照自适应动态一致性的无人机目标跟踪器，构建跟踪器模板函数为
$$ \begin{gathered} \mathcal{E}\left( {{{\boldsymbol{w}}_t}} \right) = \frac{1}{2}\left\| {{\boldsymbol{y}} - \sum\limits_{d = 1}^D {{\boldsymbol{w}}_t^d} \star {{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^d} \right)} \right\|_2^2 + \frac{1}{2}\sum\limits_{d = 1}^D {\left\| {{\boldsymbol{s}}_t^d{\boldsymbol{w}}_t^d} \right\|_2^2} + \\ \frac{{{\gamma _{\text{1}}}}}{2}\sum\limits_{d = 1}^D {\left\| {{{\boldsymbol{l}}_t} - \left( {\sum\limits_{d = 1}^D {{\boldsymbol{w}}_t^d} \star {{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^d} \right)} \right) \star {{\boldsymbol{R}}_t}\left[ {\Delta {\tau _{u,v}}} \right]} \right\|_2^2} \end{gathered} $$ (8) 总体目标损失函数包含3项：第1项为评估跟踪误差，第2项引入空间正则化，最后1项构建动态一致性正则化避免模型漂移。其中，
${{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^d} \right)$ 表示受到图像增强后的训练样本，在光照充足的场景下${{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^d} \right) = {\boldsymbol{x}}_t^d$ ；${\boldsymbol{w}}_t^d$ 表示相关滤波器的第d通道；第2项中引入空间权值函数${\boldsymbol{s}}_t^d$ 缓解边界效应；第3项中的${\gamma _1}$ 为一致性惩罚系数。为方便计算，将公式转换为频域。首先将式（8）表示为矩阵形式，即
$$ \begin{gathered} \mathcal{E}\left( {{{\boldsymbol{w}}_t}} \right) = \frac{1}{2}\left\| {{\boldsymbol{y}} - {{\boldsymbol{\chi }}_t}{{\boldsymbol{w}}_t}} \right\|_2^2 + \frac{1}{2}\left\| {{{\boldsymbol{s}}_t}{{\boldsymbol{w}}_t}} \right\|_2^2 + \\ \frac{{{\gamma _1}}}{2}\left\| {{{\boldsymbol{l}}_t} - {{\boldsymbol{R}}^ {\rm{T}} }{{\boldsymbol{\chi }}_t}{{\boldsymbol{w}}_t}} \right\|_2^2{\text{ }} + {\text{ }}\frac{{{\gamma _2}}}{2}\left\| {{{\boldsymbol{\chi }}_t}{{\boldsymbol{B}}^ {\rm{T}} }{{\boldsymbol{w}}_t} - {R_m}} \right\|_2^2 \end{gathered} $$ (9) 式中：
${\boldsymbol{y}} = {[ {{\boldsymbol{y}}(1)}\;{{\boldsymbol{y}}(2)} \;\cdots\; {\boldsymbol{y}}(N)]^ {\rm{T}} }$ ；${{\boldsymbol{w}}_t} = {\left[ {{\boldsymbol{w}}_t^{1 {\rm{T}} }}\;{{\boldsymbol{w}}_t^{2 {\rm{T}} }} \; \cdots \;{\boldsymbol{w}}_t^{D {\rm{T}} } \right]^ {\rm{T}} }$ ；${{\boldsymbol{s}}_t} = {\left[ {{\boldsymbol{s}}_t^{1 {\rm{T}} }}\;{{\boldsymbol{s}}_t^{2 {\rm{T}} }} \cdots {\boldsymbol{s}}_t^{D {\rm{T}} } \right]^ {\rm{T}}}$ ；${{\boldsymbol{\chi }}_t} = \left[ {{\boldsymbol{\varPsi}} _m}\left( {{{\boldsymbol{x}}_1}} \right){{\left[ {\Delta {\tau _1}} \right]}^ {\rm{T}} }\;{{{\boldsymbol{\varPsi}} _m}\left( {{{\boldsymbol{x}}_2}} \right){{\left[ {\Delta {\tau _2}} \right]}^ {\rm{T}} }} \cdots\right. \left. {{\boldsymbol{\varPsi}} _m}\left( {{{\boldsymbol{x}}_t}} \right){{\left[ {\Delta {\tau _N}} \right]}^ {\rm{T}} } \right]^ {\rm{T}}$ ；${{\boldsymbol{\varPsi}} _m}\left( {{{\boldsymbol{x}}_t}} \right){\left[ {\Delta {\tau _N}} \right]^ {\rm{T}} }$ 表示在增强图像上循环移位的训练样本；${\boldsymbol{R}}$ 为位移检测响应产生的圆形矩阵$ {{\boldsymbol{R}}_t}\left[ {\Delta {\tau _{u,v}}} \right] $ ；运算符$ {\rm{T}} $ 表示共轭转置操作。为了提高计算效率，将式（9）进一步转换为频域，具体如下：$$ \begin{gathered} \mathcal{E}\left( {{{\boldsymbol{w}}_t},{\hat {\boldsymbol{\alpha}}_t}} \right) = \frac{1}{2}\left\| {\hat {\boldsymbol{y}} - {\hat {\boldsymbol{\chi}}_t}{\hat {\boldsymbol{\alpha }}_t}} \right\|_2^2 + \frac{1}{2}\left\| {{{\boldsymbol{s}}_t}{{\boldsymbol{w}}_t}} \right\|_2^2\; + \\ \frac{\gamma }{2}\left\| {{\hat {\boldsymbol{1}}_t} - {\boldsymbol{\hat \chi }}_t^r{{{\boldsymbol{\hat \alpha }}}_t}} \right\|_2^2\quad{\text{s}}.{\text{t}}.\;\;{{\hat {\boldsymbol{\alpha }}}_t} = \sqrt N {\boldsymbol{F}}{{\boldsymbol{w}}_t} \end{gathered} $$ (10) 式中：
${{\boldsymbol{\hat \alpha }}_t} \in {\boldsymbol{C}^{DN \times 1}}$ 是引入的辅助变量；上标ˆ表示一个信号的离散傅里叶变换(DFT)。将矩阵${{\boldsymbol{\hat \chi }}_t}$ 和${\boldsymbol{\hat \chi }}_t^r$ 分别定义为${{\boldsymbol{\hat \chi }}_t} = \left[ {{\text{diag}}{{\left( {{{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^1} \right)} \right)}^ {\rm{T}} }}\;\;\;{{\text{diag}}{{\left( {{{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^2} \right)} \right)}^ {\rm{T}} }} \;\;\;\cdots \;\;\; {\text{diag}}{{\left( {{{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^D} \right)} \right)}^ {\rm{T}}} \right]$ 和${\boldsymbol{\hat \chi }}_t^r \;=\; \left[ {{\text{diag}}{{\left( {{\boldsymbol{\hat r}}_t^1 \;\odot\; {{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^1} \right)} \right)}^ {\rm{T}} }}\;\;\;{\rm{diag}}\left( {\boldsymbol{\hat r}}_t^1 \;\odot \right.\right.$ $\left. \left.{{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^2} \right) \right)^ {\rm{T}} \;\;\; \cdots \;\;\;{\text{diag}}{{\left( {{\boldsymbol{\hat r}}_t^1 \odot {{\boldsymbol{\varPsi}} _m}\left( {{\boldsymbol{x}}_t^1} \right)} \right)}^ {\rm{T}} } \right]$ 。其中，运算符$ \odot $ 表示元素点乘，${{\boldsymbol{\hat r}}_t}$ 是移位检测响应${{\boldsymbol{R}}_t}\left[ {\Delta {\tau _{u,v}}} \right]$ 的离散傅里叶变换。考虑式(10)具有凸性，引入交替方向乘子法，有效地获得全局最优解。将式（10）表示为增广拉格朗日形式：$$ \begin{gathered} \mathcal{L}{(w,\hat \alpha ,\hat {\boldsymbol{\zeta}} )} = \frac{1}{2}\left\| {{\hat y} - {{{\hat {\boldsymbol{\chi}} }}_t}{{{\hat {\boldsymbol{\alpha}} }}_t}} \right\|_{\text{2}}^{\text{2}} + \frac{1}{2}\left\| {{{s}_t}{{w}_t}} \right\|_{\text{2}}^{\text{2}}\; + \\ \frac{\gamma }{2}\left\| {{{{\hat {\boldsymbol{1}}}}_t} - {\hat {\boldsymbol{\chi}} }_t^r{{{\hat {\boldsymbol{\alpha}} }}_t}} \right\|_2^2\; + \;{{\hat {\boldsymbol{\zeta}} }^ {\rm{T}} }\left( {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt {N} {F}{{w}_t}} \right)\; + \\ \frac{\nu }{2}\left\| {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt {N} {F}{{w}_t}} \right\|_2^2 \\ \end{gathered} $$ (11) 式中：
$\hat {\boldsymbol{\zeta}} \in {{\bf{C}}^{DN \times 1}}$ 表示在傅里叶域中的拉格朗日向量；$ \nu $ 为惩罚因子。利用增广拉格朗日形式，第t+1帧的滤波器可以通过ADMM算法交替求解子问题方法进行求解。求解子问题
$ {w}_{t + 1}^* $ ：$$ \begin{gathered} {w}_{t + 1}^* = \mathop {\arg \min }\limits_{{{w}_t}} \Bigg\{ {\frac{1}{2}\left\| {{{s}_t}{{w}_t}} \right\|_2^2 + {{\hat {\boldsymbol{\zeta}} }^ {\rm{T}} }\left( {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt N {\boldsymbol{F}}{{w}_t}} \right)} \; + \\ {\;\;\;\;\;\frac{\nu }{2}\left\| {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt N {\boldsymbol{F}}{{w}_t}} \right\|_2^2} \Bigg\}\; = {\left( {{{{\boldsymbol{S}}}^ {\rm{T}} }{{\boldsymbol{S}}} + \nu } \right)^{ - 1}}({\boldsymbol{\zeta}} + \nu {\boldsymbol{g}}) \end{gathered} $$ (12) 式中
${{\boldsymbol{S}}}$ 由$D$ 个对角矩阵$ \text{diag}({s}) $ 连接而成。求解子问题
$ {\hat \alpha }_{t + 1}^* $ ：$$ \begin{gathered} {\hat \alpha }_{t + 1}^*{ = }\mathop {{\text{argmin}}}\limits_{{{{\hat \alpha }}_{t}}(n)} \Bigg\{ {\frac{{\text{1}}}{{\text{2}}}\left\| {{\hat y} - {{{\hat {\boldsymbol{\chi}} }}_t}{{{\hat {\boldsymbol{\alpha}} }}_t}} \right\|_{\text{2}}^{\text{2}}\;{ + }\frac{{\gamma }}{{\text{2}}}\left\| {{{{\hat {\boldsymbol{1}}}}_t} - {\hat {\boldsymbol{\chi}} }_t^r{{{\hat {\boldsymbol{\alpha}} }}_t}} \right\|_{\text{2}}^{\text{2}}{ + }} \\ {{{{\hat {\boldsymbol{\zeta}} }}^ {\rm{T}} }\left( {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt {N} {F}{{w}_t}} \right){ + }\frac{{\nu }}{{2}}\left\| {{{{\hat {\boldsymbol{\alpha}} }}_t} - \sqrt {N} {F}{{w}_t}} \right\|_{\text{2}}^{\text{2}}} \Bigg\} \end{gathered} $$ 式中的
${{{\hat {\boldsymbol{\chi}} }}_{{t}}}$ 和${{\hat {\boldsymbol{\chi}} }}_{{t}}^{{r}}$ 具有稀疏性，因此$ \hat y $ 中的每个元素只与${{\hat {\boldsymbol{\chi}} }_t}{\text{(}}n{\text{)}}{ = }{\left[ {{\hat \chi }_t^1{\text{(}}n{\text{)}},\;{\hat \chi }_{t}^{2}{\text{(}}n{\text{)}}, \;\cdots {\text{,}}\;{\hat \chi }_t^D{\text{(}}n{\text{)}}} \right]^ {\rm{T}} }$ 和${{{\hat {\boldsymbol{\alpha}} }}_t}{\text{(}}n{\text{) = }}\left[ {\text{conj}}\left( {{{\hat \alpha }}_t^1{\text{(}}n{\text{)}}} \right), \;{\text{conj}}\left( {{{\hat \alpha }}_t^2{\text{(}}n{\text{)}}} \right) , \;\cdots ,\;{\text{conj}}\left( {{{\hat \alpha }}_t^D{\text{(}}n{\text{)}}} \right) \right]^ {\rm{T}}$ 相关。运算符$ {\text{conj}}\left( {} \right) $ 表示复共轭。子问题$ {\hat \alpha }_{{t + 1}}^{*} $ 可以分解为N个独立的子目标进行求解：$$ \begin{gathered} {\hat \alpha }_{{t + 1}}^{*}{\text{(}}n{\text{)}} = \mathop {\arg \min }\limits_{{{{{\hat {\boldsymbol{\alpha}} }}}_{\boldsymbol{t}}}(n)} \Bigg\{ {\frac{1}{2}\left\| {{\hat y}{\text{(}}n{\text{)}} - {{{\hat {\boldsymbol{\chi}} }}_t}{{(n)}^ {\rm{T}} }{{{\hat {\boldsymbol{\alpha}} }}_t}{\text{(}}n{\text{)}}} \right\|_{\text{2}}^{\text{2}}} { + } \\ \frac{{\gamma }}{{\text{2}}}\left\| {{{{\hat {\boldsymbol{1}}}}_{t}}{\text{(}}n{\text{)}} - {\hat {\boldsymbol{\chi}} }_{t}^{r}{{{\text{(}}n{\text{)}}}^ {\rm{T}} }{{{\hat {\boldsymbol{\alpha}} }}_t}{\text{(}}n{\text{)}}} \right\|_{\text{2}}^{\text{2}}{ + } \\ {\hat {\boldsymbol{\zeta}} }{{\text{(}}n{\text{)}}^ {\rm{T}} }\left( {{{{\hat {\boldsymbol{\alpha}} }}_{t}}{\text{(}}n{\text{)}} - {{{\hat {\boldsymbol{w}}}}_t}{\text{(}}n{\text{)}}} \right)\;{{ + }\frac{{\nu }}{{\text{2}}}\bigg\| {{{{\hat {\boldsymbol{\alpha}} }}_t}{\text{(}}n{\text{)}} - {{{\hat {\boldsymbol{w}}}}_t}{\text{(}}n{\text{)}}} \bigg\|_{\text{2}}^{\text{2}}} \Bigg\} \end{gathered} $$ 式中
${{\boldsymbol{\hat w}}_t}(n) = \left[ {{\boldsymbol{\hat w}}_t^1(n)}\;\;{{\boldsymbol{\hat w}}_t^2(n)} \;\;\cdots \;\;{\boldsymbol{\hat w}}_t^D(n) \right]$ 。因此每个子目标可以通过以下方法求得：$$ \begin{gathered} {{\hat {\boldsymbol{a}}}}_{t + 1}^*(n) = \frac{1}{{1 + \gamma {{\hat {\boldsymbol{w}}}_t}(n){{\hat {\boldsymbol{w}}}_t}{{(n)}^ {\rm{T}} }}}\times\\ {\left( {{{{\hat {\boldsymbol{\chi}} }}_t}(n){{{\hat {\boldsymbol{\chi}} }}_t}{{(n)}^ {\rm{T}} } + \frac{\nu }{{1 + \gamma {{\hat {\boldsymbol{w}}}_t}(n){{\hat {\boldsymbol{w}}}_t}{{(n)}^ {\rm{T}} }}}} \right)^{ - 1}} \times \\ \left( {{{{{\hat {\boldsymbol{\chi}} }}}_t}(n){{{{\hat {\boldsymbol{y}}}}}_t}(n) + \gamma {{\hat{\boldsymbol {\chi}} }}_t^r(n){{{{\hat{ \boldsymbol{1}}}}}_t}(n) - \hat {\boldsymbol{\zeta}} (n) + \nu {{{{\hat{\boldsymbol {w}}}}}_t}(n)} \right) \\ \end{gathered} $$ (13) 式（13）采用谢尔曼–莫里森公式，可以表示为
$$ \begin{gathered} \hat a_{t + 1}^*{(n)^*} = \frac{1}{\nu }\left( {{{{\hat {\boldsymbol{\chi}} }}_t}(n){{\hat {\boldsymbol{y}}}_t}(n) + {{\hat{\boldsymbol{\chi}} }}_t^r(n){{\hat {\boldsymbol{1}}}_t}(n) - \hat {\boldsymbol{\zeta}} (n) + \nu {{\hat{\boldsymbol{ w}}}_t}(n)} \right) -\\ \frac{{{\hat {\boldsymbol{\chi}}_t}(n)}}{b}\left( {{\hat {\boldsymbol{s}}_{{{\boldsymbol{\chi }}_{\boldsymbol{t}}}}}(n)\hat {\boldsymbol{y}}(n) - \gamma {\hat {\boldsymbol{s}}_{{{\boldsymbol{\chi }}_t}}}(n){\hat {\boldsymbol{1}}_t}(n){{\hat{\boldsymbol {s}}}_\zeta }(n) + \nu {{\hat{\boldsymbol {s}}}_{{{\boldsymbol{w}}_t}}}(n)} \right) \end{gathered} $$ 其中
$$ \left\{ {\begin{aligned} &{{{{{\hat {\boldsymbol{s}}}}}_{{{\boldsymbol{\chi }}_{\boldsymbol{t}}}}}(n) = {{{{\hat {\boldsymbol{\chi}} }}}_t}{{(n)}^ {\rm{T}} }{{{{\hat {\boldsymbol{\chi}} }}}_t}(n)} \\ &{{{{{\hat {\boldsymbol{s}}}}}_\zeta }(n) = {{{{\hat {\boldsymbol{\chi}} }}}_t}{{(n)}^ {\rm{T}} }\hat {\boldsymbol{\zeta}} } \\ &{{{{{\hat {\boldsymbol{s}}}}}_{{{\boldsymbol{w}}_{\boldsymbol{t}}}}}(n) = {{{{\hat {\boldsymbol{\chi}} }}}_t}{{(n)}^ {\rm{T}} }{{{{\hat {\boldsymbol{w}}}}}_t}} \\ &{b = {{{{\hat {\boldsymbol{\chi}} }}}_t}{{(n)}^ {\rm{T}} }{{{{\hat {\boldsymbol{\chi}} }}}_t}(n) + \frac{\nu }{{1 + \gamma {{\hat {\boldsymbol{w}}}_t}(n){{\hat {\boldsymbol{w}}}_t}{{(n)}^ {\rm{T}} }}}} \end{aligned}} \right. $$ 拉格朗日参数
$ \zeta $ 在每次迭代中按式（14）更新:$$ \hat \zeta _{t + 1}^{j + 1} = \hat \zeta _{t + 1}^j + \nu \left( {{\boldsymbol{\hat \alpha }}_{t + 1}^{*(j + 1)} - {\boldsymbol{\hat w}}_{t + 1}^{*(j + 1)}} \right) $$ (14) 式中上标
$j$ 和$j{\text{ + }}1$ 表示第$j$ 和$j{\text{ + }}1$ 次迭代。在式（12）和式（13）中，$ {w}_{t + 1}^* $ 的解只需进行逐元素乘法和快速傅里叶反变换，因此求解$ {w}_{t + 1}^* $ 和$ {{\hat \alpha }_t} $ 的计算复杂度分别为O (D log D)和O (ND log D)。为了进一步提高算法的鲁棒性，引入在线自适应策略:
$$ {{\boldsymbol{\hat \chi }}_t} = (1 - \eta ){{\boldsymbol{\hat \chi }}_{t - 1}} + \eta {{\boldsymbol{\hat \chi }}_t} $$ (15) 式中
$ \eta $ 为外观模型的学习速率。为了实现无人机在光线不足场景进行准确跟踪，将光照自适应模块和动态一致性模块嵌入算法 ，具体流程如算法1所示。首先通过光照自适应模块判断无人机工作环境是否需要光照增强，然后利用动态一致性模块对滤波器学习进行约束，从而达到精确跟踪的目标。最后利用ADMM算法优化跟踪速度。
算法1 基于光照自适应动态一致性的无人机目标跟踪（LADCT）
输入 视频序列I 目标初始化信息；
输出 视频序列中每一帧的目标位置和尺寸。
1）通过式（2）计算出平均亮度值
$\tilde{\mathcal{G}}({\boldsymbol{I}}) $ ，并根据式（3）通过得出的环境标识符$D({\boldsymbol{I}}) $ 确定是否进行图像增强处理；若需要则通过式（4）增强图像；2）确定目标搜索区域，构建目标掩码，并提取具有目标感知的特征；
3）提取目标区域特征与已学习到的滤波器进行相关操作得到初始响应图；
4）通过式（5）和式（7）对相邻两帧的响应构建动态一致性标签及约束策略；
5）采用ADMM算法对式（11）求得最终响应，得到该帧目标位置；
6）采用式（15）策略更新模型；
7）如果是最后一帧则停止算法；否则重复执行步骤2）~6）。
返回跟踪结果。
4. 实验结果与分析
所有实验使用Ubuntu18.04，计算机配置Intel Core I9-9900K CPU和32 GB内存。LADCT算法的主要参数设置如表1所示。其中大部分是通过参数敏感性实验测试所得。LADCT采用HOG和CN对目标特征进行提取。
表 1 LADCT算法的主要参数设置Table 1 Main parameter settings of the LADCT algorithm参数名称 代表含义 设置值 $\theta $ 光照自适应模块阈值 280 $\eta $ 模型学习速率 0.042 $\gamma $ 动态一致性正则化系数 0.9 $\varsigma $ 归一化系数 50 $\beta $ 一致性评价权重系数 100 4.1 对比数据集
为了验证LADCT算法的有效性，在由无人机拍摄的视频数据集UAVDark135和UAV123上进行对比实验。UAVDark135[25]是第1个无人机黑暗场景下的跟踪基准，包含由无人机在夜间捕获的135个序列。UAV123数据集包含共计123个无人机拍摄的视频序列以及超过11万帧无人机图像。这两个数据基准包括各种跟踪场景，如十字路口、丁字路口、道路、高速公路等，以及不同种类的跟踪对象，如人、船、汽车、卡车、房子等。将LADCT与ARCF、BiCF、AutoTrack、BACF、ASRCF、SRDCF、CPCF、SASR、ADTrack这9种跟踪算法进行对比。
为更好地评估无人机跟踪器在特殊挑战下的能力，UAVDark135数据集提供了无人机跟踪中经常遇到的5个挑战属性，即视点变化(VC)、快速运动(FM)、低分辨率(LR)、遮挡(OCC)和照明变化(IV)。
此外，为了验证LADCT方法的普适性，在最具代表性的无人机UAV123数据集上进行对比验证，其具有12个挑战属性，包括长宽比变化(ARC)、背景杂波(BC)、摄像机运动(CM)、快速运动(FM)、全遮挡(FOC)、照明变化(IV)、低分辨率(LR)、视觉越界(OV)、部分遮挡(POC)、尺度变化(SV)、类似对象(SOB)和视点变化(VC)。
4.2 评价指标
为了公平且有效地评估算法的跟踪精度，采用中心误差（center location error，CLE）和重叠率（overlap rate，OR）作为评价指标。中心误差是指目标真实位置与算法所跟踪到位置的欧氏距离，其距离小于一个设定的阈值则表示跟踪成功，反之则为失败；重叠率计算的是目标真实的边界框与算法跟踪到的边界框的重叠区域占整个目标区域的比例，将重叠比例与阈值相比较来判断是否跟踪成功。本文使用这两个指标计算跟踪成功的视频帧占总视频帧的比例，对跟踪方法进行定量评估。UAVDark135数据集采用的中心误差阈值为20，重叠率阈值为0.5。
4.3 结果分析
4.3.1 总体分析
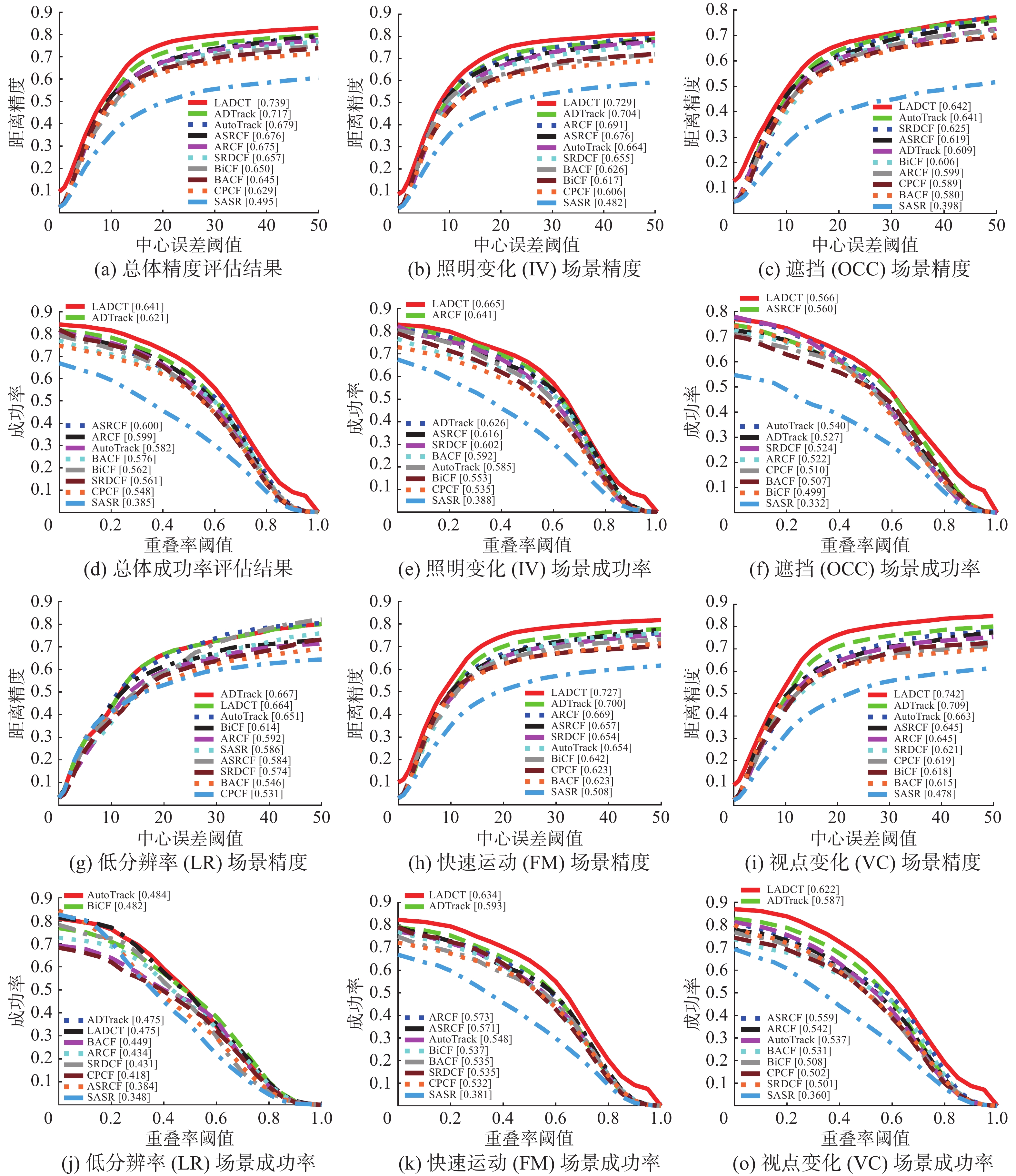
图2给出了LADCT算法与对比的9种方法的综合评估结果。实验表明：LADCT在UAVDark135和UAV123数据集上的综合精度与准确率皆取得了第一的表现。
图 2 提出的方法与9种方法的综合评价结果Fig. 2 Comprehensive evaluation results of the proposed method and nine other methods下载:
全尺寸图片
在UAVDark135数据集中，较之第2名ADTrack，LADCT算法在精度和准确率上分别提升了0.22和0.20。此外，较之基准跟踪器BACF、LADCT算法则分别提高了14.5%和11.3%。这是因为提出的光照自适应模块使跟踪算法能够在昏暗环境下自适应补偿光照信息，从而提取更多的目标信息，提高学习到目标模型的准确性。此外，构建目标掩码不仅能提取目标显著性的特征，还能保存光照增强后的语义信息，缓解光照自适应模块带来的语义信息退化问题，使得训练的滤波器对前景和背景具有更强的判别能力。最后构建动态一致性标签及采用跨帧感知语义动态一致性约束策略，进一步提高了跟踪器对目标的感知能力，降低了目标模型学习过程中受到背景干扰的影响，提高了算法的鲁棒性。
在UAV123数据集中，LADCT算法依然取得良好的表现。对比第2名ASRCF，精度和准确率分别提升0.18和0.31，而对比基准BACF、LADCT算法分别提升了15.1%和16.2%，说明LADCT算法在光照充足环境下同样具有优异的跟踪性能。这是因为提取了对目标具有感知能力的特征，保存更多的目标语义信息，从而训练更加鲁棒的滤波器。动态一致性策略利用跨帧之间的时间信息，构建一致性标签，提高滤波器对目标模型的学习效率，从而提高无人机跟踪的准确性。
4.3.2 属性分析
为了更加清晰地评估跟踪算法在特定挑战下的跟踪性能，图3给出了LADCT算法与其他9种先进跟踪器在UAVDark135数据集上5种无人机跟踪挑战属性(视点变化、快速运动、低分辨率、遮挡和照明变化)的跟踪结果。
图 3 LADCT在UAVDark135数据集上的5种挑战属性评价结果Fig. 3 Evaluation results of five challenge attributes of LADCT in the UAVDark dataset下载:
全尺寸图片
实验表明：LADCT算法在视点变化、快速运动、遮挡和照明变化4种挑战属性环境下取得较好的跟踪表现，LADCT分别取得0.742、0.727、0.642、0.729的中心位置误差和0.622、0.634、0.562、0.665的重叠率。在VC和FM挑战环境下，LADCT算法通过构建动态一致性约束策略，能够在视点或者物体快速变化时自适应学习到变化的目标外观，同时由于利用了跨帧之间的时空信息抑制响应畸变，使得算法能够更平稳更新滤波器，保证了算法的鲁棒性。在IV属性下，LADCT与ADTrack算法同样针对光照进行了弥补，而LADCT算法表现优于ADTrack算法。这是因为构建了具有目标感知能力的动态一致性标签与约束策略，使得LADCT算法鲁棒性更强，在训练过程中可以保留目标的语义信息，从而降低光照变化对学习目标模型的干扰。同时在OCC属性下，LADCT也取得较好的表现，分别取得0.642的最佳中心位置误差和0.562的重叠率精度。这是因为跨帧动态一致性约束在跟踪器丢失目标时降低了学习速率，从而保留多帧之前的目标信息。然而，在低分辨率场景下LADCT算法表现不佳，不及第1名的AutoTrack。这是因为当分辨率过低时，目标掩码会误将背景像素的信息当作目标从而使滤波器学习到背景干扰信息。此外，表2和表3给出了在UAV123数据集上，LADCT算法在12种挑战环境下的表现，可见在大多数挑战下，LADCT算法都获得了最佳的表现。再次验证LADCT算法在无人机跟踪方面具有鲁棒性和精确度。
表 2 不同算法在UAV123数据集不同挑战场景的中心位置误差结果对比Table 2 Comparison of the center position error results of different algorithms in different challenge scenarios of the UAV123 dataset算法名称 ARC BC CM FM FOC IV LR OV POC SV SOB VC CPCF 0.593 0.567 0.633 0.541 0.457 0.602 0.584 0.515 0.548 0.626 0.643 0.590 BiCF 0.600 0.556 0.651 0.569 0.504 0.618 0.602 0.580 0.583 0.653 0.634 0.628 SASR 0.590 0.597 0.649 0.558 0.540 0.645 0.639 0.554 0.598 0.636 0.707 0.643 BACF 0.576 0.531 0.639 0.518 0.436 0.525 0.520 0.543 0.564 0.617 0.673 0.587 SRDCF 0.587 0.526 0.627 0.524 0.501 0.600 0.579 0.576 0.608 0.639 0.678 0.593 AutoTrack 0.628 0.579 0.660 0.542 0.464 0.629 0.595 0.562 0.586 0.654 0.661 0.624 ASRCF 0.653 0.629 0.728 0.661 0.576 0.691 0.643 0.604 0.669 0.705 0.717 0.683 ARCF 0.602 0.552 0.647 0.515 0.445 0.595 0.565 0.531 0.573 0.630 0.682 0.596 ADTrack 0.619 0.611 0.661 0.565 0.490 0.623 0.629 0.579 0.595 0.663 0.699 0.615 LADCT 0.692 0.642 0.739 0.679 0.568 0.720 0.652 0.631 0.654 0.721 0.747 0.697 表 3 不同算法在UAV123数据集不同挑战场景的重叠率结果对比Table 3 Comparison of the overlap rate results of different algorithms in different challenge scenarios of the UAV123 dataset算法名称 ARC BC CM FM FOC IV LR OV POC SV SOB VC CPCF 0.438 0.431 0.510 0.371 0.276 0.472 0.393 0.422 0.433 0.501 0.514 0.430 BiCF 0.463 0.416 0.544 0.416 0.297 0.499 0.379 0.490 0.459 0.530 0.531 0.500 SASR 0.421 0.371 0.467 0.367 0.292 0.447 0.375 0.453 0.415 0.448 0.493 0.404 BACF 0.442 0.380 0.538 0.387 0.251 0.411 0.334 0.461 0.442 0.509 0.544 0.454 SRDCF 0.431 0.401 0.512 0.366 0.301 0.457 0.359 0.465 0.468 0.510 0.532 0.441 AutoTrack 0.467 0.413 0.542 0.402 0.269 0.469 0.388 0.455 0.456 0.525 0.529 0.463 ASRCF 0.499 0.424 0.624 0.496 0.358 0.523 0.409 0.507 0.548 0.575 0.602 0.523 ARCF 0.466 0.443 0.543 0.379 0.266 0.485 0.386 0.452 0.466 0.524 0.554 0.466 ADTrack 0.452 0.396 0.546 0.421 0.277 0.472 0.399 0.464 0.464 0.532 0.567 0.453 LADCT 0.513 0.479 0.632 0.513 0.359 0.542 0.416 0.519 0.507 0.594 0.639 0.537 4.3.3 定性分析
为了更直观展示LADCT算法的有效性，图4给出了LADCT与ADTrack、AutoTrack、SRDCF、ARCF等4种跟踪算法在5个视频上的可视化对比图。其中前3个是夜晚场景，后两个是白天跟踪场景。通过第2个视频序列可以看出，在黑暗场景下其他4种跟踪算法容易跟丢目标，尤其是面临视点变化、快速运动等挑战。而LADCT算法能较好地应对黑暗场景，准确地在黑暗场景下识别并跟踪目标。这说明LADCT算法构建的动态一致性约束策略能够在黑暗场景中较好地适应目标外观变化，更新目标模型的同时避免模型漂移的发生。此外，第1个视频和第3个视频，所有的算法都能跟踪到目标，但是由于在黑暗场景中，这些算法不能很好地估算目标的尺度变化，因此标记的目标框与实际的目标尺度差别较大。而LADCT算法通过光照自适应增强模块能够提取更多的目标信息。同时构建具有目标感知能力的跨帧动态一致性约束策略，进一步提高了滤波器的判别能力，能够更好对目标位置及尺寸进行估计。这也是LADCT在重叠率精度评估获得较好表现的原因。第4个和第5个视频给出了LADCT算法在光照充足条件下也能准确地跟踪目标并精准估计目标尺寸。这是由于LADCT构建了目标掩码增强特征对目标的感知能力，同时采用一致性标签及动态约束策略，对目标跨帧信息进行充分利用，提高了算法的鲁棒性。
图 4 5种方法在5个视频上的可视化结果Fig. 4 Visualization results of five methods on five videos下载:
全尺寸图片
此外对10种方法的跟踪速度进行了对比。其中大部分都达到了实时跟踪的要求，即25 f/s。LADCT以26.51 f/s的速度在单个CPU上运行，因此能够广泛应用于各种无人机平台完成目标跟踪任务。
4.3.4 消融实验分析
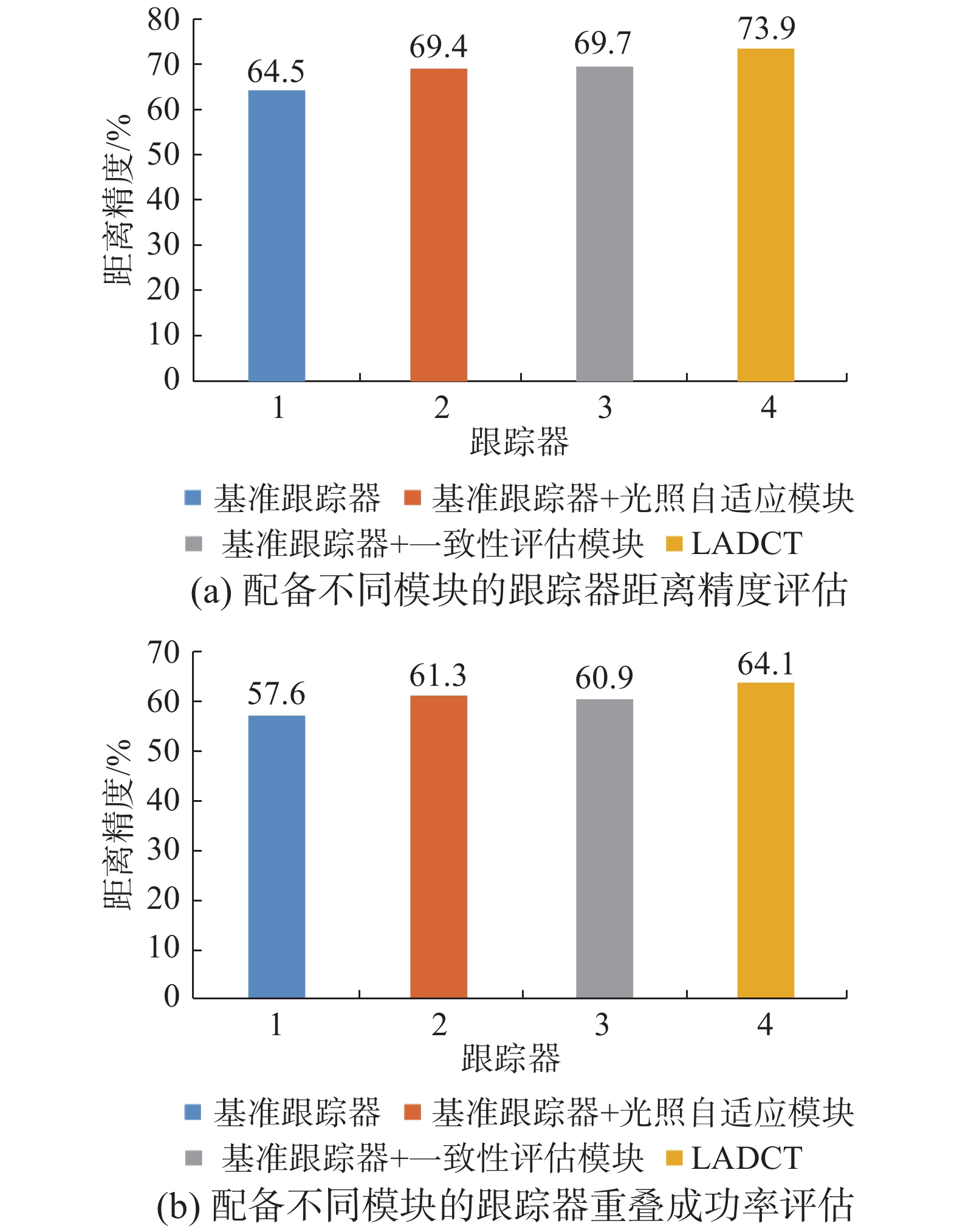
为了验证提出的光照自适应模块和动态一致性策略的有效性，在UAVDark135数据集上进行消融实验对比分析。模块A为光照自适应模块，模块B为目标感知动态一致性评估模块。如图5所示，基准跟踪器可以分别从光照自适应模块和动态一致性策略中受益。其中，光照自适应模块对基准期在黑暗光线场景进行有效跟踪助益最大，距离精度提升0.049，重叠成功率提升0.37。这说明光照自适应模块能够帮助跟踪器在光线恶劣场景精确地完成跟踪任务。引入具有目标感知能力的动态一致性策略能够提高算法有效应对光照条件不足时背景环境的干扰。
图 5 采用不同模块在UAVDark135数据集的对比结果Fig. 5 Comparison results of different modules in the UAVDark135 dataset下载:
全尺寸图片
此外，针对UAVDark135数据集中的视频序列car8进行响应值差异对比。如图6所示，当响应值差异越大时，跟踪算法越容易发生目标丢失情况。在使用基准跟踪器进行跟踪时，响应误差较大。而增加光照自适应模块，即基准跟踪器+模块A，由于目标有效信息更多，所以响应更平滑，但在遮挡、视角变化挑战发生时依然存在响应突变。当两个模块都使用时，LADCT跟踪方法的响应误差突变被抑制，因此在遭遇各种挑战场景也能较好地完成跟踪任务。
图 6 采用不同模块在单个视频上的响应值差异Fig. 6 Differences in the response values of different modules on a single video下载:
全尺寸图片
5. 结束语
本文提出一种基于光照自适应动态一致性的无人机跟踪算法，通过对场景光线的识别及自适应增强，同时构建目标语义感知动态一致性标签实现跟踪过程中跨帧间的目标一致，解决无人机跟踪在面对光线恶劣环境表现不佳的问题。LADCT算法未能及时识别遮挡并在后续跟踪及时重定位目标，影响了遮挡场景的跟踪精度。下一步将研究能够判别跟踪异常并进行目标重定位的目标重识别策略。
-
图 1 LADCT跟踪算法示意
Fig. 1 Pipeline of LADCT tracking algorithm
下载:
全尺寸图片
图 2 提出的方法与9种方法的综合评价结果
Fig. 2 Comprehensive evaluation results of the proposed method and nine other methods
下载:
全尺寸图片
图 3 LADCT在UAVDark135数据集上的5种挑战属性评价结果
Fig. 3 Evaluation results of five challenge attributes of LADCT in the UAVDark dataset
下载:
全尺寸图片
图 4 5种方法在5个视频上的可视化结果
Fig. 4 Visualization results of five methods on five videos
下载:
全尺寸图片
图 5 采用不同模块在UAVDark135数据集的对比结果
Fig. 5 Comparison results of different modules in the UAVDark135 dataset
下载:
全尺寸图片
图 6 采用不同模块在单个视频上的响应值差异
Fig. 6 Differences in the response values of different modules on a single video
下载:
全尺寸图片
表 1 LADCT算法的主要参数设置
Table 1 Main parameter settings of the LADCT algorithm
参数名称 代表含义 设置值 $\theta $ 光照自适应模块阈值 280 $\eta $ 模型学习速率 0.042 $\gamma $ 动态一致性正则化系数 0.9 $\varsigma $ 归一化系数 50 $\beta $ 一致性评价权重系数 100 表 2 不同算法在UAV123数据集不同挑战场景的中心位置误差结果对比
Table 2 Comparison of the center position error results of different algorithms in different challenge scenarios of the UAV123 dataset
算法名称 ARC BC CM FM FOC IV LR OV POC SV SOB VC CPCF 0.593 0.567 0.633 0.541 0.457 0.602 0.584 0.515 0.548 0.626 0.643 0.590 BiCF 0.600 0.556 0.651 0.569 0.504 0.618 0.602 0.580 0.583 0.653 0.634 0.628 SASR 0.590 0.597 0.649 0.558 0.540 0.645 0.639 0.554 0.598 0.636 0.707 0.643 BACF 0.576 0.531 0.639 0.518 0.436 0.525 0.520 0.543 0.564 0.617 0.673 0.587 SRDCF 0.587 0.526 0.627 0.524 0.501 0.600 0.579 0.576 0.608 0.639 0.678 0.593 AutoTrack 0.628 0.579 0.660 0.542 0.464 0.629 0.595 0.562 0.586 0.654 0.661 0.624 ASRCF 0.653 0.629 0.728 0.661 0.576 0.691 0.643 0.604 0.669 0.705 0.717 0.683 ARCF 0.602 0.552 0.647 0.515 0.445 0.595 0.565 0.531 0.573 0.630 0.682 0.596 ADTrack 0.619 0.611 0.661 0.565 0.490 0.623 0.629 0.579 0.595 0.663 0.699 0.615 LADCT 0.692 0.642 0.739 0.679 0.568 0.720 0.652 0.631 0.654 0.721 0.747 0.697 表 3 不同算法在UAV123数据集不同挑战场景的重叠率结果对比
Table 3 Comparison of the overlap rate results of different algorithms in different challenge scenarios of the UAV123 dataset
算法名称 ARC BC CM FM FOC IV LR OV POC SV SOB VC CPCF 0.438 0.431 0.510 0.371 0.276 0.472 0.393 0.422 0.433 0.501 0.514 0.430 BiCF 0.463 0.416 0.544 0.416 0.297 0.499 0.379 0.490 0.459 0.530 0.531 0.500 SASR 0.421 0.371 0.467 0.367 0.292 0.447 0.375 0.453 0.415 0.448 0.493 0.404 BACF 0.442 0.380 0.538 0.387 0.251 0.411 0.334 0.461 0.442 0.509 0.544 0.454 SRDCF 0.431 0.401 0.512 0.366 0.301 0.457 0.359 0.465 0.468 0.510 0.532 0.441 AutoTrack 0.467 0.413 0.542 0.402 0.269 0.469 0.388 0.455 0.456 0.525 0.529 0.463 ASRCF 0.499 0.424 0.624 0.496 0.358 0.523 0.409 0.507 0.548 0.575 0.602 0.523 ARCF 0.466 0.443 0.543 0.379 0.266 0.485 0.386 0.452 0.466 0.524 0.554 0.466 ADTrack 0.452 0.396 0.546 0.421 0.277 0.472 0.399 0.464 0.464 0.532 0.567 0.453 LADCT 0.513 0.479 0.632 0.513 0.359 0.542 0.416 0.519 0.507 0.594 0.639 0.537 -
[1] SPURNY V, PETRLIK M, VONASEK V, et al. Cooperative transport of large objects by a pair of unmanned aerial systems using sampling-based motion planning[C]//2019 24th IEEE International Conference on Emerging Technologies and Factory Automation. Zaragoza: IEEE, 2019: 955−962. [2] HU Chaofang, ZHANG Zelong, YANG Na, et al. Fuzzy multiobjective cooperative surveillance of multiple UAVs based on distributed predictive control for unknown ground moving target in urban environment[J]. Aerospace science and technology, 2019, 84: 329–338. doi: 10.1016/j.ast.2018.10.017 [3] LIN Shanggang, GARRATT M A, LAMBERT A J. Monocular vision-based real-time target recognition and tracking for autonomously landing an UAV in a cluttered shipboard environment[J]. Autonomous robots, 2017, 41(4): 881–901. doi: 10.1007/s10514-016-9564-2 [4] XUAN Shiyu, LI Shengyang, ZHAO Zifei, et al. Rotation adaptive correlation filter for moving object tracking in satellite videos[J]. Neurocomputing, 2021, 438: 94–106. doi: 10.1016/j.neucom.2021.01.058 [5] BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2544−2550. [6] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 37(3): 583–596. doi: 10.1109/TPAMI.2014.2345390 [7] DANELLJAN M, BHAT G, KHAN F S, et al. ECO: efficient convolution operators for tracking[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 6931−6939. [8] 戴煜彤, 陈志国, 傅毅. 相关滤波的运动目标抗遮挡再跟踪技术[J]. 智能系统学报, 2021, 16(4): 630–640. doi: 10.11992/tis.202005027 DAI Yutong, CHEN Zhiguo, FU Yi. Anti-occlusion retracking technology for a moving target based on correlation filtering[J]. CAAI transactions on intelligent systems, 2021, 16(4): 630–640. doi: 10.11992/tis.202005027 [9] 李玺, 查宇飞, 张天柱, 等. 深度学习的目标跟踪算法综述[J]. 中国图象图形学报, 2019, 24(12): 2057–2080. doi: 10.11834/jig.190372 LI Xi, ZHA Yufei, ZHANG Tianzhu, et al. Survey of visual object tracking algorithms based on deep learning[J]. Journal of image and graphics, 2019, 24(12): 2057–2080. doi: 10.11834/jig.190372 [10] 朱建章, 王栋, 卢湖川. 背景与时间感知的相关滤波实时视觉跟踪[J]. 中国图象图形学报, 2019, 24(4): 536–549. doi: 10.11834/jig.180320 ZHU Jianzhang, WANG Dong, LU Huchuan. Learning background-temporal-aware correlation filter for real-time visual tracking[J]. Journal of image and graphics, 2019, 24(4): 536–549. doi: 10.11834/jig.180320 [11] GALOOGAHI H K, FAGG A, LUCEY S. Learning background-aware correlation filters for visual tracking[C]//2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017 : 1144−1152. [12] DANELLJAN M, HÄGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]//2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 4310−4318. [13] DAI Kenan, WANG Dong, LU Huchuan, et al. Visual tracking via adaptive spatially-regularized correlation filters[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019 : 4665−4674. [14] 刘威, 靳宝, 周璇, 等. 基于特征融合及自适应模型更新的相关滤波目标跟踪算法[J]. 智能系统学报, 2020, 15(4): 714–721. doi: 10.11992/tis.201803036 LIU Wei, JIN Bao, ZHOU Xuan, et al. Correlation filter target tracking algorithm based on feature fusion and adaptive model updating[J]. CAAI transactions on intelligent systems, 2020, 15(4): 714–721. doi: 10.11992/tis.201803036 [15] 张开华, 樊佳庆, 刘青山. 视觉目标跟踪十年研究进展[J]. 计算机科学, 2021, 48(3): 40–49. doi: 10.11896/jsjkx.201100186 ZHANG Kaihua, FAN Jiaqing, LIU Qingshan. Advances on visual object tracking in past decade[J]. Computer science, 2021, 48(3): 40–49. doi: 10.11896/jsjkx.201100186 [16] LI Yiming, FU Changhong, DING Fangqiang, et al. Augmented memory for correlation filters in real-time UAV tracking[C]//2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). New York: ACM, 2020: 1559−1566. [17] FU Changhong, LIN Fuling, LI Yiming, et al. Correlation filter-based visual tracking for UAV with online multi-feature learning[J]. Remote sensing, 2019, 11(5): 549. doi: 10.3390/rs11050549 [18] 周士琪, 王耀南, 钟杭. 融合视觉显著性再检测的孪生网络无人机目标跟踪算法[J]. 智能系统学报, 2021, 16(3): 584–594. doi: 10.11992/tis.202101035 ZHOU Shiqi, WANG Yaonan, ZHONG Hang. Siamese network combined with visual saliency re-detection for UAV object tracking[J]. CAAI transactions on intelligent systems, 2021, 16(3): 584–594. doi: 10.11992/tis.202101035 [19] LI Yiming, FU Changhong, DING Fangqiang, et al. AutoTrack: towards high-performance visual tracking for UAV with automatic spatio-temporal regularization[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020 : 11920−11929. [20] FU Changhong, HUANG Ziyuan, LI Yiming, et al. Boundary effect-aware visual tracking for UAV with online enhanced background learning and multi-frame consensus verification[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Macao: IEEE, 2019: 4415−4422. [21] FU Changhong, XIONG Weijiang, LIN Fuling, et al. Surrounding-aware correlation filter for UAV tracking with selective spatial regularization[J]. Signal processing, 2020, 167: 107324. doi: 10.1016/j.sigpro.2019.107324 [22] HUANG Ziyuan, FU Changhong, LI Yiming, et al. Learning aberrance repressed correlation filters for real-time UAV tracking[C]//2019 IEEE/CVF International Conference on Computer Vision (ICCV). Seoul: IEEE, 2019: 2891−2900. [23] FU Changhong, YANG Xiaoxiao, LI Fan, et al. Learning consistency pursued correlation filters for real-time UAV tracking[C]//2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas: IEEE, 2020 : 8293−8300. [24] LIN Fuling, FU Changhong, HE Yujie, et al. BiCF: learning bidirectional incongruity-aware correlation filter for efficient UAV object tracking[C]//2020 IEEE International Conference on Robotics and Automation. Paris: IEEE, 2020 : 2365−2371. [25] LI Bowen, FU Changhong, DING Fangqiang, et al. All-day object tracking for unmanned aerial vehicle[J]. IEEE transactions on mobile computing[EB/OL]. (2021−01−21)[ 2021−10−20]. https://arxiv.org/abs/2101.08446.
