Improved barnacles mating optimizer to solve high-dimensional continuous optimization problems
-
摘要: 为增强藤壶配尾优化算法(barnacles mating optimizer, BMO)的全局探索性能和局部寻优精度，融合藤壶幼虫的沉降附着行为与正反向递减铸型策略提出一种改进藤壶配尾优化算法(improved BMO, IBMO)并将其用于求解高维连续优化问题。沉降附着行为模型受自然界藤壶幼虫随潮浮游、螺旋沉降的行为启发所构建，以增加种群多样性并改善算法的全局探索性能。正反向递减铸型策略借鉴反向学习思想并融入递减调控机制修正传统藤壶优化算法的精子铸型过程，以扩增种群的局部搜索域并改善算法的局部开采性能。实验结果表明，两种策略可分别有效改善藤壶优化算法的全局探索和局部开采性能；同时，所提IBMO算法相较于其他新近智能算法则表现出更高收敛精度、更强算法稳健性和良好高维适用性等。Abstract: To strengthen the global exploration performance and local optimization accuracy of barnacles mating optimizer (BMO), an improved BMO (IBMO) is proposed based on the sedimentation adhesion behavior (SAB) of barnacle larva and the forward-and-backward decreasing casting (FBDC) strategy, which is applied to solve high-dimensional continuous optimization problems. Inspired by the behavior of barnacle larva floating with tide and spiraling sedimentation in nature, the SAB model is built to increase the population diversity and improve the global exploration capacity. Meanwhile, in accordance with reverse learning, and by integrating into the decreasing control mechanism, FBDC modifies the sperm casting process of traditional BMO to amplify the local search domain and improve the local exploitation ability. Experimental results verify that these two strategies can effectively improve the global exploration and local optimization exploitation performance of BMO. Compared with other recent intelligence algorithms, the proposed IBMO shows higher convergence accuracy, stronger robustness and good high-dimensionality applicability.
-
优化是在满足一系列约束条件下，选择一组参数变量，寻找使其目标函数值达到最优的过程[1-2]。当前科学工程问题的复杂性和多样性驱使优化问题的变量维度越趋大规模化、函数目标越趋高维化,并进一步显著增加问题的求解难度，而牛顿法、梯度下降法等传统优化算法在求解这些问题时却容易陷入局部极值，甚至是复杂多耦合约束条件下难以运行求解的窘境[3-4]。智能优化算法(intelligence optimization algorithm, IOA)得益于其初值不敏感性、无需函数梯度信息等无严格要求的优势，而成为求解大规模、高维等复杂优化问题的一类有效的随机搜索算法[5-6]。目前，IOA算法已被成功应用于资源调度[7]、路径规划[8]、复杂函数优化[9-11]等领域。
智能优化算法根据其自然启发机理不同，大致可分为3类：基于遗传、变异的进化类算法，如遗传算法、进化策略等；基于生物群智行为的群智能优化算法，如蚁群算法、粒子群算法等；基于物理或化学机理启发的算法，如模拟退火算法、亨利气体溶解度优化算法[12]。同时受自然界新的启发机制激励，新的IOA算法也不断被构建并提出，如基于蝴蝶觅食机制的蝴蝶优化算法[13](butterfly optimization algorithm, BOA)、基于海鸥迁徙和攻击行为的海鸥优化算法[14](seagull optimization algorithm, SOA)、模拟栗翅鹰狩猎协作行为的栗翅鹰优化算法[15](harris hawks optimization, HHO)、模仿麻雀觅食−反捕食行为的麻雀搜索算法[16](sparrow search algorithm, SSA)、调控容积−质量的平衡器优化算法[17](equilibrium optimizer, EO)、基于阿基米德定律的阿基米德优化算法[18](Archimedes optimization algorithm, AOA)等、模拟蒲公英远距离飞行行为的蒲公英优化算法[19]、基于海马运动捕食和繁殖行为的海马优化算法[20]。
藤壶配尾优化算法[21](barnacles mating optimizer, BMO)是一种新的基于生物群体的IOA算法，其源于自然界成年藤壶的交配繁殖行为。BMO算法通过多个体的并行协同进化以实现问题解空间的探索并寻得全局最优解。但囿于成年藤壶固着于海底坚硬基质而无法移动，故其生殖器官长度约束下的配尾机制在一定程度上限制BMO算法对解空间的探索开采性能。受到藤壶幼虫的随潮浮游、螺旋下沉移动模式的启发，本文构建藤壶幼虫的沉降附着行为模型，以增强BMO算法的全局优化能力；同时考虑到局部反向搜索的高效寻优性能，修正性提出成年藤壶精子的正反向递减铸型策略，以进一步强化BMO算法的局部开采性能，进而融合性提出一种改进BMO算法(improved BMO, IBMO)。数值实验验证了2种改进策略优化性能的有效性以及IBMO算法优异的高维并行优性能。
1. 藤壶配尾优化算法
BMO算法[12]启发于藤壶的交配繁殖行为。每只藤壶代表一个可行解，算法通过藤壶种群在解空间中的并行迭代搜索以实现问题的优化求解。
1) 初始化阶段：在搜索空间
$ \left[ {{{{\boldsymbol{L}}}},{{{\boldsymbol{U}}}}} \right] $ 随机产生维度为$ D $ 、数量为$ n $ 的藤壶种群，其向量表示为$$ {{{\boldsymbol{X}}}} = \left[ {\begin{array}{*{20}{c}} {x_1^1}& \cdots &{x_1^D} \\ \vdots & \ddots & \vdots \\ {x_n^1}& \cdots &{x_n^D} \end{array}} \right] $$ (1) 其中每只藤壶
${{{{\boldsymbol{X}}}}_{{i}}}\left( {i = 1,2, \cdots ,n} \right)$ 的生成表达为$$ {{{X}}_{{i}}} = {{{\boldsymbol{L}}}} + {\rm{rand}}() \times ({{{\boldsymbol{U}}}} - {{{\boldsymbol{L}}}}) $$ (2) 式中：
${\rm{rand}}()$ 表示$ [0,1] $ 之间的随机数；${\boldsymbol{U}}$ 和${\boldsymbol{L}}$ 分别表示每只藤壶的上界和下界，其数学表达为$$ \begin{gathered} \;\;{\boldsymbol{L}} = \left[ {{{{l}}_1}\;{l_2}\; \cdots \;{{{l}}_i}} \right] \\ {\boldsymbol{U}} = \left[ {{{{u}}_1}\;{u_2}\; \cdots \;{{{u}}_i}} \right] \\ \end{gathered} $$ (3) 不失一般性，以最小值问题为例，则对种群
${\boldsymbol{X}}$ 按适应度值进行升序排列，最小适应度值对应的解即为当前所寻得的最优解。2) 选择过程。藤壶个体被随机选择并赋予成父本
${D_{{\rm{ad}}}}$ 和母本${M_{{\rm{um}}}}$ (本文设${p_1}$ =7)对应数学表达：$$ \begin{gathered} {D_{{\rm{ad}}}} = {\rm{randperm}}\left( n \right) \\ {M_{{\rm{um}}}} = {\rm{randperm}}\left( n \right) \\ \end{gathered} $$ (4) 式中：
${\rm{randperm}}\left( n \right)$ 表示对$ 1-n $ 个数进行随机排列，${p_1}$ 表示藤壶的生殖器官长度。3) 繁殖行为。藤壶父本
${D_{{\rm{ad}}}}$ 根据其${p_1}$ 长度分别执行子代生成和精子铸型过程。① 若被选择的藤壶母本
${M_{{\rm{um}}}}$ 位于父本${D_{{\rm{ad}}}}$ 的${p_1}$ 长度范围内，则按Hardy Weinberg原理[22]执行子代藤壶生成过程，其数学表达为$$ {\boldsymbol{X}}_{{i}}^{{{D\_}}{\rm{new}}} = {{p}}{\boldsymbol{X}}_{{{{D}}_{{\rm{ad}}}}}^{{D}} + {{q}}{\boldsymbol{X}}_{{{{M}}_{{\rm{um}}}}}^{{D}} $$ (5) 式中：
$ p $ 是服从正态分布$ N(0,1) $ 的一个随机数，$ q= 1-p $ ；${{{\boldsymbol{X}}}}_{{{\rm{D}}_{{\rm{ad}}}}}^D$ 和${{{\boldsymbol{X}}}}_{{{\rm{M}}_{{\rm{um}}}}}^D$ 表示选取藤壶父本$ {D_{\rm{ad}}} $ 和母本$ {M_{\rm{um}}} $ 的$ D $ 个变量维度。② 若被选择的藤壶母本
${M_{{\rm{um}}}}$ 超出父本${D_{{\rm{ad}}}}$ 的${p_1}$ 范围，则执行精子铸型过程，其数学表达为$$ {{{\boldsymbol{X}}}}_i^{{\rm{new}}} = {\rm{rand}}() \times {{{\boldsymbol{X}}}}_{{\rm{barnacle}}\_{\rm{m}}}^D $$ (6) 为保持种群规模的恒定性，将藤壶子代与父本藤壶合并再按适应度值升序排列，同时选择前
$ n $ 个个体作为新的子代迭代种群，其余个体消亡。2. 改进藤壶配尾优化算法
2.1 沉降附着行为模型
藤壶配尾优化算法(BMO)通过模型化成年藤壶间的繁殖行为以实现算法的探索开采性能，即以父本两藤壶间的信息交互繁殖子代并实现解空间的多个体并行迭代搜索。但囿于成年藤壶常常固着于海底岩石等坚硬基质且无法移动，一定程度上限制了其对解空间的全局探索性能。得益于藤壶幼虫在成年前随潮浮游、螺旋运动和沉降附着过程的自由运动形态。因此，数学化构建藤壶幼虫的沉降附着模型以改善传统BMO算法的全局寻优性能。
藤壶幼虫沉降附着行为(sedimentation adhesion behavior, SAB)的数学模型如下：
$$ {{{\boldsymbol{X}}}}_i^{{\rm{new}}}\left( t \right) = {{{{\boldsymbol{X}}}}_i}\left( t \right) + {\rm{Levy}}\left( \lambda \right)\left( {\alpha \times {{{{\boldsymbol{X}}}}_{{\rm{best}}}} - r \times {{{{\boldsymbol{X}}}}_i}\left( t \right)} \right) $$ (7) 式中：
${{{{\boldsymbol{X}}}}_i}\left( t \right)$ 表示第$ t $ 次迭代的藤壶位置；${\rm{Levy}}\left( \lambda \right)$ 为服从${\rm{Levy}}$ 分布的路径，其${\rm{Levy}}$ 函数与$ \sigma $ 参数同文献[23]设置；$ r $ 表示定义为对数螺旋线形状下旋转一周的半径长度，其数学表达为$$ r = u\exp \left( {v\theta } \right) $$ (8) 式中：
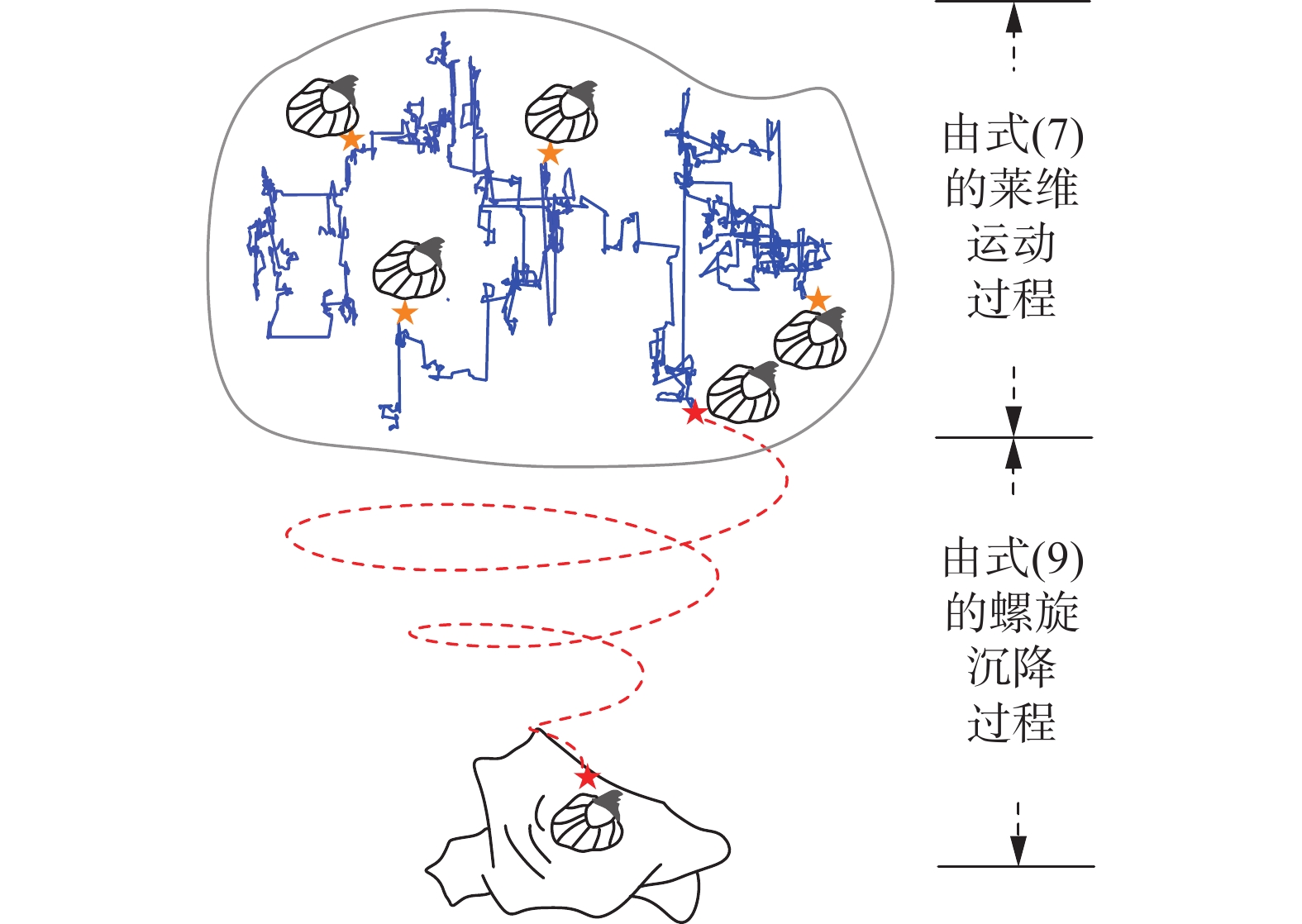
$ u $ 、$ v $ 均为常数系数(本文设$ u = 0.005 $ ，$ v = 0.5 $ )；$ \theta \in \left[ { - 2\text{π} ,2\text{π} } \right] $ 为螺旋线的旋转角度；$ \alpha $ 为藤壶幼虫定义在$ x $ 平面的螺旋行为，其数学表达为$$ \alpha=r \times \cos \theta $$ (9) 图1为SAB模型的藤壶幼虫沉降附着行为示意。SAB通过
$ {\rm{Levy}} $ 系数模拟藤壶幼虫浮游移动路线，其在高斯分布下以较大概率浮游至到其他位置。这不仅保证藤壶幼虫搜索寻优的随机性，而且能够避免算法过早收敛。启发于幼年发生的行为，SAB模型设定在父代藤壶交配繁殖后，故父代与子代藤壶评估后的前$ n $ 个个体作为藤壶幼虫进化的初始种群。融入藤壶幼虫的沉降附着行为不仅丰富种群的多样性，而且使算法更倾向于全局搜索。
图 1 藤壶幼虫的沉降附着行为示意Fig. 1 Sedimentation adhesion behavior of barnacle larvae
下载:
全尺寸图片
2.2 正反向递减铸型策略
BMO算法中，通过母本藤壶
${M_{{\rm{um}}}}$ 内模型化精子铸型过程以实现算法的局部开采性能，即遗传母本藤壶的某些优良信息。但囿于BMO算法，只通过$ \left[0,1\right] $ 内的随机数调控可行解的局部搜索域，会使邻居解仅能够朝正方向移动却忽略了其他较优的邻居解，进而导致算法的局部开采性能下降；同时随迭代次数增加，邻居解的局部开采域变化范围不明显，容易导致算法因过度开采而难以实现全局最优。因此，为改善传统BMO算法的局部开采性能需对精子铸型过程加以修正。鉴于反向学习思想[24]，考虑每个候选解的同时考虑其反向解以扩大种群的搜索范围。基于该思想，对每个可行解的邻居解均考虑其对称反向邻居解，正向和反方向邻居解分别有50%的概率靠近最优解，这有利于改善种群的收敛效率。进而，融入递减机制对局部搜索域进行再调控，避免算法在迭代后期因过度局部开采而难以寻得全局最优。所提正反向递减铸型策略(forward-and-backward decreasing casting strategy, FBDC)的数学表达为
$$ {{{\boldsymbol{X}}}}_i^{D\_{\rm{new}}} = \delta \times \left( {2 \times {\rm{rand}}() - 1} \right) \times {{{\boldsymbol{X}}}}_{{\rm{barnacle}}\_{\rm{m}}}^D $$ (10) 式中：
$ \delta \in \left[ {0,1} \right] $ 为线性递减因子，其数学表达为$$ \delta = 1 - \frac{t}{T} $$ (11) 其中：
$ t $ 为当前迭代次数，$ T $ 为最大迭代次数。图2为正反向递减铸型策略的局部开采示意。由图2可知，搜索空间
${{{\boldsymbol{X}}}}$ 中有多个局部最优解(以3个局部极值为例)，可行解通过算法的局部并行迭代搜索寻得第1个局部邻域内的最优解；其次，可行解继续全局搜索到第2个邻域内并随机分布在全局最优解两侧，通过正或反向递减搜索以趋于全局最优解；若迭代后期可行解落在第3个局部极值邻域内，正反向递减铸型策略能够使算法不会过度开采，进而在一定程度上，增加算法的全局搜索性能。
图 2 正反向递减铸型策略示意Fig. 2 Forward-and-backward decreasing casting strategy下载:
全尺寸图片
2.3 改进的BMO算法
将上述2.1节SAB与2.2节FBDC相融合而提出一种改进BMO算法。其迭代优化进程的执行伪码如下所示。
算法 IBMO伪代码
输入 设置种群规模
$ n $ ，最大迭代次数$ T $ ，维 数$ D $ ，搜索空间上下限$\left[ {{{{\boldsymbol{L}}}},{{{\boldsymbol{U}}}}} \right]$ 输出 藤壶个体
${{{{\boldsymbol{X}}}}_{{\rm{best}}}}$ ，适应度值$f\left( {{{{{\boldsymbol{X}}}}_{{\rm{best}}}}} \right)$ 1) 初始化藤壶种群
${{{\boldsymbol{X}}}}$ 2) 计算每个藤壶的适应度值
$f\left( {{{{{\boldsymbol{X}}}}_i}} \right)$ 3) 按照适应度值将个体依次从上至下升序排列
4) while (
$ t < T $ ) do5) 按式(4)随机选择父本和母本
6) if 被选择父本与母本之间距离
$< {p_1}$ 7) for i
$ \leftarrow $ 1 to$ n $ do8) 按式(5)生成子代藤壶
${{{\boldsymbol{X}}}}_i^{D\_{\rm{new}}}$ 9) end for
10) else if
11) for i
$ \leftarrow $ 1 to$ n $ do12) 按式(10)生成子代藤壶
${{{\boldsymbol{X}}}}_i^{D\_{\rm{new}}}$ 13) end for
14) end if
15) 合并父代藤壶
${{{{\boldsymbol{X}}}}_i}$ 与子代藤壶${{{\boldsymbol{X}}}}_i^{D\_{\rm{new}}}$ 16) 越界处理
17) 按适应度升序排列新种群
$\left[ {{{{{\boldsymbol{X}}}}_i}{\text{ }};{{{\boldsymbol{X}}}}_i^{D\_{\rm{new}}}} \right]$ 18) 选取前
$ n $ 个个体，保留其适应度值19) for i
$ \leftarrow $ 1 to$ n $ do20) 按式(7)更新藤壶幼体下沉后新
${{{\boldsymbol{X}}}}_i^{{\rm{new}}}$ 21) 越界处理
22) 计算个体适应度值
$f\left( {{{{\boldsymbol{X}}}}_i^{{\rm{new}}}} \right)$ 23) end for
24) 合并
$\left[ {{\boldsymbol{X}}_i^{{\rm{new}}};{\boldsymbol{X}}_i^{D\_{\rm{new}}}} \right]$ 并按适应度值升序排列25) 选取前
$ n $ 个个体，保留其适应度值26) 选择最优适应度值更新
${{{{\boldsymbol{X}}}}_{{\rm{best}}}}$ 、$f\left( {{{{{\boldsymbol{X}}}}_{{\rm{best}}}}} \right)$ 27)
$ t = t + 1 $ 28) end while
29) Return
${{{{\boldsymbol{X}}}}_{{\rm{best}}}}$ and$f\left( {{{{{\boldsymbol{X}}}}_{{\rm{best}}}}} \right)$ 2.4 算法复杂度分析
BMO算法的时间复杂度依赖于：藤壶种群规模
$ n $ 、最大迭代次数$ T $ 、变量维度$ D $ 。初始化阶段，算法执行时间有：种群随机生成、适应度值排序、适应度值寻优排序。其时间复杂度为$$ {K_1} = O\left( D \right) + 2O\left( n \right) = O\left( {D + 2n} \right) $$ 迭代阶段，BMO算法执行时间有：子代种群生成、子代种群与父代种群适应度值计算、适应度值排序。BMO算法执行时间复杂度为
$$ O\left( {{\text{BMO}}} \right) = {K_1} + O\left( {T\left( {Dn + 4n} \right)} \right) = {K_1} + O\left( {TDn} \right) $$ 而由IBMO算法的迭代阶段，其算法执行时间有：子代种群生成、子代种群适应度值计算、基于螺旋下沉行为而产生的种群、适应度值计算。故IBMO算法的时间复杂度为
$$ O\left( {{\text{IBMO}}} \right) = {K_1} + O\left( {T\left( {2Dn + 3n} \right)} \right) = {K_1} + O\left( {TDn} \right) $$ 因此，IBMO算法与BMO算法相比，时间复杂度、空间复杂度并没有发生显著变化。
3. 数值实验
为探究和验证IBMO算法的寻优性能，共进行3组实验。实验1探究SAB和FBDC策略对BMO算法性能改善的有效性；实验2以3种新近IOA算法作为对比算法以测验IBMO的高维优化性能；实验3在函数不同高维的伸缩变化下进一步探究BMO与IBMO算法的优化性能差异性。
本文选择8个国际通用基准测试函数进行测试，分别选自文献[21]的5个测试函数和CEC2017函数套件中的3个基本函数。单峰函数
$ {F_1} \sim {F_4} $ ，用于测试算法的局部开采性能与收敛速率；多峰函数$ {F_5} \sim {F_8} $ ，用于测试算法全局搜索性能与局部极值规避性等。为保证不同算法测试结果的评价公平，所有实验均按同等种群规模与最大迭代次数进行，参照文献[21]：种群规模$ n = 10 $ 、最大迭代次数$ T = 300 $ 。实验运行环境为Windows 10(64 bit)、 Intel(R) Core (TM) i7-9750H CPU @ 2.60 GHz、MATLAB 2018a。3.1 SAB和FBDC策略的性能有效性分析实验
为检验所提SAB策略和FBDC策略分别对BMO算法性能改善的有效性，分别将融入改进策略的2种BMO算法记为BMO-SAB、BMO-FBDC。以变量维度
$ D=100 $ 进行100次独立重复实验，以100次实验结果的平均值(mean)和标准差(std)作为算法性能的评价指标，统计结果如表1所示。表 1 不同改进策略下的BMO优化性能对比统计分析Table 1 Comparative statistical analysis of BMO optimization performance under different improvement strategies函数 BMO BMO-SAB 函数 BMO BMO-FBDC mean std mean std mean std mean std $ {F_1}\left( x \right) $ 4.41×10−34 2.53×10−33 2.12×10−48 1.79×10−47 $ {F_1}\left( x \right) $ 4.41×10−34 2.53×10−33 4.48×10−58 4.39×10−57 $ {F_2}\left( x \right) $ 2.41×10−60 2.41×10−59 8.31×10−88 8.18×10−87 $ {F_2}\left( x \right) $ 2.41×10−60 2.41×10−59 3.72×10−110 3.71×10−109 $ {F_3}\left( x \right) $ 1.08×10−32 8.76×10−32 3.58×10−46 2.21×10−45 $ {F_3}\left( x \right) $ 1.08×10−32 8.76×10−32 2.34×10−57 2.22×10−56 续表 1 函数 BMO BMO-SAB 函数 BMO BMO-FBDC mean std mean std mean std mean std $ {F_4}\left( x \right) $ 5.14×10−61 5.14×10−60 1.27×10−89 1.17×10−88 $ {F_4}\left( x \right) $ 5.14×10−61 5.14×10−60 2.71×10−113 2.70×10−112 $ {F_5}\left( x \right) $ −1.24×104 2.88×103 −2.17×104 1.48×103 $ {F_5}\left( x \right) $ −1.24×104 2.88×103 −1.23×104 2.81×103 $ {F_6}\left( x \right) $ 1.57×101 1.04×101 1.47×101 1.06×101 $ {F_6}\left( x \right) $ 1.57×101 1.04×101 1.84×100 5.90×100 $ {F_7}\left( x \right) $ 4.04×10−25 4.03×10−24 1.61×10−36 1.61×10−35 $ {F_7}\left( x \right) $ 4.04×10−25 4.03×10−24 1.27×10−49 1.26×10−48 $ {F_8}\left( x \right) $ 1.72×10−64 1.36×10−63 7.52×10−82 7.51×10−81 $ {F_8}\left( x \right) $ 1.72×10−64 1.36×10−63 1.63×10−113 1.62×10−112 由表1分析可知，相较于传统BMO算法，BMO-SAB与BMO-FBDC的寻优精度几乎均有所提高。在mean指标上，BMO-SAB算法均优于传统BMO算法，特别是在函数
$ {F}_{1}\sim {F}_{4}、{F}_{7}、{F}_{8} $ 上优于BMO达数十个数量级；对于std指标，BMO-SAB在7个函数上寻得更优的mean指标值，表明所提BMO-SAB算法具有更好的全局寻优性能、更强的并行寻优稳健性和良好局部极值规避性等。其次，BMO-FBDC算法在15个mean和std指标上优于传统BMO算法，其在单峰函数上均优于BMO的收敛精度，在函数
$ {F_2} $ 、$ {F_4} $ 上的平均寻优精度约提升50个数量级；同时在3个多峰函数上仍可获得更优的平均收敛精度，特别是函数$ {F_7}、{F_8} $ 的精度提升达数十个数量级；再与BMO-SAB算法在mean指标横向对比分析，BMO-FBDC相较于BMO-SAB能够更显著地提升BMO算法的收敛精度，表明所提BMO-FBDC具有更强的局部再开采性能。上述分析结果在一定程度上佐证了2种改进策略在提高BMO算法并行迭代寻优性能上的有效性。为进一步可视化验证BMO-FBDC、BMO-SAB相对于BMO算法的并行迭代搜索优异性，绘制平均适应度对比曲线见图3（维度D=100）。
图 3 BMO-SAB、BMO-FBDC与BMO平均适应度的收敛对比曲线Fig. 3 Convergence comparison curves of BMO-SAB, BMO-FBDC and BMO mean fitness values下载:
全尺寸图片
由图3分析可知，随迭代次数增大，3种算法寻优性能均呈明显递减态势，且所提BMO-SAB和BMO-FBDC算法在绝大多数函数上相比于BMO算法的迭代递减幅度更为显著。特别是在多峰函数
$ {F_5} $ 上，BMO算法在迭代后期呈现出近乎“平直”趋势，表明BMO已陷入局部极值且难以跳出局部极值而导致其相对较差的收敛精度；但BMO-SAB则可依概率跳出局部极值，并持续保持寻优态势以获得更优收敛精度，说明BMO-SAB在100次独立测试中能够保持强劲的同步局部极值规避性，并有效验证沉降附着机制的良好全局寻优性能。同时BMO-FBDC与BMO间收敛精度的跨度随迭代进程越趋增大，直至最大迭代次数时仍保持继续增大的态势，表明所提FBDC策略在并行迭代进程中良好的逐代平均寻优精度，验证了其改善BMO算法迭代搜索性能的有效性和可行性。3.2 IBMO与新进智能算法的对比分析实验
为进一步验证IBMO算法的寻优性能，以新近IOA算法中的SOA[14]、AOA[18]、GEO(golden eagle optimizer)[25]和BMO[21]作为对比算法。为保证实验评价的客观公平性，同等设置维度
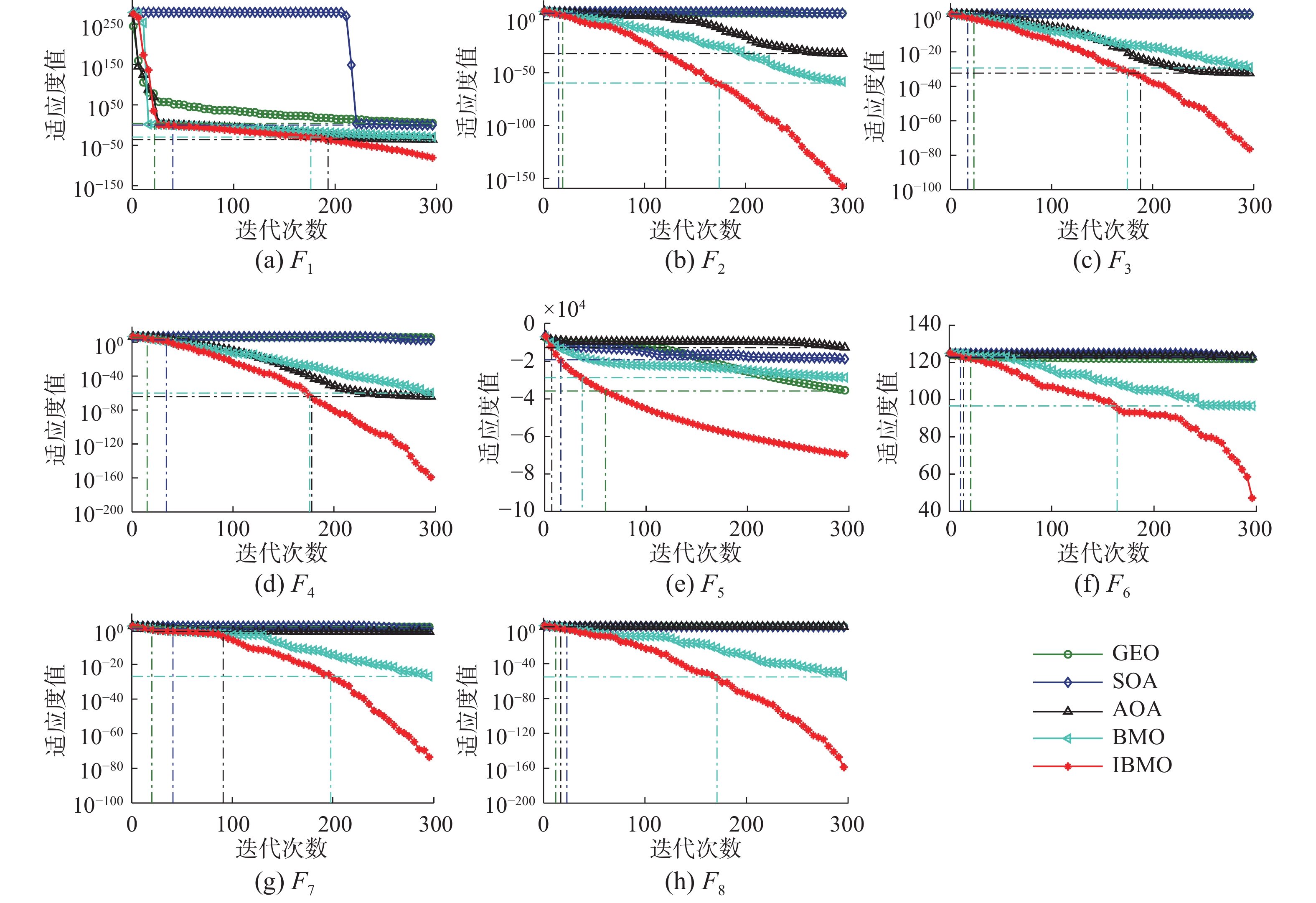
$ D= 500 $ 、最大迭代次数$ T=300 $ 、种群规模$ n = 10 $ ，而算法的其他参数按原文献设定。各实验均独立运行100次，所得统计结果见表2。为进一步有效比较各算法间的时间复杂度，以各对比算法最大迭代次数的最佳收敛精度确定出IBMO算法超过同等精度时的迭代次数，进而计算出以精度为终止条件下IBMO算法的有效运行时间并简记为te。同时为直观展示IBMO算法的良好高维适用性，绘制收敛对比曲线见图4，其中，各虚线表示各对比算法同等精度条件下IBMO的对应迭代次数。表 2 500维度不同算法优化性能对比统计分析Table 2 Comparative statistical analysis of optimization performance of different algorithms in 500 dimensions函数 指标 GEO SOA AOA BMO IBMO $ {F_1}\left( x \right) $ mean 2.46×104 1.03×100 1.40×10−36 2.48×10−30 3.82×10−84 std 1.47×105 4.33×10−1 7.77×10−36 2.41×10−29 2.62×10−83 运行时间/s 1.83×10−1 2.62×10−1 2.61×10−1 1.84×100 2.50×100 te/s 1.83×10−1≈ 3.33×10−1≈ 1.61×100− 9.42×10−1+ — $ {F_2}\left( x \right) $ mean 1.23×106 1.25×106 1.09×10−32 1.45×10−60 1.49×10−162 std 3.01×105 5.22×105 1.09×10−31 1.17×10−59 1.49×10−161 运行时间/s 1.13×100 1.28×100 1.29×100 3.97×100 5.81×100 te/s 3.68×10−1+ 3.68×10−1+ 2.34×100≈ 1.36×100+ — $ {F_3}\left( x \right) $ mean 5.18×101 9.94×101 4.60×10−33 4.08×10−30 1.88×10−81 std 3.25×100 2.47×10−1 3.17×10−32 3.48×10−29 1.81×10−80 运行时间/s 1.74×10−1 2.64×10−1 2.57×10−1 2.17×100 2.14×100 te/s 1.64×10−1+ 1.21×10−1+ 1.34×100− 7.84×10−1+ — $ {F_4}\left( x \right) $ mean 4.22×105 3.78×102 7.92×10−65 8.50×10−61 5.85×10−168 std 4.08×104 2.61×102 5.60×10−64 8.50×10−60 0.00×100 运行时间/s 1.76×10−1 2.12×10−1 2.35×10−1 1.79×100 2.16×100 te/s 1.08×10−1+ 2.45×10−1≈ 1.28×100− 7.53×10−1+ — $ {F_5}\left( x \right) $ mean −3.58×104 −1.91×104 −1.27×104 −2.87×104 −7.00×104 std 3.90×103 2.42×103 2.61×103 7.38×103 3.05×103 运行时间/s 2.05×10−1 3.24×10−1 3.12×10−1 1.85×100 2.67×100 te/s 5.34×10−1≈ 1.42×10−1+ 6.23×10−2+ 7.68×10−3+ — $ {F_6}\left( x \right) $ mean 1.22×102 1.23×102 1.23×102 9.67×101 2.52×101 std 4.60×10−1 5.80×10−1 7.39×10−1 4.86×101 4.69×101 运行时间/s 2.54×10−1 2.63×10−1 2.84×10−1 1.87×100 2.26×100 te/s 1.58×10−1+ 8.28×10−2+ 1.05×10−1+ 5.76×10−2+ — 续表 2 函数 指标 GEO SOA AOA BMO IBMO $ {F_7}\left( x \right) $ mean 4.77×101 3.41×100 9.99×10−2 9.67×101 1.98×10−74 std 2.10×100 8.37×10−1 3.09×10−5 4.86×101 1.97×10−73 运行时间/s 1.77×10−1 2.12×10−1 2.44×10−1 1.80×100 2.12×100 te/s 1.42×10−1+ 2.90×10−1≈ 6.44×10−1≈ 4.25×10−1+ — $ {F_8}\left( x \right) $ mean 3.69×102 2.22×102 2.24×102 4.47×10−25 1.60×10−167 std 5.23×101 7.18×10−1 4.28×10−13 3.75×10−24 0.00×100 运行时间/s 6.73×10−1 6.92×10−1 7.54×10−1 2.78×100 4.10×100 te/s 1.64×10−1+ 3.15×10−1+ 2.32×10−1+ 1.33×10−1+ — +/≈/− 占优次数 6/2/0 5/3/0 3/2/3 8/0/0 — 
图 4 5种算法平均适应度值的收敛对比曲线Fig. 4 Convergence comparison curves of mean fitness values of five algorithms下载:
全尺寸图片
表2给出了不同算法在500维度函数上的统计结果。“+”、“≈”或“−”分别表示IBMO的te指标比其他算法较好、略差但在同一数量级或较差且不在同一数量级。由表2分析可知，同等种群规模与最大迭代次数条件下，IBMO在8个函数上均获得最优平均收敛精度，尤其在函数
$ {F_2} $ 、$ {F_4} $ 、$ {F_8} $ 上优于对比算法达数百个数量级，而函数$ {F_1} $ 、$ {F_3} $ 、$ {F_7} $ 也能高出数十个数量级，表明所提IBMO算法具有更优的高收敛精度与强局部极值规避性等。IBMO在6个std指标上达到最小，特别是函数$ {F_4} $ 、$ {F_8} $ 的std值已达到0，表明IBMO算法的强稳健性。与GEO、SOA和BMO在预设最大迭代次数下取得的最佳结果相比，IBMO能够在更短时间内获得更优的精度。再结合图4知，对大多数函数，IBMO可在$ {T \mathord{\left/ {\vphantom {T {10}}} \right. } {10}} $ 获得比GEO和SOA更优的收敛精度，且在$ {{2T} \mathord{\left/ {\vphantom {{2T} 3}} \right. } 3} $ 获得比BMO更优的收敛精度。IBMO在多峰函数$ {F_5} $ 、$ {F_6} $ 、$ {F_6} $ 上的有效运行时间优于AOA，而对于其他函数与AOA同精度的有效运行时间数量级也在可接受范围内。特别对于多峰函数，IBMO仍保持搜寻更优精度态势而AOA几乎陷入局部极值而丧失寻优能力。上述结果有效验证了IBMO算法在处理高维问题上的高收敛精度和强稳健性。由图4再进一步对比算法间的迭代寻优趋势，不同算法在各测试函数上动态迭代进程各不相同，且以IBMO寻优精度表现最佳。对于单峰函数
$ {F_2} \sim {F_4} $ 和多峰函数$ {F_5} $ ，IBMO在迭代初期便寻得更优的函数精度且随迭代进程继续保持搜索优势直至最大迭代次数，其他算法则表现出收敛较慢或因陷入局部极值而丧失收敛能力；而对于多峰函数$ {F_7} $ 、$ {F_8} $ ，IBMO在迭代早期并没有表现出更优收敛精度，但中后期仍可跳出局部极值并寻得最优结果。另一方面，由多峰函数对比收敛曲线的发展态势可知，即使增大迭代次数使对比算法的运行时间达到IBMO的，也未必能保证寻得优于IBMO的收敛精度。上述分析结果验证了IBMO算法能够有效平衡算法的全局开采与局部搜索性能，以及在高维情况下的高收敛精度与强局部极值规避性等。
3.3 高维情形下IBMO的性能分析实验
为进一步探究IBMO对维度伸缩变化的适应性，以BMO为对比算法，在不同维度下进行实验。设置种群规模
$ n $ 与最大迭代次数$ T $ 为10和300，变量维度分别设D为100、200、300、400和500。每个实验均独立运行100次，具体统计结果见表3。表 3 BMO与IBMO算法不同维度的优化性能对比统计分析Table 3 Comparative statistical analysis of optimization performance of BMO and IBMO in different dimensions维度 算法 指标 $ {F_1}\left( x \right) $ $ {F_2}\left( x \right) $ $ {F_3}\left( x \right) $ $ {F_4}\left( x \right) $ $ {F_5}\left( x \right) $ $ {F_6}\left( x \right) $ $ {F_7}\left( x \right) $ $ {F_8}\left( x \right) $ 100 BMO mean 4.4×10−34 2.4×10−60 1.1×10−32 5.1×10−61 −1.2×104 1.6×101 4.0×10−25 1.7×10−64 std 2.5×10−33 2.4×10−59 8.8×10−32 5.1×10−60 2.9×103 1.0×101 4.0×10−24 1.4×10−63 IBMO mean 1.8×10−83 7.7×10−166 7.0×10−86 7.0×10−170 −2.2×104 5.2×100 4.9×10−76 3.5×10−166 std 1.8×10−82 0.0×100 5.8×10−85 0.0×100 1.3×103 8.9×100 4.9×10−75 0.0×100 200 BMO mean 1.1×10−32 9.9×10−58 2.2×10−32 1.7×10−60 −1.8×104 3.3×101 1.7×10−25 2.7×10−60 std 9.3×10−32 7.1×10−57 2.1×10−31 1.7×10−59 4.4×103 2.1×101 1.3×10−24 2.5×10−59 IBMO mean 1.5×10−79 2.7×10−167 1.5×10−83 6.8×10−156 −3.8×104 9.8×100 8.2×10−75 3.1×10−167 std 1.5×10−78 0.0×100 1.5×10−82 6.8×10−155 1.9×103 1.9×101 6.7×10−74 0.0×100 300 BMO mean 9.4×10−32 9.0×10−58 6.8×10−32 8.6×10−62 −2.2×104 5.2×101 1.1×10−25 2.9×10−60 std 5.9×10−31 9.0×10−57 5.4×10−31 8.6×10−61 5.1×103 3.2×101 1.1×10−24 2.2×10−59 IBMO mean 2.0×10−84 6.3×10−161 5.1×10−84 3.0×10−171 −5.0×104 1.9×101 9.6×10−75 5.1×10−159 std 1.8×10−83 6.3×10−160 5.1×10−83 0.0×100 2.5×103 3.0×101 9.6×10−74 5.1×10−158 400 BMO mean 3.6×10−30 1.0×10−58 4.4×10−32 3.3×10−56 −2.5×104 7.2×101 1.4×10−19 1.1×10−62 std 3.4×10−29 1.0×10−57 2.6×10−31 3.3×10−55 6.7×103 4.2×101 1.4×10−18 1.1×10−61 IBMO mean 8.8×10−84 1.5×10−168 1.4×10−83 8.6×10−171 −6.1×104 2.5×101 5.4×10−80 1.7×10−167 std 8.8×10−83 0.0×100 1.4×10−82 0.0×100 2.7×103 4.0×101 5.4×10−79 0.0×100 500 BMO mean 2.5×10−30 1.5×10−60 4.1×10−30 8.5×10−61 −2.9×104 9.7×101 4.5×10−25 5.3×10−56 std 2.4×10−29 1.2×10−59 3.5×10−29 8.5×10−60 7.4×103 4.9×101 3.7×10−24 5.3×10−55 IBMO mean 3.8×10−84 1.5×10−162 1.9×10−81 5.9×10−168 −7.0×104 2.5×101 2.0×10−74 1.6×10−167 std 2.6×10−83 1.5×10−161 1.8×10−80 0.0×100 3.1×103 4.7×101 2.0×10−73 0.0×100 由表3可知，IBMO在8个函数的不同维度上均达更优收敛精度。在函数
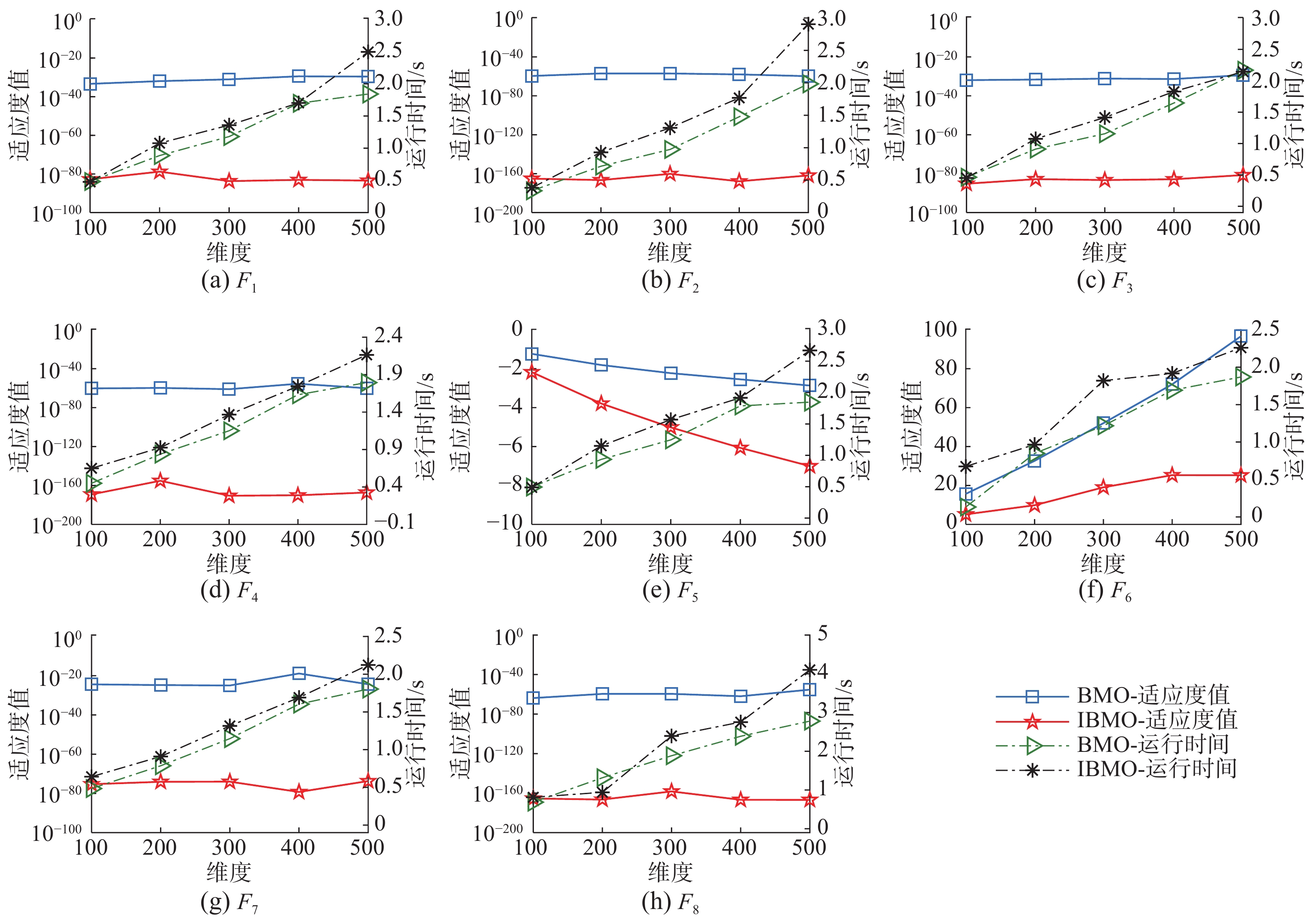
$ {F_4} $ 、$ {F_8} $ 上，IBMO优于BMO达100个数量级，在函数$ {F}_{1}\sim {F}_{3}、{F}_{7} $ 上也高达数十数量级。即使在400维、500维情形，IBMO仍能够同步追踪因维度增大所导致的优化难度增加问题，并寻得更优收敛精度。针对std指标，IBMO在大部分函数上优于BMO，表明高维度情况下所提IBMO保持强劲的算法稳健性，统计结果有效验证了IBMO算法的良好高维适用性。为对比分析维度伸缩变化对两算法的性能影响，绘制不同维度下平均适应度值与平均运行时间的对比曲线见图5。
图 5 BMO与IBMO不同维度的平均适应度值与平均运行时间的对比曲线Fig. 5 Comparison curves of average fitness values and average running time of BMO and IBMO in different dimensions下载:
全尺寸图片
由图5可知，两算法的适应度和时间跨度均随维度增加呈同步变化趋势，甚至对函数
$ {F_2} $ 、$ {F_7} $ 、$ {F_8} $ 的300维和400维情形，IBMO仍可优于维度情形并寻得更优收敛精度；而二者的平均运行时间则随函数维度增大呈递增趋势，相较而言，适应度的递变速率则变化更为缓慢，表明IBMO在高维情况下可在保持时间近似同等增幅前提下寻得更为优异的收敛精度，有效验证了所提IBMO算法在高维问题上的良好适用能力。综上分析可知，IBMO算法具有优越的全局搜索与局部开采性能、较强的鲁棒性和稳定性，以及在高维情形的良好适用性和高收敛精度，有效验证了改进IBMO在高维函数优化中的优越寻优性能。
4. 结束语
藤壶配尾优化算法是启发于自然界中藤壶交配繁殖行为的一种新的智能优化算法。为改善BMO算法在迭代过程中易陷入局部极值、开采搜索性能弱等问题，启发性构建藤壶幼虫的沉降附着行为模型、精子的正反向递减铸型策略并耦合性提出一种改进BMO算法。数值结果表明：藤壶幼虫的沉降附着行为可有效增强算法的全局搜索性能，正反向递减铸型策略则有效改善BMO算法的局部搜索性能；所提改进BMO算法具有更强的高维寻优适用性和良好算法稳健性。接下来的工作是将改进BMO用于极限学习机的超参数优选、复杂多目标问题的智能求解等领域。
-
图 1 藤壶幼虫的沉降附着行为示意
Fig. 1 Sedimentation adhesion behavior of barnacle larvae
下载:
全尺寸图片
图 2 正反向递减铸型策略示意
Fig. 2 Forward-and-backward decreasing casting strategy
下载:
全尺寸图片
图 3 BMO-SAB、BMO-FBDC与BMO平均适应度的收敛对比曲线
Fig. 3 Convergence comparison curves of BMO-SAB, BMO-FBDC and BMO mean fitness values
下载:
全尺寸图片
图 4 5种算法平均适应度值的收敛对比曲线
Fig. 4 Convergence comparison curves of mean fitness values of five algorithms
下载:
全尺寸图片
图 5 BMO与IBMO不同维度的平均适应度值与平均运行时间的对比曲线
Fig. 5 Comparison curves of average fitness values and average running time of BMO and IBMO in different dimensions
下载:
全尺寸图片
表 1 不同改进策略下的BMO优化性能对比统计分析
Table 1 Comparative statistical analysis of BMO optimization performance under different improvement strategies
函数 BMO BMO-SAB 函数 BMO BMO-FBDC mean std mean std mean std mean std $ {F_1}\left( x \right) $ 4.41×10−34 2.53×10−33 2.12×10−48 1.79×10−47 $ {F_1}\left( x \right) $ 4.41×10−34 2.53×10−33 4.48×10−58 4.39×10−57 $ {F_2}\left( x \right) $ 2.41×10−60 2.41×10−59 8.31×10−88 8.18×10−87 $ {F_2}\left( x \right) $ 2.41×10−60 2.41×10−59 3.72×10−110 3.71×10−109 $ {F_3}\left( x \right) $ 1.08×10−32 8.76×10−32 3.58×10−46 2.21×10−45 $ {F_3}\left( x \right) $ 1.08×10−32 8.76×10−32 2.34×10−57 2.22×10−56 续表 1 函数 BMO BMO-SAB 函数 BMO BMO-FBDC mean std mean std mean std mean std $ {F_4}\left( x \right) $ 5.14×10−61 5.14×10−60 1.27×10−89 1.17×10−88 $ {F_4}\left( x \right) $ 5.14×10−61 5.14×10−60 2.71×10−113 2.70×10−112 $ {F_5}\left( x \right) $ −1.24×104 2.88×103 −2.17×104 1.48×103 $ {F_5}\left( x \right) $ −1.24×104 2.88×103 −1.23×104 2.81×103 $ {F_6}\left( x \right) $ 1.57×101 1.04×101 1.47×101 1.06×101 $ {F_6}\left( x \right) $ 1.57×101 1.04×101 1.84×100 5.90×100 $ {F_7}\left( x \right) $ 4.04×10−25 4.03×10−24 1.61×10−36 1.61×10−35 $ {F_7}\left( x \right) $ 4.04×10−25 4.03×10−24 1.27×10−49 1.26×10−48 $ {F_8}\left( x \right) $ 1.72×10−64 1.36×10−63 7.52×10−82 7.51×10−81 $ {F_8}\left( x \right) $ 1.72×10−64 1.36×10−63 1.63×10−113 1.62×10−112 表 2 500维度不同算法优化性能对比统计分析
Table 2 Comparative statistical analysis of optimization performance of different algorithms in 500 dimensions
函数 指标 GEO SOA AOA BMO IBMO $ {F_1}\left( x \right) $ mean 2.46×104 1.03×100 1.40×10−36 2.48×10−30 3.82×10−84 std 1.47×105 4.33×10−1 7.77×10−36 2.41×10−29 2.62×10−83 运行时间/s 1.83×10−1 2.62×10−1 2.61×10−1 1.84×100 2.50×100 te/s 1.83×10−1≈ 3.33×10−1≈ 1.61×100− 9.42×10−1+ — $ {F_2}\left( x \right) $ mean 1.23×106 1.25×106 1.09×10−32 1.45×10−60 1.49×10−162 std 3.01×105 5.22×105 1.09×10−31 1.17×10−59 1.49×10−161 运行时间/s 1.13×100 1.28×100 1.29×100 3.97×100 5.81×100 te/s 3.68×10−1+ 3.68×10−1+ 2.34×100≈ 1.36×100+ — $ {F_3}\left( x \right) $ mean 5.18×101 9.94×101 4.60×10−33 4.08×10−30 1.88×10−81 std 3.25×100 2.47×10−1 3.17×10−32 3.48×10−29 1.81×10−80 运行时间/s 1.74×10−1 2.64×10−1 2.57×10−1 2.17×100 2.14×100 te/s 1.64×10−1+ 1.21×10−1+ 1.34×100− 7.84×10−1+ — $ {F_4}\left( x \right) $ mean 4.22×105 3.78×102 7.92×10−65 8.50×10−61 5.85×10−168 std 4.08×104 2.61×102 5.60×10−64 8.50×10−60 0.00×100 运行时间/s 1.76×10−1 2.12×10−1 2.35×10−1 1.79×100 2.16×100 te/s 1.08×10−1+ 2.45×10−1≈ 1.28×100− 7.53×10−1+ — $ {F_5}\left( x \right) $ mean −3.58×104 −1.91×104 −1.27×104 −2.87×104 −7.00×104 std 3.90×103 2.42×103 2.61×103 7.38×103 3.05×103 运行时间/s 2.05×10−1 3.24×10−1 3.12×10−1 1.85×100 2.67×100 te/s 5.34×10−1≈ 1.42×10−1+ 6.23×10−2+ 7.68×10−3+ — $ {F_6}\left( x \right) $ mean 1.22×102 1.23×102 1.23×102 9.67×101 2.52×101 std 4.60×10−1 5.80×10−1 7.39×10−1 4.86×101 4.69×101 运行时间/s 2.54×10−1 2.63×10−1 2.84×10−1 1.87×100 2.26×100 te/s 1.58×10−1+ 8.28×10−2+ 1.05×10−1+ 5.76×10−2+ — 续表 2 函数 指标 GEO SOA AOA BMO IBMO $ {F_7}\left( x \right) $ mean 4.77×101 3.41×100 9.99×10−2 9.67×101 1.98×10−74 std 2.10×100 8.37×10−1 3.09×10−5 4.86×101 1.97×10−73 运行时间/s 1.77×10−1 2.12×10−1 2.44×10−1 1.80×100 2.12×100 te/s 1.42×10−1+ 2.90×10−1≈ 6.44×10−1≈ 4.25×10−1+ — $ {F_8}\left( x \right) $ mean 3.69×102 2.22×102 2.24×102 4.47×10−25 1.60×10−167 std 5.23×101 7.18×10−1 4.28×10−13 3.75×10−24 0.00×100 运行时间/s 6.73×10−1 6.92×10−1 7.54×10−1 2.78×100 4.10×100 te/s 1.64×10−1+ 3.15×10−1+ 2.32×10−1+ 1.33×10−1+ — +/≈/− 占优次数 6/2/0 5/3/0 3/2/3 8/0/0 — 表 3 BMO与IBMO算法不同维度的优化性能对比统计分析
Table 3 Comparative statistical analysis of optimization performance of BMO and IBMO in different dimensions
维度 算法 指标 $ {F_1}\left( x \right) $ $ {F_2}\left( x \right) $ $ {F_3}\left( x \right) $ $ {F_4}\left( x \right) $ $ {F_5}\left( x \right) $ $ {F_6}\left( x \right) $ $ {F_7}\left( x \right) $ $ {F_8}\left( x \right) $ 100 BMO mean 4.4×10−34 2.4×10−60 1.1×10−32 5.1×10−61 −1.2×104 1.6×101 4.0×10−25 1.7×10−64 std 2.5×10−33 2.4×10−59 8.8×10−32 5.1×10−60 2.9×103 1.0×101 4.0×10−24 1.4×10−63 IBMO mean 1.8×10−83 7.7×10−166 7.0×10−86 7.0×10−170 −2.2×104 5.2×100 4.9×10−76 3.5×10−166 std 1.8×10−82 0.0×100 5.8×10−85 0.0×100 1.3×103 8.9×100 4.9×10−75 0.0×100 200 BMO mean 1.1×10−32 9.9×10−58 2.2×10−32 1.7×10−60 −1.8×104 3.3×101 1.7×10−25 2.7×10−60 std 9.3×10−32 7.1×10−57 2.1×10−31 1.7×10−59 4.4×103 2.1×101 1.3×10−24 2.5×10−59 IBMO mean 1.5×10−79 2.7×10−167 1.5×10−83 6.8×10−156 −3.8×104 9.8×100 8.2×10−75 3.1×10−167 std 1.5×10−78 0.0×100 1.5×10−82 6.8×10−155 1.9×103 1.9×101 6.7×10−74 0.0×100 300 BMO mean 9.4×10−32 9.0×10−58 6.8×10−32 8.6×10−62 −2.2×104 5.2×101 1.1×10−25 2.9×10−60 std 5.9×10−31 9.0×10−57 5.4×10−31 8.6×10−61 5.1×103 3.2×101 1.1×10−24 2.2×10−59 IBMO mean 2.0×10−84 6.3×10−161 5.1×10−84 3.0×10−171 −5.0×104 1.9×101 9.6×10−75 5.1×10−159 std 1.8×10−83 6.3×10−160 5.1×10−83 0.0×100 2.5×103 3.0×101 9.6×10−74 5.1×10−158 400 BMO mean 3.6×10−30 1.0×10−58 4.4×10−32 3.3×10−56 −2.5×104 7.2×101 1.4×10−19 1.1×10−62 std 3.4×10−29 1.0×10−57 2.6×10−31 3.3×10−55 6.7×103 4.2×101 1.4×10−18 1.1×10−61 IBMO mean 8.8×10−84 1.5×10−168 1.4×10−83 8.6×10−171 −6.1×104 2.5×101 5.4×10−80 1.7×10−167 std 8.8×10−83 0.0×100 1.4×10−82 0.0×100 2.7×103 4.0×101 5.4×10−79 0.0×100 500 BMO mean 2.5×10−30 1.5×10−60 4.1×10−30 8.5×10−61 −2.9×104 9.7×101 4.5×10−25 5.3×10−56 std 2.4×10−29 1.2×10−59 3.5×10−29 8.5×10−60 7.4×103 4.9×101 3.7×10−24 5.3×10−55 IBMO mean 3.8×10−84 1.5×10−162 1.9×10−81 5.9×10−168 −7.0×104 2.5×101 2.0×10−74 1.6×10−167 std 2.6×10−83 1.5×10−161 1.8×10−80 0.0×100 3.1×103 4.7×101 2.0×10−73 0.0×100 -
[1] DARWISH A. Bio-inspired computing: algorithms review, deep analysis, and the scope of applications[J]. Future computing and informatics journal, 2018, 3(2): 231–246. doi: 10.1016/j.fcij.2018.06.001 [2] AZIZI M, TALATAHARI S, GANDOMI A H. Fire Hawk optimizer: a novel metaheuristic algorithm[J]. Artificial intelligence review, 2023, 56(1): 287–363. doi: 10.1007/s10462-022-10173-w [3] SAYYADI R, AWASTHI A. A simulation-based optimisation approach for identifying key determinants for sustainable transportation planning[J]. International journal of systems science:operations & logistics, 2018, 5(2): 161–174. [4] CHEN Jing, GAN Min, ZHU Quanmin, et al. Robust standard gradient descent algorithm for ARX models using aitken acceleration technique[J]. IEEE transactions on cybernetics, 2022, 52(9): 9646–9655. doi: 10.1109/TCYB.2021.3063113 [5] PENG Xingguang, JIN Yaochu, WANG Handing. Multimodal optimization enhanced cooperative coevolution for large-scale optimization[J]. IEEE transactions on cybernetics, 2019, 49(9): 3507–3520. doi: 10.1109/TCYB.2018.2846179 [6] GU Qinghua, LIU Yingyin, CHEN Lu, et al. An improved competitive particle swarm optimization for many-objective optimization problems[J]. Expert systems with applications, 2022, 189: 116118. doi: 10.1016/j.eswa.2021.116118 [7] DOUKAKIS E, DEBATTISTA K, BASHFORD-ROGERS T, et al. Audio-visual-olfactory resource allocation for tri-modal virtual environments[J]. IEEE transactions on visualization and computer graphics, 2019, 25(5): 1865–1875. doi: 10.1109/TVCG.2019.2898823 [8] HATEM N, YUSOF Y, KADIR A Z A, et al. A novel integrating between tool path optimization using an ACO algorithm and interpreter for open architecture CNC system[J]. Expert systems with applications, 2021, 178: 114988. doi: 10.1016/j.eswa.2021.114988 [9] 赵世杰, 高雷阜, 于冬梅, 等. 融合能量周期性递减与牛顿局部增强的改进HHO算法[J]. 控制与决策, 2021, 36(3): 629–636. ZHAO Shijie, GAO Leifu, YU Dongmei, et al. Improved Harris Hawks optimization coupling energy cycle decline mechanism and Newton local enhancement strategy[J]. Control and decision, 2021, 36(3): 629–636. [10] 赵世杰, 高雷阜, 于冬梅, 等. 基于变因子加权学习与邻代维度交叉策略的改进CSA算法[J]. 电子学报, 2019, 47(1): 40–48. doi: 10.3969/j.issn.0372-2112.2019.01.006 ZHAO Shijie, GAO Leifu, YU Dongmei, et al. Improved crow search algorithm based on variable-factor weighted learning and adjacent-generations dimension crossover strategy[J]. Acta electronica sinica, 2019, 47(1): 40–48. doi: 10.3969/j.issn.0372-2112.2019.01.006 [11] 赵世杰, 马世林, 王梦晨, 等. 群集正反向回溯人工生态系统优化算法的ELM超参优选[J]. 控制与决策, 2023, 38(4): 921–928. ZHAO Shijie, MA Shilin, WANG Mengchen, et al. Super parameter optimization of ELM by artificial ecosystem-based optimization with crowding forward-backward and backtracking tips[J]. Control and decision, 2023, 38(4): 921–928. [12] HASHIM F A, HOUSSEIN E H, MABROUK M S, et al. Henry gas solubility optimization: a novel physics-based algorithm[J]. Future generation computer systems, 2019, 101: 646–667. doi: 10.1016/j.future.2019.07.015 [13] ARORA S, SINGH S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft computing, 2019, 23(3): 715–734. doi: 10.1007/s00500-018-3102-4 [14] DHIMAN G, KUMAR V. Seagull optimization algorithm: theory and its applications for large-scale industrial engineering problems[J]. Knowledge-based systems, 2019, 165: 169–196. doi: 10.1016/j.knosys.2018.11.024 [15] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris Hawks optimization: algorithm and applications[J]. Future generation computer systems, 2019, 97: 849–872. doi: 10.1016/j.future.2019.02.028 [16] XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems science & control engineering, 2020, 8(1): 22–34. [17] FARAMARZI A, HEIDARINEJAD M, STEPHENS B, et al. Equilibrium optimizer: a novel optimization algorithm[J]. Knowledge-based systems, 2020, 191: 105190. doi: 10.1016/j.knosys.2019.105190 [18] HASHIM F A, HUSSAIN K, HOUSSEIN E H, et al. Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems[J]. Applied intelligence, 2021, 51(3): 1531–1551. doi: 10.1007/s10489-020-01893-z [19] ZHAO Shijie, ZHANG Tianran, MA Shilin, et al. Dandelion optimizer: a nature-inspired metaheuristic algorithm for engineering applications[J]. Engineering applications of artificial intelligence, 2022, 114: 105075. doi: 10.1016/j.engappai.2022.105075 [20] ZHAO Shijie, ZHANG Tianran, MA Shilin, et al. Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems[J]. Applied intelligence, 2023, 53(10): 11833–11860. doi: 10.1007/s10489-022-03994-3 [21] SULAIMAN M H, MUSTAFFA Z, SAARI M M, et al. Barnacles mating optimizer: a new bio-inspired algorithm for solving engineering optimization problems[J]. Engineering applications of artificial intelligence, 2020, 87: 103330. doi: 10.1016/j.engappai.2019.103330 [22] CROW J F. Hardy, Weinberg and language impediments[J]. Genetics, 1999, 152(3): 821–825. doi: 10.1093/genetics/152.3.821 [23] MANTEGNA R N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes[J]. Physical review E, statistical physics, plasmas, fluids, and related interdisciplinary topics, 1994, 49(5): 4677–4683. [24] HERDIANTI W, GUNAWAN A A S, KOMSIYAH S. Distribution cost optimization using pigeon inspired optimization method with reverse learning mechanism[J]. Procedia computer science, 2021, 179: 920–929. doi: 10.1016/j.procs.2021.01.081 [25] MOHAMMADI-BALANI A, DEHGHAN NAYERI M, AZAR A, et al. Golden eagle optimizer: a nature-inspired metaheuristic algorithm[J]. Computers & industrial engineering, 2021, 152: 107050.
