Semi-supervised image classification method fused with relational features
-
摘要: 半监督深度学习模型具有泛化能力强，所需样本数较少等特点，经过10多年的发展，在理论和实际应用方面都取得了巨大的进步，然而建模样本内部“隐含”关系时模型缺乏解释性以及构造无监督正则化项难度较大等问题限制了半监督深度学习的进一步发展。针对上述问题，从丰富样本特征表示的角度出发，构造了一种新的半监督图像分类模型—融合关系特征的半监督分类模型（semi-supervised classification model fused with relational features，SCUTTLE），该模型在卷积神经网络模型(convolutional neural networks，CNN)基础上引入了图卷积神经网络(graph convolutional networks，GCN)，尝试通过GCN模型来提取CNN模型各层的低、高级特征间的关系，使得融合模型不仅具有特征提取能力，而且具有关系表示能力。通过对SCUTTLE模型泛化性能进行分析，进一步说明了该模型在解决半监督相关问题时的有效性。数值实验结果表明，三层CNN与一层GCN的融合模型在CIFAR10、CIFAR100、SVHN 3种数据集上与CNN监督学习模型的精度相比均可提升5%~6%的精度值，在最先进的ResNet、DenseNet、WRN（wide residual networks）与GCN的融合模型上同样证明了本文所提模型的有效性。Abstract: A semi-supervised deep learning model exhibits great generalization ability with minimal required samples and has made great progress in theory and practical application over the past ten years or so. However, the lack of the model’s interpretability when modeling the internal “implicit” relationship of samples and the difficulty in constructing unsupervised regularization items have limited the further development of semi-supervised deep learning. To solve these problems and enrich the sample feature representation, this study has developed a novel semi-supervised model for image classification—semi-supervised classification model integrating the relational features (SCUTTLE). The model introduces the graph convolutional networks (GCN) based on the convolutional neural networks (CNN) and extracts the relationships between the low- and high-level features of each layer of the CNN model via the GCN model, thus extracting features and expressing relationships. By analyzing the generalization performance of the SCUTTLE model, the paper further illustrates its effectiveness in solving semi-supervised related problems. The numerical results indicate that the classification accuracy of the hybrid model with three layers of CNN and one layer of GCN can be improved by 5%–6% compared to that of the CNN model on the CIFAR10, CIFAR100, and SVHN datasets. The effectiveness of the model proposed in this paper is also proved in the most advanced fusion models of ResNet, DenseNet, WRN (wide residual networks), and GCN.
-
半监督学习[1,2]是一种介于监督学习和无监督学习之间的学习方法，其基本思想是在训练少量标签样本的过程中引入大量无标签样本来解决监督学习由于标签样本不足所造成的模型退化问题。早期的半监督学习算法与深度学习的结合相对较少，随着深度学习在各界大放异彩，尤其在图像分类问题上超人类的识别率使得半监督学习与深度学习的结合成为一种必然趋势。
半监督深度学习的核心模型依然是卷积神经网络，不同模型的区别在于添加不同的先验假设来建立不同的损失函数。Sajjadi等[3]认为相同的样本在不同的扰动下，模型应该具有相同的输出（被称为“一致性正则化原则”）。因此将标签样本与无标签样本经过随机增强[4]、裁剪、随机池化等操作后输入模型中，强制模型对同一样本输出相同的预测类别。Laine等[5]将上述的一致性正则化原则建模为时序模型，认为模型在每次迭代的学习过程中都应该保持所谓的“一致性正则化”。Li等[6]与上述两篇文献的做法不同，将这种“一致性正则化”方法加入了模型的参数[7]之中，他们认为相同的样本在经过模型参数的随机扰动之后应该输出相同的类别。
综上所述，半监督图像分类算法主要围绕一致性原则进行建模，使用不同程度的数据增强、混合等操作强制对同类样本输出相同的预测结果，希望模型能够习得图像的本质特征。但这种建模方式仅在模型的端首与端尾进行操作，缺乏半监督模型的内部机理分析，使模型不具可解释性。
从本质上而言，半监督学习的建模思想描述为：首先建立所给样本的隐含“关系”，然后将标签样本的标签信息通过上述“关系”传递到无标签样本。而图卷积网络（graph convolutional networks，GCN）的提出，正好从关系建模的角度出发，给出解析网络数据的一种思路。与视觉卷积模型相比，模型解释性大大增加。此外，该方法还为半监督图像分类提供建模思路，本文旨在利用图卷积网络来建模前述样本的隐含“关系”，然后进一步研究与视觉卷积模型融合后的融合模型的机理性能。
一直以来，模型融合作为改进模型性能的技术被广泛使用，著名的GoogLeNet[8]模型中作者就表明视觉图像数据应在各种尺度处理后再进行融合，才能使得深度网络对输入图像的尺度具有鲁棒性。而本文将GCN与卷积分类模型相融合则需考虑以下两个问题：（1）建模“关系”的目标对象。（2）对于图像特征提取的多层神经网络模型而言，需要考虑GCN模型如何与这些多层结构相融合。
针对问题（1），首先基于图像数据构建KNN（K-nearest neighbor，KNN）图，以此来建模图像之间的一阶关系信息。这种通过建图来建模GCN模型输入的相关文献[9-11]大部分都是用随机参数化或者依靠添加损失项的方式，所得图结构很大程度上取决于模型自身性能，且这种图结构忽略了数据的原始信息，使模型不具解释性。而构建KNN图的方式可以保持数据的原始信息不丢失。
针对问题（2），本文尝试将关系学习模型融合到特征提取模型的任意一层，考虑到特征提取模型是一个复杂且多层的结构，每一层所学特征信息皆不相同，因此关系信息与特征信息不同的融合方式会对模型的泛化性能产生不同的影响。
本文主要贡献有：1）提出基于图像间的关系表示模型，该模型可以提取到图像间的不同阶的关系信息。2）设计新的半监督图像分类模型。将图像数据的关系信息与特征信息相融合，可以极大地提升表示学习模型的泛化能力。3）对模型中提取样本间隐含关系的函数进行解释，进一步阐明其运行机理。4）在5个基准图像数据集上进行数值实验，进一步验证本文提出的融合模型可以在少样本情形下有效提升监督模型的分类精度。
1. 相关工作
本节主要介绍半监督深度学习模型的建模方法。首先介绍半监督学习的基本思路。在引言中提到的（预测样本分布、聚类假设、流形假设以及前述的“一致性原则”）假设的前提下，即可约束相似的样本输出相同的结果。
以图结构的标签传播（label propagation，LP）算法[12]为例进行说明，该算法的目标函数如下：
$$ \mathop {\rm min}\limits_f {\text{ }}\sum\limits_i^L {\parallel f({{\boldsymbol{x}}_i}) - {y_i}{\parallel ^2} + \lambda \sum\limits_{i,j}^{L + U} {\parallel f({{\boldsymbol{x}}_i}) - f({{\boldsymbol{x}}_j}){\parallel ^2}{W_{ij}}} } $$ (1) 式中：样本被分为标签样本（用
$L$ 表示）和无标签样本（用$U$ 表示），其中标签样本损失为$\parallel {f_i} - {y_i}{\parallel ^2}$ ，在此基础上又添加与无标签样本相关的正则化项$\parallel {f_i} - {f_j}{\parallel ^2}{W_{ij}}$ ，意味着相同标签的样本之间会有更大的连接权重，从而使得与标签样本相连的权重较大的无标签样本更容易获得标签样本的标签信息，进而实现全图的标签信息传播。上述半监督学习方法虽然取得了不错的效果，但是随着深度学习的兴起，半监督深度学习算法成为了研究的重点。
半监督深度图像分类模型是将包含无标签样本的正则化项引入多层结构的网络模型中。Weston等[13]针对传统的半监督学习算法无法充分地学习数据的特征，通过在多层神经网络的基础上显式地引入包含无标签样本的正则化项提出3种通用的特征表示模型，从而实现半监督学习与神经网络的结合。生成对抗网络（generative adversarial nets，GAN）[14]也是一种学习数据表示的多层网络模型，由于此模型在模拟生成真实样本任务上的成功表现，自然而然的想法就是在标签样本较少的情况下，可以利用生成器生成的样本来提高模型的泛化能力。Springenberg等[15]提出的GAN模型是从部分标记数据中学习判别分类器的方法，通过在目标函数中添加标签样本的分类损失，使模型在标签样本的分布与其预测的无标签样本分布之间交换互信息，再结合判别器损失函数即可实现半监督学习。Chang等[16]改进GAN的判别器函数，强制其输出为N+1类的样本（N为样本类别数，额外的一类为生成器的样本类别），这样判别器不再是二分类函数，而是多分类的函数。同样地，上述过程也利用了无标记样本的隐含分布信息，通过结合改进的GAN模型完成半监督学习的过程。
以上半监督图像分类算法皆是利用深层卷积模型在提取数据特征方面的优势来提升模型的泛化性能，但在描述数据内部隐含的“关系”信息时均缺乏解释性。因此本文针对上述问题，在特征提取模型的基础上又设计了关系表示模型，而且给出了二者的融合方法，通过端到端的训练方式提升模型的泛化能力。
2. 融合关系特征的半监督分类模型
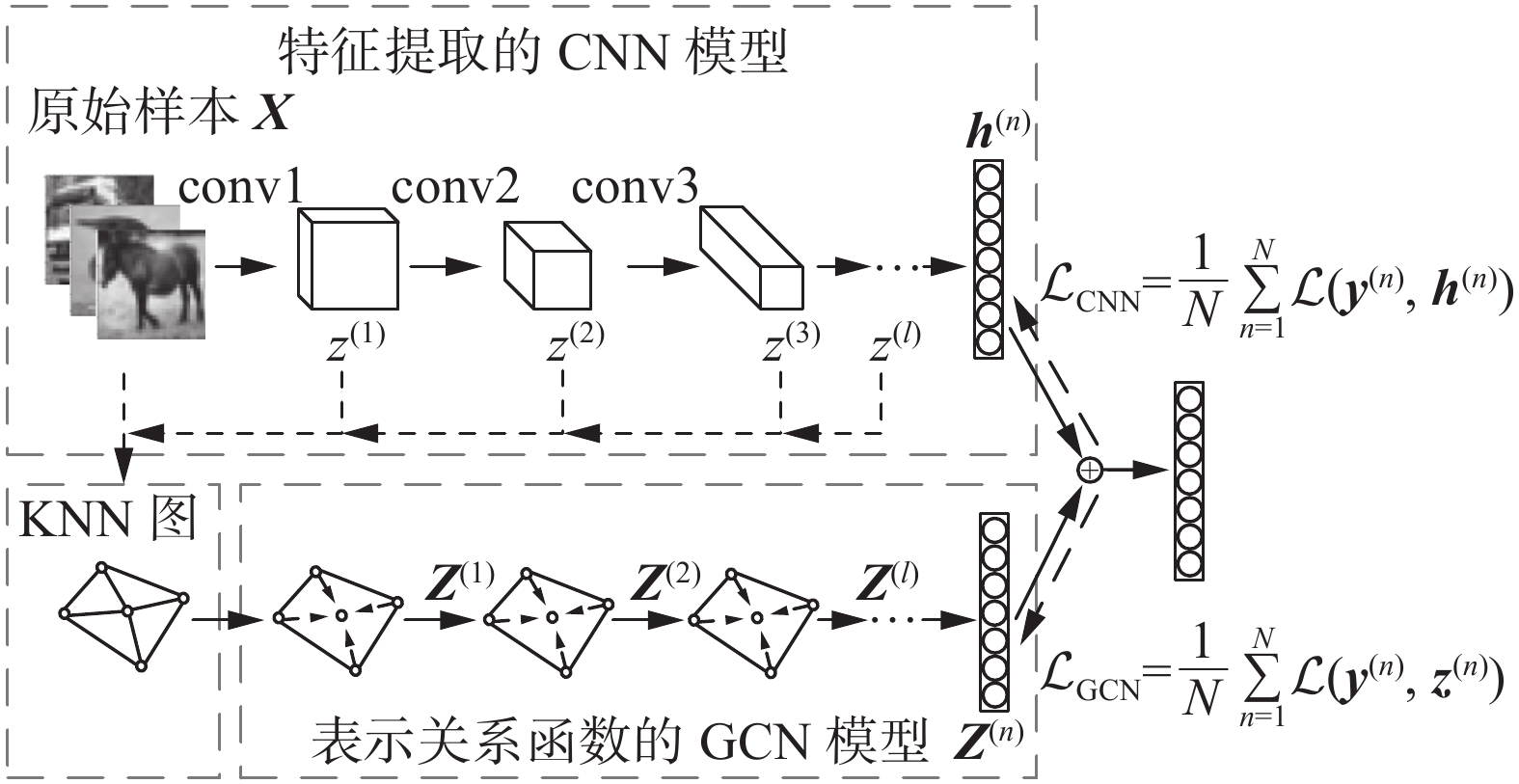
本节介绍提出的SCUTTLE模型。该模型结构如图1所示。由图可知模型大致可以分为两个模块：图像特征提取的CNN模块和表示关系函数的GCN模块。模型设计整体思路如下：
图 1 SCUTTLE模型示意图Fig. 1 Schematic diagram of SCUTTLE model
下载:
全尺寸图片
1）将原始样本数据输入CNN中学习样本的隐含特征，并且通过全连接层将学习到的样本特征映射到样本标签。
2）就监督学习而言，只依靠上述CNN模块，模型就可以取得很好的泛化性能。但是对于半监督学习，还需依赖模型习得的样本隐含“关系”函数。为了习得这些“关系”，在上述CNN提取特征的过程中，对于任意卷积层提取到的图像特征构建KNN图，图中不仅包含了样本自身的特征信息，而且将相邻样本间原本无关的样本集从离散空间映射到一个关系度量空间。此时的KNN图中仅显示了样本间的一阶关系信息．为了获取更高阶的关系信息，需要将KNN图和样本特征同时输入GCN模型中，通过多层GCN的叠加，最终将学习到的关系特征与CNN提取到的图像特征融合在一起进行端到端的学习。下面将描述模型的具体细节。
2.1 KNN图的构建
对于N个样本数据
${\boldsymbol{X}}=({x}_{1},{x}_{2},\cdots ,{x}_{N})$ ，${\boldsymbol{X}} \in {{\bf{R}}^{d \times N}}$ 。${\boldsymbol{X}}$ 中的列向量${{\boldsymbol{x}}_i}$ 代表第i个样本的特征，N为样本的数量，d表示样本的维度。对于${\boldsymbol{X}}$ 中的任何一个样本${{\boldsymbol{x}}_i}$ ，都可以通过某种映射$\varphi $ ：${{\bf R}^d} \times {{\bf R}^d} \to {\bf R}$ 来建立该样本与其他N−1个样本${{\boldsymbol{x}}_{j(i \ne j)}}$ 的相似度${S_{ij}}$ ：$$ {S}_{ij}=\phi ({\boldsymbol x}_{i}\text{，}{\boldsymbol x}_{j}) $$ (2) 上述映射函数
$\varphi $ 可以表示为$$ {S_{ij}} = \left\{ \begin{aligned} &{e^{ - \tfrac{{{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}^2}}}{t}}}\quad i \ne j \\ &{0\quad i = j } \\ \end{aligned} \right. $$ (3) 式（3）即为常用的热核定义法[17]，常用于连续型数据之间的相似度定义，通过计算样本间的距离，将d维连续空间中的两个样本映射到一维实空间中。
通过计算N个样本中任意两个样本间的相似度，可得到一个对称的相似度稠密矩阵
${\boldsymbol{S}} \in {{\bf R}^{N \times N}}$ ，即对于其中任意一个元素${S_{ij}}$ =${S_{ji}}$ ($i \ne j$ )。考虑${\boldsymbol{S}}$ 中任意行$ {S}_{i·} $ （${S_{ii}}$ 除外）的元素，分别表示第i个样本与其他N−1个样本的相似度，通过对这N−1个元素进行排序，使得${S}_{i,1}\geqslant{S}_{i,2}\geqslant \cdots \geqslant{S}_{i,N-1}$ （${S_{i,1}}$ 表示相似度最大的元素），即可找到最相似的K个元素$\{{S}_{i,1},{S}_{i,{2}},\cdots,{S}_{i,K}\}$ ，同理对于${\boldsymbol{S}}$ 中的每一行都可以执行上述操作，由此即可构建一个稀疏的KNN无向图。2.2 特征提取的CNN模型
正如引言所述，提取图像特征的CNN模型是实施半监督深度学习算法的关键。其建模过程可以描述为：
对于任意一个多层卷积神经网络，第l层卷积提取到的数据特征
${{\boldsymbol{z}}^{(l)}}$ 表示如下：$$ {{\boldsymbol{z}}^{(l)}} = {\boldsymbol{W}}_{\rm conv}^{(l)} * {{\boldsymbol{a}}^{(l - 1)}} $$ (4) 式中：
${\boldsymbol{W}}_{\rm conv}^{(l)}$ 表示第l层的卷积核参数以及偏置参数，${{\boldsymbol{a}}^{(l - 1)}}$ 表示前一层卷积提取到的特征图经过非线性激活函数（一般用ReLU[18]函数表示）后的输出。这里对于该模型的具体卷积过程不再赘述。式(4)中的${{\boldsymbol{z}}^{(l)}}$ 又可以写为$$ {\boldsymbol z}^{(l)}：=\left[{z}_{1}^{(l)};{z}_{2}^{(l)} ;{z}_{{F}_{l}}^{(l)}\right] $$ (5) 表示第l层卷积提取到的
${F_l}$ 个特征图，这些特征图再经过非线性的激活函数$\phi $ ，即可得到该层最终的输出${{\boldsymbol{a}}^{(l)}}$ ，即$$ {{\boldsymbol{a}}^{(l)}} = \phi ({{\boldsymbol{z}}^{(l)}}) $$ (6) 对于输入该模型的N个样本，该模型的目标函数为
$$ {\cal L}_{\rm CNN}=\frac{1}{N}{\displaystyle \sum _{n=1}^{N}{\cal L}({\boldsymbol y}^{(n)},{\boldsymbol h}^{(n)})} $$ (7) 式中：
${{\boldsymbol{y}}^{(n)}}$ 为第n个样本的真实标签；${{\boldsymbol{h}}^{(n)}}$ 为第n个样本的预测标签；$\cal{L}$ 为相应的损失函数。2.3 关系表示函数的GCN模型
2.2节阐述了CNN模型设计的整体思路，该模型利用不同卷积核提取到了层次化的图像特征，而忽视了图像间所蕴涵的内在联系。本节介绍图信号处理领域的GCN模型是如何通过图上节点的特征信息与图的结构信息来提取节点间的隐含关系。
GCN模型在建模之前通常需要构造一个图位移算子
${\boldsymbol{T}}$ 来表示所研究的图结构。位移算子${\boldsymbol{T}}$ 的作用就是将输入信号通过线性聚合的方式来提取节点的一阶邻域内的信息，这个过程可以类比CNN中的卷积核的作用（捕捉固定感受野范围内的信息）。其次只需要将${\boldsymbol{T}}$ 参数化后融入卷积神经网络中进行学习即可构建图上的卷积操作。常用的图位移算子包括下面3种类型：
1）图的邻接矩阵
${\boldsymbol{A}}$ 。对于其中的元素${A_{mn}}$ ，如果$({\upsilon }_{m},{\upsilon }_{n})\in \varepsilon$ ，则${A_{mn}} = 1$ ，否则为0；2）图的拉普拉斯矩阵
${\boldsymbol{L}}$ =${\boldsymbol{D}} - {\boldsymbol{A}}$ 。${\boldsymbol{D}}$ 为对角矩阵，其中的${D_{ii}}$ 表示第i个节点的度；3）
${\boldsymbol{L}}$ 归一化之后的类型：${\bar{\boldsymbol L}}{\text{ = }}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\tilde{\boldsymbol A}}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}$ 。本文采用Kipf等[19]提出的GCN模型，该模型基于归一化的图拉普拉斯矩阵
${\boldsymbol{\bar L}}$ 而提出的，也即上述图位移算子中的第3种类型。模型第$\ell $ 层学习到的特征${{\boldsymbol{Z}}^{(\ell )}}$ 可以表示为$$ {{\boldsymbol{Z}}^{(\ell )}} = \sigma ({{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\tilde{\boldsymbol A}}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{{\boldsymbol{Z}}^{(\ell - 1)}}{\boldsymbol{W}}_{\rm gcn}^{(\ell - 1)}) $$ (8) 式中：
${\tilde{\boldsymbol A}} = {\boldsymbol{A}} + {\boldsymbol{I}}$ ，${\boldsymbol{A}}$ 表示图所对应的邻接矩阵，${\boldsymbol{I}}$ 是单位对角阵，${\tilde{\boldsymbol A}}$ 表示在邻接矩阵${\boldsymbol{A}}$ 中的每个节点上添加自环的操作；${\tilde{\boldsymbol D}}$ 为对角阵，${{\tilde{\boldsymbol D}}_{ii}} = \sum\nolimits_j {{{{\tilde{\boldsymbol A}}}_{ij}}}$ 表示第i个节点（包含自己）的度，${\boldsymbol{W}}_{\rm gcn}^{(\ell - 1)}$ 表示第$\ell - 1$ 层的卷积核参数且包括偏置参数。在式(8)中，第$\ell - 1$ 层卷积提取到的特征${{\boldsymbol{Z}}^{(\ell - 1)}}$ 通过与归一化的图位移算子相乘来捕捉图中一阶邻域内的节点信息，再通过激活函数$\sigma $ （通常用ReLU函数表示）即可提取第$\ell $ 层的相关特征。与CNN模型类似，在模型的最后一层通过softmax函数来获得样本标签的预测分布。同样地，对于输入该模型的N个样本，模型的目标函数为
$$ {\cal L}_{\rm GCN}=\frac{1}{N}{\displaystyle \sum _{n=1}^{N}{\cal L}({\boldsymbol Z}^{(n)}\text{，}{\boldsymbol y}^{(n)})} $$ (9) 2.4 SCUTTLE模型
本节介绍将前述两种模型相融合的SCUTTLE模型，融合模型具有两种单一模型的双重属性，既具有特征提取能力，也具有关系表示能力。本节不仅给出模型融合的方法描述，也给出了融合模型的训练算法流程。此外，对本文提到的关系函数的构建过程也加以解释。
2.4.1 SCUTTLE模型的融合方法描述
本节介绍将2.2节中的CNN模型与2.3节中的GCN模型融合在一个end-to-end的框架中的融合方法，实施步骤如下：
1)对于输入CNN模型的N个样本，其中任意一个样本在第l层学习到的特征
${{\boldsymbol{z}}^{(l)}}$ 表示为2.2节中的式(5)。假设每个特征图的大小为$m \times n$ ，则${{\boldsymbol{z}}^{(l)}} \in {{\bf{R}}^{m \times n \times {F_l}}}$ ，可以将${{\boldsymbol{z}}^{(l)}}$ 展成维度为$ m \times n \times {F_l} $ 的一维向量。对输入模型的N样本都执行上述操作。此时的一维向量${{\boldsymbol{z}}^{(l)}}$ 依然具有特征图形状的${{\boldsymbol{z}}^{(l)}}$ 应有的特性。2)将上述样本特征
${{\boldsymbol{z}}^{(l)}}$ 作为2.1节KNN模型的输入，即可构建一个关于N个样本的稀疏KNN图，也称为权重邻接矩阵，是2.3节提到的图位移算子${\boldsymbol{T}}$ 的一种特殊形式，用${\boldsymbol{T}}'$ 来表示。3)将步骤1)和步骤2)中得到的
${{\boldsymbol{z}}^{(l)}}$ 和${\boldsymbol{T}}'$ 作为2.3节中GCN模型的输入，则GCN模型同时具有样本的高阶特征信息${{\boldsymbol{z}}^{(l)}}$ 以及连接这些信息的位移算子${\boldsymbol{T'}}$ ，通过图上的卷积操作即可学习这些特征之间的关系，GCN模型在第一层卷积学习到的特征${{\boldsymbol{Z}}^{(1)}}$ 可以表示为$$ {{\boldsymbol{Z}}^{(1)}} = \sigma ({{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\tilde{\boldsymbol T}'}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{{\boldsymbol{z}}^{(l)}}{\boldsymbol{W}}_{\rm gcn}^{(0)}) $$ (10) 式中：
${\tilde{\boldsymbol T}'} = {\boldsymbol{T}'} + {\boldsymbol{I}}$ ，${\boldsymbol{T}}'$ 为步骤2)中的权重邻接矩阵，${\tilde{\boldsymbol D}}$ 、${\boldsymbol{W}}_{\rm gcn}^{(0)}$ 与式(8)代表的含义相同。4）为了使得CNN模型与GCN模型在习得的样本特征上实现维度对齐，本文在GCN的最后一层后又添加了全连接层，假设GCN模型共有
$L''$ 层，${\boldsymbol{W}}_{fc} $ 为全连接层的权重参数，则上述过程表示为$$ {{\boldsymbol{Z}}^{(L'')}} = {\rm ReLU}\left({\boldsymbol{W}}_{fc}\left({\rm ReLU}\left({{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\tilde{\boldsymbol A}}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{{\boldsymbol{Z}}^{(L''{{ - 1}})}}{\boldsymbol{W}}_{\rm gcn}^{(L''{{ - 1}})}\right)\right)\right) $$ (11) 在融合模型的最后一层分别将两个模型得到的关系特征
${{\boldsymbol{Z}}^{(L'')}}$ 和样本特征${{\boldsymbol{a}}^{(L')}}$ 相结合得到样本的预测标签分布，这里假设CNN模型共有$L'$ 层，表示如下：$$ {\hat{\boldsymbol y}} = {\rm{softmax}}({{\boldsymbol{Z}}^{(L''')}} + {{\boldsymbol{H}}^{(L')}}) $$ (12) 5）计算模型最终的损失函数：
$$ {\cal L}_{\rm CNN\_GCN}=\frac{1}{N}{\displaystyle \sum _{n=1}^{N}{\cal L}({\widehat{y}}^{(n)}\text{，}{y}^{(n)})} $$ (13) 2.4.2 SCUTTLE模型的训练算法描述
设训练样本总数为N，每个批次的样本数量也即batch_size设定为Nbatch，则批次数量为
$\dfrac{N}{{{N_{\rm batch}}}}$ ，设每批次标记样本数量为Nlable，此时计算得到标记样本总数为${N_{\rm lable}} \times \dfrac{N}{{{N_{\rm batch}}}}$ ，后续提到的所有标记样本数量皆通过上式计算得到。算法1 SCUTTLE模型训练方法
输入 N个样本
${\boldsymbol{X}}=({\boldsymbol x}_{1},{\boldsymbol x}_{2},\cdots ,{\boldsymbol x}_{N})$ 以及Nlable个样本的标签。输出 N个样本的预测标签值。
1)随机初始化SCUTTLE模型的网络参数。
2)将全部样本作数据预处理且随机打乱顺序，同时设定样本批次数量为
$\dfrac{N}{{{N_{\rm batch}}}}$ ，且设定每批次标记样本数量为Nlable，epoch数量为e。3)将第一个批次的Nbatch个样本输入CNN模型中进行正向传播。
4)随机挑选步骤3)中CNN的任一隐层输出特征作为KNN图的输入，再经过GCN模型进行正向传播。
5)步骤3)~4)属于并行前向传播，在两个模型最后输出层通过式(12)进行特征融合并计算损失值，此时的损失值只包括步骤2)中提前设定好的Nlable个样本的损失，同时通过梯度反向传播优化模型参数。
6)测试模型精度。
7)将步骤3)~6)循环
$\dfrac{N}{{{N_{\rm batch}}}}$ 次，为全部样本一次迭代。8)步骤3)~7)循环e次，直至模型收敛。
上述算法即为SCUTTLE模型的批量训练算法，从步骤4)中可知，SCUTTLE融合算法对于任一批量的样本都会建立KNN图，相较于其他算法的随机参数化方法，本文所构建KNN图在很大程度上可以保证数据的先验性质，同时使模型具有解释性。在步骤5)中，将CNN模型的特征与GCN模型的特征进行融合，可以看作二者之间的相互约束过程，对于卷积特征不够清晰且明确的样本可以通过GCN的关系特征进行补充，从而提升泛化性能。SCUTTLE模型的训练方法流程图如图2所示。
图 2 SCUTTLE模型训练方法流程图Fig. 2 Flow chart of SCUTTLE model training method下载:
全尺寸图片
2.4.3 SCUTTLE模型的关系函数解释
对于常见的半监督学习模型（包括引言和相关工作中提到的），其优化目标函数为
$$\mathop {\rm min}\limits_W {\rm{ }}\sum\limits_i^L {\parallel f({{\boldsymbol{x}}_i}) - {y_i}{\parallel ^2}} + \sum\limits_{i,j}^{L + U} {{\cal L}(f({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j},{W_{ij}})} $$ (14) 式中：
${W_{ij}}$ 即为表示相邻两个样本间的关系参数；$L$ 表示标签样本；$U$ 表示无标签样本。为了后续表述的方便，将式(14)中的两项分别记为(141)与(142)。(141)为标签样本的损失函数，(142)为反映样本隐含关系的函数。根据前两小节所述的建模流程，CNN与GCN模型都利用标签样本的标签信息来构建监督信息的损失函数，因此(141)可以写为$$ \sum\limits_i^L {||{{({f_{\rm cnn}} + {f_{\rm gcn}})}_i} - {y_i}|{|^2}} $$ (15) 在构建样本的隐含关系函数时，CNN模型不具有建模样本间关系的能力，因此需依靠GCN模型来捕捉这些信息，因此对于(142)而言，结合式(8)或(10)，可得
$$ f({\boldsymbol{X}},{\boldsymbol{W}}) = {f_{\rm gcn}}({\boldsymbol{X}},{\boldsymbol{W}}) = {{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\tilde{\boldsymbol A}}{{\tilde{\boldsymbol D}}^{ - \frac{1}{2}}}{\boldsymbol{X}}{{\boldsymbol{W}}_{\rm gcn}} $$ (16) 对于式(16)中，任意两个样本间的关系又可以表示为
$$ f({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j},{{\boldsymbol{W}}_{ij}}) = \sum\limits_{j \in N(i)} {\frac{{{{{\tilde{\boldsymbol A}}}_{ij}}}}{{\sqrt {{{{\tilde{\boldsymbol D}}}_{ii}}} \sqrt {{{{\tilde{\boldsymbol D}}}_{jj}}} }}{{\boldsymbol{x}}_{ij}}{{\boldsymbol{W}}_{ij}}} $$ (17) $$ 令{R_{ij = }}\dfrac{{{{{\tilde{\boldsymbol A}}}_{ij}}}}{{\sqrt {{{{\tilde{\boldsymbol D}}}_{ii}}} \sqrt {{{{\tilde{\boldsymbol D}}}_{jj}}} }} $$ 其中，
$N(i)$ 表示第i个样本的邻居节点。由式(17)可以看出，相邻样本间的关系由$ {R_{ij}} $ 以及参数${{\boldsymbol{W}}_{ij}}$ 来度量，${{\boldsymbol{W}}_{ij}}$ 为模型需要学习的参数，实际值应当由所训练的样本集来确定；而$ {R_{ij}} $ 可以看作某种先验信息。从式中可以看出，对于给定的某个节点，
${{\tilde{\boldsymbol A}}_{ij}}$ 和${{\tilde{\boldsymbol D}}_{ii}}$ 是确定的，当邻居节点的度${{\tilde{\boldsymbol D}}_{jj}}$ 较大时，$ {R_{ij}} $ 较小；当邻居节点的度${{{\tilde {\boldsymbol D}}}_{jj}}$ 较小时，$ {R_{ij}} $ 较大；换言之，关系函数对于度较小的邻居分配较大的权值，对于度较大的邻居分配较小的权值。再结合视觉模型特征进行分析，假设习得的特征图不能很好地将不同类别分隔开，对应关系函数可以理解为，一个节点的邻居节点度较小，此时关系函数会赋予这些节点较大的权重，以致于不丢失这部分信息，这样无论是好的特征图还是差的特征图，关系函数总可以将他们的信息相融合，进而增强融合模型的泛化能力。2.4.4 SCUTTLE模型的复杂度分析
设N为输入模型的样本数量，CNN模型第l个卷积层的输出
${{\boldsymbol{z}}^{(l)}}$ 的维度为${M_l}$ ，卷积核维度为${K_l}$ ，上一层的输出通道数为${F_{l - 1}}$ ，全连接层的第$l'$ 层神经元数量为${C_{l'}}$ ，则CNN模型的时间复杂度为$O\left(N\left(\displaystyle\sum\limits_l {{M_l}{K_l}{F_{l - 1}} + \displaystyle\sum\limits_{l'} {{C_{l' - 1}}{C_{l'}}} } \right)\right)$ ，式(3)在构建KNN图时采用KD树算法[20]可以将时间复杂度降为$O(N{\rm log}3{M_{ \ell+1}})$ ，GCN模型第$\ell $ 层卷积${\boldsymbol{W}}_{\rm gcn}^{(\ell - 1)}$ 维度为${M_l}{d_{\ell - 1}}$ ，因此式(10)的时间复杂度为$O\left(N\displaystyle\sum\limits_\ell 2\left({M_l} + {M_l}{M_l}{d_{\ell - 1}} \right)\right)$ ，所以模型的总时间复杂度为$O\left(N\left(\displaystyle\sum\limits_l {{M_l}{K_l}{F_{l - 1}} + \sum\limits_{l'} {{C_{l' - 1}}{C_{l'}}} } \right) \right.$ +$N{\rm log}3{M_ {\ell+1}}$ +N$\left. \displaystyle\sum\limits_\ell 2\left({M_l} + {M_l}{M_l}{d_{\ell - 1}} \right)\right)$ 。由此可知，本文所提模型的时间复杂度与输入模型的样本数量之间均为线性关系。3. 数值实验与结果分析
为了更好地测试和分析半监督融合模型的泛化能力，本文采用数值实验的方式对模型进行性能评估。
3.1 数据集以及实验环境
为了验证半监督融合模型的有效性，模型需要在已知的一些公开数据集上进行测试并且给出对应的实验结果。本节介绍将要进行测试的4种数据集：MNIST、CIFAR10、CIFAR100、SVHN。由于众多研究者对于MNIST、CIFAR10、CIFAR100等常用图像数据集较为熟悉，关于它们的详细信息这里不再赘述，下面主要介绍SVHN数据集以及各数据集之间属性的对比。
SVHN：该数据集摘自Google街景图像中门牌号码，共包括73257张训练图像和26032张测试图像，每张图像像素为32
$ \times $ 32的彩色图像。MNIST数据集不同的是，每张图像中包含多个手写体数字。相比MNIST数据集，识别难度有所增加。后续全部实验所用软硬件环境为：Intel（R） Core（TM） i7-6850K CPU@3.60GHz处理器，NVIDIA GeForce GTX 1080Ti 12GB显卡，12GB内存，操作系统为CentOS 7.8.2003(Core)，编程语言为Python3.7，深度学习框架为Pytorch1.4。
表 1 4种数据集的属性信息Table 1 Attribute information of four datasets名称 样本数 训练集 测试集 类别 MNIST 70000 60000 10000 10 CIFAR10 60000 50000 10000 10 CIFAR100 60000 50000 10000 100 SVHN 99289 73257 26032 10 3.2 SCUTTLE模型(三层CNN-GCN)性能分析
3.2.1 实验模型
由于本文所提模型是CNN模型与GCN模型的融合模型，有必要设置横向对比实验来说明融合模型的有效性。鉴于2.4节所述的模型融合方法，在将二者融合时需要考虑如下问题：GCN模型应该与CNN模型哪一层的特征图相连接。
为了公平对比两种模型融合的不同方式所产生的模型性能，本文设计了简单的三层CNN（隐层通道数：128-256-512，卷积核大小：3×3）与单层GCN的融合模型。因此对比的模型共有以下5种结构（一个监督学习的基准模型和4个半监督学习融合模型）：CNN、CNN-0-GCN、CNN-1-GCN、CNN-2-GCN、CNN-3-GCN，分别代表监督模型、GCN与CNN的输入层相连接、GCN与CNN第1层卷积相连接、GCN与CNN第2层卷积相连接、GCN与CNN第3层卷积相连接。
3.2.2 实验设置
本节实验数据集划分与Jiang等[11]的划分类似，分别从4类数据集的训练样本中随机取10000个样本进行训练，与Jiang等不同的是，本文的10000个样本是随机选取，并没有针对每类样本的均衡性进行选择，其次没有设置验证集，而是直接在数据集的测试集上进行测试。其中，对于MNIST、CIFAR10、CIFAR100从10000个样本中随机选取1000、2000、3000个样本作为标记样本，剩余的9000、8000、7000个样本作为无标记样本。对于SVHN，从10000个训练样本中选取500、750、1000个样本作为标记样本，剩余的9500、9250、9000个样本作为无标记样本。
在实验过程中，对3.2.1节提到的5种模型均采用Adam优化器进行优化，且KNN图的K值设定为经验值4，设置初始学习率为0.0001，整个模型训练300次epochs，且进行10次相同的实验，将这10次实验结果的均值和标准差记录在表2中。
表 2 五种模型在四种数据集上的分类精度Table 2 Classification accuracy of five models on four datasets数据集 样本数量 分类精度/% CNN(监督) CNN-0-GCN CNN-1-GCN CNN-2-GCN CNN-3-GCN MNIST 1000 99.41±0.02 99.34±0.07 99.26±0.02 99.26±0.03 99.25±0.05 2000 99.38±0.05 99.30±0.04 99.23±0.01 99.27±0.06 3000 99.40±0.03 99.33±0.01 99.24±0.07 99.35±0.01 CIFAR10 1000 74.21±0.32 79.73±0.13 79.40±0.12 79.06±0.43 76.56±0.19 2000 79.93±0.31 80.07±0.34 79.53±0.22 79.26±0.16 3000 80.48±0.15 80.47±0.21 80.04±0.13 79.95±0.10 SVHN 500 84.46±0.27 90.07±0.24 89.67±0.08 89.57±0.10 89.74±0.23 750 89.94±0.20 89.44±0.12 89.45±0.40 89.61±0.13 1000 89.88±0.09 89.34±0.07 89.52±0.22 89.34±0.16 CIFAR100 1000 47.72±0.31 49.94±0.02 49.35±0.13 49.72±0.09 49.63±0.08 2000 50.98±0.12 49.74±0.25 50.21±0.21 50.82±0.17 3000 52.03±0.06 51.42±0.04 51.19±0.12 51.44±0.15 3.2.3 实验结果分析
分析表2实验结果，可得如下结论：
1）对比4种半监督融合模型与CNN监督模型的精度值，对于CIFAR10、CIFAR100、SVHN数据集，4种融合模型均可在CNN分类精度的基础上提升5%~6%，说明本文所提融合模型是一种有效的且分类泛化性能较好的模型。
2）单独对比4种融合模型的实验结果，总体上模型之间的精度相差不大，但是CNN-0-GCN是融合模型中表现最突出的，说明将GCN连接到CNN卷积层之后会对模型整体的性能产生轻微的影响，但是与监督学习的CNN相比融合模型的精度提升效果还是比较显著的。
3）通过对单个数据集的4种融合模型的实验结果进行对比，MNIST、CIFAR10、CIFAR100中随着标记样本的数量减少，模型的分类精度均呈现逐渐递减的趋势，但是对于SVHN数据集，随着标记样本数量的减少，模型分类泛化性能反而有所提高。考虑到SVHN数据集[21]的特殊性，单张图像中不仅包含了要识别的数字信息，还包括数字的边缘、门框、阳光产生的阴影等无关信息的干扰，但是添加了GCN模型的融合模型，相反并没有受到这些冗余信息的影响，相反较少的标记样本实现了较高的精度提升，再次说明了本文所提模型具有极好的泛化性能。
3.2.4 融合模型的特征图可视化
为了进一步验证融合模型的有效性，本节对CNN和CNN-0-GCN、CNN-1-GCN、CNN-2-GCN、CNN-3-GCN等模型的特征图进行可视化分析，从CIFAR10数据集中取了3类标签的样本（分别是马、卡车、鸟）进行可视化，如图3所示。表中从左到右的4列分别展示了4种不同的卷积核对应的特征图，其中每列从左至右依次为不同迭代次数下的可视化输出结果。从上到下每5行为一类样本的可视化结果，每类样本的第1行为CNN模型特征输出结果，第2行为CNN-0-GCN的可视化输出结果，CNN-1-GCN、CNN-2-GCN等以此类推。
图 3 5 种模型在 3 个样本不同次迭代的特征图对比Fig. 3 Comparison of feature maps of three samples of five models at different iterations下载:
全尺寸图片
对比图3中每次迭代得到的特征图，CNN-0-GCN模型的物体轮廓、清晰度、纹理特征、细腻程度相比于其他模型都有很大优势。以样本类别为马的第一类卷积核对应的特征图为例，CNN模型将图像上边缘的深黑色背景特征也提取出来，这样使得特征图中马的轮廓变的不清晰，而CNN-0-GCN模型中显然将这些冗余特征去除，通过不同的灰度值，清晰地将马的轮廓显现出来。
同样地，还是以样本类别是马的特征图为例，通过观察会发现，CNN-0-GCN模型对应的第50次迭代的特征图无论是清晰度还是纹理特征相比于CNN要差很多，但是50次迭代之后，马的轮廓以及图像的细腻程度明显好转，而且变的比50次迭代之前的特征更清晰，再一次证明了融合模型具有很好的泛化性能。
此外，通过对比CNN-0-GCN与其他3种融合模型的特征图，发现CNN-0-GCN的特征图效果依然优于其他3种模型。以鸟的特征图为例，其余3种融合模型的前150次迭代图中均有明显的噪声值；迭代到200次后，特征图的效果才有提升。其余两类样本的特征图对比情况不再详细分析。
本节从数值实验、特征图可视化两个方面对构建SCUTTLE模型过程中GCN模型与CNN模型哪一层特征图连接的问题、SCUTTLE自身泛化性能等问题做出了深入研究。实验结果表明：1) CNN-0-GCN模型相比于其他融合模型具有较好的泛化性能；2) 特征图可视化结果同时也证明了CNN-0-GCN模型的优良性；3) 4种融合模型在4种数据集上的测试结果相较于CNN模型有明显提升。研究结果充分证明本文所提SCUTTLE模型是一种良好的半监督分类模型。
3.3 SCUTTLE模型(VGG-GCN)性能分析
3.3.1 实验内容与实验设置
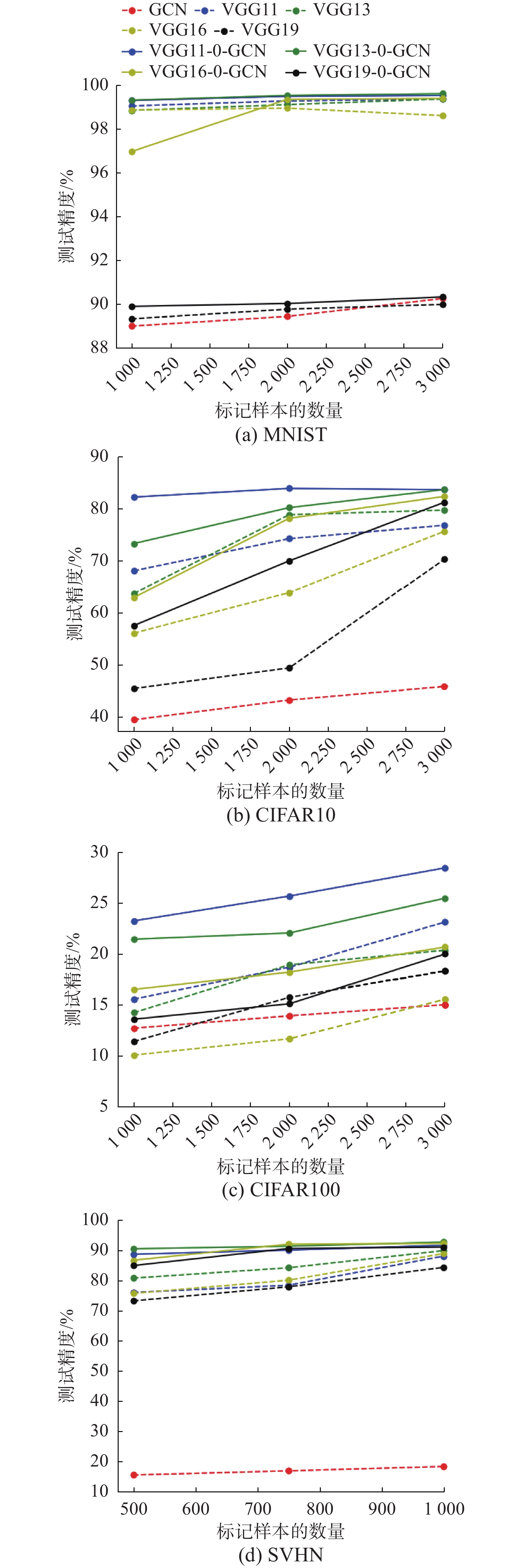
1）为了进一步验证SCUTTLE模型的泛化性能，本节将三层卷积模型替换为VGG模型[22]，分别将VGG11、VGG13、VGG16、VGG19与GCN融合在3.1节的4种数据集上测试其泛化性能，并将实验结果记录在图4中。
图 4 VGG、SCUTTLE模型在4种数据集上的精度折线图Fig. 4 Accuracy line graphs of VGG and SCUTTLE on four datasets下载:
全尺寸图片
2）设置消融实验来研究各个模型在融合模型中所起作用。在图4中，用4幅图表示所测试的4种数据集，虚线部分表示单独的VGG模型实验结果；红色虚线表示单独的GCN模型结果；而实线部分表示SCUTTLE模型的结果，通过对比虚线结果与实线结果的差异，即可分析单一VGG模型与SCUTTLE各模型之间的性能差异。
3）实验设置：本节的所有模型对于标记样本的选取都与3.2.2节所述相同。此外，超参数的设置也与3.2.2节相同。下面首先对4种融合模型实验结果进行分析。
3.3.2 实验结果分析
1) 4种SCUTTLE模型的泛化性能分析
SCUTTLE模型在4种数据集上的数值实验结果见图4。为了公平地对比每种模型的泛化性能，实验中设置4种SCUTTLE模型的参数都相同，因此在CIFAR100上的实验结果只作为对比结果而不作为最佳精度。通过分析表中结果，可得如下结论：
①对比MNIST数据集的4种融合模型的实验结果，VGG13-0-GCN获得最佳精度值；对比CIFAR10数据集，当标记样本数量为1000、2000时在VGG11-0-GCN中获得最佳精度，而当标记样本为3000时，在VGG13-0-GCN上得到最佳精度。因此对VGG-GCN的融合模型而言，并没有所谓的最优模型，不同模型在不同数量的标记样本下会呈现出不同的结果。
②对比4种融合模型各自在不同数量标记样本的结果，随着标记样本数量的增加，大部分模型的精度呈现上升趋势，而对于VGG11-0-GCN在CIFAR10数据集的标记样本数量为3000时，模型性能有所下降。此外，MNIST数据集随着标记样本数量的增加，4种融合模型的精度只有小范围的提升；而CIFAR10，VGG13-0-GCN、VGG16-0-GCN、VGG19-0-GCN随着标记样本数量的增加，模型精度提升幅度较大。综上所述，采用VGG11-0-GCN作为CIFAR10的半监督学习模型，只用1000个样本即可达到较高的精度。而其余两个数据集仍可得出类似结论。
以上只是对4种融合模型的实验结果进行简单地概括，为了充分说明模型的有效性，还需设置消融实验，分析VGG模型与GCN模型在融合模型中的作用效果。
2）消融实验结果分析
在4种数据集上，分别设置了VGG11、VGG13、VGG16、VGG19、GCN 5种模型，得到的实验结果也记录在图4中，通过对比图中实线与虚线之间的差值即可分析VGG模型与融合模型的性能差异。通过对比分析，可得如下结论：
①对比图中单一GCN的实验结果，只有在MNIST数据集上精度较高，在其余3种数据集上的精度都无法与CNN模型相比较，因此本节并没有计算GCN与融合模型的分类精度差值。
②对比虚线与实线之间的差异，几乎所有模型在不同数量的标记样本上都实现了性能提升，再次验证了本文所提融合模型的有效性，而所提升的幅度在不同数据集上自然呈现出不同的特点，对MNIST数据集，融合模型提升的精度值在1%内；对CIFAR10数据集，当标记样本数量较少时，提升幅度较大，而当标记样本数量较多时，反而提升幅度较小，此结论验证了CNN模型只有在大量标记样本的前提下才能取得不错的精度，当只有少量标记样本时，其性能急剧下降。因此融合模型在少样本上的性能较单一模型的性能更优，充分说明了融合模型在半监督图像分类任务方向上的优越性。而对于CIFAR100以及SVHN亦可得到类似的结论。
本节从数值实验的角度对VGG与GCN的融合模型性能进行分析。与前一节实验的结果对比可知三层CNN的融合模型与VGG的融合模型在性能上的差异较小，甚至在CIFAR100数据集上无论是VGG还是融合模型的性能都出现急剧下降的现象。所谓更深的模型有更好的性能，只是从理论的角度而言，但是实践中还应另当别论。
注意：后续所有模型都是将GCN与输入层进行连接，所以在命名时去掉了表示输入层的数字0。
3.4 SCUTTLE模型(ResNet、DenseNet-GCN)性能分析
3.4.1 实验内容与实验设置
1）本节选取ResNet18、ResNet32、DenseNet40、DenseNet100与GCN融合进行实验，且在CIFAR10、SVHN、CIFAR100、STL10数据集上给出对应的实验结果。
2）本节实验设置与前两节稍有不同，本节中对每个数据集均采用全部的训练集进行训练，且设定CIFAR10、CIFAR100、SVHN中的标记样本数量为500、1000、2000、4000，STL10中的标记样本数量为250、500、750、1000。以CIFAR10为例，在全部的50000个训练样本中挑选500、1000、2000、4000个样本作为标记样本，剩余49500、49000、48000、46000个样本为无标记样本进行SCUTTLE模型的性能测试。此外超参数的设置与前两节相同。
3.4.2 ResNet-GCN融合模型的实验结果分析
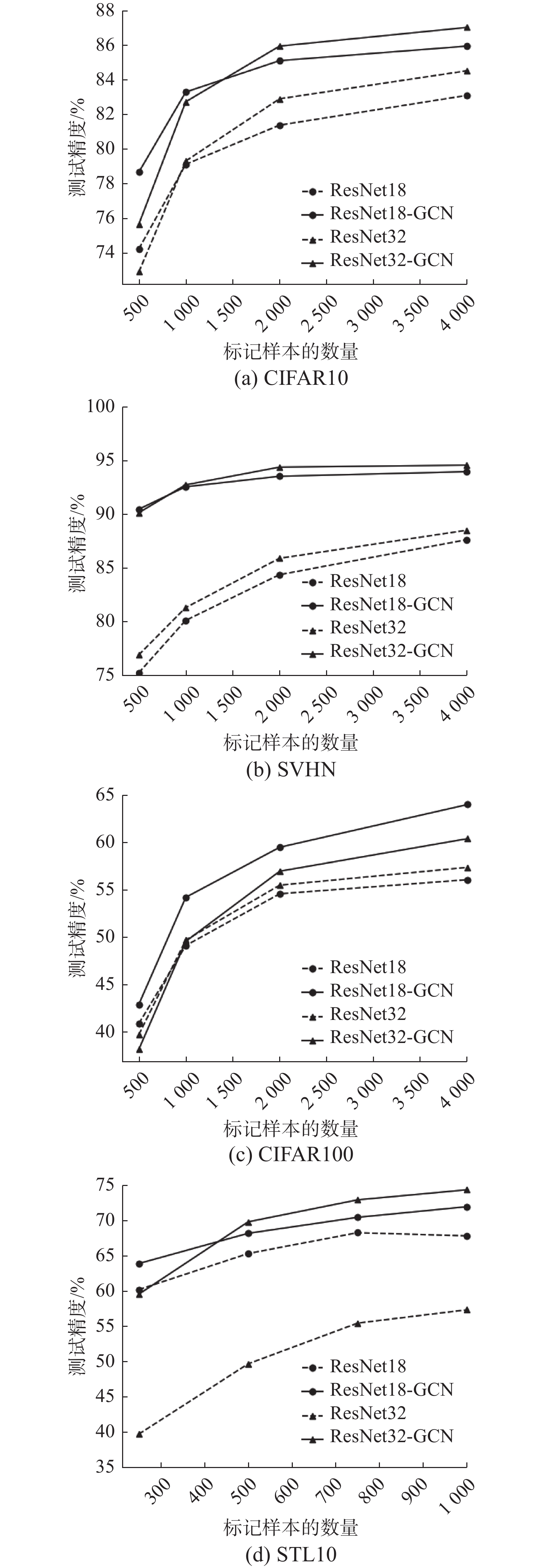
图5中的4幅图是在ResNet与GCN融合模型上测试的实验结果，图例中的ResNet18、ResNet32均指监督学习的精度折线。
图 5 ResNet18-GCN、ResNet32-GCN在4种数据集上的精度折线图Fig. 5 Accuracy line graphs of ResNet18-GCN and ResNet32-GCN on four datasets下载:
全尺寸图片
分析图5中实验统计结果可得如下结论：
1）对比4种数据集，半监督融合模型的分类精度相比ResNet18、ResNet32均有提升且提升幅度有所不同，提升幅度最大的为STL10数据集上的ResNet32-GCN模型，相比于ResNet32模型提升精度竟有20%之多。由于STL10数据集相比于其他3种数据集的特殊性，其挑战性更能检验半监督算法的相关性能，再次验证本文所提模型具有较强的泛化性能。
2）对于SVHN、CIFAR10、STL10 3种数据集，模型的深度越深其分类性能越好，因为在大部分情况下，ResNet32-GCN的精度折线图始终高于ResNet18-GCN，但是对于CIFAR100而言，ResNet18-GCN的精度折线图要高于ResNet32-GCN。因此模型越深其泛化能力越强只是从理论上给出其解释性，在实际中应进行综合分析。
3）对于CIFAR10、STL10数据集，ResNet18-GCN、ResNet32-GCN两种模型在较少数量标记样本的精度与较多数量标记样本的精度相差无几，因此ResNet模型可在这两种数据集上用最少的样本实现较高的分类精度，这对现实中的样本标注问题有极大的指导意义。
3.4.3 DenseNet-GCN融合模型的实验结果分析
本节所用的DenseNet模型为原论文中的
${{L=40}，{k=12}}$ 模型，即该模型共有40层，其中Denseblock中的卷积组合数为12，在下文叙述中都简称为DenseNet40；此外还使用了原论文中的DenseNet-BC中的${{L=100}，{k=12}}$ ，即该模型共有100层，其中Denseblock中的卷积组合数为12，在下文叙述中简称为DenseNet100。图6中的4幅图是在DenseNet与GCN融合模型上测试的实验结果。类似前一小节中的ResNet-GCN融合模型，图例中的DenseNet40、DenseNet100同样地为监督学习的精度折线。
图 6 DenseNet40-GCN、DenseNet100-GCN在4种数据集上的精度折线图Fig. 6 Accuracy line graphs of DenseNet40-GCN and DenseNet100-GCN on four datasets下载:
全尺寸图片
分析图6中实验统计结果可得如下结论：
1)观察图中的虚线结果也即DenseNet40与DenseNet100的监督学习精度，随着样本数量的增多，在4种数据集上会出现精度下降的趋势。考虑DenseNet自身的建模出发点，通过将一个卷积块中的每一层都与后面的层相连接来解决深层模型的特征重用问题，使得顶层的特征能传入模型的深层结构中。这种结构虽然在一定程度上缓减了梯度消失或者特征重用问题，但是会给模型带来更多的不确定性，因此该模型需要精心调参，调参次数成千上万才会获得最佳精度，但是本节所用参数与其他几节都相同，都为3.2.2节中的参数设置，这样每一小节之间都可以进行对比。
2)在虚线部分呈现下降趋势时，实线部分却呈现上升趋势，再次验证本文所提半监督融合模型的有效性，可以弥补单一模型自身的不足。此外，DenseNet40-GCN、DenseNet100-GCN相比监督模型都有分类精度的提升，充分说明融合模型具有较强的泛化性能。
3) DenseNet40-GCN在4种数据集上的表现均优于DenseNet100-GCN，而且DenseNet40-GCN在500个标记样本下的精度与2000个标记样本所得精度相差无几。因此在对上述4种数据集进行分类时可以优先选择DenseNet40模型，这一结论同样地对现实中的样本标注问题有极大的指导意义。
本节通过对两种经典视觉卷积ResNet、DenseNet与GCN融合模型的分类泛化性能进行数值实验分析，形成如下结论：1)融合模型在分类任务中的性能均优于单一的卷积模型；2)对于不同类型的数据集，融合模型的表现各不相同，没有最好的模型，在实践中需要根据不同类型的数据集选择不同类型的模型才能达到性能最优。研究结果显示本文所提SCUTTLE模型是一种性能较好的半监督分类模型。
3.5 与其他半监督方法的比较
为了说明本文所提半监督图像分类算法的有效性，需要在上述4种数据集上与同类算法的实验结果进行对比，而同类算法为了得到较高的精度都在泛化能力较强的WRN[23]模型上进行实验。WRN模型是ResNet模型的改进版，相比于ResNet模型浅而宽，由于ResNet模型深而窄，精度每提升1%都需要添加双倍的卷积层才能实现，因此会导致模型收敛速度较慢且重用性特征越来越少的问题，故而通过较宽且相对浅层的模型来解决上述问题，从而训练出泛化性能更好的模型。
同样地本文也采用WRN-GCN模型作为同类算法的比较模型，以此来获得较高的模型精度。由于目前大部分半监督分类模型没有统一的比较标准，因此Oliver等[24]提出了统一比较的框架，且给出了该框架下相应算法的实验结果，本文也采用该框架，将融合模型的实验结果与Oliver等记录的算法的结果进行对比。
3.5.1 实验设置
本节数据集选取以及各数据集标记样本的数量设置与3.4节相同。CNN模型采用Oliver等提到的WRN-40-4模型。模型超参数设置如下：优化器与前几小节有所不同，本节采用SGD优化器进行优化，设置KNN图的K值设定为经验值4，模型学习率采用衰减形式，设置初始学习率为0.01，模型训练200次epochs，在0~60次epochs学习率为0.01，60~120次epochs学习率为0.005，120~160 epochs学习率为0.0025，160~200 epochs学习率为0.00125，权重衰减率设置为0.0005，dropout率设置为0.2。
3.5.2 实验结果说明与分析
通过表3中与其他5种半监督学习算法的比较可以得出以下结论。
表 3 SCUTTLE与其他5种半监督分类算法精度比较Table 3 Classification accuracy of SCUTTLE model on five datasets数据集 标记样本数 半监督分类算法 Πmodel[5] Mean Teacher[25] VAT[26] Mixup[27] Pseudo-Label[28] SCUTTLE CIFAR10 500 58.18 57.99 63.89 63.83 59.45 67.14 1000 68.47 65.68 74.32 74.28 69.09 81.36 2000 76.93 81.83 83.60 81.86 78.04 85.78 4000 82.59 88.13 86.95 86.85 82.22 91.87 SVHN 250 82.35 88.55 91.59 60.03 78.84 87.91 500 88.56 92.18 92.56 70.38 85.65 92.71 1000 91.4 94.25 94.31 83.21 89.81 94.38 2000 93.06 94.55 94.75 89.53 92.46 95.05 CIFAR100 10000 61.35 64.17 — — 63.78 71.35 STL10 1000 — — — 72.01 76.16 1）本文所提SCUTTLE模型在4种数据集上的分类泛化性能均优于其他5种模型，除VAT[26] 在SVHN数据集的标记样本数量为250的结果外，但是该算法在CIFAR10数据集的精度值低于SCUTTLE的精度值，且该文中并没有给出CIFAR100、STL10两种数据集的数值实验结果。
2）表3中的5种半监督学习算法在CIFAR100、STL10数据集中没有给出相应的数值实验结果，说明这两个数据集对于检验算法分类性能具有很大挑战，本文所提SCUTTLE模型给出这两个数据集的数值实验结果，从一定程度上弥补了这一空白。
4. 结论
本文从样本间的关系提取角度出发，在图像特征提取模型基础上引入了关系表示模型，同时给出了二者的融合方法，构造了SCUTTLE模型，通过泛化性能分析和数值实验形成了如下结论：
1）SCUTTLE模型是对单一图像特征提取模型的补充和丰富，使得模型不仅具有特征提取能力也有学习图像间关系的能力。
2）针对以往视觉领域中目标检测算法在一幅图像上不同对象间构建关系的单一性以及图像分类模型中单独的特征表达所造成样本特征提取不够充分等缺点，提出建立样本间的关系与样本特征表示相融合的融合模型，SCUTTLE模型具有特征提取与聚合样本间关系的双重能力，无需其他复杂的优化算法，只需要通过简单的梯度下降即可实现end-to-end的学习。
3）数值实验结果表明：SCUTTLE模型与目前流行的卷积神经网络相比具有更强的泛化能力，通过半监督的学习方式，可以提升监督学习情况下普通卷积模型的图像分类精度。CIFAR10数据集上融合模型与卷积模型的特征图可视化对比结果验证了引入的GCN模型对CNN模型的特征图优化能力，进一步揭示了关系表示在特征提取中的重要性。
4）在VGG、ResNet、DenseNet等模型上的试验结果表明：SCUTTLE模型远远优于单一CNN模型的分类泛化性能，这一结论无疑为融合模型在少样本上的精度提升指明了方向。此外实验还发现，有时候更深特征提取层的模型可能对于监督分类学习会有好的效果，但是对于本文的半监督SCUTTLE模型而言，浅层的特征提取模型往往也会有不错的表现。
本文所做工作是针对目前计算机视觉领域单个样本上的关系不够明确和全面，而提出的样本间关系表达与特征提取融合算法的一次尝试，数值实验结果充分证明了该融合模型的可行性，扩展方法及其实际应用方面还需要进一步深入研究。
-
图 1 SCUTTLE模型示意图
Fig. 1 Schematic diagram of SCUTTLE model
下载:
全尺寸图片
图 2 SCUTTLE模型训练方法流程图
Fig. 2 Flow chart of SCUTTLE model training method
下载:
全尺寸图片
图 3 5 种模型在 3 个样本不同次迭代的特征图对比
Fig. 3 Comparison of feature maps of three samples of five models at different iterations
下载:
全尺寸图片
图 4 VGG、SCUTTLE模型在4种数据集上的精度折线图
Fig. 4 Accuracy line graphs of VGG and SCUTTLE on four datasets
下载:
全尺寸图片
图 5 ResNet18-GCN、ResNet32-GCN在4种数据集上的精度折线图
Fig. 5 Accuracy line graphs of ResNet18-GCN and ResNet32-GCN on four datasets
下载:
全尺寸图片
图 6 DenseNet40-GCN、DenseNet100-GCN在4种数据集上的精度折线图
Fig. 6 Accuracy line graphs of DenseNet40-GCN and DenseNet100-GCN on four datasets
下载:
全尺寸图片
表 1 4种数据集的属性信息
Table 1 Attribute information of four datasets
名称 样本数 训练集 测试集 类别 MNIST 70000 60000 10000 10 CIFAR10 60000 50000 10000 10 CIFAR100 60000 50000 10000 100 SVHN 99289 73257 26032 10 表 2 五种模型在四种数据集上的分类精度
Table 2 Classification accuracy of five models on four datasets
数据集 样本数量 分类精度/% CNN(监督) CNN-0-GCN CNN-1-GCN CNN-2-GCN CNN-3-GCN MNIST 1000 99.41±0.02 99.34±0.07 99.26±0.02 99.26±0.03 99.25±0.05 2000 99.38±0.05 99.30±0.04 99.23±0.01 99.27±0.06 3000 99.40±0.03 99.33±0.01 99.24±0.07 99.35±0.01 CIFAR10 1000 74.21±0.32 79.73±0.13 79.40±0.12 79.06±0.43 76.56±0.19 2000 79.93±0.31 80.07±0.34 79.53±0.22 79.26±0.16 3000 80.48±0.15 80.47±0.21 80.04±0.13 79.95±0.10 SVHN 500 84.46±0.27 90.07±0.24 89.67±0.08 89.57±0.10 89.74±0.23 750 89.94±0.20 89.44±0.12 89.45±0.40 89.61±0.13 1000 89.88±0.09 89.34±0.07 89.52±0.22 89.34±0.16 CIFAR100 1000 47.72±0.31 49.94±0.02 49.35±0.13 49.72±0.09 49.63±0.08 2000 50.98±0.12 49.74±0.25 50.21±0.21 50.82±0.17 3000 52.03±0.06 51.42±0.04 51.19±0.12 51.44±0.15 表 3 SCUTTLE与其他5种半监督分类算法精度比较
Table 3 Classification accuracy of SCUTTLE model on five datasets
数据集 标记样本数 半监督分类算法 Πmodel[5] Mean Teacher[25] VAT[26] Mixup[27] Pseudo-Label[28] SCUTTLE CIFAR10 500 58.18 57.99 63.89 63.83 59.45 67.14 1000 68.47 65.68 74.32 74.28 69.09 81.36 2000 76.93 81.83 83.60 81.86 78.04 85.78 4000 82.59 88.13 86.95 86.85 82.22 91.87 SVHN 250 82.35 88.55 91.59 60.03 78.84 87.91 500 88.56 92.18 92.56 70.38 85.65 92.71 1000 91.4 94.25 94.31 83.21 89.81 94.38 2000 93.06 94.55 94.75 89.53 92.46 95.05 CIFAR100 10000 61.35 64.17 — — 63.78 71.35 STL10 1000 — — — 72.01 76.16 -
[1] 闵帆, 王宏杰, 刘福伦, 等. SUCE: 基于聚类集成的半监督二分类方法[J]. 智能系统学报, 2018, 13(6): 974–980. MIN Fan, WANG Hongjie, LIU Fulun, et al. SUCE: semi-supervised binary classification based on clustering ensemble[J]. CAAI transactions on intelligent systems, 2018, 13(6): 974–980. [2] 姚晓红,黄恒君. 非负半监督函数型聚类方法[J]. 计算机科学与探索, 2021, 15(12): 2438–2448. doi: 10.3778/j.issn.1673-9418.2105116 YAO Xiaohong, HUANG Hengjun. Semi-supervised clustering method for non-negative functional data[J]. Journal of frontiers of computer science and technology, 2021, 15(12): 2438–2448. doi: 10.3778/j.issn.1673-9418.2105116 [3] SAJJADI M, JAVANMARDI M, TASDIZEN T. Regularization with stochastic transformations and perturbations for deep semi-supervised learning[C]//NIPS'16: Proceedings of the 30th International Conference on Neural Information Processing Systems. New York: ACM, 2016: 1171−1179. [4] CUBUK E D, ZOPH B, MANÉ D, et al. AutoAugment: learning augmentation strategies from data[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, IEEE, 2019: 113−123. [5] LAINE S, AI L A. Temporal ensembling for semi-supervised learning[EB/OL]. (2017−03−15)[2021−01−01]. https://arxiv.org/abs/1610.02242. [6] LI Yingting, LIU Lu, TAN R T. Certainty-driven consistency loss for semi-supervised learning [EB/OL]. (2017−05−07)[2021−05−01]. https://arxiv.org/abs/1901.05657v1. [7] ATHIWARATKUN B, FINZI M, IZMAILOV P, et al. There are many consistent explanations of unlabeled data: why You should average [EB/OL]. (2019−02−21)[2021−02−15]. https://arxiv.org/abs/1806.05594. [8] SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA. IEEE, 2015: 1−9. [9] CHEN Yunpeng, ROHRBACH M, YAN Zhicheng, et al. Graph-based global reasoning networks[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, IEEE, 2019: 433−442. [10] LIU Qinghui, KAMPFFMEYER M, JENSSEN R, et al. Self-constructing graph convolutional networks for semantic labeling[C]//IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium. Waikoloa, IEEE, 2020: 1801−1804. [11] JIANG Bo, ZHANG Ziyan, LIN Doudou, et al. Semi-supervised learning with graph learning-convolutional networks[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, IEEE, 2019: 11305−11312. [12] ZHUЃ Xiaojin, GHAHRAMANIЃH Zoubin. Learning from labeled and unlabeled data with label propagation. CMU-CALD-02-107[R]. Pittsburgh: Carnegie Mellon University, 2002. [13] WESTON J, RATLE F, MOBAHI H, et al. Deep learning via semi-supervised embedding[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 639−655. [14] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Advances in neural information processing systems, 2014, 27(1): 2672–2680. [15] SPRINGENBERG J T. Unsupervised and semi-supervised learning with categorical generative adversarial networks[EB/OL].(2016−04−30)[2020−05−15].https://arxiv.org/abs/1511.06390. [16] CHANG Chuanyu, CHEN T Y, CHUNG P C. Semi-supervised learning using generative adversarial networks[C]//2018 IEEE Symposium Series on Computational Intelligence. Bangalore, IEEE, 2018: 892−896. [17] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural computation, 2003, 15(6): 1373–1396. doi: 10.1162/089976603321780317 [18] NAIR V, HINTON G E. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the ICML. Haifa, Israel, 2010: 807−814. [19] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2017−02−22)[2019−12−15]. https://arxiv.org/abs/1609.02907. [20] MOORE A W. An intoductory tutorial on kd-trees. Efficient Memory-based Learning for Robot Control - 209[R]. Computer Laboratory, University of Cambridge. 1991. [21] GOODFELLOW I J, BULATOV Y, IBARZ J, et al. Multi-digit number recognition from street view imagery using deep convolutional neural networks[EB/OL]. (2014−04−14)[2019−06−05]. https://arxiv.org/abs/1312.6082. [22] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. (2015−04−10)[2020−04−20]. https://arxiv.org/abs/1409.1556 [23] ZAGORUYKO S, KOMODAKIS N. Wide residual networks[EB/OL]. (2017−06−14)[2020−12−15]. https://arxiv.org/abs/1605.07146. [24] OLIVER A, ODENA A, RAFFEL C A, et al. Realistic evaluation of deep semi-supervised learning algorithms[J]. Advances in neural information processing systems, 2018, 31(1): 3235–3246. [25] TARVAINEN A, VALPOLA H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results[J]. Advances in neural information processing systems, 2017, 30(1): 1195–1204. [26] MIYATO T, MAEDA S I, KOYAMA M, et al. Virtual adversarial training: a regularization method for supervised and semi-supervised learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(8): 1979–1993. doi: 10.1109/TPAMI.2018.2858821 [27] ZHANG Hongyi, CISSE M, DAUPHIN Y N, et al. mixup: Beyond empirical risk minimization[EB/OL].(2018−04−27)[2020−04−01]. https://arxiv.org/abs/1710.09412. [28] LEE D H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks[C]//Workshop on challenges in representation learning, ICML. 2013, 3(2): 896−901.
