随着视觉传感器解析度的不断提高，独立目标在单位时间步长内会对应一个以上的量测，学界定义此类目标为扩展目标（extended target，ET）^[1-2]。在传统目标跟踪问题中，而通常将目标视为质点考虑而忽略其物理形态^[3-5]，即被跟踪的独立目标在单位时间内最多只能生成一个量测的假设已不再适用于扩展目标跟踪。考虑到ET在单位步长内至少对应一个量测且蕴含着更多的目标运动状态信息^[6]，若采用传统点目标跟踪方法解决ET跟踪问题，当存在较多量测且存在数据关联^[7-9]时，“组合爆炸”现象会引发跟踪算法复杂度的迅速增加。

针对数据关联问题，Mahler^[10]首先提出了概率假设密度（probability hypothesis density，PHD）滤波器用于目标跟踪。在此基础上，ET高斯混合PHD（ET Gaussian mixture PHD，ET-GM-PHD）滤波器^[11-12]也应运而生。由随机集理论^[13]可知：无论采取哪种ET滤波器，为避免数据关联、降低计算量，需要将目标量测及其他运动状态信息进行有效划分。另一方面，滤波器的性能也取决于对ET量测集划分^[14]的准确程度。由于目标数目与量测数目的增加，全面考虑量测集所有可能的划分是实际应用中面临的难题之一。由此，文献[15]分析了基于距离的ET量测集划分方法，由于跟踪效果取决于目标间的距离，当目标近邻时会出现漏检与过检。在大数据背景下，文献[16]提出了k-means聚类的量测集划分方法，但k值的选取易受主观因素影响。文献[17]改进了具有噪声的基于密度的聚类（density based spatial clustering of applications with noise，DBSCAN）方法，通过牺牲收敛时间增强算法对凸集和非凸集数据划分的鲁棒性，且该算法涉及阈值的联合调参，聚类效果依赖于参数组合。文献[18]采用了基于网格聚类的ET跟踪方法，由于所使用的阈值滤波易将量测数目略低于阈值的目标作为杂波滤除，会产生漏检。文献[19]融合了密度算法和网格簇心聚类算法，但对不同属性的量测还需设置不同的空间划分步长。

综上，现有的研究大多是基于量测信息^[20-22]的某种相似度来划分目标量测集的所有子集，该子集中应包含最接近真实目标产生的量测。然而，子集划分的数量决定着跟踪算法的复杂度。为降低运算量且保证无漏检与无过检的同时，子集划分的数量尽可能少。因此，本文根据目标之间的时空关联性将采样周期内产生的目标区分为存活目标和新生目标。相对应的两类量测集各自采用不同的划分方法，且增强了算法的灵活性，降低了算法的复杂度。

1.   点目标滤波与ET滤波原理

在k时刻，假设ET运动模型和量测模型服从线性高斯分布，则目标状态方程为

式中： ${\boldsymbol{x}}_k^i$ 为目标状态； ${{\boldsymbol{F}}_{k - 1}}$ 为状态转移矩阵； ${\boldsymbol{v}}_{k - 1}^i$ 为协方差为 $ Q_{k - 1}^i $ 的0均值高斯白噪声； $ N_x^k $ 为状态数目。

量测方程为

式中： ${\boldsymbol{z}}_k^j$ 为目标量测； ${{\boldsymbol{H}}_k}$ 为观测矩阵； ${\boldsymbol{w}}_k^j$ 为协方差为 $ R_k^j $ 的零均值高斯白噪声； $ N_z^k $ 为量测数目。

1.1   GM-PHD滤波器

假设 $ {P_{D,k}} $ 为检测概率、 $ {\kappa _k} $ 为杂波强度、 $ {J_{k|k - 1}} $ 为预测的高斯分量数目、 $ q_k^{(j)}(z) $ 为量测似然函数，则点目标的PHD预测 $ {D_{k|k - 1}}(x) $ 与PHD更新 $ {D_k}(x) $ 的定义分别为^[23]

式中： $ m_{k|k - 1}^{(i)} $ 为均值， $ P_{k|k - 1}^{(i)} $ 为方差， $ \omega _k^{(j)} $ 为更新的权值：

1.2   ET-GM-PHD滤波器

在 $ k - 1 $ 时刻，ET-GM-PHD滤波器的预测公式和GM-PHD的预测公式相同。在 $ k $ 时刻，滤波器的更新为

式中伪似然函数为

式中： $ \gamma (x) $ 为泊松率； $p\angle {{\boldsymbol{Z}}_k}$ 为 ${{\boldsymbol{Z}}_k}$ 划分的 $ p $ 类簇， $ W \in p $ 为非空单元； $ \left| W \right| $ 为单元 $ W $ 中元素数目； $ {\phi _{{z_k}}}(x) = p({z_k}|x) $ 为ET的观测空间分布函数； $ {\omega _p} $ 为划分的权值， $ {d_W} $ 为划分单元 $ W $ 的权值。

2.   量测集划分方法

2.1   存活目标量测集划分

考虑到同一ET相邻时刻的量测间的关联性，对k时刻存活目标的空间位置与 $ (k - 1 )$ 时刻的距离较近，本文采用改进的模糊C均值（fuzzy C-means，FCM）算法^[24]估计ET质心，再代入式（2），转换为点目标跟踪。由于所划分样本的类别通过样本隶属度值的大小决定，引入样本隶属度函数，由隶属度值归一化样本 ${x_{{i}}}$ ：

式中： $ N $ 为样本数目； $ c $ 为类别数目； $ {u_{ij}} $ 为样本 $x_i$ 属于类 $c_j$ 的隶属度，则 $ N \times c $ 的隶属度矩阵 ${\boldsymbol{U}}$ 可定义为

该算法由隶属度大小对量测结果进行类别划分，隶属度的大小取决于量测结果 $ {x_i} $ 和类别 $c_j$ 间的距离：

式中：m为聚类的簇数， $\left\| {\cdot} \right\|$ 为距离的度量。

当在目标近邻或交叉时，位于目标之间的量测点属于不同类的隶属度存在相等的情形，即 $ {u_{ij}} = {u_{ik}}(j \ne k) $ 。隶属度矩阵 ${\boldsymbol{U}}$ 的每行元素表征了量测 $x_i$ 到不同聚类的隶属度。考虑到目标在k时刻的量测成簇，边缘点密度相对较低且对量测划分影响不大，可根据判决条件删除。这里，判断条件为

假设共删除 $ U $ 个量测点，则矩阵 ${\boldsymbol{U}}$ 可化简为

接下来，对剩余的 $ (N - \mu) $ 个量测按隶属度大小划分所属类别。当两目标相距较远时，本阶段处理的存活目标量测集不会出现 $ {u_{ij}} = {u_{ik}}(j \ne k) $ 情况。当两目标近邻时，目标的量测集会出现重叠或相交。此时，删除隶属度相等的量测点，并在邻近簇类间引入分割线，解决目标近邻时的漏检问题：

1)由式（1）预测k时刻ET的PHD。记 $ {\tilde x_{i,k}} $ 为第i个ET状态的估计值， $ o_{i,k}^{(0)} $ 为 $ {\tilde x_{i,k}} $ 位置的初始聚类中心，则FCM算法样本集表示为

式中： $ {c_k} $ 为k时刻存活目标数目， ${\boldsymbol{\tilde Z}}_k^i$ 为目标 $i$ 的量测集， $d\left( {{z_{i,k}},o_{i,k}^{\left( 0 \right)}} \right)$ 为量测值 $ {z_{i,k}} $ 与 $ o_{i,k}^{(0)} $ 的距离， $\varepsilon$ 为距离阈值。

2)将步骤(1)获得的结果代入改进的FCM算法；

3)将ET质心估计值代入式（2），对获得的更新高斯项进行裁剪合并等处理^[12]得到目标运动状态。

2.2   新生目标量测集划分

假设第i个网格包含量测数目为对应的网格密度 ${{\rho _i}}$ ，根据有效网格密度阈值^[18]滤除杂波：当有效网格密度大于有效网格密度阈值时，判为目标量测；否则，判为杂波量测。

式中： ${\Delta _\rho }$ 为密度阈值， $K$ 为有效网格数目， ${\rho _i}$ 为有效网格密度， $ \max ({\rho _i}) $ 和 $ \min ({\rho _k}) $ 分别为最大和最小有效网格密度。

上述所采用的滤波条件较为“苛刻”。一方面，当目标量测在网格密度略不大于有效网格密度阈值时，判断当前量测为杂波量测并直接滤除，进而导致漏检。另一方面，当计算有效网格密度时，将网格线上的量测点划给距离最近的有效网格，会出现远离聚类且又处于网格线上的杂波量测点。一旦把这些孤立点划分给最近的网格，则会出现过检。当两个相邻网格的共用网格线上存在数据点时，根据距离划分量测数据点的归属具有不确定性，会随机出现漏检或过检。尤其当ET近邻或交叉时，该情况更为明显。

在理想状态下，杂波位置与目标位置间有较大的距离优势，源自杂波的量测可作为异常值被直接滤除。实际上，杂波位置有可能位于目标位置附近，则杂波量测被归为新生目标量测。这时，可由ET在相邻时刻量测间的关联性及网格聚类算法的低复杂性，对新生目标量测（含杂波）网格化处理。为获得较好的网格化效果，设含有量测的有效网格数目不少于整个量测数目的1/6^[19]。首先，采用截尾均值法重定义网格密度阈值公式，去除最大网格密度 ${\rm{max}}({\rho }_{i})$ 与最小网格密度 ${{\rm{\min}}({\rho }_{k})}$ ，记新的网格密度阈值为 ${{\Delta }^{\prime }}_{\rho }$ ：

可以看出：式（5）较式（4）缩小了滤波范围，采用截尾均值法求密度阈值，去除了数列中的极端值，使求得的阈值不易受到极值影响；当网格密度测量存在坏值时，稳健性更加突出。由密度峰值聚类思想，筛选有效网格距离 $ {\delta _i} $ ：

式（7）用于 ${\rho _i}$ 为全局网格密度最大值的情况时，而式（6）则用于其他情况时。

同理，采用截尾均值法定义有效网格距离阈值，记有效网格距离阈值为 $ {\Delta '_\delta } $ ：

引入有效网格 $ i $ 的网格密度权重 ${W_{\rho ,i}}$ ：

与网格距离权重 $ {W_{\delta ,i}} $ ：

于是，位于网格线上的量测点基于距离划分步骤如下：

1)输入新生目标量测数目 $ n $ ，设步长初值为 $n/2$ 。对量测空间各维均匀划分并统计有效网格数目 $ K $ 。判断条件 $K > n/6$ 是否成立。若成立，输出步长和 $ K $ ；否则，步长减1，以新步长划分直到条件成立。

2)由式（5）计算有效网格密度阈值。判断条件 $ {\rho _i} > {\Delta '_\rho } $ 是否成立，若条件成立网格i作为新生目标量测保留下来，若不成立作为杂波量测直接滤除。由式（8）和式（9）计算权重，将位于共用网格线上的量测点划分给权重乘积最大的网格。

3)筛选 $ {\rho _i} $ 和 ${\delta _i}$ 均大于阈值的网格作为初始聚类中心。为避免出现筛选误差，引入调节参数 ${\alpha _i}$ ：

选取前若干项 $ {\alpha _i} $ 符合条件的有效网格作为初始聚类中心。这里，不包含聚类中心的网格，其类别属性与距离其最近的聚类中心保持一致。

4)对由式（3）得到的结果进行裁剪合并处理获得新生目标运动状态。

3.   仿真验证与结果分析

3.1   实验场景与参数设置

本次实验使用MATLAB 2019b软件，在Window10 64 bit、主频为2.20 GHz和12 GB内存的环境下实现。假设4个ET在x=[−1000,1000] m，y=[−1000,1000] m检测范围内运动，且具有目标新生、近邻与交叉情况，运动初始状态如表1所示。

ET的状态方程为

式中： ${\boldsymbol{x}}_k^i = {\left[ {{x_k},{y_k},v_k^x,v_k^y} \right]^{\text{T}}}$ 为ET的运动状态； ${\boldsymbol{v}}_{k - 1}^i$ 为均值为0、方差为 ${\boldsymbol{Q}}_{k - 1}^i = 20{{\boldsymbol{I}}_2}$ 的高斯噪声； ${{\boldsymbol{I}}_2}$ 为二维单位矩阵，跟踪时长为100 s。

量测方程为

式中： ${\boldsymbol{w}}_k^j$ 为均值为0、方差为 ${\boldsymbol{R}}_k^j = 20{{\boldsymbol{I}}_2}$ 的高斯噪声。目标的存活概率为 $ {P_s} = 0.99 $ ，检测概率为 $ {P_D} = 0.99 $ 。ET量测数目服从均值为20的泊松分布，杂波数服从均值为10的泊松分布，最大高斯项分量为 $ {J_{\max }} = 100 $ ，高斯项修剪门限为 $ T = {10^{ - 5}} $ ，合并门限为 $ U = 4 $ 。阈值 $ \varepsilon $ 为量测噪声协方差的2倍。采用最优子模式分配（optimal sub-pattern assignment，OSPA）距离作为评价指标：

式中： $ \beta $ 用于平衡目标数目与位置估计精度， $ \beta $ 值越大，目标数目估计重要性越明显； $ \alpha $ 用于衡量量测中的异常值， $ \alpha $ 值越大，状态估计优劣间的区分就越明显。考虑目标数目与量测集划分的影响，本文选取 $ \alpha = 4 $ 和 $ \beta = 40 $ 。

3.2   实验结果与数值分析

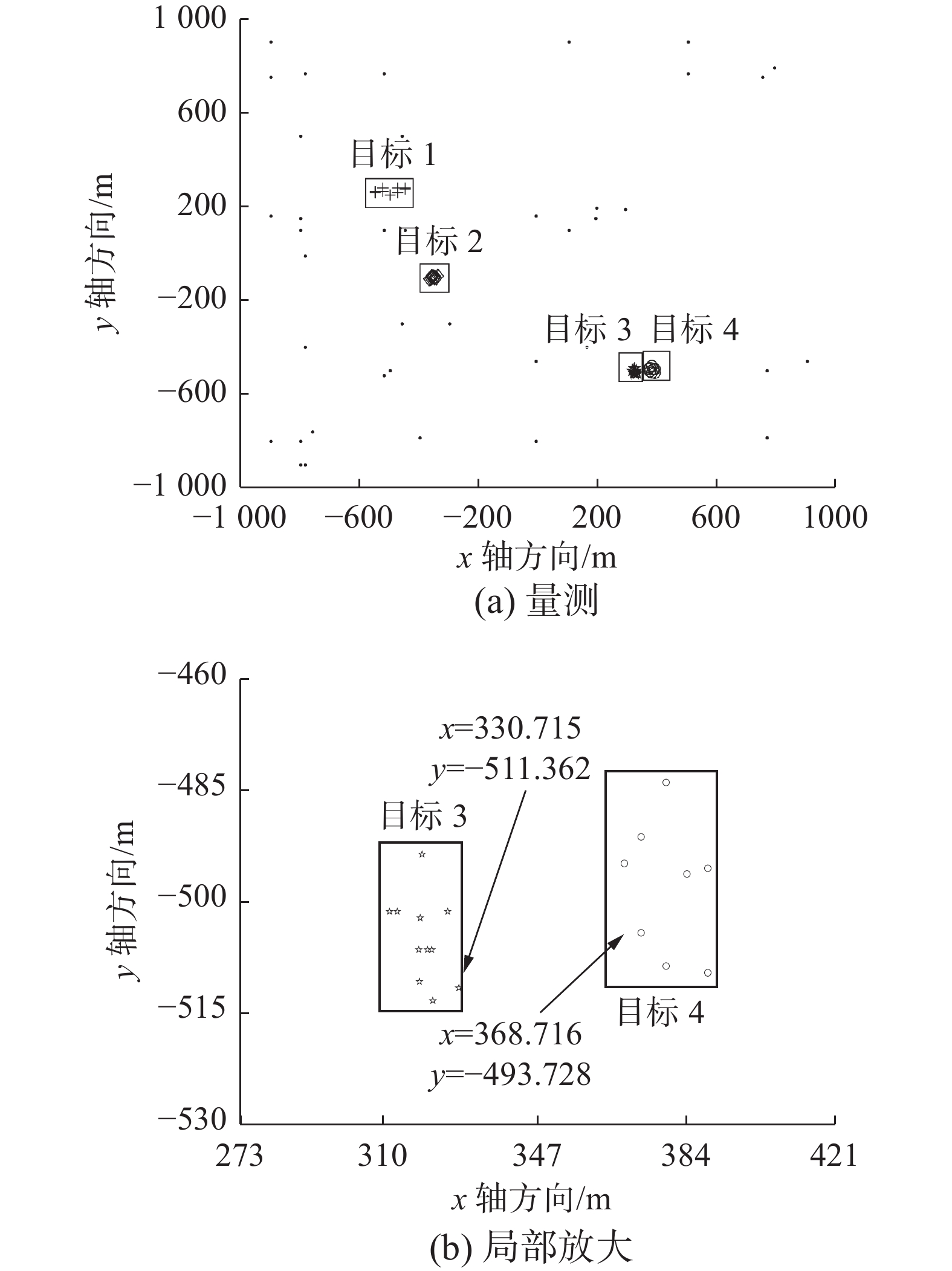
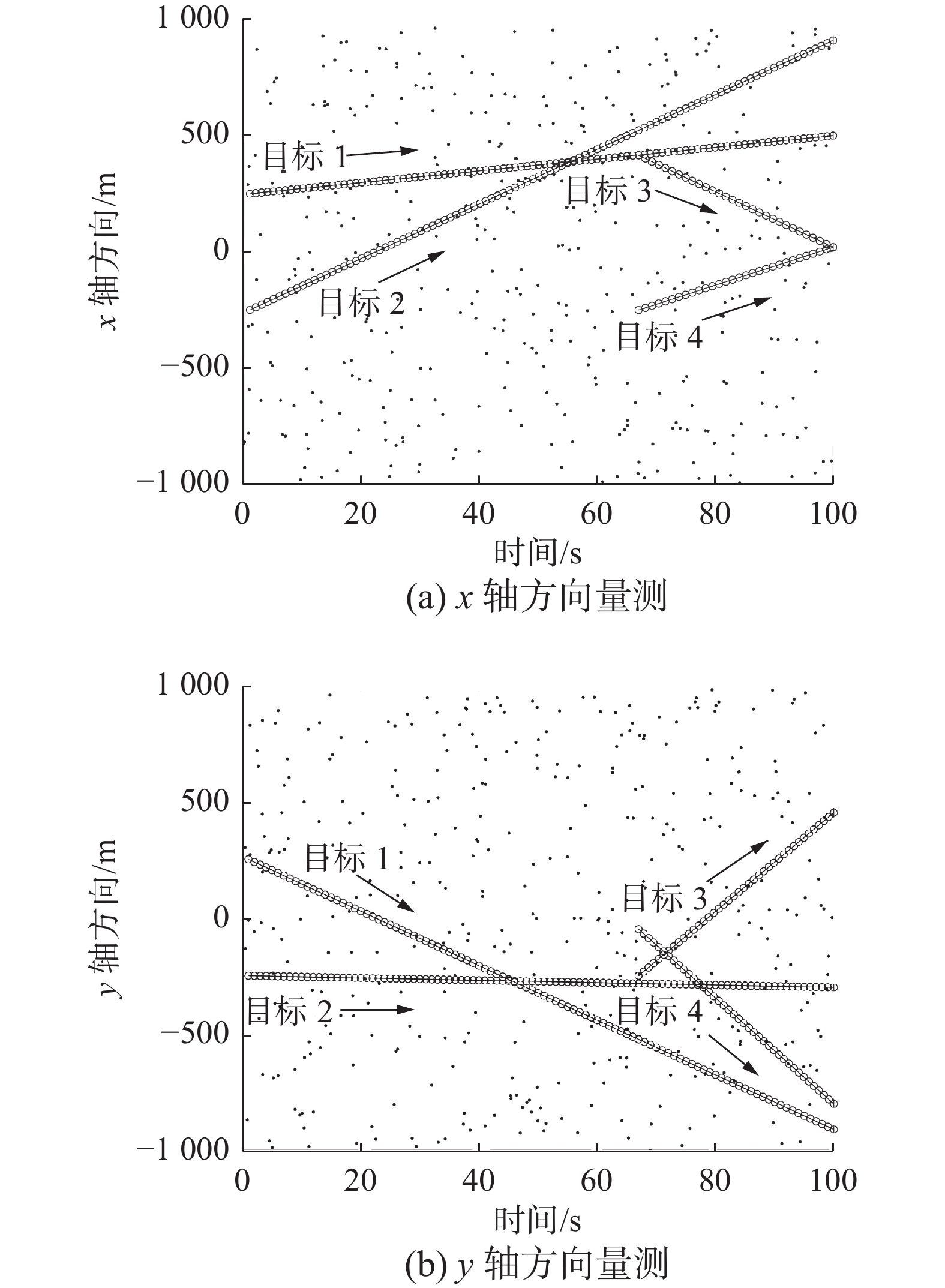
图1（a）和（b）分别描述了1~100 s内x与y方向的量测。可以看出，检测区域内包含两个存活目标和第67 s出现的两个新生目标。

图  1  1~100 s ET与杂波的量测

“$\cdot$”为杂波量测，“o”为目标量测，箭头方向为目标运动方向。

Fig.  1  Measurement of ET and clutter in 1~100 s

下载: 全尺寸图片

图2给出了第68 s时检测范围内的全部量测，包含两个存活目标和第67 s时出现的两个新生目标与杂波。矩形框内的为ET量测，其余为杂波量测。可以看出，目标3和目标4在空间上距离较为接近。图2（b）为目标3和目标4的局部放大情况展示。

图  2  第68 s时整个量测集

Fig.  2  Overall measurement set at 68 s

下载: 全尺寸图片

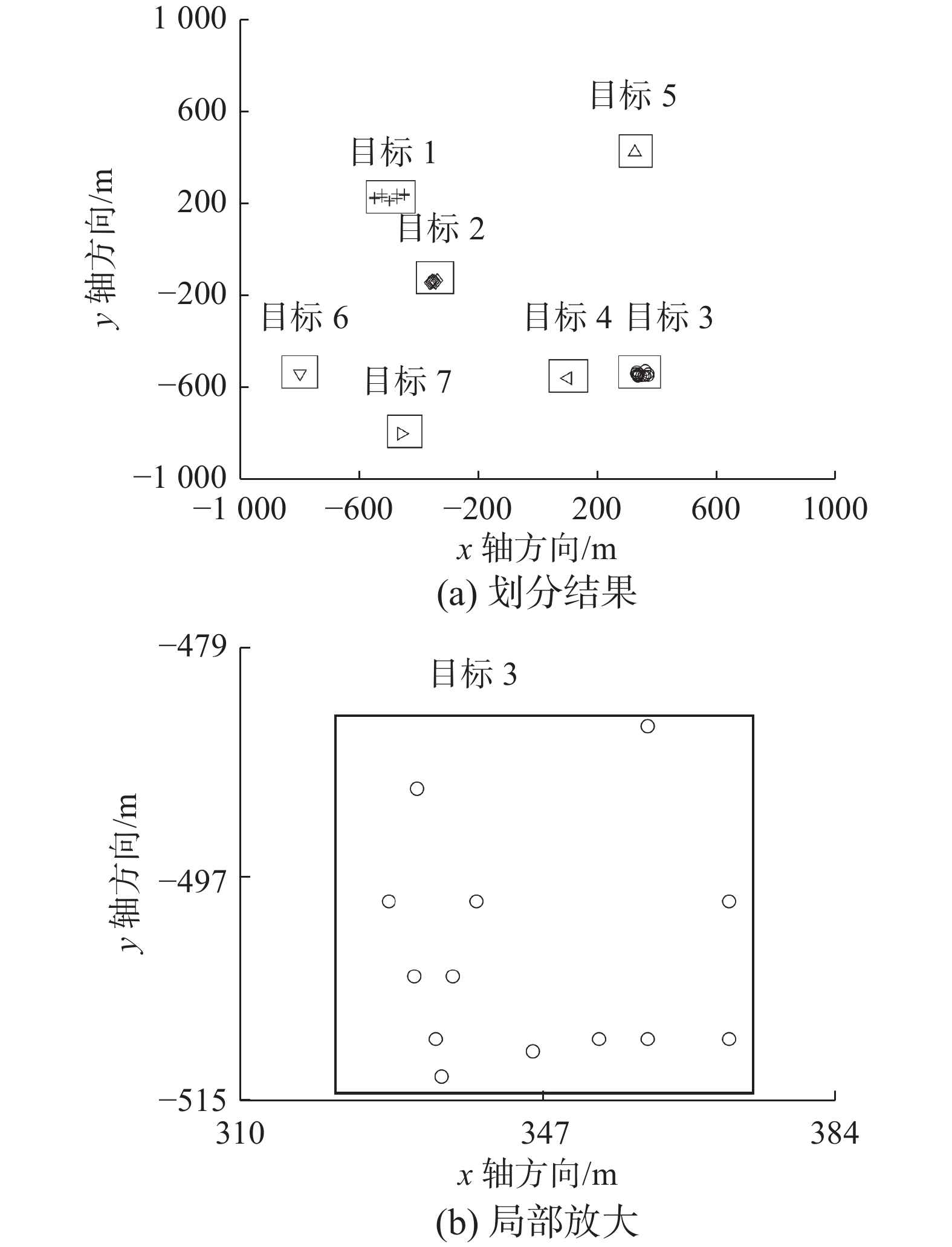
图3描述了基于距离划分算法（D=44.6328 m）在第68 s时的划分结果。可以看出，该算法获取了7个目标量测，杂波生成的量测也被划分为目标量测单元，如标注的目标4、5、6和7。量测单元数量上远超过在第68 s时的4个ET所形成的量测单元，且两个空间上靠近的ET（如图2所示的目标3和4）所生成的量测被划分为一个量测单元。

图  3  基于距离划分算法的结果（D=44.6328 m）

Fig.  3  Results of distance partitioning algorithm (D=44.6328 m)

下载: 全尺寸图片

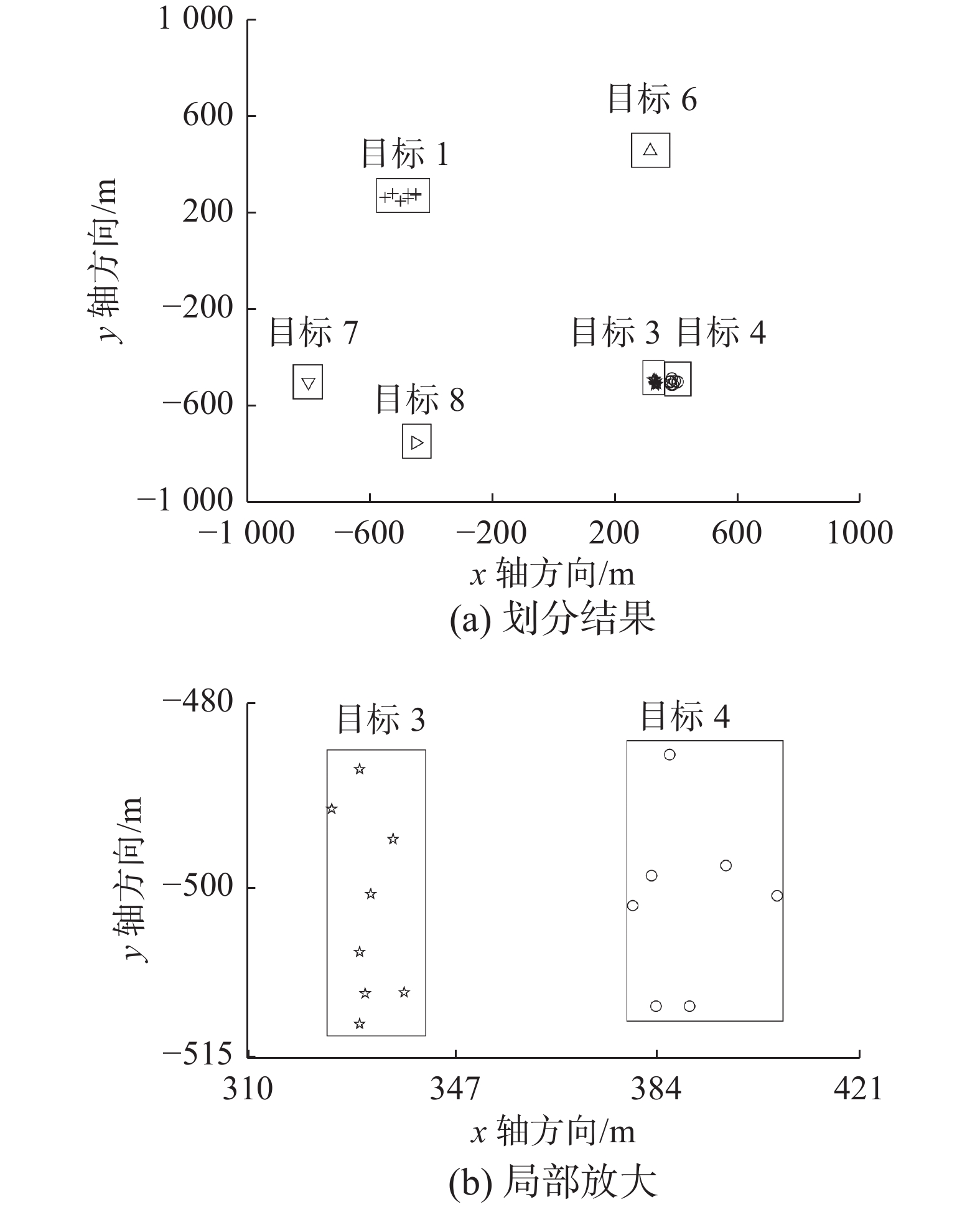
图4描述了基于距离划分算法（D=36.3526 m）在第68 s时的划分结果。可以看出，该算法获取了6个目标量测单元。对比图3和4可以得出，阈值D的大小影响着量测集的划分结果。从图2局部放大部分可知，由于相互靠近的真实目标边缘量测距离小于图3阈值，导致漏检。图4通过缩小阈值正确区分了目标3和4，但仍存在把杂波划分为目标量测单元的过检。

图  4  基于距离划分算法的结果（D=36.3526 m）

Fig.  4  Results of distance partitioning algorithm (D=36.3526 m)

下载: 全尺寸图片

图5给出本文方法的划分结果。可以看出，本文方法有效滤除了杂波，区分了图2所示检测范围内的4个真实目标，未出现将杂波量测划分为目标量测的情况。尤其是当目标近邻时，也未出现将不同的目标划分为同一目标的情况，有效避免了漏检。

图  5  本文划分方法的结果

Fig.  5  Results of the proposed partitioning method

下载: 全尺寸图片

图6对比了基于距离划分算法、k-means算法、DBSCAN算法和本文方法在100 s内对目标数目的估计。可以看出，前3种算法在ET近邻和交叉时刻未能对目标量测集进行准确划分，出现过检。DBSCAN算法虽接近真实目标数目，但在划分时间上的花费比较高。相比而言，本文方法对ET数目估计更加准确，尤其在ET近邻和交叉时，没有出现漏检与过检。

图  6  ET数目的真实值与估计值

Fig.  6  True and estimated numbers of ET

下载: 全尺寸图片

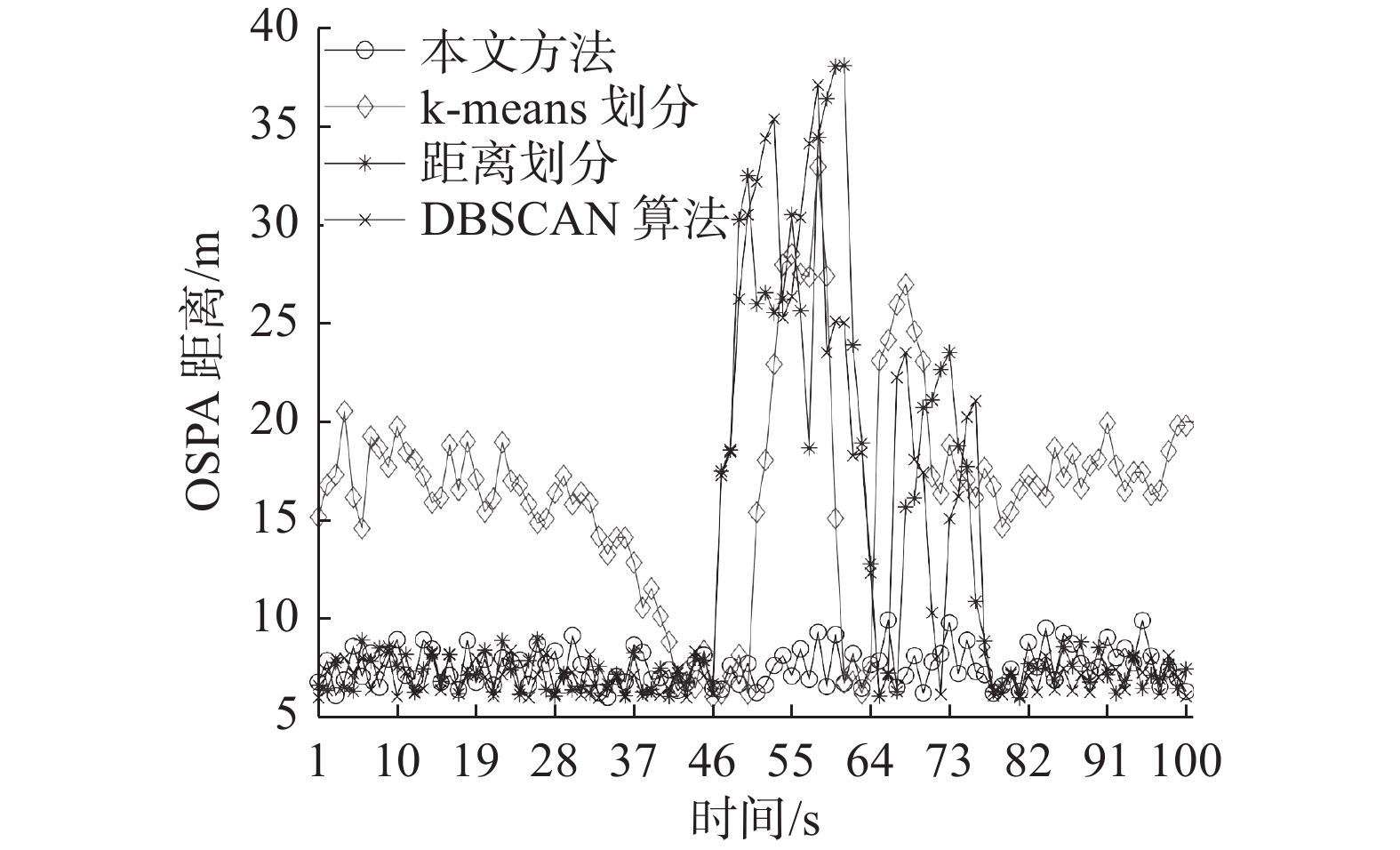
图7对比了3种算法与本文方法的OSPA距离。可以看出，本文方法的OSPA距离相对平稳，在于滤波操作除去了距离上较为孤立的杂波，避免了漏检。同时，该方法将ET附近的杂波量测则归类为目标量测，划分出近邻目标。

图  7  平均OSPA距离

Fig.  7  Average OSPA distance

下载: 全尺寸图片

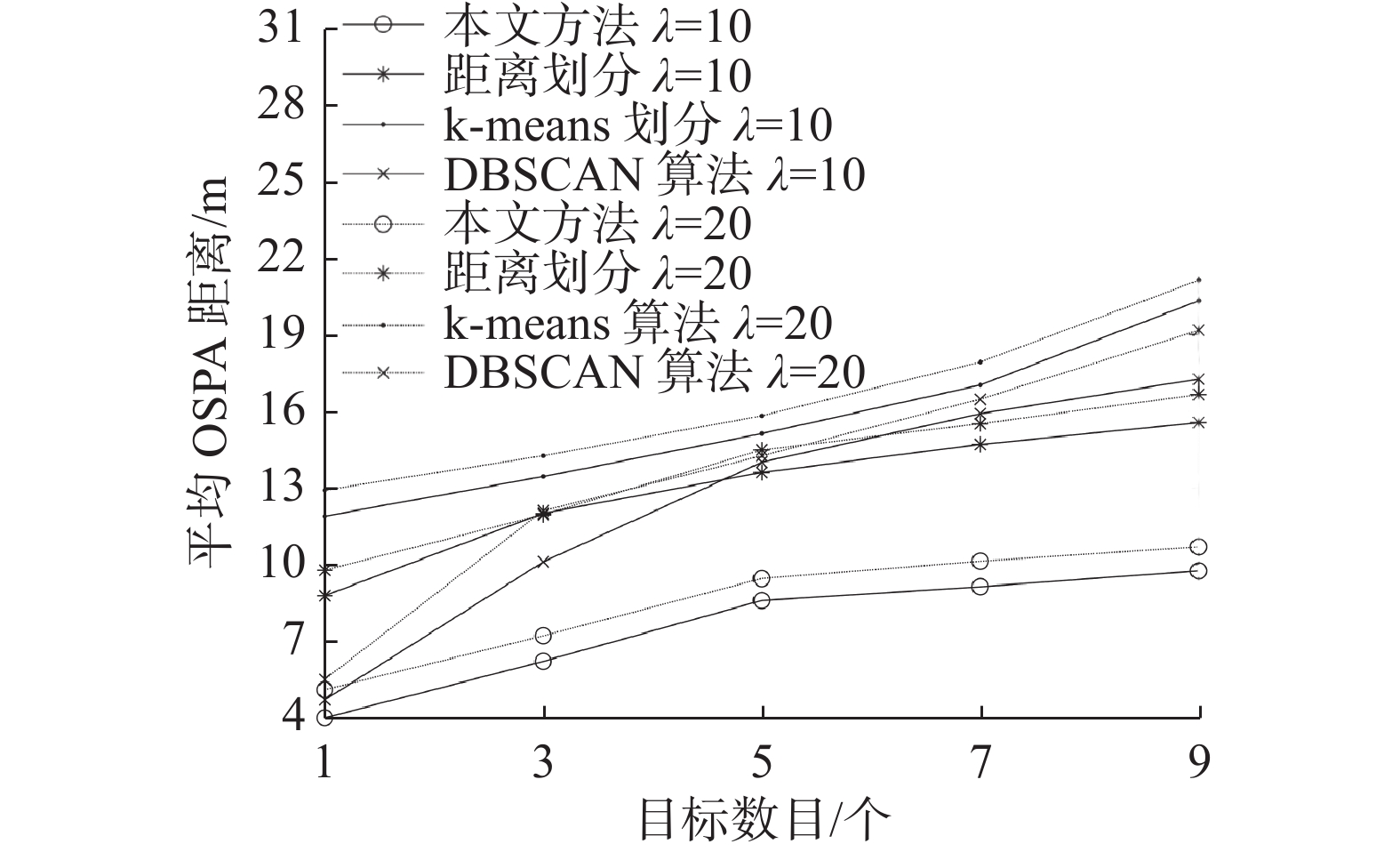
图8对比了在不同杂波率与不同目标数目情况下的平均OSPA距离。由横轴可以看出，当目标数目恒定时，随着杂波率的增大，3种算法与本文方法的平均OSPA距离逐渐增长；从纵轴来看，在同一OSPA距离的情况下，3种算法与本文方法的杂波率与目标数目均不同。综上，本文方法分别采用存活目标量测集划分步骤与新生目标量测集划分步骤，性能指标优于所对比的其他3种算法。

图  8  不同杂波率下目标数量和平均OSPA距离对比

Fig.  8  Comparison between the number of targets and averaged OSPA distance under different clutter rates

下载: 全尺寸图片

4.   结束语

针对ET跟踪过程量测集划分问题，本文提出了一种改进的方法。在目标出现近邻或交叉时刻，该方法能对量测集进行准确划分，解决了ET量测集划分困难的瓶颈，避免了传统算法在目标近邻或交叉时因划分不准确导致的漏检与过检。

在量测数据网格化的过程中，步长选取的恰当与否直接决定着网格划分的最终结果。现阶段步长的选取是对大量数据实验并统计得出的。本文中步长的选取是一个具普遍性的定值。若在网格划分过程中综合考虑网格密度与网格间距自适应设定步长，其划分效果会更加准确。因此，以后的研究将深入考虑划分步长的自适应选择与优化。