Active disturbance rejection control of the magneto-rheological shimmy damper based on the smart chaos fractional-order beetle swarm optimization algorithm
-
摘要: 为了提高飞机起飞和降落过程中的稳定性及安全性，采用磁流变阻尼器进行飞机前轮摆振控制。本文描绘了改进的Bouc-wen模型磁流变阻尼器的力学特性，并将之用于一个三自由度的飞机前起落架模型中，而后为此设计了减摆自抗扰控制器(active disturbance rejection control, ADRC)；然后采用混沌分数阶天牛群算法整定优化自抗扰控制器的参数。最后，仿真结果显示经智能算法优化参数后的减摆自抗扰控制器能够较好地控制摆振现象，并且其性能具有一定的鲁棒性。
-
关键词:
- 飞机前起落架 /
- 摆振 /
- 磁流变阻尼器 /
- 改进的Bouc-wen模型 /
- 减摆 /
- 自抗扰控制 /
- 天牛群算法 /
- 混沌分数阶天牛群算法 /
- 参数优化 /
- 鲁棒性
Abstract: To improve the stability and safety of an aircraft during the take-off and landing, a magneto–rheological damper is applied to the shimmy control of its front wheel. In this paper, the mechanical properties of a modified Bouc–Wen magneto–rheological damper are described, which is used in an aircraft landing gear model with three degrees of freedom and for which a third-order active disturbance rejection controller (ADRC) is later designed; subsequently, the chaos fractional-order beetle swarm optimization is used to optimize the controller parameters. Finally, the simulation results indicate that the controller with optimized parameters exhibits good performance in shimmy reducing control with certain robustness. -
飞机现多采用前三点式起落架，这种结构方式可以使飞机具有良好的地面运动稳定性、着陆易操纵性、飞行员视界良好等优点[1]。但是对前起落架提出了更高的要求，起飞和着陆过程中，尤其是着陆过程，前起落架会受到机身大部分的负荷，加之跑道等因素的相互作用，前轮容易产生基于中心的往复运动的摆振现象。这种现象若不加以控制，会产生安全事故。常用的方式就是加入阻尼器来控制摆振。应用较多的是油液式阻尼器，它可以提供阻尼力来抑制摆振[2]。近些年，磁流变液作为智能材料受到广泛的关注，而磁流变阻尼器则是其重要应用之一。磁流变阻尼器的应用范围较广，文献[3-4]研究了将磁流变阻尼器应用于汽车悬架及座椅的减震（振）控制中；Dyke S J等[5]将磁流变阻尼器应用于土木工程建筑物减轻地震伤害中；Nguyen团队[6]研究了一种磁流变弹性隔离器，用于结构体的减振；文献[7]中采用磁流变阻尼器进行直升机与地面共振的抑制研究。与传统的油液式阻尼器相比，磁流变阻尼器具有更快的响应速度，响应时间可以达到15 ms，有的甚至可以达到6.5 ms，且具有更大的阻尼力范围，而且其阻尼力的大小可以通过外加磁场的方式进行调节，是一种半主动控制。磁流变阻尼器阻尼力可调的功能，使得一些控制方法能够应用于起落架的减摆控制。Kang等[8]采用天棚阻尼控制对飞机起落架摆振进行控制；文献[9]采用自适应控制摆振问题；文献[10]将模糊PID控制应用于磁流变阻尼器控制；文献[11]用神经网络逆模型通过阻尼力反解电流的方式实现阻尼器控制；文献[12]通过智能算法优化PID控制器的参数实现减摆控制。上述控制方法或控制设备较复杂或控制精度较差。天棚阻尼控制需要计算阻尼系数非常依赖模型的精确性；自适应控制和神经网络逆模型设计比较复杂，难以实现，而且神经网络逆模型的准确度与训练数据息息相关；PID控制在控制效果上没有自抗扰控制精确[13]。因此，需要设计一种易于工程上实现又具有良好控制效果及鲁棒性的控制器。本文设计了自抗扰控制器（active disturbance rejection control, ADRC）来实现飞机前起落架的减摆控制。ADRC是由韩京清研究员提出的一种新型控制方法[14]。它不依赖对象模型，能够估计扰动并进行补偿，具有较高的控制精度和良好的鲁棒性。ADRC继承和发扬了PID控制和现代控制理论的优点，在某些领域表现出比PID控制更好的性能，有望能够取代PID控制在工业控制中的地位[15]。但是ADRC需要整定的参数比较多，比较依靠经验，所以这限制了它在实际工程中的推广应用。正因为ADRC参数整定的困难，一些智能优化算法被引入进行参数整定。本文主要工作为：1)一改进的Bouc-Wen模型磁流变阻尼器应用到飞机前起落架进行减摆控制。2)设计自抗扰控制器：将飞机起落架和磁流变减摆器看作一个整体，将摆角作为控制目标并进行误差反馈，将系统内部和外部的扰动看作总扰动并用扩张状态观测器进行估计，然后进行补偿。3)采用智能优化算法——混沌分数阶天牛群算法整定控制器参数通过设计适应度函数，通过智能优化算法来寻找最优解。仿真结果表明所设计控制器能够很好地控制摆振现象，而且面对参数的摄动，该控制器具有良好的鲁棒性。
1. 磁流变阻尼器
磁流变阻尼器中的磁流变液具有良好的性能，正常情况下呈现牛顿流体的特性，若外加磁场后，磁流变小颗粒在极短时间内后凝成“固体”，并且该过程是可逆的。这种特性，使得其具有良好的可控性。
1.1 磁流变阻尼器的力学模型
为方便对磁流变阻尼器的描述与研究，研究人员对其进行数学建模与分析。其中磁流变阻尼器常用的模型包括：Bingham模型、Bouc-wen模型、双曲线回归模型、Dahl模型等[16-18]。其中前两者是应用最广泛的模型。
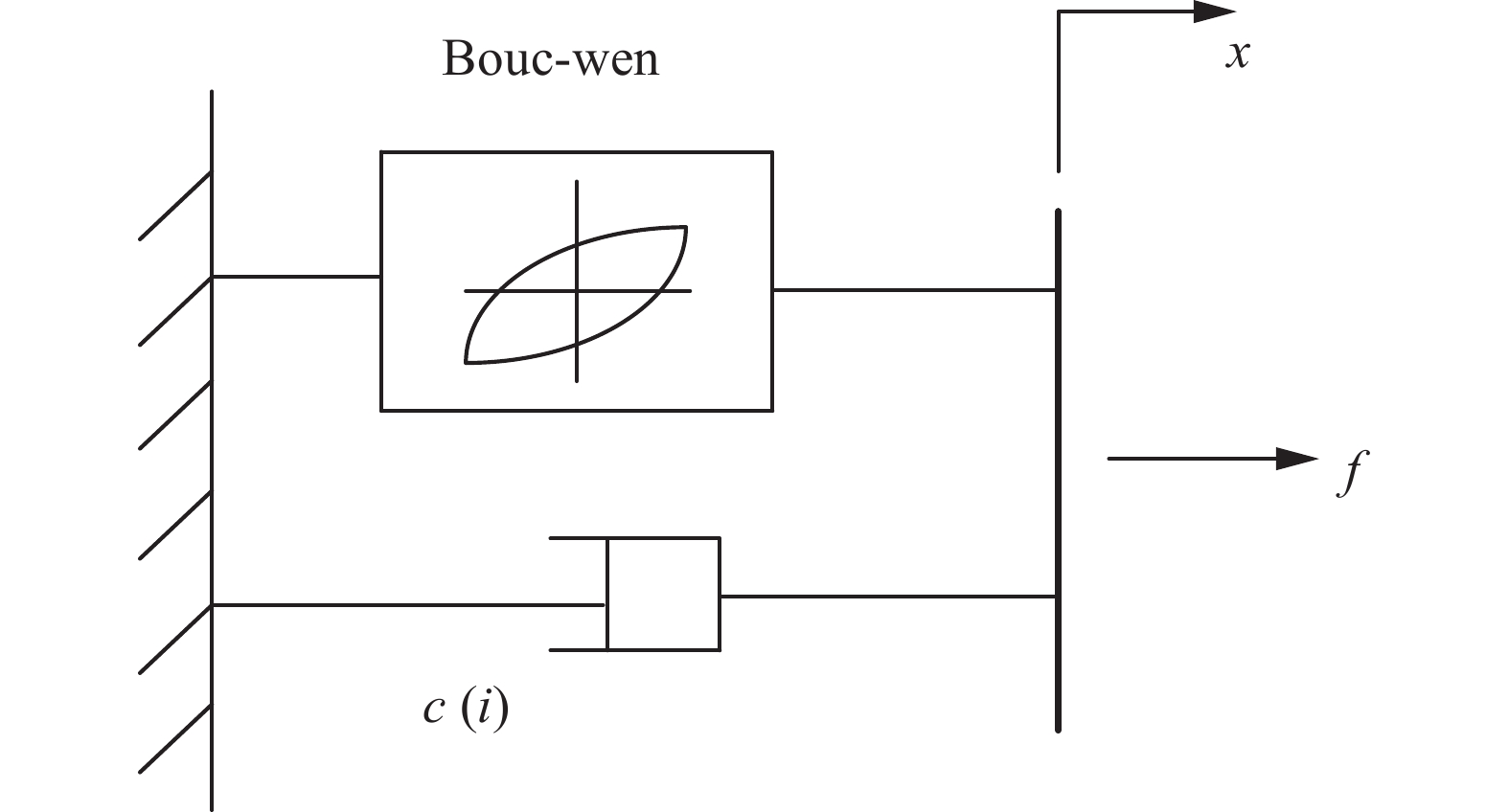
本文采用文献[9]中改进的Bouc-wen模型，与Bouc-wen模型相比，物理概念更加明显，同时也能够很好地变现出低速时的滞回特性，模型原理图如图1所示。
图 1 改进的Bouc-wen模型原理Fig. 1 Princple map of modified Bouc-wen model
下载:
全尺寸图片
模型如式(1)所示：
$$ f = c(i) \cdot \dot x + \alpha (i) \cdot z $$ (1) 式中：
$f$ 表示阻尼力；$x$ 表示阻尼器的位移；$z$ 表示滞回位移，其表达式如式（2）所示：$$ \dot z = - \gamma \cdot |\dot x| \cdot z \cdot |z{|^{n - 1}} - \beta \cdot |\dot x| \cdot |z{|^n} + A \cdot \dot x $$ (2) $c(i)$ 、$\alpha (i)$ 分别为磁流变材料的粘性系数和滞回力在阻尼器总阻尼力所占比重的调节参数，取值为电流的函数。$$ c(i) = 13.5 + 2.083i + 1.563{i^2} - 1.302{i^3}{\text{ N}} \cdot {\text{s/mm}} $$ $$ \alpha (i) = 900 + 2750i + 1875{i^2} - 1563{i^3}{\text{ N}} \cdot {\text{s/mm}} $$ 式(2)中
$ \gamma $ 、$ \beta $ 、$ A $ 为模型与滞回位移有关的参数，通过调整这些参数可以控制阻尼力变化的平稳度。$ \gamma $ 、$ \beta $ 表示滞回环宽度和高度的调节系数，取值为150；$ A $ 表示与最大阻尼力相关的参数，取值为6；$ n $ 表示滞回环圆滑系数，取值为2。1.2 改进的Bouc-wen模型的力学特性
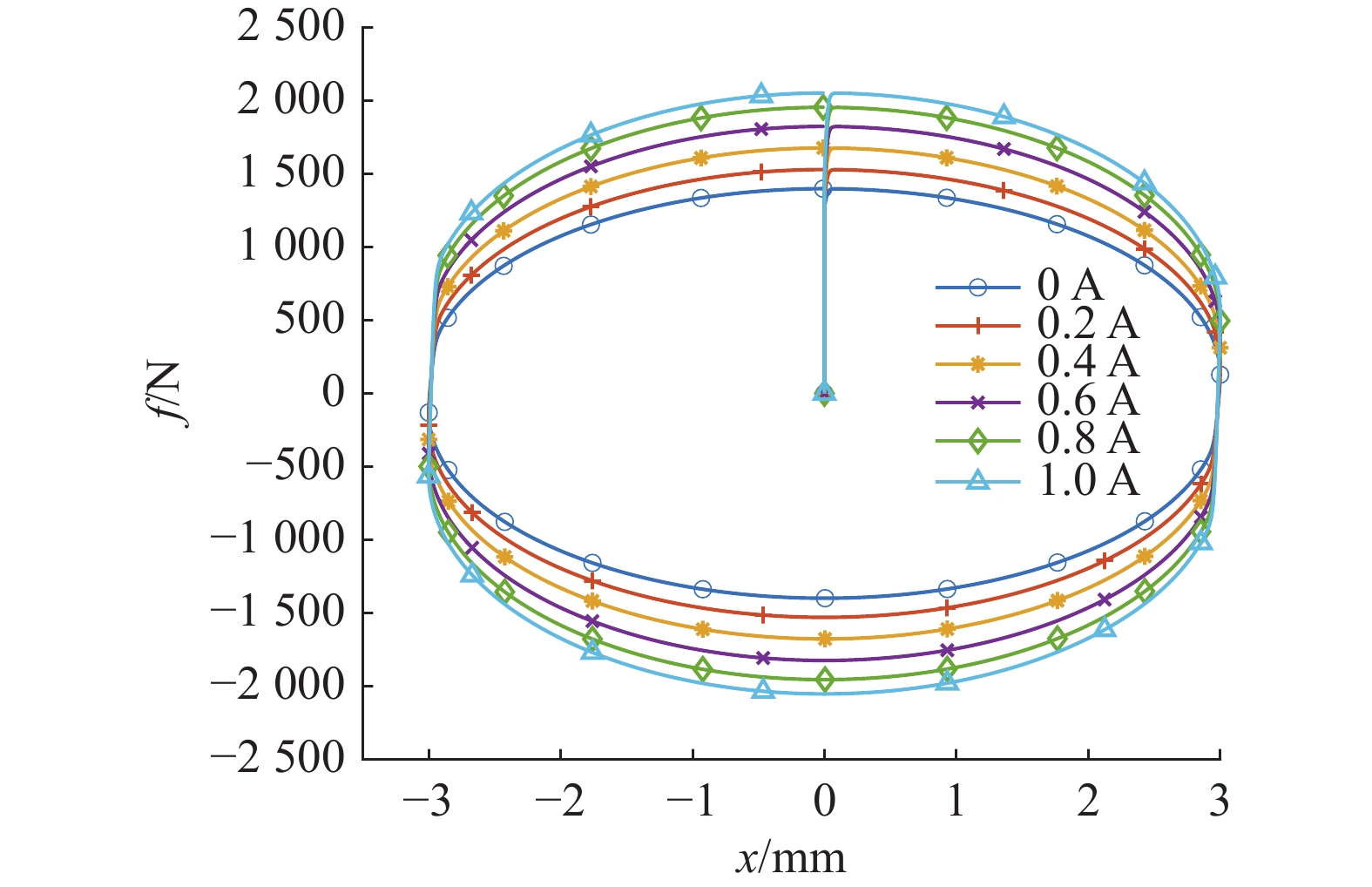
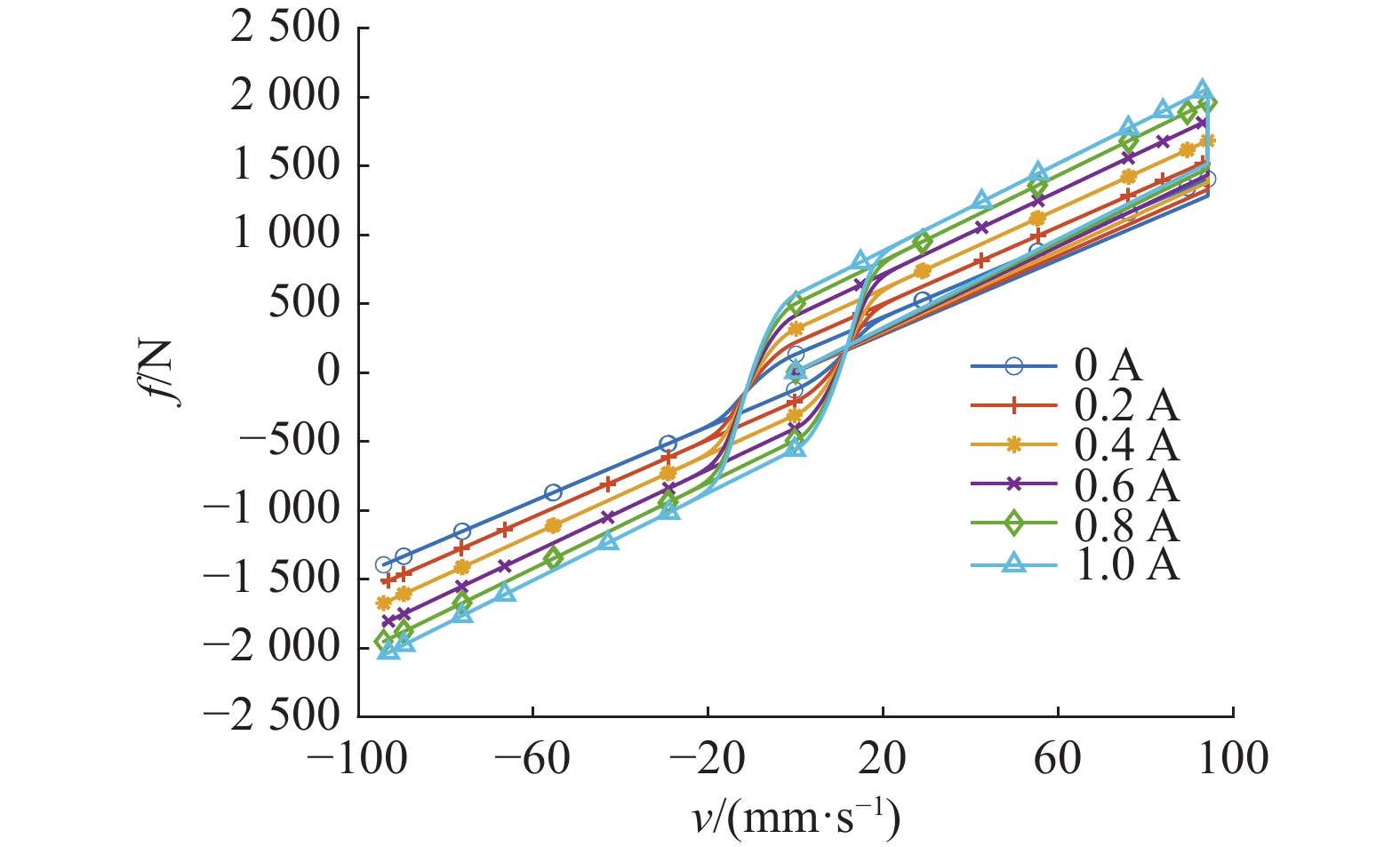
进行该模型的激励测试，输入激励信号幅值为3 mm，频率为5 Hz，输入电流一次为0、0.2、0.4、0.6、0.8、1.0 A，得到位移与阻尼力的关系如图1所示，速度与阻尼力的关系如图2所示。
图 2 位移与阻尼力的关系Fig. 2 Displacement vs. damping force下载:
全尺寸图片
从图2中可以看出，位移与阻尼力之间的关系具有良好的对称性，随着电流的增大，阻尼力增大。而且在低速运动中，阻尼力呈现了滞回特性，说明该模型能够较好地刻画磁流变阻尼器的特性。
2. 自抗扰控制
2.1 自抗扰控制基本原理
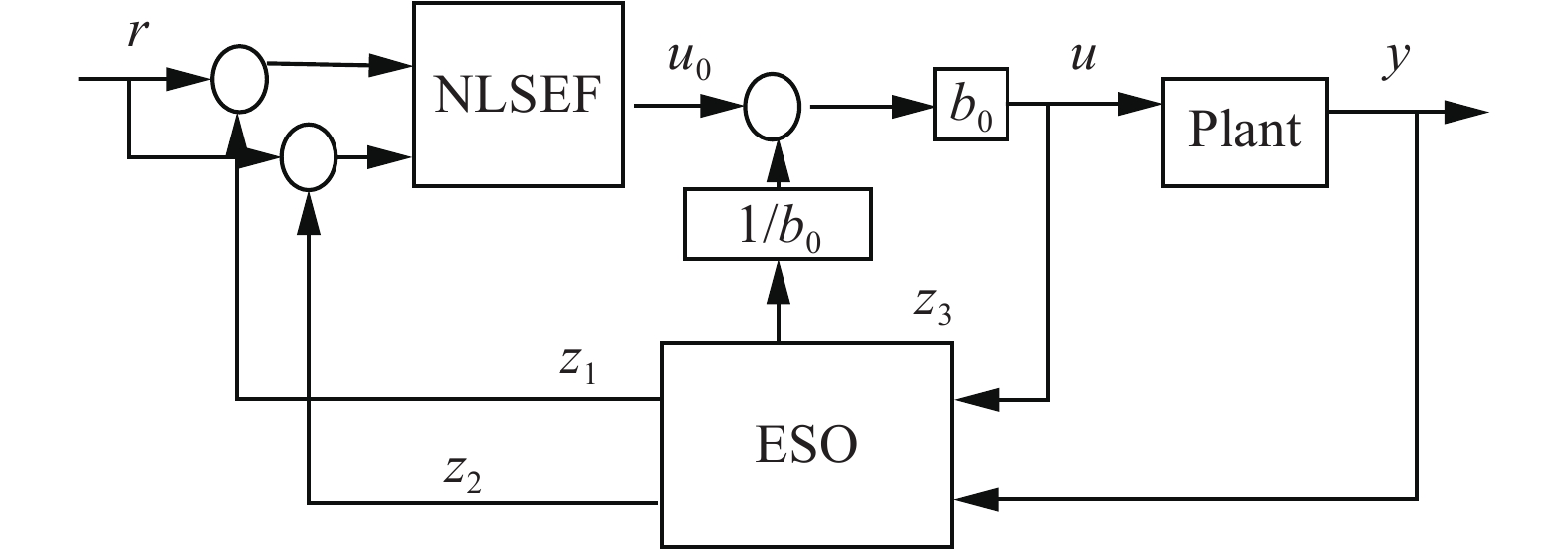
自抗扰的思想最早可以追溯到我国古代指南车的设计思想，是一种主动抗扰的方法。它主要包括跟踪–微分器(tracking differential, TD)、扩张状态观测器(extended state observer,ESO)、非线性误差反馈率(nonlinear stste error feedback, NLSEF)及扰动估计补偿等部分，其结构图如图3所示。图中
$y$ 是系统输出，$u$ 是控制信号，$r$ 是给定信号；${b_0}$ 是模型参数。
图 3 速度与阻尼力的关系Fig. 3 Velocity vs. damping force下载:
全尺寸图片
TD可以最快地跟踪给定信号的方法来提取微分信号，除此之外它还有安排过渡过程、配置系统零极点、数字整流等应用。
图 4 自抗扰控制器结构Fig. 4 Principle map of ADRC下载:
全尺寸图片
ESO是自抗扰控制的核心部分，它可以将系统内扰外扰，确定性和不确定性的扰动当作总扰动一同进行估计。
NLSEF将误差的反馈形式表示为非线性，和扰动估计补偿共同作用形成控制信号。
2.2 自抗扰控制器的设计
2.2.1 飞机前起落架模型
飞机前起落架采用一个三自由度的非线性简易模型[2,10,19]，如式(3)(4)所示：
$$ {I_z}\ddot \varphi = {M_1}(\varphi ) + {M_2}(\dot \varphi ) + {M_3}(\alpha ) + {M_4}(\dot \varphi /v) + {M_5} $$ (3) $$ \dot y + \dfrac{v}{\sigma }y = v\varphi + (e - a)\dot \varphi $$ (4) 式中：
${M_1}$ 是轮胎上方扭矩连杆和转向杆一起提供的线性弹簧扭矩；${M_2}$ 是油气式缓冲器轴承之间的粘性摩擦和减摆器的组合阻尼力矩；${M_3}$ 、${M_4}$ 分别为由侧滑和横摆引起的轮胎力矩和轮胎阻尼力矩；${M_5}$ 是磁流变阻尼器力矩。$y$ 是飞机机轮侧向位移；$v$ 是飞机滑行速度；$\varphi $ 是机轮摆角。${M_1}$ ~${M_5}$ 的表达式如式(5)~(13)所示，${M_z}$ 是围绕轮胎中心的扭转力矩；${F_y}$ 是以稳定距为杠杆作用的转弯力矩，其他变量或参数以表1的形式给出。表 1 起落架模型参数Table 1 the parameters of the landing gear model参数 数值 惯性矩Iz/(kg·m2) 1 垂直负荷Fz/N 4200 线性扭矩系数c/(N·m)·rad−1 −15000 组合阻尼系数k/(N·m·s)·rad−1 −35 稳定距e/m 0.12 轮胎力矩导数cMα/(m·rad−1) −2 侧向力导数cFα/rad−1 20 轮胎力矩极值角αg/(°) 10 轮胎力极值角δ/(°) 5 接触半长a/m 0.1 胎面宽度常数 $\kappa $/ $(\rm {N} \cdot { {m} ^2})\cdot rad^{-1}$ −126 松弛长度 $\sigma $/ $\rm{m}$ 0.3 滑行速度 $v$/ $({\rm{m\cdot s} }^{-1})$ 0~50 减摆力臂d/m 0.1 $$ {M_1} = c\varphi $$ (5) $$ {M_2} = k\dot \varphi $$ (6) $$ {M_3} = {M_z} - e{F_y} $$ (7) $$ {M_z} = \left\{ \begin{aligned} &0,\quad\alpha | \geqslant {\alpha _g} \\ &{c_{M\alpha }}{\alpha _g}/180 \cdot \sin (180/{\alpha _g} \cdot \alpha ),\quad{其他} \\ \end{aligned} \right. $$ (8) $$ {F_y} = \left\{ \begin{aligned} &{c_{F\alpha }}\alpha {F_z},\quad\alpha \leqslant \delta \\ &{c_{F\alpha }}\delta {F_z}{\rm sign} (\alpha ),\quad \alpha \geqslant \delta \\ \end{aligned} \right. $$ (9) $$ {M_4} = \kappa /v \cdot \dot \varphi $$ (10) $$ \kappa = - 0.15{a^2}{c_{F\alpha }}{F_z} $$ (11) $$ {M_5} = f \cdot d $$ (12) $$ \alpha \approx \arctan \alpha = {y_1}/\sigma $$ (13) 2.2.2 自抗扰控制
针对上述磁流变阻尼器与飞机前起落架模型，设计自抗扰控制器。因为模型的阶次为二阶，因此设计三阶的自抗扰控制器，其参考输入为0，将自抗扰简化为扩张状态观测器(extended state observer, ESO)、非线性反馈控制率(nonlinear state error feedback, NLSEF)、扰动补偿三部分。
三阶ESO模型：
$$ \left\{ \begin{aligned} &e = {z_1} - y \\ & {{\dot z}_1} = {z_2} - {\beta _{01}}e \\ &{{\dot z}_2} = {z_3} - {\beta _{02}}fal(e,0.5,\delta ) + {b_0}u \\ &{{\dot z}_3} = - {\beta _{03}}fal(e,0.25,\delta ) \\ \end{aligned} \right. $$ (14) NLSEF及扰动补偿：
$$ \left\{ \begin{aligned} &{e_1} = r - {z_1},{e_2} = \dot r - {z_2} \\ &{u_0} = {\beta _1}fal({e_1},0.5,{\delta _1}) + {\beta _2}fal({e_2},0.25,{\delta _2}) \\ &u = \dfrac{{{u_0} - {z_3}}}{{{b_0}}} \\ \end{aligned} \right. $$ (15) ${\text{fal(}} \cdot {\text{)}}$ 为一非线性函数：$$ {\rm fal} = \left\{ \begin{aligned} &\dfrac{e}{{{\delta ^{1 - \alpha }}}},\quad|e| \leqslant \delta \\ &|e{|^\alpha }{\rm sign} (e),\quad|e| > \delta \\ \end{aligned} \right. $$ (16) 将磁流变阻尼器的位移作为反馈量，产生的控制信号为电流，额定电流为1.2 A，被控对象的观测对象为机轮摆角、机轮侧滑角、侧向位移。可以看出，上述控制器中有
${\beta _{01}}$ 、${\beta _{02}}$ 、${\beta _{03}}$ 、$ {\beta _1} $ 、$ {\beta _2} $ 、$ {b_0} $ 、$\delta $ 、$ {\delta _1} $ 、$ {\delta _2} $ 等多个参数，比较难整定，因此采用智能算法进行正定参数。3. 混沌分数阶天牛群算法
混沌分数阶天牛群算法（chaos fractional order bettle swarm optimization , CFBSO）是将混沌思想、分数阶微分结构以及天牛群算法有机结合。
3.1 天牛群算法
天牛群算法(bettle swarm optimization, BSO)是天牛须算法与粒子群算法(particle swarm optimization, PSO)的融合和改进[20]。PSO中的个体用天牛来取代粒子，原来的每个粒子是一只天牛。在计算的迭代过程中位置更新，它结合了两者的长处，既有PSO算法搜索过程记录的个体历史最优解及全局最优解，又加入了天牛须算法中的增量因子来开展最优解局部范围的搜索，改善了PSO容易陷入局部最优的问题。文献[20]中将BSO算法与PSO算法、遗传算法(genetic algorithm, GA)在23组基准函数进行寻优测试，结果显示，除个别函数外，其他基准函数上，BSO算法具有良好的搜索性能和效率。
假设天牛群的种群规模为N，其中第
$i$ 个个体的位置更新公式为$$ X_i^{k + 1} = X_i^k + \lambda V_i^k + (1 - \lambda )\xi _i^k $$ (17) 式中：
$k$ 为当前时刻的迭代次数；$\lambda $ 为比例系数（取一定值）；${V_i}$ 代表第$i$ 只天牛当前时刻的速度，速度更新的公式为$$ V_i^{k + 1} = {\omega _k}V_i^k + {c_1}{r_1}({p_{{\rm best},i}} - X_i^k) + {c_2}{r_2}({g_{\rm best}} - X_i^k) $$ (18) 式中：
${\omega _k}$ 为权重因子，其更新策略为线性递减，如式(19)所示；${c_1}$ 、${c_2}$ 为学习因子；${r_1}$ 、${r_2}$ 为0~1之间的随机数；${p_{{\rm best},i}}$ 为第$i$ 只天牛的个体最优位置；${g_{\rm best}}$ 为此时全局最优位置。$$ {\omega _k} = {\omega _{\max }} - ({\omega _{\max }} - {\omega _{\min }})/K \cdot k $$ (19) 式中：
${\omega _{\max }}$ 、${\omega _{\min }}$ 分别表示权重的上下界；$K$ 为总迭代次数。除此之外，
$\xi _i^k$ 为增量因子，其更新公式如式(20)所示：$$ \xi _i^{k + 1} = {\delta ^k}V_i^k \cdot {\rm sign} (f(X_{ir}^k) - f(X_{il}^k)) $$ (20) 式中：
${\delta ^k}$ 表示第$k$ 次的迭代步长，更新公式如下：$$ {\delta ^{k + 1}} = {\rm eta} \cdot {\delta ^k} $$ (21) 式中：
$\rm eta$ 为一常数，一般取值0.95；${\rm sign}$ 为符号函数；$f(\cdot)$ 为适应度函数，$X_{il}^k$ 、$X_{ir}^k$ 分别为天牛$i$ 的左须和右须位置，其更新公式为$$ \left\{ \begin{gathered} X_{il}^{k + 1} = X_i^k + V_i^k \cdot {d^k}/2 \\ X_{ir}^{k + 1} = X_i^k - V_i^k \cdot {d^k}/2 \\ \end{gathered} \right. $$ (22) 式中：
${d^k}$ 表示天牛左右两须之间的距离，更新公式为$$ {d^k} = {\delta ^k}/c $$ (23) 式中：
$c$ 为一常数，一般取值为2。3.2 混沌分数阶天牛群算法
3.2.1 混沌化
引入混沌来初始化种群。初始种群的分布，会影响算法的收敛速度[21]。在天牛群算法中初始种群一般是随机生成，种群的分布会出现不均匀的情况，这会减少多样性，限制搜索性能。因此，采用Tent混沌映射来进行种群的初始化，提高种群的多样性，如式(24)所示：
$$ {Z_{k + 1}} = \left\{ \begin{gathered} 2{Z_k},\quad{\text{0}} \leqslant {Z_k} \leqslant 0.5 \\ 2(1 - {Z_k}),\quad 0.5 < {Z_k} < 1 \\ \end{gathered} \right. $$ (24) 而后通过式(25)映射到解空间：
$$ {X_k} = {Z_K}({U_b} - {U_l}) + {U_l} $$ (25) 式中
${U_b}$ 、${U_l}$ 分别表示参数的上界和下界。若种群大小为N，需要优化的参数为m个，则混沌初始化的过程为：首先产生m个0~1的随机数，将之作为一个m维的向量；将此向量映射到解空间，记录其位置；通过式(24)产生新的m维向量，再次映射，一共迭代
${N_m}$ 次；而后产生${N_m}$ (${N_m}$ >m)个m维的混沌序列，将混沌序列通过式(25)映射到解空间，从中选取适应度最好的N个作为初始的天牛种群。在搜索最优解过程中，在全局最优解
${g_{\rm best}}$ 的邻域内进行${K_0}$ 次混沌搜索。过程为与上文方法一样得到${K_0}$ 个m维混沌序列，而后用式(26)得到${K_0}$ 个位于${g_{\rm best}}$ 邻域内的混沌搜索点，并将其适应度与全局最优适应度值进行比较来更新或保留全局最优解：$$ {X_k} = {g_{\rm best}} + R{Z_k} $$ (26) 式中
$R$ 为一常数，一般取值为0.3。3.2.2 分数阶
将分数阶引入到BSO中，可以使算法迭代过程中天牛的运动具有分数阶微分的记忆特性[22]。
$$ {D^\alpha }[x(t)] = \frac{1}{{{T^\alpha }}}\left[ {\sum\limits_{h = 0}^r {\frac{{{{( - 1)}^h}\Gamma (\alpha + 1)x(t - hT)}}{{\Gamma (h + 1)\Gamma (\alpha - h + 1)}}} } \right] $$ (27) 式(27)为
$\alpha $ 阶G-L分数阶导数的离散形式，$T$ 为采样周期，$r$ 为截断阶次。式(19)中
${\omega _k}$ 取值为1，则$$ V_i^{k + 1} - V_i^k = {c_1}{r_1}({p_{{\rm best},i}} - X_i^k) + {c_2}{r_2}({g_{\rm best}} - X_i^k) $$ (28) $T = 1$ 时，可得$$ \begin{gathered} {D^\alpha }[V_i^{k + 1}] = \left[ {\sum\limits_{h = 0}^r {\frac{{{{( - 1)}^h}\Gamma (\alpha + 1)x(t - h)}}{{\Gamma (h + 1)\Gamma (\alpha - h + 1)}}} } \right] =\\ {c_1}{r_1}({p_{{\rm best},i}} - X_i^k) + {c_2}{r_2}({g_{\rm best}} - X_i^k) \\ \end{gathered} $$ (29) 当
$r = 4$ 时，速度更新公式可以表示为$$\begin{gathered} V_i^{k + 1} = {c_1}{r_1}({p_{{\rm best},i}} - X_i^k) + {c_2}{r_2}({g_{\rm best}} - X_i^k) + \alpha V_i^k + \\ \frac{1}{2}\alpha (1 - \alpha )V_i^{k - 1} + \frac{1}{6}\alpha (1 - \alpha )(2 - \alpha )V_i^{k - 2} + \\ \frac{1}{{24}}\alpha (1 - \alpha )(2 - \alpha )(3 - \alpha )V_i^{k - 3} \end{gathered}$$ (30) 式中：
$\alpha $ 采用式(31)更新：$$ \alpha = 0.8 - 0.5 \cdot k/K $$ (31) 式中
$K$ 为迭代总次数。3.2.3 算法流程
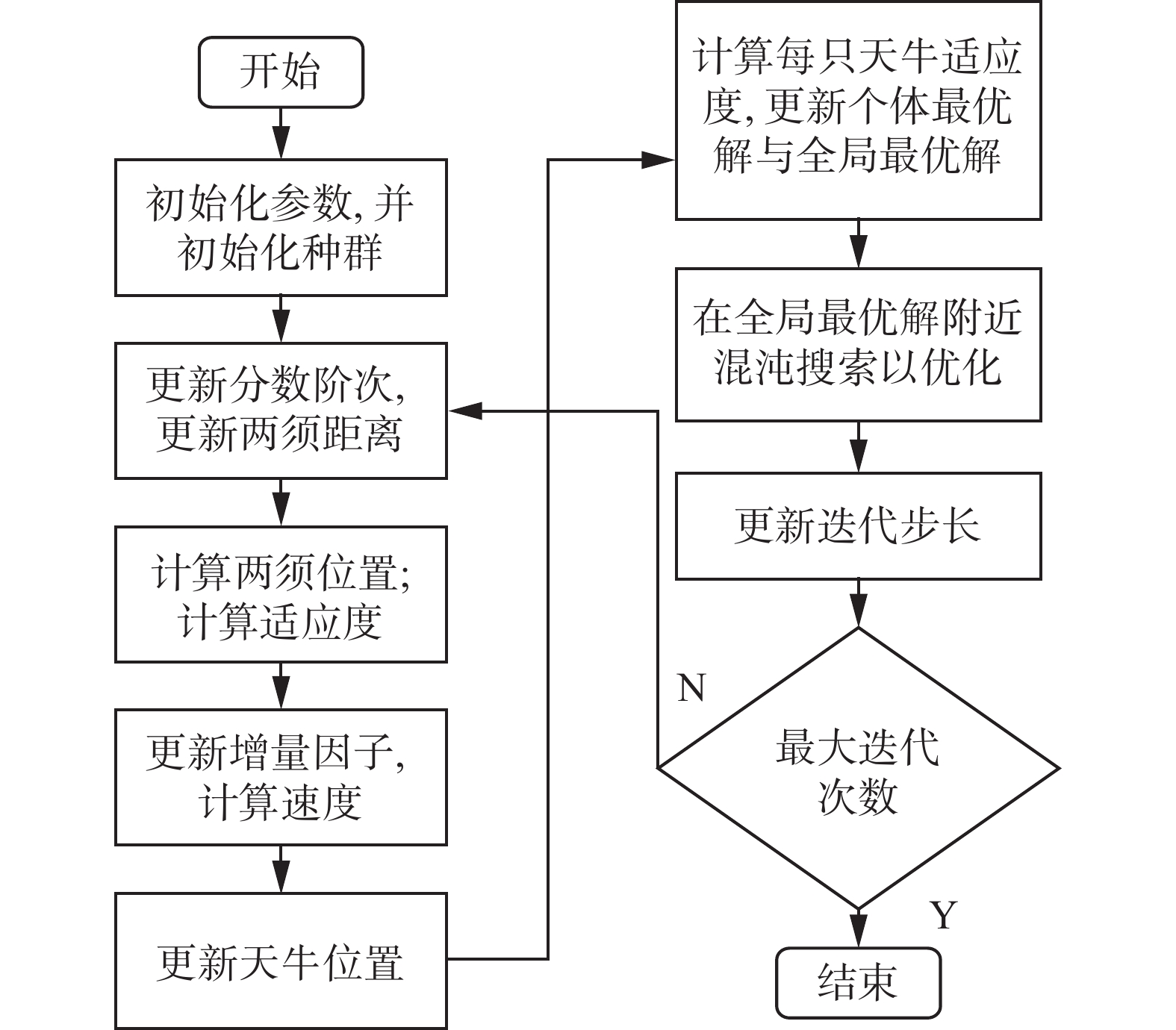
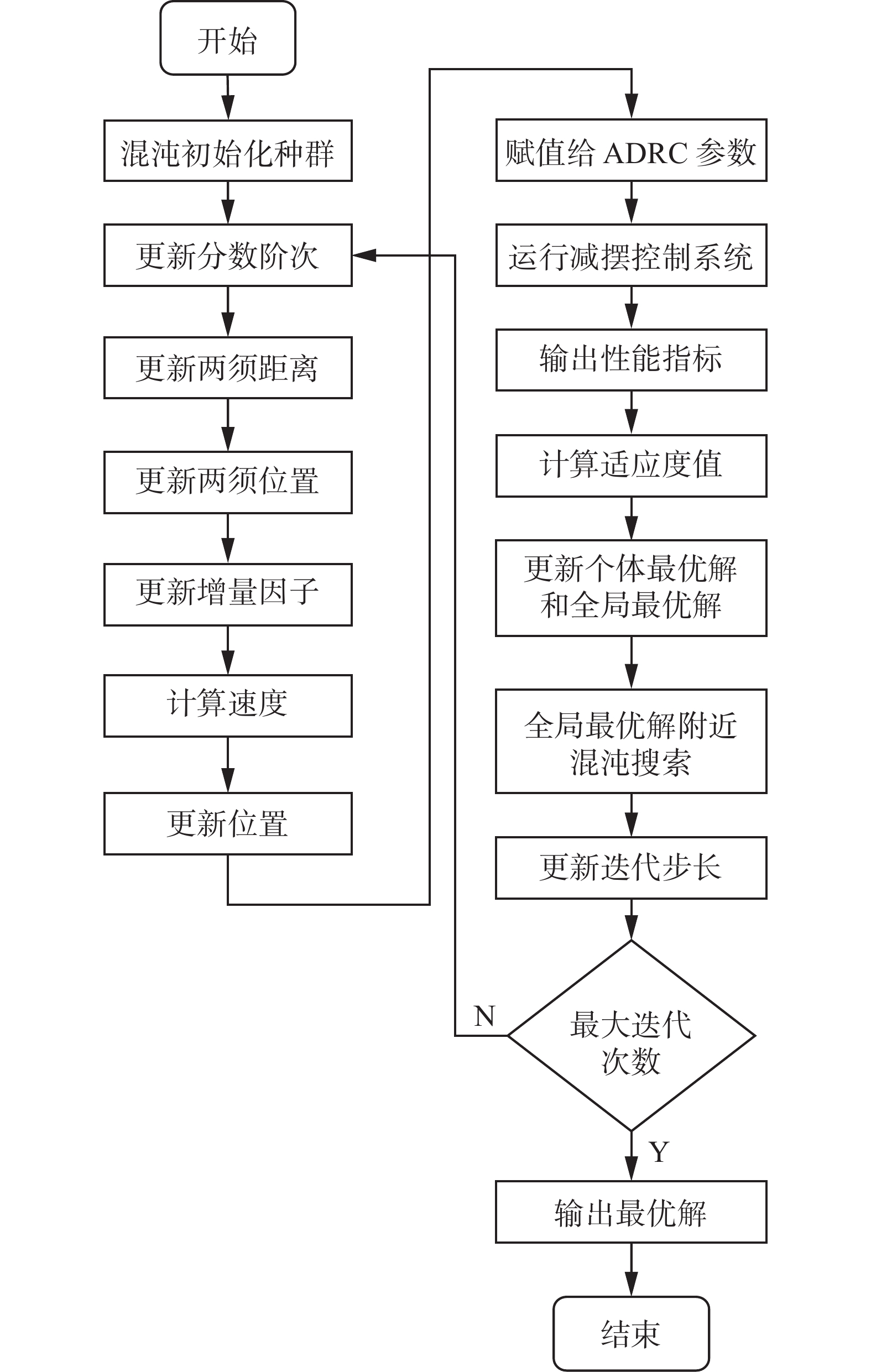
加入混沌化与分数阶后，混沌分数阶天牛群算法流程如下：
1）初始化参数，混沌化初始种群；
2）如式(30)更新分数阶的阶次
$\alpha $ ，式(23)更新两须之间的距离；3）用式(22)得到天牛两须的位置，然后计算其适应度值；
4）通过式(20)计算每个个体的增量因子，而后采用式(18)计算其速度；
5）采用式(17)更新每只天牛的位置；
6）计算每只天牛的适应度值，更新个体最优解以及全局最优解；
7）在全局最优解附近进行
${K_0}$ 次混沌搜索优化最优解；8）采用式(21)更新迭代步长；
9）判断是否终止迭代，是则输出最优解，否则返回第2)步。
算法流程如图5所示。
图 5 混沌分数阶天牛群算法流程Fig. 5 Flowchart of CFBSO下载:
全尺寸图片
4. 仿真及结果与分析
4.1 基准函数测试
将所提混沌分数阶天牛群算法与天牛群算法在23组基准函数[20]上进行性能测试，两种算法迭代次数均为1000次，测试结果如表2所示。其中ave是算法运行30次的得到的最优值，std为标准差。
表 2 基准函数在不同算法下的优化结果比较Table 2 Comparison of optimization results of benchmark function under different algorithms函数 CFBSO BSO ave std ave std F1 11.762 15.173 48.287 60.287 F2 3.3748 2.4714 6.1922 4.6076 F3 168.47 225.87 287.26 637.92 F4 0.4678 0.47890 3.9291 6.7811 F5 84.525 30.012 516.25 518.43 续表 2 函数 CFBSO BSO ave std ave std F6 13.992 10.309 54.013 50.907 F7 0.0056 0.0037 0.0044 0.0029 F8 −17934 3356.1 −12143 1097.8 F9 52.816 26.916 23.600 15.471 F10 0.34905 0.6387 0.6679 3.6334 F11 1.1906 0.1311 8.6136 17.232 F12 0.40605 0.2365 1.6958 1.1177 F13 3.0101 0.8664 10.673 11.029 F14 0.998 0 0.998 0 F15 0.0008 0.0004 0.0032 0.0069 F16 −1.0316 0 −1.0316 0 F17 0.398 0 0.398 0 F18 3 0 3 0 F19 −3.3349 0.2811 −3.2191 0.6438 F20 −1.2481 0.4047 −1.1193 0.6007 F21 −7.2404 0.3874 −0.3138 0.0676 F22 −6.8624 0.6383 −0.5227 0.8701 F23 −7.6496 0.4815 −0.5798 0.9317 F23 −7.6496 0.4815 −0.5798 0.9317 如表2所示，除函数7，CFBSO结果比BSO略差，及函数16、17、18结果一样，其余函数寻优结果都优于BSO算法。所以所提算法，在处理单峰及多峰函数问题上，比BSO算法具有显著优势。
4.2 基于CFBSO的自抗扰控制
上文描述了自抗扰控制器和混沌分数阶天牛群算法，现将两者结合，用该算法优化控制器参数。控制器中的
$\delta $ 取值为0.001，$ {\delta _1} $ 、$ {\delta _2} $ 都取值为0.01。其余控制器参数用算法进行整定，它们的取值范围为${\beta _{01}} \in [0,1\;000]$ 、${\beta _{02}} \in [0,5\;000]$ 、${\beta _{03}} \in [0, 20\;000]$ 、${\beta _1} \in [0,50]$ 、${\beta _2} \in [0,10]$ 、$ {b_0} \in [0,50] $ 。设置适应度函数：
$$ J = \int {(({\omega _1}|{e_1}|} + {\omega _2}|{e_{{z_1}}}| + {\omega _3}|{e_{{z_2}}}| + {\omega _4}|u|) \cdot t){{\rm d}t} $$ 其中
${\omega _i}(i = 1,2,3,4)$ 为权重因子；${e_1}$ 为反馈误差；${e_{{z_1}}}$ 、${e_{{z_2}}}$ 为扩张状态观测器所观测的$y$ 及$\dot y$ 的误差；$u$ 为控制量电流。权重因子的取值依次为0.59、0.2、0.2、0.01，因电流的量级与前三者的量级相差较大，所以控制信号电流的权重设置较小。加入CFBSO算法后，整个控制器的流程如图6所示。初始参数设置
$y = 0$ m,$\varphi = 0.1$ rad。
图 6 控制流程Fig. 6 Flowchart of control process下载:
全尺寸图片
4.3 仿真结果及分析
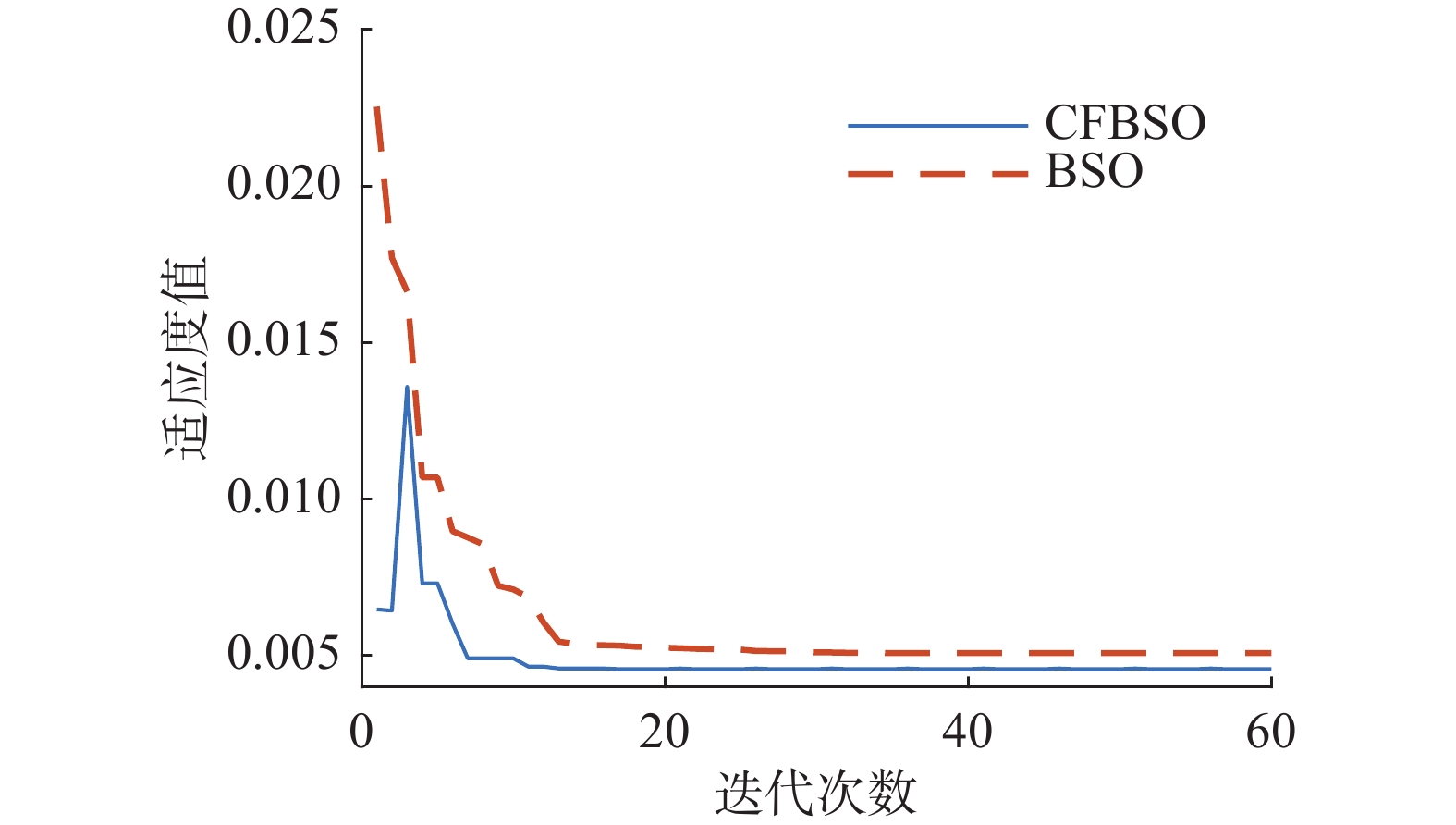
将BSO算法和CFBSO算法都应用与控制器参数寻优。各运行5次，取适应度平均值，得到其与迭代次数的关系如图7所示。在初始适应度值上CFBSO小于BSO，说明混沌初始化可以改善种群分布，达到最后的适应度收敛值，CFBSO所用次数更少，且函数值更小，体现了算法的优越性。
图 7 进化曲线图Fig. 7 The diagram of evolution curve下载:
全尺寸图片
取两种算法优化后取得的最优控制效果下的参数如表3所示。
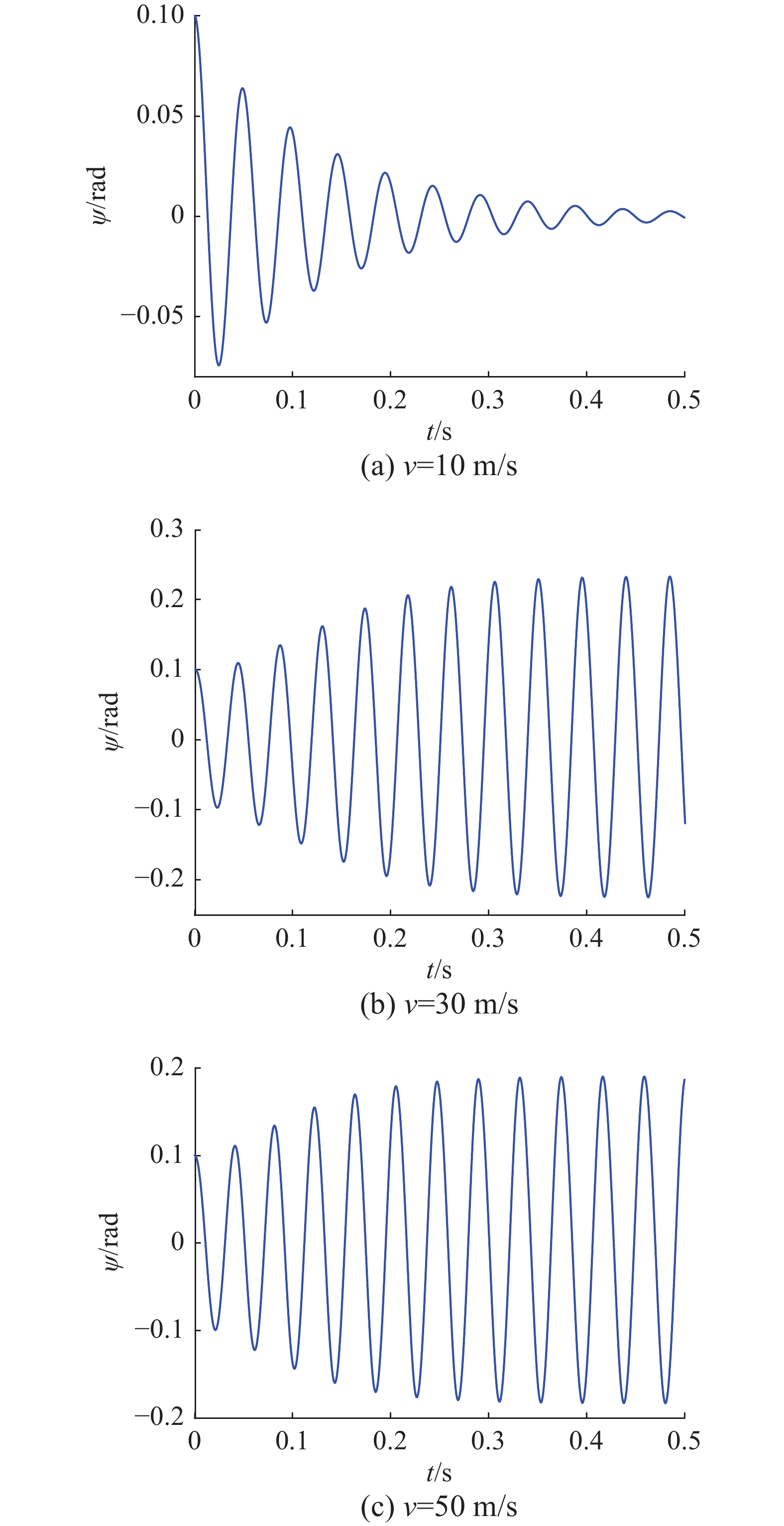
表 3 优化后控制器参数Table 3 The parameters of the controller算法 模块 参数取值 CFBSO ESO $\begin{aligned} {\beta _{01} } &= 61.88,{\beta _{02} } = 4\;999.82 \\ {\beta _{03} } &= 16\;200.11,\delta = 0.001 \\ \end{aligned}$ NLESF $\begin{aligned} {\beta _1} &= 45.65,{\beta _2} = 6.37,{b_0} = 35.94 \\ {\delta _1} &= 0.01,{\delta _2} = 0.01 \\ \end{aligned}$ BSO ESO $\begin{aligned} {\beta _{01} }& = 60.01,{\beta _{02} } = 4\;998.66 \\ {\beta _{03} }& = 13\;015.38,\delta = 0.001 \\ \end{aligned}$ NLESF $\begin{aligned} {\beta _1}& = 0.15,{\beta _2} = 9.99,{b_0} = 42.53 \\ {\delta _1} &= 0.01,{\delta _2} = 0.01 \\ \end{aligned}$ 因摆角、侧向位移以及滑移角变化趋势相同，本节仿真结果只给出摆角的变化曲线。首先，在没有加入磁流变阻尼器的情况下，摆角变化曲线如图8所示。
图 8 无MR，摆角变化曲线Fig. 8 No MR, the response of yaw angle下载:
全尺寸图片
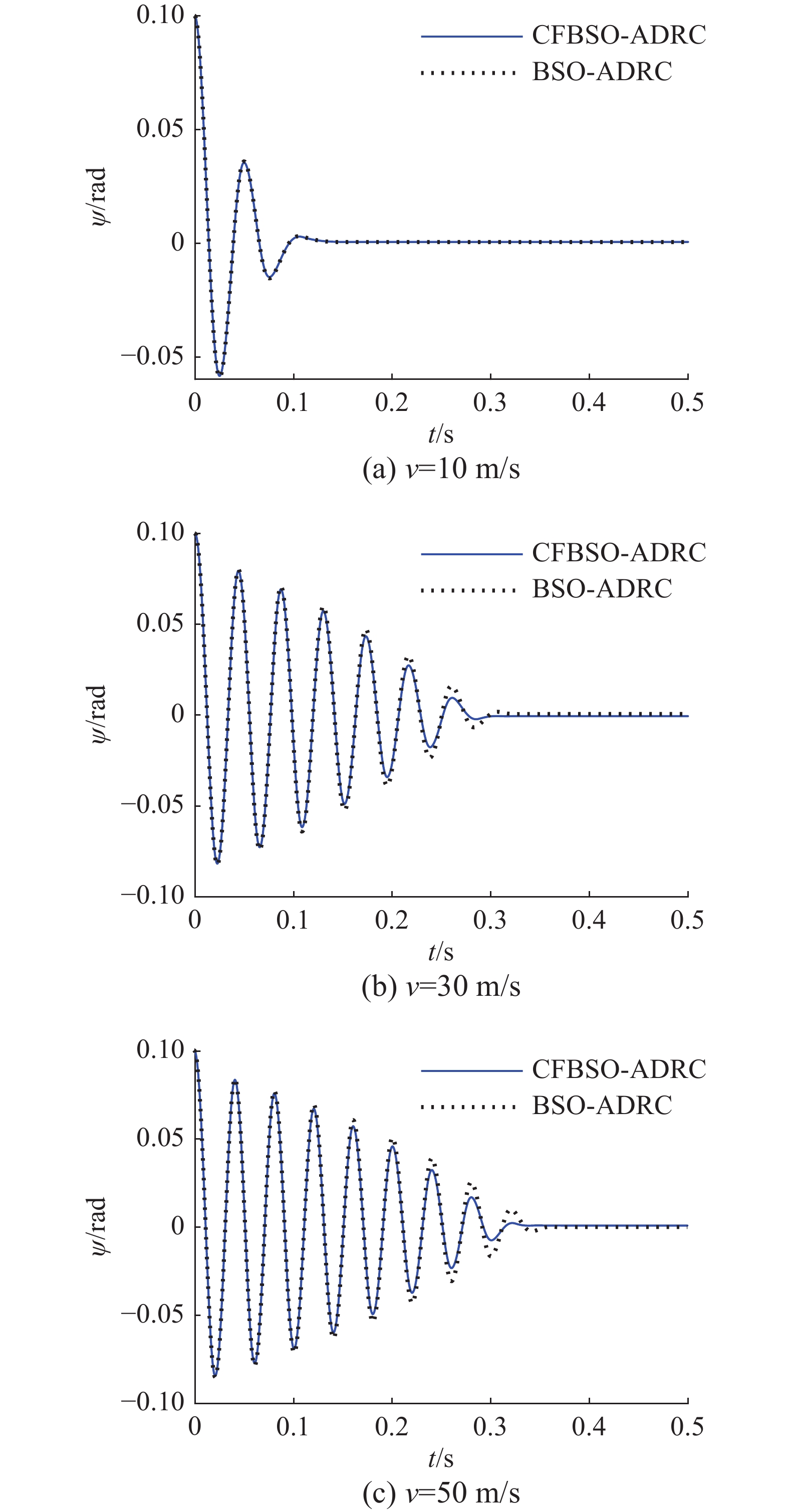
从图8和图9中可以看到在该较小的速度下，两种方式下系统都可以达到稳态，但是加入磁流变阻尼器后稳定时间和振荡周期都明显的减少，两种算法下的控制效果几乎一致，稳定时间减至0.13 s，说明加入磁流变阻尼器可以明显抑制摆振情况，然后将速度增大得到图8(b)(c)的仿真结果图。
图 9 有MR，摆角变化曲线Fig. 9 With MR, the response of yaw angle下载:
全尺寸图片
从图8中可以看出，当在一定范围内，速度增大，不加入磁流变阻尼器的情况下，前起落架的机轮的摆动会呈发散状，后会等幅振荡，造成系统的不稳定，在磁流变阻尼器的作用，摆动呈现逐渐衰减的趋势，并且可以在较短的时间内达到稳定状态。
而且在速度分别为30 m/s和50 m/s时，从图9中可以看到，在后几个振荡周期内，CFBSO-ADRC的幅值和稳定时间更小。采用时间乘绝对误差积分（integral of time and absolute error, ITAE）指标，如式(32)所示。表4为两种算法下减摆性能指标。
表 4 减摆性能指标Table 4 Performance index for shimmy reductiom控制器 速度/(m·s−1) 稳定时间/s ITAE CFBSO-ADRC 10 0.130 1.161×10−4 30 0.278 3.703×10−4 50 0.333 4.365×10−4 BSO-ADRC 10 0.130 1.165×10−4 30 0.300 3.944×10−4 50 0.353 4.706×10−4 $$ {\text{ITAE = }}\int {|e(t)|t{\rm d}t} $$ (32) 如表4所示，所提算法在稳定时间和ITAE指标上都有更好的控制效果。
4.4 鲁棒性分析
上述仿真结果图说明当速度在一定范围变化时，系统同样可以保持稳定。下面改变系统的一些参数，观察控制系统的鲁棒性。表5为参数变化后CFBSO-ADRC控制器性能指标的变化。
表 5 鲁棒性性能指标Table 5 Performance index for robustness速度/(m·s−1) 变化参数 变化范围/% 稳定时间/s 10 ${F_z}$ +5 0.143 +10 0.147 $\varphi $ +25 0.133 +50 0.170 30 ${F_z}$ +5 0.351 +10 0.440 $\varphi $ +25 0.381 +50 0.527 50 ${F_z}$ +5 0.413 +10 0.709 $\varphi $ +25 0.486 +50 0.566 从表5中可以看到垂直负荷和摆角初始值在一定范围内增加时，3种速度的情况下系统仍能保持稳定。结果显示，系统对摆角初始值变化的容忍度更高一些。
5. 结束语
本文对飞机前起落架设计减摆自抗扰控制器，并通过混沌分数阶天牛群算法进行控制器参数的整定，与天牛群算法进行了对比，通过仿真结果可知，控制器取得了良好的控制效果，并且具有较好的响应时间与鲁棒性，体现了CFBSO算法下减摆自抗扰控制的良好性能。
在未来工作中，可以就文中所提算法进行改进，比如说将反向学习和搜索的策略引入考虑算法中超参数的整定等。同时可以找寻更合适的智能优化算法来整定自抗扰控制器的参数。
-
图 1 改进的Bouc-wen模型原理
Fig. 1 Princple map of modified Bouc-wen model
下载:
全尺寸图片
图 2 位移与阻尼力的关系
Fig. 2 Displacement vs. damping force
下载:
全尺寸图片
图 3 速度与阻尼力的关系
Fig. 3 Velocity vs. damping force
下载:
全尺寸图片
图 4 自抗扰控制器结构
Fig. 4 Principle map of ADRC
下载:
全尺寸图片
图 5 混沌分数阶天牛群算法流程
Fig. 5 Flowchart of CFBSO
下载:
全尺寸图片
图 6 控制流程
Fig. 6 Flowchart of control process
下载:
全尺寸图片
图 7 进化曲线图
Fig. 7 The diagram of evolution curve
下载:
全尺寸图片
图 8 无MR，摆角变化曲线
Fig. 8 No MR, the response of yaw angle
下载:
全尺寸图片
图 9 有MR，摆角变化曲线
Fig. 9 With MR, the response of yaw angle
下载:
全尺寸图片
表 1 起落架模型参数
Table 1 the parameters of the landing gear model
参数 数值 惯性矩Iz/(kg·m2) 1 垂直负荷Fz/N 4200 线性扭矩系数c/(N·m)·rad−1 −15000 组合阻尼系数k/(N·m·s)·rad−1 −35 稳定距e/m 0.12 轮胎力矩导数cMα/(m·rad−1) −2 侧向力导数cFα/rad−1 20 轮胎力矩极值角αg/(°) 10 轮胎力极值角δ/(°) 5 接触半长a/m 0.1 胎面宽度常数 $\kappa $/ $(\rm {N} \cdot { {m} ^2})\cdot rad^{-1}$ −126 松弛长度 $\sigma $/ $\rm{m}$ 0.3 滑行速度 $v$/ $({\rm{m\cdot s} }^{-1})$ 0~50 减摆力臂d/m 0.1 表 2 基准函数在不同算法下的优化结果比较
Table 2 Comparison of optimization results of benchmark function under different algorithms
函数 CFBSO BSO ave std ave std F1 11.762 15.173 48.287 60.287 F2 3.3748 2.4714 6.1922 4.6076 F3 168.47 225.87 287.26 637.92 F4 0.4678 0.47890 3.9291 6.7811 F5 84.525 30.012 516.25 518.43 续表 2 函数 CFBSO BSO ave std ave std F6 13.992 10.309 54.013 50.907 F7 0.0056 0.0037 0.0044 0.0029 F8 −17934 3356.1 −12143 1097.8 F9 52.816 26.916 23.600 15.471 F10 0.34905 0.6387 0.6679 3.6334 F11 1.1906 0.1311 8.6136 17.232 F12 0.40605 0.2365 1.6958 1.1177 F13 3.0101 0.8664 10.673 11.029 F14 0.998 0 0.998 0 F15 0.0008 0.0004 0.0032 0.0069 F16 −1.0316 0 −1.0316 0 F17 0.398 0 0.398 0 F18 3 0 3 0 F19 −3.3349 0.2811 −3.2191 0.6438 F20 −1.2481 0.4047 −1.1193 0.6007 F21 −7.2404 0.3874 −0.3138 0.0676 F22 −6.8624 0.6383 −0.5227 0.8701 F23 −7.6496 0.4815 −0.5798 0.9317 F23 −7.6496 0.4815 −0.5798 0.9317 表 3 优化后控制器参数
Table 3 The parameters of the controller
算法 模块 参数取值 CFBSO ESO $\begin{aligned} {\beta _{01} } &= 61.88,{\beta _{02} } = 4\;999.82 \\ {\beta _{03} } &= 16\;200.11,\delta = 0.001 \\ \end{aligned}$ NLESF $\begin{aligned} {\beta _1} &= 45.65,{\beta _2} = 6.37,{b_0} = 35.94 \\ {\delta _1} &= 0.01,{\delta _2} = 0.01 \\ \end{aligned}$ BSO ESO $\begin{aligned} {\beta _{01} }& = 60.01,{\beta _{02} } = 4\;998.66 \\ {\beta _{03} }& = 13\;015.38,\delta = 0.001 \\ \end{aligned}$ NLESF $\begin{aligned} {\beta _1}& = 0.15,{\beta _2} = 9.99,{b_0} = 42.53 \\ {\delta _1} &= 0.01,{\delta _2} = 0.01 \\ \end{aligned}$ 表 4 减摆性能指标
Table 4 Performance index for shimmy reductiom
控制器 速度/(m·s−1) 稳定时间/s ITAE CFBSO-ADRC 10 0.130 1.161×10−4 30 0.278 3.703×10−4 50 0.333 4.365×10−4 BSO-ADRC 10 0.130 1.165×10−4 30 0.300 3.944×10−4 50 0.353 4.706×10−4 表 5 鲁棒性性能指标
Table 5 Performance index for robustness
速度/(m·s−1) 变化参数 变化范围/% 稳定时间/s 10 ${F_z}$ +5 0.143 +10 0.147 $\varphi $ +25 0.133 +50 0.170 30 ${F_z}$ +5 0.351 +10 0.440 $\varphi $ +25 0.381 +50 0.527 50 ${F_z}$ +5 0.413 +10 0.709 $\varphi $ +25 0.486 +50 0.566 -
[1] 聂宏, 魏小辉. 飞机起落架动力学设计与分析[M]. 西安: 西北工业大学出版社, 2013. [2] 陈大伟, 顾宏斌, 吴东苏. 基于磁流变阻尼器的起落架摆振半主动控制[J]. 中国机械工程, 2010, 21(12): 1401−1405. CHEN Dawei, GU Hongbin, WU Dongsu. Semi-active control of landing gear shimmy based on magneto-rheological (MR) damper[J]. China mechanical engineering, 2010, 21(12): 1401−1405. [3] 武柏安, 龙海洋, 李耀刚, 等. 基于遗传算法的磁流变半主动悬架最优控制[J]. 机床与液压, 2021, 49(9): 109−114. WU Boan, LONG Haiyang, LI Yaogang, et al. Optimal control of MR semi-active suspension based on genetic algorithm[J]. Machine tool & hydraulics, 2021, 49(9): 109−114. [4] ZHANG Hailong, WANG Enrong, ZHANG Ning, et al. Semi-active sliding mode control of vehicle suspension with magneto-rheological damper[J]. Chinese journal of mechanical engineering, 2015, 28(1): 63–75. doi: 10.3901/CJME.2014.0918.152 [5] DYKE S J, SPENCER B F Jr, SAIN M K, et al. Modeling and control of magnetorheological dampers for seismic response reduction[J]. Smart materials and structures, 1996, 5(5): 565–575. doi: 10.1088/0964-1726/5/5/006 [6] NGUYEN X B, KOMATSUZAKI T, IWATA Y, et al. Modeling and semi-active fuzzy control of magnetorheological elastomer-based isolator for seismic response reduction[J]. Mechanical systems and signal processing, 2018, 101: 449–466. doi: 10.1016/j.ymssp.2017.08.040 [7] 王唯, 夏品奇. 采用磁流变阻尼器的直升机“地面共振”分析[J]. 南京航空航天大学学报, 2003, 35(3): 264−267. WANG Wei, XIA Pinqi. Ground resonance analysis of helicopter with magnetorheological lag damper[J]. Journal of Nanjing university of aeronautics & astronautics, 2003, 35(3): 264−267. [8] KANG B H, YOON J Y, KIM G W, et al. Landing efficiency control of a six degrees of freedom aircraft model with magneto-rheological dampers: part 2—control simulation[J]. Journal of intelligent material systems and structures, 2021, 32(12): 1303–1315. doi: 10.1177/1045389x20942593 [9] FU Li, GUAN Wei, WANG Qi, et al. Modeling and adaptive control of magneto-rheological buffer system for aircraft landing gear[J]. Applied mathematical modelling, 2015, 39(9): 2509–2517. doi: 10.1016/j.apm.2014.10.043 [10] 李莹. 飞机起落架磁流变减摆器控制系统的设计与实现[D]. 天津: 中国民航大学, 2016: 19−26. LI Ying. Design and implementation of the aircraft landing gear of MR shimmy damper control system[D]. Tianjin: Civil Aviation University of China, 2016: 19−26. [11] 王恕浩. 基于磁流变减摆器的飞机前轮减摆控制研究[D]. 天津: 中国民航大学, 2019: 23−32. WANG Shuhao. Shimmy damping control research of aircraft's nose wheel based on magnetorheological shimmy damper[D]. Tianjin: Civil Aviation University of China, 2019: 23−32. [12] 王璐琦. 磁流变减摆器控制器改进设计与算法研究[D]. 天津: 中国民航大学, 2020: 1−22. WANG Luqi. Research on improved design and algorithm of magnetorheological shimmy damper controller[D]. Tianjin: Civil Aviation University of China, 2020: 1−22. [13] DONG Lei, CHEN Zengqiang, SUN Mingwei, et al. Study on magneto-rheological damper control of aircraft landing gear based on LADRC[M]//Lecture Notes in Electrical Engineering. Singapore: Springer Singapore, 2021: 830−840. [14] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19−23. HAN Jingqing. Auto-disturbances-rejection controller and its applications[J]. Control and decision, 1998, 13(1): 19−23. [15] 李杰, 齐晓慧, 万慧, 等. 自抗扰控制: 研究成果总结与展望[J]. 控制理论与应用, 2017, 34(3): 281−295. LI Jie, QI Xiaohui, WAN Hui, et al. Active disturbance rejection control: theoretical results summary and future researches[J]. Control theory & applications, 2017, 34(3): 281−295. [16] AHAMED R, FERDAUS M M, LI Yancheng. Advancement in energy harvesting magneto-rheological fluid damper: a review[J]. Korea-Australia rheology journal, 2016, 28(4): 355–379. doi: 10.1007/s13367-016-0035-2 [17] 邓志党, 高峰, 刘献栋, 等. 磁流变阻尼器力学模型的研究现状[J]. 振动与冲击, 2006, 25(3): 121−126, 211. DENG Zhidang, GAO Feng, LIU Xiandong, et al. State-of-art research on dynamical, models of magnetorheological damper[J]. Journal of vibration and shock, 2006, 25(3): 121−126, 211. [18] SAVAIA G, PANZANI G, CORNO M, et al. Hammerstein-Wiener modelling of a magneto-rheological dampers considering the magnetization dynamics[J]. Control engineering practice, 2021, 112: 104829. doi: 10.1016/j.conengprac.2021.104829 [19] SOMIESKI G. Shimmy analysis of a simple aircraft nose landing gear model using different mathematical methods[J]. Aerospace science and technology, 1997, 1(8): 545–555. doi: 10.1016/S1270-9638(97)90003-1 [20] WANG Tiantian, YANG Long, LIU Qiang. Beetle swarm optimization algorithm: theory and application[J]. Filomat, 2020, 34(15): 5121–5137. doi: 10.2298/fil2015121w [21] 王坚浩, 张亮, 史超, 等. 基于混沌搜索策略的鲸鱼优化算法[J]. 控制与决策, 2019, 34(9): 1893−1900. WANG Jianhao, ZHANG Liang, SHI Chao, et al. Whale optimization algorithm based on chaotic search strategy[J]. Control and decision, 2019, 34(9): 1893−1900. [22] 陈秋鑫. 分数阶粒子群优化及其在聚类分析中的应用[D]. 镇江: 江苏科技大学, 2019. CHEN Qiuxin. Fractional-order particle swarm optimization and its application in clustering analysis[D]. Zhenjiang: Jiangsu University of Science and Technology, 2019.
