当今信息化作战条件下，充分利用战场信息资源、合理进行维修任务调度，影响着我军作战胜利使命的完成。首先，战时维修时间有限，我军需合理进行任务调度以快速恢复故障装备作战能力；其次，装备的研制也需要合适的调度，以减少费用^[1-2]；再次，战时维修任务时间紧迫，维修资源有限，如何在最短的时间内合理安排各工序的顺序，分配维修保障资源使得调度方案最优也是至关重要的^[3-4]。

1.   资源约束的任务调度

资源约束的维修任务调度涉及任务的分配，以解决由谁完成何种任务的指派问题。是装备保障实施的直观表现。装备保障任务调度流程复杂、约束众多，且涉及循环往复的不断优化，详情如图1所示。

图  1  装备维修任务调度基本流程及约束条件

Fig.  1  Basic process and constraints of equipment maintenance task scheduling

下载: 全尺寸图片

1.1   维修资源分类

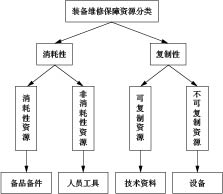
维修资源分配需要分类资源以便实际管理与后续研究。《军用装备维修基本术语》将维修保障资源表述为“人力、设备、备件、花费、技术、信息和工时的统一”^[4]。维修资源分消耗性资源和复制性资源，如图2所示。

图  2  装备维修保障资源分类图

Fig.  2  Classification chart of equipment maintenance support resources

下载: 全尺寸图片

1) 消耗性资源

主要包括维修设备、备件和技术材料等。

2) 非消耗性资源

指人力资源，如执行维修的技工和组织管理方案的人员。本文主要考虑技工。维修人力资源须有专业技能，如液压、机械等。且维修人力资源根据工作时长、学历等，可分为初、中、高级工。

3) 复制性资源

常指信息资源。维修产生的数据即为信息。

1.2   优先级评估

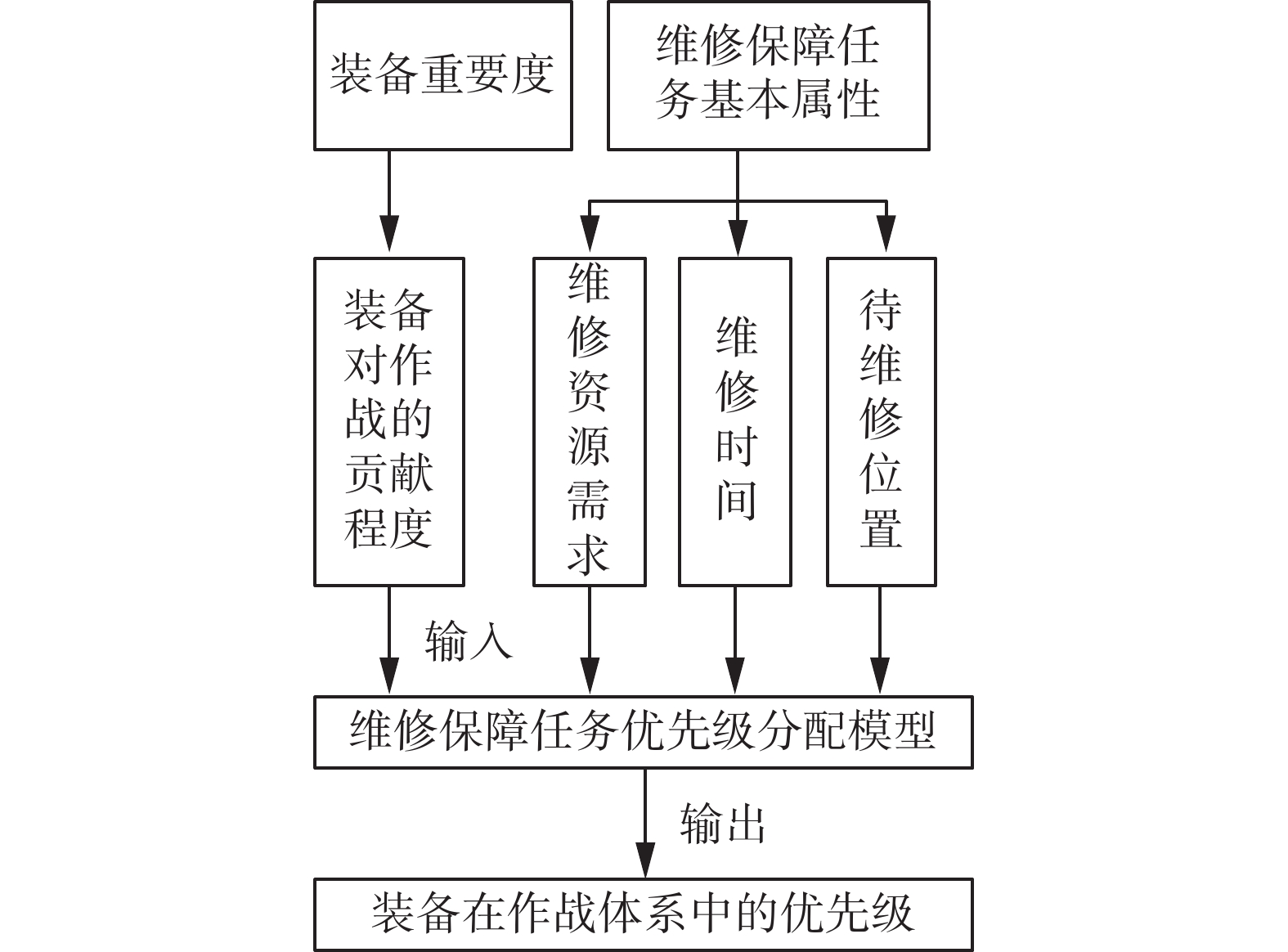
根据故障装备属性（如重要度，资源需求）及维修资源的有限性，需要为维修任务制定优先级。综合考量中外军事经验，得以下结论：战时装备作用大则先维修；故障装备易修复则先维修；耗时少则先维修；可修性好则先维修。故维修任务优先级评估指标如下^[5]：

1) 重要级别：根据作战功能大小得出；

2) 技术状态：采用技术状态系数评估；

3) 耗费工时：开始至完成维修的时间；

4) 所需设备：根据所需设备数及获取难度划分级别；

5) 所需技术：根据维修水平将所需技术划分；

6) 可维修性：采用可维修性系数评估。

优先级评估流程如图3所示。

图  3  任务优先级评估流程

Fig.  3  Task priority assessment process

下载: 全尺寸图片

1.3   维修调度模型

维修调度方案的合理性影响着维修的时效性，如缩短时间、增大效益等。陆军维修形式有自修、伴随修理、巡回修理、定点修理、战区后方修理等。野战时伴随、巡回、定点修理起至关重要的作用^[6]。

近年来，部分学者对维修任务调度进行了研究^[7]。模型方面，文献[8]研究了双目标排流车间调度问题，并采用NSGA-II算法求解；文献[9]提出了涉及剩余寿命的调度模型，采用改进遗传算法求解；文献[10]提出了鲁棒双目标混合整数线性规划模型，在不确定条件下同时最小化维修总成本和最大化任务总浮动；文献[11]在车辆正常运行的情况下，模拟车辆的周期维修，在给定的时间内安排维修任务，优化车辆运营、降低成本和提高服务可靠性；文献[12]提出了带重调度的维修方案，信息跟新后进行重调度；文献[13]利用混合粒子群遗传算法解决无人机装备军事维修任务调度问题；文献[14]提出了混合整数线性规划以优化列车运行维修延成文；文献[15]研究了任务优先级，改善马氏距离，并提出了逼近理想解排序法；文献[16]以优化维修重要度为目标，采用改进蚁群算法求解；文献[17-18]给出的方案可用于伴随维修；文献[19]利用采用离散事件仿真对定点维修任务调度求解。

1.4   动态调度算法

其中，因战时维修任务多、时间紧，维修部队赶至战损装备处的伴随维修，可参考动态车辆路径问题(dynamic vehicle routing problem, DVRP)或动态旅行商问题(dynamic traveling salesman problem, DTSP)以求解^[20]。

1) 静态化动态问题

目前研究成果常对动态调度静态化转换^[21]以求解。文献[22]分割调度时间，将动态车辆路径问题静态化；文献[23]对DVRP优化时间选择以静态化求解；文献[24]拆分DVRP为车辆选择及路线优化问题，并两阶段法数学规划求解；文献[25]动态调度多维修点、多任务、多维修队，划分时间保证任务优先级以实现静态化求解。

2) 静态问题算法

维修任务调度是NP-hard问题，需采用模拟退火、禁忌搜索等算法求解。模拟退火算法^[26]采用蒙特卡罗迭代求解，效果良好但收敛缓慢；禁忌搜索算法^[27]采用禁忌表避免重复搜索，对初始解敏感；遗传算法^[28]采用选择、交叉、变异算子对初始种群进行优化，搜索能力强但速度缓慢；人工智能方法采用智能系统动态优化，如神经网络^[29]、专家系统^[30]、蚁群算法^[31]、粒子群算法^[32]等。

综上，当前针对资源受限的任务调度问题研究仍存在以下问题：

1) 目前对于装备维修保障的研究与作战实践背景、任务装备重要度等结合不够紧密。

2) 装备维修保障任务种类多、需求大，在资源有限情况下，必须优先修复关键装备，故确定任务优先级是首要工作。现阶段对任务优先级的研究常忽略了装备重要度。

3) 信息化条件下，保障需求可及时传达，这对维修时效性要求更加苛刻。但现阶段任务调度常为静态问题，不能满足实际需求。

2.   工序调度

军用装备保障对象复杂、要素众多、环境多变。任务调度需要根据维修保障任务与资源的关系及任务间工序的关系，建立约束性规则，主要包括：

1) 资源充足前提下，任务才能开始；

2) 维修任务须按工序流程进行；

3) 正在使用的资源不得同时被任务占用，直到任务完成；

4) 维修任务独立，任务间互不影响。

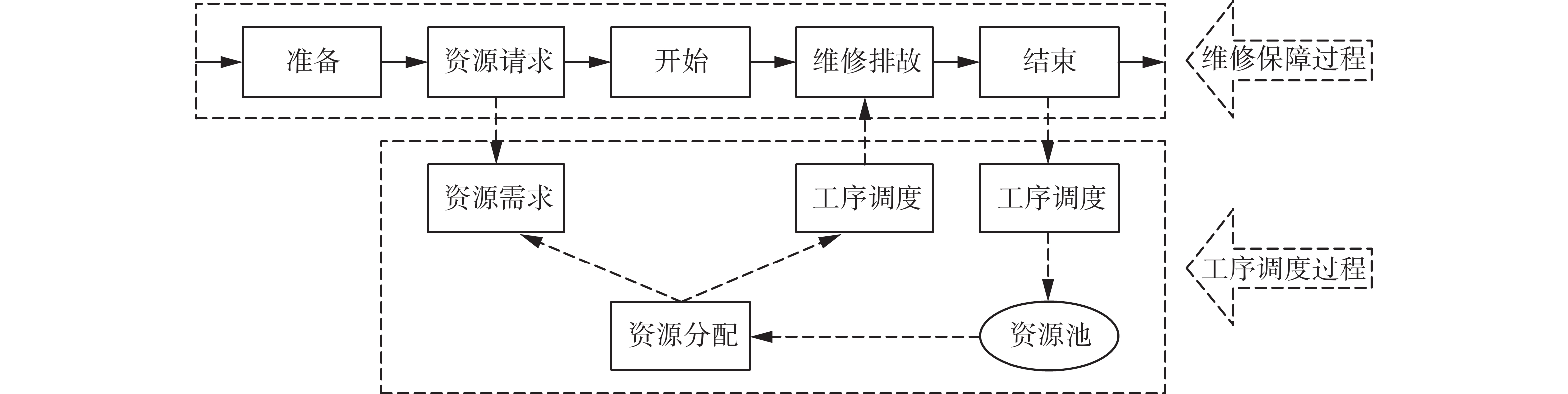
在最短时间内形成维修保障工序调度方案，可提升保障效能。维修时人员分配不当、维修调度不周等影响任务完工时间，资源受限工序调度诣在合理的安排工序调度以缩短工时、减少成本，可转化为资源受限项目调度问题(resource-constrained project scheduling problem, RCPSP)。

装备维修工序调度流程如图4所示。常见调度问题如下：

图  4  装备维修工序调度流程

Fig.  4  Equipment maintenance process scheduling process

下载: 全尺寸图片

2.1   RCPSP与PRCPSP

目前，RCPSP充分应用于各场景。此外，非抢占式RCPSP^[33]以及抢占式PRCPSP(preemptive resource-constrained project scheduling problem, PRCPSP)^[28]的应用取决于：该工序可否暂停，占用的资源被另一工序使用。研究表明，抢占可高度利用资源，减少闲置情况，从而减小工时。文献[33]对离散PRCPSP问题，在整数时刻对工序进行抢占，并分为一次抢占和多次抢占。

1) RCPSP

一个任务由 $n$ 个工序 $i = 1,2, \cdots ,n$ 组成，给定任务维修时间范围 $[0,T]$ ， $K$ 种资源中资源 $k$ 拥有量 ${R_k}$ ，工序 $i$ 需资源 $k$ 数量 ${r_{ik}}$ ，工序对资源的需求不大于该资源总量。工序 $i$ 维修时间 ${d_i}$ 。虚拟工序 $i = 0$ 和 $i = n + 1$ 表示任务的开始和结束，不占用维修时间和资源。工序 $i$ 开始时间 ${s_i}$ ，完成时间 ${c_i}$ ，则 ${s_i} + {d_i} = {c_i}$ 。假设工序不允许抢占。采用图 $G(V,E)$ 表示任务网络，工序集合为 $V = \{ 0,1, \cdots ,n + 1\} $ ，弧集合为 $E = \{ (i,j)|i,j \in V,i \to j\} $ ，表示工序 $i$ 是 $j$ 的紧前工序。工序 $i$ 紧前工序集合 ${\text{pre}}(i) = \{ j|(j,i) \in E\} $ ，工序 $i$ 的后继活动集合 ${\text{suc}}(i) = \{ j|(i,j) \in E\} $ 。RCPSP主要约束有时序和资源约束，最小化任务完成时间 ${C_{\max }} = {}_{i \in V}^{\max }\{ {C_i}\} $ 为优化目标^[34]。

RCPSP概念性模型为

${\text{s}}{\text{.t}}{\text{.}} $

其中：式(1)为目标函数；式(2)为工序时序约束；式(3)为资源约束；式(4)说明从时刻0开始维修；式(5)限制工序开始时间为非负整数。

2) PRCPSP

若允许抢占发生在整数时间点，则为离散抢占；若允许抢占发生在任意时间点，则称为连续抢占。

PRCPSP概念性模型为

${\text{s}}{\text{.t}}{\text{.}} $

其中：式(6)为目标函数；式(7)表示时刻0开始维修；式(8)为时序约束，工序 $i$ 的完成后工序 $j$ 开始；式(9)表示子工序的优先关系，子活动 ${i_{ip}}$ 结束后 ${i_{p + 1}}$ 开始；式(10)表示工序 $i$ 工时等于子工序工时之和；式(11)表示工序资源限制；式(12)表示子工序开始时刻和工时为非负整数；拆分工序 $i$ 的子工序 $p$ 开始时间 ${s_{ip}}$ ，工序工期 ${d_{ip}}$ 。

2.2   其他调度问题

1) 目标函数

经典的RCPSP数学模型是以工期最短为目标，但实际维修保障中，单一指标难以评价方案优劣，决策者常需考虑多个指标并进行权衡。

对于维修资源受限式维修工序调度问题，需要考虑的目标有以下几个：

① 最小化项目工期：

该式最小化最后虚拟活动的开始时间，等价于最小化项目工期^[35-36]。

② 最小化项目拖期：

该式最小化活动加权拖期之和，其中活动 $i$ 拖期严重程度 ${\beta _i}$ ，活动 $i$ 实际完成时间 ${f_i}$ ，计划交付时间 ${D_i}$ 。该目标适于有时间限制调度问题^[37]。

③ 资源均衡：

该式最小化资源使用量平方加权和。时刻 $t$ 需资源 $k$ 数量 ${u_{kt}} = \sum\limits_{i \in {V_t}} {{r_{ik}}} $ ，时刻 $t$ 正在执行活动集合 ${V_t} = \{ i|{s_{i,p}} \leqslant t \leqslant {s_{i,p}} + {d_{i,p}}\} $ 。资源均衡可确保资源利用稳定，是项目调度的重要目标^[38]。

④ 最小化资源可用量成本：

其中，活动中断成本 $z$ 。该目标函数增加了活动抢占成本^[39]。

2) 约束条件

对于工序调度，资源是非常重要的约束条件。装备维修保障资源分为可更新资源、消耗性资源以及双重资源。

1) 可更新资源在每个时刻的供应链是有限的，并不随维修保障的进度而消耗，例如人力、设备等。可更新资源约束表示：

对人力资源进行再进一步的划分，有不同维修作业对用的维修人员种类以及根据不同维修能力不同导致的维修时间不等将维修人员划分为不同等级：

2) 消耗性资源是在装备维修保障作业启动时以总量出现，并随着作业进展逐渐消耗的资源，例如各种原材料、能源等。消耗性资源的约束表示为

3) 时序约束：根据工艺要求限制工序顺序。如工序 $i$ 未结束，工序 $j$ 不开始。

2.3   常用算法

常用遗传算法、禁忌搜索等算法解决任务调度问题。这些算法需合理编码，产生随机方案集并不断筛选更新种群，以求解问题。

2.3.1   编码

1) 活动编码^[40]前部分表示子工序，后部分表示工序工时；

2) 资源编码^[41]表示工序维修在某时间内消耗资源量；

3) 优先级编码^[42]前部分表示子工序，后部分表示占用工时。

2.3.2   解码

调度方案(schedule generation scheme, SGS)有：

1)串行调度方案(serial SGS, SSGS)

SGS随工序展开而进行扩展^[43]，分为 $J$ 个阶段，阶段 $n$ 有对应不完全计划 ${\text{P}}{{\text{S}}_{{n}}}$ 和对应的可行工序集 ${E_n} = \left\{ {j|j \notin {\text{P}}{{\text{S}}_n},{P_j} \in {\text{P}}{{\text{S}}_n}} \right\}$ 。调度中新阶段 $n$ ，选择 ${E_n}$ 中某工序并入 ${\text{P}}{{\text{S}}_n}$ ，工序开始时间满足资源和紧前约束。设工序 $j$ 最晚开始时间 ${\text{S}}{{\text{T}}_j}$ ，在 $t$ 阶段，正在维修的工序集合 ${A_t}$ ，资源 $k$ 剩余量 ${R_{kt}}$ ，则有 ${R_{{{kt}}}}= {R_{{k}}} - \displaystyle\sum\limits_{j \in {A_t}} {{r_{jk}}}$ ，任务工期上限 $\overline D $ ，串行调度方案产生流程为

①　初始化　 $n: = 1{\text{,P}}{{\text{S}}_n}: = \left\{ 1 \right\},{\text{S}}{{\text{T}}_1} = 0$

②　当 ${\text{|P}}{{\text{S}}_n}| < j$ 时，对于每一阶段 $n$ ：计算 ${E_n}$ 和 ${R_{{{kt}}}}$ ， $t =1, 2, \cdots ,K$ ； ${j^*}{\text{:}} = {\text{mi}}{{\text{n}}_{j \in {E_n}}}\left\{ {j|v\left( j \right) = {\text{ma}}{{\text{x}}_{i \in {E_n}}}\left\{ {v\left( i \right)} \right\}} \right\} $ ； ${\text{E}}{{\text{S}}_{{j^*}}}{\text{:}} = {\text{max}}\left\{ {{\text{S}}{{\text{T}}_i}\; +\; {d_i}|i \in {p_{{j^*}}}} \right\}$ ； ${\text{S}}{{\text{T}}_{{j^*}}}: \;=\; {\text{min\{ }}t|{\text{E}}{{\text{S}}_{{j^*}}} \;\leqslant\; t \;\leqslant\; {\text{L}}{{\text{S}}_{{j^*},{r_{{j^*}k}}}} \leqslant {R_{kt}},\tau = t$ ， $t + 1,\;\cdots, t + {d_{{j^*}}} - 1,k = 1,\;2,\;\cdots,\;K{\text{\} }}$ ； ${\text{P}}{{\text{S}}_{n + 1}} = {\text{P}}{{\text{S}}_n} \cup \left\{ {{j^*}} \right\}$ ； $n: = n + 1$ 。

2)并行调度方案(parallel SGS, PSGS)

PSGS随时间进行扩展^[43]，包含 $J$ 个阶段，阶段 $n$ 调度时刻 ${t_n}$ 的3个工序集合：已完成工序 ${C_n}$ 、正在维修工序 ${A_n}$ 和可进行维修工序 ${E_n}$ ，满足： ${E_n} = \left\{ j|j \notin \left\{ {{C_n} \cup {A_n}} \right\},{P_j} \in {C_n}, {r_{jk}} \leqslant {R_{k{t_n}}},k = 1,2, \cdots ,K \right\}$ 。

并行调度方案产生从阶段 $n$ 到阶段 $n + 1$ 描述如下：

①　计算 ${t_{n + 1}}$ ， ${C_{n + 1}}$ ， ${A_{n + 1}}$ ，更新资源剩余量 $\pi {R_{kt}}$ 和 ${E_{n + 1}}$ ；

②　若 ${E_{n + 1}}$ 中的工序 $j$ 资源需求不超过资源剩余量，则执行 $j$ ，更新 ${E_{n + 1}}$ ，重复2)直至 ${E_{n + 1}}$ 为空。并行调度方案产生流程如下：

①　初始化：

$\begin{array}{l}n:=1,{t}_{n}:=0,{E}_{n}:=\left\{1\right\},{A}_{n}:{C}_{n}:=\varphi \end{array}$ ， ${R}_{k{t}_{0}}:={R}_{k},\;k= 1, 2,\cdots ,K$ 。

②　当 ${\text{|}}{{\text{A}}_n} \cup {C_n}| < J$ 时，对于每一阶段 $n$ ：

${t_n}: \;= \min \left\{ {{\text{S}}{{\text{T}}_j} + {d_j}|j \in {A_{n - 1}}} \right\}$ ， ${A_n}: \;={A_{n - 1}}\backslash \left\{ j|j \in {A_{n - 1}},\right. \left.{{\rm ST}_j} + {d_j} = {t_n} \right\}$ ， ${C_n}: = {C_{n - 1}} \cup \left\{ {j|j \in {A_{n - 1}},{{\rm ST}_j} + {d_j} = {t_n}} \right\}$ ，计算 ${R_{{{kt}}}}\left( {t = 1,\;2,\;\cdots,\;K} \right)$ 和 ${E_n}$ ； ${j^*}{\text{:}} = {\text{mi}}{{\text{n}}_{j \in {E_n}}}\left\{ j|v\left( j \right) = {\text{ma}}{{\text{x}}_{i \in {E_n}}}\right. \left.\left\{ {v\left( i \right)} \right\} \right\}$ ， ${{\rm ST}_{j*}}: = {t_n}$ ， ${A_n}: = {A_n} \cup \left\{ {{j^*}} \right\} $ ，计算R_kt(t=1, 2, ···, K)和E_n。

③　如果 ${{E}}_{n}\ne {空}$ ，继续执行②，否则 $n:=n+1 $

在解决问题方面，目前研究常建立多约束模型并利用启发式算法求解。但当前研究不能很好满足实际的RCPSP问题，文献[44]采用一种改进的离散布谷鸟搜索算法（IDCS）来解决RCPSP问题，将搜索空间划分为多个区域，每个子群体将专注于在其指定区域内搜索解决方案；文献[45]考虑到每个活动都有固定的持续时间和资源需求，将其建模为一个矩形块，其高度代表资源需求，宽度代表持续时间，将移动块序列解码为有效的时间表，根据每个区块如何从其初始位置移动到适当位置的情况，设计了4种移动模式，以最大限度地缩短项目的完成时间，并采用多智能体进化算法（MAEA）求解RCPSP问题；文献[46]通过在最大的分割次数和最小的连续执行周期的约束条件下，研究在离散时间点上分割活动的资源约束项目调度的并行调度方案产生流程问题；文献[47]通过将每个任务的处理时间被建模为其开始时间和特定退化日期的阶跃函数，利用改进的禁忌搜索算法进行求解，提出了基于问题特征的4种邻域结构和两种变异算子；文献[48]提出基于分散搜索的混合元启发式算法对工期最小资源约束项目调度问题求解；文献[49]提出基于蚁群的元启发式算法对考虑抢占惩罚的多技能资源约束项目调度问题求解；文献[50]提出两阶段优化算法对考虑人员能力差异的RCPSP求解；文献[51]研究了连续时间柔性资源配置的项目调度问题；文献[52]采用预处理和在线调度两阶段策略及两阶段局部搜索对项目时间随机的资源约束调度问题求解。

综上，在装备维修工序调度算法设计时，应当考虑以下两方面的因素：

在实际维修中，人员进行下一工序维修时需要切换时间，故可考虑带有惩罚时间的多次随机抢占方案在实际调度中的应用。

现有调度问题多以最小工期为单目标优化，但实际需考虑人员多技能、胜任力差异等问题，单一目标难以符合实际调度。

3.   结束语

现阶段的一体化作战信息系统，对取得优秀的装备维修效果具有重要意义。需要根据瞬息万变的战场情况及时更新信息，动态调度任务。目前任务调度研究存在以下问题：

1) 多数研究建立的是静态模型，或将动态模型转化为静态模型，但实际需动态的任务调度。

2) 多数研究针对定点维修调度问题，野战维修调度研究较少。

3) 对于维修任务的优先级确定也需要进一步结合战时具体情况进行分析。考虑的优化目标相对单一。

4) 对带有惩罚函数的抢占式维修工序调度问题没有很好地应用于军用装备维修保障系统内。

具体的研究方法和解决方案如下：

1) 实现平时、战时不同条件下的装备维修任务调度。

2) 单任务内部的工序调度问题需考虑备件、人员等因素，使其更加符合实际的调度问题。

3) 在抢占式的工序调度问题中，抢占的次数往往是固定的，可以将抢占次数设计为随机的，求解出最佳的抢占次数，使得抢占机制更加灵活，结果更加准确。

4) 目前所提出的任务调度算法有一定的局限性，不仅要考虑动态的调度算法，还需要将多种算法有效结合起来，使优化效果更加明显。

新时代情况下，我军装备维修调度研究急需符合实际情况。需不断探索对新型装备和技术，且根据平时、战时等情况分类研究。以合理资源分配、合理任务调度，提高保障效能。