Research status of multicenter maintenance task assignment
-
摘要: 目前战争形式发生变化，装备结构变得复杂，在作战环境多变、维修时间紧迫、维修资源有限等情况下，维修任务的合理分配显得越发重要。因此本文对多中心维修任务分配的研究现状进行了综述，总结现存的任务分配方法，以促进其进一步发展。本文首先对多中心维修任务分配问题进行了描述；然后，对基本概念进行了说明，对问题进行了分析；之后，对优先级排序、任务分配及路径规划常采用的模型与算法等进行了概述；最后，总结了当前研究的不足，并展望了未来发展的方向。Abstract: At present, the form of war is changing and the equipment structure is becoming complex. Under the circumstances of changing combat environments, low maintenance time, limited maintenance resources, and reasonable allocation of maintenance tasks are becoming increasingly important. Therefore, this study summarizes the research status of multicenter maintenance task allocation and discusses the existing task allocation methods to promote their further development. First, the problem of multicenter maintenance task assignment is described. Then, its basic concepts are discussed and related problems are analyzed. Next, the models and algorithms commonly used in priority sorting, task allocation, and path planning are summarized. Finally, the shortcomings of current research are summarized and prospects are discussed.
-
目前，战争模式趋于信息化，并演变成体系之间的对抗。由“单兵种作战”模式转变为“联合作战”“区域作战”模式，“面向装备”的维修保障转变为“面向作战区域”的维修保障，“型号保障”方式转变为“区域联合保障”方式，区域联合保障方式成为联合保障力量的基础。保障任务采用“模块化组合，积木式编组”。战时选择有效的保障模块有利于节约资源和提高效率[1]。
此外，装备维修保障是使故障装备恢复使用甚至高效运行的全部活动。一方面，指挥要根据作战要求落实指挥员意图；另一方面，指挥以行动为立足点。故在作战中，指挥起到了从需求转为行动的纽带作用。装备维修保障任务分配对指挥发挥职能与否也起到极其重要的作用。
故，有必要总结当前多中心维修任务分配研究的现状，分析存在的不足，以促进其今后的发展。
1. 问题描述
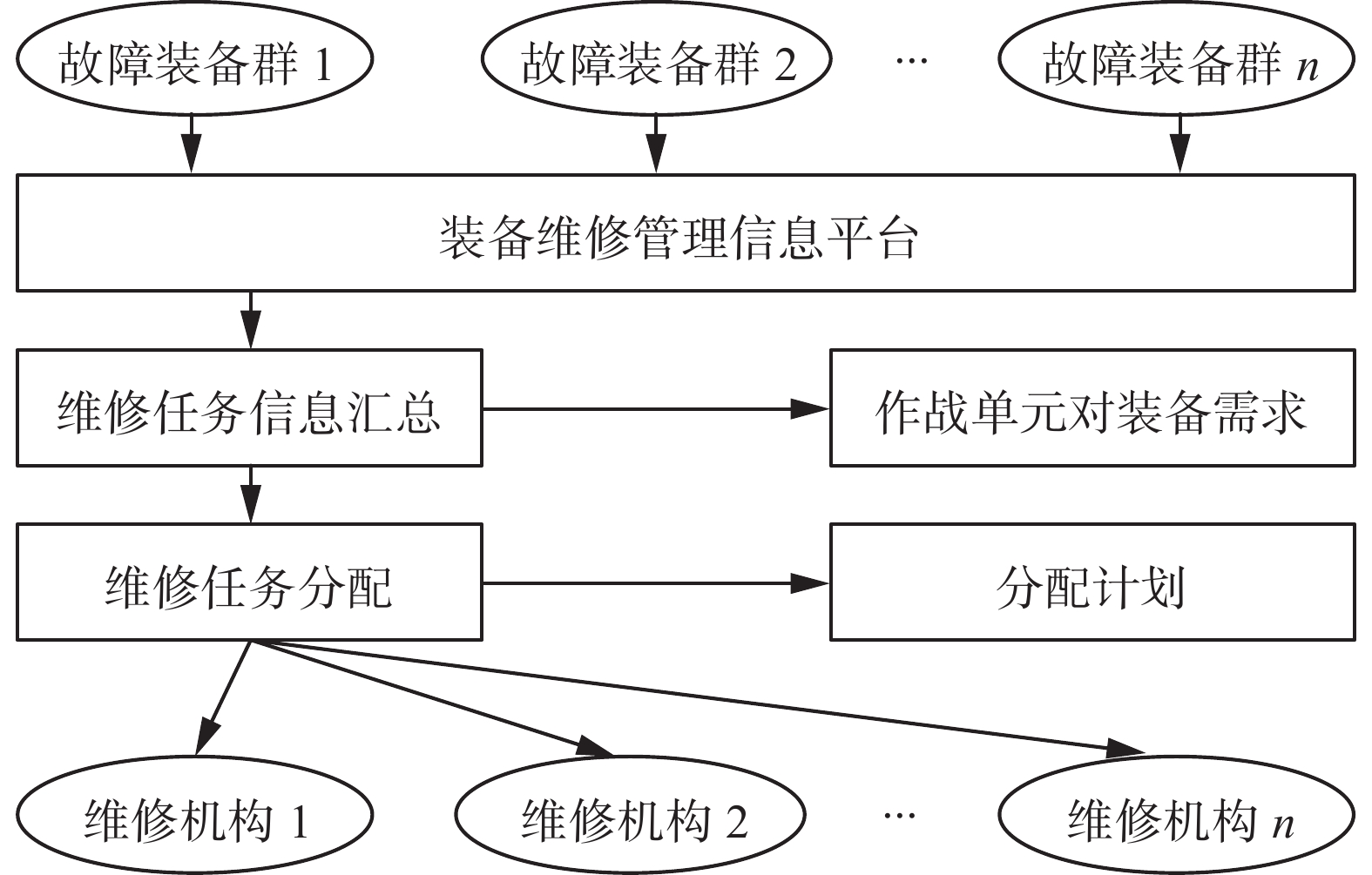
多中心维修任务分配问题是指在维修时间约束下，对任务优先级进行排序，并运用求解算法得出分配结果。详情如图1所示，任务分配框架如图2所示，任务分配功能如表1所示。
图 1 维修保障任务分配问题描述Fig. 1 Maintenance support task assignment problem description
下载:
全尺寸图片
图 2 多中心维修任务分配框架Fig. 2 Multi center maintenance tasks schedule framework下载:
全尺寸图片
表 1 任务分配功能描述Table 1 Task assignment function description功能名称 子功能名称 功能描述 状态更新 维修任务产生流程触发的状态更新 由产生自然故障维修任务和产生战损维修任务流程产生的
功能系统、装备和最小作战单元的状态更新任务管理成员触发的状态更新 在任务管理成员触发的阶段任务开始、阶段任务成功
和下个任务阶段不能开始信息下触发的功能系统、装备和最小作战单元的状态更新营组负责人触发的状态更新 营组负责人收到修复装备触发的功能系统、
装备和最小作战单元的状态更新产生自然故
障维修任务确定任务阶段第一次自然
故障维修任务发生时刻阶段任务开始时确定初始自然故障维修任务发生时刻的活动 产生自然故障维修任务并抽样下
次自然故障维修任务发生时刻最小任务单元根据自然故障维修任务
产生模型和非初始自然故障维修任务产生战损
维修任务确定战损维修任务发生时刻 任务阶段开始后确定本阶段战损维修任务发生时刻 抽样确定战损维修任务 抽样所有的战损维修任务和战损维修子任务 2. 问题分析
2.1 任务分类
任务常指分配的工作，担任的责任。在军事领域中，任务均具有军事目的。根据任务目的的不同，任务可以分为使命任务和行动任务。使命任务一般指比较重大的责任，而行动任务相对具体、细微。
根据任务时机的不同，任务可以分为训练任务和作战任务。按照新版《中国人民解放军军语》的定义，训练任务是指军事训练所要完成的任务，训练任务通常由参训兵力、训练内容、训练时间和质量指标等构成；作战任务是指作战力量为达成预定作战目的而担负的任务，由上级指挥员确定，并以作战命令的形式下达。
使用任务是指面向保障需要能够反映出作战单元构成装备的使用行为的作战行动。与一般的作战任务和作战行动相比，使用任务更为细致地描述了执行任务的每一个装备的使用过程和行为活动，并由此可与每一个装备的保障需求结合起来，而这是在保障方案制定中必须要了解的。
2.2 任务优先级排序
装备维修任务的优先级是指给定的优先等级。它决定维修任务得到维修相应及占用资源的优先次序，这主要与任务本身属性和调度算法有关。特别在实时系统中，任务优先级反应了任务的重要性与紧迫性。
任务分配中的优先级是基础，任务优先级越高须越先分配；资源分配是一个中间角色，可以合理分配资源以保证维护任务的顺利进行；任务调度是关键，可快速响应实时需求。为了使装备维修保障顺利进行以满足作战需要，优先级分类、分配和调度的合理性皆是必需的。
2.3 任务分配
合理分配任务是维修保障的前提，可充分发挥保障的力量。装备维修中的任务分配问题一般是指，为了在作战中恢复作战部队的战斗力，必须首先按照一定的机制为故障装备分配一个或多个维修机构，以充分利用保障资源，尽快恢复战斗力。无需强调维修任务的前后顺序，只考虑在哪个机构维修。
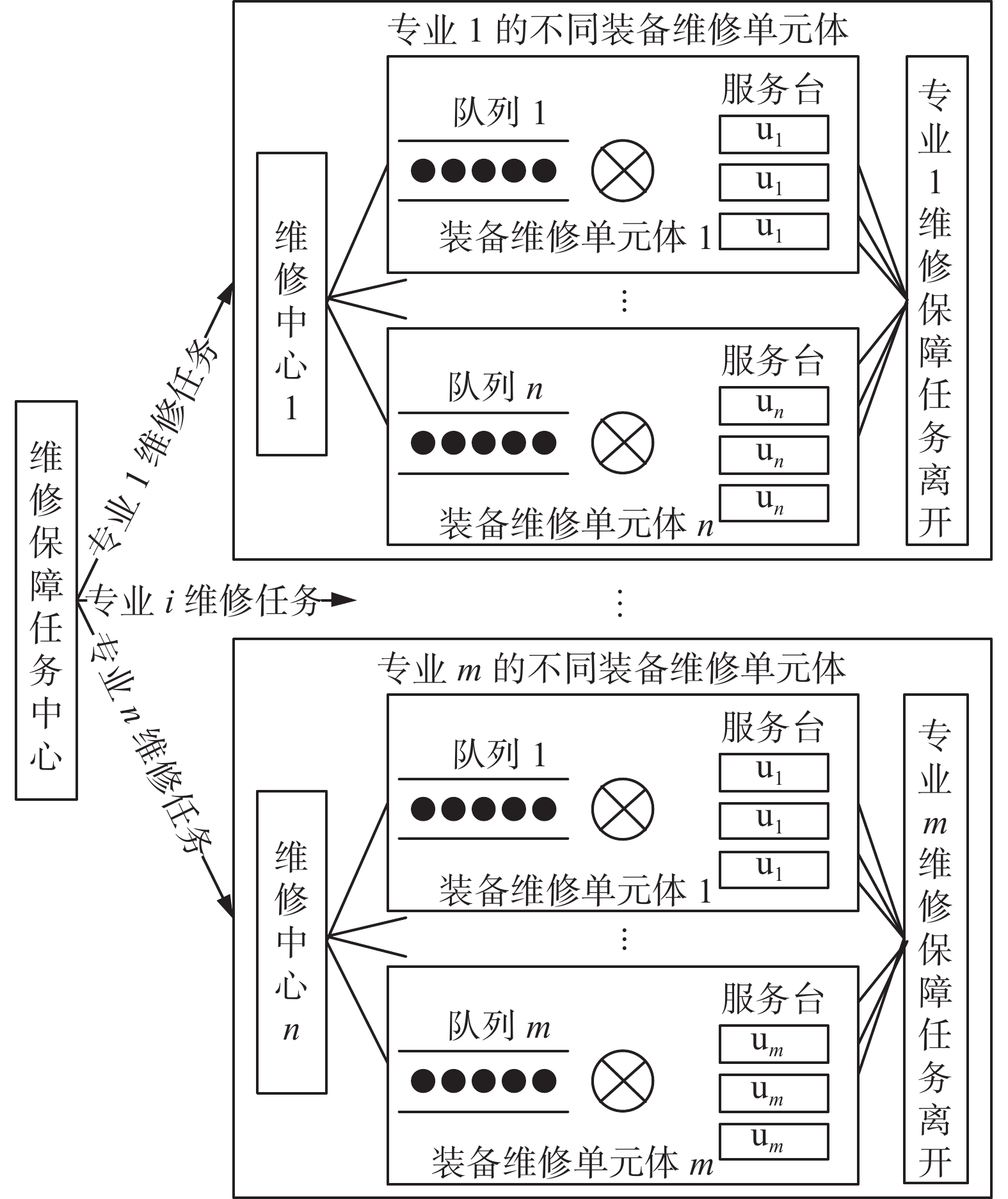
任务分配过程中，每时间段、每作战区域的每个作战单元可能出现多个故障，将其反馈到信息管理中心，并对维修需求进行汇总筛选，综合考虑维修机构负载能力、资源等因素，以及考虑故障装备受维修时间、成本、环境等影响，制定并下发维修分配计划，使维修效益最大化。维修效益指维修效果与所耗资源之比。维修分配流程如图3所示，各专业的不同装备维修单元体维修详情如图4所示。
图 3 维修任务分配流程Fig. 3 Maintenance task allocation process下载:
全尺寸图片
图 4 各专业的不同装备维修单元体维修示意图Fig. 4 Maintenance schematic diagram of different equipment maintenance units of different majors下载:
全尺寸图片
3. 模型与算法
3.1 优先级排序
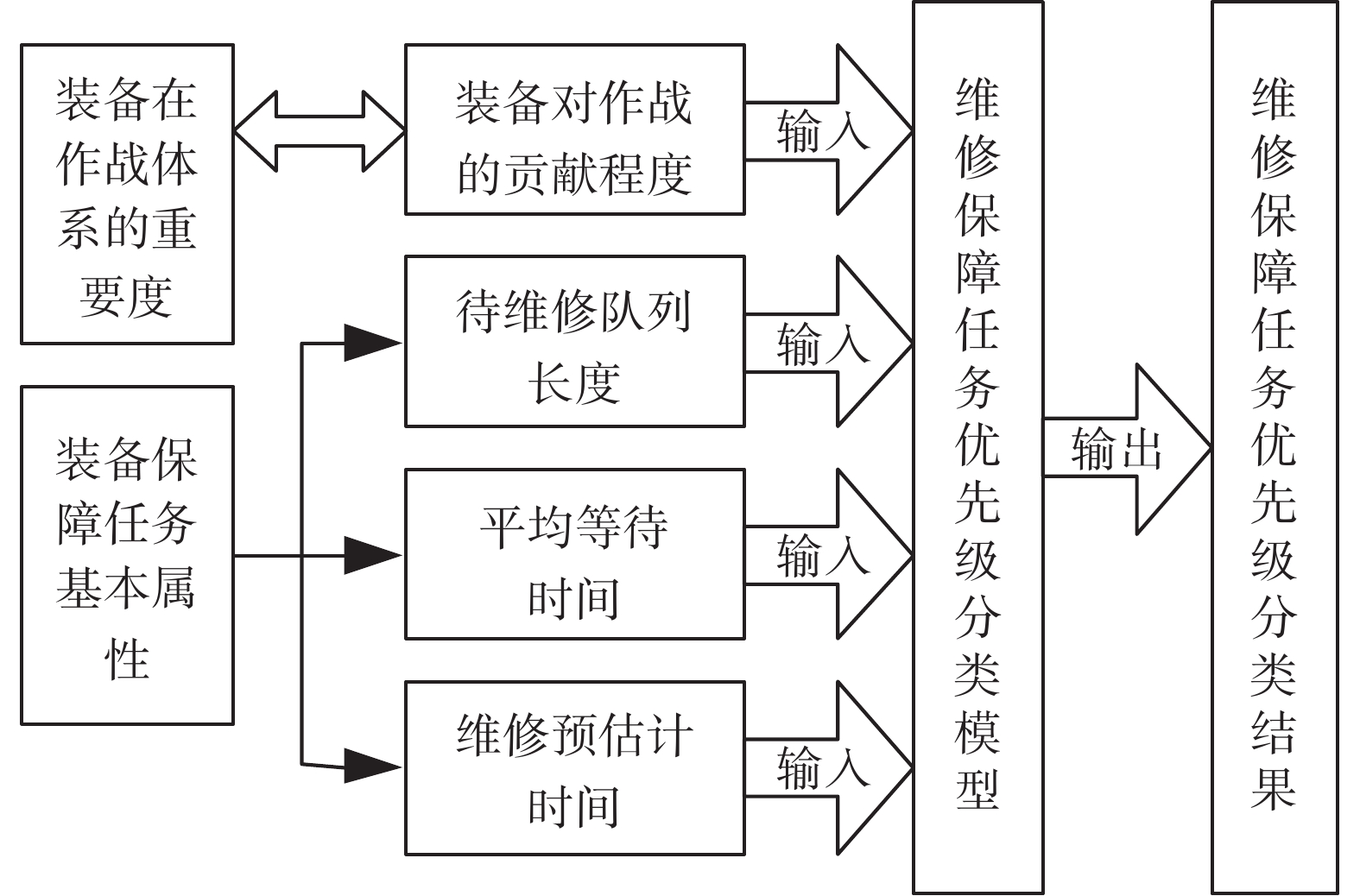
维修任务确定后，明确了资源需求和维修时间。在战斗系统中装备重要度体现在对战斗的贡献，其详情如图5所示。
任务优先级分类基于损坏级别。曾拥华等[2]分析了这一问题，战场损伤评估的流程基本由此确定。文献[3]构建并验证了战场损伤等级评价模型。然而，如果不考虑受损装备对作战的贡献，维修任务的重要性就无法得到充分的体现。通过引入装备作战贡献，推导出优先级分类模型。目前研究很少有涉及这一问题的，文献[4]以ELECTRE TRI评估了维修任务的优先级。
图 5 优先级分类Fig. 5 Priority classification下载:
全尺寸图片
多属性决策考虑各种相关属性，排序并选择令人满意的方案。研究的重点是确定指标的权重及排序的方案。
3.1.1 指标权重
确定指标权重方法：主观赋权法、客观赋权法、主客观组合赋权法和交互赋权法[5]。
1) 主客观赋权法以问卷或专家打分的数据获取到指标权重，如层次分析法[6]、D-S证据理论[7]、德尔菲法[8]等。近年优化赋权结果采用了AHP和灰色模糊结合[9]、D-S证据和灰色关联度结合[10]的混合主观方法。其优点是流程简单、对数据要求低，缺点是在赋权过程中缺乏统一原则且伴有大量的主观干扰。
2) 挖掘数据内在特征获取指标定量权重的客观赋权法包括主成分分析[11]、熵权法[12]、目标规划[13]等。其优点是权重根据已有数据得到，客观准确；缺点是对数据要求较高。
3) 主客观组合赋权法结合上述两种方法，充分发挥各自优势，如熵权法和AHP结合[14]、AHP和主成分分析结合[15]，效果良好。
4) 决策中的交互赋权法会根据信息更新调整指标权重[16]。
3.1.2 排队论
有许多排序方法可供选择，其适应条件一般不尽相同。可根据具体研究内容选择合适的方法，例如模糊综合评判法[17]、TOPSIS[18]、投影法[19]、ELECTRE[20]等。然而，在排序的过程中面临着新需求的出现与旧需求的满足，故涉及排队论。
排队论起源于电话通信。丹麦数学家A. K. Erlang在1909年研究了随机需求导致非稳态队列的问题。其后，他进一步发现了自动电话通信系统可以以两种基本概率模型模拟：泊松输入，指数分布服务时间，多服务流；泊松输入，稳定常态服务时间，单服务流。Erlang亦提出队列稳态平衡的概念与排队系统的初步优化办法。排队论源自对实际现象的研究，而后接近半个世纪，排队论主要针对理论进行研究(生灭理论，嵌入马尔可夫模型)。直到二战以后，学者开始为该理论赋予应用价值，大量研究开始导向如何精确求解先前学者留下的复杂数学模型，并直接应用于现实的管理决策中。例如：复杂排队模型，排队网络的近似解与数值模拟办法等。近现代排队论主要为管理决策软件的开发提供理论与模拟支持。
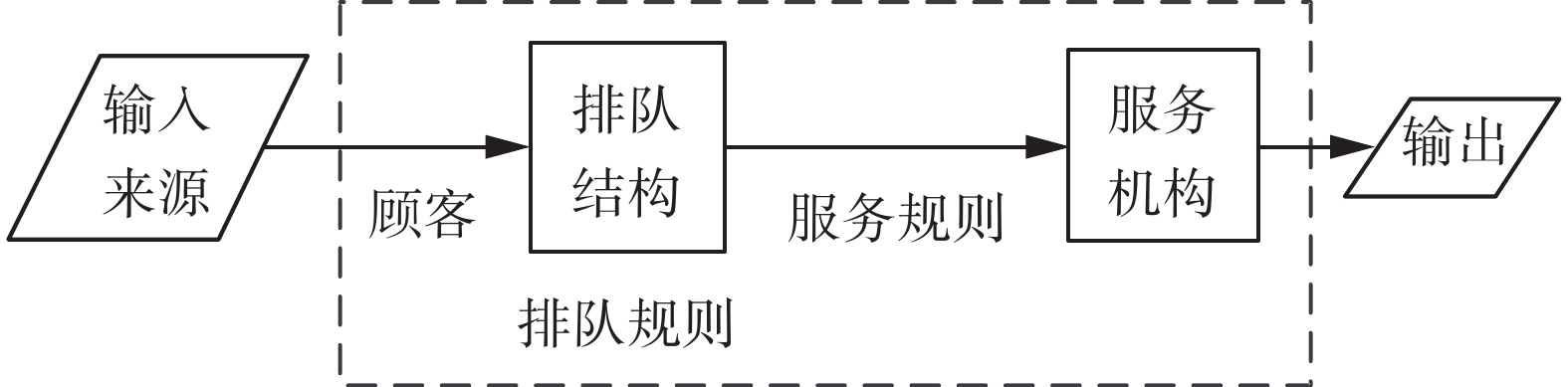
随机服务系统对服务时间进行统计研究，根据规律对服务系统进行重构，使其满足服务需要，成本又尽可能小等。排队系统在生活中一般非常复杂，常包括输入、排队和服务，如图6所示。顾客的到达称为输入，离开即为输出，顾客到达和系统服务时间常假设服从定长分布、负指数分布、几何分布[21-22]。
图 6 排队过程Fig. 6 Queuing process下载:
全尺寸图片
1) 输入过程：可采用某时间内顾客到达数或相邻两顾客到达的时间间隔来考察顾客到达系统的规律。一般有确定型和随机型。当时间
$ t $ 内到达顾客数$ n(t) $ 随机即为随机型输入，且根据统计可能服从某一分布。若服从泊松分布，时间$ t $ 内到达顾客$ n $ 的概率为$ {P_n}(t) = {{\text{e}}^{ - \lambda t}}{(\lambda t)^n}/n!\left( {n = 0,1,2, \cdots ,N} \right) $ ；若相邻顾客到达时间间隔服从负指数分布，则有$ P\left( {T \leqslant t} \right) = 1 - {{\text{e}}^{ - \lambda t}} $ ，其中$ \lambda $ 为顾客平均到达率，$ 1/\lambda $ 为相邻顾客的平均时间间隔。2) 排队规则：等待制、损失制和混合制最为常用。服务机构忙且顾客等候为等待制。服务机构忙顾客离去即为损失制。服务次序有先(后)到先服务、服从优先权服务等模式。
3) 服务机构：多个服务台平行或串联布置(也可一个服务台服务)。服务时间有确定型和随机型。
对排队论的研究常关注服务的效率、质量。排队系统评价指标如下：
1) 系统负载
$ \rho $ ：服务能力的度量。2) 系统空闲概率
$ {P_0} $ ：无顾客请求的概率。3) 队长：系统内等候和正在接受服务的客户数，均值为
$ {L_s} $ 。4) 队列长：等候接受服务的客户数，均值
$ {L_g} $ 。5) 逗留时间：一个顾客等候和接受服务时间的和，均值
$ {W_s} $ 。6) 等候时间：一个顾客的等候时间，均值
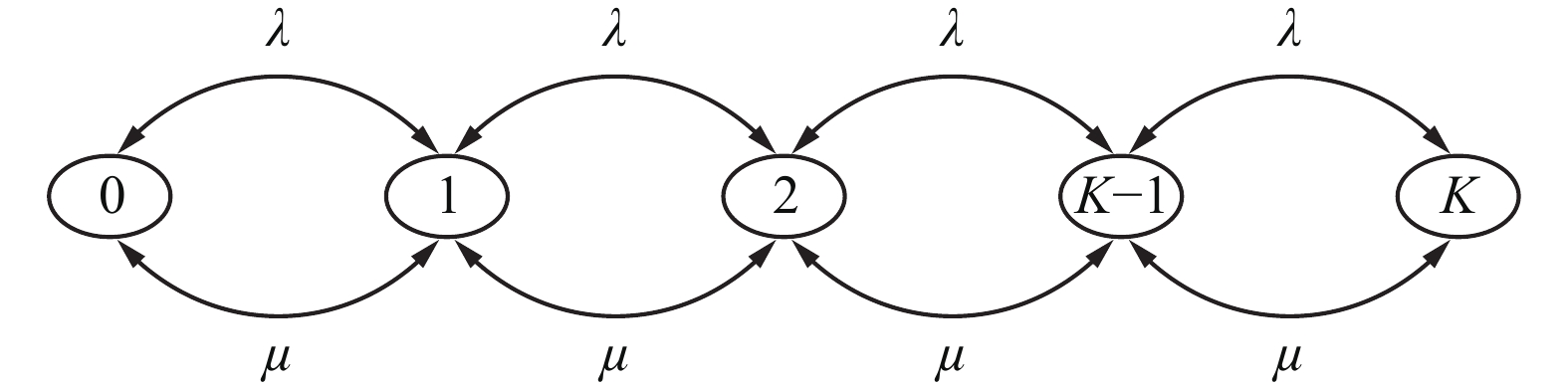
$ {W_g} $ 。系统的各项指标可由状态转移速度推算出来，如图7所示。
图 7 状态转移速度图Fig. 7 State transition velocity diagram下载:
全尺寸图片
M/M/1排队系统是最简单的排队系统，如表2所示。
表 2 M/M/1排队系统的指标Table 2 Indicators of the M/M/1 queuing system指标 $ \rho $ $ {P_0} $ $ {L_s} $ $ {L_g} $ $ {W_s} $ $ {W_g} $ 计算公式 $\dfrac{\lambda }{\mu }$ $1-\dfrac{\lambda }{\mu }$ $\dfrac{\lambda }{ {\mu -\lambda } }$ $\dfrac{ { {\lambda ^2} } }{ {\mu -\lambda } }$ $\dfrac{1}{ {\mu -\lambda } }$ $\dfrac{\lambda }{ {\mu \left( {\mu -\lambda } \right)} }$ 3.1.3 排队系统其他分类
1) 按故障特性分类
实际上完全可靠的服务系统是不存在的。按故障类型可分如下两类：
①完全故障：服务台故障时服务完全停止。
②不完全故障：服务台故障时低效服务。
此外，根据维修时间不同可分如下两类：
①即刻维修：故障后即刻维修。
②延迟维修：故障后等候维修时间随机。
Bruneel等[23-25]在经典的排队模型中考虑了故障特性。从经济学角度来看，排队系统始于2008年，Economou等[26]最早考虑了完全失效可修排队系统，根据排队长度决定是否加入的顾客均衡阈值策略由此给出。Li等[27]拓展了文献[26]，分析了不可见情况。Li等[28]关于排队系统通过对不完全故障即时维修的研究，获得了在顾客完全(不)可见排队的进入策略。Yu等[29]丰富了文献[28]成果，研究几乎(不)可见的不完全故障顾客的排队策略。Xu等[30]通过研究不完全故障延迟维修的M/M/1，考虑完全(不)可见时顾客的止步策略和平均收益。Yang等[31]研究了Geo/Geo/1队列中存在服务器故障和维护的顾客均衡行为。Boudali等[32-33]考虑有灾难的M/M/1，灾难时顾客离开系统，至服务台完成维修，采用纳什均衡策略决定新顾客接受与否。
2) 根据多类顾客分类
如优先权顾客、不耐烦顾客等存在于排队系统中，排队系统将由此变得更加难以分析。马占友等[34-35]研究了不同优先权顾客。Yang等[36-37]研究了可抵消正顾客和负顾客。刘楠[38]研究了不耐烦顾客。Balachandran[39]最早研究了优先权M/M/1，得到顾客的支付数可提高其的优先级。Adiri等[40-41]研究了两类不同优先级排队，获取了均衡进队纯阈值等策略。Lillo[42]在M/G/1中考虑不同优先级排队，获得了两个阈值的最佳控制策略。Sun等[43]研究的排队系统具有不同费用函数，在绝对优先时得到了最佳策略。Xu等[44]分析了不可见条件下具有抢占优先权顾客的M/G/1顾客均衡和全局最佳策略。
3)带启动时间的服务
启动过程是无服务时关闭服务台，服务请求开始时，经一随机启动时间恢复服务。Choudhury等[45-49]在经典的排队模型中引入了启动期的研究。排队论2007年引进了启动时间，Burnetas等[50]最早对其进行了研究，均衡分析已得可见(不可见)情况的顾客均衡排队策略和平均收益。Sun等[51-52]以马尔可夫过程和差分方程求解，分析了系统信息(不)可见情况下带有启动关闭的的队列进入策略。Zhang等[53]进一步推广了M/G/1排队系统，分析了系统信息可见情形下的均衡进队概率。Hao等[54]研究了单服务台具有启动时间，考虑了系统的阈值和完全故障。
3.2 任务分配
3.2.1 典型模型、算法概述
维修任务分配中应明确任务分工和执行路径，制订维修计划。分配时应考虑维修人员、维修能力及时间约束。
Choudhury等[55]在生产中为改善任务分配的合理性引入了柔性，并在调度中为实现优化引入了遗传算法。Yu等[56]协同无人机研究任务分配，提取有效信息以实现动态分配；Gopalakrishnan等[57]指出任务分配、复杂程度、维修能力之间存在相关性；Macedo等[58]分析了机械、电子等预防性维修的任务分配，建立了基于维修的任务分配模型，但修复性问题尚未解决；薛桂香[59]将多任务动态分配视为NP组合优化问题，提出了动态遗传算法，并根据网络系统服务节点计算能力及负载进行了动态任务分配；Shi等[60]结合蚁群、蝙蝠、狼群算法对多无人机进行了任务分配；Jia等[61]基于遗传算法对异物无人机进行了任务分配；Keiser等[62]首创并使用多维列表规划来获取任务之间的匹配方案，从而更好地全局最优化任务分配的解；Khouadjia等[63]结合DAPSO算法、VNS算法对动态的需求问题进行了车辆送货的任务分配。
Jia等[64]设计并应用了一个计算机辅助系统来解决军械维修中的任务分配，但没有对典型案例进行分析。Yuan等[65]关于任务分配构建了模型，并以蒙特卡洛法研究了石油装备维修。李龙跃等[66]对多波目标分配反导进行了研究，关于分配导弹-目标的模型由此建立，但未考虑不确定性与可靠性等因素。曾家友等[67]对分配舰载导弹的目标进行了研究，考虑了价值收益、效费比优先级排序等问题；Yang等[68]在遗传算法中引入随机移民、二元论等，可用于动态任务分配问题。
3.2.2 常用典型算法简介及对比
局部搜索算法是一种重要的求解组合优化问题的启发式算法，由于简单且易于理解，其已受到越来越广泛的重视。常见有2-Opt、2-Opt*等[63]。
模拟退火算法的思想最早由Metropolis等于1953年提出，后由Krikpatrick[69]于2002年第一次用于求解组合优化问题。此算法以一定概率选择邻域中的劣质解以克服其他算法易陷入局部最优的缺陷和对初值的依赖。
20世纪60年代，Holland[70]提出了遗传算法，随机生成初始种群，通过选择、交叉、变异产生更适应环境的个体以得到优化解。我国遗传算法从20世纪末开始研究且迅速膨胀。罗雄等[71]对遗传算法解决柔性作业、车间调度问题进行了综述。刘国强[72]根据任务分配特点，采用多目标遗传算法解决了维修任务分配问题。
上述启发式算法对比如表3所示。
表 3 启发式算法间的对比Table 3 Comparison of heuristic algorithms算法 搜索策略 影响因素 适应范围 局部搜索算法 在当前解邻域中搜索其他解，若更优则替换当前解，
重复搜索。受初始解、邻域等因
素影响。局部搜索能力、求精
能力强。模拟退火算法 采用Metro-polis原则，以冷却参数控制算法进程，可以在多项式时间内找到近似解。 受初始解、Metro-polis接受原则影响。 局部搜索能力、全局搜索
能力强。遗传算法 通过群体的遗传(选择、交叉、变异)实现进化性探索。 受遗传策
略的影响。全局搜索
能力强。3.3 路径规划
维修任务分配确定任务承担者，路径规划确定完成路径。任务划分是维修任务分配的基础，路径规划是其重点。维修任务规划是寻找最佳分配方案的问题。二者相互结合，相互影响，共同决定分配的最终结果。
装备维修任务路径规划可抽象为车辆规划最短路线遍历所有目标点的问题，此即为车辆路径问题(vehicle routing problem, VRP)。VRP随约束的增加而发展。文献[73]研究了有车辆负载能力上限约束的VRP问题。文献[74]研究了电动车辆的VRP，考虑电容量的约束，并将规划结果与燃油汽车进行了对比。文献[75]详细分析了VRP中的最优速度、垃圾倾倒、长距离运输问题，区分了时间安排原则。文献[76]考虑了无冲突VRP以解决后勤运输路径规划的冲突和死锁问题。文献[77]对多配送中心动态VRP给予了优化，采用智能优化可解决VRP这种NP问题。文献[78]使用改进遗传聚类解决了多中心配送VRP问题。文献[79]使用并行模拟退化来解决同时发送和取货的VRP问题。文献[80]采用变邻域下降算法来求解两级VRP问题。文献[57]使用混合遗传算法来解决存在车辆租借、共享等条件的多个中心配送的VRP问题。并行运算、可全局搜索的蚁群算法衍生出了混合蚁群算法[81]、量子蚁群算法[82]、蚁群系统[83]和最大–最小蚂蚁系统(max-min ant system, MMAS)[84]等。解决离散时间最佳路径规划的方法——MMAS可进一步改进。VRP和装备维修任务路径规划问题均选择最佳路径以实现某一目标，但是又存在一定差异：
1) 决策目标不同：VRP追求路径(时间)最小化，任务路径规划则追求维修效益最大化。
2) 约束条件不同：VRP及其衍生问题多以车辆的载重、最大航程、存储容量等为约束，且此问题中车辆一般要经过所有服务点；而任务路径规划是解决作战时维修的问题，不必接受所有维修任务。
4. 结束语
综上所述，已有的工作对维修任务分配问题进行了深入研究，但在装备维修任务分配的模型和算法方面还存在一定的不足，有待进一步开展，具体表现如下：
1) 目前关于装备维修任务分配的研究甚少，装备维修保障任务品种多、约束多，资源有限时，能使系统体系平稳运行的装备优先修复。现研究常忽略待修装备作战贡献值，即便有部分研究，也是针对优先级的定性排序，应同时考虑多因素以定量研究任务优先级。
2) 战争逐渐趋于信息化，未来作战空间更大。在动态作战环境下，及时合理分配维修任务，充分发挥保障系统效能，是维修保障任务分配的迫切需求与发展方向。
-
图 1 维修保障任务分配问题描述
Fig. 1 Maintenance support task assignment problem description
下载:
全尺寸图片
图 2 多中心维修任务分配框架
Fig. 2 Multi center maintenance tasks schedule framework
下载:
全尺寸图片
图 3 维修任务分配流程
Fig. 3 Maintenance task allocation process
下载:
全尺寸图片
图 4 各专业的不同装备维修单元体维修示意图
Fig. 4 Maintenance schematic diagram of different equipment maintenance units of different majors
下载:
全尺寸图片
图 5 优先级分类
Fig. 5 Priority classification
下载:
全尺寸图片
图 6 排队过程
Fig. 6 Queuing process
下载:
全尺寸图片
图 7 状态转移速度图
Fig. 7 State transition velocity diagram
下载:
全尺寸图片
表 1 任务分配功能描述
Table 1 Task assignment function description
功能名称 子功能名称 功能描述 状态更新 维修任务产生流程触发的状态更新 由产生自然故障维修任务和产生战损维修任务流程产生的
功能系统、装备和最小作战单元的状态更新任务管理成员触发的状态更新 在任务管理成员触发的阶段任务开始、阶段任务成功
和下个任务阶段不能开始信息下触发的功能系统、装备和最小作战单元的状态更新营组负责人触发的状态更新 营组负责人收到修复装备触发的功能系统、
装备和最小作战单元的状态更新产生自然故
障维修任务确定任务阶段第一次自然
故障维修任务发生时刻阶段任务开始时确定初始自然故障维修任务发生时刻的活动 产生自然故障维修任务并抽样下
次自然故障维修任务发生时刻最小任务单元根据自然故障维修任务
产生模型和非初始自然故障维修任务产生战损
维修任务确定战损维修任务发生时刻 任务阶段开始后确定本阶段战损维修任务发生时刻 抽样确定战损维修任务 抽样所有的战损维修任务和战损维修子任务 表 2 M/M/1排队系统的指标
Table 2 Indicators of the M/M/1 queuing system
指标 $ \rho $ $ {P_0} $ $ {L_s} $ $ {L_g} $ $ {W_s} $ $ {W_g} $ 计算公式 $\dfrac{\lambda }{\mu }$ $1-\dfrac{\lambda }{\mu }$ $\dfrac{\lambda }{ {\mu -\lambda } }$ $\dfrac{ { {\lambda ^2} } }{ {\mu -\lambda } }$ $\dfrac{1}{ {\mu -\lambda } }$ $\dfrac{\lambda }{ {\mu \left( {\mu -\lambda } \right)} }$ 表 3 启发式算法间的对比
Table 3 Comparison of heuristic algorithms
算法 搜索策略 影响因素 适应范围 局部搜索算法 在当前解邻域中搜索其他解，若更优则替换当前解，
重复搜索。受初始解、邻域等因
素影响。局部搜索能力、求精
能力强。模拟退火算法 采用Metro-polis原则，以冷却参数控制算法进程，可以在多项式时间内找到近似解。 受初始解、Metro-polis接受原则影响。 局部搜索能力、全局搜索
能力强。遗传算法 通过群体的遗传(选择、交叉、变异)实现进化性探索。 受遗传策
略的影响。全局搜索
能力强。 -
[1] 张守玉, 刘兵, 张炜. 美军“21世纪远征后勤”转型对我军装备保障改革的启示[J]. 装备学院学报, 2016, 27(6): 12–15. doi: 10.3783/j.issn.2095-3828.2016.06.003 ZHANG Shouyu, LIU Bing, ZHANG Wei. Enlightenments of transformation of USArmy’s 21st century expedition logistics for the PLA’s equipment support reform[J]. Journal of equipment academy, 2016, 27(6): 12–15. doi: 10.3783/j.issn.2095-3828.2016.06.003 [2] 曾拥华, 严骏, 冯柯, 等. 装备战场损伤等级评定系统分析与设计[J]. 兵工学报, 2005, 26(4): 531–534. doi: 10.3321/j.issn:1000-1093.2005.04.022 ZENG Yonghua, YAN Jun, FENG Ke, et al. Analysis and design of assessment system for damage degree of equipment on battlefield[J]. Acta armamentarii, 2005, 26(4): 531–534. doi: 10.3321/j.issn:1000-1093.2005.04.022 [3] 赵英俊, 宋文焦, 段楠楠, 等. 地空导弹装备战场损伤等级的综合指标评判[J]. 火力与指挥控制, 2011, 36(1): 108–110,117. doi: 10.3969/j.issn.1002-0640.2011.01.028 ZHAO Yingjun, SONG Wenjiao, DUAN Nannan, et al. The comprehensive index judgement to the battlefield damage level of the ground to air missile equipment[J]. Fire control and command control, 2011, 36(1): 108–110,117. doi: 10.3969/j.issn.1002-0640.2011.01.028 [4] 刘俊杰, 吕学志, 曲长征. 基于ELECTRE TRI的维修任务优先级分类方法[J]. 火力与指挥控制, 2012, 37(S1): 18–21,24. LIU Junjie, LYU Xuezhi, QU Changzheng. A priori ty sorting approach of maintenance task during mission based on ELECTRE TRI[J]. Fire control and command control, 2012, 37(S1): 18–21,24. [5] 张仕新, 昝翔, 李浩, 等. 状态维修关键技术及应用的研究现状与展望[J]. 兵工自动化, 2014, 33(10): 15–21. doi: 10.7690/bgzdh.2014.10.005 ZHANG Shixin, ZAN Xiang, LI Hao, et al. Research status and prospect of condition-based maintenance key technology and application[J]. Ordnance industry automation, 2014, 33(10): 15–21. doi: 10.7690/bgzdh.2014.10.005 [6] RACIOPPI V, MARCARELLI G, SQUILLANTE M. Modelling a sustainable requalification problem by analytic hierarchy process[J]. Quality and quantity, 2015, 49(4): 1661–1677. [7] 胡金海, 余治国, 翟旭升, 等. 基于改进D-S证据理论的航空发动机转子故障决策融合诊断研究[J]. 航空学报, 2014, 35(2): 436–443. HU Jinhai, YU Zhiguo, ZHAI Xusheng, et al. Research of decision fusion diagnosis of aero-engine rotor fault based on improved D-S theory[J]. Acta aeronautica et astronautica sinica, 2014, 35(2): 436–443. [8] NIEUWENHUIJZE M J, KORSTJENS I, DE JONGE A, et al. On speaking terms: a Delphi study on shared decision-making in maternity care[J]. BMC pregnancy and childbirth, 2014, 14(1): 1–11. doi: 10.1186/1471-2393-14-1 [9] 崔建国, 傅康毅, 陈希成, 等. 基于灰色模糊与层次分析的多属性飞机维修决策方法[J]. 航空学报, 2014, 35(2): 478–486. CUI Jianguo, FU Kangyi, CHEN Xicheng, et al. Multiple attribute maintenance decision making of aircraft based on grey-fuzziness and analytical hierarchy process[J]. Acta aeronautica et astronautica sinica, 2014, 35(2): 478–486. [10] 胡丽芳, 王晨熙, 朱靖, 等. 闭世界框架下灰色模糊多属性决策方法[J]. 控制与决策, 2014, 29(2): 246–250. HU Lifang, WANG Chenxi, ZHU Jing, et al. Approach for grey fuzzy MADA in closed world[J]. Control and decision, 2014, 29(2): 246–250. [11] CHARILAS D E, PANAGOPOULOS A D, MARKAKI O I. A unified network selection framework using principal component analysis and multi attribute decision making[J]. Wireless personal communications, 2014, 74(1): 147–165. doi: 10.1007/s11277-012-0905-y [12] 刘满凤, 任海平. 基于一类新的直觉模糊熵的多属性决策方法研究[J]. 系统工程理论与实践, 2015, 35(11): 2909–2916. doi: 10.12011/1000-6788(2015)11-2909 LIU Manfeng, REN Haiping. A study of multi-attribute decision making based on a new intuitionistic fuzzy entropy measure[J]. Systems engineering-theory and practice, 2015, 35(11): 2909–2916. doi: 10.12011/1000-6788(2015)11-2909 [13] XU Yejun, HUANG Chao, DA Qingli, et al. Linear goal programming approach to obtaining the weights of intuitionistic fuzzy ordered weighted averaging operator[J]. Journal of systems engineering and electronics, 2010, 21(6): 990–994. [14] 郭金维, 蒲绪强, 高祥, 等. 一种改进的多目标决策指标权重计算方法[J]. 西安电子科技大学学报, 2014, 41(6): 118–125. GUO Jinwei, PU Xuqiang, GAO Xiang, et al. Improved method on weights determination of indexes in multi-objective decision[J]. Journal of Xidian University, 2014, 41(6): 118–125. [15] YEH H C, CHEN Y C, WEI C. A new approach to selecting a regionalized design hyetograph by principal component analysis and analytic hierarchy process[J]. Paddy and water environment, 2013, 11(1/2/3/4): 73–85. [16] SU Chong, LI Hongguang. Approaches to affective computing and learning towards interactive decision making in process control engineering[J]. Acta automatica sinica, 2013, 39(5): 617–625. [17] HUANG Yinjuan, HUANG Liujia. Experimental teaching quality evaluation practice based on AHP-fuzzy comprehensive evaluation model[M]//Intelligent Computing Theories and Technology. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 94−100. [18] VEGA A, AGUARÓN J, GARCÍA-ALCARAZ J, et al. Notes on dependent attributes in TOPSIS[J]. Procedia computer science, 2014, 31: 308–317. doi: 10.1016/j.procs.2014.05.273 [19] ZHAO Suozhu, YANG Wei, LI Jun, et al. Aircraft concept evaluation and effectiveness-based decision-making[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2013, 30(1): 8–16. [20] YARI M, MONJEZI M, BAGHERPOUR R, et al. Developing a mathematical assessment model for blasting patterns management: Sungun copper mine[J]. Journal of Central South University, 2014, 21(11): 4344–4351. doi: 10.1007/s11771-014-2434-1 [21] 刘满凤, 陶长琪, 柳键. 运筹学教程[M]. 北京: 清华大学出版社, 2010. [22] 张波, 商豪. 应用随机过程[M]. 4版. 北京: 中国人民大学出版社, 2016. [23] BRUNEEL H, FIEMS D, WALRAEVENS J, et al. Queueing models for the analysis of communication systems[J]. TOP, 2014, 22(2): 421–448. doi: 10.1007/s11750-014-0330-3 [24] SRIDHARAN V, JAYASHREE P J. Some characteristics on a finite queue with normal partial and total failures[J]. Microelectronics reliability, 1996, 36(2): 265–267. doi: 10.1016/0026-2714(95)00088-J [25] 刘瑞芝. 服务台修复非新的可修排队系统[D]. 秦皇岛: 燕山大学, 2016. LIU Ruizhi. The queuing systems with repairabie deteriorate service station[D]. Qinhuangdao: Yanshan University, 2016. [26] ECONOMOU A, KANTA S. Equilibrium balking strategies in the observable single-server queue with breakdowns and repairs[J]. Operations research letters, 2008, 36(6): 696–699. doi: 10.1016/j.orl.2008.06.006 [27] LI Xiangyu, WANG Jinting, ZHANG Feng. New results on equilibrium balking strategies in the single-server queue with breakdowns and repairs[J]. Applied mathematics and computation, 2014, 241: 380–388. doi: 10.1016/j.amc.2014.05.025 [28] LI Le, WANG Jinting, ZHANG Feng. Equilibrium customer strategies in Markovian queues with partial breakdowns[J]. Computers and industrial engineering, 2013, 66(4): 751–757. [29] YU Senlin, LIU Zaiming, WU Jinbiao. Strategic behavior in the partially observable Markovian queues with partial breakdowns[J]. Operations research letters, 2017, 45(5): 471–474. doi: 10.1016/j.orl.2017.07.007 [30] XU Biao, XU Xiuli. Equilibrium strategic behavior of customers in the M/M/1 queue with partial failures and repairs[J]. Operational research, 2018, 18(2): 273–292. doi: 10.1007/s12351-016-0264-7 [31] YANG Tengteng, WANG Jinting, ZHANG Feng. Equilibrium balking strategies in the geo/geo/1 queues with server breakdowns and repairs[J]. Quality technology and quantitative management, 2014, 11(3): 231–243. [32] BOUDALI O, ECONOMOU A. Optimal and equilibrium balking strategies in the single server Markovian queue with catastrophes[J]. European journal of operational research, 2012, 218(3): 708–715. doi: 10.1016/j.ejor.2011.11.043 [33] BOUDALI O, ECONOMOU A. The effect of catastrophes on the strategic customer behavior in queueing systems[J]. Naval research logistics (NRL), 2013, 60(7): 571–587. doi: 10.1002/nav.21553 [34] 马占友, 王文博, 郑晓铭. 带抢占优先权和同步多重工作休假的M/M/c排队模型[J]. 重庆师范大学学报(自然科学版), 2018, 35(3): 96–100. MA Zhanyou, WANG Wenbo, ZHENG Xiaoming. The M/M/c queueing model with preemptive priority and multiple synchronous working vacation[J]. Journal of Chongqing Normal University (natural science edition), 2018, 35(3): 96–100. [35] 马占友, 王文博, 王哲, 等. 带非抢占优先权和可变服务率的离散工作休假排队[J]. 河南师范大学学报(自然科学版), 2018, 46(1): 23–28. MA Zhanyou, WANG Wenbo, WANG Zhe, et al. The discrete time working vacation queue with non-preemptive priority and variable service rates[J]. Journal of Henan Normal University (natural science edition), 2018, 46(1): 23–28. [36] YANG W S, CHAE K C. A note on the GI/M/1 queue with Poisson negative arrivals[J]. Journal of applied probability, 2001, 38(4): 1081–1085. doi: 10.1017/S0021900200019276 [37] SHIMOGAWA S, TAKAHASHI Y. On a set of interdeparture time distributions of the m/g/1 queue with server vacations[J]. Journal of the operations research society of Japan, 1993, 36(4): 206–219. doi: 10.15807/jorsj.36.206 [38] 刘楠. 带有不耐烦顾客的M/M/m排队系统的顾客损失率[D]. 秦皇岛: 燕山大学, 2015. LIU Nan. The loss probabity of an M/M/m queuing system with impatient customers[D]. Qinhuangdao: Yanshan University, 2015. [39] BALACHANDRAN K R. Purchasing priorities in queues[J]. Management science, 1972, 18(5): 319–326. [40] ADIRI I, YECHIALI U. Optimal priority-purchasing and pricing decisions in nonmonopoly and monopoly queues[J]. Operations research, 1974, 22(5): 1051–1066. doi: 10.1287/opre.22.5.1051 [41] HASSIN R, HAVIV M. Equilibrium threshold strategies: the case of queues with priorities[J]. Operations research, 1997, 45(6): 966–973. doi: 10.1287/opre.45.6.966 [42] LILLO R E. Optimal control of an M/G/1 queue with impatient priority customers[J]. Naval research logistics (NRL), 2001, 48(3): 201–209. doi: 10.1002/nav.2 [43] SUN Wei, GUO Pengfei, TIAN Naishuo, et al. Relative priority policies for minimizing the cost of queueing systems with service discrimination[J]. Applied mathematical modelling, 2009, 33(11): 4241–4258. doi: 10.1016/j.apm.2009.03.012 [44] XU Biao, XU Xiuli, WANG Xianying. Optimal balking strategies for high-priority customers in M/G/1 queues with 2 classes of customers[J]. Journal of applied mathematics and computing, 2016, 51(1/2): 623–642. [45] CHOUDHURY G. On a batch arrival Poisson queue with a random setup time and vacation period[J]. Computers and operations research, 1998, 25(12): 1013–1026. [46] ALLAHVERDI A, NG C T, CHENG T C E, et al. A survey of scheduling problems with setup times or costs[J]. European journal of operational research, 2008, 187(3): 985–1032. doi: 10.1016/j.ejor.2006.06.060 [47] 张杰. 带休假延迟和启动时间的M/M/1多重休假排队系统分析[J]. 阜阳师范学院学报(自然科学版), 2015, 32(3): 21–24,34. ZHANG Jie. Analysis of multiple vacation M/M/1 queue with delayed vacation and setup time[J]. Journal of Fuyang teachers college (natural science edition), 2015, 32(3): 21–24,34. [48] 马占友, 许敏杰, 郑晓铭, 等. 带服务台故障及启动期和备用服务台的GeomGeom 1+1排队系统[J]. 西北师范大学学报(自然科学版), 2017, 53(3): 28–33. MA Zhanyou, XU Minjie, ZHENG Xiaoming, et al. The Geom/Geom/1+1 queue system with server breakdowns and a spare server with setup time[J]. Journal of northwest normal university (natural science edition), 2017, 53(3): 28–33. [49] MACCIO V J, DOWN D G. Structural properties and exact analysis of energy-aware multiserver queueing systems with setup times[J]. Performance evaluation, 2018, 121/122: 48–66. doi: 10.1016/j.peva.2018.03.001 [50] BURNETAS A, ECONOMOU A. Equilibrium customer strategies in a single server Markovian queue with setup times[J]. Queueing systems, 2007, 56(3/4): 213–228. [51] SUN Wei, GUO Pengfei, TIAN Naishuo. Equilibrium threshold strategies in observable queueing systems with setup/closedown times[J]. Central European journal of operations research, 2010, 18(3): 241–268. doi: 10.1007/s10100-009-0104-4 [52] SUN Wei, WANG Yulan, TIAN Naishuo. Pricing and setup/closedown policies in unobservable queues with strategic customers[J]. 4OR, 2012, 10(3): 287–311. doi: 10.1007/s10288-012-0209-9 [53] ZHANG Feng, WANG Jinting, LIU Bin, et al. Equilibrium joining probabilities in observable queues with general service and setup times[J]. Journal of industrial & management optimization, 2013, 9(4): 901–917. [54] HAO Yaqian, WANG Jinting, WANG Zhongbin, et al. Equilibrium joining strategies in the M/M/1 queues with setup times under N-policy[J]. Journal of systems science and systems engineering, 2019, 28(2): 141–153. doi: 10.1007/s11518-018-5398-0 [55] CHOUDHURY B B, MISHRA D, BISWAL B B. Task assignment and scheduling in a constrained manufacturing system using GA[J]. International journal of agile systems and management, 2008, 3(1/2): 127. doi: 10.1504/IJASM.2008.019603 [56] YU Huili, MEIER K, ARGYLE M, et al. Cooperative path planning for target tracking in urban environments using unmanned air and ground vehicles[J]. IEEE/ASME transactions on mechatronics, 2015, 20(2): 541–552. doi: 10.1109/TMECH.2014.2301459 [57] GOPALAKRISHNAN M, MOHAN S, HE Z. A tabu search heuristic for preventive maintenance scheduling[J]. Computers and industrial engineering, 2001, 40(1/2): 149–160. [58] MACEDO R, BENMANSOUR R, ARTIBA A, et al. Scheduling preventive railway maintenance activities with resource constraints[J]. Electronic notes in discrete mathematics, 2017, 58: 215–222. doi: 10.1016/j.endm.2017.03.028 [59] 薛桂香. 基于动态遗传算法的网格任务调度算法研究[D]. 天津: 天津大学, 2006. XUE Guixiang. Research on task scheduling algorithms for grid computing by dynamic genetic algorithms[D]. Tianjin: Tianjin University, 2006. [60] SHI Jiaqi, TAN Li, LIAN Xiaofeng, et al. A multi- unmanned aerial vehicle dynamic task assignment method based on bionic algorithms[J]. Computers and electrical engineering, 2022, 99: 107820. doi: 10.1016/j.compeleceng.2022.107820 [61] JIA Zhenyue, YU Jianqiao, AI Xiaolin, et al. Cooperative multiple task assignment problem with stochastic velocities and time windows for heterogeneous unmanned aerial vehicles using a genetic algorithm[J]. Aerospace science and technology, 2018, 76: 112–125. doi: 10.1016/j.ast.2018.01.025 [62] KEISER C N, JONES D K, MODLMEIER A P, et al. Exploring the effects of individual traits and within-colony variation on task differentiation and collective behavior in a desert social spider[J]. Behavioral ecology and sociobiology, 2014, 68(5): 839–850. doi: 10.1007/s00265-014-1696-9 [63] KHOUADJIA M R, SARASOLA B, ALBA E, et al. A comparative study between dynamic adapted PSO and VNS for the vehicle routing problem with dynamic requests[J]. Applied soft computing, 2012, 12(4): 1426–1439. doi: 10.1016/j.asoc.2011.10.023 [64] JIA Yunxian, SUN Lei, WANG Yabin, et al. Research on maintenance task allocation and support resource requirement analysis for ordnance equipment[C]//2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering. Chengdu: IEEE, 2012: 459−465. [65] YUAN CHUN, GUO LI-BIN, YONG QI-DONG. Research on the maintenance task allocation of oil equipments[C]// 2012 IEEE Symposium on Robotics and Applications (ISRA) 2012. Chongqing: IEEE, 2012: 97−100. [66] 李龙跃, 刘付显, 赵麟锋. 对多波次目标直接分配到弹的反导火力规划方法[J]. 系统工程与电子技术, 2014, 36(11): 2206–2212. doi: 10.3969/j.issn.1001-506X.2014.11.15 LI Longyue, LIU Fuxian, ZHAO Linfeng. Direct interceptor allocation method in antimissile firepower planning for multiple wave targets[J]. Systems engineering and electronics, 2014, 36(11): 2206–2212. doi: 10.3969/j.issn.1001-506X.2014.11.15 [67] 曾家有, 王国卫, 钟建林, 等. 多平台舰舰导弹饱和攻击几个协同问题与模型[J]. 兵工学报, 2014, 35(2): 256–261. doi: 10.3969/j.issn.1000-1093.2014.02.018 ZENG Jiayou, WANG Guowei, ZHONG Jianlin, et al. Research on cooperative saturation attack problems and models of ship-to-ship missiles from multi-ship platforms[J]. Acta armamentarii, 2014, 35(2): 256–261. doi: 10.3969/j.issn.1000-1093.2014.02.018 [68] Yang Shengxiang, RENATO T. A hybrid immigrants scheme for genetic algorithms in dynamic environments[J]. International journal of automation and computing, 2007(3): 243–254. [69] KIRKPATRICK S, GELATT C D Jr, VECCHI M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671–680. doi: 10.1126/science.220.4598.671 [70] HOLLAND J H. Adaptation in natural and artificial systems[M]. Ann Arbor: University of Michigan Press, 1975. [71] 罗雄, 钱谦, 伏云发. 遗传算法解柔性作业车间调度问题应用综述[J]. 计算机工程与应用, 2019, 55(23): 15–21,34. doi: 10.3778/j.issn.1002-8331.1908-0410 LUO Xiong, QIAN Qian, FU Yunfa. Review of application of genetic algorithms for solving flexible job shop scheduling problems[J]. Computer engineering and applications, 2019, 55(23): 15–21,34. doi: 10.3778/j.issn.1002-8331.1908-0410 [72] 刘国强. 基于遗传算法的维修性分配方法及其应用[D]. 长沙: 国防科学技术大学, 2010. LIU Guoqiang. The research and application of maintainability allocation method based on genetic algorithm[D]. Changsha: National University of Defense Technology, 2010. [73] TEOH B E, PONNAMBALAM S G, KANAGARAJ G. Differential evolution algorithm with local search for capacitated vehicle routing problem[J]. International journal of bio-inspired computation, 2015, 7(5): 321. doi: 10.1504/IJBIC.2015.072260 [74] LIN J, ZHOU Wei, WOLFSON O. Electric vehicle routing problem[J]. Transportation research procedia, 2016, 12: 508–521. doi: 10.1016/j.trpro.2016.02.007 [75] LAPORTE G. Scheduling issues in vehicle routing[J]. Annals of operations research, 2016, 236(2): 463–474. doi: 10.1007/s10479-013-1423-3 [76] GAWRILOW E, KLIMM M, MÖHRING R H, et al. Conflict-free vehicle routing[J]. EURO journal on transportation and logistics, 2012, 1(1/2): 87–111. [77] 张景玲, 王万良, 赵燕伟. 基于沿途补货的多配送中心动态需求VRP建模及优化[J]. 计算机集成制造系统, 2013, 19(4): 869–878. ZHANG Jingling, WANG Wanliang, ZHAO Yanwei. Modeling and optimization for dynamic requests multi-depot vehicle routing problem with replenishment on the way[J]. Computer integrated manufacturing systems, 2013, 19(4): 869–878. [78] XU Degang, XIAO Renbin. An improved genetic clustering algorithm for the multi-depot vehicle routing problem[J]. International journal of wireless and mobile computing, 2015, 9(1): 1–7. doi: 10.1504/IJWMC.2015.071665 [79] MU Dong, WANG Chao, ZHAO Fu, et al. Solving vehicle routing problem with simultaneous pickup and delivery using parallel simulated annealing algorithm[J]. International journal of shipping and transport logistics, 2016, 8(1): 81. doi: 10.1504/IJSTL.2016.073323 [80] 曾正洋, 许维胜, 徐志宇, 等. 两级车辆路径问题的多起始点变邻域下降算法[J]. 同济大学学报(自然科学版), 2014, 42(10): 1530–1535. doi: 10.11908/j.issn.0253-374x.2014.10.011 ZENG Zhengyang, XU Weisheng, XU Zhiyu, et al. A multi-start variable neighborhood descent algorithm for two-echelon vehicle routing problem[J]. Journal of Tongji University (natural science edition), 2014, 42(10): 1530–1535. doi: 10.11908/j.issn.0253-374x.2014.10.011 [81] 刘家利, 马祖军. 存在车辆租赁及共享且有时间窗的多配送中心开环VRP[J]. 系统工程理论与实践, 2013, 33(3): 666–675. doi: 10.3969/j.issn.1000-6788.2013.03.014 LIU Jiali, MA Zujun. Multi-depot open vehicle routing problem with time windows based on vehicle leasing and sharing[J]. Systems engineering-theory and practice, 2013, 33(3): 666–675. doi: 10.3969/j.issn.1000-6788.2013.03.014 [82] ZHANG Xiao, WANG Jiangqing. Hybrid ant algorithm and applications for vehicle routing problem[J]. Physics procedia, 2012, 25: 1892–1899. doi: 10.1016/j.phpro.2012.03.327 [83] 何小锋, 马良. 带时间窗车辆路径问题的量子蚁群算法[J]. 系统工程理论与实践, 2013, 33(5): 1255–1261. doi: 10.3969/j.issn.1000-6788.2013.05.021 HE Xiaofeng, MA Liang. Quantum-inspired ant colony algorithm for vehicle routing problem with time windows[J]. Systems engineering-theory and practice, 2013, 33(5): 1255–1261. doi: 10.3969/j.issn.1000-6788.2013.05.021 [84] M’HALLAH R, ALHAJRAF A. Ant colony systems for the single-machine total weighted earliness tardiness scheduling problem[J]. Journal of scheduling, 2016, 19(2): 191–205. doi: 10.1007/s10951-015-0429-x
